A Robust Dual-Platform GMTI Method against Nonuniform Clutter
Abstract
1. Introduction
- i
- Directly calculate CCM with the range cell echoes at the location of the moving target that originated from the forward SAR images.
- ii
- By estimating CCM more accurately, the target detection threshold will also be more accurate, making the detection results more reliable.
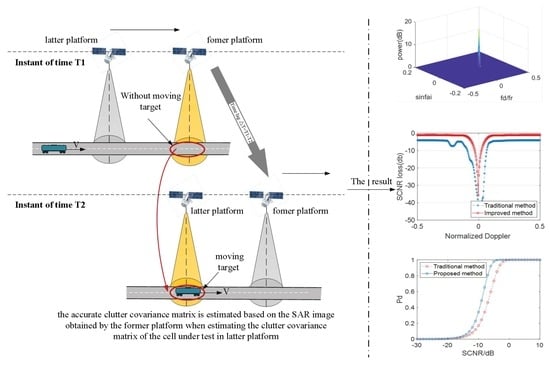
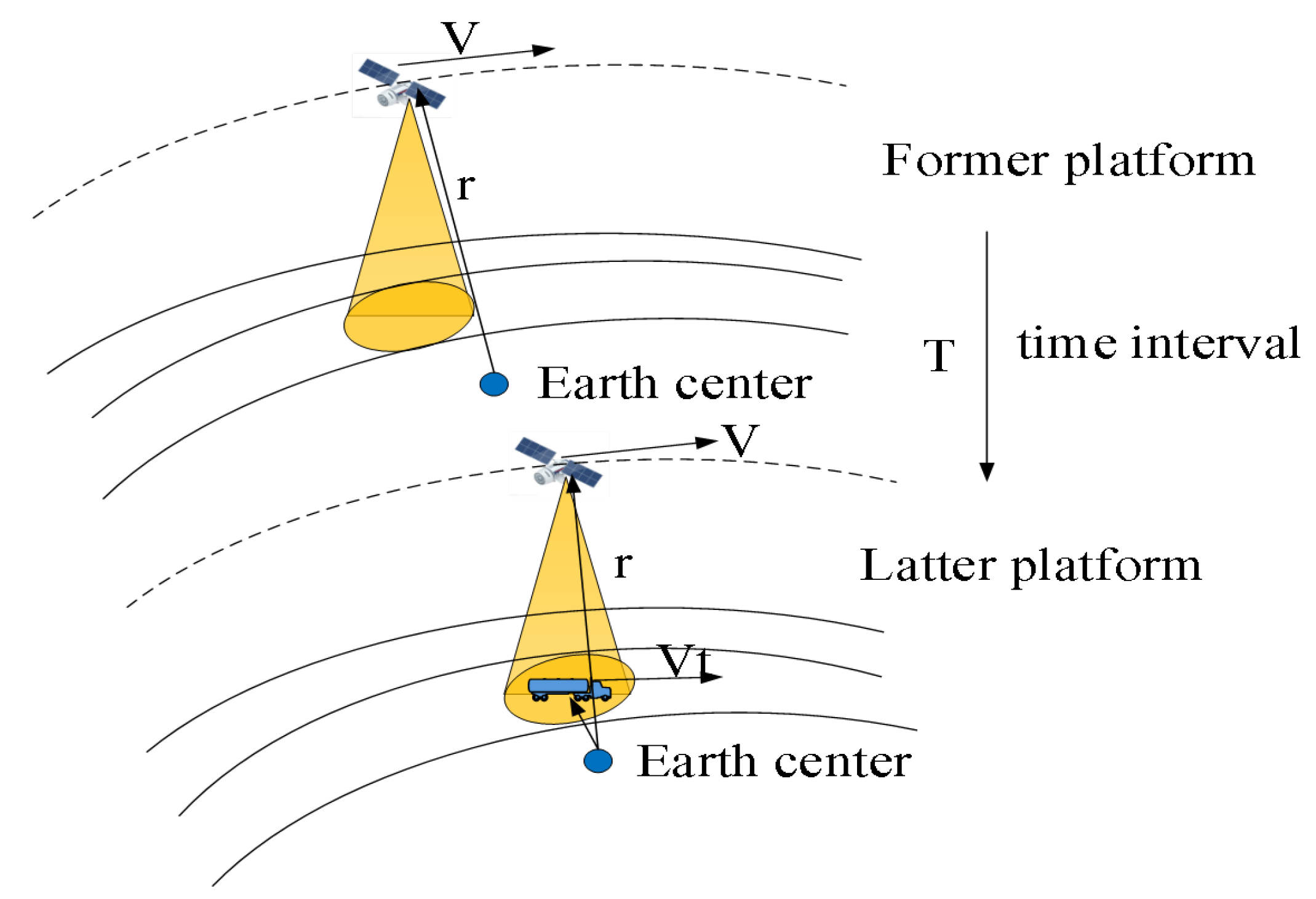
2. The Dual-Platform GMTI Method against Nonuniform Environment
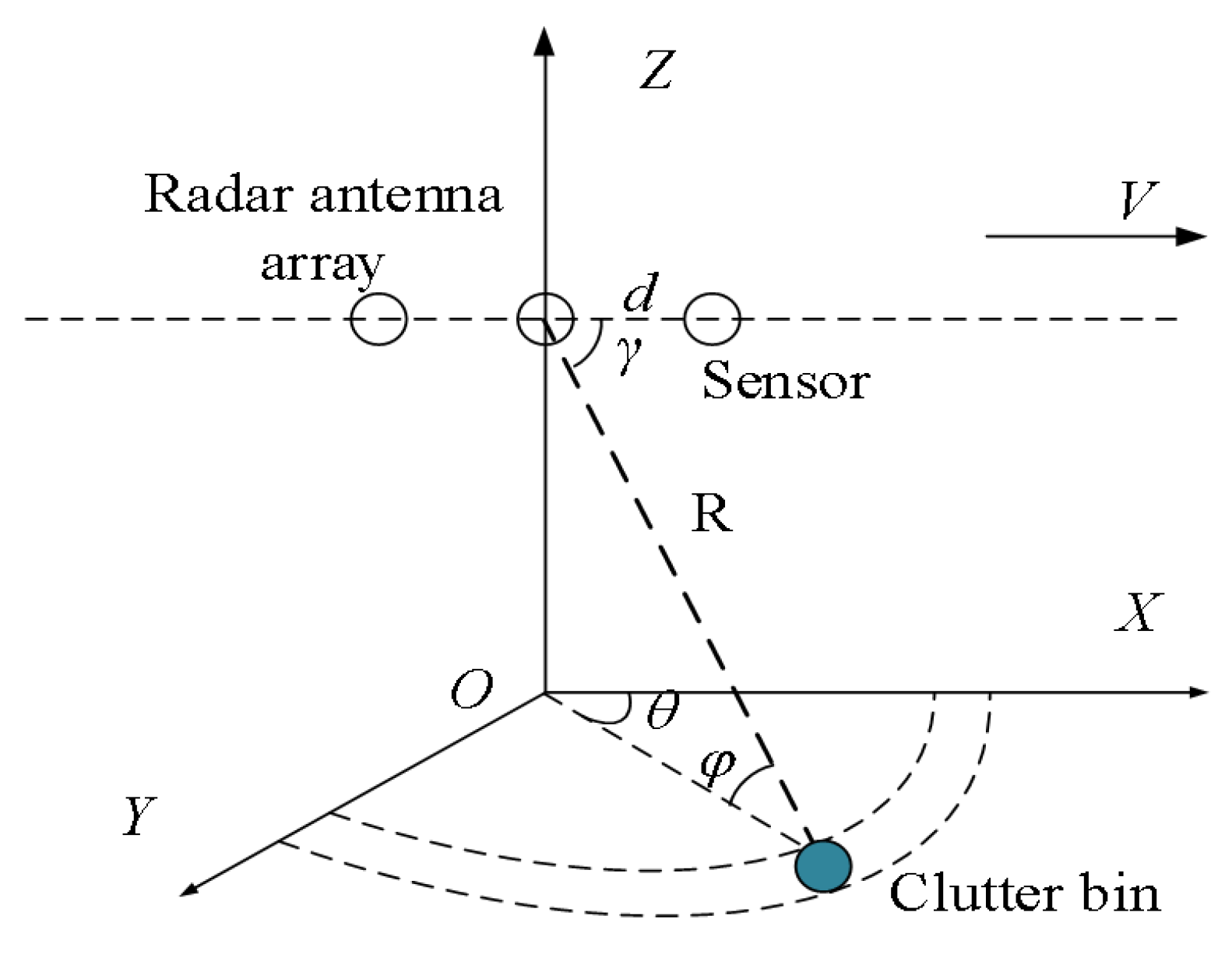
2.1. Problem Formulation
2.2. Analysis of the Influence of Heterogeneous Environment in STAP
2.2.1. Strong Pollution
2.2.2. Hot Clutter
2.2.3. Power Nonuniformity
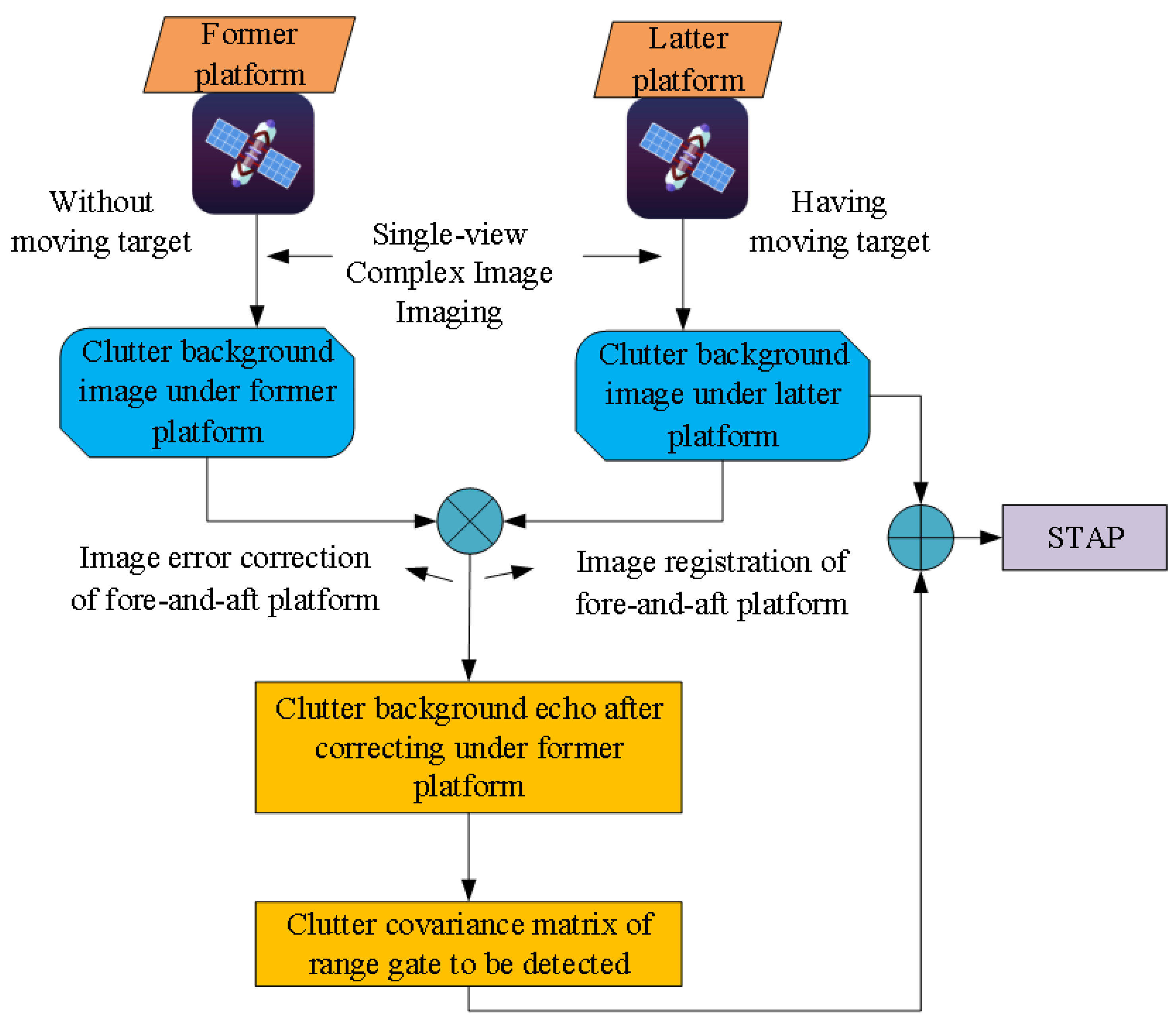
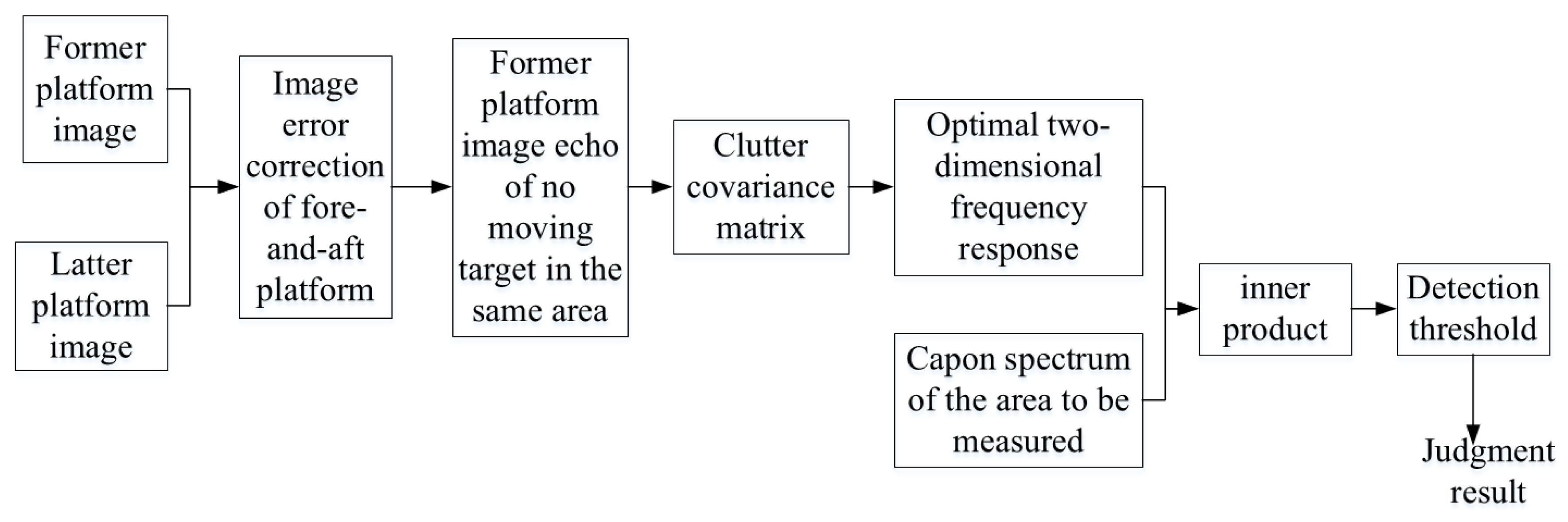
2.3. High-Precision Clutter Covariance Matrix Estimation Based on Dual-Platform SAR System
2.3.1. Image Registration of Former and Latter Platforms
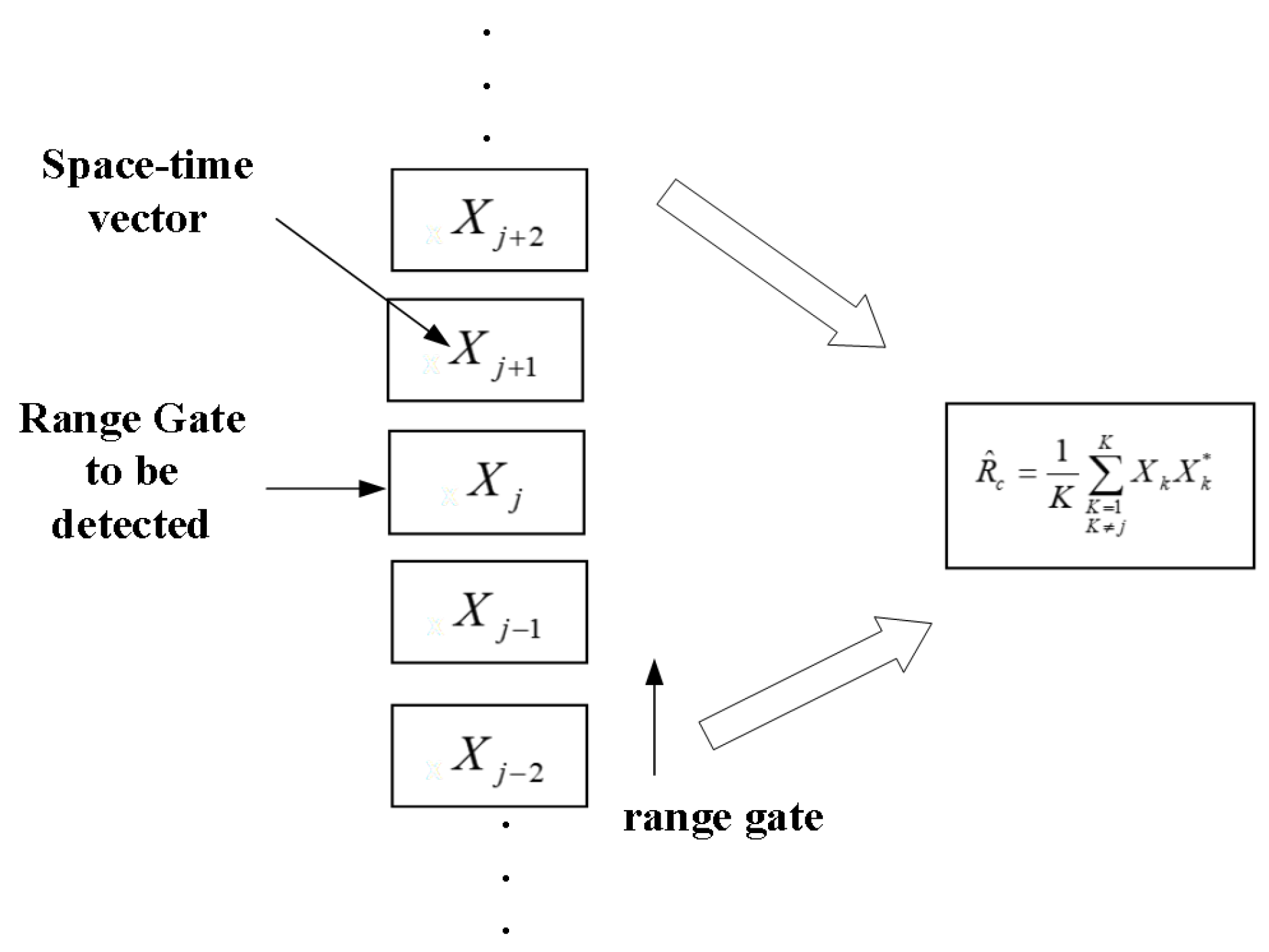
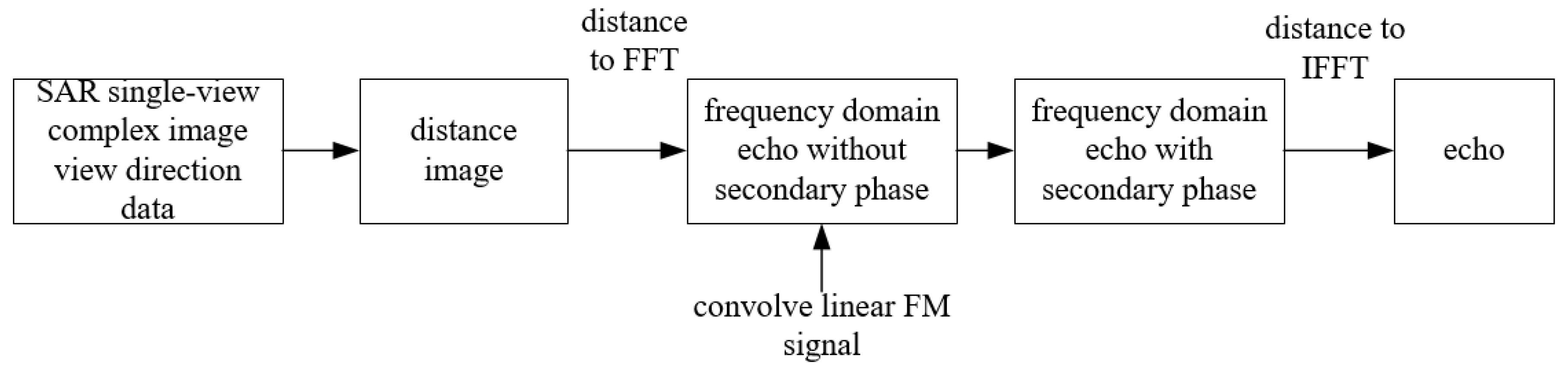
2.3.2. Calculation of Clutter Covariance Matrix Based on Echo
2.3.3. Setting the Detection Threshold
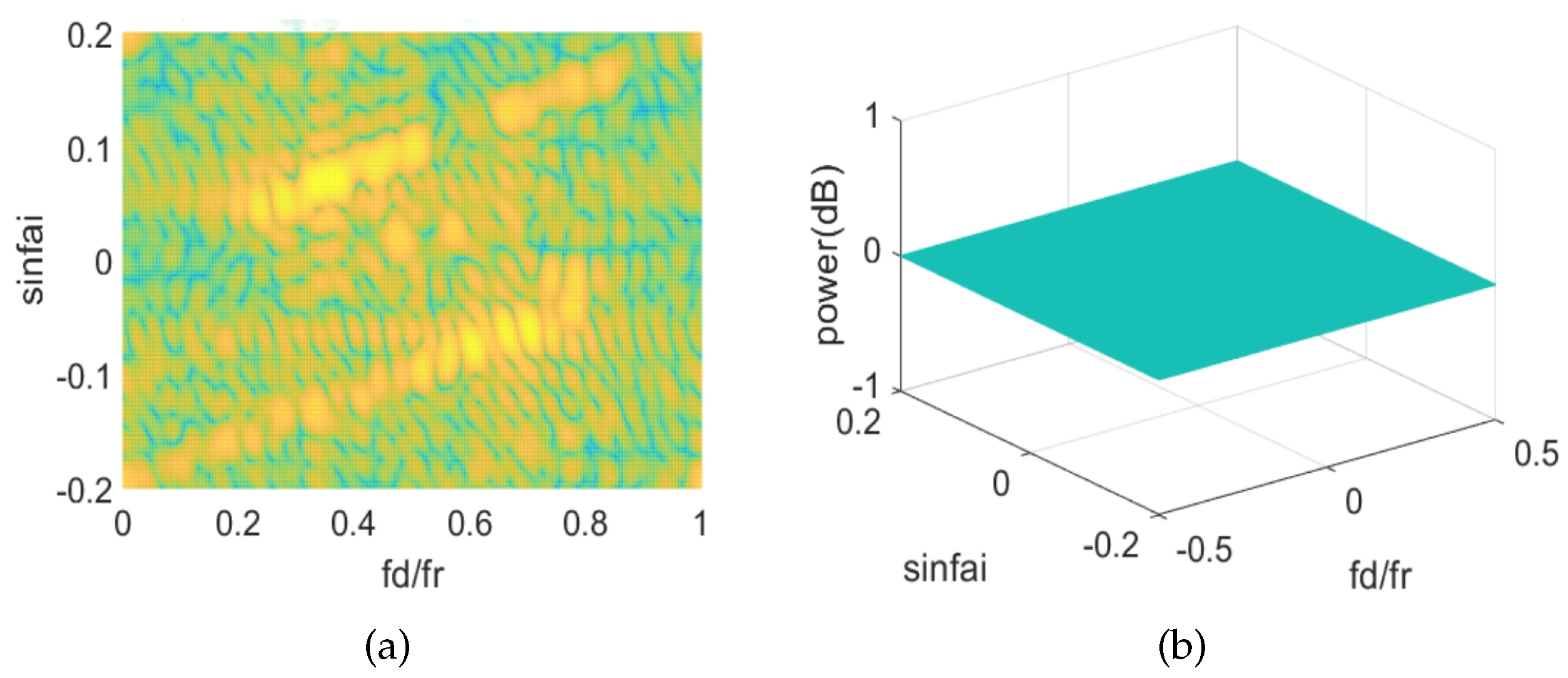
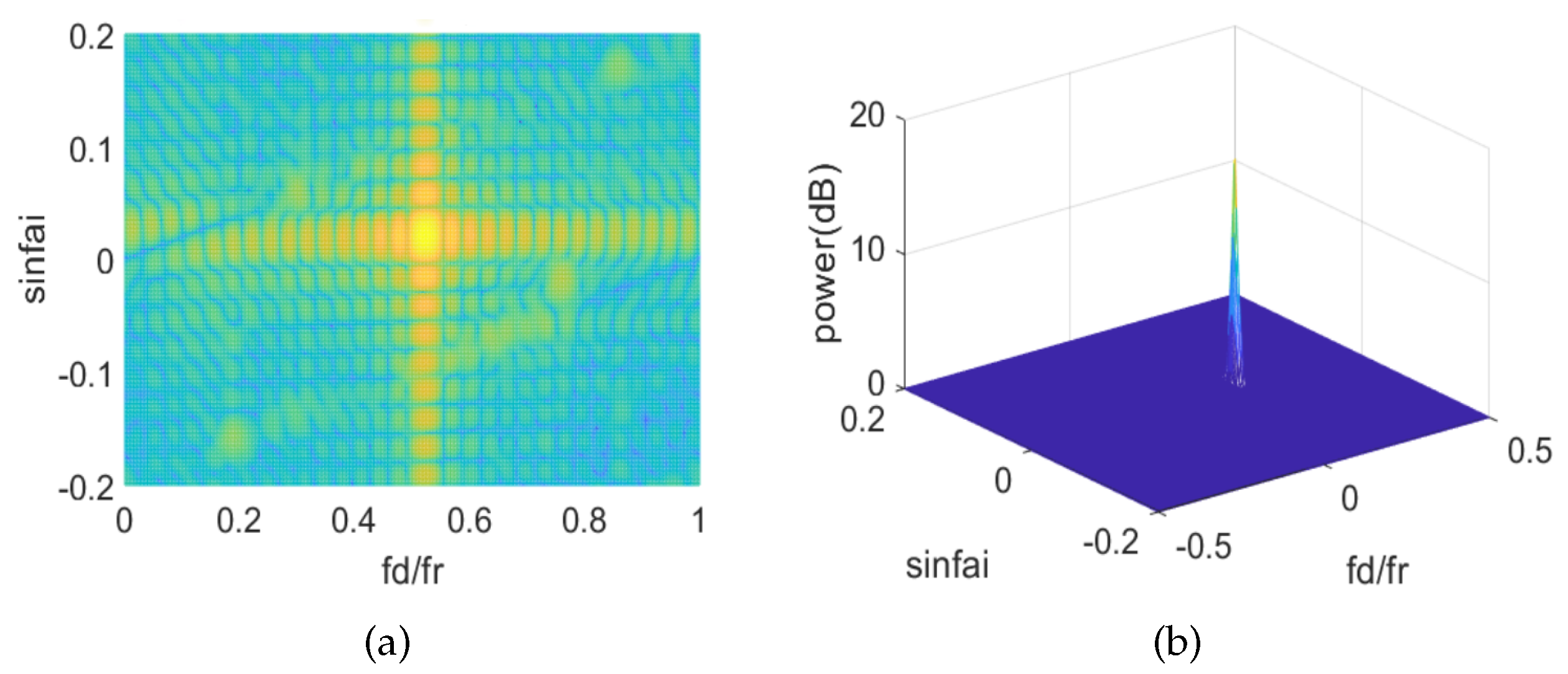
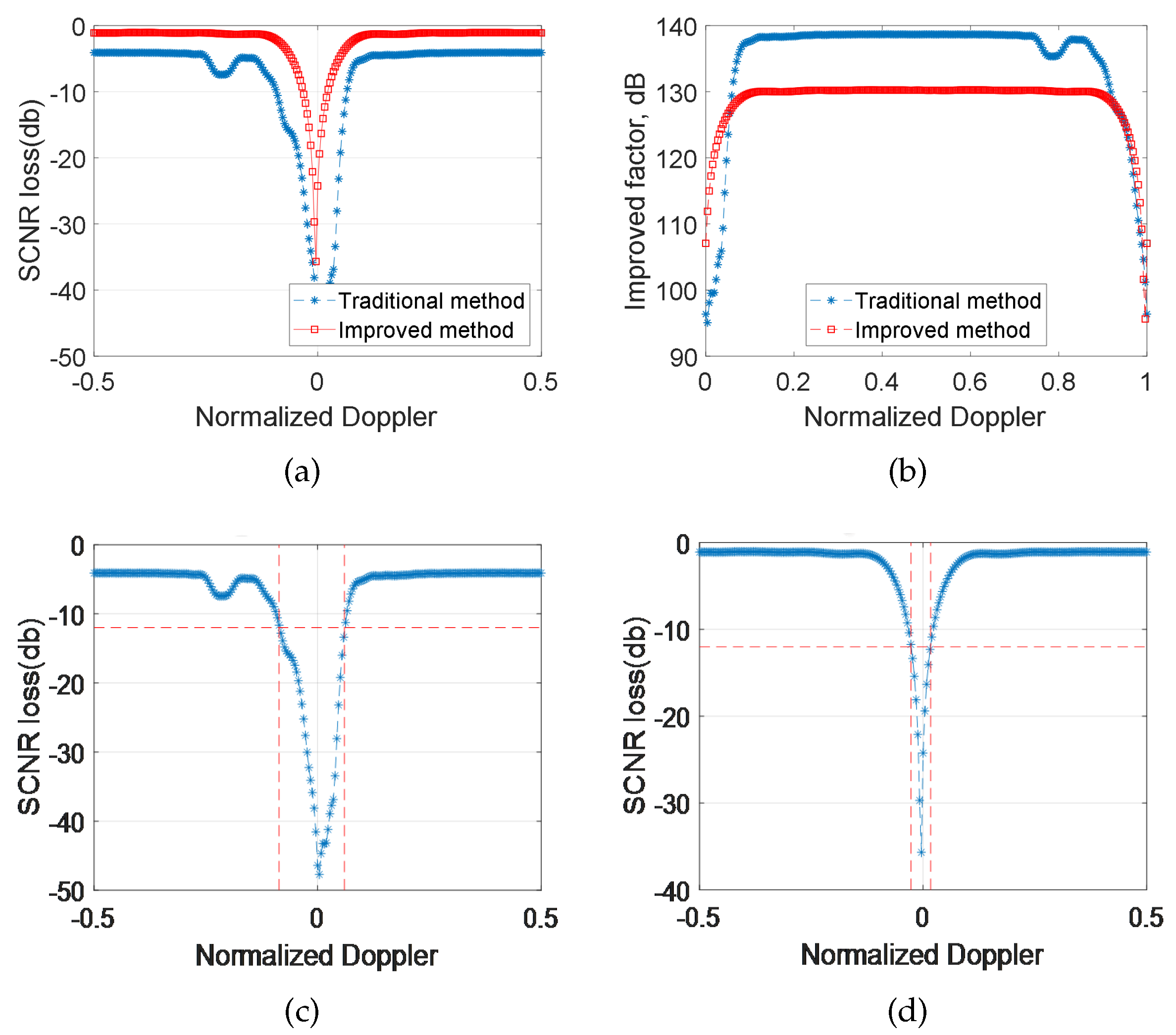
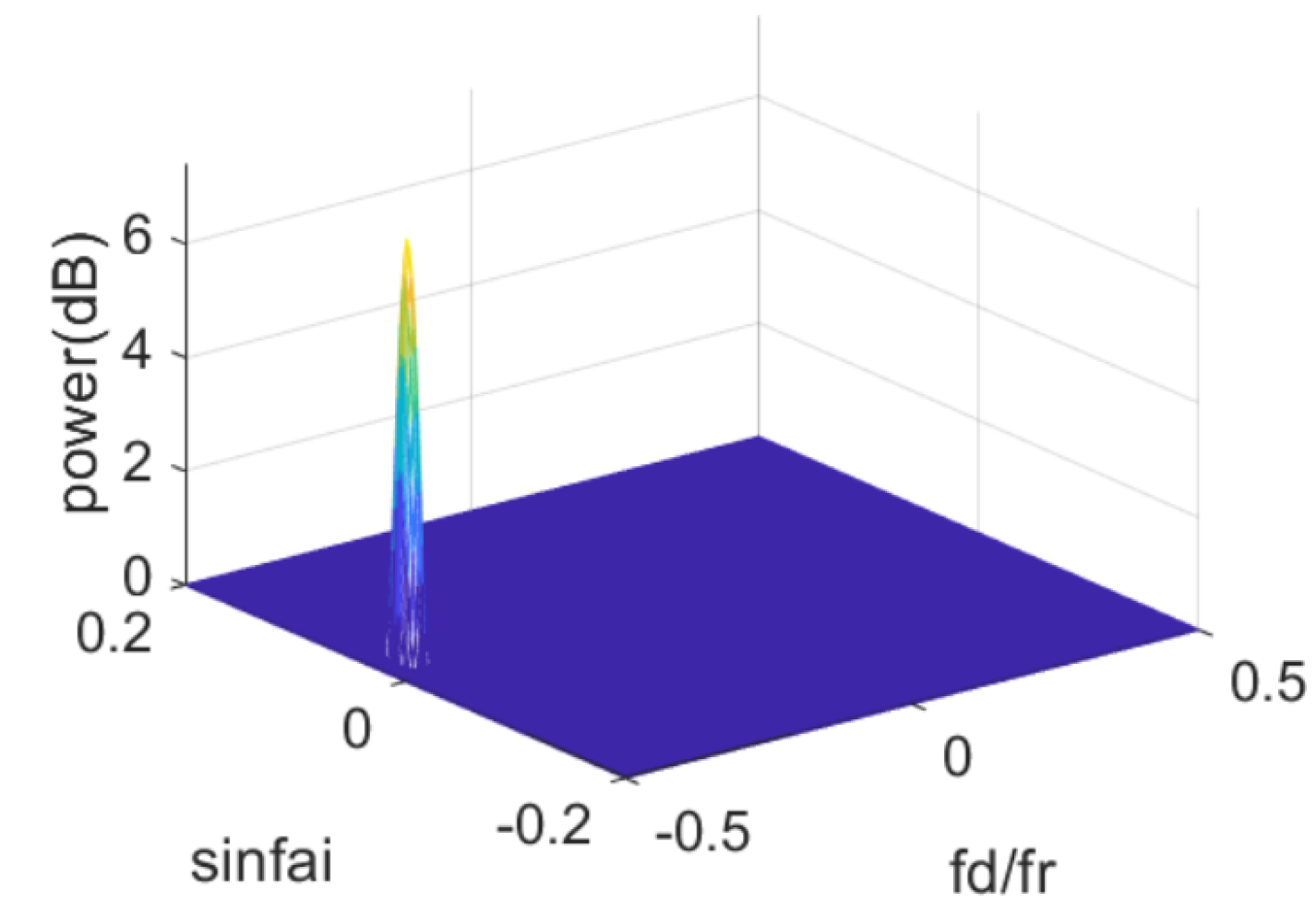
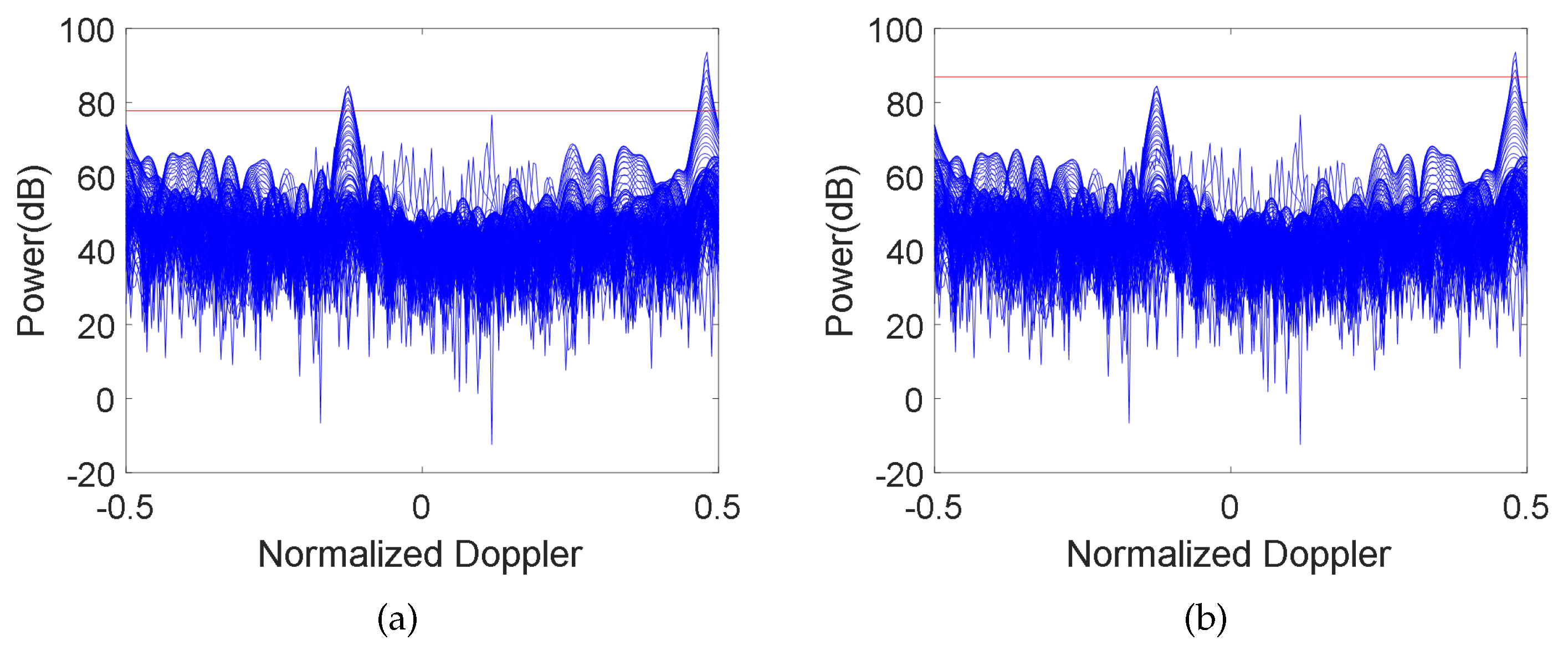
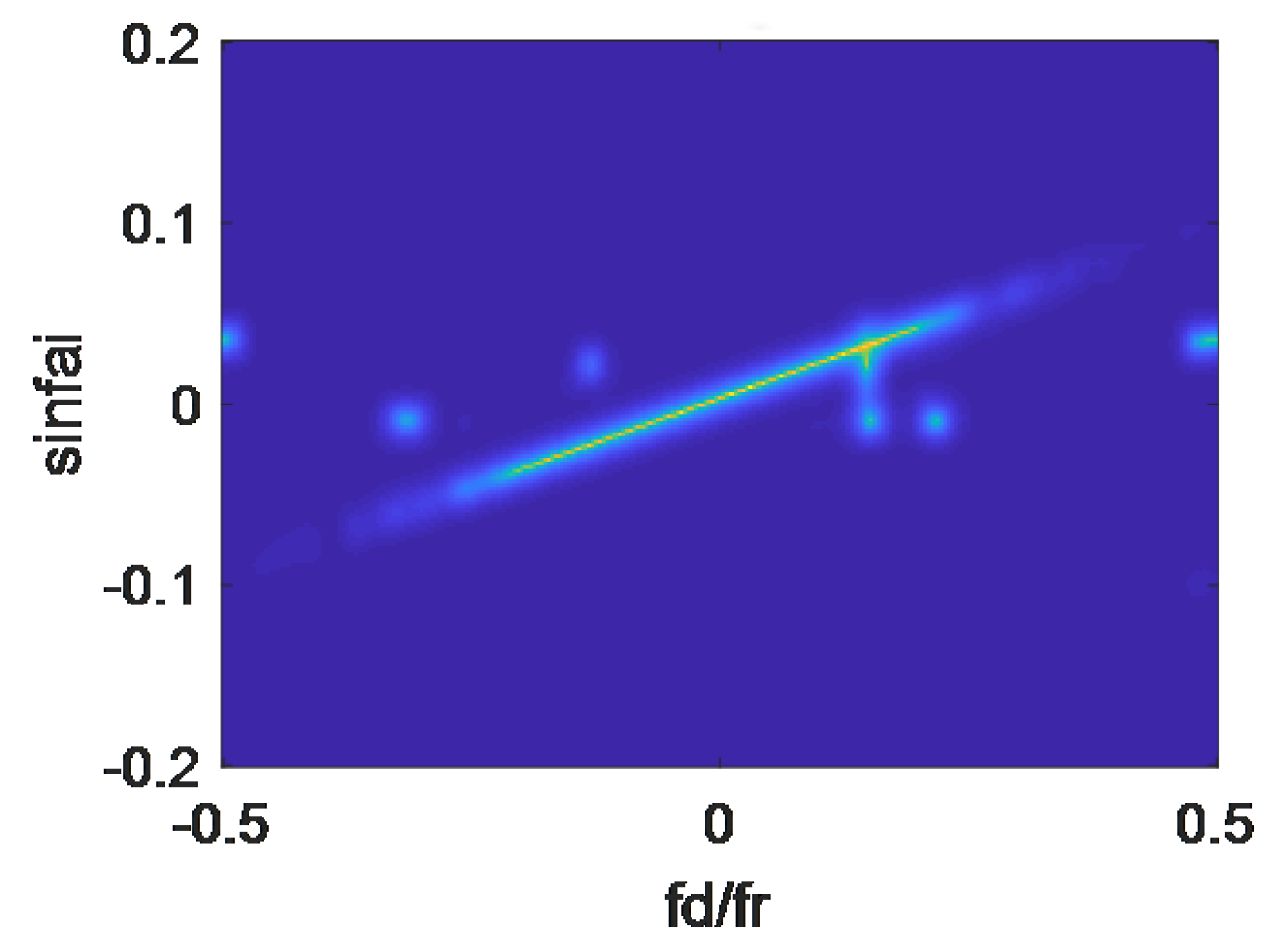
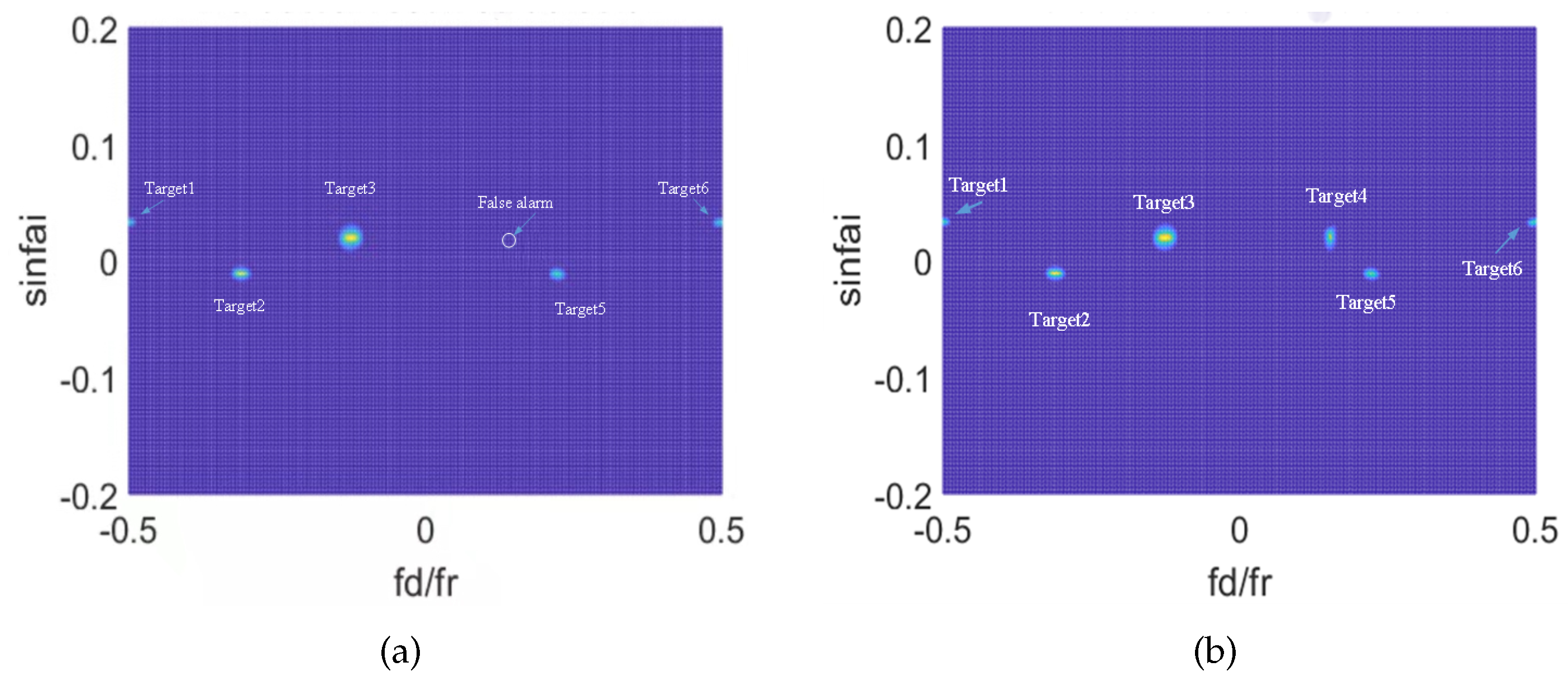
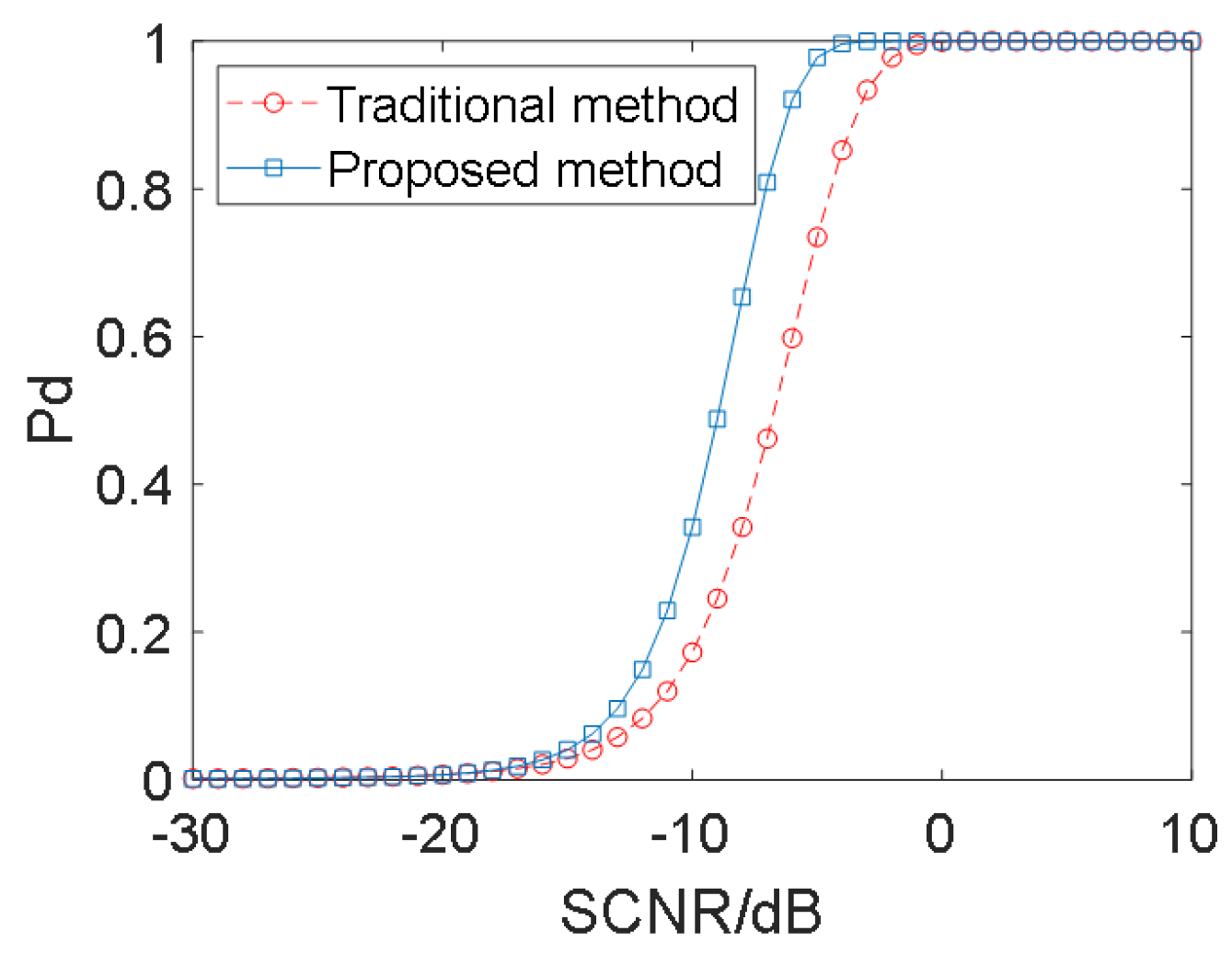
3. Results and Analysis
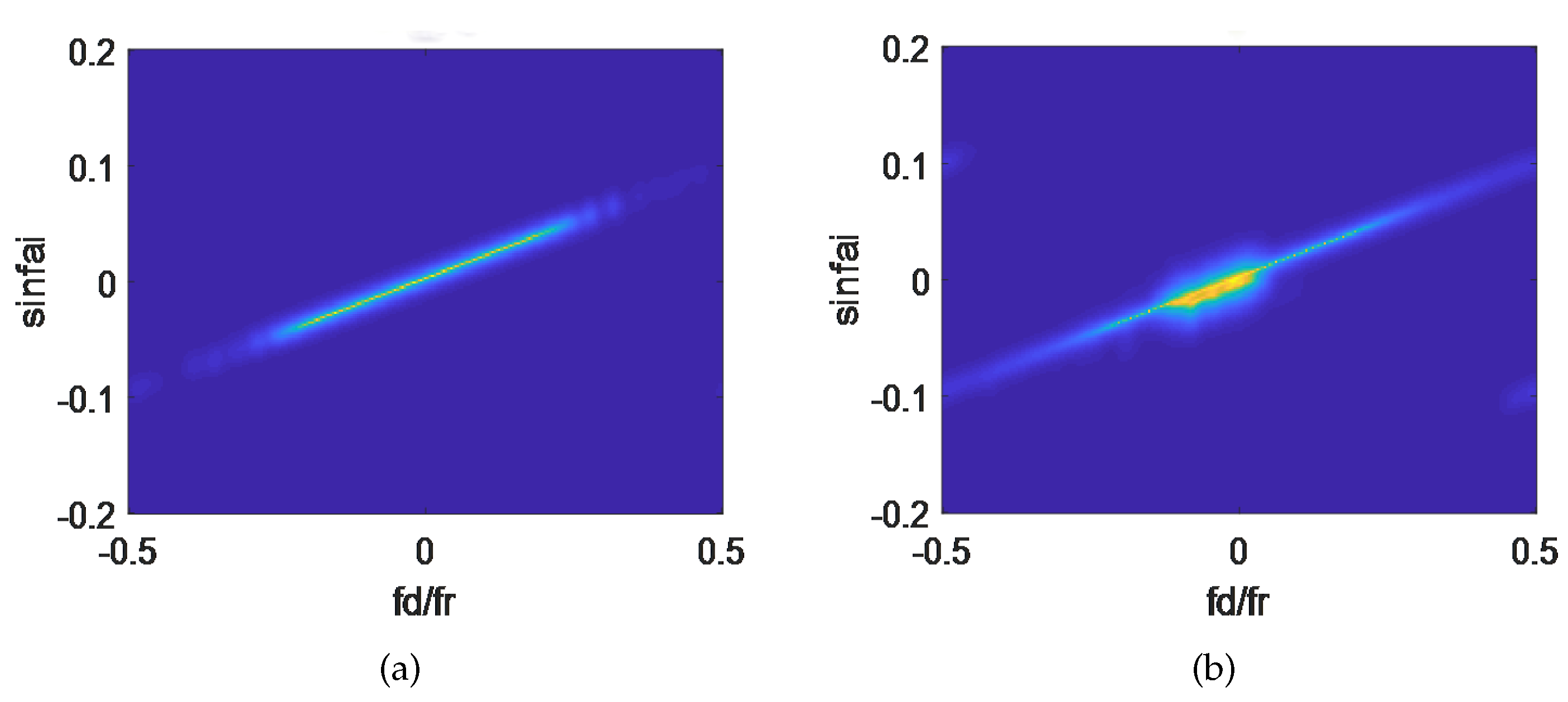
3.1. Application in Strong Pollution Environment
3.2. Application in Junction Zone of Hot and Cold Clutter
3.3. Application in Nonuniform Power Environment
4. Discussions
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zhang, Z.; Yu, W.; Zheng, M.; Zhao, L.; Zhou, Z.X. Phase Mismatch Calibration for Dual-Channel Sliding Spotlight SAR-GMTI. Remote Sens. 2022, 14, 617. [Google Scholar] [CrossRef]
- Han, J.; Cao, Y.; Wu, W.; Wang, Y.; Yeo, T.-S.; Liu, S.; Wang, F. Robust GMTI Scheme for Highly Squinted Hypersonic Vehicle-Borne Multichannel SAR in Dive Mode. Remote Sens. 2021, 13, 4431. [Google Scholar] [CrossRef]
- Kim, S.-W.; Won, J.-S. Acceleration Compensation for Estimation of Along-Track Velocity of Ground Moving Target from Single-Channel SAR SLC Data. Remote Sens. 2020, 12, 1609. [Google Scholar] [CrossRef]
- Shen, W.; Lin, Y.; Yu, L.; Xue, F.; Hong, W. Single Channel Circular SAR Moving Target Detection Based on Logarithm Background Subtraction Algorithm. Remote Sens. 2018, 10, 742. [Google Scholar] [CrossRef]
- Gracheva, V.; Ender, J. Multichannel analysis and suppression of sea clutter for airborne microwave radar systems. IEEE Trans. Geosci. Remote Sens. 2016, 54, 2385–2399. [Google Scholar] [CrossRef]
- Guo, Y.; Liao, G.; Li, J.; Gu, T. A clutter suppression method based on NSS-RPCA in heterogeneous environments for SAR-GMTI. IEEE Trans. Geosci. Remote Sens. 2020, 58, 5880–5891. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, J.; Liu, W.; Li, C.; Yang, W. A Moving Target Velocity Estimation Method Based on the MC-MASA SAR Mode. Remote Sens. 2021, 13, 1632. [Google Scholar] [CrossRef]
- Yi, N.; He, Y.; Liu, B. Improved Method to Suppress Azimuth Ambiguity for Current Velocity Measurement in Coastal Waters Based on ATI-SAR Systems. Remote Sens. 2020, 12, 3288. [Google Scholar] [CrossRef]
- Yan, H.; Hou, Q.; Jin, G.; Xu, X.; Zhang, G.; Zhu, D. Velocity Estimation of Ocean Surface Currents in along-Track InSAR System Based on Conditional Generative Adversarial Networks. Remote Sens. 2021, 13, 4088. [Google Scholar] [CrossRef]
- Yang, J.; Yuan, X.; Han, B.; Zhao, L.; Sun, J.; Shang, M.; Wang, X.; Ding, C. Phase Imbalance Analysis of GF-3 Along-Track InSAR Data for Ocean Current Measurement. Remote Sens. 2021, 13, 269. [Google Scholar] [CrossRef]
- Cui, C.; Dong, X.; Chen, Z.; Hu, C.; Tian, W. A Long-Time Coherent Integration STAP for GEO Spaceborne-Airborne Bistatic SAR. Remote Sens. 2022, 14, 593. [Google Scholar] [CrossRef]
- Li, H.; Liao, G.; Xu, J.; Zeng, C.; He, X.; Gao, P. Multi-Resolution STAP for Enhanced Ultra-Low-Altitude Target Detection. Remote Sens. 2021, 13, 4212. [Google Scholar] [CrossRef]
- Bidon, S.; Besson, O.; Tourneret, Y. A bayesian approach to adaptive detection in nonhomogeneous environments. IEEE Trans. Signal Process. 2008, 56, 205–217. [Google Scholar] [CrossRef]
- Tong, Y.; Tong, W.; Jian, W. Improving EFA-STAP performance using persymmetric covariance matrix estimation. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 925–936. [Google Scholar] [CrossRef]
- Rui, F.; de Lamare, R.C. Reduced-rank STAP algorithms using joint iterative optimization of filers. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 1668–1684. [Google Scholar]
- Sarkar, T.K.; Wang, H.; Park, S.; Adve, R.; Koh, J.; Kim, K.; Zhang, Y.; Wicks, M.C.; Brown, R.D. A deterministic least-squares approach to space-time adaptive processing (STAP). IEEE Trans. Antennas Propagat. 2001, 49, 91–103. [Google Scholar] [CrossRef]
- Aboutanios, E.; Mulgrew, B. A STAP algorithm for radar target detection in heterogeneous environments. In Proceedings of the IEEE/SP 13th Workshop on Statistical Signal Processing, Bordeaux, France, 7–20 July 2005; pp. 966–971. [Google Scholar]
- Degurse, J.F.; Savy, L.; Marcos, S. Reduced-rank STAP for target detection in heterogeneous environments. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 1153–1162. [Google Scholar] [CrossRef]
- Degurse, J.F.; Savy, L.; Marcos, S.; Molinie, J.P. Deterministic aided STAP for target detection in heterogeneous situations. Int. J. Antennas Propagat. 2013, 2013, 826935. [Google Scholar] [CrossRef][Green Version]
- Li, Z.; Ye, H.; Liu, Z.; Sun, Z.; An, H.; Wu, J.; Yang, J. Bistatic SAR Clutter-Ridge Matched STAP Method for Nonstationary Clutter Suppression. IEEE Trans. Geosci. Remote. Sens. 2021, 60, 1–14. [Google Scholar] [CrossRef]
- Hu, J.; Li, J.; Li, H.; Li, K.; Liang, J. A Novel Covariance Matrix Estimation via Cyclic Characteristic for STAP. IEEE Geosci. Remote. Sens. Lett. 2020, 11, 1871–1875. [Google Scholar] [CrossRef]
- Wang, P.; Wang, Z.; Li, H.; Himed, B. Knowledge-aided parametric adaptive matched filter with automatic combining for covariance estimation. IEEE Trans. Signal Process. 2014, 62, 4713–4722. [Google Scholar] [CrossRef]
- Hua, X.; Ono, Y.; Peng, L.; Cheng, Y.; Wang, H. Target detection within nonhomogeneous clutter via total bregman divergencebased matrix information geometry detectors. IEEE Trans. Signal Process. 2021, 69, 4326–4340. [Google Scholar] [CrossRef]
- Arnaudon, M.; Barbaresco, F.; Yang, L. Riemannian medians and means with applications to radar signal processing. IEEE J. Sel. Top. Signal Process. 2013, 7, 595–604. [Google Scholar] [CrossRef]
- Chen, X.; Cheng, Y.; Wu, H.; Wang, H. Heterogeneous Clutter Suppression for Airborne Radar STAP Based on Matrix Manifolds. Remote Sens. 2021, 13, 3195. [Google Scholar] [CrossRef]
- Kang, M.S.; Kim, K.T. Ground Moving Target Imaging Based on Compressive Sensing Framework With Single-Channel SAR. IEEE Sens. J. 2020, 20, 1238–1250. [Google Scholar] [CrossRef]
- Lee, M.-J.; Kang, M.-S.; Ryu, B.-H.; Lee, S.-J. Improved moving target detector using sequential combination of DPCA and ATI. J. Eng. 2019, 11, 7834–7837. [Google Scholar] [CrossRef]
- Lee, M.-J.; Lee, S.-J.; Ryu, B.-H.; Lim, B.-G.; Kim, K.-T. Reduction of False Alarm Rate in SAR-MTI Based on Weighted Kurtosis. IEEE Trans. Geosci. Remote Sens. 2020, 99, 1–14. [Google Scholar] [CrossRef]
- Brennan, L.E.; Reed, L.S. Theory of Adaptive Radar. IEEE Trans. Aerosp. Electron. Syst. 2007, 9, 237–252. [Google Scholar] [CrossRef]
- Brennan, L.; Mallett, J.; Reed, I. Adaptive arrays in airborne MTI radar. IRE Trans. Antennas Propag. 1976, 24, 607–615. [Google Scholar] [CrossRef]
- Klemm, R. Principles of Space-Time Adaptive Processing; Institute of Electical Engineering: London, UK, 2006. [Google Scholar]
- Guerci, J.R. Space-Time Adaptive Processing for Radar; Artech House: New York, NY, USA, 2003. [Google Scholar]
- Peckham, C.D. Reduced-rank STAP performance analysis. IEEE Trans. Aerosp. Electron. Syst. 2000, 36, 664–676. [Google Scholar] [CrossRef]
- Yang, Z.; Qin, Y.; de Lamare, R.C.; Wang, H.; Li, X. Sparsity-Based Direct Data Domain Space-Time Adaptive Processing with Intrinsic Clutter Motion. Circuits Syst. Signal Process. 2017, 36, 219–246. [Google Scholar] [CrossRef]
- Touzi, R.; Lopes, A.; Bruniquel, J.; Vachon, P.W. Coherence Estimation For Sar Imagery. IEEE Trans. Geosci. Remote. Sens. 1999, 37, 135–149. [Google Scholar] [CrossRef]
- Guarnieri, A.M.; Prati, C. SAR Interferometry: A “Quick and Dirty” Coherence Estimator for Data Browsing. IEEE Trans. Geosci. Remote Sens. 1997, 35, 660–669. [Google Scholar] [CrossRef]
- Liu, X.; Xu, S.; Tang, S. CFAR Strategy Formulation and Evaluation Based on Fox’s H-function in Positive Alpha-Stable Sea Clutter. Remote Sens. 2020, 12, 1273. [Google Scholar] [CrossRef]
- Yang, B.; Zhang, H. A CFAR Algorithm Based on Monte Carlo Method for Millimeter-Wave Radar Road Traffic Target Detection. Remote Sens. 2022, 14, 1779. [Google Scholar] [CrossRef]
- Duan, C.; Li, Y.; Wang, W.; Li, J. LEO-Based Satellite Constellation for Moving Target Detection. Remote Sens. 2022, 14, 403. [Google Scholar] [CrossRef]
- Reed, I.S.; Gau, Y.L.; Truong, K.T. CFAR detection and estimation for STAP radar. IEEE Trans. Aerosp. Electron. Syst. 1998, 34, 722–735. [Google Scholar] [CrossRef]

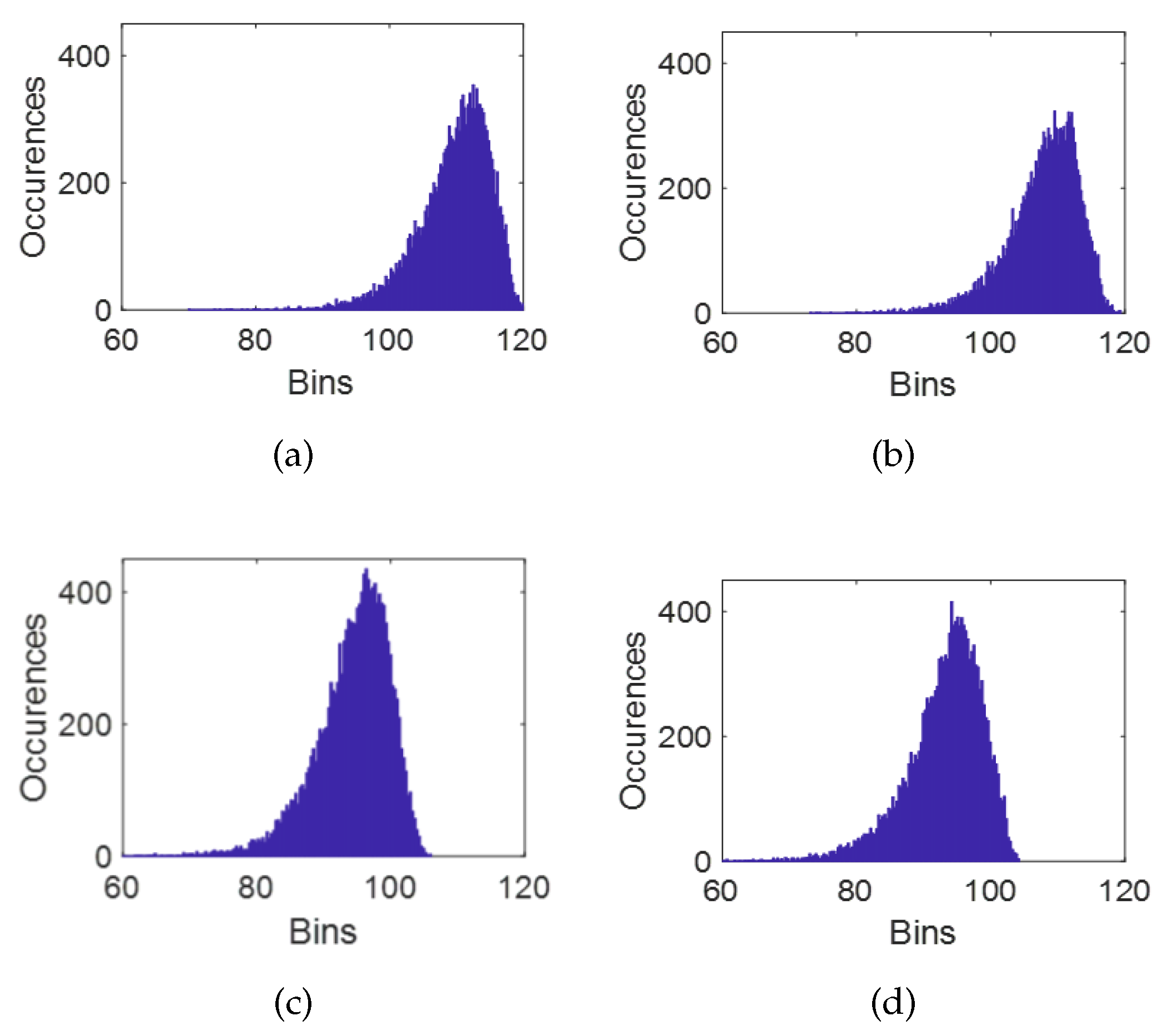




| Statistic | Area1 | Area2 | Area3 | Area4 |
|---|---|---|---|---|
| Mean value | 108 | 109 | 94 | 93 |
| Variance | 30 | 30 | 32 | 34 |
| Skewness coefficient | <0(−1.125) | <0(−1.116) | <0(−1.158) | <0(−1.194) |
| Kurtosis coefficient | 2.056 | 2.218 | 2.653 | 2.652 |
| Simulation Parameters | Value |
|---|---|
| Platform frequency | 5e9 |
| Bandwidth | 200e6 |
| PRF | 654 |
| Number of pulses in one CPI | 32 |
| Elements | 20 |
| Interval between elements | 0.12 |
| Scene | 800 × 800 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zou, M.; Jin, G.; Li, L.; He, Z. A Robust Dual-Platform GMTI Method against Nonuniform Clutter. Remote Sens. 2022, 14, 3558. https://doi.org/10.3390/rs14153558
Zou M, Jin G, Li L, He Z. A Robust Dual-Platform GMTI Method against Nonuniform Clutter. Remote Sensing. 2022; 14(15):3558. https://doi.org/10.3390/rs14153558
Chicago/Turabian StyleZou, Mulan, Guanghu Jin, Liang Li, and Zhihua He. 2022. "A Robust Dual-Platform GMTI Method against Nonuniform Clutter" Remote Sensing 14, no. 15: 3558. https://doi.org/10.3390/rs14153558
APA StyleZou, M., Jin, G., Li, L., & He, Z. (2022). A Robust Dual-Platform GMTI Method against Nonuniform Clutter. Remote Sensing, 14(15), 3558. https://doi.org/10.3390/rs14153558