Ensemble Machine Learning of Random Forest, AdaBoost and XGBoost for Vertical Total Electron Content Forecasting
Abstract
:1. Introduction
Previous Research Gaps and Our Contribution
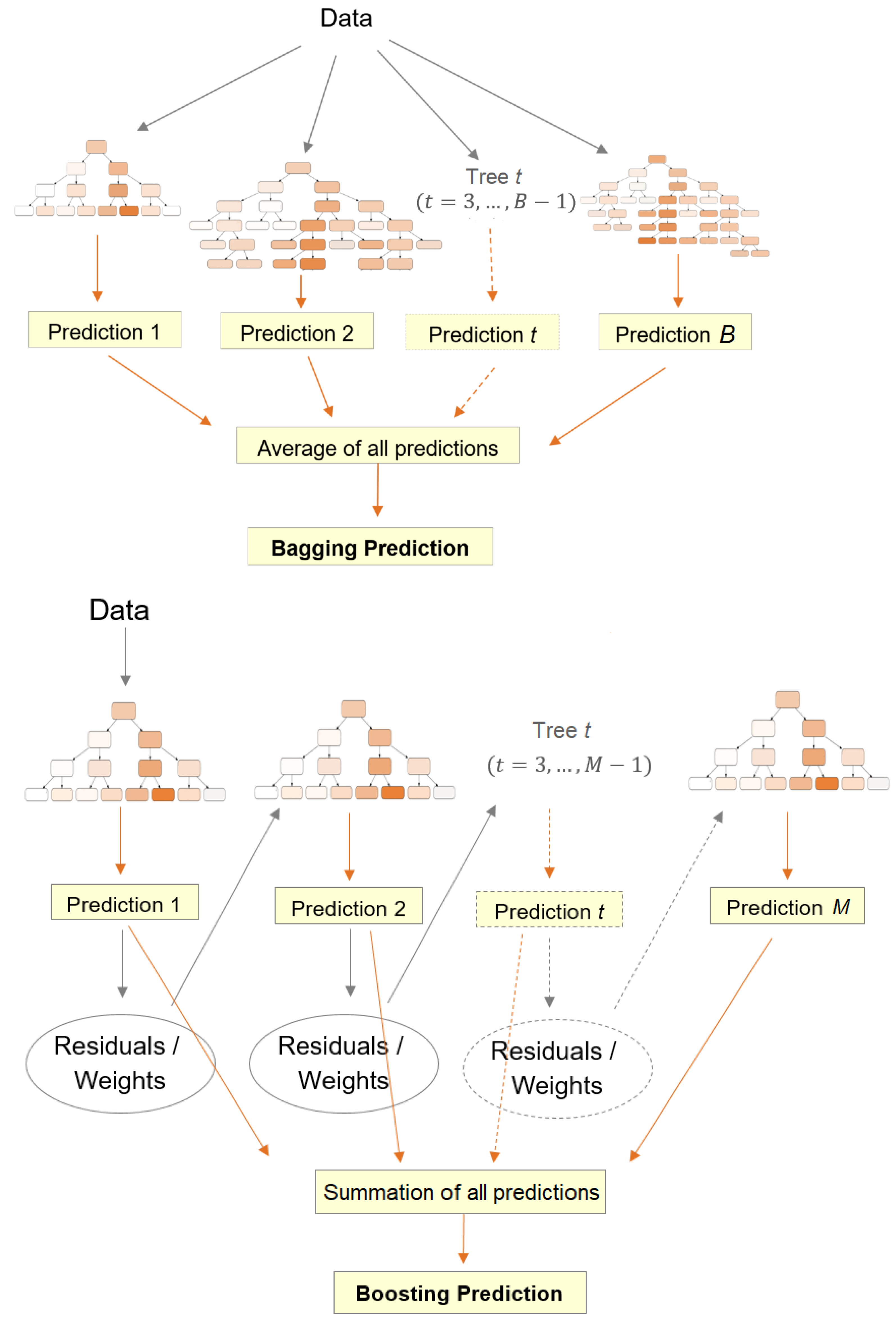
- Machine learning methods of bagging and boosting are introduced for the VTEC forecasting problem.
- Tree-based learning algorithms are applied to overcome the deficiencies of the commonly used deep learning approaches to VTEC forecasting in terms of complexity, “big data” requirements, and highly parameterized model (prone to overfitting the data). Here, we adopted learning algorithms for VTEC forecasting that are simple, fast to optimize, computationally efficient, and usable on a limited dataset.
- Moreover, we introduce an ensemble meta-model that combines predictions from multiple well-performing VTEC models to produce a final VTEC forecast with improved accuracy and generalization than each individual model.
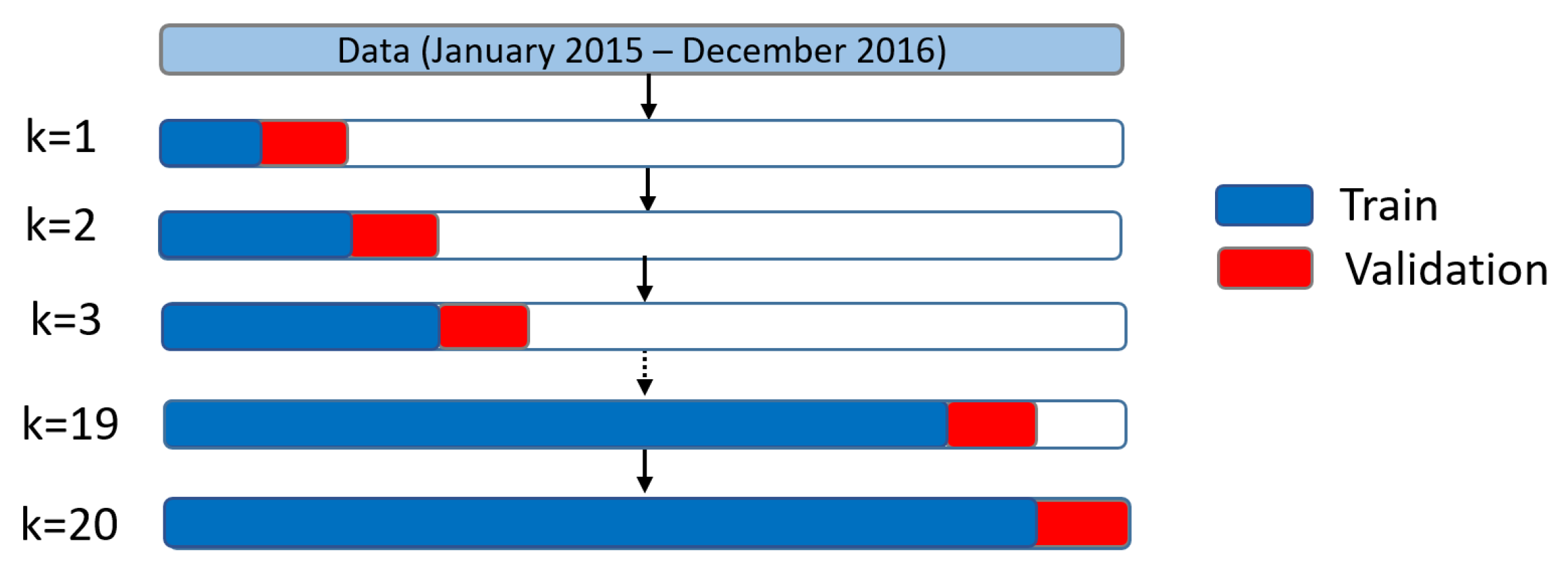
- Time series cross-validation method is proposed for VTEC model development to preserve a temporal dependency.
- Additional VTEC-related features are added, such as first and second derivatives, and moving averages. Special attention is also paid to time period selection and relations within the data to have more space weather examples and near-solar maximum conditions, as well as to enable learning and forecasting of complex VTEC variations, including space weather-related ones.
- Machine learning models are trained and optimized solely using daily differences (de-trended data) along the models with original data.
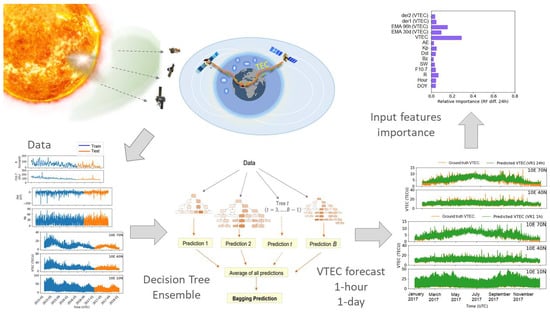
- The relative contribution of the input data to the VTEC forecast is analyzed to provide an insight into what the model has learned, and to what extent our physical understanding of important predictors has increased.
- Can other, simpler learning algorithms than ANN capture diverse VTEC variations for 1 h and 24 h VTEC forecasts?
- Can ensemble meta-model achieve better performance than a single ensemble member?
- How can VTEC models be improved in terms of data and input features? Also, does the new input dataset bring new information to the VTEC model?
- Can data modification, such as differencing, enhance the VTEC model learning and generalization?
2. Methodology
2.1. Data Selection and Preparation
- After preprocessing, the data for are used for the machine learning algorithm. In this paper this dataset is referred as non-differenced data.
- Data (except HOD, DOY, EMA and the time derivatives) are time-differenced by calculating the difference between an observation at time h and an observation at time step i, i.e., and . Differencing was used to reduce temporal dependence and trends, as well as, stabilize mean of the dataset [38], by reducing daily variations. In this paper this dataset is referred as differenced data. Values of EMA and time derivatives were calculated from differenced VTEC. At the end, predicted VTEC differences were reconstructed by adding up the VTEC values from the previous day.
2.2. Supervised Learning
2.3. Tree-Based Machine Learning Algorithms
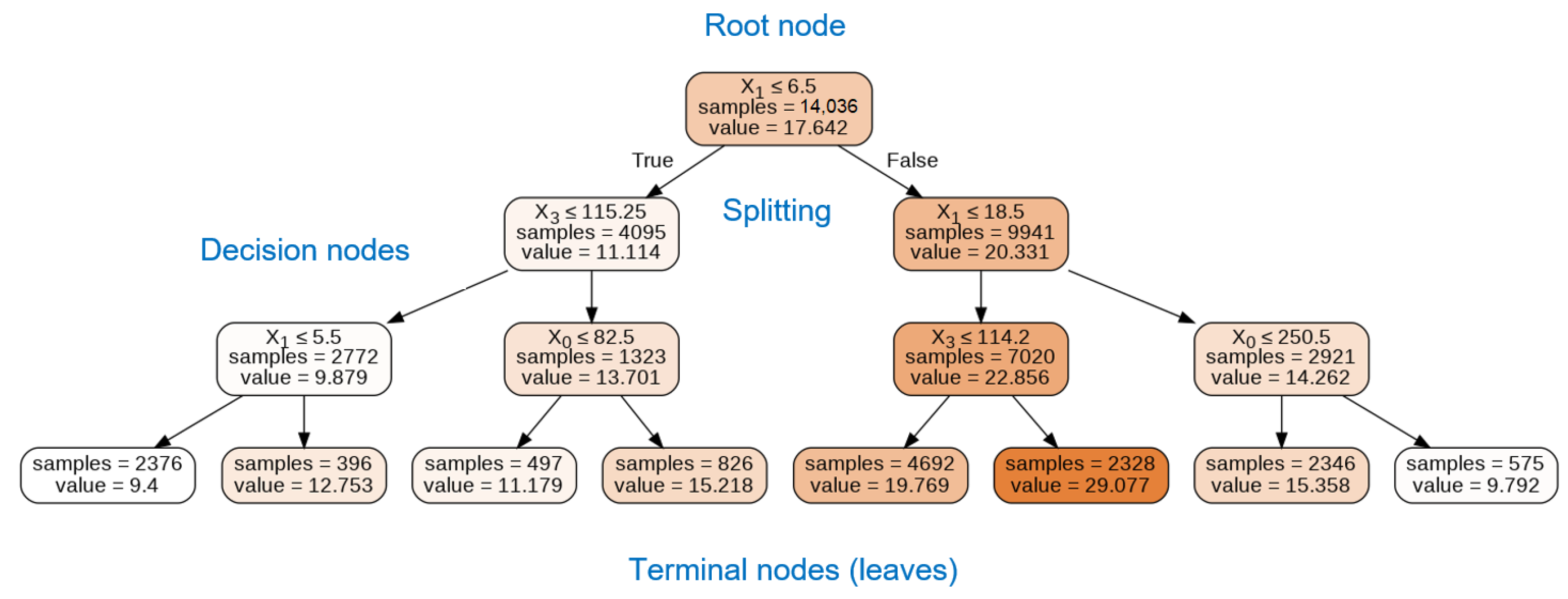
2.3.1. Regression Trees
2.3.2. Ensemble Learning
- Select random sample of v input variables from the full set of p variables;
- Find the best splitting variable and split point among the v input variables;
- Split the node into two sub-nodes.
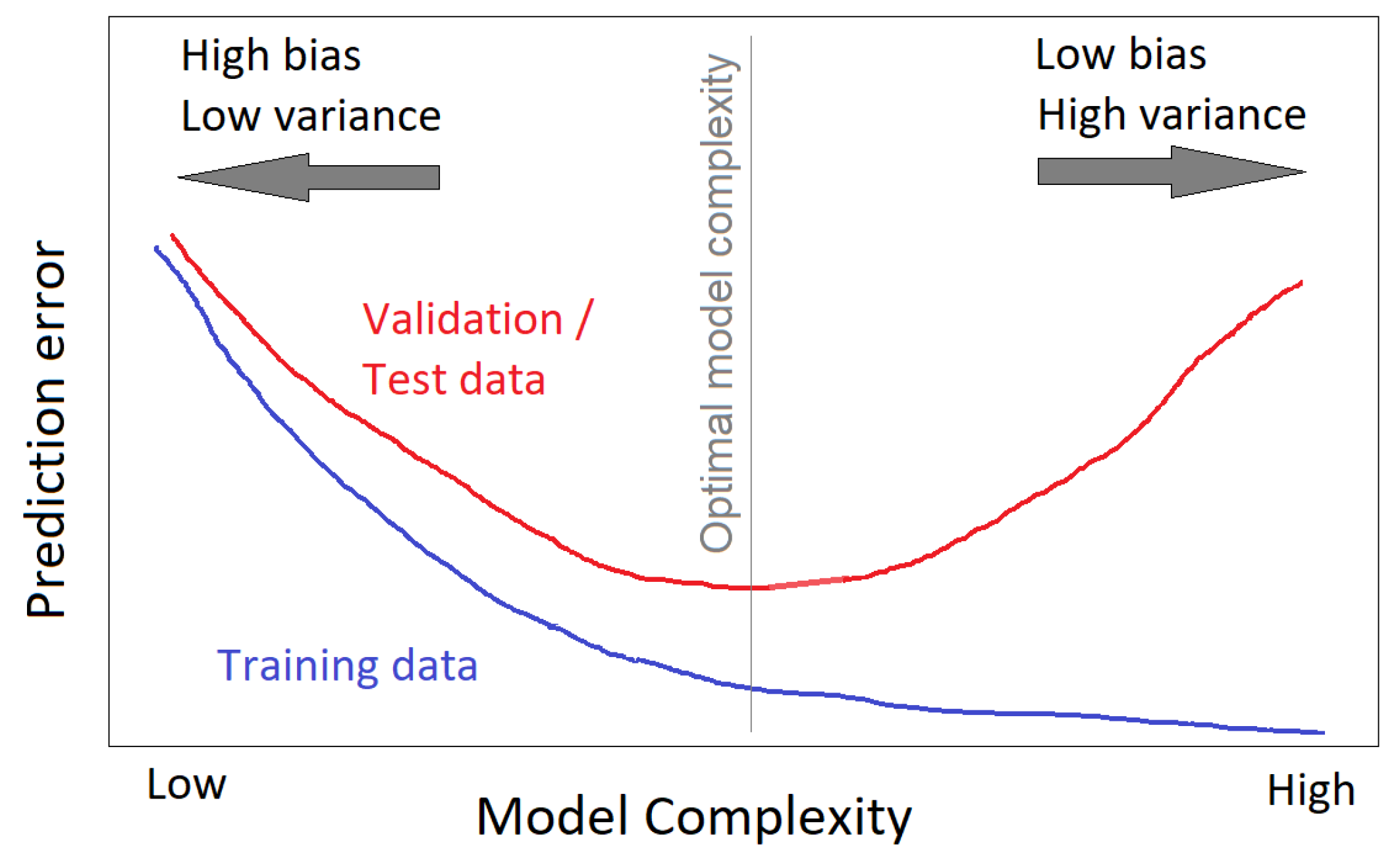
2.4. Model Selection and Validation
2.4.1. Time Series Cross-Validation
2.4.2. Model Architecture
3. Results
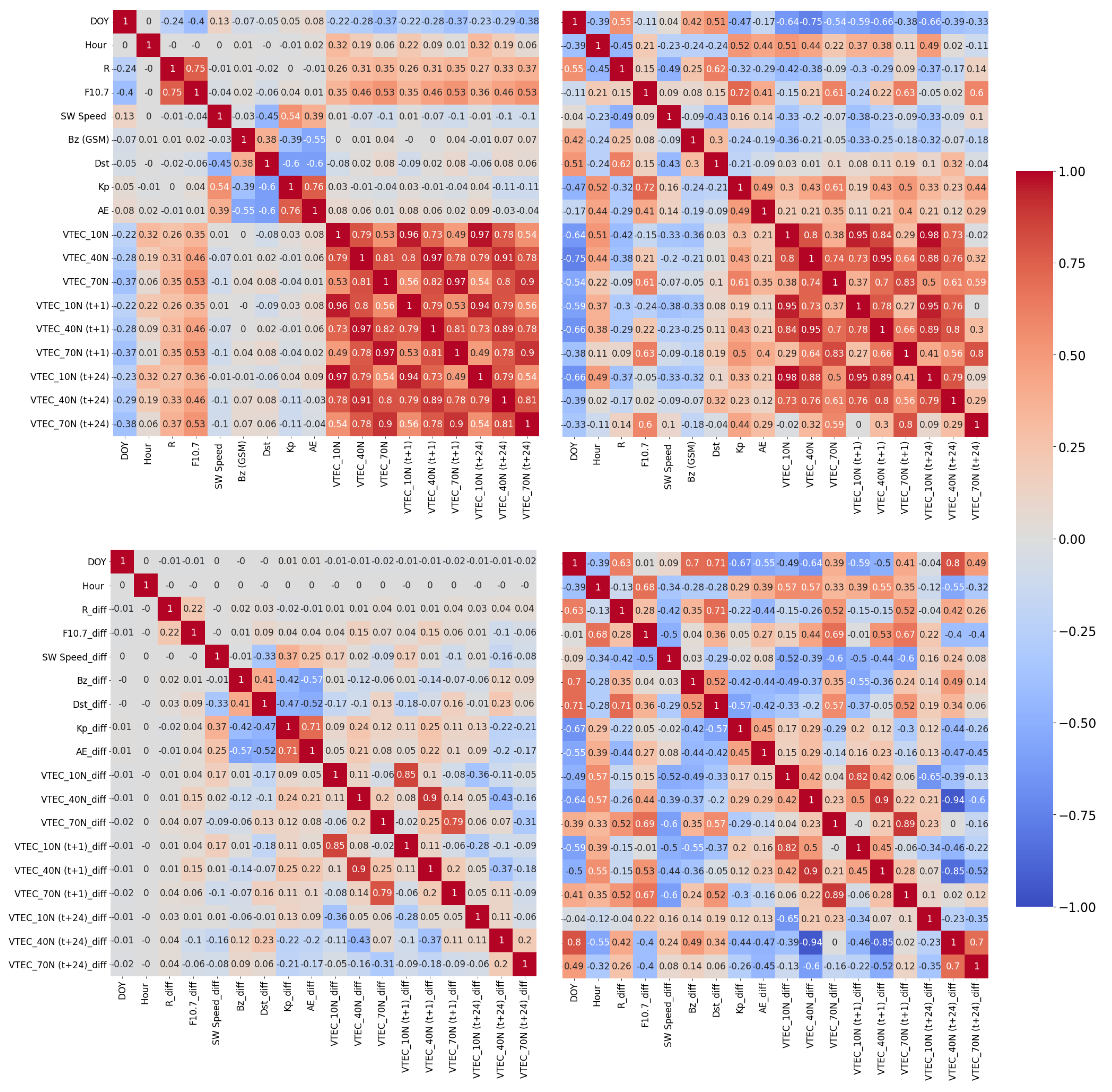
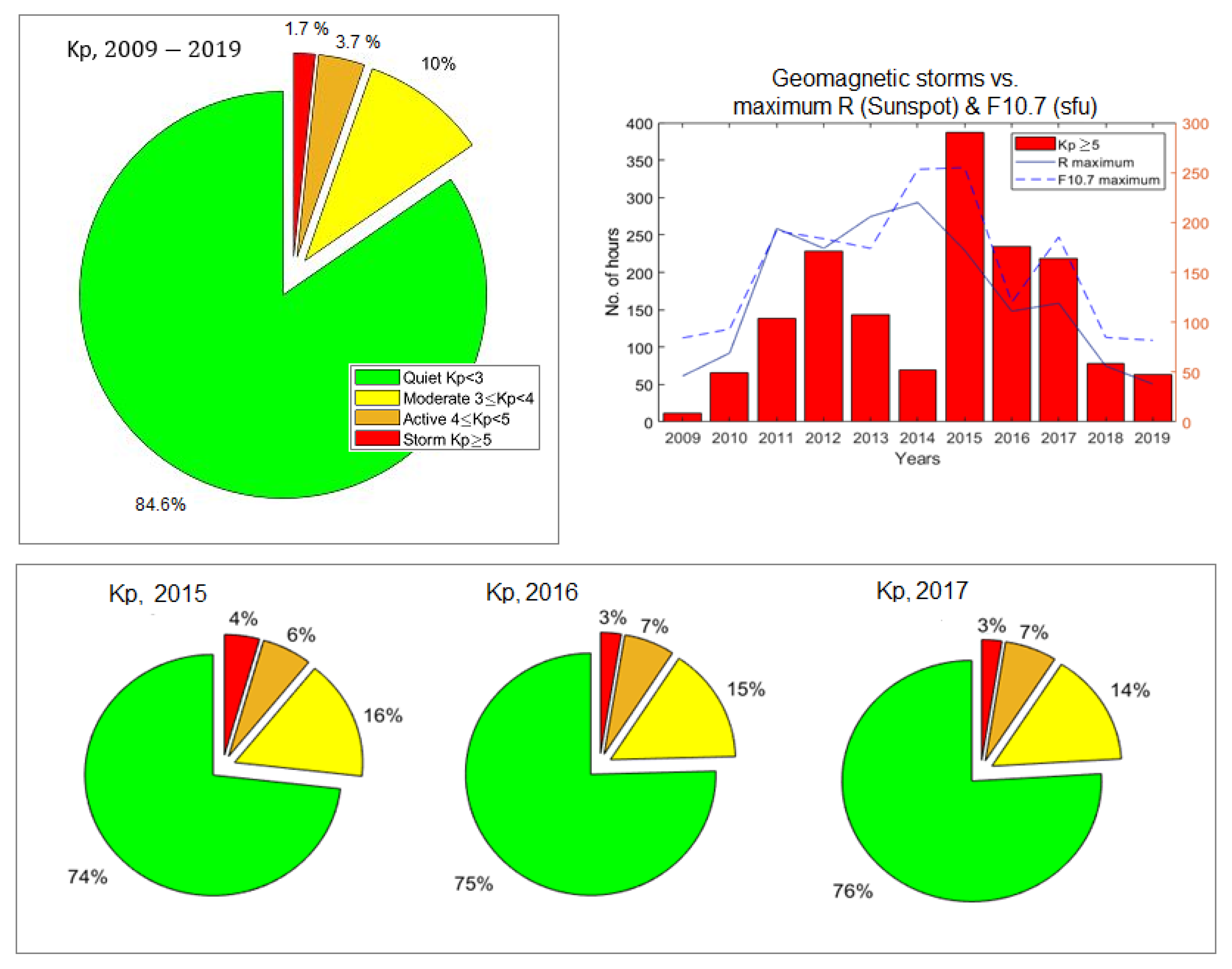
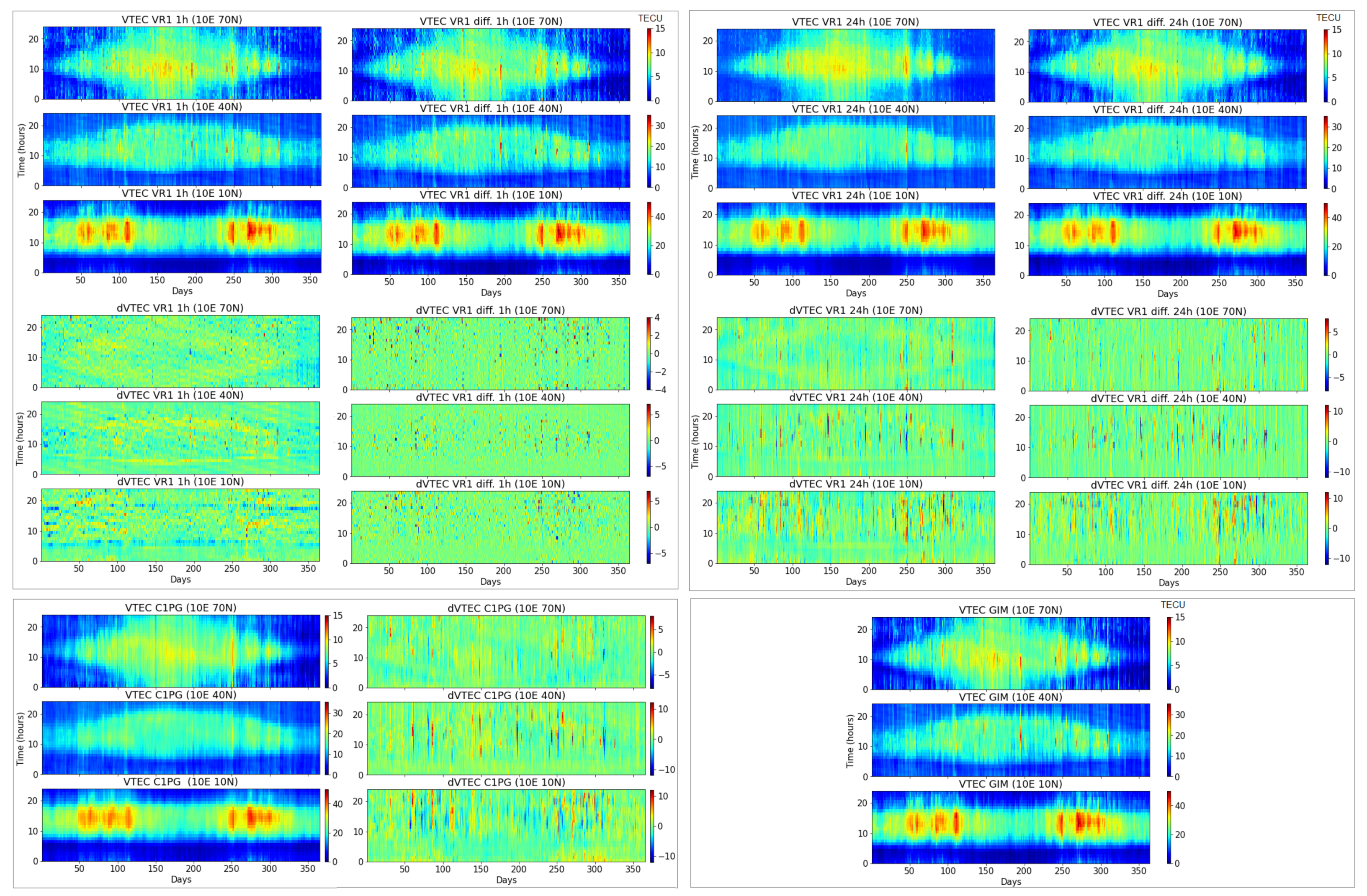
3.1. Exploratory Data Analysis
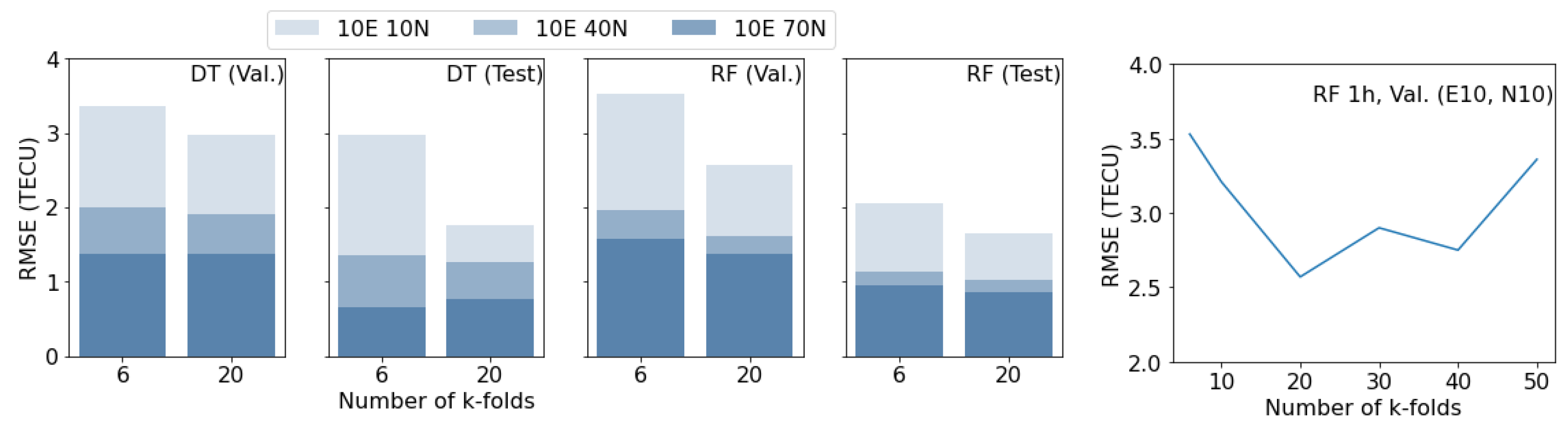
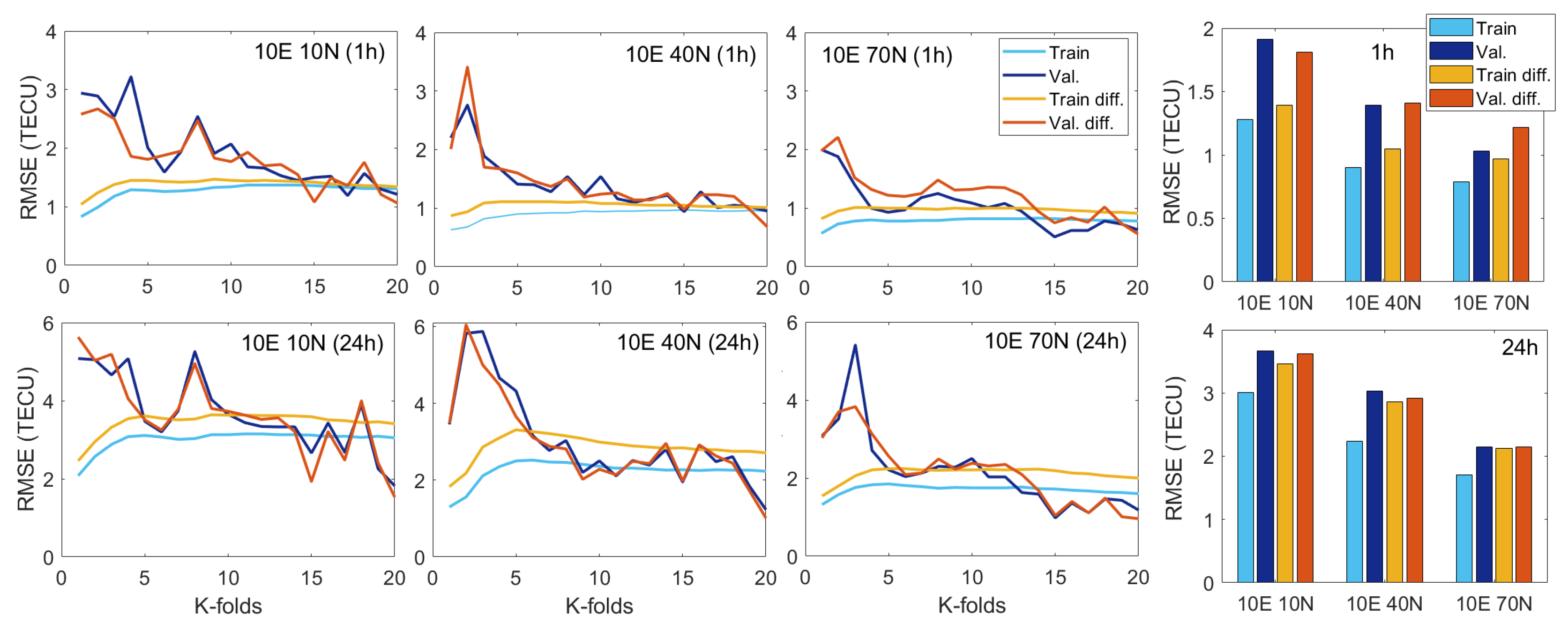
3.2. K-Fold Selection for Cross-Validation
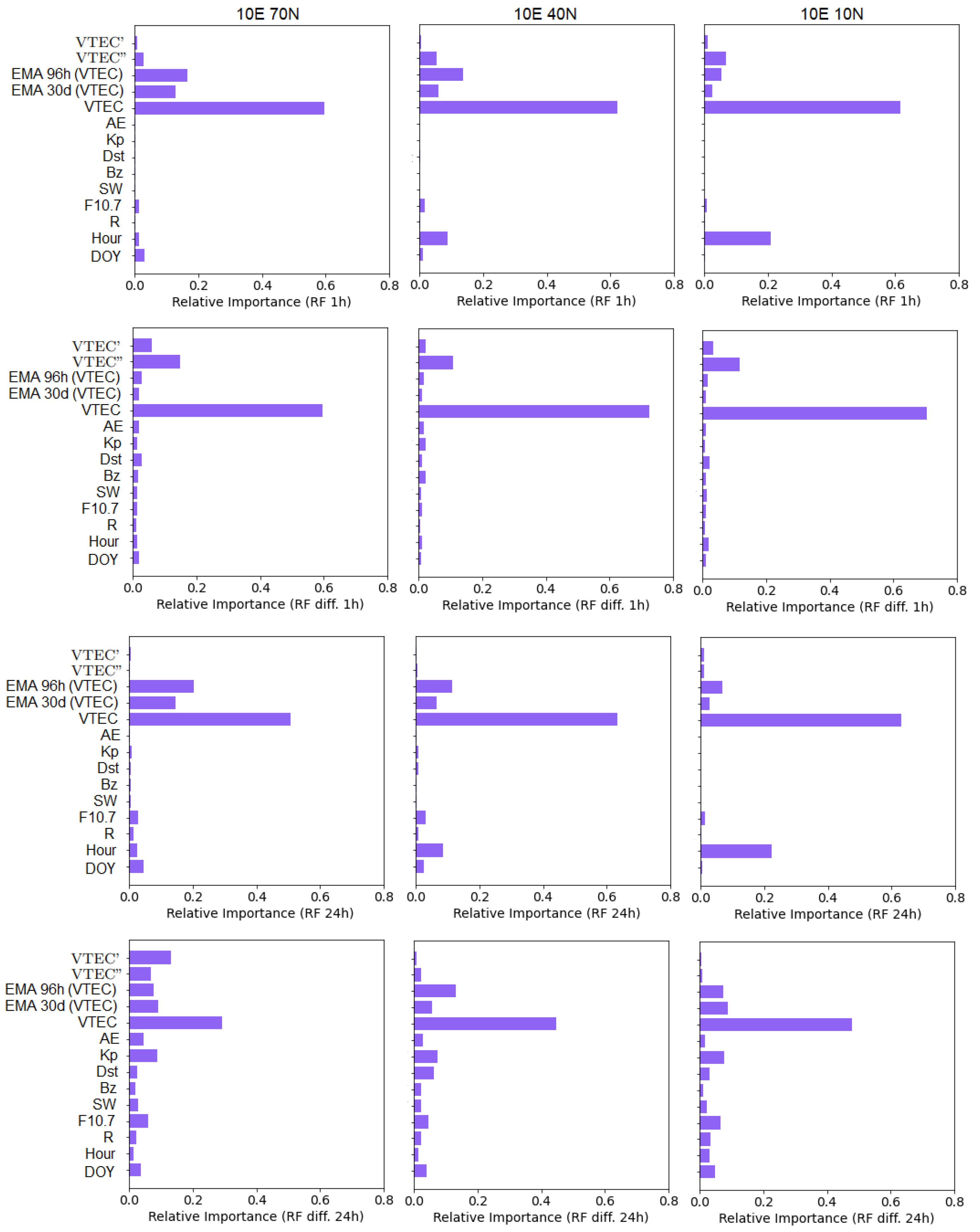
3.3. Relative Importance of Input Variables to VTEC Forecast
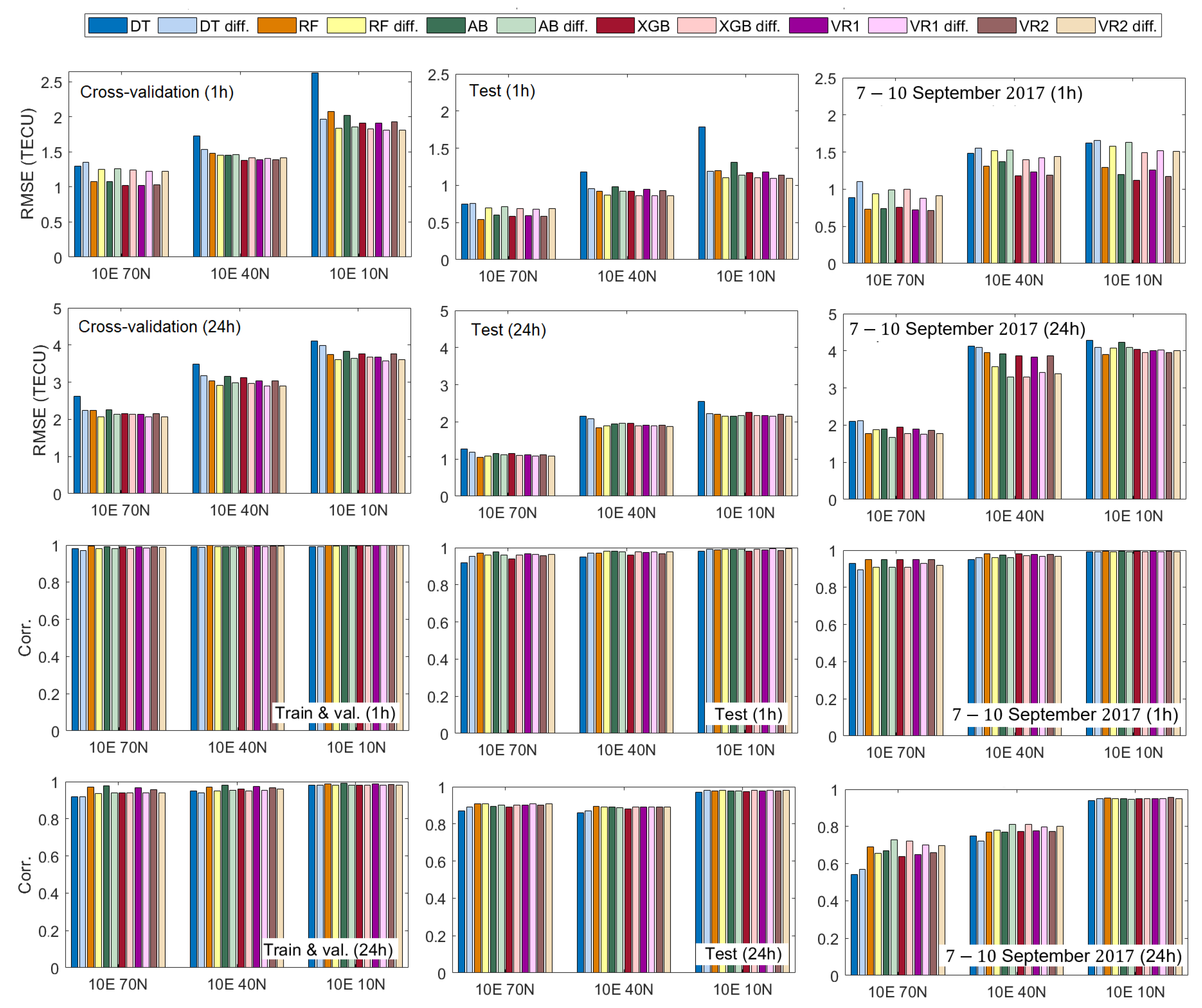
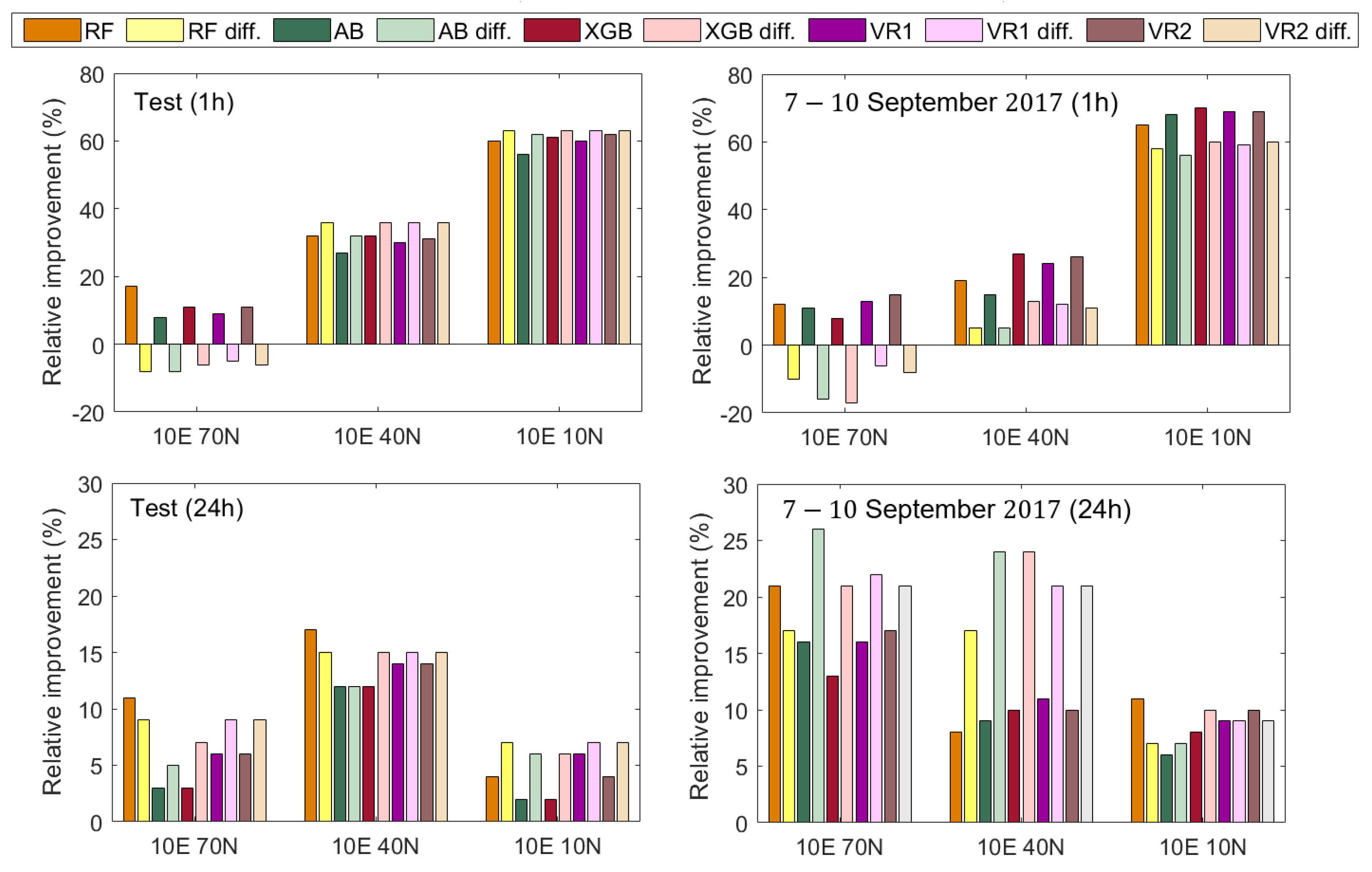
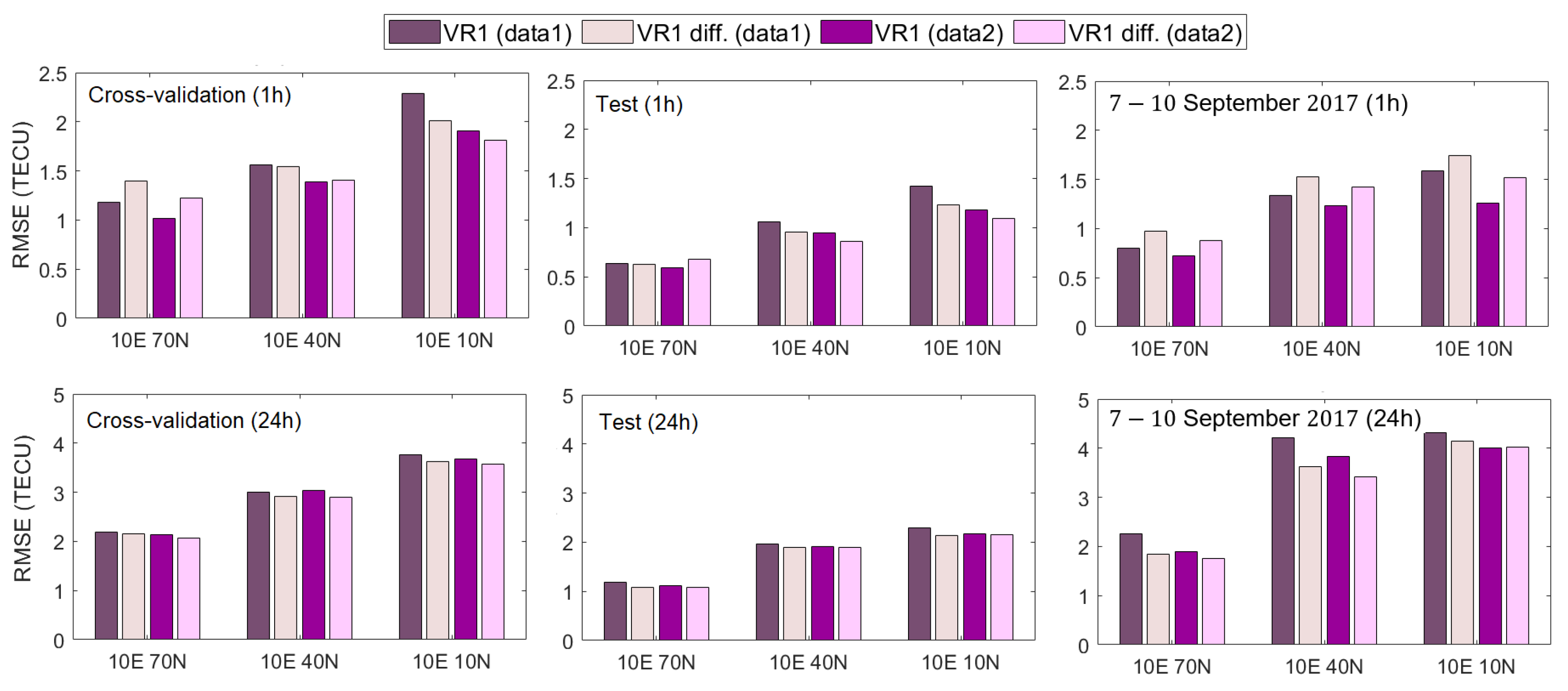
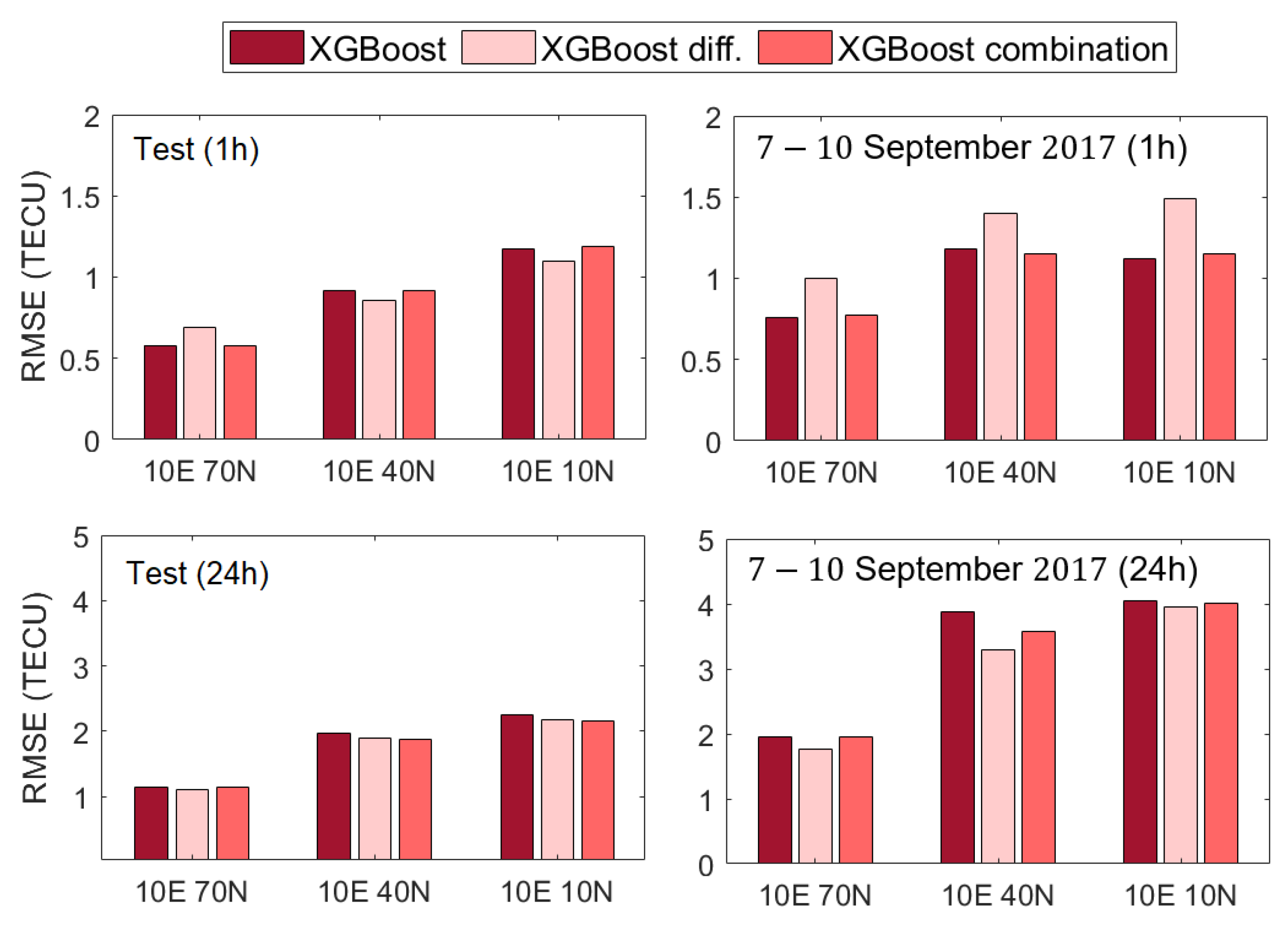
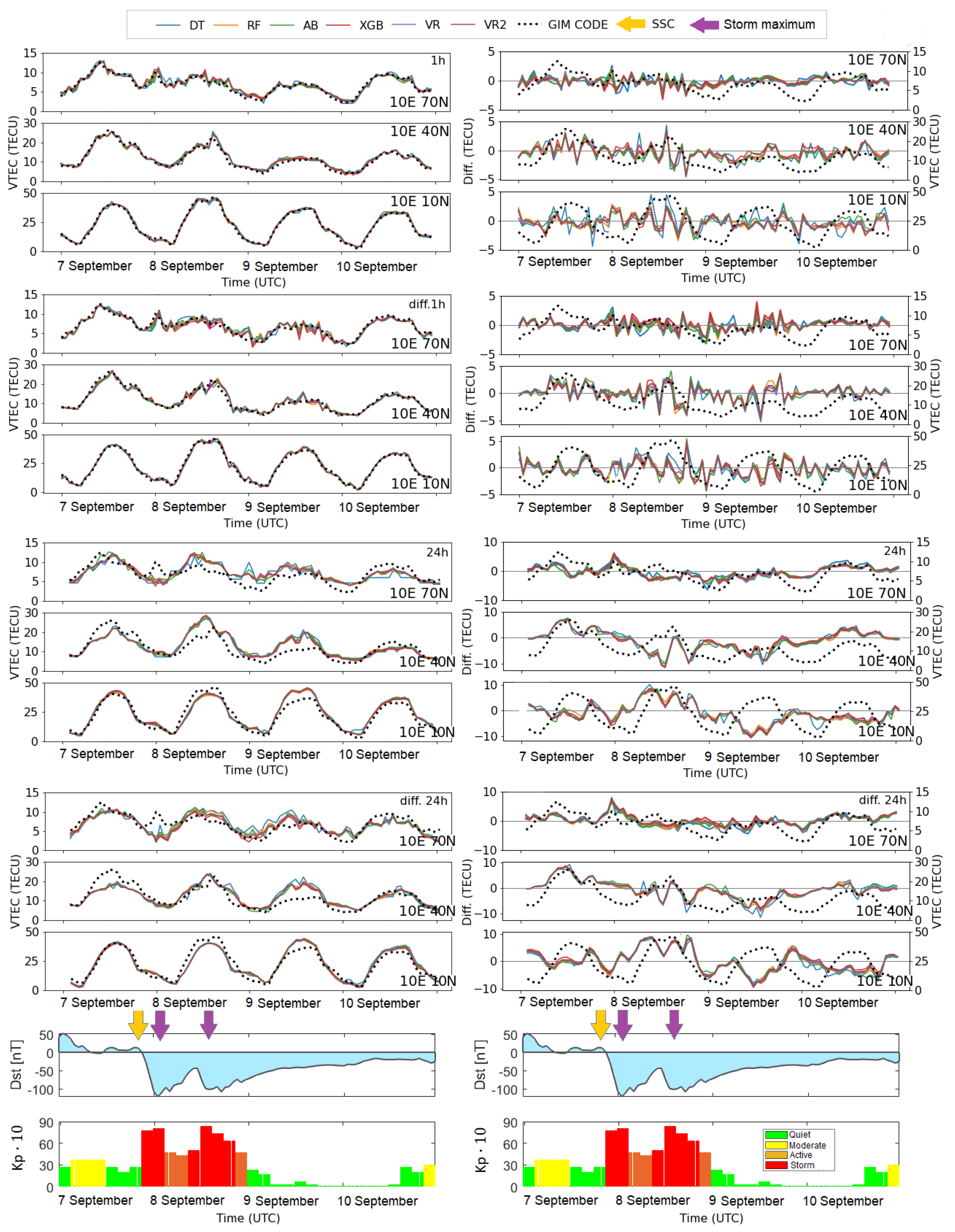
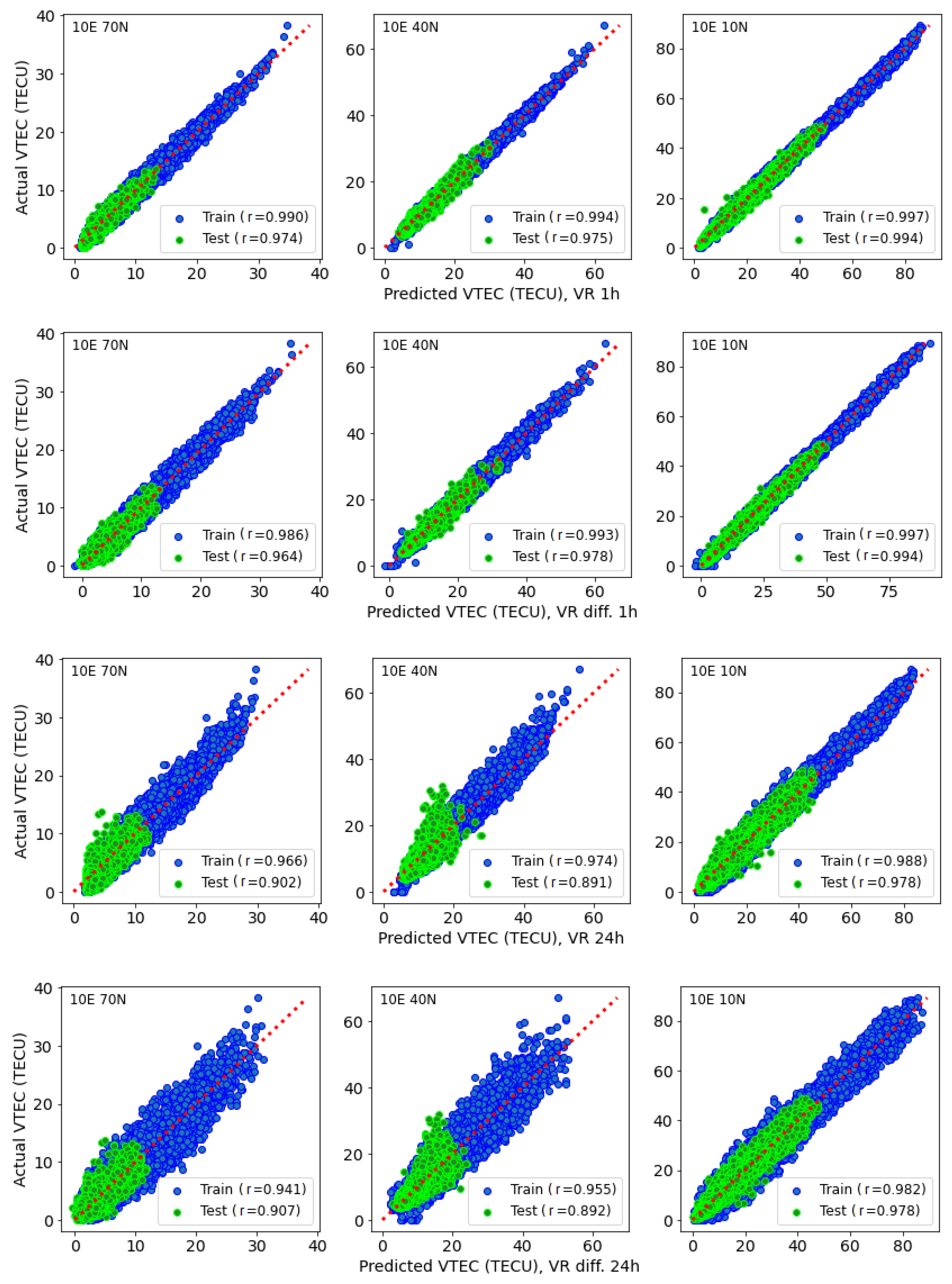
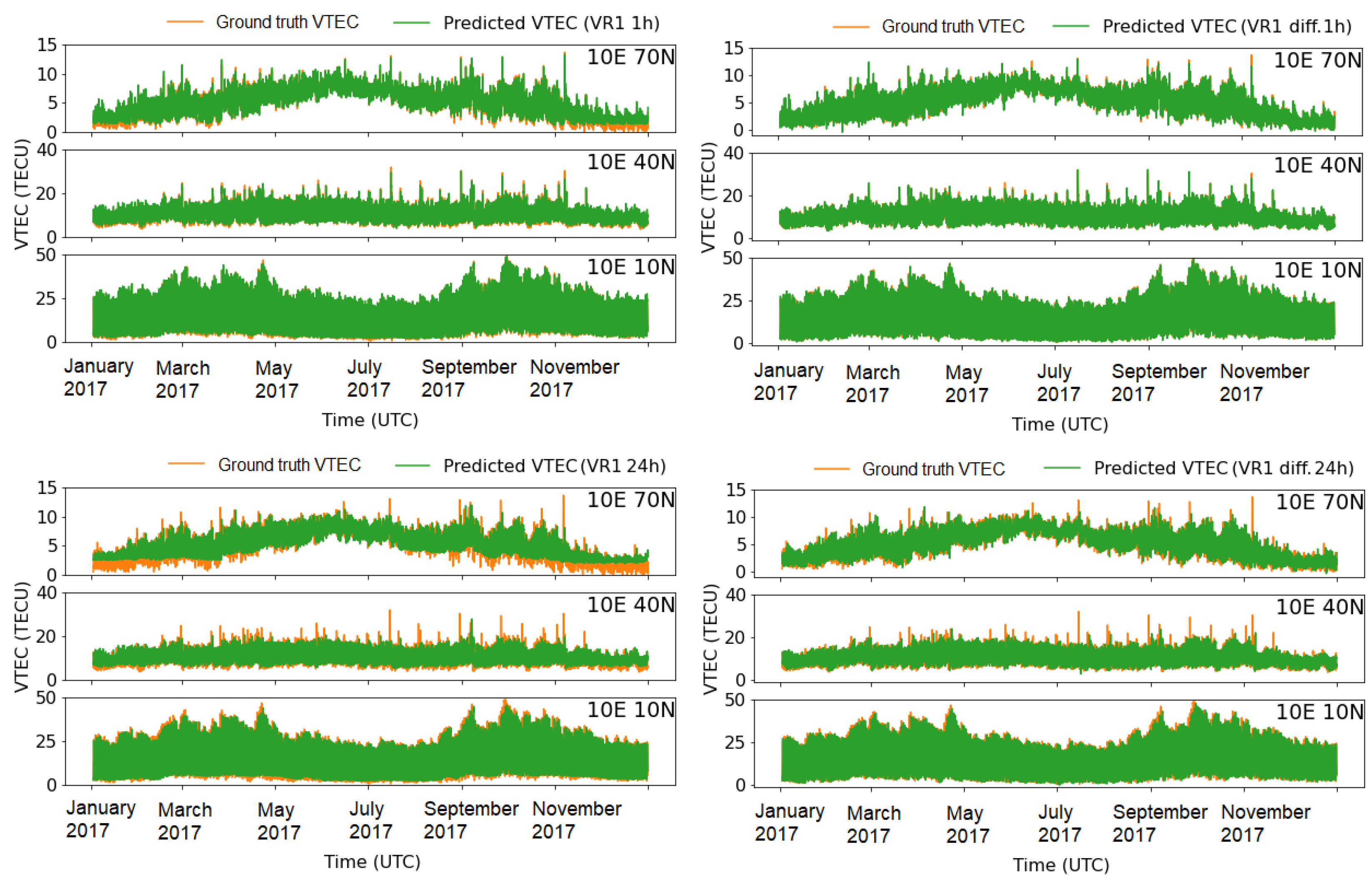
3.4. Accuracy Performance of Machine Learning Models
4. Discussion
5. Conclusions
- The new, proposed learning VTEC models can capture variations in electron content consistent with ground truth for both 1 h and 1 day forecasts.
- The ensemble meta-models (VR1 and VR2) improve the VTEC forecasting over each individual model in the ensemble and deliver optimal results.
- Including additional input features, such as moving averages and time derivatives, is beneficial to increase the accuracy of the models.
- Data modification in the form of differencing enhances the VTEC model performance for a longer (24-h) forecast, including a geomagnetic storm.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AdaBoost | Adaptive Boosting |
| AB | AdaBoost |
| DOY | Day Of Year |
| HOD | Hour Of Day |
| DT | Decision Tree |
| GIM | Global Ionosphere Map |
| GNSS | Global Navigation Satellite System |
| LSTM | Long Short-Term Memory |
| r | correlation coefficient |
| RMSE | Root Mean Square Error |
| RF | Random Forest |
| SW | Solar Wind speed |
| TECU | Total Electron Content Unit |
| VTEC | Vertical Total Electron Content |
| VR | Votting Regressor |
| XGBoost | eXtreme Gradient Boosting |
| XGB | XGBoost |
References
- Coster, A.; Komjathy, A. Space Weather and the Global Positioning System. Space Weather 2008, 6, 1–6. [Google Scholar] [CrossRef]
- Klobuchar, J.A. Ionospheric Time-Delay Algorithm for Single-Frequency GPS Users. IEEE Trans. Aerosp. Electron. Syst. 1987, AES-23, 325–331. [Google Scholar] [CrossRef]
- Roma, D.; Pajares, M.; Krankowski, A.; Kotulak, K.; Ghoddousi-Fard, R.; Yuan, Y.; Li, Z.; Zhang, H.; Shi, C.; Wang, C.; et al. Consistency of seven different GNSS global ionospheric mapping techniques during one solar cycle. J. Geod. 2017, 92, 691–706. [Google Scholar] [CrossRef] [Green Version]
- Yuan, Y.; Wang, N.; Li, Z.; Huo, X. The BeiDou global broadcast ionospheric delay correction model (BDGIM) and its preliminary performance evaluation results. Navigation 2019, 66, 55–69. [Google Scholar] [CrossRef] [Green Version]
- Cander, L.R. Ionospheric Variability. In Ionospheric Space Weather; Springer: Berlin, Germany, 2019; pp. 59–93. [Google Scholar]
- Nishimura, Y.; Verkhoglyadova, O.; Deng, Y.; Zhang, S.R. (Eds.) Cross-Scale Coupling and Energy Transfer in the Magnetosphere-Ionosphere-Thermosphere SYSTEM; Elsevier: Amsterdam, The Netherlands, 2021. [Google Scholar] [CrossRef]
- Pulinets, S.; Ouzounov, D. Lithosphere–Atmosphere–Ionosphere Coupling (LAIC) model—An unified concept for earthquake precursors validation. J. Asian Earth Sci. 2011, 41, 371–382. [Google Scholar] [CrossRef]
- Luo, X.; Du, J.; Lou, Y.; Gu, S.; Yue, X.; Liu, J.; Chen, B. A Method to Mitigate the Effects of Strong Geomagnetic Storm on GNSS Precise Point Positioning. Space Weather 2022, 20, e2021SW002908. [Google Scholar] [CrossRef]
- Luo, X.; Gu, S.; Lou, Y.; Xiong, C.; Chen, B.; Jin, X. Assessing the Performance of GPS Precise Point Positioning Under Different Geomagnetic Storm Conditions during Solar Cycle 24. Sensors 2018, 18, 1784. [Google Scholar] [CrossRef] [Green Version]
- Natras, R.; Horozovic, D.; Mulic, M. Strong solar flare detection and its impact on ionospheric layers and on coordinates accuracy in the Western Balkans in October 2014. SN Appl. Sci. 2019, 1, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Yuan, Y.; Ou, J. An improvement to ionospheric delay correction for single-frequency GPS users—The APR-I scheme. J. Geod. 2001, 75, 331–336. [Google Scholar] [CrossRef]
- Jordan, M.I.; Mitchell, T.M. Machine learning: Trends, perspectives, and prospects. Science 2015, 349, 255–260. [Google Scholar] [CrossRef]
- Natras, R.; Schmidt, M. Machine Learning Model Development for Space Weather Forecasting in the Ionosphere. In Proceedings of the CEUR Workshop, Gold Coast, Australia, 1–5 November 2021; Volume 3052. [Google Scholar]
- Camporeale, E.; Wing, S.; Johnson, J. Machine Learning Techniques for Space Weather; Elsevier: Amsterdam, The Netherlands, 2018. [Google Scholar]
- Adolfs, M.; Hoque, M.M. A Neural Network-Based TEC Model Capable of Reproducing Nighttime Winter Anomaly. Remote Sens. 2021, 13, 4559. [Google Scholar] [CrossRef]
- Natras, R.; Goss, A.; Halilovic, D.; Magnet, N.; Mulic, M.; Schmidt, M.; Weber, R. Regional ionosphere delay models based on CORS data and machine learning. Navig. J. Inst. Navig. 2022; in review. [Google Scholar]
- Tebabal, A.; Radicella, S.; Damtie, B.; Migoya-Orue’, Y.; Nigussie, M.; Nava, B. Feed forward neural network based ionospheric model for the East African region. J. Atmos. Sol.-Terr. Phys. 2019, 191, 105052. [Google Scholar] [CrossRef]
- Liu, L.; Zou, S.; Yao, Y.; Wang, Z. Forecasting Global Ionospheric TEC Using Deep Learning Approach. Space Weather 2020, 18, e2020SW002501. [Google Scholar] [CrossRef]
- Srivani, I.; Siva Vara Prasad, G.; Venkata Ratnam, D. A Deep Learning-Based Approach to Forecast Ionospheric Delays for GPS Signals. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1180–1184. [Google Scholar] [CrossRef]
- Tang, R.; Zeng, F.; Chen, Z.; Wang, J.S.; Huang, C.M.; Wu, Z. The Comparison of Predicting Storm-Time Ionospheric TEC by Three Methods: ARIMA, LSTM, and Seq2Seq. Atmosphere 2020, 11, 316. [Google Scholar] [CrossRef] [Green Version]
- Kaselimi, M.; Voulodimos, A.; Doulamis, N.; Doulamis, A.; Delikaraoglou, D. Deep Recurrent Neural Networks for Ionospheric Variations Estimation Using GNSS Measurements. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–15. [Google Scholar] [CrossRef]
- Ruwali, A.; Kumar, A.J.S.; Prakash, K.B.; Sivavaraprasad, G.; Ratnam, D.V. Implementation of Hybrid Deep Learning Model (LSTM-CNN) for Ionospheric TEC Forecasting Using GPS Data. IEEE Geosci. Remote Sens. Lett. 2021, 18, 1004–1008. [Google Scholar] [CrossRef]
- Xiong, P.; Zhai, D.; Long, C.; Zhou, H.; Zhang, X.; Shen, X. Long Short-Term Memory Neural Network for Ionospheric Total Electron Content Forecasting Over China. Space Weather 2021, 19, e2020SW002706. [Google Scholar] [CrossRef]
- Cesaroni, C.; Spogli, L.; Aragon-Angel, A.; Fiocca, M.; Dear, V.; De Franceschi, G.; Romano, V. Neural network based model for global Total Electron Content forecasting. J. Space Weather Space Clim. 2020, 10, 11. [Google Scholar] [CrossRef]
- Sivavaraprasad, G.; Lakshmi Mallika, I.; Sivakrishna, K.; Venkata Ratnam, D. A novel hybrid Machine learning model to forecast ionospheric TEC over Low-latitude GNSS stations. Adv. Space Res. 2022, 69, 1366–1379. [Google Scholar] [CrossRef]
- Lee, S.; Ji, E.Y.; Moon, Y.J.; Park, E. One day Forecasting of Global TEC Using a Novel Deep Learning Model. Space Weather 2020, 19, 2020SW002600. [Google Scholar] [CrossRef]
- Han, Y.; Wang, L.; Fu, W.; Zhou, H.; Li, T.; Chen, R. Machine Learning-Based Short-Term GPS TEC Forecasting During High Solar Activity and Magnetic Storm Periods. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 115–126. [Google Scholar] [CrossRef]
- Ghaffari Razin, M.R.; Voosoghi, B. Ionosphere time series modeling using adaptive neuro-fuzzy inference system and principal component analysis. GPS Solut. 2020, 24, 1–13. [Google Scholar] [CrossRef]
- Zhukov, A.V.; Yasyukevich, Y.V.; Bykov, A.E. Correction to: GIMLi: Global Ionospheric total electron content model based on machine learning. GPS Solut. 2021, 25, 21. [Google Scholar] [CrossRef]
- Xia, G.; Liu, Y.; Wei, T.; Wang, Z.; Huang, W.; Du, Z.; Zhang, Z.; Wang, X.; Zhou, C. Ionospheric TEC forecast model based on support vector machine with GPU acceleration in the China region. Adv. Space Res. 2021, 68, 1377–1389. [Google Scholar] [CrossRef]
- Monte-Moreno, E.; Yang, H.; Hernández-Pajares, M. Forecast of the Global TEC by Nearest Neighbour Technique. Remote Sens. 2022, 14, 1361. [Google Scholar] [CrossRef]
- Wen, Z.; Li, S.; Li, L.; Wu, B.; Fu, J. Ionospheric TEC prediction using Long Short-Term Memory deep learning network. Astrophys. Space Sci. 2021, 366, 1–11. [Google Scholar] [CrossRef]
- Natras, R.; Soja, B.; Schmidt, M. Machine Learning Ensemble Approach for Ionosphere and Space Weather Forecasting with Uncertainty Quantification. In Proceedings of the 2022 3rd URSI Atlantic and Asia Pacific Radio Science Meeting (AT-AP-RASC), Gran Canaria, Spain, 30 May–4 June 2022; pp. 1–4. [Google Scholar] [CrossRef]
- Uwamahoro, J.C.; Habarulema, J.B. Modelling total electron content during geomagnetic storm conditions using empirical orthogonal functions and neural networks. J. Geophys. Res. Space Phys. 2015, 120, 11000–11012. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference and Prediction, 2nd ed.; Springer: Berlin, Germany, 2009. [Google Scholar] [CrossRef]
- Blum, A.; Kalai, A.; Langford, J. Beating the Hold-out: Bounds for K-Fold and Progressive Cross-Validation. In Proceedings of the Twelfth Annual Conference on Computational Learning Theory, Santa Cruz, CA, USA, 7–9 July 1999; Association for Computing Machinery: New York, NY, USA, 1999; pp. 203–208. [Google Scholar] [CrossRef]
- Arlot, S.; Celisse, A. A survey of cross-validation procedures for model selection. Stat. Surv. 2010, 4, 40–79. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Athanasopoulos, G. Forecasting: Principles and Practice, 3rd ed.; OTexts: Melbourne, Australia, 2021. [Google Scholar]
- King, J.H.; Papitashvili, N.E. Solar wind spatial scales in and comparisons of hourly Wind and ACE plasma and magnetic field data. J. Geophys. Res. Space Phys. 2005, 110, 1–9. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Freund, Y.; Schapire, R.E. A Decision-Theoretic Generalization of On-Line Learning and an Application to Boosting. J. Comput. Syst. Sci. 1997, 55, 119–139. [Google Scholar] [CrossRef] [Green Version]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Breiman, L.; Friedman, J.; Stone, C.; Olshen, R. Classification and Regression Trees; Taylor & Francis: Abingdon, UK, 1984. [Google Scholar]
- Wong, T.T.; Yeh, P.Y. Reliable Accuracy Estimates from k-Fold Cross Validation. IEEE Trans. Knowl. Data Eng. 2020, 32, 1586–1594. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy Function Approximation: A Gradient Boosting Machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Esposito, D. Introducing Machine Learning, 1st ed.; Microsoft Press: Redmond, WA, USA; Safari: Boston, MA, USA, 2020. [Google Scholar]
- Badeke, R.; Borries, C.; Hoque, M.M.; Minkwitz, D. Empirical forecast of quiet time ionospheric Total Electron Content maps over Europe. Adv. Space Res. 2018, 61, 2881–2890. [Google Scholar] [CrossRef]
- García-Rigo, A.; Monte, E.; Hernández-Pajares, M.; Juan, J.M.; Sanz, J.; Aragón-Angel, A.; Salazar, D. Global prediction of the vertical total electron content of the ionosphere based on GPS data. Radio Sci. 2011, 46, 1–3. [Google Scholar] [CrossRef] [Green Version]
- Verkhoglyadova, O.; Meng, X.; Mannucci, A.J.; Shim, J.S.; McGranaghan, R. Evaluation of Total Electron Content Prediction Using Three Ionosphere-Thermosphere Models. Space Weather 2020, 18, e2020SW002452. [Google Scholar] [CrossRef]
- Imtiaz, N.; Younas, W.; Khan, M. Response of the low- to mid-latitude ionosphere to the geomagnetic storm of September 2017. Ann. Geophys. 2020, 38, 359–372. [Google Scholar] [CrossRef] [Green Version]
- Wang, G.; Yin, Z.; Hu, Z.; Chen, G.; Li, W.; Bo, Y. Analysis of the BDGIM Performance in BDS Single Point Positioning. Remote Sens. 2021, 13, 3888. [Google Scholar] [CrossRef]
- Liu, Q.; Hernández-Pajares, M.; Lyu, H.; Goss, A. Influence of temporal resolution on the performance of global ionospheric maps. J. Geod. 2021, 95, 34. [Google Scholar] [CrossRef]
- Goss, A.; Schmidt, M.; Erdogan, E.; Görres, B.; Seitz, F. High-resolution vertical total electron content maps based on multi-scale B-spline representations. Ann. Geophys. 2019, 37, 699–717. [Google Scholar] [CrossRef] [Green Version]
- Erdogan, E.; Schmidt, M.; Goss, A.; Görres, B.; Seitz, F. Real-Time Monitoring of Ionosphere VTEC Using Multi-GNSS Carrier-Phase Observations and B-Splines. Space Weather 2021, 19, e2021SW002858. [Google Scholar] [CrossRef]
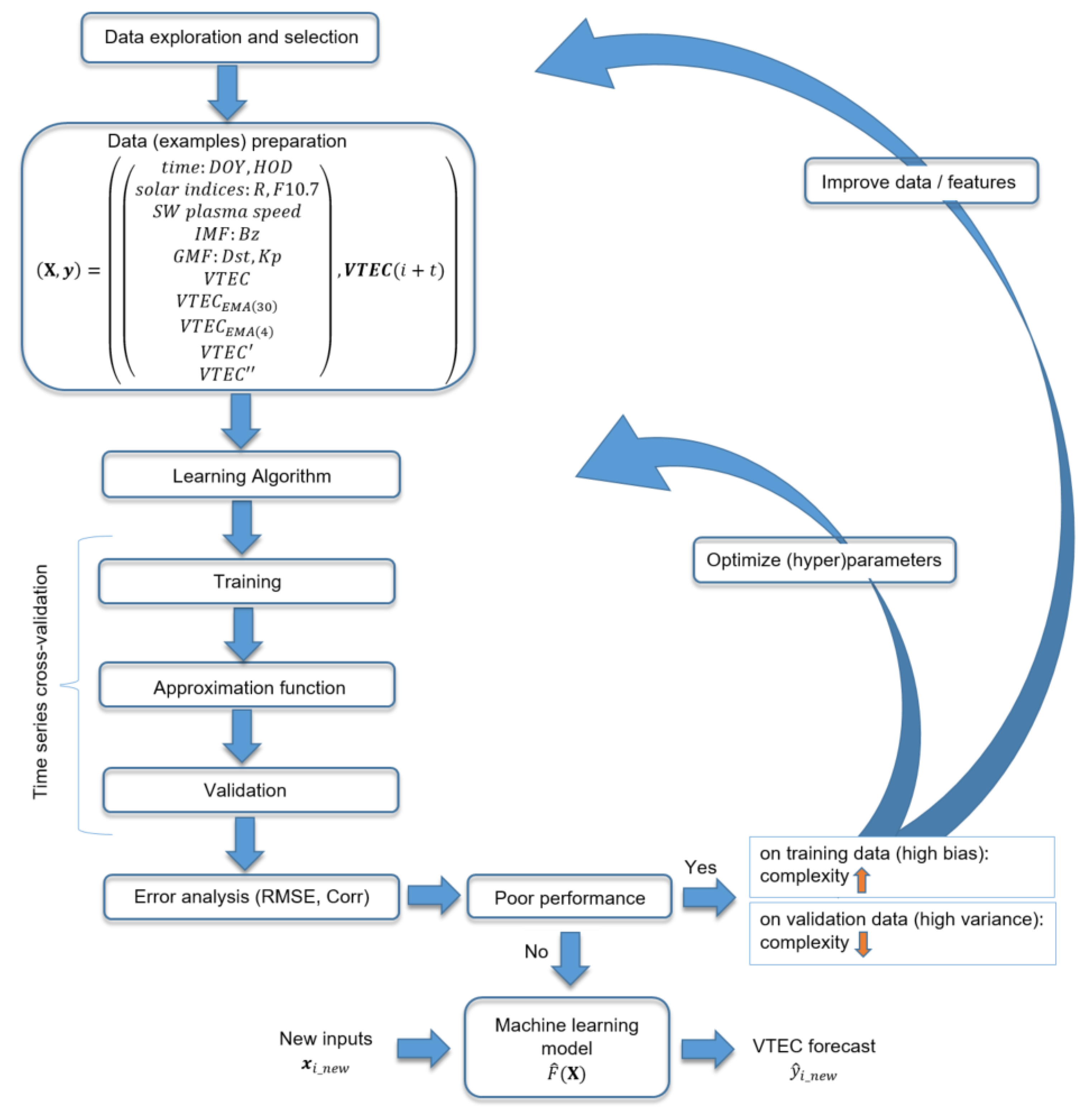

| Input Data (Time Moment: i) | Output Data (i + 1 h, i + 24 h) |
|---|---|
| Day of year (DOY) | |
| Hour of day (HOD) | |
| Sunspot number (R) | |
| Solar radio flux (F10.7) | |
| Solar wind (SW) plasma speed | |
| Interplanetary magnetic field (IMF) Bz index | VTEC |
| Geomagnetic field (GMF) Dst index | (10°70°, 10°40°, 10°10°) |
| GMF Kp index·10 | |
| AE index | |
| VTEC (10°70°, 10°40°, 10°10°) | |
| EMA of VTEC over previous 30 days | |
| EMA of VTEC over previous 4 days (96 h) | |
| First VTEC derivative (VTEC′) | |
| Second VTEC derivative (VTEC″) |
| Model | Selected Hyperparameters | Range of Search |
|---|---|---|
| max_depth = 5–8 | [4, 5, 6, 7, 8, 9, 10, 15, 20] | |
| Decision Tree | min_samples_split = 10–20 | [2, 5, 10, 15, 20] |
| min_samples_leaf = 10 | [2, 5, 10, 15, 20] | |
| max_features = 6 | [4, 5, 6, 7, 8] | |
| max_depth = 8–10 | [4, 6, 8, 10, 12, 15, 20] | |
| Random Forest | min_samples_split = 10 | [2, 5, 10, 15, 20] |
| min_samples_leaf = 5 | [2, 5, 10, 15, 20] | |
| n_estimators = 300 | [50–500] interval of 50 | |
| AdaBoost | max_depth = 6–8 | [3, 4, 5, 6, 7, 8, 9, 10, 15] |
| n_estimators = 50 | [50, 100, 150, 200, 300] | |
| max_depth = 4–6 | [3, 4, 5, 6, 7, 8, 9, 10, 15] | |
| XGBoost | n_estimators = 100 | [50, 100, 150, 200, 300] |
| learning_rate = | [0.01, 0.05, 0.1, 0.15, 0.2, 0.25, 0.3] | |
| subsample = | [0.3, 0.5, 0.7, 1] |
| Abbreviation | Machine Learning Model | Approach |
|---|---|---|
| DT | Decision (Regression) Tree | Single tree |
| RF | Random Forest | Bagging ensemble |
| AB | AdaBoost | Boosting ensemble |
| XGB | XGBoost | Boosting ensemble |
| VR1 | Random Forest, AdaBoost & XGBoost | Meta-ensemble |
| VR2 | Random Forest & XGBoost | Meta-ensemble |
| Machine Learning Model | Training and Validation (s) | Testing (s) |
|---|---|---|
| DT | 2–4 | <0.01 |
| RF | 300–330 | ∼0.30 |
| AB | 65–85 | ∼0.10 |
| XGB | 30–40 | ∼0.05 |
| VR1 | ∼250 | ∼0.35 |
| VR2 | ∼200 | ∼0.25 |
| DT | RF | AB | XGB | VR1 | VR2 | |
|---|---|---|---|---|---|---|
| 70N, 40N, 10N | 70N, 40N, 10N | 70N, 40N, 10N | 70N, 40N, 10N | 70N, 40N, 10N | 70N, 40N, 10N | |
| 2017 | RMSE (TECU) | RMSE (TECU) | RMSE (TECU) | RMSE (TECU) | RMSE (TECU) | RMSE (TECU) |
| 1 h | 0.75, 1.18, 1.79 | 0.54, 0.92, 1.20 | 0.60, 0.98, 1.31 | 0.59, 0.92, 1.17 | 0.59, 0.95, 1.18 | 0.58, 0.93, 1.14 |
| 1 hdiff. | 0.76, 0.96, 1.19 | 0.70, 0.87, 1.10 | 0.71, 0.92, 1.14 | 0.69, 0.86, 1.10 | 0.68, 0.86, 1.09 | 0.69, 0.86, 1.09 |
| 24 h | 1.28, 2.15, 2.55 | 1.06, 1.86, 2.20 | 1.15, 1.95, 2.26 | 1.15, 1.96, 2.25 | 1.11, 1.91, 2.17 | 1.11, 1.92, 2.21 |
| 24 hdiff. | 1.18, 2.08, 2.22 | 1.08, 1.89, 2.15 | 1.12, 1.96, 2.17 | 1.10, 1.89, 2.17 | 1.08, 1.89, 2.15 | 1.08, 1.88, 2.15 |
| 7–10 September | ||||||
| 1 h | 0.89, 1.48, 1.62 | 0.73, 1.31, 1.29 | 0.74, 1.37, 1.20 | 0.76, 1.18, 1.12 | 0.72, 1.23, 1.16 | 0.71, 1.19, 1.17 |
| 1 hdiff. | 1.10, 1.55, 1.66 | 0.94, 1.52, 1.58 | 0.99, 1.53, 1.63 | 1.00, 1.40, 1.49 | 0.88, 1.42, 1.52 | 0.91, 1.44, 1.51 |
| 24 h | 2.10, 4.12, 4.29 | 1.77, 3.95, 3.95 | 1.89, 3.92, 4.23 | 1.95, 3.87, 4.04 | 1.90, 3.84, 4.01 | 1.86, 3.87, 3.96 |
| 24 hdiff. | 2.12, 4.09, 4.10 | 1.87, 3.57, 4.08 | 1.67, 3.29, 4.09 | 1.77, 3.29, 3.96 | 1.76, 3.41, 4.02 | 1.78, 3.39, 4.00 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Natras, R.; Soja, B.; Schmidt, M. Ensemble Machine Learning of Random Forest, AdaBoost and XGBoost for Vertical Total Electron Content Forecasting. Remote Sens. 2022, 14, 3547. https://doi.org/10.3390/rs14153547
Natras R, Soja B, Schmidt M. Ensemble Machine Learning of Random Forest, AdaBoost and XGBoost for Vertical Total Electron Content Forecasting. Remote Sensing. 2022; 14(15):3547. https://doi.org/10.3390/rs14153547
Chicago/Turabian StyleNatras, Randa, Benedikt Soja, and Michael Schmidt. 2022. "Ensemble Machine Learning of Random Forest, AdaBoost and XGBoost for Vertical Total Electron Content Forecasting" Remote Sensing 14, no. 15: 3547. https://doi.org/10.3390/rs14153547
APA StyleNatras, R., Soja, B., & Schmidt, M. (2022). Ensemble Machine Learning of Random Forest, AdaBoost and XGBoost for Vertical Total Electron Content Forecasting. Remote Sensing, 14(15), 3547. https://doi.org/10.3390/rs14153547