Retrieving Pigment Concentrations Based on Hyperspectral Measurements of the Phytoplankton Absorption Coefficient in Global Oceans
Abstract
1. Introduction
2. Study Area and Data
2.1. Study Area
2.2. Data and Preprocessing
2.2.1. Phytoplankton Pigments
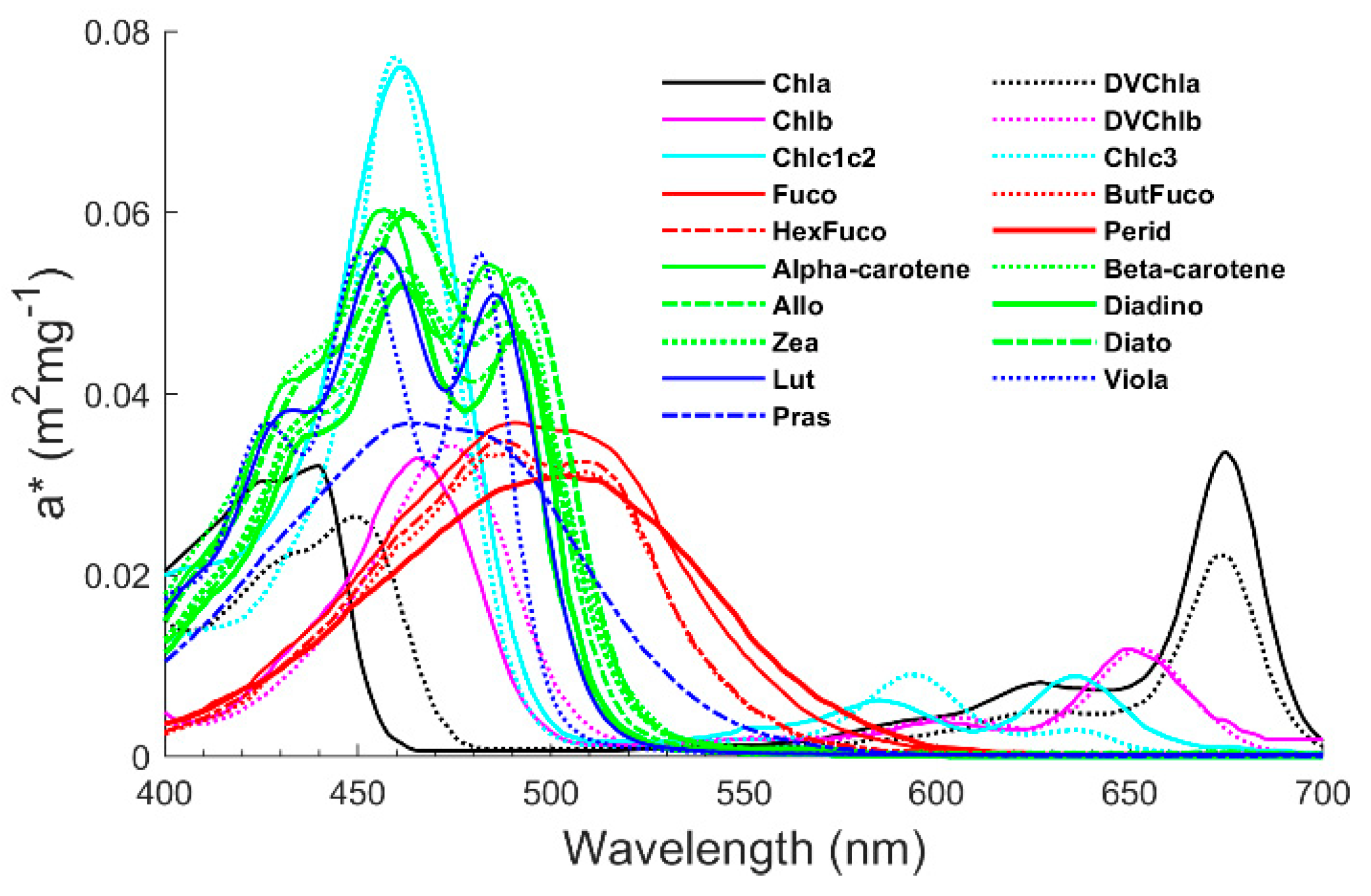
2.2.2. Phytoplankton Absorption Coefficient
3. ES-SR Method
3.1. Variable Form for Inversion
3.2. Ideas and Rationale for the Establishment of the ES-SR Method
3.3. Procedures of the ES-SR Method
- Criterion 1: Stop after epoch t + k with ROCd (m) < 0.01 sequentially, where m = t, t + 1, …, t + k.
- Criterion 2: Stop after epoch t + k with ROCr (m) < 0.01 sequentially, where m = t, t + 1, …, t + k.
4. Method Evaluation and Discussion
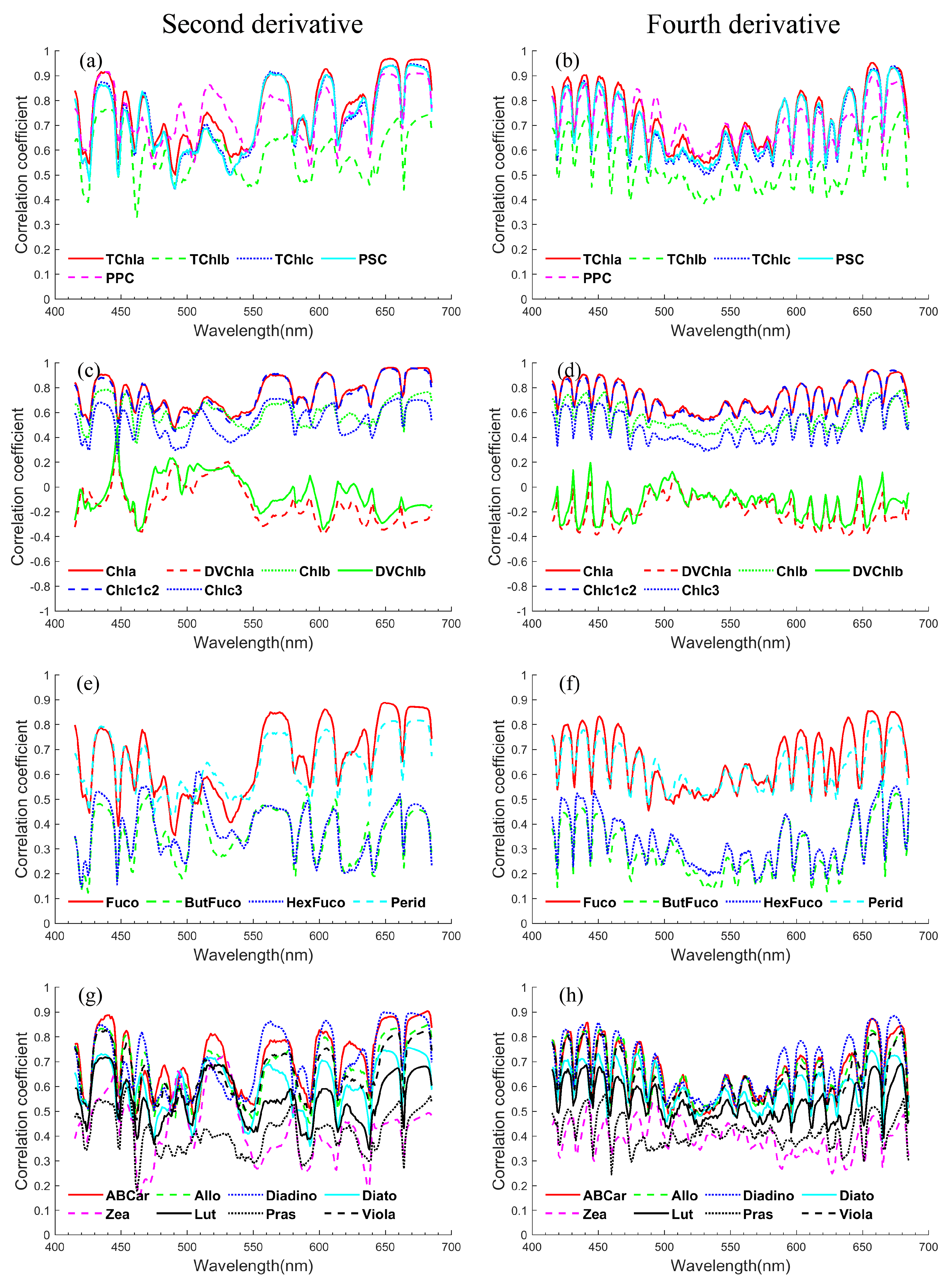
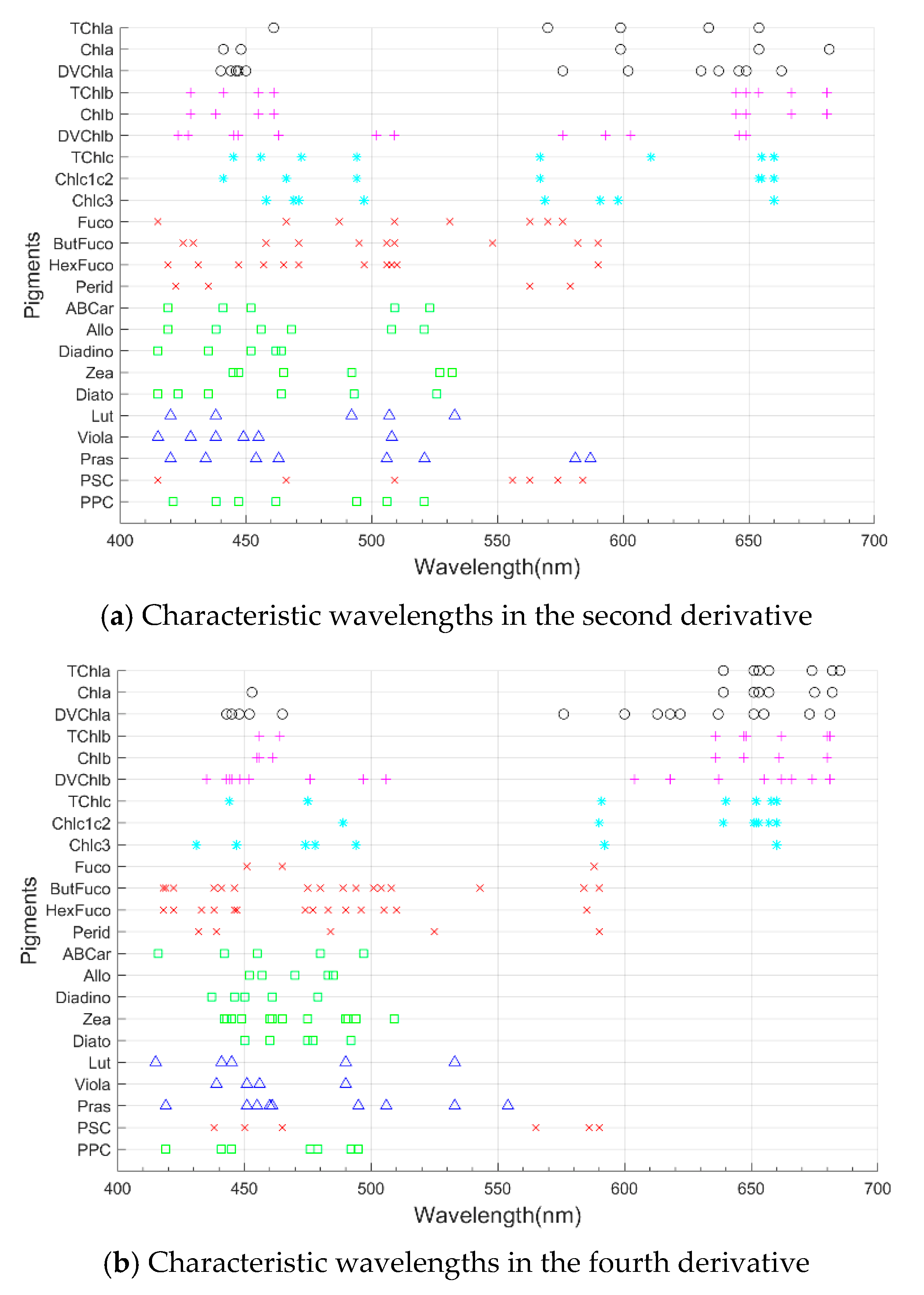
4.1. Characteristic Wavelength Analysis from the ES-SR Method
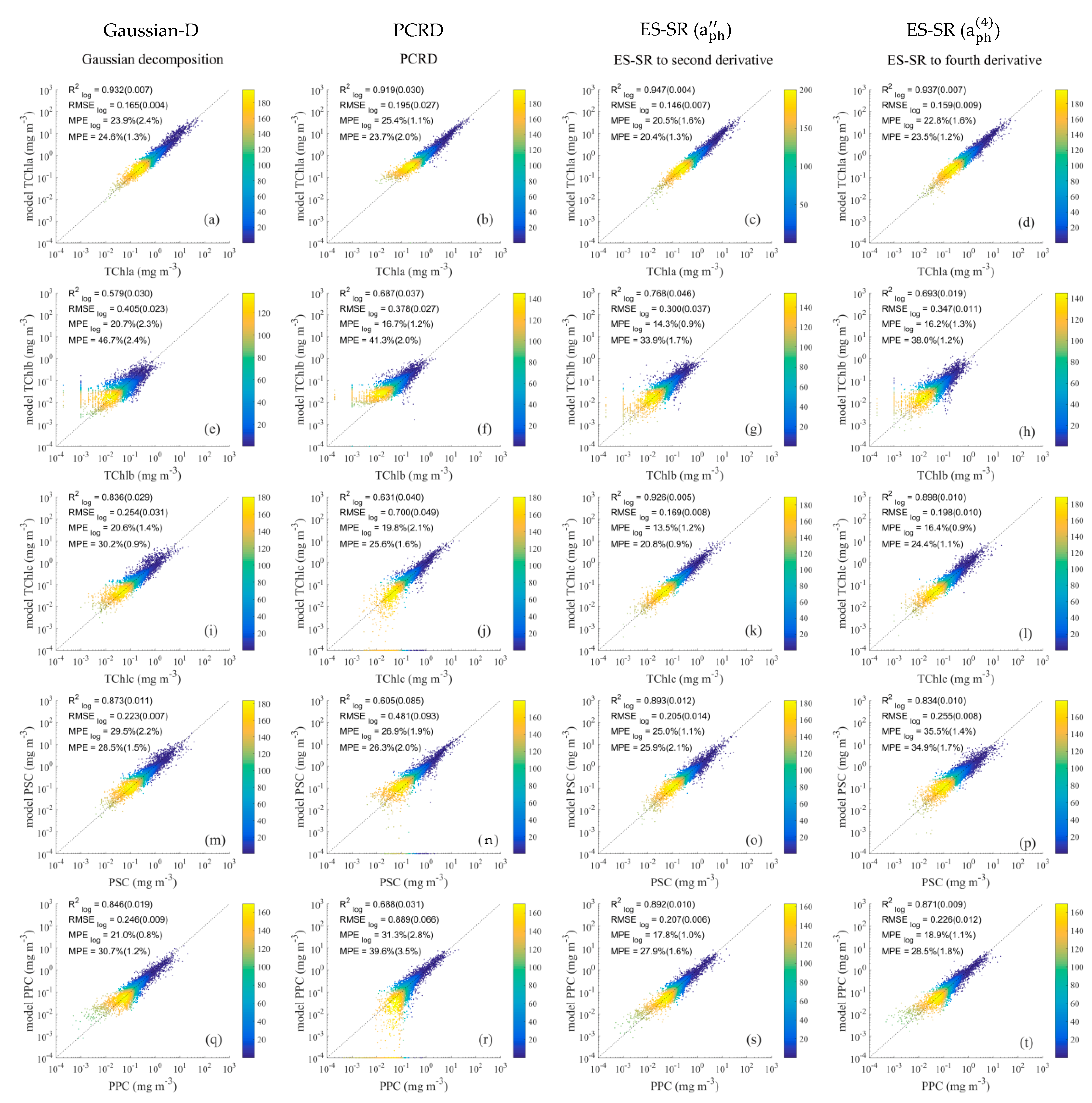
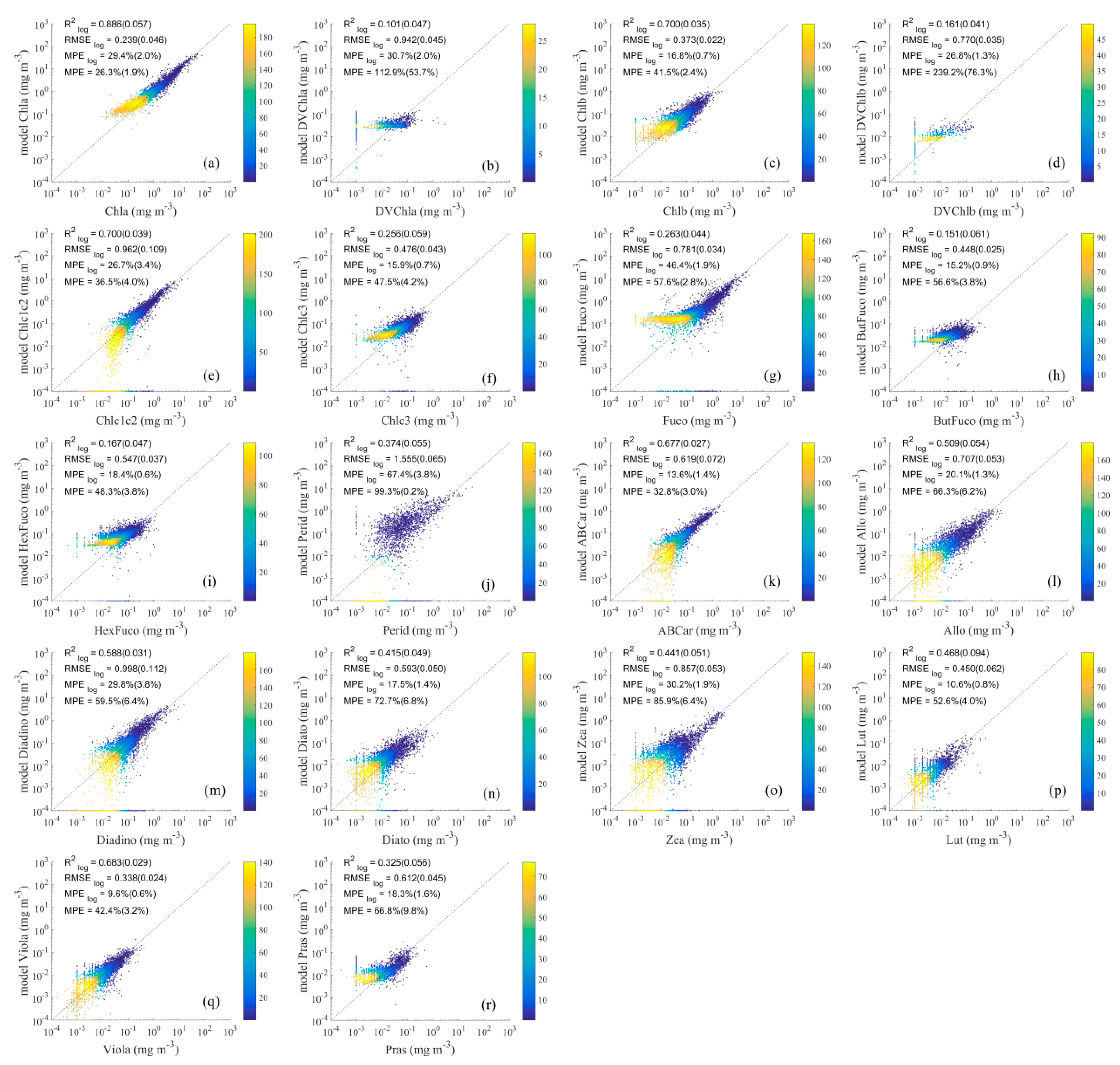
4.2. Result Comparison
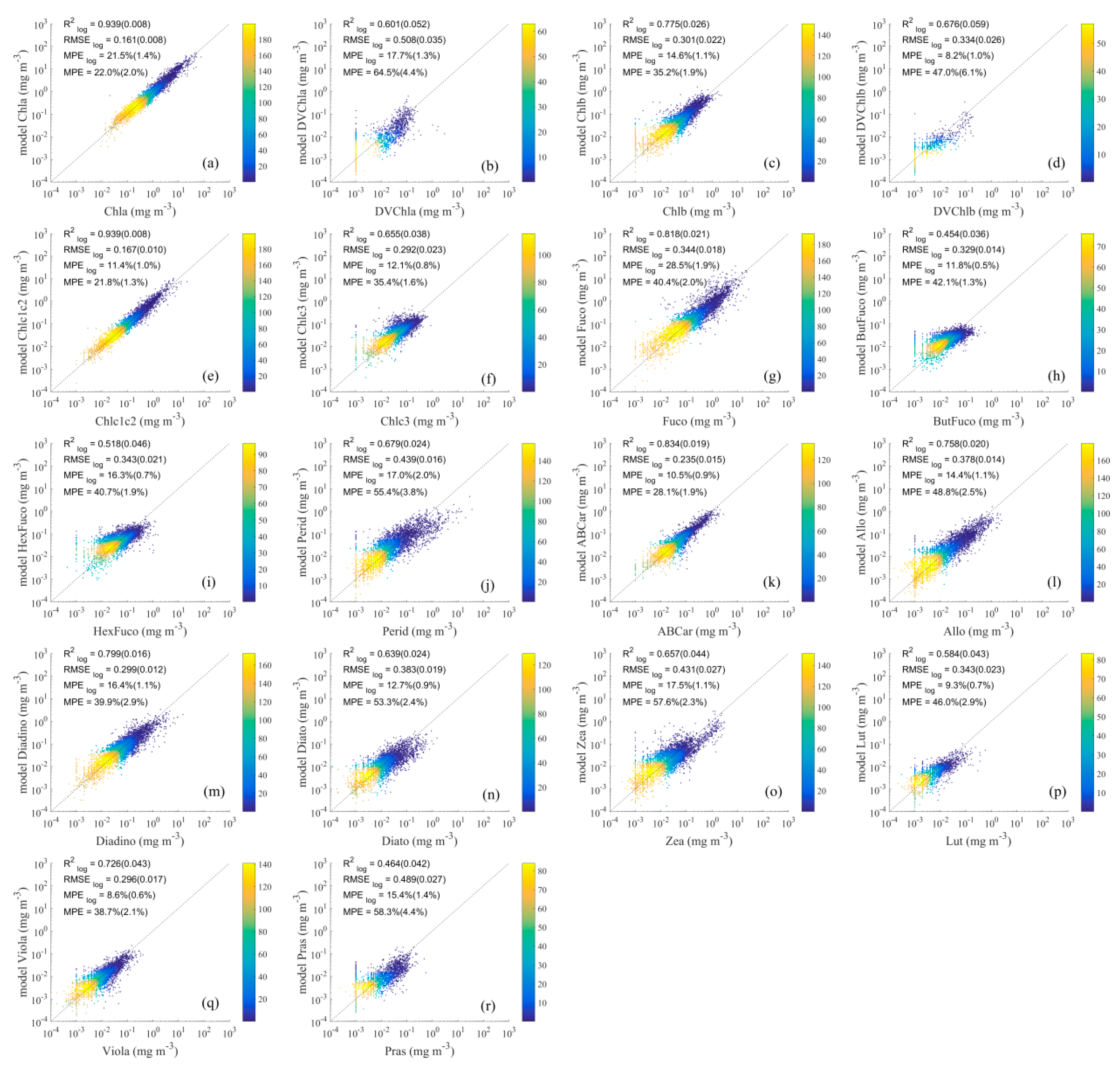
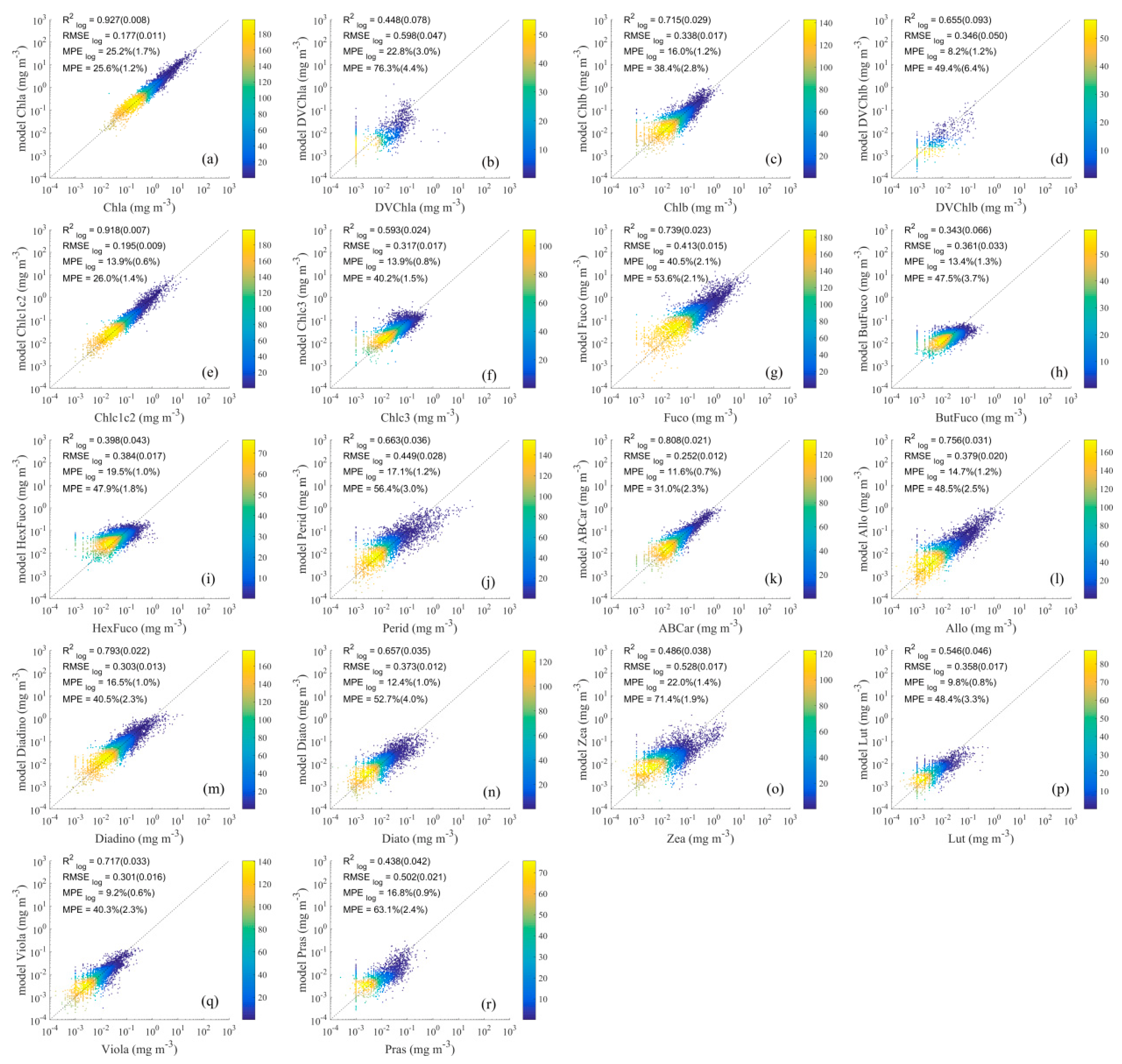
4.2.1. Results of Pigment Group Comparison
4.2.2. Results of Detailed Pigment Comparison
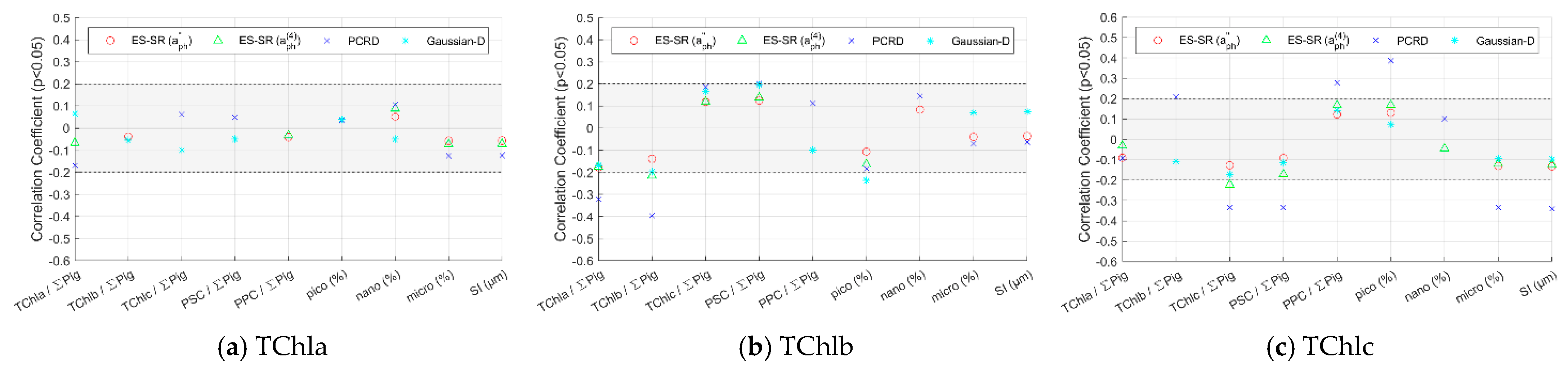
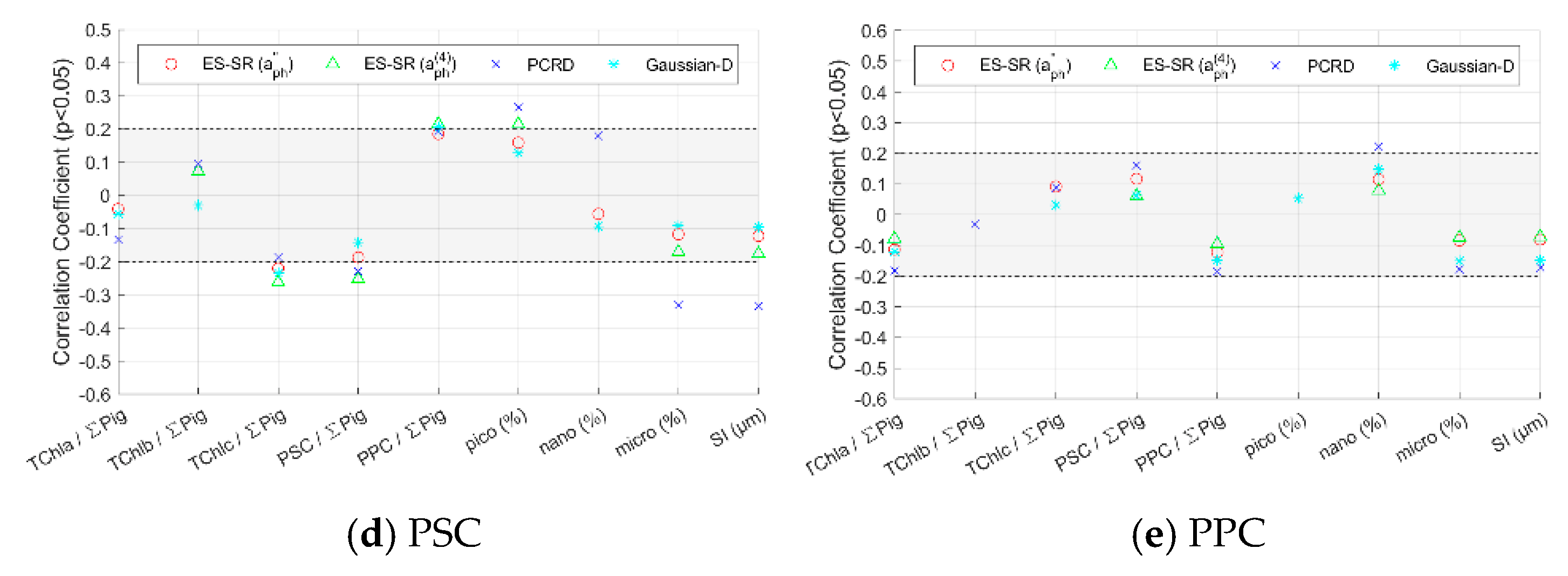
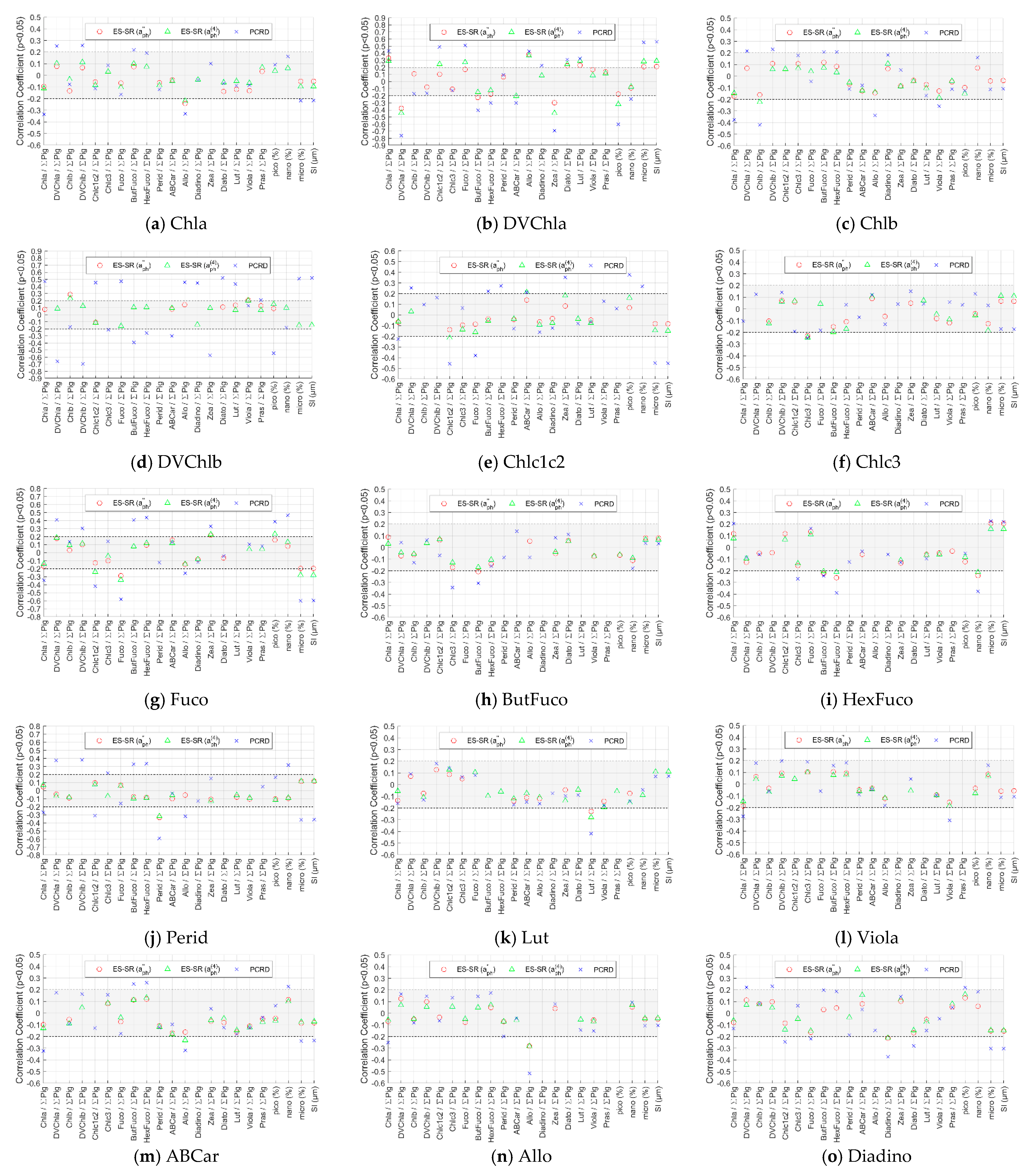
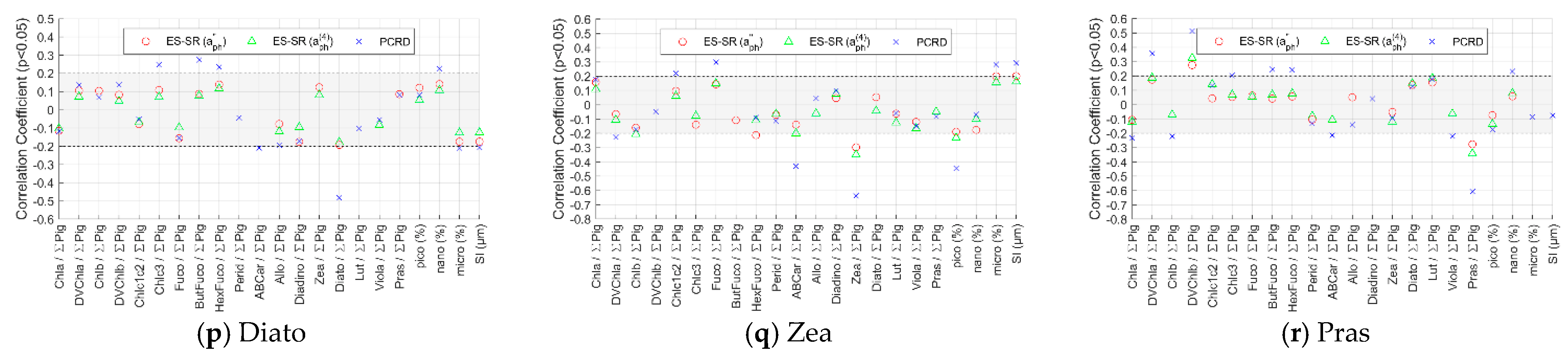
4.3. Effects of Impact Factors on Inversion Methods
4.3.1. Methods Evaluation for Pigment Groups Based on Impact Factors
4.3.2. Methods Evaluation for Detailed Pigments Based on Impact Factors
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Information on Phytoplankton Pigments
| Abbreviation | Pigment (Pigment Group) | Taxonomic Distribution (Corresponding Phytoplankton Groups) |
|---|---|---|
| TChla | Total chlorophyll a (TChla = Chla + DVChla + Chlorophyllide a) | All taxa |
| Chla | chlorophyll a | All taxa, with the exception of some cyanobacteria |
| DVChla | Divinyl chlorophyll a | Cyanobacteria, prochlorophytes |
| TChlb | Total chlorophyll b (TChlb = Chlb + DVChlb) | Prochlorophytes, cyanobacteria, chlorarachniophytes, mesostigmatophytes, chlorophytes, prasinophytes, green algae, euglenophytes, dinoflagellates |
| Chlb | chlorophyll b | Prochlorophytes, cyanobacteria, chlorarachniophytes, mesostigmatophytes, chlorophytes, prasinophytes, green algae, euglenophytes, dinoflagellates |
| DVChlb | Divinyl chlorophyll b | Prochlorophytes |
| TChlc | Total chlorophyll c (TChlc = Chlc1c2 + Chlc3) | All red algae except rhodophytes and eustigmatophytes |
| Chlc1c2 | Chlorophylls c1 and c2 | Diatoms, chrysophytes, cryptophytes, dictyophytes, pelagophytes, raphidophytes, synurophytes, haptophytes, dinoflagellates |
| Chlc3 | Chlorophyll c3 | Diatoms, dictyophytes, pelagophytes, haptophytes, dinoflagellates |
| Fuco | Fucoxanthin | Diatoms, bolidophytes, chrysophytes, dictyophytes, pelagophytes, raphidophytes, silicoflagellates, phaetamniophytes, pinguiophytes, synurophytes, haptophytes, dinoflagellates |
| ButFuco | 19′-Butanoyloxyfucoxanthin | Diatoms, dictyophytes, raphidophytes, silicoflagellates, pelagophytes, chrysophytes, dinoflagellates, haptophytes |
| HexFuco | 19′-Hexanoyloxyfucoxanthin | Haptophytes, dinoflagellates |
| Perid | Peridinin | Dinoflagellates (Not all pigmented dinoflagellates contain peridinin.) |
| ABCar | Alpha-beta-carotene (β, β-carotene + β, ε-carotene) | All taxa |
| Allo | Alloxanthin | Cryptophytes, dinoflagellates, chlorophytes |
| Diadino | Diadinoxanthin | Diatoms, bolidophytes, dictyophytes, pelagophytes, xanthophytes, haptophytes, dinoflagellates, euglenophytes, |
| Zea | Zeaxanthin | Cyanobacteria, prochlorophytes, glaucocystophytes, rhodophytes, chrysophytes, eustigmatophytes, pinguiophytes, raphidophytes, pelagophytes, dinoflagellates, chlorarachniophytes, prasinophytes, chlorophytes, diatoms, dictyophytes |
| Diato | Diatoxanthin | Diatoms, bolidophytes, dictyophytes, pelagophytes, xanthophytes, haptophytes, dinoflagellates, euglenophytes |
| Lut | Lutein | Chlorarachniophytes, chlorophytes, prasinophytes, green algae, Mesostigmatophytes |
| Viola | Violaxanthin | Diatoms, dictyophytes, raphidophytes, synurophytes, mesostigmatophytes, green algae, prasinophytes, chlorophytes, chlorarachniophytes, dinoflagellates, eustigmatophytes, chrysophytes |
| Pras | Prasinoxanthin | Prasinophytes, dinoflagellates |
| PSC | Photosynthetic carotenoids (PSC = Fuco + ButFuco + HexFuco + Perid) | |
| PPC | Photoprotective carotenoids (PPC = Allo + Diadino + Diato + Zea + ABCar) | |
| Pig_sum (∑Pig) | The sum of pigments (Pig_sum = TChla + TChlb + TChlc + PSC + PPC + Lut + Viola + Pras) |
Appendix B. Analysis of Research Data
Appendix B.1. Phytoplankton Pigment Concentration Analysis
| Pigment | Min (mg m−3) | Max (mg m−3) | Mean (mg m−3) | Skew | Kurt | Skew (log10) | Kurt (log10) |
|---|---|---|---|---|---|---|---|
| Chla | 0 | 78.04 | 2.26 | 6.15 | 58.68 | −0.16 | −0.43 |
| DVChla | 0 | 3.00 | 0.01 | 31.15 | 1249.67 | 0.00 | −1.40 |
| Chlb | 0 | 2.32 | 0.10 | 4.09 | 33.40 | −0.76 | 0.52 |
| DVChlb | 0 | 0.19 | 0.00 | 9.39 | 102.29 | 0.40 | −0.34 |
| Chlc1c2 | 0 | 21.86 | 0.35 | 9.95 | 176.01 | −0.15 | −0.35 |
| Chlc3 | 0 | 0.86 | 0.07 | 2.46 | 10.56 | −0.69 | 0.55 |
| Fuco | 0 | 27.57 | 0.75 | 7.00 | 75.02 | −0.43 | −0.27 |
| ButFuco | 0 | 0.56 | 0.03 | 3.74 | 29.77 | −1.28 | 3.79 |
| HexFuco | 0 | 1.57 | 0.09 | 4.23 | 31.82 | −0.68 | 1.25 |
| Perid | 0 | 35.53 | 0.16 | 21.63 | 620.80 | −0.02 | 0.53 |
| ABCar | 0 | 2.83 | 0.09 | 5.36 | 44.80 | −0.18 | −0.01 |
| Allo | 0 | 2.48 | 0.06 | 6.51 | 62.07 | −0.35 | −0.18 |
| Diadino | 0 | 15.13 | 0.19 | 13.22 | 283.45 | −0.29 | 0.01 |
| Zea | 0 | 3.02 | 0.08 | 6.15 | 45.02 | −0.28 | 0.32 |
| Diato | 0 | 1.52 | 0.03 | 8.04 | 109.17 | −0.60 | 0.43 |
| Lut | 0 | 0.58 | 0.01 | 13.21 | 275.38 | −0.47 | −0.05 |
| Viola | 0 | 0.41 | 0.02 | 4.90 | 41.94 | −0.37 | −0.08 |
| Pras | 0 | 0.56 | 0.01 | 6.29 | 84.14 | −0.28 | −1.12 |
| TChla | 0.009 | 78.95 | 2.44 | 5.87 | 53.73 | −0.11 | −0.42 |
| TChlb | 0 | 2.32 | 0.11 | 3.91 | 30.18 | −0.77 | 0.53 |
| TChlc | 0 | 21.87 | 0.42 | 9.35 | 160.36 | −0.30 | −0.11 |
| PSC | 0 | 37.61 | 1.02 | 7.13 | 78.85 | −0.21 | −0.23 |
| PPC | 0 | 20.36 | 0.45 | 7.28 | 98.21 | −0.37 | 0.62 |
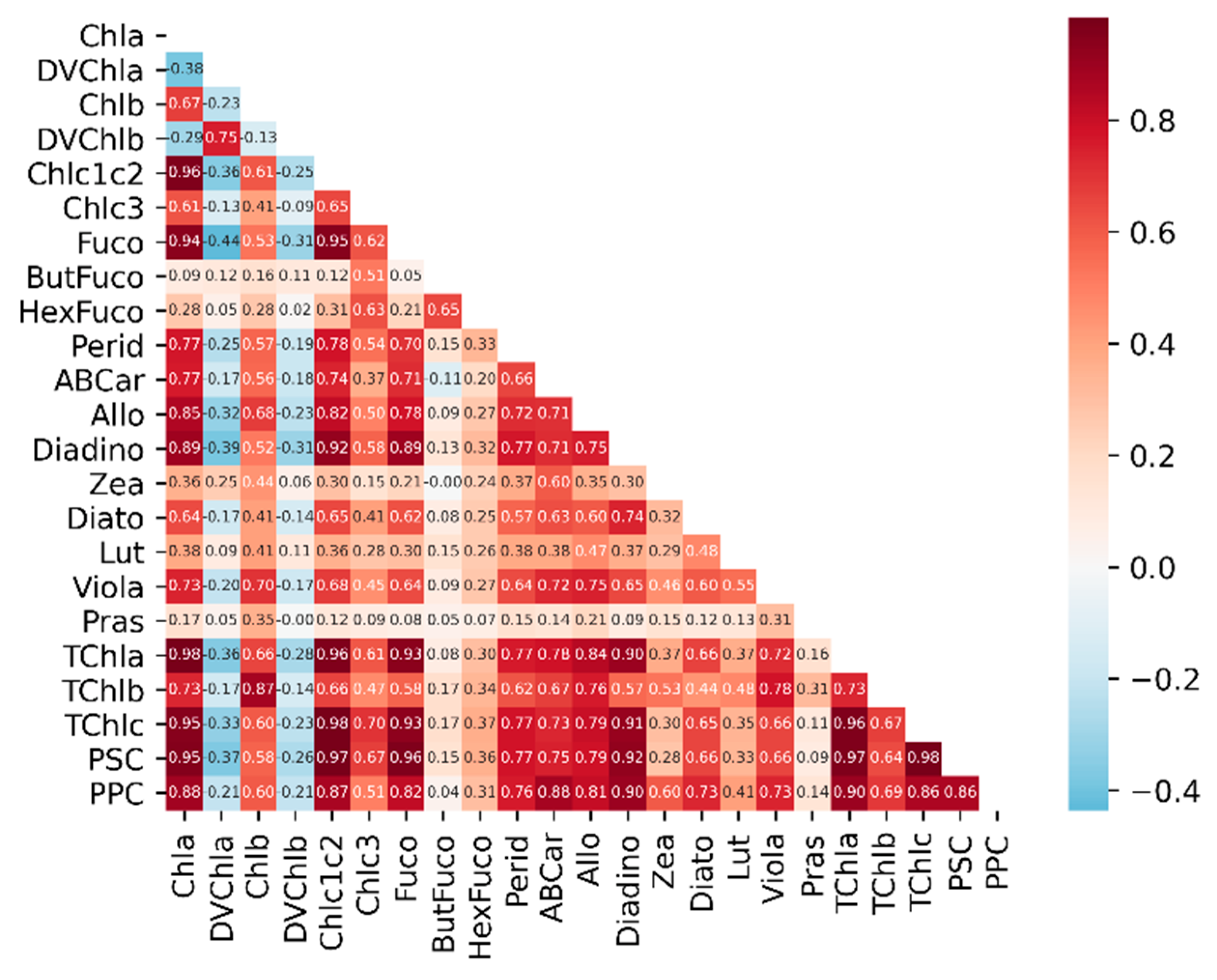
Appendix B.2. Correlation Coefficients of Phytoplankton Pigment Concentrations
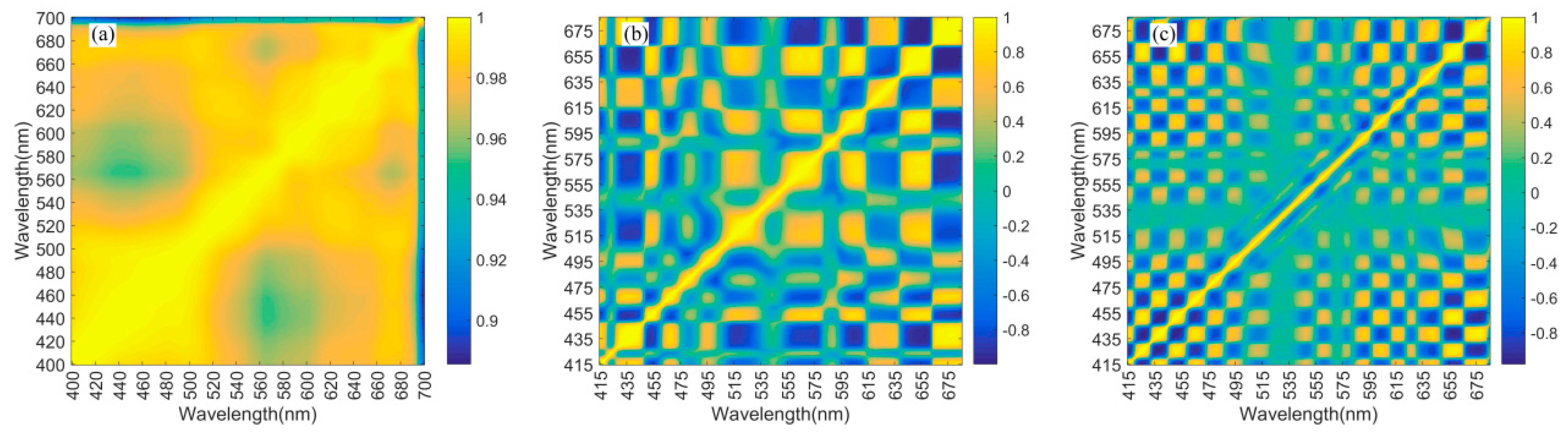
Appendix B.3. Correlation Coefficients of Phytoplankton Absorption and Derivative Spectra
Appendix C. Additional Information on Method Evaluation
Appendix C.1. Statistics
Appendix C.2. Comparison Methods
Appendix C.2.1. Gaussian Decomposition Method
Appendix C.2.2. PCRD Method
Appendix C.3. Impact Factors of the Inversion Method
References
- Behrenfeld, M.J.; Boss, E.; Siegel, D.A.; Shea, D.M. Carbon-based ocean productivity and phytoplankton physiology from space. Glob. Biogeochem. Cycles 2005, 19, GB1006. [Google Scholar] [CrossRef]
- Le Quéré, C.L.; Harrison, S.P.; Prentice, I.C.; Buitenhuis, E.T.; Aumont, O.; Bopp, L.; Claustre, H.; Cunha, L.C.D.; Geider, R.; Giraud, X.; et al. Ecosystem dynamics based on plankton functional types for global ocean biogeochemistry models. Glob. Chang. Biol. 2005, 11, 2016–2040. [Google Scholar]
- Nair, A.; Sathyendranath, S.; Platt, T.; Morales, J.; Stuart, V.; Forget, M.-H.; Devred, E.; Bouman, H. Remote sensing of phytoplankton functional types. Remote Sens. Environ. 2008, 112, 3366–3375. [Google Scholar] [CrossRef]
- Muller-Karger, F.; Kavanaugh, M.T.; Montes, E.; Balch, W.M.; Breitbart, M.; Chavez, F.P.; Doney, S.C.; Johns, E.M.; Letelier, R.M.; Lomas, M.W.; et al. A Framework for a Marine Biodiversity Observing Network within Changing Continental Shelf Seascapes. Oceanography 2014, 27, 18–23. [Google Scholar] [CrossRef][Green Version]
- Edwards, K.F.; Thomas, M.K.; Klausmeier, C.A.; Litchman, E. Phytoplankton growth and the interaction of light and temperature: A synthesis at the species and community level. Limnol. Oceanogr. 2016, 61, 1232–1244. [Google Scholar] [CrossRef]
- Chase, A.P.; Boss, E.; Cetinić, I.; Slade, W. Estimation of phytoplankton accessory pigments from hyperspectral reflectance spectra: Toward a global algorithm. J. Geophys. Res. Ocean. 2017, 122, 9725–9743. [Google Scholar] [CrossRef]
- IOCCG. Phytoplankton Functional Types from Space; Sathyendranath, S., Ed.; Reports of the International Ocean-Colour Coordinating Group, No. 15; IOCCG: Dartmouth, NS, Canada, 2014. [Google Scholar]
- Lorenzoni, L.; Toro-Farmer, G.; Varela, R.; Guzman, L.; Rojas, J.; Montes, E.; Muller-Karger, F. Characterization of phytoplankton variability in the Cariaco Basin using spectral absorption, taxonomic and pigment data. Remote Sens. Environ. 2015, 167, 259–268. [Google Scholar] [CrossRef]
- Catlett, D.; Siegel, D.A. Phytoplankton pigment communities can be modeled using unique relationships with spectral absorption signatures in a dynamic coastal environment. J. Geophys. Res. 2018, 123, 246–264. [Google Scholar] [CrossRef]
- Chase, A.; Boss, E.; Zaneveld, R.; Bricaud, A.; Claustre, H.; Ras, J.; Dall’Olmo, G.; Westberry, T.K. Decomposition of in situ particulate absorption spectra. Methods Oceanogr. 2013, 7, 110–124. [Google Scholar] [CrossRef]
- Bracher, A.; Bouman, H.A.; Brewin, R.J.W.; Bricaud, A.; Brotas, V.; Ciotti, A.M.; Clementson, L.; Devred, E.; Di Cicco, A.; Dutkiewicz, S.; et al. Obtaining Phytoplankton Diversity from Ocean Color: A Scientifific Roadmap for Future Development. Front. Mar. Sci. 2017, 4, 55. [Google Scholar] [CrossRef]
- Liu, Y.; Boss, E.; Chase, A.; Xi, H.; Zhang, X.; Röttgers, R.; Pan, Y.; Bracher, A. Retrieval of Phytoplankton Pigments from Underway Spectrophotometry in the Fram Strait. Remote Sens. 2019, 11, 318. [Google Scholar] [CrossRef]
- Dickey, T.; Lewis, M.; Chang, G. Optical oceanography: Recent advances and future directions using global remote sensing and in situ observations. Rev. Geophys. 2006, 44, RG1001. [Google Scholar] [CrossRef]
- Lee, Z.; Shang, S.; Hu, C.; Zibordi, G. Spectral interdependence of remote-sensing reflectance and its implications on the design of ocean color satellite sensors. Appl. Opt. 2014, 53, 3301–3310. [Google Scholar] [CrossRef]
- Uitz, J.; Stramski, D.; Reynolds, R.A.; Dubranna, J. Assessing phytoplankton community composition from hyperspectral measurements of phytoplankton absorption coefficient and remote-sensing reflectance in open-ocean environments. Remote Sens. Environ. 2015, 171, 58–74. [Google Scholar] [CrossRef]
- Garver, S.A.; Siegel, D.A. Inherent optical property inversion of ocean color spectra and its biogeochemical interpretation: 1. Time series from the Sargasso Sea. J. Geophy. Res. 1997, 102, 18607–18625. [Google Scholar] [CrossRef]
- Lee, Z.; Carder, K.L. Absorption spectrum of phytoplankton pigments derived from hyperspectral remote-sensing reflectance. Remote Sens. Environ. 2004, 89, 361–368. [Google Scholar] [CrossRef]
- Isada, T.; Hirawake, T.; Kobayashi, T.; Nosaka, Y.; Natsuike, M.; Imai, I.; Suzuki, K.; Saitoh, S.-I. Hyperspectral optical discrimination of phytoplankton community structure in Funka Bay and its implications for ocean color remote sensing of diatoms. Remote Sens. Environ. 2015, 159, 134–151. [Google Scholar] [CrossRef]
- Bidigare, R.R.; Morrow, J.H.; Kiefer, D.A. Derivative analysis of spectral absorption by photosynthetic pigments in the western Sargasso Sea. J. Mar. Res. 1989, 47, 323–341. [Google Scholar] [CrossRef]
- Staehr, P.A.; Cullen, J.J. Detection of Karenia mikimotoi by spectral absorption signatures. J. Plankton Res. 2003, 25, 1237–1249. [Google Scholar] [CrossRef]
- Devred, E.; Sathyendranath, S.; Stuart, V.; Maass, H.; Ulloa, O.; Platt, T. A two-component model of phytoplankton absorption in the open ocean: Theory and applications. J. Geophys. Res. 2006, 111, C03011. [Google Scholar] [CrossRef]
- Barlow, R.; Kyewalyanga, M.; Sessions, H.; van den Berg, M.; Morris, T. Phytoplankton pigments, functional types, and absorption properties in the Delagoa and Natal Bights of the Agulhas ecosystem. Estuar. Coast. Shelf Sci. 2008, 80, 201–211. [Google Scholar] [CrossRef]
- Moisan, J.R.; Moisan, T.A.H.; Linkswiler, M.A. An inverse modeling approach to estimating phytoplankton pigment concentrations from phytoplankton absorption spectra. J. Geophys. Res. 2011, 116, C09018. [Google Scholar] [CrossRef]
- Xi, H.; Hieronymi, M.; Röttgers, R.; Krasemann, H.; Qiu, Z. Hyperspectral Differentiation of Phytoplankton Taxonomic Groups: A Comparison between Using Remote Sensing Reflectance and Absorption Spectra. Remote Sens. 2015, 7, 14781–14805. [Google Scholar] [CrossRef]
- Organelli, E.; Nuccio, C.; Lazzara, L.; Uitz, J.; Bricaud, A.; Massi, L. On the discrimination of multiple phytoplankton groups from light absorption spectra of assemblages with mixed taxonomic composition and variable light conditions. Appl. Opt. 2017, 56, 3952–3968. [Google Scholar] [CrossRef]
- Mackey, M.D.; Mackey, D.J.; Higgins, H.W.; Wright, S.W. CHEMTAX—A program for estimating class abundances from chemical markers: Application to HPLC measurements of phytoplankton. Mar. Ecol. Prog. Ser. 1996, 144, 265–283. [Google Scholar] [CrossRef]
- Latasa, M. Improving estimations of phytoplankton class abundances using CHEMTAX. Mar. Ecol. Proj. Ser. 2007, 329, 13–21. [Google Scholar] [CrossRef]
- Sañé, E.; Valente, A.; Fatela, F.; Cabral, M.C.; Beltrán, C.; Drago, T. Assessment of sedimentary pigments and phytoplankton determined by CHEMTAX analysis as biomarkers of unusual upwelling conditions in summer 2014 off the SE coast of Algarve. J. Sea Res. 2019, 146, 33–45. [Google Scholar] [CrossRef]
- Jeffrey, S.W.; Mantoura, R.F.C.; Wright, S.W. Phytoplankton Pigments in Oceanography: Guidelines to Modern Methods, 1st ed.; UNESCO: Paris, France, 1997. [Google Scholar]
- Bricaud, A.; Claustre, H.; Ras, J.; Oubelkheir, K. Natural variability of phytoplanktonic absorption in oceanic waters: Influence of the size structure of algal populations. J. Geophys. Res. 2004, 109, C11010. [Google Scholar] [CrossRef]
- Uitz, J.; Claustre, H.; Morel, A.; Hooker, S.B. Vertical distribution of phytoplankton communities in open ocean: An assessment based on surface chlorophyll. J. Geophy. Res. 2006, 111, C08005. [Google Scholar] [CrossRef]
- Roy, S.; Llewellyn, C.; Egeland, E.S.; Johnsen, G. Phytoplankton Pigments: Characterization, Chemotaxonomy and Applications in Oceanography, 1st ed.; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Hoepffner, N.; Sathyendranath, S. Determination of the major groups of phytoplankton pigments from the absorption spectra of total particulate matter. J. Geophys. Res. 1993, 98, 22789–22803. [Google Scholar] [CrossRef]
- Wang, G.; Lee, Z.; Mouw, C.B. Concentrations of Multiple Phytoplankton Pigments in the Global Oceans Obtained from Satellite Ocean Color Measurements with MERIS. Appl. Sci. 2018, 8, 2678. [Google Scholar] [CrossRef]
- Moisan, T.A.; Moisan, J.R.; Linkswiler, M.A.; Steinhardt, R.A. Algorithm development for predicting biodiversity based on phytoplankton absorption. Cont. Shelf Res. 2013, 55, 17–28. [Google Scholar] [CrossRef]
- Kirkpatrick, G.J.; Millie, D.F.; Moline, M.A.; Schofield, O. Optical Discrimination of a Phytoplankton Species in Natural Mixed Populations. Limnol. Oceanogr. 2000, 45, 467–471. [Google Scholar] [CrossRef]
- Aguirre-Gómez, R.; Weeks, A.R.; Boxall, S. The identification of phytoplankton pigments from absorption spectra. Int. J. Remote Sens. 2001, 22, 315–338. [Google Scholar] [CrossRef]
- Craig, S.E.; Lohrenz, S.E.; Lee, Z.; Mahoney, K.L.; Kirkpatrick, G.J.; Schofield, O.M.; Steward, R.G. Use of hyperspectral remote sensing reflectance for detection and assessment of the harmful alga, Karenia brevis. Appl. Opt. 2006, 45, 5414–5425. [Google Scholar] [CrossRef]
- Lubac, B.; Loisel, H.; Guiselin, N.; Astoreca, R.; Artigas, L.F.; Mériaux, X. Hyperspectral and multispectral ocean color inversions to detect Phaeocystis globosa blooms in coastal waters. J. Geophys. Res. 2008, 113, C06026. [Google Scholar]
- Torrecilla, E.; Piera, J.; Vilasec, M. Derivative analysis of hyperspectral oceanographic data. In Advances in Geoscience and Remote Sensing; Jedlovec, G., Ed.; IntechOpen: London, UK, 2009; pp. 597–618. [Google Scholar]
- Torrecilla, E.; Stramski, D.; Reynolds, R.A.; Millán-Núñez, E.; Piera, J. Cluster analysis of hyperspectral optical data for discriminating phytoplankton pigment assemblages in the open ocean. Remote Sens. Environ. 2011, 115, 2578–2593. [Google Scholar] [CrossRef]
- Wolanin, A.; Soppa, M.; Bracher, A. Investigation of Spectral Band Requirements for Improving Retrievals of Phytoplankton Functional Types. Remote Sens. 2016, 8, 871. [Google Scholar] [CrossRef]
- Bidigare, R.R.; Ondrusek, M.E.; Morrow, J.H.; Kiefer, D.A. In-vivo absorption properties of algal pigments. Ocean Opt. X 1990, 1302, 290–302. [Google Scholar]
- Robinson, C.M.; Huot, Y.; Schuback, N.; Ryan-Keogh, T.J.; Thomalla, S.J.; Antoine, D. High latitude Southern Ocean phytoplankton have distinctive bio-optical properties. Opt. Express 2021, 29, 21084. [Google Scholar] [CrossRef]
- Allali, K.; Bricaud, A.; Claustre, H. Spatial variations in the chlorophyll-specific absorption coefficients of phytoplankton and photosynthetically active pigments in the equatorial Pacific. J. Geophys. Res. 1997, 102, 12413–12423. [Google Scholar] [CrossRef]
- Stuart, V.; Sathyendranath, S.; Platt, T.; Maass, H.; Irwin, B.D. Pigments and species composition of natural phytoplankton populations: Effect on the absorption spectra. J. Plankton Res. 1998, 20, 187–217. [Google Scholar] [CrossRef]
- Whittingham, M.J.; Stephens, P.A.; Bradbury, R.B.; Freckleton, R.P. Why do we still use stepwise modelling in ecology and behaviour? J. Anim. Ecol. 2006, 75, 1182–1189. [Google Scholar] [CrossRef]
- Prost, L.; Makowski, D.; Jeuffroy, M.-H. Comparison of stepwise selection and Bayesian model averaging for yield gap analysis. Ecol. Model. 2008, 219, 66–76. [Google Scholar] [CrossRef]
- Smith, D. Step away from stepwise. J. Big Data 2018, 5, 32. [Google Scholar] [CrossRef]
- Werdell, P.J.; Bailey, S.; Fargion, G.; Pietras, C.; Knobelspiesse, K.; Feldman, G.; McClain, C. Unique data repository facilitates ocean color satellite validation. Eos Trans. Am. Geophys. Union 2003, 84, 377–387. [Google Scholar] [CrossRef]
- Hirata, T.; Aiken, J.; Hardman-Mountford, N.; Smyth, T.J.; Barlow, R.G. An absorption model to determine phytoplankton size classes from satellite ocean colour. Remote Sens. Environ. 2008, 112, 3153–3159. [Google Scholar] [CrossRef]
- Specific Criteria of SeaBASS Data. Available online: https://seabass.gsfc.nasa.gov (accessed on 30 December 2018).
- Kishino, M.; Takahashi, M.; Okami, N.; Ichimura, S. Estimation of the Spectral Absorption Coefficients of Phytoplankton in the Sea. Bull. Mar. Sci. 1985, 37, 634–642. [Google Scholar]
- Clementson, L.A.; Wojtasiewicz, B. Dataset on the in vivo absorption characteristics and pigment composition of various phytoplankton species. Data Brief 2019, 25, 104020. [Google Scholar] [CrossRef]
- Kim, T.; White, H. On More Robust Estimation of Skewness and Kurtosis: Simulation and Application to the S&P500 Index; Department of Economics, UCSD, UC: San Diego, CA, USA, 2003. [Google Scholar]
- Kim, H.-Y. Statistical notes for clinical researchers: Assessing normal distribution (2) using skewness and kurtosis. Restor. Dent. Endod. 2013, 38, 52–54. [Google Scholar] [CrossRef]
- Calude, C.S.; Longo, G. The Deluge of Spurious Correlations in Big Data. Found. Sci. 2016, 22, 595–612. [Google Scholar] [CrossRef]
- Ginzburg, L.R.; Jensen, C.X.J. Rules of thumb for judging ecological theories. Trends Ecol. Evol. 2004, 19, 121–126. [Google Scholar] [CrossRef]
- Guthery, F.S.; Brennan, L.A.; Peterson, M.J.; Lusk, J.J. Information theory in wildlife science: Critique and viewpoint. J. Wildl. Manag. 2005, 69, 457–465. [Google Scholar] [CrossRef]
- Finnoff, W.; Hergert, F.; Zimmermann, H.G. Improving model selection by nonconvergent methods. Neural Netw. 1993, 6, 771–783. [Google Scholar] [CrossRef]
- Prechelt, L. Automatic early stopping using cross validation: Quantifying the criteria. Neural Netw. 1998, 11, 761–767. [Google Scholar] [CrossRef]
- Dodge, J.; Ilharco, G.; Schwartz, R.; Farhadi, A.; Hajishirzi, H.; Smith, N. Fine-Tuning Pretrained Language Models: Weight Initializations, Data Orders, and Early Stopping. arXiv 2020, arXiv:2002.06305. [Google Scholar]
- Simon, R. Resampling strategies for model assessment and selection. In Fundamentals of Data Mining in Genomics and Proteomics; Dubitzky, W., Granzow, M., Berrar, D., Eds.; Springer: Boston, MA, USA, 2007; pp. 173–186. [Google Scholar]
- Berrar, D. Cross-Validation. In Encyclopedia of Bioinformatics and Computational Biology; Ranganathan, S., Gribskov, M., Nakai, K., Schönbach, C., Eds.; Elsevier Inc.: Cambridge, UK, 2019; pp. 542–545. [Google Scholar]
- Hoepffner, N.; Sathyendranath, S. Effect of pigment composition on absorption properties of phytoplankton. Mar. Ecol. Prog. Ser. 1991, 73, 11–23. [Google Scholar] [CrossRef]
- Massy, W.F. Principal components regression in exploratory statistical research. J. Am. Stat. Assoc. 1965, 60, 234–256. [Google Scholar] [CrossRef]
- Vidussi, F.; Claustre, H.; Manca, B.B.; Luchetta, A.; Marty, J.-C. Phytoplankton pigment distribution in relation to upper thermocline circulation in the eastern Mediterranean Sea during winter. J. Geophy. Res. 2001, 106, 19939–19956. [Google Scholar] [CrossRef]
- Higgins, H.W.; Wright, S.W.; Schlüter, L. Quantitative interpretation of chemotaxonomic pigment data. In Phytoplankton Pigments: Characterization, Chemotaxonomy and Applications in Oceanography; Roy, S., Llewellyn, C., Egeland, E., Johnsen, G., Eds.; Cambridge University Press: Cambridge, UK, 2011; pp. 257–313. [Google Scholar]
- Suzuki, K.; Kishino, M.; Sasaoka, K.; Saitoh, S.; Saino, T. ChlorophylI-specific absorption coefficients and pigments of phytoplankton off Sanriku, Northwestern North Pacific. J. Oceanogr. 1998, 54, 517–526. [Google Scholar] [CrossRef]
- Longhurst, A.R. Ecological Geography of the Sea, 2nd ed.; Academic Press: New York, USA, 2007. [Google Scholar]
- Blondeau-Patissier, D.; Gower, J.F.R.; Dekker, A.G.; Phinn, S.R.; Brando, V.E. A review of ocean color remote sensing methods and statistical techniques for the detection, mapping and analysis of phytoplankton blooms in coastal and open oceans. Prog. Oceanogr. 2014, 123, 123–144. [Google Scholar] [CrossRef]
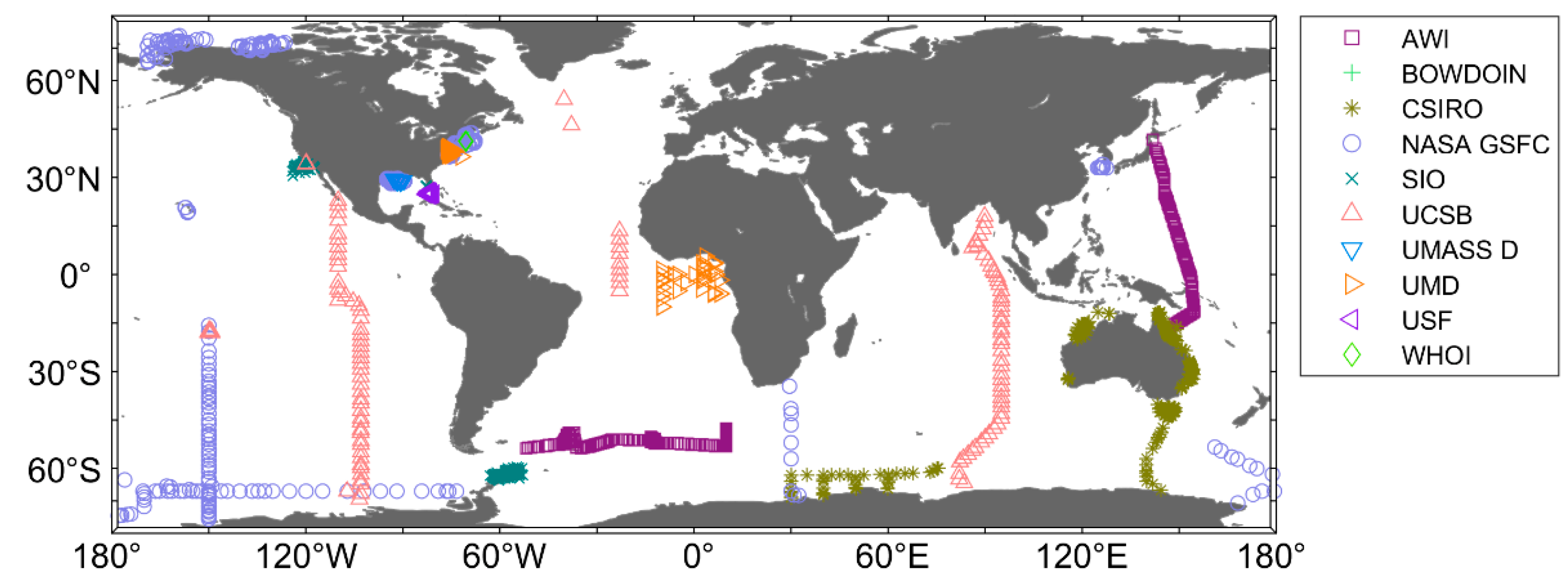
| Institution | Time | Size (N) | Depth (m) |
|---|---|---|---|
| AWI | 2009–2012 | 281 | 0–12 |
| BOWDOIN | 2011–2011 | 26 | 0.5–10 |
| CSIRO | 1997–2010 | 629 | 0–150 |
| NASA GSFC | 2005–2014 | 906 | 0–140 |
| SIO | 2004–2008 | 889 | 0–200 |
| UCSB | 2003–2017 | 803 | 0–150 |
| UMASS D | 2008–2008 | 16 | 1–30 |
| UMD | 1996–2007 | 328 | 0–80 |
| USF | 2012–2016 | 48 | 0.5–30 |
| WHOI | 2006–2014 | 678 | 0–40 |
| Pigment (Pigment Group) | Wavelength (nm) |
|---|---|
| TChla, Chla, DVChla | 415–475, 570–685 |
| TChlb, Chlb, DVChlb | 415–515, 575–685 |
| TChlc, Chlc1c2, Chlc3 | 415–505, 538–660 |
| PSC, Fuco, ButFuco, HexFuco, Perid | 415–590 |
| PPC, Allo, Diadino, Diato, Zea, ABCar, Lut, Viola | 415–535 |
| Pras | 415–560 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Teng, J.; Zhang, T.; Sun, K.; Gao, H. Retrieving Pigment Concentrations Based on Hyperspectral Measurements of the Phytoplankton Absorption Coefficient in Global Oceans. Remote Sens. 2022, 14, 3516. https://doi.org/10.3390/rs14153516
Teng J, Zhang T, Sun K, Gao H. Retrieving Pigment Concentrations Based on Hyperspectral Measurements of the Phytoplankton Absorption Coefficient in Global Oceans. Remote Sensing. 2022; 14(15):3516. https://doi.org/10.3390/rs14153516
Chicago/Turabian StyleTeng, Jing, Tinglu Zhang, Kunpeng Sun, and Hong Gao. 2022. "Retrieving Pigment Concentrations Based on Hyperspectral Measurements of the Phytoplankton Absorption Coefficient in Global Oceans" Remote Sensing 14, no. 15: 3516. https://doi.org/10.3390/rs14153516
APA StyleTeng, J., Zhang, T., Sun, K., & Gao, H. (2022). Retrieving Pigment Concentrations Based on Hyperspectral Measurements of the Phytoplankton Absorption Coefficient in Global Oceans. Remote Sensing, 14(15), 3516. https://doi.org/10.3390/rs14153516







