Analysis of PM2.5 Variations Based on Observed, Satellite-Derived, and Population-Weighted Concentrations
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data Collection and Pre-Processing
2.2.1. In Situ Site-Based PM2.5 Measurements
2.2.2. Satellite AOD
2.2.3. PM2.5 Emission Data
2.2.4. PM2.5 Dispersion Conditions Data
2.3. TSAM Modeling
2.3.1. Structure of the TSAM Model
2.3.2. TSAM Model Fitting, Validation, and Prediction
2.4. Calculation of Population-Weighted PM2.5 Concentration
3. Results
3.1. Analysis of TSAM Model Structure
3.2. Fitting and Validation of TSAM Models
3.3. Temporal Variations in Observed and TSAM-Derived PM2.5
3.4. Spatial Variations in TSAM-Derived PM2.5
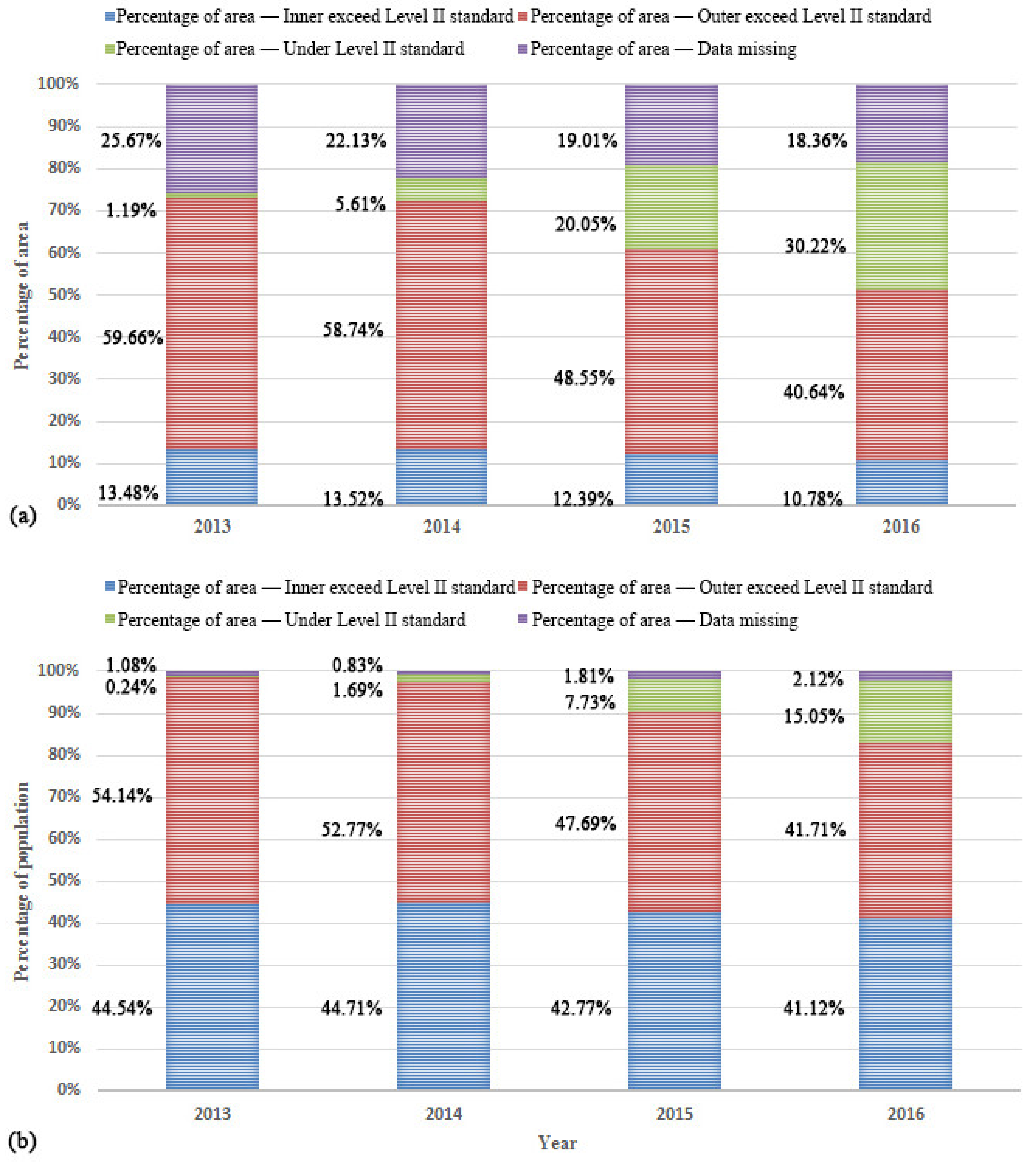
3.5. PM2.5 Variation Analysis Based on Percentage of Area and Population
3.6. Comparison between Observed and Population-Weighted PM2.5 Values for Key Regions
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Emmanuela, G.; Ashkan, A.; Amanuel, A.A.; Kalkidan, H.A.; Cristiana, A.; Kaja, M.A.; Foad, A.; Abdishakur, M.A.; Semaw, F.A.; Victor, A. Global, regional, and national comparative risk assessment of 84 behavioural, environmental and occupational, and metabolic risks or clusters of risks, 1990–2016: A systematic analysis for the Global Burden of Disease Study 2016. Lancet 2017, 390, 1345–1422. [Google Scholar]
- Lelieveld, J.; Evans, J.S.; Fnais, M.; Giannadaki, D.; Pozzer, A.A. The contribution of outdoor air pollution sources to premature mortality on a global scale. Nature 2017, 525, 367–371. [Google Scholar] [CrossRef] [PubMed]
- Yin, P.; Brauer, M.; Cohen, A.; Burnett, R.T.; Liu, J.; Liu, Y.; Liang, R.; Wang, W.; Qi, J.; Wang, L.; et al. Long-term fine particulate matter exposure and nonaccidental and cause-specific mortality in a large national cohort of Chinese men. Environ. Health Perspect. 2017, 125, 117002. [Google Scholar] [CrossRef] [PubMed]
- Shen, M.; Gu, X.; Li, S.; Yu, Y.; Zou, B.; Chen, X. Exposure to black carbon is associated with symptoms of depression: A retrospective cohort study in college students. Environ. Int. 2021, 157, 106870. [Google Scholar] [CrossRef]
- Varotsos, C.; Tzanis, C.; Cracknell, A. The enhanced deterioration of the cultural heritage monuments due to air pollution. Environ. Sci. Pollut. Res. 2009, 16, 590–592. [Google Scholar] [CrossRef]
- Van Donkelaar, A.; Martin, R.V.; Brauer, M.; Kahn, R.; Levy, R.; Verduzco, C.; Villeneuve, P.J. Global estimates of ambient fine particulate matter concentrations from satellite-based aerosol optical depth: Development and application. Enivron. Health Persp. 2010, 118, 847. [Google Scholar] [CrossRef] [Green Version]
- Zhao, P.; Zhang, X.; Xu, X.; Zhao, X. Long-term visibility trends and characteristics in the region of Beijing, Tianjin, and Hebei, China. Atmos. Res. 2011, 101, 711–718. [Google Scholar] [CrossRef]
- Brimblecombe, P. Visibility Driven Perception and Regulation of Air Pollution in Hong Kong, 1968–2020. Environments 2021, 8, 51. [Google Scholar] [CrossRef]
- Liu, Z.; Qi, Z.; Ni, X.; Dong, M.; Ma, M.; Xue, W.; Zhang, Q.; Wang, J. How to apply O3 and PM2.5 collaborative control to practical management in China: A study based on meta-analysis and machine learning. Sci. Total Environ. 2021, 772, 145392. [Google Scholar] [CrossRef]
- Liu, Z.; Xue, W.; Ni, X.; Qi, Z.; Zhang, Q.; Wang, J. Fund gap to high air quality in China: A cost evaluation for PM2.5 abatement based on the Air Pollution Prevention and control Action Plan. J. Clean. Prod. 2021, 319, 128715. [Google Scholar] [CrossRef]
- Shi, W.; Bi, J.; Liu, R.; Liu, M.; Ma, Z. Decrease in the chronic health effects from PM2.5 during the 13th Five-Year Plan in China: Impacts of air pollution control policies. J. Clean. Prod. 2021, 317, 128433. [Google Scholar] [CrossRef]
- Van Donkelaar, A.; Martin, R.V.; Spurr, R.J.D.; Burnett, R.T. High-resolution satellite-derived PM2.5 from optimal estimation and geographically weighted regression over north America. Environ. Sci. Tech. 2015, 49, 10482–10491. [Google Scholar] [CrossRef]
- Rohde, R.A.; Muller, R.A. Air pollution in China: Mapping of concentrations and sources. PLoS ONE. 2015, 10, e0135749. [Google Scholar] [CrossRef]
- Zou, B.; Luo, Y.; Wan, N.; Zheng, Z.; Sternberg, T.; Liao, Y. Performance comparison of LUR and OK in PM2.5 concentration mapping: A multidimensional perspective. Sci. Rep. 2015, 5, 8698. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; Christakos, G. Spatiotemporal characterization of ambient PM2.5 concentration in Shandong province (China). Environ. Sci. Tech. 2015, 49, 13431–13438. [Google Scholar] [CrossRef]
- Di, Q.; Kloog, I.; Koutrakis, P.; Lyapustin, A.; Wang, Y.; Schwartz, J. Assessing PM2.5 exposures with high spatiotemporal resolution across the continental United States. Envion. Sci. Tech. 2016, 50, 4712–4721. [Google Scholar] [CrossRef] [Green Version]
- Lee, H.J.; Chatfield, R.B.; Strawa, A.W. Enhancing the applicability of satellite remote sensing for PM2.5 estimation using MODIS deep blue AOD and land use regression in California, United States. Environ. Sci. Tech. 2016, 50, 6546–6555. [Google Scholar] [CrossRef]
- Cracknell, A.P.; Varotsos, C.A. New aspects of global climate-dynamics research and remote sensing. Int. J. Remote Sens. 2011, 32, 579–600. [Google Scholar] [CrossRef]
- Kahn, R.; Banerjee, P.; McDonald, D.; Diner, D.J. Sensitivity of multiangle imaging to aerosol optical depth, and to pure-particle size distribution and composition over ocean. J. Geophys. Res. Atmos. 1998, 103, 32195–32213. [Google Scholar] [CrossRef]
- Kahn, R.; Banerjee, P.; McDonald, D. Sensitivity of multiangle imaging to natural mixtures of aerosols over ocean. J. Geophys. Res. Atmos. 2001, 106, 18219–18238. [Google Scholar] [CrossRef] [Green Version]
- Ma, Z.; Hu, X.; Huang, L.; Bi, J.; Liu, Y. Estimating ground-level PM2.5 in China using satellite remote sensing. Environ. Sci. Tech. 2014, 48, 7436–7444. [Google Scholar] [CrossRef]
- Fang, X.; Zou, B.; Liu, X.; Sternberg, T.; Zhai, L. Satellite-based ground PM2.5 estimation using timely structure adaptive modeling. Remote Sens. Enivron. 2016, 186, 152–163. [Google Scholar] [CrossRef]
- Wang, J.; Christopher, S.A. Intercomparison between satellite-derived ground-level fine aerosol optical thickness and PM2.5 mass: Implications for air quality studies. Geophys. Res. Lett. 2003, 30, 2067–2283. [Google Scholar] [CrossRef]
- Liu, Y.; Sarnat, J.A.; Kilaru, V.; Jacob, D.J.; Koutrakis, P. Estimating ground-level PM2.5 in the eastern United States using satellite remote sensing. Environ. Sci. Tech. 2005, 39, 3269–3278. [Google Scholar] [CrossRef] [Green Version]
- Zou, B.; Pu, Q.; Bilal, M.; Weng, Q.; Zhai, L.; Nichol, J.E. High-resolution satellite mapping of fine particulates based on geographically weighted regression. IEEE Geosci. Remote Sens. Lett. 2016, 13, 495–499. [Google Scholar] [CrossRef]
- Ma, Z.; Liu, Y.; Zhao, Q.; Liu, M.; Zhou, Y.; Bi, J. Satellite-derived high resolution PM2.5 concentrations in Yangtze River Delta region of China using improved linear mixed effects model. Atmos. Environ. 2016, 133, 156–164. [Google Scholar] [CrossRef]
- Pu, Q.; Yoo, E. Spatio-temporal modeling of PM2.5 concentrations with missing data problem: A case study in Beijing, China. Int. J. Geogr. Inf. Sci. 2020, 34, 423–447. [Google Scholar] [CrossRef]
- Zou, B.; Wang, M.; Wan, N.; Wilson, J.G.; Fang, X.; Tang, Y. Spatial modeling of PM2.5 concentrations with a multifactorial radial basis function neural network. Environ. Sci. Pollut. Res. 2015, 22, 10395–10404. [Google Scholar] [CrossRef]
- Chen, Z.Y.; Zhang, T.-H.; Zhang, R.; Zhu, Z.-M.; Yang, J.; Chen, P.-Y.; Ou, C.-Q.; Guo, Y. Extreme gradient boosting model to estimate PM2.5 concentrations with missing-filled satellite data in China. Atmos. Environ. 2019, 202, 180–189. [Google Scholar] [CrossRef]
- Yan, X.; Zang, Z.; Luo, N.; Jiang, Y.; Li, Z. New interpretable deep learning model to monitor real-time PM2.5 concentrations from satellite data. Environ. Int. 2020, 144, 106060. [Google Scholar] [CrossRef]
- Hu, H.Y. The distribution of population in China, with statistics and maps. Acta Geograph. Sin. 1935, 2, 33–74. (In Chinese) [Google Scholar] [CrossRef]
- Lee, H.J.; Liu, Y.; Coull, B.A.; Schwartz, J.; Koutrakis, P. A novel calibration approach of MODIS AOD data to predict PM2.5 concentrations. Atmos. Chem. Phys. 2011, 11, 7991–8002. [Google Scholar] [CrossRef] [Green Version]
- Puttaswamy, S.J.; Nguyen, H.M.; Braverman, A.; Hu, X.; Liu, Y. Statistical data fusion of multi-sensor AOD over the Continental United States. Geocarto. Int. 2014, 29, 48–64. [Google Scholar] [CrossRef]
- Tian, J.; Chen, D. A semi-empirical model for predicting hourly ground-level fine particulate matter (PM2.5) concentration in southern Ontario from satellite remote sensing and ground-based meteorological measurements. Remote Sens. Environ. 2010, 114, 221–229. [Google Scholar] [CrossRef]
- Rodriguez, J.D.; Perez, A.; Lozano, J.A. Sensitivity analysis of k-fold cross validation in prediction error estimation. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 569–575. [Google Scholar] [CrossRef]
- Zou, B.; Zeng, Y.; Zhan, F.B.; Charles, Y.; Liu, X. Performance of kriging and EWPM for relative air pollution exposure risk assessment. Int. J. Environ. Res. 2011, 5, 769–778. [Google Scholar]
- Ma, Z.; Hu, X.; Sayer, A.M.; Levy, R.; Zhang, Q.; Xue, Y.; Tong, S.; Bi, J.; Huang, L.; Liu, Y. Satellite-based spatiotemporal trends in PM2.5 concentrations: China, 2004–2013. Environ. Health Perspect. 2016, 124, 184–192. [Google Scholar] [CrossRef] [Green Version]
- Li, T.; Shen, H.; Zeng, C.; Yuan, Q.; Zhang, L. Point-surface fusion of station measurements and satellite observations for mapping PM2.5 distribution in China: Methods and assessment. Atmos. Environ. 2017, 152, 477–489. [Google Scholar] [CrossRef] [Green Version]



| Fitting | Cross-Validation | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Year | Season | N | Mean | RMSE | MPE | RPE | RMPE | RMSE | MPE | RPE | RMPE |
| 2013 | Spring | 6451 | 66.80 | 14.58 | 10.55 | 21.04% | 15.79% | 16.82 | 12.84 | 25.18% | 19.22% |
| Summer | 7133 | 47.54 | 12.97 | 9.45 | 27.28% | 19.87% | 14.92 | 11.02 | 31.38% | 23.18% | |
| Autumn | 11,958 | 70.79 | 16.16 | 12.25 | 22.83% | 17.31% | 18.38 | 14.16 | 25.97% | 20.00% | |
| Winter | 11,593 | 94.39 | 18.23 | 14.43 | 19.31% | 15.29% | 20.48 | 16.42 | 21.69% | 17.39% | |
| 2014 | Spring | 16,972 | 61.56 | 14.57 | 11.25 | 23.67% | 18.27% | 16.19 | 12.65 | 26.29% | 20.54% |
| Summer | 14,147 | 49.26 | 12.99 | 9.91 | 26.37% | 20.11% | 14.53 | 11.24 | 29.49% | 22.83% | |
| Autumn | 17,574 | 57.20 | 14.58 | 11.12 | 25.50% | 19.45% | 16.42 | 12.70 | 28.71% | 22.21% | |
| Winter | 18,123 | 69.73 | 15.86 | 12.71 | 22.75% | 18.22% | 17.33 | 14.01 | 24.86% | 20.01% | |
| 2015 | Spring | 25,116 | 49.37 | 13.31 | 10.47 | 26.96% | 21.21% | 14.41 | 11.42 | 29.18% | 23.14% |
| Summer | 20,475 | 38.31 | 11.46 | 8.91 | 29.91% | 23.25% | 12.59 | 9.86 | 32.86% | 25.72% | |
| Autumn | 20,857 | 46.88 | 13.23 | 10.32 | 28.22% | 22.02% | 14.43 | 11.38 | 30.79% | 24.28% | |
| Winter | 11,212 | 58.68 | 15.46 | 12.32 | 26.34% | 21.00% | 16.68 | 13.44 | 28.43% | 22.90% | |
| 2016 | Spring | 19,325 | 44.95 | 13.17 | 10.23 | 29.29% | 22.76% | 14.39 | 11.29 | 32.01% | 25.12% |
| Summer | 19,673 | 31.43 | 10.07 | 7.66 | 32.03% | 24.37% | 11.27 | 8.64 | 35.87% | 27.49% | |
| Autumn | 18,222 | 45.23 | 13.18 | 10.23 | 29.13% | 22.63% | 14.60 | 11.46 | 32.28% | 25.34% | |
| Winter | 5596 | 74.80 | 16.52 | 13.44 | 22.09% | 17.96% | 17.75 | 14.59 | 23.72% | 19.51% | |
| Regions | 2013 | 2016 | Difference between 2013 and 2016 | |||
|---|---|---|---|---|---|---|
| ExpCon | ObsCon | ExpCon | ObsCon | ExpDiff | ObsDiff | |
| BTH Delta | 87.55 | 85.41 | 62.64 | 67.02 | −24.91 | −18.39 |
| Wuhan Region | 86.25 | 104.95 | 55.57 | 59.76 | −30.68 | −45.19 |
| Shandong Province | 85.68 | 97.01 | 60.62 | 60.52 | −25.06 | −36.49 |
| Chengdu–Chongqing | 84.37 | 75.37 | 48.51 | 52.44 | −35.86 | −22.93 |
| Shaanxi Guanzhong | 83.99 | 94.11 | 53.78 | 58.66 | −30.21 | −35.45 |
| Yangtze River Delta | 77.74 | 71.28 | 52.25 | 51.24 | −25.49 | −20.04 |
| Changsha–Zhuzhou–Xiangtan | 74.58 | 77.90 | 48.41 | 54.66 | −26.17 | −23.24 |
| Urumqi, Xinjiang | 72.59 | 71.00 | 33.54 | 31.62 | −39.05 | −39.38 |
| Pearl River Delta | 64.76 | 70.04 | 42.19 | 41.80 | −22.57 | −28.24 |
| Gansu–Ningxia | 60.14 | 53.12 | 42.98 | 49.18 | −17.16 | −3.94 |
| Central and northern areas of Shanxi | 58.67 | 62.77 | 48.88 | 56.96 | −9.79 | −5.81 |
| Central Liaoning | 57.39 | 52.23 | 44.18 | 41.02 | −13.21 | −11.21 |
| Straits Fujian | 47.09 | 42.43 | 35.45 | 33.86 | −11.64 | −8.57 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, X.; Li, S.; Xiong, L.; Zou, B. Analysis of PM2.5 Variations Based on Observed, Satellite-Derived, and Population-Weighted Concentrations. Remote Sens. 2022, 14, 3381. https://doi.org/10.3390/rs14143381
Fang X, Li S, Xiong L, Zou B. Analysis of PM2.5 Variations Based on Observed, Satellite-Derived, and Population-Weighted Concentrations. Remote Sensing. 2022; 14(14):3381. https://doi.org/10.3390/rs14143381
Chicago/Turabian StyleFang, Xin, Shenxin Li, Liwei Xiong, and Bin Zou. 2022. "Analysis of PM2.5 Variations Based on Observed, Satellite-Derived, and Population-Weighted Concentrations" Remote Sensing 14, no. 14: 3381. https://doi.org/10.3390/rs14143381
APA StyleFang, X., Li, S., Xiong, L., & Zou, B. (2022). Analysis of PM2.5 Variations Based on Observed, Satellite-Derived, and Population-Weighted Concentrations. Remote Sensing, 14(14), 3381. https://doi.org/10.3390/rs14143381






