Using a Multiobjective Genetic Algorithm to Design Satellite Constellations for Recovering Earth System Mass Change
Abstract
:1. Introduction
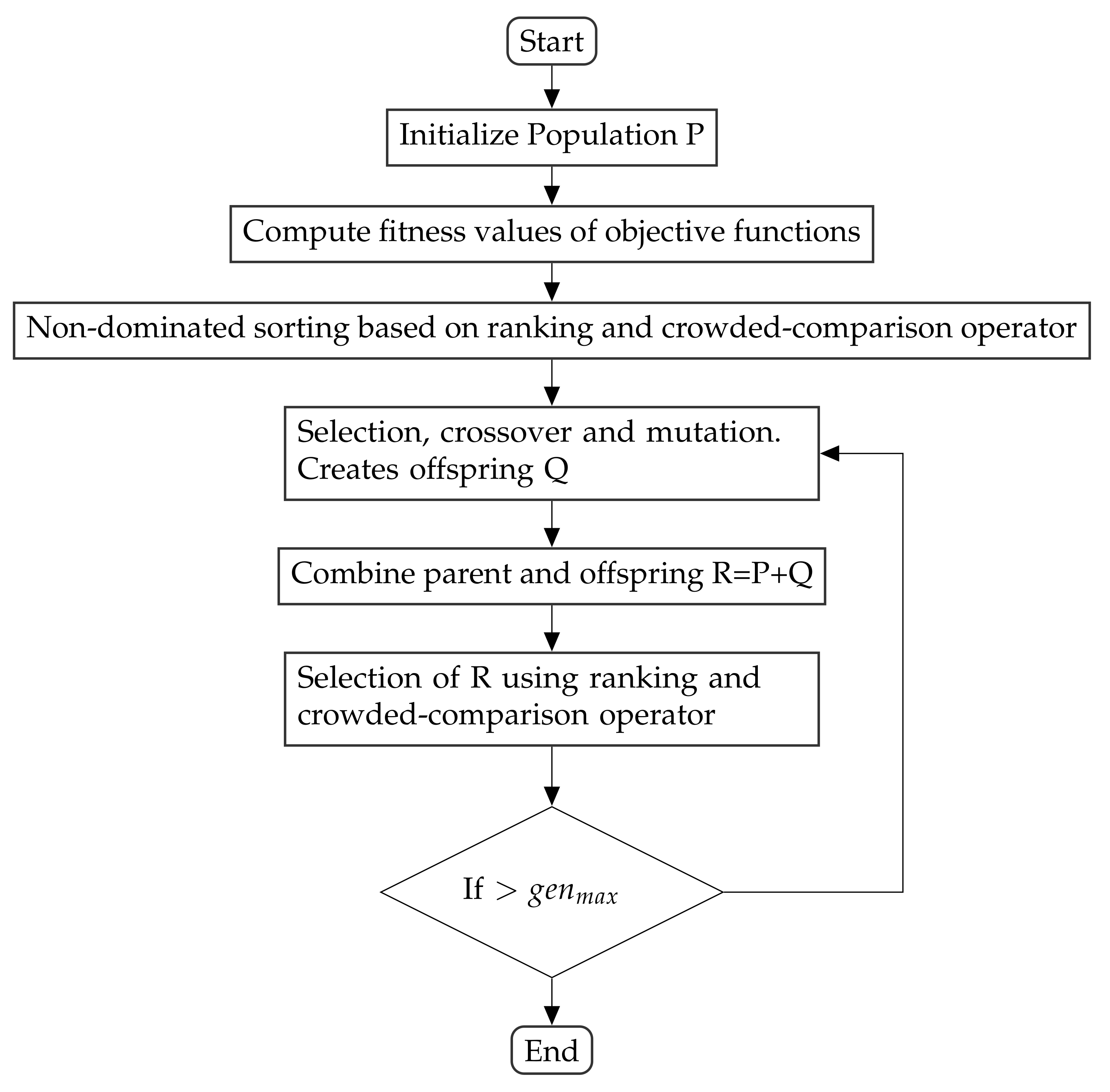
2. Methodology
2.1. Objective Function
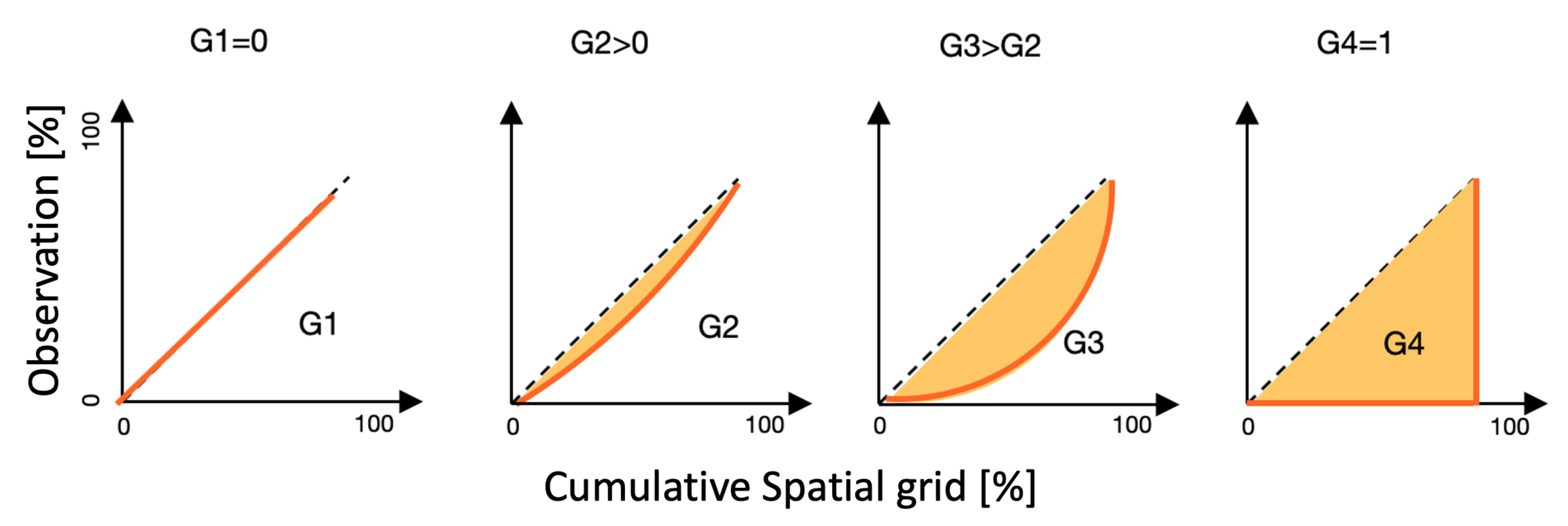
2.1.1. Spatial Objective Function
2.1.2. Weight Calibration
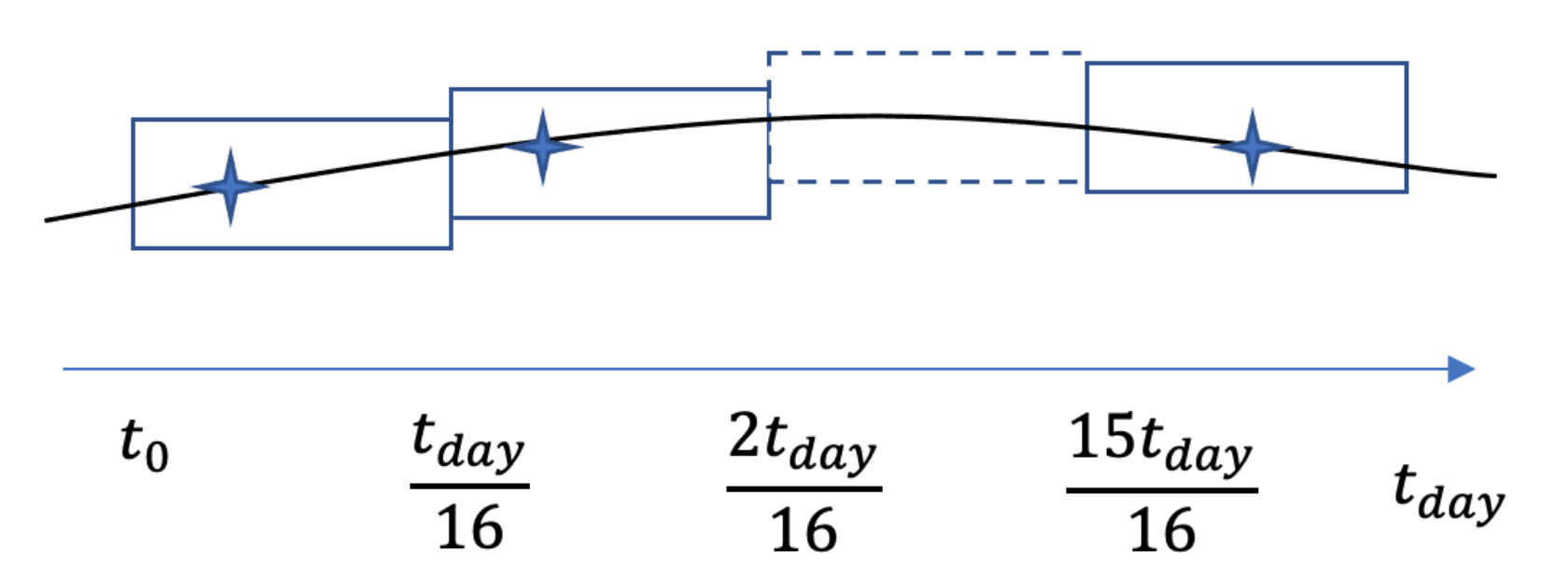
2.1.3. Temporal Objective Function
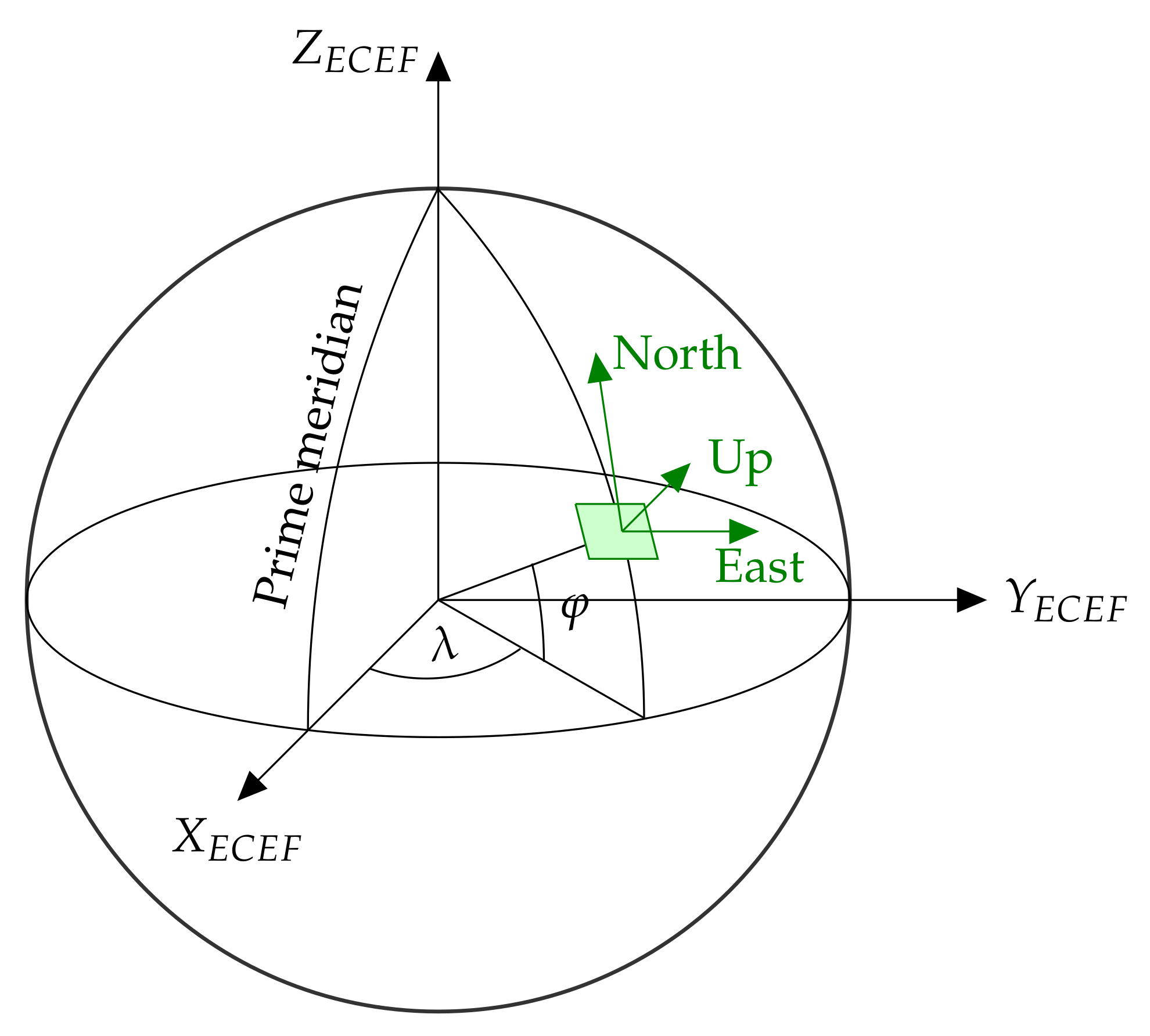
3. Orbital Considerations
4. Simulation Setup
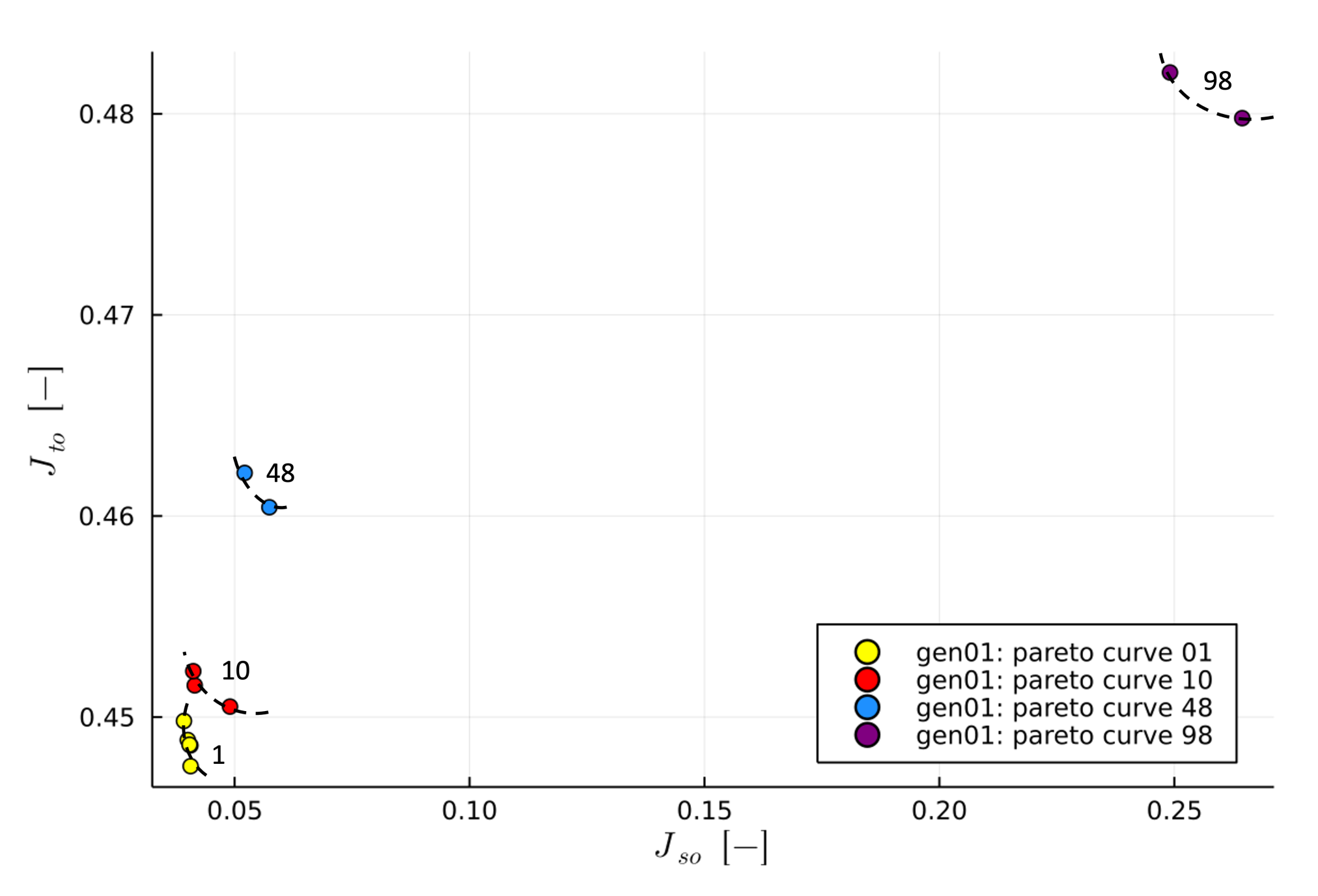
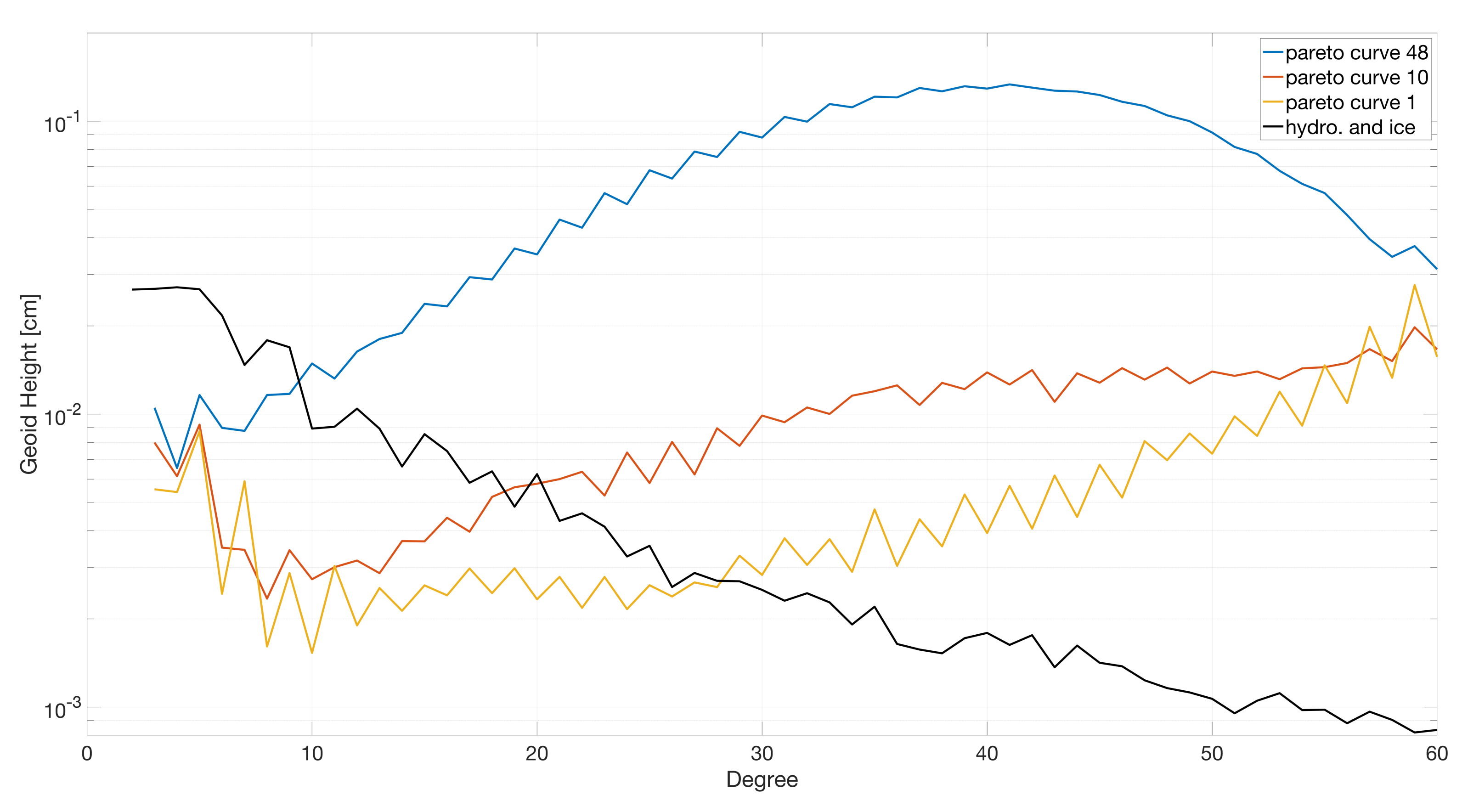
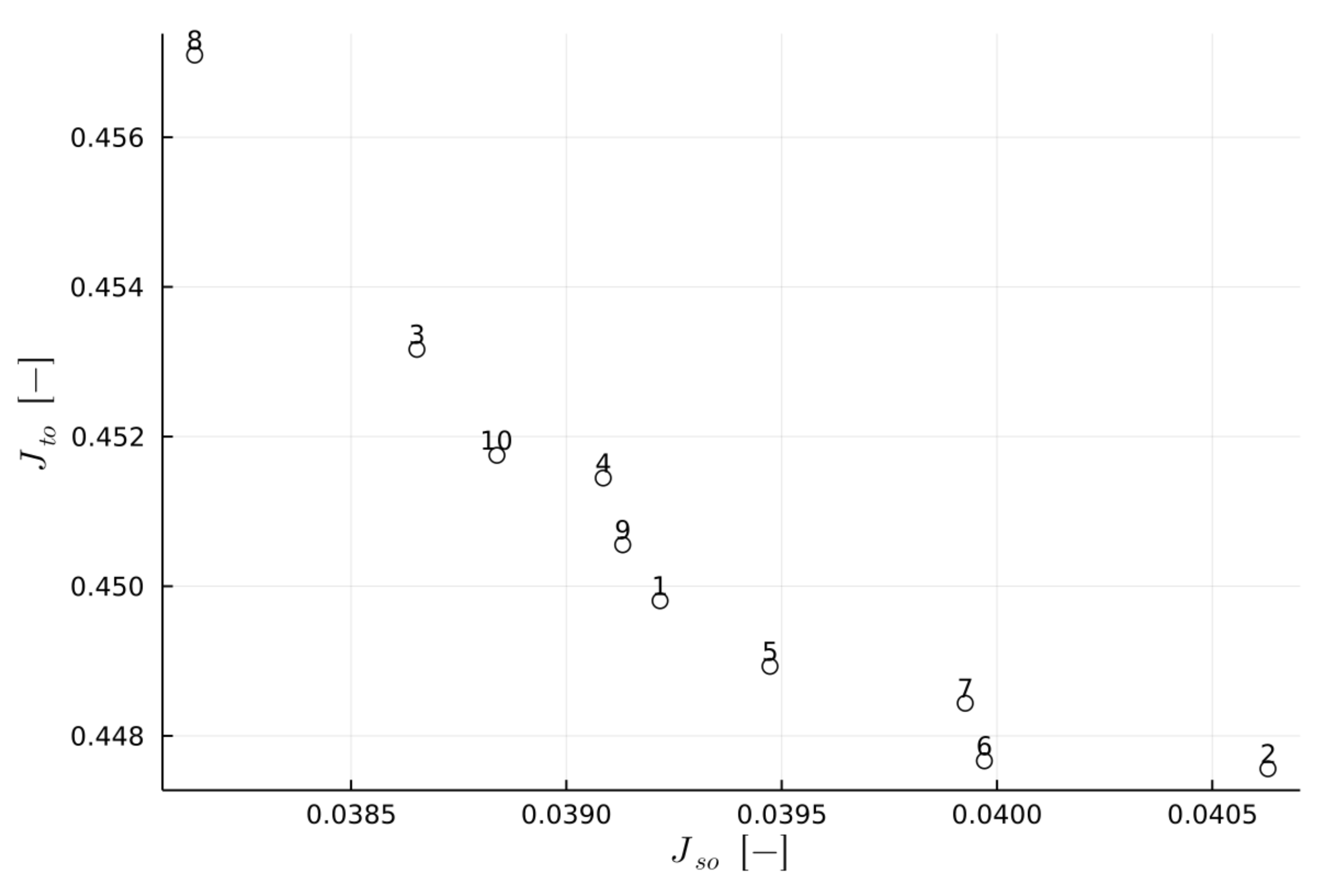
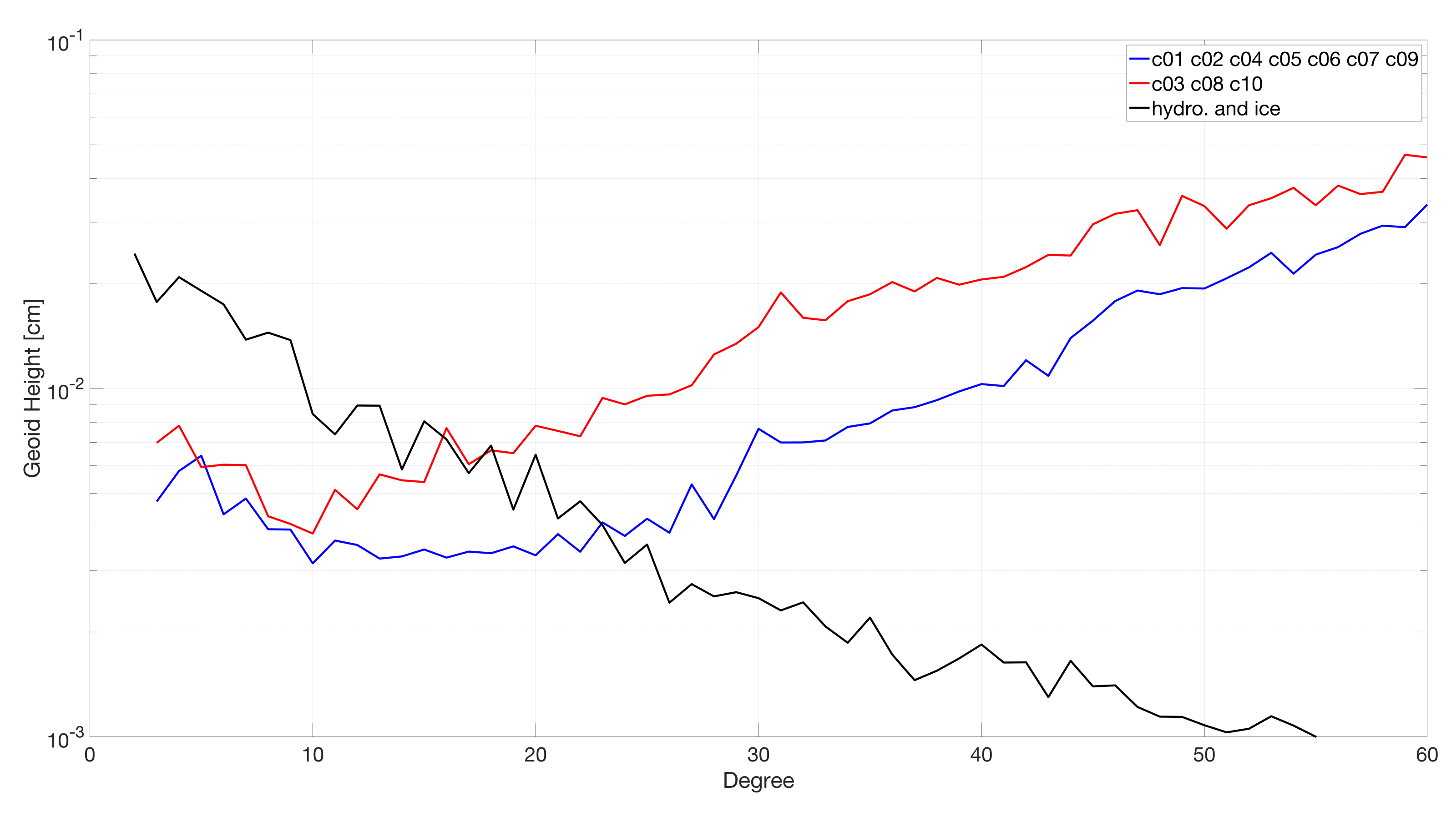
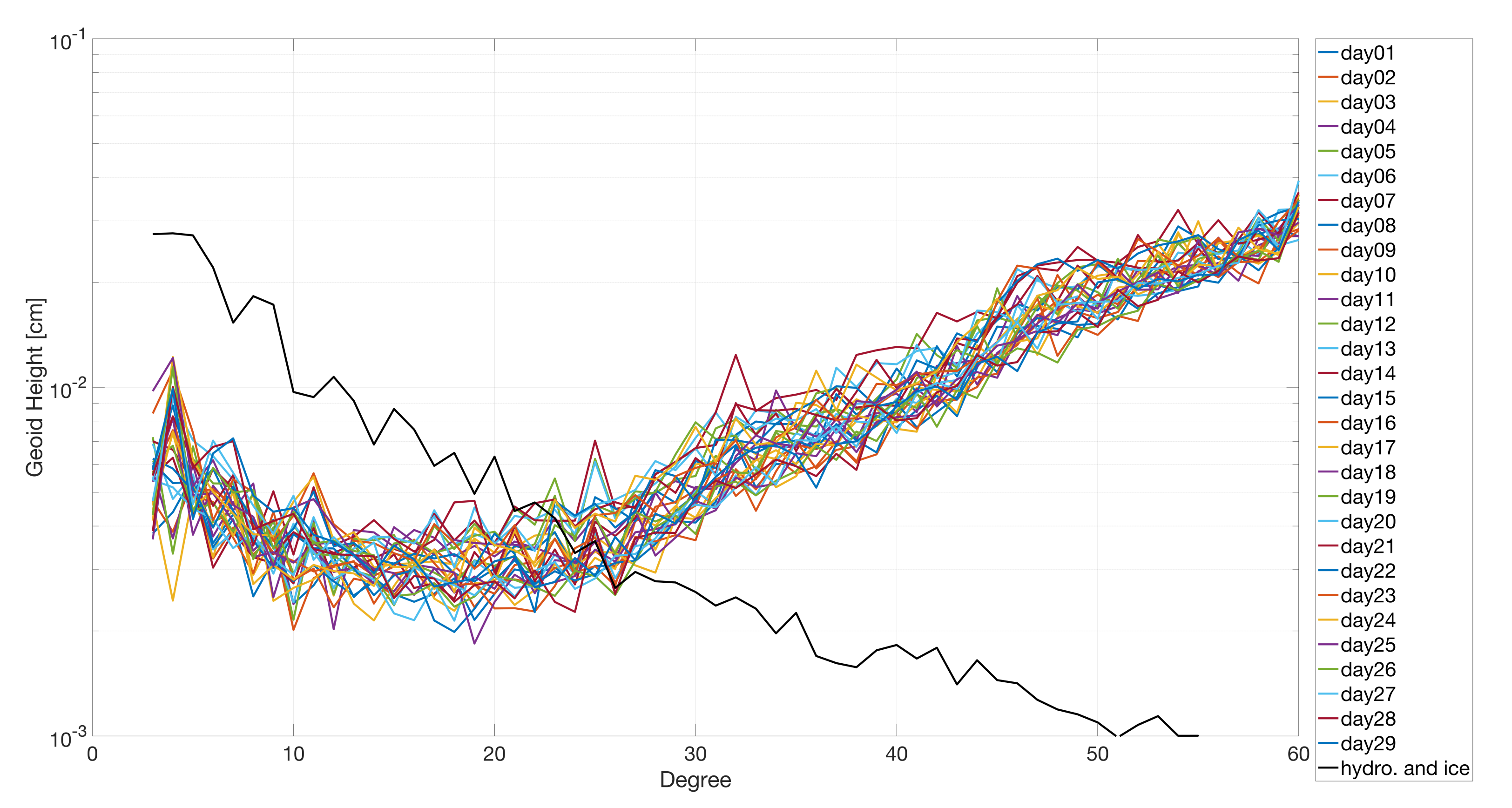
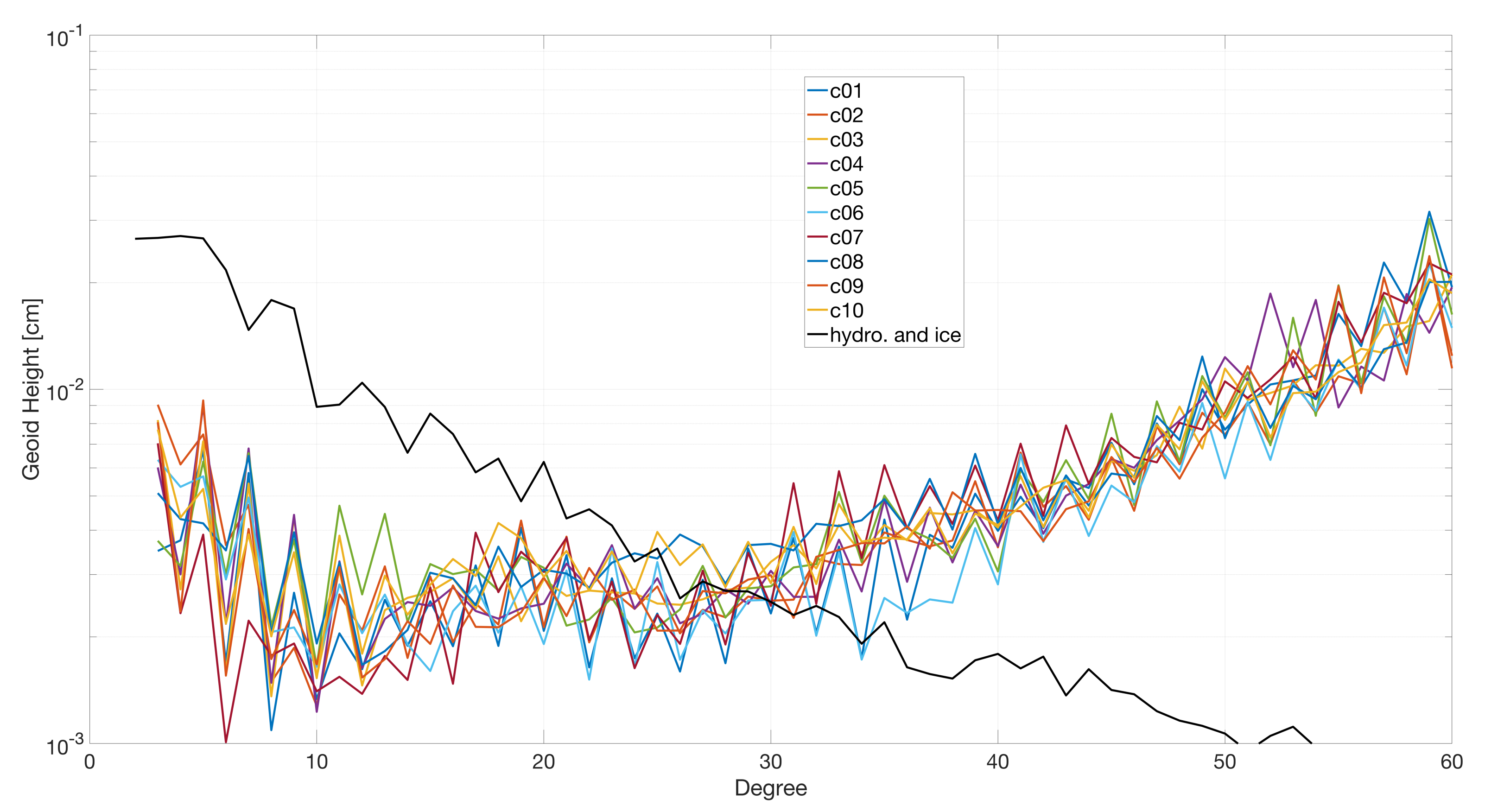
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| c | Constellation |
| ew | East–West |
| i | Inclination |
| id | Identification |
| ns | North–South |
| ob | Observation |
| rev | Revisit |
| ro | Repeat observations |
| so | Spatial objective function |
| to | Temporal objective function |
| ECEF | Earth-centered, Earth-fixed coordinate system |
| ECMWF | European Centre for Medium-Range Weather Forecasts |
| EWH | Equivalent Water Height |
| FES | Finite Element Solution tidal model |
| GA | Genetic Algorithm |
| GOT | Goddard Ocean Tide Model |
| GRACE | Gravity Recovery and Climate Experiment |
| GRACE-FO | GRACE Follow-On |
| GSFC | Goddard Space Flight Center |
| M | Mean Anomaly |
| MOGA | Multiobjective Genetic Algorithm |
| MOG2D | 2-Dimensional Gravity Waves model |
| NASA | National Aeronautics and Space Administration |
| NCEP | National Centers for Environmental Prediction |
| OMCT | Ocean Model for Circulation and Tides |
| RAAN | Right Ascension of the Ascending Node |
| ROSES | Research Opportunities in Space and Earth Science |
| RP | Repeat period |
| SC | Spatial cell |
| TC | Temporal cell |
References
- Tapley, B.D.; Bettadpur, S.; Ries, J.C.; Thompson, P.F.; Watkins, M.M. GRACE measurements of mass variability in the Earth system. Science 2004, 305, 503–505. [Google Scholar] [CrossRef] [Green Version]
- Tapley, B.D.; Bettadpur, S.; Watkins, M.; Reigber, C. The gravity recovery and climate experiment: Mission overview and early results. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef] [Green Version]
- Tapley, B.D.; Watkins, M.M.; Flechtner, F.; Reigber, C.; Bettadpur, S.; Rodell, M.; Sasgen, I.; Famiglietti, J.S.; Landerer, F.W.; Chambers, D.P.; et al. Contributions of GRACE to understanding climate change. Nat. Clim. Chang. 2019, 9, 358–369. [Google Scholar] [CrossRef] [PubMed]
- Johnson, G.C.; Chambers, D.P. Ocean bottom pressure seasonal cycles and decadal trends from GRACE Release-05: Ocean circulation implications. J. Geophys. Res. Ocean. 2013, 118, 4228–4240. [Google Scholar] [CrossRef]
- Velicogna, I.; Mohajerani, Y.; Landerer, F.; Mouginot, J.; Noel, B.; Rignot, E.; Sutterley, T.; van den Broeke, M.; van Wessem, M.; Wiese, D.N. Continuity of ice sheet mass loss in Greenland and Antarctica from the GRACE and GRACE Follow-On missions. Geophys. Res. Lett. 2020, 47, e2020GL087291. [Google Scholar] [CrossRef] [Green Version]
- Nerem, R.S.; Leuliette, E.; Cazenave, A. Present-day sea-level change: A review. C. R. Geosci. 2006, 338, 1077–1083. [Google Scholar] [CrossRef]
- National Academies of Sciences, Engineering and Medicine. Thriving on Our Changing Planet: A Decadal Strategy for Earth Observation from Space; The National Academies Press: Washington, DC, USA, 2018. [Google Scholar] [CrossRef]
- Landerer, F.W.; Flechtner, F.M.; Save, H.; Webb, F.H.; Bandikova, T.; Bertiger, W.I.; Bettadpur, S.V.; Byun, S.H.; Dahle, C.; Dobslaw, H.; et al. Extending the global mass change data record: GRACE Follow-On instrument and science data performance. Geophys. Res. Lett. 2020, 47, e2020GL088306. [Google Scholar] [CrossRef]
- Sneeuw, N.; Flury, J.; Rummel, R. Science requirements on future missions and simulated mission scenarios. In Future Satellite Gravimetry and Earth Dynamics; Springer: New York, NY, USA, 2005; pp. 113–142. [Google Scholar]
- Pail, R.; Bingham, R.; Braitenberg, C.; Dobslaw, H.; Eicker, A.; Güntner, A.; Horwath, M.; Ivins, E.; Longuevergne, L.; Panet, I.; et al. Science and user needs for observing global mass transport to understand global change and to benefit society. Surv. Geophys. 2015, 36, 743–772. [Google Scholar] [CrossRef]
- Wiese, D.N.; Nerem, R.S.; Lemoine, F.G. Design considerations for a dedicated gravity recovery satellite mission consisting of two pairs of satellites. J. Geod. 2012, 86, 81–98. [Google Scholar] [CrossRef] [Green Version]
- Loomis, B.D.; Nerem, R.S.; Luthcke, S.B. Simulation study of a follow-on gravity mission to GRACE. J. Geod. 2012, 86, 319–335. [Google Scholar] [CrossRef]
- Elsaka, B.; Forootan, E.; Alothman, A. Improving the recovery of monthly regional water storage using one year simulated observations of two pairs of GRACE-type satellite gravimetry constellation. J. Appl. Geophys. 2014, 109, 195–209. [Google Scholar] [CrossRef] [Green Version]
- Hauk, M.; Wiese, D.N. New Methods for Linking Science Objectives to Remote Sensing Observations: A Concept Study Using Single-and Dual-Pair Satellite Gravimetry Architectures. Earth Space Sci. 2020, 7, e2019EA000922. [Google Scholar] [CrossRef] [Green Version]
- Baker, D.N.; Worden, S.P. The large benefits of small-satellite missions. EOS Trans. Am. Geophys. Union 2008, 89, 301–302. [Google Scholar] [CrossRef] [Green Version]
- Bock, D.; Tajmar, M. Highly miniaturized FEEP propulsion system (NanoFEEP) for attitude and orbit control of CubeSats. Acta Astronaut. 2018, 144, 422–428. [Google Scholar] [CrossRef]
- Sandau, R.; Roeser, H.P.; Valenzuela, A. small satellite missions for earth observation. In New Developments and Trends; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Nolde, M.; Plank, S.; Richter, R.; Klein, D.; Riedlinger, T. The DLR FireBIRD Small Satellite Mission: Evaluation of Infrared Data for Wildfire Assessment. Remotesensing 2021, 13, 1459. [Google Scholar] [CrossRef]
- Caspi, A.; Barthelemy, M.; Bussy-Virat, C.D.; Cohen, I.J.; DeForest, C.E.; Jackson, D.R.; Vourlidas, A.; Nieves-Chinchilla, T. Small Satellite Mission Concepts for Space Weather Research and as Pathfinders for Operations. Space Weather 2022, 20, e2020SW002554. [Google Scholar] [CrossRef]
- Christophe, B.; Foulon, B.; Liorzou, F.; Lebat, V.; Boulanger, D.; Huynh, P.A.; Zahzam, N.; Bidel, Y.; Bresson, A. Status of development of the future accelerometers for next generation gravity missions. In International Symposium on Advancing Geodesy in a Changing World; Springer: Cham, Switzerland, 2018; pp. 85–89. [Google Scholar]
- Yang, G.; Chen, J.; Numata, K.; Luthcke, S.; Yu, T. Compact Coherent Laser Ranging (CCLR); No. GSFC-E-DAA-TN72283; NASA: Washington, DC, USA, 2019.
- Alonso, I.; Alpigiani, C.; Altschul, B.; Araujo, H.; Arduini, G.; Arlt, J.; Badurina, L.; Balaz, A.; Bandarupally, S.; Barone, B.C.; et al. Cold Atoms in Space: Community Workshop Summary and Proposed Road-Map. arXiv 2022, arXiv:2201.07789. [Google Scholar]
- Deccia, C.M.A.; Nerem, R.S.; Yunck, T. A SmallSat constellation mission architecture for a GRACE-type mission design. In Proceedings of the 2017 AGU Fall Meeting, New Orleans, LA, USA, 11–15 December 2017. [Google Scholar]
- Deccia, C.M.A.; Nerem, R.S.; Wiese, D.N. Designing a GRACE-type satellite constellation for hydrologic science. In Proceedings of the 2018 AGU Fall Meeting, Washington, DC, USA, 10–14 December 2018. [Google Scholar]
- Deccia, C.M.A.; Wiese, D.N.; Loomis, B.D.; Nerem, R.S. Design of GRACE-like Small Satellite Constellations for Improved Temporal Gravity Measurements. In Proceedings of the GRACE/GRACE-FO Science Team Meeting 2020, Online, 27–29 October 2020. [Google Scholar] [CrossRef]
- Deccia, C.M.A.; Wiese, D.N.; Loomis, B.D.; Nerem, R.S. Design of future Earth observing mass change constellations using small satellites. In Proceedings of the 2020 AGU Fall Meeting, Online, 1–17 December 2020. [Google Scholar]
- Deccia, C.M.A.; Nerem, R.S.; Wiese, D.N. Designing an n-pair satellite constellation for recovering daily Earth system mass change using a multi-objective genetic algorithm. In Proceedings of the 2021 GRACE-FO Science Team Meeting, Online, 12–20 October 2021. [Google Scholar]
- Deccia, C.M.A.; Wiese, D.N.; Nerem, R.S. Using genetic algorithms to design satellite constellations for recovering daily Earth system mass change. In Proceedings of the 2021 AGU Fall Meeting, Online, 13–17 December 2021. [Google Scholar]
- Yunck, T.; Saltman, A.; Bettadpur, S.V.; Nerem, R.S.; Abel, J.; Widner, M.V., IV; Deccia, C.M.A.; Fountain, E.; Franklin, G.; Esterhuizen, S. The Earth Gravitational Observatory Smallsat Constellation for Advanced Gravity Mapping. In Proceedings of the 2017 AGU Fall Meeting, New Orleans, LA, USA, 11–15 December 2017. [Google Scholar]
- Yunck, T.; Saltman, A.; Bettadpur, S.V.; Nerem, R.S.; Widner, M.V., IV; Deccia, C.M.A.; Veneziano, A. Design For A Permanent Earth Gravitational Observatory. In Proceedings of the 2018 AGU Fall Meeting, Washington, DC, USA, 10–14 December 2018. [Google Scholar]
- Wiese, D.N. Optimizing Two Pairs of GRACE-like Satellites for Recovering Temporal Gravity Variations. Ph.D. Thesis, University of Colorado at Boulder, Boulder, CO, USA, 2011. [Google Scholar]
- Sastry, K.; Goldberg, D.; Kendall, G. Genetic algorithms. In Search Methodologies; Springer: Boston, MA, USA, 2005; pp. 97–125. [Google Scholar]
- Deccia, C.M.A. Comprehensive Exam Document: Design of a GRACE-Type Small Satellite Constellation to Improve Temporal and Spatial Resolution of Satellite; University of Colorado at Boulder: Boulder, CO, USA, 2019. [Google Scholar]
- Schaefer, R. Foundations of Global Genetic Optimization; Springer: Berlin/Heidelberg, Germany, 2007; Volume 74. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T.A.M.T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef] [Green Version]
- Savitri, T.; Kim, Y.; Jo, S.; Bang, H. Satellite constellation orbit design optimization with combined genetic algorithm and semianalytical approach. Int. J. Aerosp. Eng. 2017, 2017, 1235692. [Google Scholar] [CrossRef] [Green Version]
- Stern, J.; Wachtel, S.; Colombi, J.; Meyer, D.; Cobb, R. Multiobjective optimization of geosynchronous earth orbit space situational awareness systems via parallel executable architectures. In Disciplinary Convergence in Systems Engineering Research; Springer: Cham, Switzerland, 2018; pp. 599–615. [Google Scholar]
- Dai, C.Q.; Yu, T.; Chen, Q. Capacity-Oriented Satellite Constellation Design in Disaster Emergency Communication Network. In Proceedings of the 2020 International Conference on Wireless Communications and Signal Processing (WCSP), Nanjing, China, 21–23 October 2020; pp. 666–671. [Google Scholar]
- Wijayatunga, M.; Wu, X. An Optimised Satellite Constellation for Bushfire Detection through Edge Computing. Preprints 2021, 2021030071. [Google Scholar] [CrossRef]
- Sheng, M.; Zhou, D.; Bai, W.; Liu, J.; Li, J. 6G service coverage with mega satellite constellations. China Commun. 2022, 19, 64–76. [Google Scholar] [CrossRef]
- Bender, T.; McNabb, J.; Birbasov, N.; Bowne, M.; Robertson, B.E.; Sudol, A.; Mavris, D.N.; Lourenco, N. Satellite Formation Design to Enhance Passive Millimeter Wave Imaging Mission Performance. In Proceedings of the AIAA SCITECH 2022 Forum, San Diego, CA, USA, 3–7 January 2022; p. 1881. [Google Scholar]
- Watkins, M.M.; Wiese, D.N.; Yuan, D.N.; Boening, C.; Landerer, F.W. Improved methods for observing Earth’s time variable mass distribution with GRACE using spherical cap mascons. J. Geophys. Res. Solid Earth 2015, 120, 2648–2671. [Google Scholar] [CrossRef]
- Croteau, M.J.; Nerem, R.S.; Merrifield, M.A.; Thompson, P.R.; Loomis, B.D.; Wiese, D.N.; Zlotnicki, V.; Larson, J.; Talpe, M.; Hardy, R.A. Interactive and Approachable Web-Based Tools for Exploring Global Geophysical Data Records. In Proceedings of the 2017 AGU Fall Meeting, New Orleans, LA, USA, 11–15 December 2017. [Google Scholar]
- Gini, C. Variabilità e mutabilità. In Memorie di Metodologica Statistica; Pizetti, E., Ed.; Libreria Eredi Virgilio Veschi: Rome, Italy, 1912. [Google Scholar]
- Swenson, S.; Wahr, J. Post-processing removal of correlated errors in GRACE data. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Bender, P.L.; Wiese, D.N.; Nerem, R.S. A possible dual-GRACE mission with 90 degree and 63 degree inclination orbits. In Proceedings of the 3rd International Symposium on Formation Flying, Missions and Technologies. European Space Agency Symposium Proceedings, SP-654 jILA Pub, Noordwijk, The Netherlands, 23–25 April 2018; Volume 8161, pp. 1665–1669. [Google Scholar]
- Pavlis, D.E.; Deng, C.; McCarthy, J.J. GEODYN Operations Manual; Contractor Report; SGT, Inc.: Greenbelt, MD, USA, 2010.
- Ullman, R. SOLVE Program Mathematical Formulation. Rep. HSTX- G and G-9201; Raytheon ITSS: Greenbelt, MD, USA, 1997. [Google Scholar]
- Förste, C.; Schmidt, R.; Stubenvoll, R.; Flechtner, F.; Meyer, U.; König, R.; Neumayer, H.; Biancale, R.; Lemoine, J.; Bruinsma, S.; et al. The GFZ/GRGS satellite and combined gravity field models EIGEN-GL04S1 and EIGEN-GL04C. J. Geod. 2008, 82, 331–346. [Google Scholar] [CrossRef] [Green Version]
- Lyard, F.; Lefèvre, F.; Letellier, T.; Francis, O. Modelling the global ocean tides: Modern insights from FES2004. Ocean. Dyn. 2006, 56, 394–415. [Google Scholar] [CrossRef]
- Ray, R.D. A global ocean tide model from TOPEX/POSEIDON altimetry: GOT99.2. In NASA Technical Memorandum 209478; Goddard Space Flight Center: Greenbelt, MD, USA, 1999. [Google Scholar]
- Klinker, E.; Rabier, F.; Kelly, G.; Mahfouf, J.F. The ECMWF operational implementation of four-dimensional variational assimilation. III: Experimental results and diagnostics with operational configuration. Q. J. R. Meteorol. Soc. 2000, 126, 1191–1215. [Google Scholar] [CrossRef]
- Kalnay, E.; Kanamitsu, M.; Kistler, R.; Collins, W.; Deaven, D.; Gandin, L.; Iredell, M.; Saha, S.; White, G.; Woollen, J.; et al. The NCEP/NCAR 40-year reanalysis project. Bull. Am. Meteorol. Soc. 1996, 77, 437–470. [Google Scholar] [CrossRef] [Green Version]
- Flechtner, F. AOD1B Product Description Document for Product Releases 01 to 04; GRACE 327–750, CSR Publ. GR-GFZ-AOD-0001 Rev. 3.1; University of Texas at Austin: Austin, TX, USA, 2007; 43p. [Google Scholar]
- Carrère, L.; Lyard, F. Modeling the barotropic response of the global ocean to atmospheric wind and pressure forcing. Geophys. Res. Lett. 2003, 30, 1275. [Google Scholar] [CrossRef] [Green Version]
- Rodell, M.; House, P.; Jambor, U.; Gottschalck, J.; Mitchell, K.; Meng, C.J.; Arsenault, K.; Cosgrove, B.; Radakovich, J.; Bosilovich, M.; et al. The global land data assimilation system. Bull. Am. Meteorol. Soc. 2004, 85, 381–394. [Google Scholar] [CrossRef] [Green Version]
- Van Dam, T.; Visser, P.; Sneeuw, N.; Losch, M.; Gruber, T.; Bamber, J.; Bierkens, M.; King, M.; Smit, M. Monitoring and Modelling Individual Sources of Mass Distributions and Transport in the Earth System by Means of Satellites; Technical Report; Final Report, ESA Contract 20403; ESA: Paris, France, 2008. [Google Scholar]
- Kang, Z.; Tapley, B.; Bettadpur, S.; Ries, J.; Nagel, P. Precise orbit determination for GRACE using accelerometer data. Adv. Space Res. 2006, 38, 2131–2136. [Google Scholar] [CrossRef]
- Wiese, D.N.; Bienstock, B.; Blackwood, C.; Chrone, J.; Loomis, B.D.; Sauber-Rosenberg, J.M.; Rodell, M.; Baize, R.R.; Bearden, D.; Case, K.; et al. The Mass Change Designated Observable Study: Overview and Results; Earth and Space Science Open Archive: Washington, DC, USA, 2022. [Google Scholar] [CrossRef]
- Rowlands, D.D.; Ray, R.D.; Chinn, D.S.; Lemoine, F.G. Short-arc analysis of intersatellite tracking data in a gravity mapping mission. J. Geod. 2002, 76, 307–316. [Google Scholar] [CrossRef] [Green Version]
- Farrell, W.E. Deformation of the Earth by surface loads. Rev. Geophys. 1972, 10, 761–797. [Google Scholar] [CrossRef]


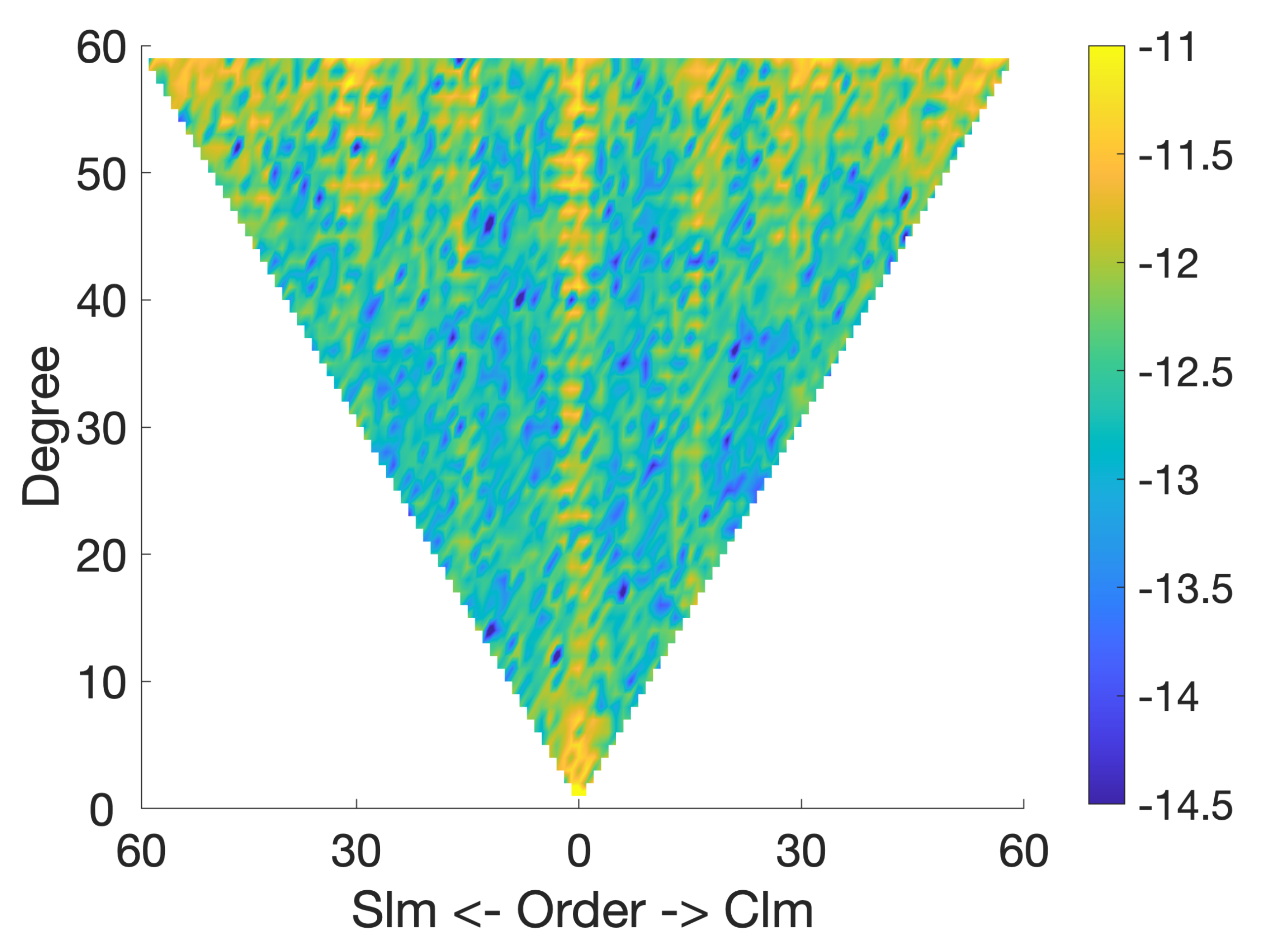
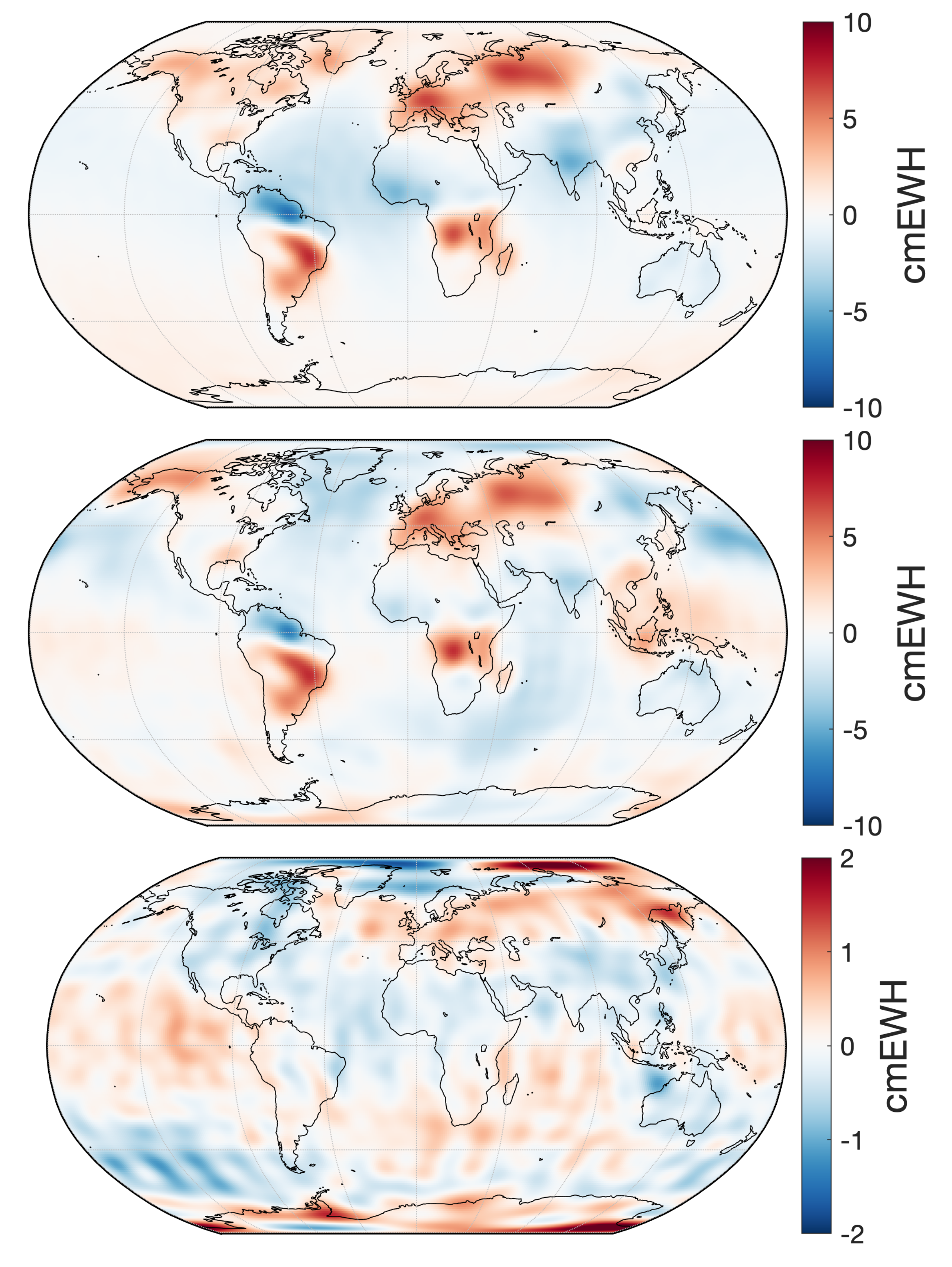
| Weight | Value [−] |
|---|---|
| 100 | |
| 1 | |
| 1 | |
| 10 |
| Parameter | Value | Unit |
|---|---|---|
| Propagation time (T) | 29 | (day) |
| Satellite pairs () | 6 | (pairs) |
| Orbit altitude () | (km) | |
| Repeat period (RP) | 29 | (day) |
| Eccentricity (e) | 0 | (-) |
| Arg. of perigee () | 90 | () |
| Intersatellite distance () | 100 | (km) |
| Spatial cell (SC) | 4551 | (-) |
| Temporal cell (TC) | 16 | (per-day) |
| Inclination (i) | [0–180] | () |
| RAAN () | [0–360] | () |
| Mean anomaly (M) | [0–360] | () |
| Models | Truth | Nominal | Source |
|---|---|---|---|
| Static gravity field | EIGEN-GL04C | EIGEN-GL04C | [49] |
| Ocean tide | FES2004 | GOT00 | [50,51] |
| Atmospheric | ECMWF | NCEP | [52,53] |
| Ocean | OMCT | MOG2D | [54,55] |
| Hydrological | GLDAS | - | [56] |
| Ice | ESA | - | [57] |
| id (-) | () | () | () | () | () | () | () | () | () |
|---|---|---|---|---|---|---|---|---|---|
| c01 | 87.13 | 78.55 | 236.16 | 99.52 | 168.61 | 269.94 | 116.55 | 33.52 | 134.84 |
| c02 | 23.97 | 258.68 | 224.9 | 139.26 | 146.1 | 157.35 | 102.35 | 157.35 | 67.29 |
| c03 | 81.39 | 179.87 | 67.29 | 66.29 | 112.32 | 191.13 | 116.55 | 292.45 | 348.74 |
| c04 | 58.42 | 134.84 | 202.39 | 89.0 | 44.77 | 247.42 | 91.0 | 360.0 | 33.52 |
| c05 | 144.55 | 112.32 | 326.23 | 133.58 | 247.42 | 33.52 | 96.68 | 112.32 | 292.45 |
| c06 | 92.87 | 269.94 | 112.32 | 102.35 | 360.0 | 44.77 | 116.55 | 337.48 | 247.42 |
| c07 | 98.61 | 236.16 | 157.35 | 108.03 | 44.77 | 33.52 | 86.16 | 360.0 | 314.97 |
| c08 | 64.16 | 292.45 | 326.23 | 89.0 | 337.48 | 67.29 | 83.32 | 146.1 | 56.03 |
| c09 | 87.13 | 269.94 | 224.9 | 54.94 | 157.35 | 202.39 | 77.65 | 179.87 | 56.03 |
| c10 | 35.45 | 247.42 | 269.94 | 110.87 | 281.19 | 101.06 | 89.0 | 134.84 | 112.32 |
| id (-) | () | () | () | () | () | () | () | () | () |
| c01 | 32.23 | 202.39 | 168.61 | 52.1 | 67.29 | 112.32 | 91.0 | 292.45 | 11.0 |
| c02 | 125.06 | 67.29 | 326.23 | 93.84 | 224.9 | 360.0 | 108.03 | 191.13 | 78.55 |
| c03 | 86.16 | 258.68 | 78.55 | 89.0 | 22.26 | 236.16 | 125.06 | 236.16 | 360.0 |
| c04 | 66.29 | 33.52 | 281.19 | 133.58 | 213.65 | 168.61 | 71.97 | 303.71 | 202.39 |
| c05 | 63.45 | 269.94 | 112.32 | 89.0 | 326.23 | 247.42 | 71.97 | 303.71 | 67.29 |
| c06 | 96.68 | 236.16 | 112.32 | 136.42 | 157.35 | 247.42 | 147.77 | 236.16 | 269.94 |
| c07 | 66.29 | 191.13 | 348.74 | 142.1 | 56.03 | 157.35 | 133.58 | 281.19 | 191.13 |
| c08 | 71.97 | 112.32 | 67.29 | 83.32 | 281.19 | 78.55 | 99.52 | 269.94 | 360.0 |
| c09 | 153.45 | 89.81 | 348.74 | 108.03 | 337.48 | 78.55 | 89.0 | 22.26 | 213.65 |
| c10 | 116.55 | 247.42 | 67.29 | 83.32 | 67.29 | 314.97 | 86.16 | 191.13 | 326.23 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deccia, C.M.A.; Wiese, D.N.; Nerem, R.S. Using a Multiobjective Genetic Algorithm to Design Satellite Constellations for Recovering Earth System Mass Change. Remote Sens. 2022, 14, 3340. https://doi.org/10.3390/rs14143340
Deccia CMA, Wiese DN, Nerem RS. Using a Multiobjective Genetic Algorithm to Design Satellite Constellations for Recovering Earth System Mass Change. Remote Sensing. 2022; 14(14):3340. https://doi.org/10.3390/rs14143340
Chicago/Turabian StyleDeccia, Carlos M. A., David N. Wiese, and Robert S. Nerem. 2022. "Using a Multiobjective Genetic Algorithm to Design Satellite Constellations for Recovering Earth System Mass Change" Remote Sensing 14, no. 14: 3340. https://doi.org/10.3390/rs14143340
APA StyleDeccia, C. M. A., Wiese, D. N., & Nerem, R. S. (2022). Using a Multiobjective Genetic Algorithm to Design Satellite Constellations for Recovering Earth System Mass Change. Remote Sensing, 14(14), 3340. https://doi.org/10.3390/rs14143340






