Abstract
Accurate knowledge of soil moisture is crucial for agricultural drought monitoring. Data assimilation has proven to be a promising technique for improving soil moisture estimation, and various studies have been conducted on soil moisture data assimilation based on land surface models. However, crop growth models, which are ideal tools for agricultural simulation applications, are rarely used for soil moisture assimilation. Moreover, the role of data assimilation in agricultural drought monitoring is seldom investigated. In the present work, we assimilated the European Space Agency (ESA) Climate Change Initiative (CCI) soil moisture product into the Decision Support System for Agro-technology Transfer (DSSAT) model to estimate surface and root-zone soil moisture, and we evaluated the effect of data assimilation on agricultural drought monitoring. The results demonstrate that the soil moisture estimates were significantly improved after data assimilation. Root-zone soil moisture had a better agreement with in situ observation. Compared with the drought index based on soil moisture modeled without remotely-sensed observations, the drought index based on assimilated data could improve at least one drought level in agricultural drought monitoring and performed better when compared with winter wheat yield. In conclusion, crop growth model-based data assimilation effectively improves the soil moisture estimation and further strengthens soil moisture-based drought indices for agricultural drought monitoring.
1. Introduction
Drought is a fairly complex and disastrous climate disaster, which can cause tremendous damages to the economy and environment, especially for the agriculture sector. Typically, meteorological, agricultural, hydrological, and socioeconomic droughts are recognized as the four common types of drought [1]. Compared with other types of drought, agricultural drought provides a more immediate and obvious influence [2] and threatens regional and even national food security [3,4]. Under the scenario of global climate change, future drought may be exacerbated [5], and along with other climate hazards, drought may still pose a heightened threat to humanity [6]. Thus, accurate and effective agricultural drought monitoring is of great significance for impact assessment and targeted adaption planning.
Agricultural drought involves insufficient soil moisture due to the imbalance between water supply and crop water demand, which detrimentally affects crop growth and yield [7]. Hence, soil moisture becomes an essential indicator for assessing agricultural drought [2]. Several soil moisture-based drought indices have been proposed, which are generally divided into two categories: (1) based on soil moisture time series (e.g., SMP [8], NSM [9], ESSMI [10]); and (2) based on soil properties and other parameters (e.g., SMI [11,12], SWDI [2], RSMI [13]). Although the rationales of these indices are not completely identical, the accuracy of soil moisture is a critical factor affecting their performances for agricultural drought monitoring. Currently, methods for estimating soil moisture include field measurement, model simulation, and remote sensing retrieval. Field measurement is accurate but time-consuming and limited in coverage, making it unsuitable for large-scale and frequent soil moisture collection. The main advantage of using a land surface model to simulate soil moisture is that it has a clear physical mechanism, has good spatiotemporal consistency, and can obtain soil moisture throughout the soil profile; the drawback is that it requires many input parameters, and its accuracy depends largely on the model structure, model parameters and forcings. Over the past few decades, great advances in remote sensing techniques have enabled users to obtain soil moisture over large areas. Soil moisture can be estimated using remote sensing techniques with different spectra from optical to microwave ranges, i.e., the visible/near infrared (VIS/NIR, 350~2500 nm), thermal infrared (TIR, 3500~14,000 nm) and microwave (P—band, L—band, C—band, and X—band) [14,15,16]. Li et al. [15] reviewed the soil moisture retrieval from satellite remote sensing measurements, with emphasis on estimations from the visible/near infrared (VIS/NIR) and thermal infrared (TIR) observations. Babaeian et al. [16] elaborated on recent advances in soil moisture estimation using ground, proximal, and airborne and spaceborne remote sensing techniques, and they summarized the available soil moisture data sources. According to the above related literature, the satellite-based microwave remote sensing method is still the mainstream of soil moisture estimation. However, remote sensing measurements are limited to a few centimeters at the top of the soil and do not provide information on the moisture of the deep soil [17,18]. In fact, root-zone soil moisture is more appropriate than that from a fixed soil depth for assessing agricultural drought [19].
Given that each method has its own advantages and limitations in estimating soil moisture, data assimilation (DA) is a promising approach for improving soil moisture estimation by integrating a process model and observation. Benefiting from the rapid progress of remote sensing techniques, the accuracy of satellite soil moisture products has gradually increased in recent years, and they have become the core observations for soil moisture data assimilation. Many previous studies have assimilated remotely sensed products into hydrological or land surface models [17,20,21,22,23] and agricultural drought estimation [24,25,26,27,28,29]. For example, Baldwin et al. [17] assimilated the AMSR-E soil moisture into the Soil Moisture Analytical Relationship (SMAR) infiltration model for predicting root-zone soil moisture. De Lannoy and Reichle [28] conducted the assimilation of SMOS products into the Goddard Earth Observing System Model to improve estimates of surface and root-zone soil moisture. Seo et al. [29] assimilated the SMAP and ASCAT soil moisture into the JULES land surface model for improving soil moisture and drought monitoring. Kumar et al. [24] presented the assimilation of three remotely sensed soil moisture products into the Noah land surface model for soil moisture and drought estimation. The results of these studies showed that data assimilation contributes to the improvement of soil moisture estimation, but significant room for improvement exists for each component (model, observation, and algorithm) of the data assimilation system [25]. For the time being, land surface models are still the dominant model operators for moisture assimilation. As far as crops are concerned, the occurrence of agricultural drought has a close bearing on soil moisture, crop water demand, growth stage, and irrigation condition. Most land surface models, however, rely on observations or empirical functions to simulate the effects of vegetation and lack a more mechanistic representation [30], while generally ignoring the effect of human activities (e.g., irrigation) on soil moisture change. In contrast, crop models are more capable of explicitly characterizing the entire growth process and simulating the interactions between the root-zone soil moisture and crop water uptake during the growing season. Hence, crop growth models are ideal tools to characterize the relationship between crop growth and environmental factors, and drought indices combined with the agronomic parameters from the model output can better monitor agricultural drought. In current studies, crop growth model-based data assimilation is generally used for leaf area index, as well as yield or biomass estimation and prediction [31,32,33,34,35]. The linkage between crop models and remote sensing observations for improving surface and root-zone soil moisture is relatively rare, and evaluations of the impact of DA-based soil moisture estimates on agricultural drought monitoring are still lacking. Consequently, the goals of this study were: (1) to assimilate remote sensing data into a crop model to estimate soil moisture; (2) to investigate the impacts of different strategies (simultaneous state-parameter estimation, ensemble size, and assimilation interval) on soil moisture data assimilation; and (3) to evaluate the extent to which soil moisture assimilation enhances the level of agricultural drought monitoring.
2. Study Area and Data
2.1. Study Area
The focus of this article is on the Huang-Huai-Hai (HHH) Plain, the second largest plain in China, which is located between 32° and 41°N and 112° and 123°E, covering 390,000 km2 (Figure 1). The HHH Plain is an important food-producing base in China, accounting for approximately 16% of the total cultivated land area [36,37,38]. The prevailing cropping system is the rotation of winter wheat and summer corn, and wheat and corn production account for 70% and 30% of the national total production, respectively [39]. The HHH Plain is affected by a warm-temperate monsoon climate, and the average temperatures in winter and summer are approximately 0 °C and 26 °C, respectively. In terms of precipitation, significant differences exist in time and space dimensions. The average annual precipitation ranges from 400 to 1000 mm, increasing from north to south, but 60–80% of the annual precipitation is concentrated in the summer corn growing season. Since winter wheat is more susceptible to drought than corn, the experimental period was selected during the winter wheat growing season. Considering the differences in topography, climate, hydrology, and agricultural production conditions, the HHH Plain consists of four divisions, as shown in Figure 1. Eight agro-meteorological sites were selected in this study, which were distributed in the four agricultural subregions.
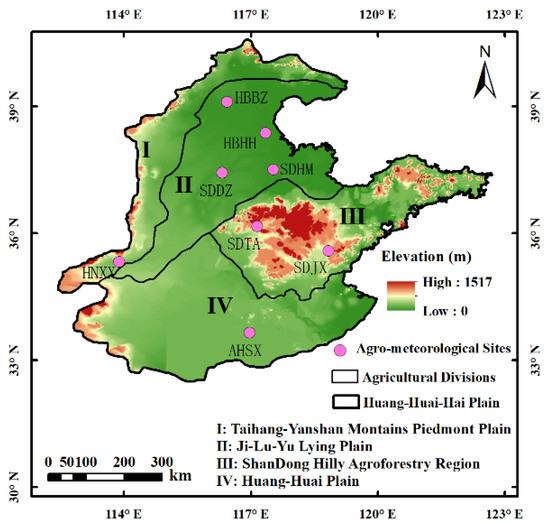
Figure 1.
Study area and distribution of agro-meteorological sites.
2.2. Data
2.2.1. Meteorological Data
Meteorological variables of daily precipitation, air temperature, wind speed, and solar radiation were required to drive the crop growth simulation. Solar radiation was calculated from sunshine duration using the Ångström equation [40]. The other four meteorological variables and sunshine duration were observed by meteorological stations in China (http://data.cma.cn/ (accessed on 1 June 2022)).
2.2.2. Agro-Meteorological Data
Agro-meteorological data, including wheat phenology, yield, soil moisture, and soil properties, were also collected in this study; these data were derived from the observations of agro-meteorological sites affiliated with the China Meteorological Administration. Wheat phenology and yield were primarily used for crop growth model calibration. The phenology was measured every 10 days during the growing season, and yield was measured after harvest. Soil moisture was used for model initialization and data assimilation evaluation. We collected soil moisture at 10, 20, 30, 40 and 50 cm depths at the representative HBBZ site, as well as at 10, 20 and 50 cm depths at seven other sites. Soil moisture was measured every 10 days during the growing season. Gravimetric measurement was adopted with four replicates, and the averaged value was used. The soil moisture obtained in this way is gravimetric water content. In order to match the satellite soil moisture data, it was then multiplied by soil bulk density and converted to volumetric water content. The soil moisture used in this study refers to volumetric water content. Soil properties included the soil texture, bulk density, field water-holding capacity, and wilting point at the corresponding layers, and these properties were used for model input and soil moisture index calculation. Soil properties were measured every 5–10 years depending on the actual condition of each site.
2.2.3. Satellite Soil Moisture
Soil moisture from the ESA (European Space Agency) CCI (Climate Change Initiative) was used as the observation for soil moisture data assimilation. ESA CCI soil moisture contains the passive, active and combined products based on various microwave sensors, which have been extensively applied in a great deal of earth system applications, e.g., climate change, land-atmosphere interactions, drought monitoring and assessment, and land surface modeling [18]. The latest version is v07.1, which can be obtained from http://www.esa-soilmoisture-cci.org (accessed on 1 June 2022). This product covers the time range from November 1978 to December 2021, with spatial and temporal resolutions of 0.25° and 1 day, respectively. The combined product during the period from 2002 to 2011 was used in this study. For more details regarding this product, please refer to Liu et al. [41], Dorigo et al. [18] and Gruber et al. [42].
3. Methods
3.1. Crop Model Description and Verification
The Decision Support System for Agro-technology Transfer (DSSAT)—Cropping System Model (CSM)—Wheat model (herein referred to as the DSSAT model [43]) was used as the model operator for data assimilation. The DSSAT model was developed by the US Department of Agriculture, and it can simulate the vegetative and reproductive growth, physiological and ecological processes, and soil water balance on a daily basis. Input data include four categories: weather; crop; soil; and management data. The weather data should at least include daily maximum and minimum temperature, solar radiation, and precipitation. Crop data indicates the genetic and ecological parameters, which describe crop photosynthesis, respiration, phenological stage and other physiological processes. Soil data represent the soil physical, chemical, and morphological parameters throughout the soil profile. Management data include a number of parameters regarding planting, irrigation, fertilization, etc.
The soil moisture simulation in the DSSAT model was implemented using the soil water balance module [44]. Soil water balance involves the following processes: infiltration; evapotranspiration (ET); runoff; and drainage. Soil water infiltration is calculated as the sum of rainfall and irrigation minus surface runoff. Surface runoff is computed based on the SCS-CN model [45] developed by the US Department of Agriculture. The soil-plant-atmosphere module (SPAM) was developed to compute the daily ET, and it provides two methods—the Priestley–Taylor [46] and FAO-56 Penman–Monteith [40] methods, to calculate the potential ET. Actual ET is calculated based on potential ET and soil water stress factors [47].
Before using the DSSAT model, the model parameters should be calibrated according to the local climate, soil conditions, management methods, and cropping system, in order to enable the model to accurately measure the characteristics of local crops. Crop phenology and yield were used to calibrate seven critical cultivar parameters (P1V, P1D, P5, G1, G2, G3, and PHINT; for a detailed description, see Jones et al. [43]). The suitable parameters in the study area were well calibrated and validated in our previous study; for more details about the model verification process, please refer to Zhou et al. [13].
3.2. Assimilation Algorithms
The Augmented Ensemble Kalman Filter (AEnKF) [30,48] was used as the assimilation algorithm in the present paper. On the basis of EnKF (Ensemble Kalman Filter; [49]), AEnKF also takes model parameters as state variables to achieve the aim of simultaneously estimating these two categorical parameters (state variables and model parameters). Hence, EnKF is the foundation of AEnKF. The implementation of EnKF involves the following steps: initialization; forecast; and analysis.
Suppose as the state variable, where represents the soil moisture in the different soil layers and crop model parameters in this study. First, the state ensemble is initialized as follows (Equation (1)):
where is the i-th initial state member (i = 1, 2, …, n; n is the ensemble size), is the expectation of the background field, is the random error, indicates the Gaussian distribution, and is background covariance matrix. Note that the initial state ensemble can also be generated by perturbing model parameters.
Second, each ensemble member is forecasted by the model operator as follows (Equation (2)):
where is the forecasted state variable of the i-th ensemble member at the time t + 1; M(•) is the model operator, represents the model forcing data, is model parameter; is the model error, and is the model covariance matrix.
Third, when the observations are available, each ensemble member is analyzed based on the following linear combination of forecasted state and observation (Equation (3)).
where is the analysis state variable, is the observation, is the observation error, R is the observation covariance matrix, H(•) is the observation operator, and is the Kalman gain matrix defined as follows:
where is the forecasted covariance matrix, and is the average value of forecasted ensemble members.
Finally, the analysis state variable is calculated by averaging each ensemble member (Equation (9)). When the next observation occurs, the state variable continues to repeat the above process until the end of data assimilation.
3.3. Data Assimilation Implementation
Data assimilation framework includes three key components: model operator; observation; and algorithm. The soil water balance module of the DSSAT model was used as the model operator for soil moisture data assimilation. Soil moisture simulations of nine winter wheat growing seasons from 2002 to 2011 were conducted at the eight agro-meteorological sites in the HHH Plain. Management parameters, such as planting date, density, depth, soil properties, fertilization, and irrigation, were set according to the records of the agro-meteorological sites.
The ESA CCI soil moisture product was used as observation data of the assimilation framework. Given the differences in the climatology and spatial resolution of in situ and satellite observations, bias correction of satellite soil moisture was required prior to data assimilation. In this study, the cumulative distribution function matching approach was applied for bias correction, which has been widely applied in data assimilation studies (e.g., [24,29,50]). Referring to existing studies [18,24,34,51], the observation error was set to 0.06 m3·m−3.
The AEnKF was selected as the algorithm for soil moisture data assimilation, which was described in detail in Section 3.2. In this study, the state variable vector consists of soil moisture at different depths and model parameters that were sensitive to soil moisture. Soil parameters such as lower limit (SLLL), drained upper limit (SDUL), saturated limit (SSAT), drainage rate (SLDR) and runoff curve number (SLRO) in the DSSAT model have significant impacts on soil moisture estimation [47]. Thus, these soil parameters were also included as state variables, and the state variable vector was as follows:
where is the state variable vector at the time t, SMi is the soil moisture at soil layer i, and n is the number of soil layers. Since the ESA CCI data only reflects soil moisture information for the top layer, the observation operator H was set to . Following the study of Ines et al. [34], an uncertainty level of 10% of the model soil parameters was introduced to perturb the initial state variables.
The ensemble size was set to 20 by considering the estimation accuracy and computational time. Additionally, with the increase in assimilation time, the standard EnKF algorithm tends to exhibit a “filter divergence” phenomenon; that is, the analysis value gradually approaches the model forecast and ignores the observation. According to existing studies [33,34], when the observation error covariance is greater than four times the model forecast error covariance (), an inflation factor of 1.05 was used to enlarge the Kalman gain to reduce this phenomenon. In addition, the impacts of ensemble size, model parameter, and assimilation interval on data assimilation are discussed in Section 4.2.
3.4. Agricultural Drought Index
The root-weighted soil moisture index (RSMI [13]) was used as an agricultural drought index to evaluate the role of data assimilation. There are two main reasons for choosing the RSMI as an indicator: (a) RSMI considers the influence of soil properties and root distribution on crop water uptake, and (b) RSMI does not require long-term time series data. RSMI is as follows:
where SMI is the soil moisture index, is the weight value, n is the number of soil layers, in which roots reach the deepest part of the soil, which varies with the crop growth stage, z is the soil thickness, RLD is the root length density, and , and represent soil moisture, field capacity and wilting point, respectively. The drought classifications of the RSMI are shown in Table 1. For more details regarding the RSMI, please refer to Zhou et al. [13].

Table 1.
Drought categories of the RSMI.
3.5. Evaluation Criteria
The root-mean-square error (RMSE, m3·m−3), correlation coefficient (R), and effectiveness (Eff, %) [52] were used to quantitatively measure the capability of data assimilation. These indicators were calculated as follows:
where is the estimated (simulated or assimilated) soil moisture at the time i, is the measured soil moisture; n is the number of measurements, and represent the average value of the estimated and measured soil moisture, respectively, and are the soil moisture before and after data assimilation, respectively, and Eff indicates the efficiency of the data assimilation. If Eff is greater than 0, this situation indicates that the soil moisture accuracy is improved after data assimilation; otherwise, a negative value denotes a degraded performance.
4. Results
4.1. Comparisons of Open-Loop and Assimilated Soil Moisture
4.1.1. Soil Moisture at Different Depths
A data assimilation experiment was first conducted and validated in the representative Bazhou (HBBZ) agro-meteorological site. The experimental period incorporated the growing seasons of winter wheat from 2002 to 2011. Figure 2 shows the comparison of the open-loop and assimilated soil moisture at the HBBZ site. Open-loop soil moisture is the direct simulation from the DSSAT model without data assimilation. As shown, relatively large errors were present in the open-loop simulations compared with the measured soil moisture, and open-loop soil moisture was significantly lower than observed data in the late growth stage of winter wheat. In contrast, assimilated results were in good agreement with the observations. Quantitatively, the goodness-of-fit statistics (RMSE, R, and Eff) at the HBBZ site are shown in Table 2. The RMSEs of open-loop soil moisture in the 10–50 cm depth during the 2002–2011 growing season were 0.084, 0.087, 0.088, 0.092, and 0.066 m3·m−3, respectively, and the RMSEs of assimilated soil moisture were 0.048, 0.031, 0.074, 0.060, and 0.043 m3·m−3, respectively. Except for the depths of 10 and 50 cm, the correlation coefficients of soil moisture at other soil layers increased slightly compared with those in the open-loop simulations. The effectiveness Eff values of soil moisture at a depth of 10–50 cm were 66.9%, 87.4%, 27.9%, 57.9%, and 56.0%, respectively, indicating that the soil moisture at each layer improved after data assimilation.
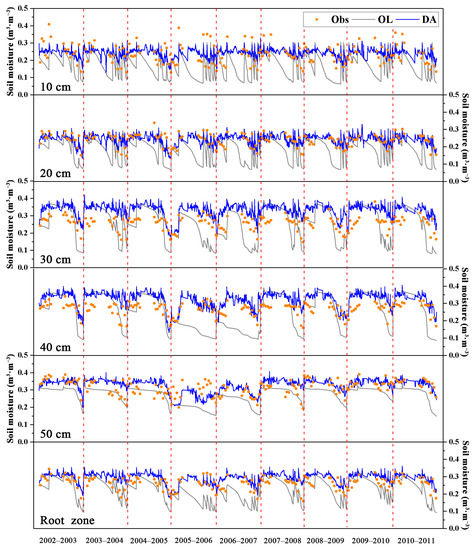
Figure 2.
Comparison of open loop (OL) and assimilated (DA) soil moisture with observations (Obs) during the winter wheat growing seasons (2002–2011) at the HBBZ site.

Table 2.
Statistics of open-loop (OL) and assimilated (DA) soil moisture at the HBBZ site.
We also compared the open-loop and assimilated soil moisture with in situ observations at all eight agro-meteorological sites. Except for the HBBZ site, measured soil moisture at the other sites was collected at three depths: 10, 20, and 50 cm. Figure 3 shows the scatter plots and histograms of soil moisture estimates and observations. The results indicated that assimilated soil moisture matched better with in situ observations than open-loop simulations. Additionally, compared with open-loop simulations, the histograms of assimilated soil moisture were more similar to these of observations. For the eight sites, the average RMSEs of open-loop simulations at depths of 10, 20, and 50 cm were 0.088, 0.091, and 0.056 m3·m−3, respectively, and the average RMSEs of assimilated soil moisture were 0.047, 0.046, and 0.045 m3·m−3, respectively (Table 3). The correlations between the assimilated soil moisture with observations at each layer were improved. The Eff values of the soil moisture at each layer were greater than zero, indicating that moisture estimates throughout the soil profile were improved via data assimilation.
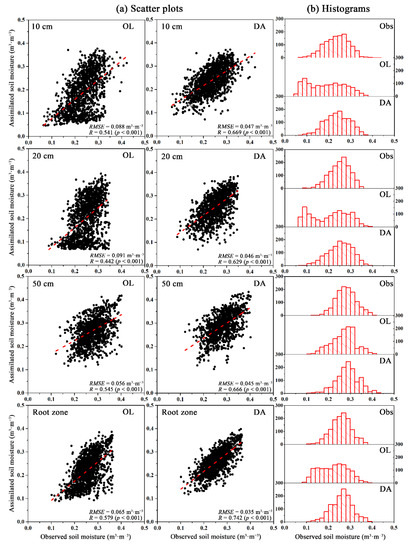
Figure 3.
Comparisons of open-loop (OL) and assimilated (DA) soil moisture with observations (Obs) in the different soil depths: (a) scatter plots between OL (DA) and Obs; (b) histograms of OL, DA, and Obs. The red lines represent the linear regressions between open-loop/assimilated soil moisture and observed soil moisture.

Table 3.
Statistics of open-loop (OL) and assimilated (DA) soil moisture at all eight sites.
4.1.2. Root-Zone Soil Moisture
Root-zone soil moisture plays a significant role in agricultural drought monitoring. For cereal crops, roots are mainly distributed at a depth of 0–50 cm; thus, soil moisture within these depths has often been used to monitor and predict agricultural drought [2,53]. In this study, the average of soil moisture in each layer within 0–50 cm was regarded as the root-zone value. The assimilation results and error statistics of the root-zone soil moisture at HBBZ site are also shown in Figure 2 and Table 2. The RMSEs of open-loop and assimilated soil moistures were 0.067 and 0.038 m3·m−3, respectively. Similarly, Figure 3 and Table 3 display the results of the root-zone soil moisture at the eight sites. In comparison with the open-loop simulations, the RMSE of the root-zone soil moisture was reduced from 0.065 to 0.035 m3·m−3, and R was increased from 0.579 to 0.742. Furthermore, compared with the soil moisture at each layer, root-zone soil moisture also had a better agreement with in situ observations.
4.2. Impacts of Different Strategies on Data Assimilation
4.2.1. Impact of Simultaneous State-Parameter Estimation
During the progress of data assimilation, initial conditions, model parameters, external observations and algorithm are the main factors affecting the accuracy of state variable estimation. Hence, the accuracy of the model parameters is important for improving state variable estimation when other conditions are the same. In the AEnKF algorithm, state variables and model parameters are updated at the same time according to the Kalman gain, which is theoretically expected to enhance the soil moisture measurement. Here we compared the utilities of the results based on the AEnKF algorithm (simultaneous state–parameter estimation) and EnKF algorithm (state-only estimation) at the HHBZ site during the growing seasons of 2004–2005 and 2005–2006.
Figure 4 and Figure 5 display the time series and RMSEs of soil moisture estimates based on the AEnKF and EnKF algorithms, respectively. The results show that, influenced by the model structure, the error of the soil moisture estimates based on EnKF were still large in the late growth season. The RMSEs of the assimilated soil moisture at depths of 10–50 cm and root zone based on the EnKF (AEnKF) algorithm were 0.048 (0.048), 0.030 (0.029), 0.085 (0.061), 0.084 (0.047), 0.071 (0.057), and 0.049 (0.029), respectively. The errors of assimilated soil moisture at each soil layer based on AEnKF were less than those based on the EnKF algorithm. According to the time series data and error statistics, the performance of the AEnKF-based soil moisture data assimilation was better, which also indicated that the simultaneous state-parameter estimation was effective for improving state variable estimation in data assimilation.
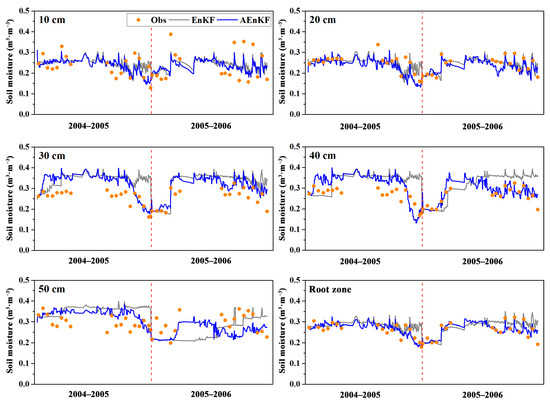
Figure 4.
Soil moisture assimilation estimates using AEnKF and EnKF algorithms at different soil depths during the growing seasons of 2004–2005 and 2005–2006.
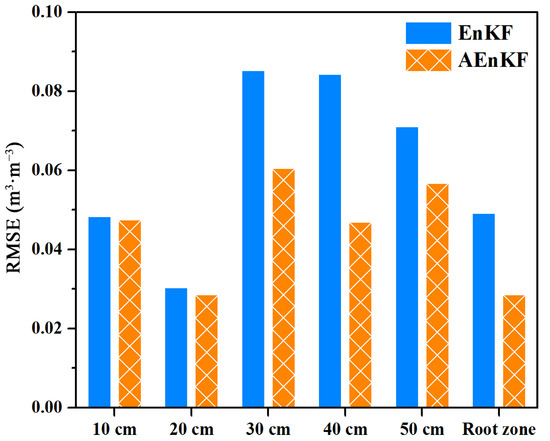
Figure 5.
Root-mean-square errors (RMSEs) of assimilated soil moisture at different soil depths using AEnKF and EnKF algorithms.
4.2.2. Impact of Ensemble Size
The EnKF algorithm uses a Monte Carlo approach to generate the model error distribution. Theoretically, as ensemble size increases, the model error distribution can be better characterized. However, a significant expansion of ensemble size leads to a dramatic increase in model calculation costs. Therefore, ensemble size is often selected with the compromise of accuracy and time cost in practical applications, especially in the case of complex models with many parameters, which can not only ensure accuracy but also reduce calculation time. In this section, we compared the accuracy of the assimilated soil moisture with five, ten, twenty, and fifty ensemble members during the growing seasons of 2004–2005 and 2005–2006.
Figure 6 shows the time series of soil moisture estimates with different ensemble members. Generally, the fluctuations of the assimilated soil moisture time series under different ensemble members were similar. When the ensemble size was small, the fluctuations in soil moisture were relatively large; conversely, when the ensemble size was large, the change was relatively small. As ensemble size increased, the error of assimilated soil moisture decreased to some extent (Figure 7). However, overall, no obvious difference in the error of assimilation results occurred under the different ensemble members. The error of the root-zone soil moisture was the smallest, with RMSEs of 0.033, 0.029, 0.029, and 0.027 m3·m−3 under 5, 10, 20, and 50 ensemble members, respectively. In previous studies, ensemble size was mostly set between 10 and 50 [24,33,34,54]. According to the error statistics, the RMSEs of the assimilated soil moisture under 20 and 50 members were similar. Compared with the observation data and model structure error, the influence of ensemble size on the soil moisture data assimilation was marginal. In view of the high dimensionality of the state variables in this study, the calculation cost of larger ensemble size was relatively expensive. Thus, considering the calculation accuracy and time cost, 20 ensemble members were deemed more appropriate for soil moisture assimilation at the other sites.
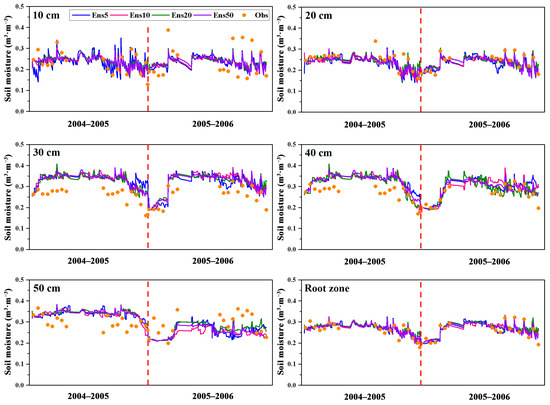
Figure 6.
Soil moisture assimilation estimates with different ensemble sizes at different soil depths during the growing seasons of 2004–2005 and 2005–2006.
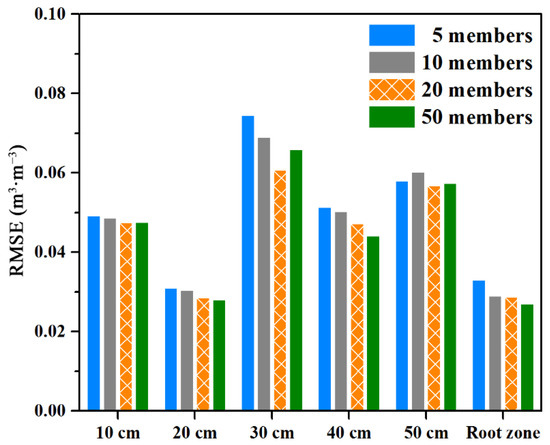
Figure 7.
Root-mean-square errors (RMSEs) of assimilated soil moisture with five, ten, twenty and fifty members at different soil depths.
4.2.3. Impact of Temporal Interval
Although the ESA CCI soil moisture product has a one-day temporal resolution, the acquisition of continuous daily data during the growing season is difficult. This problem can be caused by many reasons, including satellite orbit changes, radio frequency interference (RFI), underlying surface (e.g., snow and ice), and physical limitations of satellite sensors [18,55,56]. Under the circumstances of incomplete observations, an exploration of the influence of observation frequency on soil moisture data assimilation is necessary.
An assimilation experiment was conducted with observation data at intervals of three, five and ten days for two winter wheat growing seasons from 2004 to 2006. The results showed that the fluctuation of soil moisture estimated with observation data at a ten-day interval was more obvious than that at three- and five-day intervals (Figure 8). When the temporal interval of observations was large, the assimilated soil moisture tended to approach the model simulation results. The model simulation values were lower in the late growth season, which led to an increase in soil moisture fluctuation. The detailed RMSEs of soil moisture with different assimilation intervals are shown in Figure 9. Generally, as the frequency of observation increased, the error of assimilated soil moisture decreased, but the difference in soil moisture error at intervals of three and five days was small. Therefore, the interval of observation data within five days was identified as the ideal time frequency for obtaining soil moisture with high accuracy, in agreement with the conclusion of Walker and Houser [57].
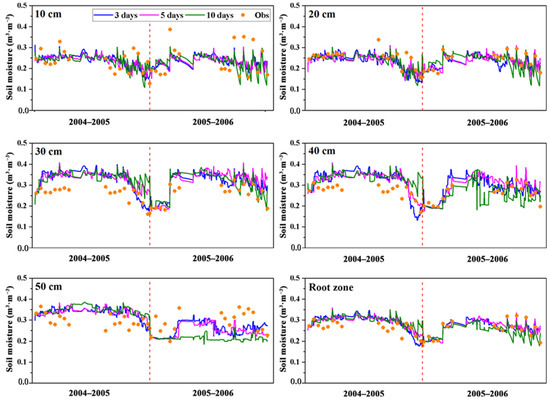
Figure 8.
Soil moisture assimilation estimates with the observation intervals of three, five, and ten days at different soil depths during the growing seasons of 2004–2005 and 2005–2006.
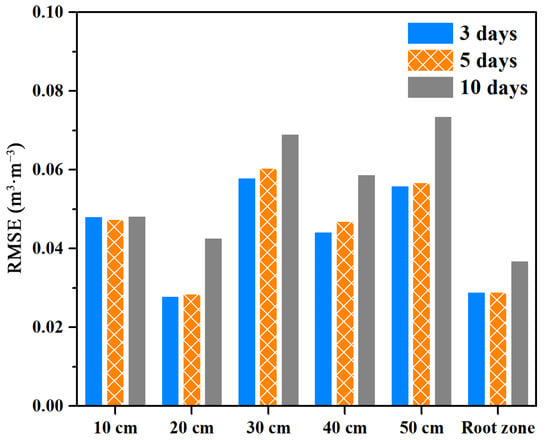
Figure 9.
Comparison of the RMSEs of assimilated soil moisture with observation intervals of three, five, and ten days at different soil depths.
4.3. Effect of Data Assimilation on Agricultural Drought Monitoring
4.3.1. Comparison with Observed Soil Moisture-Based Drought Index
In this study, the RSMI was used as an indicator for agricultural drought monitoring. We compared the RSMI based on assimilated soil moisture () and open-loop simulations () with the RSMI based on in situ observations (), with the aim of investigating the extent to which soil moisture data assimilation improved the level of agricultural drought monitoring.
Firstly, from the perspective of qualitative assessment, time series graphs and scatter plots were used to show the fluctuations and consistency of the RSMI. Figure 10 displays the RSMI time series during the growing seasons from 2002 to 2011 at eight sites. The results illustrate that the and had similar fluctuations during the growing seasons. In the HHH Plain, due to the huge water demand for water in the late growing season of winter wheat, a decrease in soil moisture often occurred during this period. Both the and showed this characteristic. showed a good match with in the early growth season of winter wheat, however, in the late growth season, the values for were significantly lower than those for . According to the drought levels of RSMI, the low value of in the late growth season indicated a severe or extreme drought, which might be inconsistent with the reality.
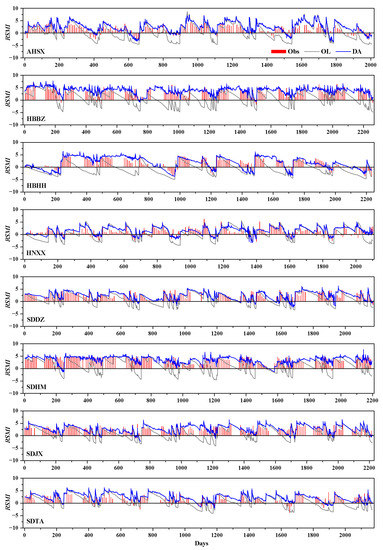
Figure 10.
RSMI time series calculated from the observed, simulated and assimilated soil moisture for nine winter wheat growing seasons at the eight sites.
Secondly, from the perspective of quantitative assessment, Table 4 displayed the error statistics of RSMI based on open-loop and assimilated soil moisture at eight agro-meteorological sites. The average RMSEs of and at the eight sites were 2.60 and 1.38, respectively, and the corresponding average R values were 0.62 and 0.68, respectively. Compared with the , the of all sites had a higher correlation at the 0.01 significance level, and the RMSE of was smaller than that of for all sites. According to the drought category of RSMI (Table 1), a value of less than zero indicated that drought occurred; when the RSMI value was decreased by one, the drought intensity was increased by one level. Therefore, the difference between the average RMSEs of and was 1.22, which implied that, compared with the drought index based on open-loop simulations, the index based on assimilated data could improve at least one drought level in agricultural drought monitoring.

Table 4.
Root-mean-square errors (RMSEs) and correlation coefficients (R) for the RSMI based on open-loop (OL) and assimilated soil moisture (DA) at the eight sites. R values are shown in brackets.
4.3.2. Comparison with Winter Wheat Yield
Crop yield reduction is a major manifestation of crop growth threatened by drought. Here, we discuss the relationship between agricultural drought and crop yield reduction to further evaluate the effect of data assimilation on agricultural drought monitoring. Yield loss ratio (YLR) was utilized to quantify the degree of crop yield reduction, calculated as follows: , where represents the annual crop yield, and is the multiyear average yield. According to the disaster record dataset of agro-meteorological sites from 2002 to 2011, six sites (AHSX, HBHH, SDDZ, SDHM, SDJX, and SDTA) experienced agricultural droughts. Figure 11 shows the relationship between the RSMI ( and ) and crop yield loss ratio (YLR). Overall, the RSMI matched well with the YLR during the nine growing seasons; that is, when the RSMI value was small (drought), the crop yield was reduced, and when the RSMI value was large (wetness), the crop yield increased.
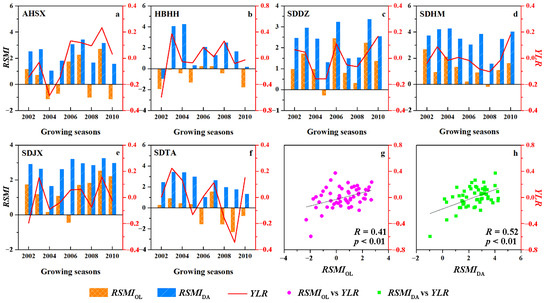
Figure 11.
The relationship between the RSMI and yield loss ratio (YLR) during the growing seasons from 2002 to 2011: (a–f) the dynamics of RSMI and YLR at each site; (g,h) the scatter plots between RSMI and YLR at the six sites. , RSMI based on open-loop soil moisture; , RSMI based on assimilated soil moisture.
As a result of the small sample size per site, the RSMIs from the six sites were used together to statistically investigate the correlation with YLR (Figure 11g,h). The correlation coefficients between the RSMI ( and ) and YLR were 0.41 and 0.52 (p < 0.01), respectively. The results demonstrated that the RSMI was significantly correlated with YLR, and the RSMI based on assimilated soil moisture performed better than that based on open-loop simulations. Therefore, data assimilation could further strengthen the skill of the drought index to reflect the yield losses by improving soil moisture estimation.
5. Discussion
In this study, we established a data assimilation scheme to estimate surface and root zone soil moisture, and we evaluated the effect of data assimilation on agricultural drought monitoring. The main advantage of this scheme is that, combined with a crop models and remote sensing observations, the process of crop growth and development can be simulated, and soil moisture information can also be obtained [19,58]. Such results are very helpful for constructing a drought index with agronomic traits [13,19]. The assimilated results demonstrate that soil moisture estimates were significantly improved after data assimilation (Figure 2 and Figure 3; Table 2 and Table 3). Although the observation data in the data assimilation framework was surface satellite soil moisture, deeper layers also showed the improved results after assimilation. From the perspective of different soil depths, the improvement of surface soil moisture accuracy after data assimilation was greater than that of the deep layers. As the soil depth increased, the ability of assimilating surface soil moisture to improve the accuracy of deep soil moisture decreased. These findings also agree with previous studies [20,30]. We can also find that the results of soil moisture assimilation at depths of 30 and 40 cm were less accurate. Soil water balance is a very complex physical process, and the possible reasons for the poor performance include the following: (1) the inability of the model structure to perfectly describe the soil water balance process; (2) the uncertainties of the input data (soil attribute data and management data) [58]. Due to the influence of many factors (models, observations, and forcings), the estimation of soil moisture at a fixed depth may have some uncertainties. Root-zone soil moisture (averaged at each layer within the root zone) was observed to be a better estimate (Table 3). Root-zone soil moisture plays a significant role in agricultural drought monitoring [2,53]. Our study found that compared with the drought index based on open-loop soil moisture, the index based on assimilated data could improve at least one drought level in agricultural drought monitoring. Therefore, it is an important and feasible approach to improve the accuracy of root-zone soil moisture through data assimilation, thereby enhancing the estimation of agricultural drought.
Model and observation are key components for data assimilation. In this study, we found that the performance of the AEnKF-based soil moisture data assimilation was better, which also indicated that the simultaneous state-parameter estimation was more effective for improving soil moisture estimation. This conclusion highlights the importance of simultaneous estimation of model parameters and state variables, which is consistent with related research [30,48,59,60]. In addition to model parameters, observation has a crucial impact on data assimilation. Errors caused by observations include the bias between model and observation and the error of the observation itself. Discrepancies between model and observation are caused by a variety of factors, including uncertainty of model parameters, a difference in spatial scales. Bias correction is effective to reduce the discrepancies between model and observation [59,60]. In this study, the CDF matching approach was used to reduce the impact of scale difference between the gridded satellite observation and point-scale model prior to data assimilation. The error of observation itself is generally set based on empirical values [24,34,59,60]. In our study, we set it based on the relevant studies on soil moisture validation [18,51], and we obtained good estimation results. Recently, several studies have proposed new methods for bias correction and model parameter estimation to further improve the performance of data assimilation. Instead of bias correction prior to data assimilation, Qin et al. [59] proposed on-line bias correction during data assimilation and obtained a good estimate. Tian et al. [60] developed a novel assimilation method to estimate both model and observation errors to improve soil moisture retrievals, in which model state, model parameters, model error, and observation error were estimated simultaneously. Overall, model parameters and observation errors are still worthy of continued research to further improve the estimation accuracy of state variables.
Through this study, we found that the crop growth model-based data assimilation scheme effectively improved soil moisture estimation and was significantly beneficial for agricultural drought monitoring. It is worth noting that this study also had some limitations that need to be further discussed. On one hand, the study was conducted on a point scale, as accurate regional crop model parameterization and high-precision gridded data (meteorological forcings, soil data, and field management data) used for crop modeling are still challenging. Some studies have investigated the gridded data assimilation scheme [32,33,61,62], however, generally gridded meteorological data are used, whereas soil data, and management data (e.g., irrigation), and crop parameters over large areas are still replaced by empirical values or coarse-resolution data. Therefore, observations at higher spatial and temporal resolution (e.g., SMAP product [63]) and more accurate model parameterization schemes can further improve the gridded data assimilation framework, help analyze the variations in drought characteristics in different regions, and better understand the mechanism of drought formation. On the other hand, a single remote sensing data source was used in this study. Multi-source remote sensing can provide land surface monitoring from different perspectives. Some scholars carried out data assimilation based on various remote sensing data sources [24,61,62,64,65]; however, so far collaborative applications based on multi-source remote sensing data are still rare in agricultural drought monitoring. With the launch of subsequent remote sensing satellites, data quality and spatial-temporal resolution will be further improved. The combination of multi-source remote sensing data and crop models will help to further strengthen the application of drought indicators in agricultural drought monitoring.
6. Conclusions
In this study, the DSSAT crop model and satellite soil moisture were integrated for data assimilation to improve soil moisture estimation. The assimilated results were validated using in situ observations of agro-meteorological sites. The impacts of different strategies (simultaneous state-parameter estimation, ensemble size and temporal interval) on data assimilation were also discussed. Furthermore, we evaluated the effect of data assimilation on agricultural drought monitoring through comparisons with the observed soil moisture-based drought index and winter wheat yield. The main conclusions are summarized as follows:
- (1)
- Compared with open-loop simulations, crop growth model-based data assimilation effectively improved soil moisture estimation throughout the soil profile. Soil moisture in the root zone was more consistent with in situ observation (RMSE = 0.035 m3·m−3, R = 0.742) than that in other soil layers;
- (2)
- Simultaneous state-parameter estimation (based on AEnKF algorithm) performed better than state-only estimation (based on EnKF algorithm). As the observation frequency and ensemble size increased, the accuracy of soil moisture estimates also increased. In the case of a comprehensive consideration of estimation accuracy and calculation cost, observation frequency within five days with twenty ensemble members could meet the requirement of soil moisture accuracy;
- (3)
- Compared with the drought index based on open-loop soil moisture, the drought index based on assimilated results improves at least one drought level in agricultural drought monitoring. Additionally, the drought index based on assimilated soil moisture was better correlated with winter wheat yield than that based on open-loop simulation.
Author Contributions
Conceptualization, H.Z.; methodology, H.Z. and J.Y.; software, H.Z. and J.Y.; validation, H.Z., G.G. and J.Y.; writing—original draft preparation, H.Z., G.G. and J.Y.; writing—review and editing, H.Z., G.G., J.Y., H.H., L.S. and W.L.; funding acquisition, H.Z. and L.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (Grant No. 41907394, 41901360); Zhejiang Provincial Natural Science Foundation of China (Grant No. LY21D010004).
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
We are grateful to those who participated in the data processing and manuscript revisions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Mishra, A.K.; Singh, V.P. A review of drought concepts. J. Hydrol. 2010, 391, 202–216. [Google Scholar] [CrossRef]
- Martínez-Fernández, J.; González-Zamora, A.; Sánchez, N.; Gumuzzio, A. A soil water based index as a suitable agricultural drought indicator. J. Hydrol. 2015, 522, 265–273. [Google Scholar] [CrossRef]
- AghaKouchak, A.; Farahmand, A.M.; Melton, F.S.; Teixeira, J.P.; Anderson, M.; Wardlow, B.; Hain, C.R. Remote sensing of drought: Progress, challenges and opportunities. Rev. Geophys. 2015, 53, 452–480. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.; Pan, Y.; Zhu, X.; Yang, T.; Bai, J.; Sun, Z. Drought evolution and its impact on the crop yield in the North China Plain. J. Hydrol. 2018, 564, 984–996. [Google Scholar] [CrossRef]
- Samaniego, L.; Thober, S.; Kumar, R.; Wanders, N.; Rakovec, O.; Pan, M.; Zink, M.; Sheffield, J.; Wood, E.F.; Marx, A. Anthropogenic warming exacerbates European soil moisture droughts. Nat. Clim. Chang. 2018, 8, 421–426. [Google Scholar] [CrossRef]
- Mora, C.; Spirandelli, D.; Franklin, E.C.; Lynham, J.; Kantar, M.B.; Miles, W.; Smith, C.Z.; Freel, K.; Moy, J.; Louis, L.V.; et al. Broad threat to humanity from cumulative climate hazards intensified by greenhouse gas emissions. Nat. Clim. Chang. 2018, 8, 1062–1071. [Google Scholar] [CrossRef]
- Crow, W.T.; Kumar, S.V.; Bolten, J.D. On the utility of land surface models for agricultural drought monitoring. Hydrol. Earth Syst. Sci. 2012, 16, 3451–3460. [Google Scholar] [CrossRef] [Green Version]
- Sheffield, J.; Goteti, G.; Wen, F.; Wood, E. A simulated soil moisture based drought analysis for the United States. J. Geophys. Res. D Atmos. 2004, 109, D24108. [Google Scholar] [CrossRef]
- Dutra, E.; Viterbo, P.; Miranda, P.M.A. ERA-40 reanalysis hydrological applications in the characterization of regional drought. Geophys. Res. Lett. 2008, 35, L19402. [Google Scholar] [CrossRef]
- Carrão, H.; Russo, S.; Sepulcre-Canto, G.; Barbosa, P. An empirical standardized soil moisture index for agricultural drought assessment from remotely sensed data. Int. J. Appl. Earth Obs. Geoinf. 2016, 48, 74–84. [Google Scholar] [CrossRef]
- Sridhar, V.; Hubbard, K.G.; You, J.; Hunt, E.D. Development of the Soil Moisture Index to Quantify Agricultural Drought and Its “User Friendliness” in Severity-Area-Duration Assessment. J. Hydrometeorol. 2008, 9, 660–676. [Google Scholar] [CrossRef] [Green Version]
- Hunt, E.D.; Hubbard, K.G.; Wilhite, D.A.; Arkebauer, T.J.; Dutcher, A.L. The development and evaluation of a soil moisture index. Int. J. Climatol. 2009, 29, 747–759. [Google Scholar] [CrossRef]
- Zhou, H.; Wu, J.; Geng, G.; Li, X.; Wang, Q.; Lei, T.; Mo, X.; Liu, L. Enhancing the Ability of a Soil Moisture-based Index for Agricultural Drought Monitoring by Incorporating Root Distribution. JAWRA J. Am. Water Resour. Assoc. 2017, 53, 1409–1423. [Google Scholar] [CrossRef]
- Peng, J.; Albergel, C.; Balenzano, A.; Brocca, L.; Cartus, O.; Cosh, M.H.; Crow, W.T.; Dabrowska-Zielinska, K.; Dadson, S.; Davidson, M.W.; et al. A roadmap for high-resolution satellite soil moisture applications—Confronting product characteristics with user requirements. Remote Sens. Environ. 2020, 252, 112162. [Google Scholar] [CrossRef]
- Li, Z.-L.; Leng, P.; Zhou, C.; Chen, K.-S.; Zhou, F.-C.; Shang, G.-F. Soil moisture retrieval from remote sensing measurements: Current knowledge and directions for the future. Earth-Sci. Rev. 2021, 218, 103673. [Google Scholar] [CrossRef]
- Babaeian, E.; Sadeghi, M.; Jones, S.B.; Montzka, C.; Vereecken, H.; Tuller, M. Ground, Proximal, and Satellite Remote Sensing of Soil Moisture. Rev. Geophys. 2019, 57, 530–616. [Google Scholar] [CrossRef] [Green Version]
- Baldwin, D.; Manfreda, S.; Keller, K.; Smithwick, E. Predicting root zone soil moisture with soil properties and satellite near-surface moisture data across the conterminous United States. J. Hydrol. 2017, 546, 393–404. [Google Scholar] [CrossRef]
- Dorigo, W.; Wagner, W.; Albergel, C.; Albrecht, F.; Balsamo, G.; Brocca, L.; Chung, D.; Ertl, M.; Forkel, M.; Gruber, A.; et al. ESA CCI Soil Moisture for improved Earth system understanding: State-of-the art and future directions. Remote Sens. Environ. 2017, 203, 185–215. [Google Scholar] [CrossRef]
- Mishra, A.K.; Ines, A.V.M.; Das, N.N.; Prakash Khedun, C.; Singh, V.P.; Sivakumar, B.; Hansen, J.W.; Mishra, A.K.; Sivakumar, B.; Singh, V.P. Anatomy of a local scale drought; application of assimilated remote sensing products, crop model, and statistical methods to an agricultural drought study. J. Hydrol. 2015, 526, 15–29. [Google Scholar] [CrossRef]
- Sahoo, A.K.; De Lannoy, G.J.; Reichle, R.H.; Houser, P.R. Assimilation and downscaling of satellite observed soil moisture over the Little River Experimental Watershed in Georgia, USA. Adv. Water Resour. 2013, 52, 19–33. [Google Scholar] [CrossRef]
- Parrens, M.; Mahfouf, J.-F.; Barbu, A.L.; Calvet, J.-C. Assimilation of surface soil moisture into a multilayer soil model: Design and evaluation at local scale. Hydrol. Earth Syst. Sci. 2014, 18, 673–689. [Google Scholar] [CrossRef] [Green Version]
- Sabater, J.M.; Jarlan, L.; Calvet, J.-C.; Bouyssel, F.; De Rosnay, P. From Near-Surface to Root-Zone Soil Moisture Using Different Assimilation Techniques. J. Hydrometeorol. 2007, 8, 194–206. [Google Scholar] [CrossRef]
- Huang, C.; Li, X.; Lu, L. Retrieving soil temperature profile by assimilating MODIS LST products with ensemble Kalman filter. Remote Sens. Environ. 2008, 112, 1320–1336. [Google Scholar] [CrossRef]
- Kumar, S.; Peters-Lidard, C.; Mocko, D.; Reichle, R.; Liu, Y.; Arsenault, K.; Xia, Y.; Ek, M.; Riggs, G.; Livneh, B.; et al. Assimilation of Remotely Sensed Soil Moisture and Snow Depth Retrievals for Drought Estimation. J. Hydrometeorol. 2014, 15, 2446–2469. [Google Scholar] [CrossRef]
- Han, E.; Crow, W.T.; Holmes, T.; Bolten, J. Benchmarking a Soil Moisture Data Assimilation System for Agricultural Drought Monitoring. J. Hydrometeorol. 2014, 15, 1117–1134. [Google Scholar] [CrossRef]
- Bolten, J.D.; Crow, W.T.; Zhan, X.; Jackson, T.J.; Reynolds, C.A. Evaluating the Utility of Remotely Sensed Soil Moisture Retrievals for Operational Agricultural Drought Monitoring. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2009, 3, 57–66. [Google Scholar] [CrossRef] [Green Version]
- Sun, X.; Lai, P.; Wang, S.; Song, L.; Ma, M.; Han, X. Monitoring of Extreme Agricultural Drought of the Past 20 Years in Southwest China Using GLDAS Soil Moisture. Remote Sens. 2022, 14, 1323. [Google Scholar] [CrossRef]
- De Lannoy, G.J.M.; Reichle, R.H. Assimilation of SMOS brightness temperatures or soil moisture retrievals into a land surface model. Hydrol. Earth Syst. Sci. 2016, 20, 4895–4911. [Google Scholar] [CrossRef] [Green Version]
- Seo, E.; Lee, M.-I.; Reichle, R.H. Assimilation of SMAP and ASCAT soil moisture retrievals into the JULES land surface model using the Local Ensemble Transform Kalman Filter. Remote Sens. Environ. 2020, 253, 112222. [Google Scholar] [CrossRef]
- Monsivais-Huertero, A.; Graham, W.; Judge, J.; Agrawal, D. Effect of simultaneous state–parameter estimation and forcing uncertainties on root-zone soil moisture for dynamic vegetation using EnKF. Adv. Water Resour. 2010, 33, 468–484. [Google Scholar] [CrossRef]
- Dong, T.; Liu, J.; Qian, B.; Zhao, T.; Jing, Q.; Geng, X.; Wang, J.; Huffman, T.; Shang, J. Estimating winter wheat biomass by assimilating leaf area index derived from fusion of Landsat-8 and MODIS data. Int. J. Appl. Earth Obs. Geoinf. 2016, 49, 63–74. [Google Scholar] [CrossRef]
- Huang, J.; Sedano, F.; Huang, Y.; Ma, H.; Li, X.; Liang, S.; Tian, L.; Zhang, X.; Fan, J.; Wu, W. Assimilating a synthetic Kalman filter leaf area index series into the WOFOST model to improve regional winter wheat yield estimation. Agric. For. Meteorol. 2016, 216, 188–202. [Google Scholar] [CrossRef]
- Huang, J.; Tian, L.; Liang, S.; Ma, H.; Becker-Reshef, I.; Huang, Y.; Su, W.; Zhang, X.; Zhu, D.; Wu, W. Improving winter wheat yield estimation by assimilation of the leaf area index from Landsat TM and MODIS data into the WOFOST model. Agric. For. Meteorol. 2015, 204, 106–121. [Google Scholar] [CrossRef] [Green Version]
- Ines, A.V.; Das, N.N.; Hansen, J.W.; Njoku, E.G. Assimilation of remotely sensed soil moisture and vegetation with a crop simulation model for maize yield prediction. Remote Sens. Environ. 2013, 138, 149–164. [Google Scholar] [CrossRef] [Green Version]
- Jiang, Z.; Chen, Z.; Chen, J.; Ren, J.; Li, Z.; Sun, L. The Estimation of Regional Crop Yield Using Ensemble-Based Four-Dimensional Variational Data Assimilation. Remote Sens. 2014, 6, 2664–2681. [Google Scholar] [CrossRef] [Green Version]
- Ren, S.; Guo, B.; Wu, X.; Zhang, L.; Ji, M.; Wang, J. Winter wheat planted area monitoring and yield modeling using MODIS data in the Huang-Huai-Hai Plain, China. Comput. Electron. Agric. 2021, 182, 106049. [Google Scholar] [CrossRef]
- National Bureau of Statistics of China. China Statistical Yearbook; National Bureau of Statistics of China: Beijing, China, 2021.
- Hou, M. Study of Agricultural Structure Adjustment and Agricultural Development Stratagem on HuangHuaiHai Plain. Ph.D. Thesis, China Agricultural University, Beijing, China, 2004. [Google Scholar]
- Xu, J.; Ju, H.; Mei, X.; Liu, Q.; Yang, J. Simulation on potential effects of drought on winter wheat in Huang-Huai-Hai Plain from 1981 to 2010. Trans. Chin. Soc. Agric. Eng. 2015, 31, 150–158. (In Chinese) [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration—Guidelines for Computing Reference Crop Evapo-Transpiration; FAO Irrigation and Drainage Paper No. 56; FAO: Rome, Italy, 1998; pp. 1–15. [Google Scholar]
- Liu, Y.Y.; Dorigo, W.A.; Parinussa, R.M.; de Jeu, R.A.M.; Wagner, W.; McCabe, M.F.; Evans, J.P.; van Dijk, A.I.J.M. Trend-preserving blending of passive and active microwave soil moisture retrievals. Remote Sens. Environ. 2012, 123, 280–297. [Google Scholar] [CrossRef]
- Gruber, A.; Dorigo, W.A.; Crow, W.; Wagner, W. Triple Collocation-Based Merging of Satellite Soil Moisture Retrievals. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6780–6792. [Google Scholar] [CrossRef]
- Jones, J.W.; Hoogenboom, G.; Porter, C.H.; Boote, K.J.; Batchelor, W.D.; Hunt, L.A.; Wilkens, P.W.; Singh, U.; Gijsman, A.J.; Ritchie, J.T. The DSSAT cropping system model. Eur. J. Agron. 2003, 18, 235–265. [Google Scholar] [CrossRef]
- Ritchie, J.T. Model for predicting evaporation from a row crop with incomplete cover. Water Resour. Res. 1972, 8, 1204–1213. [Google Scholar] [CrossRef] [Green Version]
- SCS. National Engineering Handbook, Section 4: Hydrology; Soil Conservation Service: Washington, DC, USA, 1972.
- Priestley, C.H.B.; Taylor, R.J. On the assessment of surface heat flux and evaporation using large-scale parameters. Mon. Weather Rev. 1972, 100, 81–92. [Google Scholar] [CrossRef]
- Soldevilla-Martinez, M.; Quemada, M.; López-Urrea, R.; Muñoz-Carpena, R.; Lizaso, J. Soil water balance: Comparing two simulation models of different levels of complexity with lysimeter observations. Agric. Water Manag. 2014, 139, 53–63. [Google Scholar] [CrossRef]
- Chen, W.; Huang, C.; Shen, H.; Li, X. Comparison of ensemble-based state and parameter estimation methods for soil moisture data assimilation. Adv. Water Resour. 2015, 86, 425–438. [Google Scholar] [CrossRef]
- Evensen, G. The Ensemble Kalman Filter: Theoretical formulation and practical implementation. Ocean. Dyn. 2003, 53, 343–367. [Google Scholar] [CrossRef]
- Nair, A.S.; Indu, J. Improvement of land surface model simulations over India via data assimilation of satellite-based soil moisture products. J. Hydrol. 2019, 573, 406–421. [Google Scholar] [CrossRef]
- An, R.; Zhang, L.; Wang, Z.; Quaye-Ballard, J.A.; You, J.; Shen, X.; Gao, W.; Huang, L.; Zhao, Y.; Ke, Z. Validation of the ESA CCI soil moisture product in China. Int. J. Appl. Earth Obs. Geoinf. 2016, 48, 28–36. [Google Scholar] [CrossRef]
- Aubert, D.; Loumagne, C.; Oudin, L. Sequential assimilation of soil moisture and streamflow data in a conceptual rainfall–runoff model. J. Hydrol. 2003, 280, 145–161. [Google Scholar] [CrossRef]
- Narasimhan, B.; Srinivasan, R. Development and evaluation of Soil Moisture Deficit Index (SMDI) and Evapotranspiration Deficit Index (ETDI) for agricultural drought monitoring. Agric. For. Meteorol. 2005, 133, 69–88. [Google Scholar] [CrossRef]
- Chakrabarti, S.; Bongiovanni, T.; Judge, J.; Zotarelli, L.; Bayer, C. Assimilation of SMOS Soil Moisture for Quantifying Drought Impacts on Crop Yield in Agricultural Regions. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 3867–3879. [Google Scholar] [CrossRef]
- Almendra-Martín, L.; Martínez-Fernández, J.; Piles, M.; González-Zamora, Á. Comparison of gap-filling techniques applied to the CCI soil moisture database in Southern Europe. Remote Sens. Environ. 2021, 258, 112377. [Google Scholar] [CrossRef]
- Zhang, L.; Liu, Y.; Ren, L.; Teuling, A.J.; Zhang, X.; Jiang, S.; Yang, X.; Wei, L.; Zhong, F.; Zheng, L. Reconstruction of ESA CCI satellite-derived soil moisture using an artificial neural network technology. Sci. Total Environ. 2021, 782, 146602. [Google Scholar] [CrossRef]
- Walker, J.P.; Houser, P.R. Requirements of a global near-surface soil moisture satellite mission: Accuracy, repeat time, and spatial resolution. Adv. Water Resour. 2004, 27, 785–801. [Google Scholar] [CrossRef]
- Jin, X.; Kumar, L.; Li, Z.; Feng, H.; Xu, X.; Yang, G.; Wang, J. A review of data assimilation of remote sensing and crop models. Eur. J. Agron. 2018, 92, 141–152. [Google Scholar] [CrossRef]
- Qin, J.; Tian, J.; Yang, K.; Lu, H.; Li, X.; Yao, L.; Shi, J. Bias correction of satellite soil moisture through data assimilation. J. Hydrol. 2022, 610, 127947. [Google Scholar] [CrossRef]
- Tian, J.; Qin, J.; Yang, K.; Zhao, L.; Chen, Y.; Lu, H.; Li, X.; Shi, J. Improving surface soil moisture retrievals through a novel assimilation algorithm to estimate both model and observation errors. Remote Sens. Environ. 2022, 269, 112802. [Google Scholar] [CrossRef]
- Huang, J.; Ma, H.; Sedano, F.; Lewis, P.; Liang, S.; Wu, Q.; Su, W.; Zhang, X.; Zhu, D. Evaluation of regional estimates of winter wheat yield by assimilating three remotely sensed reflectance datasets into the coupled WOFOST–PROSAIL model. Eur. J. Agron. 2019, 102, 1–13. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, Z.; Chen, Y.; Zhang, L.; Tao, F. Improving regional wheat yields estimations by multi-step-assimilating of a crop model with multi-source data. Agric. For. Meteorol. 2020, 290, 107993. [Google Scholar] [CrossRef]
- Colliander, A.; Jackson, T.J.; Bindlish, R.; Chan, S.; Das, N.; Kim, S.B.; Cosh, M.H.; Dunbar, R.S.; Dang, L.; Pashaian, L.; et al. Validation of SMAP surface soil moisture products with core validation sites. Remote Sens. Environ. 2017, 191, 215–231. [Google Scholar] [CrossRef]
- Jin, N.; Tao, B.; Ren, W.; He, L.; Zhang, D.; Wang, D.; Yu, Q. Assimilating remote sensing data into a crop model improves winter wheat yield estimation based on regional irrigation data. Agric. Water Manag. 2022, 266, 107583. [Google Scholar] [CrossRef]
- Rahman, A.; Maggioni, V.; Zhang, X.; Houser, P.; Sauer, T.; Mocko, D.M. The Joint Assimilation of Remotely Sensed Leaf Area Index and Surface Soil Moisture into a Land Surface Model. Remote Sens. 2022, 14, 437. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).