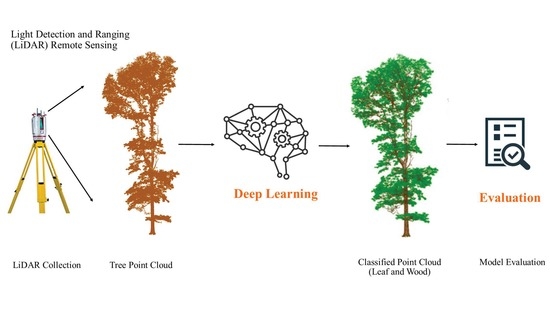
A Deep Learning Time Series Approach for Leaf and Wood Classification from Terrestrial LiDAR Point Clouds
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area and Data
2.2. Data Processing
2.2.1. Predictor Variables
2.2.2. Data Labeling
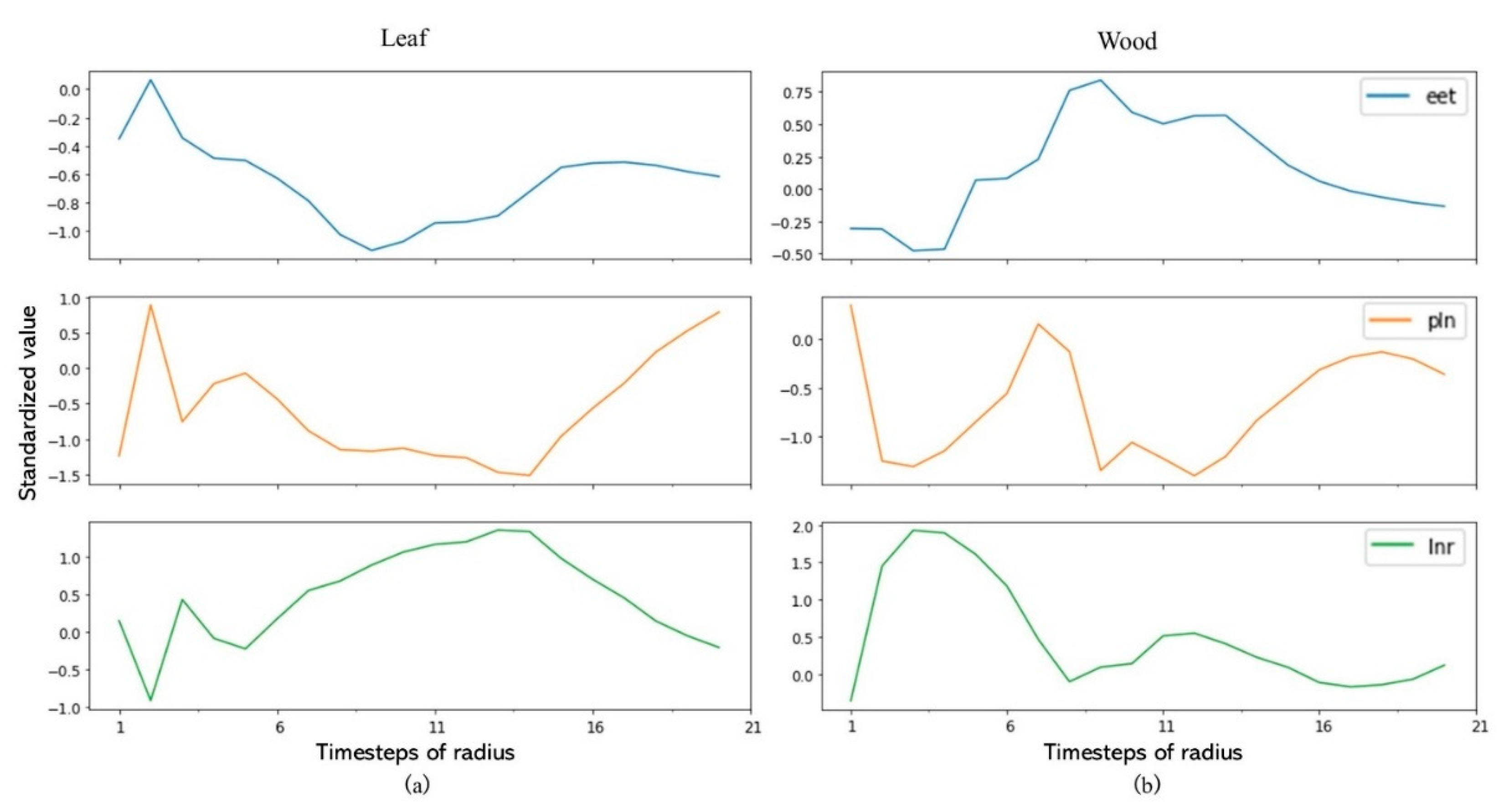
2.2.3. Time-Series Data
2.2.4. End-to-End Deep Learning Model
- A.
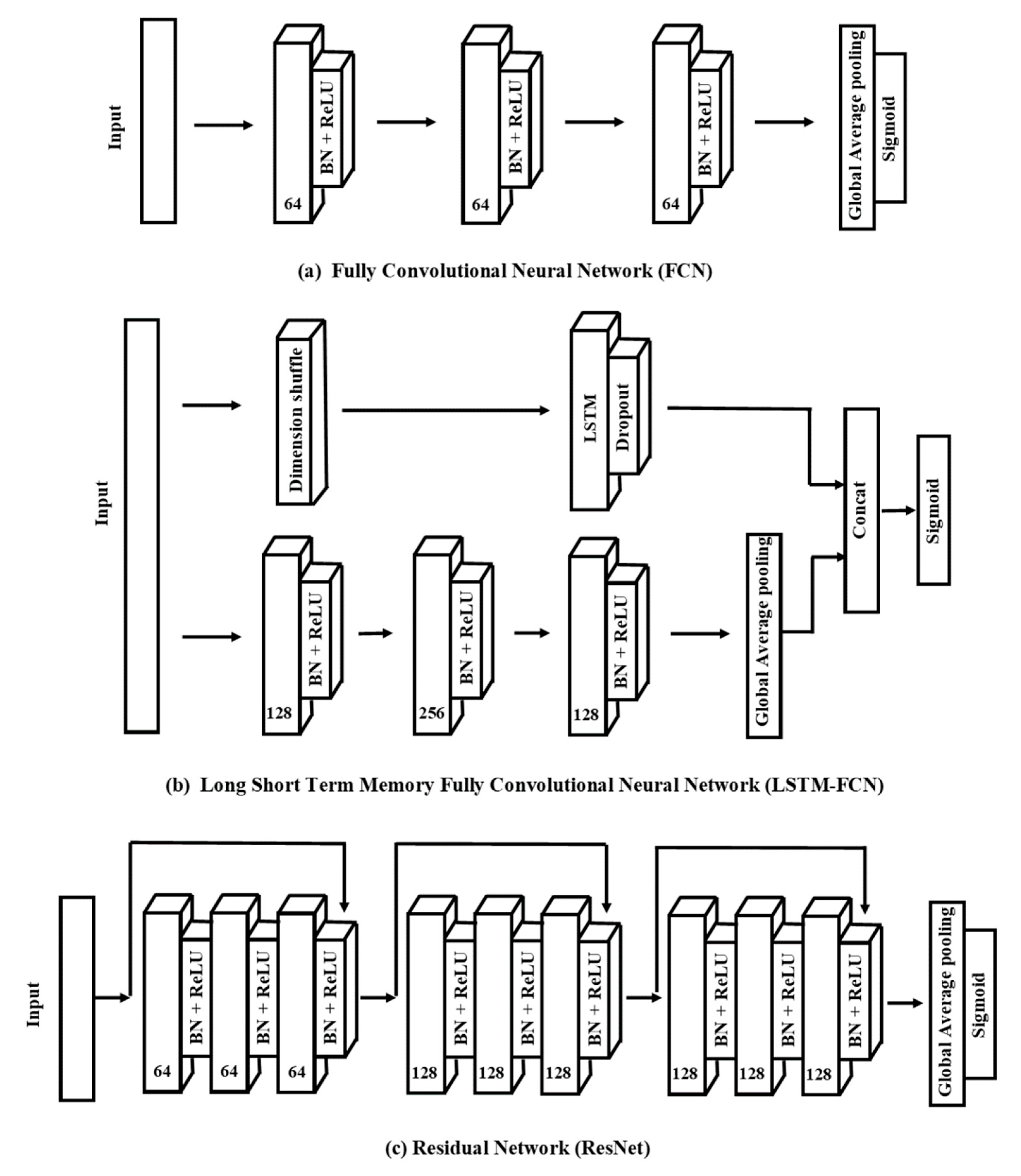
- Fully Convolutional Neural NetworksFully convolutional neural networks (FCNs) were originally proposed by Wang et al. [32]. This architecture outperformed other approaches (i.e., multilayer perceptrons, residual networks) for classifying UTS and MTS data according to the University of California Riverside/University of East Anglia (UCR/UEA) archive [32]. There are three convolutional blocks in this network, where each block also has three operations:where: x = input data; w = weight matrix; b = bias; y = output neuron; z = batch normalization on output neuron; h = activation of the output neuron, ⊗ = convolutional operator, and BN = batch normalization (BN).BN can help speed up convergence and improve generalization. Those three blocks are performed as feature extractors, and are fed into a global average pooling (GAP) layer instead of the traditional fully connected layer, thus reducing the number of parameters [46]. Finally, a sigmoid function connects the GAP layer’s output to produce the final label (Figure 2a).
- B.
- Long Short-Term Memory-Fully Convolutional Neural NetworksLong short-term memory (LSTM) is one of advanced RNN architecture, which handles vanishing gradient problems [47]. Karim et al. [48] proposed combined utilization of LSTM and FCN on time series classification, and the obtained LSTM-FCN method further increased the performance of FCN on the UCR archive.With the same network of FCN, LSTM-FCN incorporated a sub-module which contained two layers (Figure 2b). The original time series will be input into the first layer, also called the dimensional shuffle. This layer transforms a univariable time series with N timesteps into a multivariable time series (N variables with one timestep). The transformed time series is then passed into a LSTM layer followed by a dropout, with the dropout layer helping to prevent overfitting. The outputs of the LSTM and GAP layers are concatenated and then input into a final sigmoid layer.
- C.
- Residual NetworksResNet is also a high-performance deep neural network in time series classification tasks [49]. Xi et al. [12] compared the performance of 15 machine learning and deep learning methods on leaf and wood classification and determined that ResNet is one of the most competitive classifiers among them.Figure 2c presents the network structure of ResNet used in this study. The ResNet network includes three residual blocks and connects with the GAP layer and a sigmoid function. We used the convolutional blocks in Equation (1) to develop each residual block. Here, the Blockn indicates the residual block with n filters, which have the following operations: x, input data; sn, output of each convolutional block; y, output neuron after adding shortcut connection; s, output of the residual block.
2.2.5. Evaluation
3. Results
3.1. UTS vs. MTS
3.2. Class Activation Map
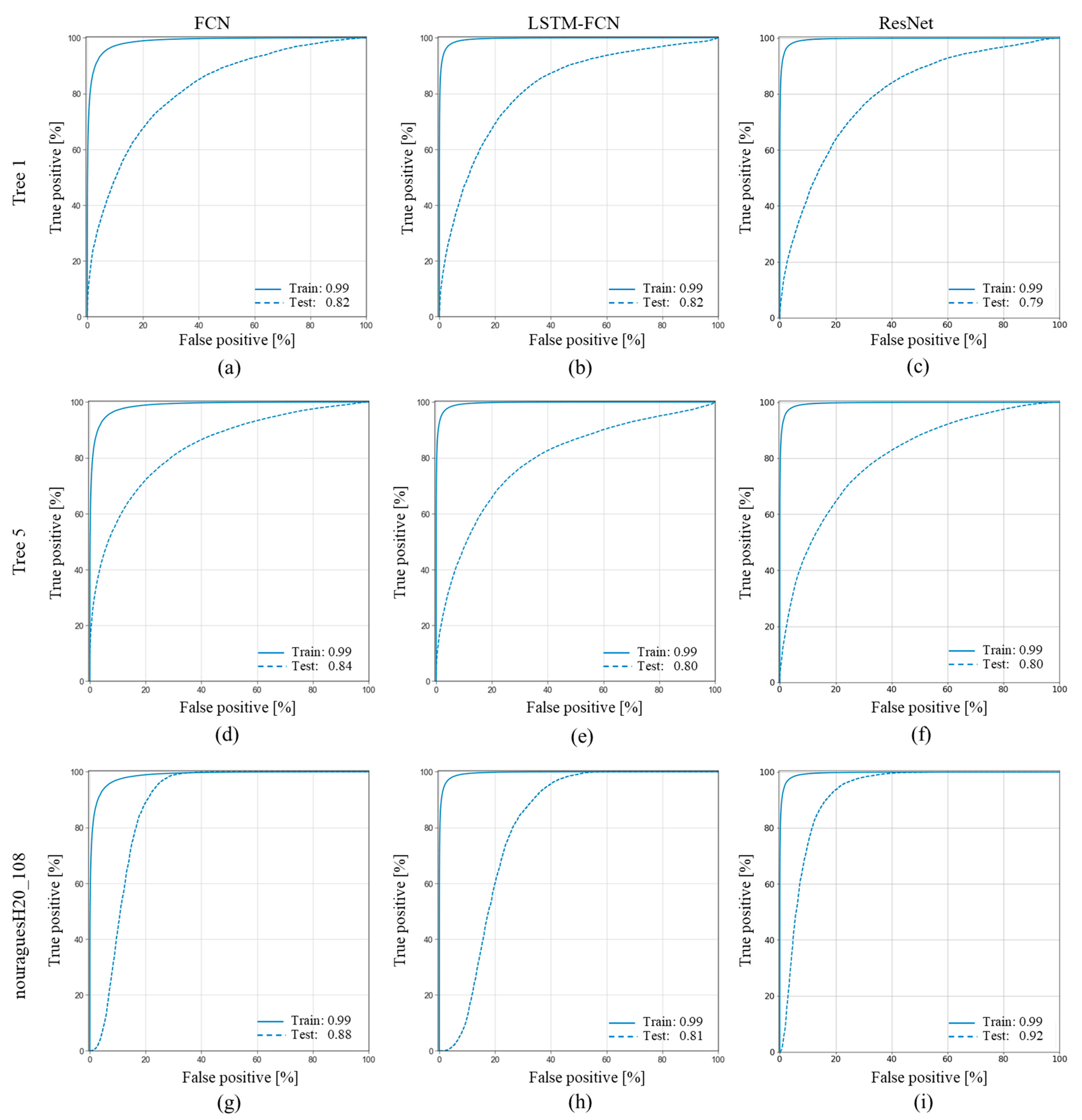
3.3. Model Generalization
4. Discussion
4.1. UTS or MTS
4.2. Comparison with Other Leaf-Wood Classification Methods
4.3. Model Generalization
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| LiDAR | Light detection and ranging |
| TLS | Terrestrial laser scanning |
| LAI | Leaf area index |
| AGB | Above-ground biomass |
| FCNs | Fully convolutional neural networks |
| TSC | Time series classification |
| UTS | Univariable time series |
| UTS | Univariable time series |
| MTS | Multivariable time series |
| CAM | Class activation map |
| NN | Neural networks |
| RF | Random forest |
| LSTM | Long short-term memory |
| RNN | Recurrent neural network |
| CNN | Convolutional neural network |
| DTW | Dynamic time warping |
| PR curve | Precision-recall curve |
Appendix A
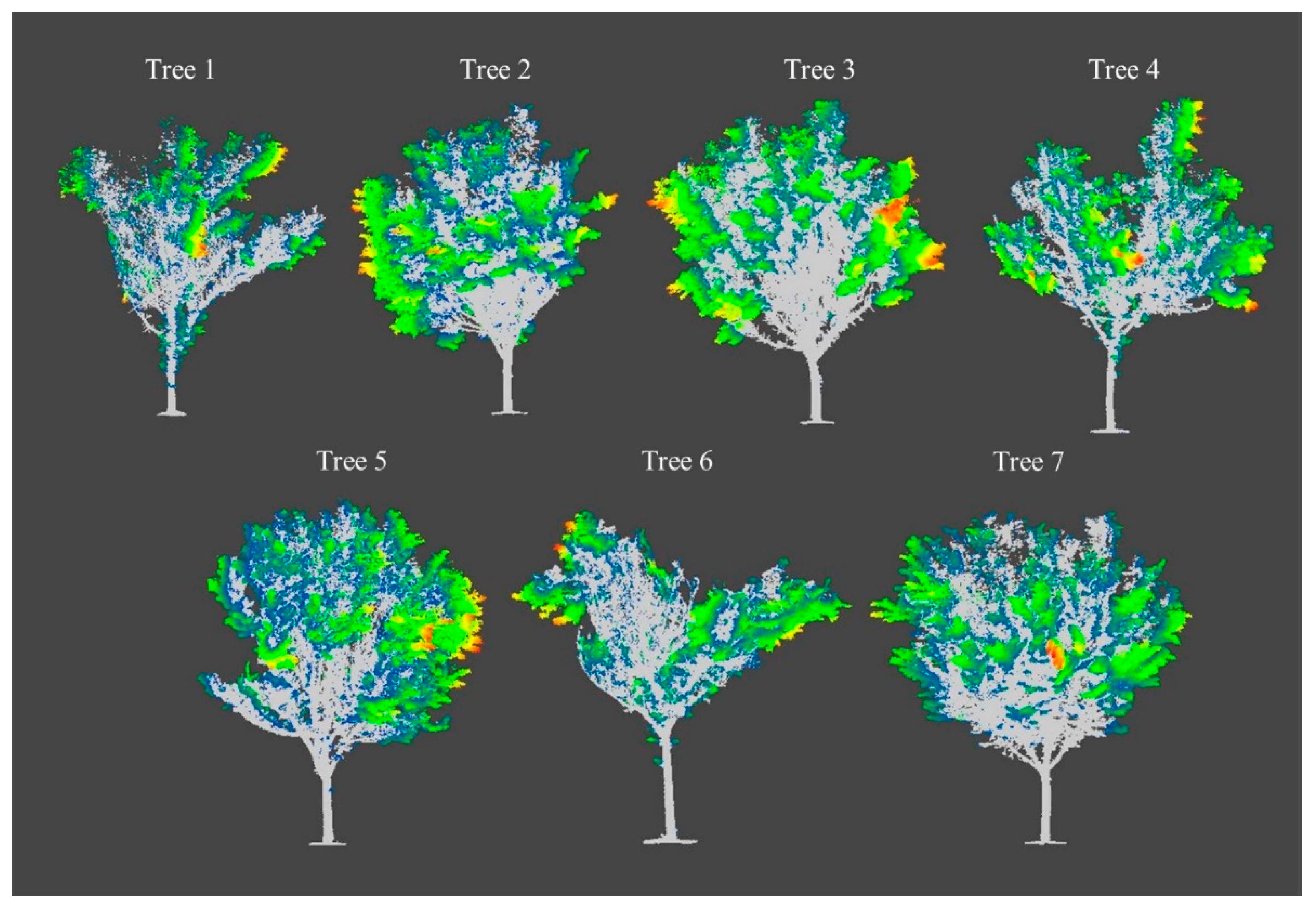
| Tree ID | Sample Points | Total Points |
|---|---|---|
| Tree 1 | 32,000 | 319,037 |
| Tree 2 | 70,000 | 668,950 |
| Tree 3 | 96,000 | 947,704 |
| Tree 4 | 56,000 | 540,369 |
| Tree 5 | 80,000 | 802,740 |
| Tree 6 | 32,000 | 302,494 |
| Tree 7 | 66,000 | 653,643 |
Appendix B
References
- Hosoi, F.; Omasa, K. Voxel-Based 3-D Modeling of Individual Trees for Estimating Leaf Area Density Using High-Resolution Portable Scanning Lidar. IEEE Trans. Geosci. Remote Sens. 2006, 44, 3610–3618. [Google Scholar] [CrossRef]
- Béland, M.; Widlowski, J.L.; Fournier, R.A.; Côté, J.F.; Verstraete, M.M. Estimating Leaf Area Distribution in Savanna Trees from Terrestrial LiDAR Measurements. Agric. For. Meteorol. 2011, 151, 1252–1266. [Google Scholar] [CrossRef]
- Tao, S.; Guo, Q.; Xu, S.; Su, Y.; Li, Y.; Wu, F. A Geometric Method for Wood-Leaf Separation Using Terrestrial and Simulated Lidar Data. Photogramm. Eng. Remote Sens. 2015, 81, 767–776. [Google Scholar] [CrossRef]
- Zhu, X.; Skidmore, A.K.; Darvishzadeh, R.; Niemann, K.O.; Liu, J.; Shi, Y.; Wang, T. Foliar and Woody Materials Discriminated Using Terrestrial LiDAR in a Mixed Natural Forest. Int. J. Appl. Earth Obs. Geoinf. 2018, 64, 43–50. [Google Scholar] [CrossRef]
- Calders, K.; Adams, J.; Armston, J.; Bartholomeus, H.; Bauwens, S.; Bentley, L.P.; Chave, J.; Danson, F.M.; Demol, M.; Disney, M.; et al. Terrestrial Laser Scanning in Forest Ecology: Expanding the Horizon. Remote Sens. Environ. 2020, 251, 112102. [Google Scholar] [CrossRef]
- Disney, M.I.; Boni Vicari, M.; Burt, A.; Calders, K.; Lewis, S.L.; Raumonen, P.; Wilkes, P. Weighing Trees with Lasers: Advances, Challenges and Opportunities. Interface Focus 2018, 8, 20170048. [Google Scholar] [CrossRef] [Green Version]
- Calders, K.; Newnham, G.; Burt, A.; Murphy, S.; Raumonen, P.; Herold, M.; Culvenor, D.; Avitabile, V.; Disney, M.; Armston, J.; et al. Nondestructive Estimates of Above-Ground Biomass Using Terrestrial Laser Scanning. Methods Ecol. Evol. 2015, 6, 198–208. [Google Scholar] [CrossRef]
- Moorthy, S.M.; Calders, K.; Vicari, M.B.; Verbeeck, H. Improved Supervised Learning-Based Approach for Leaf and Wood Classification from LiDAR Point Clouds of Forests. IEEE Trans. Geosci. Remote Sens. 2020, 58, 3057–3070. [Google Scholar] [CrossRef] [Green Version]
- Ma, L.; Zheng, G.; Eitel, J.U.H.; Moskal, L.M.; He, W.; Huang, H. Improved Salient Feature-Based Approach for Automatically Separating Photosynthetic and Nonphotosynthetic Components within Terrestrial Lidar Point Cloud Data of Forest Canopies. IEEE Trans. Geosci. Remote Sens. 2016, 54, 679–696. [Google Scholar] [CrossRef]
- Vicari, M.B.; Disney, M.; Wilkes, P.; Burt, A.; Calders, K.; Woodgate, W. Leaf and Wood Classification Framework for Terrestrial LiDAR Point Clouds. Methods Ecol. Evol. 2019, 10, 680–694. [Google Scholar] [CrossRef] [Green Version]
- Béland, M.; Baldocchi, D.D.; Widlowski, J.L.; Fournier, R.A.; Verstraete, M.M. On Seeing the Wood from the Leaves and the Role of Voxel Size in Determining Leaf Area Distribution of Forests with Terrestrial LiDAR. Agric. For. Meteorol. 2014, 184, 82–97. [Google Scholar] [CrossRef]
- Xi, Z.; Hopkinson, C.; Rood, S.B.; Peddle, D.R. See the Forest and the Trees: Effective Machine and Deep Learning Algorithms for Wood Filtering and Tree Species Classification from Terrestrial Laser Scanning. ISPRS J. Photogramm. Remote Sens. 2020, 168, 1–16. [Google Scholar] [CrossRef]
- Belton, D.; Moncrieff, S.; Chapman, J. Processing Tree Point Clouds Using Gaussian Mixture Models. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2013, 2, 43–48. [Google Scholar] [CrossRef] [Green Version]
- Thomas, H.; Goulette, F.; Deschaud, J.-E.; Marcotegui, B.; LeGall, Y. Semantic Classification of 3D Point Clouds with Multiscale Spherical Neighborhoods. In Proceedings of the 2018 International Conference on 3D Vision (3DV), Verona, Italy, 5–8 September 2018; pp. 390–398. [Google Scholar]
- Joaquin, Q.-C.; Masashi, S.; Anton, S.; Lawrence, N.D. Dataset Shift in Machine Learning; Quiñonero-Candela, J., Sugiyama, M., Schwaighofer, A., Lawrence, N.D., Eds.; The MIT Press: Cambridge, MA, USA, 2008; ISBN 9780262170055. [Google Scholar]
- Wei, Q.; Dunbrack, R.L. The Role of Balanced Training and Testing Data Sets for Binary Classifiers in Bioinformatics. PLoS ONE 2013, 8, e67863. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep Learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Dargan, S.; Kumar, M.; Ayyagari, M.R.; Kumar, G. A Survey of Deep Learning and Its Applications: A New Paradigm to Machine Learning. Arch. Comput. Methods Eng. 2020, 27, 1071–1092. [Google Scholar] [CrossRef]
- Qi, C.R.; Yi, L.; Su, H.; Guibas, L.J. PointNet++: Deep Hierarchical Feature Learning on Point Sets in a Metric Space. Adv. Neural Inf. Process. Syst. 2017, 30, 5105–5114. [Google Scholar]
- Fawaz, I.H.; Forestier, G.; Weber, J.; Idoumghar, L.; Muller, P.A. Deep Learning for Time Series Classification: A Review. Data Min. Knowl. Discov. 2019, 33, 917–963. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Wang, Z.; Liu, S. An Effective Multivariate Time Series Classification Approach Using Echo State Network and Adaptive Differential Evolution Algorithm. Expert Syst. Appl. 2016, 43, 237–249. [Google Scholar] [CrossRef]
- Zheng, Y.; Liu, Q.; Chen, E.; Ge, Y.; Zhao, J.L. Exploiting Multi-Channels Deep Convolutional Neural Networks for Multivariate Time Series Classification. Front. Comput. Sci. 2016, 10, 96–112. [Google Scholar] [CrossRef]
- Esling, P.; Agon, C. Time-Series Data Mining. ACM Comput. Surv. 2012, 45, 1–34. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Wu, Y.; Gao, X.; Zhang, X. A Simple Method of Mapping Landslides Runout Zones Considering Kinematic Uncertainties. Remote Sens. 2022, 14, 668. [Google Scholar] [CrossRef]
- Rajkomar, A.; Oren, E.; Chen, K.; Dai, A.M.; Hajaj, N.; Hardt, M.; Liu, P.J.; Liu, X.; Marcus, J.; Sun, M.; et al. Scalable and Accurate Deep Learning with Electronic Health Records. NDJ Digit. Med. 2018, 1, 18. [Google Scholar] [CrossRef]
- Nweke, H.F.; Teh, Y.W.; Al-garadi, M.A.; Alo, U.R. Deep Learning Algorithms for Human Activity Recognition Using Mobile and Wearable Sensor Networks: State of the Art and Research Challenges. Expert Syst. Appl. 2018, 105, 233–261. [Google Scholar] [CrossRef]
- Mehdiyev, N.; Lahann, J.; Emrich, A.; Enke, D.; Fettke, P.; Loos, P. Time Series Classification Using Deep Learning for Process Planning: A Case from the Process Industry. Procedia Comput. Sci. 2017, 114, 242–249. [Google Scholar] [CrossRef]
- Lines, J.; Bagnall, A. Time Series Classification with Ensembles of Elastic Distance Measures. Data Min. Knowl. Discov. 2015, 29, 565–592. [Google Scholar] [CrossRef]
- Keogh, E.; Ratanamahatana, C.A. Exact Indexing of Dynamic Time Warping. Knowl. Inf. Syst. 2005, 7, 358–386. [Google Scholar] [CrossRef]
- Bagnall, A.; Lines, J.; Bostrom, A.; Large, J.; Keogh, E. The Great Time Series Classification Bake off: A Review and Experimental Evaluation of Recent Algorithmic Advances. Data Min. Knowl. Discov. 2017, 31, 606–660. [Google Scholar] [CrossRef] [Green Version]
- Baydogan, M.G.; Runger, G.; Tuv, E. A Bag-of-Features Framework to Classify Time Series. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 2796–2802. [Google Scholar] [CrossRef]
- Wang, Z.; Yan, W.; Oate, T. Time Series Classification from Scratch with Deep Neural Networks: A Strong Baseline. In Proceedings of the 2017 International Joint Conference on Neural Networks (IJCNN), Anchorage, AK, USA, 14–19 May 2017; pp. 1578–1585. [Google Scholar] [CrossRef] [Green Version]
- Wang, P.; Wang, L.; Leung, H.; Zhang, G. Super-Resolution Mapping Based on Spatial-Spectral Correlation for Spectral Imagery. IEEE Trans. Geosci. Remote Sens. 2021, 59, 2256–2268. [Google Scholar] [CrossRef]
- Xu, X.; Chen, Y.; Zhang, J.; Chen, Y.; Anandhan, P.; Manickam, A. A Novel Approach for Scene Classification from Remote Sensing Images Using Deep Learning Methods. Eur. J. Remote Sens. 2021, 54, 383–395. [Google Scholar] [CrossRef]
- Dou, P.; Shen, H.; Li, Z.; Guan, X. Time Series Remote Sensing Image Classification Framework Using Combination of Deep Learning and Multiple Classifiers System. Int. J. Appl. Earth Obs. Geoinf. 2021, 103, 102477. [Google Scholar] [CrossRef]
- Antonio Guzmán, Q.J.; Sharp, I.; Alencastro, F.; Sánchez-Azofeifa, G.A. On the Relationship of Fractal Geometry and Tree–Stand Metrics on Point Clouds Derived from Terrestrial Laser Scanning. Methods Ecol. Evol. 2020, 11, 1309–1318. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, L.; Fang, T.; Mathiopoulos, P.T.; Tong, X.; Qu, H.; Xiao, Z.; Li, F.; Chen, D. A Multiscale and Hierarchical Feature Extraction Method for Terrestrial Laser Scanning Point Cloud Classification. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2409–2425. [Google Scholar] [CrossRef]
- Wang, D.; Hollaus, M.; Pfeifer, N. Feasibility of Machine Learning Methods for Separating Wood and Leaf Points from Terrestrial Laser Scanning Data. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, 4, 157–164. [Google Scholar] [CrossRef] [Green Version]
- van Kuppevelt, D.; Meijer, C.; Huber, F.; van der Ploeg, A.; Georgievska, S.; van Hees, V.T. Mcfly: Automated Deep Learning on Time Series. SoftwareX 2020, 12, 100548. [Google Scholar] [CrossRef]
- Oguiza, I. Tsai-A State-of-the-Art Deep Learning Library for Time Series and Sequential Data. Retrieved April 2020, 20, 2021. [Google Scholar]
- Burt, A.; Disney, M.; Calders, K. Extracting Individual Trees from Lidar Point Clouds Using Treeseg. Methods Ecol. Evol. 2019, 10, 438–445. [Google Scholar] [CrossRef] [Green Version]
- Ruiz, A.P.; Flynn, M.; Large, J.; Middlehurst, M.; Bagnall, A. The Great Multivariate Time Series Classification Bake off: A Review and Experimental Evaluation of Recent Algorithmic Advances. Data Min. Knowl. Discov. 2021, 35, 401–449. [Google Scholar] [CrossRef]
- Ordóñez, F.J.; Roggen, D. Deep Convolutional and LSTM Recurrent Neural Networks for Multimodal Wearable Activity Recognition. Sensors 2016, 16, 115. [Google Scholar] [CrossRef] [Green Version]
- Gamboa, J.C.B. Deep Learning for Time-Series Analysis. arXiv 2017, arXiv:1701.01887. [Google Scholar]
- Karim, F.; Majumdar, S.; Darabi, H.; Harford, S. Multivariate LSTM-FCNs for Time Series Classification. Neural Netw. 2019, 116, 237–245. [Google Scholar] [CrossRef] [Green Version]
- Lin, M.; Chen, Q.; Yan, S. Network in Network. In Proceedings of the ICLR 2014 2nd International Conference on Learning Representations, Banff, AB, Canada, 14–16 April 2014; pp. 1–10. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Karim, F.; Majumdar, S.; Darabi, H.; Chen, S. LSTM Fully Convolutional Networks for Time Series Classification. IEEE Access 2017, 6, 1662–1669. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. Indian J. Chem.-Sect. B Org. Med. Chem. 2015, 45, 1951–1954. [Google Scholar] [CrossRef]
- Zhou, B.; Khosla, A.; Lapedriza, A.; Oliva, A.; Torralba, A. Learning Deep Features for Discriminative Localization. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 2921–2929. [Google Scholar] [CrossRef] [Green Version]
- van Laarhoven, T. L2 Regularization versus Batch and Weight Normalization. arXiv 2017, arXiv:1706.05350. [Google Scholar]
- Rhys, H.I. Machine Learning with R, the Tidyverse, and Mlr; Manning: Shelter Island, NY, USA, 2020; ISBN 9781617296574. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. In Proceedings of the 3rd International Conference on Learning Representations, ICLR 2015, San Diego, CA, USA, 7–9 May 2015; pp. 1–15. [Google Scholar]
- Smith, L.N. A Disciplined Approach to Neural Network Hyper-Parameters: Part 1—Learning Rate, Batch Size, Momentum, and Weight Decay. arXiv 2018, arXiv:1803.09820. [Google Scholar]
- Raskutti, G.; Wainwright, M.J.; Yu, B. Early Stopping and Non-Parametric Regression: An Optimal Data-Dependent Stopping Rule. J. Mach. Learn. Res. 2013, 15, 335–366. [Google Scholar]


| Feature | Name | Equation |
|---|---|---|
| 1 | Planarity | ( |
| 2 | Linearity | ( |
| 3 | Eigentropy |
| FCN | LSTM-FCN | ResNet | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Method | Accuracy | F1 Score (Leaf) | F1 Score (Wood) | Accuracy | F1 Score (Leaf) | F1 Score (Wood) | Accuracy | F1 Score (Leaf) | F1 Score (Wood) |
| Planarity | 0.67 ± 0.01 | 0.67 ± 0.07 | 0.66 ± 0.04 | 0.74 ± 0.00 | 0.74 ± 0.00 | 0.74 ± 0.01 | 0.80 ± 0.01 | 0.80 ± 0.01 | 0.80 ± 0.01 |
| Linearity | 0.69 ± 0.02 | 0.65 ± 0.07 | 0.72 ± 0.02 | 0.76 ± 0.01 | 0.76 ± 0.01 | 0.76 ± 0.01 | 0.79 ± 0.01 | 0.79 ± 0.01 | 0.79 ± 0.01 |
| Eigentropy | 0.82 ± 0.01 | 0.81 ± 0.01 | 0.82 ± 0.02 | 0.85 ± 0.01 | 0.85 ± 0.01 | 0.85 ± 0.01 | 0.88 ± 0.01 | 0.87 ± 0.01 | 0.88 ± 0.01 |
| MTS | 0.92 ± 0.01 | 0.92 ± 0.00 | 0.92 ± 0.01 | 0.96 ± 0.01 | 0.96 ± 0.00 | 0.96 ± 0.00 | 0.96 ± 0.01 | 0.96 ± 0.01 | 0.96 ± 0.01 |
| FCN | LSTM-FCN | ResNet | ||||
|---|---|---|---|---|---|---|
| Method | Epochs | Time (Minutes) | Epochs | Time (Minutes) | Epochs | Time (Minutes) |
| Planarity | 227 | 74 | 222 | 29 | 253 | 548 |
| Linearity | 226 | 75 | 335 | 45 | 187 | 405 |
| Eigentropy | 159 | 54 | 234 | 30 | 234 | 508 |
| Average | 204 ± 39 | 68 ± 12 | 264 ± 62 | 35 ± 9 | 225 ± 34 | 487 ± 74 |
| MTS | 185 | 62 | 223 | 54 | 255 | 553 |
| FCN | LSTM-FCN | ResNet | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Tree Name | Accuracy | F1 Score (Leaf) | F1 Score (Wood) | Accuracy | F1 Score (Leaf) | F1 Score (Wood) | Accuracy | F1 Score (Leaf) | F1 Score (Wood) |
| Tree 1 | 0.75 | 0.76 | 0.75 | 0.74 | 0.72 | 0.76 | 0.73 | 0.71 | 0.75 |
| Tree 5 | 0.78 | 0.77 | 0.79 | 0.75 | 0.74 | 0.75 | 0.73 | 0.72 | 0.74 |
| alice_1 | 0.76 | 0.75 | 0.83 | 0.73 | 0.72 | 0.69 | 0.65 | 0.66 | 0.64 |
| alice_2 | 0.81 | 0.81 | 0.81 | 0.74 | 0.74 | 0.74 | 0.77 | 0.76 | 0.78 |
| alice_3 | 0.79 | 0.78 | 0.81 | 0.75 | 0.74 | 0.78 | 0.78 | 0.77 | 0.82 |
| caxiuanA_117 | 0.61 | 0.52 | 0.76 | 0.63 | 0.59 | 0.76 | 0.66 | 0.60 | 0.78 |
| nouraguresH20_108 | 0.84 | 0.84 | 0.85 | 0.82 | 0.81 | 0.85 | 0.78 | 0.79 | 0.80 |
| Pan_33 | 0.67 | 0.64 | 0.71 | 0.63 | 0.59 | 0.69 | 0.63 | 0.58 | 0.76 |
| Ave ± Sd | 0.75 ± 0.08 | 0.73 ± 0.10 | 0.79 ± 0.05 | 0.72 ± 0.06 | 0.71 ± 0.08 | 0.75 ± 0.05 | 0.72 ± 0.06 | 0.70 ± 0.08 | 0.76 ± 0.06 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, T.; Sánchez-Azofeifa, G.A. A Deep Learning Time Series Approach for Leaf and Wood Classification from Terrestrial LiDAR Point Clouds. Remote Sens. 2022, 14, 3157. https://doi.org/10.3390/rs14133157
Han T, Sánchez-Azofeifa GA. A Deep Learning Time Series Approach for Leaf and Wood Classification from Terrestrial LiDAR Point Clouds. Remote Sensing. 2022; 14(13):3157. https://doi.org/10.3390/rs14133157
Chicago/Turabian StyleHan, Tao, and Gerardo Arturo Sánchez-Azofeifa. 2022. "A Deep Learning Time Series Approach for Leaf and Wood Classification from Terrestrial LiDAR Point Clouds" Remote Sensing 14, no. 13: 3157. https://doi.org/10.3390/rs14133157
APA StyleHan, T., & Sánchez-Azofeifa, G. A. (2022). A Deep Learning Time Series Approach for Leaf and Wood Classification from Terrestrial LiDAR Point Clouds. Remote Sensing, 14(13), 3157. https://doi.org/10.3390/rs14133157