Latent Low-Rank Projection Learning with Graph Regularization for Feature Extraction of Hyperspectral Images
Abstract
:1. Introduction
2. Related Work
2.1. Low-Rank Representation for Feature Extraction
2.2. Latent Low-Rank Representation for Feature Extraction
2.3. Locality Preserving Projection for Feature Extraction
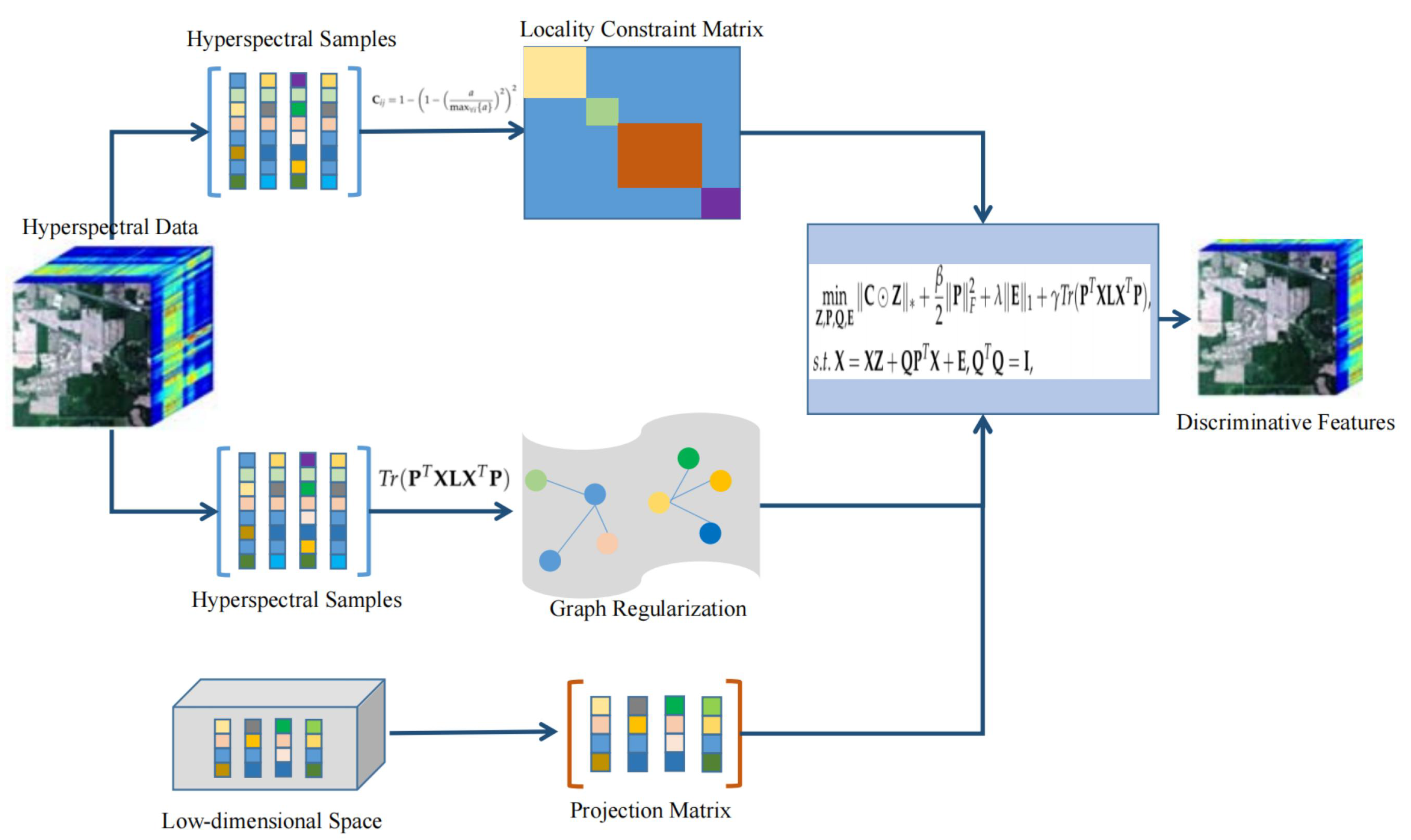
3. Proposed Unsupervised Projection Learning Method
3.1. Model Construction of LatLRPL
3.2. Optimization of LatLRPL
| Algorithm 1: ADMM for solving LatLRPL. |
| Input: N unlabeled samples , regularization parameters , , and , number of preserved features d. Initialize: , , , , , , , , , , maxIter = 200, . 1. Compute decomposition matrix by . 2. Construct the spectral constraint according to (10). 3. Construct the neighborhood graph according to (3). 4. Repeat: 5. Compute , , , , , according to (16)–(18), (20)–(22). 6. Update the Lagrangian multipliers according to (23). 7. Update : . 8. Check convergence conditions: , , . 9. . 10. Until convergence conditions are satisfied or > maxIter. Output: Discriminative projection matrix . |
3.3. Spatial Extension of LatLRPL
4. Experiments and Discussions
4.1. Hyperspectral Datasets
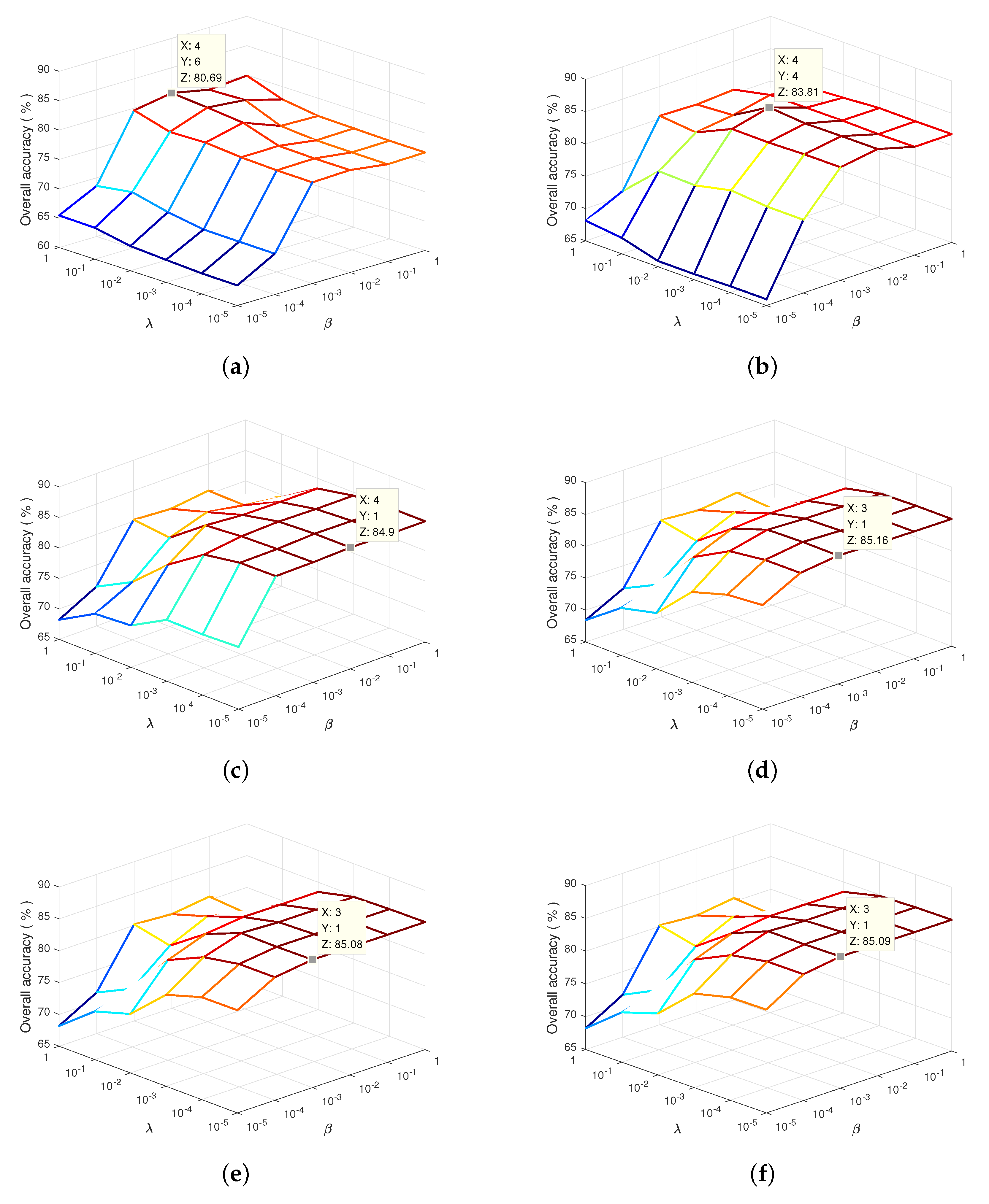
4.2. Analysis of the Regularization Parameters
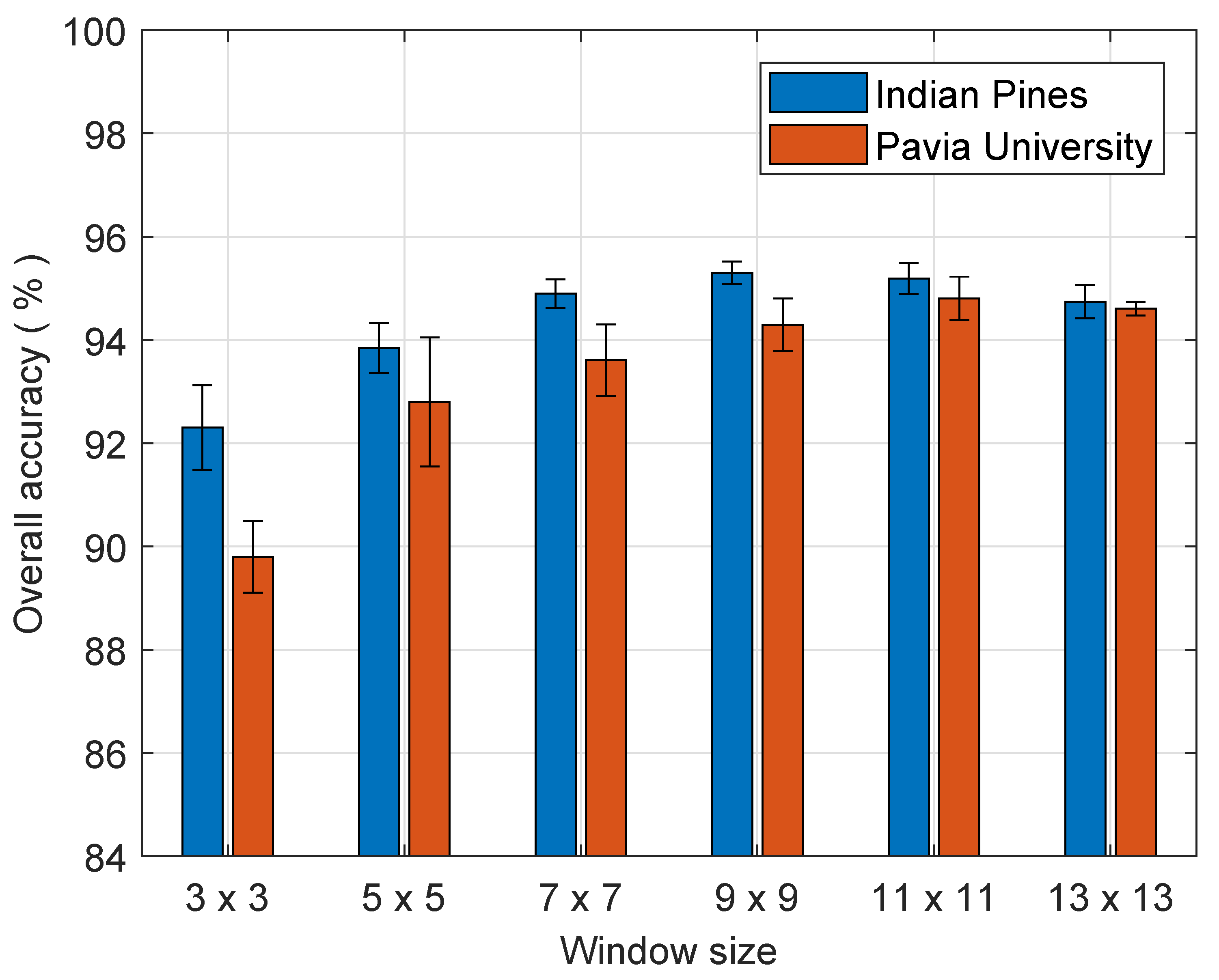
4.3. Analysis of the Sliding Window Size
4.4. Analysis of the Number of Features
4.5. Comparison of the Classification Performance
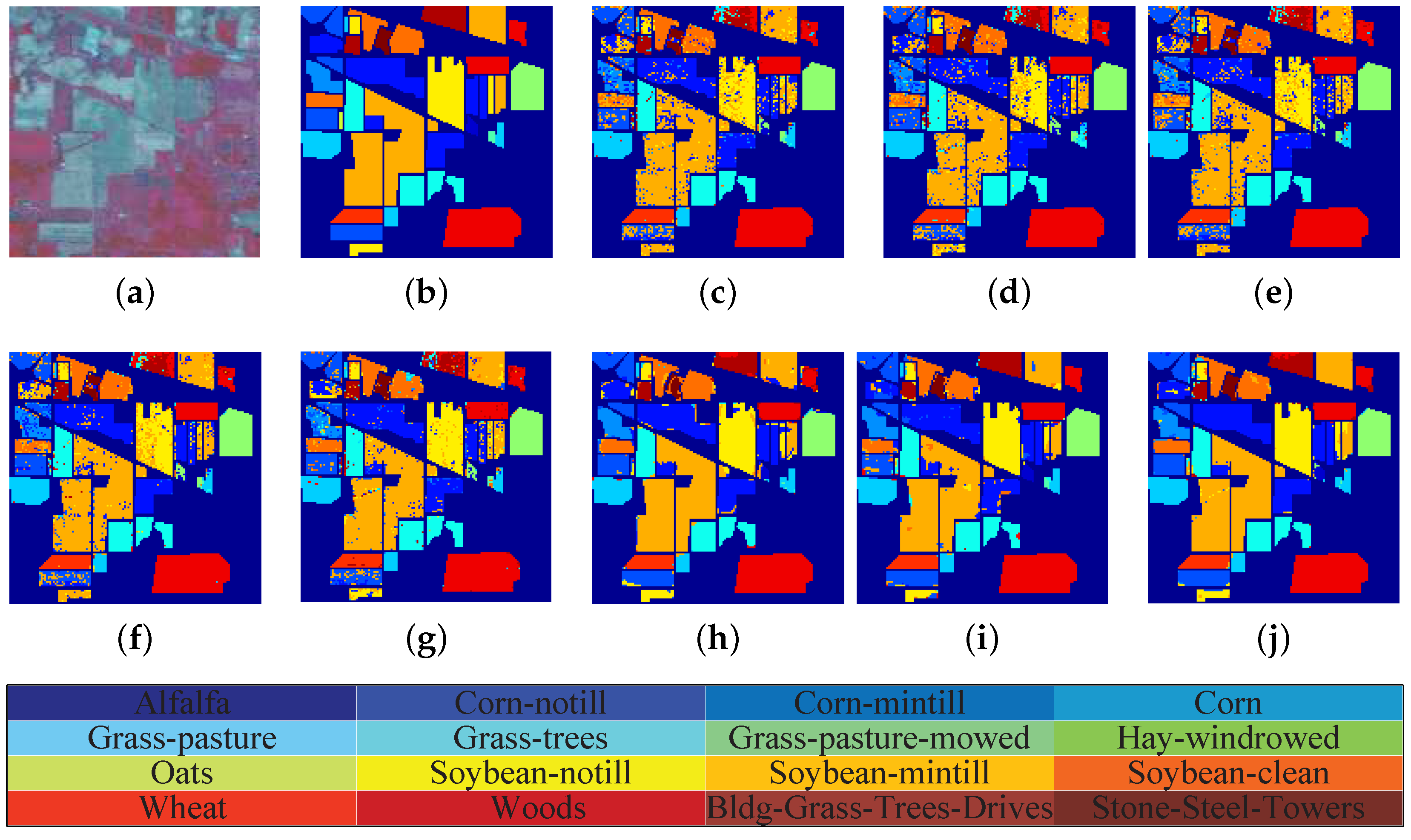
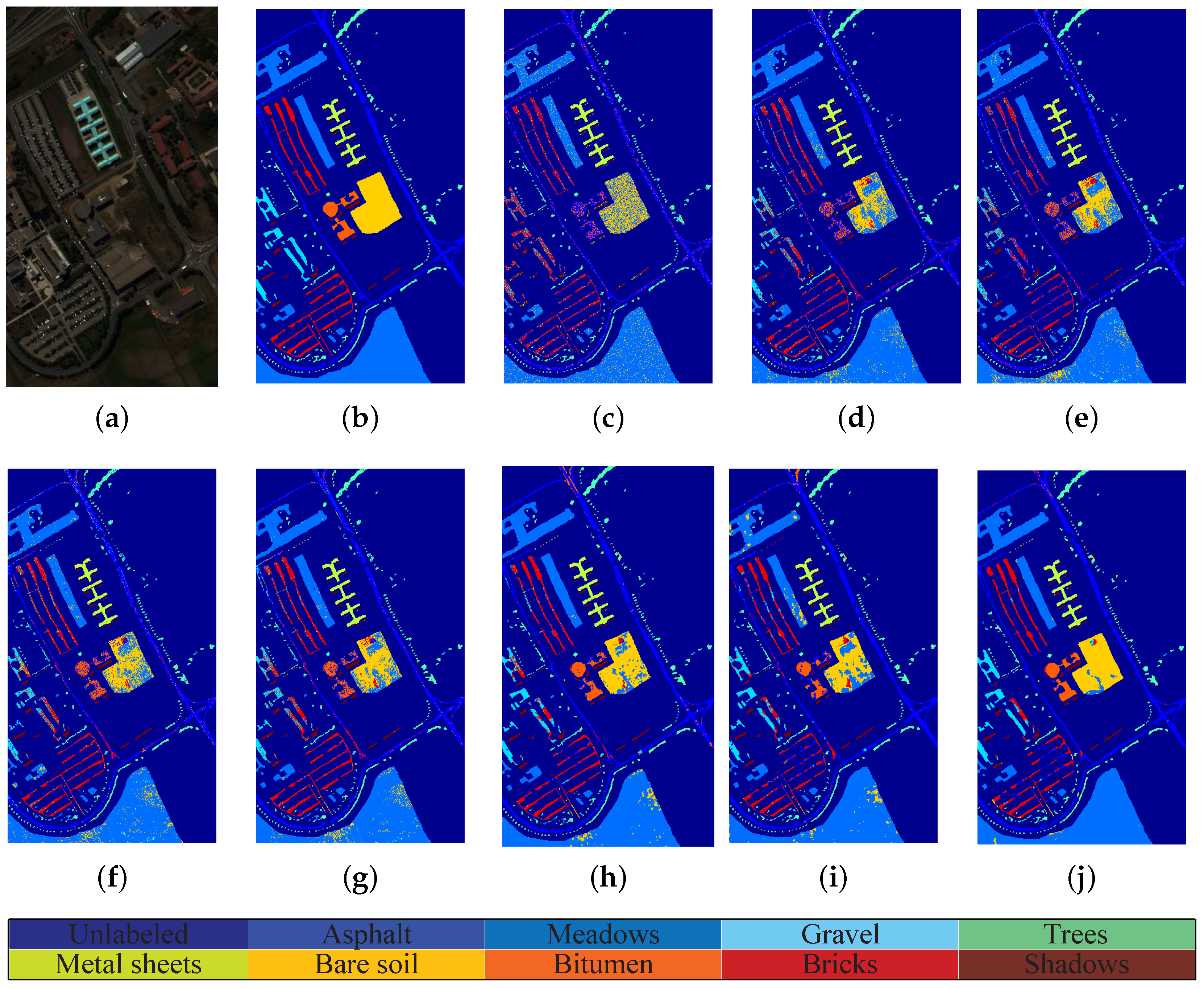
4.6. Presentation of Classification Maps
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ghamisi, P.; Yokoya, N.; Li, J.; Liao, W.; Liu, S.; Plaza, J.; Rasti, B.; Plaza, A. Advances in hyperspectral image and signal processing: A comprehensive overview of the state of the art. IEEE Geosci. Remote Sens. Mag. 2017, 5, 37–78. [Google Scholar] [CrossRef] [Green Version]
- Wen, J.; Fowler, J.E.; He, M.; Zhao, Y.Q.; Deng, C.; Menon, V. Orthogonal nonnegative matrix factorization combining multiple features for spectral-spatial dimensionality reduction of hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4272–4286. [Google Scholar] [CrossRef]
- An, J.L.; Zhang, X.R.; Zhou, H.Y.; Jiao, L.C. Tensor-based low-rank graph with multimanifold regularization for dimensionality reduction of hyperspectral images. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4731–4746. [Google Scholar] [CrossRef]
- Sun, W.W.; Du, Q. Hyperspectral band selection: A review. IEEE Geosci. Remote Sens. Mag. 2019, 7, 118–139. [Google Scholar] [CrossRef]
- Feng, J.; Feng, X.L.; Chen, J.T.; Cao, X.H.; Zhang, X.R.; Jiao, L.C.; Yu, T. Generative adversarial networks based on collaborative learning and attention mechanism for hyperspectral image classification. Remote Sens. 2020, 12, 1149. [Google Scholar] [CrossRef] [Green Version]
- Feng, J.; Wu, X.D.; Shang, R.H.; Sui, C.H.; Li, J.; Jiao, L.C. Attention multibranch convolutional neural network for hyperspectral image classification based on adaptive region search. IEEE Trans. Geosci. Remote Sens. 2020, 59, 5054–5070. [Google Scholar] [CrossRef]
- Yang, L.X.; Zhang, R.; Yang, S.Y.; Jiao, L.C. Hyperspectral Image Classification via Slice Sparse Coding Tensor Based Classifier With Compressive Dimensionality Reduction. IEEE Access 2020, 8, 145207–145215. [Google Scholar] [CrossRef]
- Hang, R.L.; Liu, Q.S.; Sun, Y.B.; Yuan, X.T.; Pei, H.C.; Plaza, J.; Plaza, A. Robust matrix discriminative analysis for feature extraction from hyperspectral images. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2017, 10, 2002–2011. [Google Scholar] [CrossRef]
- Varga, D. Multi-pooled inception features for no-reference image quality assessment. Appl. Sci. 2020, 10, 2186. [Google Scholar] [CrossRef] [Green Version]
- Varga, D. No-reference video quality assessment using multi-pooled, saliency weighted deep features and decision fusion. Sensors 2022, 22, 2209. [Google Scholar] [CrossRef]
- Lin, C.Z.; Lu, J.W.; Wang, G.; Zhou, J. Graininess-aware deep feature learning for pedestrian detection. IEEE Trans. Image Process. 2020, 29, 3820–3834. [Google Scholar] [CrossRef] [PubMed]
- Sethy, P.K.; Barpanda, N.K.; Rath, A.K.; Behera, S.K. Deep feature based rice leaf disease identification using support vector machine. Comput. Electron. Agric. 2020, 175, 105527. [Google Scholar] [CrossRef]
- Zhang, W.B.; Zhang, L.M.; Pfoser, D.; Zhao, L. Disentangled dynamic graph deep generation. arXiv 2020, arXiv:2010.07276. [Google Scholar]
- Jia, S.; Liao, J.H.; Xu, M.; Li, Y.; Zhu, J.S.; Sun, W.W.; Jia, X.P.; Li, Q.Q. 3-D gabor convolutional neural network for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5509216. [Google Scholar] [CrossRef]
- Wan, S.; Pan, S.R.; Zhong, P.; Chang, X.J.; Yang, J.; Gong, C. Dual interactive graph convolutional networks for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5510214. [Google Scholar] [CrossRef]
- Jolliffe, I.T. Principal Component Analysis; Springer: New York, NY, USA, 2002. [Google Scholar]
- Bandos, T.V.; Bruzzone, L.; Camps-Valls, G. Classification of hyperspectral images with regularized linear discriminant analysis. IEEE Trans. Geosci. Remote Sens. 2009, 47, 862–873. [Google Scholar] [CrossRef]
- Sugiyama, M. Dimensionality reduction of multimodal labeled data by local fisher discriminant analysis. J. Mach. Learn. Res. 2007, 8, 1027–1061. [Google Scholar]
- Ma, L.; Crawford, M.M.; Yang, X.Q.; Guo, Y. Local-mainfold-learning-based graph construction for semisupervised hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2832–2844. [Google Scholar] [CrossRef]
- Liao, D.P.; Qian, Y.T.; Tang, Y.Y. Constrained manifolding learning for hyperspectral imagery visualization. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2017, 11, 1213–1226. [Google Scholar] [CrossRef] [Green Version]
- He, X.F.; Niyogi, P. Locality preserving projections. In Proceedings of the 17th Annual Conference on Neural Information Processing Systems (NIPS 2003), Vancouver, BC, Canada, 8–13 December 2003; pp. 234–241. [Google Scholar]
- Roweis, S.T.; Saul, L.K. Nonlinear dimensionality reduction by locally linear embedding. Science 2000, 290, 2323–2326. [Google Scholar] [CrossRef] [Green Version]
- He, X.F.; Cai, D.; Yan, S.C.; Zhang, H.J. Neighborhood preserving embedding. In Proceedings of the Tenth IEEE International Conference on Computer Vision (ICCV’05), Beijing, China, 17–21 October 2005; pp. 1208–1213. [Google Scholar]
- Belkin, M.; Niyogi, P. Laplacian eigenmaps for dimensionality reduction and data representation. Neural Comput. 2003, 15, 1373–1396. [Google Scholar] [CrossRef] [Green Version]
- Yan, S.C.; Xu, D.; Zhang, B.Y.; Zhang, H.-J.; Yang, Q.; Lin, S. Graph embedding and extensions:a general framework for dimensionality reduction. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 29, 40–51. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wright, J.; Yang, A.Y.; Ganesh, A.; Sastry, S.S.; Ma, Y. Robust face recognition via sparse representation. IEEE Trans. Pattern Anal. Mach. Intell. 2009, 31, 210–227. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Peng, J.T.; Li, L.Q.; Tang, Y.Y. Maximum likelihood estimation based joint sparse representation for the classification of hyperspectral remote sensing images. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 1790–1802. [Google Scholar] [CrossRef] [PubMed]
- Gu, Y.F.; Wang, Y.T.; Zheng, H.; Hu, Y. Hyperspectral target detection via exploiting spatial-spectral joint sparsity. Neurocomputing 2015, 169, 5–12. [Google Scholar] [CrossRef]
- Cheng, B.; Yang, J.C.; Yan, S.C.; Fu, Y.; Huang, T.S. Learning with l1-graph for image analysis. IEEE Trans. Image Process. 2015, 23, 2241–2253. [Google Scholar]
- Qiao, L.S.; Chen, S.C.; Tan, X.Y. Sparsity preserving projections with applications to face recognition. Pattern Recognit. 2010, 43, 331–341. [Google Scholar] [CrossRef] [Green Version]
- Ly, N.H.; Du, Q.; Fowler, J.E. Sparse graph-based discriminant analysis for hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2014, 52, 3872–3884. [Google Scholar]
- He, W.; Zhang, H.Y.; Zhang, L.P.; Philips, W.; Liao, W.Z. Weighted sparse graph based dimensionality reduction for hyperspectral images. IEEE Geosci. Remote Sens. Lett. 2016, 13, 686–690. [Google Scholar] [CrossRef] [Green Version]
- Ly, N.H.; Du, Q.; Fowler, J.E. Collaborative graph-based discriminant analysis for hyperspectral imagery. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2014, 7, 2688–2696. [Google Scholar] [CrossRef]
- Zhang, L.; Yang, M.; Feng, X.H. Sparse representation or collaborative representation: Which helps face recognition? In Proceedings of the 2011 International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011. [Google Scholar]
- Liu, G.C.; Lin, Z.C.; Yan, S.C.; Sun, J.; Yu, Y.; Ma, Y. Robust recovery of subspace structure by low-rank representation. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 171–184. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhuang, L.S.; Gao, S.H.; Tang, J.H.; Wang, J.J.; Lin, Z.C.; Ma, Y.; Yu, N.H. Constructing a nonnegative low-rank and sparse graph with data-adaptive features. IEEE Trans. Image Process. 2015, 24, 3717–3728. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- de Morsier, F.; Borgeaud, M.; Gass, V.; Thiran, J.-P.; Tuia, D. Kernel low-rank and sparse graph for unsupervised and semi-supervised classification of hyperspectral images. IEEE Trans. Geosci. Remote Sens. 2016, 54, 3410–3420. [Google Scholar] [CrossRef]
- Li, W.; Liu, J.B.; Du, Q. Sparse and low-rank graph for discriminant analysis of hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4094–4105. [Google Scholar] [CrossRef]
- Pan, L.; Li, H.-C.; Li, W.; Chen, X.-D.; Wu, G.-N.; Du, Q. Discriminant analysis of hyperspectral imagery using fast kernel sparse and low-rank graph. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6085–6098. [Google Scholar] [CrossRef]
- Pan, L.; Li, H.-C.; Deng, Y.J.; Zhang, F.; Chen, X.-D.; Du, Q. Hyperspectral dimensionality reduction by tensor sparse and low-rank graph-based discriminant analysis. Remote Sens. 2017, 9, 452. [Google Scholar] [CrossRef] [Green Version]
- Mei, S.H.; Bi, Q.Q.; Ji, J.Y.; Hou, J.H.; Du, Q. Hyperspectral image classification by exploring low-rank property in spectral or/and spatial domain. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2017, 10, 2910–2921. [Google Scholar] [CrossRef]
- He, W.; Zhang, H.Y.; Zhang, L.P.; Shen, H.F. Total-variation-regularized low-rank matrix factorization for hyperspectral image restoration. IEEE Trans. Geosci. Remote Sens. 2016, 54, 178–188. [Google Scholar] [CrossRef]
- Xue, J.Z.; Zhao, Y.Q.; Liao, W.Z.; Kong, S.G. Joint Spatial and Spectral Low-Rank Regularization for Hyperspectral Image Denoising. IEEE Trans. Geosci. Remote Sens. 2018, 56, 1940–1958. [Google Scholar] [CrossRef]
- Liu, G.C.; Yan, S.C. Latent low-rank representation for subspace segementation and feature extraction. In Proceedings of the 2011 International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011. [Google Scholar]
- Pan, L.; Li, H.-C.; Sun, Y.-J.; Du, Q. Hyperspectral image reconstruction by latent low-rank representation for classification. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1422–1426. [Google Scholar] [CrossRef]
- Fang, X.Z.; Han, N.; Wu, J.G.; Xu, Y. Approximate low-rank projection learning for feature extraction. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 5228–5241. [Google Scholar] [CrossRef] [PubMed]
- Pan, L.; Li, H.-C.; Meng, H.; Li, W.; Du, Q.; Emery, W.J. Hyperspectral image classification via low-rank and sparse representation with spectral consistency constraint. IEEE Geosci. Remote Sens. Lett. 2017, 14, 2117–2121. [Google Scholar] [CrossRef]
- Boyd, S.; Parikh, N.; Chu, E.; Peleato, B.; Eckstein, J. Distributed optimization and statistical learning via the alternating direction method of multipliers. Found. Trends Mach. Learn. 2011, 3, 1–122. [Google Scholar] [CrossRef]
- Cai, J.-F.; Candés, E.J.; Shen, Z. A singular value thresholding algorithm for matrix completion. SIAM J. Optim. 2010, 24, 1956–1982. [Google Scholar] [CrossRef]
- Zou, H.; Hastie, T.; Tibshirani, R. Sparse principle component analysis. J. Comput. Graph. Stat. 2006, 15, 265–286. [Google Scholar] [CrossRef] [Green Version]


| Class | LPP | NPE | SGE | LRGE | LatLRPL | MPCA | TLPP | SpaLatLRPL |
|---|---|---|---|---|---|---|---|---|
| 1 | 39.59 | 37.55 | 42.45 | 33.06 | 29.80 | 59.18 | 90.48 | 66.67 |
| ± 16.2 | ± 12.6 | ± 13.1 | ± 4.87 | ± 16.2 | ± 5.40 | ± 9.43 | ± 8.25 | |
| 2 | 75.83 | 79.95 | 79.36 | 82.08 | 83.41 | 93.21 | 89.88 | 94.45 |
| ± 1.82 | ± 2.24 | ± 1.56 | ± 0.99 | ± 2.06 | ± 1.39 | ± 1.93 | ± 0.74 | |
| 3 | 64.61 | 67.06 | 66.79 | 70.39 | 77.20 | 93.96 | 83.89 | 95.83 |
| ± 3.00 | ± 2.82 | ± 4.51 | ± 2.15 | ± 2.81 | ± 0.27 | ± 5.86 | ± 0.70 | |
| 4 | 52.70 | 57.35 | 53.93 | 53.93 | 50.71 | 84.68 | 89.89 | 86.73 |
| ± 9.30 | ± 6.72 | ± 6.93 | ± 8.71 | ± 9.33 | ± 7.29 | ± 6.00 | ± 9.25 | |
| 5 | 92.98 | 92.53 | 93.42 | 92.66 | 91.81 | 94.71 | 95.82 | 97.39 |
| ± 3.21 | ± 2.76 | ± 3.22 | ± 3.68 | ± 4.33 | ± 1.37 | ± 3.48 | ± 1.06 | |
| 6 | 95.39 | 96.49 | 96.19 | 95.62 | 94.88 | 97.67 | 98.46 | 97.57 |
| ± 1.55 | ± 1.27 | ± 1.48 | ± 1.20 | ± 1.22 | ± 1.08 | ± 0.56 | ± 0.73 | |
| 7 | 20.00 | 13.04 | 31.30 | 6.08 | 38.26 | 0.00 | 55.07 | 0.00 |
| ± 22.1 | ± 13.4 | ± 29.1 | ± 8.48 | ± 24.9 | ± 0.00 | ± 6.64 | ± 0.00 | |
| 8 | 99.27 | 99.36 | 99.45 | 99.23 | 98.27 | 97.35 | 99.92 | 98.33 |
| ± 0.41 | ± 0.19 | ± 0.20 | ± 0.59 | ± 1.77 | ± 1.74 | ± 0.13 | ± 0.65 | |
| 9 | 3.33 | 0.00 | 4.44 | 0.00 | 8.88 | 1.85 | 33.33 | 11.11 |
| ± 7.45 | ± 0.00 | ± 6.09 | ± 0.00 | ± 12.2 | ± 3.21 | ± 24.2 | ± 19.2 | |
| 10 | 58.05 | 62.80 | 60.32 | 63.51 | 77.57 | 88.94 | 89.55 | 93.61 |
| ± 3.02 | ± 5.24 | ± 6.38 | ± 4.03 | ± 2.60 | ± 1.35 | ± 1.92 | ± 0.43 | |
| 11 | 80.87 | 82.97 | 82.35 | 87.28 | 89.30 | 95.02 | 92.65 | 97.63 |
| ± 2.78 | ± 0.60 | ± 1.28 | ± 1.62 | ± 1.52 | ± 0.61 | ± 1.50 | ± 0.60 | |
| 12 | 77.07 | 79.46 | 80.83 | 85.06 | 85.75 | 87.22 | 87.10 | 92.77 |
| ± 2.89 | ± 1.68 | ± 4.72 | ± 2.28 | ± 2.94 | ± 5.27 | ± 4.76 | ± 2.20 | |
| 13 | 98.32 | 97.91 | 98.43 | 98.12 | 94.87 | 96.16 | 97.21 | 95.29 |
| ± 0.77 | ± 1.39 | ± 0.97 | ± 1.32 | ± 0.86 | ± 2.69 | ± 1.98 | ± 2.40 | |
| 14 | 96.21 | 95.93 | 96.64 | 97.65 | 96.07 | 96.31 | 99.43 | 98.43 |
| ± 2.47 | ± 3.05 | ± 2.33 | ± 0.90 | ± 1.17 | ± 1.12 | ± 0.84 | ± 0.13 | |
| 15 | 57.66 | 57.43 | 60.76 | 54.74 | 57.43 | 85.19 | 91.91 | 92.11 |
| ± 4.27 | ± 5.50 | ± 4.92 | ± 0.95 | ± 6.42 | ± 4.69 | ± 2.21 | ± 5.87 | |
| 16 | 82.59 | 80.47 | 83.29 | 83.06 | 87.53 | 80.39 | 84.31 | 87.45 |
| ± 8.74 | ± 9.58 | ± 7.64 | ± 6.31 | ± 8.71 | ± 13.2 | ± 5.43 | ± 8.76 | |
| OA | 79.29 | 81.20 | 81.07 | 83.15 | 85.46 | 92.79 | 92.41 | 95.34 |
| ± 0.65 | ± 0.72 | ± 0.73 | ± 0.51 | ± 0.58 | ± 0.51 | ± 1.01 | ± 0.22 | |
| AA | 68.40 | 68.77 | 70.62 | 68.90 | 72.61 | 78.24 | 86.18 | 81.58 |
| ± 1.18 | ± 0.47 | ± 2.06 | ± 0.46 | ± 2.01 | ± 0.85 | ± 0.59 | ± 0.74 | |
| 76.25 | 78.46 | 78.30 | 80.65 | 83.36 | 91.77 | 91.35 | 94.68 | |
| ± 0.68 | ± 0.83 | ± 0.89 | ± 0.60 | ± 0.67 | ± 0.58 | ± 1.16 | ± 0.33 |
| Class | LPP | NPE | SGE | LRGE | LatLRPL | MPCA | TLPP | SpaLatLRPL |
|---|---|---|---|---|---|---|---|---|
| 1 | 81.75 | 83.528 | 83.13 | 84.05 | 85.99 | 92.75 | 93.80 | 95.54 |
| ± 4.30 | ± 2.9 | ± 3.46 | ± 2.95 | ± 4.33 | ± 1.06 | ± 0.55 | ± 3.63 | |
| 2 | 94.21 | 95.05 | 94.52 | 95.26 | 96.47 | 97.86 | 95.65 | 99.40 |
| ± 1.34 | ± 0.54 | ± 1.06 | ± 1.82 | ± 1.23 | ± 0.60 | ± 1.14 | ± 0.14 | |
| 3 | 37.39 | 39.73 | 53.90 | 48.79 | 49.72 | 75.22 | 75.38 | 77.90 |
| ± 12.2 | ± 19.9 | ± 6.78 | ± 7.13 | ± 11.1 | ± 3.16 | ± 4.00 | ± 4.93 | |
| 4 | 82.34 | 77.74 | 79.79 | 77.42 | 81.64 | 87.58 | 91.84 | 91.92 |
| ± 3.54 | ± 3.84 | ± 5.43 | ± 2.76 | ± 2.41 | ± 2.67 | ± 2.41 | ± 1.84 | |
| 5 | 99.22 | 99.14 | 99.20 | 98.02 | 99.07 | 99.13 | 99.98 | 99.27 |
| ± 0.54 | ± 0.50 | ± 0.69 | ± 1.72 | ± 0.62 | ± 0.81 | ± 0.03 | ± 0.75 | |
| 6 | 51.97 | 55.59 | 55.79 | 58.05 | 60.92 | 77.55 | 72.93 | 93.39 |
| ± 4.58 | ± 3.78 | ± 2.87 | ± 3.46 | ± 5.71 | ± 3.78 | ± 3.61 | ± 1.73 | |
| 7 | 36.28 | 40.35 | 43.95 | 61.47 | 57.48 | 81.96 | 67.49 | 92.28 |
| ± 8.19 | ± 9.21 | ± 6.51 | ± 3.87 | ± 9.14 | ± 7.08 | ± 9.61 | ± 1.60 | |
| 8 | 70.95 | 73.48 | 72.34 | 80.71 | 84.47 | 87.19 | 80.52 | 84.57 |
| ± 7.86 | ± 10.8 | ± 2.81 | ± 3.01 | ± 3.91 | ± 2.22 | ± 3.01 | ± 3.34 | |
| 9 | 73.39 | 80.26 | 63.77 | 98.76 | 93.26 | 97.89 | 88.93 | 92.00 |
| ± 7.60 | ± 11.4 | ± 34.4 | ± 2.20 | ± 4.23 | ± 1.14 | ± 4.59 | ± 1.29 | |
| OA | 79.57 | 80.91 | 81.14 | 83.45 | 85.07 | 91.46 | 89.23 | 94.84 |
| ± 0.94 | ± 0.99 | ± 0.76 | ± 0.90 | ± 0.80 | ± 0.56 | ± 0.97 | ± 0.34 | |
| AA | 69.72 | 71.65 | 71.82 | 78.06 | 78.78 | 88.57 | 85.17 | 91.81 |
| ± 1.68 | ± 2.41 | ± 4.09 | ± 0.31 | ± 1.59 | ± 0.60 | ± 0.87 | ± 0.61 | |
| 72.32 | 74.08 | 74.46 | 77.63 | 79.81 | 88.56 | 85.61 | 93.13 | |
| ± 1.22 | ± 1.39 | ± 1.13 | ± 1.12 | ± 1.06 | ± 0.76 | ± 1.29 | ± 0.66 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, L.; Li, H.; Dai, X.; Cui, Y.; Huang, X.; Dai, L. Latent Low-Rank Projection Learning with Graph Regularization for Feature Extraction of Hyperspectral Images. Remote Sens. 2022, 14, 3078. https://doi.org/10.3390/rs14133078
Pan L, Li H, Dai X, Cui Y, Huang X, Dai L. Latent Low-Rank Projection Learning with Graph Regularization for Feature Extraction of Hyperspectral Images. Remote Sensing. 2022; 14(13):3078. https://doi.org/10.3390/rs14133078
Chicago/Turabian StylePan, Lei, Hengchao Li, Xiang Dai, Ying Cui, Xifeng Huang, and Lican Dai. 2022. "Latent Low-Rank Projection Learning with Graph Regularization for Feature Extraction of Hyperspectral Images" Remote Sensing 14, no. 13: 3078. https://doi.org/10.3390/rs14133078
APA StylePan, L., Li, H., Dai, X., Cui, Y., Huang, X., & Dai, L. (2022). Latent Low-Rank Projection Learning with Graph Regularization for Feature Extraction of Hyperspectral Images. Remote Sensing, 14(13), 3078. https://doi.org/10.3390/rs14133078






