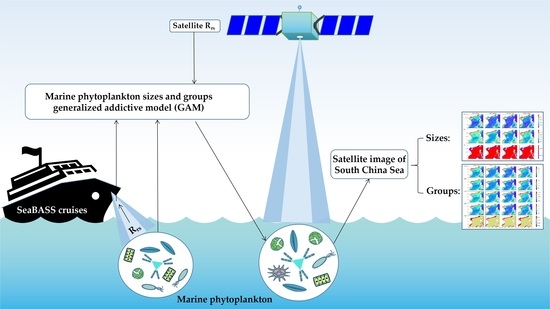
3.2. Establishment of GAMs
The in situ Rrs at 412, 443, 490, 555, and 670 nm (corresponding to the SeaWiFS band setting) were used as the predictors and the in situ Chl a was used as the response variable.
The fitted GAM result for Chl a is summarized in
Table 2. The Chl a GAM-fitted results show that the five predictors explained 79.2% of the total variance, with all the covariates being highly significant (
p value < 0.01). The EDF value of the five predictors indicated that each of them has a nonlinear relationship with the change in Chl a. The adj-R
2 (0.781) and GCV (0.106 mg·m
−3) showed that the Chl a GAM has a good fitting effect.
Similar to the Chl a GAM, the GAM was also used to fit the phytoplankton groups (Micro, Nano, Pico, diatoms, dinoflagellates, chrysophytes, prymnesiophytes, chlorophyceae, prasinophyceae, cyanobacteria and cryptophytes). The result of each fitted GAM is summarized in
Table 3,
Table 4,
Table 5,
Table 6,
Table 7,
Table 8,
Table 9,
Table 10,
Table 11,
Table 12 and
Table 13.
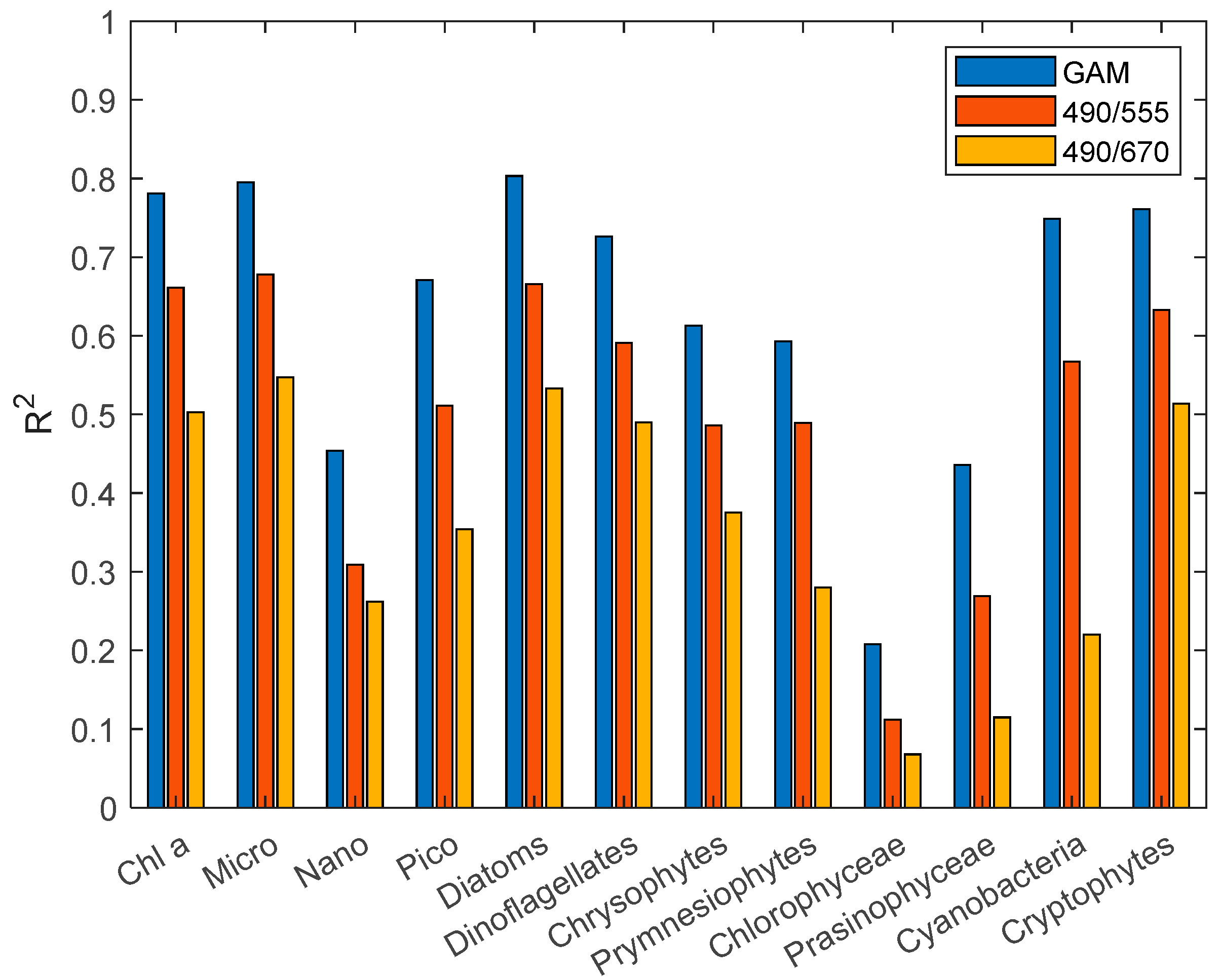
In the establishment of models, except for Nano, Chlorophyceae, and prasinophyceae, the deviance explained by the chlorophyll a, Micro, Pico, diatoms, dinoflagellates, chrysophytes, prymnesiophytes, cyanobacteria, and cryptophytes fitted model is more than 60%.
The different cell sizes of the phytoplankton present different spectral features, including their absorption and backscattering properties in a wide band range from 400 to 700 nm. This difference in the absorption and backscattering induces the variability in spectral shape of remote sensing reflectance [
37]. Li et al. [
17] found that the spectral features with particular importance around 440–555 nm have a significant response to phytoplankton size. Brewin et al. [
38] found there are contrasting spectral shapes between the three phytoplankton sizes in the green part of the spectrum (500–600 nm). It is consistent with our results that R
rs555 has a significant response to micro-, nano- and picophytoplankton concentrations (the F value is high in
Table 3,
Table 4 and
Table 5). R
rs412, R
rs443, and R
rs555 have a significant contribution for estimation of all three sizes’ concentration. In addition, Brewin et al. [
38] also demonstrated that nanophytoplankton has a distinct absorption at ~450 nm. In our study, the nanophytoplankton GAM (adj-R
2 = 0.454) is a little worse than the pico- and microphytoplankton model (adj-R
2 = 0.671 and adj-R
2 = 0.795). R
rs412, R
rs443, and R
rs555 contribute significantly in estimating the nanophytoplankton concentration, while R
rs490 and R
rs670 have a limited contribution to nanophytoplankton estimation (
Table 4). In the blue-green part of the spectrum (400–600 nm), R
rs490 has a lower contribution to the phytoplankton size GAM compared with other spectral bands, especially for the nanophytoplankton retrieval model. Sun et al. [
39] applied remote sensing reflectance at 488 nm and 555 nm to obtain the phytoplankton size. They found that the microphytoplankton retrievals show a greater sensitivity than that of the nano- and picophytoplankton on R
rs488 or R
rs555. In the red part of the spectrum, Roy et al. [
40] developed a semi-analytical algorithm based on phytoplankton absorption features at a red wavelength (676 nm) to obtain the phytoplankton size distribution. However, our results illustrate that R
rs670 have the smallest (not significant) contribution to the micro-, nano- and picophytoplankton retrieval estimation.
Satellites detect some phytoplankton species (such as cyanobacteria, diatoms, dinoflagellates, etc.) with a similar chlorophyll biomass, provided they have contrasting optical signatures. Some studies demonstrated that satellite spectra have a distinct response for cyanobacteria and diatoms [
41,
42]. Isada et al. [
43] found that diatom and cyanobacteria have differences in absorption in the green-red part of the spectrum. The diatoms absorption normalized at 443 nm is higher in the green-red part of the spectrum than that of cyanobacteria, resulting in lower remote sensing reflectance for diatoms. Our results demonstrate that the contribution of R
rs(670) to the diatom model is lower than that for cyanobacteria (
Table 6 and
Table 12). Aguirre-Gomez et al. [
44] also indicated that cyanobacteria has a more obvious optical signal at ~670 nm than diatoms. Stuart et al. [
45] found that the absorption at 443 and 490 nm normalized at 555 nm is significantly lower for the diatom-dominated population than for the prymnesiophyte-rich population, indicating that there are larger R
rs443 and R
rs490 for the diatom-dominated population. The prymnesiophytes GAM model developed in this study is mainly contributed by R
rs490 and R
rs555. It was thought that diatoms and dinoflagellates contain some of the same pigments, and therefore their light absorption features are similar [
46]; however, their optical backscattering features are different due to their structure difference. Discriminating between these two groups depends on the variability in the R
rs spectral shape induced by backscattering [
47]. In fact, there are some difference in the absorption between these two groups. The absorption peak of the dinoflagellates at ~440 nm is steeper than that of diatoms. In the case of absorption peaks of the same magnitude, the absorption curve of dinoflagellates drops faster at ~490 nm. It is also found that dinoflagellates have a stronger absorption at ~670 nm [
48]. Our results indicate that, compared with diatoms, the contribution of R
rs490 for the dinoflagellates model decreases and the contribution of R
rs670 increases (
Table 6 and
Table 7). Based on the steeper absorption peak characteristics of the dinoflagellates, Bracher et al. [
49] also retrieved cyanobacteria and diatoms based on their spectral variability within 429–495 nm. Sadeghi et al. [
50] retrieved diatoms, coccolithophores, and dinoflagellates based on a spectral absorption difference over the 429–521 nm spectral range. Relatively little research has been done on remote sensing of chrysophytes and cryptophytes. In this study, their retrieval accuracy performs well. R
rs412, R
rs443, and R
rs555 have larger contributions for chrysophytes estimation (
Table 8). R
rs at all five bands demonstrate a more near-equivalent contribution for cryptophytes estimation (
Table 13). Compared to other species models, the contribution of R
rs at 490 and 670 nm also increases.
To test the effectiveness of the GAM, we used random sampling to extract 70% of the data as the training data set and the remaining 30% of the data as the test data set and randomly cycle 1000 times to test the prediction accuracy. This helps to test whether our models are effective or an effect caused by the randomness of the data set. We take the root mean squared error (RMSE), median absolute percentage error (MED), and coefficient of determination (R2) as the indicators of the models’ prediction accuracy.
From the training results of various phytoplankton GAM (
Table 14), eight GAM models achieve a good fitted effect (R
2 > 0.5). They are chlorophyll a, Micro, Pico, diatoms, dinoflagellates, chrysophytes, cyanobacteria, and cryptophytes models. The prymnesiophytes model performs a little worse than the above eight models with an R
2 of 0.403. The correlation coefficient is relatively small for the Nano, chlorophyceae, and prasinophyceae models.
In addition, the GAM of the various marine phytoplankton groups studied and developed in this paper was constructed based on different depths. Therefore, theoretically, as long as the R
rs data at different depths can be accurately obtained, the distribution information of the phytoplankton groups in the research area can be estimated by using the marine phytoplankton group GAM developed in this study, whether it is surface or deep water [
51].
3.3. Comparison between GAMs and Other Algorithms
In addition to the training models, the GAM models are also compared with other inversion algorithms. The empirical ocean chlorophyll (OC) algorithm from O’Reilly et al. [
52] is the current default chlorophyll a algorithm for SeaWiFS and MODIS. The OC algorithm is a fourth-order polynomial calculated using an empirical relationship derived from in situ measurements of Chl a and R
rs in the blue-to-green region of the visible spectrum.
where a
0–a
4 are the empirical regression coefficients, for which the current values of OC4v6 (the ocean chlorophyll 4 algorithm vision 6) are 0.3272, 2.9940, 2.7218, 1.2259, and 0.5683, respectively.
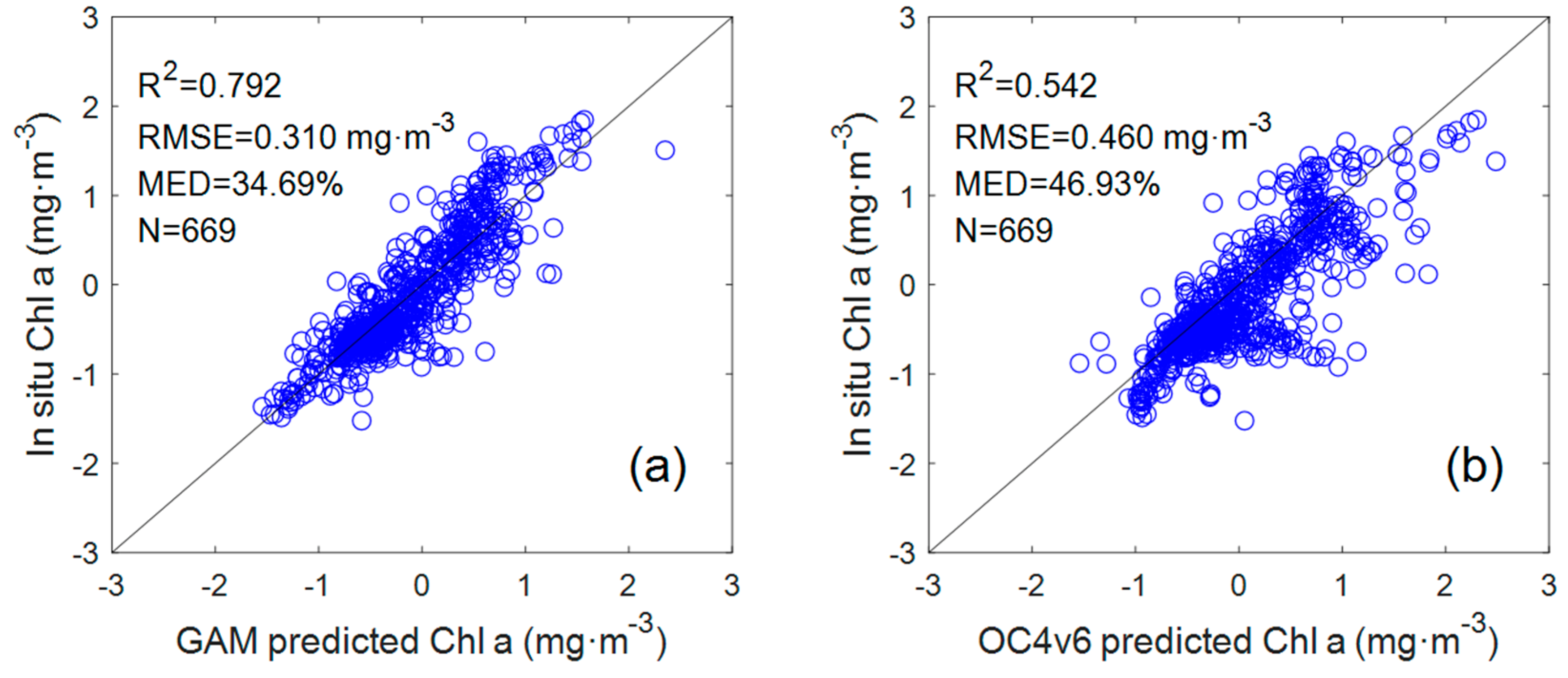
To compare with the GAM, the data set used for the OC4v6 algorithm was also taken from 669 coincident in situ data points corresponding to the GAM. From the comparison results of the Chl a GAM and OC4v6 algorithms (
Figure 3), it can be seen that the OC4v6-retrieved Chl a showed a lower coefficient of determination (R
2 = 0.542, n = 669) and higher RMSE and MED from the in situ Chl a (RMSE = 0.46 mg·m
−3, MED = 46.93%). Indeed, as the current default chlorophyll a algorithm, the OC algorithm has achieved acceptable inversion results in most Case I waters, but it has limitations in some areas, such as coastal waters with complex optical characteristics. The data set in this study was collected in both Case I waters and coastal waters, which may be the reason for the poor performance of the OC algorithm.
Similar to the OC algorithm, Pan et al. [
25] adopted a set of third-order polynomial functions to develop algorithms for individual pigment concentrations from R
rs ratios:
where A
0–A
3 are the empirical regression coefficients.
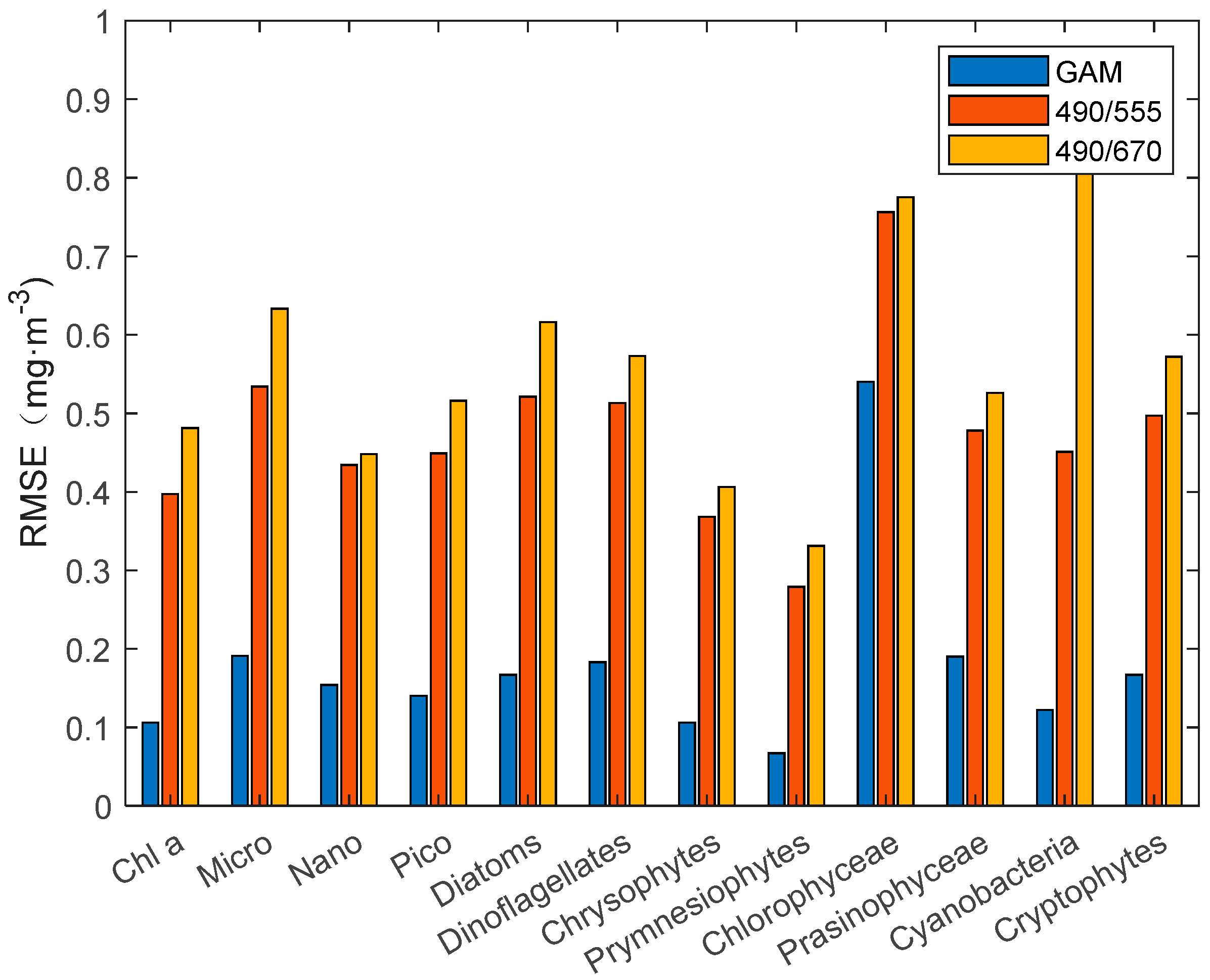
Therefore, similar to O’Reilly et al. [
52] and Pan et al. [
25], we constructed a third-order polynomial algorithm for individual groups of phytoplankton. The statistical results (
Figure 4 and
Figure 5) of R
2 and RMSE show that the third-order polynomial algorithm based on the R
rs490/R
rs555 band ratio is better than the R
rs490/R
rs670 band ratio. In the comparison results between the GAM and third-order polynomial algorithm, the GAM performs better than the third-order polynomial algorithm, with a higher R
2 and lower RMSE. The RMSE of the third-order polynomial algorithm generally exceeds 0.3 mg·m
−3. In addition, the poor performance (R
2 < 0.5) of the Nano, chlorophyceae, and prasinophyceae models can be seen concisely and clearly from
Figure 4 and
Figure 5.
3.4. Model Evaluation Using Satellite Data
In
Section 3.2, we established the GAM of the marine phytoplankton groups using in situ data, and obtained nine models with good performance, namely, chlorophyll a, Micro, Pico, diatoms, dinoflagellates, chrysophytes, prymnesiophytes, cyanobacteria, and cryptophytes. In addition, although the R
2 of the Nano model is only 0.454, it is also included in the scope of the discussion in this section. In
Section 2.1, we mentioned that there are four cruises without in situ R
rs data matching the HPLC data in the western Pacific Ocean. Therefore, these four cruises (a total of 32 coincident satellite data) independent of the construction GAM data are very suitable for evaluating the performance of the GAM in remote sensing satellites.
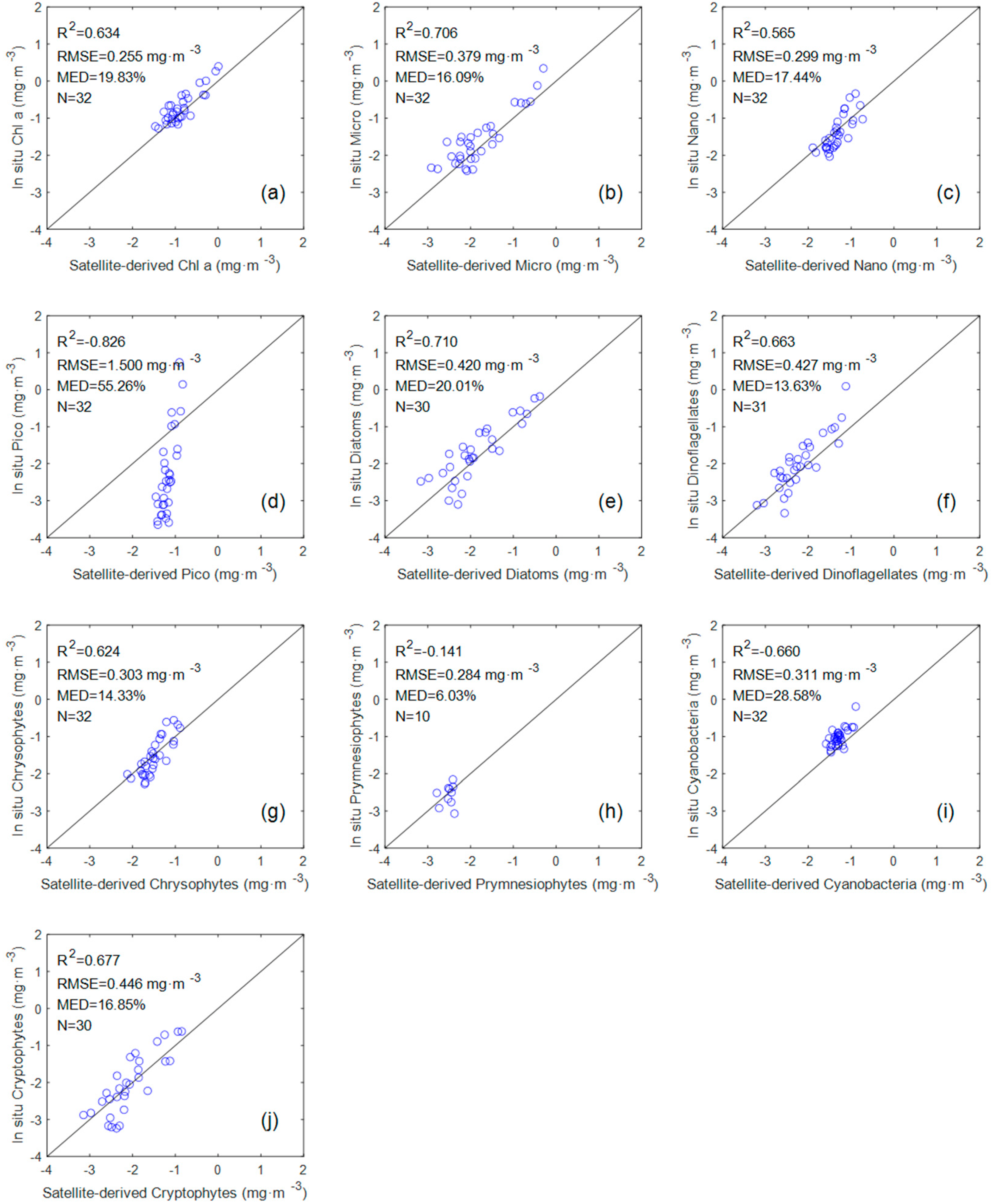
Ten models were applied to the ocean color satellite Level 3 binned Rrs products of MODIS-Terra, and the derived values were compared with the in situ data. Rrs488 and Rrs667 in MODIS were assumed to be equal to their values at 490 and 670 nm (SeaWiFS band setting).
The evaluation results (
Figure 6) of seven groups (Chl a, Micro, Nano, diatoms, dinoflagellates, chrysophytes, and cryptophytes) showed a good tendency towards accuracy (R
2 > 0.5 and MED < 20%). However, the evaluation results of Pico, premnesiophytes, and cyanobacteria exhibit dispersion and poor statistical correlation. The R
2 value of the three groups are −0.826, −0.141, and −0.66, respectively. A negative value of R
2 indicates that the sum of squares of errors (SSE) in the predicted value of the model is much greater than the sum of squares of the total deviations (SST). We are surprised by the performance of the Pico and cyanobacteria models in this comparison, because they perform well in the previous in situ measurements.
3.5. Application of GAMs in the South China Sea
The seven models with good performance in
Section 3.4 were applied to the SCS, to obtain the spatial–temporal distribution and seasonal variation map of each phytoplankton group in 2020. Among them, December to February is winter, March to May is spring, June to August is summer, and September to November is autumn.
The open deep basin of the South China Sea is characterized as an oligotrophic water type, which is similar with that of the oligotrophic western Pacific water. Furthermore, the seawater in the coastal area of the South China Sea has the typical optical complex water characteristics of the coastal waters in China. According to the results of the dominant optical water class by Jackson et al. [
53], the central deep basin of the South China Sea has the same optical water class as the lower and middle latitude waters of the western Pacific. Coastal water of the South China Sea has the same optical water class as some areas of the Yellow River region of China. In addition, due to the water exchange between the western Pacific and the South China Sea, the distribution and concentration of the algae type in the western Pacific Ocean are closely related to that of the South China Sea [
54].
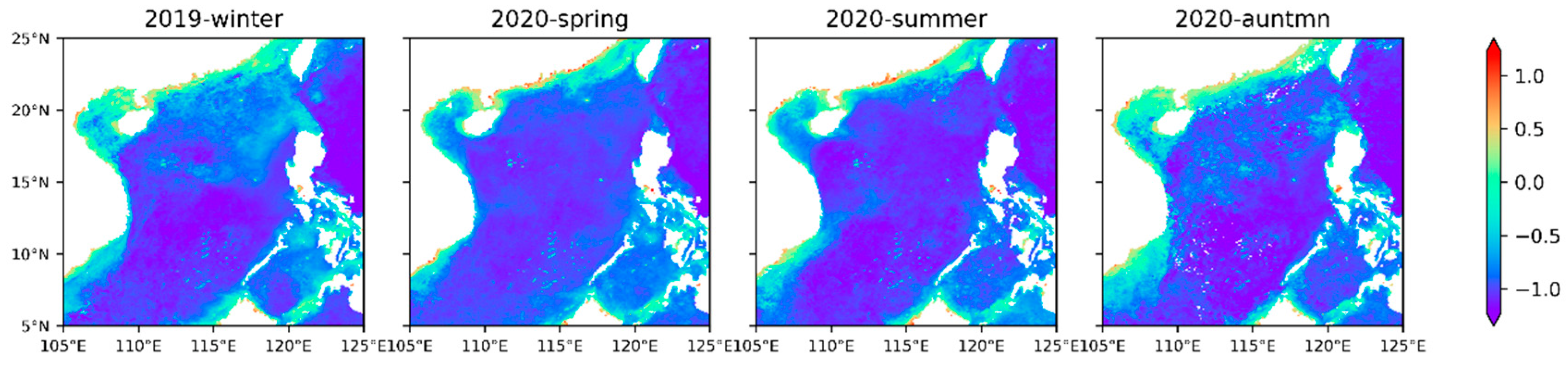
Figure 7 shows that the Chl a abundance generally decrease from the inner shelf to outer shelf and the higher abundance in the inner shelf is strongly influenced by river discharge (e.g., Pearl River, Red River, and Mekong River). The shallow water depths near the shore and the rich nutrient supplements are very suitable for the growth and reproduction of phytoplankton [
55]. Higher Chl a abundance in the winter relative to the summer are consistent with a previous study in the SCS [
56]. The higher abundance of Chl a are associated with lower temperature and higher nutrients, and temperature and nutrients are usually the limiting factors for phytoplankton growth [
22]. In winter and spring,
Figure 7 clearly shows that there is a high abundance of chlorophyll in the southwestern Taiwan Strait, northern Luzon Island, and western Hainan Island, with an average concentration of 1 mg·m
−3. There is a strong northeast monsoon prevailing in the SCS from October to April, which makes the seawater offshore Ekman transport in these areas, causing the upwelling of low-temperature and high-nutrient seawater from the bottom. The violent agitation of the monsoon also enhances the vertical mixing of seawater, resulting in high chlorophyll levels in the SCS in winter and spring. In summer, the southwest monsoon prevailing in the SCS leads to the emergence of upwelling areas along the coast of Guangdong, the east of Hainan Island, and Vietnam. In addition, in eastern Vietnam, approximately 12°N usually forms a chlorophyll belt from the upwelling of Vietnam to the SCS basin. This is because an offshore jet from southwest to northeast is formed between the cold and warm eddies to transport the cold-water mass generated in the upwelling area to the SCS basin [
57,
58,
59].
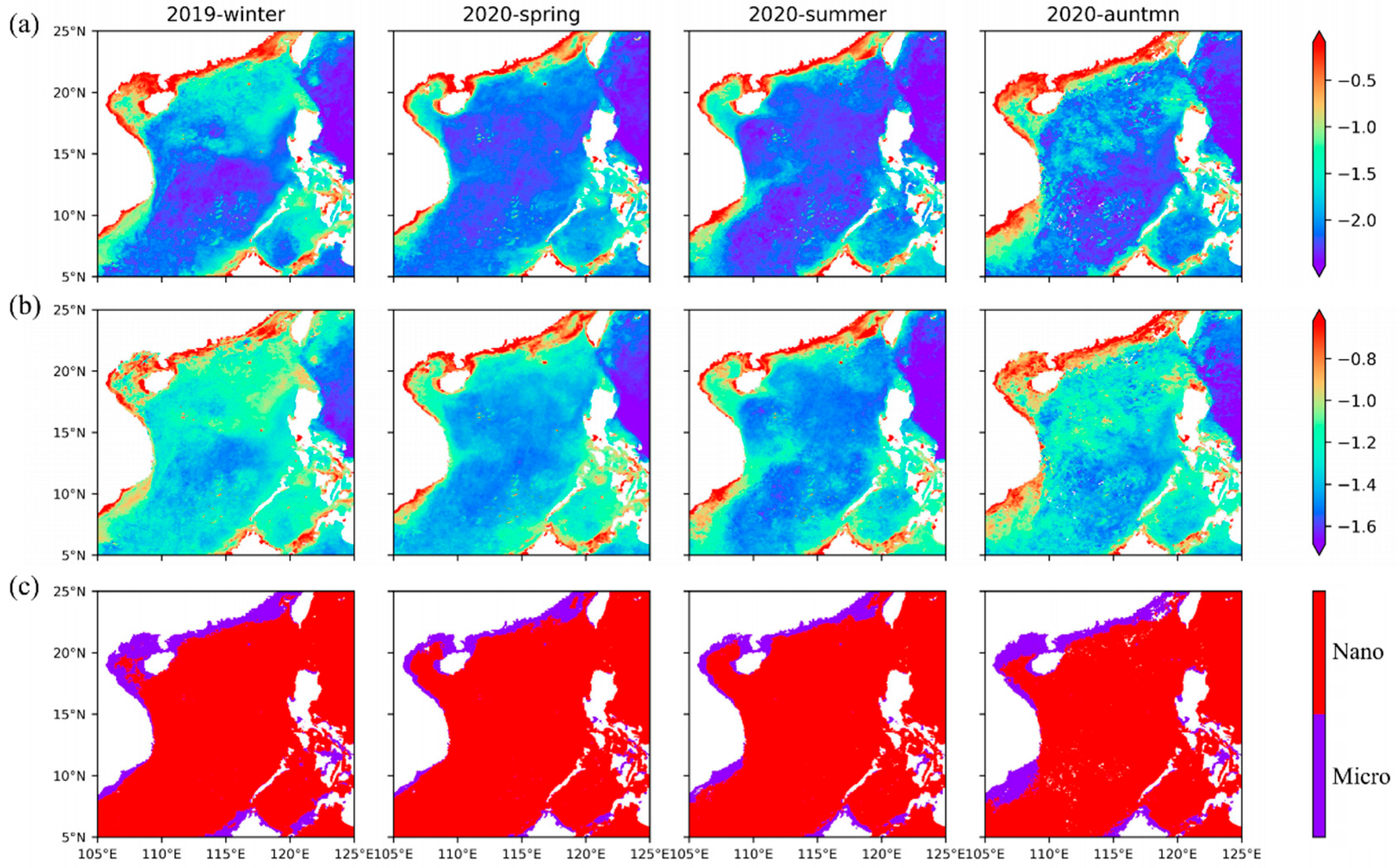
Among the two size classes retrieved by our model, both Micro (
Figure 8a) and Nano (
Figure 8b) show the distribution characteristics of high abundance in winter and low abundance in summer. The distribution map of the dominant group (
Figure 8c) shows well-defined and persistent large-scale structures characterized to the first order by the dominance of Nano in oligotrophic waters; the average concentration reached 0.1 mg·m
−3, whereas Micro prevails in the coastal and continental shelf, and the average concentration reaches 0.5 mg·m
−3. The main groups of Micro are diatoms and dinoflagellates, which generally occupy an absolute advantage in the nearshore [
60]. These patterns are consistent with the expected nutrient conditions in these regions, as diatoms are favored under more nutrient-replete conditions, while Nano is favored in nutrient-depleted water [
22,
61]. The higher efficiency of nutrient utilization due to their small size (higher surface-to-volume ratio) permits Nano to grow faster than Micro in nutrient-poor waters [
25]. These results are also consistent with those estimated from field samples [
30,
62]. In addition, it is also indicated that turbid coastal water conditions with limited light intensity may stimulate the growth of microphytoplankton, possibly due to large superficial areas of these large-sized algal particles that possess stronger light availability than small one [
63,
64]. The small-sized nanophytoplankton growth would be suppressed by the turbid coastal water.
Among the four groups retrieved by our model, the four groups show the characteristics of a gradually decreasing abundance from winter to summer, especially in the open ocean, while the abundance of the four groups increased toward the coast. Among them, diatoms (
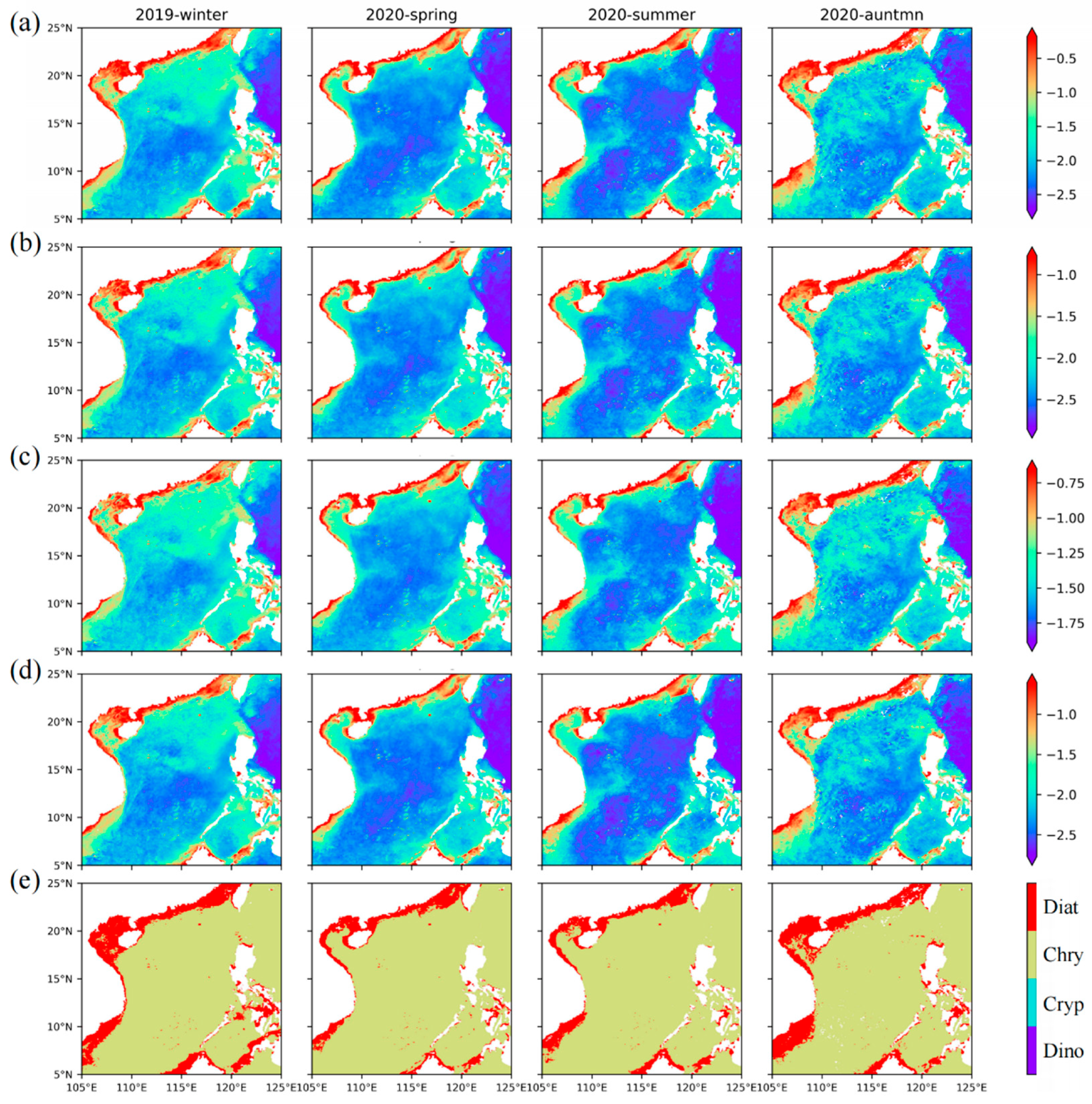
Figure 9a) are mainly distributed in the nearshore, and the average concentration can reach 0.3 mg·m
−3. Indeed, silicate is very important for the growth of diatoms, and the rivers bring abundant silicate to the nearshore [
65]. In addition, the distribution range of diatoms gradually decreases from winter to summer, but diatoms are still common in the upwelling area year-round, and the concentration is greater than 0.1 mg·m
−3. Dinoflagellates (
Figure 9b) also mainly occur in the nearshore area with abundant nutrients, with an average concentration of approximately 0.1 mg·m
−3 and approximately 0.03 mg·m
−3 in the upwelling area. Aiken et al. [
66] also found the diatom and dinoflagellate populations are located in shallow water or upwelled water. Nanophytoplankton chrysophytes (
Figure 9c) and cryptophytes (
Figure 9d) also have a high abundance in the oligotrophic ocean in summer, with average concentrations of approximately 0.025 mg·m
−3 and 0.01 mg·m
−3, respectively. In autumn and winter, the average concentrations reached 0.063 mg·m
−3 and 0.031 mg·m
−3, respectively. In the seasonal upwelling area, the average concentrations of chrysophytes and cryptophytes can reach 0.158 mg·m
−3 and 0.056 mg·m
−3, respectively.
The distribution map of the dominant groups (
Figure 9e) shows that diatoms (nearshore) and chrysophytes (outside the continental shelf) are the dominant groups in the SCS throughout the year. Dinoflagellates only become dominant in some coastal areas, but compared with diatoms, dinoflagellates have a limited dominant range. Among the four groups, cryptophytes rarely become the dominant group in the SCS. Compared with the chrysophytes, cryptophytes contribute less to Nano, but the sum of their abundance makes individual areas dominated by Micro change to Nano. Combined with the dominant groups of Micro and Nano, it can be seen that the main contribution of Micro comes from diatoms, while Nano comes from chrysophytes. The suitable growth conditions near the shore make the groups with large size classes, such as diatoms and dinoflagellates, dominant, while nanophytoplankton, such as chrysophytes and cryptophytes, are dominant offshore, where there are fewer nutrients. In addition, a clear seasonal cycle is also evidenced west of Hainan Island, where chrysophytes dominate in summer and large-scale diatom blooms occur in winter. These consistencies validate our inversion models proposed in this study for estimating the phytoplankton sizes and groups from satellite remote sensing.
The satellite retrievals of phytoplankton sizes and groups using our empirical models were relatively successful. However, some models show instability in the process of training the models and evaluation using satellite data. This instability might be partly explained by the differences in the dynamic range of the measured data (spatial mismatch exists between in situ and satellite data) or because there was not enough matching data [
67]. In addition, there might be some possible sources of uncertainty: (1) we assumed R
rs488 and R
rs667 to be equal to R
rs490 and R
rs670; and (2) we quantified the phytoplankton composition and abundance by using the proposed modified classification (DPA and HPLC-CHEMTAX). The regression coefficient in DPA comes from the regression results in the ocean pigment data, and CHEMTAX also depends on the initial input pigment ratio. These factors may have induced the deviations in our models.