Abstract
Many Ground-Based Synthetic Aperture Radar (GBSAR) applications demand preliminary analysis to select areas with high-quality signal. That is, areas in which the phase can be processed to extract the desired information. The interferometric coherence and the amplitude dispersion index are important tools widely used in the literature to assess the quality of GBSAR images. So far, no direct relation has been found between the two. Indeed, they are parameters of different natures: amplitude dispersion index is calculated with only amplitude values, while coherence provides information also on the signal phase. The purpose of this article is to find a relation between the two parameters. Indeed, the amplitude dispersion index provides some practical advantages if compared to coherence estimators, especially to perform fast preliminary analysis. In this article, a theoretical relation between amplitude dispersion index and coherence is retrieved. GBSAR measurements acquired in different scenarios, at different working frequencies are presented and used to validate such a relation.
1. Introduction
Ground-Based Synthetic Aperture Radar (GBSAR) [1] interferometry is a powerful tool that enables the measurement of target displacements with sub-wavelength precision. This popular technique is currently applied for monitoring natural and urban scenarios. Interferometry techniques exploit the signal phase information and give reliable results only when applied to signals with a sufficient phase quality. Therefore, preliminary studies to single out areas of the investigated scene characterized by high-quality signal are demanded.
One of the main problems that affects radar interferometry is the temporal decorrelation of the radar echoes [2]. In fact, there are several factors that can degrade the phase information as changes in atmospheric conditions or modifications in the physical properties of the scene between acquisitions. This effect is particularly evident in vegetated scenarios, where (due to wind, vegetation growth, etc.) targets are subject to non-coherent displacements between successive acquisitions. For instance, authors of [3] showed that the short-term variable reflectivity induced by wind, typical of vegetated scenarios, can be theoretically characterized and modeled. In [4] different theoretical models for the temporal decorrelation of GBSAR images in vegetated scenarios are examined. For the short-term signal variability, a model with dependence on the wind speed is presented and validated for experimental data acquired in different scenarios.
To estimate the decorrelation degree of GBSAR images, the interferometric coherence [5] and the amplitude dispersion index [6] parameters are largely employed.
The interferometric coherence of radar images is a benchmark of the achievable interferogram quality [5] and is widely used to select image pixels with a sufficiently stable phase.
The amplitude dispersion index (DA) [6,7] was introduced for the determination of the so-called permanent scatterers, i.e., targets whose signal amplitude remains stable over time, and it is a popular tool currently employed in interferometric analysis.
Whereas the coherence is calculated on complex image values, the DA is based only on the signal amplitudes and seems to provide no information on phase content. Nevertheless, the authors of [7] showed that the amplitude dispersion index can provide an estimate for the phase dispersion, under the hypothesis of high signal-to-noise ratio.
As will be further discussed in the following section of this paper, the DA provides practical advantages with respect to the interferometric coherence in assessing the image quality. For instance, being based on amplitude values, it is less sensitive to changes in the atmospheric parameters. Thus, it does not require atmospheric phase compensation before calculation, which implies less computational effort. Furthermore, the amplitude dispersion index parameter gives reliable results if calculated on a limited measurement time series.
Given the paramount importance and theoretical relevance of the coherence parameter on the one hand, and the practical advantages provided by amplitude dispersion index on the other, it would be interesting to find a way to relate them. Up to now, no direct relation has been established between the two parameters. The aim of this article is to find a theoretical relation between coherence and DA.
In order to give the DA a theoretical formulation, the authors of this paper start from the theory of radar scattering statistics [8,9,10]. Indeed, as the amplitude dispersion index involves first and second momenta of the amplitude distribution, it is possible to retrieve an analytic expression of this parameter.
The analytic expression retrieved, which relates DA and coherence, is tested using GBSAR experimental data resulting from three measurement campaigns performed in different scenarios.
2. Materials and Methods
In this section, after having reviewed the theoretical definition of the signal coherence, some estimators commonly used to evaluate the phase quality of radar images are introduced and discussed. Then, to theoretically relate the amplitude dispersion index to the coherence, a statistical description of the radar backscattered signal is introduced, and an analytic formula that relates the two parameters is derived for the most common signal distributions. Finally, the theoretical relation is validated by simulations.
2.1. The Coherence Estimator
Given two zero-mean complex signals In and Im, the complex coherence is defined as follows [5]:
where is the expectation value operator. The magnitude of this quantity is called the degree of coherence. The coherence is defined within [0, 1]. High values of γnm correspond to high coherent signals. Generally, a signal is considered coherent when .
In the context of GBSAR analysis, we are interested in evaluating the coherence between radar images of the same scenario, acquired at different times, say at time t1, and t2. Then, the above expression is called temporal or interferometric coherence and quantifies the signal quality of the image’s pixel value I, between time t1, and t2.
There are several factors that lead to a degradation of a radar image in terms of phase information, such as thermal effects, noise, atmospheric phase screen or physical changes in the scene [2,3,11,12]. In GBSAR applications, we are particularly interested in the degradation related to physical changes in the scene. Indeed, these changes could fatally affect the interferometric image.
Other sources of de-coherence, such as the atmospheric condition, could be compensated during the signal analysis. Indeed, these contributions are not related with the quality of the signal and can be removed by using specific techniques [13,14,15,16,17,18] before coherence computing.
Throughout the last decades, different models [2,19,20,21] and estimators for the temporal coherence have been defined, mostly for SAR applications [4,5,22,23].
An efficient tool for retrieving information on the signal autocorrelation and coherence is provided by the signal spectral analysis. In the frequency domain, the coherence is usually computed as the amplitude of normalized cross spectral density [24,25,26].
The signal power spectral density function can provide important information also about the characterization of GBSAR signals. For instance, in [27] the power spectral density is proposed in the context of synthetic aperture radar (SAR) processing as a tool for the statistical characterization of the different SAR modes and interferograms.
To understand how the signal power spectral density is related to the coherence, let us write the autocorrelation function C(τ) for a certain time interval τ, of a signal time series I(t) acquired at generic times t, and its power spectral density S(f), respectively, as,
where f is the conjugate variable of τ.
The Wiener–Kinchin theorem states that, under the assumption of a stationary random process, the Fourier transform (FT) of the autocorrelation signal (2) is equal to the signal power spectral density,
Under the assumption of stationary processes, the spectral density itself can provide information on the overall coherence degree of the time series images. Indeed, the autocorrelation, if properly normalized is a common coherence estimator. For a stationary process it is for any , and normalization factors in Equation (1) do not depend on time. Therefore, by applying the Fourier transform to Equation (1), and combining Equations (2) and (4), we have
Equation (5) provides us with an expression of the signal coherence, in the frequency domain. If only one frequency dominates the spectral density , then, the peak value of the spectral density, properly normalized, is an estimator for the coherence degree, relative to that frequency in the spectrum. Indeed, if the investigated area is stationary, or subject to a constant uniform movement, the spectrum will be characterized by a single peak at zero or at a constant frequency, respectively. This method provides us with an estimate of the temporal coherence averaged over the time interval.
It is worth noting that almost regular sampling times are required to properly calculate the Fourier transform, hence, the signal spectral density. The GBSAR systems usually acquire long time series of images of the same scenario, with regular return times in the order of minutes. Thus, Equation (5) may represent an excellent tool for estimating the signal coherence in GBSAR applications.
Finally, it is worth saying that the coherence estimate of Equation (5) presents great sensitivity to changes in atmospheric conditions, since the variations of the signal phase values over time influence the evaluation of the Fourier transform.
2.2. The Amplitude Dispersion Index
The amplitude dispersion index is an important tool for evaluating the signal stability over time, and was introduced in the context of permanent scatterers determination for interferometric analysis [6,7,28,29]. It is defined as
where is the image amplitude, and STDA, mA are the standard deviation and the mean value of the amplitude time series, respectively. Low values of DA correspond to high coherent signals. Generally, the threshold below which a pixel is considered a permanent scatterer is set to 0.25.
Since the DA evaluation is based on amplitude values, it is not very sensitive on changes in atmospheric conditions. Indeed, a time variation of the air refractive index profoundly changes the atmospheric phase contribution, hence, the signal phase information. Conversely, amplitude values are almost insensitive to these effects, and the DA evaluation does not demand atmospheric phase corrections.
As already said, despite being calculated with amplitude values, it has been shown that the DA provides a good estimate of the phase dispersion in the hypothesis of high signal-to-noise ratio [7]. This result was obtained investigating the statistical properties of the signal amplitude. As it suggests a connection between DA and coherence of the interferometric phase, in the following section a statistical description of radar signal amplitudes is reviewed.
2.3. Amplitude Statistics of Radar Data
Statistical descriptions of radar signals have been studied at the very beginning of this technology [8,9,10,30,31,32,33]. Depending on the radar signal characteristics or the physically investigated scenario, different statistics have been proposed for both the interferometric phase and the signal amplitude. In what follows, we review basic concepts related to the statistical properties of the backscattered signal from distributed targets. Indeed, the signal amplitude statistics can provide important insights on the amplitude dispersion index and on its relation to the other parameters of interest.
Let us start modelling the response of the so-called Gaussian scatterers, i.e., scatterers that can be decomposed into a sufficiently high number of random independent scatterers within a resolution cell [33]. If no scatterer dominates the others, for the central limit theorem, the radar image pixel value I(t) is a zero mean complex circular Gaussian random variable, arising from the contribution of independent scatterers located in the same resolution cell. Thus, the joint probability density function for the real and imaginary part of I(t) reads
where σ is the standard deviation. By performing a change of variables, one can derive a joint probability distribution for the amplitude A and phase φ of the signal. Specifically, by substituting
into Equation (7), and after integration over the variable φ, we get the following expression for the signal amplitude statistics,
Equation (9) is a Rayleigh distribution [8], with scale parameter σ. Given the assumptions made (large number of independent contributions and no scatterer that dominates the others), this model has been regarded in the literature as that describing the speckle pattern [8]. Good agreement with the Rayleigh distribution has been observed for the amplitude of SAR experimental data in homogeneous regions with coarse spatial resolution [9]. Conversely, it fails in describing the radar statistics of heterogeneous areas imaged with fine spatial resolution.
Let us now consider the case when a coherent background signal is summed to the independent scatterers contributions [8]. That is, a part of the scatterers within the resolution cell remains stable over time. Indeed, this may be the case in natural scenarios, when investigating land partially covered by vegetation. In this case the signal can be modeled as the sum of a random circular Gaussian variable and a constant complex phasor. In the following, we assume that the Gaussian scatterers are completely independent from the coherent background. Without loss of generality, we also assume the coherent background image value to be real, equal to AS. As a result, the real part of the image pixel I(t) has mean value equal to AS. Under these hypotheses, the joint probability distribution for the real and imaginary part of the image pixel value I(t), reads
By performing the change of variables defined in Equation (8), and after integration over the phase variable φ, we retrieve the following relation:
which is called the Rice distribution [8]. The Rician model was found appropriate to describe low resolution SAR images [10], where strong scatterers are embedded into the surrounding weak clutter environment. Our intent is to understand whether this simple model can account for GBSAR amplitude images, acquired in vegetated scenarios.
2.4. Relation between Amplitude Dispersion Index and Coherence
An a-priori expression of the amplitude dispersion index can be retrieved by considering the first (mA) and the second (STDA) moment of the proper amplitude radar statistic.
For example, considering the Rayleigh distribution (9), the value of dispersion index is constant, equal to
Indeed, this value corresponds to the dispersion index of radar clutter, which typically follows the Rayleigh distribution.
If the amplitude signal is instead Rice distributed, it depends on the parameters AS, and σ, according to
where is the Laguerre polynomial of degree . Equation (13) relates the amplitude dispersion index values to the ratio . Under the same assumptions on the statistical distribution, it is possible to retrieve an expression for the coherence of radar images, as a function of the parameters AS, and σ. Let us recall the expressions of the first and second distribution moment for the variables Re(I) and Im(I),
where, without loss of generality, we assumed the coherent background image value to be real, equal to AS (see Section 2.3).
By writing Equation (1) in terms of real and imaginary parts of the image I, and using the expressions in (14), we end with
Then, by combining Equations (13) and (15), we obtain an expression that relates the coherence with the amplitude dispersion index.
This equation establishes a direct relation between the DA and the coherence, under the hypothesis of Rician amplitude statistics. As will be shown in the next section, for GBSAR systems, in rural environments where low vegetation is present, this condition is met, and Equation (16) successfully reproduces the parameters relation.
It is worth noting that the method used to retrieve Equation (16) is rather general and could also be used for signals characterized by different statistics.
2.5. Simulations
With the aim to provide solid basis for the above formulation, and to assess the validity of Equation (16), the two models considered in the above section have been simulated.
The echo of a continuous wave stepped frequency signal operative in Ku-band were simulated. For the sake of simplicity, we limited the analysis in one dimension, by simulating the signal of a monostatic radar. The echo reflected from 100 scatterers, uniformly distributed inside the same one-dimensional resolution cell, was simulated. The amplitude reflectivity of each scatterer was uniformly distributed between 0 and 1.
All the scatterers were subject to random displacements inside the resolution cell, between each acquisition, in order to simulate a model, in which the signal amplitude mimics the Rayleigh distribution. The Rice statistics were instead reproduced by fixing the position of a certain number of scatterers, while moving randomly the others, always inside the resolution cell. In the following we refer to these two models to as the “Rayleigh” and “Rice” model, respectively. We simulated acquisitions of Nt consecutive measurements. For the Rice model, the simulation was replicated for different values of the ratio of stable to total scatterers, which was tuned from 0 to 1.
To collect statistics and averaging over the initial positions of the scatterers, in every run of the simulation, the time series was repeated 100 times; before starting any new time series, the scatterers position inside the resolution cell was changed randomly.
Figure 1 shows the obtained results concerning the amplitude values, both for Rayleigh (a), and Rice model (b). Histograms in gray represent simulated data, while the red and green curves are the Rayleigh and Rice functions (Equations (9) and (11), respectively), that result from a fit of the simulated data.
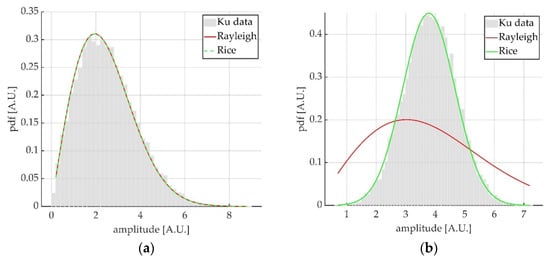
Figure 1.
Comparison between amplitude histograms and theoretical distributions for simulated data: (a) represents the model where only random scatterers are present; in (b) both random and fixed scatterers are present. The red curve is the Rayleigh function resulting from the fitting of simulated data, while the green curve is the Rice function.
It is worth noting that, in Figure 1a, when only random scatterers are present, the Rice distribution that best fits the data, reduces to the Rayleigh one. On the other hand, if both fixed and random scatterers are present (Figure 1b), the Rayleigh distribution no longer fits simulated data. Simulated models successfully reproduced the expected theoretical amplitude distributions.
For each time series, the coherence and the DA were computed. The coherence was calculated by using the spectral density estimator defined in Equation (5). Indeed, this expression provides a coherence value for the whole time series, as the amplitude dispersion index, thus enabling the parameter comparison. Hence, for each run of the simulation, a single value of DA and coherence is calculated. Specifically, we evaluated the spectral density of the signal and set the coherence equal to the peak value, properly normalized.
Figure 2 shows the results obtained regarding the relationship between DA and coherence for the Rayleigh model (red circles), and for the Rice model (blue circles). Each circle corresponds to a different run of the simulation. For the Rice model each circle corresponds to the simulated result obtained for a specific value of the ratio of stable to total scatterers. If almost all scatterers are stable, low (high) values of DA (coherence) are obtained. If instead nearly 100% of scatterers are subject to random displacements, values of DA correspond to that of the Rayleigh model. Good agreement between simulations and theoretical curves was obtained.
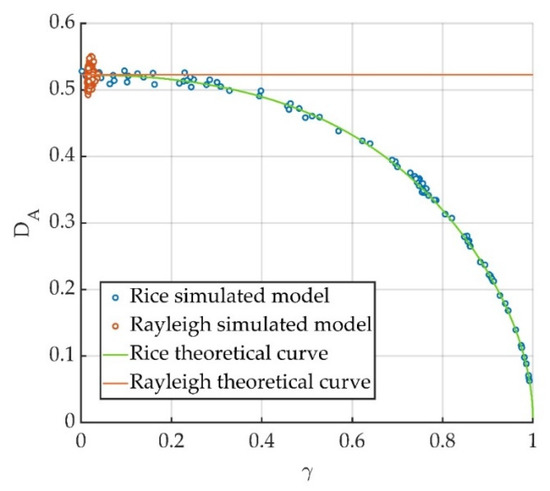
Figure 2.
Relation between amplitude dispersion index DA and coherence γ obtained in simulated data: red circles are obtained for the Rayleigh model where only random scatterers are present; blue circles for the Rice model with different values for the ratio of stable to total scatterers. The theoretical curves correspond to the analytic expressions obtained in Equations (12) and (16) for the Rayleigh and for the Rice model, respectively.
3. Results
Given the promising results obtained with simulations, authors of this paper aimed to validate Equation (16) for experimental data acquired in natural scenarios. That is, determining whether the simplified model introduced in Section 2, could effectively describe the scattering properties of different physical scenarios. To give solid basis to the relation between amplitude dispersion index and coherence, data from three GBSAR measurement campaigns were analyzed. This enabled us to test the relation in different scenarios and with different working frequencies.
The image was focused on a range–azimuth grid using a backpropagation algorithm [34]. Using this algorithm, each range–azimuth resolution cell was covered by several pixels. The amplitude statistics were evaluated by averaging over an ensemble of the pixels whose overall size is approximately equal to that of a single resolution cell. Indeed, this ensemble of pixels properly represents the backscattered signal of the physical illuminated target. For each measurement series, we selected only resolution cells where the scatterers were present. Then, the amplitude dispersion index and the coherence were calculated to test the theoretical relation (16).
3.1. Formigal Measurement Campaign
For our scope, we analyzed GBSAR measurements acquired in Formigal, Spain, from 13 to 22 November 2006. The purpose of this campaign was to monitor a vegetated slope, subject to a landslide. The radar used was a C-band GBSAR able to acquire an image about every hour. Figure 3 shows an amplitude radar image (a) and a picture (b) the illuminated scene. The area was characterized by the presence of rocks, grass, and low vegetation.
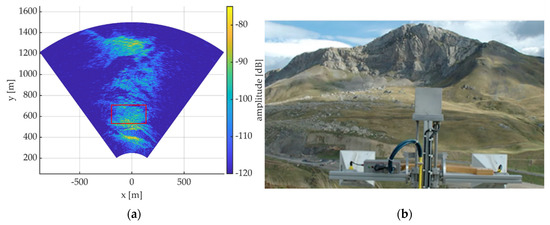
Figure 3.
(a) Amplitude GBSAR image on the monitored slope, in Formigal, Spain; the red box highlights the area chosen for analysis. (b) Picture of the illuminated area.
Figure 4 shows the histogram of signal amplitude values, obtained for the resolution cells in the region highlighted by the red box in Figure 3a. This region was a vegetated area characterized by meadows. The colored curves correspond to the theoretical distributions that best fit the experimental data. One can notice a good agreement between the experimental data and the Rice distribution.
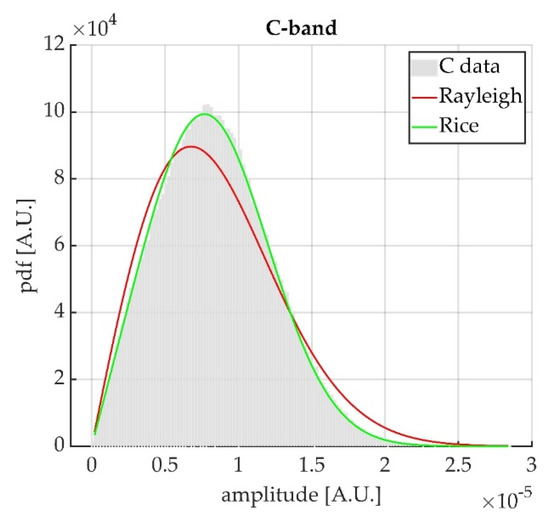
Figure 4.
Histogram of the signal amplitude values of the GBSAR image, compared with theoretical Rayleigh (red curve) and Rice (green curve) distributions.
On such areas, amplitude dispersion index and coherence were calculated for each resolution cell. As done with simulated data, coherence was computed by using the spectral density function (5). As already stressed, changes in the atmospheric parameters affect the coherence values. Thus, a processing to remove the atmospheric phase screen was implemented. Results concerning DA and coherence values are shown in Figure 5a. Experimental data appear to be arranged according to the theoretical curve, thus, validating the relation (16) in this specific case. To quantify the agreement between experimental and theoretical data, we calculated the squared deviation between the theoretical (16) and experimental value of DA, by averaging on a group of almost one hundred targets with similar coherence. Figure 6b shows the obtained results.
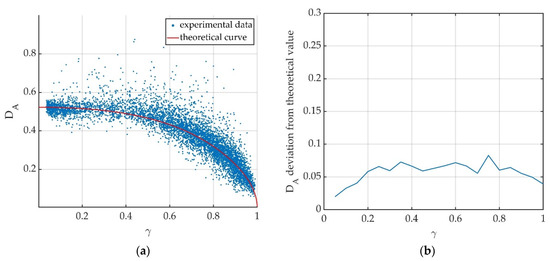
Figure 5.
(a) Values of the amplitude dispersion index DA as function of the coherence γ, calculated for resolution cells of the investigated area, in Formigal. (b) Deviation of DA values from the theoretical ones.
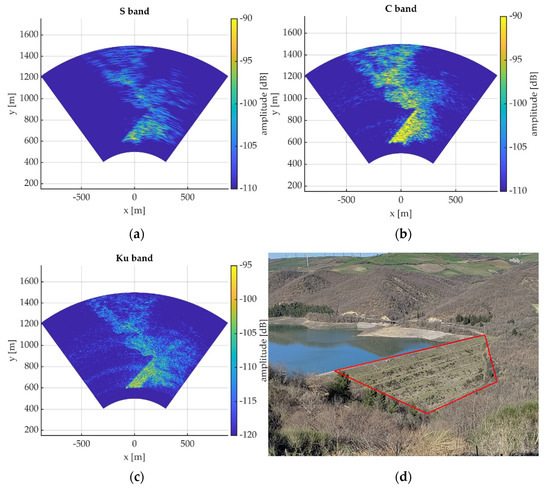
Figure 6.
Amplitude GBSAR images of a vegetated dam, acquired at Aquilonia (Avellino), Italy, in S-band (a), C-band (b), and Ku-band (c). (d) shows a top view of the investigated area. The area highlighted in red was chosen for the analysis.
3.2. Aquilonia Test Site: Validation with Different Frequencies
To investigate the relation between DA and coherence for different frequency bands, measurements of a multi-frequency GBSAR campaign, acquired in Aquilonia, Italy, were analyzed. During this measurement campaign, three GBSAR systems working in C, S, and Ku-band illuminated a vegetated tailing dam [35]. The acquisition rate of the radars in C and S-band were about 580 s. The acquisition rate of the Ku-band radar was 240 s.
For the present analysis, measurements acquired from 12 March to 3 April 2022 were studied, for a total of almost 4000 radar images.
In Figure 6 amplitude images acquired in the three bands are shown, together with a picture of the illuminated scene. As can be seen in Figure 6d, the dam body is covered by grass and low vegetation.
We focused the analysis on the dam body highlighted in red in Figure 6d. First, we tested the Rician statistics of the amplitude distribution. Areas for which we obtained excellent agreement are those characterized by meadows, without higher vegetations.
In order to test whether Equation (16) could also apply for the other parts of the dam body, amplitude dispersion index and coherence have been calculated for each resolution cell in the area contoured in red. Figure 7a, Figure 8a and Figure 9a show the results concerning the relation between the two parameters obtained for S, C, and Ku-band data, respectively. Each blue dot corresponds to a specific resolution cell. It is worth noting good agreement between experimental data and the theoretical curve (16), represented by the red line, at least for high values of coherence. Figure 7b, Figure 8b and Figure 9b show the deviation of the experimental DA values from the theoretical ones, for each value of coherence measured.
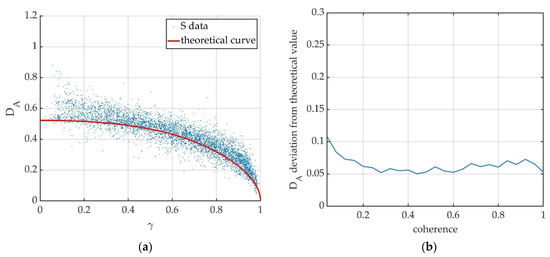
Figure 7.
Results obtained for S-band data. (a) Relation between amplitude dispersion index DA and coherence γ of experimental data compared to the theoretical red curve, Equation (14). Each dot represents a resolution cell in the analyzed area. (b) Deviation of experimental DA values from theoretical ones.
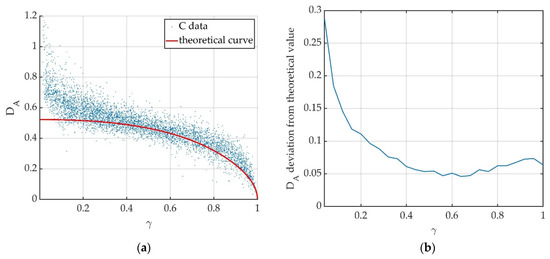
Figure 8.
Results obtained for C-band data. (a) Relation between amplitude dispersion index DA and coherence γ of experimental data compared to the theoretical red curve, Equation (14). Each dot represents a resolution cell in the analyzed area. (b) Deviation of experimental DA values from theoretical ones.
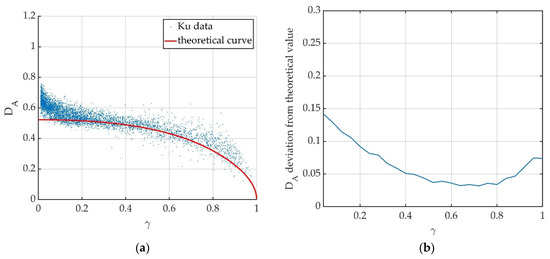
Figure 9.
Results obtained for Ku-band data. (a) Relation between amplitude dispersion index DA and coherence γ of experimental data compared to the theoretical red curve, Equation (14). Each dot represents a resolution cell in the analyzed area. (b) Deviation of experimental DA values from theoretical ones.
3.3. Measurements in Urban Scenario: Validation with Different Frequencies
Finally, to further test the relation in an environment with different characteristics, a measurement series acquired in an urban scenario in the premises of the University of Florence is presented. In this case, the same GBSAR systems employed in the test site at Aquilonia, acquired images for 5 days. Figure 10 shows an amplitude image (a) and a picture (b) the illuminated scene. As can be observed, various kinds of targets are present in the area; namely, grass, some bushes, a tree, and buildings.
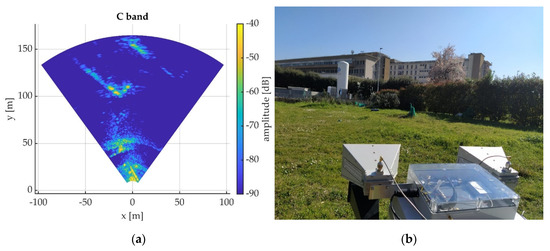
Figure 10.
(a) Amplitude GBSAR image acquired in C-band of the illuminated urban area, in Florence, Italy; (b) a picture of the illuminated scene.
In this case, the previous analysis was computed for the area corresponding to the whole focused image in Figure 10a. Results obtained are shown in Figure 11, Figure 12 and Figure 13 for the S, C, and Ku-band, respectively. For all the three bands, good agreement with the theoretical curve is found.
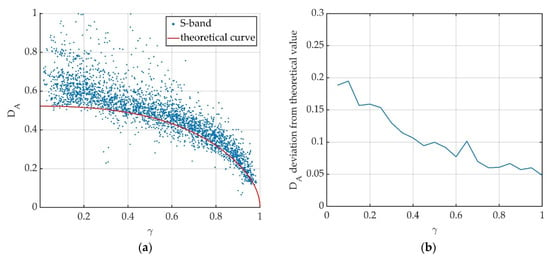
Figure 11.
Results obtained for S-band data. (a) Values of DA as function of the coherence, calculated for resolution cells of the investigated area, in the urban scenario, in Florence. (b) Deviation of experimental DA values from theoretical ones.
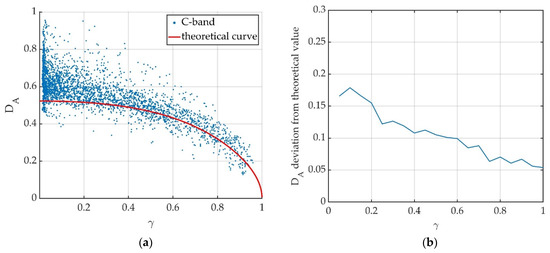
Figure 12.
Results obtained for C-band data. (a) Values of DA as function of the coherence, calculated for resolution cells of the investigated area, in the urban scenario, in Florence. (b) Deviation of experimental DA values from theoretical ones.
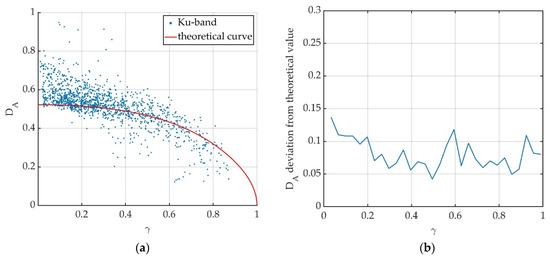
Figure 13.
Results obtained for Ku-band data. (a) Values of DA as function of the coherence, calculated for resolution cells of the investigated area, in the urban scenario, in Florence. (b) Deviation of experimental DA values from theoretical ones.
4. Discussion
Amplitude dispersion index and coherence are widely used in GBSAR interferometric analysis as tools for selecting high quality pixels in the image. Since the coherence evaluation demands preprocessing analysis to give reliable results, the amplitude dispersion index could represent a precious efficient tool. Starting from simple general assumptions, we found a theoretical relation between the two parameters.
The purpose of the experimental data analysis was to determine whether such theoretical relation would apply for GBSAR images acquired in scenarios with different characteristics. The three measurement campaigns considered for the analysis were performed in the following environments: on a slope characterized by the presence of rocks and partially covered by grass; on a dam, covered by low vegetation; on an urban scenario, characterized by the presence of both buildings and vegetation.
For each data set, the agreement between experimental data and Rice statistics was tested for several areas in the wide range of scenarios considered. Excellent agreement was found for areas characterized by the presence of meadows. Then, both amplitude dispersion index and coherence were evaluated for all these areas. Results reported in Figure 5, Figure 7, Figure 8, Figure 9, Figure 11, Figure 12 and Figure 13 seem to confirm the relation between amplitude dispersion index and coherence retrieved analytically in Equation (16). Specifically, good agreement is found for low values of coherence (high values of ), that is, for targets characterized by high signal-to-noise ratio.
Indeed, as can be noted in Figure 7, Figure 8 and Figure 9 and Figure 11, Figure 12 and Figure 13, some points close to γ = 0, overcome the Rayleigh threshold (). These results were obtained by performing the analysis for the whole dam body (Figure 7, Figure 8 and Figure 9) and for the entire focused image in the urban scenario (Figure 11, Figure 12 and Figure 13). The points with , probably correspond to the targets of wooded areas, or in any case where there is more incoherent scatterers, and low signal-to-noise ratio.
Anyway, results obtained using data acquired at Formigal (Figure 5) in C-band, also show good agreement with the theoretical ones for low values of coherence. This is probably because the analysis has been carried out for a homogeneous area characterized by high signal-to-noise ratio.
The results shown suggest the use of this relation as a quantitative reference to relate coherence and amplitude dispersion index, for targets with DA < 0.5, that is, with a sufficiently high signal-to-noise ratio. This method can represent a powerful tool when searching for high-signal quality pixels in GBSAR images, in a wide range of scenarios. The validation with different frequency bands also contributes to give solid basis to the relation.
5. Conclusions
In this paper, the estimation of the coherence of GBSAR images has been addressed. First, we reviewed some common estimators used to evaluate the phase stability of pixels in the radar image. Then, a statistical description of the backscattered signal amplitude is presented, and a relationship between the so-called amplitude dispersion index and the interferometric coherence was analytically found.
The preliminary estimation of the targets signal quality usually performed in interferometric analysis, could benefit from this relation. Indeed, the amplitude dispersion index provide practical advantages, and represent an efficient tool for estimating the signal quality. A theoretical quantitative relation between coherence and amplitude dispersion index can give solid basis to the DA parameter: it relates a threshold on coherence to thresholds on DA. Thus, such a relation allows the obtaining of information on the coherence of the image, greatly simplifying the processing.
Some simulations have been implemented to test the reliability of such a function under specific hypotheses. The theoretical relation was confirmed by experimental data acquired in different environments and with different working frequencies. Obtained results suggest the general character of this quantitative relation and its applicability in a wide range of situations.
Author Contributions
Conceptualization, A.B. and M.P.; methodology, A.B. and A.M.; validation, A.B., L.M. and M.P.; formal analysis, A.B.; data curation, A.B. and L.M.; writing—original draft preparation, A.B.; writing—review and editing, L.M.; visualization, A.M.; supervision, M.P.; project administration, M.P.; funding acquisition, M.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by IDS Georadar Pisa 56121, Italy.
Data Availability Statement
Data available on request.
Acknowledgments
The authors would like to thank DIAN s.r.l., Matera, Italy, especially Giovanni Nico and Olimpia Masci, for their valuable support and cooperation.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wang, Y.; Hong, W.; Zhang, Y.; Lin, Y.; Li, Y.; Bai, Z.; Zhang, Q.; Lv, S.; Liu, H.; Song, Y. Ground-Based Differential Interferometry SAR: A Review. IEEE Geosci. Remote Sens. Mag. 2020, 8, 43–70. [Google Scholar] [CrossRef]
- Zebker, H.; Villasenor, J. Decorrelation in interferometric radar echoes. IEEE Trans. Geosci. Remote Sens. 1992, 30, 950–959. [Google Scholar] [CrossRef] [Green Version]
- Lort, M.; Aguasca, A.; Lopez-Martinez, C.; Fabregas, X. Impact of Wind-Induced Scatterers Motion on GB-SAR Imaging. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 3757–3768. [Google Scholar] [CrossRef] [Green Version]
- Monti-Guarnieri, A.; Manzoni, M.; Giudici, D.; Recchia, A.; Tebaldini, S. Vegetated Target Decorrelation in SAR and Interferometry: Models, Simulation, and Performance Evaluation. Remote Sens. 2020, 12, 2545. [Google Scholar] [CrossRef]
- Touzi, R.; Lopes, A.; Bruniquel, J.; Vachon, P.W. Coherence estimation for SAR imagery. IEEE Trans. Geosci. Remote Sens. 1999, 37, 135–149. [Google Scholar] [CrossRef] [Green Version]
- Crosetto, M.; Monserrat, O.; Cuevas-González, M.; Devanthéry, N.; Crippa, B. Persistent Scatterer Interferometry: A review. ISPRS J. Photogramm. Remote Sens. 2016, 115, 78–89. [Google Scholar] [CrossRef] [Green Version]
- Ferretti, A.; Prati, C.; Rocca, F. Permanent scatterers in SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2001, 39, 8–20. [Google Scholar] [CrossRef]
- Goodman, J.W. Statistical Properties of Laser Speckle Patterns. In Laser Speckle and Related Phenomena; Dainty, J.C., Ed.; Springer: Berlin/Heidelberg, Germany, 1975; pp. 9–75. [Google Scholar] [CrossRef]
- Chitroub, S.; Houacine, A.; Sansal, B. Statistical characterisation and modelling of SAR images. Signal Process. 2002, 82, 69–92. [Google Scholar] [CrossRef]
- Gao, G. Statistical Modeling of SAR Images: A Survey. Sensors 2010, 10, 775–795. [Google Scholar] [CrossRef]
- Luzi, G.; Pieraccini, M.; Mecatti, D.; Noferini, L.; Guidi, G.; Moia, F.; Atzeni, C. Ground-based radar interferometry for landslides monitoring: Atmospheric and instrumental decorrelation sources on experimental data. IEEE Trans. Geosci. Remote Sens. 2004, 42, 2454–2466. [Google Scholar] [CrossRef]
- Wei, M.; Sandwell, D.T. Decorrelation of L-Band and C-Band Interferometry Over Vegetated Areas in California. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2942–2952. [Google Scholar] [CrossRef]
- Iglesias, R.; Fabregas, X.; Aguasca, A.; Mallorqui, J.J.; Lopez-Martinez, C.; Gili, J.A.; Corominas, J. Atmospheric Phase Screen Compensation in Ground-Based SAR with a Multiple-Regression Model Over Mountainous Regions. IEEE Trans. Geosci. Remote Sens. 2013, 52, 2436–2449. [Google Scholar] [CrossRef]
- Iannini, L.; Guarnieri, A.M. Atmospheric Phase Screen in Ground-Based Radar: Statistics and Compensation. IEEE Geosci. Remote Sens. Lett. 2010, 8, 537–541. [Google Scholar] [CrossRef]
- Izumi, Y.; Nico, G.; Sato, M. Time-Series Clustering Methodology for Estimating Atmospheric Phase Screen in Ground-Based InSAR Data. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–9. [Google Scholar] [CrossRef]
- Hu, C.; Deng, Y.; Tian, W.; Zhao, Z. A Compensation Method for a Time–Space Variant Atmospheric Phase Applied to Time-Series GB-SAR Images. Remote Sens. 2019, 11, 2350. [Google Scholar] [CrossRef] [Green Version]
- Deng, Y.; Hu, C.; Tian, W.; Zhao, Z. A Grid Partition Method for Atmospheric Phase Compensation in GB-SAR. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–13. [Google Scholar] [CrossRef]
- Falabella, F.; Perrone, A.; Stabile, T.A.; Pepe, A. Atmospheric Phase Screen Compensation on Wrapped Ground-Based SAR Interferograms. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–15. [Google Scholar] [CrossRef]
- Rocca, F. Modeling Interferogram Stacks. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3289–3299. [Google Scholar] [CrossRef]
- Tang, P.; Zhou, W.; Tian, B.; Chen, F.; Li, Z.; Li, G. Quantification of Temporal Decorrelation in X-, C-, and L-Band Interferometry for the Permafrost Region of the Qinghai–Tibet Plateau. IEEE Geosci. Remote Sens. Lett. 2017, 14, 2285–2289. [Google Scholar] [CrossRef]
- Morishita, Y.; Hanssen, R.F. Temporal Decorrelation in L-, C-, and X-band Satellite Radar Interferometry for Pasture on Drained Peat Soils. IEEE Trans. Geosci. Remote Sens. 2014, 53, 1096–1104. [Google Scholar] [CrossRef]
- Guarnieri, A.; Prati, C. SAR interferometry: A “Quick and dirty” coherence estimator for data browsing. IEEE Trans. Geosci. Remote Sens. 1997, 35, 660–669. [Google Scholar] [CrossRef] [Green Version]
- Lee, J.-S.; Cloude, S.; Papathanassiou, K.; Grunes, M.; Woodhouse, I. Speckle filtering and coherence estimation of polarimetric sar interferometry data for forest applications. IEEE Trans. Geosci. Remote Sens. 2003, 41, 2254–2263. [Google Scholar] [CrossRef]
- Carter, G.; Knapp, C.; Nuttall, A. Estimation of the magnitude-squared coherence function via overlapped fast Fourier transform processing. IEEE Trans. Audio Electroacoust. 1973, 21, 337–344. [Google Scholar] [CrossRef] [Green Version]
- Hinich, M.J.; Clay, C.S. The application of the discrete Fourier transform in the estimation of power spectra, coherence, and bispectra of geophysical data. Rev. Geophys. 1968, 6, 347–363. [Google Scholar] [CrossRef]
- Blasch, E.; Yang, C. FFT-based auto-correlation estimation (FACE) for extended radar pulse integration subject to large doppler change. In Proceedings of the 2012 11th International Conference on Information Science, Signal Processing and their Applications (ISSPA), Montreal, QC, Canada, 2–5 July 2012; pp. 1153–1158. [Google Scholar] [CrossRef]
- Holzner, J. Analysis and statistical characterization of interferometric SAR signals based on the power spectral density function. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1116–1121. [Google Scholar] [CrossRef]
- Qiu, Z.; Ma, Y.; Guo, X. Atmospheric phase screen correction in ground-based SAR with PS technique. SpringerPlus 2016, 5, 1594. [Google Scholar] [CrossRef] [Green Version]
- Noferini, L.; Pieraccini, M.; Mecatti, D.; Luzi, G.; Atzeni, C.; Tamburini, A.; Broccolato, M. Permanent scatterers analysis for atmospheric correction in ground-based SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1459–1471. [Google Scholar] [CrossRef]
- Tough, R.J.A.; Blacknell, D.; Quegan, S. A statistical description of polarimetric and interferometric synthetic aperture radar data. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1995, 449, 567–589. [Google Scholar] [CrossRef]
- Donati, S.; Martini, G. Speckle-pattern intensity and phase: Second-order conditional statistics. J. Opt. Soc. Am. 1979, 69, 1690–1694. [Google Scholar] [CrossRef]
- Bamler, R.; Just, D. Phase statistics and decorrelation in SAR interferograms. In Proceedings of the IGARSS’93—IEEE International Geoscience and Remote Sensing Symposium, Tokyo, Japan, 18–21 August 2002. [Google Scholar] [CrossRef]
- Bamler, R.; Hartl, P. Synthetic aperture radar interferometry. Inverse Probl. 1998, 14, R1–R54. [Google Scholar] [CrossRef]
- Pieraccini, M.; Miccinesi, L. ArcSAR: Theory, Simulations, and Experimental Verification. IEEE Trans. Microw. Theory Tech. 2016, 65, 293–301. [Google Scholar] [CrossRef]
- Di Pasquale, A.; Nico, G.; Pitullo, A.; Prezioso, G. Monitoring Strategies of Earth Dams by Ground-Based Radar Interferometry: How to Extract Useful Information for Seismic Risk Assessment. Sensors 2018, 18, 244. [Google Scholar] [CrossRef] [PubMed] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).