Abstract
In this paper, we characterize the sea-ice elevation distribution by using NASA’s Operation IceBridge (OIB) Airborne Topographic Mapper (ATM) L1B data over the Arctic Ocean during 94 Spring campaigns between 2009 and 2019. The ultimate objective of this analysis is to better understand sea-ice topography to improve the estimation of the sea-ice freeboard for nadir-looking altimeters. We first introduce the use of an exponentially modified Gaussian (EMG) distribution to fit the surface elevation probability density function (PDF). The characteristic function of the EMG distribution can be integrated in the modeling of radar altimeter waveforms. Our results indicate that the Arctic sea-ice elevation PDF is dominantly positively skewed and the EMG distribution is better suited to fit the PDFs than the classical Gaussian or lognormal PDFs. We characterize the elevation correlation characteristics by computing the autocorrelation function (ACF) and correlation length (CL) of the ATM measurements. To support the radar altimeter waveform retracking over sea ice, we perform this study typically on 1.5 km ATM along-track segments that reflect the footprint diameter size of radar altimeters. During the studied period, the mean CL values range from 20 to 30 m, which is about 2% of the radar altimeter footprint diameter (1.5 km).
1. Introduction
The satellite altimeter footprint size ranges from 17 m (ICESat-2) [1] to 70 m (ICESat) [2] to more than 1 km for radar altimeters [3,4]. Assuming the height variations in these footprints arise from a stationary random process, aspects of the altimeter’s measurement can be related to low-order moments of the surface height probability density function (PDF) [5,6], provided that the horizontal correlation scale of the random process is small compared to the horizontal dimensions of the footprint [5], so that both high and low random height fluctuations are contained within the footprint. Satellite altimeters measure the mean (or median) height, root-mean-square roughness, etc., within the footprint area, and retrieval of this information is simplified if the PDF or its Fourier transform has a simple functional form.
Conventional satellite radar altimetry was developed to measure ocean surfaces, on which the surface height variations produced by wind waves and swell have a very near-Gaussian distribution [7] and a correlation length less than the footprint size [5]. Our motivation is to support the satellite radar altimetry of sea ice by the CryoSat-2 and Sentinel-3 missions, the pulse echoes of which arise from rough surface backscatter distributed over an area approximately 1.5 km in diameter. We, therefore, are interested in characterizing the sea-ice elevation fluctuations that occur over distances of 1.5 km and less. Applying Doppler beam sharpening to the pulse echoes of these missions can narrow the measurement footprint in the direction of flight [3,8,9,10]; thus, we also aim to characterize the horizontal correlation scale of the elevation variations.
The sea-ice height variations that occur over 1.5 km are not well-approximated by a Gaussian distribution [11,12,13,14,15,16]. Many studies of sea ice have used a lognormal distribution [13,14,15,16]. Landy et al. [11] demonstrated that at the radar altimeter footprint scale, a lognormal distribution can better describe sea-ice topography than a Gaussian; assuming a Gaussian distribution for the surface elevation of sea ice may be introducing significant error into the Cryosat-2 waveform retracking process. We characterize the PDF of sea-ice elevation using an exponentially modified Gaussian (EMG) distribution, as this form can be incorporated into a radar altimeter waveform retracker. We also compare the EMG to the Gaussian and lognormal distributions in this study.
2. Data
This study used NASA Operation IceBridge (OIB) Airborne Topographic Mapper (ATM) L1B [17,18] and Digital Mapping System (DMS) imagery [19] L1B data [20] from the National Snow and Ice Data Center (NSIDC) collected over the Arctic Ocean in March, April, and May from 2009 to 2019. The geographical coverage of these data is shown in Figure 1. OIB is a NASA airborne mission that monitored Arctic and Antarctic ice sheets, ice shelves, and sea ice. It collected data between the ICESat (2003–2009) and ICESat-2 (2018-present) missions in an effort to fill the data gap of the two satellites. Its airborne conical-scanning laser ranging system has an off-nadir angle (15 degrees for wide swath) and a scan rate of 20 Hz. Its output laser wavelength is 532 nm and the pulse repetition rate is 5 kHz [17,18]. At its wide swath scan angle and at an altitude of 500 m above the surface, the laser footprint diameter is about 1 m and the laser swath width is about 250 m. The absolute elevation accuracy is about 0.1 m or better [21,22]. For IceBridge campaigns, the estimated elevation accuracy and precision are 0.066 and 0.030 m, respectively [18].
The ATM elevation data are heights with respect to the WGS-84 ellipsoid. We adjusted these to measure height with respect to the Danish Technical University mean sea surface (MSS) model DTU18 [23,24]. Because DTU18 gives the MSS height with respect to the TOPEX ellipsoid, we accounted for the difference in ellipsoidal heights [25] and then used bilinear interpolation of the DTU18 grid to evaluate the height correction to apply to each ATM footprint. We did not apply the ATM-azimuth-scan-angle-related elevation bias correction [26] in this study. We tested the application of the bias correction and found the impact on the 1.5 km section mean/STD insignificant.
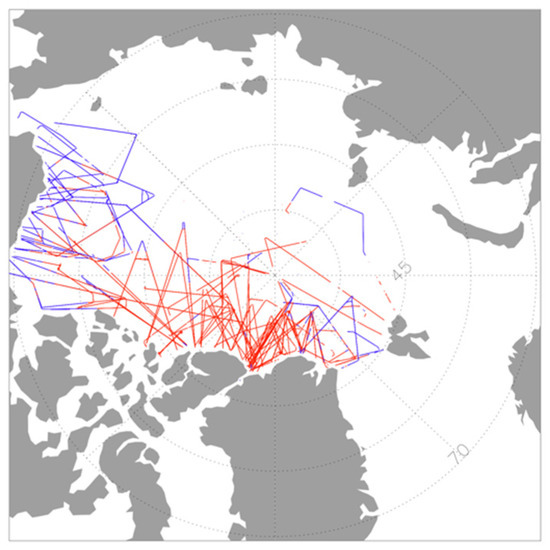
Figure 1.
OIB ground tracks from 2009 to 2019. There are 94 spring flights over the Arctic Ocean. Land cover is in gray. Blue tracks are for first-year ice (FYI) and red tracks are for multi-year ice (MYI). FYI and MYI are based on OSISAF sea surface types [27]. The majority of the campaigns are between March and April. There are three campaigns from early May in 2015 and 2016. For overlapping tracks, later tracks will cover early tracks.
The DMS is an airborne digital camera system that records natural color and panchromatic imagery [19]. The DMS level-1b image spatial resolution ranges from 0.015 to 2.5 m. The pixel size is dependent on flight altitude. For a flight at 460 m above ground level, the pixel size is about 0.1 m.
The OSISAF sea ice surface type data of 2009–2019 [27] were used to estimate FYI and MYI. Each ATM footprint can be assigned to an OSISAF sea ice surface type, FYI or MYI, based on the OSISAF sea ice surface type grids.
3. Methods and Analysis
We grouped the ATM data into segments, each segment spanning 1.5 km in the along-track direction of the OIB aircraft. We calculated the sea-ice surface elevation PDF for each 1.5 km segment. In this section, we discuss candidate models that describe the PDFs, cluster analysis to distinguish floe heights from lead heights, ATM elevation measurement noise, and elevation correlation length (CL).
3.1. Candidate Models for the PDFs
Three different surface elevation distribution models: (1) Gaussian, (2) lognormal, and (3) EMG, are evaluated here to describe the sea-ice surface elevation distribution PDFs.
3.1.1. Gaussian Distribution
A Gaussian distribution with mean μ and standard deviation σ is defined as:
While this model has been widely used to describe the sea-ice surface elevation distribution, over the satellite radar altimeter scale of 1.5 km horizontally, the Gaussian distribution may not fit the elevation PDF very well and other distribution models need to be considered [11,12].
3.1.2. Lognormal Distribution
A lognormal distribution with mean = exp( + /2) and variance = [exp() − 1] × exp(2 + ) is defined as:
This model is also used in the sea-ice study [11,13,14,15,16]. Landy and others [11] demonstrated that at the satellite radar altimeter scale, a lognormal distribution can better describe sea-ice topography than a Gaussian.
3.1.3. EMG Distribution
The EMG distribution [28] with mean = + 1/λ2 and variance = + 1/λ is defined as:
where erfc is the complementary error function defined as erfc(x) = 1 − erf(x) = .
In this study, we introduce the EMG distribution, as it fits the sea-ice surface elevation PDF nicely and its characteristic function can be applied in an algorithm for floe height retrieval from satellite radar altimeter waveforms.
3.2. Cluster Analysis to Distinguish Floe Heights from Lead Heights
Over sea ice, a satellite radar altimeter will receive specular reflections from leads and rough surface backscatter from the floes [4]; the latter process will sense the entire footprint as one realization of a single random process. Onana et al. [29] applied a sophisticated method to distinguish leads for the ATM data. Here, we apply a more efficient cluster analysis to separate the floe and lead. This enables us to analyze data with and without leads. Especially when there are a large number of lead footprints, the elevation PDFs will have more than one peak and all three models used here, Gaussian, Lognormal, and EMG, will not fit. Generally, the lead surface has a lower RTratio and lower elevation, and the scatterplot of elevation vs. RTratio will show 2 distinguished clusters of the two types of surfaces. The cluster function used here is from Interactive Data Language (IDL) [30,31]. Figure 2 shows an example of the cluster analysis method. Figure 2b,c show the ATM elevation and the ratio of the received power to transmitted power (RTratio) on top of the DMS images. Figure 2f shows an elevation-RTratio scatterplot and the result from cluster analysis. Figure 2g shows the PDFs of the floe and lead.
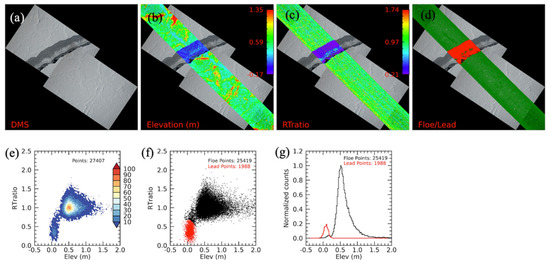
Figure 2.
An example from 21 April 2016 shows the cluster analysis method results. (a) DMS images. (b–d) ATM elevation, RTratio, and floe (green) and lead (red) footprints on top of the DMS images. (e) Color-coded Elevation-RTratio scatter plot. (f) Elevation-RTratio scatterplot, and floe (black) and lead (red) from the cluster analysis. (g) The pdf of floe (black) and lead (red) normalized by floe pdf amplitude.
The following data analysis is restricted to the floe elevations identified by this cluster analysis method and separated from the lead elevations.
3.3. Weakly Stationary Surface Processes
We suppose that the floe heights within any data segment are a realization of a random process that is at least weakly stationary over the segment. At any horizontal point position in the segment, the height , where is the mean height and is a zero-mean random process having variance . If and are two points within the ice floe segment, the semi-variogram can be defined as:
in which indicates the statistical expectation and is the normalized auto-covariance function for , so . In these expressions, and are the distance and azimuth from to , respectively; stationarity requires that and are even functions of and have period , not , in .
3.4. ATM Measurement Noise
We suppose that at each ATM measurement point , the measured floe elevation above the MSS contains a random measurement error, , so the elevation is measured as . Assuming that the random processes for and for are independent and weakly stationary over a segment, the PDF for is the convolution of the individual PDFs of and taken separately, and means and variances will combine additively. Then, by estimating the variance of the measured elevations and subtracting the variance of the measurement noise process, we can obtain the noise-free variance of the ice surface heights. In addition, the semi-variogram estimated from noisy ATM measurements, , is related to the noise-free process semi-variogram, , simply as , where is the variance of the measurement noise.
For each ATM L1b data file, we found all point pairs such that and the distance between and was less than 0.25 m. For each such pair, we formed the measured height difference , and then we tested the set of all values obtained from the file to see whether it fit a Gaussian distribution. The Kolmogorov–Smirnov and Anderson–Darling tests for normality found that the data appear Gaussian at the 99.99% confidence level, and quantile-quantile (QQ) plots show a straight line out to ±3.7 standard deviations. The fact that appears Gaussian is particularly convenient, as it allows us to simply remove the measured measurement noise from the elevation statistics, and describe the noise-free process by the aforementioned Gaussian, log-normal, or EMG distribution.
As the ATM measurement footprint diameter is ~1 m, for a 0.25 m footprint separation, the ATM measurement footprint overlap in area is about 68%. If the slope of the noise-free surface is small enough that the mean square change in the noise-free height over 0.25 m is less than , then is a good estimate of . The standard deviation of ranges between 2 and 7 cm, as shown in Figure 3, as the laser instrument, aircraft and aircraft altitude, weather condition, and other phenomena change during OIB flights and can influence this parameter. It is very likely that the measurement noise decreases after 2016 are due to the instrument improvement (for example, the decreased laser pulse width) [32]. We computed for each file and used this to estimate for each segment. This assumes that changes only slowly during each flight. We made this assumption in order to obtain a large number of samples of to make a reliable estimate of the measurement noise.
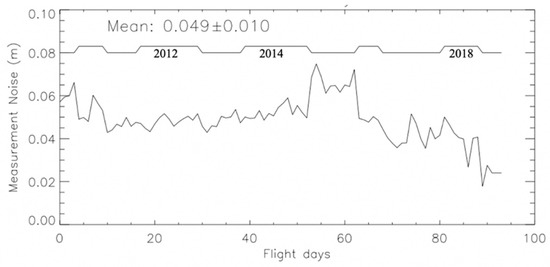
Figure 3.
ATM measurement noise for the 94 campaigns from 2009 to 2019. The upper curve marks the measurement years.
Analysis of cannot determine . The spatial resolution of the MSS is such that the mean MSS error will be effectively constant over any one segment of data, consistent with the weak stationarity assumption for . If , the effect of this is a shift in location between the PDFs of the noisy and the noise-free processes. This is not a problem for our application, as the location of is a parameter to be estimated during satellite radar altimeter waveform modeling; our study aims to determine the shape of the PDF for , but its accurate location is not needed for our purpose.
3.5. Local Anisotropy and Segment-Scale Isotropy
Figure 4 shows two 1.5 km segments of ATM data, one typical of FYI and one typical of MYI. In each elevation map, there are features that are clearly elongated in one direction or another, and over a horizontal scale of approximately 100 m, the surfaces appear anisotropic. Because the elevations of the elongated features are more pronounced in the MYI segment in Figure 4, we estimated for this segment, at sample steps of 0.1 m in and 10° in , by forming all possible point pairs and assigning each pair’s measured height difference to the bin it was closest to, and then taking the sample average over all values assigned in each bin. We found that the resulting estimates appeared to show the same variation with at all estimated values; that is, the height variation appears statistically isotropic when the expectation is taken over the entire 1.5 km long segment. The limitation of the swath width is not a problem, because the correlation length estimated is quite short compared to the swath width.
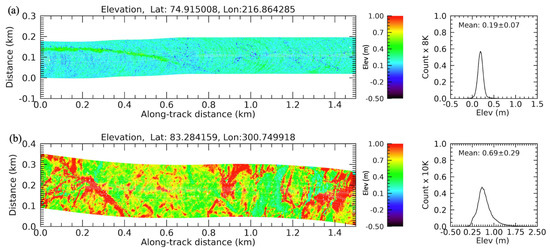
Figure 4.
(a) Typical first-year flat thin ice and the histogram of a 1.5 km section, 21 April 2016. (b) Typical multi-year rough thick ice and the histogram of a 1.5 km section in central Arctic, 9 March 2017. The cross-track swath width is related to the ATM laser scan angle and airplane flight height. Latitude and longitude are the center locations of the two 1.5 km sections.
We believe this apparent isotropy is due to the fact that there are many elongated structures in a segment, and over the length of the segment, the elongation directions vary randomly enough that the overall behavior appears isotropic over a 1.5 km scale. This is convenient, because it simplifies the surface statistical description needed for satellite radar altimetry, and it also allowed us to simplify our subsequent analyses by assuming that and are independent of , which saved considerable computation. We did not test a large set of surfaces, because this is computationally prohibitive.
3.6. Correlation Length Estimation
For our application, the exact specification of the surface process-normalized autocorrelation function is not needed if we can determine that the process decorrelates over a distance that is short compared to the satellite radar altimeter footprint. If this is true, then we may use any reasonable estimate of correlation length (CL), so long as we use it consistently. Here, we define CL as that horizontal distance at which drops to [33].
One may obtain CL from , but this is computationally expensive, so we also tried a less computationally expensive approach as follows. We projected the data in each 1.5 km segment into distance coordinates along-track and across-track and gridded the data to a grid with samples every 5 by 5 m. We also tried using a 2 by 2 m grid to calculate CL. The CL results from 2 by 2 and 5 by 5 m grids are very similar. We chose to use the 5 by 5 m grid in this study. Along each row of constant values in the grid, we removed the sample mean elevation and then computed the sample autocovariance function:
where is a lag step along the direction and is the height that remains after removing the mean along each row. We then averaged, across the direction, the ACF estimates obtained from each row. We then normalized the averaged ACF by its value at lag . Finally, we estimated CL from the averaged and normalized ACF.
We applied both the ACF method (method 2) and the method (method 1) to all segments from two days of OIB flight data and compared the results. Figure 5 shows the CL estimates obtained by applying the two methods to 1191 1.5 km long segments from the flight data of 9 March 2017. The mean CL difference between the two methods is 0.2 ± 9.5 m. As the mean difference is small, we decided to use the faster ACF method for the data analyses for all 94 ATM campaigns.
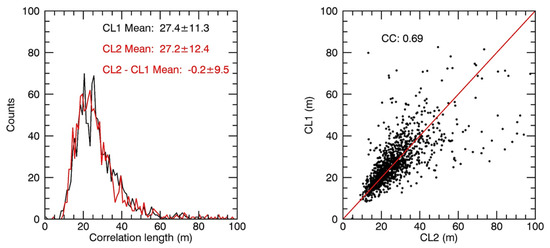
Figure 5.
CL values calculated from method 1 (CL1) and method 2 (CL2) for 9 March 2017. The mean of CL1 is 27.4 11.3 m. The mean of CL2 is 27.2 12.4 m. The mean of CL2 − CL1 is −0.2 9.5 m. The correlation coefficient (CC) of CL1 and CL2 is 0.69.
4. Results and Discussion
As described in the previous section, for the calculation of the PDF parameters and CL, we grouped the ATM data into segments, each segment spanning 1.5 km in the along-track direction of the OIB aircraft; we applied the cluster analysis presented in Section 3.2 to discriminate between floe and lead returns. We then computed the histogram of sea-ice floe elevations and fitted the data with the PDF candidate models presented in Section 3.1, and we obtained the segment CL as explained in Section 3.6.
4.1. Elevation PDF Model Fitting
Model fitting to the 1.5 km ATM elevation PDFs: Examples of ATM 1.5 km floe elevation PDFs and their lognormal and EMG model Levenberg–Marquart fitting are shown in Figure 6. A typical PDF is asymmetric and positively skewed, with a shorter, steeper leading edge and a longer, more gradual trailing edge. As a Gaussian model is not fitting the unsymmetric PDF very well, only lognormal and EMG fitting results are presented here. Both the lognormal and the EMG models fit the PDFs. While the lognormal model requires elevation x > 0, the EMG does not have this requirement. The PDF mean and STD are compared with the mean and STD calculated from lognormal and EMG fitting parameters for all 11 years of ATM data in Figure 7. There are a total of 108,309 1.5 km segments that have both EMG and lognormal fitting results. The overall mean elevation is 0.670 ± 0.238 m and the overall STD of the elevation is 0.254 ± 0.108 m. The correlation coefficient between the PDF elevation and elevation calculated from lognormal parameters is 0.980, slightly smaller than the value calculated from EMG parameters, 0.993. The correlation coefficient between the PDF elevation STD and the elevation STD calculated from lognormal parameters is 0.807, smaller than the value calculated from EMG parameters, 0.914. Figure 7g shows that the EMG modeled elevation will have an overall elevation bias of 0.006 ± 0.030 m and the lognormal modeled elevation will have an overall elevation bias of −0.010 ± 0.049 m. Both biases are small. The elevation STD biases are −0.017 ± 0.052 and −0.032 ± 0.084 for EMG and lognormal models, respectively (Figure 7h). These results allow us to conclude that EMG is an excellent candidate PDF and, in some cases, superior to log-normal, for the description of sea-ice roughness.
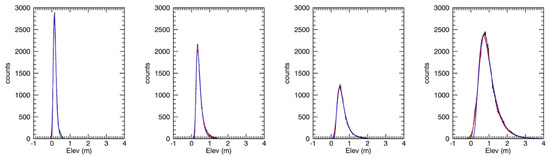
Figure 6.
Examples of lognormal (blue) and EMG (red) pdf fitting.
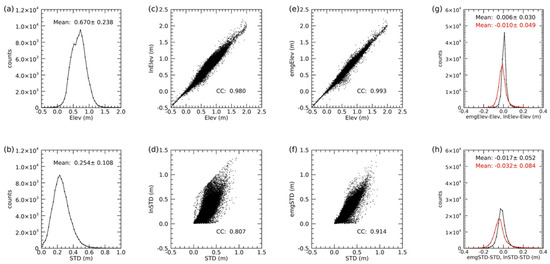
Figure 7.
Mean elevation and standard deviation of elevation for each 1.5 km section along-track compared with values calculated from EMG and lognormal fitting parameters. (a) 1.5 km mean elevation histogram. (b) 1.5 km STD of the elevation histogram. (c) Mean elevation (Elev) vs. mean elevation from lognormal model (lnElev). (d) STD vs. STD from lognormal model (lnSTD). (e) Mean elevation vs. mean elevation from EMG model (emgElev). (f) STD vs. STD from EMG model (emgSTD). (g) Histograms of emgElev–Elev (black) and lnElev–Elev (red). (h) Histograms of emgSTD–STD (black) and lnSTD–STD (red). Measurement noise is removed from STD, lnSTD, and emgSTD.
The spatial variation in the eight parameters derived from the surface elevation (mean, STD, skewness, and kurtosis) and EMG model fitting to the elevation PDF (, 1/λ, and ) and from ACF functions (CL) for 2014 are shown in Figure 8. There are five parameters (mean, STD, , 1/λ, and ) that show smaller values over the thinner-ice-dominated Chukchi and Beaufort seas and larger values over the Arctic Ocean north of Ellesmere Islands and Greenland dominated by thicker ice. The skewness and kurtosis show the opposite pattern, smaller values over the thicker ice and larger values over the thinner ice. The mean elevation for 2014 is 0.704 ± 0.251 m and the mean STD is 0.265 ± 0.110 m. The dominant positive skewness values 1.332 ± 0.362 indicate that the elevation PDFs are skewed positively most of the time. The pattern for CL spatial distribution is less obvious. Both smaller and larger values are shown in the FYI regions in the Chukchi and Beaufort seas.
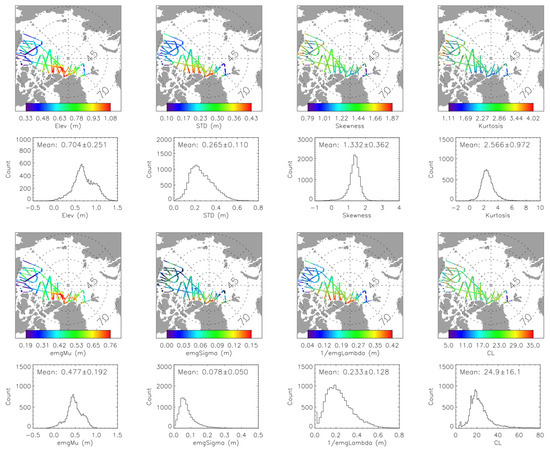
Figure 8.
The mean elevation, standard deviation of elevation, skewness, kurtosis, (emgMu), (emgSigma), 1/λ (emgLambda), and CL of the 1.5 km sections of 2014. Measurement noise is removed from the standard deviation of elevation.
4.2. CL Distribution over the Arctic
Examples of ACFs and CL for 8 April 2018 are shown in Figure 9. Although outliers for CL can be as large as over 200 m (typically for “irregular” surfaces that have more than one distinguished peak in floe elevation PDFs), the mean is about 30 m with a standard deviation of about 20 m. The box-whisker plot of CL from 2009 to 2019 for FYI, MYI, and all ice are shown in Figure 10. The mean CL values of the FYI are slightly smaller than those of the MYI. The FYI and MYI CL differences are not significant. The mean and standard deviation of CL for each year, for FYI and MYI, are summarized in Table 1. The 20~30 m of CL values are less than 2% of the radar altimeter footprint diameter (1.5 km).
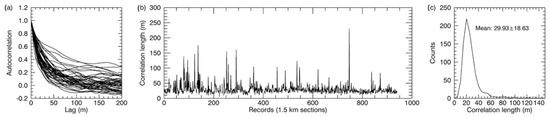
Figure 9.
An example of autocorrelation and correlation length of 8 April 2018. All data here are over FYI. (a) Examples of autocorrelation vs. lag along the profiles (one for every 20 1.5 km sections is plotted). (b) Correlation length for each 1.5 km section. (c) Histogram of correlation length. The mean correlation length for the day is 29.93 ± 18.63 m.
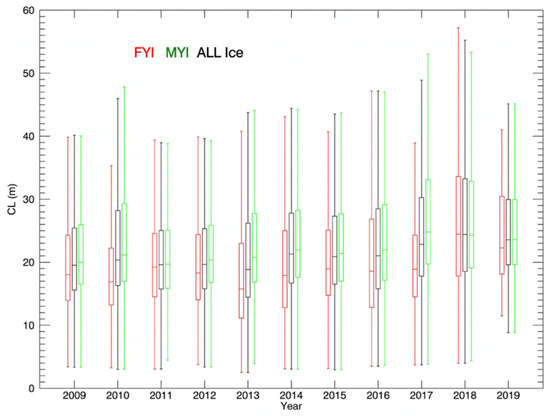
Figure 10.
The box-whisker plot of correlation length (CL) of FYI (red), MYI (green), and all ice (black) from 2009 to 2019. The medians of CL show a trend of increase for all FYI, MYI, and all ice.

Table 1.
The mean and standard deviation of correlation length (CL) of FYI, MYI, and all ice.
A previous study by Rivas et al. [12] using ATM data in March 2003 over the Alaskan Arctic [34] derived CL values of 3 to 8 m over deformed FYI and 6 to 9 m over the MYI. Their data were from regions close to the coast and the data sample sizes were relatively small. Similar CL values for similar regions can be found in this study. However, their CL values were at the lower end of the CL values we observe here. It is not clear why the CL results from the two studies differ. A possible reason could be the different sampling sizes used by the two studies.
4.3. Snow Depth Impact and Future Work
A radar altimeter signal typically penetrates a dry snow surface and the main return power is from the snow/ice interface [4]. The return power can also be impacted by the snow depth and snow density [35]. The surface elevation distribution from the ATM laser altimeter is for the snow/air interface. The elevation PDF for the snow/air interface and snow/ice interface can be different due to the irregular snow depth and snow density distributions. Applying the EMG surface elevation distribution derived from ATM data to the modeling of radar altimeter return waveforms inherently assumes that the snow/ice interface has a similar elevation distribution within its footprint. Landy et al. [13] found that the snow and sea ice surfaces exhibit similar roughness properties, and their results support the argument that snow surface roughness is primarily controlled by the roughness of the underlying sea ice [36,37,38]. Landy et al. [13] also found that the variable ice surface roughness contributes a systematic uncertainty in sea ice thickness of up to 20% over FYI and 30% over MYI. The error due to the irregular snow distribution impact needs to be studied further.
In this study, we focused on the 1.5 km segments of the ATM along-track data for the typical radar altimeter footprint. For studies related to different altimeter footprint sizes, such as ICESat (~70 m) and ICESat-2 (~17 m), further studies are needed and the PDFs should be evaluated from data grids similar to their corresponding footprint sizes.
5. Conclusions
In this study, we re-analyzed the entirety of NASA’s OIB ATM lidar data over the Arctic sea ice for the spring season to better characterize the sea-ice surface elevation PDF. The ultimate objective of this analysis was to better understand the sea-ice surface topography to improve the estimation of the sea-ice freeboard, particularly from nadir-looking radar altimeters. We found that the EMG function fit the surface elevation PDF extremely well for a wide range of sea-ice conditions, from thin FYI to rough MYI, and, therefore, it is possible to characterize the sea-ice surface roughness by just the three parameters describing the EMG function. In addition, the EMG function has a closed mathematical form for its characteristic function, allowing us to integrate this surface elevation PDF in the modeling of radar altimeter waveforms. Our results indicate that the Arctic sea-ice surface elevation PDF is dominantly positively skewed and this function is better suited to fit the PDFs than the classical Gaussian or lognormal functions.
The results presented in this paper are relevant to researchers studying sea-ice dynamics in the Arctic as sea-ice surface roughness modulates the energy and momentum exchange between the atmosphere and ocean and controls the distribution of melt ponds through spring and summer. All of the surface roughness PDF data from the re-analyzed ATM data will be shared through the NOAA’s Laboratory for Satellite Altimetry public ftp.
We also characterized the surface elevation correlation characteristics by computing ACF and CL of the ATM measurements along the ground tracks. During the studied period, the mean CL values ranged from 20 to 30 m, which is about 29–43% of the size of the ICESat laser footprint (~70 m), larger than the ICESat-2 footprints (~17 m), and about 2% of the radar altimeter footprint diameter (1.5 km).
Author Contributions
Each of the authors were actively involved in the preparation of the paper. Conceptualization and methodology, A.E., D.Y., C.B. and W.H.F.S.; software, D.Y., A.E., L.C., W.H.F.S. and D.Z.; investigation, validation, and formal analysis, D.Y., A.E., W.H.F.S., L.C., C.B. and D.Z.; writing—original draft preparation, D.Y., A.E. and W.H.F.S.; supervision, A.E. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially funded by the NASA ROSES, Studies with ICESat-2, grant number NNH19ZDA001N and by the NOAA Product Development, Readiness, and Application (PDRA)/Jason Program.
Data Availability Statement
Sea ice surface elevation distribution data derived from the methodology described in this publication are freely available and accessible at https://www.star.nesdis.noaa.gov/socd/lsa/SeaIce/SurfaceTopography.php.
Acknowledgments
The scientific results and conclusions, as well as any views or opinions expressed herein, are those of the authors and do not necessarily reflect the views of NOAA or the Department of Commerce. We thank the five reviewers for their useful and detailed comments that improved this paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kwok, R.; Petty, A.; Cunningham, G.F.; Hancock, D.W.; Ivanoff, A.; Wimert, J.T.; Bagnardi, M.; Kurtz, N. Algorithm Theoretical Basis Document (ATBD) For Sea Ice Products. In ICESat-2 Algorithm Theoretical Basis Document, Version 4; NASA Goddard Space Flight Center: Greenbelt, MD, USA, 2021. [Google Scholar]
- Brenner, A.C.; Zwally, H.J.; Bentley, C.R.; Csatho, B.M.; Harding, D.J.; Hufton, M.A.; Minster, J.B.; Roberts, L.; Saba, J.L.; Thomas, R.H.; et al. Derivation of Range and Range Distributions from Laser Pulse Waveform Analysis for Surface Elevations, Roughness, Slope, and Vegetation Heights. In ICESat Algorithm Theoretical Basis Document, Version 5; NASA Goddard Space Flight Center: Greenbelt, MD, USA, 2011. [Google Scholar]
- Wingham, D.J.; Francis, C.R.; Baker, S.; Bouzinac, C.; Brockley, D.; Cullen, R.; Chateau-Thierry, P.; Laxon, S.W.; Mallow, U.; Mavrocordatos, C.; et al. Cryosat: A mission to determine the fluctuations in Earth’s land and marine ice fields. Adv. Space Res. 2006, 37, 841–871. [Google Scholar] [CrossRef]
- Laxon, S.W.; Giles, K.A.; Ridout, A.L.; Wingham, D.J.; Willatt, R.; Cullen, R.; Kwok, R.; Schweiger, A.; Zhang, J.; Haas, C.; et al. CryoSat-2 estimates of Arctic sea ice thickness and volume. Geophys. Res. Lett. 2013, 40, 732–737. [Google Scholar] [CrossRef] [Green Version]
- Berger, T. Satellite altimetry using ocean backscatter. IEEE Trans. Antennas Propag. 1972, 20, 295–309. [Google Scholar] [CrossRef]
- Brown, G.S. The average impulse response of a rough surface and its applications. IEEE Trans. Antennas Propag. 1977, 25, 67–74. [Google Scholar] [CrossRef]
- Tayfun, M.A. Narrow-Band Nonlinear Sea Waves. J. Geophys. Res. 1980, 85, 1548–1582. [Google Scholar] [CrossRef]
- Raney, R.K. The Delay/Dopper Radar Altimeter. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1578–1588. [Google Scholar] [CrossRef]
- Egido, A.W.; Smith, H.F. Fully Focused SAR Altimetry: Theory and Applications. IEEE Trans. Geosci. Remote Sens. 2017, 55, 392–406. [Google Scholar] [CrossRef]
- Egido, A.; Smith, W.H.F. Pulse-to-Pulse Correlation Effects in High PRF Low-Resolution Mode Altimeters. IEEE Trans. Geosci. Remote Sens. 2019, 57, 2610–2617. [Google Scholar] [CrossRef]
- Landy, J.C.; Tsamados, M.; Scharien, R.K. A Facet-Based Numerical Model for Simulating SAR Altimeter Echoes from Heterogeneous Sea Ice Surfaces. IEEE Trans. Geosci. Remote Sens. 2019, 57, 4164–4180. [Google Scholar] [CrossRef] [Green Version]
- Rivas, M.B.; Maslanik, J.A.; Sonntag, J.G.; Axelrad, P. Sea Ice Roughness from Airborne LIDAR Profiles. IEEE Trans. Geosci. Remote Sens. 2006, 44, 3032–3037. [Google Scholar] [CrossRef]
- Landy, J.C.; Petty, A.A.; Tsamados, M.; Stroeve, J.C. Sea ice roughness overlooked as a key source of uncertainty in CryoSat-2 ice freeboard retrievals. J. Geophys. Res. Ocean 2020, 125, e2019JC015820. [Google Scholar] [CrossRef]
- Hughes, B.A. On the use of lognormal statistics to simulate one- and two-dimensional under-ice draft profiles. J. Geophys. Res. 1991, 96, 22101–22111. [Google Scholar] [CrossRef]
- Davis, N.; Wadhams, P. A statistical analysis of Arctic pressure ridge morphology. J. Geophys. Res. 1995, 100, 10915–10925. [Google Scholar] [CrossRef]
- Castellani, G.; Lüpkes, C.; Hendricks, S.; Gerdes, R. Variability of Arctic sea-ice topography and its impact on the atmospheric surface drag. J. Geophys. Res. Ocean 2014, 119, 6743–6762. [Google Scholar] [CrossRef]
- Krabill, W.B.; Abdalati, W.; Frederick, E.B.; Manizade, S.S.; Martin, C.F.; Sonntag, J.; Swift, R.N.; Thomas, R.H.; Yungel, J.G. Aircraft laser altimetry measurement of elevation changes of the Greenland ice sheet: Technique and accuracy assessment. J. Geodyn. 2002, 34, 357–376. [Google Scholar] [CrossRef]
- Martin, C.F.; Krabill, W.B.; Manizade, S.S.; Russell, R.L.; Sonntag, J.G.; Swift, R.N.; Yungel, J.K. Airborne Topographic Mapper Calibration Procedures and Accuracy Assessment; Technical Report NASA/TM-2012-215891; NASA Goddard Space Flight Center: Greenbelt, MD, USA, 2012. Available online: https://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/20120008479.pdf (accessed on 1 March 2022).
- Dominguez, R. IceBridge DMS L1B Geolocated and Orthorectified Images, Version 1; Technical Report updated 2018; NASA National Snow Ice Data Center Distributed Active Archive Center: Boulder, CO, USA, 2018. [Google Scholar] [CrossRef]
- Studinger, M. IceBridge ATM L1B Elevation and Return Strength, Version 2; updated 2020; NASA National Snow and Ice Data Center Distributed Active Archive Center: Boulder, CO, USA, 2020. [Google Scholar] [CrossRef]
- Krabill, W.B.; Thomas, R.H.; Martin, C.F.; Swift, R.N.; Frederick, E.B. Accuracy of airborne laser altimetry over the Greenland ice sheet. Int. J. Remote Sens. 1995, 16, 1211–1222. [Google Scholar] [CrossRef]
- Brunt, K.M.; Hawley, R.L.; Lutz, E.R.; Studinger, M.; Sonntag, J.G.; Hofton, M.A.; Andrews, L.C.; Neumann, T.A. Assessment of NASA airborne laser altimetry data using ground-based GPS data near Summit Station, Greenland. Cryosphere 2017, 11, 681–692. [Google Scholar] [CrossRef] [Green Version]
- Andersen, O.B.; Stenseng, L.; Piccioni, G.; Knudsen, P. The DTU15 MSS (Mean Sea Surface) and DTU15LAT (Lowest Astronomical Tide) Reference Surface. In Proceedings of the ESA Living Planet Symposium, Prague, Czech Republic, 9–13 May 2016; Available online: https://ftp.space.dtu.dk/pub/DTU15/DOCUMENTS/MSS/DTU15MSS+LAT.pdf (accessed on 1 March 2022).
- Andersen, O.B.; Knudsen, P. DNSC08 mean sea surface and mean dynamic topography models. J. Geophys. Res. 2009, 114, C11001. [Google Scholar] [CrossRef]
- Smith, W.H.F. Direct conversion of latitude and height from one ellipsoid to another. J. Geod. 2022, in press. [Google Scholar] [CrossRef]
- Yi, D.; Harbeck, J.P.; Manizade, S.S.; Kurtz, N.T.; Studinger, M.; Hofton, M. Arctic Sea Ice Freeboard Retrieval with Waveform Characteristics for NASA’s Airborne Topographic Mapper (ATM) and Land, Vegetation, and Ice Sensor (LVIS). IEEE Trans. Geosci. Remote Sens. 2015, 53, 1403–1410. [Google Scholar] [CrossRef]
- Aaboe, S.; Breivik, L.-A.; Sorense, A.; Eastwood, S.; Lavergne, T. Ocean & Sea Ice SAF, Global Sea Ice Edge and Type, Product User’s Manual, OSI-402-c & OSI-403-c, Version 2.3; Norwegian Meteorological Institute: Oslo, Norway, 2018.
- Exponentially Modified Gaussian Distribution. Available online: https://en.wikipedia.org/wiki/Exponentially_modified_Gaussian_distribution (accessed on 1 March 2021).
- Onana, V.D.P.; Kurtz, N.T.; Farrell, S.L.; Koenig, L.S.; Studinger, M.; Harbeck, J.P. A sea-ice lead detection algorithm for use with high resolution airborne visible imagery. IEEE Trans. Geosci. Remote Sens. 2013, 51, 38–56. [Google Scholar] [CrossRef]
- CLUSTER. Available online: https://www.l3harrisgeospatial.com/docs/cluster.html (accessed on 15 March 2021).
- Everitt, B.S. Cluster Analysis; Halsted Press: New York, NY, USA, 1993; ISBN 0-470-22043-0. [Google Scholar]
- MacGregor, J.A.; Boisvert, L.N.; Medley, B.; Petty, A.A.; Harbeck, J.P.; Bell, R.E.; Blair, J.B.; Blanchard-Wrigglesworth, E.; Buckley, E.M.; Christoffersen, M.S.; et al. The scientific legacy of NASA’s Operation IceBridge. Rev. Geophys. 2021, 59, e2020RG000712. [Google Scholar] [CrossRef]
- Church, E.L. Comments on the Correlation Length. In Proceedings of the SPIE 0680, Surface Characterization and Testing, Bay Point, FL, USA, 23 March 1987. [Google Scholar] [CrossRef]
- Cavalieri, D.J.; Markus, T.; Maslanik, J.; Sturm, M.; Lobl, E. March 2003 EOS Aqua AMSR-E Arctic Sea Ice Field Campaign. IEEE Trans. Geosci. Remote Sens. 2006, 44, 3003–3008. [Google Scholar] [CrossRef]
- Willatt, R.; Laxon, S.; Giles, K.; Cullen, R.; Haas, C.; Helm, V. Ku-band radar penetration into snow cover Arctic sea ice using airborne data. Ann. Glaciol. 2011, 52, 197–205. [Google Scholar] [CrossRef] [Green Version]
- Doble, M.; Skourup, H.; Wadhams, P.; Geiger, C. The relation between Arctic sea ice surface elevation and draft: A case study using coincident AUV sonar and air-borne scanning laser. J. Geophys. Res. 2011, 116, C00E03. [Google Scholar] [CrossRef] [Green Version]
- Iacozza, J.; Barber, D. An examination of the distribution of snow on sea-ice. Atmos. Ocean 1999, 37, 21–51. [Google Scholar] [CrossRef]
- Kurtz, N.T.; Farrell, S.L.; Studinger, M.; Galin, N.; Harbeck, J.P.; Lindsay, R.; Onana, V.D.; Panzer, B.; Sonntag, J.G. Sea ice thickness, freeboard, and snow depth products from Operation IceBridge air-borne data. Cryosphere 2013, 7, 1035–1056. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).