Evidence of Ocean Waves Signature in the Space–Time Turbulent Spectra of the Lower Marine Atmosphere Measured by a Scanning LiDAR
Abstract
1. Introduction
2. Experimental Campaign
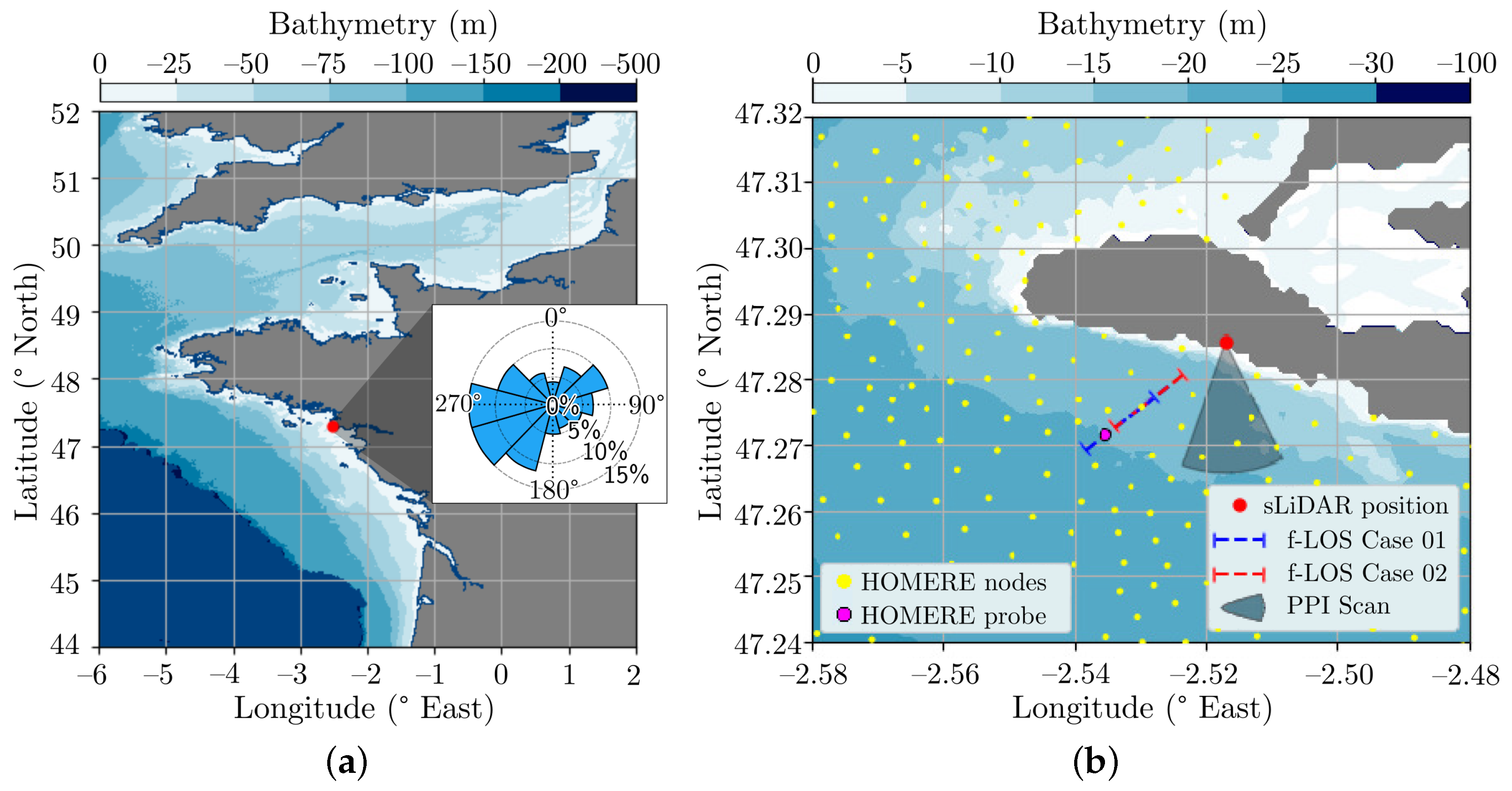
2.1. Test Site
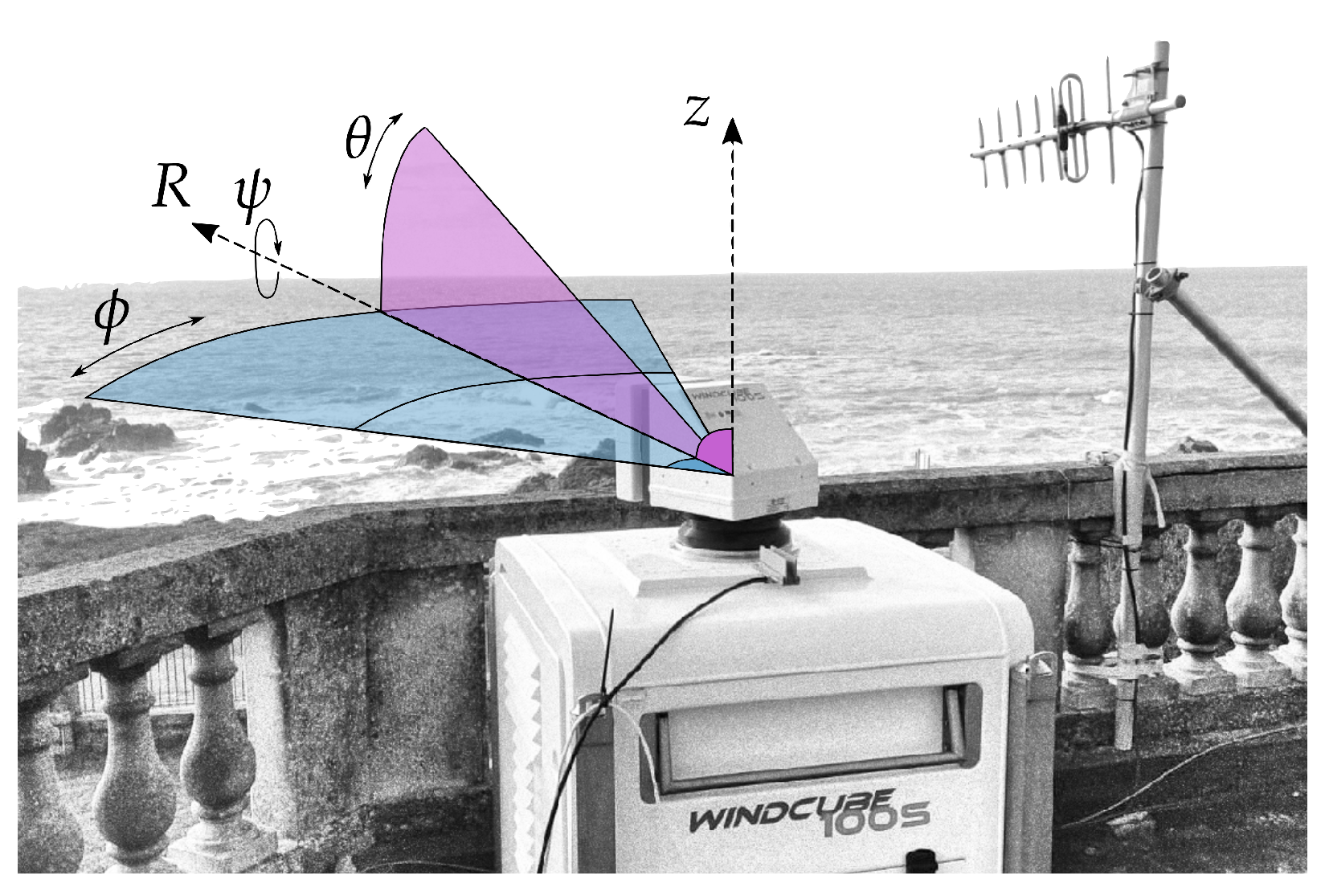
2.2. sLiDAR Technology and Experimental Setup
2.2.1. Technology and Challenges
2.2.2. Calibration and Configuration
2.3. Environmental Description and Test-Case Selection
2.3.1. Meteocean Conditions
2.3.2. Test Cases
3. Data Treatment and Analyses
3.1. Energy Density Functions
3.2. Two-Dimensional Fourier Transform
4. Results
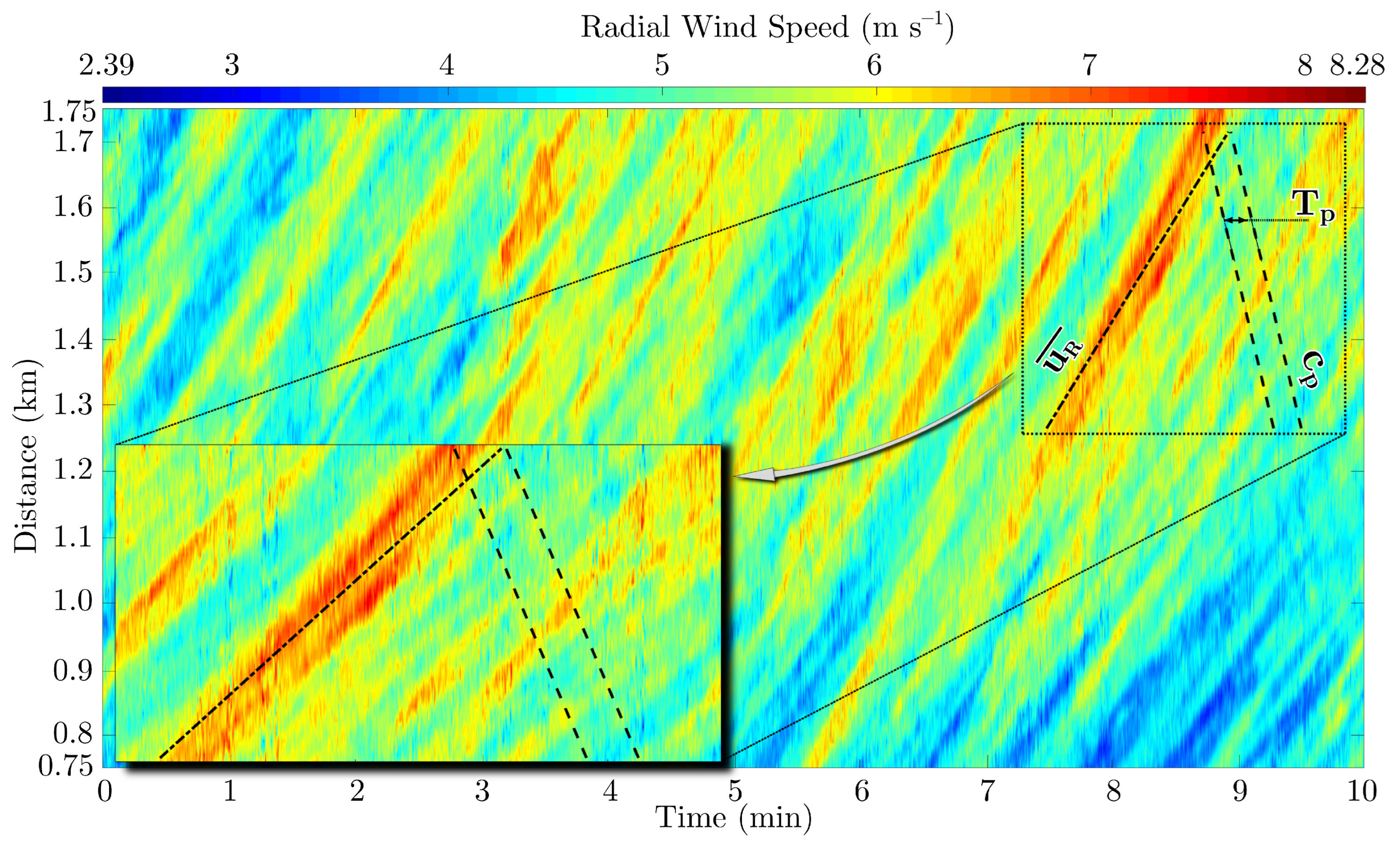
4.1. Radial Wind Speed Fluctuations
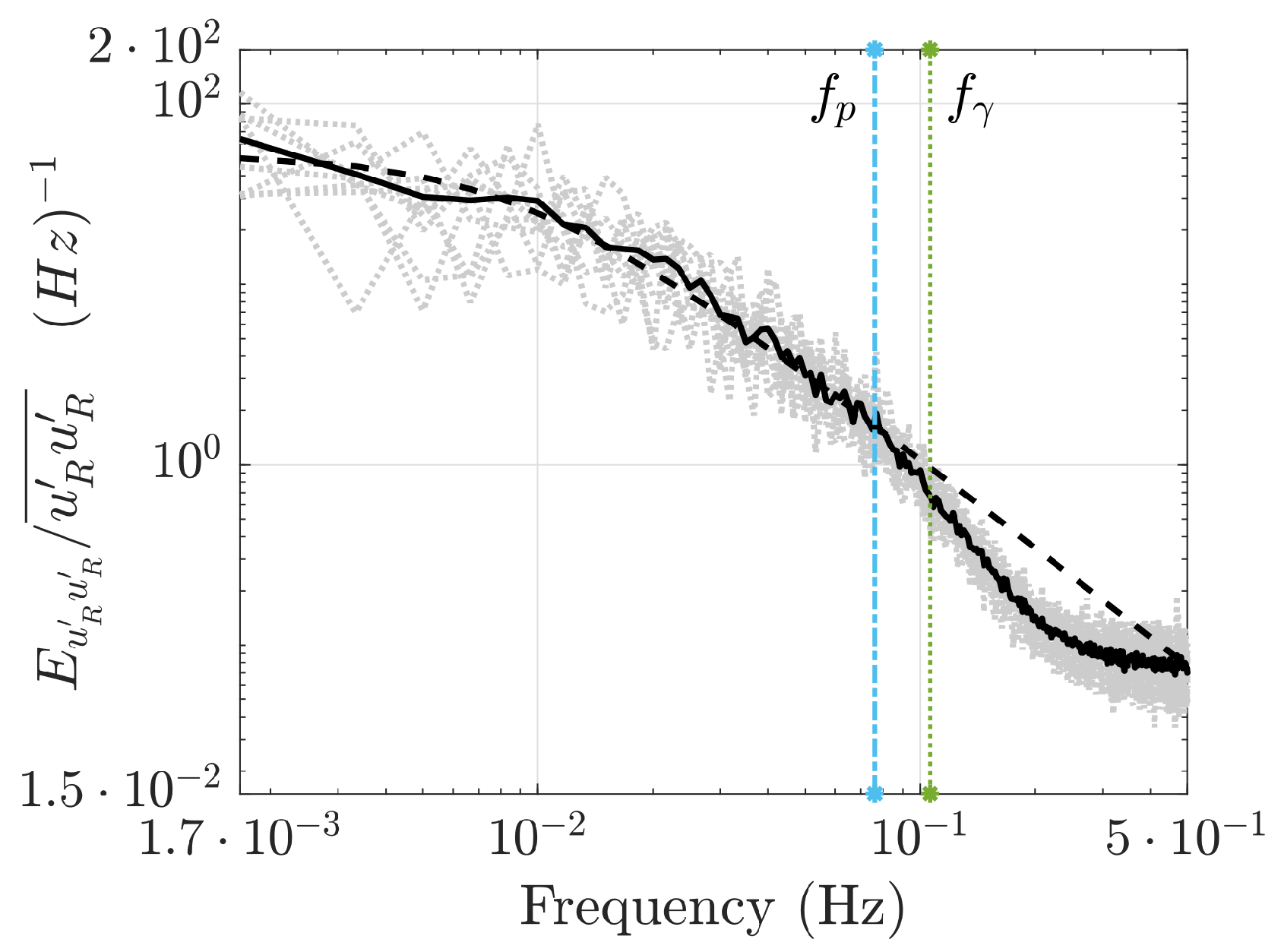
4.2. One-Dimensional Turbulent Spectra
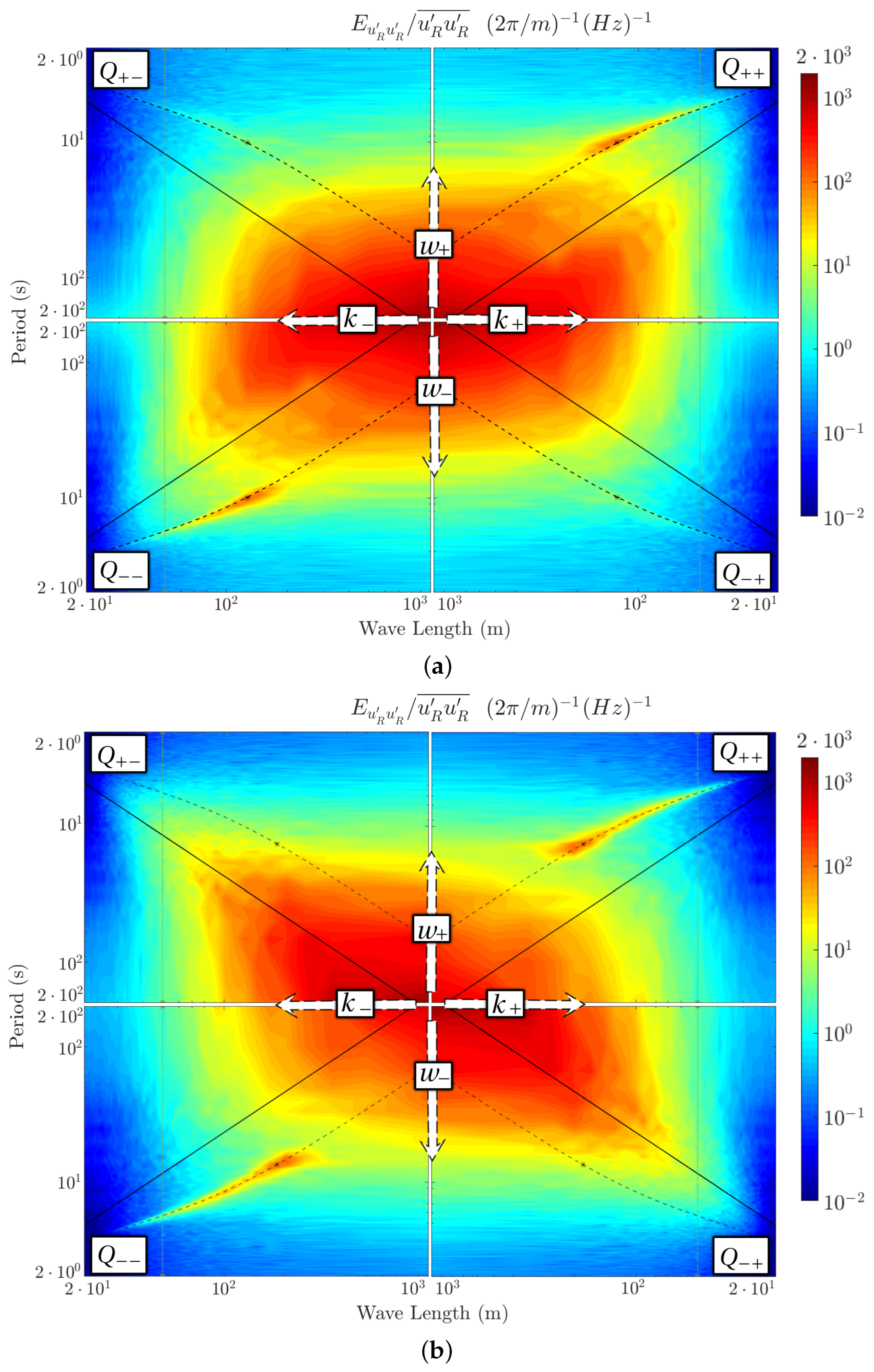
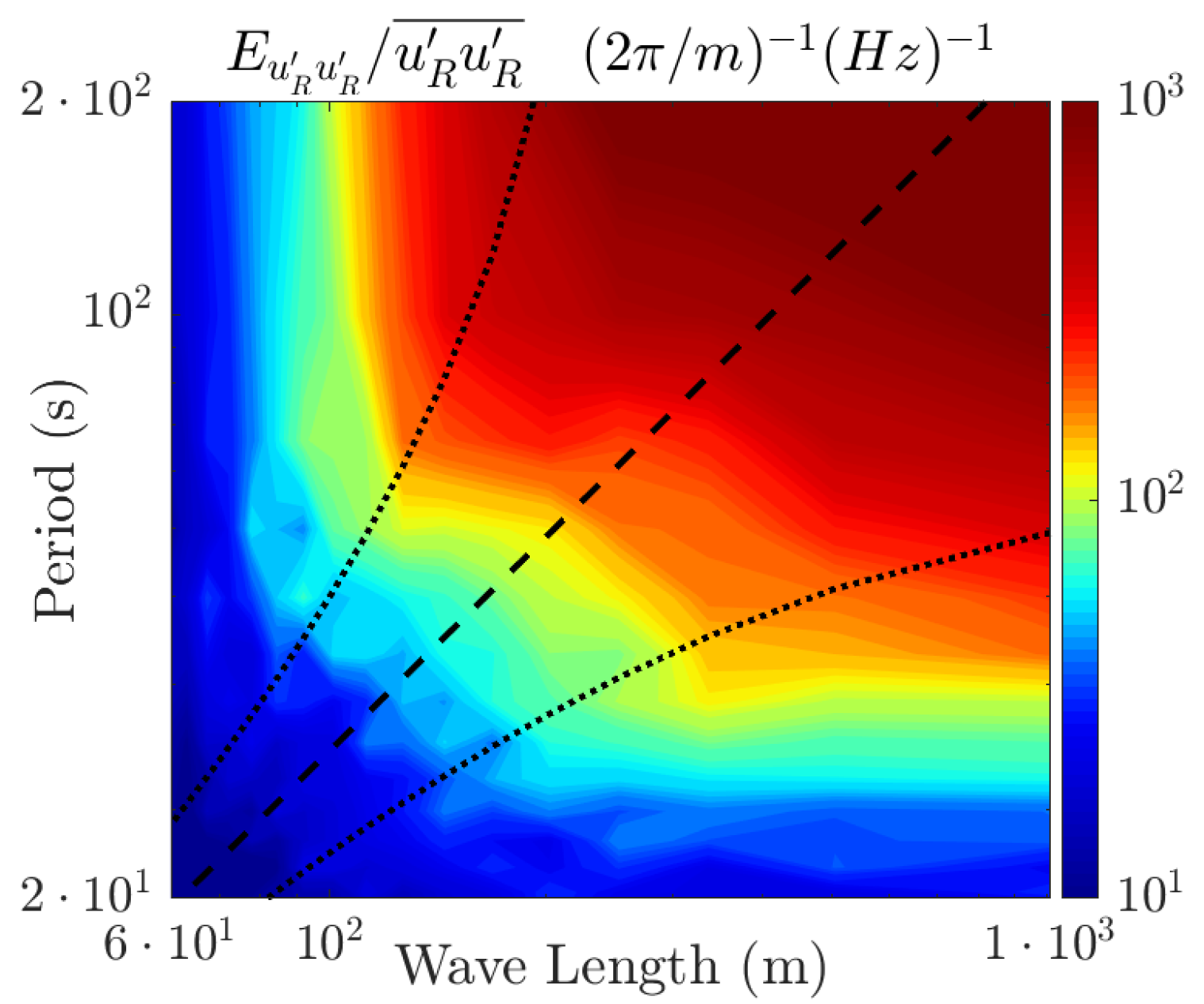
4.3. Two-Dimensional Turbulent Spectrum
4.3.1. Resultant Single-Sided Spectrum
4.3.2. Opposing Directions and the Four-Quadrant Spectrum
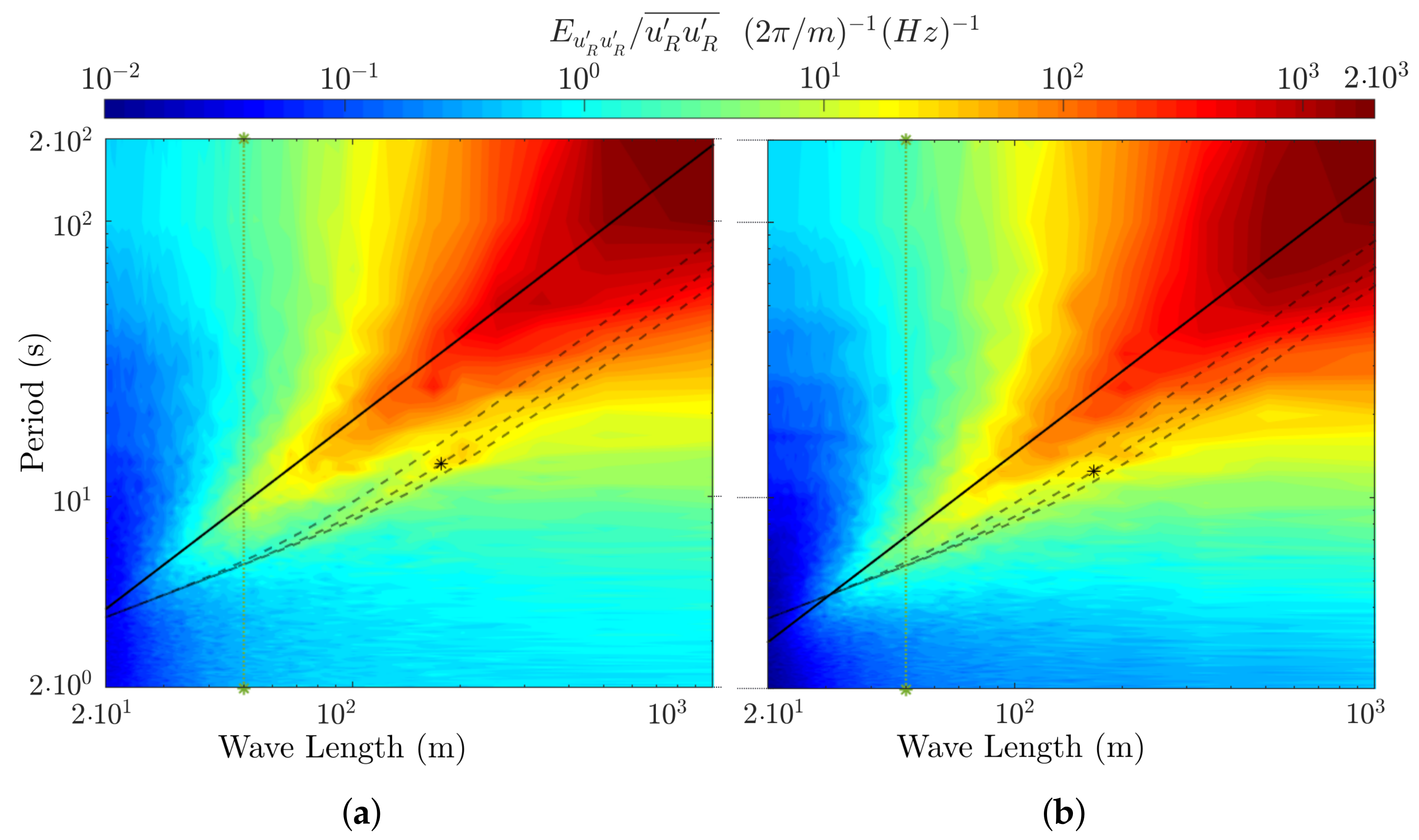
4.4. Rising Wind and Diminishing Sea-State
5. Discussion
5.1. Deviations from the Taylor and Random Sweeping Hypotheses
5.2. Coherence and Correlation in a Space–Time Perspective
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| 1D | One-dimensional |
| 2D | Two-dimensional |
| ABL | Atmospheric Boundary Layer |
| CNR | Carrier-to-noise-ratio |
| EDF | Energy Density Function |
| ESDU | Engineering Sciences Data Unit |
| f-LOS | fixed LOS |
| FT | Fourier Transform |
| FFT | Fast FT |
| LiDAR | Light Detection and Ranging System |
| LHEEA | Laboratory in Hydrodynamics, Energetics and Atmospheric Environment |
| LOS | Line of Sight |
| MABL | Marine ABL |
| MSL | Mean Sea Level |
| PPI | Plan Position Indicator |
| RWS | Radial Wind Speed |
| sLiDAR | scanning LiDAR |
| SST | Sea Surface Temperature |
| TI | Turbulence Intensity |
| TKE | Turbulent Kinetic Energy |
| UTC | Universal Time Coordinated |
| WA | Wave Age |
| WBL | Wave Boundary Layer |
| WC | Wave-Coherent |
| WD | Wind Direction |
| WI | Wave-Induced |
| WS | Wind Speed |
| WWIII | WAVEWATCH III |
Appendix A. Data Quality and Filter
Appendix A.1. Carrier-To-Noise Ratio
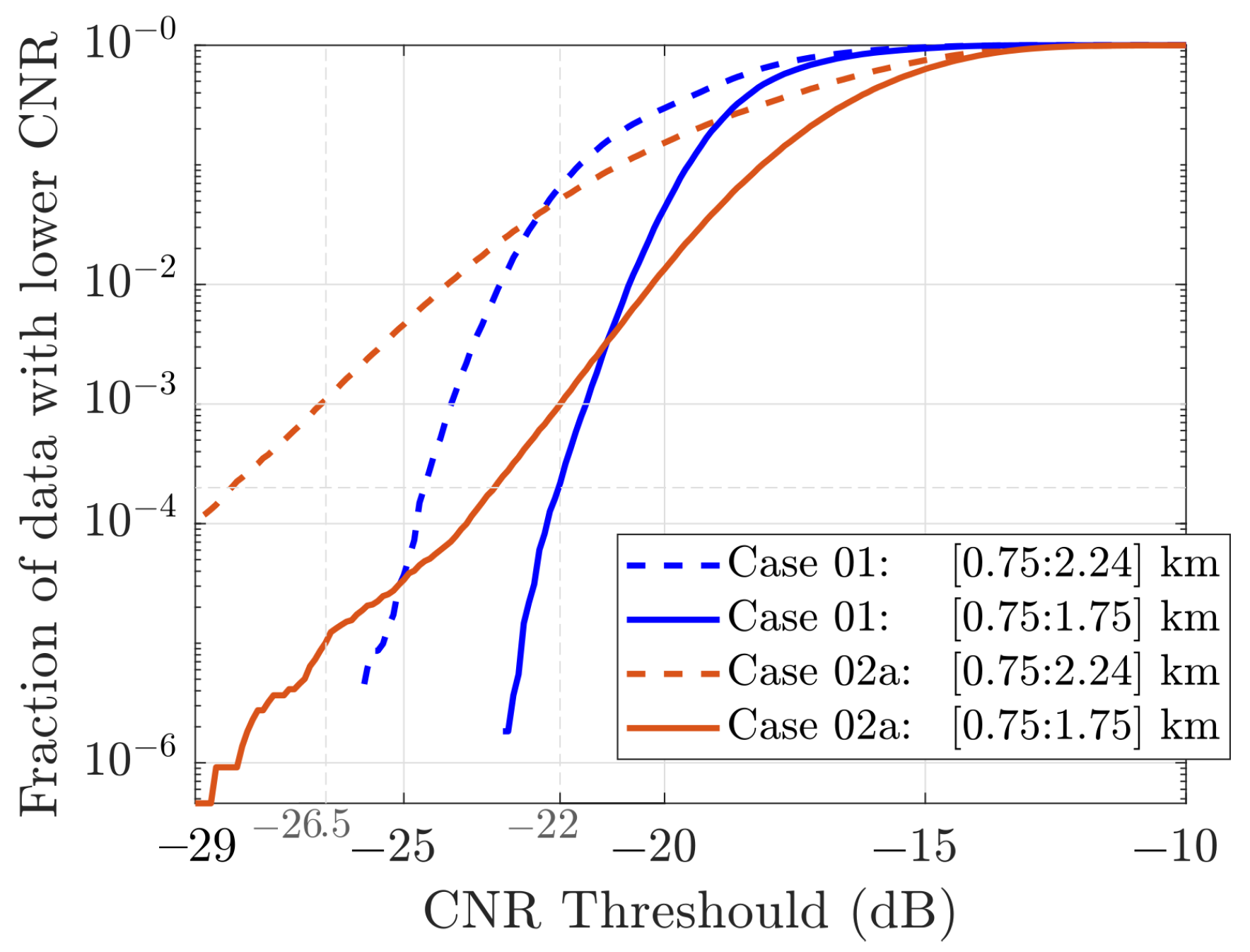
Appendix A.2. Spike Detection and Removal
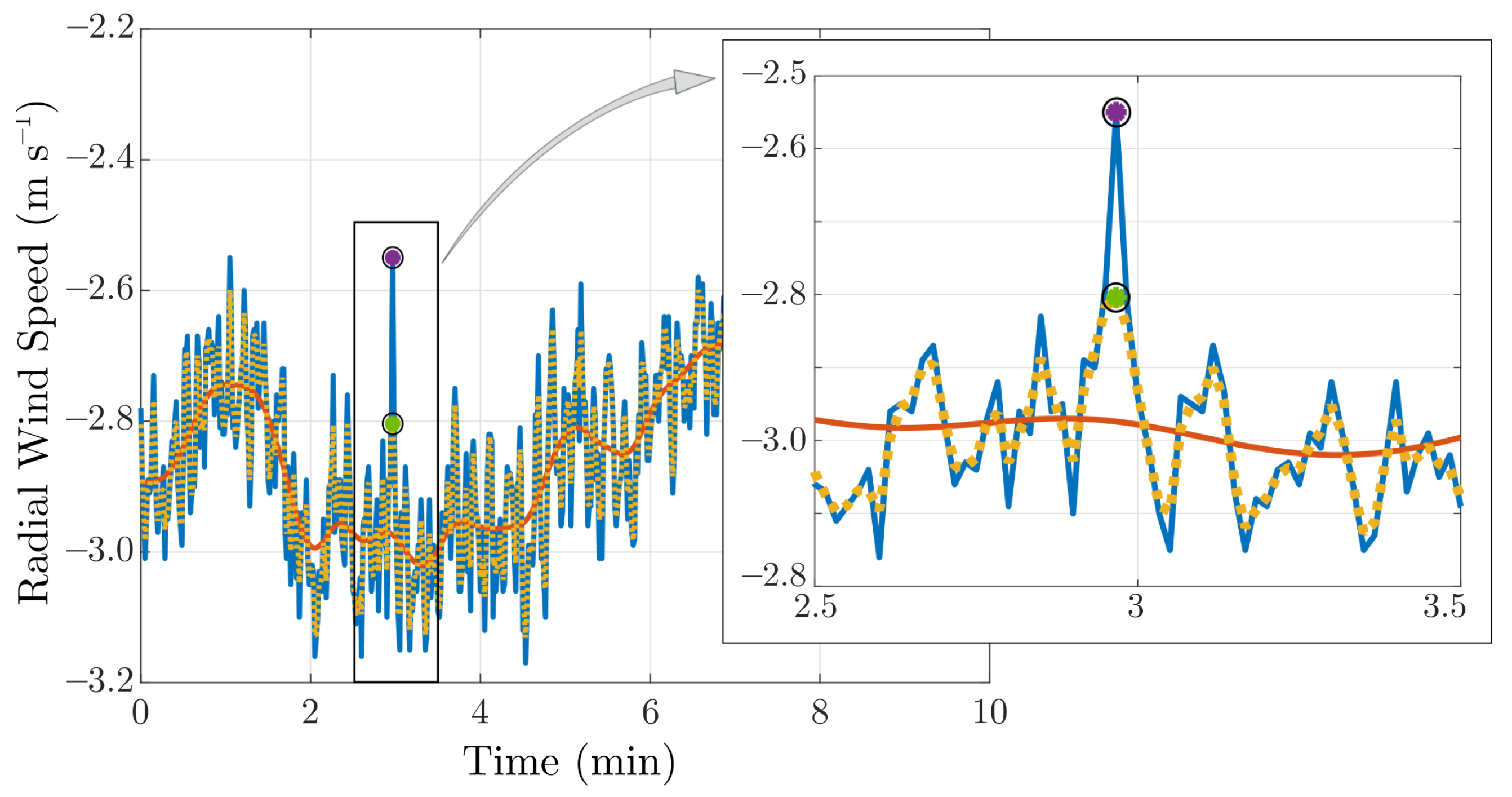
Appendix A.3. Signal Reconstruction
References
- Thomson, W. Hydrokinetic Solutions and Observations. Philos. Mag. 1871, 42, 326–378. [Google Scholar] [CrossRef]
- Jeffreys, H. On the formation of water waves by wind. Proc. R. Soc. Lond. 1925, 107, 189–206. [Google Scholar]
- Miles, J.W. On The Generation Of Surface Waves By Shear Flows, Part I. J. Fluid Mech. 1957, 3, 185–204. [Google Scholar] [CrossRef]
- Phillips, O.M. On The Generation Of Waves By Turbulent Wind. J. Fluid Mech. 1957, 2, 417–445. [Google Scholar] [CrossRef]
- Belcher, S.E.; Hunt, J.C.R. Turbulent Shear Flow Over Slowly Moving Waves. J. Fluid Mech. 1993, 251, 109–148. [Google Scholar] [CrossRef]
- Edson, J.B.; Zappa, C.J.; Ware, J.A.; McGillis, W.R.; Hare, J.E. Scalar flux profile relationships over the open ocean. J. Geophys. Res. Ocean. 2004, 109, C08S09. [Google Scholar] [CrossRef]
- Hristov, T. Mechanistic, empirical and numerical perspectives on wind-waves interaction. Procedia IUTAM 2018, 26, 102–111. [Google Scholar] [CrossRef]
- Tamura, H.; Drennan, W.M.; Collins, C.O.; Graber, H.C. Turbulent Airflow and Wave-Induced Stress Over the Ocean. Bound.-Layer Meteorol. 2018, 169, 47–66. [Google Scholar] [CrossRef]
- Patton, E.G.; Sullivan, P.P.; Kosović, B.; Dudhia, J.; Mahrt, L.; Žagar, M.; Marić, T. On the Influence of Swell Propagation Angle on Surface Drag. J. Appl. Meteorol. Climatol. 2019, 58, 1039–1059. [Google Scholar] [CrossRef]
- Porchetta, S.; Temel, O.; Muñoz Esparza, D.; Reuder, J.; Monbaliu, J.; van Beeck, J.; van Lipzig, N. A new roughness length parameterization accounting for wind–wave (mis)alignment. Atmos. Chem. Phys. 2019, 19, 6681–6700. [Google Scholar] [CrossRef]
- Sullivan, P.P.; McWilliams, J.C.; Moeng, C.H. Simulation of turbulent flow over idealized water waves. J. Fluid Mech. 2000, 404, 47–85. [Google Scholar] [CrossRef]
- Yang, D.; Shen, L. Direct-simulation-based study of turbulent flow over various waving boundaries. J. Fluid Mech. 2010, 650, 131–180. [Google Scholar] [CrossRef]
- Yang, D.; Meneveau, C.; Shen, L. Effect of downwind swells on offshore wind energy harvesting—A large-eddy simulation study. Renew. Energy 2014, 70, 11–23. [Google Scholar] [CrossRef]
- Sullivan, P.P.; McWilliams, J.C.; Patton, E.G. Large-Eddy Simulation of Marine Atmospheric Boundary Layers above a Spectrum of Moving Waves. J. Atmos. Sci. 2014, 71, 4001–4027. [Google Scholar] [CrossRef]
- Hao, X.; Shen, L. Wind-wave coupling study using LES of wind and phase-resolved simulation of nonlinear waves. J. Fluid Mech. 2019, 874, 391–425. [Google Scholar] [CrossRef]
- Obukhov, A.M. Turbulence in an Atmosphere with a Non-Uniform Temperature. Bound.-Layer Meteorol. 1946, 2, 7–29. [Google Scholar] [CrossRef]
- Monin, A.S.; Obukhov, A.M. Basic Laws of Turbulent Mixing in the Surface Layer of the Atmosphere. Contrib. Geophys. Inst. Acad. Sci. USSR 1954, 24, 163–187. [Google Scholar]
- Businger, J.A.; Wyngaard, J.C.; Izumi, Y.; Bradley, E.F. Flux-Profile Relationships in the Atmospheric Surface Layer. J. Atmos. Sci. 1971, 28, 181–189. [Google Scholar] [CrossRef]
- Sjöblom, A.; Smedman, A.S. The turbulent kinetic energy budget in the marine atmospheric surface layer. J. Geophys. Res. Ocean. 2002, 107, 6-1–6-18. [Google Scholar] [CrossRef]
- Donelan, M.A.; Dobson, F.W.; Smith, S.D.; Anderson, R.J. On the Dependence of Sea Surface Roughness on Wave Development. J. Phys. Oceanogr. 1993, 23, 2143–2149. [Google Scholar] [CrossRef]
- Cifuentes-Lorenzen, A.; Edson, J.B.; Zappa, C.J. Air–Sea Interaction in the Southern Ocean: Exploring the Height of the Wave Boundary Layer at the Air–Sea Interface. Bound.-Layer Meteorol. 2018, 169, 461–482. [Google Scholar] [CrossRef]
- Hristov, T.; Ruiz-Plancarte, J. Dynamic Balances in a Wavy Boundary Layer. J. Phys. Oceanogr. 2014, 44, 3185–3194. [Google Scholar] [CrossRef]
- Pierson, W.J.; Marks, W. The power spectrum analysis of ocean-wave records. Eos Trans. Am. Geophys. Union 1952, 33, 834–844. [Google Scholar] [CrossRef]
- Kitaigorodskii, S.A. On the Theory of the Equilibrium Range in the Spectrum of Wind-Generated Gravity Waves. J. Phys. Oceanogr. 1983, 13, 816–827. [Google Scholar] [CrossRef]
- Ōkubo, A. Oceanic diffusion diagrams. Deep Sea Res. Oceanogr. Abstr. 1971, 18, 789–802. [Google Scholar] [CrossRef]
- Golitsyn, G. Coefficient of Horizontal Eddy Diffusion of a Tracer on the Water Surface as a Function of the Wave Age. Izv. Atmos. Ocean. Phys. 2011, 47, 393–398. [Google Scholar] [CrossRef]
- Hristov, T.S.; Miller, S.D.; Friehe, C.A. Dynamical coupling of wind and ocean waves through wave-induced air flow. Nature 2003, 422, 55–58. [Google Scholar] [CrossRef]
- Kolmogorov, A. The Local Structure of Turbulence in Incompressible Viscous Fluid for Very Large Reynolds’ Numbers. Akad. Nauk. SSSR Dokl. 1941, 30, 301–305. [Google Scholar]
- Harris, D.L. The Wave-Driven Wind. J. Atmos. Sci. 1966, 23, 688–693. [Google Scholar] [CrossRef]
- Hanley, K.E.; Belcher, S.E. Wave-Driven Wind Jets in the Marine Atmospheric Boundary Layer. J. Atmos. Sci. 2008, 65, 2646–2660. [Google Scholar] [CrossRef]
- Cathelain, M. Development of a Deterministic Numerical Model for the Study of the Coupling between an Atmospheric Flow and a Sea State. Ph.D. Thesis, Ecole Centrale de Nantes (ECN), Nantes, France, 2017. [Google Scholar]
- Edson, J.B.; Jampana, V.; Weller, R.A.; Bigorre, S.P.; Plueddemann, A.J.; Fairall, C.W.; Miller, S.D.; Mahrt, L.; Vickers, D.; Hersbach, H. On the Exchange of Momentum over the Open Ocean. J. Phys. Oceanogr. 2013, 43, 1589–1610. [Google Scholar] [CrossRef]
- Mastenbroek, C. Wind-Wave Interaction. Ph.D. Thesis, TU Delft, Delft, The Netherlands, 1996. [Google Scholar]
- Edson, J.B.; Fairall, C.W. Similarity Relationships in the Marine Atmospheric Surface Layer for Terms in the TKE and Scalar Variance Budgets. J. Atmos. Sci. 1998, 55, 2311–2328. [Google Scholar] [CrossRef]
- Yousefi, K.; Veron, F. Boundary layer formulations in orthogonal curvilinear coordinates for flow over wind-generated surface waves. J. Fluid Mech. 2020, 888, A11. [Google Scholar] [CrossRef]
- Benilov, A.Y.; Kouznetsov, O.A.; Panin, G.N. On the analysis of wind wave-induced disturbances in the atmospheric turbulent surface layer. Bound.-Layer Meteorol. 1974, 6, 269–285. [Google Scholar] [CrossRef]
- Snyder, R.L.; Dobson, F.W.; Elliott, J.A.; Long, R.B. Array measurements of atmospheric pressure fluctuations above surface gravity waves. J. Fluid Mech. 1981, 102, 1–59. [Google Scholar] [CrossRef]
- Grare, L.; Lenain, L.; Melville, W.K. Wave-Coherent Airflow and Critical Layers over Ocean Waves. J. Phys. Oceanogr. 2013, 43, 2156–2172. [Google Scholar] [CrossRef]
- Taylor, G.I. The Spectrum of Turbulence. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1938, 164, 476–490. [Google Scholar] [CrossRef]
- Wilczek, M.; Narita, Y. Wave-number–frequency spectrum for turbulence from a random sweeping hypothesis with mean flow. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2012, 86, 066308. [Google Scholar] [CrossRef]
- Craik, A.D. The origins of water wave theory. Annu. Rev. Fluid Mech. 2004, 36, 1–28. [Google Scholar] [CrossRef]
- Janssen, P. The Interaction of Ocean Waves and Wind; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Desmars, N. Real-Time Reconstruction and Prediction of Ocean Wave Fields from Remote Optical Measurements. Ph.D. Thesis, École Centrale de Nantes, Nantes, France, 2020. [Google Scholar]
- Leckler, F.; Ardhuin, F.; Peureux, C.; Benetazzo, A.; Bergamasco, F.; Dulov, V. Analysis and Interpretation of Frequency–Wavenumber Spectra of Young Wind Waves. J. Phys. Oceanogr. 2015, 45, 2484–2496. [Google Scholar] [CrossRef]
- Plant, W.J. Short wind waves on the ocean: Wavenumber-frequency spectra. J. Geophys. Res. Ocean. 2015, 120, 2147–2158. [Google Scholar] [CrossRef]
- Cheng, Y.; Sayde, C.; Li, Q.; Basara, J.; Selker, J.; Tanner, E.; Gentine, P. Failure of Taylor’s hypothesis in the atmospheric surface layer and its correction for eddy-covariance measurements. Geophys. Res. Lett. 2017, 44, 4287–4295. [Google Scholar] [CrossRef]
- Kraichnan, R.H. Kolmogorov’s Hypotheses and Eulerian Turbulence Theory. Phys. Fluids 1964, 7, 1723–1734. [Google Scholar] [CrossRef]
- He, G.W.; Zhang, J.B. Elliptic model for space-time correlations in turbulent shear flows. Phys. Rev. E 2006, 73, 055303. [Google Scholar] [CrossRef]
- Narita, Y. Spectral moments for the analysis of frequency shift, broadening, and wavevector anisotropy in a turbulent flow. Earth Planets Space 2017, 69, 73–83. [Google Scholar] [CrossRef][Green Version]
- Peña, A.; Mann, J. Turbulence Measurements with Dual-Doppler Scanning Lidars. Remote Sens. 2019, 11, 2444. [Google Scholar] [CrossRef]
- Chan, P.W. Generation of an Eddy Dissipation Rate Map at the Hong Kong International Airport Based on Doppler Lidar Data. J. Atmos. Ocean. Technol. 2011, 28, 37–49. [Google Scholar] [CrossRef]
- Nijhuis, A.C.P.O.; Thobois, L.P.; Barbaresco, F.; Haan, S.D.; Dolfi-Bouteyre, A.; Kovalev, D.; Krasnov, O.A.; Vanhoenacker-Janvier, D.; Wilson, R.; Yarovoy, A.G. Wind Hazard and Turbulence Monitoring at Airports with Lidar, Radar, and Mode-S Downlinks: The UFO Project. Bull. Am. Meteorol. Soc. 2018, 99, 2275–2293. [Google Scholar] [CrossRef]
- Lothon, M.; Lenschow, D.H.; Mayor, S.D. Doppler Lidar Measurements of Vertical Velocity Spectra in the Convective Planetary Boundary Layer. Bound.-Layer Meteorol. 2009, 132, 205–226. [Google Scholar] [CrossRef]
- Barlow, J.F.; Dunbar, T.M.; Nemitz, E.G.; Wood, C.R.; Gallagher, M.W.; Davies, F.; O’Connor, E.; Harrison, R.M. Boundary layer dynamics over London, UK, as observed using Doppler lidar during REPARTEE-II. Atmos. Chem. Phys. 2011, 11, 2111–2125. [Google Scholar] [CrossRef]
- Smalikho, I.N.; Banakh, V.A.; Pichugina, Y.L.; Brewer, W.A.; Banta, R.M.; Lundquist, J.K.; Kelley, N.D. Lidar Investigation of Atmosphere Effect on a Wind Turbine Wake. J. Atmos. Ocean. Technol. 2013, 30, 2554–2570. [Google Scholar] [CrossRef]
- Pichugina, Y.L.; Brewer, W.A.; Banta, R.M.; Choukulkar, A.; Clack, C.T.M.; Marquis, M.C.; McCarty, B.J.; Weickmann, A.M.; Sandberg, S.P.; Marchbanks, R.D.; et al. Properties of the offshore low level jet and rotor layer wind shear as measured by scanning Doppler Lidar. Wind Energy 2017, 20, 987–1002. [Google Scholar] [CrossRef]
- Désert, T.; Knapp, G.; Aubrun, S. Quantification and Correction of Wave-Induced Turbulence Intensity Bias for a Floating LIDAR System. Remote Sens. 2021, 13, 2973. [Google Scholar] [CrossRef]
- Bastine, D.; Wächter, M.; Peinke, J.; Trabucchi, D.; Kühn, M. Characterizing Wake Turbulence with Staring Lidar Measurements. J. Phys. Conf. Ser. 2015, 625, 012006. [Google Scholar] [CrossRef]
- Global Wind Atlas (Version 3.1). Technical University of Denmark (DTU). 2021. Available online: https://globalwindatlas.info (accessed on 29 May 2022).
- Shimada, S.; Goit, J.P.; Ohsawa, T.; Kogaki, T.; Nakamura, S. Coastal wind measurements using a single scanning LiDAR. Remote Sens. 2020, 12, 1347. [Google Scholar] [CrossRef]
- Stull, R.B. An Introduction to Boundary Layer Meteorology; Cambridge University Press: Cambridge, UK, 1989; p. 177. [Google Scholar]
- Spiegel, E.A.; Veronis, G. On the Boussinesq Approximation for a Compressible Fluid. Astrophys. J. 1960, 131, 442. [Google Scholar] [CrossRef]
- Sekimoto, A.; Kawahara, G.; Sekiyama, K.; Uhlmann, M.; Pinelli, A. Turbulence- and buoyancy-driven secondary flow in a horizontal square duct heated from below. Phys. Fluids 2011, 23, 075103. [Google Scholar] [CrossRef]
- Lazure, P.; Dumas, F. An external–internal mode coupling for a 3D hydrodynamical model for applications at regional scale (MARS). Adv. Water Resour. 2008, 31, 233–250. [Google Scholar] [CrossRef]
- Boudière, E.; Maisondieu, C.; Ardhuin, F.; Accensi, M.; Pineau-Guillou, L.; Lepesqueur, J. A suitable metocean hindcast database for the design of Marine energy converters. Int. J. Mar. Energy 2013, 3–4, e40–e52. [Google Scholar] [CrossRef]
- Perignon, Y. Assessing accuracy in the estimation of spectral content in wave energy resource on the French Atlantic test site SEMREV. Renew. Energy 2017, 114, 145–153. [Google Scholar] [CrossRef]
- Accensi, M.; Alday, M.; Maisondieu, C.; Raillard, N.; Darbynian, D.; Old, C.; Sellar, B.; Thilleul, O.; Perignon, Y.; Payne, G.S.; et al. ResourceCODE framework: A high-resolution wave parameter dataset for the European Shelf and analysis toolbox. In Proceedings of the 14th European Wave and Tidal Energy Conference, Plymouth, UK, 5–9 September 2021; pp. 2182-1–2182-9. [Google Scholar]
- Gryning, S.E.; Floors, R.; Peña, A.; Batchvarova, E.; Brümmer, B. Weibull Wind-Speed Distribution Parameters Derived from a Combination of Wind-Lidar and Tall-Mast Measurements Over Land, Coastal and Marine Sites. Bound.-Layer Meteorol. 2016, 159, 329–348. [Google Scholar] [CrossRef]
- Gryning, S.E.; Floors, R. Carrier-to-Noise-Threshold Filtering on Off-Shore Wind Lidar Measurements. Sensors 2019, 19, 592. [Google Scholar] [CrossRef] [PubMed]
- Beck, H.; Kühn, M. Dynamic Data Filtering of Long-Range Doppler LiDAR Wind Speed Measurements. Remote Sens. 2017, 9, 561. [Google Scholar] [CrossRef]
- Suomi, I.; Gryning, S.E.; O’Connor, E.J.; Vihma, T. Methodology for obtaining wind gusts using Doppler lidar. Q. J. R. Meteorol. Soc. 2017, 143, 2061–2072. [Google Scholar] [CrossRef]
- Jiménez, J. Coherent structures in wall-bounded turbulence. J. Fluid Mech. 2018, 842, P1. [Google Scholar] [CrossRef]
- Engineering Sciences Data Unit. Characteristics of atmospheric turbulence near the ground. Part 2: Single point data for strong winds (neutral atmosphere). In ESDU 85020; Engineering Sciences Data Unit: London, UK, 1985. [Google Scholar]
- Yang, D.; Shen, L. Characteristics of coherent vortical structures in turbulent flows over progressive surface waves. Phys. Fluids 2009, 21, 125106. [Google Scholar] [CrossRef]
- Nappo, C.J.; Hiscox, A.L.; Miller, D.R. A Note on Turbulence Stationarity and Wind Persistence Within the Stable Planetary Boundary Layer. Bound.-Layer Meteorol. 2010, 136, 165–174. [Google Scholar] [CrossRef]
- Paskin, L.; Perignon, Y.; Conan, B.; Aubrun, S. Numerical study on the Wave Boundary Layer, its interaction with turbulence and consequences on the wind energy resource in the offshore environment. J. Phys. Conf. Ser. 2020, 1618, 062046. [Google Scholar] [CrossRef]
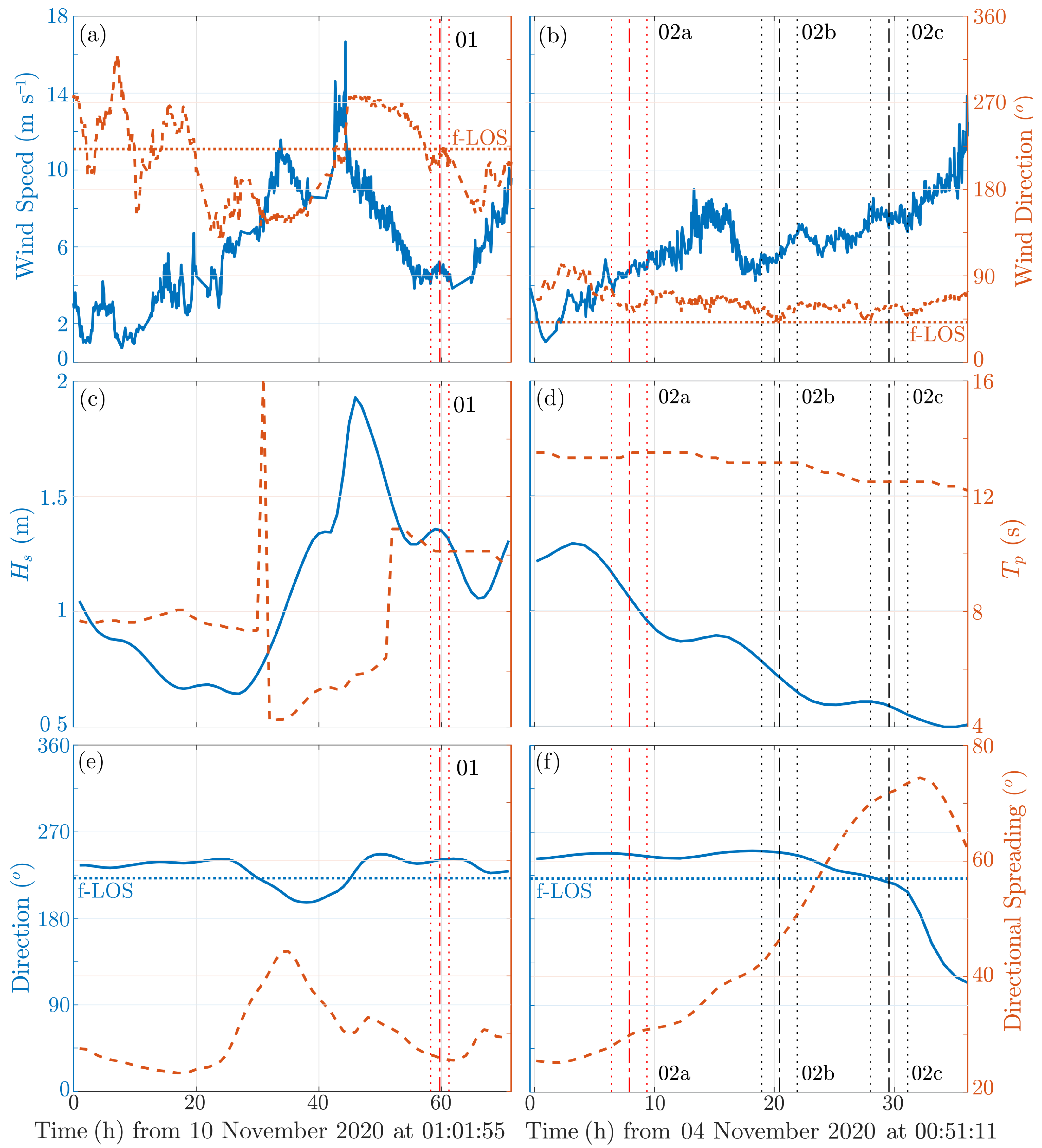
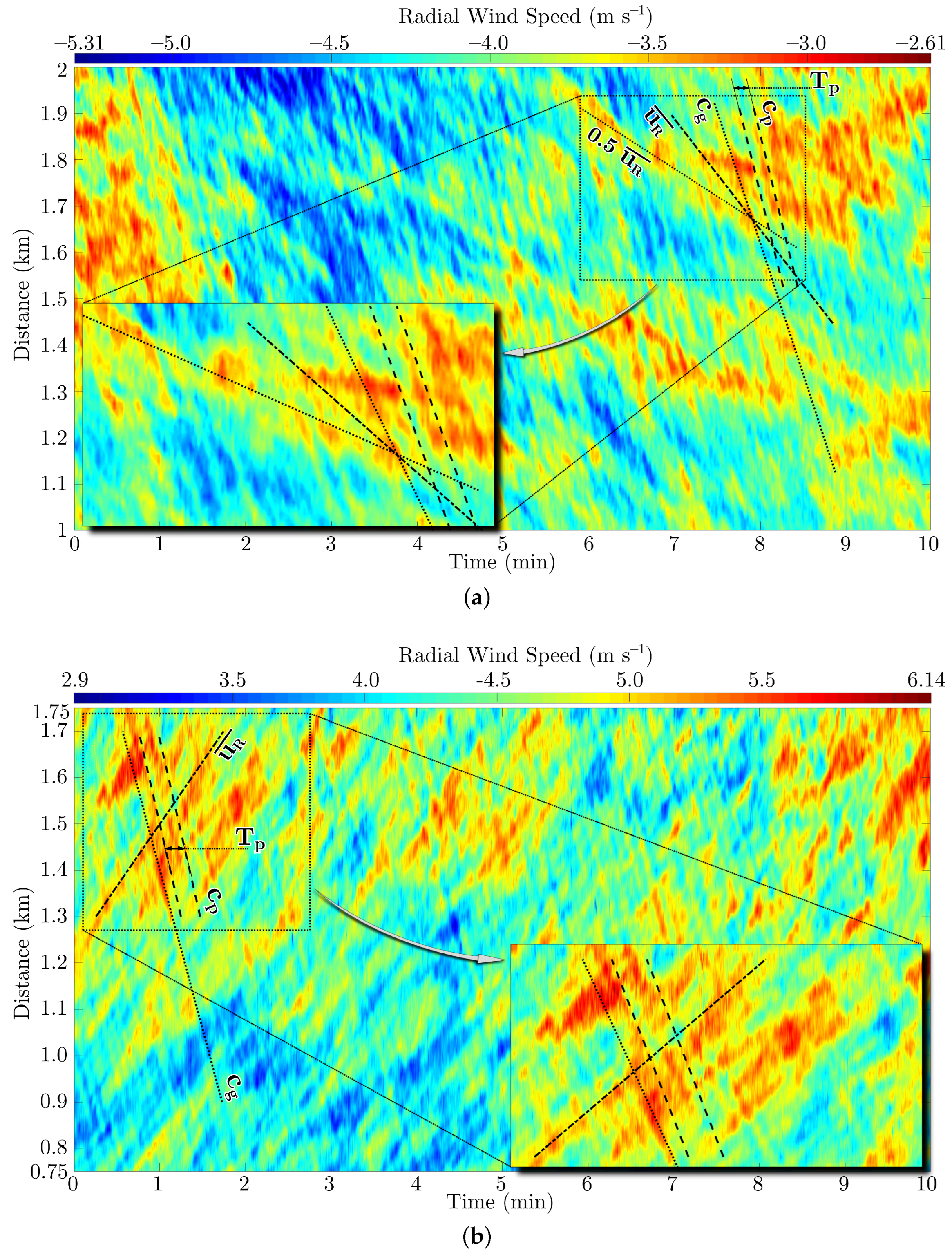
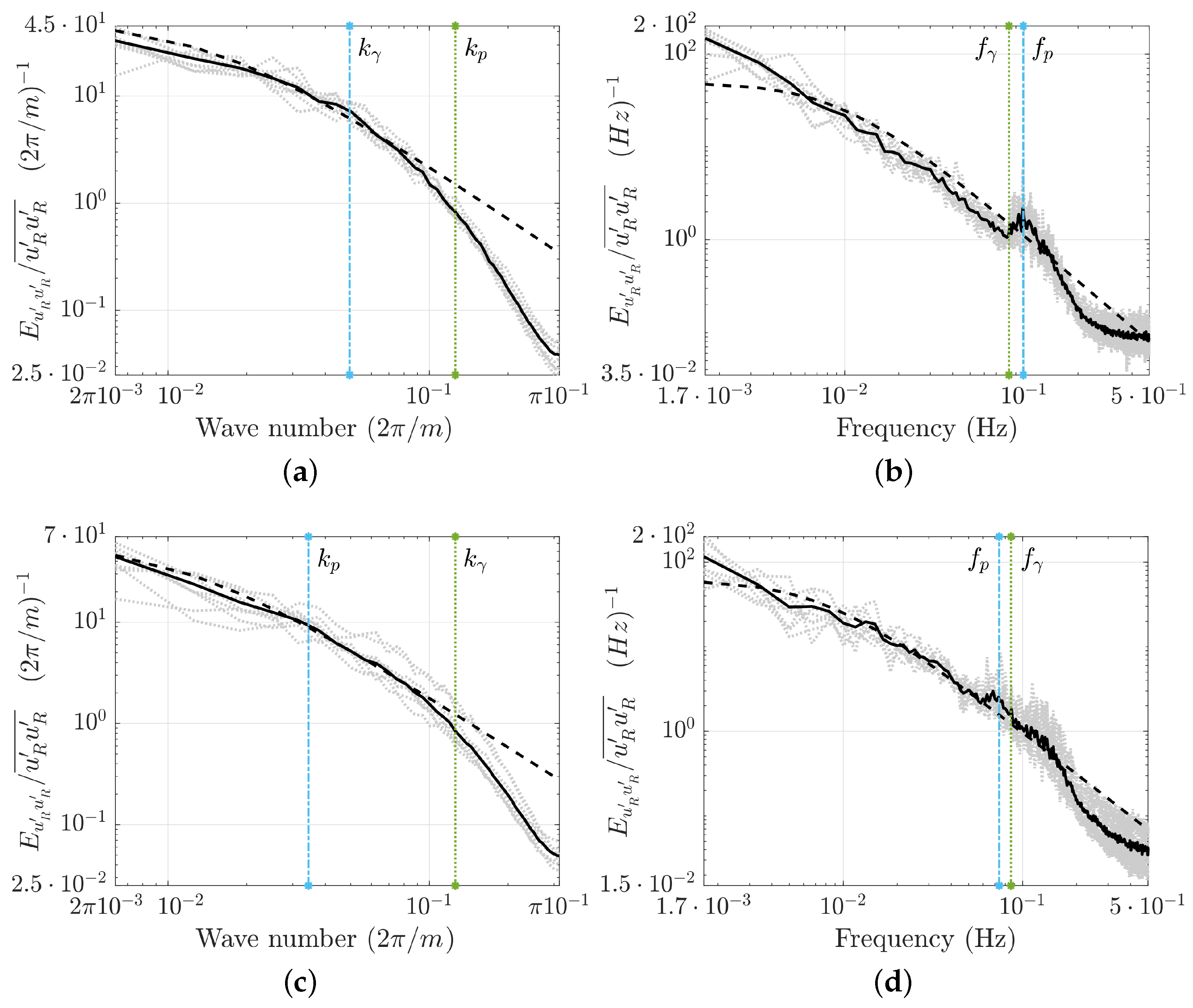
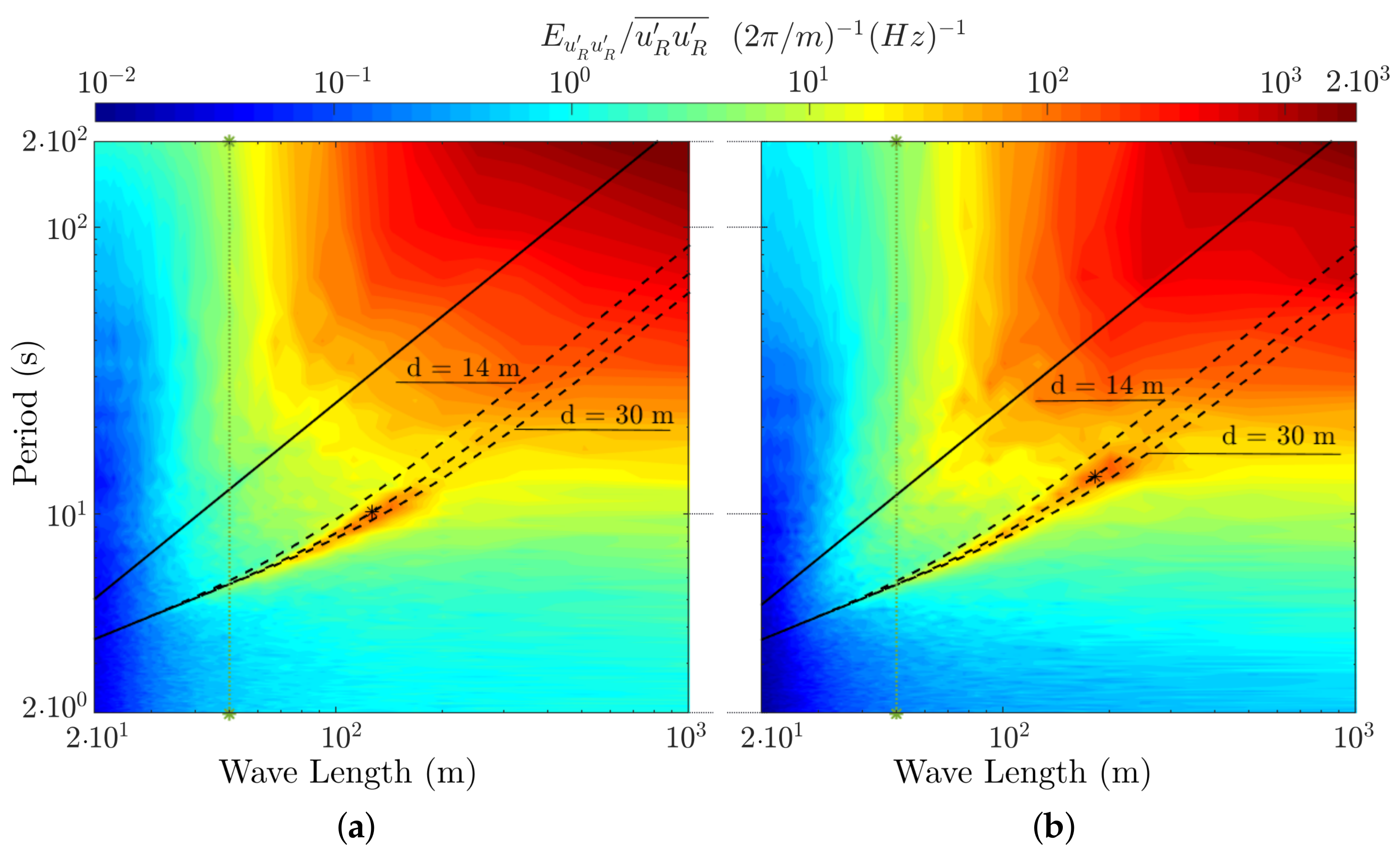

| Scan | Rot. Speed | Gate Spacing | First Gate | Last Gate | Acc. Time | Duration | |
|---|---|---|---|---|---|---|---|
| (°) | (°s) | (m) | (km) | (km) | (s) | (s) | |
| f-LOS 01 | 221.8 | 0 | 10 | 1.00 | 2.00 | 1.00 | 600 |
| f-LOS 02 | 221.8 | 0 | 10 | 0.75 | 1.75 | 0.25 | 600 |
| PPI | [154–199] | 3 | 25 | 0.50 | 1.75 | 1.00 | 16 |
| Case ID | Day | Start Time | WD | TI | |||
|---|---|---|---|---|---|---|---|
| (UTC) | (m s) | (°) | (%) | (°C) | (Stability) | ||
| 01 | 12 November 2020 | 11:10:32 | 4.12 | 212 | 8.6 | 1.4 | 0.04 (Stable) |
| 02a | 4 November 2020 | 07:10:24 | 4.29 | 60 | 10.0 | −6.2 | −0.17 (Unstable) |
| 02b | 4 November 2020 | 19:41:19 | 5.31 | 51 | 13.7 | −4.6 | −0.09 (Unstable) |
| 02c | 5 November 2020 | 04:44:30 | 6.93 | 56 | 12.1 | −7.2 | −0.08 (Unstable) |
| Case ID | WA | |||||||
|---|---|---|---|---|---|---|---|---|
| (m) | (s) | (m) | (m s) | (m s) | (°) | (°) | ||
| 01 | 3.0 | 1.3 | 10.1 | 127 | 12.5 | 9.4 | 241 | 26 |
| 02a | −3.1 | 1.0 | 13.5 | 181 | 13.5 | 11.4 | 247 | 30 |
| 02b | −2.5 | 0.7 | 13.2 | 177 | 13.4 | 11.3 | 249 | 46 |
| 02c | −1.9 | 0.6 | 12.5 | 166 | 13.3 | 11.0 | 219 | 71 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Paskin, L.; Conan, B.; Perignon, Y.; Aubrun, S. Evidence of Ocean Waves Signature in the Space–Time Turbulent Spectra of the Lower Marine Atmosphere Measured by a Scanning LiDAR. Remote Sens. 2022, 14, 3007. https://doi.org/10.3390/rs14133007
Paskin L, Conan B, Perignon Y, Aubrun S. Evidence of Ocean Waves Signature in the Space–Time Turbulent Spectra of the Lower Marine Atmosphere Measured by a Scanning LiDAR. Remote Sensing. 2022; 14(13):3007. https://doi.org/10.3390/rs14133007
Chicago/Turabian StylePaskin, Liad, Boris Conan, Yves Perignon, and Sandrine Aubrun. 2022. "Evidence of Ocean Waves Signature in the Space–Time Turbulent Spectra of the Lower Marine Atmosphere Measured by a Scanning LiDAR" Remote Sensing 14, no. 13: 3007. https://doi.org/10.3390/rs14133007
APA StylePaskin, L., Conan, B., Perignon, Y., & Aubrun, S. (2022). Evidence of Ocean Waves Signature in the Space–Time Turbulent Spectra of the Lower Marine Atmosphere Measured by a Scanning LiDAR. Remote Sensing, 14(13), 3007. https://doi.org/10.3390/rs14133007






