Abstract
Globally, estimating crop acreage and yield is one of the most critical issues that policy and decision makers need for assessing annual crop productivity and food supply. Nowadays, satellite remote sensing and geographic information system (GIS) can enable the estimation of these crop production parameters over large geographic areas. The present work aims to estimate the wheat (Triticum aestivum) acreage and yield of Maharajganj, Uttar Pradesh, India, using satellite-based data products and the Carnegie-Ames-Stanford Approach (CASA) model. Uttar Pradesh is the largest wheat-producing state in India, and this district is well known for its quality organic wheat. India is the leader in wheat grain export, and, hence, its monitoring of growth and yield is one of the top economic priorities of the country. For the calculation of wheat acreage, we performed supervised classification using the Random Forest (RF) and Support Vector Machine classifiers and compared their classification accuracy based on ground-truthing. We found that RF performed a significantly accurate acreage assessment (kappa coefficient 0.84) compared to SVM (0.68). The CASA model was then used to calculate the winter crop (Rabi, winter-sown, and summer harvested) wheat net primary productivity (NPP) in the study area for the 2020–2021 growth season using the RF-based acreage product. The model used for wheat NPP-yield conversion (CASA) showed 3100.27 to 5000.44 kg/ha over 148,866 ha of the total wheat area. The results showed that in the 2020–2021 growing season, all the districts of Uttar Pradesh had similar wheat growth trends. A total of 30 observational data points were used to verify the CASA model-based estimates of wheat yield. Field-based verification shows that the estimated yield correlates well with the observed yield (R2 = 0.554, RMSE = 3.36 Q/ha, MAE −0.56 t ha−1, and MRE = −4.61%). Such an accuracy for assessing regional wheat yield can prove to be one of the promising methods for calculating the whole region’s agricultural yield. The study concludes that RF classifier-based yield estimation has shown more accurate results and can meet the requirements of a regional-scale wheat grain yield estimation and, thus, can prove highly beneficial in policy and decision making.
1. Introduction
Accurate and real-time estimates of agricultural production at local, regional, and global scales are crucial for agricultural strategy formation and decision making worldwide [1,2]. Field surveys are a traditional method of collecting this information, but due to technological advances, the use of a combination of crop modeling and satellite image analysis appears to be one of the best strategies for yield estimation over large areas [3]. Since the 1960s, crop simulation models have become more complex and potentially more valuable, particularly after the green revolution [4]. When the research aim is precise and accurate, such as crop water usage, many simple statistical models, such as SSM (Simple Simulation Model), may perform well or even outperform more complicated models in calculating the agricultural production indices [5,6]. However, such models are inadequate in compensating for the direct influence of abiotic stresses on the growth of plants and have limitations in using lesser data for understanding the overall processes associated with growth and development [7,8]. More complex models, on the other hand, can be used to forecast crop development and growth regularly throughout the crop’s entire life cycle [9]. These models take into account various elements that influence crop growth and development, including plant-accessible abiotic factors such as water, temperature, wind, and biotic factors such as genetics, pest infestations, and management decisions [10]. The ability of these models to represent soil–environment–plant interactions is their strength as research tools. However, their initialization typically necessitates a series of biological and pedological characteristics that are difficult to obtain [11]. Hence, both simpler and more complex models have significant drawbacks, especially when assessing yields on a regional basis, and while choosing the best technique, it is always within the purview of the research objectives and the data availability that the decision is based [12].
Recently, an integrated method based on optical remotely sensed data has been developed to address these issues. Throughout the world, remote sensing data is employed as a source of knowledge for model driving, delivering spatially explicit, regularly acquired model parameter estimations [13,14]. The empirical correlations among the dry biomass produced by different crops and ratios of visible and near-infrared bands are used in contemporary crop yield estimation techniques based on data from satellites [15]. In this regard, the normalized difference vegetation index (NDVI) is the most widely used parameter in such methods [16]. Although this method is basically straightforward, the linkages discovered are only of local importance and cannot be simply expanded to other locations. Integrating remote sensing data with crop simulation models can explain the physiological and biological systems that drive crop growth and development and is one viable option for overcoming this difficulty and making yield estimating methods more robust and deliverables-based [17]. Raza and Mahmood (2018) assessed the Net primary production (NPP) of the rice in Zoige Plateau, China, using the CASA model. Using a hierarchy model and real-time field observations, they were able to achieve good estimates of yield. They concluded such integrated methods are useful to agronomists for precise estimates of NPP [18]. Li et al. (2020) used remote sensing and GIS for wheat yield estimations using the hierarchical linear modeling (HLM) algorithm by integrating meteorological and hyperspectral data. Using HLM, they concluded such methods could improve yield and grain protein content estimations at interannual scales [19].
The present study has been carried out in Uttar Pradesh, India. Agriculture in India plays a strategic role because the sector is the cornerstone of the country’s economy [20]. Approximately 19.9% of the GDP of India is based on agriculture, which employs approximately half of the country’s labor force [21]. Wheat is mainly a winter crop (Rabi season crop), a vital food grain, and in Eastern India, the staple food is wheat-based. Thus, most foods are based on wheat flour, and its assessment is therefore very significant to monitor [22,23,24]. Uttar Pradesh is India’s major wheat-growing state and contributes 32% of the country’s wheat production from just 7.34% of the country’s total geographical area. Economic policies related to agriculture and prices of yield are affected by the accuracy and speed of crop yield estimates [25,26]. The crop yield is estimated to play an essential role in economic development. With precise crop yield estimations, decision makers can decide whether production conditions exceed or fall below and, hence, can make timely export and import decisions [27]. Due to population growth, the demand for planning at micro-levels is increasing, especially the need for ensuring crops, which increases the demand for field-level production estimates [28].
The calculation of the yield using yield estimation models such as the Carnegie-Ames-Stanford Approach (CASA) depends on the precise estimations of the acreage [29]. In order to calculate precise yield, this study first compares wheat acreage area evaluated from two machine learning (ML) image classifier algorithms, the random forest (RF) and support vector machine (SVM), two of the most used techniques to calculate acreage worldwide [30,31]. After comparison, one of the accurate models is then used to calculate the wheat yield using the Carnegie-Ames-Stanford Approach (CASA) model. Such an integrated approach is the first of its type used in India. As discussed above, in India, the precise assessment of the wheat yield is critical, as it is the second staple crop of the country (between 2018 and 2022, an average of 101,232 (1000 MT) of wheat was consumed every year in India). Because of this significance, supported by the fact that India’s water stress scenario and climate change implications are worsening, the integrated wheat acreage and yield assessment study performed in this research is of great importance [32,33].
2. Study Area
Uttar Pradesh is the largest wheat-producing state in India. For the present study, we selected the Maharajganj district in Uttar Pradesh which lies between 26°53′20″ and 27°28′37″N latitude and 03°07′03″ and 83°56′30″E longitude as a case study. Given that it was impossible to perform ground-truthing for the accuracy assessment of the yield calculations for the entire state of UP in one growing season, only a single district was chosen for this study. Moreover, the fact that no such work has been conducted in this district before, and the wheat production in this district is considered completely organic were the reasons this district was selected for this research. The total area of the district is 2934.1 sq. km. Nepal is bounded by it in the north, Gorakhpur in the south, Siddhartha Nagar in the west, and Deoria in the north (Figure 1). The district is part of the Central Gangetic Plain and is under the Quaternary Alluvial Layer from the Pleistocene. The average rainfall in this district is 1327.7 mm. Climate is humid to semi-humid and is affected by the presence of the regional Tarai marshes. About 87% of the rainfall takes place between June and September. January is the coldest, with a daily maximum temperature (Tmax) of 23 °C and an average daily minimum temperature (Tmin) of 9.9 °C. At the same time, May is the hottest, with a mean daily (Tmax) of 39 °C and a mean daily (Tmin) of 25.9 °C. The highest mean monthly temperature (Tmean) is 31.9 °C, and the lowest monthly (Tmin) is 19.8 °C. During, and after monsoons, the relative humidity (Rh) is high and declines with approaching winters. The monthly mean Rh in the morning is 69%, and the monthly mean Rh in the evening is 53%. The mean wind speed is 4.1 km/h, whereas 1422.7 mm is the evapotranspiration. The fertile alluvial soils in the region are of two types, old and young alluvial soils. High lands occupy the older alluvium, whereas the younger alluvium is found along the marginal tracts of River Gandak.
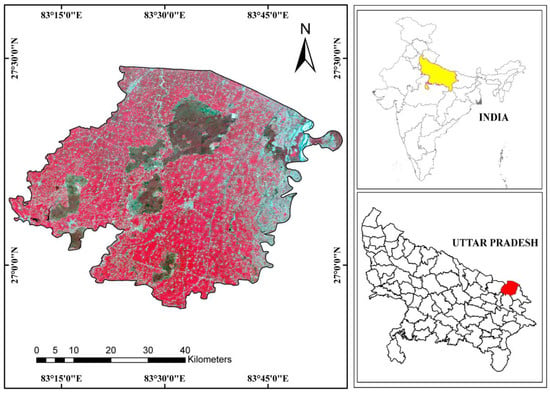
Figure 1.
Location of the study area. The upper right inset is the union of India, showing the state of Uttar Pradesh in yellow. In the lower right inset are the districts of UP, with the red color depicting the study area, Maharajganj. The left inset is the Sentinel-2A image of the study area. The map coordinates are in the UTM coordinate system and WGS 84 North datum.
3. Materials and Methods
3.1. Datasets
We used Sentinel 2A imagery (Bands 2, 3, 4, and 8, each 10 m spatial resolution, dated 21 May 2021) for calculating the winter crop (Rabi, winter-sown, and summer harvested) wheat acreage. The images were corrected for atmospheric corrections and preprocessed into Orth photo (TOA) and the bottom same orthodontic reflection (BOA) for removing the atmospheric errors and converted into 1C product corrected product. It was ascertained that the images used in the analysis must cover the stem extension (January), heading (February), flowering, and early ripening (March) stages of the wheat crop. The march image was used for the optimum acreage and yield calculations, whereas the earlier images were analyzed for fPAR variations. The mosaicking was performed on T44RQR and T44RQQ Tile of Sentinel-2A that covered the study area. We used the ERDAS Imagine 2014 software for all the image processing and GIS analysis [34]. Since the image of the study area was available in various scenes, we performed mosaicking within the ERDAS platform. For CASA, mean daily temperature, sunshine hours, daily precipitation, and average solar radiation were downloaded for the study area from the National Aeronautics and Space Administration’s (NASA) (https://giovanni.gsfc.nasa.gov/giovanni/, (accessed on 25 April 2021)) website [35]. The Government of India’s census department provided the state and district boundaries of Uttar Pradesh and Maharajganj District. For validating the acreage generated from SVM and RF, we conducted extensive ground-truthing and performed the accuracy assessment using the user’s accuracy, producer’s accuracy, and the kappa coefficient [36,37], and took about 120 ground-truthing points (randomly distributed, covering almost whole of the district) for this purpose. We used Garmin GPS explorer to record the GPS locations [38] (Figure 2). Daily average temperature, sunshine data, daily rainfall, and average solar energy data used here were downloaded from the NASA Power Data Access Viewer (https://power.larc.nasa.gov/data-access-viewer/ (accessed on 25 April 2021)). The processing included monthly averaging of temperature, solar radiation data, and precipitation data.
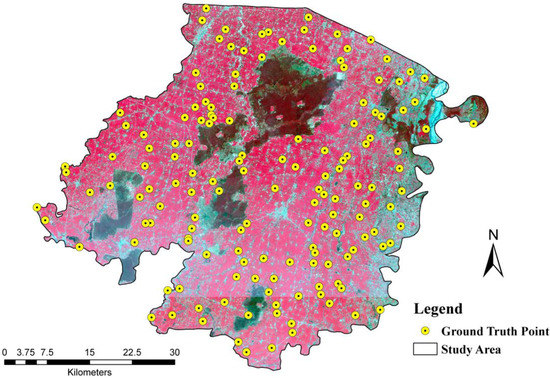
Figure 2.
Distribution of the ground-truthing points for validating the acreage results from SVM and RF classifiers. Random well-distributed field verification sampling of acreage accuracy assessment was performed in this study.
3.2. Methods
In this section, we first discuss the methods related to the calculation of acreage, followed by the estimation of yield. The overall methodology is shown in Figure 3.
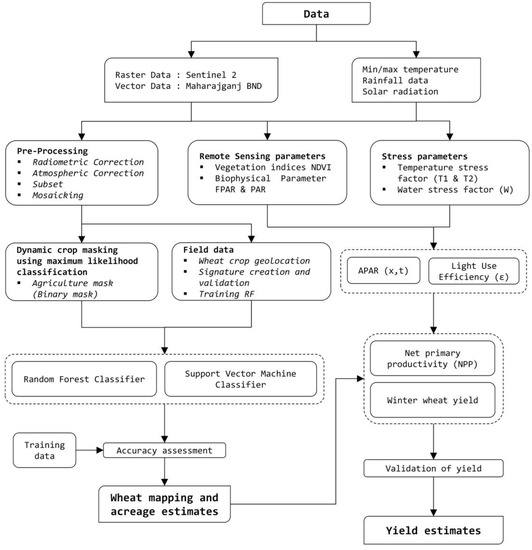
Figure 3.
The overall methodology employed in the present work. NDVI Normalized Difference Vegetation Index, FPAR Fraction Photosynthetically Active Radiation, PAR Photosynthetically Active Radiation, APAR Absorbed Photosynthetically Active Radiation, NPP Net Primary Productivity.
3.2.1. Acreage Estimation
Wheat crop forecasting comprises crop identification area estimation [39]. Crop identification and discernment are based on each crop’s detail with a matchless spectral signature. The maximum likelihood classification technique was first used to mask uncultivated areas, including sand, plantations, built-up forests, and water bodies [40], a technique called dynamic cropland masking. It results in a binary map that separates the annual target crop area from other areas [41]. The logic behind creating such a mask is based on the fact that yearly arable land is well-defined as an area of land that can be planted and harvested at least 0.25 hectares within one year after the date of sowing [42]; there are some small crops also sown in the vicinity, such as mustard, that were required to be separated from the analysis. Therefore, masking was important. Training signatures of wheat were selected based on the visual image interpretation, augmented with statistical training class estimates in the form of mean, variance, and covariance matrix, the data product that was masked in the previous step [43]. Training samples were used for classifying the wheat class in the masked raster based on two techniques, SVM and RF [44]. ERDAS Imagine was used for the SVM and RF supervised classification.
Support vector machine (SVM) is a supervised non-parametric statistical learning approach that was previously designed for binary classification [45]. The SVM is based on the hypothesis that the training set is linearly unique. The SVM detects the optimal line, which splits up the training set without errors and maximizes the gap between the objects of each class and the optima line. SVM uses only those training samples that designate class boundaries (support vectors). The SVM essentially involves parameterizing a Support Vector Classifier (SVC) based totally on the reference information and the classification of the image data.
On the other hand, the Random Forest (RF) algorithm is a set of decision tree structure classifiers, each consisting of a random subset of the training data and classification variables [46,47]. It is swift, resistant to overfitting, and can include as many decision trees as the user requires. The user must specify two parameters to configure it [48]. These parameters are m and N, which are the number of variables and the number of growing trees used to split each node. First, bootstrap N examples were extracted from 2/3 of the training dataset [49]. The left-behind third training data, also called out-of-bag (OOB), were used to assess the prediction error. A tree was then developed, uncut to each boot example so that the predictors of each random node were selected as a subclass of the predictor variables, and the most appropriate among these was selected. Determining the variable numbers of an adequately low association with good predictive power is critical. Assessing the variable numbers (m) equivalent to the square root of M (the number of total variables) gives almost perfect outcomes. RF is based on the Classification and Regression Tree (CART) algorithm to generate trees [49]. The segmentation in every node is performed as per the condition known as the GINI index within the CART algorithm. In this study, an accuracy assessment was carried out to assess the performance of SVM and RF classification. For this purpose, we took 120 ground truth points to evaluate the SVM and RF product’s user accuracy, producer accuracy, overall accuracy, and kappa coefficient [50,51,52].
The accuracy was assessed using the user’s accuracy, producer’s accuracy and the kappa coefficient. Kappa coefficient () is mathematically expressed as [53,54,55,56]:
where, r represents no. of rows in the error matrix; Xii represents no. of observations in row I and column I; Xi+ is the total of observations in row I; X+I is the total of observations in column I; N is the total number of observations included in the matrix.
3.2.2. Wheat Yield Estimation
This study used the updated CASA model to estimate the NPP from wheat and then estimate its yield. The CASA equations were structured within ArcGIS 10.1 (ESRI)using the ArcGIS model builder. The CASA model parameters were generated from remote sensing and weather data, and the following is its equation [57],
where NPP is the Net Primary Productivity, t is time, x number of pixels in the NPP (x, t) [g 100 m−2] at time t, and the distance (x, t) [1000 m−2] is at time t. APAR is the Absorbed Photosynthetically Active Radiation. The effective absorption, photosynthetically, of the radiation pixel x, and ε (x, t) is used for the light use efficiency of the pixel x time t.
NPP(x, t) = APAR(x, t) × ε (x, t)
Absorbed photosynthetically active energy for grasses mainly depends on Solar Radiation (SOL) and the fraction of Photosynthetically Active Radiation (fPAR). The calculation is as follows [58],
where, SOL (x, t) [1000 sqm] is the sum of solar energy of pixel x at T. fPAR (x, t) is the part of all photosynthetically active energy, and the proportion of element 1/2 is the proportion of effective solar radiation used by vegetation to the total solar energy.
For wheat, fPAR is dependent on a growing period of time. The normalized difference vegetation index (NDVI) indicates flora and growth conditions and the Linear in fPAR. In this study, the NDVI max and min fPAR is calculated by the HJ-1 A/B image, and fPAR (x, t) is calculated as follows [59],
where, fPARmax, 0.950 and fPAR min, 0.001 are the maximum and minimum constant values of fPAR.
The constants maximum and minimum NDVI are the NDVI maximum and minimum for wheat. After assembling a relative analysis, the lower-end 95% value and lower-end 5% value of the wheat NDVI were used. The present study analyses the complete growth season of wheat, rendered into two Sentinel-2 satellite data scenes. Thus, Sentinel-2 images for every month with the NDVIs for wheat were used. The light utilization efficiency (ε) is calculated using following equation [60],
where Tε₁ (x, t) and Tε₂ (x, t) are temperature (T) stress parameters of the light use efficiency for pixel x at time t, Wε(x, t) is the water (W) stress parameter of the light use efficiency for pixel x at time t, ε∗ [g C MJ−1] is the maximum light use efficiency under ideal conditions. Ε is the CASA model’s significant factor, called the maximum efficiency [61]. It directly affects the calculated value for the efficiency of light usage by the plants. The value of this parameter, as deduced by field et al. (1995), is 0.389 g C MJ−1 for global ε of vegetation, independent of geography and vegetation types [62]. Different vegetation types have dissimilar biological and functional characteristics, so their ε is different. Since the present study focuses on wheat, for the environmental settings of the study area, ε was fixed for the wheat between 0.42 and 2.93 g C MJ−1 using literature-based parameter calculations. The mean of this range, i.e., ε∗ of 1.7 g C MJ−1, was used in the present study as a factor of the CASA model [63]. The yield of wheat is the wheat harvest and is finally calculated using the equation below [64],
ε(x, t) = Tε₁ (x, t) × Tε₂ (x, t) × Wε(x, t) × ε
4. Results and Discussion
In this section, first the results of acreage calculation are discussed using SVM and RF methods, followed by the estimation of the wheat yield.
4.1. Wheat Acreage Estimation
Before SVM and RF for classifying wheat areas, a cropland area was extracted from the study area for all the stages of the wheat. Figure 4a is the sentinel image of the study for the month of March (flowering and early ripening stage). Figure 4b is binary map showing agriculture-only classification products, with the symbology yellow depicting agriculture for the same date. SVM and RF were then applied on the dynamic cropland mask (binary map).
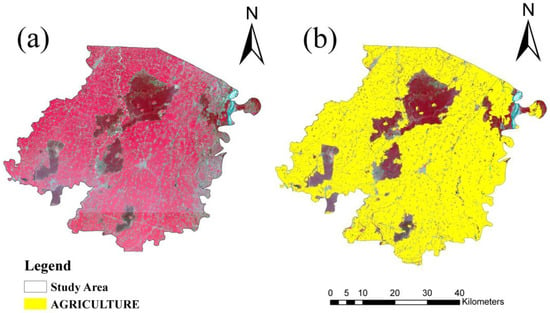
Figure 4.
(a) Sentinel 2A cropped image of the study area that was masked to extract the agricultural land. The red tone is the tone of vegetation observed in false color composite (FCC) (b) Agriculture only classification product with the symbology yellow depicting agriculture (binary map extracted using the maximum likelihood classifier).
Using SVM, it was observed that the total acreage of wheat in 2020-2021 was 148,866 Ha. The wheat crop map shows the classified output of only wheat plots in the Maharajganj district’s four Talukas (Figure 5). Here, the acreage estimates show that the highest acreage can be seen in Nuchal Taluka (62,672 Ha), and the lowest acreage observed in Maharajganj Taluka is 21,673 ha for 2020–2021 (Table 1). About 120 ground truth points were taken, resulting in an overall accuracy of 85.58%. The wheat acreage map accurately depicts what was on the field in 2020–2021. Producer’s accuracy and user’s accuracy for wheat crop using the support vector classifier were 91.04% and 87.14%, respectively. The Kappa value for this assessment was calculated to be 0.68, indicating that there is 68 percent greater agreement than would be expected by chance alone (Figure 5).

Figure 5.
Wheat acreage map of Maharajganj district using support vector machine (SVM) supervised classification for the flowering and early ripening stage (March).

Table 1.
Taluka wise comparative acreage estimates of wheat in 2020–2021 using SVM and RF.
Using RF, the total derived acreage of wheat 2020–2021 was 146,499 Ha. Thus, the wheat crop map shows the classified output of only wheat plots in the Maharajganj district’s selected four Talukas, with the total acreage of Taluka-wise estimates presented in Table 1. About 120 ground truth points were taken, resulting in an overall accuracy of 93.20 percent using RF. This implies that the wheat crop acreage map, utilizing a random forest classifier, correlates to what was actually on the ground in 2020–2021, about 93.20 times out of 100. The producer’s accuracy and user’s accuracy for wheat crop using RF were 95.65% and 94.29%, respectively. The kappa estimates for this evaluation were obtained at 0.84, indicating that there is an 84 percent greater agreement than would be expected by chance alone (Figure 6, Table 1).
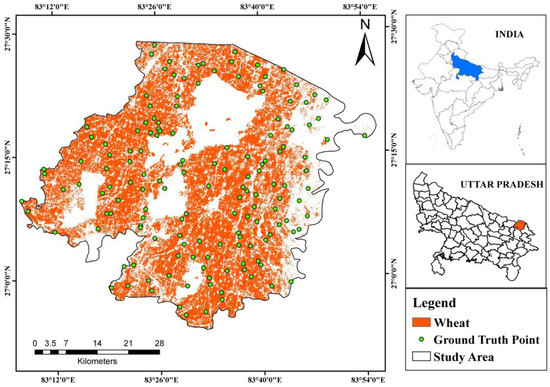
Figure 6.
Wheat acreage map of Maharajganj district using Random Forest supervised classification algorithm for the flowering and early ripening stage (March).
The analysis and comparison of the two classification techniques show that the highest accuracy for the wheat acreage estimation of the Maharajganj district of Uttar Pradesh was obtained using the RF classifier in terms of producers, users, and overall accuracy, as well as Kappa values (Table 2).

Table 2.
Error matrix-based performance analysis of SVM and RF classifiers.
Based on the results obtained and accuracy assessment carried out for Wheat Crop obtained using different prominent classifiers, Table 3 below shows the performance evaluation.

Table 3.
Relative Deviation of Wheat Yield.
4.2. Wheat Yield Estimation Using the CASA Model
Although the study analyses the spread of wheat yield during the whole growing season, the fPAR, NPP, and the light-use efficiency parameters of the study area had to be parametrized for improved CASA model results [64]. The calculated NDVI maximum and minimum values for fPAR evaluation is an essential step beforehand. The NDVI min and NDVI max values for FPAR calculated are −0.0126 and 0.839. Figure 7 shows the results for fPAR. The fPAR calculated for January is 0.72 and is less than compared to February (0.71) and March (0.78). In January, the fPAR for wheat continued to rise due to photosynthesis and exceeded 0.72. The greatest average fPAR of 0.78 was seen in February 2021, while the lowest mean fPAR was 0.71 in January 2021. This is due to an increase in wheat photosynthetic activity and the corresponding increase in growth, which supports the geographical importance of the study area for the suitability of wheat growth [65].
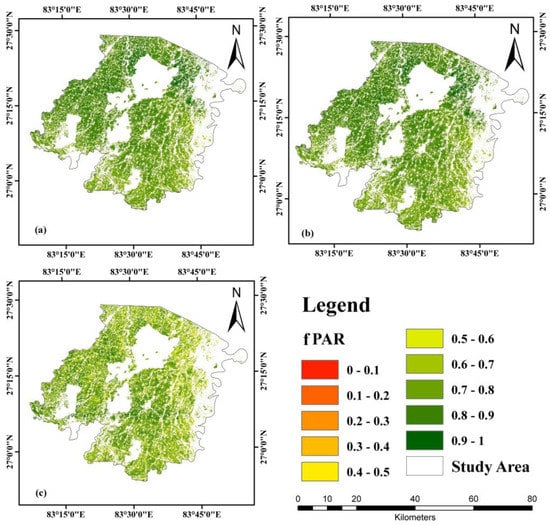
Figure 7.
Spatial distribution of wheat fPAR (fractionally Photosynthetically Active Radiation) for (a) January, (b) February, and (c) March.
In 2020–2021, wheat light use efficiency in the whole study area remained comparatively constant every month. However, minor alterations are due to the variability in atmospheric and climatic factors. Hence, the mean monthly efficiency of light use was 0.2806 g C MJ−1. Geoenvironmental conditions (i.e., temperature, sunshine, and precipitation) in January helped grow wheat; hence, the ε in January had an average range of 0.2806 g CMJ−1. Again, this reflects favorable environmental conditions for growing wheat in Maharajganj from November to March, helping proper development and growth [66].
Figure 8 shows the distribution of wheat average NPP for the total growth season, obtained by adding the NPP of each month. Wheat gradually moves towards the greening and erecting stages. The total NPP distribution of wheat in the Maharajganj district was calculated to be between 26.21 and 43.47 g C m2, with a mean NPP of 37.81 g C m2. The wheat growth improved unceasingly, and dry matter quality increased rapidly.
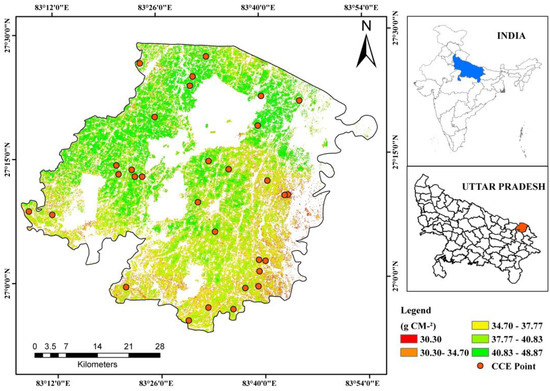
Figure 8.
Spatial distribution of wheat NPP averaged for the 2020–2021 growing season. Randomly selected well-distributed crop-cutting experiment (CCE) points selected for validation are also shown.
We estimated the wheat economic yield using the derived NPP. The updated CASA model used to calculate the NPP of the wheat at Maharajganj, Uttar Pradesh, for the 2020–2021 growth season provided insightful results. The results of the NPP-yield conversion model utilized to convert the NPP into the fiscal yield were 31.27 to 50.44 q/ha, over 148,866 ha of the total study area. Figure 9 shows the distribution of the calculated wheat yield. The results of the complete study area were about fifty percent for the range less than 38.98 Q/ha and about the other 50% for the range 38.98–55.44 Q/ha.
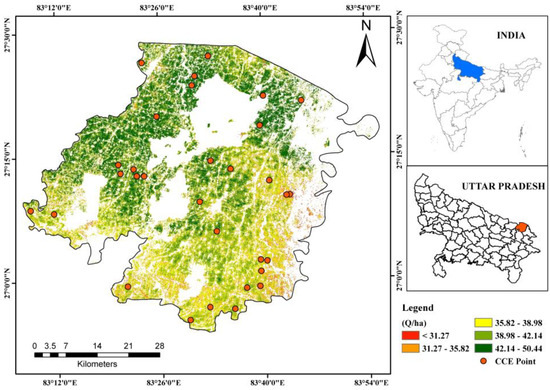
Figure 9.
Spatial distribution of estimated Wheat yield for the 2020–2021 growing season. Randomly selected well-distributed crop cutting experiment points (CCE) for the validation are also shown.
The results showed that in the 2020–2021 growing season, all the districts of Uttar Pradesh had similar wheat growth trends. For assessing the accuracy of the yield estimates from the CASA model and the NPP-yield conversions, we used 30 CCE (crop cutting experiment) data points to verify the results. Each pixel around the CCE points was averaged with the eight corresponding pixels to attain the projected yield for the specified CCE point [67]. Figure 10 shows the assessed yield as a derivative of the estimated yield and the coefficient of determination R2 = 0.5544, and the root mean square error (RMSE) was 3.361 Q/ha (Table 3). This analysis revealed a mean absolute error of −0.56 t ha−1 and a mean relative error of −4.61%, showing a promising accuracy for assessing regional wheat yield using this method. Moreover, the Pearson’s correlation coefficient observed between the two is 0.74, which depicts a very good correlation between the modeled and observed wheat yield. In 2020–2021, the estimated yield of wheat in India was approximately 35 quintals per hectare. This is in close agreement with the results obtained from the current study.
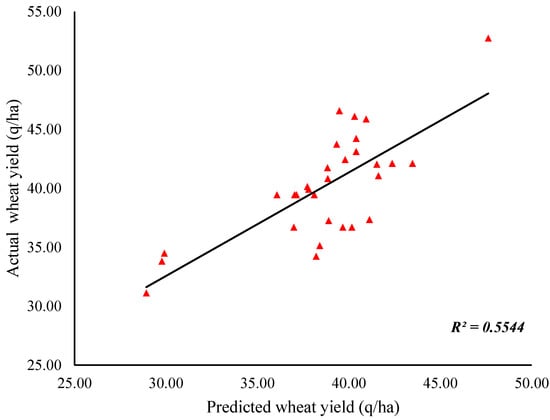
Figure 10.
Predicted versus observed wheat yield for the entire study area for the 2020–2021 growing season. The Pearson’s correlation coefficient between the two is 0.74, depicting a good correlation between the modeled and observed wheat yield.
The use of integrated wheat acreage estimations, the net primary productivity and yield have been conducted by various researchers across the globe. This method may be used to estimate grain yield on a large scale, evaluate food security on a regional level, and make some valuable recommendations for the government to improve food security. In this context, Shi et al. (2022) used the CASA model to calculate annual net primary production (NPP) and anticipate annual grain yields in Egypt, using the NPP-yield conversion procedure. They classified arable terrain that grows grains using the support vector technique. The CASA model was used to compute the yearly net primary production (NPP) using the classified results, weather parameters, and NDVI data. Then, the NPP-yield conversion formula was utilized to forecast the annual grain yield using the NPP-yield conversion formula. The evaluation results suggest that Egypt’s food security is deteriorating, supply and quality security are highly variable and economic and resource protection are reasonably steady [68]. Furthermore, for designing agricultural product import and export plans, regulating grain markets, and altering the planting structure, timely and accurate monitoring and reviews of regional grain crop production are more important, and have been one of this study’s objectives. Similar to this study, Wang et al. (2019) used an enhanced Carnegie–Ames–Stanford Approach (CASA) model combined with time-series satellite remote sensing imagery to predict winter wheat production. The modified CASA model was used to estimate the Net Primary Production (NPP) of winter wheat using HJ-1A/B satellite data. MOD17A2H data products were interpolated to determine the spatial patterns of winter wheat NPP during the whole growing season of winter wheat. The method for estimating winter wheat yield with remote sensing photos was validated by comparing the results to ground-measured yield. This study substantiates the findings of this study that this method can be used in the field and can serve as a benchmark for a variety of crop yield estimation algorithms worldwide. Some studies have shown that it is possible to simulate alpine grassland NPP using satellite remote sensing data rather than ground measurements [69]. Wu et al. (2022) have shown that remote sensing data can be used to provide real-time information at a regional scale, thereby substituting ground observation data as the driving force behind the CASA model. They used DEM data generated from the Moderate Resolution Imaging Spectroradiometer satellite sensor to improve the CASA model to model the NPP of alpine grasslands in China’s Qinghai Lake Basin, northeastern Qinghai-Tibetan Plateau. In July 2020, the NPP simulated using RS data-driven CASA produces values similar to those published and comparable to the observed NPP [70]. Furthermore, net primary productivity (NPP) is an important component in terrestrial ecosystem carbon cycles. Quantitatively calculating and monitoring NPP fluctuations have thus become critical components of understanding the carbon cycle in terrestrial ecosystems. Human impact, such as urbanization, has a considerable impact on NPP and puts more demand on a region’s natural resources. Wu et al. (2022) conducted a study in Hubei Province, China to study the spatiotemporal distribution of NPP from 2001 to 2012 and its associated connection with urbanization. The spatial variability and fluctuation of population and gross domestic product (GDP) were simulated using a new method that included elevation-adjusted human settlement index and nighttime lights data so as to deduce the degree of urbanization. The main findings of their research revealed that high NPP locations were found in highlands with extensive woods. Low NPP locations were mostly found in metropolitan areas and values had been steadily declining. Such studies could be used as a starting point for future research on the interaction of the natural environment and socio-economic processes in the context of worldwide fast urbanization [71].
To predict winter wheat yield using time-series satellite remote sensing data, our study improves the CASA model and integrates it with the NPP. When the estimated findings are compared to the ground-measured yield data, it is clear that the prediction accuracy meets the criteria for forecasting regional winter wheat in comparison to other researchers’ studies. It is still an important goal to increase the accuracy of agricultural production estimates. The CASA model is straightforward and practical to use, with only a few parameters to setup and calibrate. However, while the CASA model can only simulate net primary productivity (NPP), we must construct an HI to convert NPP to crop yield. However, the transition from photosynthetic absorption to biomass accumulation and final crop yields involves many complex physiological mechanisms that an HI cannot capture through a simple formula. It is thus a critical parameter in the model and is given a constant value in the current study based on earlier research. The other critical parameter is the ε∗, which was also given a constant value based on literature. Variable analysis should be performed in addition to appropriate testing, which could be the subject of future research, as various geoenvironmental settings influence these two parameters. Another issue is data source optimization. Crop yield estimation is influenced by the quality and quantity of input data. Such information is frequently unavailable at sufficiently fine geographic scales and is derived from a soil classification map with a lower spatial and temporal resolution. When paired with the Monteith model, an optimization model to correct missing data can enhance the validity of crop yield estimation. Moreover, our study examined a maximum of 30 CCEs of wheat yield data. The use of 30 CCEs in this study area achieved an ideal outcome, but if the study is regional, more research is needed to test the correctness and validation of the proposed models.
5. Conclusions
This study involved wheat acreage estimation using different machine-learning classification algorithms and the subsequent calculation of wheat yield using the CASA model. This study again justifies Sentinel-2 remote sensing data’s utility for assessing acreage estimation, as the results corroborated well with the observational data. The wheat crop area, analyzed using SVM and RF classifiers, is 148,866 Ha and 146,499 Ha, respectively. Of the two methods tested for classifying the Sentinel-2 data, RF had a higher mapping accuracy. The Sentinel 2A satellite data-based acreage data product used as input in the CASA model was utilized to assess the net primary production (NPP) during the 2020–2021 wheat growing season. The NPP-yield conversion model was thereafter utilized to calculate winter wheat yield at a regional scale. R2 = 0.554 was estimated between the observed and calculated wheat yield, with RMSE equal to 3.36 Q/ha and a relative deviation error of −4.61%. These results showed that the updated CASA model integrated with the model for NPP-yield conversion could provide reliable regional-scale calculations of wheat yield from satellite-based remote sensing and biophysical modeling approaches.
Author Contributions
Conceptualization, G.M., S.K. and S.K.S.; methodology, G.M., S.K., S.K.S., A.A., B.A.J. and M.F.; software, G.M., A.A., S.K. and M.F.; validation, G.M., S.K., A.A., A.R.; formal analysis, S.K.S., G.M., A.A., A.R., S.K., P.K. and N.S.; investigation, G.M., S.K., A.A., A.R. and M.F.; resources, B.A.J. and P.K.; data curation, G.M., S.K., A.A. and M.F.; writing—original draft preparation, G.M., S.K. and A.A; writing—review and editing, G.M.; visualization, G.M., A.A., S.K. and M.F.; supervision, P.K. and B.A.J.; project administration, G.M. and S.K.S.; funding acquisition, P.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data is available on request to the corresponding author.
Acknowledgments
The authors are thankful to the three anonymous reviewers whose critical reviews in two rounds of review have improved the quality of this manuscript. The first author, G.M. is thankful to the Department of Science and Technology, Government of India (DST-GoI) for providing the Fellowship under the Scheme for Young Scientists and Technology (SYST-SEED) [Grant no. SP/YO/2019/1362(G) & (C)].
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bolten, J.D.; Crow, W.T.; Zhan, X.; Jackson, T.J.; Reynolds, C.A. Evaluating the utility of remotely sensed soil moisture retrievals for operational agricultural drought monitoring. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2009, 3, 57–66. [Google Scholar] [CrossRef] [Green Version]
- Chlingaryan, A.; Sukkarieh, S.; Whelan, B. Machine learning approaches for crop yield prediction and nitrogen status estimation in precision agriculture: A review. Comput. Electron. Agric. 2018, 151, 61–69. [Google Scholar] [CrossRef]
- Mateo-Sanchis, A.; Piles, M.; Muñoz-Marí, J.; Adsuara, J.E.; Pérez-Suay, A.; Camps-Valls, G. Synergistic integration of optical and microwave satellite data for crop yield estimation. Remote Sens. Environ. 2019, 234, 111460. [Google Scholar] [CrossRef] [PubMed]
- Zeng, N.; Zhao, F.; Collatz, G.J.; Kalnay, E.; Salawitch, R.J.; West, T.O.; Guanter, L. Agricultural Green Revolution as a driver of increasing atmospheric CO2 seasonal amplitude. Nature 2014, 515, 394–397. [Google Scholar]
- Lobell, D.B.; Burke, M.B. On the use of statistical models to predict crop yield responses to climate change. Agric. For. Meteorol. 2010, 150, 1443–1452. [Google Scholar] [CrossRef]
- Roberts, M.J.; Braun, N.O.; Sinclair, T.R.; Lobell, D.B.; Schlenker, W. Comparing and combining process-based crop models and statistical models with some implications for climate change. Environ. Res. Lett. 2017, 12, 095010. [Google Scholar] [CrossRef]
- Stehfest, E.; Heistermann, M.; Priess, J.A.; Ojima, D.S.; Alcamo, J. Simulation of global crop production with the ecosystem model DayCent. Ecol. Model. 2007, 209, 203–219. [Google Scholar] [CrossRef]
- Lamichhane, J.R.; Debaeke, P.; Steinberg, C.; You, M.P.; Barbetti, M.J.; Aubertot, J.N. Abiotic and biotic factors affecting crop seed germination and seedling emergence: A conceptual framework. Plant Soil 2018, 432, 1–28. [Google Scholar] [CrossRef]
- Lawless, C.; Semenov, M.A. Assessing lead-time for predicting wheat growth using a crop simulation model. Agric. For. Meteorol. 2005, 135, 302–313. [Google Scholar] [CrossRef]
- Orcutt, D.M.; Nilsen, E.T. Physiology of Plants under Stress: Soil and Biotic Factors; John Wiley & Sons: Hoboken, NJ, USA, 2000; Volume 2. [Google Scholar]
- Rembold, F.; Atzberger, C.; Savin, I.; Rojas, O. Using low resolution satellite imagery for yield prediction and yield anomaly detection. Remote Sens. 2013, 5, 1704–1733. [Google Scholar] [CrossRef] [Green Version]
- Gower, S.T.; Kucharik, C.J.; Norman, J.M. Direct and indirect estimation of leaf area index, fAPAR, and net primary production of terrestrial ecosystems. Remote Sens. Environ. 1999, 70, 29–51. [Google Scholar] [CrossRef]
- Kumar, A.; Giri, R.K.; Taloor, A.K.; Singh, A.K. Rainfall trend, variability and changes over the state of Punjab, India 1981–2020: A geospatial approach. Remote Sens. Appl. Soc. Environ. 2021, 23, 100595. [Google Scholar] [CrossRef]
- Meraj, G.; Farooq, M.; Singh, S.K.; Islam, M.; Kanga, S. Modeling the sediment retention and ecosystem provisioning services in the Kashmir valley, India, Western Himalayas. Model. Earth Syst. Environ. 2021, 1–26. [Google Scholar] [CrossRef]
- Penuelas, J.; Filella, I. Visible and near-infrared reflectance techniques for diagnosing plant physiological status. Trends Plant Sci. 1998, 3, 151–156. [Google Scholar] [CrossRef]
- Singh, S.K.; Meraj, G.; Mondal, N.; Bera, A.; Verma, M.K.; Tomar, J.S.; Kanga, S. Assessment of seasonal vegetation dynamics over parts of thar desert using geospatial techniques. J. Res. ANGRAU 2021, 49, 105–109. [Google Scholar]
- Technow, F.; Messina, C.D.; Totir, L.R.; Cooper, M. Integrating crop growth models with whole genome prediction through approximate Bayesian computation. PLoS ONE 2015, 10, e0130855. [Google Scholar]
- Raza, S.M.; Mahmood, S.A. Estimation of net rice production through improved CASA model by addition of soil suitability constant (ħα). Sustainability 2018, 10, 1788. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; Taylor, J.; Yang, H.; Casa, R.; Jin, X.; Li, Z.; Song, X.; Yang, G. A hierarchical interannual wheat yield and grain protein prediction model using spectral vegetative indices and meteorological data. Field Crops Res. 2020, 248, 107711. [Google Scholar] [CrossRef]
- Ahlawat, A.; Bhat, A.; Gupta, V.; Sharma, M.; Sharma, S.; Rai, S.K.; Singh, S.P. Market Share and Promotional Approaches of Pesticide Companies for Vegetable Crops in Jammu District. Int. J. Soc. Sci. 2021, 10, 115–121. [Google Scholar] [CrossRef]
- Renwick, A.; Dynes, R.; Johnstone, P.; King, W.; Holt, L.; Penelope, J. Challenges and opportunities for land use transformation: Insights from the Central Plains Water scheme in New Zealand. Sustainability 2019, 11, 4912. [Google Scholar] [CrossRef] [Green Version]
- Eli-Chukwu, N.C. Applications of artificial intelligence in agriculture: A review. Eng. Technol. Appl. Sci. Res. 2019, 9, 4377–4383. [Google Scholar] [CrossRef]
- Saini, R.; Ghosh, S.K. Crop classification on single date sentinel-2 imagery using random forest and suppor vector machine. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2018, 42, 683–688. [Google Scholar] [CrossRef] [Green Version]
- Ge, G.; Shi, Z.; Zhu, Y.; Yang, X.; Hao, Y. Land use/cover classification in an arid desert-oasis mosaic landscape of China using remote sensed imagery: Performance assessment of four machine learning algorithms. Glob. Ecol. Conserv. 2020, 22, e00971. [Google Scholar] [CrossRef]
- Mehrotra, S. The cornerstone of a planning strategy for the 21st Century. In Planning in the 20th Century and Beyond: India’s Planning Commission and the NITI Aayog; Cambridge University Press: Cambridge, UK, 2020; p. 208. [Google Scholar]
- Asseng, S.; Ewert, F.; Rosenzweig, C.; Jones, J.W.; Hatfield, J.L.; Ruane, A.C.; Boote, K.J.; Thorburn, P.J.; Rötter, R.P.; Cammarano, D.; et al. Uncertainty in simulating wheat yields under climate change. Nat. Clim. Chang. 2013, 3, 827–832. [Google Scholar] [CrossRef] [Green Version]
- Meraj, G.; Singh, S.K.; Kanga, S.; Islam, M. Modeling on comparison of ecosystem services concepts, tools, methods and their ecological-economic implications: A review. Model. Earth Syst. Environ. 2022, 8, 15–34. [Google Scholar]
- Jain, H. Trade Liberalization, Economic Growth and Environmental Externalities: An Analysis of Indian Manufacturing Industries; Springer: Singapore, 2016. [Google Scholar]
- Patel, N.R.; Dadhwal, V.K.; Saha, S.K.; Garg, A.; Sharma, N. Evaluation of MODIS data potential to infer water stress for wheat NPP estimation. Trop. Ecol. 2010, 51, 93. [Google Scholar]
- Mangiameli, M.; Mussumeci, G.; Gagliano, A. Evaluation of the Urban Microclimate in Catania using Multispectral Remote Sensing and GIS Technology. Climate 2022, 10, 18. [Google Scholar] [CrossRef]
- Kiefer, M.T.; Andresen, J.A.; Doubler, D.; Pollyea, A. Development of a gridded reference evapotranspiration dataset for the Great Lakes region. J. Hydrol. Reg. Stud. 2019, 24, 100606. [Google Scholar] [CrossRef]
- Taloor, A.K.; Kumar, V.; Singh, V.K.; Singh, A.K.; Kale, R.V.; Sharma, R.; Khajuria, V.; Raina, G.; Kouser, B.; Chowdhary, N.H. Land use land cover dynamics using remote sensing and GIS Techniques in Western Doon Valley, Uttarakhand, India. In Geoecology of Landscape Dynamics; Springer: Singapore, 2020; pp. 37–51. [Google Scholar]
- Khan, A.; Govil, H.; Taloor, A.K.; Kumar, G. Identification of artificial groundwater recharge sites in parts of Yamuna River basin India based on Remote Sensing and Geographical Information System. Groundw. Sustain. Dev. 2020, 11, 100415. [Google Scholar] [CrossRef]
- Bera, A.; Taloor, A.K.; Meraj, G.; Kanga, S.; Singh, S.K.; Đurin, B.; Anand, S. Climate vulnerability and economic determinants: Linkages and risk reduction in Sagar Island, India; A geospatial approach. Quat. Sci. Adv. 2021, 4, 100038. [Google Scholar] [CrossRef]
- Qadir, A.; Mondal, P. Synergistic use of radar and optical satellite data for improved monsoon cropland mapping in India. Remote Sens. 2020, 12, 522. [Google Scholar] [CrossRef] [Green Version]
- Guptha, G.C.; Swain, S.; Al-Ansari, N.; Taloor, A.K.; Dayal, D. Assessing the role of SuDS in resilience enhancement of urban drainage system: A case study of Gurugram City, India. Urban Clim. 2022, 41, 101075. [Google Scholar] [CrossRef]
- Romshoo, S.A.; Fayaz, M.; Meraj, G.; Bahuguna, I.M. Satellite-observed glacier recession in the Kashmir Himalaya, India, from 1980 to 2018. Environ. Monit. Assess. 2020, 192, 1–17. [Google Scholar] [CrossRef]
- Farooq, M.; Meraj, G.; Kanga, S.; Nathawat, R.; Singh, S.K.; Ranga, V. Slum Categorization for Efficient Development Plan—A Case Study of Udhampur City, Jammu and Kashmir Using Remote Sensing and GIS. In Geospatial Technology for Landscape and Environmental Management; Springer: Singapore, 2022; pp. 283–299. [Google Scholar]
- Verma, U.; Dabas, D.S.; Hooda, R.S.; Kalubarme, M.H.; Yadav, M.; Grewal, M.S.; Sharma, M.P.; Prawasi, R. Remote sensing based wheat acreage and spectral-trend-agrometeorological Yield Forecasting: Factor Analysis Approach. Stat. Appl. 2011, 9, 1–13. [Google Scholar]
- Konda, V.G.R.K.; Chejarla, V.R.; Mandla, V.R.; Voleti, V.; Chokkavarapu, N. Vegetation damage assessment due to Hudhud cyclone based on NDVI using Landsat-8 satellite imagery. Arab. J. Geosci. 2018, 11, 35. [Google Scholar] [CrossRef]
- Phalke, A.R.; Özdoğan, M.; Thenkabail, P.S.; Erickson, T.; Gorelick, N.; Yadav, K.; Congalton, R.G. Mapping croplands of Europe, middle east, Russia, and central Asia using Landsat, random forest, and google earth engine. ISPRS J. Photogramm. Remote Sens. 2020, 167, 104–122. [Google Scholar] [CrossRef]
- Dimitrov, P.; Dong, Q.; Eerens, H.; Gikov, A.; Filchev, L.; Roumenina, E.; Jelev, G. Sub-pixel crop type classification using PROBA-V 100 m NDVI time series and reference data from Sentinel-2 classifications. Remote Sens. 2019, 11, 1370. [Google Scholar] [CrossRef] [Green Version]
- Górriz, J.M.; Ramírez, J.; Suckling, J.; Illan, I.A.; Ortiz, A.; Martínez-Murcia, F.J.; Segovia, F.; Salas-Gonzalez, D.; Wang, S. Case-based statistical learning: A non-parametric implementation with a conditional-error rate SVM. IEEE Access 2017, 5, 11468–11478. [Google Scholar] [CrossRef]
- Hasan, M.A.M.; Nasser, M.; Pal, B.; Ahmad, S. Support vector machine and random forest modeling for intrusion detection system (IDS). J. Intell. Learn. Syst. Appl. 2014, 6, 42869. [Google Scholar] [CrossRef] [Green Version]
- Xu, Y.; Yu, L.; Zhao, F.R.; Cai, X.; Zhao, J.; Lu, H.; Gong, P. Tracking annual cropland changes from 1984 to 2016 using time-series Landsat images with a change-detection and post-classification approach: Experiments from three sites in Africa. Remote Sens. Environ. 2018, 218, 13–31. [Google Scholar] [CrossRef]
- Do, T.N.; Lenca, P.; Lallich, S.; Pham, N.K. Classifying very-high-dimensional data with random forests of oblique decision trees. In Advances in Knowledge Discovery and Management; Springer: Berlin/Heidelberg, Germany, 2010; pp. 39–55. [Google Scholar]
- Wang, X.; Liu, T.; Zheng, X.; Peng, H.; Xin, J.; Zhang, B. Short-term prediction of groundwater level using improved random forest regression with a combination of random features. Appl. Water Sci. 2018, 8, 125. [Google Scholar] [CrossRef] [Green Version]
- Hastie, T.; Tibshirani, R.; Friedman, J. Random forests. In The Elements of Statistical Learning; Springer: New York, NY, USA, 2009; pp. 587–604. [Google Scholar]
- Watts, J.D. Satellite Monitoring of Cropland-Related Carbon Sequestration Practices in North Central Montana. Ph.D. Thesis, College of Agriculture, Montana State University, Bozeman, MT, USA, 2008. [Google Scholar]
- Kanga, S.; Singh, S.K.; Meraj, G.; Kumar, A.; Parveen, R.; Kranjčić, N.; Đurin, B. Assessment of the Impact of Urbanization on Geoenvironmental Settings Using Geospatial Techniques: A Study of Panchkula District, Haryana. Geographies 2022, 2, 1–10. [Google Scholar] [CrossRef]
- Shyam, M.; Meraj, G.; Kanga, S.; Farooq, M.; Singh, S.K.; Sahu, N.; Kumar, P. Assessing the Groundwater Reserves of the Udaipur District, Aravalli Range, India, Using Geospatial Techniques. Water 2022, 14, 648. [Google Scholar] [CrossRef]
- Piñeiro, G.; Oesterheld, M.; Paruelo, J.M. Seasonal variation in aboveground production and radiation-use efficiency of temperate rangelands estimated through remote sensing. Ecosystems 2006, 9, 357–373. [Google Scholar] [CrossRef]
- Prince, S.D.; Goward, S.N. Global primary production: A remote sensing approach. J. Biogeogr. 1995, 22, 815–835. [Google Scholar] [CrossRef]
- Zhao, L.; Liu, Z.; Xu, S.; He, X.; Ni, Z.; Zhao, H.; Ren, S. Retrieving the diurnal FPAR of a maize canopy from the jointing stage to the tasseling stage with vegetation indices under different water stresses and light conditions. Sensors 2018, 18, 3965. [Google Scholar] [CrossRef] [Green Version]
- Guang-Sheng, Z.; Xin-Shi, Z. A natural vegetation NPP model. Chin. J. Plant Ecol. 1995, 19, 193. [Google Scholar]
- Ye, X.C.; Meng, Y.K.; Xu, L.G.; Xu, C.Y. Net primary productivity dynamics and associated hydrological driving factors in the floodplain wetland of China’s largest freshwater lake. Sci. Total Environ. 2019, 659, 302–313. [Google Scholar] [CrossRef]
- Nayak, R.K.; Patel, N.R.; Dadhwal, V.K. Estimation and analysis of terrestrial net primary productivity over India by remote-sensing-driven terrestrial biosphere model. Environ. Monit. Assess. 2010, 170, 195–213. [Google Scholar] [CrossRef]
- Coventry, D.R.; Gupta, R.K.; Yadav, A.; Poswal, R.S.; Chhokar, R.S.; Sharma, R.K.; Yadav, V.K.; Gill, S.C.; Kumar, A.; Mehta, A.; et al. Wheat quality and productivity as affected by varieties and sowing time in Haryana, India. Field Crops Res. 2011, 123, 214–225. [Google Scholar] [CrossRef]
- Singh, K.M.; Singh, A. Lentil in India: An Overview. 2014. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=2510906 (accessed on 21 April 2022).
- Barma, N.C.D.; Hossain, A.; Hakim, M.; Mottaleb, K.A.; Alam, M.; Reza, M.; Ali, M.; Rohman, M. Progress and challenges of wheat production in the era of climate change: A Bangladesh perspective. In Wheat Production in Changing Environments; Springer: Singapore, 2019; pp. 615–679. [Google Scholar]
- Lambert, M.J.; Traoré, P.C.S.; Blaes, X.; Baret, P.; Defourny, P. Estimating smallholder crops production at village level from Sentinel-2 time series in Mali’s cotton belt. Remote Sens. Environ. 2018, 216, 647–657. [Google Scholar] [CrossRef]
- Field, C.B.; Randerson, J.T.; Malmström, C.M. Global net primary production: Combining ecology and remote sensing. Remote Sens. Environ. 1995, 51, 74–88. [Google Scholar] [CrossRef] [Green Version]
- Ajour, S. Evaluation of FAO’s Water Productivity Portal (WaPOR) Yield over the Beqaa Valley, Lebanon. Master’s Thesis, American University of Beirut, Beirut, Lebanon, 2021. Available online: https://scholarworks.aub.edu.lb/bitstream/handle/10938/22922/AjourSalma_2021.pdf?sequence=3 (accessed on 25 May 2022).
- Yao, F.; Tang, Y.; Wang, P.; Zhang, J. Estimation of maize yield by using a process-based model and remote sensing data in the Northeast China Plain. Phys. Chem. Earth Parts A B C 2015, 87, 142–152. [Google Scholar] [CrossRef]
- Bhatt, R.; Kaur, R.; Ghosh, A. Strategies to practice climate-smart agriculture to improve the livelihoods under the rice-wheat cropping system in South Asia. In Sustainable Management of Soil and Environment; Springer: Singapore, 2019; pp. 29–71. [Google Scholar]
- Sure, A.; Dikshit, O. Estimation of root zone soil moisture using passive microwave remote sensing: A case study for rice and wheat crops for three states in the Indo-Gangetic basin. J. Environ. Manag. 2019, 234, 75–89. [Google Scholar] [CrossRef] [PubMed]
- Gumma, M.K.; Kadiyala, M.D.M.; Panjala, P.; Ray, S.S.; Akuraju, V.R.; Dubey, S.; Smith, A.P.; Das, R.; Whitbread, A.M. Assimilation of remote sensing data into crop growth model for yield estimation: A case study from India. J. Indian Soc. Remote Sens. 2022, 50, 257–270. [Google Scholar] [CrossRef]
- Shi, S.; Ye, Y.; Xiao, R. Evaluation of Food Security Based on Remote Sensing Data—Taking Egypt as an Example. Remote Sens. 2022, 14, 2876. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, X.; Huang, L.; Yang, G.; Fan, L.; Wei, P.; Chen, G. An improved CASA model for estimating winter wheat yield from remote sensing images. Remote Sens. 2019, 11, 1088. [Google Scholar] [CrossRef] [Green Version]
- Wu, C.; Chen, K.; You, X.; He, D.; Hu, L.; Liu, B.; Wang, R.; Shi, Y.; Li, C.; Liu, F. Improved CASA model based on satellite remote sensing data: Simulating net primary productivity of Qinghai Lake Basin alpine grassland. Geosci. Model Dev. Discuss. 2022, 10, 1–24. [Google Scholar]
- Wu, K.; Zhou, C.; Zhang, Y.; Xu, Y. Long-Term Spatiotemporal Variation of Net Primary Productivity and Its Correlation with the Urbanization: A Case Study in Hubei Province, China. Front. Environ. Sci. 2022, 9, 656. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).