Effects of Human Activities on Urban Vegetation: Explorative Analysis of Spatial Characteristics and Potential Impact Factors
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data
2.3. Methodology
2.3.1. Spatial Gridding with the Area Weighting Method
2.3.2. Feature Selection with RFR
2.3.3. Contribution Assessment with GWR
2.3.4. Evaluation Parameters for Models
3. Results
3.1. Spatial Distributions of Socio-Economic Factors
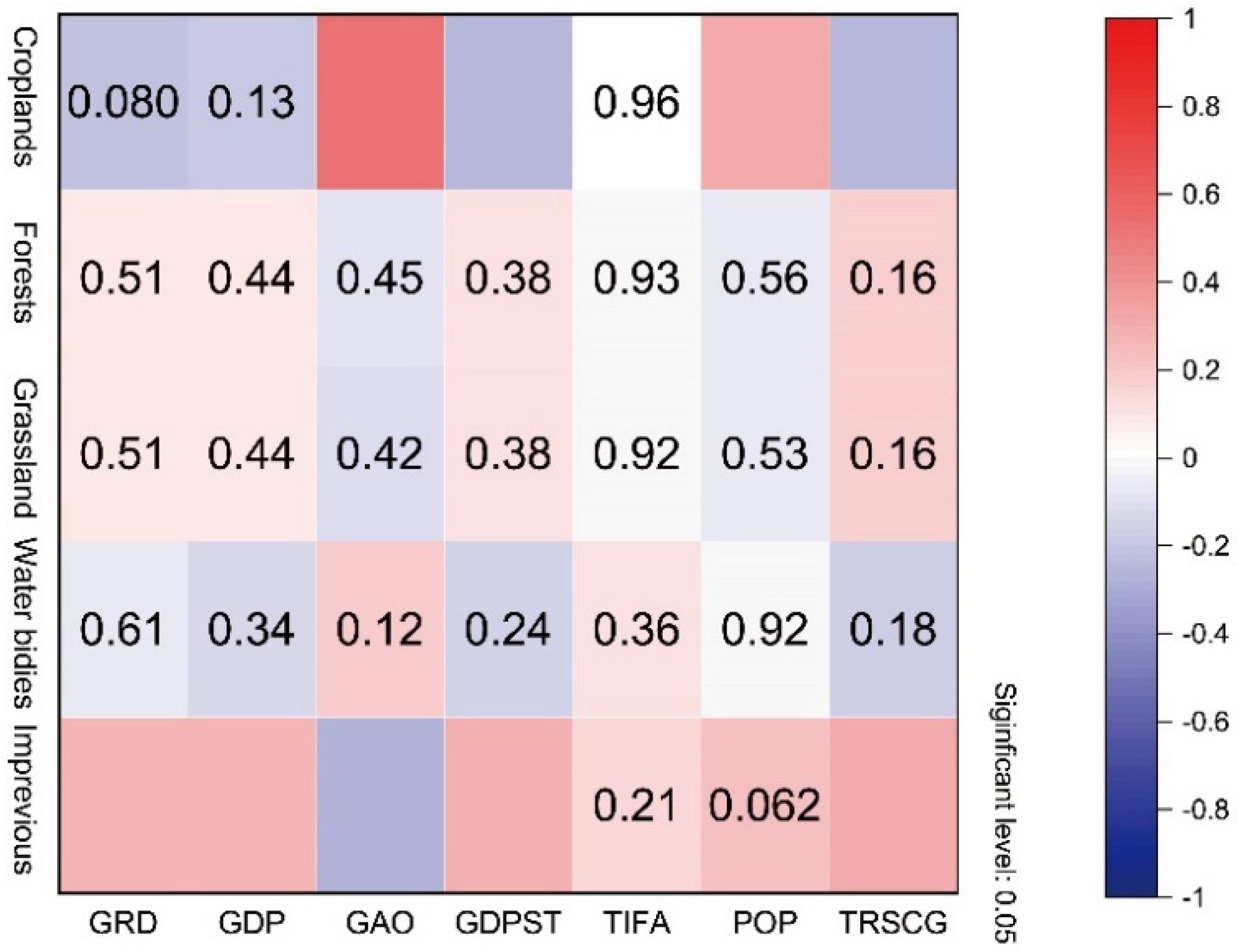
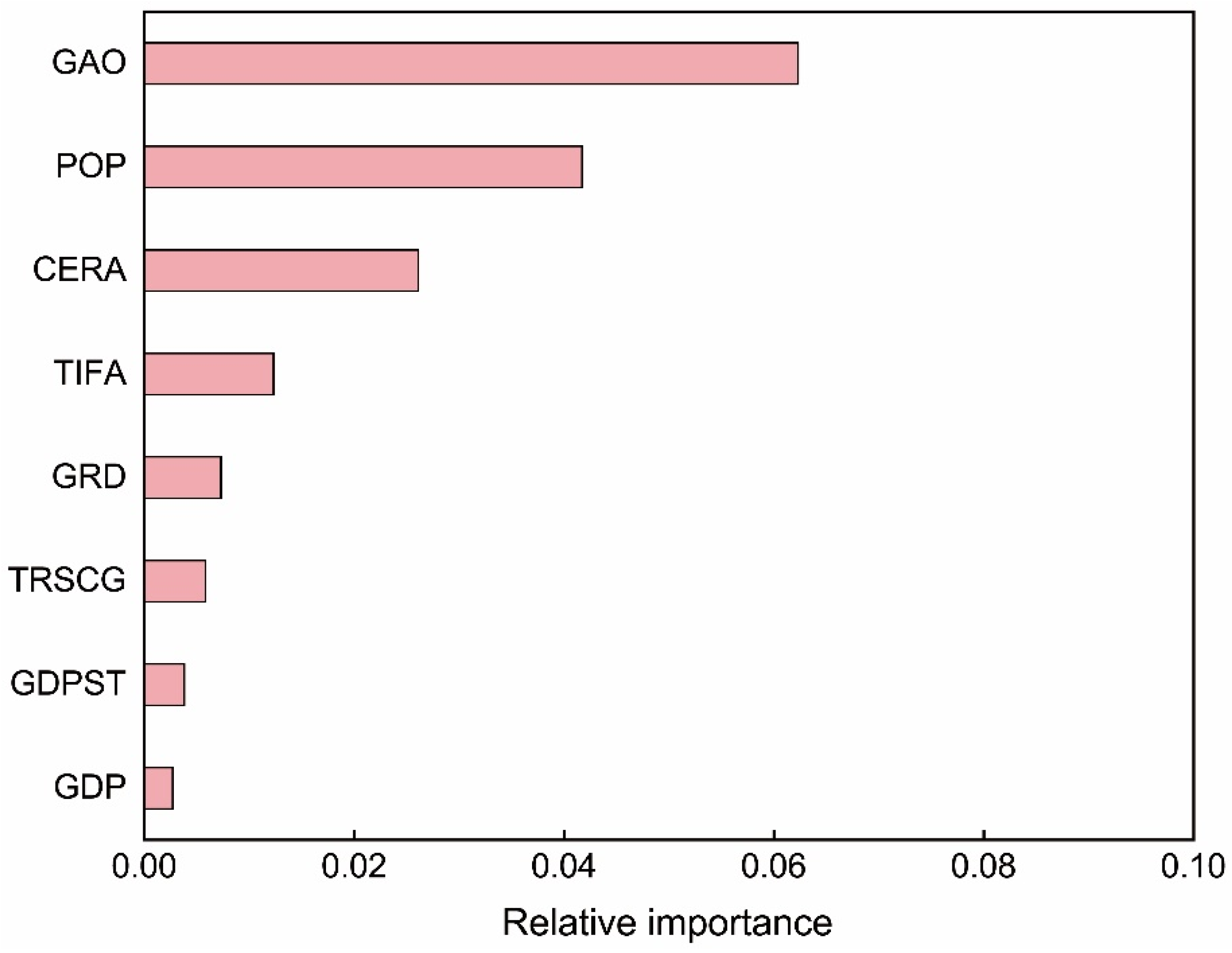
3.2. Major Factors’ Contribution Assessment
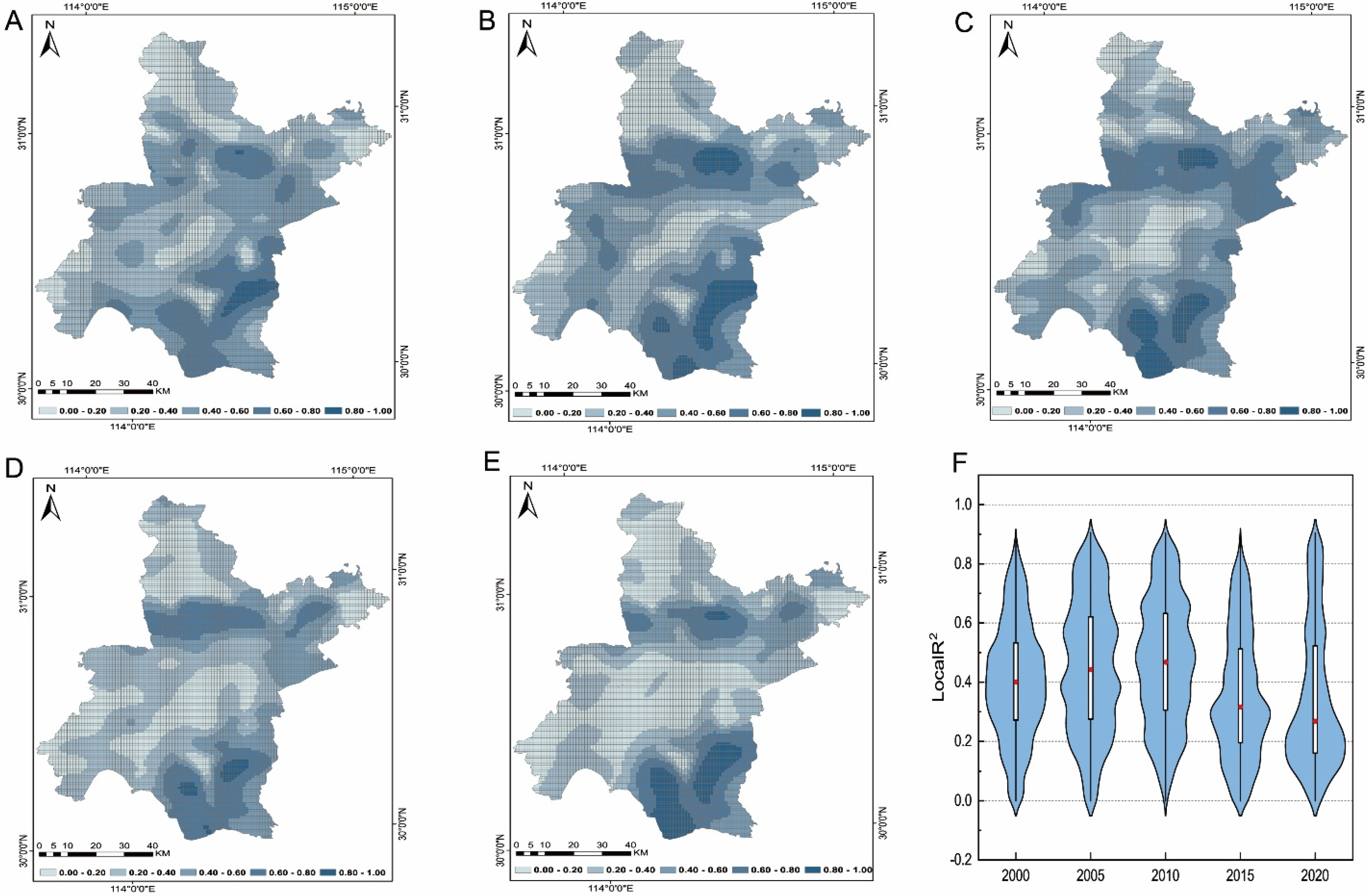
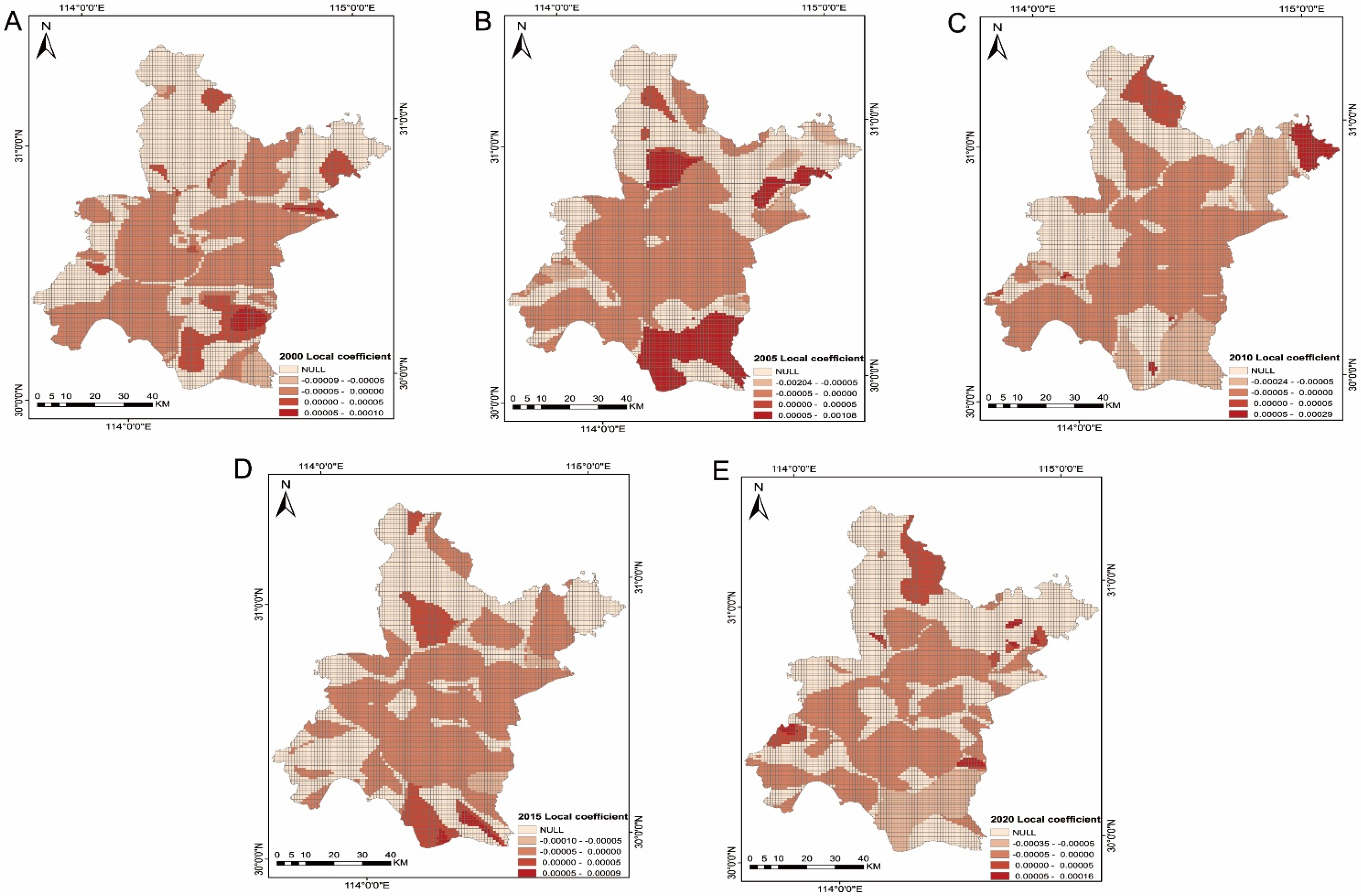
3.3. Spatial Correlation of Major Factors with NDVI
4. Discussion
4.1. Driving Factors of Vegetation Coverage
4.2. Quantitative Evaluation Models
4.3. Spatial Characteristic of the Impact of Human Activities on NDVI
4.4. Limitations
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Xin, Z.; Xu, J.; Zheng, W. Spatiotemporal variations of vegetation cover on the Chinese Loess Plateau (1981–2006): Impacts of climate changes and human activities. Sci. China Ser. D Earth Sci. 2008, 51, 67–78. [Google Scholar] [CrossRef]
- Lu, D.; Xu, X.; Tian, H.; Moran, E.; Zhao, M.; Running, S. The Effects of Urbanization on Net Primary Productivity in Southeastern China. Environ. Manag. 2010, 46, 404–410. [Google Scholar] [CrossRef] [PubMed]
- Feng, Q.; Ma, H.; Jiang, X.; Wang, X.; Cao, S. What Has Caused Desertification in China? Sci. Rep. 2015, 5, 15998. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shen, Q.; Gao, G.; Han, F.; Xiao, F.; Ma, Y.; Wang, S.; Fu, B. Quantifying the effects of human activities and climate variability on vegetation cover change in a hyper-arid endorheic basin. Land Degrad. Dev. 2018, 29, 3294–3304. [Google Scholar] [CrossRef]
- Jiang, M.; Tian, S.; Zheng, Z.; Zhan, Q.; He, Y. Human Activity Influences on Vegetation Cover Changes in Beijing, China, from 2000 to 2015. Remote Sens. 2017, 9, 271. [Google Scholar] [CrossRef] [Green Version]
- Jin, J.; Gergel, S.E.; Lu, Y.; Coops, N.C.; Wang, C. Asian Cities are Greening While Some North American Cities are Browning: Long-Term Greenspace Patterns in 16 Cities of the Pan-Pacific Region. Ecosystems 2020, 23, 383–399. [Google Scholar] [CrossRef]
- Yao, R.; Cao, J.; Wang, L.; Zhang, W.; Wu, X. Urbanization effects on vegetation cover in major African cities during 2001–2017. Int. J. Appl. Earth Obs. Geoinf. 2019, 75, 44–53. [Google Scholar] [CrossRef]
- Foley, J.A.; DeFries, R.; Asner, G.P.; Barford, C.; Bonan, G.; Carpenter, S.R.; Chapin, F.S.; Coe, M.T.; Daily, G.C.; Gibbs, H.K.; et al. Global consequences of land use. Science 2005, 309, 570–574. [Google Scholar] [CrossRef] [Green Version]
- Kaufmann, R.K.; Seto, K.C.; Schneider, A.; Liu, Z.; Zhou, L.; Wang, W. Climate response to rapid urban growth: Evidence of a human-induced precipitation deficit. J. Clim. 2007, 20, 2299–2306. [Google Scholar] [CrossRef]
- Zhang, C.; Tian, H.; Pan, S.; Liu, M.; Lockaby, G.; Schilling, E.B.; Stanturf, J. Effects of Forest Regrowth and Urbanization on Ecosystem Carbon Storage in a Rural-Urban Gradient in the Southeastern United States. Ecosystems 2008, 11, 1211–1222. [Google Scholar] [CrossRef]
- Chen, C.; Park, T.; Wang, X.; Piao, S.; Xu, B.; Chaturvedi, R.K.; Fuchs, R.; Brovkin, V.; Ciais, P.; Fensholt, R.; et al. China and India lead in greening of the world through land-use management. Nat. Sustain. 2019, 2, 122–129. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Xu, Z. A Study of Spatialization Methods of Human Factors Based on IPAT Model. J. Glaciol. Geocryol. 2012, 34, 740–747. [Google Scholar]
- Liu, H.; Zheng, L.; Liao, M. Dynamics of Vegetation Change and Its Relationship with Nature and Human Activities—A Case Study of Poyang Lake Basin, China. J. Sustain. For. 2021, 40, 47–67. [Google Scholar] [CrossRef]
- Mueller, T.; Dressler, G.; Tucker, C.J.; Pinzon, J.E.; Leimgruber, P.; Dubayah, R.O.; Hurtt, G.C.; Bohning-Gaese, K.; Fagan, W.F. Human Land-Use Practices Lead to Global Long-Term Increases in Photosynthetic Capacity. Remote Sens. 2014, 6, 5717–5731. [Google Scholar] [CrossRef] [Green Version]
- Shi, Y.; Jin, N.; Ma, X.; Wu, B.; He, Q.; Yue, C.; Yu, Q. Attribution of climate and human activities to vegetation change in China using machine learning techniques. Agric. For. Meteorol. 2020, 294, 108146. [Google Scholar] [CrossRef]
- Jin, K.; Wang, F.; Li, P. Responses of Vegetation Cover to Environmental Change in Large Cities of China. Sustainability 2018, 10, 270. [Google Scholar] [CrossRef] [Green Version]
- Wu, Z.; Li, Z.; Zeng, H. Using Remote Sensing Data to Study the Coupling Relationship between Urbanization and Eco-Environment Change: A Case Study in the Guangdong-Hong Kong-Macao Greater Bay Area. Sustainability 2020, 12, 7875. [Google Scholar] [CrossRef]
- Leroux, L.; Begue, A.; Seen, D.L.; Jolivot, A.; Kayitakire, F. Driving forces of recent vegetation changes in the Sahel: Lessons learned from regional and local level analyses. Remote Sens. Environ. 2017, 191, 38–54. [Google Scholar] [CrossRef] [Green Version]
- Wu, S.P.; Gao, X.; Lei, J.Q.; Zhou, N.; Wang, Y.D. Spatial and Temporal Changes in the Normalized Difference Vegetation Index and Their Driving Factors in the Desert/Grassland Biome Transition Zone of the Sahel Region of Africa. Remote Sens. 2020, 12, 4119. [Google Scholar] [CrossRef]
- Hunter, L.M. People and pixels: Linking remote sensing and social science. Contemp. Sociol. J. Rev. 1999, 28, 362–363. [Google Scholar] [CrossRef]
- Gaffin, S.R.; Rosenzweig, C.; Xing, X.S.; Yetman, G. Downscaling and geo-spatial gridding of socio-economic projections from the IPCC Special Report on Emissions Scenarios (SRES). Glob. Environ. Chang. 2004, 14, 105–123. [Google Scholar] [CrossRef]
- Brinegrar, S.J.; Popick, S.J. A Comparative Analysis of Small Area Population Estimation Methods. Cartogr. Geogr. Inf. Sci. 2010, 37, 273–284. [Google Scholar] [CrossRef]
- Zhuo, L.; Ichinose, T.; Zheng, J.; Chen, J.; Shi, P.J.; Li, X. Modelling the population density of China at the pixel level based on DMSP/OLS non-radiance-calibrated night-time light images. Int. J. Remote Sens. 2009, 30, 1003–1018. [Google Scholar] [CrossRef]
- Han, X.; Zhou, Y.; Wang, S.; Liu, R.; Yao, Y. GDP Spatialization in China based on DMSP/OLS Data and Land Use Data. Remote Sens. Technol. Appl. 2012, 27, 396–405. [Google Scholar]
- Lu, D.; Weng, Q.; Li, G. Residential population estimation using a remote sensing derived impervious surface approach. Int. J. Remote Sens. 2006, 27, 3553–3570. [Google Scholar] [CrossRef]
- Peng, C.; Jin, X.; Wong, K.-C.; Shi, M.; Lio, P. Collective Human Mobility Pattern from Taxi Trips in Urban Area. PLoS ONE 2012, 7, e34487. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Yan, Q.; Hu, M. Spatial-Temporal Evolution of Vegetation and Dominant Factors inEnergy Golden TriangleRegion Based on Geographically Weighted Regression Model. J. Ecol. Rural Environ. 2018, 34, 700–708. [Google Scholar]
- Shi, S.; Yu, J.; Wang, F.; Wang, P.; Zhang, Y.; Jin, K. Quantitative contributions of climate change and human activities to vegetation changes over multiple time scales on the Loess Plateau. Sci. Total Environ. 2021, 755, 142419. [Google Scholar] [CrossRef]
- Jin, Y.; Zhang, H.; Yan, Y.; Cong, P. A Semi-Parametric Geographically Weighted Regression Approach to Exploring Driving Factors of Fractional Vegetation Cover: A Case Study of Guangdong. Sustainability 2020, 12, 7512. [Google Scholar] [CrossRef]
- Peng, J.; Li, Y.; Tian, L.; Liu, Y.; Wang, Y. Vegetation Dynamics and Associated Driving Forces in Eastern China during 1999–2008. Remote Sens. 2015, 7, 13641–13663. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.Z.; Feng, X.M.; Tian, H.Q.; Wu, X.T.; Gao, Z.; Feng, Y.; Piao, S.L.; Lv, N.; Pan, N.Q.; Fu, B.J. Accelerated increase in vegetation carbon sequestration in China after 2010: A turning point resulting from climate and human interaction. Glob. Chang. Biol. 2021, 27, 5848–5864. [Google Scholar] [CrossRef] [PubMed]
- Zaimes, G.N.; Gounaridis, D.; Symenonakis, E. Assessing the impact of dams on riparian and deltaic vegetation using remotely-sensed vegetation indices and Random Forests modelling. Ecol. Indic. 2019, 103, 630–641. [Google Scholar] [CrossRef]
- Clauss, K.; Ottinger, M.; Leinenkugel, P.; Kuenzer, C. Estimating rice production in the Mekong Delta, Vietnam, utilizing time series of Sentinel-1 SAR data. Int. J. Appl. Earth Obs. Geoinf. 2018, 73, 574–585. [Google Scholar] [CrossRef]
- Huang, S.; Zheng, X.; Ma, L.; Wang, H.; Huang, Q.; Leng, G.; Meng, E.; Guo, Y. Quantitative contribution of climate change and human activities to vegetation cover variations based on GA-SVM model. J. Hydrol. 2020, 584, 124687. [Google Scholar] [CrossRef]
- Luo, D.; Goodin, D.G.; Caldas, M.M. Spatial-Temporal Analysis of Land Cover Change at the Bento Rodrigues Dam Disaster Area Using Machine Learning Techniques. Remote Sens. 2019, 11, 2548. [Google Scholar] [CrossRef] [Green Version]
- Hua, W.J.; Chen, H.S.; Zhou, L.M.; Xie, Z.H.; Qin, M.H.; Li, X.; Ma, H.D.; Huang, Q.H.; Sun, S.L. Observational Quantification of Climatic and Human Influences on Vegetation Greening in China. Remote Sens. 2017, 9, 425. [Google Scholar] [CrossRef] [Green Version]
- Ma, B.; Wang, S.S.; Mupenzi, C.; Li, H.R.; Ma, J.Y.; Li, Z.B. Quantitative Contributions of Climate Change and Human Activities to Vegetation Changes in the Upper White Nile River. Remote Sens. 2021, 13, 3648. [Google Scholar] [CrossRef]
- Dong, J. Study on the progress of spatialization of anthrop factors. J. Gansu Sci. 2007, 19, 91–94. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Yu, H.R.; Gong, H.L.; Chen, B.B.; Liu, K.S.; Gao, M.L. Analysis of the influence of groundwater on land subsidence in Beijing based on the geographical weighted regression (GWR) model. Sci. Total Environ. 2020, 738, 139405. [Google Scholar] [CrossRef]
- da Silva, A.R.; Fotheringham, A.S. The Multiple Testing Issue in Geographically Weighted Regression. Geogr. Anal. 2016, 48, 233–247. [Google Scholar] [CrossRef]


| Area (2000, km2) | Area (2020, km2) | ||||||
|---|---|---|---|---|---|---|---|
| Croplands | Forest | Grasslands | Water | Impervious | Others | Total | |
| Croplands | 22.96 | 1.71 | 99.33 | 425.49 | 2.39 | 551.88 | |
| Forest | 18.84 | 1.38 | 4.29 | 18.67 | 0.21 | 43.39 | |
| Grasslands | 1.58 | 1.68 | 4.66 | 4.48 | 0.26 | 12.66 | |
| Water bodies | 46.66 | 3.37 | 2.45 | 66.11 | 3.51 | 122.10 | |
| Impervious | 25.70 | 1.90 | 0.26 | 9.29 | 0.31 | 37.46 | |
| Others | 2.28 | 0.18 | 0.07 | 4.83 | 4.00 | 11.36 | |
| Total | 95.06 | 30.10 | 5.87 | 122.40 | 518.74 | 6.67 | 778.85 |
| Year | Model | MSE | R2 |
|---|---|---|---|
| 2000 | GWR | 0.006 | 0.64 |
| RFR | 0.010 | 0.39 | |
| 2005 | GWR | 0.008 | 0.65 |
| RFR | 0.013 | 0.42 | |
| 2010 | GWR | 0.009 | 0.67 |
| RFR | 0.013 | 0.52 | |
| 2015 | GWR | 0.013 | 0.61 |
| RFR | 0.022 | 0.35 | |
| 2020 | GWR | 0.016 | 0.59 |
| RFR | 0.028 | 0.29 |
| Year | Factor | DIFF of Criterion | Geographical Variability |
|---|---|---|---|
| 2000 | POP | −3695.16 | √ |
| GAO | −10,758.93 | √ | |
| 2005 | POP | −214.69 | √ |
| GAO | −318.15 | √ | |
| 2010 | POP | −709.31 | √ |
| GAO | −2272.61 | √ | |
| 2015 | POP | −361.90 | √ |
| GAO | −440.05 | √ | |
| 2020 | POP | −366.56 | √ |
| GAO | −283.35 | √ |
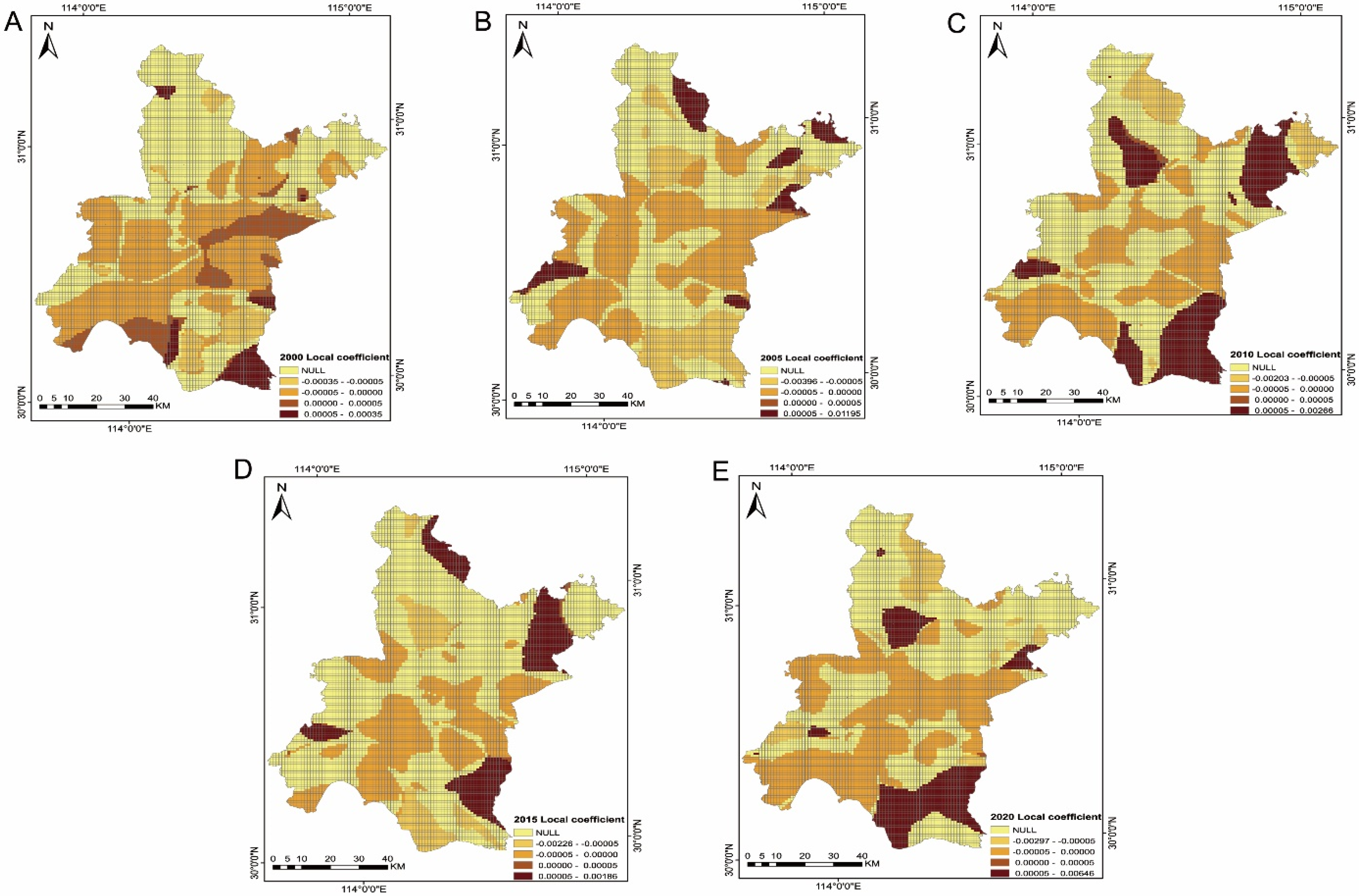
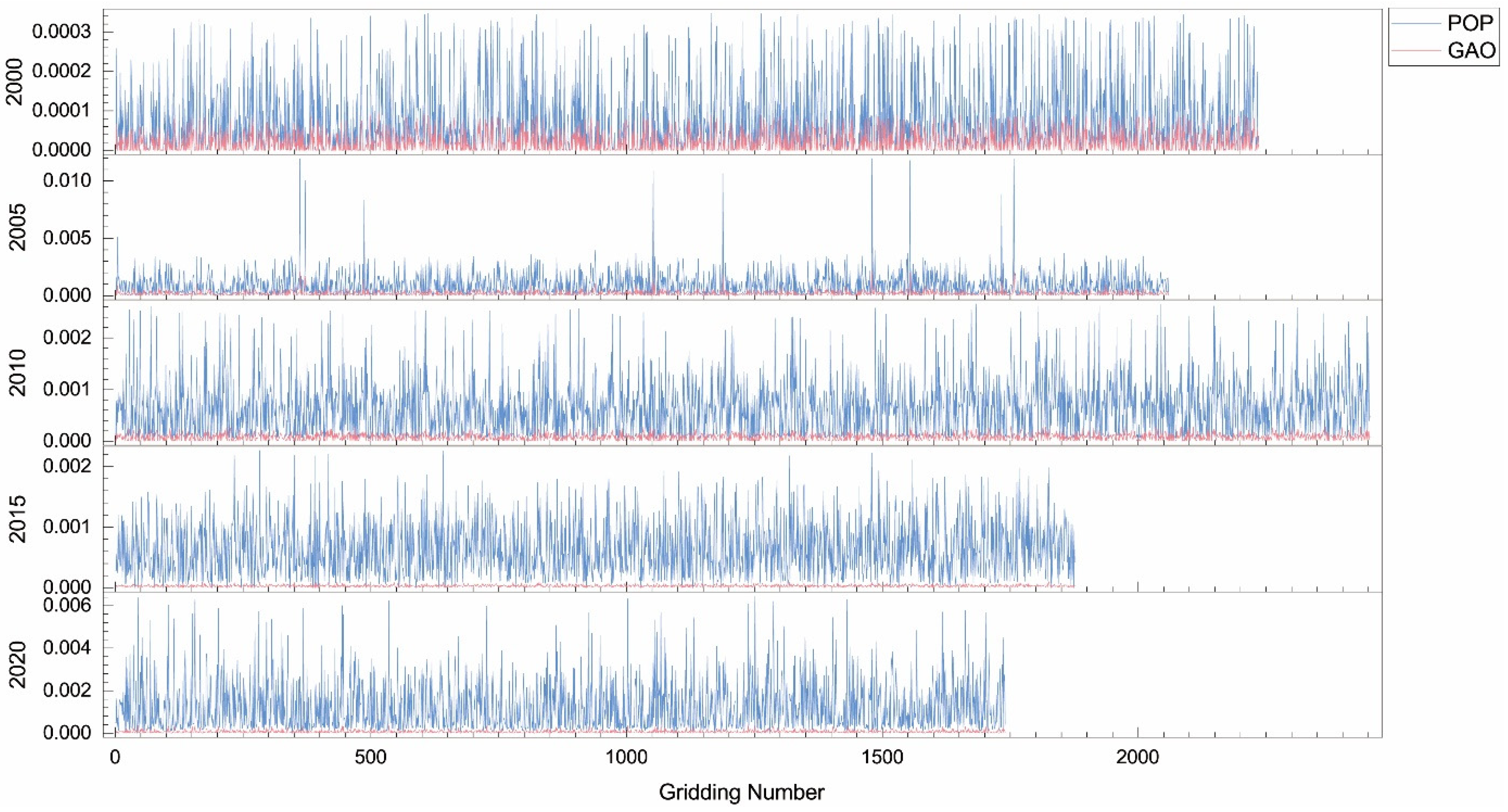
| Year | Factor | Min | Max | Mean | Positive/% | Negative/% | Moran’ I | Z |
|---|---|---|---|---|---|---|---|---|
| 2000 | POP | −0.000345 | 0.000348 | 0 | 58.80 | 41.19 | 0.97 | 127.04 |
| GAO | −0.000089 | 0.000096 | 0.000001 | 59.85 | 40.15 | 0.97 | 127.23 | |
| 2005 | POP | −0.003956 | 0.011951 | −0.000169 | 64.21 | 35.79 | 0.85 | 111.53 |
| GAO | −0.002043 | 0.001081 | 0.000023 | 64.57 | 35.43 | 0.85 | 111.53 | |
| 2010 | POP | −0.00203 | 0.002657 | 0.000218 | 75.70 | 24.30 | 0.87 | 91.72 |
| GAO | −0.00024 | 0.000294 | −0.000019 | 24.32 | 75.68 | 0.87 | 91.92 | |
| 2015 | POP | −0.002264 | 0.001864 | 0.000067 | 61.89 | 38.11 | 0.95 | 98.27 |
| GAO | −0.000102 | 0.000089 | −0.000004 | 38.22 | 61.78 | 0.95 | 98.28 | |
| 2020 | POP | −0.002966 | 0.006459 | 0.000307 | 64.08 | 35.92 | 0.95 | 124.48 |
| GAO | −0.000351 | 0.000161 | −0.000017 | 36.10 | 63.90 | 0.95 | 124.46 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Du, L.; Li, X.; Yao, P.; Luo, Z.; Wu, Z. Effects of Human Activities on Urban Vegetation: Explorative Analysis of Spatial Characteristics and Potential Impact Factors. Remote Sens. 2022, 14, 2999. https://doi.org/10.3390/rs14132999
Li X, Du L, Li X, Yao P, Luo Z, Wu Z. Effects of Human Activities on Urban Vegetation: Explorative Analysis of Spatial Characteristics and Potential Impact Factors. Remote Sensing. 2022; 14(13):2999. https://doi.org/10.3390/rs14132999
Chicago/Turabian StyleLi, Xiangyuan, Lin Du, Xiong Li, Panfeng Yao, Zhuoran Luo, and Zhiyuan Wu. 2022. "Effects of Human Activities on Urban Vegetation: Explorative Analysis of Spatial Characteristics and Potential Impact Factors" Remote Sensing 14, no. 13: 2999. https://doi.org/10.3390/rs14132999
APA StyleLi, X., Du, L., Li, X., Yao, P., Luo, Z., & Wu, Z. (2022). Effects of Human Activities on Urban Vegetation: Explorative Analysis of Spatial Characteristics and Potential Impact Factors. Remote Sensing, 14(13), 2999. https://doi.org/10.3390/rs14132999





