View-Agnostic Point Cloud Generation for Occlusion Reduction in Aerial Lidar
Abstract
:1. Introduction
- View occlusion describes a scenario in which an object of interest is outside the sensor’s field of view;
- Self-occlusion is when the position of the sensor causes a portion of an object to be obscured from view. In this scenario, the object itself is causing the occlusion;
- Ambient occlusion describes a scenario in which an object is hidden from view by a completely different object.
- A new dataset, DALES Viewpoints Version 2, for aerial lidar occlusions. This dataset contains over nine times the number of points per scene compared to Version 1 and does not require point replication when generating new scenes;
- A task-specific point sampling method that can learn to select key points that highly contribute to point clouds features;
- A loss function that promotes the structure transfer between point clouds with the same underlying shape but different physical locations.
2. Related Works
2.1. Point Cloud Completion Networks
2.1.1. PointNet Features
2.1.2. Folding-Based Decoders
2.1.3. Skip Attention Network
2.2. Sampling Methods
2.2.1. Farthest Point Sampling
2.2.2. SampleNet
2.3. Loss Functions
2.3.1. Chamfer Distance
2.3.2. Earth Mover’s Distance
3. Materials and Methods
3.1. Point Cloud Network Dataset
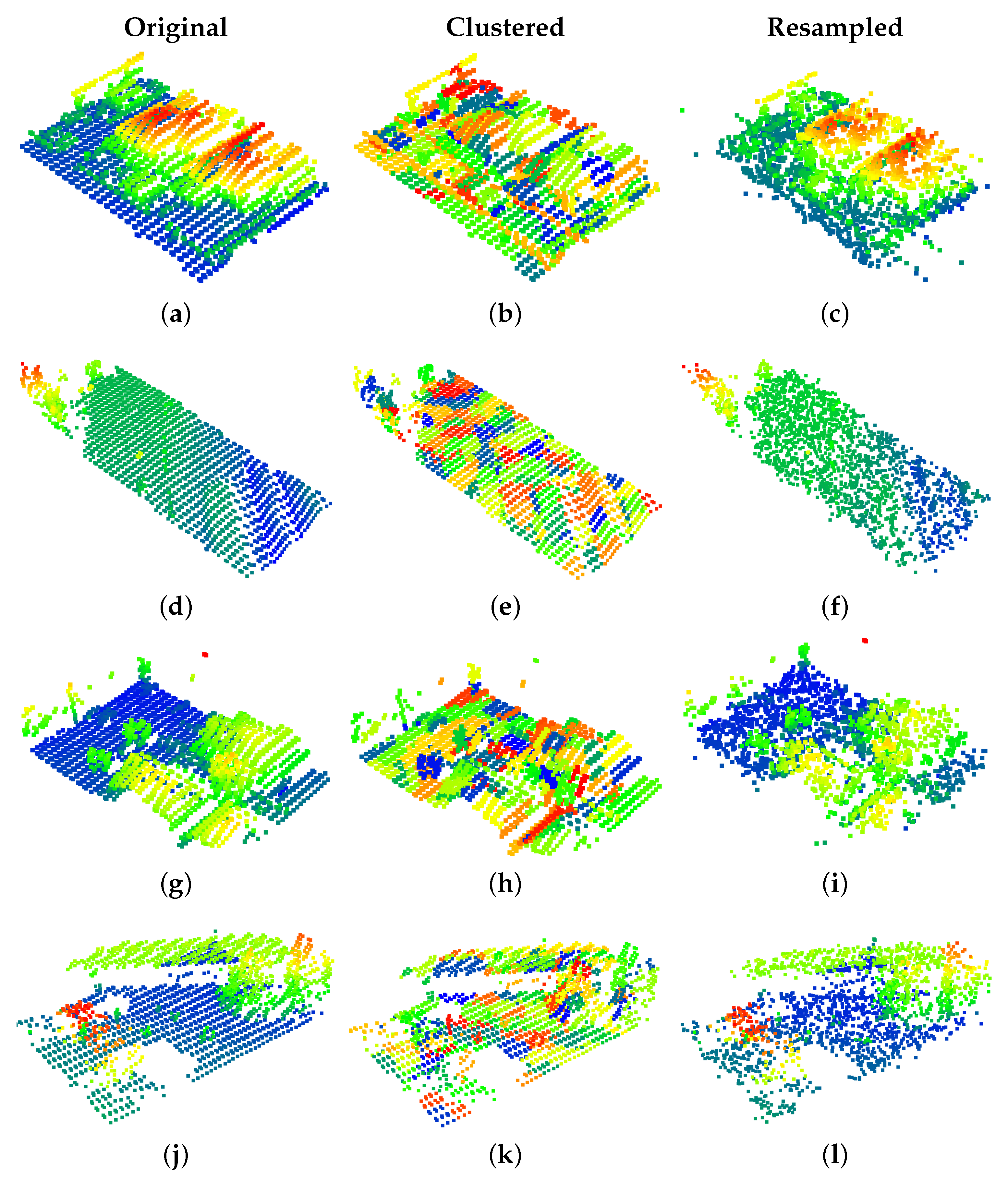
3.2. DALES Viewpoints Version 2 Dataset
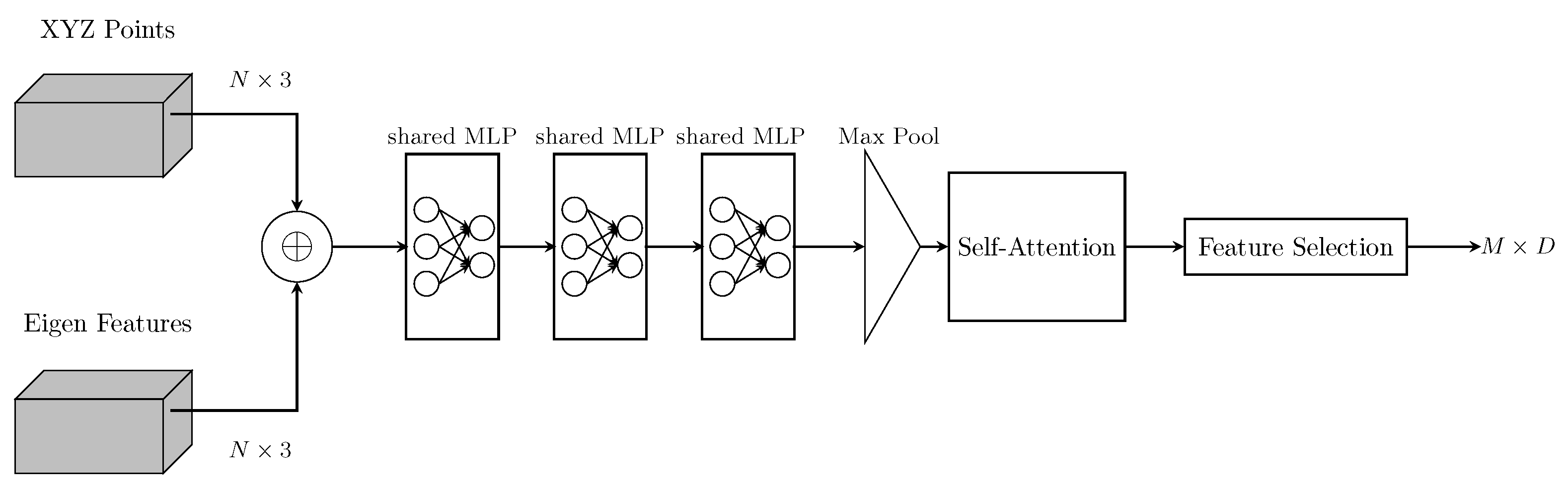
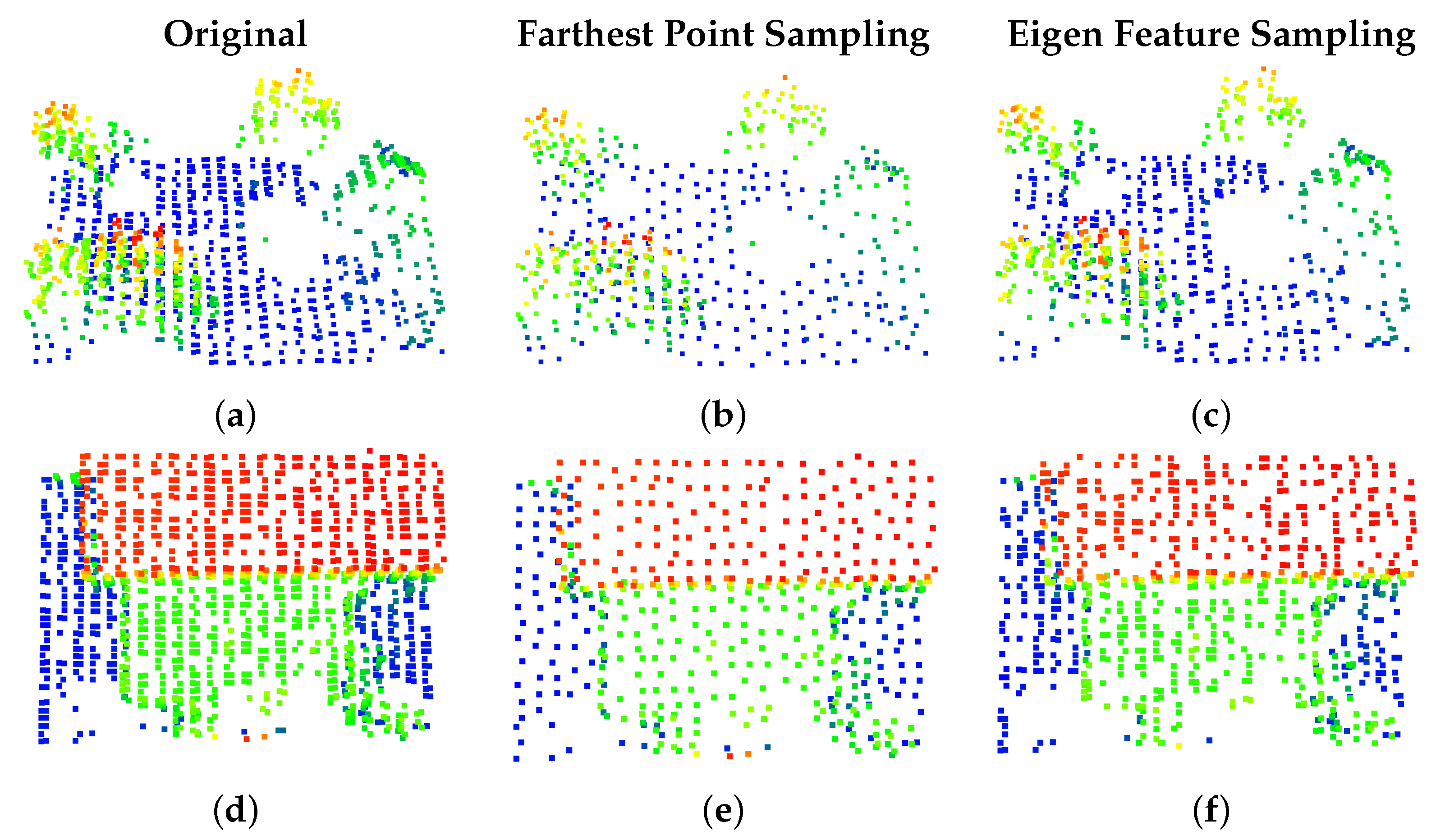
3.3. Eigen-Based Heiarchical Sampling
3.4. Point Correspondence Loss
3.5. Parallel Network
4. Results
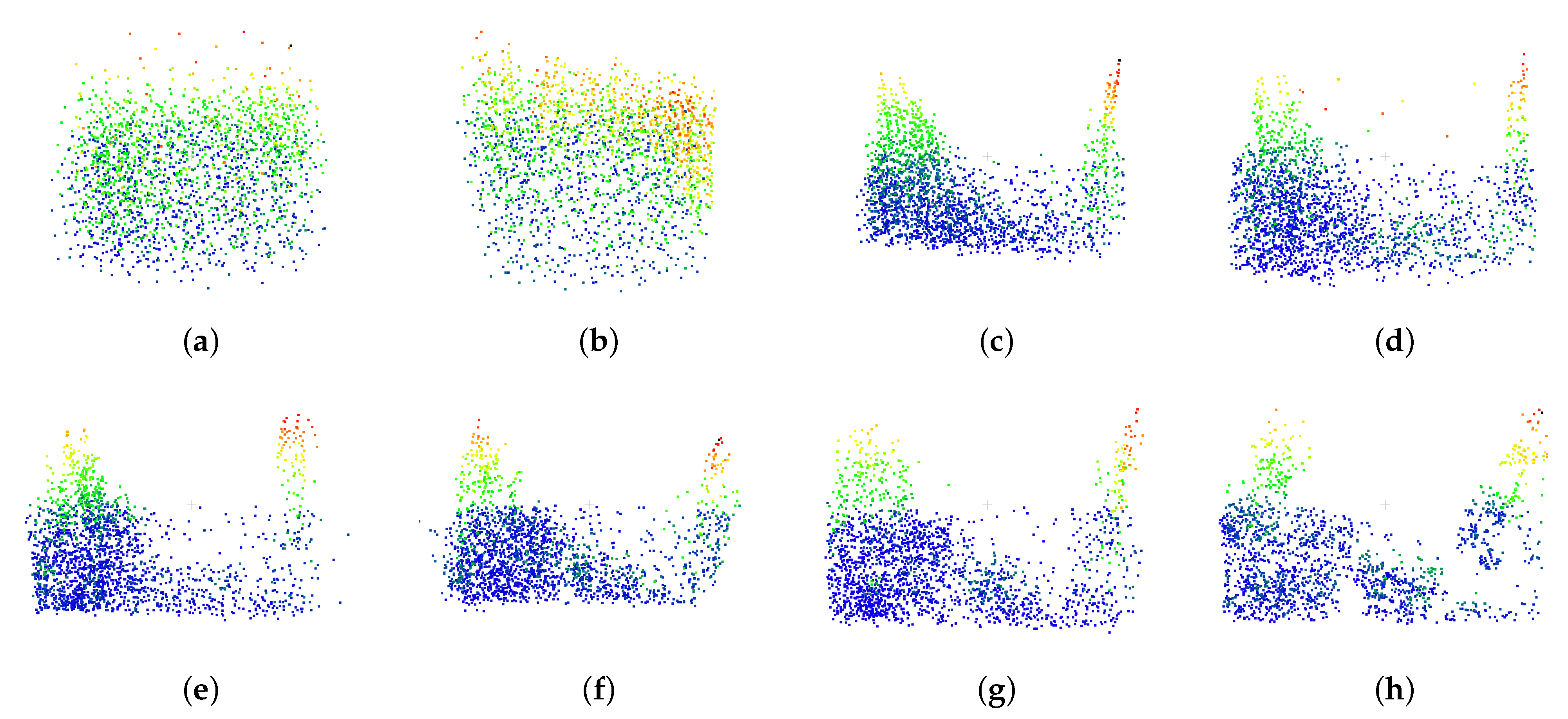
4.1. DALES Viewpoints Version 2
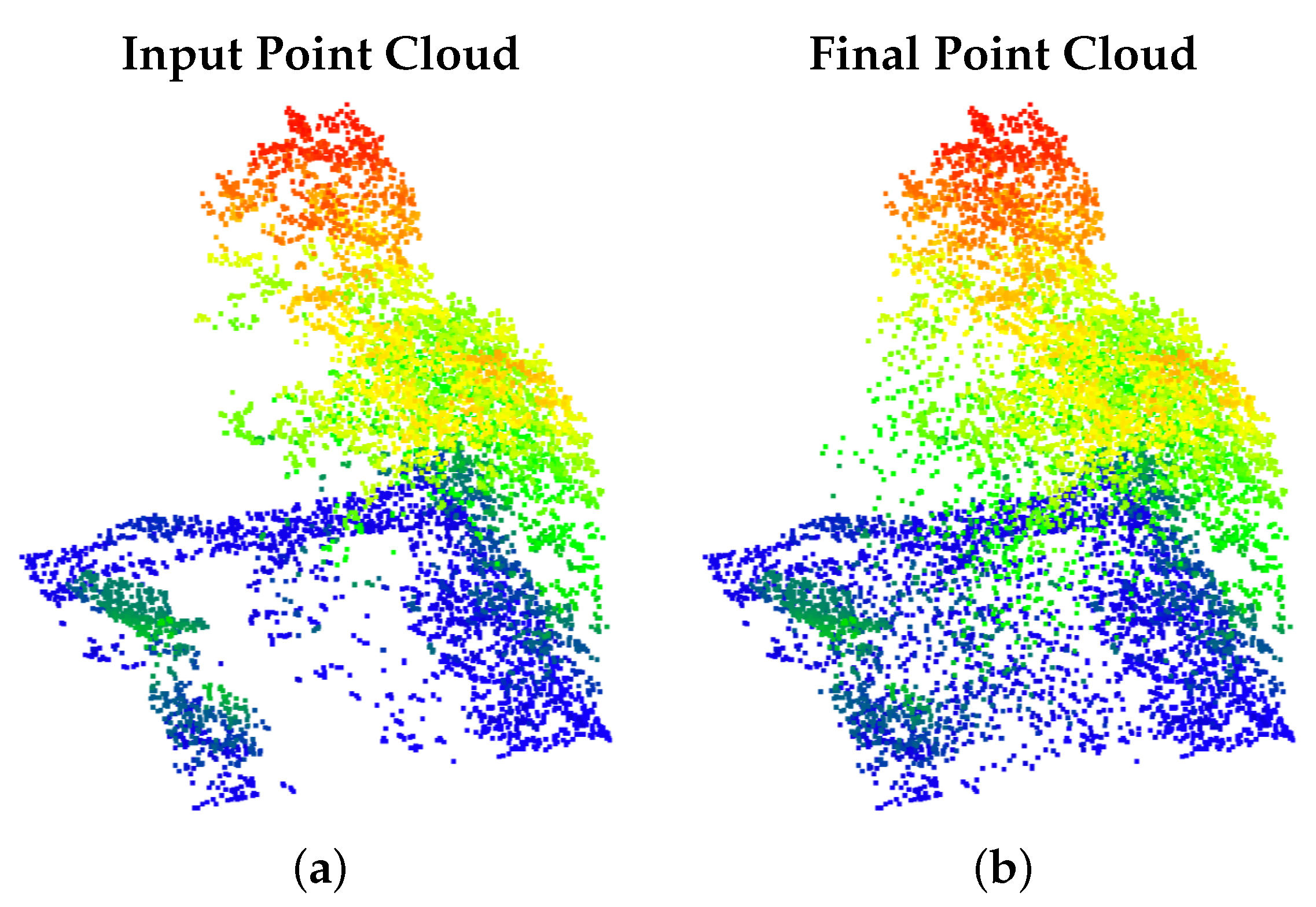
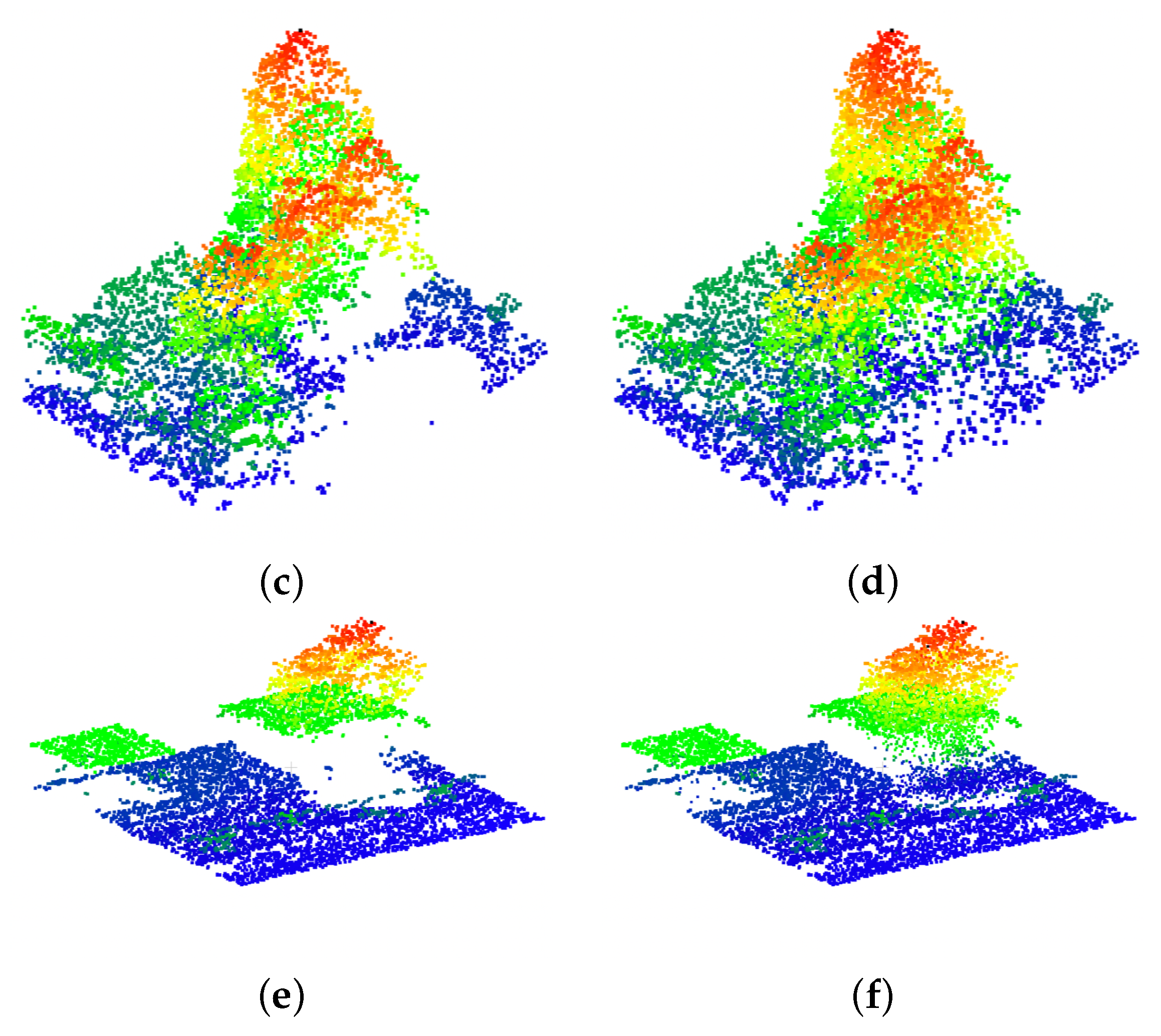
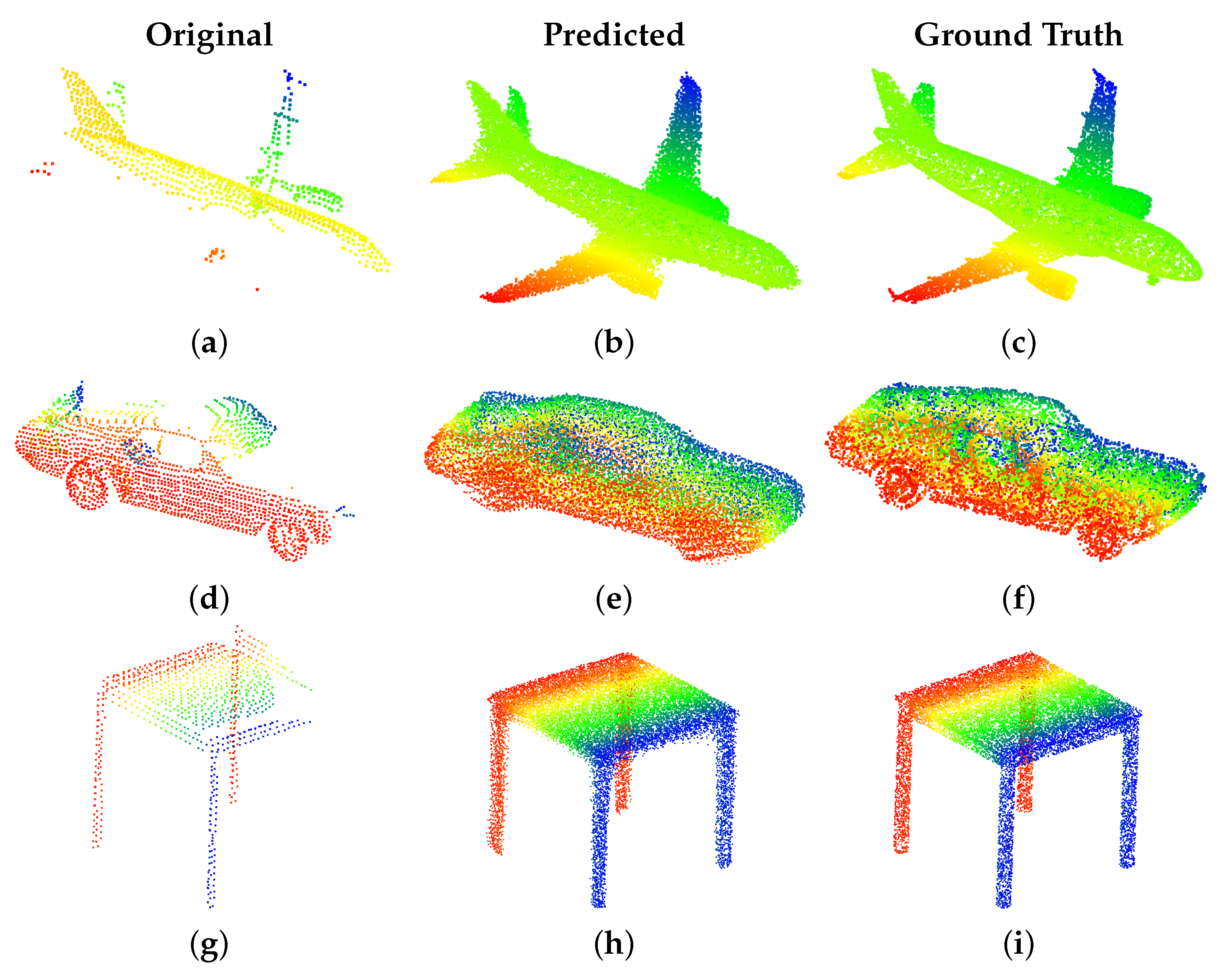
4.2. Point Cloud Completion Network
4.3. Discussion
4.3.1. Eigen Feature Selection Sampling
4.3.2. Point Projection for Stabilizing Point Correspondences
4.3.3. Timing
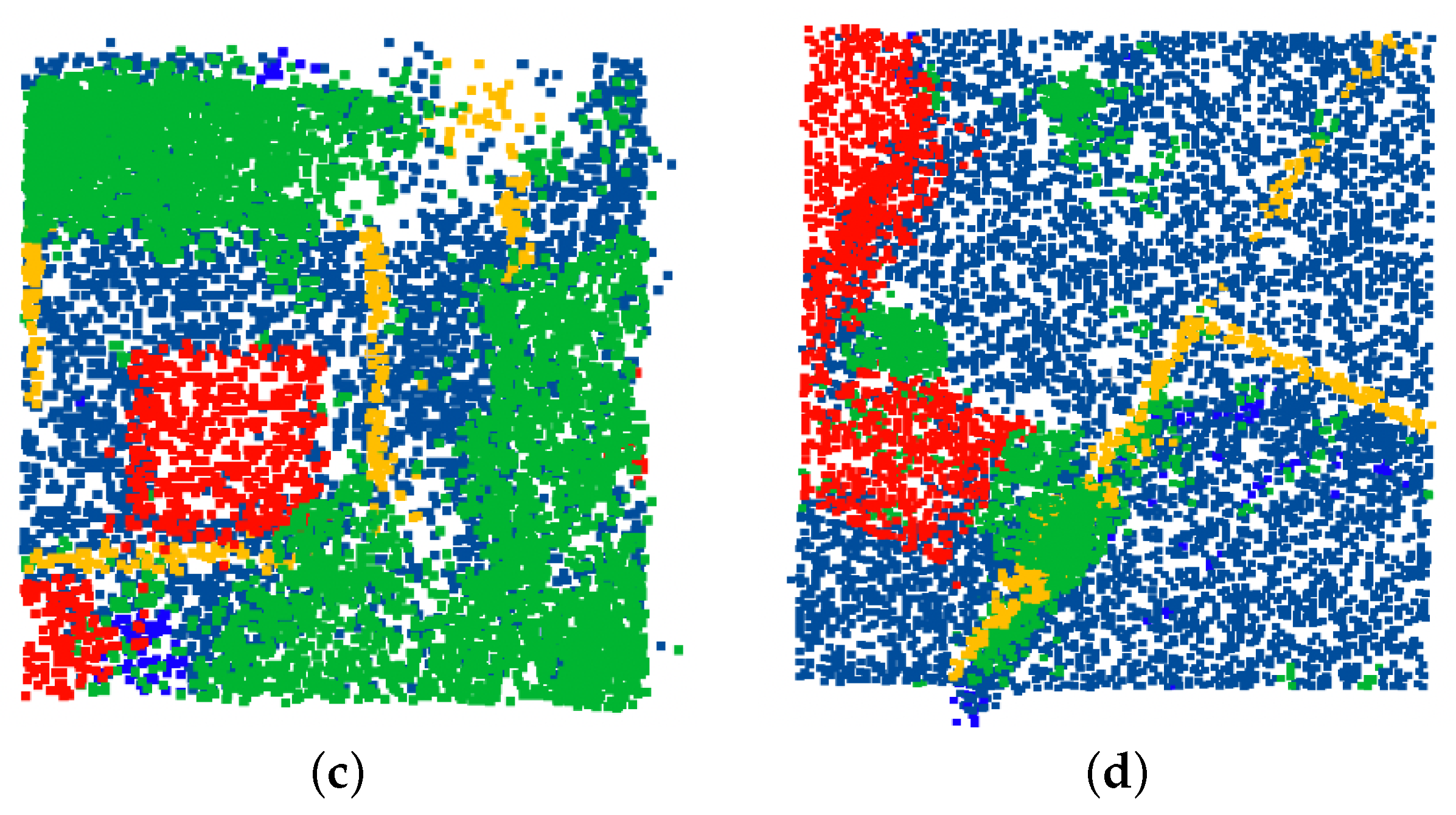
4.4. Semantic Segmentation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wu, Z.; Song, S.; Khosla, A.; Yu, F.; Zhang, L.; Tang, X.; Xiao, J. 3d shapenets: A deep representation for volumetric shapes. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1912–1920. [Google Scholar]
- Chang, A.X.; Funkhouser, T.; Guibas, L.; Hanrahan, P.; Huang, Q.; Li, Z.; Savarese, S.; Savva, M.; Song, S.; Su, H.; et al. Shapenet: An information-rich 3d model repository. arXiv 2015, arXiv:1512.03012. [Google Scholar]
- Lemmens, M. Airborne lidar sensors. GIM Int. 2007, 21, 24–27. [Google Scholar]
- Lehtola, V.V.; Kaartinen, H.; Nüchter, A.; Kaijaluoto, R.; Kukko, A.; Litkey, P.; Honkavaara, E.; Rosnell, T.; Vaaja, M.T.; Virtanen, J.P.; et al. Comparison of the selected state-of-the-art 3D indoor scanning and point cloud generation methods. Remote Sens. 2017, 9, 796. [Google Scholar] [CrossRef] [Green Version]
- Carson, W.W.; Andersen, H.E.; Reutebuch, S.E.; McGaughey, R.J. LIDAR applications in forestry—An overview. In Proceedings of the ASPRS Annual Conference, Denver, CO, USA, 23–28 May 2004; pp. 1–9. [Google Scholar]
- Li, Y.; Ma, L.; Zhong, Z.; Liu, F.; Chapman, M.A.; Cao, D.; Li, J. Deep learning for LiDAR point clouds in autonomous driving: A review. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 3412–3432. [Google Scholar] [CrossRef] [PubMed]
- Eitel, J.U.; Höfle, B.; Vierling, L.A.; Abellán, A.; Asner, G.P.; Deems, J.S.; Glennie, C.L.; Joerg, P.C.; LeWinter, A.L.; Magney, T.S.; et al. Beyond 3-D: The new spectrum of lidar applications for earth and ecological sciences. Remote Sens. Environ. 2016, 186, 372–392. [Google Scholar] [CrossRef] [Green Version]
- Liu, W.; Sun, J.; Li, W.; Hu, T.; Wang, P. Deep learning on point clouds and its application: A survey. Sensors 2019, 19, 4188. [Google Scholar] [CrossRef] [Green Version]
- Endo, Y.; Javanmardi, E.; Kamijo, S. Analysis of Occlusion Effects for Map-Based Self-Localization in Urban Areas. Sensors 2021, 21, 5196. [Google Scholar] [CrossRef]
- Böhm, J. Facade detail from incomplete range data. In Proceedings of the ISPRS Congress, Beijing, China, 3–11 July 2008; Volume 1, p. 2. [Google Scholar]
- Goyal, A.; Law, H.; Liu, B.; Newell, A.; Deng, J. Revisiting point cloud shape classification with a simple and effective baseline. In Proceedings of the International Conference on Machine Learning, PMLR, Online, 18–24 July 2021; pp. 3809–3820. [Google Scholar]
- Chen, X.; Chen, B.; Mitra, N.J. Unpaired point cloud completion on real scans using adversarial training. arXiv 2019, arXiv:1904.00069. [Google Scholar]
- Sarmad, M.; Lee, H.J.; Kim, Y.M. Rl-gan-net: A reinforcement learning agent controlled gan network for real-time point cloud shape completion. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 5898–5907. [Google Scholar]
- Yuan, W.; Khot, T.; Held, D.; Mertz, C.; Hebert, M. Pcn: Point completion network. In Proceedings of the 2018 International Conference on 3D Vision (3DV), Verona, Italy, 5–8 September 2018; pp. 728–737. [Google Scholar]
- Huang, Z.; Yu, Y.; Xu, J.; Ni, F.; Le, X. Pf-net: Point fractal network for 3d point cloud completion. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 7662–7670. [Google Scholar]
- Tchapmi, L.P.; Kosaraju, V.; Rezatofighi, H.; Reid, I.; Savarese, S. Topnet: Structural point cloud decoder. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 383–392. [Google Scholar]
- Bello, S.A.; Yu, S.; Wang, C.; Adam, J.M.; Li, J. Deep learning on 3D point clouds. Remote Sens. 2020, 12, 1729. [Google Scholar] [CrossRef]
- Guo, Y.; Wang, H.; Hu, Q.; Liu, H.; Liu, L.; Bennamoun, M. Deep learning for 3d point clouds: A survey. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 43, 4338–4364. [Google Scholar] [CrossRef] [PubMed]
- Aoki, Y.; Goforth, H.; Srivatsan, R.A.; Lucey, S. Pointnetlk: Robust & efficient point cloud registration using pointnet. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 7163–7172. [Google Scholar]
- Sarode, V.; Li, X.; Goforth, H.; Aoki, Y.; Srivatsan, R.A.; Lucey, S.; Choset, H. Pcrnet: Point cloud registration network using pointnet encoding. arXiv 2019, arXiv:1908.07906. [Google Scholar]
- Ge, L.; Cai, Y.; Weng, J.; Yuan, J. Hand pointnet: 3d hand pose estimation using point sets. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 8417–8426. [Google Scholar]
- Qi, C.R.; Su, H.; Mo, K.; Guibas, L.J. Pointnet: Deep learning on point sets for 3d classification and segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 652–660. [Google Scholar]
- Qi, C.R.; Yi, L.; Su, H.; Guibas, L.J. Pointnet++: Deep hierarchical feature learning on point sets in a metric space. arXiv 2017, arXiv:1706.02413. [Google Scholar]
- Geiger, A.; Lenz, P.; Stiller, C.; Urtasun, R. Vision meets Robotics: The KITTI Dataset. Int. J. Robot. Res. 2013, 32, 1231–1237. [Google Scholar] [CrossRef] [Green Version]
- Lu, H.; Shi, H. Deep Learning for 3D Point Cloud Understanding: A Survey. arXiv 2020, arXiv:2009.08920. [Google Scholar]
- Thomas, H.; Qi, C.R.; Deschaud, J.E.; Marcotegui, B.; Goulette, F.; Guibas, L.J. Kpconv: Flexible and deformable convolution for point clouds. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Korea, 27 October–2 November 2019; pp. 6411–6420. [Google Scholar]
- Hu, Q.; Yang, B.; Xie, L.; Rosa, S.; Guo, Y.; Wang, Z.; Trigoni, N.; Markham, A. Randla-net: Efficient semantic segmentation of large-scale point clouds. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 11108–11117. [Google Scholar]
- Wu, W.; Qi, Z.; Fuxin, L. Pointconv: Deep convolutional networks on 3d point clouds. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 9621–9630. [Google Scholar]
- Maturana, D.; Scherer, S. Voxnet: A 3d convolutional neural network for real-time object recognition. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 922–928. [Google Scholar]
- Yang, B.; Wang, J.; Clark, R.; Hu, Q.; Wang, S.; Markham, A.; Trigoni, N. Learning object bounding boxes for 3d instance segmentation on point clouds. arXiv 2019, arXiv:1906.01140. [Google Scholar]
- Makhzani, A.; Shlens, J.; Jaitly, N.; Goodfellow, I.; Frey, B. Adversarial autoencoders. arXiv 2015, arXiv:1511.05644. [Google Scholar]
- Moenning, C.; Dodgson, N.A. A new point cloud simplification algorithm. In Proceedings of the 3rd IASTED International Conference on Visualization, Imaging, and Image Processing (VIIP 2003), Benalmadena, Spain, 8–10 September 2003; pp. 1027–1033. [Google Scholar]
- Moenning, C.; Dodgson, N.A. Fast marching farthest point sampling for implicit surfaces and point clouds. Comput. Lab. Tech. Rep. 2003, 565, 1–12. [Google Scholar]
- Landrieu, L.; Simonovsky, M. Large-scale point cloud semantic segmentation with superpoint graphs. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 4558–4567. [Google Scholar]
- Yin, K.; Chen, Z.; Huang, H.; Cohen-Or, D.; Zhang, H. LOGAN: Unpaired shape transform in latent overcomplete space. ACM Trans. Graph. (TOG) 2019, 38, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Yu, L.; Fu, C.W.; Cohen-Or, D.; Heng, P.A. Unsupervised detection of distinctive regions on 3D shapes. ACM Trans. Graph. 2020, 39, 1–14. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, Q.; Ni, B.; Li, L.; Liu, J.; Zhou, M.; Tian, Q. Modeling point clouds with self-attention and gumbel subset sampling. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 3323–3332. [Google Scholar]
- Lang, I.; Manor, A.; Avidan, S. Samplenet: Differentiable point cloud sampling. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 7578–7588. [Google Scholar]
- Dovrat, O.; Lang, I.; Avidan, S. Learning to sample. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 2760–2769. [Google Scholar]
- Berger, J.O. Certain standard loss functions. In Statistical Decision Theory and Bayesian Analysis, 2nd ed.; Springer: New York, NY, USA, 1985; pp. 60–64. [Google Scholar]
- Fan, H.; Su, H.; Guibas, L.J. A point set generation network for 3d object reconstruction from a single image. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 605–613. [Google Scholar]
- Moore, A. The case for approximate Distance Transforms. In Proceedings of the The 14th Annual Colloquium of the Spatial Information Research Centre, University of Otago, Dunedin, New Zealand, 3–5 December 2002. [Google Scholar]
- Fix, E.; Hodges, J.L., Jr. Discriminatory Analysis-Nonparametric Discrimination: Small Sample Performance; Technical Report; University of California: Berkeley, CA, USA, 1952. [Google Scholar]
- Goldberger, J.; Hinton, G.E.; Roweis, S.; Salakhutdinov, R.R. Neighbourhood components analysis. Adv. Neural Inf. Process. Syst. 2004, 17. [Google Scholar]
- Plötz, T.; Roth, S. Neural nearest neighbors networks. arXiv 2018, arXiv:1810.12575. [Google Scholar]
- Wang, Y.; Sun, Y.; Liu, Z.; Sarma, S.E.; Bronstein, M.M.; Solomon, J.M. Dynamic graph cnn for learning on point clouds. ACM Trans. Graph. 2019, 38, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Levina, E.; Bickel, P. The earth mover’s distance is the mallows distance: Some insights from statistics. In Proceedings of the Proceedings Eighth IEEE International Conference on Computer Vision, ICCV 2001, Vancouver, BC, Canada, 7–14 July 2001; Volume 2, pp. 251–256. [Google Scholar]
- Liu, M.; Sheng, L.; Yang, S.; Shao, J.; Hu, S.M. Morphing and Sampling Network for Dense Point Cloud Completion. arXiv 2019, arXiv:1912.00280. [Google Scholar] [CrossRef]
- Singer, N.; Asari, V.K.; Aspiras, T.; Schierl, J.; Stokes, A.; Keaffaber, B.; Van Rynbach, A.; Decker, K.; Rabb, D. Attention Focused Generative Network for Reducing Self-Occlusions in Aerial LiDAR. In Proceedings of the 2021 IEEE Applied Imagery Pattern Recognition Workshop (AIPR), Washington, DC, USA, 12–14 October 2021; pp. 1–7. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; pp. 234–241. [Google Scholar]
- Groueix, T.; Fisher, M.; Kim, V.G.; Russell, B.C.; Aubry, M. A papier-mâché approach to learning 3d surface generation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 216–224. [Google Scholar]
- Wen, X.; Li, T.; Han, Z.; Liu, Y.S. Point cloud completion by skip-attention network with hierarchical folding. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 1939–1948. [Google Scholar]
- Yang, Y.; Feng, C.; Shen, Y.; Tian, D. Foldingnet: Point cloud auto-encoder via deep grid deformation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 206–215. [Google Scholar]

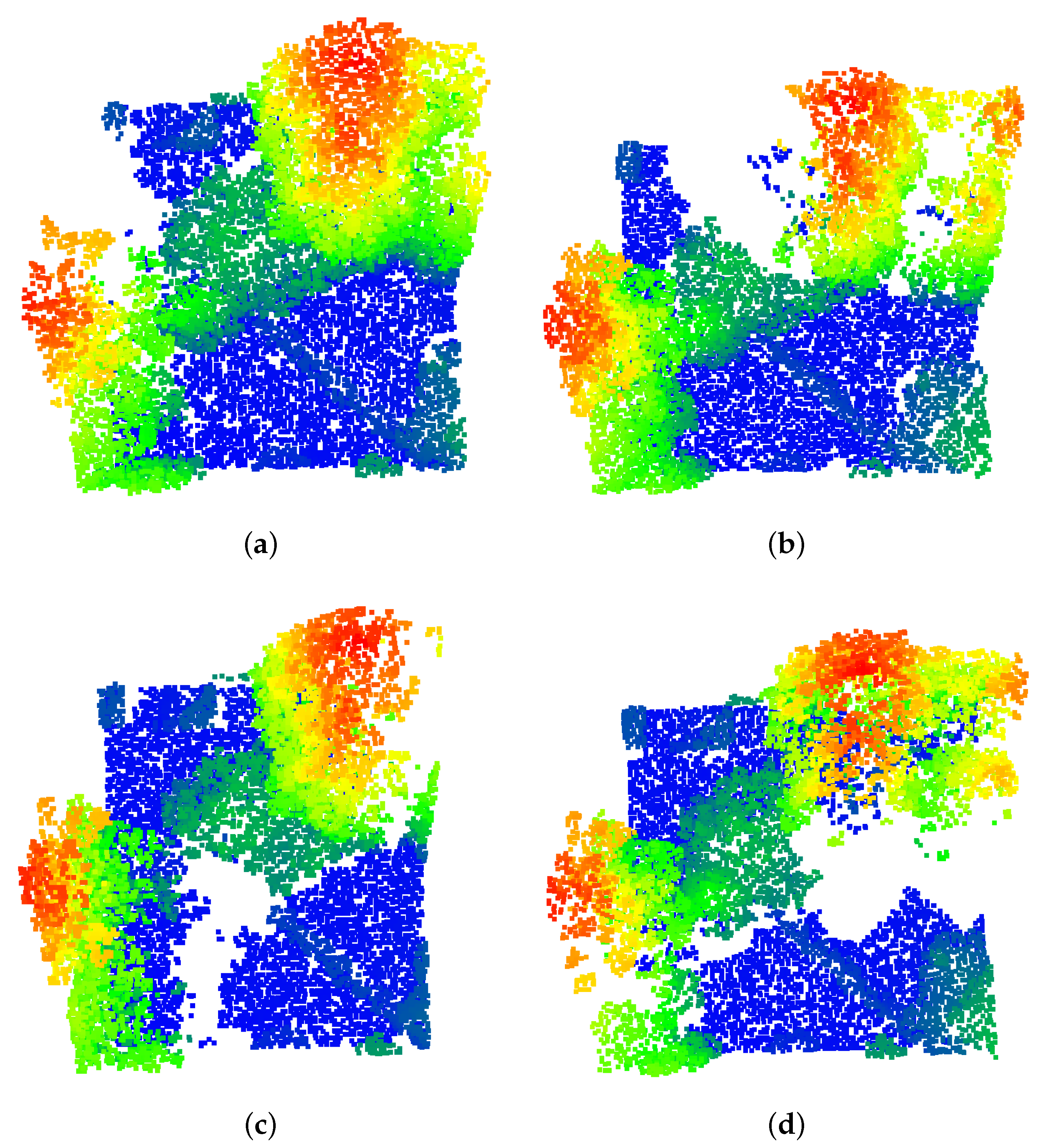
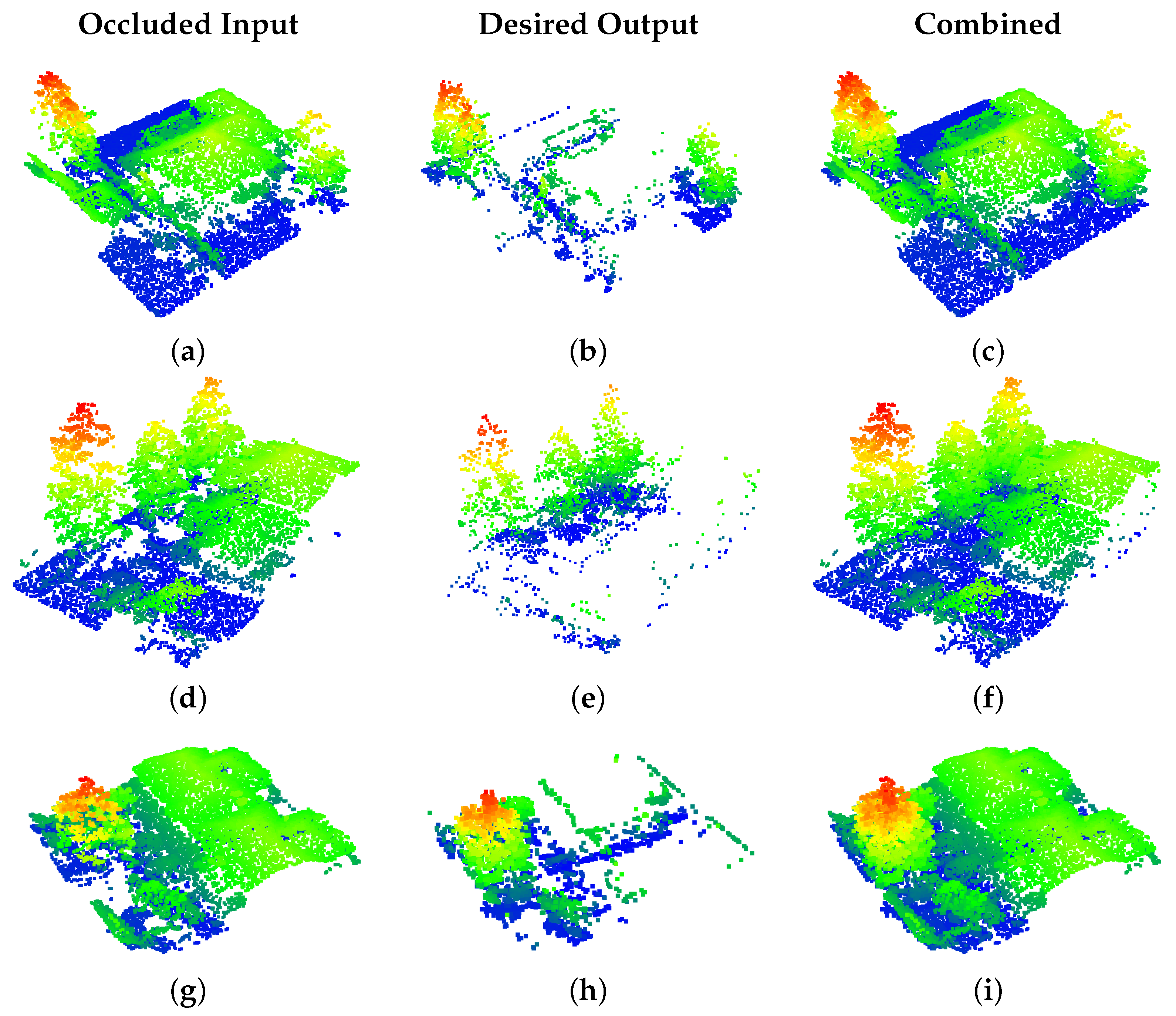
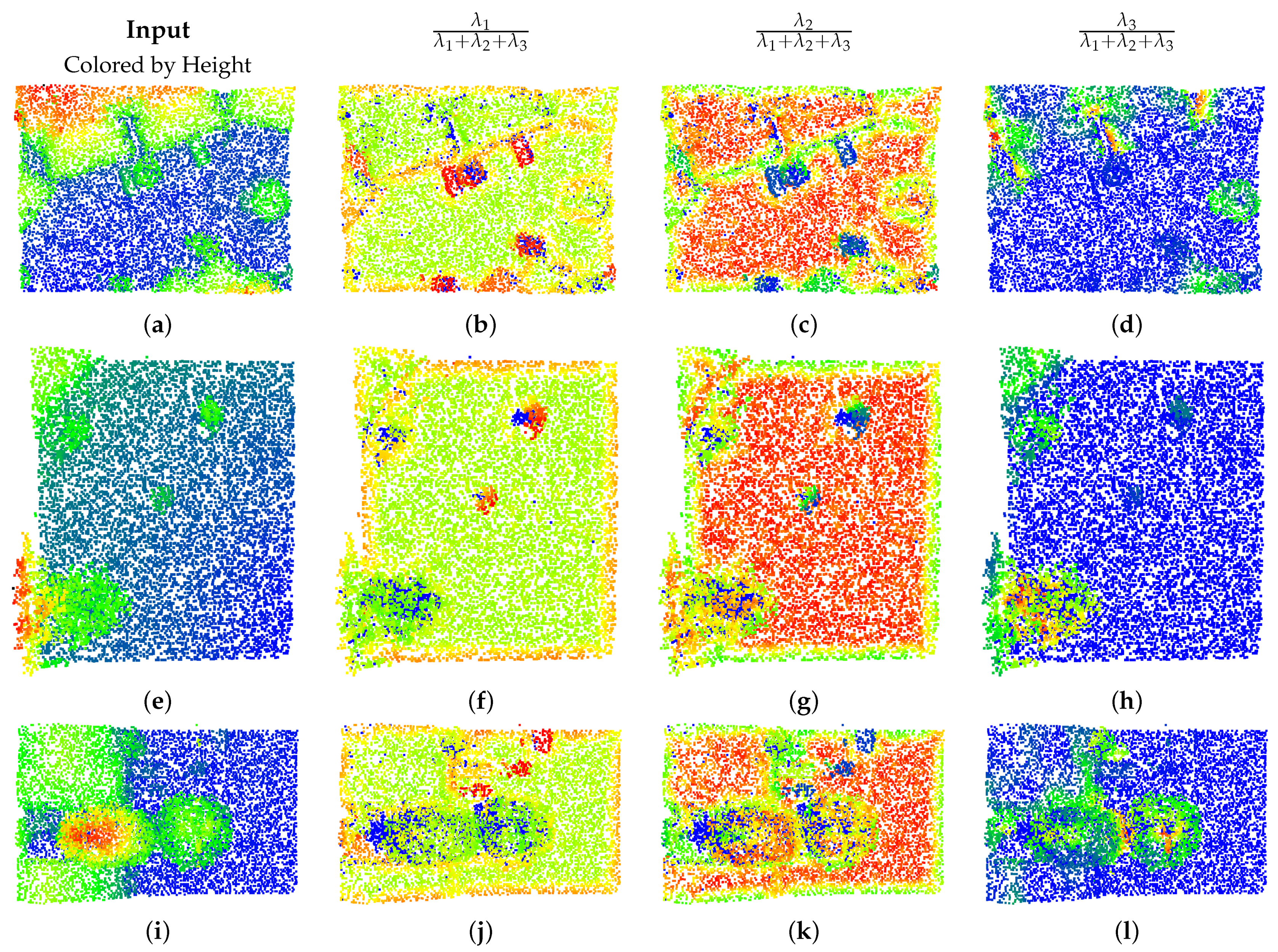






| Overall Results: DALES Viewpoints Version 2 Dataset | ||
|---|---|---|
| Method | Mean CD ↓ | Mean EMD ↓ |
| TopNet [16] | 0.002167 | 0.071537 |
| PCN [14] | 0.001802 | 0.068283 |
| ATLASNet [51] | 0.000474 | 0.067515 |
| PointNetFCAE [16] | 0.000468 | 0.112022 |
| SA-Net [52] | 0.000433 | 0.039664 |
| FoldingNet [53] | 0.000424 | 0.097007 |
| Ours | 0.000375 | 0.035604 |
| Overall Results: Point Cloud Completion Network Dataset | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Methods | Mean | Plane | Cab. | Car | Chair | Lamp | Couch | Table | Boat |
| AtlasNet [51] | 17.69 | 10.37 | 23.4 | 13.41 | 24.16 | 20.24 | 20.82 | 17.52 | 11.62 |
| FoldingNet [53] | 16.48 | 11.18 | 20.15 | 13.25 | 21.48 | 18.19 | 19.09 | 17.8 | 10.69 |
| PCN [14] | 14.72 | 8.09 | 18.32 | 10.53 | 19.33 | 18.52 | 16.44 | 16.34 | 10.21 |
| TopNet [16] | 9.72 | 5.5 | 12.02 | 8.9 | 12.56 | 9.54 | 12.2 | 9.57 | 7.51 |
| SA-Net [52] | 7.74 | 2.18 | 9.11 | 5.56 | 8.94 | 9.98 | 7.83 | 9.94 | 7.23 |
| Ours | 7.10 | 2.51 | 10.29 | 10.29 | 8.07 | 6.54 | 6.64 | 6.61 | 5.87 |
| Ablation Study: Eigen Feature Sampling | ||
|---|---|---|
| Sampling Method | Mean CD ↓ | Mean EMD ↓ |
| FPS | 0.00208 | 0.07594 |
| SampleNet [38] | 0.00282 | 0.13035 |
| Eigen Feature Sampling (Ours) | 0.00184 | 0.05244 |
| Ablation Study: Point Projection for Stabilizing Point Correspondences | ||
|---|---|---|
| Method | Mean CD ↓ | Mean EMD ↓ |
| Single Network | 0.00208 | 0.07594 |
| Parallel Network (Ours) | 0.00167 | 0.04951 |
| Semantic Segmentation: Overall Results | ||
|---|---|---|
| Overall Accuracy | Mean IoU | |
| Dataset 1 | 0.685 | 0.395 |
| Dataset 2 | 0.865 | 0.451 |
| Semantic Segmentation: Per Class IoU | ||||||||
|---|---|---|---|---|---|---|---|---|
| ground | buildings | cars | trucks | poles | power lines | fences | veg | |
| Dataset 1 | 0.740 | 0.713 | 0.266 | 0.262 | 0.204 | 0.660 | 0.148 | 0.556 |
| Dataset 2 | 0.871 | 0.724 | 0.245 | 0.256 | 0.214 | 0.667 | 0.152 | 0.769 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Singer, N.; Asari, V.K. View-Agnostic Point Cloud Generation for Occlusion Reduction in Aerial Lidar. Remote Sens. 2022, 14, 2955. https://doi.org/10.3390/rs14132955
Singer N, Asari VK. View-Agnostic Point Cloud Generation for Occlusion Reduction in Aerial Lidar. Remote Sensing. 2022; 14(13):2955. https://doi.org/10.3390/rs14132955
Chicago/Turabian StyleSinger, Nina, and Vijayan K. Asari. 2022. "View-Agnostic Point Cloud Generation for Occlusion Reduction in Aerial Lidar" Remote Sensing 14, no. 13: 2955. https://doi.org/10.3390/rs14132955
APA StyleSinger, N., & Asari, V. K. (2022). View-Agnostic Point Cloud Generation for Occlusion Reduction in Aerial Lidar. Remote Sensing, 14(13), 2955. https://doi.org/10.3390/rs14132955








