Abstract
Theoretically, the spectral efficiency of in-band full-duplex underwater acoustic communications (IBFD-UWAC) is twice that of a half-duplex one. However, the actual achievable spectral efficiency of IBFD-UWAC is determined by the performance of the self-interference cancellation (SIC). In addition, the hostile underwater environment poses a challenge to the tracking performance of the SIC due to its complexity and variability. In this paper, we propose a digital SIC method based on the improved variable step-size least mean square (IVSS-LMS) algorithm where we modify the step-size adjustment criterion in the classical LMS filter and establishes a nonlinear relationship with the Sigmoid function to control the step-size using the instantaneous state error, thus improving the robustness and tracking performance of IVSS-LMS. Hardware-in-loop simulation (HLS) based on Simulink platform verifies the real-time implementability and effectiveness of the proposed IVSS-LMS algorithm. Furthermore, the sea trial results show that the digital SIC method based on the proposed algorithm can be implemented in real-time and the convergence speed, and steady-state performance are significantly improved.
1. Introduction
To improve the spectrum utilization of underwater communications, scholars have proposed the in-band full-duplex (IBFD) communication technique for an underwater acoustic medium. IBFD underwater acoustic communication (IBFD-UWAC) can simultaneously transmit and receive signals in the same frequency band, which can theoretically achieve twice the frequency utilization compared to a half-duplex one. In the context of the severely limited spectrum resources available for underwater acoustic channels [1], the main challenge in the implementation of IBFD-UWAC is the SI cancellation (SIC) [2,3,4,5].
Currently, most of the available SIC methods are implemented in the digital or analog domain. The self-interference (SI) signal is first cancelled in the analog domain, and the cancelled residuals enters into the digital domain for further cancellation [6,7,8]. The key part of the implementation of analog SIC is to reconstruct the analog domain copy of the self-interference signal using a dedicated link. Depending on the type of input signal to the dedicated link, analog SIC can be divided into pure analog SIC and digitally assisted analog SIC. In digitally assisted analogy SIC, the dedicated chain connects the transmitter’s digital baseband to the receiver’s analog passband, and the input to the dedicated link is a digital copy of SI. On the other hand, in pure analogy SIC, the dedicated chain connects the transmitter’s analog passband to the receiver’s analog passband, and the input to the dedicated link is an analog copy of the SI [8,9,10]. Analog SIC results determine the upper limit of theoretical performance of SIC for IBFD-UWAC systems, while digital SIC determines the final practical performance of the cancellation. Thus, how to design the digital SIC scheme is of crucial importance.
S. Chen et al. proposed division-free duplex for future wireless systems, with results from an experimental RF system yielding some 72 dB duplex isolation at 1.8 GHz in 1998 [2]. In 2013, S. Li et al. used the power amplifier output as a reference signal to convert the nonlinear problem into a linear problem, and achieved a SI cancellation effect of nearly 70 dB when the antenna isolation reached 20 dB through a two-step digital SI cancellation method [11]. In 2018, S. Gan et al. proposed a ML algorithm with sparse constraints to realize digital SI cancellation of sparse SI channels. The method was simulated and experimentally verified in the literature, and the maximum digital SI cancellation effect of 43 dB was obtained. Compared with the LS algorithm, the convergence is faster and the cancellation effect is better [12].
However, the literatures mentioned above have focused on offline SIC algorithms conducted in the laboratory without considering the limitations of real-time implementation and therefore cannot be directly applied to practical engineering application. In 2015, Tom Vermeulen et al. proposed a real-time IBFD RF SIC scheme for wireless communications, which achieved a 60 dB SIC [13]. However, to the best of the authors’ knowledge, there is no literature that has studied real-time digital SIC techniques for IBFD-UWA systems. Based on the above, this paper first proposes a real-time digital domain SIC scheme, using a hardware-in-loop simulation (HLS) technique.
So far, many VSS-LMS algorithms with different step size adjustment criteria have been developed, and the step size adjustment criteria are used to optimize the performance of LMS algorithm, so as to solve some engineering application problems [14,15,16,17,18,19,20,21,22,23]. Among them, Kwong et al. first proposed the variable step size minimum mean square error (VSS-LMS) algorithm and used the instantaneous error signal to adjust the step size in real time [14]. Then, Jalal, B et al. proposed the step size adjustment principle based on Sigmoid function which can be applied to engineering practice [24,25,26,27], and compared it with the traditional LMS algorithm to verify the superiority of the proposed algorithm; Sui Zeping et al. proposed the NRVSLMS algorithm with double Sigmoid functions, and applied this algorithm to OFDM underwater acoustic channel equalization to obtain lower BER and MSE [28].
It is worth noting that in the field of IBFD-UWA, the far-end desired signal, although is useful in the demodulation, acts like an interference signal in the SIC, specifically, in the process of SI channel estimation, thus degrading the performance of SIC. Therefore whether the influence of the far-end communication signal can be handled correctly is the key to the performance of SIC. In this paper, an improved VSS-LMS (IVSS-LMS) algorithm for IBFD-UWAC is designed, which modifies the step size adjustment criterion based on the modified Sigmoid function and uses the instantaneous state error to adaptively determine the arrival state of the far-end desired signal and the degree of cancellation in real-time and adjust the step size. This greatly reduces the influence of the desired signal on the residual SI channel estimation process, improves the accuracy of the residual SI channel estimation, and in turn, improves the digital domain SIC performance.
2. Fundamentals
2.1. System Model
In a IBFD-UWAC system, any communication node can send and receive data in the same frequency band simultaneously. Therefore, as shown in Figure 1, for any node, it not only receives the far-end communication signal, but also receives the SI signal formed by its own transmitting signal. Due to the high power of the local SI signal, causing the far-end desired signal to be overwhelmed in the SI signal, the analog SIC process is first needed to cancel out most of the SI signal, and, after the analog cancellation, there is a part of the interference signal remaining, which needs to be further cancelled in digital domain, i.e., digital SIC. In this paper, we focus on the digital SIC method.
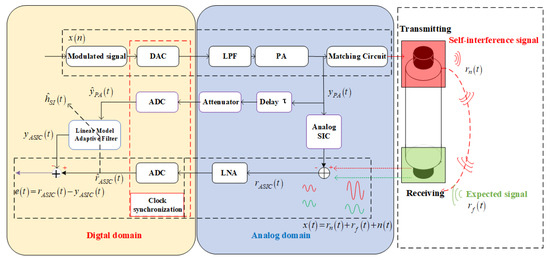
Figure 1.
IBFD-UWAC system SIC model.
From Figure 1, it can be seen that the received signal is:
where is the local transmit signal at the near-end (SI signal), is the far-end desired signal, and is the underwater ambient noise signal. Assuming that the channel between the local transmitter and the receiver is , we have:
where ⊗ imply convolution. After the analog domain SIC, the output signal passes through the LNA and is captured locally to obtain the desired signal for digital interference cancellation. In order to fully consider the impact of amplifier nonlinear distortion on the SIC process, in the scheme, the amplifier output signal is collected locally through the attenuator to obtain as the reference signal for the digital domain SIC, and the desired signal is simultaneously passed through the adaptive filter to estimate the SI channel. After the SI channel is obtained, the SI signal can be reconstructed as . The cancelled signal after the digital domain SIC can be expressed as .
2.2. IVSS-LMS Algorithm
In general, considering the real-time implementation purpose, SI channels are generally estimated using the LMS family algorithms. For traditional LMS algorithm, the squared error is used instead of the mean squared error. The cost function is denoted as
Then, the derivative of the cost function can be expressed as:
Based on Equations (3) and (4), the following update rule for the weight coefficients of the LMS algorithm can be obtained:
where are the adaptive filter weight coefficients, which, in this system, can be viewed as the local SI channel estimated in real-time state and is the convergence step of the adaptive filter algorithm.
Reference signal and the linear filter tapped weight coefficients are, respectively, given as:
The SIC performance depends on the degree of fitting of the filter’s real-time estimate of to the real SI channel , based on Figure 1 and the convolution rule, which also means the degree of fitting of to . However, the step-size of the conventional LMS algorithm is fixed, so the convergence speed, the tracking capability of the time-varying channel, and the steady-state error are constrained. To address the above problems, scholars have studied the VSS-LMS algorithm, and the core idea is to establish constraints between the state error and the step-size factor so that the step-size can be adaptively modified and adjusted according to the current condition to obtain better filter effects. The principle of step-size adjustment in VSS-LMS mentioned in literature [13] is shown in the following equation:
where controls the convergence speed of the step change principle, b controls the trend of the step change after the filter converges to the steady state, and c controls the maximum value of the step adjustment principle. In literature [13], after experimental analysis, it proves that when and the system has the best results; however, in literature simulation, the number of taps is 2, which does not match the IBFD-UWAC channel, Figure 2 shows the state error and step factor relationship in this paper, where Figure shows the case of and the case of .
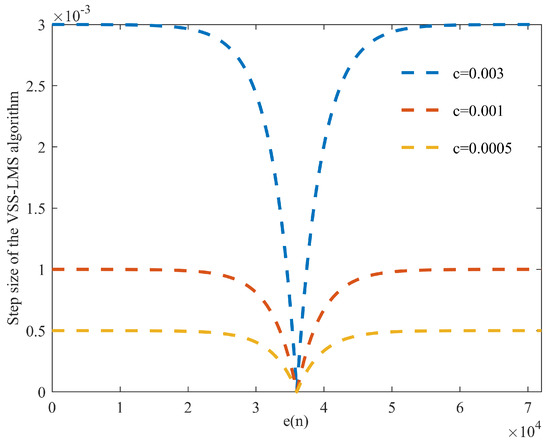
Figure 2.
Relationship between error and step factor in literature [28].
As can be seen from Figure 2, although the algorithm proposed in literature [28] can reduce the step-size adaptively when the error tends to zero (the filter is close to the steady state), for the IBFD-UWAC system, the arrival of the far-end desired signal causes the error to fluctuate, causing the filter step-size to increase, which leads to a decrease in the accuracy of the SI channel estimation, thus degrading the SIC effect.
To solve the above mentioned problems, this paper takes LMS filter as the main body and divides the cancellation process into three cases:
- When the SI signal is energetically large and the far-end desired signal is overwhelmed in the high-power SI signal, or when there is no desired signal and the error mainly originates from the SI signal;
- When the filter iteration is close to the steady state, the error floating due to the arrival of the desired signal, and the error mainly comes from the desired signal;
- When the filter iteration is close to the steady state, there is no arrival of the desired signal, and the error mainly comes from the environmental noise.
In order to solve the problems faced in the above three cases, this paper proposes a segmented variable step-size criterion adjusted according to the instantaneous state error, which is based on the Sigmoid function for correction. In the IBFD-UWAC system, the energy range of the desired signal arrival is generally predicted, which is due to the fact that, in general, the desired signal at the far-end needs to occur after SIC and needs to satisfy the signal to interference plus noise ratio (SINR) condition required for the final demodulation; therefore, in this paper, we introduce parameters to constrain the step-size variation. Inspired by the literature [29] and the Hampel trigonometric function, the step-size adjustment criterion is set as follows:
where , is the square root of the error variance in the instantaneous update state at n moments, and is the lower threshold value that is related to and , allowing the step-size to be adjusted using the second branch, which is calculated as follows:
where is the variance of the underwater ambient noise, which can be easily collected, is defined as the minimum SINR that guarantees the system’s bit error rate (BER) performance. In this paper, we assume that the transmit power of the far-end desired signal is sufficient to ensure that the SINR of the desired signal is when it reaches the near-end receiver. is the square root of the variance of the instantaneous desired signal , is a compensation factor, and are the parameters that control the shape of the modified Sigmoid function.
It is worth noting that, compared to other conventional VSS-LMS algorithms, such as Equation (7) proposed in [28], the proposed algorithm for the IBFD-UWAC system novelty sets a threshold that reduces the desired signal impact on the SIC by decreasing the step-size when the desired signal with predicted energy arrives
Algorithm Steps
The basic flow of the proposed IVSS-LMS algorithm is explained in Table 1.

Table 1.
The specific steps of the proposed algorithm.
To sum up, this paper designs an novel adjustment criterion that is different from the conventional IVSS-LMS algorithm, and the design idea of this criterion is as follows:
- When the error is large, , the algorithm judges that a large SI signal or sudden change in the local environment occurs in this state, so we adjusted step-size to the maximum value , in order to improve the convergence speed of the algorithm.
- When the error is close to the predetermined desired signal arrival threshold, . We adjust the step-size to the minimum value , in order to reduce the steady-state error, improve the steady-state performance, and avoid the influence of the system expectation signal on the filter, which causes a decrease in the channel estimation accuracy.
- When , the algorithm uses the Sigmoid function as a constraint that causes step-size to vary between the maximum values and minimum values for change.
2.3. Hardware-in-Loop Simulation (HLS)
The time of traditional digital simulation is determined by the execution speed of the program code itself, and in most cases, the execution speed of the SIC algorithm is much slower than the real-world system operation speed, which results non-real-time simulation. On the other side, the real-time implementation means that the simulation process program execution time is synchronized with the actual time, and the HLS can be directly performed. In this paper, we use Matlab/Simulink real-time simulation toolbox for real-time simulation, and the experimental platform for IBFD-UWAC SIC simulation is built in External mode under Desktop Real-time, with a simulation step-size of 1/18,000 s, which is sufficient for real-time IBFD-UWAC system.
In what follows we describe the architecture of the HLS and its implementation. The architecture of the HLS consists of two parts: simulation platform and the actual hardware components. Figure 3 shows the NI-DAQ hardware interface and explaining the device connection scheme.
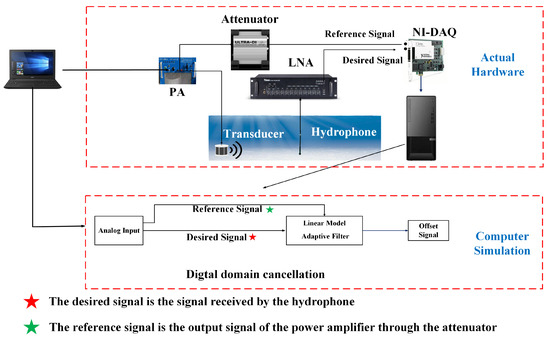
Figure 3.
NI-DAQ hardware interface and the device connection scheme.
This paper mainly focuses on the digital SIC algorithm. However, if the energy of the SI signal fed to the LNA is too high, the resulting saturation effect causes a decrease in the SNR of the far-end desired signal. Therefore, this paper assumes that the SI signal has been preliminary processed by analog SIC to ensure that the saturation effect of the LNA is not triggered. The signal being processed by the proposed digital SIC algorithm is the output signal of the LNA, that is, . In this paper, in order to fully consider the effect of amplifier nonlinear distortion, the reference signal is the power amplifier output signal . The output signal of attenuator is collected locally, and the digital domain SIC is performed by passing and through each of the adaptive filter algorithms described above, where the signals are captured locally by NI-DAQ devices.
The top of Figure 4 shows the flow chart of the program in Simulink Desktop Real-time EXTERN mode.
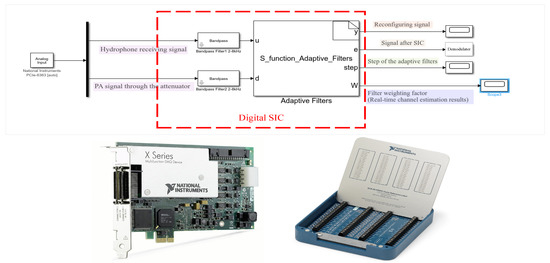
Figure 4.
The top is Simulink program block diagram and the bottom is PCIe-6363 device and NI SCB-68A Terminal Block, respectively.
Analog Input: Based on the NI PCIE-6363 DAQ device (shown in the bottom left figure of Figure 4), the analog signal input is completed, the device has 16-bit analog to digital Converters, the transmission rate reaches 2.00 MSample/s, and the sampling frequency is set to 18 kHz. The hardware is connected to the computer through the SCB-68A (shown in the bottom right figure of Figure 4) and the RTSI bus, and the data is transferred to the Simulink platform to complete the hardware-in-the-loop simulation.
Desktop Real-time: The experiment is conducted in EXTERN mode; the System target file is selected as “sldrtert.tlc” file; the simulation solver is selected as fixed step ode5 (Dormand-Prince); the simulation step is determined as 1/18,000 s.
Algorithm: S-function Builder in Simulink is used for the design and optimization of the algorithm. The IVSS-LMS algorithm proposed in this paper has two inputs: the reference signal and the desired signal, and four outputs: the reconstructed signal, the signal after SIC, the step-size of the adaptive filter, and the filter weight coefficients (in IBFD-UWAC system, it is treated as the estimated channel in real-time).
Data Inspector: During real-time simulation, you can set the simulation duration, during which all data can be exported through this module in order to check the validity of the data.
3. HLS and Experimental Results Analysis
3.1. Normalized Mean Squared Error (NMSE) Criterion
To evaluate the estimation performance of each scheme for the SI channel estimation, the normalized mean squared error (NMSE) is used as the performance evaluation criterion for each scheme, which is calculated as follows:
where denotes the simulated channel at time n, and denotes the estimated channel at time n.
To better demonstrate the tracking and steady-state performance of the SIC algorithm under time-varying channels, we obtained the modified NMSE (M-NMSE) performance metrics by replacing the SI channel in (10) with the SI signal , which is calculated using the following equation:
where is the SI signal, denotes the transpose of the estimated channel at time n, is the reference signal. M-NMSE curves can better illustrate the effect of SIC in real-time.
3.2. HLS Results
The simulation in this section is divided into two parts:
3.2.1. Optimal Parameters of IVSS-LMS
The first part simulates the case of high SNR of input signal, and clarifies the specific meaning of each parameter in the IVSS-LMS algorithm, finding the optimal parameter in the IVSS-LMS algorithm.In this simulation, is 60 dB, the simulation time is 10 s and the parameters , the simulation under different , and , are shown in Figure 5, respectively.
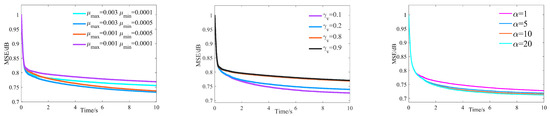
Figure 5.
The MSE curves of the IVSS-LMS algorithm with different parameters. Left shows the MSE curves of the IVSS-LMS algorithm with different step-size, middle shows the MSE curves of the IVSS-LMS algorithm with different and right shows the MSE curves of the IVSS-LMS algorithm with different .
It can be seen that compensation factor is the parameter that controls when to start adjusting the step-size, which is taken as 0.1 in the subsequent simulations in this paper, and is the maximum and minimum step-size of the IVSS-LMS filter, and is the parameter that controls the rate of change of the step-size in the filter.
3.2.2. Practical Considerations
In the second part, we consider the following scenario, where the local SI signal is a direct sequence spread spectrum signal with a frequency band of 2–4 KHz. is set as 40 dB, and the number of channel taps is 1000. To better demonstrate the comparison of each algorithm under the three different cases in Section 2.2, we consider three cases in the following simulations.
The time-frequency diagram of the original near-end transmitting signal and the original far-end transmitting signal are shown in Figure 6 and Figure 7, the DSSS signal is used in the simulation and sea trial experiment. The number of spread spectrum chips is 127, and the chip duration is 0.5 millisecond, the communication bandwidth is 2000 Hz, the carrier center frequency is 3000 Hz, the sampling rate is 18,000 Hz, each spread spectrum sequence can carry 3 bits of information each time, and the communication rate is 47.2 bps.
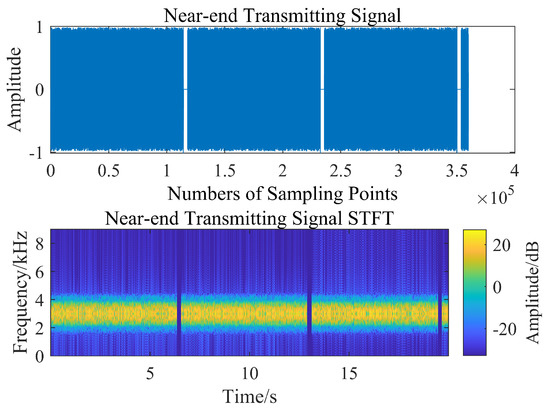
Figure 6.
Time-frequency diagram of the original near-end transmitting signal.
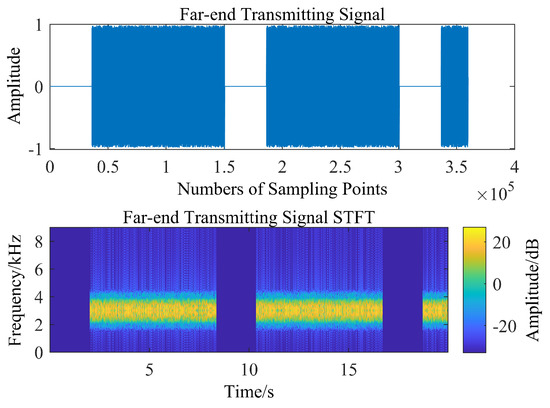
Figure 7.
Time-frequency diagram of the original far-end transmitting signal.
The first case: There is no far-end desired signal in IBFD-UWAC system. The parameters are set as follows: , and for the IVSS-LMS algorithm, for the VSS-LMS algorithm, for the LMS algorithm. According to Section 2.3, this simulation experiment sets , then the threshold is obtained as follows: .
From Figure 8 and Figure 9, we can learn that, when there is no far-end desired signal, the VSS-LMS and the IVSS-LMS algorithms start with a good convergence speed. Since the SNR of the SI signal is 40 dB, and the minimum SINR of desired signal to guarantee the system’s BER performance is 25 dB, therefore, the minimum amount of SIC is required to reach 40 dB, which means the value of M-NMSE should be lower than −15 dB, as labeled as lower limit of desired signal demodulation in Figure 9. From Figure 9, we can see that thanks to the threshold setting, IVSS-LMS can adaptively reduce the convergence rate when it approaches the value of −15 dB of M-NMSE, thus improving the steady-state performance of the algorithm; however, the conventional VSS-LMS cannot adaptively optimize the convergence rate when it reaches the same limit, resulting in a degradation of the steady-state performance.
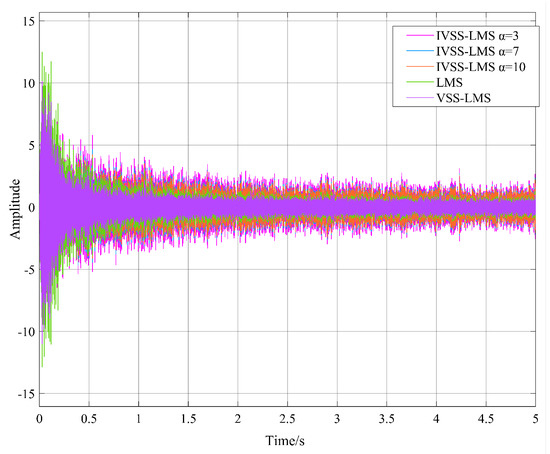
Figure 8.
Real-time cancellation results for each algorithm.
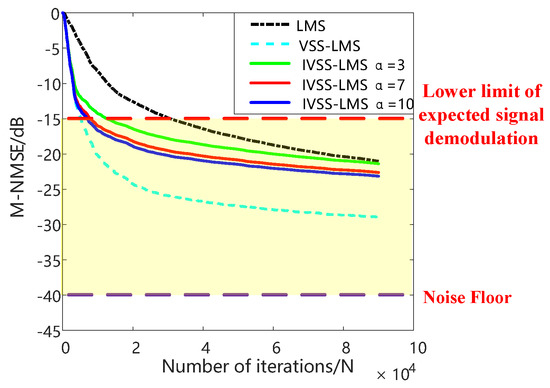
Figure 9.
M-NMSE results for each algorithm.
The second case: the far-end desired signal is always present in the IBFD-UWAC system. Figure 10 and Figure 11, respectively, represent the time-frequency diagram of the signal prior to SIC and the signal after SIC. From Figure 12 and Figure 13, it can be seen that when the far-end desired signal is always present, both the IVSS-LMS and VSS-LMS show good convergence speed; however, when the VSS-LMS algorithm approaches the steady-state, the desired signal affects the local SIC process, making the algorithm less stable and less effective in the steady-state, while the IVSS-LMS algorithm proposed in this paper can converge smoothly with no impact.
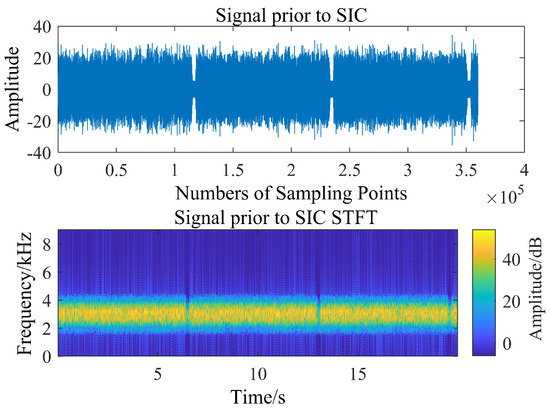
Figure 10.
Time-frequency diagram of the signal prior to SIC.
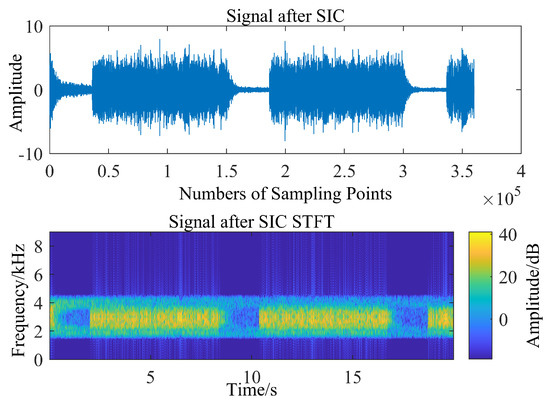
Figure 11.
Time-frequency diagram of the signal after SIC.
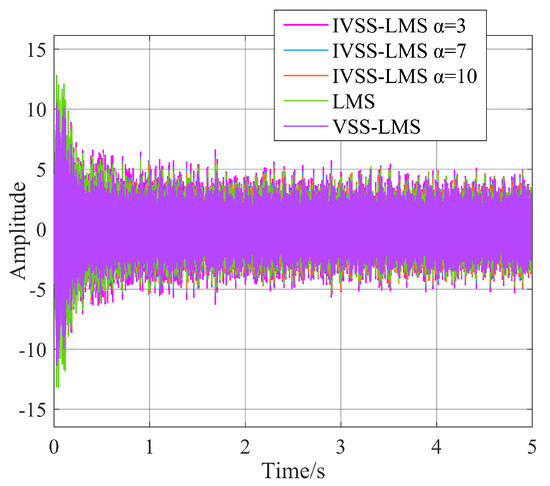
Figure 12.
Real-time cancellation results for each algorithm.
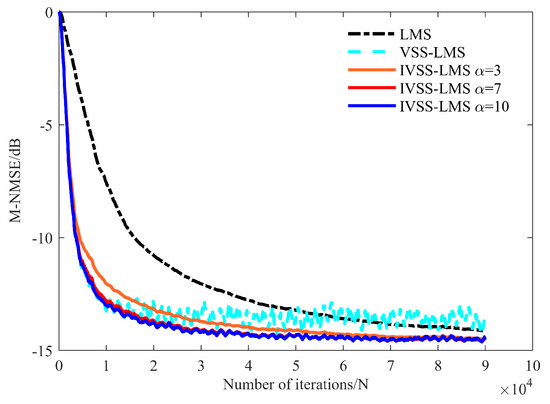
Figure 13.
M-NMSE results for each algorithm.
The third case: Sudden arrival of a desired signal in the IBFD-UWAC system. Figure 14 and Figure 15, respectively, represent the time-frequency diagram of the signal prior to SIC and the signal after SIC. It can be clearly seen from Figure 14 and Figure 15 that after SIC, the SI signal is canceled, and the signal to be demodulated is obtained. Figure 16 shows the real-time cancellation results for each algorithm. Figure 17 shows the M-NMSE results for each algorithm, it can be seen that the far-end desired signal arrives at 4s, and the steady-state effect remains consistent with the simulation results, showing that the algorithm mentioned in this paper can both speed up the convergence at the beginning and reach the set threshold as soon as possible. After that, it adaptively decreases the step-size to achieve the steady-state effect.
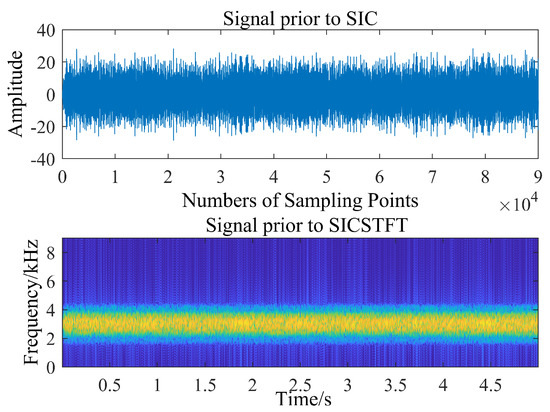
Figure 14.
Time-frequency diagram of the signal prior SIC.
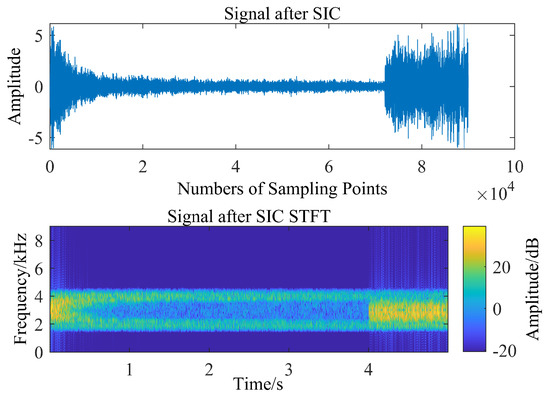
Figure 15.
Time-frequency diagram of the signal after SIC.
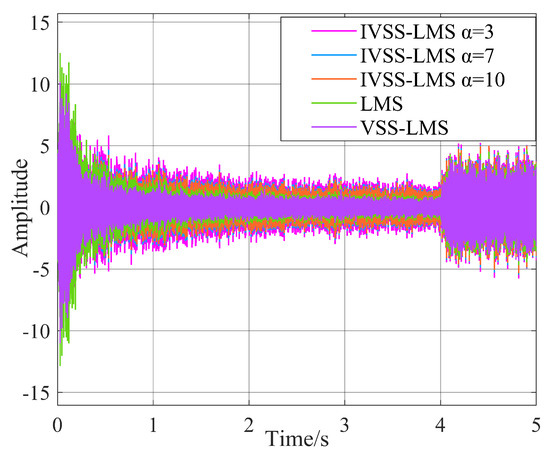
Figure 16.
Real-time cancellation results for each algorithm.
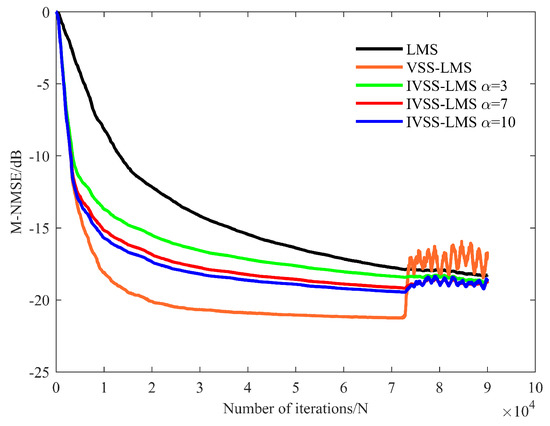
Figure 17.
M-NMSE results for each algorithm.
The fourth case: simulation of sudden changes in the local environment (simulation with local randomly issued impulsive noise for simulation). In practical engineering applications, unexpected situations, such as sudden changes in waves and sea breeze, will occur, which will lead to sudden changes in the local environment. Therefore, in the fourth case, we simulate each algorithm and compares the cancellation performance in the presence of local random impulsive noise.
In this paper, we simulate the scenario with and without the presence of the far-end desired signal, and the simulation results are shown in Figure 18 and Figure 19. Figure 18 and Figure 19 clearly show that both IVSS-LMS and VSS-LMS can show strong adaptability with abrupt changes in the environment and can finish SIC with a faster convergence rate when abrupt changes occur, but close to the steady-state, the IVSS-LMS algorithm shows the optimal results.
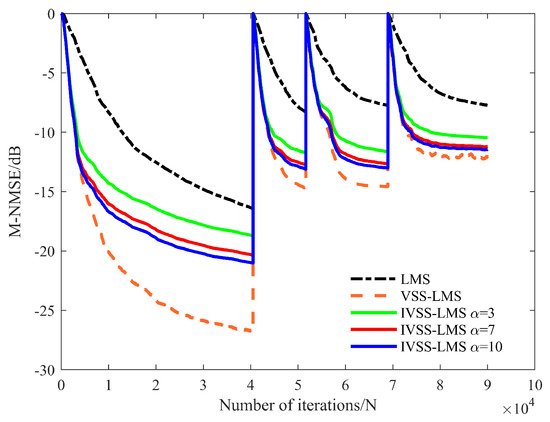
Figure 18.
M-NMSE results of each algorithm when there is no far-end desired signal.
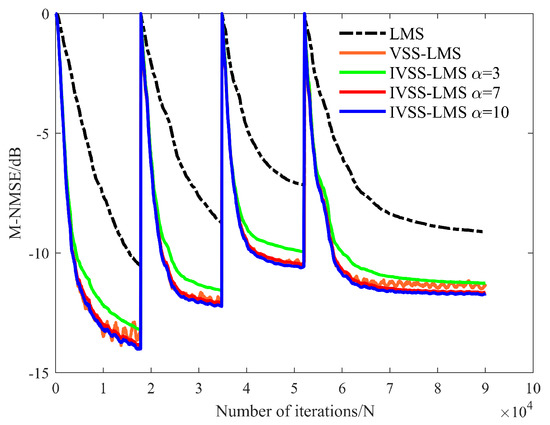
Figure 19.
M-NMSE results of each algorithm when there is a far-end desired signal.
3.3. Sea Trial Test
After the simulation analyses in the previous sections, in order to verify the practicality of the algorithm in this paper, this section will give the results of real-time HLS during the sea trial. This experiment was conducted in May 2021, in the Yellow Sea of Weihai, Shandong Province. The experimental equipment connection diagram is shown in Figure 20; The sampling frequency is 18 kHz, the frequency range of the transducer is 2–8 kHz, the maximum working power of the power amplifier (PA) is 2000 W, we use the 8105 standard hydrophone, the attenuator reduces the output signal of the power amplifier by 40 dB without distortion, and the signal passes Simulink through SCB-68A according to the wiring shown in Figure 21 to complete real-time SIC. The sea trial completed the IBFD-UWAC experiments and the experiments were conducted for the case of no far-end desired signal, as well as a desired signal existing at 5 km in the distance.

Figure 20.
The experimental equipment connection diagram.

Figure 21.
Wiring diagram of SCB-68A in the sea trial.
Experimental scenario 1: There is no far-end desired signal in the IBFD-UWAC system, the experimental scenario shows in Figure 22 and Figure 23, and Figure 24 shows the SI channel estimated at a certain moment in HLS. The role of the adaptive filter in the IBFD-UWAC system is to estimate the SI channel, so the weight coefficient of the adaptive filter in the real-time state is the estimated SI channel in that real-time state. Due to the time-varying characteristics of the underwater acoustic channel, we take the SI channel at a certain moment to show.
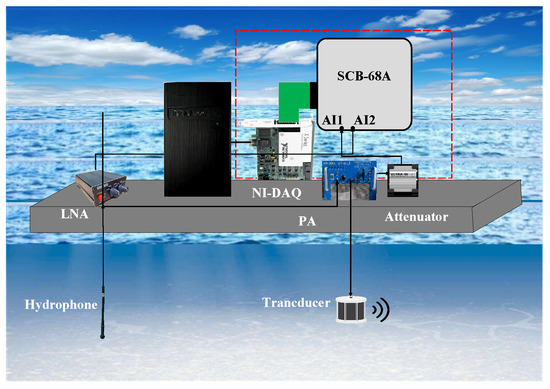
Figure 22.
Experimental scenario 1.

Figure 23.
Experimental coordinates and GPS.
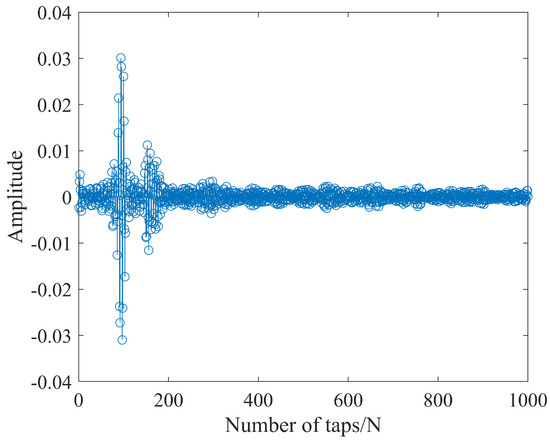
Figure 24.
Channel response at a moment during the sea trial.
For the experiment, we sent direct sequence spread spectrum signal with a frequency band of 2–4 KHz, and the equals . Threshold is calculated as follows:
Following the device connection scheme mentioned in Section 2.3 for the experiments, Figure 25 shows the M-NMSE curves for each algorithm when no far-end desired signal present.
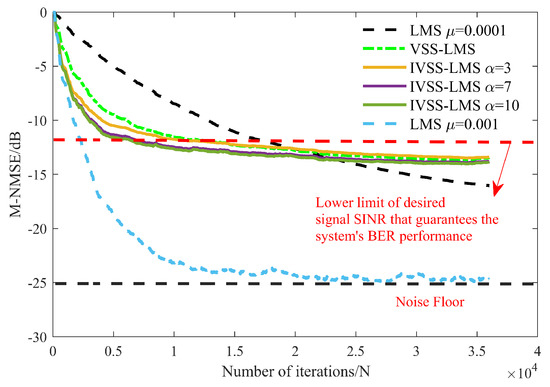
Figure 25.
M-NMSE results for each algorithm during the sea trial.
From Figure 26, we can see that the step-size of the VSS-LMS algorithm decreases adaptively with the transient state error when no far-end desired signal present, and gradually reaches steady state subsequently. Thanks to the threshold, the IVSS step-size reduces to the minimum step-size when the energy of the SI signal is canceled to −13 dB, in order to prevent the degradation of the SI channel estimation accuracy caused by the far-end desired signal.
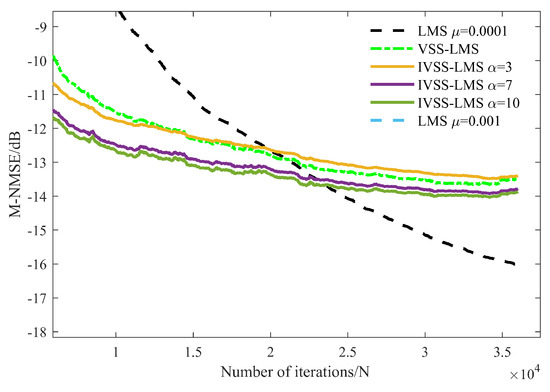
Figure 26.
Partial enlargement of Figure 25.
Experimental scenario 2: The far-end desired signal transmitted from 5KM away and the near-end SI signal are the direct spread spectrum sequence signal of the same frequency. We show the experimental scenario in Figure 27.
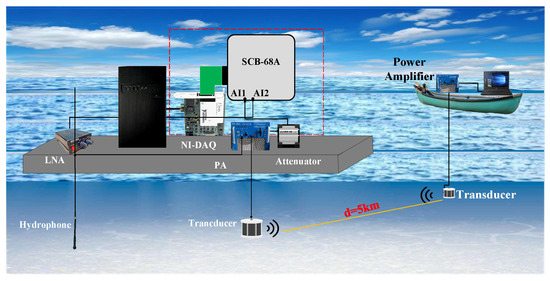
Figure 27.
Experimental scenario 2: Desired signal exists at 5 km.
Figure 28 shows the time-frequency diagram of the signal prior to SIC, including the SI signal and the desired signal at the far-end, Figure 29 is the time-frequency diagram of the signal after SIC.
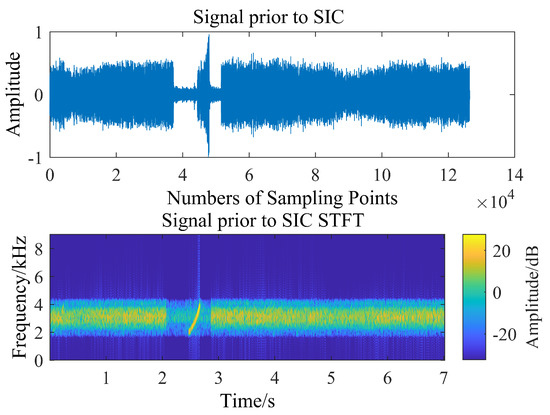
Figure 28.
Time-frequency diagram of the signal prior to SIC.
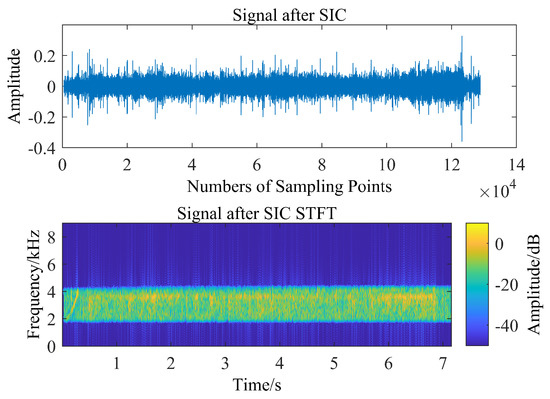
Figure 29.
Time-frequency diagram of the signal after SIC.
Figure 30 gives the M-NMSE curves of each algorithm in the second experiment and Figure 31 shows the local enlargement of the red position of Figure 30. According to the processing results of the sea trial data, the cancellation performance of IVSS-LMS is more superior to the conventional LMS and the VSS-LMS algorithm proposed in the literature [28]. Although the effect of IVSS-LMS and the VSS-LMS algorithm in the literature [28] is the same after the filter approaches the steady-state, the convergence speed of the IVSS-LMS algorithm is higher than that of the VSS-LMS algorithm, and the steady-state performance is best for the IVSS-LMS when .
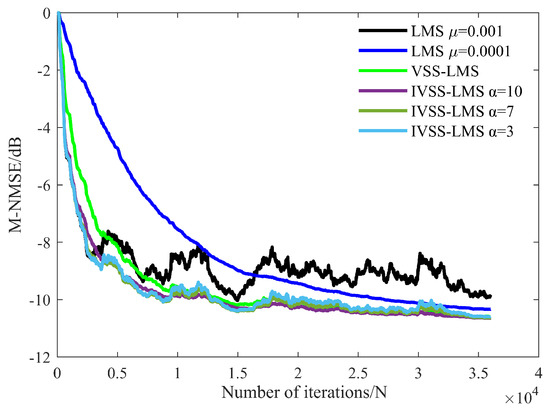
Figure 30.
Comparison of M-NMSE curves of each algorithm in the sea trial.
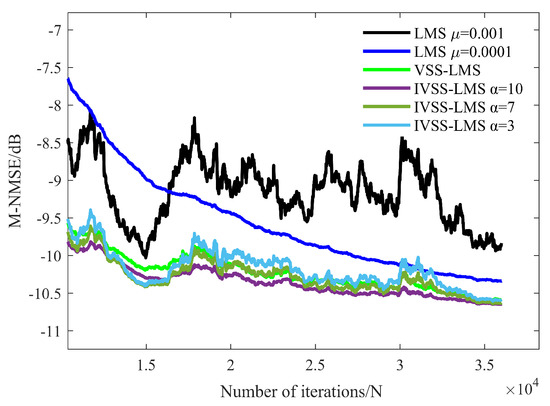
Figure 31.
Local enlargement of the red position of Figure 30.
Further, to consider the BER performance in the IBFD-UWAC system, the BER curves for the sea trial data will be given in this paper. It should be noted that during the sea trial, the power amplifier of the far-end transmitting ship was kept at its maximum value. Moreover, the energy of the near-end SI signal remains constant. Therefore, the larger the distance of the far-end transmitting ship, the smaller the value of SINR. We calculated the BER performance when the far-end transmittering ship is at 1.2 km, 2 km, 3.5 km and 5 km, respectively, using the sea trial data as shown in Figure 32.
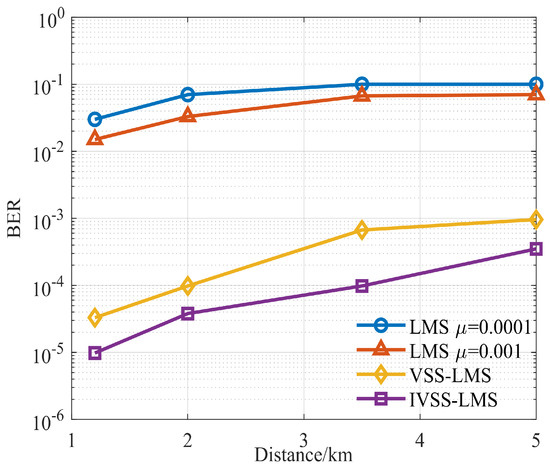
Figure 32.
BER in the sea trial.
As can be seen from Figure 32, our proposed algorithm, i.e., IVSS-LMS has the best performance among all algorithms at all distances. In particular, even at 5 km, using our proposed algorithm, the BER is still less than to maintain stable IBFDM-UWAC link, while other algorithms can no longer guarantee the BER performance of the communication system within an acceptable level.
4. Discussion
4.1. Significance of the Proposed Method
The real-time digital SIC method proposed in this paper provides a new technical approach for implementing IBFD-UWAC. In Simulink Desktop Real-time mode, we have implemented the real-time digital SIC using the HLS technique, which can greatly improves the communication efficiency of IBFD-UWAC. For the IBFD-UWAC system, the proposed IVSS-LMS algorithm can effectively reduce the influence of the far-end desired signal on the SIC process. The application scenario of the proposed method in this paper is the implementation of real-time IBFD-UWAC, which can be subsequently easily ported to the FPGA platform using tools such as MATLAB coder of Simulink platform, and can be used as the basis for the fabrication of an IBFD-UWAC modem.
4.2. Limitations of the Proposed Method
The algorithm utilizes NI-DAQ devices for the digital domain SIC process. NI-DAQ devices have a certain range, which makes the digital domain SIC with a certain upper limit, which is due to the fact that our SI signals need to be acquired; however, digital SIC is usually in the analog domain after the range can usually meet the requirements. In addition, the program described in this paper is implemented using Desktop Real-time of Simulink platform, its sampling frequency can reach up to 20 kHz, which creates a certain constraint on the frequency band range of communication signals, and fortunately in Simulink, the program can be easily ported using tools such as MATLAB Coder. The last point is about the limitation of the application scenario of the algorithm: the algorithm has better convergence speed and steady-state effect only for the SIC process of IBFD-UWAC system, where the desired signal generally has a SINR that can satisfy the system BER performance, and the core of the algorithm proposed in this article is that the threshold can be set according to the SINR of the desired signal, which can adaptively judge the degree of SIC to prevent the SI signal from being over-canceled. However, often in communication systems with two-party communication, the desired signal is generally known, so the algorithm proposed in this paper has some value.
5. Conclusions
As the final stage of the SIC for IBFD-UWAC, digital SIC needs to reduce the SI signal to the level that is suitable for desired signal demodulation. On the other side, the desired signal and the SI signal are mostly in the overlapping state in practical applications. The traditional digital interference cancellation does not consider the impact of the presents of the desired signal. At the same time, most digital interference cancellation algorithms are based on offline processing, which is difficult to be applied in the engineering application, as the complexity of the algorithm and equipment is high. To address the above problems, we design and implement the real-time digital SIC in IBFD-UWAC, and implement the simulation and experiment using Simulink Desktop Real-time mode, which increases the engineering applicability compared with the current offline processing algorithms. This paper proposes an IVSS-LMS algorithm for an IBFD-UWAC system, which fully considers the unique problem in IBFD-UWAC, that is, the desired signal arrival will destroy the steady-state of the filter and thus affect the SI channel estimation accuracy. By modifying the variable step-size criterion in the conventional VSS-LMS algorithms and setting the parameters according to different environments, we can use IVSS-LMS to achieve the best results, and enables the algorithm to both reduce the SI signal to a preset level at the initial state with a large convergence rate and to reduce the step-size to obtain a smaller mean square error as it approaches the steady-state. It is worth mentioning that the program can be easily ported to FPGA implementation through Simulink Desktop Real-time mode, which lays the foundation for engineering implementation of an IBFD underwater acoustic modem. This paper proves the effectiveness of the proposed scheme through simulation, sea trial experiments, and theoretical analyses.
Author Contributions
Conceptualization, Y.L.; methodology, Y.L. and C.Y.; software, G.Q.; validation, Y.L., C.Y., Y.Z., G.Y. and H.L.; formal analysis, G.Q. and G.Y.; investigation, Y.L.; resources, G.Q.; data curation, Y.L.; writing—original draft preparation, Y.L. and C.Y.; writing—review and editing, Y.L. and G.Q.; visualization, Y.Z.; supervision, G.Q.; project administration, Y.L.; funding acquisition, G.Q. All authors have read and agreed to the published version of the manuscript.
Funding
The work was supported in part by the Natural Science Foundation of Heilongjiang under Grant No. LH2021F010.
Data Availability Statement
The data presented in this paper are available after contacting the corresponding author.
Acknowledgments
The authors would like to thank the anonymous reviewers for their careful reading and valuable comments.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Stojanovic, M.; Preisig, J. Underwater acoustic communication channels: Propagation models and statistical characterization. IEEE Commun. Mag. 2009, 47, 84–89. [Google Scholar] [CrossRef]
- Chen, S.; Beach, M.A.; Mcgeehan, J.P. Division-free duplex for wireless applications. Electron. Lett. 1998, 34, 147–148. [Google Scholar] [CrossRef]
- Zhou, J.; Krishnaswamy, H. System-level analysis of phase noise in full-duplex wireless transceivers. IEEE Trans. Circuits Syst. II Express Briefs 2018, 65, 1189–1193. [Google Scholar] [CrossRef]
- Shen, L.; Henson, B.; Zakharov, Y.; Mitchell, P. Digital self-interference cancellation for full-duplex underwater acoustic systems. IEEE Trans. Circuits Syst. II Express Briefs 2019, 67, 192–196. [Google Scholar] [CrossRef] [Green Version]
- Li, S.; Lu, H.T.; Shao, S.H.; Tang, Y.X. Impact of the amount of RF self-interference cancellation on digital self-interference cancellation in full duplex communications. J. Electron. Inf. Technol. 2017, 39, 1278–1283. [Google Scholar]
- Bharadia, D.; Mcmilin, E.; Katti, S. Full duplex radios. Comput. Commun. Rev. 2013, 43, 375–386. [Google Scholar] [CrossRef]
- Hong, S.; Brand, J.; Choi, J.I.; Jain, M.; Mehlman, J.; Katti, S.; Levis, P. Applications of self-interference cancellation in 5G and beyond. IEEE Commun. Mag. 2014, 52, 114–121. [Google Scholar] [CrossRef]
- Liu, Y.; Roblin, P.; Quan, X.; Pan, W.; Shao, S.; Tang, Y. A full-duplex transceiver with two-stage analog cancellations for multipath self-interference. IEEE Trans. Microw. Theory Tech. 2017, 65, 5263–5273. [Google Scholar] [CrossRef]
- Liu, Y.; Quan, X.; Pan, W.; Tang, Y. Digitally assisted analog interference cancellation for in-band full-duplex radios. IEEE Commun. Lett. 2017, 21, 1079–1082. [Google Scholar] [CrossRef]
- Huang, X.; Le, A.T.; Guo, Y.J. ALMS loop analyses with higher-order statistics and strategies for joint analog and digital self-interference cancellation. IEEE Trans. Wirel. Commun. 2021, 20, 6467–6480. [Google Scholar] [CrossRef]
- Li, S.; Murch, R.D. An investigation into baseband techniques for single-channel fullduplex wireless communication systems. IEEE Trans. Wirel. Commun. 2014, 13, 4794–4806. [Google Scholar] [CrossRef]
- Qiao, G.; Gan, S.W.; Liu, S.Z.; Song, Q.J. Self-interference channel estimation algorithm based on maximum-likelihood estimator in in-band fullduplex underwater acoustic communication system. IEEE Access 2019, 6, 62324–62334. [Google Scholar] [CrossRef]
- Vermeulen, T.; van Liempd, B.; Hershberg, B.; Pollin, S. Real-time RF self-interference cancellation for in-band full duplex. In Proceedings of the 2015 IEEE International Symposium on Dynamic Spectrum Access Networks (DySPAN), Stockholm, Sweden, 28 September–2 October 2015; pp. 275–276. [Google Scholar]
- Kwong, R.H.; Johnston, E.W. A variable step size LMS algorithm. IEEE Trans. Signal Process. 1992, 40, 1633–1642. [Google Scholar] [CrossRef] [Green Version]
- Aboulnasr, T.; Mayyas, K. A robust variable step-size LMS-type algorithm: Analysis and simulations. IEEE Trans. Signal Process. 1997, 45, 631–639. [Google Scholar] [CrossRef]
- Pazaitis, D.I.; Constantinides, A.G. A novel kurtosis driven variable step-size adaptive algorithm. IEEE Trans. Signal Process. 1999, 47, 864–872. [Google Scholar] [CrossRef]
- Benesty, J.; Rey, H.; Vega, L.R.; Tressens, S. A nonparametric VSS NLMS algorithm. IEEE Signal Process. Lett. 2006, 13, 581–584. [Google Scholar] [CrossRef]
- Zhao, S.; Man, Z.; Khoo, S.; Wu, H.R. Variable step-size LMS algorithm with a quotient form. Signal Process 2009, 89, 67–76. [Google Scholar] [CrossRef]
- Hwang, J.K.; Li, Y.P. A gradient-based variable step size scheme for kurtosis of estimated error. IEEE Signal Process. Lett. 2010, 17, 331–334. [Google Scholar] [CrossRef]
- Huang, H.C.; Lee, J. A new variable step-size NLMS algorithm and its performance analysis. IEEE Trans. Signal Process. 2012, 60, 2055–2060. [Google Scholar] [CrossRef]
- Shin, H.C.; Sayed, A.H.; Song, W.J. Variable step-size NLMS and affine projection algorithms. IEEE Signal Process. Lett. 2004, 11, 132–135. [Google Scholar] [CrossRef]
- Mandic, D.P. A generalized normalized gradient descent algorithm. IEEE Signal Process. Lett. 2004, 11, 115–118. [Google Scholar] [CrossRef]
- Huang, B.Y.; Xiao, Y.G.; Ma, Y.P.; Wei, G.; Sun, J.W. A simplified variable step-size LMS algorithm for Fourier analysis and its statistical properties. Signal Process. 2015, 117, 69–81. [Google Scholar] [CrossRef]
- Choi, Y.S.; Shin, H.C.; Song, W.J. Robust regularization for nor-malized LMS algorithms. IEEE Trans. Circuits Syst. II Express Briefs 2006, 53, 627–631. [Google Scholar] [CrossRef]
- Jalal, B.; Yang, X.; Liu, Q.; Long, T.; Sarkar, T.K. Fast and robust variable-step-size LMS algorithm for adaptive beamforming. IEEE Antennas Wirel. Propag. Lett. 2020, 19, 1206–1210. [Google Scholar] [CrossRef]
- Garg, R.; Kohli, A.K. Parameter estimation and tracking of sinusoid using variable-step-size LMS algorithms. Optik 2016, 127, 10953–10960. [Google Scholar] [CrossRef]
- Kohli, A.K.; Sharma, J. Nonlinear acoustic echo canceller to combat sigmoid-type nonlinearities under noisy environment. Wirel. Pers. Commun. 2020, 114, 3489–3506. [Google Scholar] [CrossRef]
- Sui, Z.P.; Yan, S.F. Noise-robust variable-step LMS algorithm and its application in OFDM underwater acoustic channel equalization. Syst. Eng. Electron. Technol. 2020, 42, 1605–1613. [Google Scholar]
- Qiao, G.; Zhao, Y.J.; Liu, S.Z.; Ahmed, N. The effect of acoustic-shell coupling on near-end self-interference signal of in-band full-duplex underwater acoustic communication modem. In Proceedings of the 2020 17th International Bhurban Conference on Applied Sciences and Technology (IBCAST)), Islamabad, Pakistan, 14–18 January 2020; pp. 606–610. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).