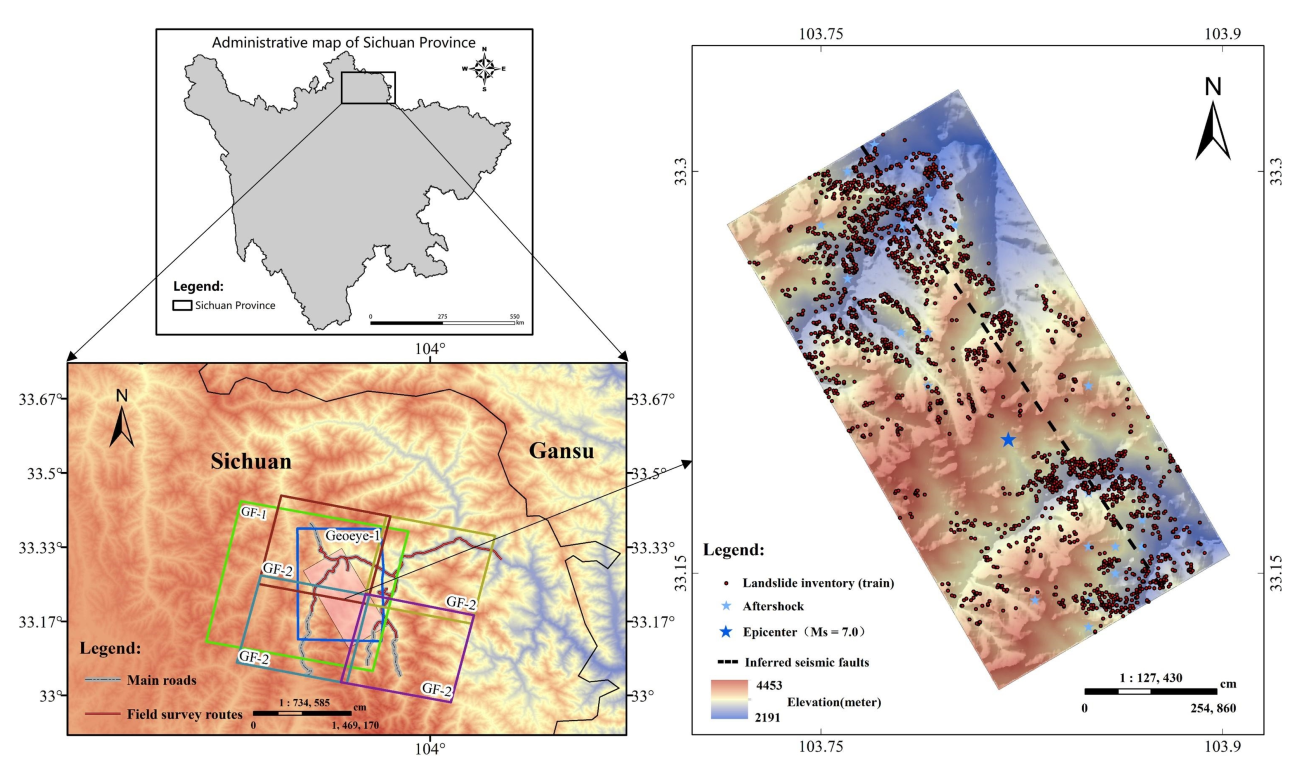
1. Introduction
Landslides are one of the most catastrophic natural disasters in the world triggered by anthropogenic and natural factors [
1]. Earthquakes, as one of the triggering factors for landslides, are prone to cause thousands of landslides in mountainous areas due to the special geomorphic environment [
2]. High spatial resolution remote sensing images and unoccupied airborne vehicles have been broadly applied to landslide investigation and identification [
3]. However, it is difficult to predict the probability of landslides in the future based on image band information alone. Therefore, landslide susceptibility mapping (LSM) is of great significance to post-earthquake emergency response and disaster prevention and mitigation [
4].
Landslide susceptibility is a prediction of the likelihood of a landslide occurring at a site based on topography, geology, and other factors [
5]. Several methods have been applied to LSM and tested to be usable and effective, including geomorphological mapping, physics-based models, heuristic terrain and susceptibility zoning, and machine learning (ML) methods [
6]. In this paper, we focus on a critical review of ML, especially deep learning (DL), for landslide susceptibility modelling due to the latest development trends. Traditional statistical ML methods mainly include decision trees [
7], random forests [
8], support vector machines [
9], artificial neural networks [
10], and naïve Bayes [
11]. These methods proved that due to shallow structures, the methods are unable to learn more representative deep features [
12]. Deep learning, especially convolutional neural networks (CNNs) with deep network structures and powerful feature learning capabilities, is being increasingly applied in the field of LSM [
13]. The rich environmental information and the influence between factors were taken into account in CNN-based LSM, leading to better performance than the benchmark models [
14]. The application of deep learning can achieve very good assessment results without a significant geoscience background. This is the strength and also the weakness of deep learning, which indirectly reflect the landslide formation law in a black box way.
Although there have been some excellent studies on LSM applying DL methods, especially CNNs, to the best of our knowledge, there have been few reputable studies on landslide inventory optimization for LSM. Generally, the traditional approaches of constructing a landslide inventory indicated that positive samples represented by landslides were marked as “1”, while negative samples represented by non-landslides were marked as “0” [
15]. Positive samples were often true and reliable. However, the selection of negative samples is considered subjective or selected based on certain rules. For example, Chen et al. (2018) used a randomly selected negative sample from the area outside a landslide and participated in the training of the model [
16]. Hu et al. (2020) proposed and compared three rules for selecting negative samples and compared their characteristics. The selection rules were random sampling of non-landslide areas, sampling of low-slope areas, and sampling using fractal theory [
17,
18,
19]. Yi et al. (2020) proposed a method to select negative samples through a certain distance buffer. The accuracy of the model was proved to be improved by optimizing negative samples [
20]. The starting point for these negative sample selections is the assumption that there is no possibility of future landslides in the area, and the optimized negative samples make the model easier to classify, meaning that the samples are not representative during the training process.
As expressed above, although optimizing the quality of negative samples at the input step of a deep learning model can improve the accuracy of the model, the existing methods of directly applying positive and negative samples for LSM mainly have the following two shortcomings: (1) Relying solely on positive and negative samples to participate in CNN model training often led to results approaching the maximum and minimum susceptibility index. Instead, the reality is that several different levels of LSM results are desired to be classified. (2) The existing studies mainly addressed the overfitting issue by simplifying the network structure and reducing the number of epochs [
21,
22,
23]. These strategies could contribute to the model’s inability to learn rich features and thus affect model performance. Therefore, it is worthwhile to study in depth how to refine and improve this dataset sampling method.
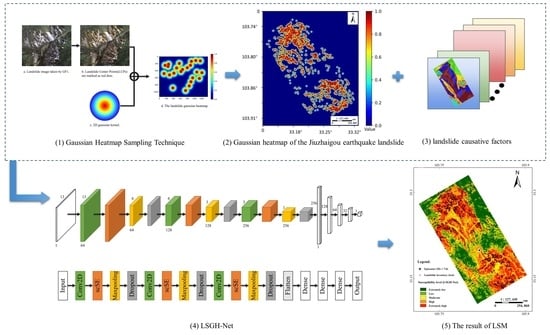
Gaussian heatmap regression was applied to DL model-based target detection owing to its powerful spatial generalization ability [
24]. Unlike traditional landslide inventory, the Gaussian heatmap sampling technique can generate samples in the range of 0~1 by a two-dimensional Gaussian kernel function. The advantages of this method mainly include (1) expansion of partially credible samples in the case of insufficient samples and consideration of environmental information around landslides. (2) These smooth samples (ranging from zero to one) were considered hard to classify, thus enhancing the spatial generalization ability of the model and avoiding extreme susceptibility index distributions. (3) The generated new samples avoided the risk of overfitting while ensuring excellent model performance.
In this study, a landslide susceptibility Gaussian heatmap network (LSGH-Net) was innovatively applied to LSM. The main goal of this paper is to use the Gaussian heat map sampling technique to enrich the variety of landslide inventory at the input step of the deep learning model to improve the accuracy of the LSM results. This strategy took into account the rich environmental information and the possibility of future landslides in the surrounding environment due to disasters. LSGH-Net is an improved convolutional neural network of LeNet-5 [
25]. A series of optimization strategies such as attention mechanism, dropout, etc., were applied to enhance model performance and efficiency. This paper chose Jiuzhaigou as an experimental site to verify the feasibility and efficiency of the proposed network. In addition, a series of evaluation metrics, Precision and Recall (PR) curves, Average Precision (AP) values, and landslide densities, were applied to evaluate the model performance and compare it with the traditional CNN, an unoptimized model.
3. Experiments and Results
3.1. Implementation Details
The hardware configuration of this experiment was as follows: the processor was an Intel(R) Xeon(R) Silver 4210R CPU @ 2.40GHZ (Santa Clara, CA, USA), the graphics card was an NVIDIA GeForce RTX 3090 (Santa Clara, CA, USA), and the memory (RAM) was 64.0GB. The software environment was a Windows 10 Professional 64-bit operating system (version number: 21H1), the programming language used was Python, and the tensorflow-gpu-1.4.0 and Keras-2.0.8 DL framework was selected as tool to build the model, corresponding to the Python-3.6 version.
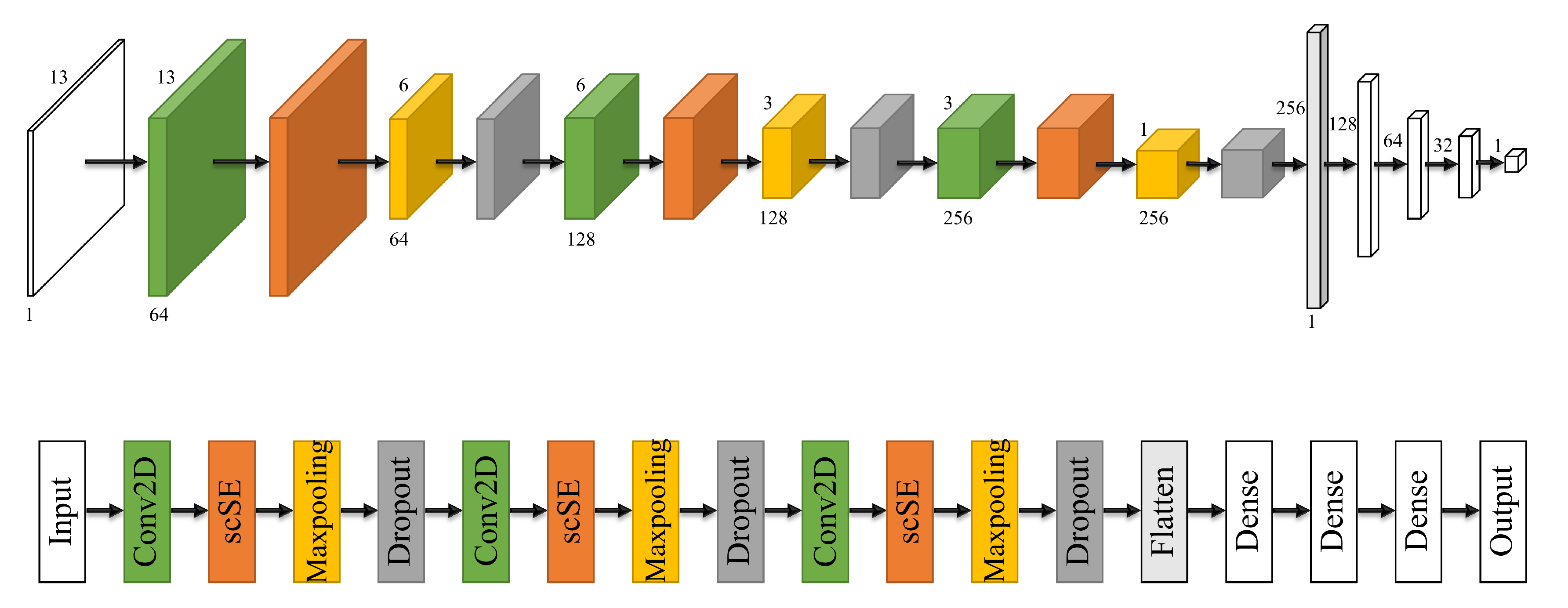
The application of a CNN to LSM needs to solve the problem of model applicability, that is, to convert a one-dimensional landslide causative factor vector into a two-dimensional image. We referred to the CNN-2D method proposed by Wang, Fan, and Hong (2019), which followed one-hot encoding [
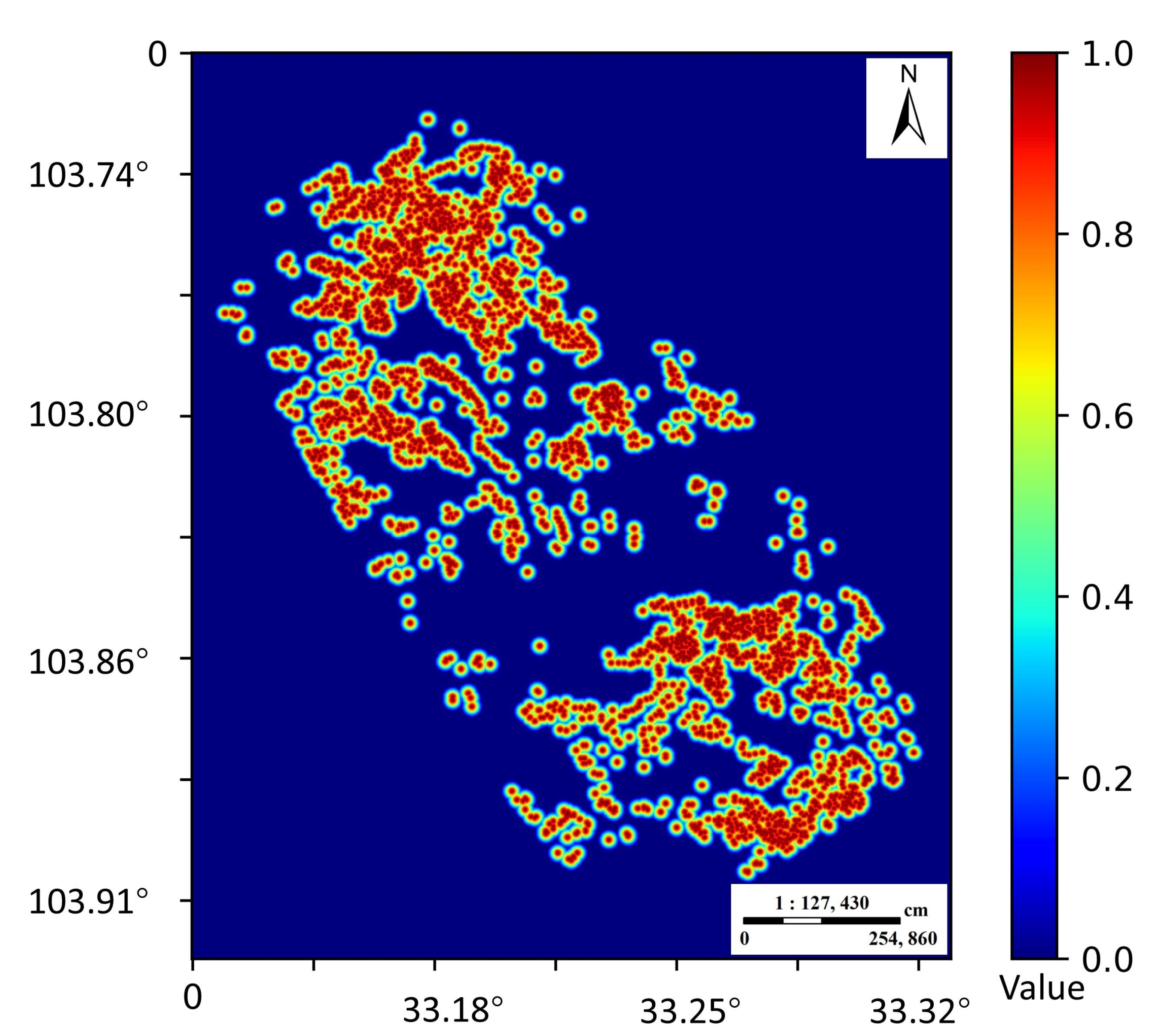
41]. By extracting 3592 landslide points, the Gaussian heatmap of landslide in the whole Jiuzhaigou earthquake area was generated by a two-dimensional Gaussian kernel function (
Figure 7). The values of the corresponding pixels in the heatmap were equally divided into five parts and randomly selected as new samples at equal intervals. It should be noted that since the selection of landslides and non-landslides was based on credible traditional methods, we only needed to generate new samples in the middle three intervals. We had a total of 10,376 samples and divided them into a training set and test set according to a 7:3 ratio. In the end, we converted these samples into 2D images to participate in model building.
For LSGH-Net, the attention model was added after each convolution operation. By comparing the loss of the training set and the validation set, we set the dropout rate to 0.5. Considering the size of the data set, the batch size in BN was set to 32. We set the maximum number of epochs to 200 in order to ensure adequate training. When the accuracy of the validation set did not increase significantly in 50 epochs, it was terminated early to avoid invalid training. The Adam algorithm was used as an optimizer to accelerate model training. Since LSM is a regression problem between factors and samples, we chose MSE as the loss function. In the DL model, the final feature map is obtained from the activation function to obtain the landslide susceptibility index (between 0 and 1).
3.2. Evaluation Metrics
In the study of landslide susceptibility based on the DL method, the results of evaluation mapping are often reflected by various metrics. At the same time, the effectiveness of different models or improved methods is verified by comparing the differences in metrics. In this paper, five single thresholds, i.e., accuracy, precision, specificity, sensitivity, and the F1 score, were selected as evaluation metrics. The calculation formula and detailed description of each evaluation metric are illustrated in
Table 3. The mean square error (MSE) was used to compare model errors, which reflects the degree of difference between the two estimated quantities. The PR curve and AP value of multi-threshold metrics can more intuitively reflect the predictive ability of the model. The PR curve was chosen because it focuses more on positive samples than the ROC curve. The AP value is the area of the graph enclosed by the PR curve and the X-axis.
TP and FN represent landslides that are correctly or incorrectly predicted, respectively. TN and FP represent non-landslides that are correctly or incorrectly predicted, respectively.
3.3. Comparative Experiments of Different Methods
In this part, we first compared the differences between the proposed LSGH-Net, Random forests (RF), and CNN models. The difference between the RF and CNN methods is that the input data are one-dimensional and two-dimensional, respectively. The structure of the CNN was consistent with the proposed network. The difference was that the Gaussian heatmap sampling technique to generate smooth samples was not applied to the CNN. We compared the impact of adopting improved strategies such as the
scSE block in the proposed model. The results of comparative experiments are shown in
Table 4.
First, we used GridSearchCV for RF parameter tuning. The RF model, as a statistical machine learning method, is generally less accurate than deep learning. On the one hand, a deep learning model has a deep network structure and strong feature learning ability. On the other hand, one-hot encoding is used to convert a one-dimensional vector into a two-dimensional vector. Using one-hot encoding for discrete features will make the calculation of the distance between features more reasonable. For overall accuracy, the proposed network and improved strategy using the Gaussian heatmap sampling technique performed better than the traditional CNN (93.67%). LSGH-Net outperformed the CNN in terms of all metrics, especially sensitivity (about 3% improvement). The FI score is an indicator reflecting the overall performance of a DL model. The score of the CNN (93.34%) was lower than that of LSGH-Net (95.13%), indicating that the proposed approach has better predictive performance in LSM. Compared with LSGH-Net, removing the
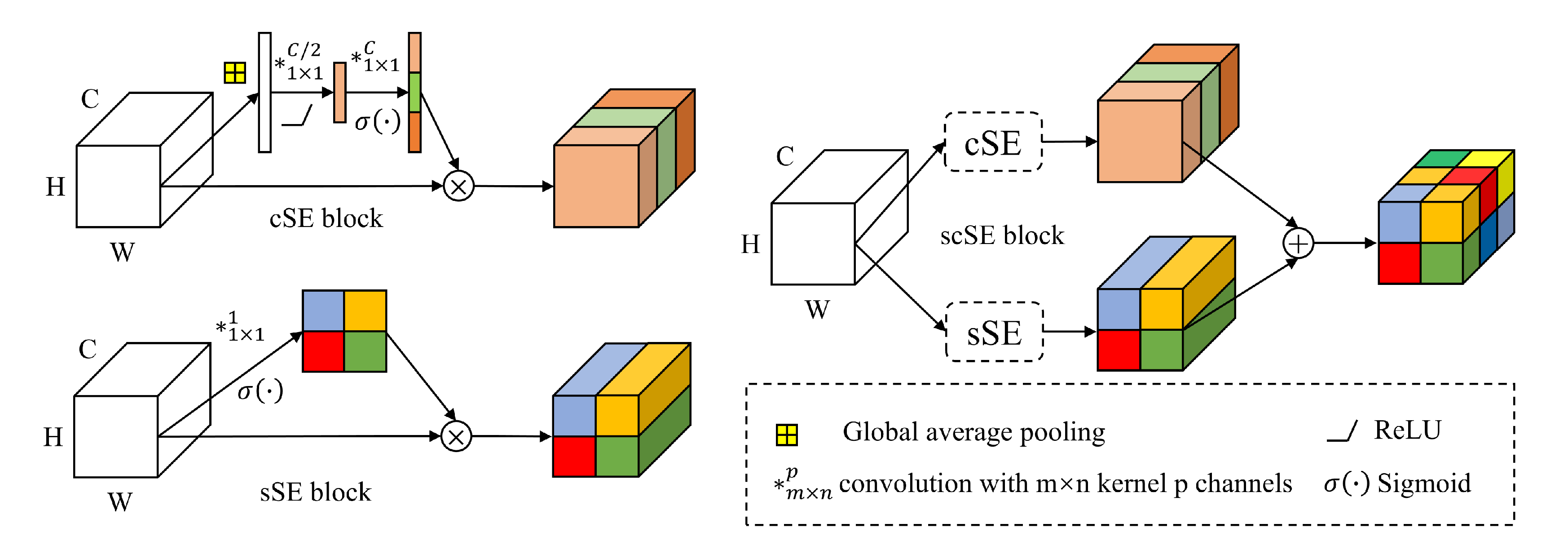
scSE strategy will make some changes to the model, namely, higher specificity (99.23%) and lower sensitivity (89.28%). The implementation of the
scSE strategy improved the overall accuracy (1.04%) and F1 score (1.17%) of the model.
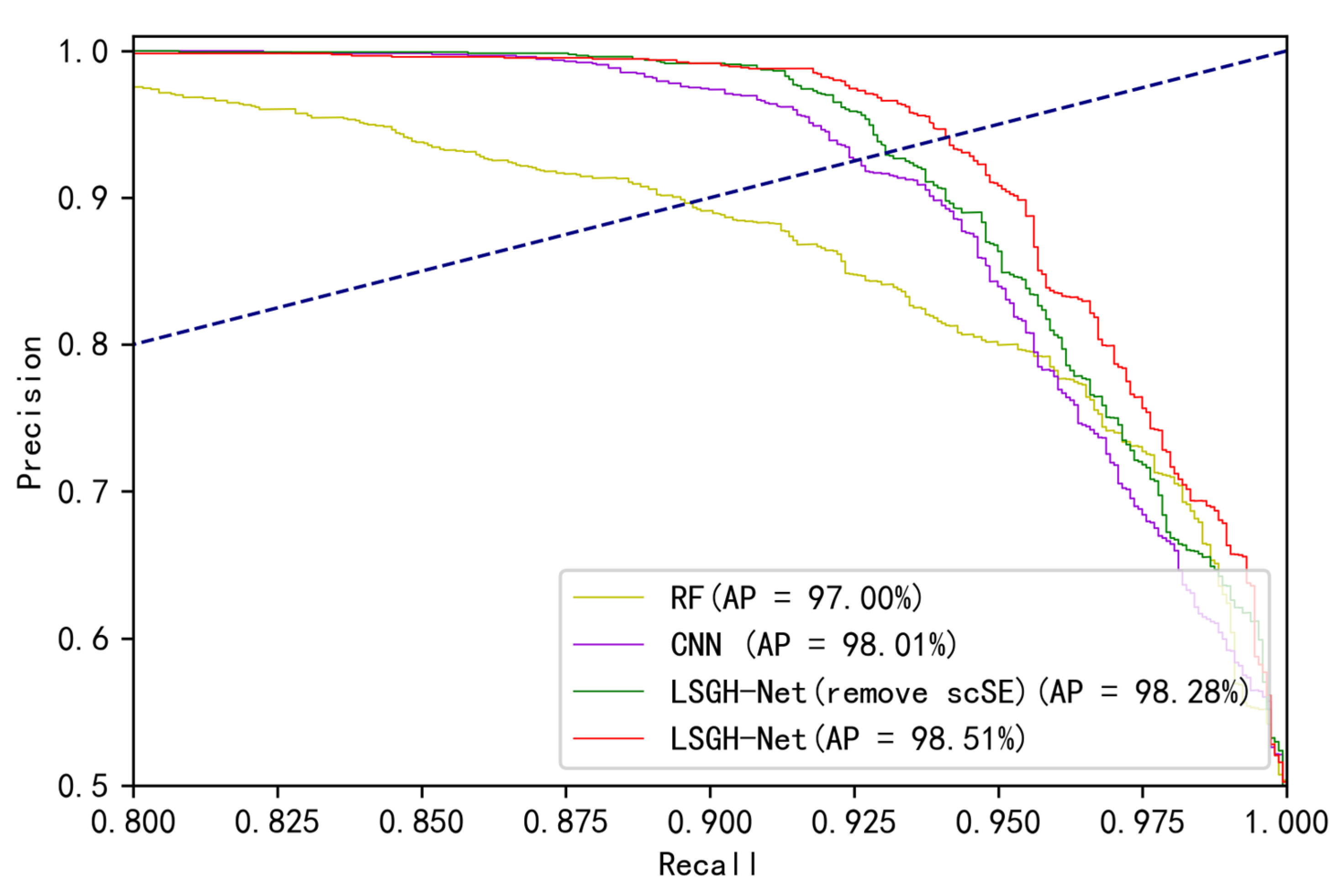
Figure 8 shows the comparison of the PR curves and AP values of different models. If the PR curve of classifier A completely wraps around another classifier B, then A outperforms B. Through analysis and comparison of AP values, the regression performance of the three models all achieved excellent scores, of which LSGH-Net was the best and the CNN was relatively poor. The MSE value of LSGH-NET was the smallest (0.0485), indicating that this predicted value was more consistent with the real value.
3.4. LSM Results
This paper used the Python package Keras with Tensorflow as the backend for LSM. The generated results were imported into ArcGIS 10.6, and Jenks natural break approach was used to divide the susceptibility index into five categories from low to high. It is worth noting that this paper mainly studied the influence of smooth samples generated by the Gaussian heatmap sampling technique on landslide susceptibility. Although the improved strategies such as the scSE block improved the model performance, the difference was not significant in the mapping results, and they had a similar susceptibility index frequency distribution. Therefore, this paper only compared the mapping results of the optimized LSGH-Net and the traditional CNN.
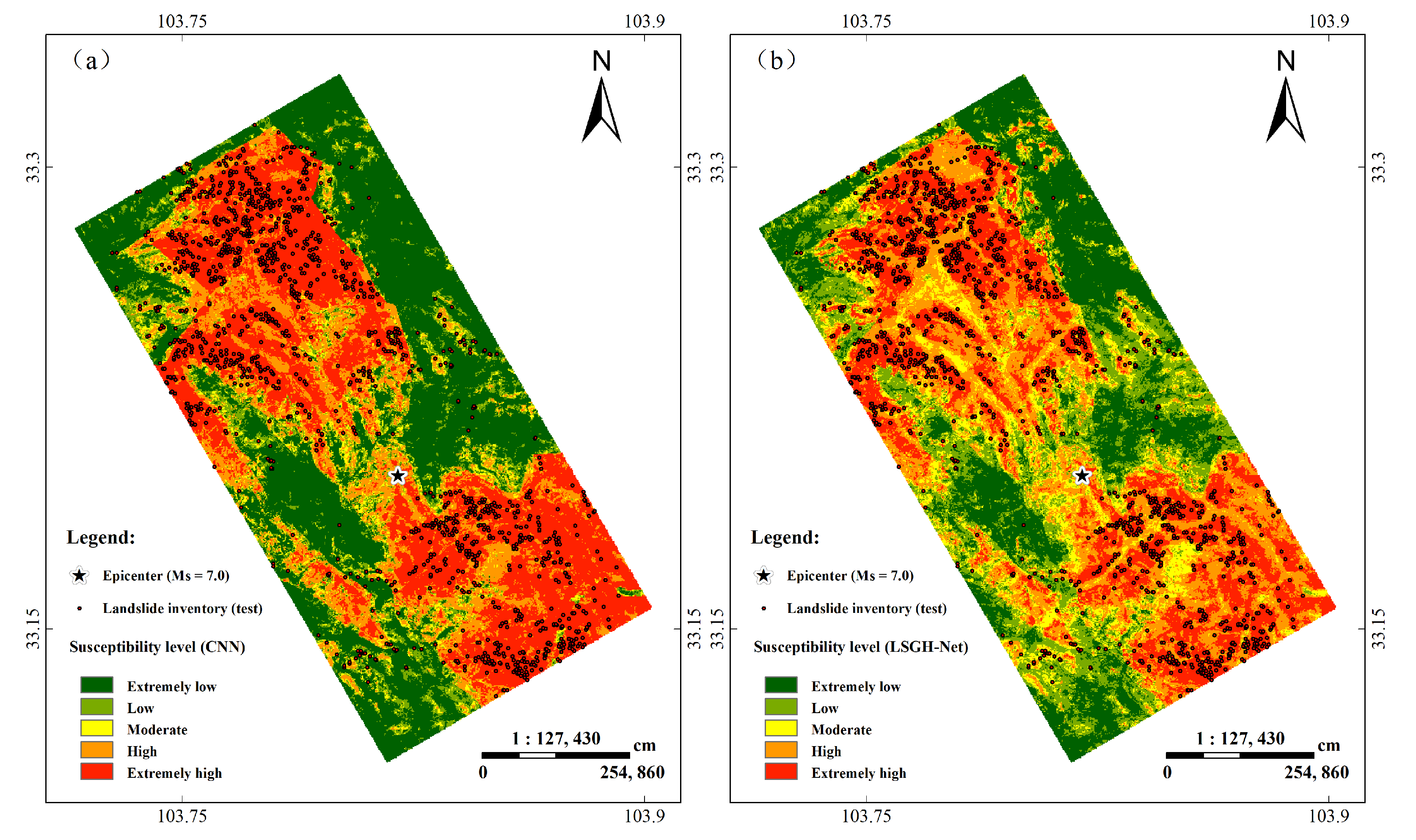
Figure 9 shows that the two maps were similar in the spatial distribution of landslides. Landslides were mainly concentrated in the northwest and southeast of the earthquake region. From the perspective of the landslide susceptibility index, there was a significant difference between the two models. For the CNN, high and very high landslide susceptibility occupied approximately 52% (108.16 km
2) of the total area. Pourghasemi et al. (2013) proposed that susceptibility mapping should consider reasonableness [
42]. There is the reasonable expectation that LSM will have the ground-truthed landslides occupying the high and very-high areas. Meanwhile, the proportion of highly and very highly prone areas should be as small as possible because the occurrence of landslides is still small relative to the entire area. Compared with the results of the CNN, the proportion of highly and very highly prone areas in LSGH-Net (approximately 33%) is more reasonable.
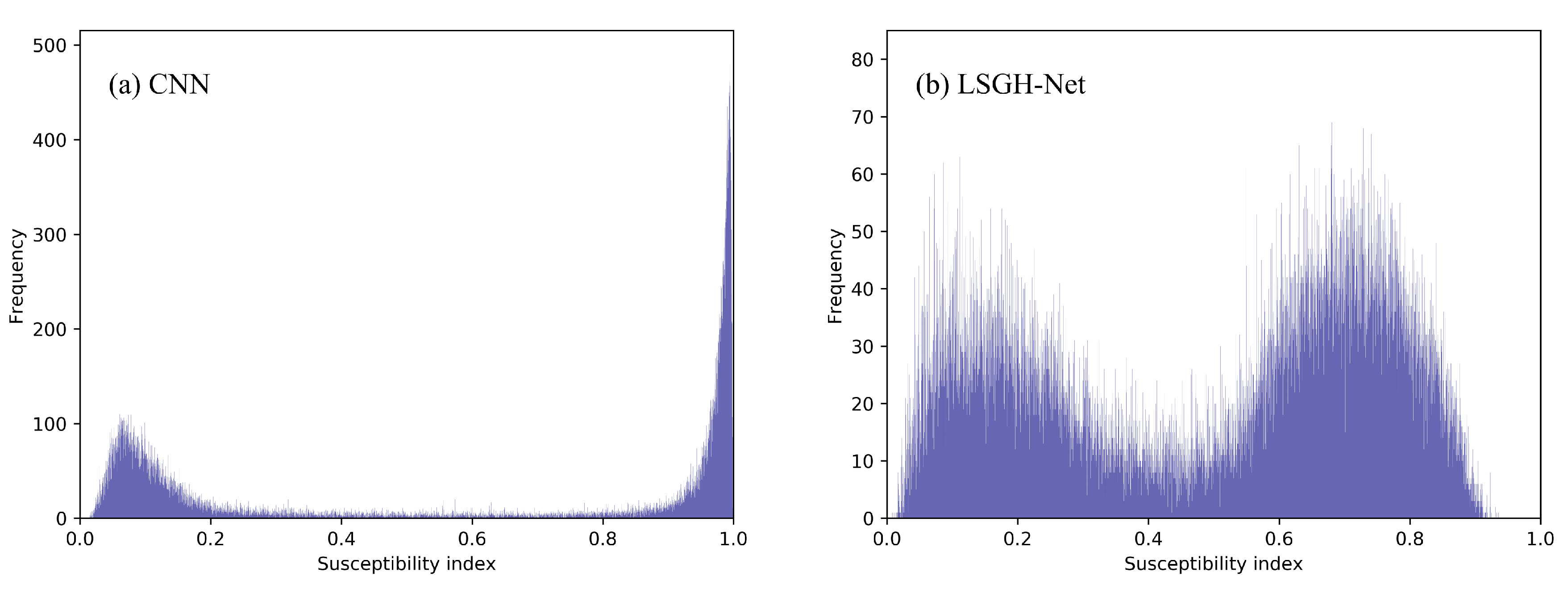
As shown in
Figure 10, the quantitative relationship between index and frequency is more intuitively reflected through the frequency histogram of the landslide susceptibility index. For the CNN, most of the susceptibility indexes were in the range of 0~0.2 and 0.8~1.0. This phenomenon quantitatively explains why highly and very highly prone areas accounted for a large proportion. For LSGH-Net, the frequency distribution of the susceptibility index was more reasonable, that is, there was still a considerable frequency distribution in the moderately prone areas. Therefore, the Gaussian heatmap sampling technique can improve the frequency distribution of the susceptibility index. This result can provide more precise mapping details and accurate predictions.
4. Discussion
4.1. Effectiveness of the LSGH-Net and Improved Strategies
The main research of this paper is the development of an LSM method based on the Gaussian heatmap sampling technique and a CNN. The application of the method is mainly based on the first law of geography and the accepted assumptions of landslide susceptibility research. Traditional CNN models trained only by landslide and non-landslide samples tend to show several drawbacks. As shown in
Figure 9 and
Table 4 in the previous chapter, if model prediction accuracy is the primary concern, the mapping results of the CNN model often show that the high and extremely high susceptibility levels account for a large pixel proportion. The reason for this phenomenon is that the large number of epochs cause the model to overfit. The contradiction is that if the number of epochs is reduced, the risk of overfitting can be decreased but the accuracy of the model will be greatly reduced. Similarly, if overfitting is avoided by simplifying the network such as reducing the feature map, it will also affect the prediction accuracy.
Therefore, the advantage of the LSGH-Net proposed in this paper is that it can effectively avoid the contradiction between overfitting caused by excessive epochs and hard-to-classify reduced accuracy caused by model simplification or reduced epochs. This method can ensure a sufficient number of epochs without overfitting, and it is suitable for complex networks and improved strategies to extract advanced features of landslide causative factors. These hard-to-classify smooth samples make the model more complex and robust. Therefore, these smooth samples generated by the Gaussian heatmap sampling technique can effectively improve the generalization ability of the model and avoid overfitting. The successful application of various strategies in the network improved the evaluation metrics and efficiency of the LSM. In the attention mechanism, the performance improvement can be explained as follows: the scSE block strengthens the important feature maps and ignores the minor ones.
4.2. Reasonableness Analysis of Landslide Density
As previously expressed, the frequency histogram of landslide susceptibility index should consider the rationality of the mapping. The study of landslide susceptibility was to use past landslides to predict the probability of occurrence in the future, but it was often difficult to verify whether a landslide would happen in the future. Analysis of the spatial distribution relationship between the susceptibility index and known landslides could further evaluate the rationality and scientificity of the model. Landslide susceptibility zoning is used to divide the probability of landslide susceptibility and the number and proportion of evaluation units and landslide units. It is also possible to calculate the landslide density and analyze the trend, and through the evaluation, landslide unit ratio, and landslide density analysis, it is possible to better quantify the intrinsic difference between LSM and the interpretability of model differences. The specific zoning statistics are shown in the table.
Although there are similarities between the two models in terms of the LSM results, it can be seen from
Table 5 and
Table 6 that there are large differences in the models in terms of statistical performance. First, in terms of the proportion of evaluation units, the CNN model takes up a large proportion in the range of 0–0.2 and 0.8–1, with a total of 87.2%, that is, most of the assessment results show extremely low or extremely high susceptibility, which is obviously overestimated. Compared with the LSGH-Net model, there is a certain proportion in each interval, and the proportion of 0.8~1.0 in the evaluation unit is the smallest (10%), which is consistent with the actual situation. At the same time, for the proportion of landslide units, a large number of landslides are distributed in the interval of 0.6–1, while compared with the CNN model, there are 6.9% of landslides in the interval of 0–0.2, which is a large error. In the range of 0.6~0.8, there should be a higher landslide ratio, but the ratio of 2.3% is much smaller than that of the LSGH-Net model. This is because the CNN has overestimated it and predicted it into the extremely high susceptibility range.
Landslide density refers to the proportion of a landslide inventory in the total mapping units within a certain susceptibility index interval. Through landslide density analysis, the predicted susceptibility index and landslide inventory can be better explained in terms of rationality.
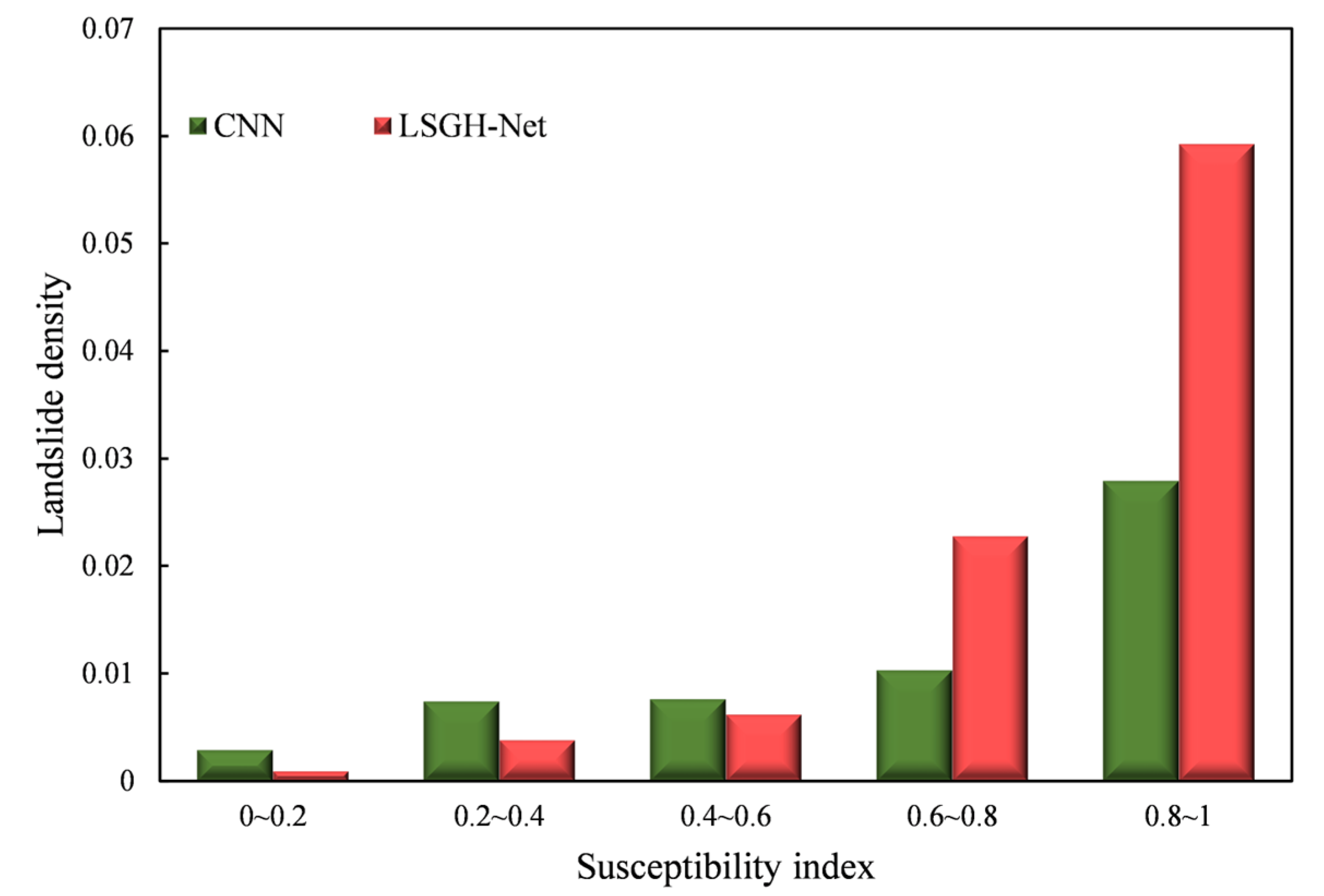
Figure 11 illustrates the landslide density results of the CNN and LSGH-Net in different index intervals. From the overall trend, landslide density increases with increasing susceptibility index. This trend is particularly significant for LSGH-Net, which is manifested in exponential growth. For the CNN, the landslide density in the interval of 0~0.2 still has a higher value than the model proposed in this paper. This phenomenon may be a result of overfitting that causes the CNN model to overpredict the very low prone areas, and there is no significant difference in landslide density in the 0.2~0.8 interval. Compared with the CNN, LSGH-Net had a higher landslide density in the 0.8~1 interval, which shows that the model has more accurate spatial prediction. Through the above analysis and comparison, the network proposed in this paper satisfied the assumption of reasonableness in landslide density.
To sum up, the Gaussian heatmap sampling technique can adjust the susceptibility index histogram, which makes the landslide more accurately distributed in the very highly prone areas. This method makes the distribution of landslide density at different levels of susceptibility more reasonable.
4.3. Sensitivity of the Gaussian Heatmap Sampling Technique
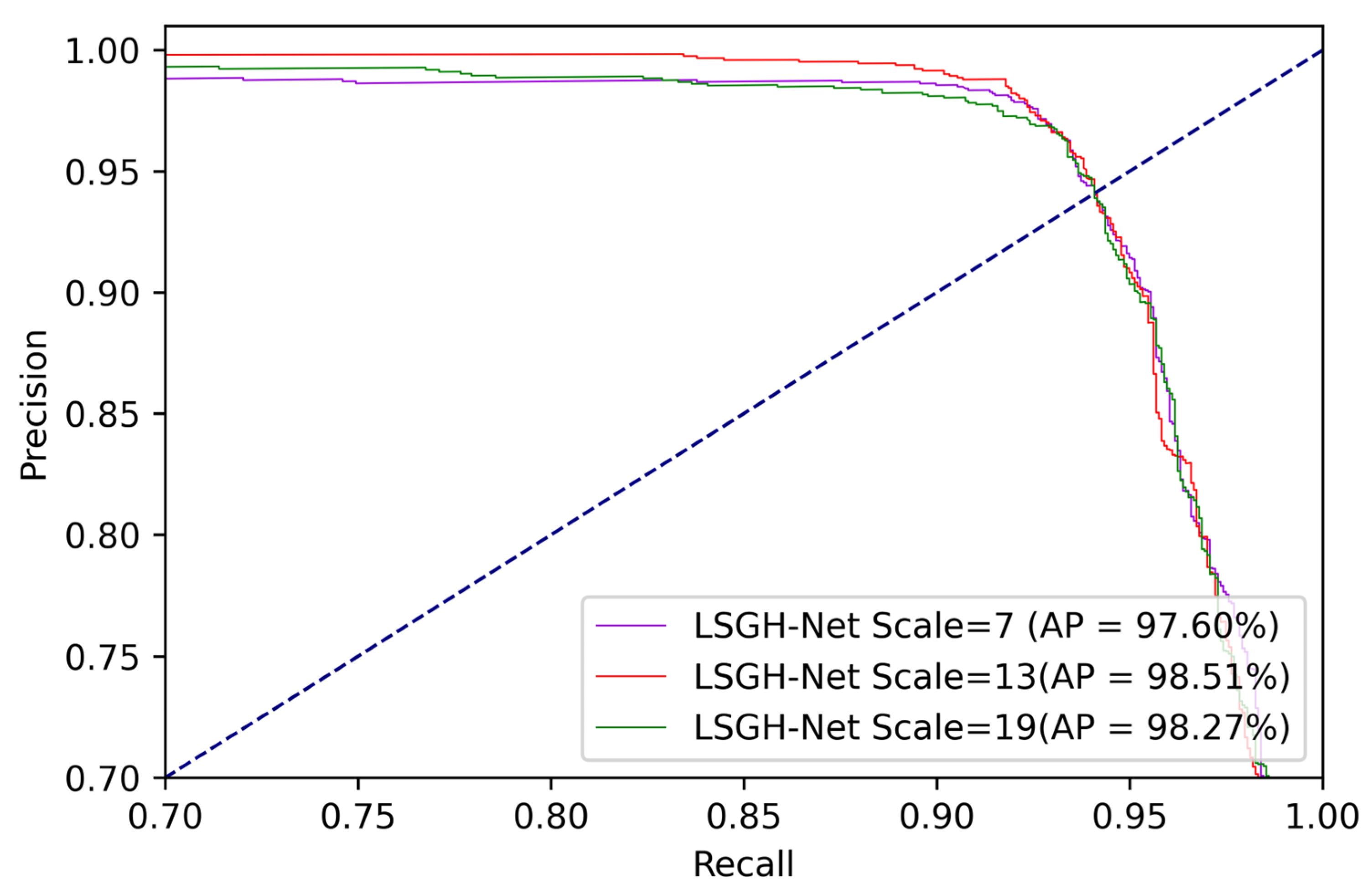
The application of the Gaussian heatmap sampling technique is based on the fact that the occurrence of landslides is closely related to the surrounding environment. The area near the landslide will be more susceptible due to similar geographical environment factors. However, determination of the extent or scale of surrounding environmental factors affected by landslides remains a challenge. Different scale parameters were set to explore the effect on landslide susceptibility based on the Gaussian heatmap diameter size. The size of the diameter (7, 13, and 19) was classified into small, medium, and large scales in LSM. The small scale was more concerned with information about the landslide itself while the large scale was more focused on information about the surrounding environment.
Figure 12 shows the performance of different scale data sets by comparing the PR curve and AP value. The AP values corresponding to small, medium, and large scales were 97.60%, 98.51%, and 98.27%, respectively. This indicates that excellent fits were obtained for data sets of different scales. Furthermore, the medium scale achieved the best overall score, indicating the suitability of the scale for landslide susceptibility studies in the Jiuzhaigou region. The results show that the appropriate scale selection takes into account the information of the landslide itself and the surrounding causative factors. Meanwhile, the causative factors selected in this paper, such as the distance from the road, distance from the water system, etc., showed a high susceptibility index at the mesoscale. To sum up, the Gaussian heatmap scale parameters had a certain impact on LSM, and different regions and environments may require trial and error to select the best parameters.
5. Conclusions
In this paper, a novel intelligent CNN-based approach, LSGH-Net, was proposed for landslide susceptibility based on the Gaussian heatmap sampling technique. To address the inadequacy of traditional landslide inventory sampling, the Gaussian heatmap sampling technique was added to LSGH-Net to optimize the performance of the model. A series of optimization strategies such as attention mechanism, dropout, etc., were applied to the network to improve the accuracy and efficiency. The new landslide inventory and causative factors were input into the designed network for training and prediction. The main conclusions were as follows: (1) The accuracy and F1 score of the LSGH-Net approach were 95.30% and 95.13%, respectively, approximately 1.63% and 1.79% higher than that of the traditional CNN sample selection approach. The results demonstrated that LSGH-Net had strong predictive performance and generalization ability. (2) The frequency histogram of the susceptibility index was effectively improved by the Gaussian heatmap sampling technique. The improved histogram provided more fine-grained mapping details and a more reasonable landslide density. (3) The final evaluation results of landslide susceptibility show that the northwest and southeast of the Jiuzhaigou earthquake area are highly and extremely prone areas, and the possibility of landslides in the future is very high. (4) Based on scale sensitivity analysis, the medium-scale Gaussian heatmap was more suitable for the mapping of landslide susceptibility in the Jiuzhaigou earthquake region. Given the above, based on the basic laws and assumptions of susceptibility, the Gaussian heatmap sampling technique is considered to be effective and feasible in different regions and other disaster susceptibility studies.