A New Probability Distribution for SAR Image Modeling
Abstract
1. Introduction
- A new probability model is proposed, which is an extension of an important texture model of SAR imagery;
- The maximum likelihood theory is developed for parameter estimation;
- Numerical experiments with synthetic signals are performed to validate the proposed model and inference theory;
- Based on three measured SAR images, we show that the proposed model outperforms several well-known SAR image descriptors;
- A collection of computational codes are available to guarantee reproducibility of the results and future applications of the proposal.
2. The Exponentiated Transmuted Inverted Beta Distribution
2.1. Statistical Preliminaries
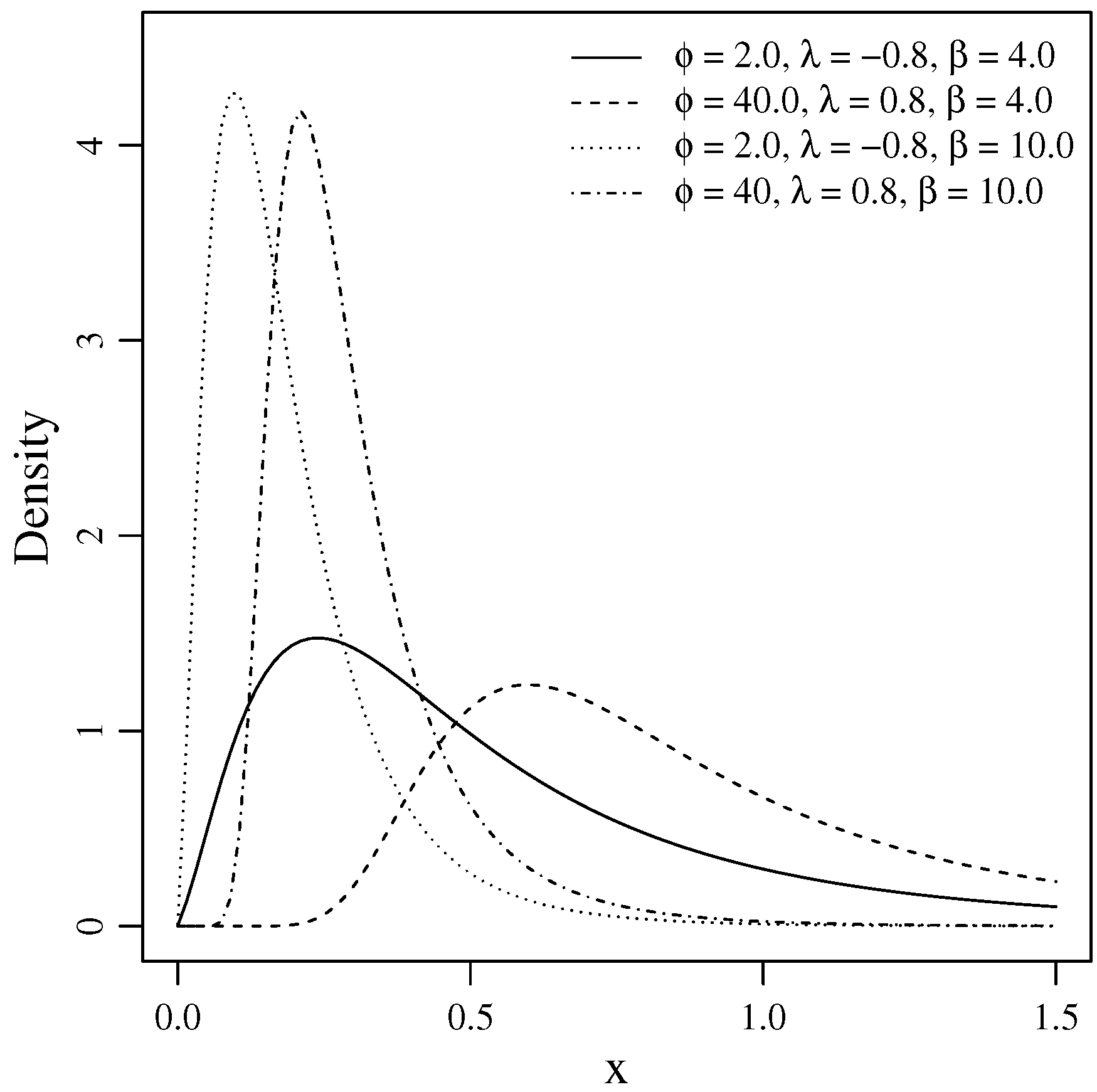
2.2. The Model Description
2.3. Likelihood Inference
3. Numerical Results
3.1. Analysis with Simulated Data
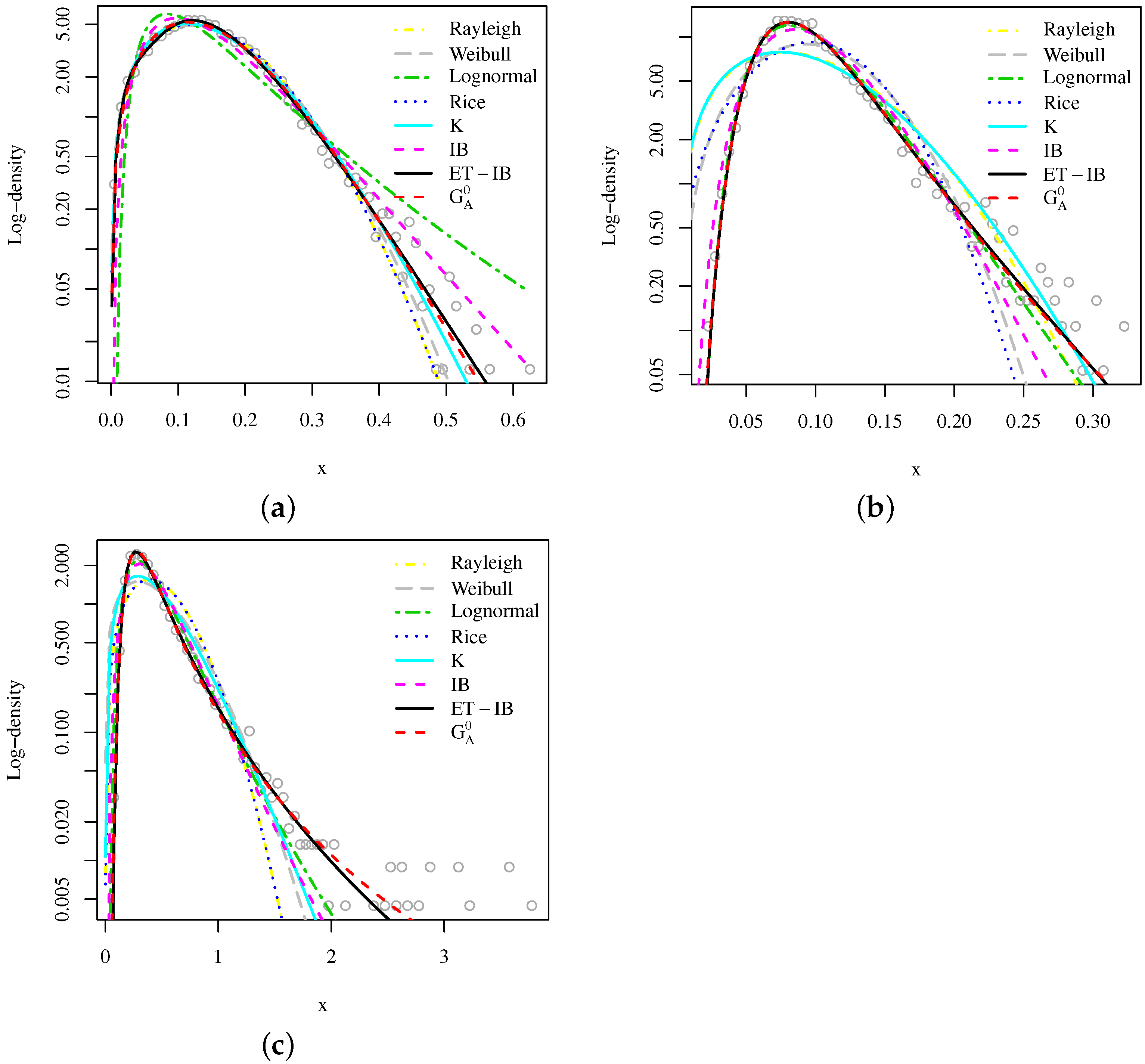
3.2. Analysis with SAR Amplitude Data
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gao, G. Statistical modeling of SAR images: A survey. Sensors 2010, 10, 775–795. [Google Scholar] [PubMed]
- Feng, J.; Cao, Z.; Pi, Y. Multiphase SAR image segmentation with G0-statistical-model-based active contours. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4190–4199. [Google Scholar] [CrossRef]
- Jain, A.; Singh, D. An optimal selection of probability distribution functions for unsupervised land cover classification of PALSAR-2 data. Adv. Space Res. 2018, 63, 813–825. [Google Scholar] [CrossRef]
- Karine, A.; Toumi, A.; Khenchaf, A.; Hassouni, M.E. Target recognition in Radar images using weighted statistical dictionary-based sparse representation. IEEE Geosci. Remote Sens. Lett. 2017, 14, 2403–2407. [Google Scholar] [CrossRef]
- Nadarajah, S.; Kotz, S. Intensity models for non Rayleigh speckle distributions. Int. J. Remote Sens. 2008, 2, 529–541. [Google Scholar]
- Frery, A.C.; Muller, H.J.; Yanasse, C.C.F.; Sant’Anna, S.J.S. A model for extremely heterogeneous clutter. IEEE Trans. Geosci. Remote Sens. 1997, 35, 648–659. [Google Scholar]
- Cintra, R.J.; Rêgo, L.C.; Cordeiro, G.M.; Nascimento, A.D.C. Beta generalized normal distribution with an application for SAR image processing. Statistics 2012, 2, 279–294. [Google Scholar] [CrossRef]
- Gao, G.; Qin, X.; Zhou, S. Modeling SAR images based on a generalized gamma distribution for texture component. Prog. Electromagn. Res. 2013, 137, 669–685. [Google Scholar] [CrossRef][Green Version]
- Cordeiro, G.M.; Cintra, R.J.; Rêgo, L.C.; Nascimento, A.D.C. The gamma generalized normal distribution: A descriptor of SAR imagery. J. Comput. Appl. Math. 2019, 347, 257–272. [Google Scholar]
- Vasconcelos, J.M.; Cintra, R.J.; Nascimento, A.D.C.; Rêgo, L.C. The compound truncated Poisson Cauchy model: A descriptor for multimodal data. J. Comput. Appl. Math. 2020, 378, 112887. [Google Scholar]
- Karakus, O.; Kuruoglu, E.E.; Achim, A. A generalized Gaussian extension to the Rician distribution for SAR image modeling. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5205615. [Google Scholar] [CrossRef]
- McDonald, J.B. Some generalized functions for the size distribution of income. Econometrica 1984, 52, 647–665. [Google Scholar] [CrossRef]
- Deng, X.; López-Martínez, C.; Chen, J.; Han, P. Statistical modeling of polarimetric SAR data: A survey and challenges. Remote Sens. 2017, 9, 348. [Google Scholar] [CrossRef]
- MingChun, W.; JiaFeng, Z.; Tao, L. Constant false alarm rate detection method in polarimetric synthetic aperture radar imagery based on whitening filter under inverse beta distribution. J. Eng. 2019, 2019, 5574–5579. [Google Scholar] [CrossRef]
- Merovci, F.; Alizadeh, M.; Yousof, H.M.; Hamedani, G.G. The exponentiated transmuted-G family of distributions: Theory and applications. Commun. Stat. Theory Methods 2017, 46, 10800–10822. [Google Scholar] [CrossRef]
- Okereke, E.W. Exponentiated transmuted Lindley distribution with applications. Open J. Math. Anal. 2019, 3, 1–18. [Google Scholar] [CrossRef]
- Abbas, S.; Mohsin, M.; Pilz, J. A new life time distribution with applications inreliability and environmental sciences. J. Stat. Manag. Syst. 2020, 24, 453–479. [Google Scholar]
- Freitas, C.C.; Frery, A.C.; Correia, A.H. The polarimetric distribution for SAR data analysis. Environmetrics 2005, 16, 13–31. [Google Scholar] [CrossRef]
- Guo, R.; Cui, J.; Jing, G.; Zhang, S.; Xing, M. Validating GEV model for reflection symmetry-based ocean ship detection with Gaofen-3 dual-polarimetric data. Remote Sens. 2020, 12, 1148. [Google Scholar] [CrossRef]
- Liao, M.; Wang, C.; Wang, Y.; Jiang, L. Using SAR images to detect ships from sea clutter. IEEE Geosci. Remote Sens. Lett. 2008, 5, 194–198. [Google Scholar] [CrossRef]
- Atteia, G.E.; Collins, M.J. On the use of compact polarimetry SAR for ship detection. ISPRS J. Photogramm. Remote Sens. 2012, 80, 1–9. [Google Scholar] [CrossRef]
- McDonald, J.B.; Xu, Y.J. A generalization of the beta distribution with applications. J. Econ. 1995, 66, 133–152. [Google Scholar] [CrossRef]
- Sagrillo, M.; Guerra, R.R.; Bayer, F.M.; Machado, R. Shiny Application of ET-IB Distribution. Available online: https://estmsp.shinyapps.io/etib/ (accessed on 15 May 2022).
- Kenney, J.F.; Keeping, E.S. Mathematics of Statistics, 3rd ed.; Chapman and Hall Ltd.: London, UK, 1962. [Google Scholar]
- Moors, J.J.A. A quantile alternative for kurtosis. J. R. Stat. Soc. Ser. D Stat. 1988, 37, 25–32. [Google Scholar] [CrossRef]
- Pawitan, Y. In All Likelihood: Statistical Modelling and Inference Using Likelihood; Oxford University Press: Oxford, UK, 2001. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2021. [Google Scholar]
- Kuttikkad, S.; Chellappa, R. Statistical modeling and analysis of high-resolution Synthetic Aperture Radar images. Stat. Comput. 2000, 10, 133–145. [Google Scholar] [CrossRef]
- Sagrillo, M.; Guerra, R.R.; Bayer, F.M.; Machado, R. R Implementations of ET-IB Distribution. Available online: https://github.com/murilosagrillo/ETIB (accessed on 20 May 2022).
- Lundberg, M.; Ulander, L.M.H.; Pierson, W.E.; Gustavsson, A. A challenge problem for detection of targets in foliage. In Proceedings of the Defense and Security Symposium, Orlando, FL, USA, 17–21 April 2006; Volume 6237, p. 62370K. [Google Scholar]
- Nascimento, A.D.C.; Horta, M.M.; Frery, A.C.; Cintra, R.J. Comparing edge detection methods based on stochastic entropies and distances for PolSAR imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 7, 648–663. [Google Scholar] [CrossRef]
- Johnsen, H. Multi-look versus single-look processing of synthetic aperture radar images with respect to ocean wavespectra estimation. Int. J. Remote Sens. 1992, 13, 1627–1643. [Google Scholar] [CrossRef]
- Gong, L.; Wang, C.; Wu, F.; Zhang, J.; Zhang, H.; Li, Q. Earthquake-induced building damage detection with post-event sub-meter VHR terra SAR-X staring spotlight imagery. Remote Sens. 2016, 8, 887. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Marinho, P.R.D.; Silva, R.B.; Bourguignon, M.; Cordeiro, G.M.; Nadarajah, S. AdequacyModel: An R package for probability distributions and general purpose optimization. PLoS ONE 2019, 14, e0221487. [Google Scholar] [CrossRef]
- Akbari, V.; Anfinsen, S.N.; Doulgeris, A.P.; Eltoft, T.; Moser, G.; Serpico, S.B. Polarimetric SAR change detection with the complex Hotelling–Lawley Trace Statistic. IEEE Trans. Geosci. Remote Sens. 2016, 64, 3853–3966. [Google Scholar] [CrossRef]
- Yao, J.; Cao, X.; Zhao, Q.; Meng, D.; Xu, Z. Robust subspace clustering via penalized mixture of Gaussians. Neurocomputing 2018, 278, 4–11. [Google Scholar] [CrossRef]
- Yao, J.; Meng, D.; Zhao, Q.; Cao, W.; Xu, Z. Nonconvex-sparsity and Nonlocal-smoothness Based Blind Hyperspectral Unmixing. IEEE Trans. Image Process. 2019, 28, 2991–3006. [Google Scholar] [CrossRef] [PubMed]
- Palm, B.G.; Bayer, F.M.; Cintra, R.J.; Pettersson, M.I.; Machado, R. Rayleigh regression model for ground type detection in SAR imagery. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1660–1664. [Google Scholar] [CrossRef]
- Bayer, D.M.; Bayer, F.M.; Gamba, P. A 3-D spatiotemporal model for remote sensing data cubes. IEEE Trans. Geosci. Remote Sens. 2020, 59, 1082–1093. [Google Scholar] [CrossRef]
- Hong, D.; Gao, L.; Yokoya, N.; Yao, J.; Chanussot, J.; Du, Q.; Zhang, B. More diverse means better: Multimodal deep learning meets remote-sensing imagery classification. IEEE Trans. Geosci. Remote Sens. 2020, 59, 4340–4354. [Google Scholar] [CrossRef]
- Nguyen, H.H.; Cho, S.; Jeong, J.; Choi, M. A D-vine copula quantile regression approach for soil moisture retrieval from dual polarimetric SAR Sentinel-1 over vegetated terrains. Remote Sens. Environ. 2021, 255, 112283. [Google Scholar] [CrossRef]

| Scenario | ||||
|---|---|---|---|---|
| Forest | (6.3, 36.2, 0.4, −0.9) | |||
| 60 × 60 | 90 × 90 | 120 × 120 | ||
| mean | (6.46, 36.76, 0.40, −0.89) | (6.36, 36.40, 0.40, −0.90) | (6.33, 36.29, 0.40, −0.90) | |
| Bias | (0.16, 0.53, 0.00, 0.00) | (0.06, 0.20, 0.00, 0.00) | (0.03, 0.09, 0.00, 0.00) | |
| SD | (0.68, 2.42, 0.06, 0.05) | (0.43, 1.56, 0.04, 0.03) | (0.35, 1.19, 0.03, 0.05) | |
| TRB | 0.06 | 0.02 | 0.01 | |
| Ocean | (3.0, 37.5, 3.7, 0.8) | |||
| 60 × 60 | 90 × 90 | 120 × 120 | ||
| mean | (2.89, 37.28, 4.26, 0.78) | (2.94, 37.23, 3.95, 0.79) | (2.98, 37.47, 3.81, 0.80)⊤ | |
| Bias | (−0.11, −0.22, 0.56, −0.02) | (−0.06, −0.27, 0.25, 0.00) | (−0.02, −0.03, 0.11, 0.00) | |
| SD | (0.56, 5.66, 1.54, 0.11) | (0.39, 4.15, 0.87, 0.07) | (0.31, 3.27, 0.59, 0.05) | |
| TRB | 0.22 | 0.10 | 0.04 | |
| Urban | (0.4, 5.3, 66.9, 0.9) | |||
| 60 × 60 | 90 × 90 | 120 × 120 | ||
| mean | (0.46, 5.28, 54.04, 0.89) | (0.44, 5.29, 59.60, 0.90) | (0.43, 5.31, 60.96, 0.90) | |
| Bias | (0.06, −0.02, −12.86, −0.01) | (0.04, 0.00, −7.30, 0.00) | (0.03, 0.01, −5.94, 0.00) | |
| SD | (0.09, 0.43, 17.31, 0.03) | (0.07, 0.29, 17.63, 0.02) | (0.06, 0.21, 17.33, 0.02) | |
| TRB | 0.36 | 0.21 | 0.18 |
| Dataset | Min. | Max. | Mean | Median | CV(%) | CS | CK |
|---|---|---|---|---|---|---|---|
| Forest region | 7.72 × 10 | 0.62 | 0.15 | 0.14 | 54.45 | 0.92 | 4.32 |
| Ocean region | 0.02 | 0.32 | 0.10 | 0.09 | 41.19 | 1.47 | 6.25 |
| Urban region | 0.09 | 3.75 | 0.45 | 0.37 | 68.86 | 3.21 | 21.22 |
| Scenario | Model | NP | AIC | W* | KS (p-Value) |
|---|---|---|---|---|---|
| Forest | ET-IB | 4 | −18,752.34 | 0.028 | 0.005 (0.973) |
| IB | 2 | −18,468.01 | 3.923 | 0.040 (<0.001) | |
| Rayleigh | 1 | −18,658.60 | 0.732 | 0.021 (<0.001) | |
| Weibull | 2 | −18,680.15 | 0.602 | 0.017 (0.014) | |
| Log-normal | 2 | −17,521.40 | 15.139 | 0.108 (<0.001) | |
| Rician | 2 | −18,656.60 | 0.732 | 0.021 (<0.001) | |
| K | 2 | −18,722.74 | 0.299 | 0.017 (0.022) | |
| 3 | −18,735.88 | 0.248 | 0.012 (0.180) | ||
| Ocean | ET-IB | 4 | −14,354.08 | 0.110 | 0.013 (0.456) |
| IB | 2 | −14,215.73 | 2.023 | 0.047 (<0.001) | |
| Rayleigh | 1 | −13,194.10 | 6.811 | 0.115 (<0.001) | |
| Weibull | 2 | −13,536.55 | 9.690 | 0.083 (<0.001) | |
| Log-normal | 2 | −14,329.52 | 0.501 | 0.843 (<0.001) | |
| Rician | 2 | −13,432.68 | 11.544 | 0.090 (<0.001) | |
| K | 2 | −13,158.91 | 5.720 | 0.157 (<0.001) | |
| 3 | −14,350.44 | 0.117 | 0.015 (0.348) | ||
| Urban | ET-IB | 4 | −1418.99 | 0.030 | 0.008 (0.927) |
| IB | 2 | −1072.49 | 4.301 | 0.054 (<0.001) | |
| Rayleigh | 1 | 633.11 | 22.517 | 0.161 (<0.001) | |
| Weibull | 2 | 181.21 | 17.077 | 0.105 (<0.001) | |
| Log-normal | 2 | 312.87 | 0.381 | 0.484 (<0.001) | |
| Rician | 2 | 635.11 | 22.517 | 0.161 (<0.001) | |
| K | 2 | −321.22 | 11.406 | 0.091 (<0.001) | |
| 3 | −1406.31 | 0.092 | 0.012 (0.543) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sagrillo, M.; Guerra, R.R.; Bayer, F.M.; Machado, R. A New Probability Distribution for SAR Image Modeling. Remote Sens. 2022, 14, 2853. https://doi.org/10.3390/rs14122853
Sagrillo M, Guerra RR, Bayer FM, Machado R. A New Probability Distribution for SAR Image Modeling. Remote Sensing. 2022; 14(12):2853. https://doi.org/10.3390/rs14122853
Chicago/Turabian StyleSagrillo, Murilo, Renata R. Guerra, Fábio M. Bayer, and Renato Machado. 2022. "A New Probability Distribution for SAR Image Modeling" Remote Sensing 14, no. 12: 2853. https://doi.org/10.3390/rs14122853
APA StyleSagrillo, M., Guerra, R. R., Bayer, F. M., & Machado, R. (2022). A New Probability Distribution for SAR Image Modeling. Remote Sensing, 14(12), 2853. https://doi.org/10.3390/rs14122853







