Sparse Approximation of the Precision Matrices for the Wide-Swath Altimeters

Abstract

The upcoming technology of wide-swath altimetry from space will deliver a large volume of data on the ocean surface at unprecedentedly high spatial resolution. These data are contaminated by errors caused by the uncertainties in the geometry and orientation of the on-board interferometer and environmental conditions, such as sea surface roughness and atmospheric state. Being highly correlated along and across the swath, these errors present a certain challenge for accurate processing in operational data assimilation centers. In particular, the error covariance matrix $\mathit{R}$ of the Surface Water and Ocean Topography (SWOT) mission may contain trillions of elements for a transoceanic swath segment at kilometer resolution, and this makes its handling a computationally prohibitive task. Analysis presented here shows, however, that the SWOT precision matrix ${\mathit{R}}^{-1}$ and its symmetric square root can be efficiently approximated by a sparse block-diagonal matrix within an accuracy of a few per cent. A series of observational system experiments with simulated data shows that such approximation comes at the expense of a relatively minor reduction in the assimilation accuracy, and, therefore, could be useful in operational systems targeted at the retrieval of submesoscale variability of the ocean surface.

1. Introduction

The upcoming Surface Water and Ocean Topography (SWOT, [1,2]) and Coastal and Ocean Measurement with Precise and Innovative Radar Altimeter (COMPIRA, [3]) missions are planned to deliver high resolution maps of the ocean surface topography using radar interferometers. This new type of observations of the sea surface height (SSH) will deliver gridded data along 100–150 km wide swaths at kilometer resolution. To achieve the target SSH accuracy of a few centimeters, this new remote sensing technology requires taking into the account multiple observation errors of instrumental and environmental origin that are spatially correlated.

Dealing with spatial correlations of swath altimetry errors in presents a certain challenge for the operational data assimilation systems, mostly because of the huge dimension of the respective error covariance matrices. As an example, a 3000 km long swath segment will contain on order of a million of spatially correlated observations whose error covariance matrix will have ${10}^{12}$ elements, and, therefore will be computationally expensive to handle.

In preparation for the SWOT mission, the Jet Propulsion Laboratory (JPL) developed the observation error covariance model [2,4] which served as a basis for numerous experiments aimed at assessing both the added value of the mission in monitoring the global ocean (e.g., [5,6,7,8,9]) and at dealing with spatial correlations of the errors contaminating SWOT observations (e.g., [10,11,12]).

In particular, ref. [10] proposes employing high-order differential operators to penalize the grid-scale components along the swath, while [11,13] explore a method of removing SSH errors caused by the uncertainties in interferometer geometry and orientation (hereinafter referred to as geometric and orientation errors, GOEs). In their recent study, Yaremchuk et al. [12] proposed a separable approximation to the GOE covariance matrix and its inverse, which provide significant computational savings at the expense of a slight modification of the along-swath error spectra of the JPL model. Heuristic sparse approximations of the inverse error covariance for the SWOT mission were also proposed in the earlier studies by Ruggiero et al. [7] and Yaremchuk et al. [14].

In a more general perspective, the problem of introducing non-diagonal observation error covariances into data assimilation systems requires an efficient algorithm for statistically consistent normalization of the innovations (i.e., multiplication of the innovations by the inverse square root of the respective observational error covariance matrix $\mathit{R}$). This necessity is evident from from the relationship between the model increment $\delta \mathit{x}$ and the normalized innovation vector $\delta \mathit{d}={\mathit{R}}^{-1/2}[\mathit{d}-\widehat{\mathit{H}}\left({\mathit{x}}_b\right)]$:

$$\delta \mathit{x}=\mathit{V}\mathit{C}{\mathit{H}}^{\mathrm{T}}{(\mathit{H}\mathit{C}{\mathit{H}}^{\mathrm{T}}+\mathit{I})}^{-1}\delta \mathit{d};\mathit{H}={\mathit{R}}^{-1/2}{\mathit{H}}_b\mathit{V}.$$

(1)

Here, $\widehat{\mathit{H}}\left({\mathit{x}}_b\right)$ is the observation operator projecting the background model state ${\mathit{x}}_b$ on observations $\mathit{d}$, ${\mathit{H}}_b$ is its linearization in the vicinity of ${\mathit{x}}_b$, $\mathit{V}$ is the diagonal matrix of the background standard deviations, $\mathit{C}$ is the respective correlation matrix, $\mathit{I}$ is the identity matrix, and the superscript $\mathrm{T}$ denotes transposition.

In this study, we explore a possibility of approximating the SWOT precision matrix ${\mathit{R}}^{-1}$ and its symmetric square root ${\mathit{R}}^{-1/2}$ by sparse matrices. Such approximations facilitate computationally efficient performance of the data assimilation systems in both dual (Equation (1)) and primal (state space) formulations.

The paper is organized as follows. In the next section we analyze the structure of the SWOT error covariance matrix and propose approximations reducing it to the block-diagonal form that is also separable in the across- and along-swath directions. In Section 3 the numerical testing methodology of these approximations is described and the respective errors are computed, as well as the results of observation system simulation experiments with several versions of the precision matrix approximations with different accuracy. The findings are summarized and discussed in Section 4.

2. Structure of the Wide-Swath Error Covariance Matrix

The JPL error covariance model [4], developed in preparation for the SWOT mission, is represented by the sum of three major constituents, associated with the errors caused by uncertainties in the geometry and orientation of the on-board interferometer, uncertainties in the environmental conditions (state of the atmosphere and ocean waves), and the intrinsic noise of the Ka-band Radar Interferometer (KaRIn) itself:

$$\mathit{R}={\mathit{R}}^g+{\mathit{R}}^e+\mathit{D}.$$

(2)

Here, ${\mathit{R}}^g$, ${\mathit{R}}^e$ and $\mathit{D}$ denote the respective (GOE, environmental and KaRIn) covariance matrices in the above-mentioned order. We denote the KaRIn noise error covariance by $\mathit{D}$ to distinguish its diagonal positive-definite structure, whereas the other two components are generally rank-deficient (positive semi-definite) and non-diagonal (i.e., have significant error correlations in the across- and along-swath directions). In the following, these directions are denoted by respectively x and y, while all the matrices operating in these directions will be subscripted accordingly.

2.1. Separable Approximation of the GOE Covariance Matrix

The general structure of the GOE model [4,12] is given by

$${\mathit{R}}^g=\sum _{p=1}^4[{\mathit{R}}_x^p\otimes {\mathit{F}}_y^{\mathrm{T}}{\mathit{S}}_y^p{\mathit{F}}_y]$$

(3)

where p enumerates the four GOE components associated with uncertainties in the roll, phase, baseline length and timing of the on-board interferometer, ⊗ denotes the tensor product, ${\mathit{R}}_x^p$, are the respective across-swath covariance matrices, ${\mathit{S}}_y^p=\mathrm{diag}{\mathit{S}}^p$ are the along-swath power spectra shown in the left panel of Figure 1, and $\mathit{F}$, ${\mathit{F}}^{\mathrm{T}}$ denote, respectively, the Fourier transformation matrix in the along-swath direction and its inverse.

Similarity in the shape of the spectra in Figure 1 allows to rescale them and introduce their “optimal mean” spectral shape ${\mathit{S}}_y$ shown in Figure 1 by the thick black line. After plugging the inverses of the spectral rescaling factors $s_p$ into ${\mathit{R}}_x^p$, the GOE covariance can be approximated by the matrix of the form

$${\mathit{R}}^{g\ast }=\left(\sum _{p=1}^4{\mathit{R}}_x^p\right)\otimes {\mathit{F}}_y^{\mathrm{T}}{\mathit{S}}_y{\mathit{F}}_y,$$

(4)

where ${\mathit{R}}_x^p$ now denote the across-swath covariances rescaled by $s_p$. As it was shown in [12], the error of such approximation does not exceed several per cent, which is likely to be well within the modeling uncertainty of the original spectra shown in Figure 1. Further reduction can be achieved by performing singular value decomposition of the sum in the rhs of Equation (4):

$${\mathit{R}}^{g\ast }={\mathit{F}}_x^{\mathrm{T}}{\mathit{S}}_x{\mathit{F}}_x\otimes {\mathit{F}}_y^{\mathrm{T}}{\mathit{S}}_y{\mathit{F}}_y,$$

(5)

where ${\mathit{F}}_x$ is the $4\times n_x$ matrix of the orthonormal eigenmodes shown in the right panel of Figure 1, and ${\mathit{S}}_x$ is the $4\times 4$ diagonal matrix of the respective eigenvalues. Equation (5) can also be rewritten in the more compact form

$${\mathit{R}}^{g\ast }={\mathit{F}}_x^{\mathrm{T}}{\mathit{S}}_x{\mathit{F}}_x\otimes {\mathit{F}}_y^{\mathrm{T}}{\mathit{S}}_y{\mathit{F}}_y\equiv {\Phi }^{\mathrm{T}}\mathit{S}\Phi$$

(6)

with $\Phi ={\mathit{F}}_x\otimes {\mathit{F}}_y$ and $\mathit{S}={\mathit{S}}_x\otimes {\mathit{S}}_y$. This representation allows one to obtain the pseudoinverse of ${\mathit{R}}^{g\ast }$ by computing the reciprocals of the diagonal entries of $\mathit{S}$.

It is also worthwhile to note that the approximation (5) also implies separability of the SWOT covariance (2) in the across- and along-swath directions if $\mathit{D}$ and ${\mathit{R}}^e$ can be represented in the form $\mathit{D}={\mathit{D}}_x\otimes {\mathit{D}}_y$ and ${\mathit{R}}^e={\mathit{R}}_x^e\otimes {\mathit{R}}_y^e$. Separability is a useful property from the computational point of view, as it allows one to easily compute and parallelize the action of $\mathit{R}$, ${\mathit{R}}^{-1}$ and ${\mathit{R}}^{-1/2}$ on a vector employing operations only involving small ($n_x\times n_x$ and $n_y\times n_y$) matrices operating in the across- and along-swath directions.

Separable approximations could be made under realistic assumptions about environmental factors affecting the structure of these matrices. First, the diagonal elements of $\mathit{D}$ depend on the significant wave height (SWH) underneath the satellite [4], and one may assume that SWH varies on spatial scales of the dominant atmospheric disturbances (≃500 km) that are much larger than the typical half-width (50 km) of the swath. In this case, spatial variation of the diagonal elements of $\mathit{D}$ could be approximated by the product of the across-swath structure function $D\left(x\right)$ corresponding to the mean SWH over the swath segment, and a slowly varying function $D\left(y\right)$ in the along-swath direction. So, neglecting SWH variation across the swath appears to be a reasonably good approximation, at least for relatively short swath segments in the open ocean. Similarly, the structure of ${\mathit{R}}^e$ is also defined by the scales of atmospheric disturbances in the water vapor and aerosol content, so a separable representation of ${\mathit{R}}^e$ (e.g., using a Gaussian kernel in the spectral space) appears to be a reasonable option.

2.2. Sparse Approximation of the Precision Matrix and Its Square Root

In what follows, we neglect ${\mathit{R}}^e$ in Equation (2), as the magnitude of the respective noise appears to be several times smaller than the magnitude of KaRIn and GOE constituents, at least in the two-beam radiometer configuration [4]. Assuming separability of the KaRIn noise error covariance matrix, consider separable approximation ${(\mathit{D}+{\mathit{R}}^{g\ast })}^{-1}$ of the precision matrix ${\mathit{R}}^{-1}$. Combining the representation (6) with the Woodbury identity, and rewriting the precision matrix in the form

$${\mathit{R}}^{-1}={\mathit{D}}^{-1}-{\mathit{D}}^{-1}{\Phi }^{\mathrm{T}}{({\mathit{S}}^{-1}+\Phi {\mathit{D}}^{-1}{\Phi }^{\mathrm{T}})}^{-1}\Phi {\mathit{D}}^{-1},$$

(7)

consider a polynomial expansion of the matrix inverse in the right-hand side. The latter is valid if one of the matrices under the inversion sign is sufficiently small compared to the other, so that the inverse of their sum could be represented by a convergent Taylor series. Inspection of the rms magnitudes of the KaRIn noise errors [4] indicates that within a realistic range (1 to 8 m) of the SWH conditions, the typical magnitude of $\left|\mathit{D}\right|$ (1–2 cm) is considerably (3–5 times) smaller than the magnitude of the sum of GOEs $\left|\mathit{S}\right|$, so we could consider the second term in the sum to dominate, and rearrange the inverted matrix in (7) by rewriting it in the form:

$${({\mathit{S}}^{-1}+\Phi {\mathit{D}}^{-1}{\Phi }^{\mathrm{T}})}^{-1}\equiv {({\mathit{S}}^{-1}+{\mathit{Q}}^{-1}{\mathit{Q}}^{-1})}^{-1}=\mathit{Q}{(\mathit{Q}{\mathit{S}}^{-1}\mathit{Q}+\mathit{I})}^{-1}\mathit{Q},$$

(8)

where $\mathit{I}$ is the $4n_y\times 4n_y$ identity matrix and

$$\mathit{Q}={(\Phi {\mathit{D}}^{-1}{\Phi }^{\mathrm{T}})}^{-1/2}={\mathit{Q}}_x\otimes {\mathit{Q}}_y={\left({\mathit{F}}_x{\mathit{D}}_x^{-1}{\mathit{F}}_x^{\mathrm{T}}\right)}^{-1/2}\otimes {\mathit{F}}_y{\mathit{D}}_y^{1/2}{\mathit{F}}_y^{\mathrm{T}}$$

(9)

is the symmetric square root of ${(\Phi {\mathit{D}}^{-1}{\Phi }^{\mathrm{T}})}^{-1}$.

The matrix inverse in the rhs of Equation (8) can be expanded in the convergent series if all the eigenvalues of the expansion matrix $\mathit{Q}{\mathit{S}}^{-1}\mathit{Q}$ do not exceed 1. Because of the matrix separability,

$$\mathit{Q}{\mathit{S}}^{-1}\mathit{Q}={\mathit{Q}}_x{\mathit{S}}_x^{-1}{\mathit{Q}}_x\otimes {\mathit{Q}}_y{\mathit{S}}_y^{-1}{\mathit{Q}}_y$$

(10)

the eigenvalues can be inexpensively obtained by decomposition of the respective $n_x\times n_x$ and $n_y\times n_y$ matrices in the rhs of (10) given their definition in the rhs of (9).

The eigenvalues of the expansion matrix in the lhs of (10) are then obtained as a tensor product of two vectors containing eigenvalues of the matrices in the rhs of (10) operating in the across- and along-swath directions. Results of these computations are shown in the left panel of Figure 2 for a 512 km long swath segment at 2 km resolution. It is seen that for SWH values less than 6 m, just a few terms of the Taylor expansion provide a good approximation of the precision matrix as the largest eigenvalue does not exceed 0.22.

It is also noteworthy that since we are interested in retrieval of submesoscale SSH variability with spatial frequencies above 10${}^{-2}$ km${}^{-1}$ (wavelengths below the half-width of the satellite swath, which is 50–60 km), the respective part of the along-swath precision matrix spectrum is nearly flat (Figure 1) and contributes more than 90% to the total precision (inverse error variance). Therefore, the white noise ${\mathit{S}}_y^{-1}\approx \alpha {\mathit{I}}_y$ could be a reasonable approximation of the along-swath spectrum if we are particularly interested in retrieving the submesoscale components of the SSH variability. What is more important, this approximation sparsifies the SWOT precision matrix estimate reducing Equation (7) to the block-diagonal form:

$${\mathit{R}}^{-1}={\mathit{D}}^{-1}-\sum _{m=0}^{\infty }{(-1)}^m{\mathit{D}}_x^{-1}{\mathit{F}}_x^{\mathrm{T}}{\mathit{Q}}_x^2{\left({\mathit{S}}_x^{-1}{\mathit{Q}}_x^2\right)}^m{\mathit{F}}_x{\mathit{D}}_x^{-1}\otimes {\alpha }^m{\mathit{D}}_y^{m-1}$$

(11)

In the case of constant SWH, ${\mathit{D}}_y$ in the rhs of Equation (11) turns into the identity matrix, and all the blocks become identical (see Appendix A for more details). Equation (11) demonstrates that the precision matrix can be decoupled in the along- and across-swath directions if the inverse of the along-swath GOE spectrum is approximated by the white noise. Inspection of Figure 1 shows that such approximation is rather accurate, because the inverse of the optimized spectrum is nearly flat for wavelengths $\lambda$ below 50 km ($k_y>0.02$ km${}^{-1}$) and quickly falls down at longer wavelengths, which contribute less than 1% to the wavenumber integral.

To summarize, these analytical considerations indicate that block-diagonal approximations of ${\mathit{R}}^{-1}$ and ${\mathit{R}}^{-1/2}$ may have a reasonable accuracy, especially for the purpose of retrieving submesocale SSH variability within the swath.

Although Equation (11) provides a simple way to obtain the diagonal blocks of the precision matrix, it still requires first to get reliable approximations of ${\mathit{S}}_y$ [12], $\alpha$ and ${\mathit{D}}_y$. A more general and accurate way of doing this in practice, is to minimize the Frobenius norm of the following expressions in the space of symmetric block-diagonal matrices $\mathit{C}$:

$$\begin{array}{ccc}\hfill {\mathit{R}}_a^{-1}& =& {\mathrm{argmin}}_{\mathit{C}}{|\mathit{R}\mathit{C}-\mathit{I}|}^2;\hfill \end{array}$$

(12)

$$\begin{array}{ccc}\hfill {\mathit{R}}_a^{-\frac{1}{2}}& =& {\mathrm{argmin}}_{\mathit{C}}{|\mathit{C}\mathit{R}\mathit{C}-\mathit{I}|}^2\hfill \end{array}$$

(13)

with the structure of $\mathit{R}$ given by the JPL error model, and Equation (3) in particular. Note that due to the block-diagonal form of the target matrix $\mathit{C}$, these problems can be executed in parallel for each of the $n_y$ blocks, each having a rather moderate size of the control vector which is equal to the number of elements $n_x(n_x+1)/2$ in the upper triangle of the across-swath covariance matrix. Similar approach is routinely used in computing the approximate sparse preconditioners for iterative solvers (e.g., [15]).

3. Numerical Tests

3.1. Methodology

To test the proposed approach, we conducted a series of twin data assimilation experiments with a 512 km long swath segment defined on rectangular grid with $dx=2$ km resolution (Figure 3). The true (reconstructed) SSH field $\mathit{x}$ was defined on the same grid and computed as a single realization of a Gaussian field with zero mean, the decorrelation scale of $\rho =5$ km and the amplitude a of 2 cm shown in the top panel of Figure 3.

To simulate the data assimilation process, two 100-member ensembles of the “model fields” $\left\{{\mathit{x}}_m\right\}$ and “SWOT observations” $\left\{{\mathit{x}}_o\right\}$ were created, and then the estimates of the true state were reconstructed for each pair of the ensemble members. The model fields were generated by contaminating $\mathit{x}$ with realizations of the background noise (model errors) ${\mathit{x}}_m^{\prime }$ characterized by the decorrelation scale $\rho =3$ km and the amplitude of 1 cm. The Gaussian random fields used for generating both the true sea surface height field and the background noise were defined by the covariance function

$$\mathbf{B}=\frac{a^2}{{\rho }^2\sqrt{2\pi }}exp(\frac{{\rho }^2}{2}\Delta ),$$

(14)

where $\Delta$ is the Laplacian operator (e.g., [16,17]) on the model grid with Neumann boundary conditions.

As mentioned above, the information on the true field was provided by the simulated model fields $\left\{{\mathit{x}}_m\right\}=\mathit{x}+\left\{{\mathit{x}}_m^{\prime }\right\}$ and SWOT “observations” $\left\{{\mathit{x}}_o\right\}=\mathit{x}+\left\{{\mathit{x}}_o^{\prime }\right\}$ at 2 km resolution. Realizations of the respective error fields were computed by

$${\mathit{x}}^{\prime }={\mathbf{B}}^{1/2}\mathit{n};{\mathit{x}}_o={\mathit{R}}^{1/2}\mathit{n}$$

(15)

where $\mathit{n}$ is the normally distributed 2d field, and ${\mathbf{B}}^{1/2}$, ${\mathit{R}}^{1/2}$ are the square roots of the background (14) and SWOT (2) error covariances. Two realizations of the “modelled” and “observed” fields are shown in the middle and bottom panels of Figure 3.

Given 100 realizations of the “model output” and “observations”, three hundred data assimilation experiments using Equation (1) were conducted to compute the optimal correction $\delta \mathit{x}$ to the model field. These experiments employed three types of representation (diagonal, block-diagonal and exact) for the inverse square root of $\mathit{R}$ in Equation (1). The first two approximations were obtained by the respective restrictions of the sparsity patterns for $\mathit{C}$ in Equation (13).

To quantify the results of assimilation experiments, the mean relative deviations e of the analyses ${\mathit{x}}_a=\mathit{x}+{\mathit{x}}^{\prime }+\delta \mathit{x}$ from the true state $\mathit{x}$ were computed

$$e=\frac{|{\mathit{x}}_a-\mathit{x}|}{\left|\mathit{x}\right|}=\frac{|{\mathit{x}}^{\prime }+\delta \mathit{x}|}{\left|\mathit{x}\right|},$$

(16)

as well as their ensemble means $\langle e\rangle$.

3.2. Results

The block-diagonal approximation of ${\mathit{R}}^{-1/2}$ was computed under the condition of constant SWH over the swath (${\mathit{D}}_y={\mathit{I}}_y$ in Equation (11)) currently available in the SWOT simulator. At 2 km resolution of the SWOT grid, this problem had a moderate size of $n_x(n_x+1)/2=1275$ and was not computationally expensive. To check the block-diagonal approximation quality, we also computed the exact precision matrix and a series of its sparsifications ${\mathit{R}}_k$. The latter were obtained by setting to zero all the elements of ${\mathit{R}}^{-1}$ whose absolute value was less than a given threshold ${\mathit{C}}_k$. Results of these computations as a function of the sparsity parameter $\gamma =N\left({\mathit{R}}^{-1}\right)/{\left(n_x{n}_y\right)}^2$, (here N is the number of non-zero elements of a matrix), are presented in the left panel of Figure 2. The approximation errors ${ϵ}_k$ were defined by the Frobenius norm ratio $|{\mathit{R}}_k-\mathit{R}|/|\mathit{R}|$. The plot gives an evidence that; (a) the block-diagonal approximation of ${\mathit{R}}^{-1}$ is an order in magnitude better than just taking the diagonal of ${\mathit{R}}^{-1}$, and (b) provides an accuracy $ϵ$ of roughly 2%, which is nearly identical to accuracy obtained by the above described sparsification method when $\gamma$ is equal to its block-diagonal value of $n_y^{-1}$.

For the symmetric square root of the precision matrix, the errors are somewhat larger, but still remain within the reasonably accurate limits of 2–2.7%, even for larger SWH values that magnify the KaRIn noise quite significantly. Results of these preliminary computations are assembled in

Table 1. Block-diagonal approximation errors for the SWOT precision matrix ${\mathit{R}}^{-1}$ and its symmetric square root for various values of the significant sea surface height.

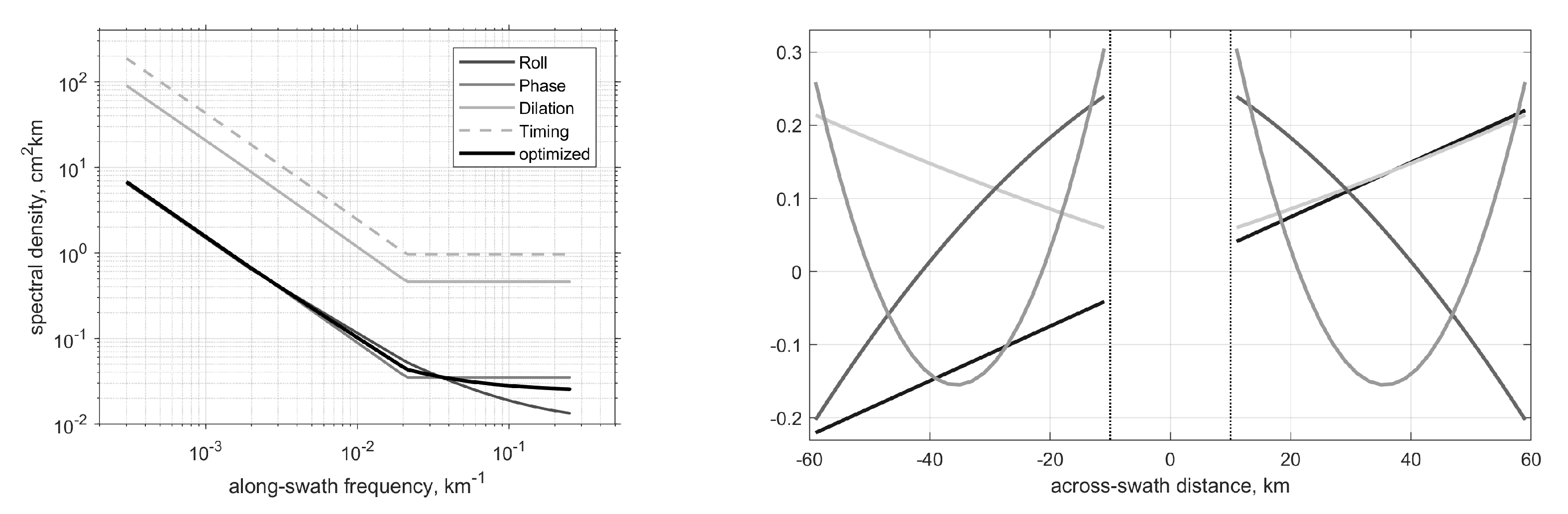
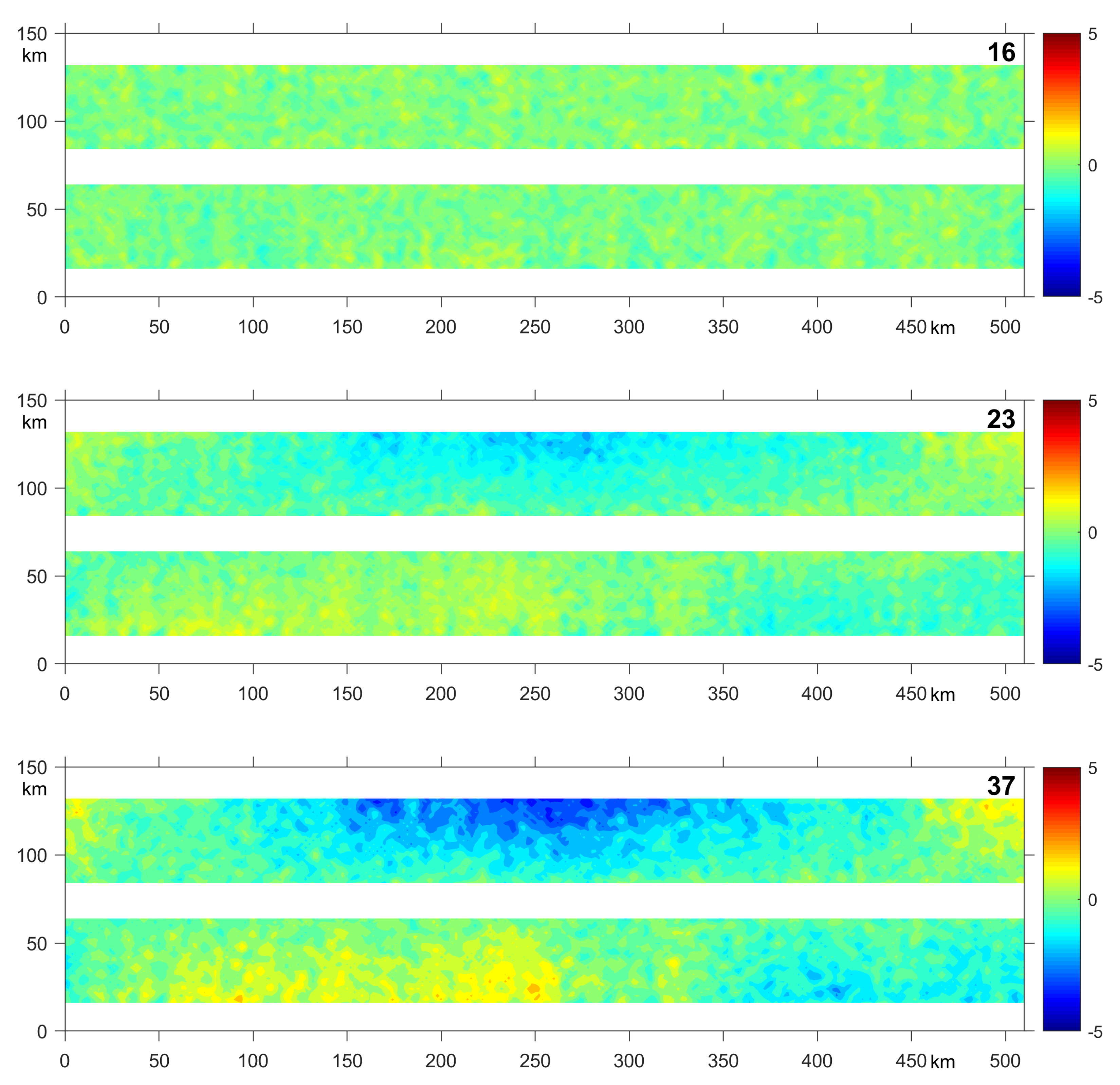
SWH, m	2	4	6	7	8
$ϵ\left({\mathit{R}}^{-1}\right)$	0.0188	0.0198	0.0209	0.0221	0.0242
$ϵ\left({\mathit{R}}^{-1/2}\right)$	0.0204	0.0215	0.0233	0.0250	0.0267

. It should be also noted that the SWOT covariance matrix does not have a similar sparse approximation as the respective errors were found to be quite close to a hundred per cent, and ranged within 0.98–0.997 for the tested swath configuration.

To estimate the impact of assimilating SWOT data, we computed the increments $\delta \mathit{x}$ in Equation (1) for the 100-member ensembles of realizations of the background and simulated SWOT error fields. A couple of ensemble members of the background and observed fields are shown in the middle and bottom panels of Figure 3. In each of the ensembles of the assimilation solutions, three forms of the square root of the SWOT precision matrix were used: the exact symmetric square root of the inverse covariance, its block-diagonal ${\mathit{R}}_{bd}^{-1/2}$ and diagonal ${\mathit{R}}_d^{-1/2}$ approximations. The latter was obtained by inverting the square root of the ensemble-based estimate of diag(R) derived from the SWOT simulator output by squaring the ensemble members in each grid point and averaging the result.

An example of such a twin-data assimilation experiment is shown in Figure 4 for an ensemble member with moderate sea surface roughness SWH = 2 m.

To assess the overall impact of the block-diagonal approximation on the accuracy of submesoscale retrievals from SWOT observations, we conducted a series of numerical experiments with sea surface roughness parameter increasing from 2 to 8 m. Results of these experiments are assembled in

Table 2. Ensemble-averaged deviations e (Equation (16)) from the true SSH obtained in the assimilation experiments with the exact square root of the precision matrix in the definition of the normalized observation operator in Equation (1) (first line), with its block-diagonal ${\mathit{R}}_{bd}^{-1/2}$ and diagonal ${\mathit{R}}_d^{-1/2}$ approximations shown in the middle. The contribution of the KaRIn noise to the total error covariance (in %) is displayed at the bottom line.

SWH, m	2	4	6	7	8
$\langle e\left({\mathit{R}}^{-1/2}\right)\rangle$	0.16	0.17	0.19	0.21	0.22
$\langle e\left({\mathit{R}}_{bd}^{-1/2}\right)\rangle$	0.23	0.24	0.25	0.26	0.26
$\langle e\left({\mathit{R}}_d^{-1/2}\right)\rangle$	0.37	0.35	0.34	0.33	0.31
$\eta$	0.41	0.46	0.59	0.70	0.77

.

The major tendencies are the general increase of the analysis error e, and reduction of its range (the difference between lines 1 and 3) with the increasing SWH. It is also remarkable that the analysis errors obtained with the diagonal approximation of ${\mathit{R}}^{-1/2}$ (line 3) decrease from 0.37 to 0.31 with the increase of the significant wave height from 2 to 8 m. This can be explained by the growth of the KaRIn noise contribution to the error budget

$$\eta =\sqrt{\frac{\langle {\mathit{n}}^{\mathrm{T}}\mathit{D}\mathit{n}\rangle }{\langle {\mathit{n}}^{\mathrm{T}}(\mathit{D}+{\mathit{R}}^g)\mathit{n}\rangle }}$$

(17)

shown in the bottom line of Table 2. Indeed, rougher seas reduce the overall accuracy of the SSH retrieval at submesoscale (upper line in Table 2) and at the same time increase the covariance matrix diagonal $\mathit{D}$, improving the quality of the diagonal approximation for the precision matrix (third line). The growing diagonal dominance of the SWOT covariance matrix reduces the importance of taking the spatial error covariances into the account with the increase of the sea surface roughness.

Quantitatively, improvement in the accuracy of submesoscale retrievals using the block-diagonal approximation (computed as the ratio $e\left({\mathit{R}}_d^{-1/2}\right)/e\left({\mathit{R}}_{bd}^{-1/2}\right)$ of the respective errors) degrades from 1.6 to 1.3 with the growth of SWH from 2 to 7 m. These numbers indicate utility of the proposed approximation of the SWOT precision matrix in a wide range of sea surface roughness conditions.

4. Conclusions and Discussion

Analysis of the structure of the SWOT error covariance matrix has shown a possibility to approximate its inverse square root by a sparse matrix within the accuracy of a few per cent. The approximation was successfully tested in a series of twin data assimilation experiments, and demonstrated a capability to improve the assimilation accuracy 1.3–1.6 times compared to a simple diagonal approximation of the error covariance. The improvement is observed over the range of significant sea surface heights of 2–8 m, and could be even better for calmer seas.

The analytical analysis of precision matrix and its square root indicate that their block-diagonal approximations are more accurate for retrieval of the SSH structures with typical wavelengths below the swath half-width (scales less than 20 km). This makes the proposed approximation technique especially suitable for multi-scale data assimilation (e.g., [18,19]) at its final stage, after correction of the larger-scale (mesoscale) structures of the model state. Furthermore, since the typical magnitude of SSH perturbations at submesoscale (2–4 cm, [20]) is comparable to (and often less than) SWOT errors [4], statistically consistent treatment of the spatial structure of the observation error covariances becomes especially important in the analysis and assimilation of the SWOT data at the wavelengths below 50 km. Comparison of the analysis error fields (shown in middle and bottom panels of Figure 4) provides a particular demonstration of the necessity to properly take into account spatial correlations of the observational errors within the swath.

In this study, we did not consider the contribution of uncertainties in atmospheric water content ${\mathit{R}}^e$ and nadir altimeter observations on the overall accuracy of the SSH reconstruction. Preliminary consideration indicates that the magnitude of ${\mathit{R}}^e$ is several times smaller than the contributions from KaRIn noise $\mathit{D}$ and ${\mathit{R}}^g$, at least in the two-beam radiometer configuration, which removes the linear trend of the vapor-related path delay across the swath [4]. The relatively small magnitude of ${\mathit{R}}^e$ may provide an asymptotic guidance for updating the sparsity pattern of the precision matrix by taking the wet atmosphere corrections into the account. Similar asymptotic techniques can be possibly used for treatment of spatial variations of the SWH field and dry atmosphere corrections. These modifications are planned to be implemented in the JPL model in the near future.

Comparison of the first and second rows in Table 2 shows that there is still a considerable room for improving the block-diagonal approximation of the sparsity pattern for the precision matrices. Solutions to this challenging problem could be further developed by the joint analysis of real data from the forthcoming satellite missions and ensemble simulations of the ocean surface topography by state-of-the-art numerical models. In particular, the specific structure of the wide-swath altimetry error covariances may be exploited to improve the sparsity patterns of the precision matrices by the deep learning techniques (e.g., [21,22]) and other methods involving neural networks. Extensive literature (e.g., [23,24,25,26]) also exists on purely algebraic methods of approximating the inverse covariances. These methods do not explicitly take into account the specific structure of the covariance model, as it was done in the present study. Of particular interest are applications of the modified Cholesky decomposition [24], under the sparsifying assumption of conditional independence of the observation errors beyond a given localization scale in the along-swath direction. This approach is suitable for efficient parallelization [25] of the precision matrix approximations specifically tailored for retrieving SSH variability at submesoscale.

In the SWOT application, one may think of combining the above-mentioned methods to obtain accurate and computationally efficient approximations of the precision matrices. The presented study could be considered as another step towards this ultimate goal.