Sparse Approximation of the Precision Matrices for the Wide-Swath Altimeters
Abstract
:1. Introduction
2. Structure of the Wide-Swath Error Covariance Matrix
2.1. Separable Approximation of the GOE Covariance Matrix
2.2. Sparse Approximation of the Precision Matrix and Its Square Root
3. Numerical Tests
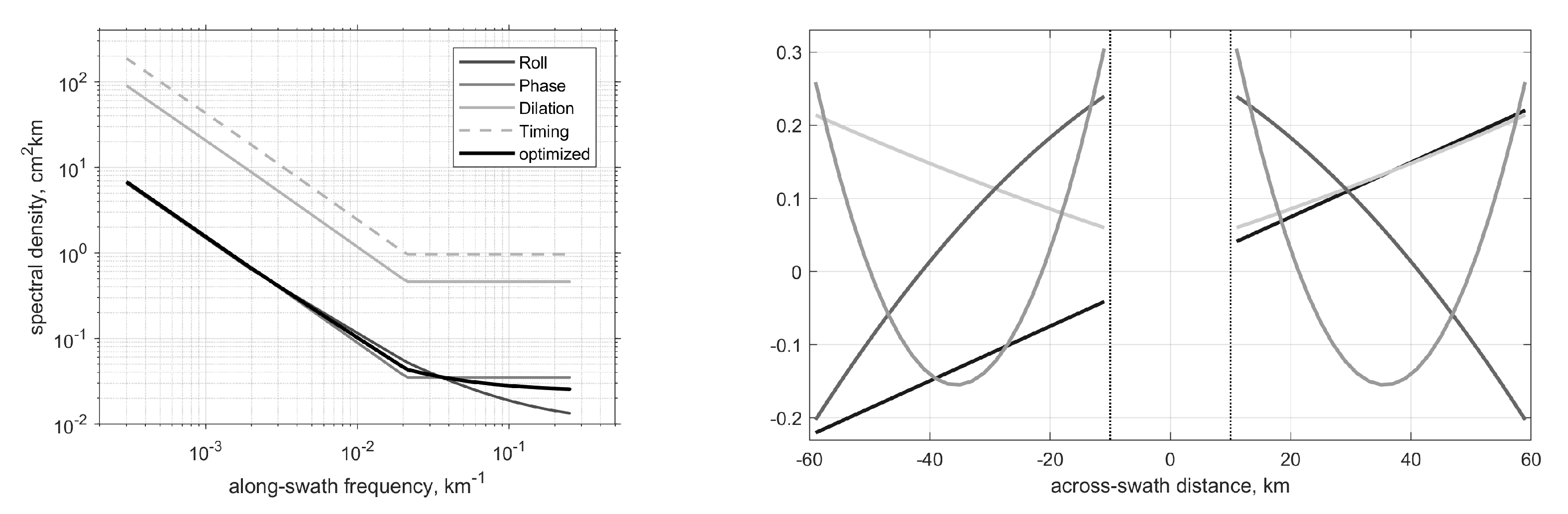
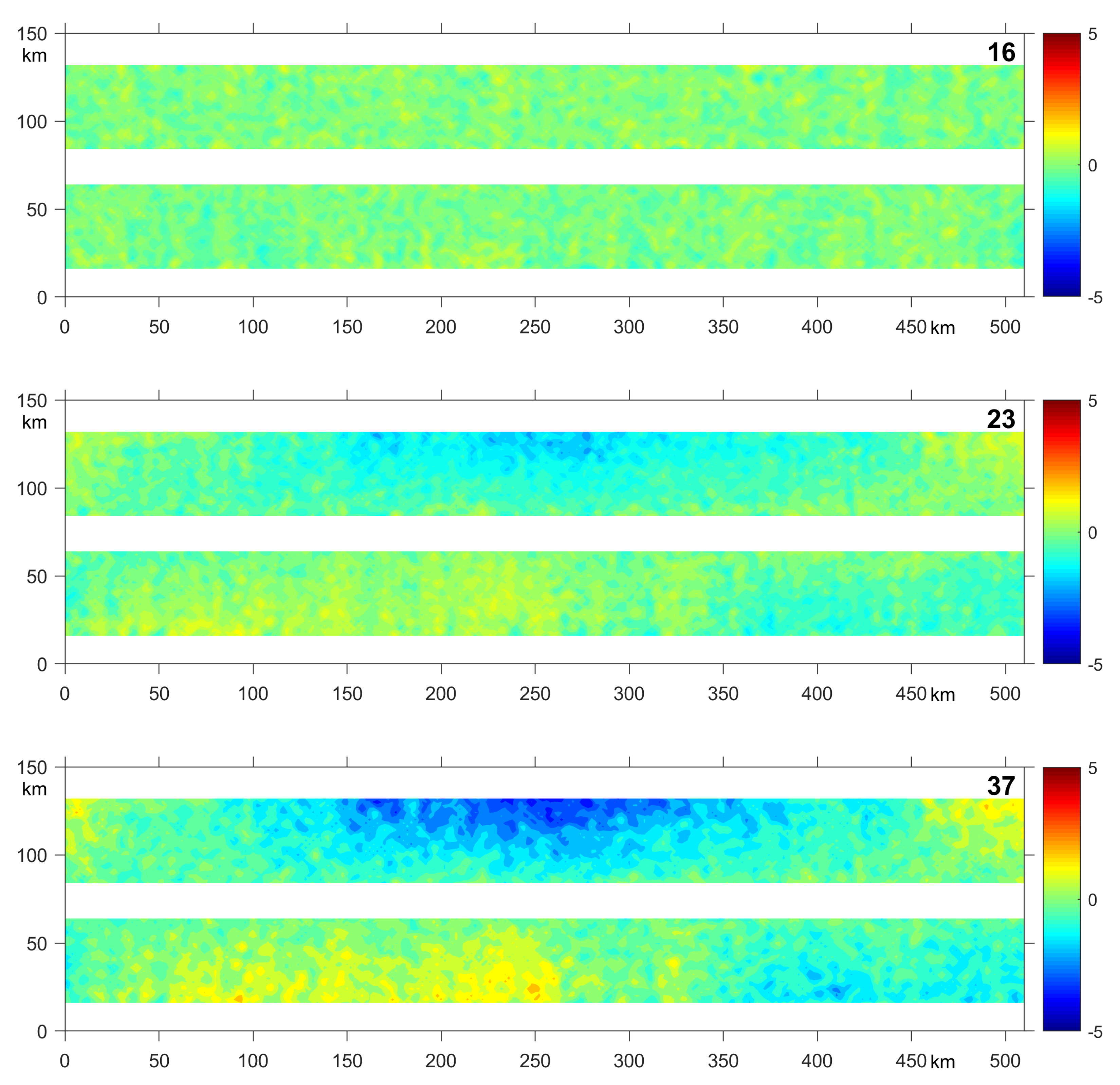
3.1. Methodology
3.2. Results
4. Conclusions and Discussion
Funding
Conflicts of Interest
Appendix A. White Noise Approximation of the Along-Swath Covariance
References
- Durand, M.; Fu, L.L.; Lettenemaier, D.; Alsdorf, D.; Rodriguers, E.; Esteban-Fernandez, D. The surface water and ocean topography mission: Observing terrestrial surface water and oceanic submesoscale eddies. Proc. IEEE 2010, 98, 766–779. [Google Scholar] [CrossRef]
- Esteban-Fernandez, D. SWOT Project: Mission Performance and Error Budget. Revision A. NASA/JPL Tech. Rep. JPL D-79084. 2013. Available online: http://https://ieeexplore.ieee.org/document/8517385 (accessed on 12 June 2022).
- Ito, N.; Uematsu, A.; Yajima, Y.; Isoguchi, O. A Japanese new altimetry mission COMPIRA—Towards high temporal and spatial sampling of sea surface height. AGU Fall Meet. 2014, OS34B-05. Available online: https://agu.confex.com/agu/fm14/webprogram/Paper21766.html (accessed on 12 June 2022).
- Gaultier, L.; Ubelmann, C.; Fu, L.-L. SWOT Simulator Documentation; Tech. Rep. 2.3.0; Jet Propulsion Laboratory, CalTech: Pasadena, CA, USA, 2017.
- Gaultier, L.; Ubelmann, C.; Fu, L.-L. The challenge of using future SWOT data for oceanic field reconstruction. J. Atm. Ocean. Technol. 2016, 33, 119–126. [Google Scholar] [CrossRef]
- Li, Z.; Wang, J.; Fu, L.-L. An observing system simulation experiment for ocean state estimation to assess the performance of the SWOT mission: Part 1—A twin experiment. J. Geophys. Res. Ocean. 2019, 124, 4838–4855. [Google Scholar] [CrossRef]
- Ruggiero, G.A.; Cosme, E.; Brankart, J.M.; Le Sommer, J.; Ubelmann, C. An efficient way to account for observation error correlations in the assimilation of data from the future SWOT high-resolution altimeter mission. J. Atmos. Ocean. Technol. 2016, 33, 2755–2768. [Google Scholar] [CrossRef]
- Ubelmann, C.; Klein, E.; Fu, L.L. Dynamic interpolation of sea surface height and potential applications for future high-resolution altimetry mapping. J. Atmos. Ocean. Technol. 2015, 32, 177–184. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Fu, L.L.; Qui, B.; Menemenlis, D.; Farrar, J.T.; Chao, Y.; Thompson, A.F.; Flexas, M.M. An observing system simulation experiment for the calibration and validation of the SWOT sea surface height measurement using in situ platforms. J. Atmos. Ocean. Technol. 2018, 35, 281–297. [Google Scholar] [CrossRef]
- Gomez-Navarro, L.; Cosme, E.; Sommer, J.L.; Papadakis, N.; Pascual, A. Development of an image de-noising method in preparation for SWOT satellte mission. Remote Sens. 2020, 12, 734. [Google Scholar] [CrossRef] [Green Version]
- Metref, S.; Cosme, E.; Guillou, F.L.; Sommer, J.L.; Brankart, J.-M.; Verron, J. Wide-swath altimetric satellite data assimilation with correlated error reduction. Front. Mar. Sci. 2020, 6, 822. [Google Scholar] [CrossRef] [Green Version]
- Yaremchuk, M.; D’Addezio, J.; Jacobs, G. Facilitating inversion of the error covariance models for the wide-swath altimeters. Remore Sens. 2020, 12, 1823. [Google Scholar] [CrossRef]
- Metref, S.; Cosme, E.; Sommer, J.L.; Poel, N.; Brankart, J.-M.; Verron, J.; Gomez Navarro, L. Reduction of spatially structured errors in wide-swath altimetric satellite data using data assimilation. Remote Sens. 2019, 11, 1336. [Google Scholar] [CrossRef] [Green Version]
- Yaremchuk, M.; D’Addezio, J.; Panteleev, G.; Jacobs, G. On the approximation of the inverse error covariances of high-resolution altimetry data. Q. J. R. Meteorol. Soc. 2018, 144, 1995–2000. [Google Scholar] [CrossRef]
- Chow, E.; Saad, Y. Approximate inverse preconditioners via sparse-sparse iterations. SIAM J. Sci. Comp. 1998, 19, 995–1023. [Google Scholar] [CrossRef] [Green Version]
- Yaremchuk, M.; Smith, S. On the correlation functions associated with polynomials of the diffusion operator. Q. J. R. Meteorol. Soc. 2011, 137, 1927–1932. [Google Scholar] [CrossRef]
- Yaremchuk, M.; Carrier, M.; Smith, S.; Jacobs, G. Background error correlation modeling with diffusion operators. In Data Assimilation for Atmospheric, Oceanic and Hydrologic Applications; Park, S.K., Xu, L., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; Volume II, pp. 177–203. [Google Scholar] [CrossRef]
- Li, Z.; McWiliams, J.C.; Ide, K.; Farrara, J.D. A multi-scale variational data assimilation scheme: Formulation and illustration. Mon. Wea. Rev. 2015, 143, 3804–3822. [Google Scholar] [CrossRef]
- Souopgui, I.; D’Addezio, J.M.; Rowley, C.; Smith, S.; Jacobs, G.A.; Helber, R.; Yaremchuk, M. Multi-scale assimilation of simulated SWOT observations. Ocean Model. 2020, 154, 101683. [Google Scholar] [CrossRef]
- D’Addezio, J.M.; Jacobs, J.M.G.A.; Yaremchuk, M.; Souopgui, I. Submesoscale eddy vertical covariances and dynamical constraints from high-resolution numerical simulations. J. Phys. Oceanogr. 2020, 50, 1087–1115. [Google Scholar] [CrossRef] [Green Version]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comp. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Tavakkoli, V.; Chedjou, J.C.; Kyamakaya, K. A novel recurrent neural network-based ultra-fast, robust, and scalable solver for inverting a time-varying matrix. Sensors 2019, 19, 4002. [Google Scholar] [CrossRef] [Green Version]
- Chang, C.; Tsay, R.S. Estimation of covariance matrix via the sparse Cholesky factor with the lasso. J. Stat. Plan. Inference 2010, 140, 3858–3873. [Google Scholar] [CrossRef]
- Nino-Ruiz, E.D.; Sandu, A.; Deng, X. An ensemble Kalman filter implementation based on modified Cholesky decomposition for inverse covariance matrix estimation. SIAM J. Sci. Comp. 2018, 40, A867–A886. [Google Scholar] [CrossRef]
- Nino-Ruiz, E.D.; Sandu, A.; Deng, X. A parallel implementation of the ensemble Kalman filter implementation based on modified Cholesky decomposition. J. Comp. Sci. 2019, 36, 100654. [Google Scholar] [CrossRef] [Green Version]
- Zhang, W.; Leng, C. A moving average Cholesky factor model in covariance modeling for longitudinal data. Biometrika 2012, 99, 141–150. [Google Scholar] [CrossRef]


| SWH, m | 2 | 4 | 6 | 7 | 8 |
|---|---|---|---|---|---|
| 0.0188 | 0.0198 | 0.0209 | 0.0221 | 0.0242 | |
| 0.0204 | 0.0215 | 0.0233 | 0.0250 | 0.0267 |
| SWH, m | 2 | 4 | 6 | 7 | 8 |
|---|---|---|---|---|---|
| 0.16 | 0.17 | 0.19 | 0.21 | 0.22 | |
| 0.23 | 0.24 | 0.25 | 0.26 | 0.26 | |
| 0.37 | 0.35 | 0.34 | 0.33 | 0.31 | |
| 0.41 | 0.46 | 0.59 | 0.70 | 0.77 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yaremchuk, M. Sparse Approximation of the Precision Matrices for the Wide-Swath Altimeters. Remote Sens. 2022, 14, 2827. https://doi.org/10.3390/rs14122827
Yaremchuk M. Sparse Approximation of the Precision Matrices for the Wide-Swath Altimeters. Remote Sensing. 2022; 14(12):2827. https://doi.org/10.3390/rs14122827
Chicago/Turabian StyleYaremchuk, Max. 2022. "Sparse Approximation of the Precision Matrices for the Wide-Swath Altimeters" Remote Sensing 14, no. 12: 2827. https://doi.org/10.3390/rs14122827
APA StyleYaremchuk, M. (2022). Sparse Approximation of the Precision Matrices for the Wide-Swath Altimeters. Remote Sensing, 14(12), 2827. https://doi.org/10.3390/rs14122827





