Analysis of BDS-3 PPP-B2b Positioning and Time Transfer Service

Abstract

With the completion of the BeiDou global navigation satellite system (BDS-3), the BeiDou Navigation Satellite System Signal In Space Interface Control Document Precise Point Positioning Service Signal PPP-B2b (Version 1.0) was officially announced, and BDS-3 officially broadcast PPP-B2b correction to broadcast ephemeris through geostationary earth orbit (GEO) satellites to provide precise point positioning services for users in the Asia–Pacific region. This study comprehensively analyzes the application of the PPP-B2b product to time transfer and positioning. On a daily basis, the PPP-B2b positioning accuracy after convergence is calculated using the four ionosphere-free (IF) combinations in static and simulated kinematic modes: BDS B1I/B3I, BDS B1C/B2a, BDS B1I/B3I + GPS, and BDS B1C/B2a + GPS. Observations of time laboratories including the National Time Service Center of the Chinese Academy of Sciences (NTSC) and the Telecommunication Laboratories (TL) are employed to conduct zero-baseline common clock difference (CCD) time comparison experiments and long-baseline time comparison experiments using the PPP-B2b product and the GBM product. The results indicate that the PPP-B2b position accuracy in static mode by only BDS is 1.5/2.7/3.9 cm, and by GPS + BDS is within 1.5/2.5/3.5 cm in North, East, and Up directions, respectively. Regarding simulated kinematic PPP-B2b, the average root mean square (RMS) values of the position errors in the North, East, and Up directions for the combination of BDS B1I/B3I + GPS and BDS B1I/B3I are 3.4/5.8/7.6 cm and 3.8/6.6/7.8 cm, respectively. Simultaneously, the average RMS values of position errors using BDS B1C/B2a + GPS and BDS B1C/B2a are 3.6/4.9/8.1 cm and 4/6.1/8.5 cm. In the time comparison study, the results of zero-baseline CCD using the PPP-B2b product and the GBM product are within the fluctuation range of 0.1 ns, respectively. Particularly, the long-baseline time comparison difference between results employing the PPP-B2b product and the GBM product is within the range of ±0.5 ns.

1. Introduction

The BeiDou navigation satellite system (BDS) independently established and operated by China, as one of the four major global navigation satellite systems, aims to provide global users with positioning, navigation, and timing services. The BeiDou navigation satellite system is developed in three stages, with services ranging from China to the Asia–Pacific region, and finally to the world [1]. In May 2003, the third geostationary earth orbit satellite was launched, and the BeiDou demonstration navigation system (BDS-1) was established, providing China with positioning, timing, and short message communication services [2]. By the end of 2012, with the launch of 14 networked satellites including 5 geostationary earth orbit satellites, 5 inclined geosynchronous orbit (IGSO) satellites, and 4 medium earth orbit (MEO) satellites, the BeiDou regional navigation system (BDS-2) was established and its service scope was extended to the Asia–Pacific region. At the end of July 2020, it was officially announced that the BeiDou global navigation satellite system, comprising 24 MEO satellites, 3 GEO satellites, and 3 IGSO satellites, was completed. Since then, BDS-3 has provided global users with positioning, navigation and timing (PNT), global short message communication (GSMC), and international search and rescue (SAR), and provided a satellite-based augmentation system (SBAS), a ground augmentation system (GAS) as well as precise point positioning (PPP) and regional short message communication (RSMC) services for users in China and its surrounding areas [3,4,5,6,7,8].

PPP [9,10,11] plays an important role in the global navigation satellite system (GNSS) high-precision positioning applications. It receives carrier phase observations and pseudorange observations through a single GNSS receiver, uses precise products and model empirical formulas to correct errors, and uses least squares, Kalman filtering, and other methods to determine high-precision absolute coordinates [11]. Initially, the international GNSS service (IGS) only provides precise satellite clock and orbit products with a certain delay, which limits the PPP study to focus on post-processing. In order to obtain precise products with the shortest possible latency, the IGS launched a real-time pilot project (RTPP) in 2007. In 2013, real-time data streaming services via Networked Transport of RTCM (Radio Technical Commission for Maritime Services) via Internet Protocol (NTRIP) was officially provided, serving users with real-time and free correction products required for PPP [12,13,14]. The emergence of real-time products has promoted the research of PPP in positioning and time transfer. Refs. [14,15,16,17,18,19,20] demonstrated that the simulated kinematic positioning accuracy using real-time products is better than one decimeter and that time transfer can achieve sub-nanosecond accuracy. However, the NTRIP protocol requires a communication network, making it impossible to be applied in areas with limited network connections. Some navigation systems provide users with PPP services by broadcasting corrections to the navigation ephemeris through satellites to solve the problem of real-time correction products’ dependence on the communication network. The Quasi-Zenith Satellite System (QZSS) uses an L6 signal to provide centimeter-level augmentation services (CLAS) for users in the Japanese area. Currently, the CLAS services support GPS, QZSS, and Galileo systems [21]. Galileo provides free high-precision PPP services for GPS and Galileo users through E6-B signals [22]. In August 2020, the China Satellite Navigation Office released the interface control document dealing with the PPP service signal, PPP-B2b. The document points out that BDS-3 uses GEO satellites to provide BDS-3, GPS, GLONASS, and GALILEO with satellite orbit correction, clock correction, and many others, providing decimeter-level positioning accuracy in the kinematic mode for users in the Asia–Pacific region [23]. However, the PPP-B2b service currently only provides correction products for the BDS-3 and GPS systems.

The PPP-B2b signal broadcasts the I-component and the Q-component but the first three GEO satellites of BDS-3 only broadcast the I-component [23].

Table 1. Defined message types.

Message Types (in Decimal)	Information Content
1	Satellite mask
2	Satellite orbit correction and user range accuracy index
3	Differential code bias
4	Satellite clock correction
5	User range accuracy index
6	Clock correction and orbit correction–combination 1
7	Clock correction and orbit correction–combination 2
8–62	Reserved
63	Null message

summarizes the types of messages defined by the PPP-B2b interface control document [23]. The user receives the PPP-B2b signal in real time to restore satellite orbit correction, satellite clock correction, and differential code bias, and finally corrects the broadcast ephemeris to obtain precise satellite orbit and clock, achieving decimeter-level positioning accuracy in kinematic mode using PPP. The research on the PPP-B2b product and services is becoming a hotspot. Among them, Tao et al. evaluated the PPP-B2b product using the multi-GNSS Wuhan University (WHU) final product as a reference. Their results show that the satellite orbit error of the PPP-B2b product is 0.1 m in both the BDS-3 and GPS in the radial component, and the error in the along-track and cross-track components is three to four times the radial component, respectively [24]. Meanwhile, the standard deviation (STD) of satellite clock error for the GPS and BDS-3 PPP-B2b clock product is 0.13 and 0.11 ns [24]. Xu et al. reported that the accuracy of the BDS-3 satellite orbit corrected by the PPP-B2b product in the radial, along-track, and cross-track directions is 6.8, 33.4, and 36.6 cm, respectively, and the clock product reaches an accuracy of 0.2 ns, improved by about 85.1% compared to the broadcast clock [25]. Nie et al. define that PPP positioning utilizing PPP-B2b corrections converges after 10 consecutive epochs to an accuracy of better than 0.6 m in the vertical component and better than 0.3 m in the horizontal component. Their results showed that PPP average convergence time is 17.7 min utilizing the PPP-B2b signal [26]. Positioning accuracy using the PPP-B2b product can reach decimeter-level by Multi-GNSS PPP-B2b in simulated kinematic mode in China [24,25,26]. Meanwhile, PPP-B2b augmentation information availability for GPS and BDS satellites is 91.5% and 97.5%, respectively [24]. These studies focus on the evaluation of the PPP-B2b product, and the positioning research mainly focuses on the use of B1I/B3I observations for stations within China. There are few studies on PPP-B2b positioning accuracy in static and simulated kinematic modes using the BDS-3 B1C and B2a new signals, and a lack of research on the application of the PPP-B2b product to time transfer.

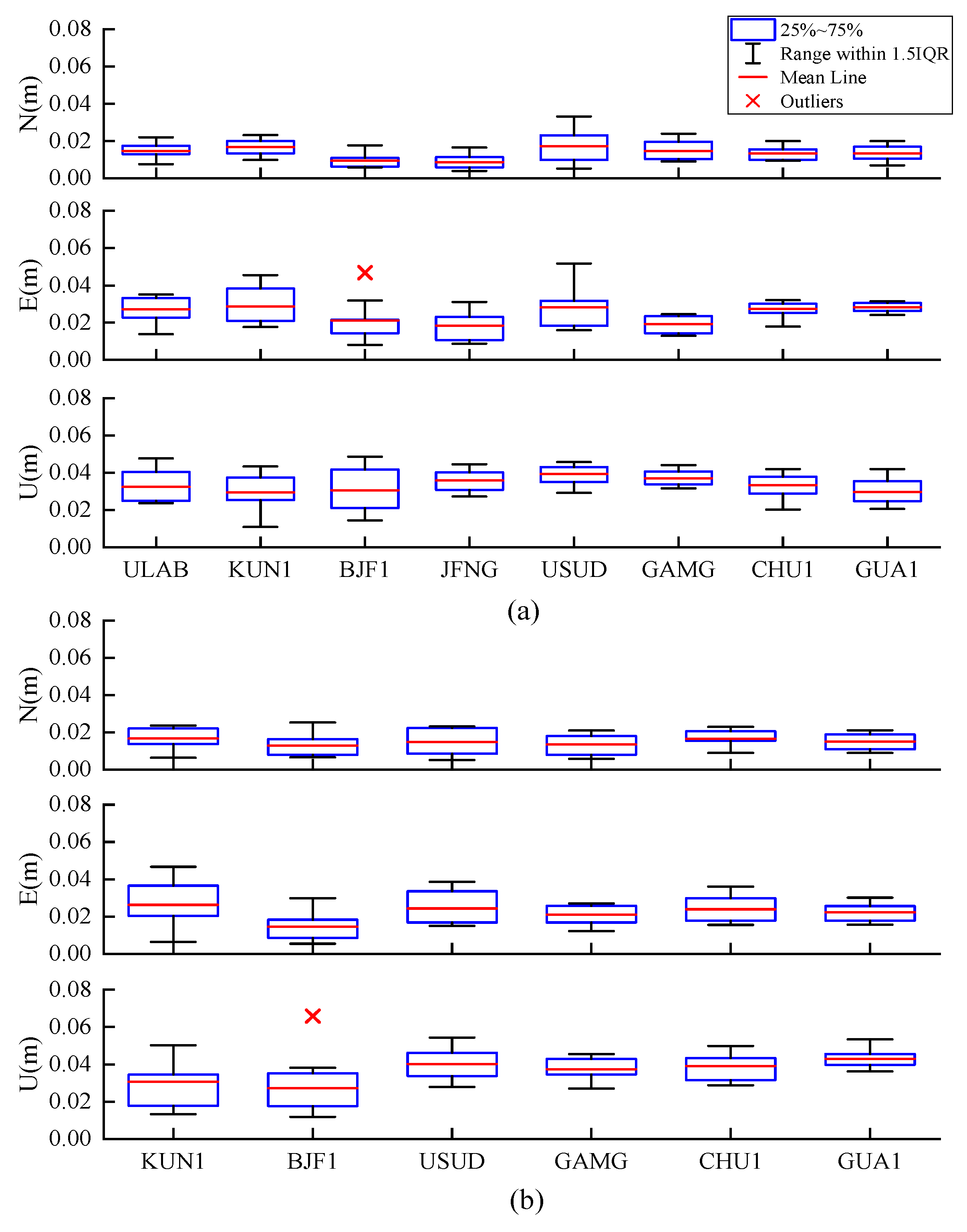
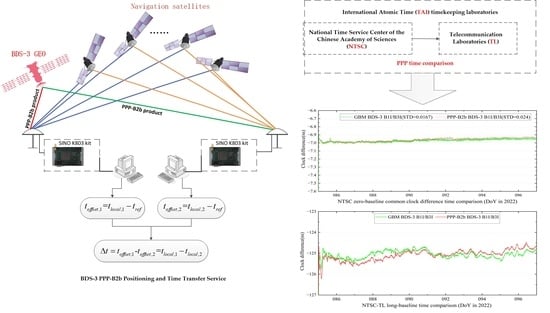
In this contribution, stations with uniform distribution in the Asia–Pacific region were selected, and the daily RMS values of the PPP-B2b positioning errors using BDS B1I/B3I and BDS B1C/B2a were calculated in static and simulated kinematic modes. Meanwhile, the PPP-B2b time comparison of two international atomic time (TAI) timekeeping laboratories in the Asia–Pacific region was studied, including the National Time Service Center of the Chinese Academy of Sciences and the Telecommunication Laboratories. Based on the 10-day observation data of 8 IGS/international GNSS monitoring and assessment system (IGMAS) stations in the Asia–Pacific region from day of year (DoY) 67 to 76 in 2022, the RMS values of the PPP-B2b positioning errors in North, East, and Up (N, E, and U) directions employing four combinations of BDS B1I/B3I + GPS, BDS B1I/B3I, BDS B1C/B2a + GPS, and BDS B1C/B2a were analyzed in static and simulated kinematic modes. In addition, two baseline time links were used to investigate the accuracy and stability of PPP-B2b time comparison, taking the GeoForschungZentrum (GFZ) multi-GNSS final product (GBM) as a reference, including the NTSC zero-baseline common clock difference and NTSC-TL long-baseline. The rest of the article is arranged as follows. Section 2 introduces the matching strategy of PPP-B2b correction information and the method of using the PPP-B2b product to restore precise satellite orbit and satellite clock; secondly, theories of PPP and PPP time transfer are introduced. Section 3 predominately covers the experimental data, methodology, experimental results, and analysis discussion. Section 4 presents several conclusions.

2. Materials and Methods

2.1. Matching Strategy

The connection between PPP-B2b message types is identified by the issue of data (IOD), which consists of IOD SSR (issue of data, state space representation), IODP (issue of data, PRN mask), IODN (issue of data, navigation), and IOD Corr (issue of data, orbit and clock correction).

Table 2. Defined issue of data.

Issue of Data	Message Types
IOD SSR	1, 2, 3, 4, 5, 6, 7
IODP	1, 4, 5, 6
IODN	2, 6, 7
IOD Corr	2, 4, 6, 7

lists the IOD contained in the message types. Currently, the first four message types of the PPP-B2b product can be combined into a complete correction message version. The IOD SSR plays a decisive role in the connection of different message types, and different message types of the same IOD SSR can be matched. IODP indicates the issue number of the satellite mask where the identification position of “1” denotes that the differential information of the satellite broadcast ephemeris corrected by the PPP-B2b product is provided. Meanwhile, the message type 4 arranges satellite clock products in the order of slot locations with the mask of “1” in the message type 1. Satellite clock and satellite orbit corrections can only be used if the IOD Corr of the satellite orbit and satellite clock was consistent. IODN matches IODE (issue of data, ephemeris) of different navigation messages, establishes a connection between the navigation messages and the PPP-B2b IOD, and the matched navigation messages are corrected by the PPP-B2b product to obtain precise satellite orbit and clock. The corrected navigation message differs due to the navigation system. For BDS-3 PPP-B2b, the CNAV1 navigation message carried by the B1C signal is corrected, whereas the LNAV navigation message is corrected for GPS.

Each PPP-B2b message has two timestamps: the time when the receiver receives the PPP-B2b correction information (marked as time a) and the time carried by the epoch time field in the PPP-B2b correction signal frame (marked as time b). There are two options for the reference time for updating the PPP-B2b message in post-processing. If time b is selected, the IOD Corr of the satellite orbit and clock will be mismatched when message type 2 and message type 4 match [25]. Figure 1 shows the BDS C23 orbit and clock IOD Corr every second with time b as the reference for updating the correction product. At time t1, the IOD Corr of the satellite clock is updated, and the IOD Corr of the satellite orbit is updated at t2, and there is a short IOD Corr mismatch from t1 to t2. Figure 2 shows the BDS C23 orbit and clock IOD Corr every 1 s and every 2 s with time a as the reference time for updating the correction product. Using time a as the reference time for updating the correction information can weaken the mismatch phenomenon, and the occurrence rate of this mismatch is significantly reduced when updating every 2 s because there is a random lag between time a and time b. This mismatch can be eliminated using the observation data with an interval of 30 s in post-processing, using time a as the reference time for updating the correction information.

2.2. Correction Algorithm

2.2.1. Differential Code Bias Correction

The pseudorange observations generated using different tracking methods contain hardware delay deviations [27]. The PPP-B2b product provides a differential code bias, which can be used to correct the satellite hardware delay of pseudorange observations. Taking RINEX3.05 as a reference, the PPP-B2b product currently provides the hardware delay correction product for signals such as BDS C2I, C2Q, C1P, etc., but does not provide hardware delay correction of BDS C1X and C5X. The pseudorange hardware delay correction algorithm [23] can be applied according to (1):

$${\tilde{l}}_{sig}=l_{sig}-DC{B}_{sig}$$

(1)

${\tilde{l}}_{sig}$ denotes the pseudorange observation value in meters corrected by the PPP-B2b differential code bias product, $l_{sig}$ denotes the pseudorange observation value in meters directly obtained by the GNSS receiver, $DC{B}_{sig}$ denotes the correction in meters of the pseudorange observation in the sig tracking mode.

2.2.2. Recovery of Precise Satellite Orbit

Equation (2) is the algorithm for recovering a precise satellite position from broadcast ephemeris [23].

$$\left[\begin{array}{c}{X}_{pre}\\ Y_{pre}\\ Z_{pre}\end{array}\right]=\left[\begin{array}{c}{X}_{brd}\\ Y_{brd}\\ Z_{brd}\end{array}\right]-\left[\begin{array}{c}\delta x\\ \delta y\\ \delta z\end{array}\right]$$

(2)

where $\left(X_{pre},Y_{pre},Z_{pre}\right)$ is the precise satellite coordinate vector in earth-centered-earth fixed (ECEF), $(X_{brd},Y_{brd},Z_{brd})$ represents satellite ECEF coordinate vector calculated from the broadcast ephemeris, and $(\delta x,\delta y,\delta z)$ denotes corrections in the x, y, and z directions of the satellite in the ECEF frame.

The orbit correction vector $(\delta O_r,\delta O_a,\delta O_c)$ broadcasted by the PPP-B2b product contains the correction parameters in radial, along-track, and cross-track components. It should be transformed into the ECEF coordinate system using Formulas (3) and (4).

$$\left[\begin{array}{c}\delta x\\ \delta y\\ \delta z\end{array}\right]=[{\mathit{e}}_{radical}\hspace{0.33em} {\mathit{e}}_{along} \hspace{0.33em}{\mathit{e}}_{cross}]\cdot \left[\begin{array}{c}\delta O_r\\ \delta O_a\\ \delta O_c\end{array}\right]$$

(3)

$$\left\{\begin{array}{c}{\mathit{e}}_{radial}=\frac{\mathit{r}}{\left|\mathit{r}\right|}\\ {\mathit{e}}_{cross}=\frac{\mathit{r}\times \dot{\mathit{r}}}{\left|\left.\mathit{r}\times \dot{\mathit{r}}\right|\right.}\\ {\mathit{e}}_{along}={\mathit{e}}_{cross}\times {\mathit{e}}_{radial}\end{array}\right.$$

(4)

where $\mathit{r}=(X_{brd},Y_{brd},Z_{brd})$ is the broadcast ephemeris satellite position vector and $\dot{\mathit{r}}$ represents the broadcast ephemeris satellite velocity vector.

2.2.3. Recovery of Precise Satellite Clock

The broadcast satellite clock recovers the precise clock through Formula (5).

$$t_{pre}=t_{brd}-\frac{C_0}{c}$$

(5)

where $t_{brd}$ is the satellite clock offset in seconds calculated from the broadcast ephemeris, $t_{pre}$ represents the satellite clock offset in seconds corrected by the PPP-B2b clock correction product, $c$ denotes the speed of light, and $C_0$ is the PPP-B2b product satellite clock correction in meters.

2.3. PPP Model

The GNSS observation equations are expressed as Equations (6)–(8) [28] after the Sagnac effect [29], relativistic effect, phase windup effect [30], and receiver and satellite antenna phase centers are corrected.

$$P_{r,j}^s=\rho +c(d{t}_r-d{t}^s)+T_r^s+{\gamma }_j^{}\cdot I_{r,1}^s+c(d_{r,j}^s-d_j^s)+{\epsilon }_{r,j}^s$$

(6)

$$L_{r,j}^s=\rho +c(d{t}_r-d{t}^s)+T_r^s-{\gamma }_j^{}\cdot I_{r,1}^s+{\lambda }_j^s(N_{r,j}^s+b_{r,j}^s-b_j^s)+{\xi }_{r,j}^s$$

(7)

$${\gamma }_j=\frac{f_1^2}{f_j^2}$$

(8)

where $r$ and $s$ refer to receiver-related, satellite-related, respectively; subscript $j$ represents the band number of the satellite signal, L1 and L2 of GPS refer to 1 and 2, respectively, while B1I, B3I, B1C, and B2a of BDS refer to 2, 6, 1, and 5, respectively; $P$ and $L$ represent raw code and carrier phase observations in meters; $\rho$ represents geometric distance from the satellite to a receiver in meters. $c$ is the speed of light, $d{t}_r$ and $d{t}^s$ denote clock offset of the GNSS receiver and satellite; $T_r^s$ is tropospheric delay (m); ${\gamma }_j$ denotes a frequency-dependent scaling factor, $I_{r,1}^s$ represents the ionospheric delay in meters at frequency $j=1$; $d_{r,j}^s$ and $d_j^s$ denote uncalibrated code delays (UCD) at the receiver and satellite; ${\epsilon }_{r,j}^s$ and ${\xi }_{r,j}^s$ represent the error in the pseudorange and carrier phase measurements; $b_{r,j}^s$ and $b_j^s$ represent uncalibrated phase delays (UPD) at the receiver and satellite; ${\lambda }_j^s$ denotes the carrier wavelength at the frequency $j$ of satellite $s$, $N_{r,j}^s$ is the integer ambiguity of the $j$ frequency signal from satellite $s$ to receiver $r$.

For convenience, Equation (9) is defined, $\rho$ can be linearized to the calculated satellite-receiver distance ${\rho }_0$ and ${\mu }_r^s\Delta x$. ${\mu }_r^s$ represents the receiver-to-satellite unit vector and $\Delta x$ represents the vector of receiver position increments.

$$\left\{\begin{array}{c}{\alpha }_{ij}=\frac{f_i^2}{f_i^2-f_j^2},{\beta }_{ij}=-\frac{f_j^2}{f_i^2-f_j^2}\\ d_{I{F}_{ij}}^s={\alpha }_{ij}{d}_i^s+{\beta }_{ij}{d}_j^s,d_{r,I{F}_{ij}}^s={\alpha }_{ij}{d}_{r,i}^s+{\beta }_{ij}{d}_{r,j}^s& i\ne j\hfill \\ DC{B}_{P_i{P}_j}^s=d_i^s-d_j^s,DC{B}_{r,P_i{P}_j}^s=d_{r,i}^s-d_{r,j}^s\\ \rho ={\rho }_0+{\mu }_r^s\Delta x\end{array}\right.$$

(9)

The GPS broadcast clock offset refers to a P1 and P2 hardware delay linear combination, while the BDS broadcast clock offset introduces a B3I hardware delay [27]

$$cd{t}_{I{F}_{12}}^s=cd{t}^s+c{d}_{I{F}_{12}}^s$$

(10)

$$cd{t}_{brd}^s=cd{t}^s+c{d}_6^s$$

(11)

In this study, Equations (12)–(15) express the dual-frequency ionospheric-free (IF) combination of L1 and L2 observations of the GPS.

$$\begin{array}{l}{P}_{r,I{F}_{12}}^s={\alpha }_{12}{P}_{r,1}^s+{\beta }_{12}{P}_{r,2}^s\\ \hspace{1em}\hspace{1em}\hspace{0.17em}=\rho +cd{t}_{r,I{F}_{12}}-cd{t}_{I{F}_{12}}^s+T_r^s+{\epsilon }_{r,{\mathrm{IF}}_{12}}^s\end{array}$$

(12)

$$\begin{array}{l}{L}_{r,I{F}_{12}}^s={\alpha }_{12}{L}_{r,1}^s+{\beta }_{12}{L}_{r,2}^s\\ \hspace{0.33em}\hspace{1em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.17em}=\rho +cd{t}_{r,I{F}_{12}}-cd{t}_{I{F}_{12}}^s+T_r^s+{\overline{\lambda }}_{I{F}_{12}}{\overline{N}}_{r,I{F}_{12}}^s+{\xi }_{r,I{F}_{12}}^s\end{array}$$

(13)

$${\overline{\lambda }}_{I{F}_{12}}{\overline{N}}_{r,I{F}_{12}}^s={\alpha }_{12}{\lambda }_1^s(N_{r,1}^s+b_{r,1}^s-b_1^s)+{\beta }_{12}{\lambda }_2^s(N_{r,2}^s+b_{r,2}^s-b_2^s)-c{d}_{r,I{F}_{12}}^s+c{d}_{I{F}_{12}}^s$$

(14)

$$cd{t}_{r,I{F}_{12}}=cd{t}_r+c{d}_{r,I{F}_{12}}^s$$

(15)

Replace $d{t}_{I{F}_{12}}^s$ in Equations (12) and (13) with the broadcasted satellite clock corrected by PPP-B2b, and the unknown parameters are expressed as a vector $[\Delta x,cd{t}_{r,I{F}_{12}},T_r^s,{\overline{N}}_{r,I{F}_{12}}^s]$.

Equations (16)–(19) express the dual-frequency ionospheric-free combination of the BDS B1I/B3I and the BDS B1C/B2a.

$$\begin{array}{l}{P}_{r,I{F}_{ij}}^s={\alpha }_{ij}{P}_{r,i}^s+{\beta }_{ij}{P}_{r,j}^s\\ \hspace{1em}\hspace{1em}\hspace{0.17em}=\rho +cd{t}_{r,I{F}_{ij}}+T_r^s+c{\alpha }_{ij}{\mathrm{DCB}}_{p_6{p}_i}^s+c{\beta }_{ij}{\mathrm{DCB}}_{p_6{p}_j}^s-cd{t}_{brd}^s+{\epsilon }_{r,{\mathrm{IF}}_{ij}}^s\end{array}$$

(16)

$$\begin{array}{l}{L}_{r,I{F}_{ij}}^s={\alpha }_{ij}{L}_{r,i}^s+{\beta }_{ij}{L}_{r,j}^s\\ \hspace{1em}\hspace{0.33em}\hspace{1em}=\rho +cd{t}_{r,I{F}_{ij}}+T_r^s-cd{t}_{brd}^s+{\overline{\lambda }}_{I{F}_{ij}}{\overline{N}}_{r,I{F}_{ij}}^s+{\xi }_{r,I{F}_{ij}}^s\end{array}$$

(17)

$${\overline{\lambda }}_{I{F}_{ij}}{\overline{N}}_{r,I{F}_{ij}}^s={\alpha }_{ij}{\lambda }_i^s(N_{r,i}^s+b_{r,i}^s-b_i^s)+{\beta }_{ij}{\lambda }_j^s(N_{r,j}^s+b_{r,j}^s-b_j^s)-c{d}_{r,I{F}_{ij}}^s+c{d}_6^s$$

(18)

$$cd{t}_{r,I{F}_{ij}}=cd{t}_r+c{d}_{r,I{F}_{ij}}^s$$

(19)

Replace $d{t}_{brd}^s$ in Equations (16) and (17) with the broadcasted satellite clock corrected by the PPP-B2b product, and the unknown parameters are expressed as a vector $[\Delta x,cd{t}_{r,I{F}_{ij}},T_r^s,{\overline{N}}_{r,I{F}_{ij}}^s]$.

2.4. PPP Time Transfer

The receiver clock offset $t_{offset,a}$ of a station is the difference between the local time $t_{local,a}$ of $a$ station and the GNSS reference clock $t_{ref}$, as shown in Equation (20). The difference in the receiver clock offset of the two stations for time transfer eliminates $t_{ref}$, which is equivalent to the difference in the local time of the two stations, as shown in Equation (21). Only two GNSS receivers are required, and the all-weather, long-distance and high-precision time transfer can be achieved using PPP. Equations (15) and (19) show that the receiver clock offset introduces a hardware delay which must be calibrated in engineering applications [31].

$$t_{offset,a}=t_{local,a}-t_{ref}$$

(20)

$$\Delta t=t_{offset,1}-t_{offset,2}=(t_{local,1}-t_{ref})-(t_{local,2}-t_{ref})=t_{local,1}-t_{local,2}$$

(21)

3. Experiments, Results, and Discussion

3.1. Dataset

Figure 3 shows 8 IGMAS/IGS stations equipped with BDS-3 and GPS receivers in the Asia–Pacific region participating in our analysis of PPP-B2b in the static and simulated kinematic mode. SINO K803 kit which is a multi-GNSS receiver with a PPP-B2b signal receiving module is used to collect the original binary PPP-B2b correction number information which is automatically ordered and saved into files by the data collection program in daily bins for 10 days from DoY 67 to 76 in 2022. The static and simulated kinematic PPP-B2b positioning analysis in this study is divided into four cases by model and observation type: BDS B1I/B3I IF combination (abbreviated as BDS B1I/B3I), BDS B1I/B3I and GPS L1/L2 dual-system IF combination (abbreviated as BDS B1I/B3I + GPS), BDS B1C/B2a IF combination (abbreviated as BDS B1C/B2a), and BDS B1C/B2a and GPS L1/L2 dual-system IF combination (abbreviated as BDS B1C/B2a + GPS). Because the PPP-B2b product does not contain the differential code bias correction products of the C1X and C5X observations of JFNG and ULAB stations, BDS B1C/B2a and BDS B1C/B2a + GPS use 6 stations except JFNG and ULAB for PPP-B2b positioning experiments in static and simulated kinematic modes. PPP was processed using the open-source MG_APP software [32].

NTSC and TL are the two time laboratories in the Asia–Pacific region involved in maintaining TAI.

Table 3. Receiver information.

Receiver ID	Time Laboratory	Receiver (Firmware Version)
NTTS	NTSC	SEPT POLARX5TR(5.4.0)
NT07	NTSC	SEPT POLARX5TR(5.4.0)
TLM2	TL	SEPT POLARX5TR(5.4.0)

lists the GNSS receiver’s information for the PPP-B2b time comparison. NTTS and NT07 are GNSS receivers with a common atomic clock and antenna in the NTSC laboratory. NTSC-TL represents a pair of long-baseline time comparison links in the Asia–Pacific region. NTTS, NT07, and TLM2 are all connected to local UTC (k). Using the 12-day observation data from DoY 85 to 96 in 2022, the BDS IF combination PPP-B2b time comparison using B1I/B3I and the reference GBM product BDS PPP time comparison were conducted simultaneously.

Table 4. Time links.

Time Link	Region	Approximate Distance (km)
NTTS-NT07	Asia	0
NTTS-TLM2	Asia	1551.5

lists the time links participating in the time comparison.

3.2. PPP-B2b Strategy

Table 5. Data processing strategies for PPP-B2b.

Items	Models
Constellations	BDS, GPS
Cutoff angle	10°
Estimator	Kalman filter
Observations	Ionospheric-free linear combination code and carrier-phase measurements
Data interval	30 s
Tropospheric delay	Dry component: corrected with Saastamoinen model [33] Wet component: estimated as a random-walk process; GMF Mapping function is applied [34].
Phase wind-up	Corrected [30]
Receiver antenna phase center	PCO is corrected by the “atx” file
Satellite orbit and clock	BDS:B1C CNAV1 broadcast ephemeris + BDS-3 PPP-B2b. GPS: LNAV broadcast ephemeris + BDS-3 PPP-B2b.
Satellite DCB	Corrected using the PPP-B2b product [23]
Station coordinates	Estimated as constant for the static mode, Estimated as white noise for the simulated kinematic mode
Receiver clock offset	Estimated as white noise
Phase ambiguities	Estimated as floating-point constant each continuous epoch

summarizes the processing strategies for PPP. Daily PPP-B2b position solutions in four combinations in the static and simulated kinematic modes are conducted. Because the kalman filter must converge when calculating the positioning errors RMS of the N, E, and U directions, the first 25 min of data are removed from the daily data used in positioning. Meanwhile, the 12-day data were solved continuously to determine the accuracy and stability of the time transfer of the PPP-B2b product.

3.3. Convergence Time

According to the official document [35], the precise point positioning performance using the PPP-B2b product with the BDS single-system and the BDS + GPS dual-system is better than 30 cm, 20 cm in the horizontal component with a confidence level of 95%, respectively, while position accuracy is better than 60 cm, 40 cm in the vertical component, respectively. To guarantee a 95% confidence level, the convergence time was defined to achieve accuracy prescribed in the official document, and to keep such a converged positioning accuracy for five minutes. Figure 4 shows the average convergence time per station from DoY 67 to 76 and from DoY 85 to 96 in 2022. Average convergence time using the PPP-B2b product with BDS B1I/B3I + GPS, BDS B1C/B2a + GPS, BDS B1I/B3I, BDS B1C/B2a is 15.1/17.8/17.3/20.5 min. Although the convergence time is long using B1C/B2a, it also meets the official document requirements of less than 30 min for the BDS single-system and less than 20 min for the BDS + GPS dual-system.

3.4. Static Positioning of PPP-B2b

Figure 5 shows the average number of satellites participating in the PPP-B2b solution from DoY 67 to 76 in 2022. The average number of GPS and BDS satellites participating in the PPP-B2b calculation per epoch is 5.68 and 8.56, respectively. Considering the influence of the number of GPS satellites, the PPP-B2b positioning accuracy is investigated using the BDS and GPS dual-system rather than GPS single-system. The USUD station has the fewest satellites of the eight stations, resulting in poor PPP-B2b positioning accuracy in both static and simulated kinematic modes.

As an example, taking station GAMG on DoY 72 in 2022 the static positioning results in the N, E, and U directions (green-N, red-E, and blue-U, respectively) over time are shown in Figure 6, which displays four sequences (BDS B1I/B3I + GPS, BDS B1C/B2a + GPS, BDS B1I/B3I, and BDS B1C/B2a) of static position error in N, E, and U directions from top to bottom. The vertical orange line daily at 0:25 h separates the converged PPP-B2b static positioning results from the non-converged positioning results. The convergent positioning error RMS values in the N, E, and U directions for 2830 epochs of 30 s intervals on DoY 67 in 2022 is calculated. The position error of the four combinations fluctuates within the range of ±0.05 m after the PPP-B2b static positioning of the GAMG station converges. The position error RMS was about 2 cm for the horizontal component and 4 cm for the vertical component.

The RMS values of the station’s static PPP-B2b positioning in N, E, and U directions from DoY 67 to 76 in 2022 are shown in form of box plots in Figure 7 and Figure 8. Figure 7 and Figure 8 show the 25–75% range, mean, and outliers of 10-day static position errors RMS using the PPP-B2b product in the N, E, and U directions. In addition,

Table 6. Mean RMS values of PPP-B2b static positioning of each station using B1I/B3I.

Station	BDS B1I/B3I + GPS			BDS B1I/B3I
	N (cm)	E (cm)	U (cm)	N (cm)	E (cm)	U (cm)
KUN1	1.7	2.9	2.9	1.7	2.6	3.5
BJF1	1.0	2.1	3.1	0.9	2.1	3.5
USUD	1.7	2.8	3.9	2.1	2.8	4.3
GAMG	1.5	1.9	3.7	1.5	2.7	4.2
CHU1	1.3	2.7	3.3	1.3	3.3	3.4
GUA1	1.3	3.1	3.0	1.2	3.2	3.9
ULAB	1.5	2.7	3.2	1.5	3.6	3.6
JFNG	0.9	1.8	3.6	0.9	1.2	4.0
MEAN	1.4	2.5	3.3	1.4	2.7	3.8

and

Table 7. Mean RMS values of PPP-B2b static positioning of each station using B1C/B2a.

Station	BDS B1C/B2a + GPS			BDS B1C/B2a
	N (cm)	E (cm)	U (cm)	N (cm)	E (cm)	U (cm)
KUN1	1.7	2.6	3.1	1.2	2.3	3.7
BJF1	1.3	1.5	2.7	1.3	1.5	3.4
USUD	1.5	2.4	4.0	1.8	2.4	4.0
GAMG	1.4	2.1	3.7	1.2	2.0	4.1
CHU1	1.7	2.4	3.9	1.8	2.2	4.0
GUA1	1.5	2.2	4.3	1.6	2.8	4.2
MEAN	1.5	2.2	3.6	1.5	2.2	3.9

list the average RMS values of the position errors of the BDS B1I/B3I + GPS, BDS B1I/B3I, BDS B1C/B2a + GPS, and BDS B1C/B2a in N, E, and U directions. Figure 7 and Figure 8 show that the RMS values of the position errors in the N direction for the four positioning combinations are less than 2 cm of most test days, with a minimum value of less than 1 cm, and the accuracy in E and U directions is poor and concentrated within 3 and 4 cm, respectively. Due to the number of satellites, USUD and GUA1 deliver a poor positioning accuracy compared with other stations. The average RMS values of the PPP-B2b static positioning of the BDS + GPS dual-system in the N direction concentrate around 1.5 cm, which is better than 2.5 cm in the E direction and 3.6 cm in the U direction. Table 6 and Table 7 show that the average RMS values of the BDS PPP-B2b static positioning in the N, E, and U directions are 1.5/2.7/3.9 cm, respectively.

3.5. Kinematic Positioning of PPP-B2b

Figure 9 shows the position errors of the GAMG station using four combinations in simulated kinematic mode in N, E, and U directions (green-N, red-E, and blue-U, respectively) on DoY 72 in 2022 from top to bottom, BDS B1I/B3I + GPS, BDS B1C/B2a + GPS, BDS B1I/B3I, and BDS B1C/B2a. The vertical orange line daily at 0:25 h separates the converged PPP-B2b simulated kinematic positioning results from the non-converged positioning results. After convergence, the errors in the N and E directions fluctuate within the range of ±10 cm, and the RMS is 3 and 5 cm, respectively. The U direction is poor, and most of the epoch position errors fluctuate within the range of ±15 cm. Some epochs can reach up to 20 cm but cannot increase further. The RMS value of the B1C/B2a combination in the U direction is the worst at 8 cm, while the other three combinations are 7 cm. Using only the BDS single-system has a longer convergence time and a lower convergence accuracy than the BDS + GPS dual-system.

The RMS values of the kinematic PPP-B2b errors in the N, E, and U directions from DoY 67 to 76 in 2s022 are shown in form of box plots in Figure 10 and Figure 11, and the average RMS values of position errors are recorded in

Table 8. Mean RMS values of PPP-B2b kinematic positioning at each station using B1I/B3I.

Station	BDS B1I/B3I + GPS			BDS B1I/B3I
	N (cm)	E (cm)	U (cm)	N (cm)	E (cm)	U (cm)
KUN1	3.2	6.8	7.3	3.8	7.4	7.9
BJF1	3.8	5.4	7.3	3.9	6.6	7.2
USUD	4.4	5.3	8.2	3.8	6.5	8.9
GAMG	3.1	4.7	7.9	4.3	6.2	7.9
CHU1	3.4	6.3	7.6	3.3	6.8	7.4
GUA1	3.4	6.5	7.7	3.3	6.1	7.3
ULAB	3.5	6.8	7.0	4.3	6.4	8.3
JFNG	2.7	4.7	7.6	3.4	6.6	7.3
MEAN	3.4	5.8	7.6	3.8	6.6	7.8

and

Table 9. Mean RMS values of PPP-B2b kinematic positioning at each station using B1C/B2a.

Station	BDS B1C/B2a + GPS			BDS B1C/B2a
	N (cm)	E (cm)	U (cm)	N (cm)	E (cm)	U (cm)
KUN1	3.1	5.9	7.6	3.8	7.1	9.9
BJF1	4.3	5.6	8.4	4.0	7.1	8.3
USUD	3.6	3.5	8.6	4.7	5.0	8.0
GAMG	3.4	5.0	8.0	3.5	5.3	7.5
CHU1	3.6	4.7	8.2	4.6	6.2	8.6
GUA1	3.3	4.5	8.0	3.6	5.8	8.4
MEAN	3.6	4.9	8.1	4.0	6.1	8.5

. Figure 10 and Figure 11 show that the best simulated kinematic positioning results are in the N direction, which is concentrated at 2–4 cm; the simulated kinematic positioning results are concentrated at 3–7 cm using the BDS + GPS dual-system in the E direction, and at 6–9 cm using the single BDS system; the kinematic positioning results in the U direction are the worst, with the largest RMS value being 0.1181 m. The average RMS line positions in Figure 10 and Figure 11 show that the mean RMS line in the E direction of the dual-system is lower than that in the single system; using B1I and B3I is higher in the E direction than B1C and B2a, and lower in the U direction. Table 8 shows that the average RMS values of the position errors of the combination of BDS B1I/B3I + GPS and BDS B1I/B3I in the N, E, and U directions are 3.4/5.8/7.6 cm and 3.8/6.6/7.8 cm, respectively. The average RMS values of the position errors of BDS B1C/B2a + GPS and BDS B1C/B2a in the N, E, and U directions are 3.6/4.9/8.1 cm and 4/6.1/8.5 cm, respectively. Compared with B1C/B2a, the positioning accuracy of PPP-B2b using B1I/ B3I observations is improved by 5–7 mm in the U direction but decreased by 5–9 mm in the E direction. Compared with the BDS single-system, the dual-system PPP-B2b improved by nearly 1 cm in the E direction.

3.6. Time Transfer

CCD is often used to analyze the noise level of time comparison [36,37,38]. Consecutive days with CCD can reflect the uncertainty of receiver noise and time comparison. Figure 12 shows the zero-baseline CCD time comparison results of NTTS and NT07 using the GBM product and the PPP-B2b product from DoY 85 to 96 in 2022. A hardware delay is absorbed in the receiver clock offset, and the results of the time comparison have systematic deviations. Figure 12 shows that the PPP time comparison noise using the GBM and PPP-B2b products fluctuates within the range of 0.1 ns, the standard deviation of time comparison is 0.0167 and 0.024, respectively, which are consistent, and the time comparison of the two products has good continuity.

Figure 13 shows the long-baseline BDS-3 PPP time comparison results of NTTS and TLM2 using the GBM product and the PPP-B2b product from DoY 85 to 96 in 2022. Using the difference in the NTTS-TLM2 time comparison results between the GBM product and the PPP-B2b product, the residual sequence of NTTS-TLM2 BDS-3 PPP time comparison is obtained in Figure 14. The residual of the time comparison of the two products fluctuates within the range of ±0.5 ns after convergence, demonstrating the uncertainty of the time comparison of the two products within ±0.5 ns. Meanwhile, Figure 15 shows the Allan variance of the GBM product and the PPP-B2b product time transfer.

4. Conclusions

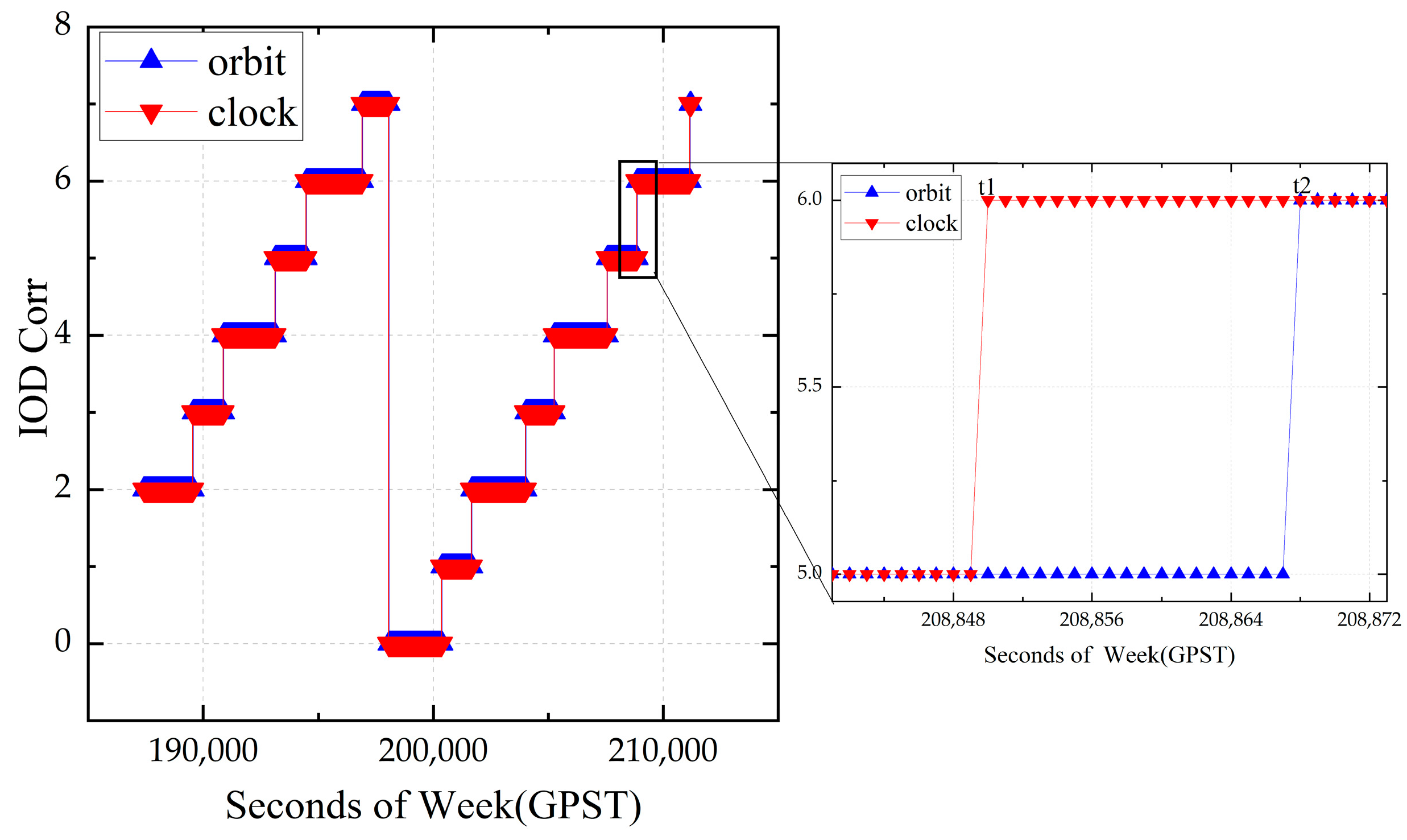
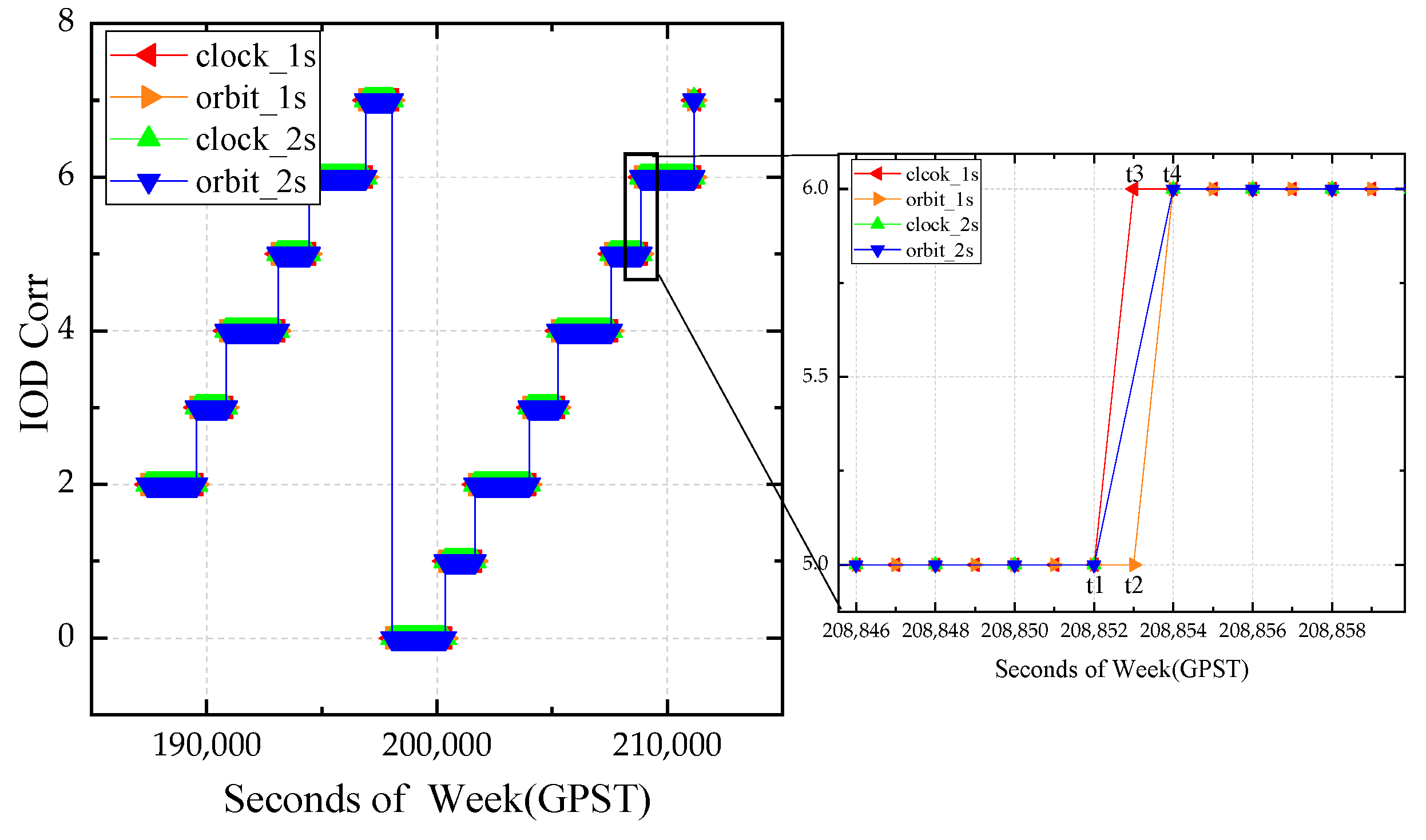
The BDS-3 can provide PPP services to the Asia–Pacific region via GEO satellites following the official announcement of the PPP-B2b signal document. In this contribution, by employing distributed IGS/IGMAS stations in the Asia–Pacific region, a comprehensive analysis of the time transfer and positioning accuracy using the PPP-B2b product was undertaken. Initially, the matching strategy of the PPP-B2b product was discussed. The post-processing observations were updated at the rate of 1 s, and the epoch time field in the PPP-B2b information frame was used as a reference for updating the PPP-B2b correction product. The IOD Corr of the satellite orbit and clock were mismatched when the message type 2 and message type 4 match. Using the time when the receiver gets the PPP-B2b correction message as the reference time, and updating the observation value at 1 s intervals, the mismatch between the PPP-B2b satellite clock and orbit products will be significantly reduced. When the observation update interval is increased to 2 s, the probability of mismatch occurrence is significantly reduced. In this study, the observation value update interval in PPP-B2b positioning was investigated with a time comparison of 30 s.

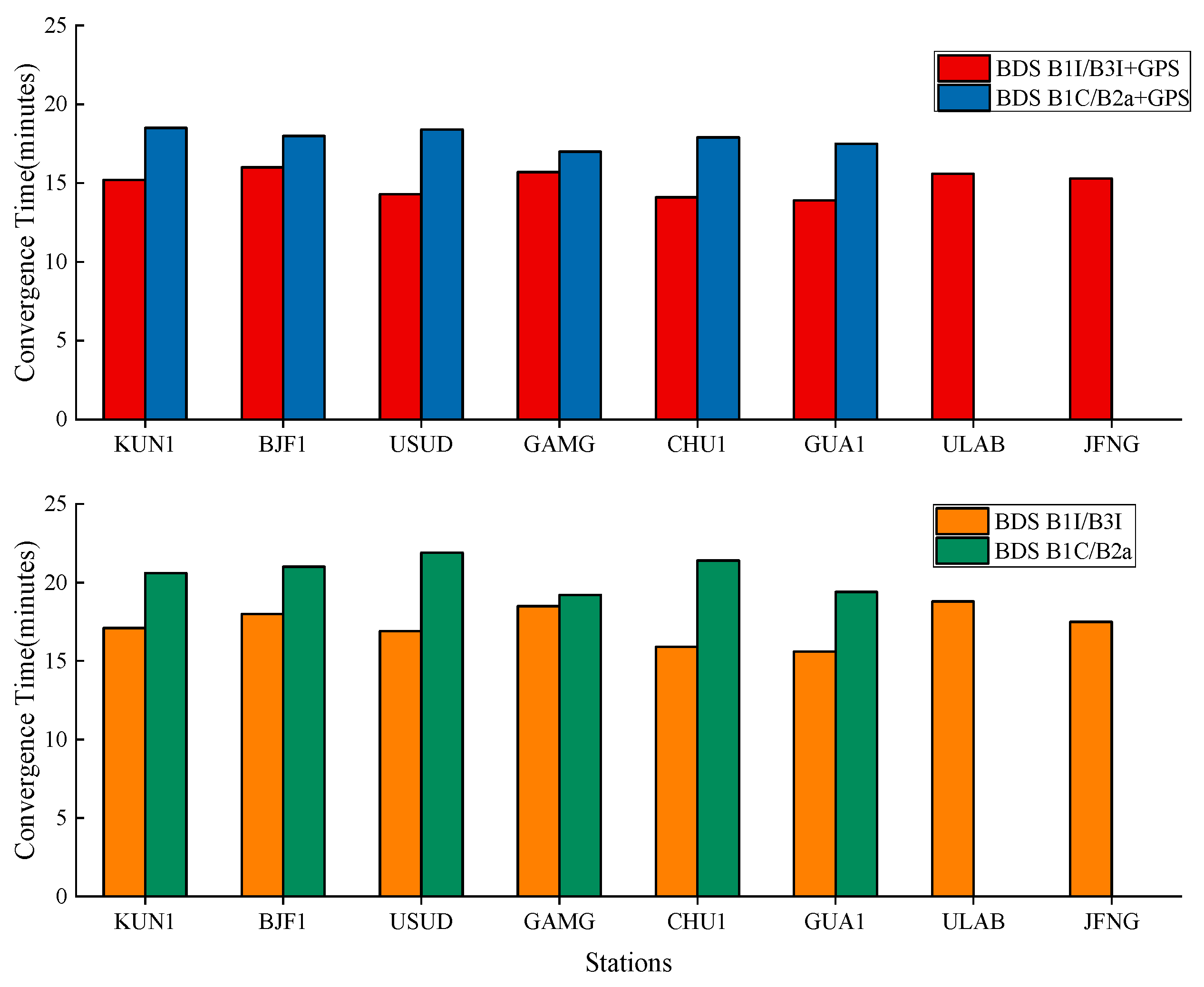
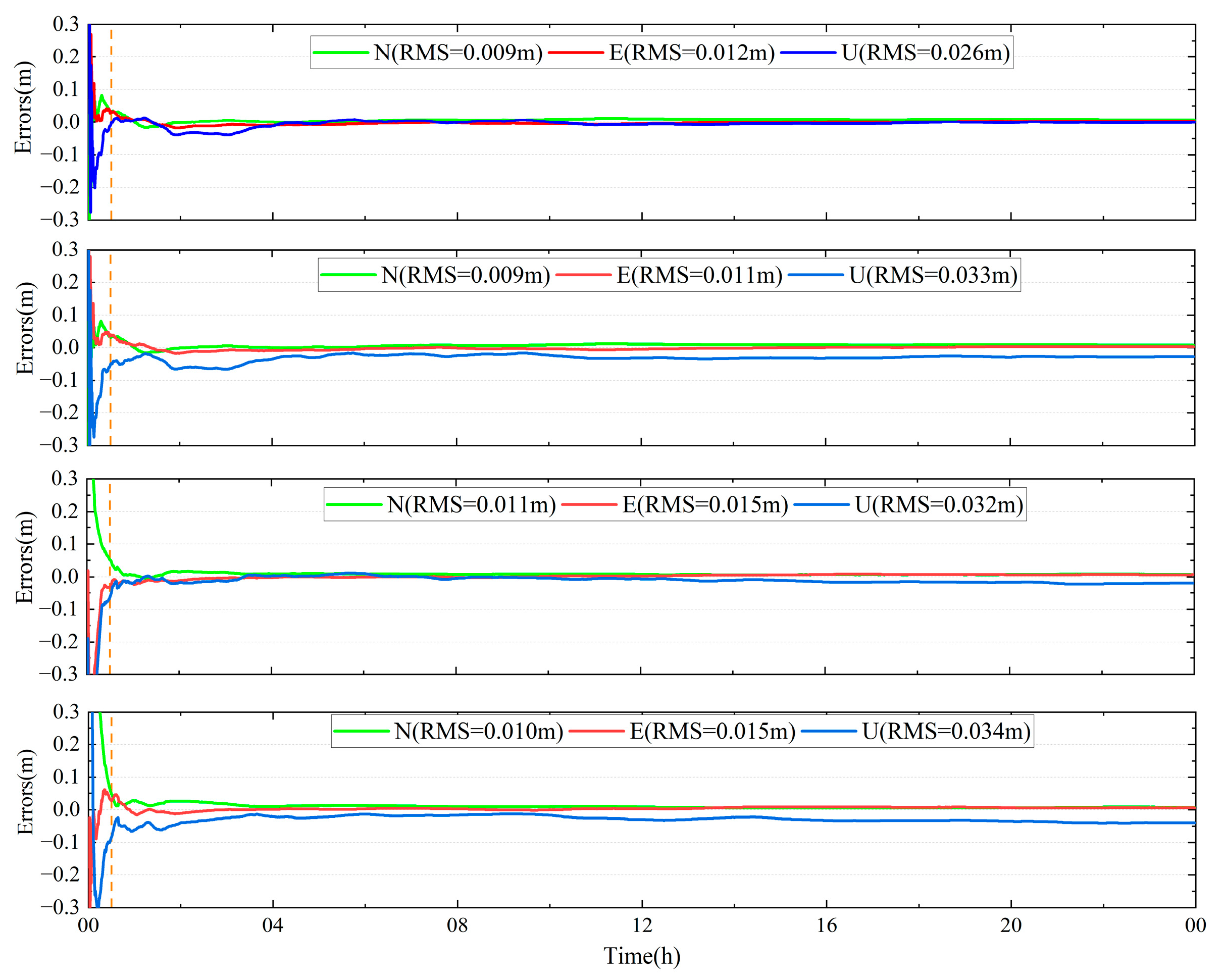
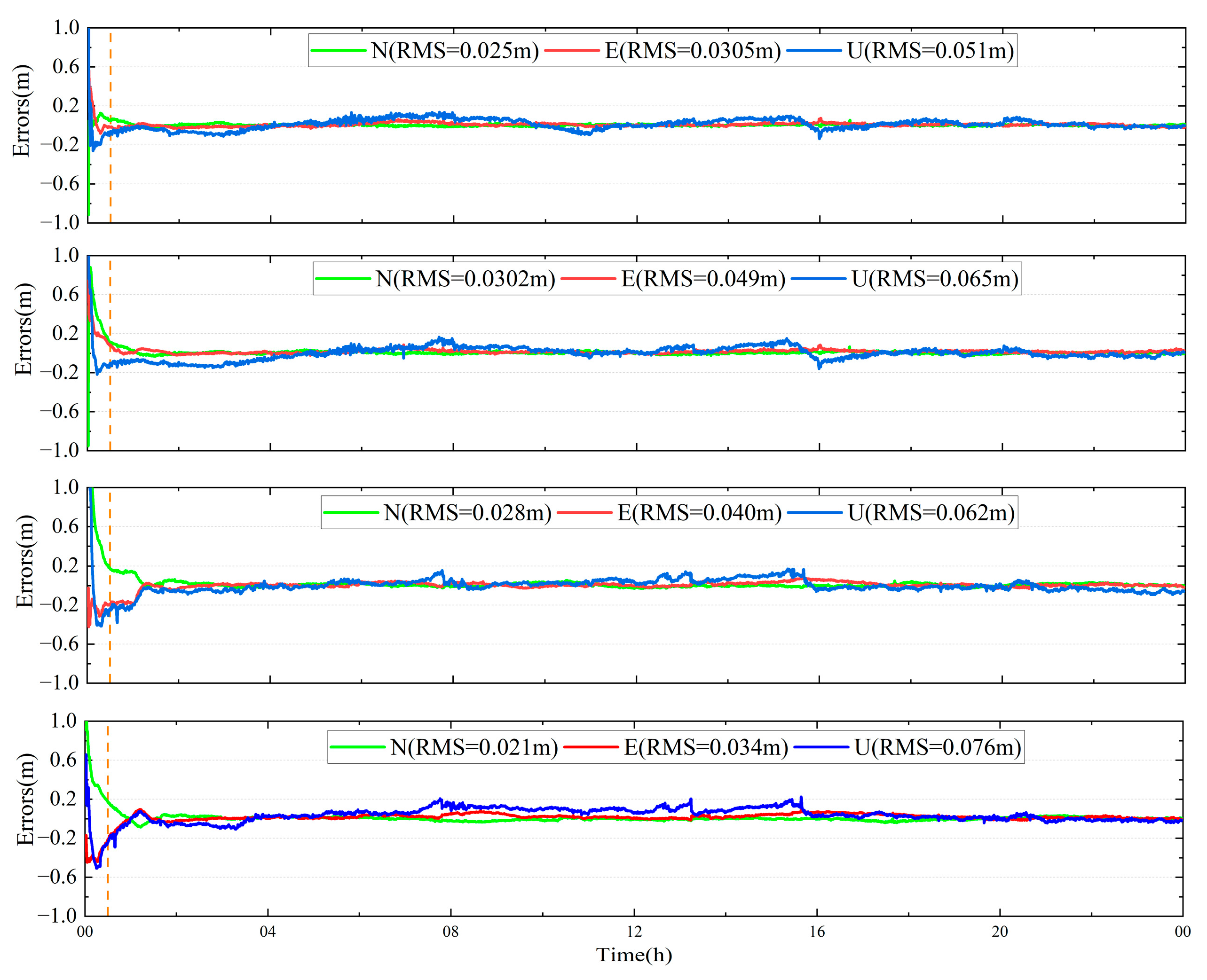
The PPP-B2b positioning study was analyzed using the four IF combinations in static and simulated kinematic mode: BDS B1I/B3I, BDS B1C/B2a, BDS B1I/B3I + GPS, and BDS B1C/B2a + GPS. According to the official document, the average convergence time was analyzed. Average convergence time using the PPP-B2b product with BDS B1I/B3I + GPS, BDS B1C/B2a + GPS, BDS B1I/B3I, BDS B1C/B2a was 15.1/17.8/17.3/20.5 min, respectively. Regarding the PPP-B2b static position results, the average RMS values in the N, E, and U directions of only BDS PPP-B2b were within 1.5/2.7/3.9 cm, respectively, and the positioning accuracies in the E and U directions can be improved to 2.5/3.5 cm using BDS and GPS dual-system. Compared with BDS B1C/B2a, BDS B1I/B3I has comparable positioning accuracy in the N direction, and the accuracy in the U direction can be improved by 3-4 mm. In the PPP-B2b simulated kinematic positioning study, the average RMS values of the positioning errors in the N, E, and U directions for the combination of BDS B1I/B3I + GPS and BDS B1I/B3I were 3.4/5.8/7.6 and 3.8/6.6/7.8 cm, respectively. Meanwhile, the RMS values of the position errors using BDS B1C/B2a + GPS and BDS B1C/B2a were 3.6/4.9/8.1 and 4/6.1/8.5 cm, respectively. The results show that (1) the PPP-B2b positioning accuracy using B1I/B3I and B1C/B2a can approach centimeter-level in the static mode and decimeter-level in the simulated kinematic mode; and (2) compared with B1I/B3I IF combination, the positioning accuracy is improved in the E direction but reduced in the U direction at millimeter-level.

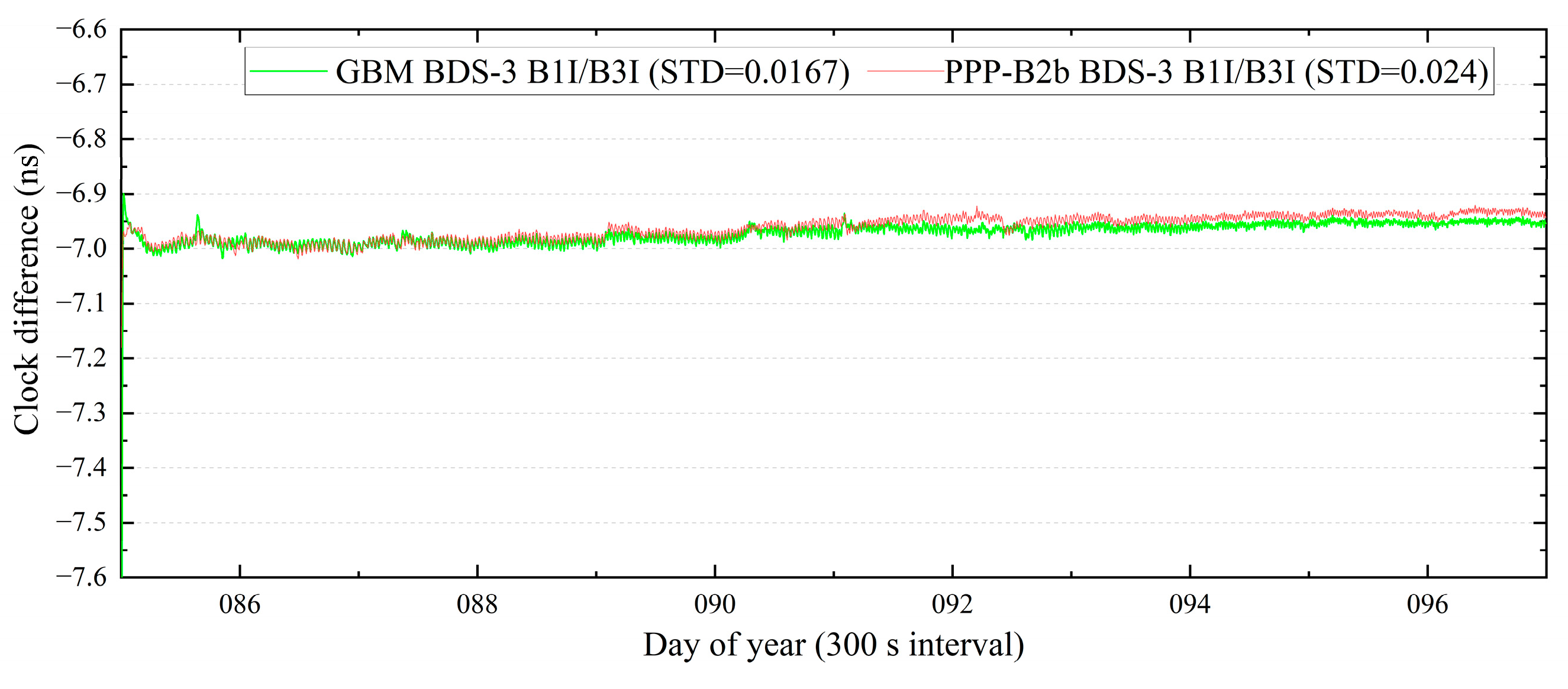
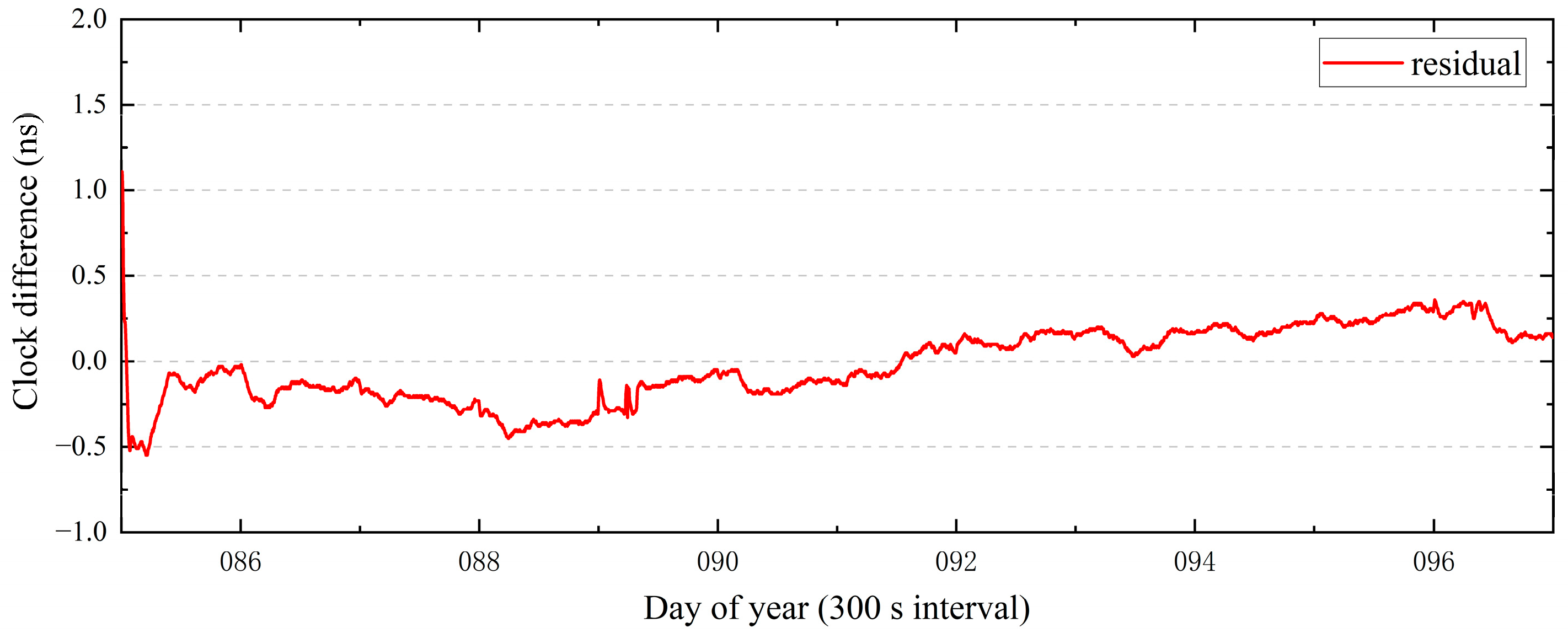
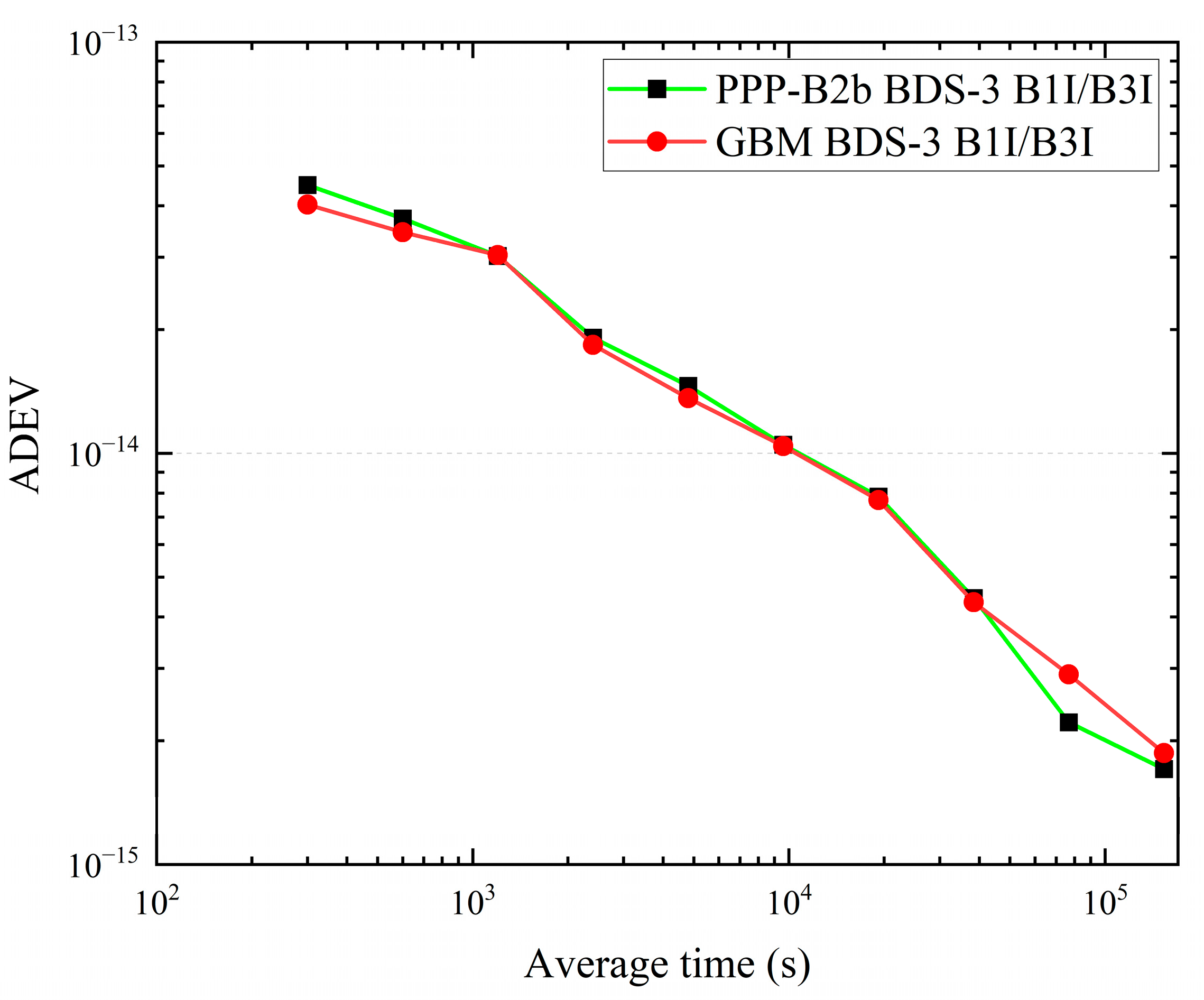
In the PPP-B2b time transfer study, observations of NTSC and TL time laboratories in the Asia–Pacific region involved in maintaining TAI were used. The zero-baseline CCD was used to evaluate the uncertainty of receiver noise level and time comparison using precise products. The results show that (1) the zero baseline CCD time comparison noise level using the GBM product and the PPP-B2b product is within the fluctuation range of 0.1 ns, respectively; (2) the long-baseline time comparison difference between results using the PPP-B2b product and the GBM product is within the range of ±0.5 ns; and (3) according to the Allan’s calculations, the time comparison of the two products exhibits consistent stability.