Inversion of Coniferous Forest Stock Volume Based on Backscatter and InSAR Coherence Factors of Sentinel-1 Hyper-Temporal Images and Spectral Variables of Landsat 8 OLI
Abstract
:1. Introduction
2. Study Area and Data
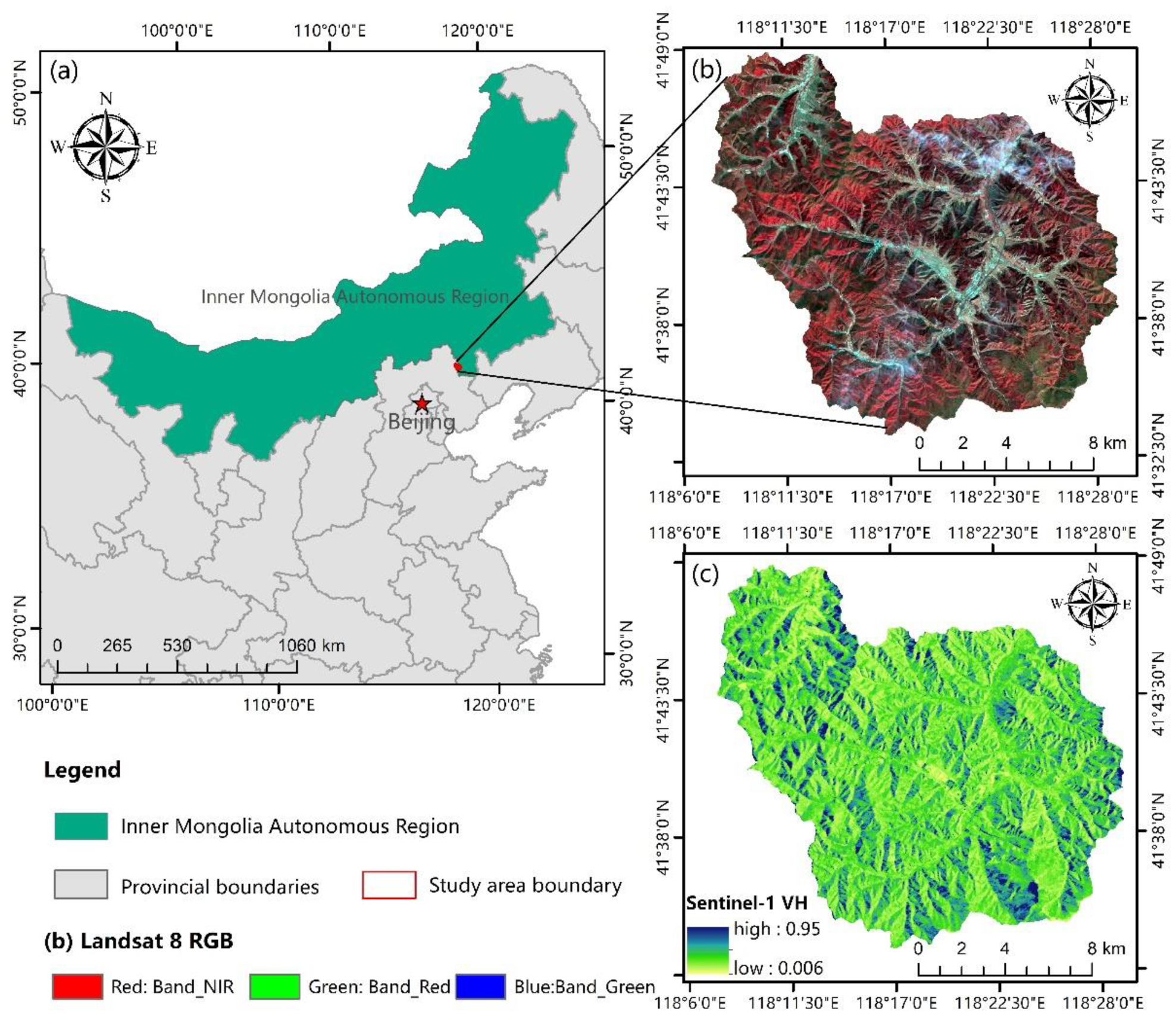
2.1. Study Area
2.2. Sample Plot Design and FSV Data Collection
2.3. Optical and SAR Remote Sensing Data Preprocessing
3. Methods
3.1. Optical Remote Sensing Feature Variable Extraction
3.2. SAR Feature Variable Extraction
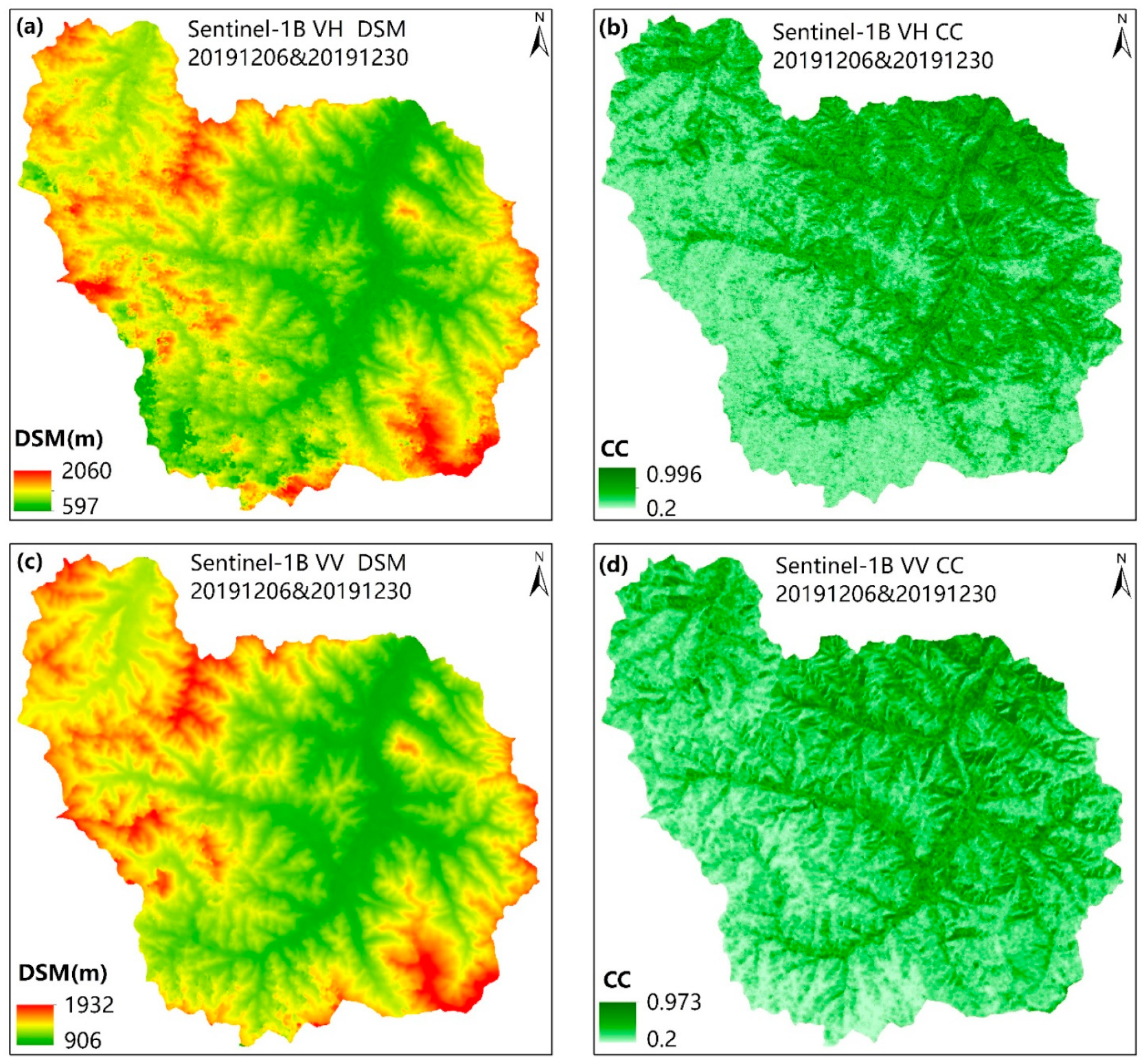
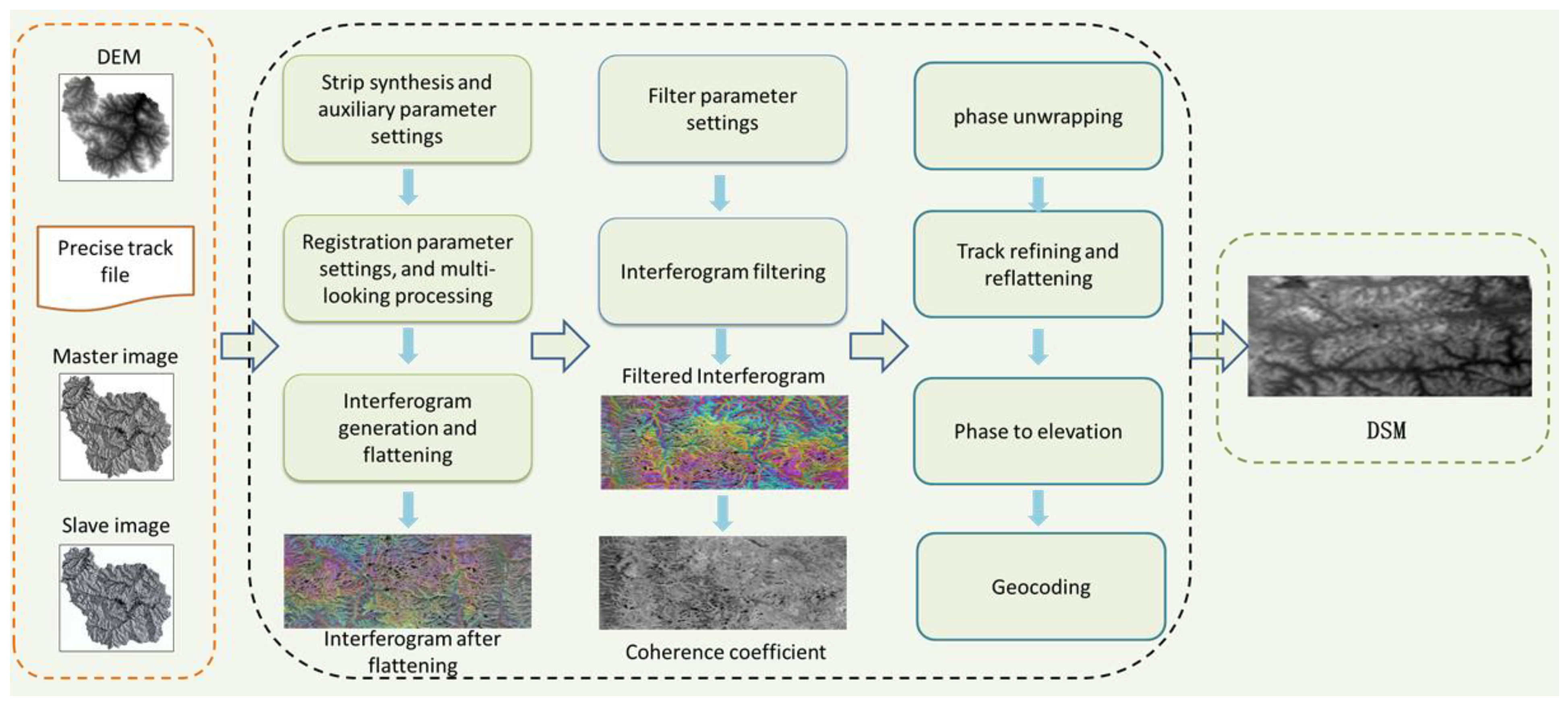
3.3. InSAR Feature Variable Extraction
3.4. Feature Variable Selection Method Based on SVR
3.5. FSV Modeling and Accuracy Evaluation
4. Results
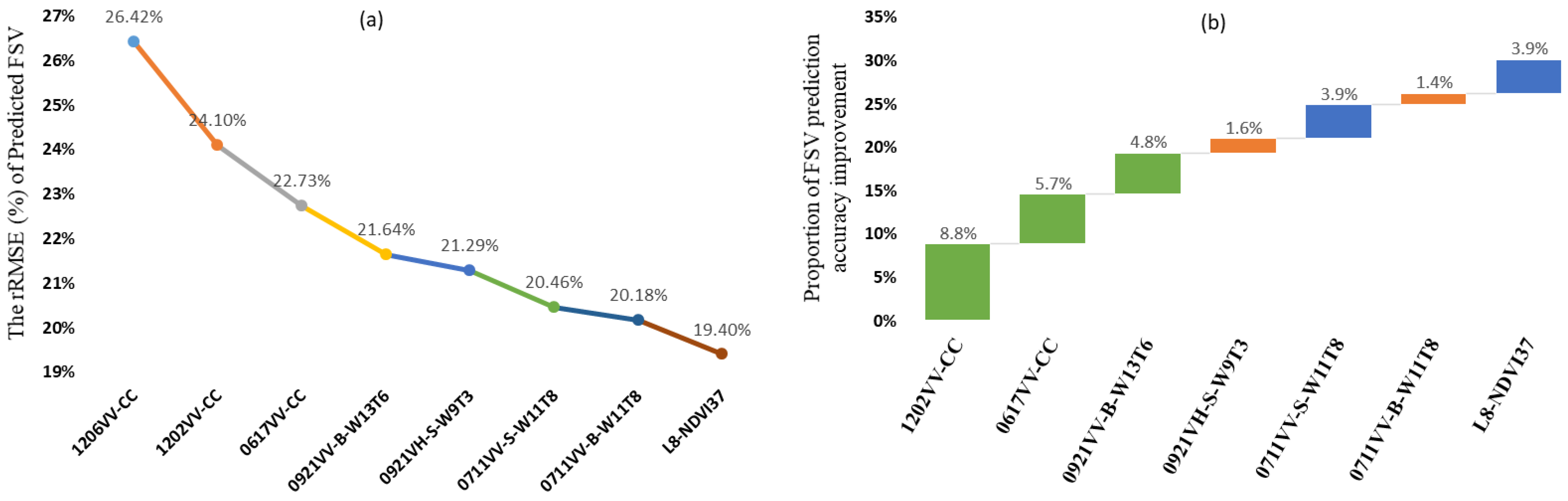
4.1. Feature Variables Extracted and Selected by Different Methods
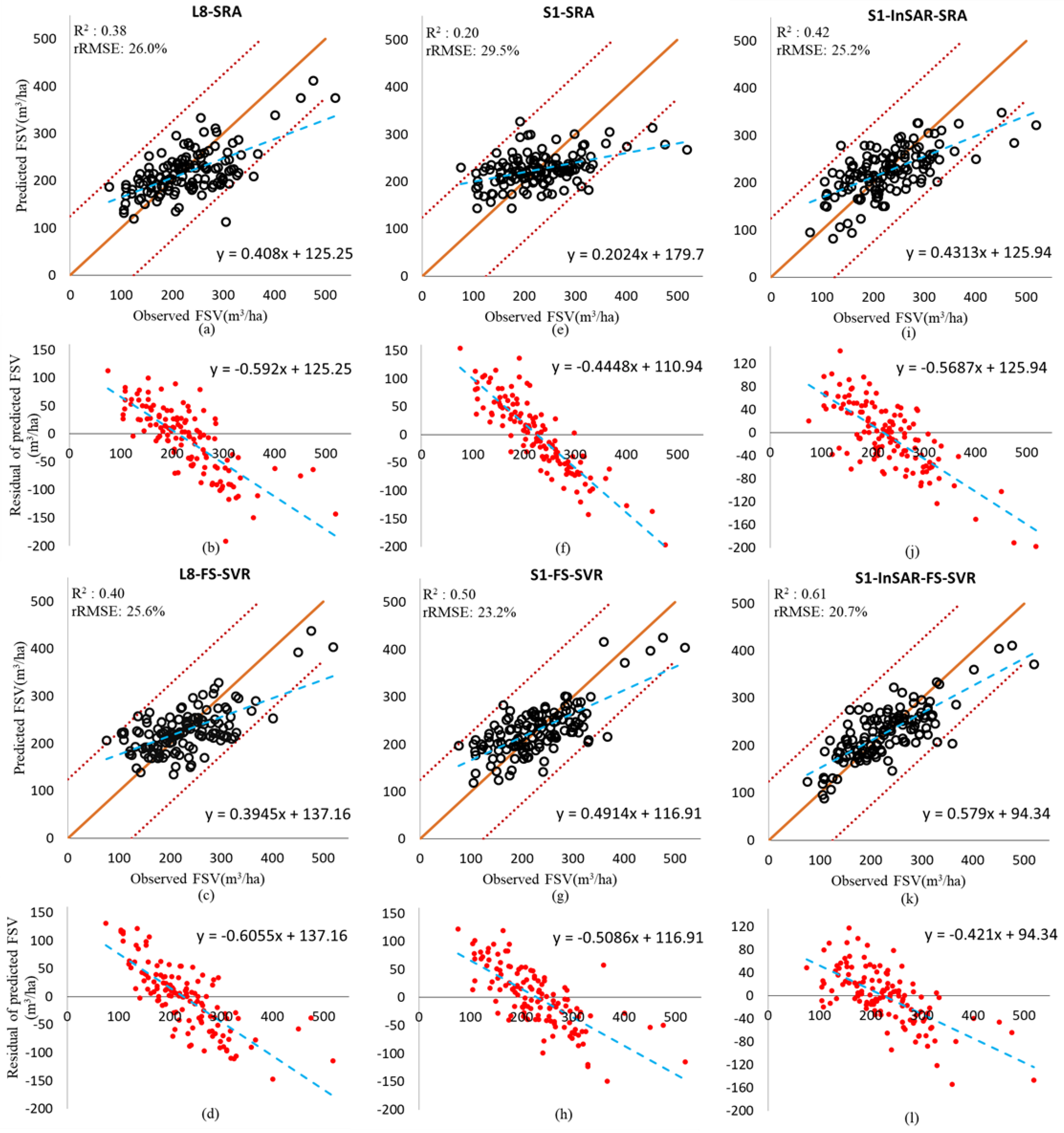
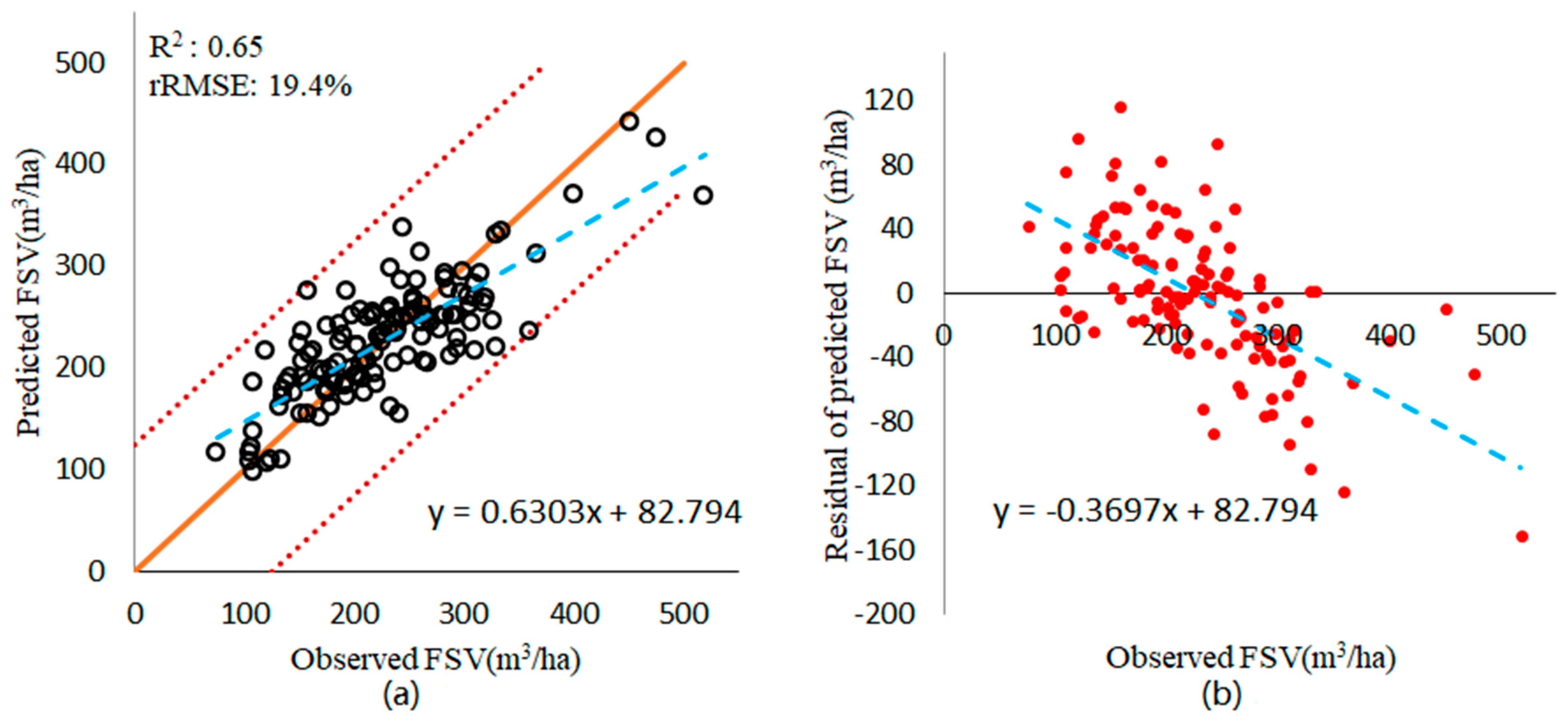
4.2. FSV Prediction Result
4.3. Predicting and Mapping the Stock Volume of Coniferous Plantation
5. Discussion
5.1. Feature Variables Selection in FSV Estimation
5.2. Analysis of FSV Estimation Performance
5.3. Limitations and Prospects
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Image Category | Image Identification | Acquisition Date |
|---|---|---|
| Landsat 8 | LC08_L1TP_122031_20190927_20191017_01_T1 | 20190927 |
| Sentinel-1B | S1B_IW_SLC__1SDV_20191230T221132_20191230T221159_019600_0250B0_2899 | 20191230 |
| S1B_IW_SLC__1SDV_20191218T221133_20191218T221200_019425_024B1B_4D83 | 20191218 | |
| S1B_IW_SLC__1SDV_20191206T221133_20191206T221200_019250_024587_75B0 | 20191206 | |
| S1B_IW_SLC__1SDV_20191124T221134_20191124T221201_019075_023FFC_F9D2 | 20191124 | |
| S1B_IW_SLC__1SDV_20191112T221134_20191112T221201_018900_023A5C_5D48 | 20191112 | |
| S1B_IW_SLC__1SDV_20191019T221134_20191019T221201_018550_022F3E_5B86 | 20191019 | |
| S1B_IW_SLC__1SDV_20191007T221134_20191007T221201_018375_0229DE_E289 | 20191007 | |
| S1B_IW_SLC__1SDV_20190925T221134_20190925T221201_018200_022459_AE9B | 20190925 | |
| S1B_IW_SLC__1SDV_20190901T221133_20190901T221200_017850_02197D_522E | 20190901 | |
| S1B_IW_SLC__1SDV_20190820T221132_20190820T221159_017675_02140F_526D | 20190820 | |
| S1B_IW_SLC__1SDV_20190810T095659_20190810T095725_017522_020F3E_BC60 | 20190810 | |
| S1B_IW_SLC__1SDV_20190808T221132_20190808T221159_017500_020E97_6E25 | 20190808 | |
| S1B_IW_SLC__1SDV_20190727T221131_20190727T221158_017325_02094E_08A7 | 20190727 | |
| S1B_IW_SLC__1SDV_20190715T221130_20190715T221157_017150_020438_6966 | 20190715 | |
| S1B_IW_SLC__1SDV_20190703T221129_20190703T221156_016975_01FF10_9955 | 20190703 | |
| S1B_IW_SLC__1SDV_20190621T221129_20190621T221156_016800_01F9E2_C83C | 20190621 | |
| S1B_IW_SLC__1SDV_20190609T221128_20190609T221155_016625_01F4AC_6072 | 20190609 | |
| S1B_IW_SLC__1SDV_20190528T221127_20190528T221154_016450_01EF78_A431 | 20190528 | |
| S1B_IW_SLC__1SDV_20190516T221127_20190516T221154_016275_01EA17_1542 | 20190516 | |
| S1B_IW_SLC__1SDV_20190504T221126_20190504T221153_016100_01E499_637A | 20190504 | |
| S1B_IW_SLC__1SDV_20190422T221126_20190422T221153_015925_01DEBD_37CA | 20190422 | |
| S1B_IW_SLC__1SDV_20190329T221125_20190329T221152_015575_01D321_91C4 | 20190329 | |
| S1B_IW_SLC__1SDV_20190317T221124_20190317T221151_015400_01CD68_5402 | 20190317 | |
| Sentinel-1A | S1A_IW_SLC__1SDV_20191226T095744_20191226T095812_030518_037E99_1211 | 20191226 |
| S1A_IW_SLC__1SDV_20191214T095744_20191214T095812_030343_037891_1BF4 | 20191214 | |
| S1A_IW_SLC__1SDV_20191202T095745_20191202T095813_030168_037286_5B2A | 20191202 | |
| S1A_IW_SLC__1SDV_20191120T095745_20191120T095813_029993_036C78_D64C | 20191120 | |
| S1A_IW_SLC__1SDV_20191108T095745_20191108T095813_029818_036669_AAD4 | 20191108 | |
| S1A_IW_SLC__1SDV_20191015T095745_20191015T095813_029468_035A34_B673 | 20191015 | |
| S1A_IW_SLC__1SDV_20190921T095745_20190921T095813_029118_034E23_9420 | 20190921 | |
| S1A_IW_SLC__1SDV_20190909T095745_20190909T095812_028943_034826_7BA8 | 20190909 | |
| S1A_IW_SLC__1SDV_20190828T095744_20190828T095812_028768_034210_B0B1 | 20190828 | |
| S1A_IW_SLC__1SDV_20190816T095743_20190816T095811_028593_033BF0_21BC | 20190816 | |
| S1A_IW_SLC__1SDV_20190804T095743_20190804T095811_028418_033619_59BC | 20190804 | |
| S1A_IW_SLC__1SDV_20190723T095742_20190723T095810_028243_0330C2_ECFE | 20190723 | |
| S1A_IW_SLC__1SDV_20190711T095741_20190711T095809_028068_032B79_A792 | 20190711 | |
| S1A_IW_SLC__1SDV_20190629T095740_20190629T095808_027893_03262C_B424 | 20190629 | |
| S1A_IW_SLC__1SDV_20190617T095739_20190617T095807_027718_0320F1_5DB1 | 20190617 | |
| S1A_IW_SLC__1SDV_20190605T095739_20190605T095807_027543_031BAA_448C | 20190605 |
| Number | Paired Image | Satellite and Track | Vertical Baseline Length (m) | Time Baseline Interval (Days) | Interference Processing |
|---|---|---|---|---|---|
| 1 | 20190317 and 20190329 | S1B-Descending | 12.462 | 12 | No |
| 2 | 20190317 and 20190422 | S1B-Descending | 46.479 | 36 | Yes |
| 3 | 20190329 and 20190422 | S1B-Descending | 58.387 | 24 | Yes |
| 4 | 20190422 and 20190504 | S1B-Descending | 81.720 | 12 | Yes |
| 5 | 20190422 and 20190516 | S1B-Descending | 35.526 | 24 | Yes |
| 6 | 20190504 and 20190516 | S1B-Descending | 48.376 | 12 | Yes |
| 7 | 20190504 and 20190528 | S1B-Descending | 74.800 | 24 | Yes |
| 8 | 20190516 and 20190528 | S1B-Descending | 26.943 | 12 | Yes |
| 9 | 20190605 and 20190617 | S1A-Ascending | 46.979 | 12 | Yes |
| 10 | 20190609 and 20190621 | S1B-Descending | 55.835 | 12 | Yes |
| 11 | 20190617 and 20190629 | S1A-Ascending | 74.956 | 12 | Yes |
| 12 | 20190621 and 20190703 | S1B-Descending | 91.912 | 12 | Yes |
| 13 | 20190629 and 20190711 | S1A-Ascending | 11.979 | 12 | No |
| 14 | 20190703 and 20190715 | S1B-Descending | 31.498 | 12 | Yes |
| 15 | 20190711 and 20190723 | S1A-Ascending | 58.018 | 12 | Yes |
| 16 | 20190715 and 20190727 | S1B-Descending | 69.089 | 12 | Yes |
| 17 | 20190723 and 20190804 | S1A-Ascending | 70.665 | 12 | Yes |
| 18 | 20190727 and 20190808 | S1B-Descending | 3.070 | 12 | No |
| 19 | 20190804 and 20190816 | S1A-Ascending | 12.535 | 12 | No |
| 20 | 20190808 and 20190820 | S1B-Descending | 34.460 | 12 | Yes |
| 21 | 20190816 and 20190828 | S1A-Ascending | 12.676 | 12 | No |
| 22 | 20190820 and 20190901 | S1B-Descending | 10.237 | 12 | No |
| 23 | 20190828 and 20190909 | S1A-Ascending | 65.810 | 12 | Yes |
| 24 | 20190901 and 20190925 | S1B-Descending | 42.950 | 24 | Yes |
| 25 | 20190909 and 20190921 | S1A-Ascending | 17.108 | 12 | Yes |
| 26 | 20190921 and 20191015 | S1A-Ascending | 149.681 | 24 | Yes |
| 27 | 20190925 and 20191007 | S1B-Descending | 85.305 | 12 | Yes |
| 28 | 20191007 and 20191019 | S1B-Descending | 46.193 | 12 | Yes |
| 29 | 20191015 and 20191108 | S1A-Ascending | 111.245 | 24 | Yes |
| 30 | 20191019 and 20191112 | S1B-Descending | 68.399 | 24 | Yes |
| 31 | 20191108 and 20191120 | S1A-Ascending | 30.156 | 12 | Yes |
| 32 | 20191112 and 20191124 | S1B-Descending | 8.064 | 12 | No |
| 33 | 20191112 and 20191206 | S1B-Descending | 82.270 | 24 | Yes |
| 34 | 20191120 and 20191202 | S1A-Ascending | 57.503 | 12 | Yes |
| 35 | 20191124 and 20191206 | S1B-Descending | 74.109 | 12 | Yes |
| 36 | 20191202 and 20191214 | S1A-Ascending | 49.938 | 12 | Yes |
| 37 | 20191206 and 20191230 | S1B-Descending | 60.980 | 24 | Yes |
| 38 | 20191214 and 20191226 | S1A-Ascending | 44.198 | 12 | Yes |
| 39 | 20191218 and 20191230 | S1B-Descending | 55.525 | 12 | Yes |
References
- Sun, W.; Liu, X. Review on carbon storage estimation of forest ecosystem and applications in China. For. Ecosyst. 2020, 7, 37–50. [Google Scholar] [CrossRef] [Green Version]
- Ali, F.; Khan, N.; Abd_Allah, E.; Ahmad, A. Species Diversity, Growing Stock Variables and Carbon Mitigation Potential in the Phytocoenosis of Monotheca buxifolia Forests along Altitudinal Gradient across Pakistan. Appl. Sci. 2022, 12, 1292. [Google Scholar] [CrossRef]
- Yan, W.; Wang, W.; Peng, Y.; Chen, X. Evaluation of Biomass and Carbon Stocks in Three Pine Forest Types in Karst Area of Southwestern China. J. Sustain. For. 2022, 41, 18–32. [Google Scholar] [CrossRef]
- Sasaki, N.; Myint, Y.; Abe, I.; Venkatappa, M. Predicting carbon emissions, emissions reductions, and carbon removal due to deforestation and plantation forests in Southeast Asia. J. Clean. Prod. 2021, 312, 127728. [Google Scholar] [CrossRef]
- Zhao, J.; Zhao, L.; Chen, E.; Li, Z.; Xu, K.; Ding, X. An Improved Generalized Hierarchical Estimation Framework with Geostatistics for Mapping Forest Parameters and Its Uncertainty: A Case Study of Forest Canopy Height. Remote Sens. 2022, 14, 568. [Google Scholar] [CrossRef]
- Gschwantner, T.; Alberdi, I.; Bauwens, S.; Bender, S.; Borota, D.; Bosela, M.; Bouriaud, O.; Breidenbach, J.; Donis, J.; Fischer, C.; et al. Growing stock monitoring by European National Forest Inventories: Historical origins, current methods and harmonisation. For. Ecol. Manag. 2022, 505, 119868. [Google Scholar] [CrossRef]
- Rees, W.G.; Tomaney, J.; Tutubalina, O.; Zharko, V.; Bartalev, S. Estimation of Boreal Forest Growing Stock Volume in Russia from Sentinel-2 MSI and Land Cover Classification. Remote Sens. 2021, 13, 4483. [Google Scholar] [CrossRef]
- Persson, H.J. Estimation of Boreal Forest Attributes from Very High Resolution Pléiades Data. Remote Sens. 2016, 8, 736. [Google Scholar] [CrossRef] [Green Version]
- Astola, H.; Hame, T.; Sirro, L.; Molinier, M.; Kilpi, J. Comparison of Sentinel-2 and Landsat 8 imagery for forest variable prediction in boreal region. Remote Sens. Environ. 2019, 223, 257–273. [Google Scholar] [CrossRef]
- Li, X.; Liu, Z.; Lin, H.; Wang, G.; Sun, H.; Long, J.; Zhang, M. Estimating the growing stem volume of Chinese Pine and Larch Plantations based on fused optical data using an improved variable screening method and stacking algorithm. Remote Sens. 2020, 12, 871. [Google Scholar] [CrossRef] [Green Version]
- Fassnacht, F.E.; Hartig, F.; Latifi, H.; Berger, C.; Hernández, J.; Corvalán, P.; Koch, B. Importance of sample size, data type and prediction method for remote sensing-based estimations of aboveground forest biomass. Remote Sens. Environ. 2014, 154, 102–114. [Google Scholar] [CrossRef]
- Li, X.; Lin, H.; Long, J.; Xu, X. Mapping the Growing Stem Volume of the Coniferous Plantations in North China Using Multispectral Data from Integrated GF-2 and Sentinel-2 Images and an Optimized Feature Variable Selection Method. Remote Sens. 2021, 13, 2740. [Google Scholar] [CrossRef]
- Rutishauser, E.; Wrigh, S.; Condit, R.; Hubbell, S.; Davies, S.; Muller-Landau, H.C. Testing for changes in biomass dynamics in large-scale forest datasets. Glob. Change Biol. 2020, 26, 1485–1498. [Google Scholar] [CrossRef] [PubMed]
- Sebastian, W.; Christian, H.; Mikhail, K.; Christiane, S. Large Area Mapping of Boreal Growing Stock Volume on an Annual and Multi-Temporal Level Using PALSAR L-Band Backscatter Mosaics. Forests 2014, 5, 1999–2015. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Liang, S. Fusion of Multiple Gridded Biomass Datasets for Generating a Global Forest Aboveground Biomass Map. Remote Sens. 2020, 12, 2559. [Google Scholar] [CrossRef]
- Lindberg, E.; Hollaus, M. Comparison of methods for estimation of stem volume, stem number and basal area from airborne laser scanning data in a hemi-boreal forest. Remote Sens. 2012, 4, 1004–1023. [Google Scholar] [CrossRef] [Green Version]
- Wijaya, A.; Kusnadi, S.; Gloaguen, R.; Heilmeier, H. Improved strategy for estimating stem volume and forest biomass using moderate resolution remote sensing data and GIS. J. For. Res. Jpn. 2010, 21, 1–12. [Google Scholar] [CrossRef]
- Zhao, P.; Lu, D.; Wang, G.; Wu, C.; Huang, Y.; Yu, S. Examining spectral reflectance saturation in Landsat imagery and corresponding solutions to improve forest aboveground biomass estimation. Remote Sens. 2016, 8, 469. [Google Scholar] [CrossRef] [Green Version]
- Bogan, S.A.; Antonarakis, A.S.; Moorcroft, P.R. Imaging spectrometry-derived estimates of regional ecosystem composition for the Sierra Nevada, California. Remote Sens. Environ. 2019, 228, 14–30. [Google Scholar] [CrossRef]
- Lu, D.; Chen, Q.; Wang, G.; Li, G.; Moran, E. A survey of remote sensing-basedd aboveground biomass estimation methods in forest ecosystems. Int. J. Digit. Earth 2016, 9, 63–105. [Google Scholar] [CrossRef]
- Puliti, S.; Saarela, S.; Gobakken, T.; Stahl, G.; Naesset, E. Combining UAV and Sentinel-2 auxiliary data for forest growing stock volume estimation through hierarchical model-based inference. Remote Sens. Environ. 2018, 204, 485–497. [Google Scholar] [CrossRef]
- Bilous, A.; Myroniuk, V.; Holiaka, D.; Bilous, S.; See, L.; Schepaschenko, D. Mapping growing stock volume and forest live biomass: A case study of the Polissya region of Ukraine. Environ. Res. Lett. 2017, 12, 105001. [Google Scholar] [CrossRef] [Green Version]
- Chrysafis, I.; Mallinis, G.; Gitas, I.; Tsakiri-Strati, M. Estimating Mediterranean forest parameters using multi seasonal Landsat 8 OLI imagery and an ensemble learning method. Remote Sens. Environ. 2017, 199, 154–166. [Google Scholar] [CrossRef]
- García-Gutiérrez, J.; Martínez-álvarez, F.; Troncoso, A.; Riquelme, J.C. A comparison of machine learning regression techniques for lidar-derived estimation of forest variables. Neurocomputing 2015, 167, 24–31. [Google Scholar] [CrossRef]
- Neuenschwander, A.L.; Magruder, L.A. Canopy and terrain height retrievals with ICESat-2: A first look. Remote Sens. 2019, 11, 1721. [Google Scholar] [CrossRef] [Green Version]
- Narine, L.L.; Popescu, S.; Neuenschwander, A.; Zhou, T.; Srinivasan, S. Estimating aboveground biomass and forest canopy cover with simulated ICESat-2 data. Remote Sens. Environ. 2019, 224, 1–11. [Google Scholar] [CrossRef]
- Fu, L.; Liu, Q.; Sun, H.; Wang, S.; Li, Z.; Chen, E.; Pang, Y.; Song, X.; Wang, G. Development of a system of compatible individual tree diameter and aboveground biomass prediction models using error-in-variable regression and airborne LiDAR data. Remote Sens. 2018, 10, 325. [Google Scholar] [CrossRef] [Green Version]
- Chen, Q.; Laurin, G.V.; Battles, J.J.; Saah, D. Integration of airborne LiDAR and vegetation types derived from aerial photography for mapping aboveground live biomass. Remote Sens. Environ. 2012, 121, 108–117. [Google Scholar] [CrossRef]
- Zhang, Y.; Shao, Z.F. Assessing of urban vegetation biomass in combination with LiDAR and high-resolution remote sensing images. Int. J. Remote Sens. 2021, 42, 964–985. [Google Scholar] [CrossRef]
- Cao, L.; Coops, N.C.; Innes, J.L.; Sheppard, S.R.J.; Fu, L.; Ruan, H.; She, G. Estimation of forest biomass dynamics in subtropical forests using multi-temporal airborne LiDAR data. Remote Sens. Environ. 2016, 178, 158–171. [Google Scholar] [CrossRef]
- Sinha, S.; Jeganathan, C.; Sharma, L.K.; Nathawat, M.S. A review of radar remote sensing for biomass estimation. Int. J. Environ. Sci. Technol. 2015, 12, 1779–1792. [Google Scholar] [CrossRef] [Green Version]
- Soja, M.J.; Quegan, S.; D’Alessandro, M.M.; Banda, F.; Scipal, K.; Tebaldini, S.; Ulander, L.M.H. Mapping above-ground biomass in tropical forests with ground-cancelled P-band SAR and limited reference data. Remote Sens. Environ. 2021, 253, 112153. [Google Scholar] [CrossRef]
- Vafaei, S.; Soosani, J.; Adeli, K.; Fadaei, H.; Naghavi, H.; Pham, T.D.; Bui, D.T. Improving accuracy estimation of forest aboveground biomass based on incorporation of ALOS-2 PALSAR-2 and Sentinel-2A imagery and machine learning: A case study of the Hyrcanian Forest area (Iran). Remote Sens. 2018, 10, 172. [Google Scholar] [CrossRef] [Green Version]
- Kumar, L.; Mutanga, O. Remote sensing of above-ground biomass. Remote Sens. 2017, 9, 935. [Google Scholar] [CrossRef] [Green Version]
- Cai, Y.; Li, X.; Zhang, M.; Lin, H. Mapping wetland using the object-based stacked generalization method based on multi-temporal optical and SAR data. Int. J. Appl. Earth Obs. Geoinf. 2020, 92, 102164. [Google Scholar] [CrossRef]
- Santoro, M.; Beaudoin, A.; Beer, C.; Cartus, O.; Fransson, J.E.S.; Hall, R.J.; Pathe, C.; Schmullius, C.; Schepaschenko, D.; Shvidenko, A. Forest growing stock volume of the northern hemisphere: Spatially explicit estimates for 2010 derived from Envisat ASAR. Remote Sens. Environ. 2015, 168, 316–334. [Google Scholar] [CrossRef]
- Zhu, Y.; Liu, K.; Myint, S.W.; Du, Z.; Wu, Z. Integration of GF2 Optical, GF3 SAR, and UAV Data for Estimating Aboveground Biomass of China’s Largest Artificially Planted Mangroves. Remote Sens. 2020, 12, 2039. [Google Scholar] [CrossRef]
- Zhao, Q.; Yu, S.; Zhao, F.; Tian, L.; Zhao, Z. Comparison of machine learning algorithms for forest parameter estimations and application for forest quality assessments. For. Ecol. Manag. 2019, 434, 224–234. [Google Scholar] [CrossRef]
- Long, J.; Lin, H.; Wang, G.; Sun, H.; Yan, E. Estimating the growing stem volume of the planted forest using the general linear model and time series quad-polarimetric sar images. Sensors 2020, 20, 3957. [Google Scholar] [CrossRef]
- Purohit, S.; Aggarwal, S.P.; Patel, N.R. Estimation of forest aboveground biomass using combination of Landsat 8 and Sentinel-1A data with random forest regression algorithm in Himalayan Foothills. Trop. Ecol. 2021, 62, 288–300. [Google Scholar] [CrossRef]
- Liu, G.; Zbigniew, P.; Stefano, S.; Benni, T.; Wu, L.; Fan, J.; Bai, S.; Wei, L.; Yan, S.; Song, R.; et al. Land Surface Displacement Geohazards Monitoring Using Multi-temporal InSAR Techniques. J. Geod. Geoinf. Sci. 2021, 4, 77–87. [Google Scholar] [CrossRef]
- Chen, L.; Wang, Y.; Ren, C.; Zhang, B.; Wang, Z. Assessment of multi-wavelength SAR and multispectral instrument data for forest aboveground biomass mapping using random forest kriging. For. Ecol. Manag. 2019, 447, 12–25. [Google Scholar] [CrossRef]
- Tomppo, E.; Antropov, O.; Praks, J. Boreal Forest Snow Damage Mapping Using Multi-Temporal Sentinel-1 Data. Remote Sens. 2019, 11, 384. [Google Scholar] [CrossRef] [Green Version]
- Tanase, M.A.; BorlafMena, I.; Santoro, M.; Aponte, C.; Marin, G.; Apostol, B.; Badea, O. Growing Stock Volume Retrieval from Single and Multi-Frequency Radar Backscatter. Forests 2021, 12, 944. [Google Scholar] [CrossRef]
- BorlafMena, I.; Badea, O.; Tanase, M.A. Assessing the Utility of Sentinel-1 Coherence Time Series for Temperate and Tropical Forest Mapping. Remote Sens. 2021, 13, 4814. [Google Scholar] [CrossRef]
- Zhang, R.; Xiang, W.; Liu, G.; Wang, X.; Mao, W.; Fu, Y.; Cai, J.; Zhang, B. Interferometric coherence and seasonal deformation characteristics analysis of saline soil based on Sentinel-1A time series imagery. J. Syst. Eng. Electron. 2021, 32, 1270–1283. [Google Scholar] [CrossRef]
- Jänichen, J.; Schmullius, C.; Baade, J.; Last, K.; Bettzieche, V.; Dubois, C. Monitoring of Radial Deformations of a Gravity Dam Using Sentinel-1 Persistent Scatterer Interferometry. Remote Sens. 2022, 14, 1112. [Google Scholar] [CrossRef]
- Tong, X.; Xu, X.; Chen, S. Coseismic Slip Model of the 2021 Maduo Earthquake, China from Sentinel-1 InSAR Observation. Remote Sens. 2022, 14, 436. [Google Scholar] [CrossRef]
- Dai, K.; Xu, Q.; Li, Z.; Tomás, R.; Fan, X.; Dong, X.; Li, W.; Zhou, Z.; Gou, J.; Ran, P. Post-disaster assessment of 2017 catastrophic Xinmo landslide (China) by spaceborne SAR interferometry. Landslides 2019, 16, 1189–1199. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Long, J.; Zhang, M.; Liu, Z.; Lin, H. Coniferous Plantations Growing Stock Volume Estimation Using Advanced Remote Sensing Algorithms and Various Fused Data. Remote Sens. 2021, 13, 3468. [Google Scholar] [CrossRef]
- Luo, M.; Wang, Y.; Xie, Y.; Zhou, L.; Qiao, J.; Qiu, S.; Sun, Y. Combination of feature selection and catboost for prediction: The first application to the estimation of aboveground biomass. Forests 2021, 12, 216. [Google Scholar] [CrossRef]
- Li, X.; Zhang, M.; Long, J.; Lin, H. A Novel Method for Estimating Spatial Distribution of Forest Above-Ground Biomass Based on Multispectral Fusion Data and Ensemble Learning Algorithm. Remote Sens. 2021, 13, 3910. [Google Scholar] [CrossRef]
- Jiang, F.; Kutia, M.; Ma, K.; Chen, S.; Long, J.; Sun, H. Estimating the aboveground biomass of coniferous forest in Northeast China using spectral variables, land surface temperature and soil moisture. Sci. Total Environ. 2021, 785, 147335. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Ma, J.; Liang, S.; Li, X.; Li, M. An evaluation of eight machine learning regression algorithms for forest aboveground biomass estimation from multiple satellite data products. Remote Sens. 2020, 12, 4015. [Google Scholar] [CrossRef]
- Lobert, F.; Holtgrave, A.-K.; Schwieder, M.; Pause, M.; Vogt, J.; Gocht, A.; Erasmi, S. Mowing event detection in permanent grasslands: Systematic evaluation of input features from Sentinel-1, Sentinel-2, and Landsat 8 time series. Remote Sens. Environ. 2021, 267, 112751. [Google Scholar] [CrossRef]
- Doyog, N.D.; Lin, C.; Lee, Y.J.; Lumbres, R.I.C.; Daipan, B.P.O.; Bayer, D.C.; Parian, C.P. Diagnosing pristine pine forest development through pansharpened-surface-reflectance Landsat image derived aboveground biomass productivity. For. Ecol. Manag. 2021, 487, 119011. [Google Scholar] [CrossRef]
- Chrysafis, I.; Mallinis, G.; Siachalou, S.; Patias, P. Assessing the relationships between growing stock volume and Sentinel-2 imagery in a Mediterranean forest ecosystem. Remote Sens. Lett. 2017, 8, 508–517. [Google Scholar] [CrossRef]
- Granero-Belinchon, C.; Adeline, K.; Briottet, X. Impact of the number of dates and their sampling on a NDVI time series reconstruction methodology to monitor urban trees with Venμs satellite. Int. J. Appl. Earth Obs. Geoinf. 2021, 95, 102257. [Google Scholar] [CrossRef]
- Sarker, M.; Nichol, J.; Iz, H.B.; Ahmad, B.B. Forest biomass estimation using texture measurements of high-resolution dual-polarization C-band SAR data. IEEE Trans. Geosci. Remote Sens. 2013, 51, 3371–3384. [Google Scholar] [CrossRef]
- Wang, J.; Wu, F.; Shang, J.; Zhou, Q.; Ahmad, I.; Zhou, G. Saline soil moisture mapping using Sentinel-1A synthetic aperture radar data and machine learning algorithms in humid region of China’s east coast. Catena 2022, 213, 106189. [Google Scholar] [CrossRef]
- Chen, L. Modeling of Forest Aboveground Biomass Based on Optical and Interferometric Synthetic Aperture Radar. Ph.D Thesis, University of Chinese Academy of Sciences, Beijing, China, 2020. [Google Scholar] [CrossRef]
- Bucha, T.; Papčo, J.; Sačkov, I.; Pajtík, J.; Sedliak, M.; Barka, I.; Feranec, J. Woody Above-Ground Biomass Estimation on Abandoned Agriculture Land Using Sentinel-1 and Sentinel-2 Data. Remote Sens. 2021, 13, 2488. [Google Scholar] [CrossRef]
- Dube, T.; Mutanga, O. The impact of integrating WorldView-2 sensor and environmental variables in estimating plantation forest species aboveground biomass and carbon stocks in uMgeni Catchment, South Africa. ISPRS J. Photogramm. Remote Sens. 2016, 119, 415–425. [Google Scholar] [CrossRef]
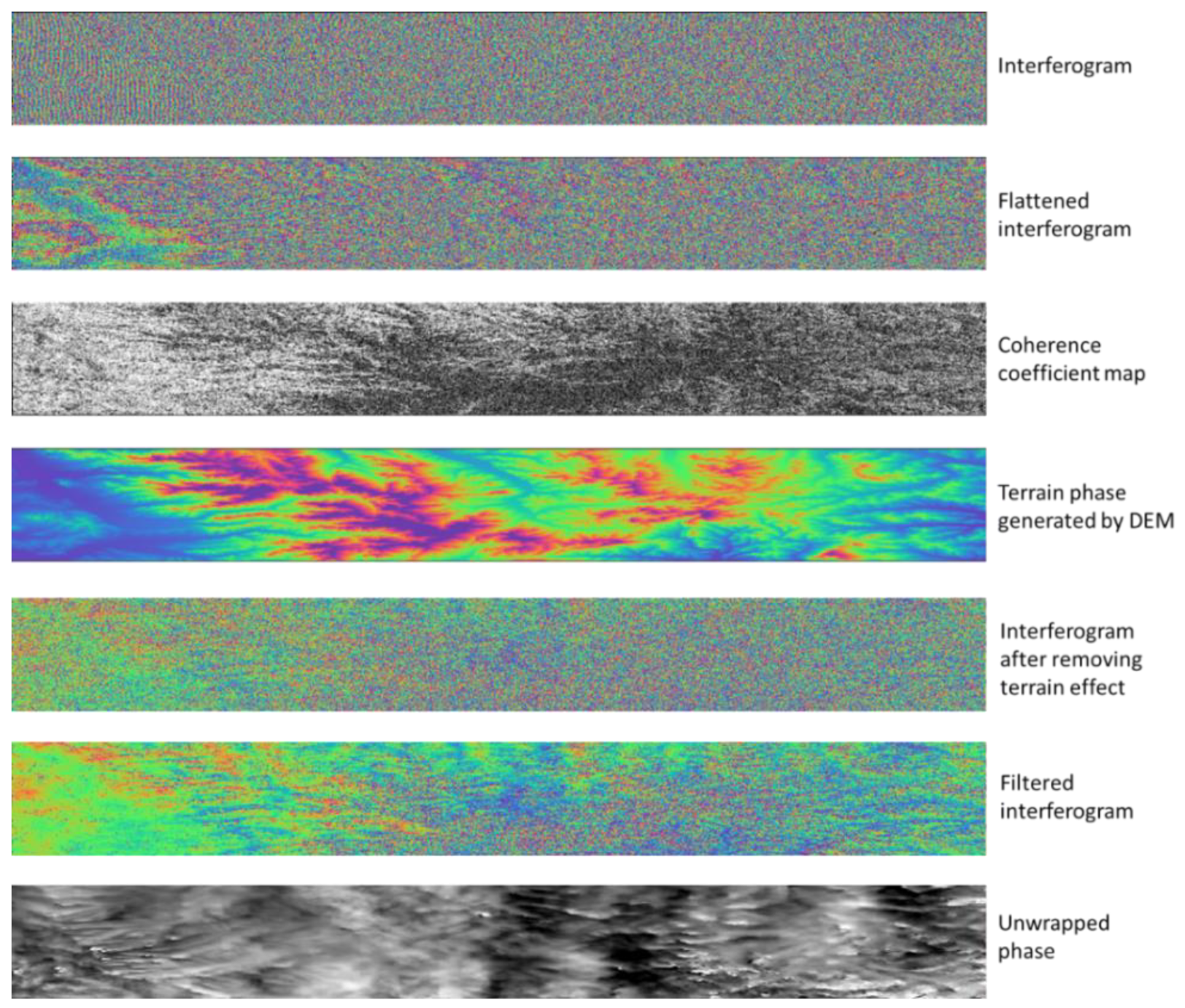

| Tree Species | FSV Calculation Formula | Remarks |
|---|---|---|
| Larch | FSV= −0.001498 + 0.00007 × D2 + 0.000901 × H + 0.000032 × H × D2 | D: DBH H: Tree height |
| Chinese pine | FSV= 0.013464 − 0.001967 × D + 0.000089 × D2 + 0.000628 × D × H + 0.000032 × H × D2 − 0.003173 × H |
| Tree Species | Numbers of Plots | Minimum | Maximum | Mean | Standard Deviation | Coefficient of Variation (%) |
|---|---|---|---|---|---|---|
| Chinese pine | 76 | 105 | 519 | 230.8 | 83.2 | 36.1 |
| Larch | 54 | 76 | 360 | 223.4 | 63.5 | 28.4 |
| All | 130 | 76 | 519 | 227.7 | 75.5 | 33.2 |
| Variable Type | Variable Name | Variable Description |
|---|---|---|
| Band reflectance | Band i, (i = 1, …, 7) | Band 1: Coastal, Band 2: Blue, Band 3: Green, Band 4: Red, Band 5: NIR, Band 6: SWIR 1, Band 7: SWIR 2 |
| Vegetation indices | NDVI | (Nir − Red)/(Nir + Red) |
| RVI_ij | Band i/Band j, i ≠ j | |
| DVI_ij | Band i/Band j, i ≠ j | |
| EVI | 2.5 × (NIR − Red)/(NIR + 6 × Red − 7.5 × Blue + 1) | |
| SAVI | (Nir − Red)(1 + 0.5)/(Nir + Red + 0.5) | |
| Texture (GLCM) | Mean (M) | |
| Variance (Var) | ||
| Contrast (Con) | ||
| Homogeneity (Hom) | ||
| Entropy (Ent) | ||
| Dissimilarity (Dis) | ||
| Second Moment (SM) | ||
| Correlation (Cor) |
| Variable Type | Variable Description |
|---|---|
| Backscattering coefficients | VV(Sigma0), VH(Sigma0), VV(Gamma0), VH(Gamma0), VV(Beta0), VH(Beta0) |
| Radar indices | (VH − VV)/(VH + VV), VV/VH |
| Texture features extracted from Backscattering coefficients | Mean (M), Variance (Var), Homogeneity (Hom), Contrast (Con), Dissimilarity (Dis), Entropy (Ent), Second moment (SM), Correlation (Cor) |
| Variables | Coefficient | t | Sig. | 95% Confidence Interval | Collinearity Statistics | Correlation with FSV | ||
|---|---|---|---|---|---|---|---|---|
| Lower | Upper | Tolerance | VIF | |||||
| Constant | 66.627 | 1.654 | 0.101 | −13.129 | 146.383 | |||
| b3-W5-T7 | 164.945 | 5.189 | 0.000 | 102.017 | 227.874 | 0.601 | 1.665 | 0.531 |
| b6-W9-T1 | −6.315 | −3.632 | 0.000 | −9.757 | −2.873 | 0.546 | 1.832 | −0.428 |
| RVI24 | −81.817 | −5.116 | 0.000 | −113.481 | −50.154 | 0.296 | 3.382 | −0.400 |
| RVI47 | 266.994 | 5.144 | 0.000 | 164.239 | 369.750 | 0.281 | 3.564 | −0.184 |
| b4-W5-T4 | 4.610 | 3.874 | 0.000 | 2.255 | 6.966 | 0.297 | 3.369 | −0.129 |
| b2-W7-T5 | −50.827 | −2.646 | 0.009 | −88.858 | −12.796 | 0.223 | 4.493 | −0.357 |
| b4-W5-T8 | 50.507 | 3.033 | 0.003 | 17.539 | 83.475 | 0.755 | 1.325 | −0.032 |
| b5-W9-T5 | 12.153 | 2.310 | 0.023 | 1.736 | 22.570 | 0.640 | 1.561 | −0.124 |
| Variables | Coefficient | t | Sig. | 95% Confidence Interval | Collinearity Statistics | Correlation with FSV | ||
|---|---|---|---|---|---|---|---|---|
| Lower | Upper | Tolerance | VIF | |||||
| Constant | 108.650 | 4.181 | 0.000 | 57.212 | 160.087 | |||
| 0921VH-B-W13-T1 | 196.682 | 7.254 | 0.000 | 143.009 | 250.354 | 0.070 | 14.193 | 0.142 |
| 0921VH-G-W9-T1 | −95.474 | −4.152 | 0.000 | −140.989 | −49.959 | 0.062 | 16.029 | 0.014 |
| 0711VV-S-W9-T1 | −49.330 | −4.976 | 0.000 | −68.956 | −29.705 | 0.159 | 6.290 | −0.095 |
| 0711VH-B-W15-T8 | 129.218 | 2.976 | 0.004 | 43.268 | 215.168 | 0.695 | 1.438 | 0.146 |
| 0828VH-S-W9-T8 | −102.517 | −3.402 | 0.001 | −162.157 | −42.876 | 0.697 | 1.435 | −0.091 |
| 0921VV-B-W13-T5 | 518.921 | 2.270 | 0.025 | 66.369 | 971.473 | 0.516 | 1.937 | −0.010 |
| Variables | Coefficient | t | Sig. | 95% Confidence Interval | Collinearity Statistics | Correlation with FSV | ||
|---|---|---|---|---|---|---|---|---|
| Lower | Upper | Tolerance | VIF | |||||
| Constant | 447.447 | 5.463 | 0.000 | 285.288 | 609.606 | |||
| 1206VV-CC | −200.281 | −3.052 | 0.003 | −330.227 | −70.335 | 0.570 | 1.755 | −0.600 |
| 1124VV-CC | −186.394 | −3.564 | 0.001 | −289.943 | −82.846 | 0.559 | 1.789 | −0.564 |
| 0711VV-DSM | 0.309 | 4.680 | 0.000 | 0.178 | 0.439 | 0.405 | 2.470 | 0.451 |
| 0703VV-CC | −72.551 | −2.813 | 0.006 | −123.617 | −21.485 | 0.947 | 1.056 | −0.061 |
| 0723VH-CC | −117.975 | −2.622 | 0.010 | −207.063 | −28.886 | 0.859 | 1.164 | −0.295 |
| 0621VV-CC | 94.824 | 2.640 | 0.009 | 23.710 | 165.939 | 0.835 | 1.197 | −0.122 |
| 1019VV-CC | −350.079 | −4.001 | 0.000 | −523.304 | −176.855 | 0.539 | 1.857 | −0.576 |
| 1108VV-CC | −159.089 | −2.811 | 0.006 | −271.156 | −47.021 | 0.498 | 2.008 | −0.567 |
| 1019VV-DSM | −0.147 | −2.287 | 0.024 | −0.275 | −0.020 | 0.293 | 3.408 | 0.491 |
| Datasets | Variables | DC | PC | MIC | Importance |
|---|---|---|---|---|---|
| L8 OLI | b4-W9-T1 | 0.365 | −0.363 | 0.266 | 0.248 |
| b1-W9-T7 | 0.363 | 0.294 | 0.356 | 0.148 | |
| b5-W3-T7 | 0.292 | 0.300 | 0.291 | 0.029 | |
| NDVI37 | 0.254 | −0.221 | 0.299 | 0.155 | |
| b6-W9-T7 | 0.365 | 0.338 | 0.298 | 0.148 | |
| b5-W9-T7 | 0.272 | 0.339 | 0.240 | 0.055 | |
| b4-W9-T7 | 0.388 | 0.392 | 0.295 | 0.095 | |
| b1-W7-T4 | 0.363 | −0.251 | 0.335 | 0.150 | |
| S1 | 0711VV-B-W7-T1 | 0.184 | −0.146 | 0.272 | 0.370 |
| 0921VH-B-W13-T1 | 0.183 | 0.142 | 0.239 | 0.488 | |
| 0711VH-G-W3-T7 | 0.164 | 0.067 | 0.213 | 0.067 | |
| 0711VH-B-W13-T4 | 0.163 | −0.031 | 0.296 | 0.115 | |
| 0921VH-S-W9-T3 | 0.160 | 0.109 | 0.230 | 0.071 | |
| 0711VV-B | 0.220 | −0.203 | 0.257 | 0.190 | |
| 0711VV-B-W13-T7 | 0.156 | 0.033 | 0.210 | 0.078 | |
| 0828VH-S-W9-T3 | 0.162 | 0.056 | 0.291 | 0.089 | |
| S1-InSAR | 1206VV-CC | 0.590 | −0.600 | 0.415 | 0.194 |
| 1124VV-CC | 0.544 | −0.564 | 0.401 | 0.126 | |
| 0617VV-CC | 0.280 | −0.059 | 0.301 | 0.034 | |
| 0703VV-CC | 0.261 | −0.061 | 0.358 | 0.075 | |
| 0921VV-CC | 0.273 | −0.080 | 0.310 | 0.034 | |
| 1108VV-CC | 0.581 | −0.567 | 0.439 | 0.130 | |
| 1019VV-CC | 0.581 | −0.576 | 0.508 | 0.160 | |
| 1214VV-CC | 0.361 | −0.340 | 0.314 | 0.034 | |
| 0317VH-CC | 0.269 | −0.132 | 0.264 | 0.042 | |
| 0422VH-DSM | 0.315 | −0.238 | 0.308 | 0.152 |
| Datasets | Methods | C | Gamma | R2 | RMSE (m3/ha) | rRMSE (%) | r |
|---|---|---|---|---|---|---|---|
| L8 | SRA | 100 | 0.38 | 59.0 | 25.9 | 0.63 | |
| FS-SVR | 150 | 2.8 | 0.40 | 58.4 | 25.6 | 0.63 | |
| S1 | SRA | 200 | 0.20 | 67.3 | 29.5 | 0.45 | |
| FS-SVR | 350 | 1.4 | 0.50 | 52.9 | 23.2 | 0.71 | |
| S1-InSAR | SRA | 51 | 0.42 | 57.3 | 25.2 | 0.65 | |
| FS-SVR | 150 | 4.8 | 0.61 | 47.2 | 20.7 | 0.78 | |
| The integrated dataset | FS-SVR | 270 | 2.4 | 0.65 | 44.3 | 19.4 | 0.81 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Ye, Z.; Long, J.; Zheng, H.; Lin, H. Inversion of Coniferous Forest Stock Volume Based on Backscatter and InSAR Coherence Factors of Sentinel-1 Hyper-Temporal Images and Spectral Variables of Landsat 8 OLI. Remote Sens. 2022, 14, 2754. https://doi.org/10.3390/rs14122754
Li X, Ye Z, Long J, Zheng H, Lin H. Inversion of Coniferous Forest Stock Volume Based on Backscatter and InSAR Coherence Factors of Sentinel-1 Hyper-Temporal Images and Spectral Variables of Landsat 8 OLI. Remote Sensing. 2022; 14(12):2754. https://doi.org/10.3390/rs14122754
Chicago/Turabian StyleLi, Xinyu, Zilin Ye, Jiangping Long, Huanna Zheng, and Hui Lin. 2022. "Inversion of Coniferous Forest Stock Volume Based on Backscatter and InSAR Coherence Factors of Sentinel-1 Hyper-Temporal Images and Spectral Variables of Landsat 8 OLI" Remote Sensing 14, no. 12: 2754. https://doi.org/10.3390/rs14122754
APA StyleLi, X., Ye, Z., Long, J., Zheng, H., & Lin, H. (2022). Inversion of Coniferous Forest Stock Volume Based on Backscatter and InSAR Coherence Factors of Sentinel-1 Hyper-Temporal Images and Spectral Variables of Landsat 8 OLI. Remote Sensing, 14(12), 2754. https://doi.org/10.3390/rs14122754








