Estimation of Daily Average Shortwave Solar Radiation under Clear-Sky Conditions by the Spatial Downscaling and Temporal Extrapolation of Satellite Products in Mountainous Areas
Abstract
1. Introduction
2. Study Area and Data
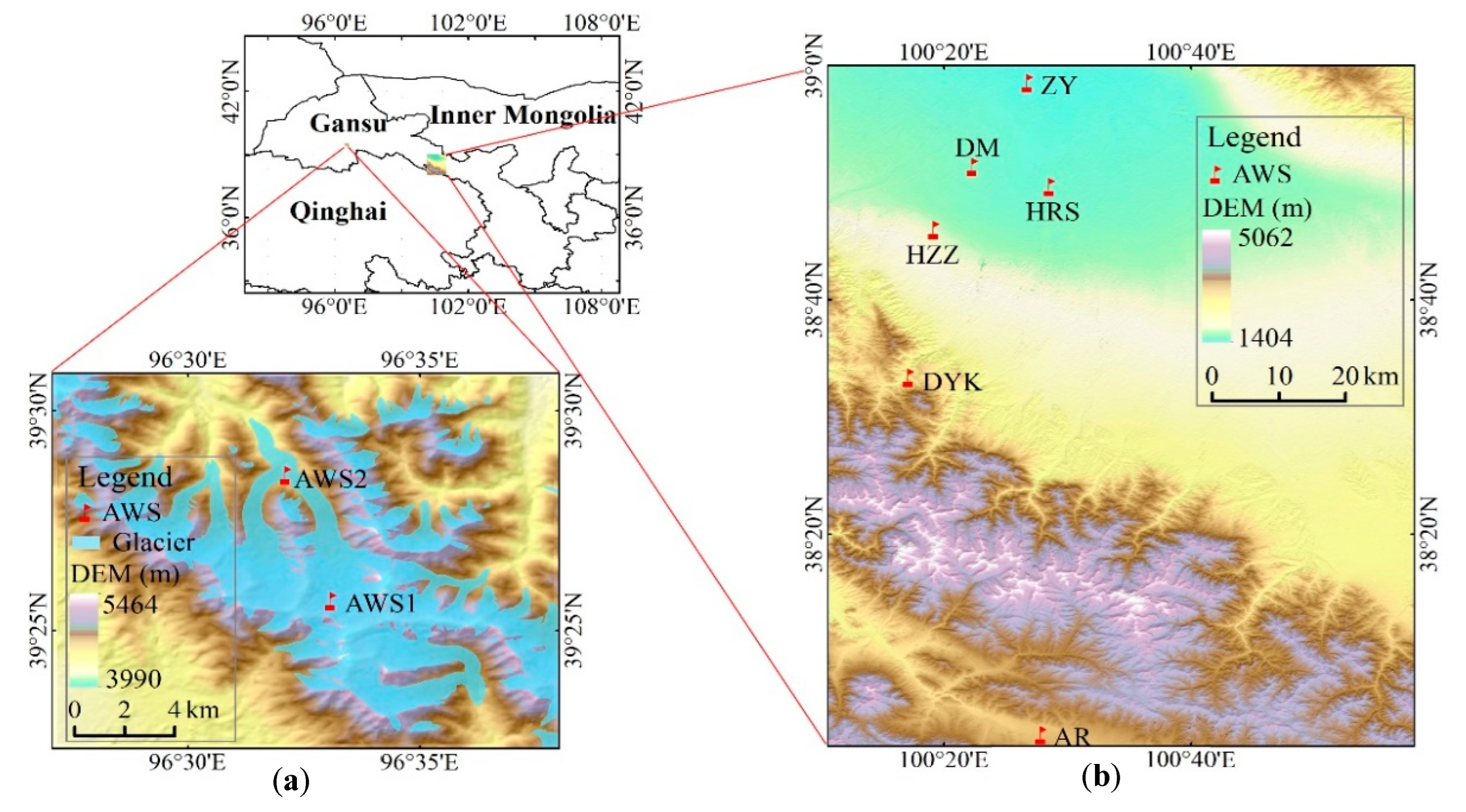
2.1. Study Area
2.2. Data
2.2.1. Himawari-8 Radiation Products
2.2.2. Sentinel-2 Instantaneous DSSR
2.2.3. Digital Elevation Model
2.2.4. In-Situ Measurements
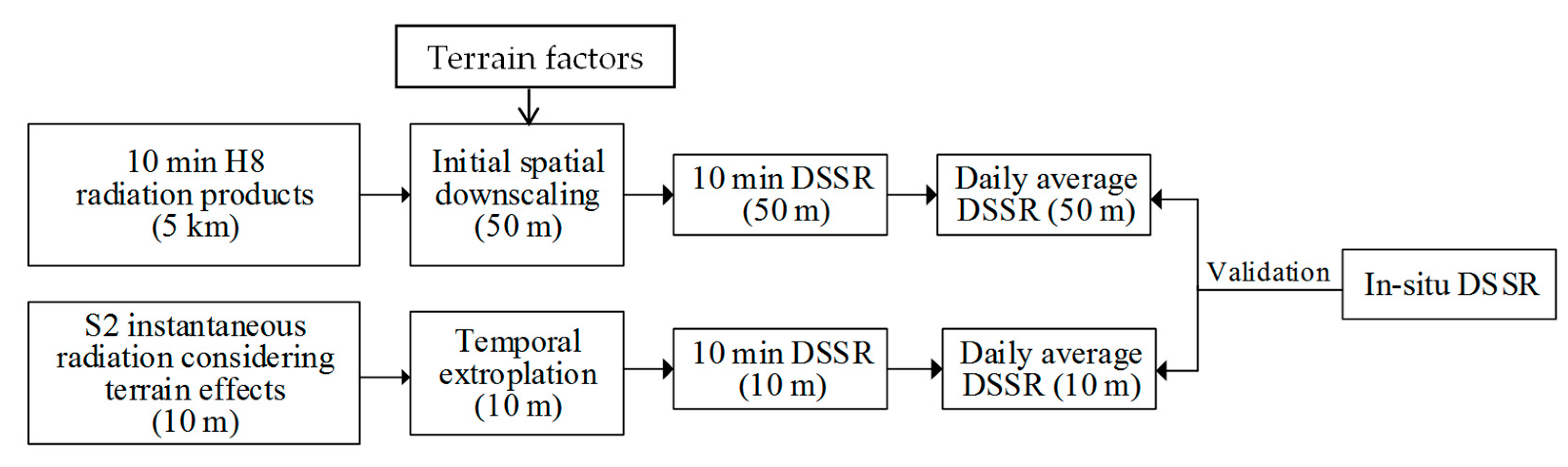
3. Methods
3.1. Spatial Downscaling
3.2. Temporal Extrapolation
4. Results
4.1. Evaluation against Ground-Based Measurements
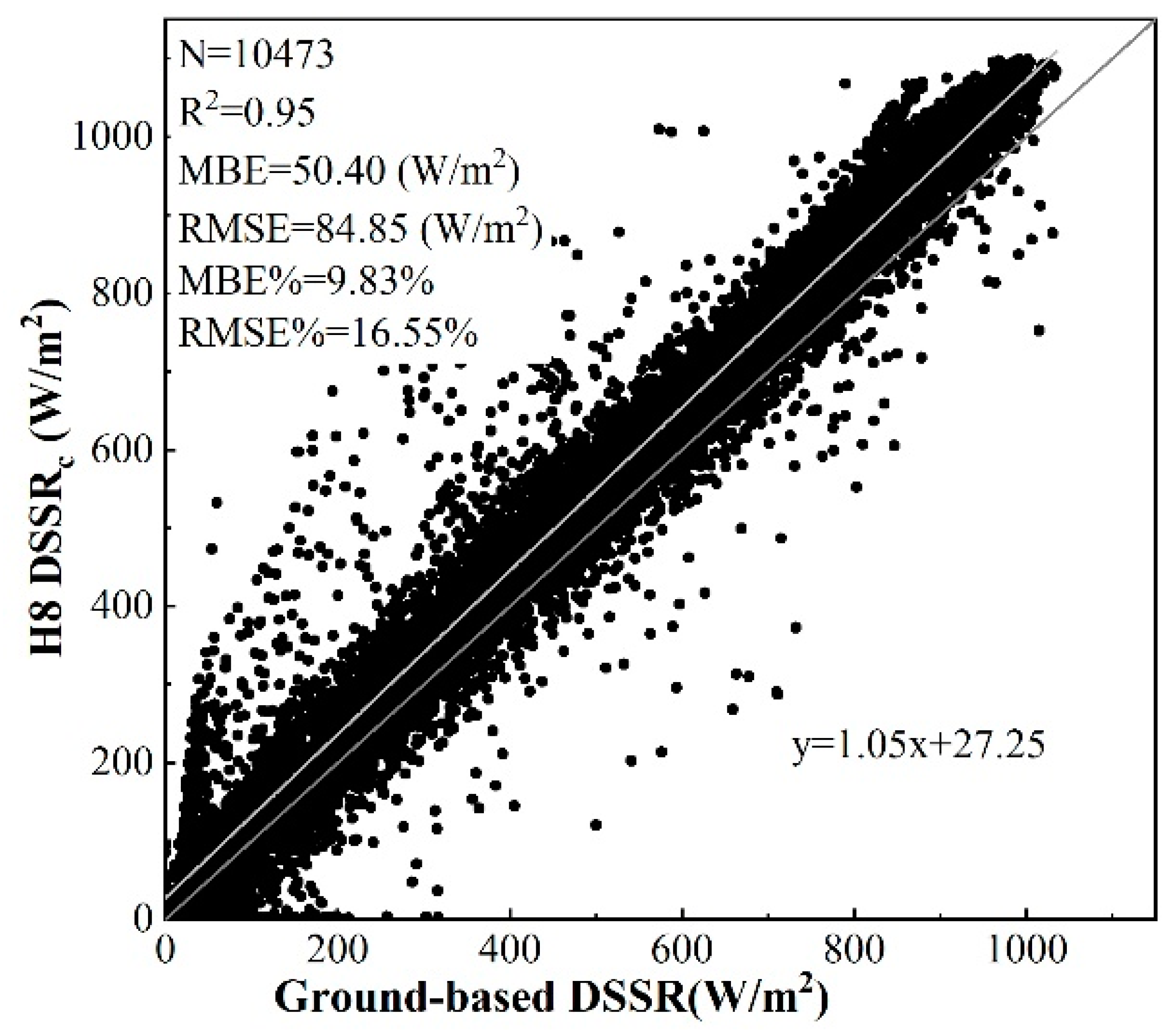
4.1.1. Evaluation of the Original H8 Radiation Products
4.1.2. Evaluation of the Spatial Downscaling
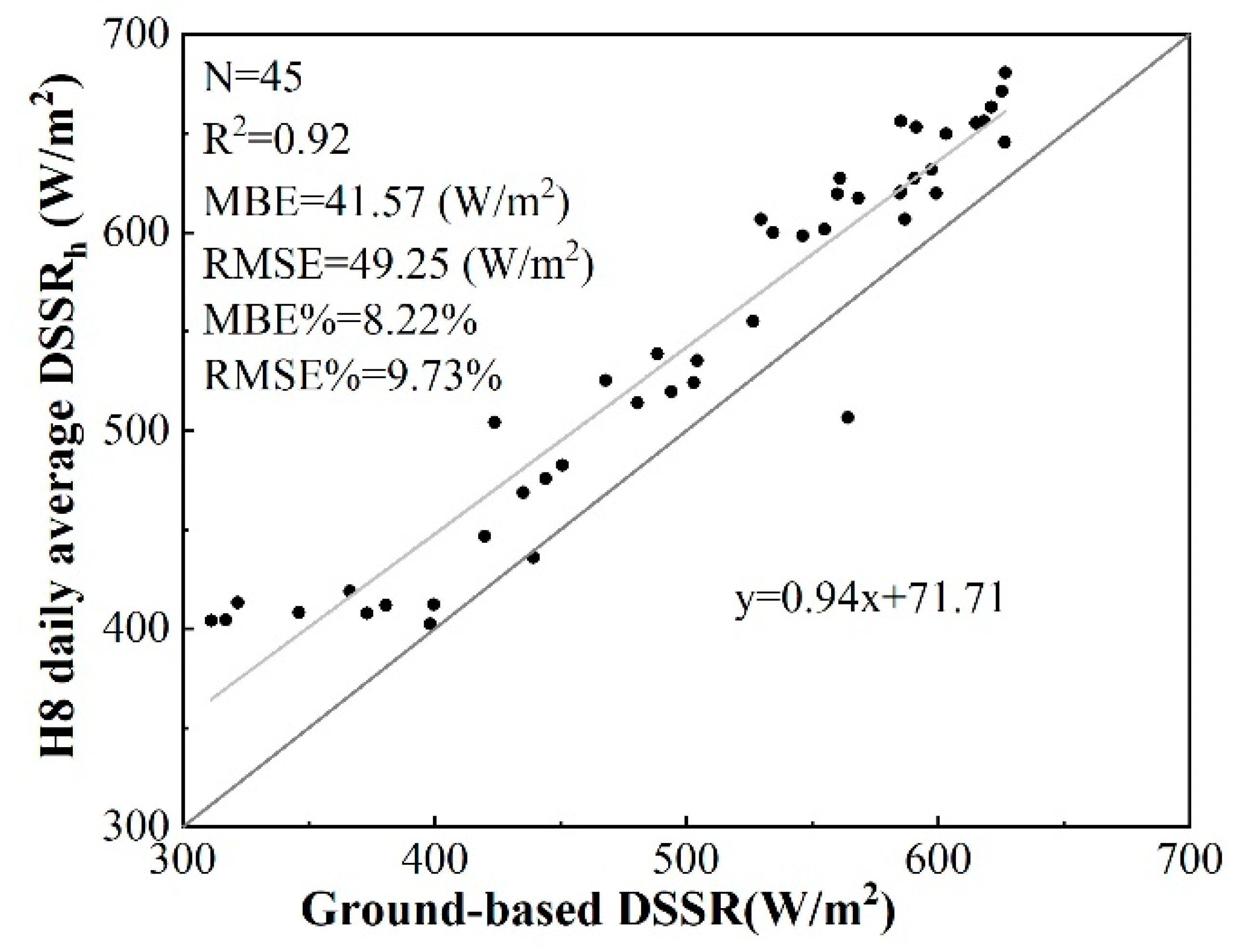
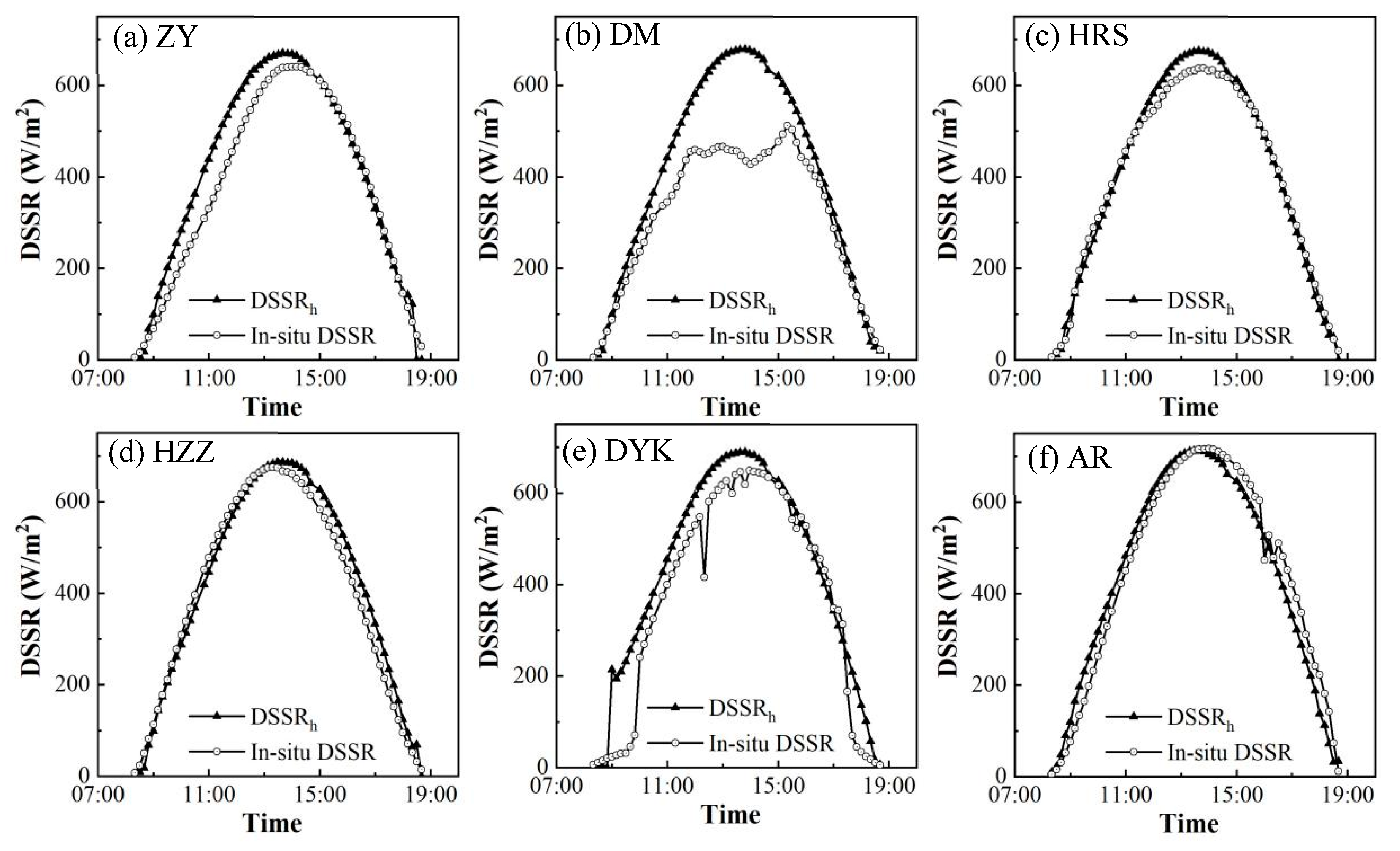
4.1.3. Evaluation of Temporal Extrapolation
4.2. Mapping of DSSR
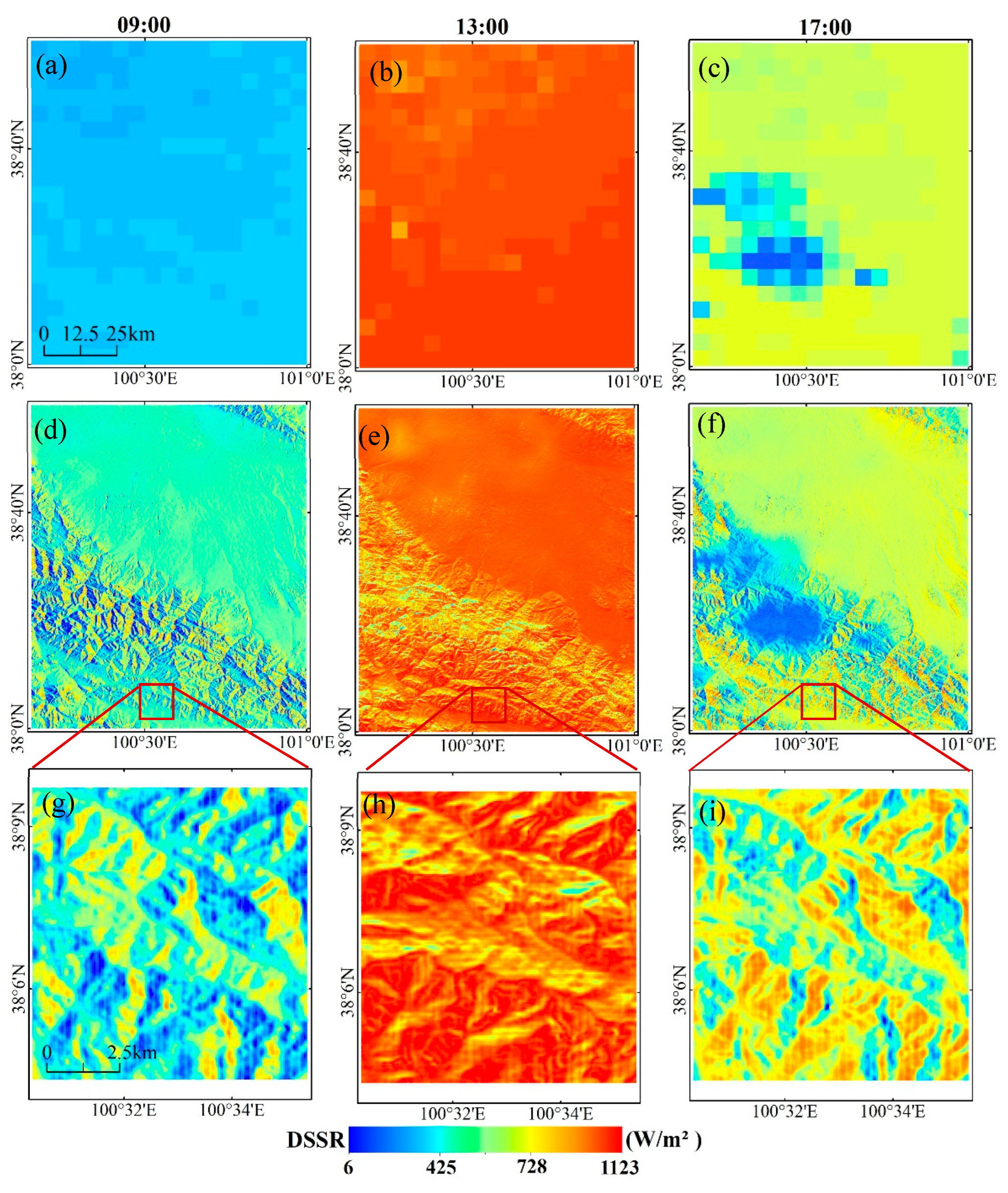
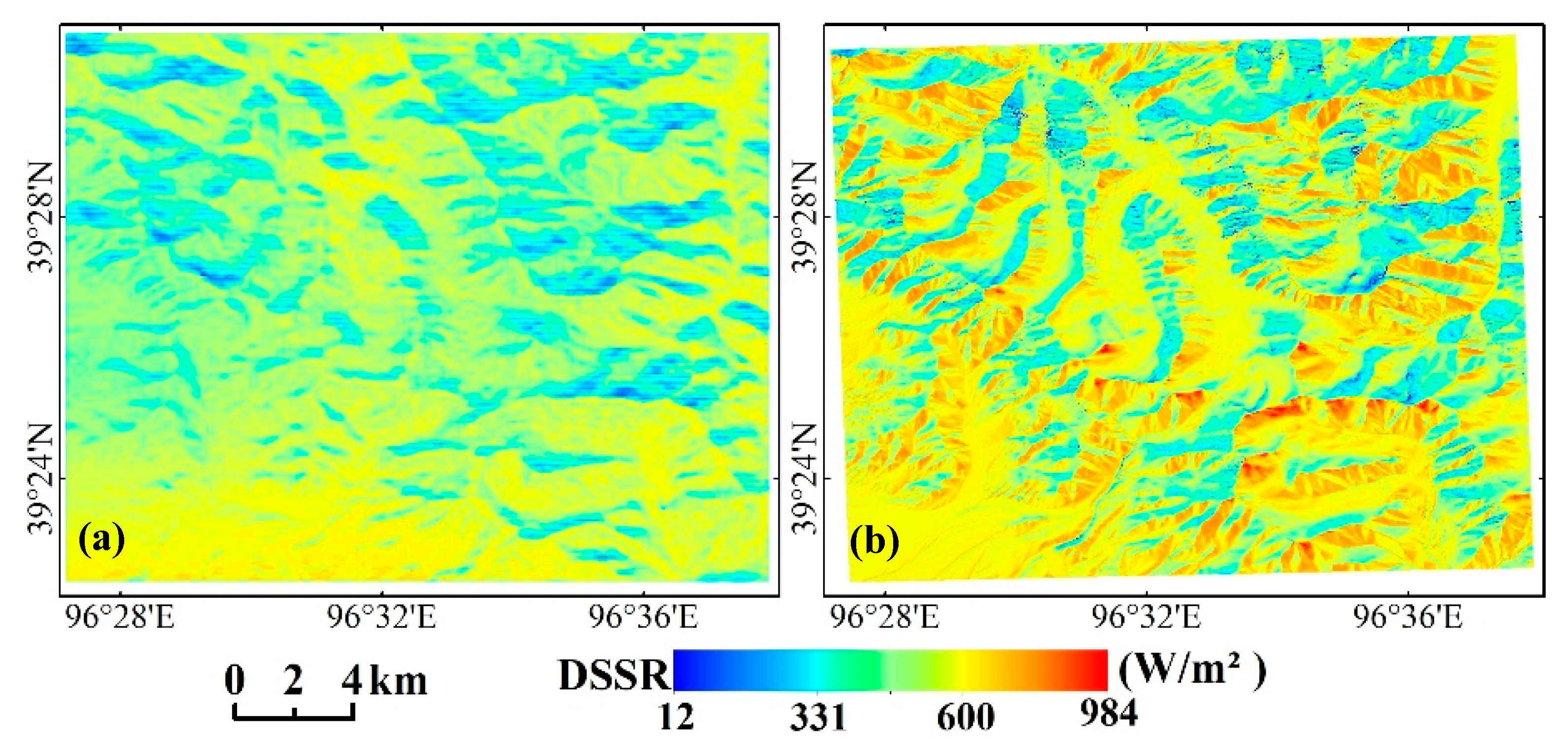
4.2.1. Mapping of Downscaled DSSR
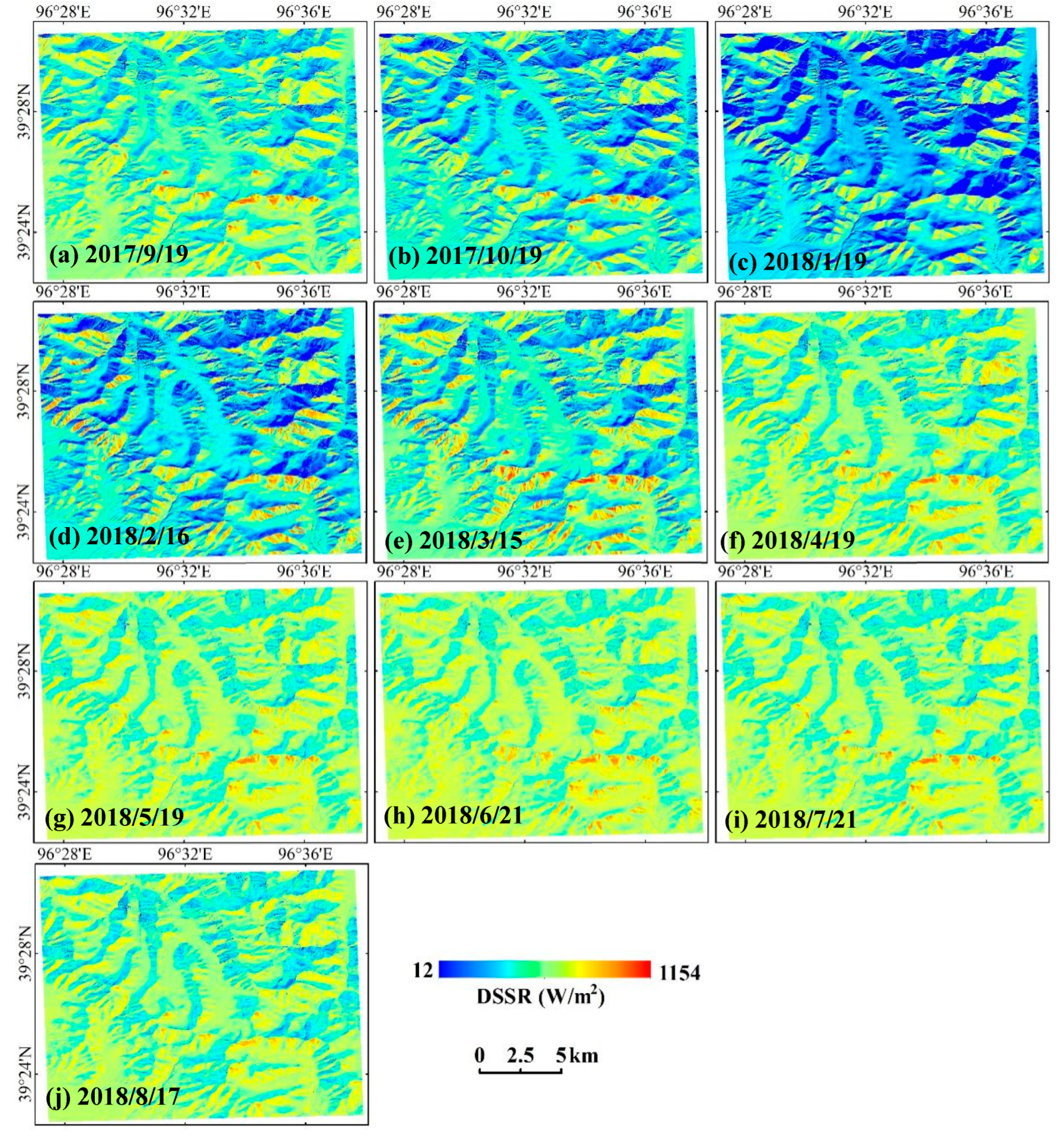
4.2.2. Mapping of the Temporal Extrapolation DSSR
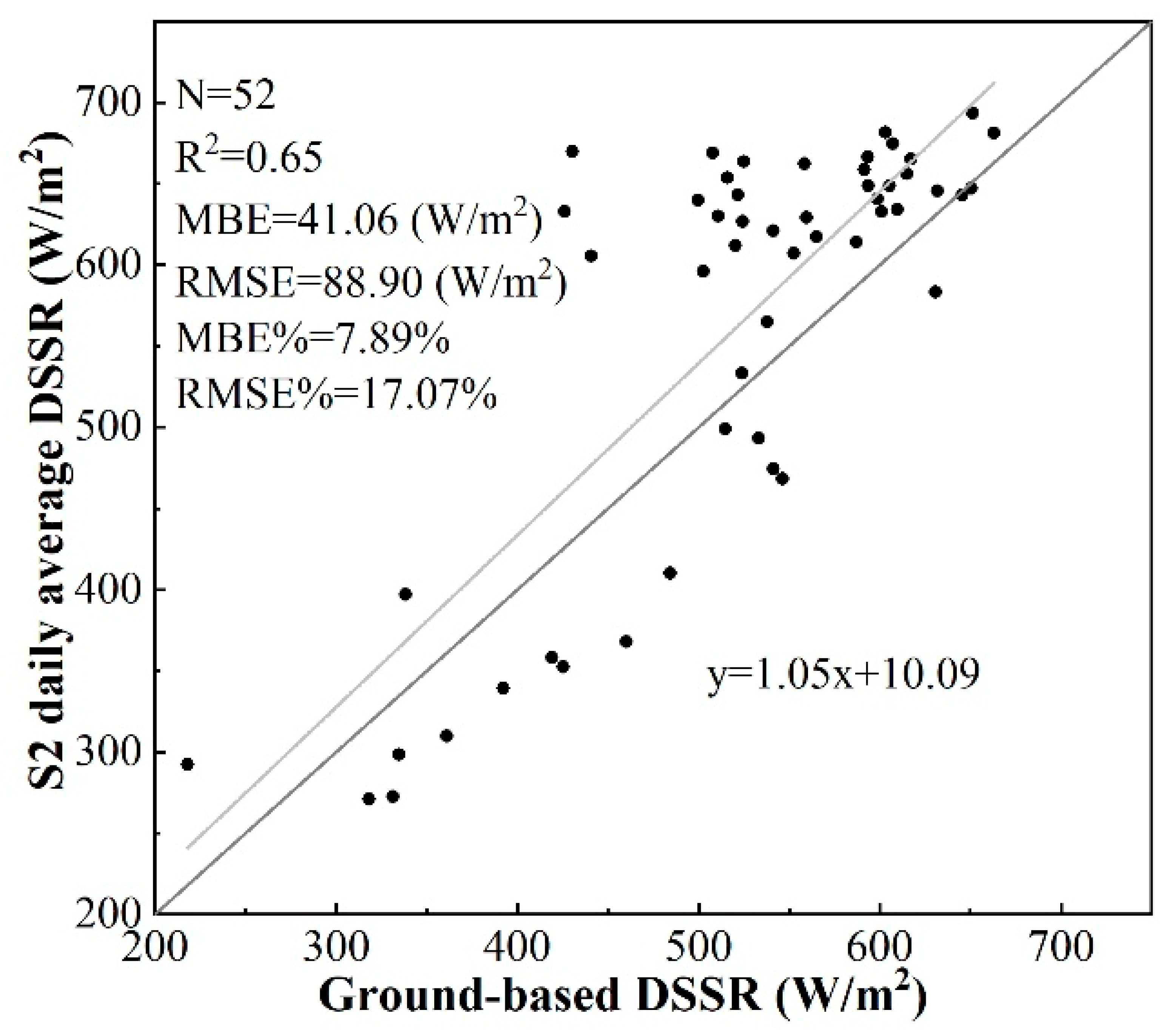
4.3. Comparison of the Daily Average DSSR Estimated by Two Methods
5. Discussion
5.1. Uncertainty Analysis of the Spatial Downscaling
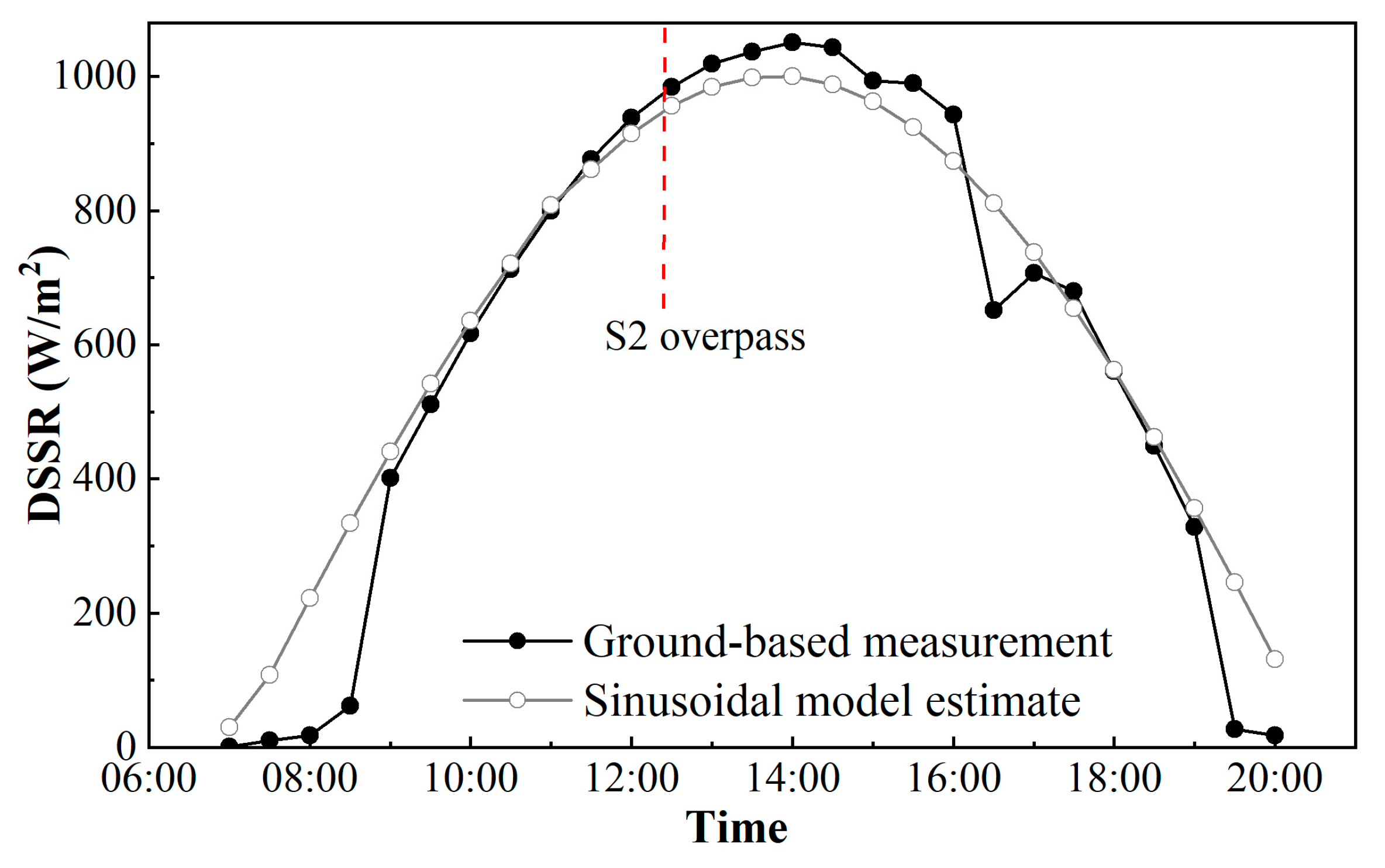
5.2. Uncertainty Analysis of the Temporal Extrapolation
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Yang, K.; Koike, T.; Ye, B. Improving estimation of hourly, daily, and monthly solar radiation by importing global data sets. Agric. For. Meteorol. 2006, 137, 43–55. [Google Scholar] [CrossRef]
- Journée, M.; Bertrand, C. Improving the spatio-temporal distribution of surface solar radiation data by merging ground and satellite measurements. Remote Sens. Environ. 2010, 114, 2692–2704. [Google Scholar] [CrossRef]
- Zhang, R.; Liu, Y.; Bian, S. Mathematical criterion of Gauss function fitting parameters. Hydrogr. Surv. Charting 2018, 38, 5–8. [Google Scholar]
- Huang, G.; Li, Z.; Li, X.; Liang, S.; Yang, K.; Wang, D.; Zhang, Y. Estimating surface solar irradiance from satellites: Past, present, and future perspectives. Remote Sens. Environ. 2019, 233, 111371. [Google Scholar] [CrossRef]
- Zou, L.; Wang, L.; Li, J.; Lu, Y.; Gong, W.; Niu, Y. Global surface solar radiation and photovoltaic power from Coupled Model Intercomparison Project Phase 5 climate models. J. Clean. Prod. 2019, 224, 304–324. [Google Scholar] [CrossRef]
- Hou, N.; Zhang, X.; Zhang, W.; Xu, J.; Feng, C.; Yang, S.; Jia, K.; Yao, Y.; Cheng, J.; Jiang, B. A New Long-Term Downward Surface Solar Radiation Dataset over China from 1958 to 2015. Sensors 2020, 20, 6167. [Google Scholar] [CrossRef] [PubMed]
- Chen, F.; Zhou, Z.; Lin, A.; Niu, J.; Qin, W.; Yang, Z. Evaluation of direct horizontal irradiance in China using a physically-based model and machine learning methods. Energies 2019, 12, 150. [Google Scholar] [CrossRef]
- Fan, J.; Wang, X.; Zhang, F.; Ma, X.; Wu, L. Predicting daily diffuse horizontal solar radiation in various climatic regions of China using support vector machine and tree-based soft computing models with local and extrinsic climatic data. J. Clean. Prod. 2020, 248, 119264. [Google Scholar] [CrossRef]
- Feng, L.; Lin, A.; Wang, L.; Qin, W.; Gong, W. Evaluation of sunshine-based models for predicting diffuse solar radiation in China. Renew. Sustain. Energy Rev. 2018, 94, 168–182. [Google Scholar] [CrossRef]
- Wang, H.; Sun, F.; Wang, T.; Liu, W. Estimation of daily and monthly diffuse radiation from measurements of global solar radiation a case study across China. Renew. Energy 2018, 126, 226–241. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, X.; Bai, Y. An integrated approach to estimate shortwave solar radiation on clear-sky days in rugged terrain using MODIS atmospheric products. Sol. Energy 2015, 113, 347–357. [Google Scholar] [CrossRef]
- Wang, D.; Liang, S.; Zhang, Y.; Gao, X.; Brown, M.G.; Jia, A. A New Set of MODIS Land Products (MCD18): Downward Shortwave Radiation and Photosynthetically Active Radiation. Remote Sens. 2020, 12, 168. [Google Scholar] [CrossRef]
- Zhang, H.; Xin, X.; Liu, Q. Modeling daily net shortwave radiation over rugged surfaces using MODIS atmospheric products. In Proceedings of the 2011 IEEE International Geoscience and Remote Sensing Symposium, Vancouver, BC, Canada, 25–29 July 2011; pp. 3787–3790. [Google Scholar]
- Kambezidis, H.; Psiloglou, B.; Karagiannis, D.; Dumka, U.; Kaskaoutis, D. Meteorological Radiation Model (MRM v6.1): Improvements in diffuse radiation estimates and a new approach for implementation of cloud products. Renew. Sustain. Energy Rev. 2017, 74, 616–637. [Google Scholar] [CrossRef]
- Psiloglou, B.; Kambezidis, H.; Kaskaoutis, D.; Karagiannis, D.; Polo, J.M. Comparison between MRM simulations, CAMS and PVGIS databases with measured solar radiation components at the Methoni station, Greece. Renew. Energy 2020, 146, 1372–1391. [Google Scholar] [CrossRef]
- Xu, X.; Du, H.; Zhou, G.; Mao, F.; Li, P.; Fan, W.; Zhu, D. A method for daily global solar radiation estimation from two instantaneous values using MODIS atmospheric products. Energy 2016, 111, 117–125. [Google Scholar] [CrossRef]
- Bisht, G.; Bras, R.L. Estimation of net radiation from the MODIS data under all sky conditions: Southern Great Plains case study. Remote Sens. Environ. 2010, 114, 1522–1534. [Google Scholar] [CrossRef]
- Bisht, G.; Venturini, V.; Islam, S.; Jiang, L. Estimation of the net radiation using MODIS (moderate resolution imaging spectroradiometer) data for clear sky days. Remote Sens. Environ. 2005, 97, 52–67. [Google Scholar] [CrossRef]
- Hou, J.; Jia, G.; Zhao, T.; Wang, H.; Tang, B. Satellite-based estimation of daily average net radiation under clear-sky conditions. Adv. Atmos. Sci. 2014, 31, 705–720. [Google Scholar] [CrossRef]
- Kim, H.; Liang, S. Development of a hybrid method for estimating land surface shortwave net radiation from MODIS data. Remote Sens. Environ. 2010, 114, 2393–2402. [Google Scholar] [CrossRef]
- Olofsson, P.; Van Laake, P.E.; Eklundh, L. Estimation of absorbed PAR across Scandinavia from satellite measurements: Part I: Incident PAR. Remote Sens. Environ. 2007, 110, 252–261. [Google Scholar] [CrossRef]
- Wang, D.; Liang, S.; Liu, R.; Zheng, T. Estimation of daily-integrated PAR from sparse satellite observations: Comparison of temporal scaling methods. Int. J. Remote Sens. 2010, 31, 1661–1677. [Google Scholar] [CrossRef]
- Yan, G.; Tong, Y.; Yan, K.; Mu, X.; Chu, Q.; Zhou, Y.; Zhou, H. Temporal extrapolation of daily downward shortwave radiation over cloud-free rugged terrains. Part 1: Analysis of topographic effects. IEEE Trans. Geosci. Remote Sens. 2018, 56, 6375–6394. [Google Scholar] [CrossRef]
- Letu, H.; Yang, K.; Nakajima, T.Y.; Ishimoto, H.; Nagao, T.M.; Riedi, J.; Khatri, P. High-resolution retrieval of cloud microphysical properties and surface solar radiation using Himawari-8/AHI next-generation geostationary satellite. Remote Sens. Environ. 2020, 239, 111583. [Google Scholar] [CrossRef]
- Peng, Z.; Letu, H.; Wang, T.; Shi, C.; Zhao, C.; Tana, G.; Shi, J. Estimation of shortwave solar radiation using the artificial neural network from Himawari-8 satellite imagery over China. J. Quant. Spectrosc. Radiat. Transf. 2020, 240, 106672. [Google Scholar] [CrossRef]
- Tang, W.; Qin, J.; Yang, K.; Liu, S.; Lu, N.; Niu, X. Retrieving high-resolution surface solar radiation with cloud parameters derived by combining MODIS and MTSAT data. Atmos. Chem. Phys. 2016, 16, 2543–2557. [Google Scholar] [CrossRef]
- Ruiz-Arias, J.; Cebecauer, T.; Tovar-Pescador, J.; Suri, M. Spatial disaggregation of satellite-derived irradiance using a high-resolution digital elevation model. Sol. Energy 2010, 84, 1644–1657. [Google Scholar] [CrossRef]
- Wang, W.; Yin, G.; Zhao, W.; Wen, F.; Yu, D. Spatial Downscaling of MSG Downward Shortwave Radiation Product Under Clear-Sky Condition. IEEE Trans. Geosci. Remote Sens. 2019, 58, 3264–3272. [Google Scholar] [CrossRef]
- Loghmari, I.; Timoumi, Y.; Messadi, A. Performance comparison of two global solar radiation models for spatial interpolation purposes. Renew. Sustain. Energy Rev. 2018, 82, 837–844. [Google Scholar] [CrossRef]
- Rivington, M.; Miller, D.; Matthews, K.; Russell, G.; Bellocchi, G.; Buchan, K. Downscaling regional climate model estimates of daily precipitation, temperature and solar radiation data. Clim. Res. 2008, 35, 181–202. [Google Scholar] [CrossRef][Green Version]
- Haurant, P.; Muselli, M.; Pillot, B.; Oberti, P. Disaggregation of satellite derived irradiance maps: Evaluation of the process and application to Corsica. Sol. Energy 2012, 86, 3168–3182. [Google Scholar] [CrossRef]
- Bessafi, M.; Oree, V.; Khoodaruth, A.; Jumaux, G.; Bonnardot, F.; Jeanty, P.; Dauhoo, M. Downscaling solar irradiance using DEM-based model in young volcanic islands with rugged topography. Renew. Energy 2018, 126, 584–593. [Google Scholar] [CrossRef]
- Ohmura, A.; Dutton, E.G.; Forgan, B.; Fröhlich, C.; Gilgen, H.; Hegner, H.; Heimo, A.; König-Langlo, G.; McArthur, B.; Müller, G.; et al. Baseline Surface Radiation Network (BSRN/WCRP): New Precision Radiometry for Climate Research. Bull. Am. Meteorol. Soc. 1998, 79, 2115–2136. [Google Scholar] [CrossRef]
- Zhang, Y.; Qin, X.; Li, X.; Zhao, J.; Liu, Y. Estimation of Shortwave Solar Radiation on Clear-Sky Days for a Valley Glacier with Sentinel-2 Time Series. Remote Sens. 2020, 12, 927. [Google Scholar] [CrossRef]
- Bessho, K.; Date, K.; Hayashi, M.; Ikeda, A.; Imai, T.; Inoue, H.; Okuyama, A. An introduction to Himawari-8/9—Japan’s new-generation geostationary meteorological satellites. J. Meteorol. Soc. Jpn. Ser. II 2016, 94, 151–183. [Google Scholar] [CrossRef]
- Cheng, G.; Li, X.; Zhao, W.; Xu, Z.; Xiao, H. Integrated study of the water–ecosystem–economy in the Heihe River Basin. Natl. Sci. Rev. 2014, 1, 413–428. [Google Scholar] [CrossRef]
- Zhang, X.; Qin, X.; Wu, J.; Zhang, X. Analysis of the characteristics of runoff yield and confluence in the Laohugou basin, Qilian Mountains. J. Glaciol. Geocryol. 2017, 39, 140–147. [Google Scholar]
- Damiani, A.; Irie, H.; Horio, T.; Takamura, T.; Khatri, P.; Takenaka, H.; Cordero, R.R. Evaluation of Himawari-8 surface downwelling solar radiation by ground-based measurements. Atmos. Meas. Tech. 2018, 11, 2501–2521. [Google Scholar] [CrossRef]
- Qi, Y.; Zhang, J.; Zhou, S.; Wang, H. The DEM Data of 30 m in Qilian Mountain (2018); National Tibetan Plateau Data Center: Beijing, China, 2019. [Google Scholar]
- Zakšek, K.; Oštir, K.; Kokalj, Ž. Sky-view factor as a relief visualization technique. Remote Sens. 2011, 3, 398–415. [Google Scholar] [CrossRef]
- Li, X.; Toshio, K.; Cheng, G. Retrieval of snow reflectance from Landsat data in rugged terrain. Ann. Glaciol. 2002, 34, 31–37. [Google Scholar]
- Yang, K.; Koike, T. A general model to estimate hourly and daily solar radiation for hydrological studies. Water Resour. Res. 2005, 41, 10. [Google Scholar] [CrossRef]
- Huang, G.; Liu, S.; Liang, S. Estimation of net surface shortwave radiation from MODIS data. Int. J. Remote Sens. 2012, 33, 804–825. [Google Scholar] [CrossRef]
- Shi, H.; Li, W.; Fan, X.; Zhang, J.; Hu, B.; Husi, L.; Xia, X. First assessment of surface solar irradiance derived from Himawari-8 across China. Sol. Energy 2018, 174, 164–170. [Google Scholar] [CrossRef]
- Yu, Y.; Shi, J.; Wang, T.; Letu, H.; Yuan, P.; Zhou, W.; Hu, L. Evaluation of the Himawari-8 Shortwave Downward Radiation (SWDR) Product and its Comparison with the CERES-SYN, MERRA-2, and ERA-Interim Datasets. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 12, 519–532. [Google Scholar] [CrossRef]
- Huang, G.; Li, X.; Ma, M.; Li, H.; Huang, C. High resolution surface radiation products for studies of regional energy, hydrologic and ecological processes over Heihe river basin, northwest china. Agric. For. Meteorol. 2016, 230, 67–78. [Google Scholar] [CrossRef]
- Chen, Z.; Hu, D.; Jiang, W.; Cao, R. Land surface radiation budget parameterization and spatial analysis over China using GLASS data. Geogr. Res. 2016, 35, 25–36. [Google Scholar]


| Datasets | Spatial Resolution | Temporal Resolution | Date | Region | Amount of Data | Applications |
|---|---|---|---|---|---|---|
| S2 DSSR | 10 m | 2–5 days | 1 September 2017– 25 August 2018 | LHG | 52 scenes | Temporal extrapolation |
| H8 product | 5 km | 10 min | 13 January 2018– 29 September 2019 | UM-HRB | 531 scenes | Spatial downscaling |
| LHG | 84 scenes | |||||
| DEM | 30 m | \ | \ | UMHRB/LHG | 1 scene | Terrain factors |
| Pyranometer | \ | 10 min | 13 January 2018– 29 September 2019 | UM-HRB | \ | Precision verification |
| \ | 30 min | 1 September 2017–25 August 2018 | LHG | \ |
| Region | Station | Lon (°) | Lat (°) | 50 m DEM | Number of Measurement Points | ||
|---|---|---|---|---|---|---|---|
| Alt (m) | Slope (°) | Aspect (°) | |||||
| UM-HRB | Zhangye (ZY) | 100.45 | 38.98 | 1460 | 5.40 | 64.29 | 531 |
| Huazhaizi (HZZ) | 100.32 | 38.77 | 1731 | 2.68 | 90.00 | ||
| Arou (AR) | 100.46 | 38.05 | 3033 | 1.59 | 18.44 | ||
| Heihe remote sensing (HRS) | 100.48 | 38.83 | 1560 | 2.15 | 51.34 | ||
| Dayekou (DYK) | 100.29 | 38.56 | 2703 | 7.40 | 284.35 | 409 | |
| Daman (DM) | 100.37 | 38.86 | 1556 | 1.66 | 135.00 | 469 | |
| LHG | AWS2 (4550 m) | 96.54 | 39.48 | 4549 | 7.78 | 30.96 | 42 |
| AWS1 (5040 m) | 96.56 | 39.43 | 5028 | 6.35 | 0.00 | 37 | |
| Datasets | MBE (W/m2) | MBE % | RMSE (W/m2) | RMSE% | R2 | Number of Measurement Points |
|---|---|---|---|---|---|---|
| H8 DSSRh | 40.95 | 7.93 | 69.00 | 13.37 | 0.96 | 3002 |
| H8 DSSRc | 45.85 | 8.88 | 71.29 | 13.81 | 0.97 |
| Data | MBE (W/m2) | MBE% | RMSE (W/m2) | RMSE% | R2 |
|---|---|---|---|---|---|
| H8 DSSRh (50 m) | −2.39 | −0.39 | 76.69 | 12.60 | 0.96 |
| Sinusoidal model (10 m) | 16.66 | 5.09 | 94.77 | 15.41 | 0.97 |
| Sinusoidal model (50 m) | 10.70 | 1.76 | 95.97 | 15.77 | 0.97 |
| Station | MBE (W/m2) | MBE% | RMSE (W/m2) | RMSE% | R2 | Number of Measurement Points |
|---|---|---|---|---|---|---|
| ZY | 38.25 | 7.48 | 55.42 | 10.83 | 0.98 | 531 |
| HZZ | 43.36 | 8.43 | 64.81 | 12.60 | 0.97 | |
| AR | 35.17 | 6.47 | 60.16 | 11.07 | 0.98 | |
| HRS | 29.73 | 5.73 | 60.16 | 11.59 | 0.99 | |
| DYK | 30.19 | 5.85 | 102.91 | 19.93 | 0.89 | 409 |
| DM | 69.93 | 14.29 | 82.53 | 16.86 | 0.98 | 469 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Chen, L. Estimation of Daily Average Shortwave Solar Radiation under Clear-Sky Conditions by the Spatial Downscaling and Temporal Extrapolation of Satellite Products in Mountainous Areas. Remote Sens. 2022, 14, 2710. https://doi.org/10.3390/rs14112710
Zhang Y, Chen L. Estimation of Daily Average Shortwave Solar Radiation under Clear-Sky Conditions by the Spatial Downscaling and Temporal Extrapolation of Satellite Products in Mountainous Areas. Remote Sensing. 2022; 14(11):2710. https://doi.org/10.3390/rs14112710
Chicago/Turabian StyleZhang, Yanli, and Linhong Chen. 2022. "Estimation of Daily Average Shortwave Solar Radiation under Clear-Sky Conditions by the Spatial Downscaling and Temporal Extrapolation of Satellite Products in Mountainous Areas" Remote Sensing 14, no. 11: 2710. https://doi.org/10.3390/rs14112710
APA StyleZhang, Y., & Chen, L. (2022). Estimation of Daily Average Shortwave Solar Radiation under Clear-Sky Conditions by the Spatial Downscaling and Temporal Extrapolation of Satellite Products in Mountainous Areas. Remote Sensing, 14(11), 2710. https://doi.org/10.3390/rs14112710






