MIMO FMCW Radar with Doppler-Insensitive Polyphase Codes

Abstract

Co-located MIMO is used to enlarge the antenna aperture virtually and increase the angular resolution. This paper shows FMCW radar using MIMO VAA. Polyphase codes are designed for modulating the successive chirps of transmitting signals. The codes are optimized to have low cross-correlations regardless of the Doppler filter mismatch. Compared with orthogonal codes, the designed codes show robust performance for Doppler mismatch and lower angle estimation errors. The entire procedure is explained, and the simulation results are provided.

1. Introduction

Frequency-modulated continuous waveform (FMCW), also known as linear frequency modulation (LFM), is commonly utilized in the automotive industry. Targets are detected by the frequency difference between the transmitted and received signals, and the range resolution is inversely proportional to the bandwidth. Conventional methods use two or more slopes to resolve the range and velocity but are unsuitable for multiple targets because they inherently produce ghost targets. Thus, multiple fast chirps are now widely used for detecting multiple targets, where the distance is determined by the frequency difference and the velocity (Doppler frequency) is estimated by the phase differences of multiple consecutive chirps [1]. On the other hand, high-resolution angle estimation capability is one of the important requirements of automotive radars for collision avoidance or adaptive cruise control. Because the resolution capability is primarily dependent on the physical size of the array (i.e., the antenna aperture), it is very difficult for a small-sized automotive radar to achieve high angular resolution. Several studies on high-resolution angle estimation based on beamforming techniques have been conducted, including subspace-based algorithms [2,3,4] like Multiple Signal Classification (MUSIC) and parameter estimation algorithms using the maximum likelihood (ML) function [5,6]. However, the recent virtual array antenna (VAA) by the Multiple-Input and Multiple-Output (MIMO) method provides a more efficient way to achieve high-resolution capability with a large virtual antenna, which can be combined with conventional methods.

MIMO radar has attracted the attention of many researchers in recent years [7,8,9,10,11,12,13], as it effectively improves radar performance by transmitting multiple signals concurrently. The MIMO method can be used to increase the antenna aperture in collocated antennas, which improves the angular resolution [14], or it can be used in a multi-static manner that is transmitted and received from different sites [15]. Automobile applications typically use the co-located MIMO method to emulate a much larger aperture than its physical aperture, which is called VAA. In any case, the essential issue of MIMO is to design the orthogonal transmit waveforms in at least one domain: the frequency, time, or code domain. Time division multiplexing (TDM) is the easiest method to achieve orthogonality because only one waveform is transmitted each time. However, radar signal processing requires multiple pulses or chirps, and TDM with many transmitters reduces the effective repetition frequency. Therefore, TDM is inadequate for operations with a high repetition frequency. Frequency division multiplexing (FDM) basically means that each transmitter divides the operating frequency domain without overlap. Particular FDM with orthogonality in the beat frequency domain that is compatible with FMCW radar has been introduced [16,17,18]. This approach used the spectrum more efficiently than the classical frequency division method. Finally, code division multiplexing (CDM) uses orthogonal code modulation instead of frequency modulation. CDM in FMCW radar used binary phase shift keying (BPSK) or random code to ensure each transmitter sends a different coded waveform, provided the code bandwidth is small to ensure proper FMCW radar operation [19,20]. In this paper, we use the CDM method for an FMCW radar using multiple fast chirps by modulating the orthogonal polyphase codes to successive chirps.

This paper proposes a design method of polyphase codes for multi-chirp FMCW radar to improve the angular resolution by MIMO VAA [21]. VAA beamforming and angle estimation are performed after the range Doppler processing. If the codes modulated to the successive chirps are orthogonal, the output of the corresponding Doppler bin only contains a matched code signal. However, if the code is not perfectly orthogonal, the cross-correlation remains as additive interference and reduces the signal-to-interference-and-noise ratio (SINR). Additionally, if the center of the Doppler filter does not precisely coincide with the target velocity, the same is true. The remaining cross-correlations reduce the SINR and degrade the angle estimation accuracy. Therefore, we designed the polyphase codes maintaining low cross-correlation regardless of the Doppler filter mismatch using the simulated annealing (SA) algorithm of the statistical optimization method [22,23,24,25]. Section 2 explains the basic principles of MIMO FMCW, the SA algorithm for code design, and VAA beamforming. Section 3 evaluates the performance by simulation, and Section 4 summarizes and concludes the paper.

2. Basic Principles

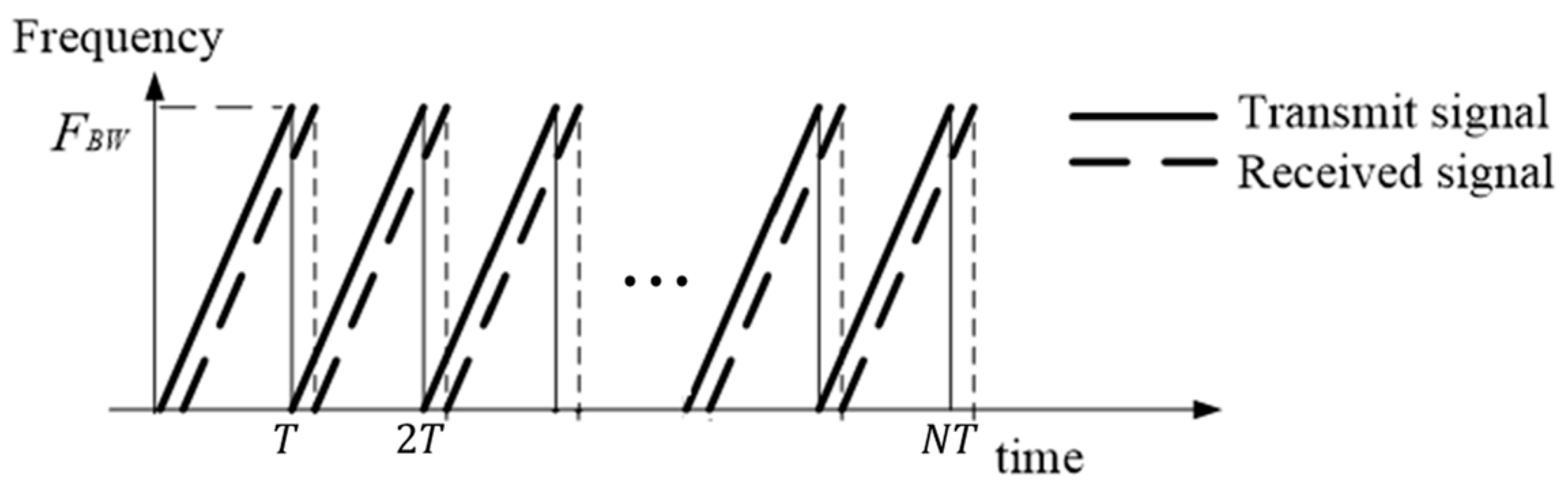
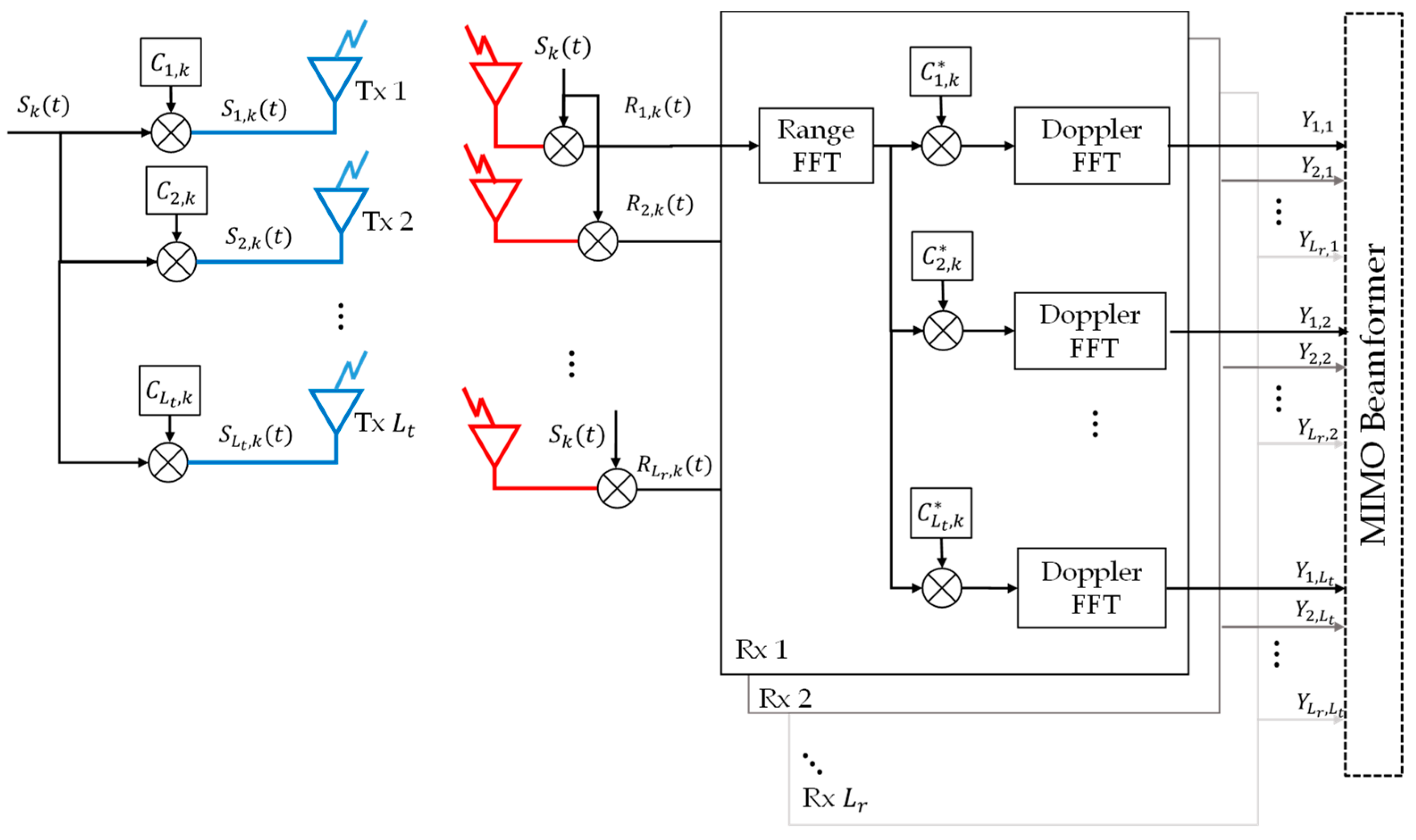
2.1. MIMO FMCW

The source signal for all transmitters is the multi-chirp FMCW waveform where the chirp is repeated N times, as shown in Figure 1.

Figure 1. Multi-chirp FMCW waveform.

Then, the kth chirp is expressed as

$$S_k\left(t\right)=S\left(t-kT\right)=\exp j\left[2\pi f_{c}t+\left(\frac{\pi F_{BW}}{T}\right){\left(t-\frac{T}{2}-kT\right)}^2\right], kT\le t<\left(k+1\right)T$$

(1)

where $k=0,1,2,\dots \left(N-1\right)$, $f_c$ is the center frequency, $F_{BW}$ is the bandwidth, $T$is the repetition period, and N is the number of chirps. Each transmitter modulates N chirps by its own code [26]. We designed the MIMO system with different transmitting phase codes as shown in Figure 2. The mth transmitter’s code $C_m$ and signal $S_{m,k}\left(t\right)$can be expressed as

$$C_m={\left[C_{m,0} C_{m,1} \dots C_{m,\left(N-1\right)}\right]}^T, m=1,\dots L_t$$

(2)

$$S_{m,k}\left(t\right)=C_{m,k}{S}_k\left(t\right)=C_{m,k}S\left(t-kT\right)$$

(3)

where $L_t$ is the number of transmitters. If there is one target, the received signal after dechirping via mixing the transmit and receive signals is represented by the sum of the reflective signals as follows:

$$R_{i,k}\left(t\right)={\displaystyle \sum }_{m=1}^{L_t}{\overline{A}}_{m,i}{S}_{m,k}^{*}\left(t-\tau \right)S_k\left(t\right)+noise, \tau =\frac{2\left(R-vt\right)}{c}, i=1,\dots ,L_r$$

(4)

where * means the complex conjugate, R is the distance to the target, c is the light speed, $L_r$ is the number of receivers, and ${\overline{A}}_{m,i}$ is the complex reflective coefficient from the mth transmitter to the ith receiver, assuming that it does not fluctuate during the coherent integration time of NT. Though we assumed additive noise, we do not describe it in detail because it has little influence on this study.

Figure 2. Overall description of the MIMO FMCW radar.

After discarding the small, high-order terms and combining the constant phase terms into $A_{m,i},$ the received signal in multi-chirp FMCW is rewritten with the following equation. The detailed derivation is in Appendix A:

$$R_{i,k}\left(t\right)\cong {\displaystyle \sum }_{m=1}^{L_t}{A}_{m,i}{C}_{m,k}^{*}\exp 2\pi j\left[f_b\left(t-kT\right)+f_{d}t\right]+noise$$

(5)

where $f_b$ is the beat frequency by the target distance and $f_d$ is the Doppler frequency:

$$f_b=\left(\frac{F_{BW}}{T}\right)\frac{2R}{c} \mathrm{and} f_d=-f_c\frac{2v}{c}.$$

(6)

$f_b+f_d$ is estimated via the first range FFT processing of fast-sampling data in one chirp, and $f_d$ is measured via the second Doppler FFT of inter-chirp data with a sampling rate of T. The waveform is usually designed for $f_b$ and $f_d$ to differ by two or more orders of magnitude.

A single transmit signal is extracted by multiplying its code to the consecutive chirps of the received signal before Doppler processing:

$$\begin{array}{cc}\hfill C_{j,k}^{*}{R}_{i,k}\left(t\right)& ={\displaystyle {\displaystyle \sum }_{m=1}^{L_t}}{A}_{m,i}{C}_{j,k}^{*}{C}_{m,k}\exp 2\pi j\left[f_b\left(t-kT\right)+f_{d}t\right]+noise\hfill \\ & =\exp 2\pi j\left[f_b\left(t-kT\right)+f_{d}t\right]\left\{A_{j,i}N+{\displaystyle {\displaystyle \sum }_{\begin{array}{c}m=1\\ \left(m\ne j\right)\end{array}}^{L_t}}{A}_{m,i}{C}_{j,k}^{*}{C}_{m,k}\exp 2\pi j\left(f_{d}t\right)\right\}+noise\hfill \end{array}$$

(7)

The second term in Equation (7) is removed after Doppler processing if $C_m$and $C_j$are orthogonal and the center of the filter is exactly matched with $f_d$. Otherwise, this term will not be zero and will remain as interference.

Figure 2 describes the whole structure of the proposed MIMO FMCW radar. Each transmitting signal $S_{m,k}\left(t\right)$, expressed in Equation (3), is modulated by the different phase code, and the received signals are downconverted by dechirping, which is represented by $R_{i,k}\left(t\right)$ in Equation (5). Because the range FFT is a linear transformation performed within one chirp with the same code, it is executed before decoding to reduce the computational power. Then, the code decoding for successive chirps and Doppler processing are followed. VAA beamforming is performed last.

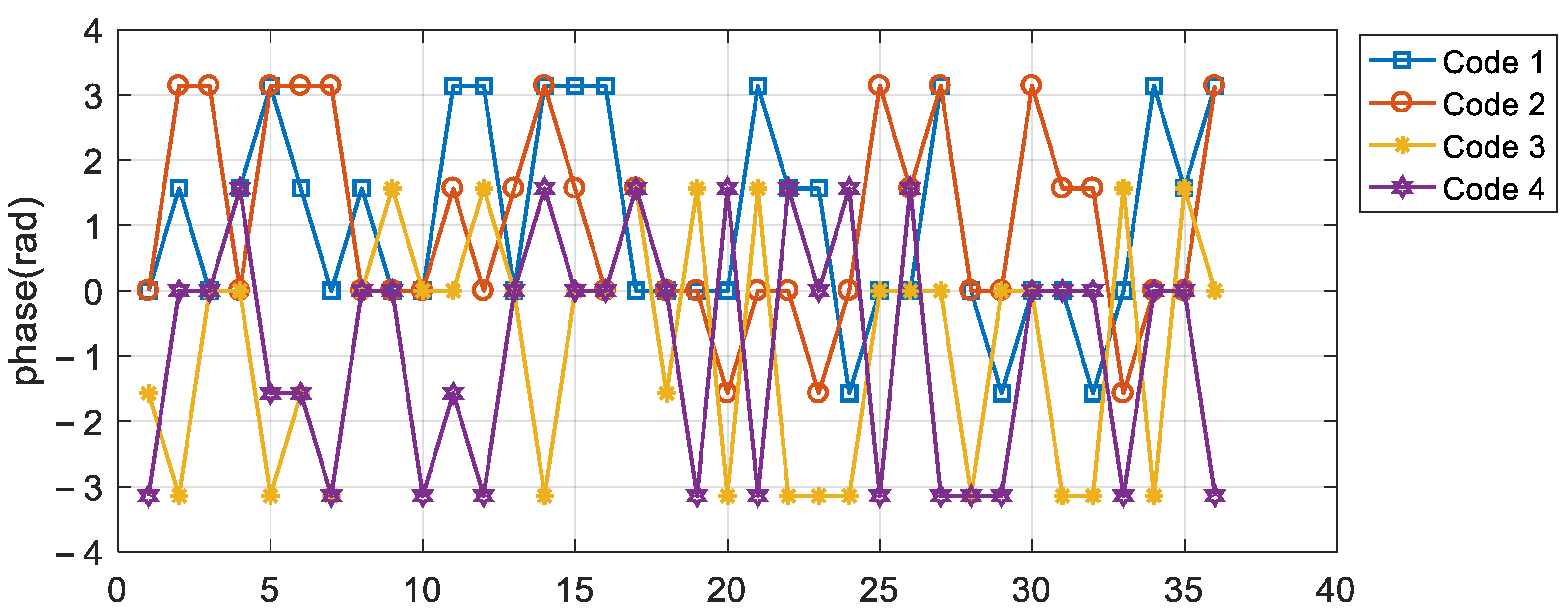
2.2. Design of the Doppler-Insensitive Polyphase Code

The polyphase code in Equation (2) with the unit amplitude is represented by

$$C_{m,k}=\exp \left(j {\phi }_m\left(k\right)\right),\hspace{1em}\hspace{1em}{\phi }_m\left(k\right)\in \left\{0,\hspace{0.17em}\frac{2\pi }{M},\hspace{0.17em}2\cdot \frac{2\pi }{M},\hspace{0.17em}\dots \hspace{0.17em},\hspace{0.17em}\left(M-1\right)\cdot \frac{2\pi }{M}\right\}$$

(8)

where $M$ is the number of distinct phases in $\left[0 2\pi \right)$ [22]. If $M=2$, then the code becomes a biphase code with 1 and −1. The auto-correlation (AC) and the cross-correlation (CC) are defined by

$$\mathrm{AC}={\displaystyle \sum }_{k=1}^N{C}_{m,k}^{*}{C}_{m,k}=N,{\hspace{1em}\hspace{1em}\mathrm{CC}}_{jm}={\displaystyle \sum }_{k=1}^N{C}_{j,k}^{*}{C}_{m,k}\left(j\ne m\right)$$

(9)

and CC is zero if the codes are orthogonal with each other.

As shown in the second term of Equation (7), if the received signal from the moving targets has Doppler shift, and the center of the Doppler filter does not exactly coincide with it, the outputs of the correlators are changed by the mismatch $\mathsf{\Delta }f$ as follows:

$$\mathrm{AC}\left(\mathsf{\Delta }f\right)={\displaystyle \sum }_{k=1}^N\exp \left[j\frac{2\pi k}{N}\mathsf{\Delta }f\right],{ \mathrm{CC}}_{jm}\left(\mathsf{\Delta }f\right)={\displaystyle \sum }_{k=1}^N{C}_{j,k}^{*}{C}_{m,k}\exp \left[j\frac{2\pi k}{N}\mathsf{\Delta }f\right]$$

(10)

where $\mathsf{\Delta }f$ is a dimensionless number which is the frequency mismatch between the target Doppler and the center of the Doppler filter divided by the Doppler resolution. The average signal-to-interference ratio (SIR) at the ith receiver from Equation (7) can be defined by

$$\mathrm{SIR}\left(\mathsf{\Delta }f\right)=\frac{{\left|A_{j,i} \mathrm{AC}\left(\mathsf{\Delta }f\right)\right|}^2}{\left[\frac{1}{L_t}{{\displaystyle \sum }}_{j=1}^{L_t}{\left|{{\displaystyle \sum }}_{\begin{array}{c}m=1\\ \left(m\ne j\right)\end{array}}^{L_t}{A}_{m,i}{ \mathrm{CC}}_{jm}\left(\mathsf{\Delta }f\right)\right|}^2\right]}=\frac{\mathrm{power} \mathrm{of} \mathrm{signal}}{\mathrm{average} \mathrm{power} \mathrm{of} \mathrm{interference}}.$$

(11)

$A_{j,i}$ is the complex reflective coefficient from the jth transmitter to the ith receiver. Because the transmitters and the receivers are collocated at the same site, $A_{j,i}$ and $A_{m,i} \left(m\ne j\right)$ are assumed to be the same in amplitude and only be different in phase. The phase difference is explained in Section 2.3. Given that

$$\left|{\displaystyle \sum }_{\begin{array}{c}m=1\\ \left(m\ne j\right)\end{array}}^{L_t}{A}_{m,i}{ \mathrm{CC}}_{jm}\left(\mathsf{\Delta }f\right)\right|\le {\displaystyle \sum }_{\begin{array}{c}m=1\\ \left(m\ne j\right)\end{array}}^{L_t}\left|A_{m,i}{ \mathrm{CC}}_{jm}\left(\mathsf{\Delta }f\right)\right|=\left|A_{j.i} \right|{\displaystyle \sum }_{\begin{array}{c}m=1\\ \left(m\ne j\right)\end{array}}^{L_t}\left|{\mathrm{CC}}_{jm}\left(\mathsf{\Delta }f\right)\right|,$$

(12)

Then, the low bound of SIR can be written as follows.

$$\mathrm{SIR}\left(\mathsf{\Delta }f\right)\ge {\mathrm{SIR}}_{min}\left(\mathsf{\Delta }f\right)=\frac{{\left[\mathrm{AC}\left(\mathsf{\Delta }f\right)\right]}^2}{\left[\frac{1}{L_t}{{\displaystyle \sum }}_{j=1}^{L_t}{\left[{{\displaystyle \sum }}_{\begin{array}{c}m=1\\ \left(m\ne j\right)\end{array}}^{L_t}\left|{\mathrm{CC}}_{jm}\left(\mathsf{\Delta }f\right)\right|\right]}^2\right]}=\frac{{\left[\mathrm{AC}\left(\mathsf{\Delta }f\right)\right]}^2}{I_{max}\left(\mathsf{\Delta }f\right)}$$

(13)

Typically, the goal of orthogonal code design is to make $\mathrm{CC}$ zero at $\mathsf{\Delta }f=0$. One of the conventional methods to design orthogonal codes is using the Hadamard matrix [27]. Figure 3 shows quadratic phase orthogonal codes with 36 lengths designed by the Hadamard matrix. Four codes among the length of 36 are displayed. Figure 4a shows that the denominator $I_{max}\left(\mathsf{\Delta }f\right)$in Equation (13) is zero at $\mathsf{\Delta }f=0$ but grows with $\mathsf{\Delta }f$. As a result, ${\mathrm{SIR}}_{min}\left(\mathsf{\Delta }f\right)$ drops abruptly, as shown in Figure 4b.

Figure 3. Example of orthogonal quadratic phase codes of length of 36.

Figure 4. Performance degradation of orthogonal code by filter mismatch. (a) AC and CC according to doppler mismatch (b) Minimum SIR.

Therefore, in this paper, we design the polyphase codes of which the cross-correlation is low and insensitive to Doppler mismatch $\mathsf{\Delta }f$. The computational cost for searching the best polyphase code set with a set size of $L_t$, a code length of N, and the distinct phase number of M through exhaustive search is to the order of $M^{\left(L_t\times N\right)}$, which grows exponentially with $N$ and $L_t$. Thus, we used the statistical optimization algorithm proposed in [22] which combines the simulated annealing (SA) algorithm with a traditional iterative code selection algorithm. The SA algorithm exploits an analogy between the search for a minimum of a cost function and the physical process by which a material changes state while minimizing its energy [23]. The major advantage of the SA algorithm is the ability to avoid trapping in local optima during the search process because it accepts some changes that also increase the cost function with a probability of

$$P=\exp \left(-\frac{\mathsf{\Delta }E}{T_c}\right)$$

(14)

The control parameter is known as the system “temperature”, which slowly decreases from a large value to a very small one during the annealing process. The SA algorithm can find the global optimum of a nonlinear multivariable function by carefully controlling the change rate of the system temperature.

We define the objective function $E\left(C\right)$ to be minimized as the peak of the cross-correlation for $\mathsf{\Delta }f\in \left[0,1\right)$:

$$E\left(C\right)=\underset{\mathsf{\Delta }f\in \left[0, 1\right)}{\max }\left[\underset{j,m\left(j\ne m\right)}{\max }\left|C{C}_{jm}\left(\mathsf{\Delta }f\right)\right| \right]=\underset{\mathsf{\Delta }f\in \left[0, 1\right)}{\max }\left[\underset{j,m\left(j\ne m\right)}{\max }\left|{\displaystyle \sum }_{k=1}^N{C}_{j,k}^{*}{C}_{m,k}\exp \left[j\frac{2\pi k}{N}\mathsf{\Delta }f\right] \right|\right]$$

(15)

Therefore, the problem is to find C for minimizing the function $E\left(C\right)$. The resulting codes may not be perfectly orthogonal but have very low cross-correlation and are tolerable to Doppler mismatching. The SA algorithm used in this paper is summarized in Table 1.

Table 1. Process of polyphase codes design using SA algorithm.

Step	Description
0.	◆ $\mathrm{For} \mathrm{given} L_t,N, \mathrm{and} M,$ generate initial C at random
1.	◆ $\mathrm{Set} \mathrm{the} \mathrm{initial} \mathrm{temperature} T_0$$\mathrm{and} \mathrm{initialize} \mathrm{temperature} \mathrm{index} c=0$
2.	◆ $\mathrm{Evaluate} \mathrm{the} \mathrm{objective} \mathrm{function} E_0$$\mathrm{at} T_c$ with current C ◆ $\mathrm{Initialize} \mathrm{the} \mathrm{index} i=0$
3.	◆ $\mathrm{Choose} \mathrm{one} \mathrm{of} L_t\times N$phases in matrix C at random ◆ $\mathrm{Perturb} \mathrm{the} \mathrm{selected} \mathrm{phase} \mathrm{to} \mathrm{another} \mathrm{value} \mathrm{in} M-1$ at random ◆ $\mathrm{Increase} \mathrm{the} \mathrm{index} i (i=i+1)$
4.	◆ $\mathrm{Evaluate} \mathrm{the} \mathrm{objective} \mathrm{function} E_i$ with perturbed phase matrix ◆ $\mathrm{Calculate} \mathrm{the} \mathrm{increment} \mathrm{of} \mathrm{functions} \mathrm{as} \mathsf{\Delta }E=E_i-E_{i-1}$
5.	◆ $\mathrm{Calculate} \mathrm{the} \mathrm{transition} \mathrm{probability} \mathrm{by} \mathsf{\Delta }E$ as follows:                $P=\{\begin{array}{c}\exp \left(-\frac{\mathsf{\Delta }E}{T_c}\right), if \Delta E>0\\ 1 , otherwise\end{array}$ ◆ Update the matrix C according to the probability
6.	◆ $\mathrm{Repeat} \mathrm{steps} 3–5 \mathrm{during} i<I_{max}$1
7.	◆ $\mathrm{If} E_i$$\mathrm{changes} \mathrm{from} E_0,$go to step 8; otherwise go to step 9
8.	◆ $\mathrm{Increase} c$ and reduce temperature 1        $c=c+1,T_c=\alpha T_{c-1} (0<\alpha <1)$ ◆ Go to step 2
9.	◆ $\mathrm{If} c>c_{max}$ or stop condition is satisfied, then quit; otherwise, go to step 8 2

¹ Maximum number of iterations $I_{max}$ in step 6 and $\alpha$ in step 8 determine the convergence speed. We use $I_{max}=10\times \left(N_{T}ML\right), \alpha =0.95$ in this work. ² Stop condition in step 9 is that there are no changes in the objective function for more than three successive temperature cycles in this work.

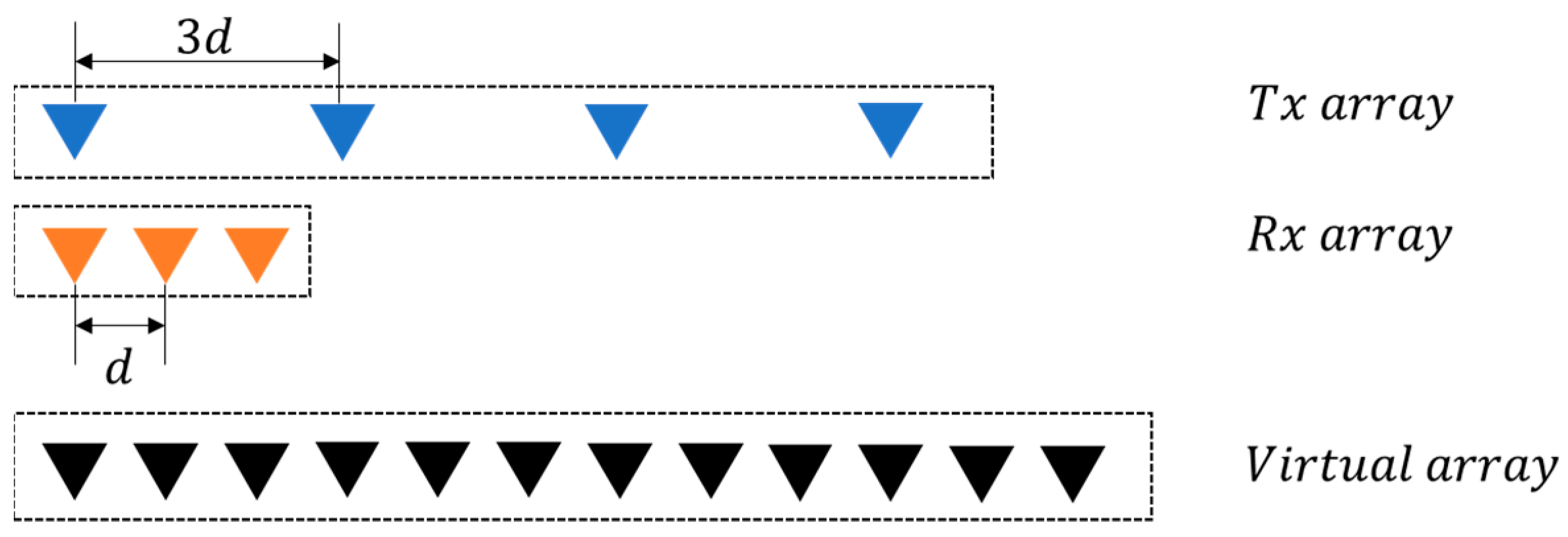
2.3. MIMO VAA

The beampattern of the VAA is made by multiplication of the transmit pattern and receive pattern. Thus, the virtual aperture is dependent on the configuration of the transmit arrays and receive arrays. To maximize the VAA in a uniform linear array (ULA), one ULA, either transmitter or receiver, is built with $L_r$ arrays with an interval d, and its physical aperture $d\times L_r$ becomes the interval of the other ULA with $L_t$ arrays. The final aperture size is then $d\times L_r\times L_t$. The spacing $d$is set by the field of view (FOV) and should be less than or equal to half of the wavelength in order to have the whole FOV of $\pm 90$ deg. Figure 5 shows the virtual array antenna with $L_r=3$receive arrays and $L_t=4$transmit arrays.

Figure 5. MIMO virtual array example where $L_r=4$ and $L_r=3$.

The phase difference vectors for the transmit, receiving, and virtual arrays are

$$v_{tx}=\left[1 e^{j\left(L_{r}kd\sin \theta \right)} e^{j\left(2L_{r}kd\sin \theta \right)}\cdots e^{j\left(\left(L_t-1\right)L_{r}kd\sin \theta \right)}\right],$$

(16)

$$v_{rx}=\left[1\hspace{1em}{e}^{j\left(kd\sin \theta \right)}\cdots \hspace{1em}{e}^{j\left(\left(L_r-1\right)kd\sin \theta \right)} \right],$$

(17)

and

$$v=v_{tx}\otimes v_{rx}=\left[1\hspace{1em}{e}^{jkd\sin \theta }\hspace{1em}{e}^{j\left(2kd\sin \theta \right)}\cdots e^{j\left(\left(L_t{L}_r-1\right)kd\sin \theta \right)} \right]$$

(18)

where ⨂ is the Kronecker product and $k \left(=2\pi ⁄\lambda \right)$ is the wave number. Then, v is identical to that of a ULA composed of $L_r\times L_t$ elements. Therefore, the complex coefficient $A_{m,i}$in Equation (7) is related to $A_{1,1}$ as

$$A_{m,i}=v_{\left(m-1\right)\times L_r+i} A_{1,1}=e^{j\left[\left(m-1\right)L_r+i-1\right]kd\sin \theta } A_{1,1}$$

(19)

In addition, VAA beamforming can be performed by

$$Y\left(\theta \right)=\left[\begin{array}{ccccccccc}{Y}_{1,1}& Y_{2,1}& \cdots & Y_{L_r,1}& Y_{2,1}& Y_{2,2}& \cdots & Y_{L_r-1,L_t}& Y_{L_r,L_t}\end{array}\right]v^H$$

(20)

where H is the conjugate transpose and $Y_{i,j}$ is the output of the jth code-correlated Doppler FFT in the ith receiver in Figure 2.

3. Simulation Results

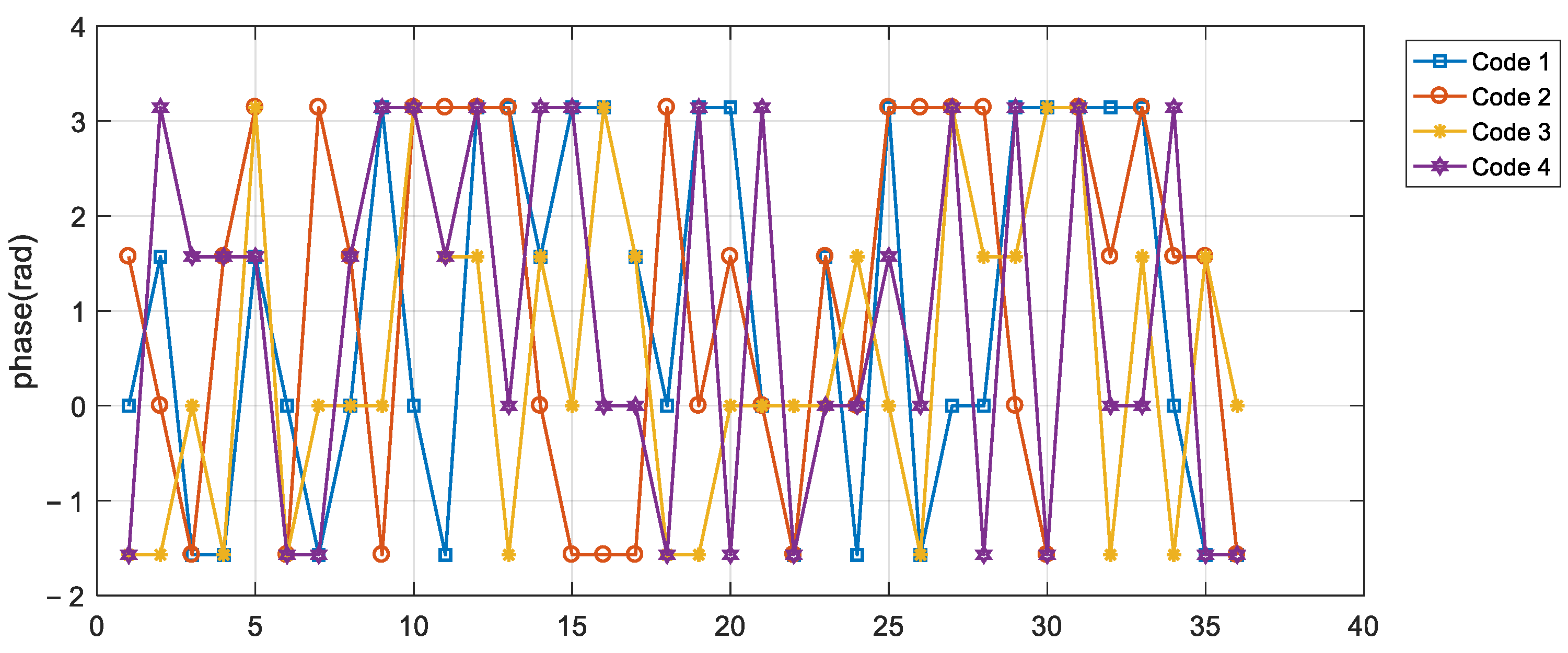
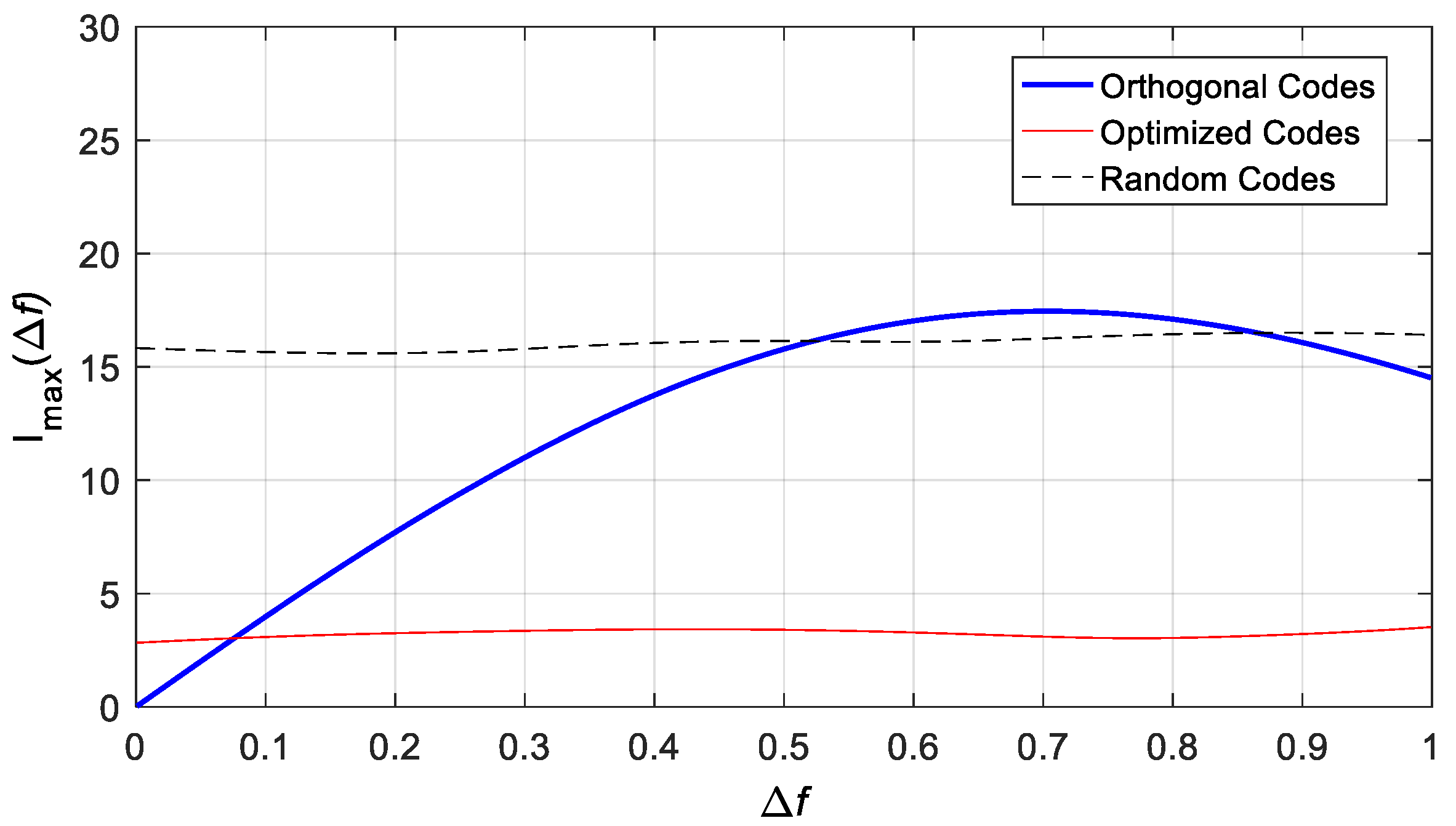
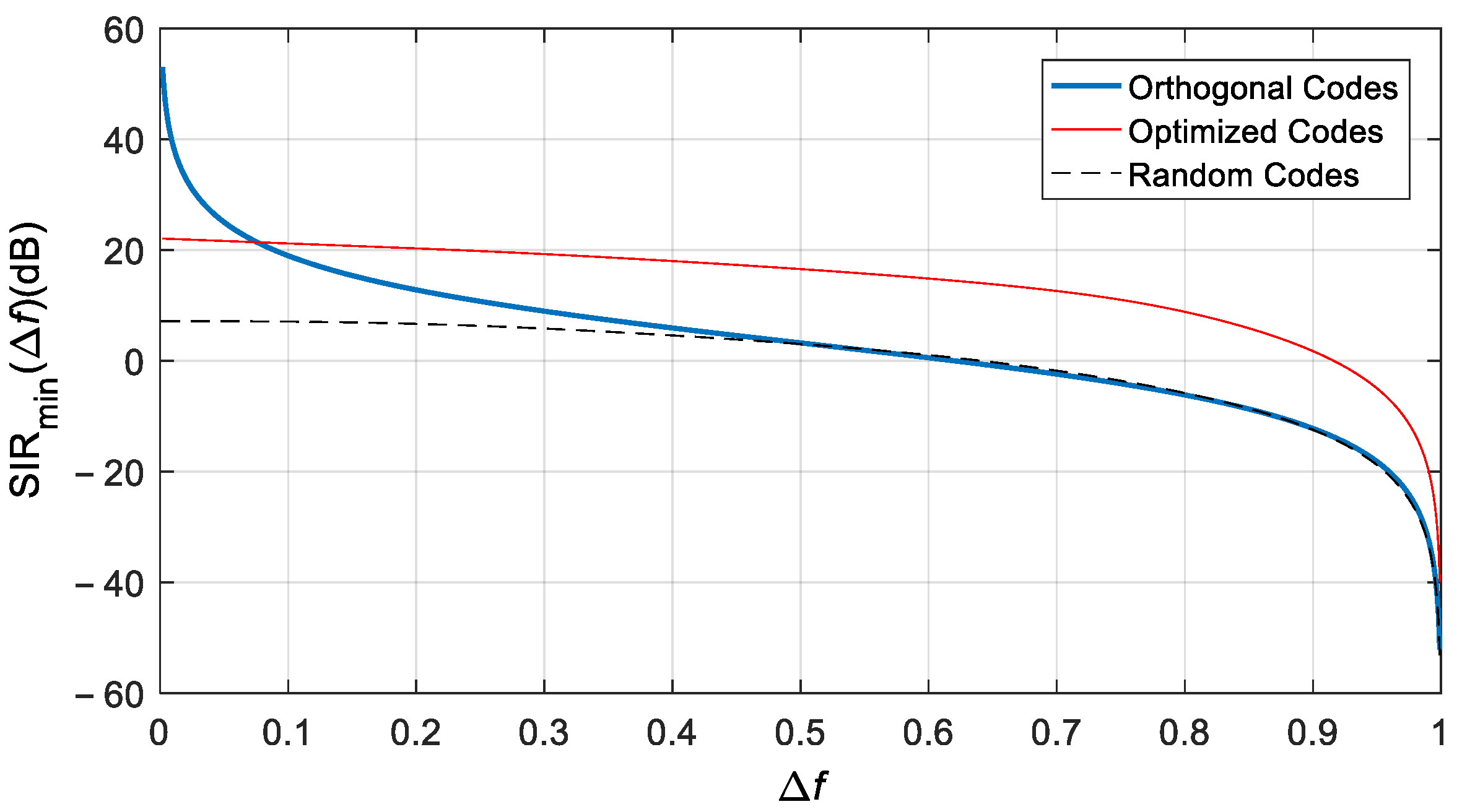
3.1. Doppler-Insensitive Code Design (36 Length, 4 Transmitters)

According to the process in Table 1, we designed four codes of a length of 36 and compared them with the orthogonal code in Figure 3. Figure 6 shows the phase of the optimized codes.

Figure 6. SA Optimized codes ($L=4, M=4, N=36$).

Figure 7 shows $I_{max}(\mathsf{\Delta }f$) defined by the denominator in Equation (13). The optimized codes have a lower value than that of the orthogonal codes if the filter mismatch $\mathsf{\Delta }f$ is greater than 0.075. It also indicates a reasonably consistent value within the entire interval. The black line represents the mean value of 1000 randomly generated codes. As a result, $SI{R}_{min}\left(\mathsf{\Delta }f\right)$ of the optimized codes was greater than that of the orthogonal codes or random codes. It was about 15 dB higher than that of the random codes, as shown in Figure 8.

Figure 7. Comparison of the interference power $I_{max}\left(\mathsf{\Delta }f\right)$.

Figure 8. Comparison of $SI{R}_{min}\left(\mathsf{\Delta }f\right)$.

3.2. Performance according to M

Figure 9 represents $SI{R}_{min}$at $\mathsf{\Delta }f=0.5$ according to the number of phases M for different code lengths of 32, 64, and 128.

Figure 9. Improvement of the performance according to the number of phases M.

The performance of the optimized codes improved as the number of phases M increased, but the rate of improvement gradually reduced. Aside from the longer time for optimization, utilizing more phases was restricted by the hardware configuration. Thus, there must be trade-offs for implementation. Figure 9 also shows that ${\mathrm{SIR}}_{min}$was improved with the code length N, similar to coherent integration.

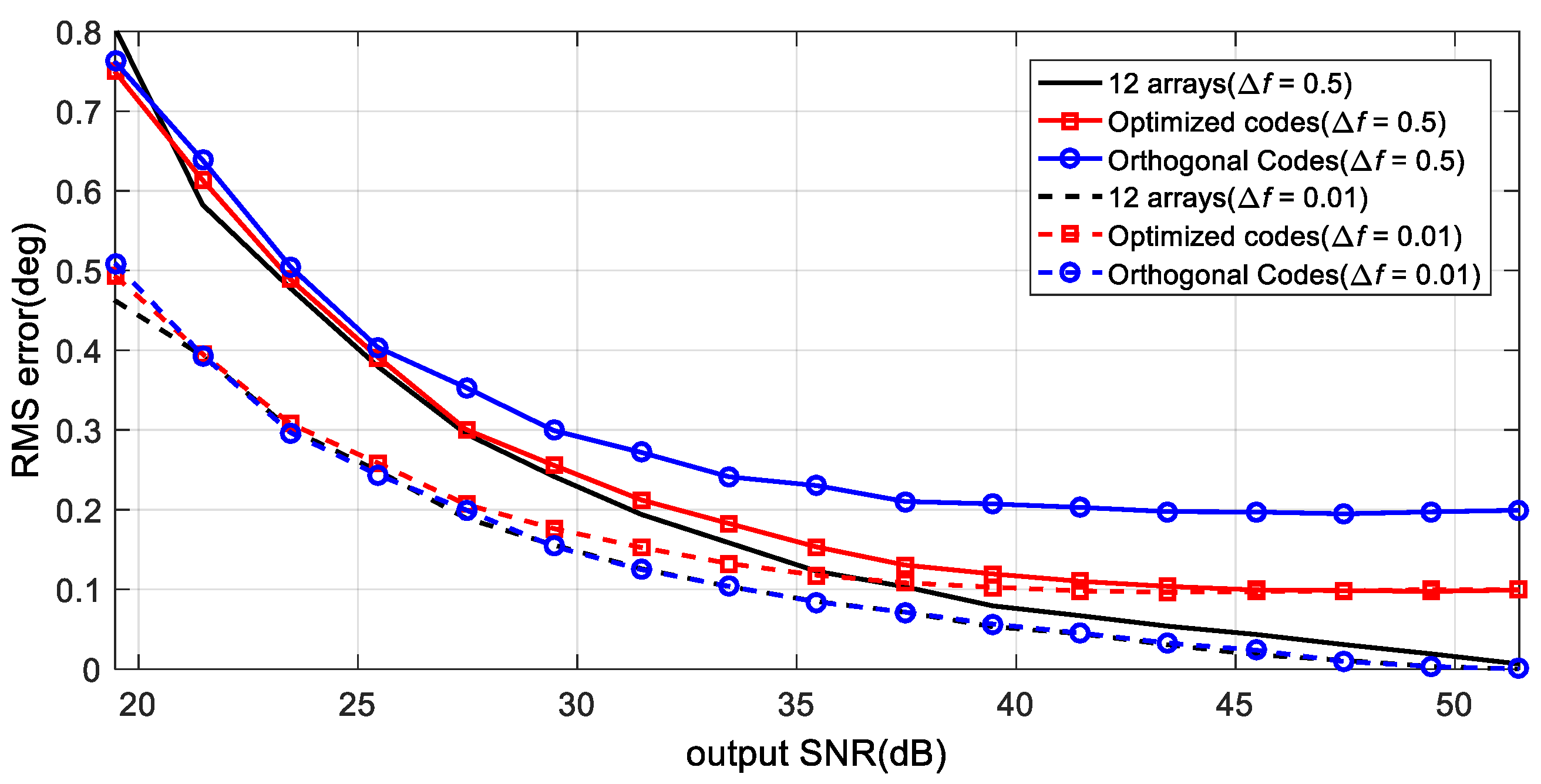
3.3. FMCW Simulation and MIMO Angle Accuracy

In this section, we show the simulation results of the MIMO FMCW radar using the optimized codes. The simulation was performed by Monte Carlo methods in 1000 runs for each SNR. The processing followed Figure 2, and the parameters are listed in Table 2.

Table 2. Simulation parameters.

Parameter	Value
$\mathrm{Operating} \mathrm{frequency} \left(f_c\right)$	77 (GHz)
$\mathrm{Bandwidth} \left(F_{BW}\right)$	1 (GHz)
$\mathrm{Chirp} \mathrm{period} \left(T\right)$	30 (usec)
$\mathrm{Number} \mathrm{of} \mathrm{transmitters} \left(L_t\right)$	4
$\mathrm{Number} \mathrm{of} \mathrm{receivers} \left(L_r\right)$	3
$\mathrm{Number} \mathrm{of} \mathrm{coherent} \mathrm{chirps}{ }^1 \left(N\right)$	64
$\mathrm{Number} \mathrm{of} \mathrm{phases} \mathrm{in} \mathrm{code} \left(M\right)$	4
$\mathrm{Sampling} \mathrm{frequency} \left(F_s\right)$	50 (MHz)
Target velocity	$5.57 (\mathrm{m}/\mathrm{s}) (\mathsf{\Delta }f=0.5)$
Initial target distance	40 (m)
Array interval	$0.5 \lambda$

¹ It is equal to the code length.

Figure 10 shows the root mean square (RMS) error of the estimated angle for a single target at a direction of 10 degrees. The angle was calculated in MIMO VAA via conventional beamforming, which was described in Section 2.3.

Figure 10. Comparison of RMS errors according to SNR.

The RMS error is normally dependent on the SNR and, in this case, the SINR. When the SNR was low, the noise power was dominant over the interference power. Thus, the RMS error of the VAA was almost the same as 12 ULAs, either using orthogonal codes or optimized codes. However, as the SNR rose, the interference became dominant. This interference could not be eliminated and remained as angle error because it consisted of the cross-correlations of multiple transmit signals and was proportional to the signal power. At $\mathsf{\Delta }f=0.5$, the remaining RMS errors in Figure 10 are 0.1 and 0.2 for the optimized and orthogonal codes, respectively. The optimized codes outperformed the orthogonal codes. Of course, the performance of the orthogonal codes was better at $\mathsf{\Delta }f=0.01$ with only a slight mismatch and approached the 12 ULA case. The optimal codes showed similar performance for $\mathsf{\Delta }f$, which is also indicated in Figure 7 and Figure 8.

The interference power is dependent on the target direction, which is included in $A_{m,i}$ in Equations (7) and (19). As a result, the remaining RMS error is dependent on the direction. Figure 11 depicts the RMS error in relation to the direction. The error of the optimized codes was smaller than that of the orthogonal codes, and the angle impact was less noticeable.

Figure 11. RMS error according to the target direction at $\mathsf{\Delta }f=0.5$ for high SNR.

4. Conclusions

In this paper, we suggest an MIMO FMCW radar system including the design method of polyphase codes for multiple transmitters, receive processing chains, and VAA antenna configuration. Polyphase codes with low cross-correlations were optimized by the SA algorithm and modulated to the successive chirps of transmitting signals. Compared with the orthogonal codes, the proposed optimum codes showed robust performance for Doppler mismatching. As a result, the performance of VAA angle estimation using the proposed codes outperformed that of the orthogonal codes.