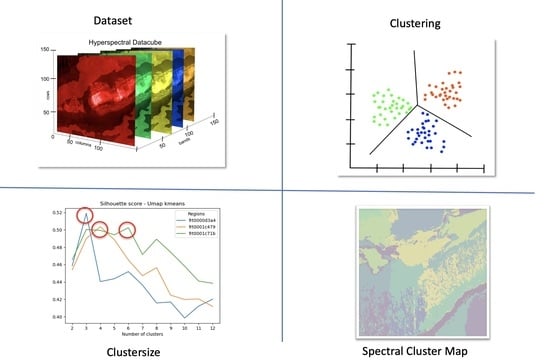
Generation and Optimization of Spectral Cluster Maps to Enable Data Fusion of CaSSIS and CRISM Datasets
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Source
2.2. Data and Location
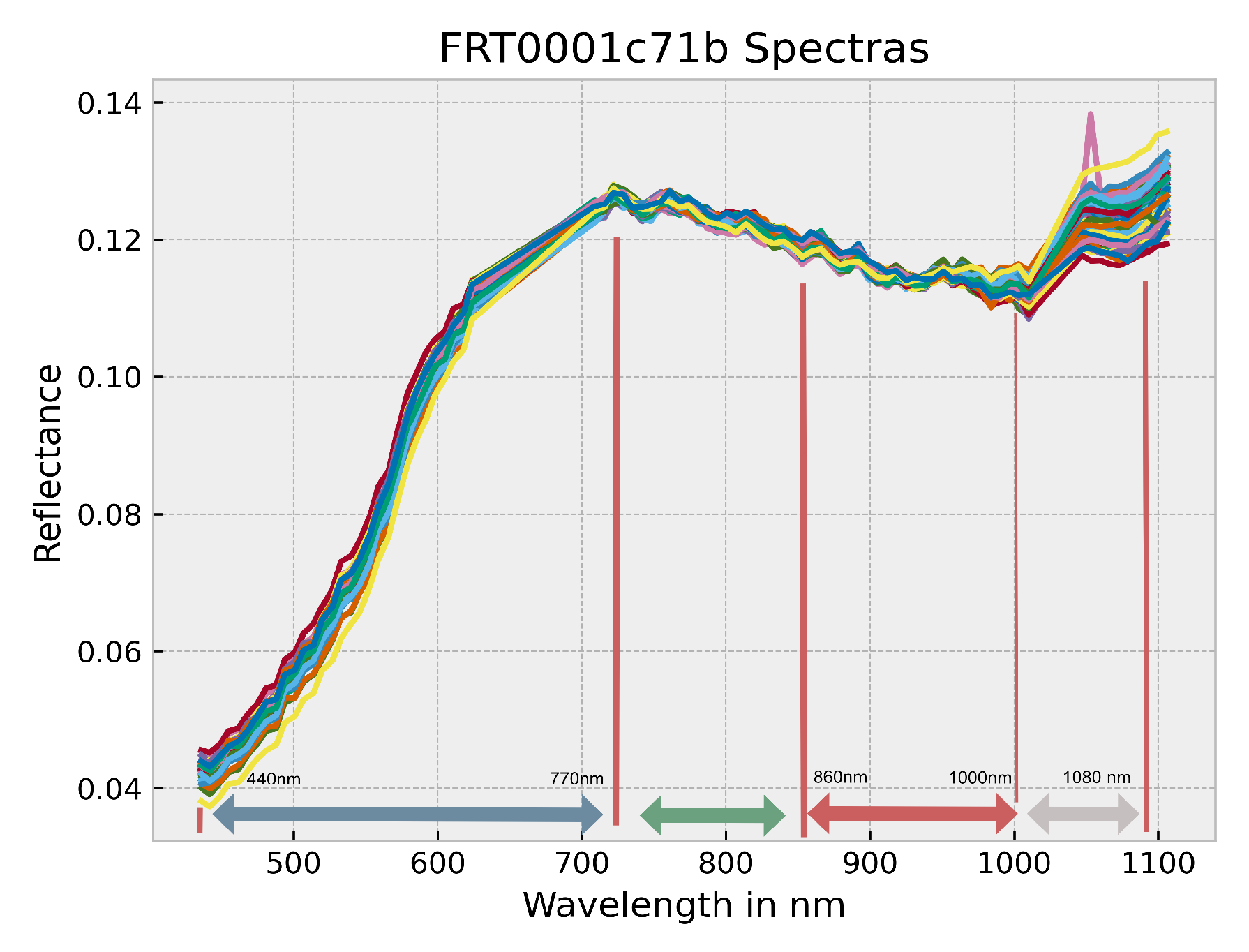
2.3. Preprocessing
2.4. Dimensionality Reduction Techniques
- Autoencoder
- t-SNE
- UMAP
2.5. Clustering Algorithms
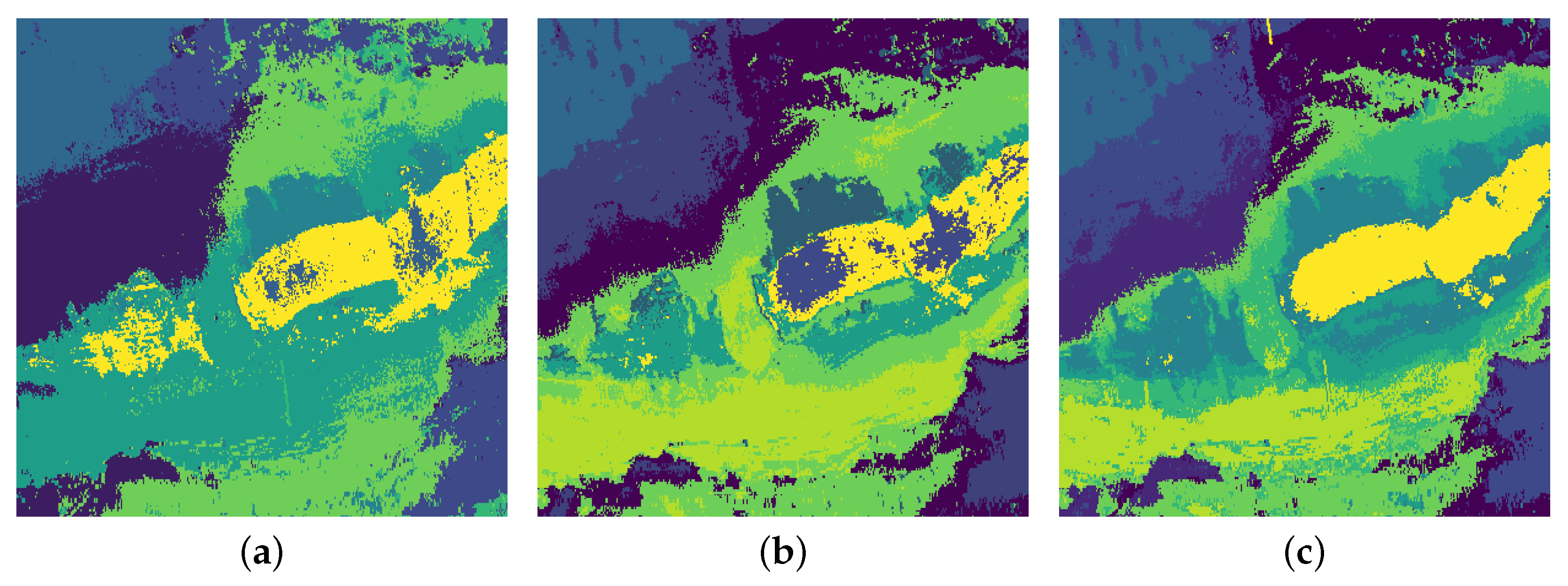
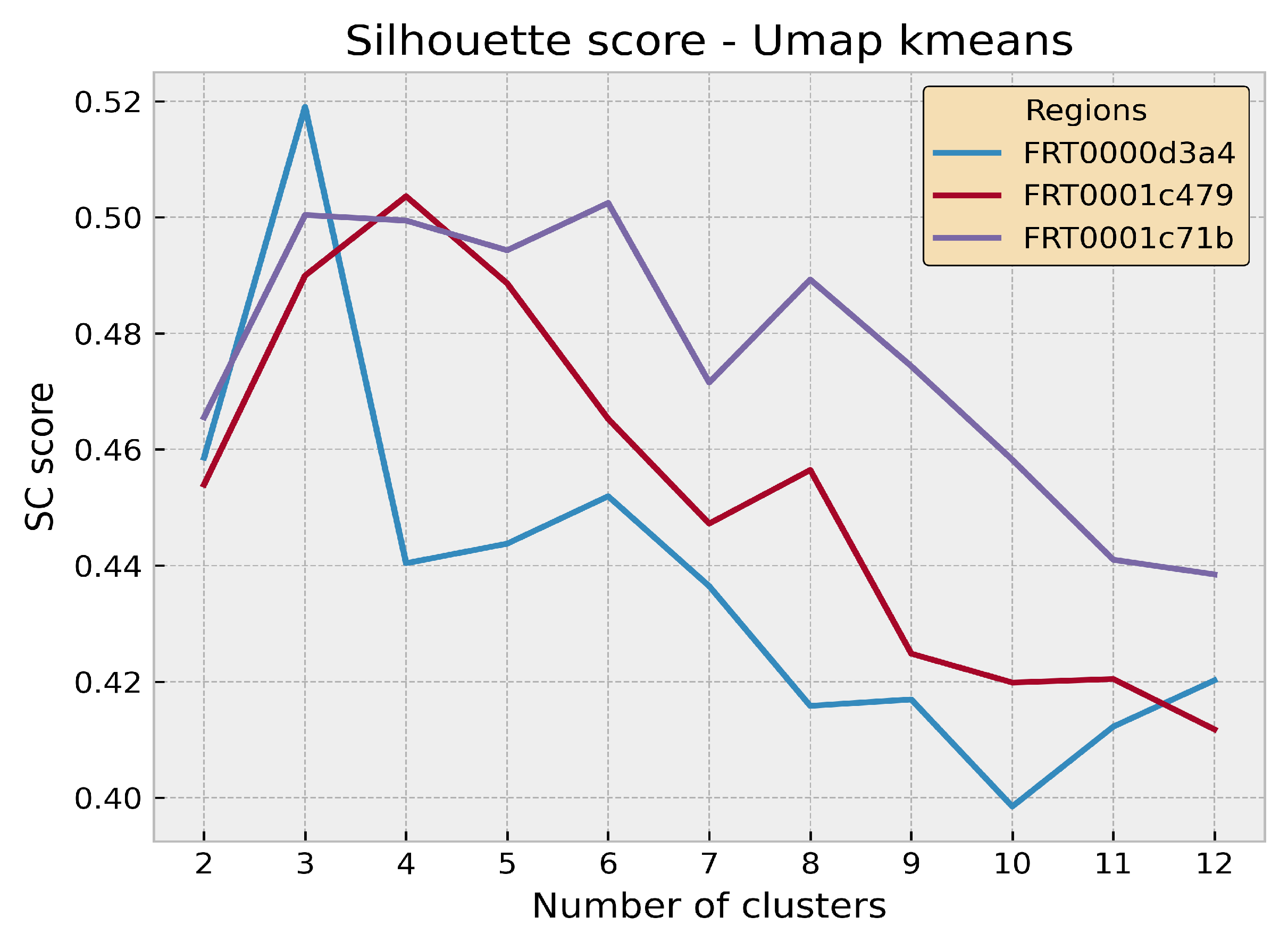
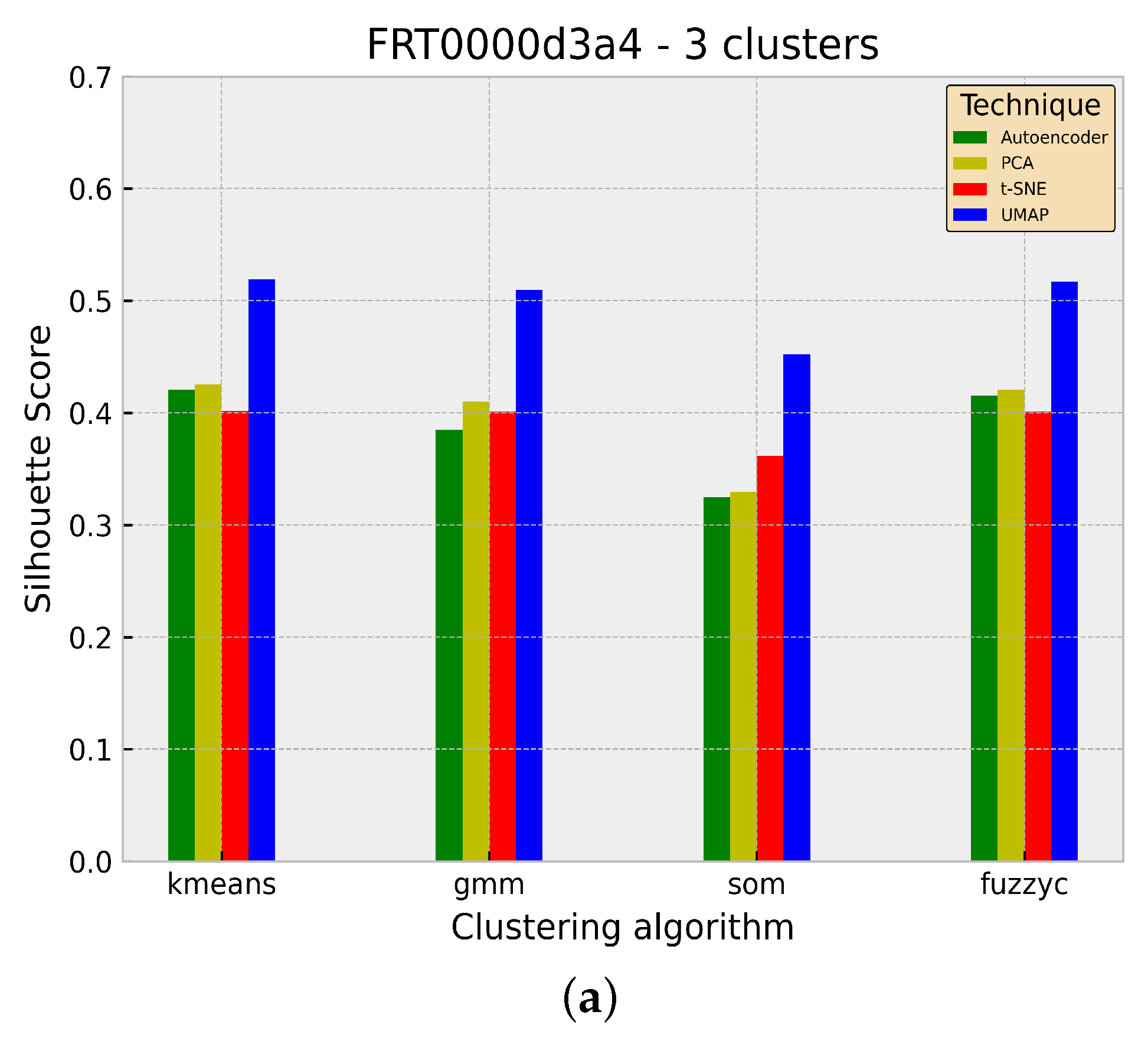
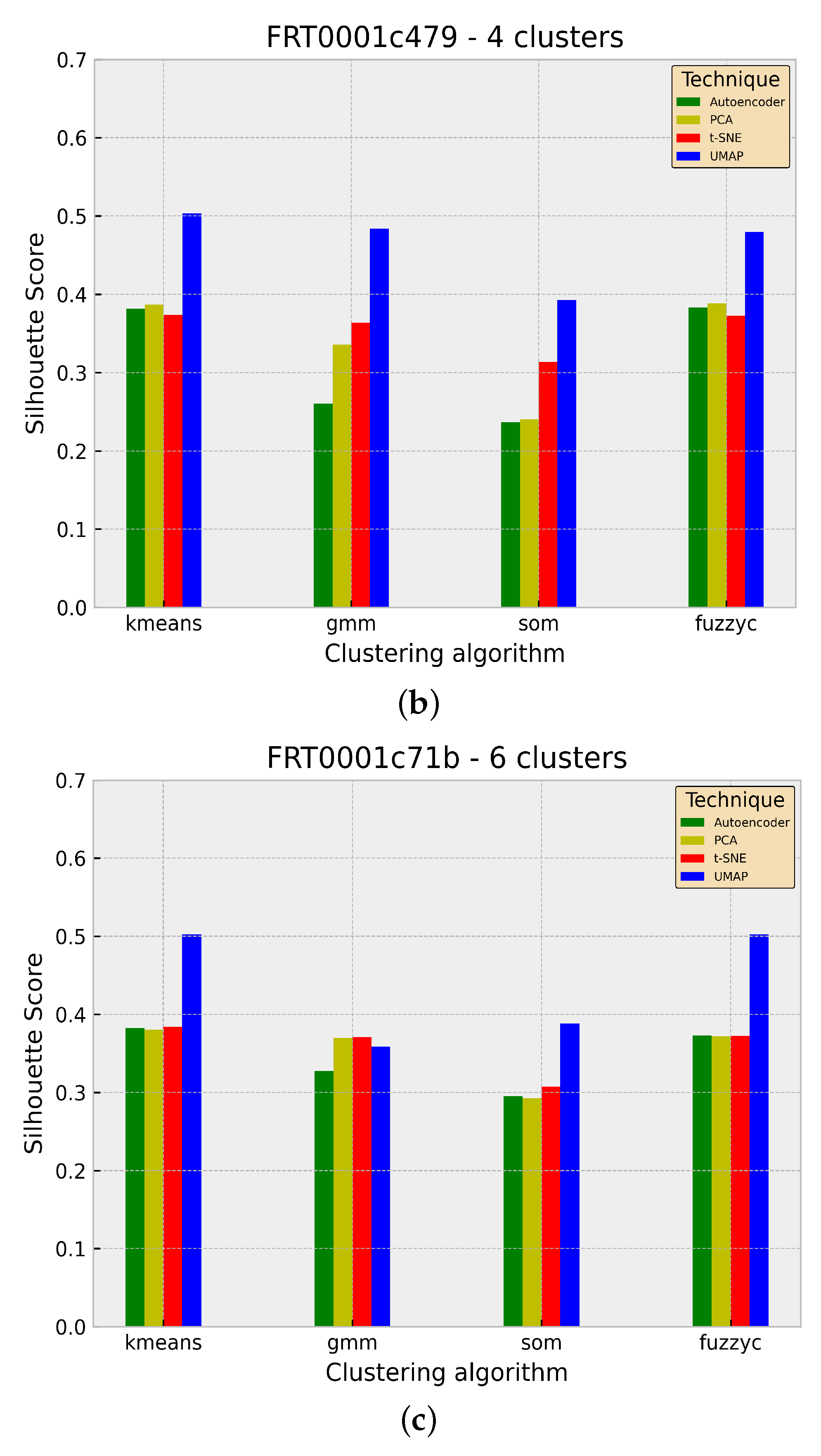
3. Results
3.1. Experiment
3.2. Evaluation
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CaSSIS | Color and Stereo Surface Imaging System |
| CH | Calinski–Harabasz |
| CRISM | Compact Reconnaissance Imaging Spectrometer |
| DB | Davies–Bouldin |
| GMM | Gaussian Mixture model |
| HiRISE | High Resolution Imaging Science Experiment |
| MRO | Mars Reconnaissance Orbiter |
| MTRDR | Map-projected Targeted Reduced Data Record |
| PCA | Principal omponent analysis |
| SC | Silhouette Coefficient |
| SCM | Spectral Cluster Map |
| SOM | Self-organizing map |
| t-SNE | t-distributed Stochastic Neighbor Embedding |
| TGO | ExoMars Trace Gas Orbiter |
| UMAP | Uniform Manifold Approximation and Projection |
Appendix A
| Regions | |||
|---|---|---|---|
| Methods | FRT0000d3a4 | FRT0001c479 | FRT0001c71b |
| Autoencoder + K-Means | 0.8775 | 0.9128 | 0.7967 |
| Autoencoder + GMM | 2.9242 | 2.2085 | 0.8964 |
| Autoencoder + SOM | 1.2979 | 1.1723 | 0.9601 |
| Autoencoder + Fuzzy-c-Means | 1.0237 | 0.9387 | 0.8412 |
| PCA + K-Means | 0.8678 | 0.9009 | 0.8000 |
| PCA + GMM | 1.9057 | 1.7879 | 0.8214 |
| PCA + SOM | 1.2301 | 1.1618 | 0.9572 |
| PCA + Fuzzy-c-Means | 1.0105 | 0.9256 | 0.8434 |
| t-SNE + K-Means | 0.8332 | 0.8347 | 0.8369 |
| t-SNE + GMM | 0.8454 | 0.8614 | 0.8660 |
| t-SNE + SOM | 0.9658 | 0.9936 | 1.0490 |
| t-SNE + Fuzzy-c-Means | 0.8673 | 0.8438 | 0.8507 |
| UMAP + K-Means | 0.7425 | 0.6971 | 0.6523 |
| UMAP + GMM | 0.7322 | 0.7178 | 0.7142 |
| UMAP + SOM | 1.0230 | 0.8936 | 0.7817 |
| UMAP + Fuzzy-c-Means | 0.7682 | 0.7178 | 0.6542 |
Appendix B. Citation of PDS Data Products
Appendix C. HiRISE and CaSSIS Filter Bandpasses
| HiRISE Name | HiRISE Color Band | CaSSIS Name | CaSSIS Color Band | CaSSIS Effective Central Wavelength |
|---|---|---|---|---|
| BG | <580 nm | BLU | <570 nm | 494 nm |
| RED | 570–830 nm | PAN | 550–800 nm | 678 nm |
| NIR | >790 nm | RED | 785–880 nm | 836 nm |
| NIR | >870 nm | 939 nm |
References
- McEwen, A.S.; Eliason, E.M.; Bergstrom, J.W.; Bridges, N.T.; Hansen, C.J.; Delamere, W.A.; Grant, J.A.; Gulick, V.C.; Herkenhoff, K.E.; Keszthelyi, L.; et al. Mars reconnaissance orbiter’s high resolution imaging science experiment (HiRISE). J. Geophys. Res. Planets 2007, 112, E05S02. [Google Scholar] [CrossRef]
- Murchie, S.; Arvidson, R.; Bedini, P.; Beisser, K.; Bibring, J.P.; Bishop, J.; Boldt, J.; Cavender, P.; Choo, T.; Clancy, R.T.; et al. Compact Reconnaissance Imaging Spectrometer for Mars (CRISM) on Mars Reconnaissance Orbiter (MRO). J. Geophys. Res. Planets 2007, 112, E05S02. [Google Scholar] [CrossRef]
- Thomas, N.; Cremonese, G.; Ziethe, R.; Gerber, M.; Brändli, M.; Bruno, G.; Erismann, M.; Gambicorti, L.; Gerber, T.; Ghose, K.; et al. The Colour and Stereo Surface Imaging System (CaSSIS) for the ExoMars Trace Gas Orbiter. Space Sci. Rev. 2017, 212, 1897–1944. [Google Scholar] [CrossRef]
- Schubert, G. Treatise on Geophysics; Elsevier: Amsterdam, The Netherlands, 2015; ISBN 978-0-444-53803-1. [Google Scholar]
- Gao, A.F.; Rasmussen, B.; Kulits, P.; Scheller, E.L.; Greenberger, R.; Ehlmann, B.L. Generalized Unsupervised Clustering of Hyperspectral Images of Geological Targets in the Near Infrared. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 4294–4303. [Google Scholar]
- Timmerman, M.E. Principal Component Analysis. J. Am. Stat. Assoc. 2003, 98, 1082–1083. [Google Scholar] [CrossRef]
- Martel, E.; Lazcano, R.; López, J.; Madroñal, D.; Salvador, R.; López, S.; Juarez, E.; Guerra, R.; Sanz, C.; Sarmiento, R. Implementation of the Principal Component Analysis onto High-Performance Computer Facilities for Hyperspectral Dimensionality Reduction: Results and Comparisons. Remote Sens. 2018, 10, 864. [Google Scholar] [CrossRef]
- Rodarmel, C.; Shan, J. Principal component analysis for hyperspectral image classification. Surv. Land Inf. Sci. 2002, 62, 115–122. [Google Scholar]
- Melit Devassy, B.; George, S.; Nussbaum, P. Unsupervised Clustering of Hyperspectral Paper Data Using t-SNE. J. Imaging 2020, 6, 29. [Google Scholar] [CrossRef]
- Pouyet, E.; Rohani, N.; Katsaggelos, A.K.; Cossairt, O.; Walton, M. Innovative data reduction and visualization strategy for hyperspectral imaging datasets using t-SNE approach. Pure Appl. Chem. 2018, 90, 493–506. [Google Scholar] [CrossRef]
- Song, W.; Wang, L.; Liu, P.; Choo, K.K.R. Improved t-SNE based manifold dimensional reduction for remote sensing data processing. Multimed. Tools Appl. 2019, 78, 4311–4326. [Google Scholar] [CrossRef]
- Kohonen, T. Adaptive, associative, and self-organizing functions in neural computing. Appl. Opt. 1987, 26, 4910–4918. [Google Scholar] [CrossRef]
- Picollo, M.; Cucci, C.; Casini, A.; Stefani, L. Hyper-Spectral Imaging Technique in the Cultural Heritage Field: New Possible Scenarios. Sensors 2020, 20, 2843. [Google Scholar] [CrossRef] [PubMed]
- Wander, L.; Vianello, A.; Vollertsen, J.; Westad, F.; Braun, U.; Paul, A. Exploratory analysis of hyperspectral FTIR data obtained from environmental microplastics samples. Anal. Methods 2020, 12, 781–791. [Google Scholar] [CrossRef]
- D’Amore, M.; Padovan, S. Chapter 7—Automated surface mapping via unsupervised learning and classification of Mercury Visible–Near-Infrared reflectance spectra. In Machine Learning for Planetary Science; Helbert, J., D’Amore, M., Aye, M., Kerner, H., Eds.; Elsevier: Amsterdam, The Netherlands, 2022; pp. 131–149. ISBN 978-0-12-818721-0. [Google Scholar]
- Ferrer-Font, L.; Mayer, J.U.; Old, S.; Hermans, I.F.; Irish, J.; Price, K.M. High-Dimensional Data Analysis Algorithms Yield Comparable Results for Mass Cytometry and Spectral Flow Cytometry Data. Cytom. Part A 2020, 97, 824–831. [Google Scholar] [CrossRef]
- Yang, Y.; Sun, H.; Zhang, Y.; Zhang, T.; Gong, J.; Wei, Y.; Duan, Y.G.; Shu, M.; Yang, Y.; Wu, D.; et al. Dimensionality reduction by UMAP reinforces sample heterogeneity analysis in bulk transcriptomic data. Cell Rep. 2021, 36, 109442. [Google Scholar] [CrossRef] [PubMed]
- Zambon, F.; Carli, C.; Wright, J.; Rothery, D.; Altieri, F.; Massironi, M.; Capaccioni, F.; Cremonese, G. Spectral units analysis of quadrangle H05-Hokusai on Mercury. J. Geophys. Res. Planets 2022, 27, e2021JE006918. [Google Scholar] [CrossRef]
- Massironi, M.; Rossi, A.P.; Wright, J.; Zambon, F.; Poheler, C.; Giacomini, L.; Carli, C.; Ferrari, S.; Semenzato, A.; Luzzi, E.; et al. From Morpho-Stratigraphic to Geo(Spectro)-Stratigraphic Units: The PLANMAP Contribution. In Proceedings of the 2021 Annual Meeting of Planetary Geologic Mappers, Virtual, 14–15 June 2021; Volume 2610, p. 7045. Available online: https://ui.adsabs.harvard.edu/abs/2021LPICo2610.7045M (accessed on 31 March 2022).
- Semenzato, A.; Massironi, M.; Ferrari, S.; Galluzzi, V.; Rothery, D.A.; Pegg, D.L.; Pozzobon, R.; Marchi, S. An Integrated Geologic Map of the Rembrandt Basin, on Mercury, as a Starting Point for Stratigraphic Analysis. Remote Sens. 2020, 12, 3213. [Google Scholar] [CrossRef]
- Giacomini, L.; Carli, C.; Zambon, F.; Galluzzi, V.; Ferrari, S.; Massironi, M.; Altieri, F.; Ferranti, L.; Palumbo, P.; Capaccioni, F. Integration between morphological and spectral characteristics for the geological map of Kuiper quadrangle (H06). In Proceedings of the EGU General Assembly Conference, Online, 19–30 April 2021; p. EGU21-15052. [Google Scholar]
- Pajola, M.; Lucchetti, A.; Semenzato, A.; Poggiali, G.; Munaretto, G.; Galluzzi, V.; Marzo, G.; Cremonese, G.; Brucato, J.; Palumbo, P.; et al. Lermontov crater on Mercury: Geology, morphology and spectral properties of the coexisting hollows and pyroclastic deposits. Planet. Space Sci. 2021, 195, 105136. [Google Scholar] [CrossRef]
- Seelos, F. Mars Reconnaissance Orbiter Compact Reconnaissance Imaging Spectrometer for Mars Map-Projected Targeted Reduced Data Record; MRO-M-CRISM-5-RDR-MPTARGETED-V1.0; NASA Planetary Data System: St. Louis, MO, USA, 2016. [CrossRef]
- Pelkey, S.M.; Mustard, J.F.; Murchie, S.; Clancy, R.T.; Wolff, M.; Smith, M.; Milliken, R.; Bibring, J.P.; Gendrin, A.; Poulet, F.; et al. CRISM multispectral summary products: Parameterizing mineral diversity on Mars from reflectance. J. Geophys. Res. Planets 2007, 112, E08S14. [Google Scholar] [CrossRef]
- Viviano, C.E.; Seelos, F.P.; Murchie, S.L.; Kahn, E.G.; Seelos, K.D.; Taylor, H.W.; Taylor, K.; Ehlmann, B.L.; Wiseman, S.M.; Mustard, J.F.; et al. Revised CRISM spectral parameters and summary products based on the currently detected mineral diversity on Mars. J. Geophys. Res. Planets 2014, 119, 1403–1431. [Google Scholar] [CrossRef]
- Tornabene, L.L.; Seelos, F.P.; Pommerol, A.; Thomas, N.; Caudill, C.M.; Becerra, P.; Bridges, J.C.; Byrne, S.; Cardinale, M.; Chojnacki, M.; et al. Image Simulation and Assessment of the Colour and Spatial Capabilities of the Colour and Stereo Surface Imaging System (CaSSIS) on the ExoMars Trace Gas Orbiter. Space Sci. Rev. 2018, 214, 18. [Google Scholar] [CrossRef]
- Parkes Bowen, A.; Mandon, L.; Bridges, J.; Quantin-Nataf, C.; Tornabene, L.; Page, J.; Briggs, J.; Thomas, N.; Cremonese, G. Using band ratioed CaSSIS imagery and analysis of fracture morphology to characterise Oxia Planum’s clay-bearing unit. In Proceedings of the European Planetary Science Congress, Virtual, 21 September–9 October 2020; p. EPSC2020-877. [Google Scholar] [CrossRef]
- Parkes Bowen, A.; Bridges, J.; Tornabene, L.; Mandon, L.; Quantin-Nataf, C.; Patel, M.R.; Thomas, N.; Cremonese, G.; Munaretto, G.; Pommerol, A.; et al. A CaSSIS and HiRISE map of the Clay-bearing Unit at the ExoMars 2022 landing site in Oxia Planum. Planet. Space Sci. 2022, 214, 105429. [Google Scholar] [CrossRef]
- Thomas, N.; Pommerol, A.; Almeida, M.; Read, M.; Cremonese, G.; Simioni, E.; Munaretto, G.; Weigel, T. Absolute calibration of the Colour and Stereo Surface Imaging System (CaSSIS). Planet. Space Sci. 2021, 211, 105394. [Google Scholar] [CrossRef]
- Tulyakov, S.; Ivanov, A.; Thomas, N.; Roloff, V.; Pommerol, A.; Cremonese, G.; Weigel, T.; Fleuret, F. Geometric calibration of Colour and Stereo Surface Imaging System of ESA’s Trace Gas Orbiter. Adv. Space Res. 2018, 61, 487–496. [Google Scholar] [CrossRef]
- Weitz, C.M.; Irwin III, R.P.; Chuang, F.C.; Bourke, M.C.; Crown, D.A. Formation of a terraced fan deposit in Coprates Catena, Mars. Icarus 2006, 184, 436–451. [Google Scholar] [CrossRef]
- Grindrod, P.M.; Warner, N.; Hobley, D.; Schwartz, C.; Gupta, S. Stepped fans and facies-equivalent phyllosilicates in Coprates Catena, Mars. Icarus 2018, 307, 260–280. [Google Scholar] [CrossRef]
- Chojnacki, M.; Hynek, B.M. Geological context of water-altered minerals in Valles Marineris, Mars. J. Geophys. Res. Planets 2008, 113, E12005. [Google Scholar] [CrossRef]
- Weitz, C.M.; Bishop, J.L. Stratigraphy and formation of clays, sulfates, and hydrated silica within a depression in Coprates Catena, Mars. J. Geophys. Res. Planets 2016, 121, 805–835. [Google Scholar] [CrossRef]
- Murchie, S.L.; Bibring, J.P.; Arvidson, R.E.; Bishop, J.L.; Carter, J.; Ehlmann, B.L.; Langevin, Y.; Mustard, J.F.; Poulet, F.; Riu, L.; et al. Visible to Short-Wave Infrared Spectral Analyses of Mars from Orbit Using CRISM and OMEGA. In Remote Compositional Analysis: Techniques for Understanding Spectroscopy, Mineralogy, and Geochemistry of Planetary Surfaces; Cambridge Planetary Science; Cambridge University Press: Cambridge, UK, 2019; pp. 453–483. [Google Scholar] [CrossRef]
- Fueten, F.; Racher, H.; Stesky, R.; MacKinnon, P.; Hauber, E.; McGuire, P.; Zegers, T.; Gwinner, K. Structural analysis of interior layered deposits in Northern Coprates Chasma, Mars. Earth Planet. Sci. Lett. 2010, 294, 343–356. [Google Scholar] [CrossRef][Green Version]
- Buczkowski, D.; Seelos, K.; Viviano, C.; Murchie, S.; Seelos, F.; Malaret, E.; Hash, C. Anomalous Phyllosilicate-Bearing Outcrops South of Coprates Chasma: A Study of Possible Emplacement Mechanisms. J. Geophys. Res. Planets 2020, 125, e2019JE006043. [Google Scholar] [CrossRef]
- Le Deit, L.; Flahaut, J.; Quantin, C.; Hauber, E.; Mège, D.; Bourgeois, O.; Gurgurewicz, J.; Massé, M.; Jaumann, R. Extensive surface pedogenic alteration of the Martian Noachian crust evidenced by plateau phyllosilicates around Valles Marineris. J. Geophys. Res. 2012, 117, E00J05. [Google Scholar] [CrossRef]
- Kovenko, V.; Bogach, I. A Comprehensive Study of Autoencoders’ Applications Related to Images. In Proceedings of the IT&I Workshops, Kyiv, Ukraine, 2–3 December 2020. [Google Scholar]
- Le, Q.V. A tutorial on deep learning part 2: Autoencoders, convolutional neural networks and recurrent neural networks. Google Brain 2015, 20, 1–20. [Google Scholar]
- Van der Maaten, L.; Hinton, G. Visualizing data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2625. [Google Scholar]
- Kullback, S.; Leibler, R.A. On Information and Sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- McInnes, L.; Healy, J.; Melville, J. UMAP: Uniform Manifold Approximation and Projection for Dimension Reduction. arXiv 2018, arXiv:1802.03426. [Google Scholar]
- Allaoui, M.; Kherfi, M.L.; Cheriet, A. Considerably Improving Clustering Algorithms Using UMAP Dimensionality Reduction Technique: A Comparative Study. In Image and Signal Processing; El Moataz, A., Mammass, D., Mansouri, A., Nouboud, F., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 317–325. [Google Scholar]
- Vermeulen, M.; Smith, K.; Eremin, K.; Rayner, G.; Walton, M. Application of Uniform Manifold Approximation and Projection (UMAP) in spectral imaging of artworks. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2021, 252, 119547. [Google Scholar] [CrossRef]
- MacQueen, J. Some methods for classification and analysis of multivariate observations. In Proceedings of the 5th Berkeley Symposium on Mathematical Statistics and Probability, Oakland, CA, USA; 1967; Volume 1, pp. 281–297. [Google Scholar]
- Bishop, C.M.; Nasrabadi, N.M. Pattern Recognition and Machine Learning; Springer: Berlin/Heidelberg, Germany, 2006; Volume 4, ISBN 978-0-387-31073-2. [Google Scholar]
- Bezdek, J.C.; Ehrlich, R.; Full, W. FCM: The fuzzy c-means clustering algorithm. Comput. Geosci. 1984, 10, 191–203. [Google Scholar] [CrossRef]
- Kohonen, T. Self-Organizing Maps; Springer: Berlin/Heidelberg, Germany, 1997; ISBN 978-3-642-97966-8. [Google Scholar]
- Bioucas-Dias, J.M.; Nascimento, J.M.P. Hyperspectral Subspace Identification. IEEE Trans. Geosci. Remote Sens. 2008, 46, 2435–2445. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Sklearn-Som v. 1.1.0 Master Documentation. Available online: https://sklearn-som.readthedocs.io/en/latest/ (accessed on 17 March 2022).
- Dias, M.L.D. Fuzzy-c-Means: An Implementation of Fuzzy C-Means Clustering Algorithm; Zenodo: Geneva, Switzerland, 2019. [Google Scholar] [CrossRef]
- Caliński, T.; Harabasz, J. A dendrite method for cluster analysis. Commun. Stat.-Theory Methods 1974, 3, 1–27. [Google Scholar] [CrossRef]
- Davies, D.L.; Bouldin, D.W. A Cluster Separation Measure. IEEE Trans. Pattern Anal. Mach. Intell. 1979, PAMI-1, 224–227. [Google Scholar] [CrossRef]
- Rousseeuw, P.J. Silhouettes: A graphical aid to the interpretation and validation of cluster analysis. J. Comput. Appl. Math. 1987, 20, 53–65. [Google Scholar] [CrossRef]
- Milligan, G.W.; Cooper, M.C. An examination of procedures for determining the number of clusters in a data set. Psychometrika 1985, 50, 159–179. [Google Scholar] [CrossRef]
- Loizeau, D.; Quantin-Nataf, C.; Carter, J.; Flahaut, J.; Thollot, P.; Lozac’h, L.; Millot, C. Quantifying widespread aqueous surface weathering on Mars: The plateaus south of Coprates Chasma. Icarus 2018, 302, 451–469. [Google Scholar] [CrossRef]
- Gambicorti, L.; Piazza, D.; Gerber, M.; Pommerol, A.; Roloff, V.; Ziethe, R.; Zimmermann, C.; Da Deppo, V.; Cremonese, G.; Veltroni, I.F.; et al. Thin-film optical pass band filters based on new photo-lithographic process for CaSSIS FPA detector on Exomars TGO mission: Development, integration, and test. In Advances in Optical and Mechanical Technologies for Telescopes and Instrumentation II; International Society for Optics and Photonics: Bellingham, WA, USA, 2016; Volume 9912, p. 99122Y. [Google Scholar]
- Gambicorti, L.; Piazza, D.; Pommerol, A.; Roloff, V.; Gerber, M.; Ziethe, R.; El-Maarry, M.R.; Weigel, T.; Johnson, M.; Vernani, D.; et al. First light of Cassis: The stereo surface imaging system onboard the exomars TGO. In Proceedings of the International Conference on Space Optics—ICSO 2016, Biarritz, France, 18–21 October 2016; International Society for Optics and Photonics: Bellingham, WA, USA, 2017; Volume 10562, p. 105620A. [Google Scholar]



| Regions | |||
|---|---|---|---|
| Methods | FRT0000d3a4 | FRT0001c479 | FRT0001c71b |
| Autoencoder + K-Means | 96.371 | 135.768 | 221.408 |
| Autoencoder + GMM | 49.838 | 62.005 | 185.458 |
| Autoencoder + SOM | 69.396 | 108.513 | 192.581 |
| Autoencoder + Fuzzy-c-Means | 81.773 | 133.995 | 214.217 |
| PCA + K-Means | 97.718 | 138.611 | 220.849 |
| PCA + GMM | 50.756 | 82.344 | 202.702 |
| PCA + SOM | 71.086 | 110.939 | 192.436 |
| PCA + Fuzzy-c-Means | 83.132 | 136.640 | 213.769 |
| t-SNE + K-Means | 137.141 | 138.955 | 138.998 |
| t-SNE + GMM | 132.889 | 128.090 | 127.752 |
| t-SNE + SOM | 120.052 | 114.351 | 113.640 |
| t-SNE + Fuzzy-c-Means | 134.679 | 138.300 | 137.684 |
| UMAP + K-Means | 207.836 | 246.825 | 284.543 |
| UMAP + GMM | 178.341 | 216.898 | 224.978 |
| UMAP + SOM | 162.585 | 198.219 | 222.445 |
| UMAP + Fuzzy-c-Means | 206.015 | 245.274 | 284.117 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fernandes, M.; Pletl, A.; Thomas, N.; Rossi, A.P.; Elser, B. Generation and Optimization of Spectral Cluster Maps to Enable Data Fusion of CaSSIS and CRISM Datasets. Remote Sens. 2022, 14, 2524. https://doi.org/10.3390/rs14112524
Fernandes M, Pletl A, Thomas N, Rossi AP, Elser B. Generation and Optimization of Spectral Cluster Maps to Enable Data Fusion of CaSSIS and CRISM Datasets. Remote Sensing. 2022; 14(11):2524. https://doi.org/10.3390/rs14112524
Chicago/Turabian StyleFernandes, Michael, Alexander Pletl, Nicolas Thomas, Angelo Pio Rossi, and Benedikt Elser. 2022. "Generation and Optimization of Spectral Cluster Maps to Enable Data Fusion of CaSSIS and CRISM Datasets" Remote Sensing 14, no. 11: 2524. https://doi.org/10.3390/rs14112524
APA StyleFernandes, M., Pletl, A., Thomas, N., Rossi, A. P., & Elser, B. (2022). Generation and Optimization of Spectral Cluster Maps to Enable Data Fusion of CaSSIS and CRISM Datasets. Remote Sensing, 14(11), 2524. https://doi.org/10.3390/rs14112524