Regional Ionospheric Corrections for High Accuracy GNSS Positioning
Abstract
:1. Introduction
2. Methodology
2.1. Ionosphere Delay Estimation Using PPP Technique
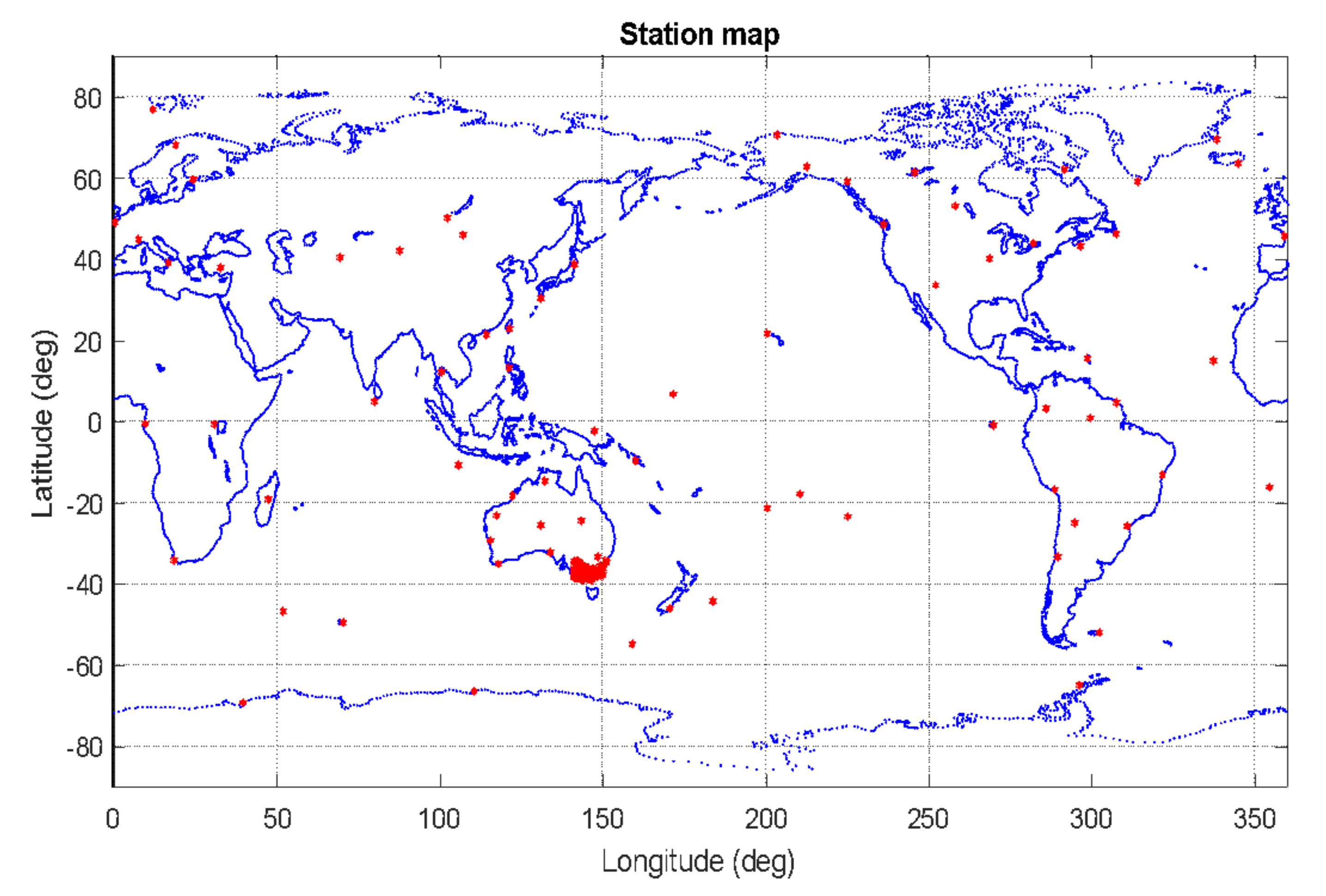
2.2. GINAN Parameter Estimation Algorithm Processing
3. Results
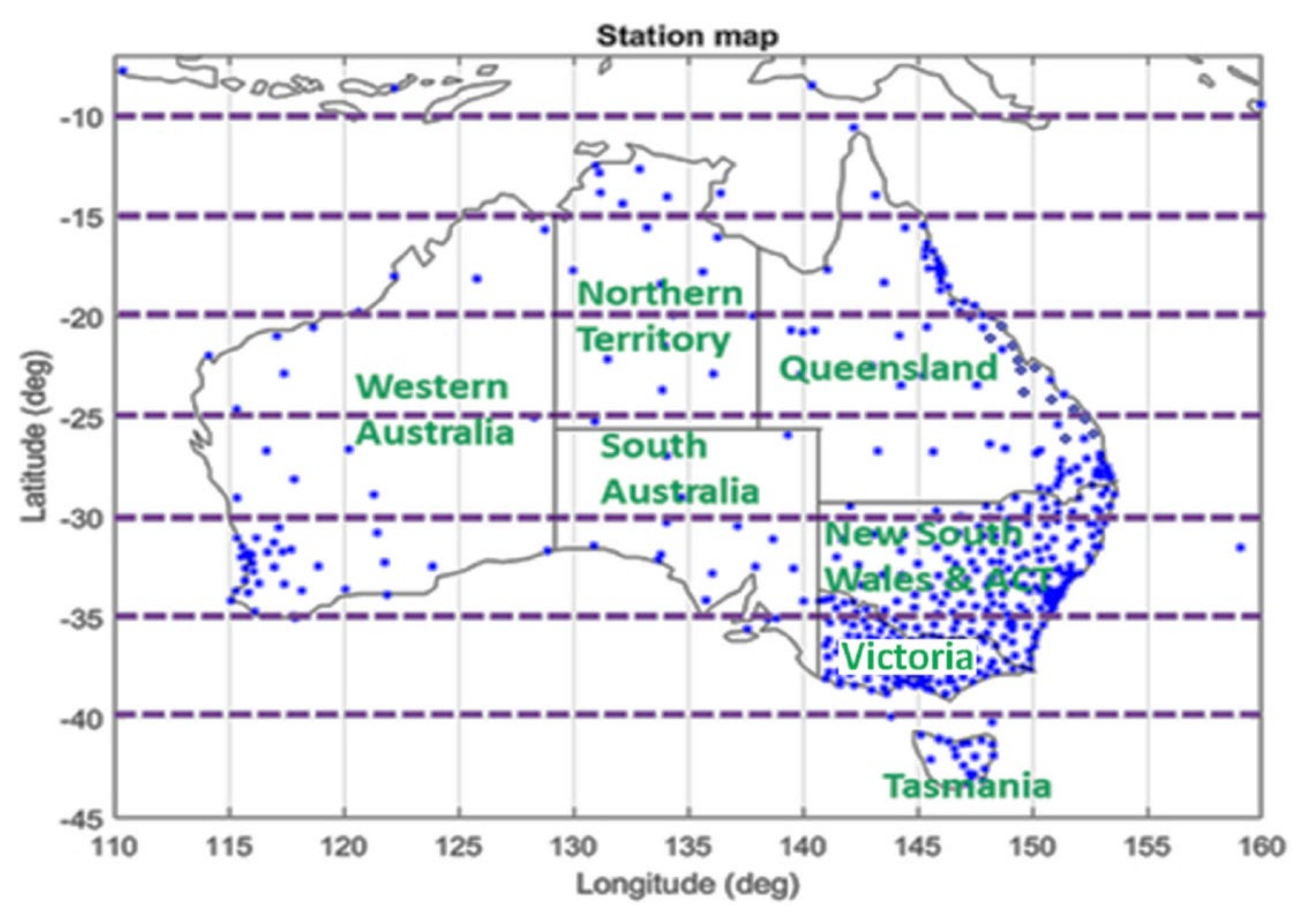
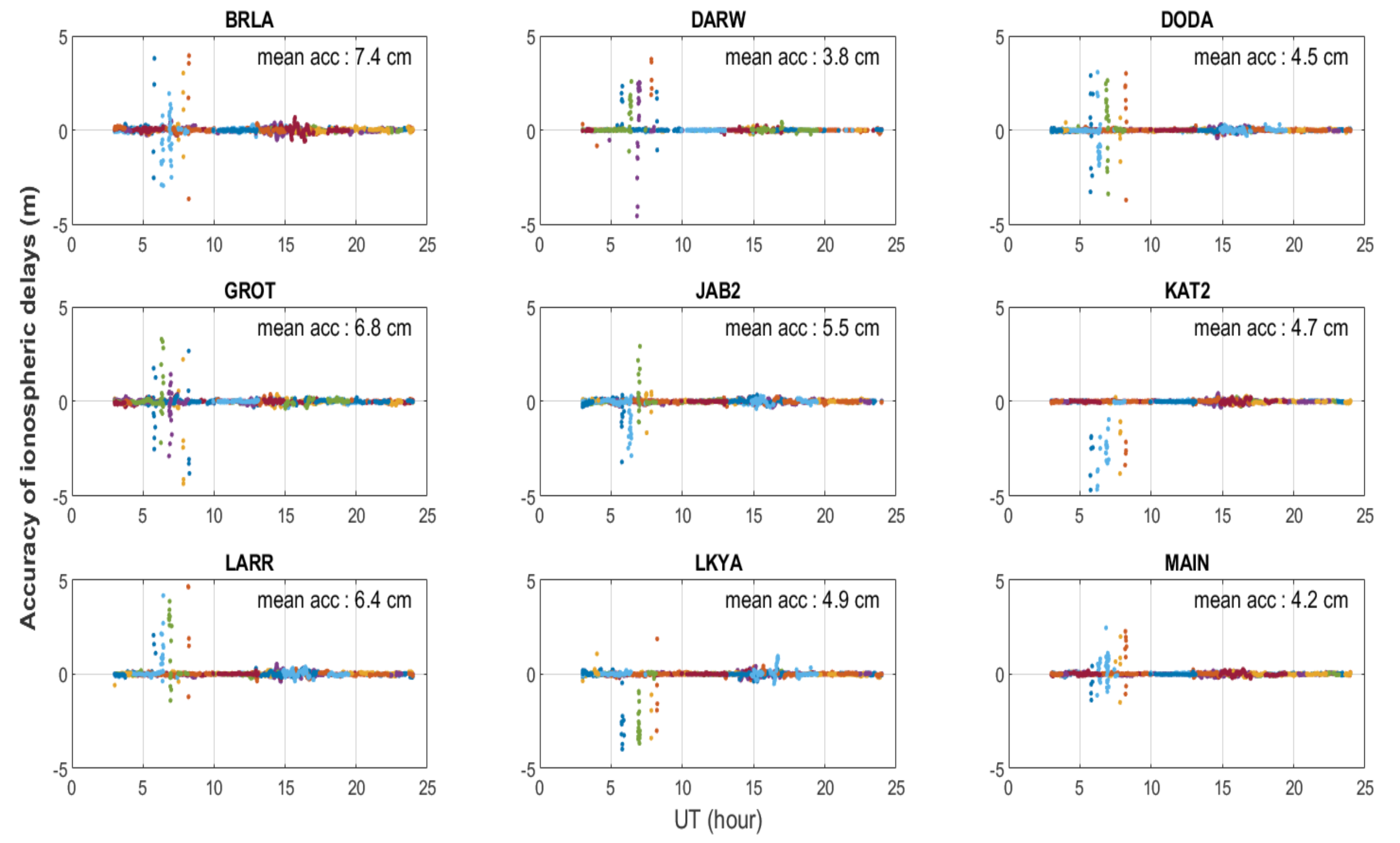
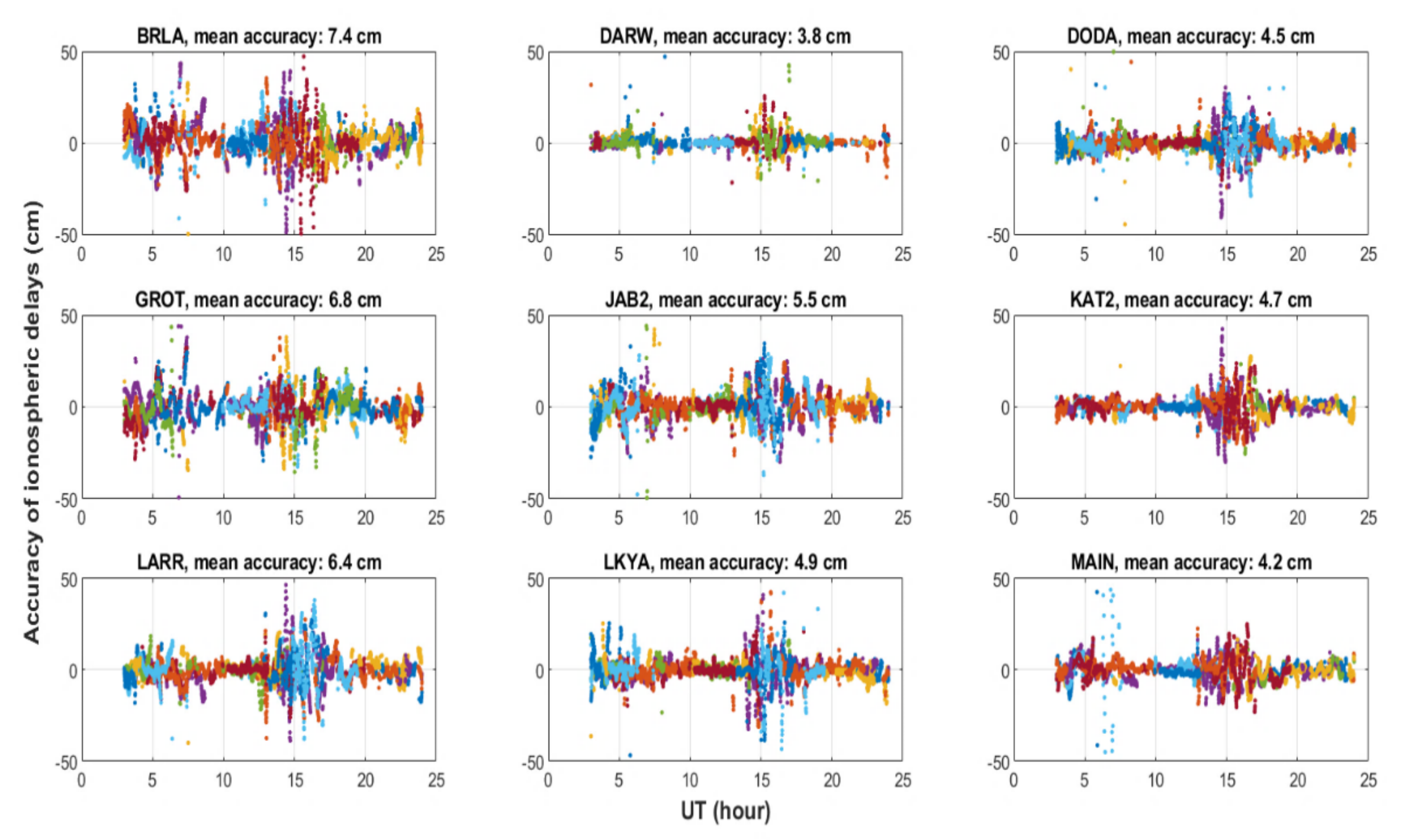
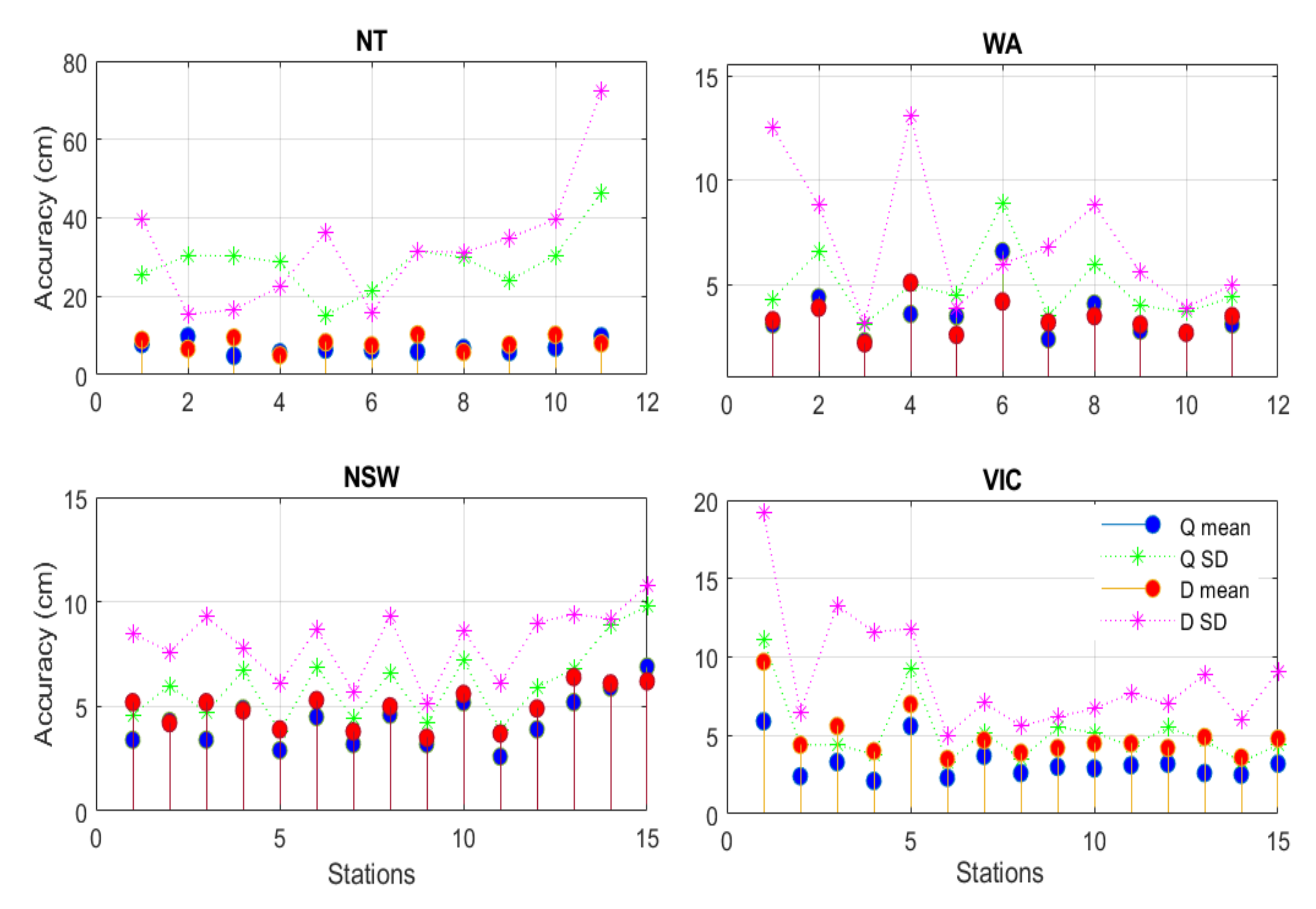
3.1. Evaluation of the Ionospheric Corrections in Different Parts of Australia
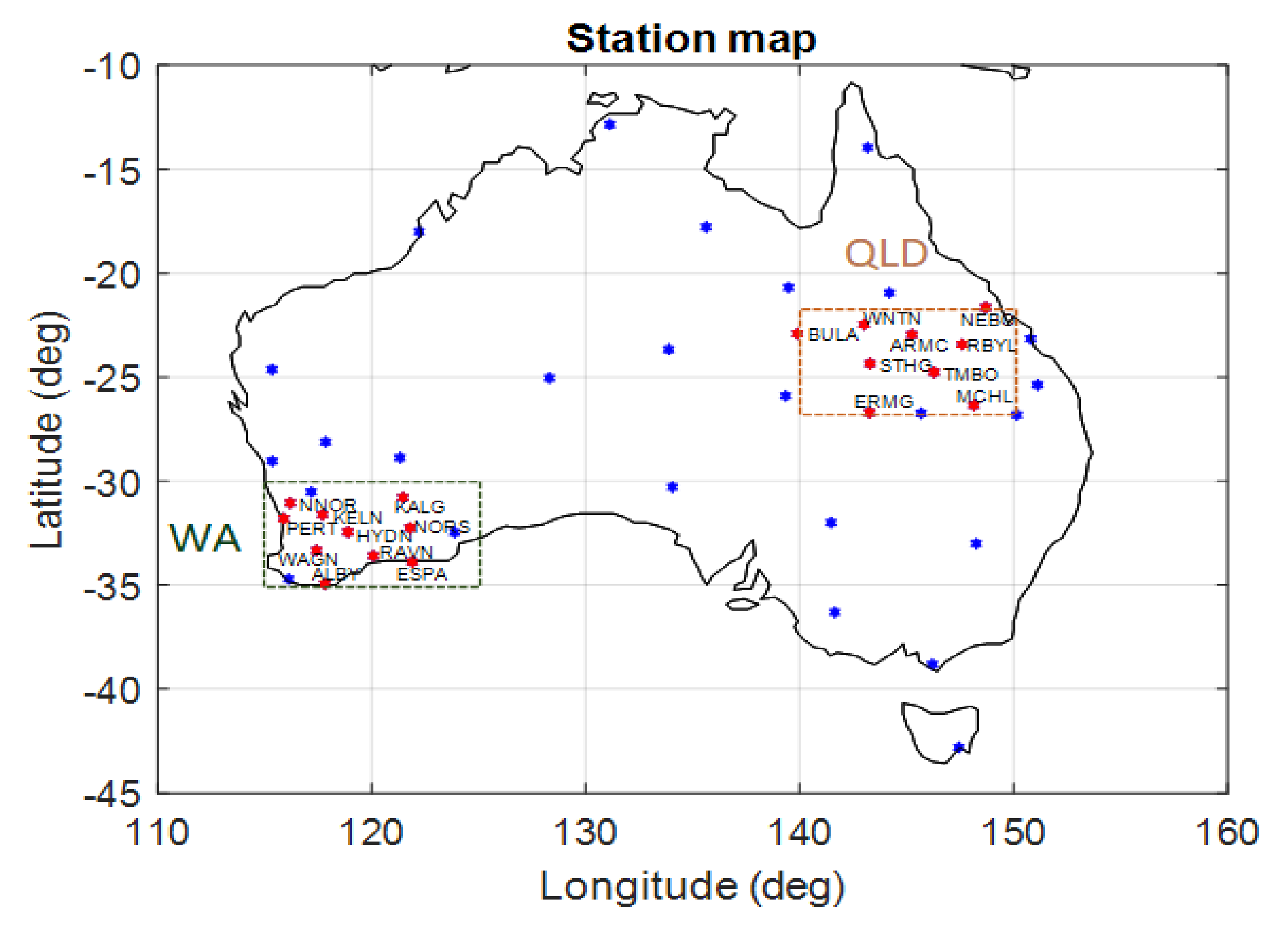
3.1.1. Victoria (VIC), New South Wales (NSW) and Canberra (ACT)
3.1.2. North Territory (NT) and East Coast of Queensland (QLD)
3.1.3. South Australia (SA), Western Australia (WA) and Central Australia
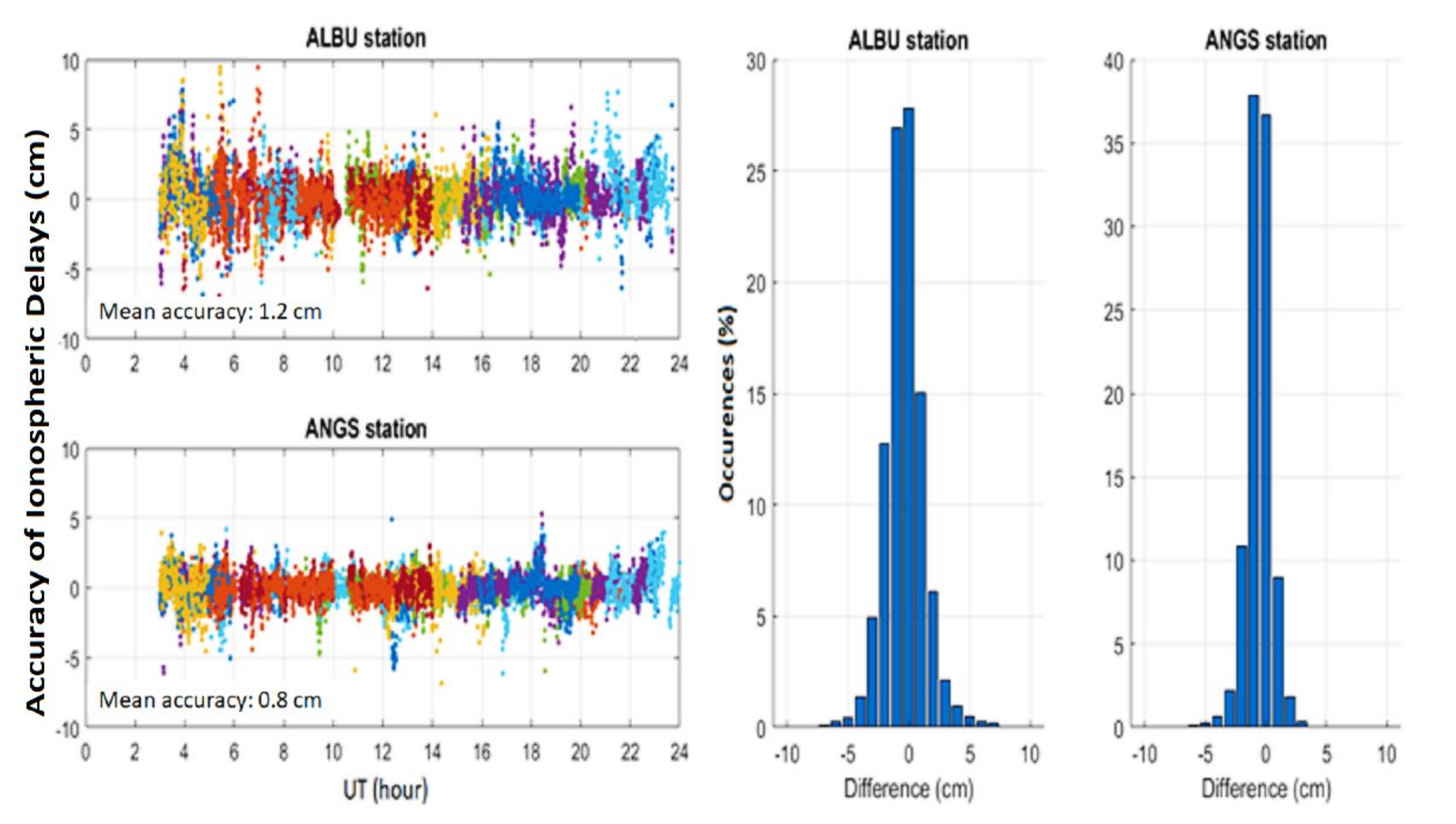
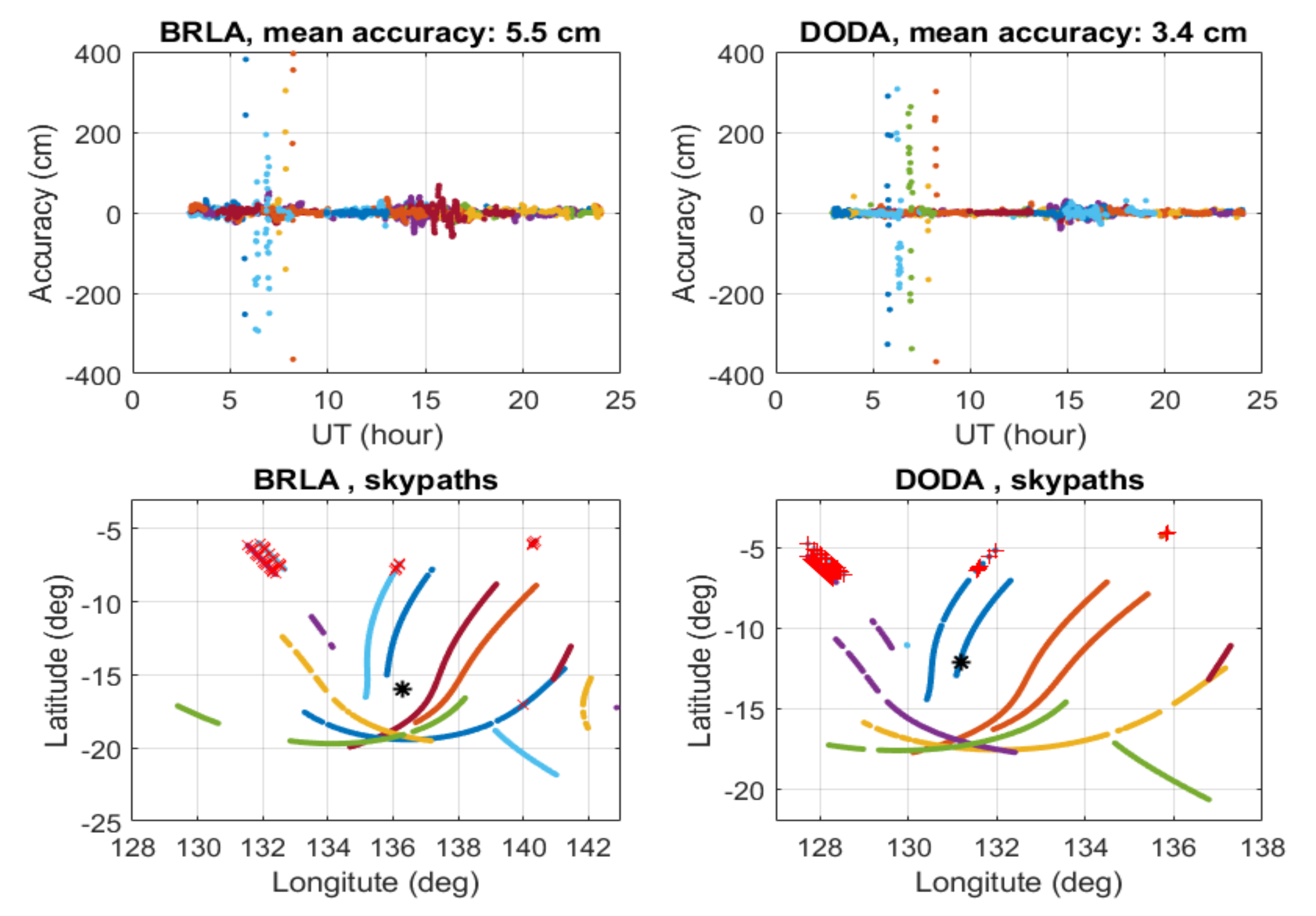
3.2. Day-to-Day Accuracy of the Ionospheric Corrections during Ionosphere Quiet and Disturbed Days
4. Discussion
- (1)
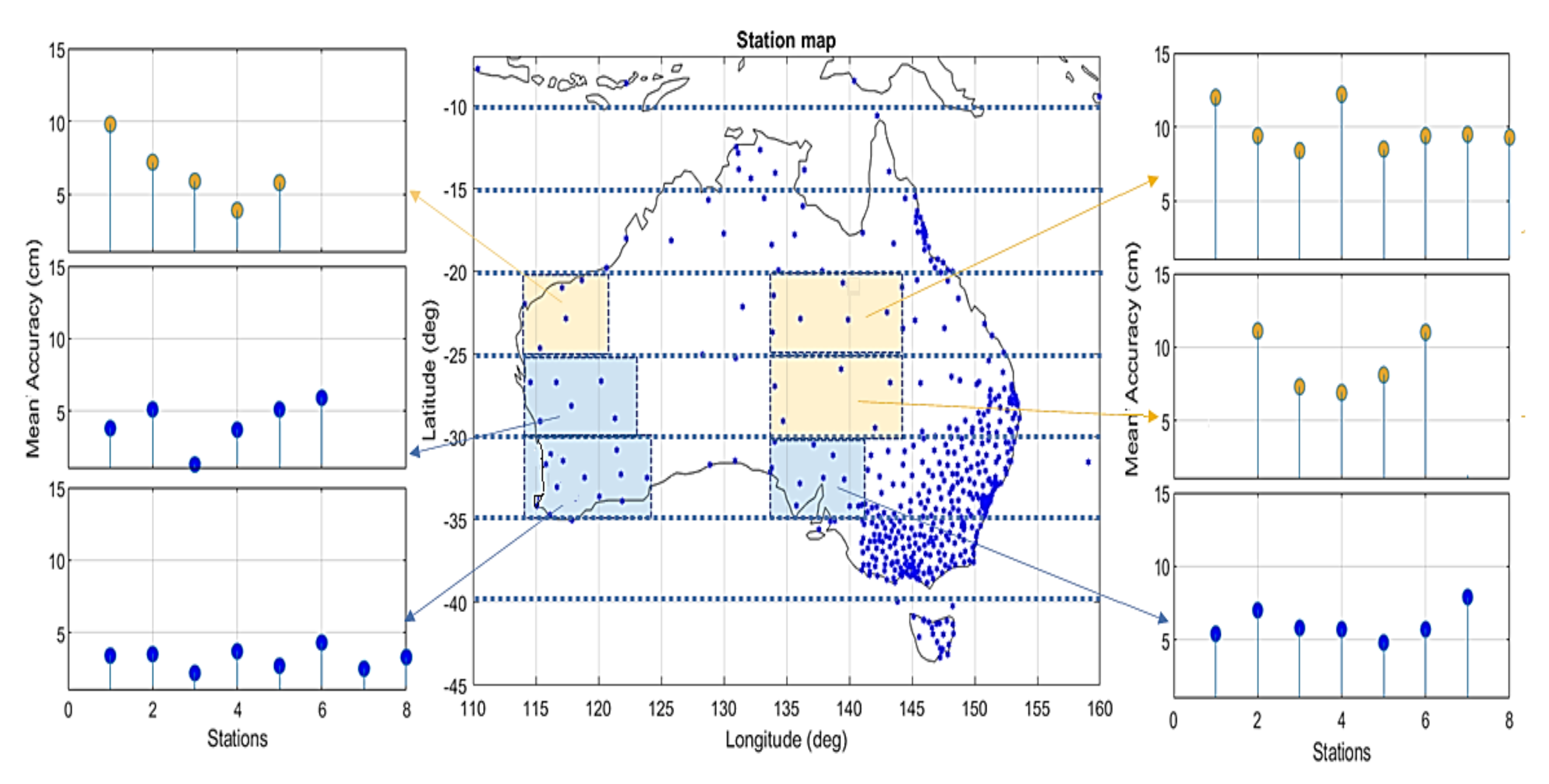
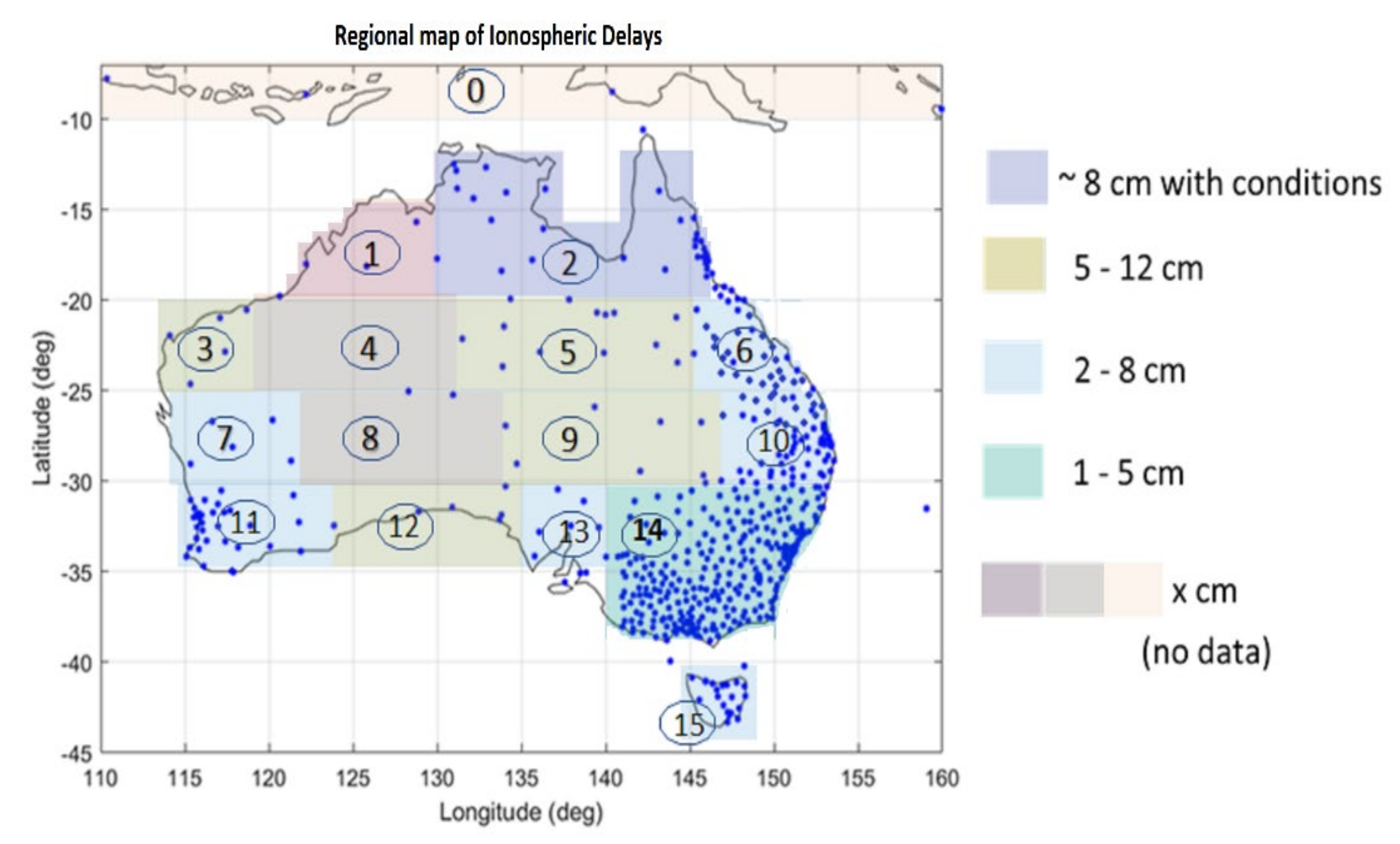
- Region 0 covers multiple islands of Indonesia and there were no available GNSS stations; therefore, it is not included for analysis.
- (2)
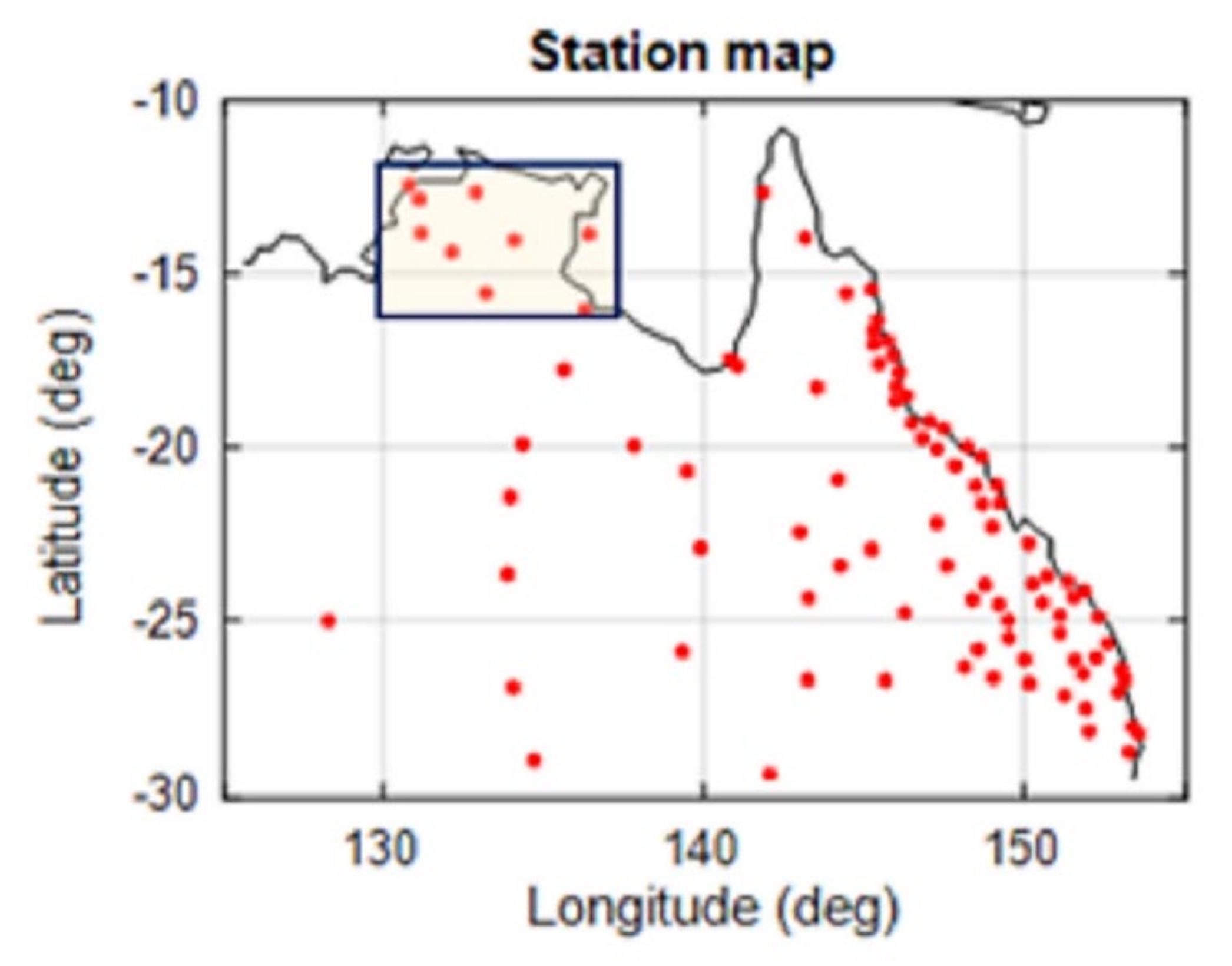
- Regions 1 and 2 are in the low latitudes of 10° to 20°S, where the high electron density and the variation in the equatorial ionospheric anomaly are found. The ionospheric corrections around midnight or low-elevation GNSS satellites below 20 deg during daytime can be high. With the current available CORS networks in NT and northern QLD, 8 cm level ionospheric corrections can be obtained in Region 2, while additional GNSS stations will be required to be installed in Region 1 (northern WA) if centimetre-level accurate ionospheric corrections will be needed in this area.
- (3)
- Regions 3, 5, 9 and 12 are in the mid latitudes from approximately 20° to 35°S. The mid-latitude regions were less impacted by equatorial ionospheric disturbances. In these regions, the current available GNSS CORS networks are sparse. Nevertheless, it was found that 5 to 12 cm level accurate ionospheric corrections can be obtained in these regions. In the eastern corner of WA, where the borders of SA and NT meet, i.e., Regions 4 and 8, no evaluation was undertaken due to an insufficient number of GNSS stations.
- (4)
- Regions 6, 7, 10, 11, 13, 14 and 15 are also in the mid latitudes covering 20° to 45°S. For these regions, a high number and dense CORS networks exist. Therefore, the average obtainable accuracy of the ionospheric corrections is within 2 to 8 cm.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Choy, S.; Zhang, K.; Silcock, D. An Evaluation of Various Ionospheric Error Mitigation Methods used in Single Frequency PPP. Positioning 2008, 1, 62–71. [Google Scholar] [CrossRef] [Green Version]
- Choy, S.; Bisnath, S.; Rizos, C. Uncovering common misconceptions in GNSS Precise Point Positioning and its future prospect. GPS Solut. 2016, 21, 13–22. [Google Scholar] [CrossRef]
- Choy, S. High accuracy precise point positioning using a single frequency GPS receiver. J. Appl. Geod. 2011, 5, 59–69. [Google Scholar] [CrossRef]
- Zumberge, J.F.; Heflin, M.B.; Jefferson, D.C.; Watkins, M.M.; Webb, F.H. Precise point positioning for the efficient and robust analysis of GPS data from large networks. J. Geophys. Res. 1997, 102, 5005–5017. [Google Scholar] [CrossRef] [Green Version]
- Kouba, J.; Héroux, P. Precise point positioning using IGS orbit and clock products. GPS Solut. 2001, 5, 12–28. [Google Scholar] [CrossRef]
- Samper, M.D.; Merino, M.M. Advantages and Drawbacks of the Precise Point Positioning (PPP) Technique for Earthquake, Tsunami Prediction and Monitoring. In Proceedings of the ION 2013 Pacific PNT Meeting, Honolulu, HI, USA, 25 April 2013; pp. 9–26. [Google Scholar]
- Wabbena, G.; Schmitz, M.; Bagge, A. PPP-RTK: Precise Point Positioning Using State-Space Representation in RTK Networks. In Proceedings of the 18th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS 2005), Long Beach, CA, USA, 16 September 2005; pp. 2584–2594. [Google Scholar]
- Leick, A.; Rapoport, L.; Tatarnikov, D. GPS Satellite Surveying; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Alkan, R.M.; Erol, S.; Ozulu, I.M.; Ilci, V. Accuracy comparison of post-processed PPP and real-time absolute positioning techniques. Geomat. Nat. Hazards Risk 2020, 11, 178–190. [Google Scholar] [CrossRef]
- Rovira-Garcia, A.; Juan, J.M.; Sanz, J.; González-Casado, G.; Bertran, E. Fast Precise Point Positioning: A System to Provide Corrections for Single and Multi-frequency Navigation. J. Inst. Navig. 2016, 63, 231–247. [Google Scholar] [CrossRef] [Green Version]
- Juan, J.M.; Hernández-Pajares, M.; Sanz, J.; Ramos-Bosch, P.; Aragon-Angel, A.; Orus, R.; Ochieng, W.; Feng, S.; Jofre, M.; Coutinho, P.; et al. Enhanced Precise Point Positioning for GNSS Users. IEEE Trans. Geosci. Remote Sens. 2012, 50, 4213–4222. [Google Scholar] [CrossRef]
- Psychas, D.; Verhagen, S.; Liu, X.; Memarzadeh, Y.; Visser, H. Assessment of ionospheric corrections for PPP-RTK using regional ionosphere modelling. Meas. Sci. Technol. 2019, 30, 014001. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Zhang, X.; Ge, M. Regional reference network augmented precise point positioning for instantaneous ambiguity resolution. J. Geod. 2011, 85, 151–158. [Google Scholar] [CrossRef]
- Hernández-Pajares, M.; Juan, J.M.; Sanz, J.; Orus, R.; Garcia-Rigo, A.; Feltens, J.; Komjathy, A.; Schaer, S.C.; Krankowski, A. The IGS VTEC maps: A reliable source of ionospheric information since 1998. J. Geod. 2011, 83, 263–275. [Google Scholar] [CrossRef]
- Rovira-Garcia, A.; Juan, J.M.; Sanz, J.; González-Casado, G.; Ibáñez, D. Accuracy of ionospheric models used in GNSS and SBAS: Methodology and analysis. J. Geod. 2016, 90, 229–240. [Google Scholar] [CrossRef]
- Banville, S.; Collins, P.; Zhang, W.; Langley, R.B. Global and regional ionospheric corrections for faster PPP convergence. J. Inst. Navig. 2014, 61, 115–124. [Google Scholar] [CrossRef]
- Choy, S.; Harima, K. Satellite delivery of high-accuracy GNSS precise point positioning service: An overview for Australia. J. Spat. Sci. 2019, 64, 197–208. [Google Scholar] [CrossRef]
- Brown, N.; Dawson, J.; Ruddick, R. Positioning Australia for the Future. Engineering 2020, 6, 857–859. [Google Scholar] [CrossRef]
- Harima, K.; Choy, S.; Elneser, L.; Kogure, S. Local augmentation to wide area PPP systems: A case study in Victoria, Australia. In Proceedings of the IGNSS Conference, Sydney, Australia, 6–8 December 2016. [Google Scholar]
- Melbourne, W. The case for ranging in GPS based geodetic systems. In Proceedings of the 1st International Symposium on Precise Positioning with the Global Positioning System, Rockville, MD, USA, 15–19 April 1985; pp. 373–386. [Google Scholar]
- Wübbena, G. Software developments for geodetic positioning with GPS using TI 4100 code and carrier measurements. In Proceedings of the 1st International Symposium on Precise Positioning with the Global Positioning System, Rockville, MD, USA, 15–19 April 1985; pp. 403–412. [Google Scholar]
- Subirana, J.S.; Zornoza, J.J.; Hernández-Pajares, M. Detector Based in Code and Carrier Phase Data: The Melburne–Wübbena Combination. ESA Navipedia. Available online: https://gssc.esa.int/navipedia/index.php/Detector_based_in_code_and_carrier_phase_data:_The_Melbourne-W%C3%BCbbena_combination (accessed on 12 April 2022).
- The PEA Packet. Available online: https://bitbucket.org/geoscienceaustralia/pea/src/master/ (accessed on 15 June 2021).
- Johnston, H.F. Mean, K-Indices from Twenty-One Magnetic Observatories and Five Quiet Days and Five Disturbed Days for 1942. Terr. Magn. Atmos. Electr. 1943, 47, 219. [Google Scholar] [CrossRef]
- The International 5 and 10 Quietest and 5 Most Disturbed Days in Each Month. Available online: https://wdc.kugi.kyoto-u.ac.jp/qddays/ (accessed on 15 April 2022).
- Newell, T.P.; Gjerloev, J.W. Evaluation of SuperMAG auroral electrojet indices as indicators of substorms and auroral power. J. Geophys. Res. 2011, 116, A12211. [Google Scholar] [CrossRef]
- Gjerloev, J.W. The SuperMAG data processing technique. J. Geophys. Res. 2012, 117, A09213. [Google Scholar] [CrossRef]
- Pradipta, R.; Valladares, C.E.; Carter, B.A.; Doherty, P.H. Interhemispheric propagation and in-teractions of auroral traveling ionospheric disturbances near the equator. J. Geophys. Res. Space Phys. 2016, 121, 2462–2474. [Google Scholar] [CrossRef] [Green Version]
- Valdés-Abreu, J.C.; Diaz, M.A.; Báez, J.C.; Stable-Sánchez, Y. Effects of the 12 May 2021 Geomgagnetic Storm on Georeferencing Precision. Remote Sens. 2022, 14, 38. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dao, T.; Harima, K.; Carter, B.; Currie, J.; McClusky, S.; Brown, R.; Rubinov, E.; Choy, S. Regional Ionospheric Corrections for High Accuracy GNSS Positioning. Remote Sens. 2022, 14, 2463. https://doi.org/10.3390/rs14102463
Dao T, Harima K, Carter B, Currie J, McClusky S, Brown R, Rubinov E, Choy S. Regional Ionospheric Corrections for High Accuracy GNSS Positioning. Remote Sensing. 2022; 14(10):2463. https://doi.org/10.3390/rs14102463
Chicago/Turabian StyleDao, Tam, Ken Harima, Brett Carter, Julie Currie, Simon McClusky, Rupert Brown, Eldar Rubinov, and Suelynn Choy. 2022. "Regional Ionospheric Corrections for High Accuracy GNSS Positioning" Remote Sensing 14, no. 10: 2463. https://doi.org/10.3390/rs14102463
APA StyleDao, T., Harima, K., Carter, B., Currie, J., McClusky, S., Brown, R., Rubinov, E., & Choy, S. (2022). Regional Ionospheric Corrections for High Accuracy GNSS Positioning. Remote Sensing, 14(10), 2463. https://doi.org/10.3390/rs14102463





