Forest Fire Monitoring and Positioning Improvement at Subpixel Level: Application to Himawari-8 Fire Products
Abstract
:1. Introduction
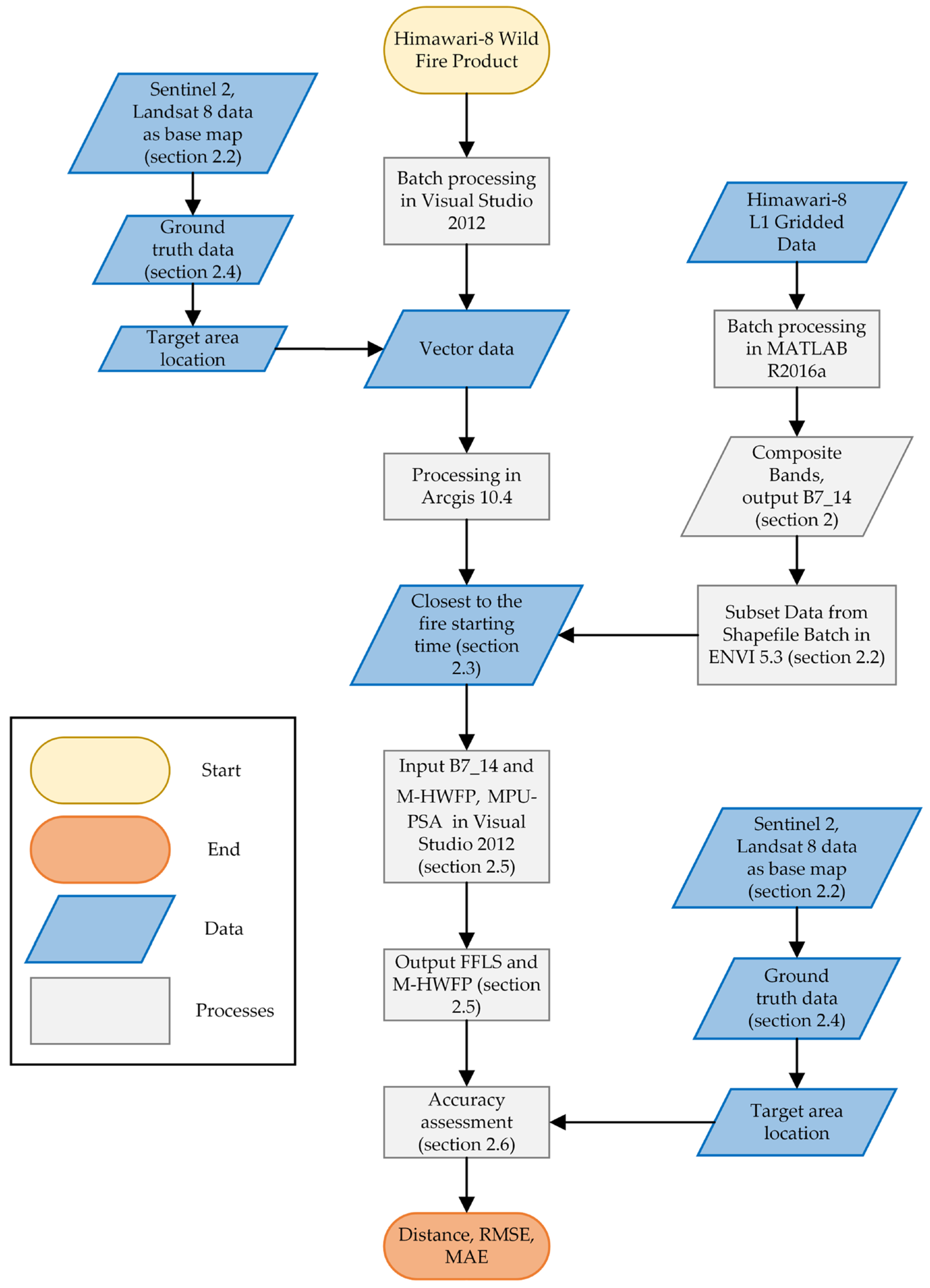
2. Materials and Methods
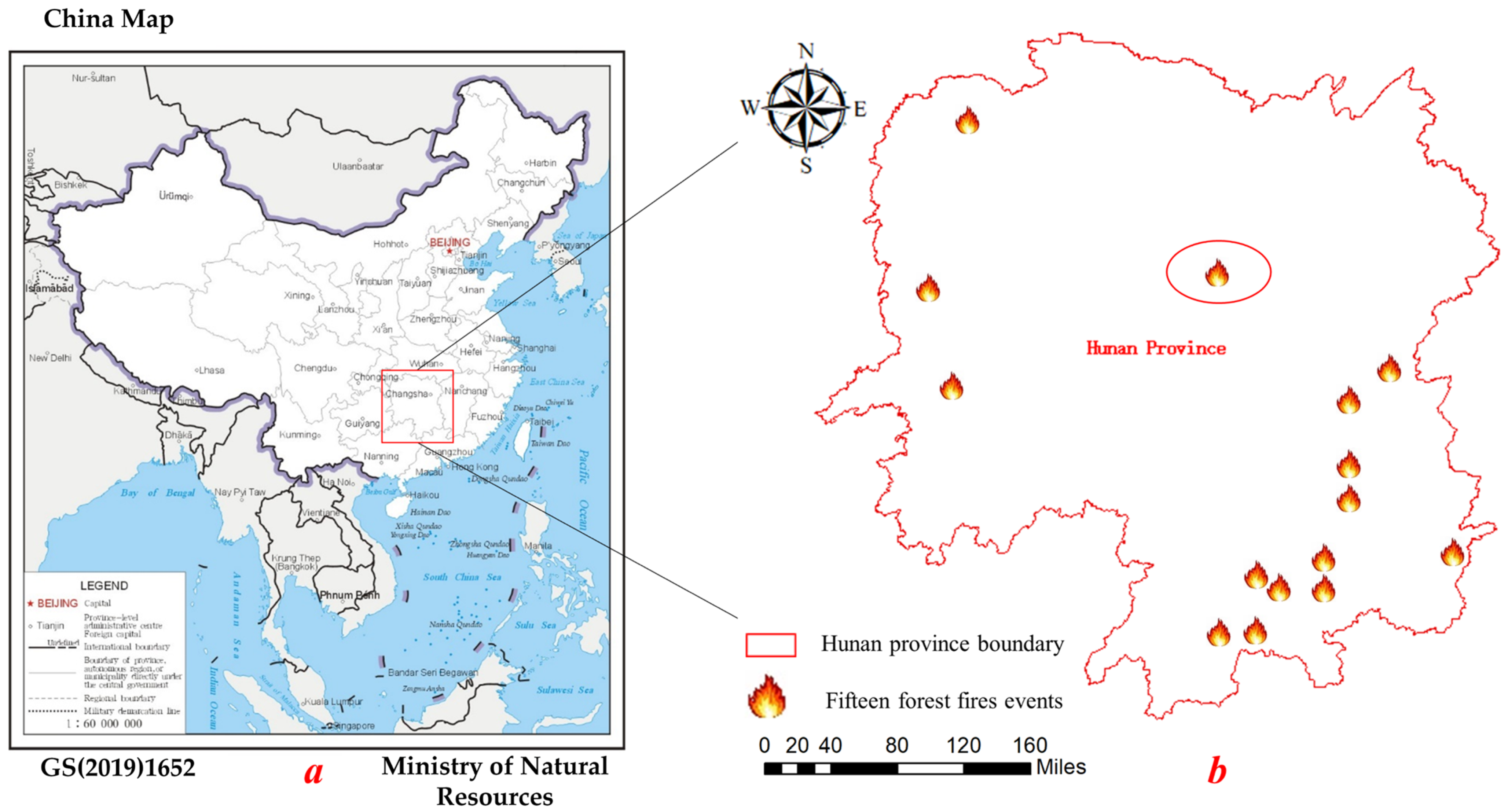
2.1. Study Area
2.2. Satellite Data Processing
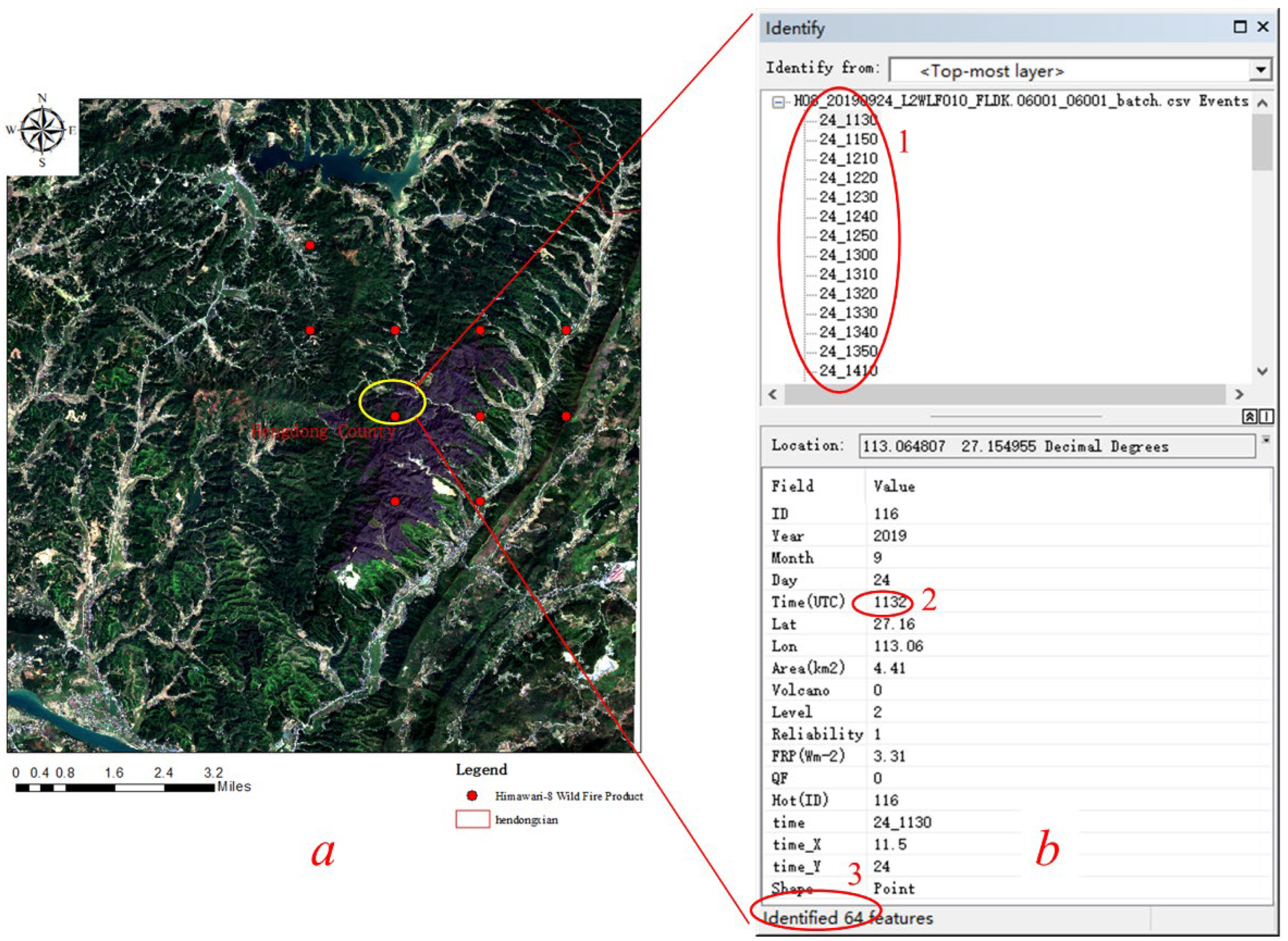
2.3. Input Data Preparation
2.4. Ground Truth Data
2.5. The Proposed MPU-PSA Model
2.5.1. Mixed Pixel-Unmixing (MPU) Analysis
2.5.2. Pixel-Swapping Algorithm (PSA)
2.6. Accuracy Assessment
3. Results
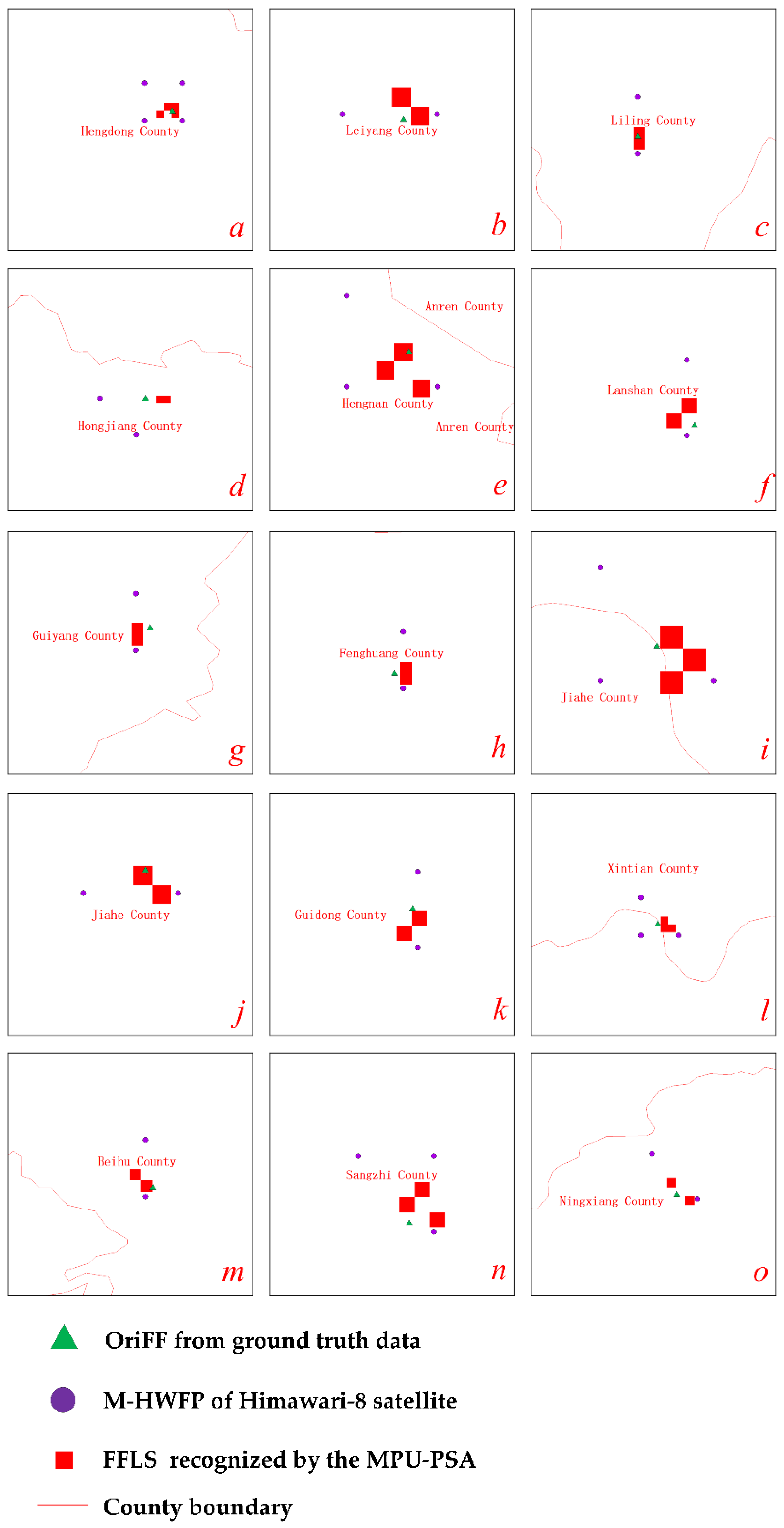
3.1. Forest-Fire Detection
3.2. Comparison of M-HWFP and FFLS in Positioning Accuracy
3.3. Accuracy Comparison between M-HWFP and FFLS
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Administration, N.F. (Ed.) National Forest Fire Prevention Plan (2016–2025); FAO: Beijing, China, 2016. [Google Scholar]
- Sannigrahi, S.; Pilla, F.; Basu, B.; Basu, A.S.; Sarkar, K.; Chakraborti, S.; Joshi, P.K.; Zhang, Q.; Wang, Y.; Bhatt, S.; et al. Examining the effects of forest fire on terrestrial carbon emission and ecosystem production in India using remote sensing approaches. Sci. Total Environ. 2020, 725, 138331. [Google Scholar] [CrossRef] [PubMed]
- Fernandez-Carrillo, A.; McCaw, L.; Tanase, M.A. Estimating prescribed fire impacts and post-fire tree survival in eucalyptus forests of Western Australia with L-band SAR data. Remote Sens. Environ. 2019, 224, 133–144. [Google Scholar] [CrossRef]
- Matin, M.A.; Chitale, V.S.; Murthy, M.S.R.; Uddin, K.; Bajracharya, B.; Pradhan, S. Understanding forest fire patterns and risk in Nepal using remote sensing, geographic information system and historical fire data. Int. J. Wildland Fire 2017, 26, 276–286. [Google Scholar] [CrossRef] [Green Version]
- Forest Fire in Sichuan Province, China in 2019. 4 April 2019. Available online: http://www.lsz.gov.cn/ztzl/lszt/2019ztzl/mlxslhztbbd/yw/201904/t20190404_1171588.html (accessed on 24 December 2021). (In Chinese)
- Forest Fire in Sichuan Province, China in 2020. 31 March 2020. Available online: http://www.xuezhangbb.com/news/tag/67379390 (accessed on 24 December 2021). (In Chinese).
- Forest Fire in Sichuan Province, China in 2021. 20 April 2021. Available online: https://baike.baidu.com/item/4%C2%B720%E5%86%95%E5%AE%81%E6%A3%AE%E6%9E%97%E7%81%AB%E7%81%BE/56798303?fr=aladdin (accessed on 24 December 2021). (In Chinese).
- Jolly, C.; Nimmo, D.; Dickman, C.; Legge, S.; Woinarski, J. Estimating Wildlife Mortality during the 2019–20 Bushfire Season; NESP Threatened Sprecies Recovery Hub Project 8.3.4 Report; NESP: Brisbane, Australia, 2021. [Google Scholar]
- De Bem, P.P.; de Carvalho Júnior, O.A.; Matricardi, E.A.T.; Guimarães, R.F.; Gomes, R.A.T. Predicting wildfire vulnerability using logistic regression and artificial neural networks: A case study in Brazil’s Federal District. Int. J. Wildland Fire 2019, 28, 35–45. [Google Scholar] [CrossRef]
- Cardil, A.; Monedero, S.; Ramirez, J.; Silva, C.A. Assessing and reinitializing wildland fire simulations through satellite active fire data. J. Environ. Manag. 2019, 231, 996–1003. [Google Scholar] [CrossRef]
- Dwomoh, F.K.; Wimberly, M.C.; Cochrane, M.A.; Numata, I. Forest degradation promotes fire during drought in moist tropical forests of Ghana. For. Ecol. Manag. 2019, 440, 158–168. [Google Scholar] [CrossRef]
- He, Y.; Chen, G.; De Santis, A.; Roberts, D.A.; Zhou, Y.; Meentemeyer, R.K. A disturbance weighting analysis model (DWAM) for mapping wildfire burn severity in the presence of forest disease. Remote Sens. Environ. 2019, 221, 108–121. [Google Scholar] [CrossRef]
- Jang, E.; Kang, Y.; Im, J.; Lee, D.-W.; Yoon, J.; Kim, S.-K. Detection and Monitoring of Forest Fires Using Himawari-8 Geostationary Satellite Data in South Korea. Remote Sens. 2019, 11, 271. [Google Scholar] [CrossRef] [Green Version]
- Filizzola, C.; Corrado, R.; Marchese, F.; Mazzeo, G.; Paciello, R.; Pergola, N.; Tramutoli, V. RST-FIRES, an exportable algorithm for early-fire detection and monitoring: Description, implementation, and field validation in the case of the MSG-SEVIRI sensor. Remote Sens. Environ. 2016, 186, 196–216. [Google Scholar] [CrossRef]
- Tien Bui, D.; Hoang, N.D.; Samui, P. Spatial pattern analysis and prediction of forest fire using new machine learning approach of Multivariate Adaptive Regression Splines and Differential Flower Pollination optimization: A case study at Lao Cai province (Viet Nam). J. Environ. Manag. 2019, 237, 476–487. [Google Scholar] [CrossRef]
- Xie, Z.; Song, W.; Ba, R.; Li, X.; Xia, L. A Spatiotemporal Contextual Model for Forest Fire Detection Using Himawari-8 Satellite Data. Remote Sens. 2018, 10, 1992. [Google Scholar] [CrossRef] [Green Version]
- Vikram, R.; Sinha, D.; De, D.; Das, A.K. EEFFL: Energy efficient data forwarding for forest fire detection using localization technique in wireless sensor network. Wirel. Netw. 2020, 26, 5177–5205. [Google Scholar] [CrossRef]
- Kaur, I.; Hüser, I.; Zhang, T.; Gehrke, B.; Kaiser, J. Correcting Swath-Dependent Bias of MODIS FRP Observations With Quantile Mapping. Remote Sens. 2019, 11, 1205. [Google Scholar] [CrossRef] [Green Version]
- Hua, L.; Shao, G. The progress of operational forest fire monitoring with infrared remote sensing. J. For. Res. 2016, 28, 215–229. [Google Scholar] [CrossRef]
- Dozier, J. A Method for Satellite Identification of Surface Temperature Fields of Subpixel Resolution. Remote Sens. Environ. 1981, 11, 221–229. [Google Scholar] [CrossRef]
- Eckmann, T.; Roberts, D.; Still, C. Using multiple endmember spectral mixture analysis to retrieve subpixel fire properties from MODIS. Remote Sens. Environ. 2008, 112, 3773–3783. [Google Scholar] [CrossRef]
- Zhukov, B.; Lorenz, E.; Oertel, D.; Wooster, M.; Roberts, G. Spaceborne detection and characterization of fires during the bi-spectral infrared detection (BIRD) experimental small satellite mission (2001–2004). Remote Sens. Environ. 2006, 100, 29–51. [Google Scholar] [CrossRef]
- Giglio, L.; Schroeder, W. A global feasibility assessment of the bi-spectral fire temperature and area retrieval using MODIS data. Remote Sens. Environ. 2014, 152, 166–173. [Google Scholar] [CrossRef] [Green Version]
- Kaufman, Y.J.; Tucker, C.J.; Fung, I.Y. Remote sensing of biomass burning in the tropics. J. Geophys. Res. 1990, 95, 9927–9939. [Google Scholar] [CrossRef]
- Giglio, L.; Schroeder, W.; Justice, C.O. The collection 6 MODIS active fire detection algorithm and fire products. Remote Sens. Environ. 2016, 178, 31–41. [Google Scholar] [CrossRef] [Green Version]
- Lin, Z.; Chen, F.; Niu, Z.; Li, B.; Yu, B.; Jia, H.; Zhang, M. An active fire detection algorithm based on multi-temporal FengYun-3C VIRR data. Remote Sens. Environ. 2018, 211, 376–387. [Google Scholar] [CrossRef]
- Robinson, J.M. Fire from space: Global fire evaluation using infrared remote sensing. Int. J. Remote Sens. 2007, 12, 3–24. [Google Scholar] [CrossRef]
- Roberts, G.; Wooster, M.J. Development of a multi-temporal Kalman filter approach to geostationary active fire detection & fire radiative power (FRP) estimation. Remote Sens. Environ. 2014, 152, 392–412. [Google Scholar] [CrossRef]
- Moreno, M.V.; Laurent, P.; Ciais, P.; Mouillot, F. Assessing satellite-derived fire patches with functional diversity trait methods. Remote Sens. Environ. 2020, 247, 111897. [Google Scholar] [CrossRef]
- Liu, X.; He, B.; Quan, X.; Yebra, M.; Qiu, S.; Yin, C.; Liao, Z.; Zhang, H. Near Real-Time Extracting Wildfire Spread Rate from Himawari-8 Satellite Data. Remote Sens. 2018, 10, 1654. [Google Scholar] [CrossRef] [Green Version]
- Atkinson, P.M. Mapping Sub-Pixel Boundaries from Remotely Sensed Images; Taylor and Francis: London, UK, 1997; Volume 4, pp. 166–180. [Google Scholar]
- Atkinson, P.M.; Cutler, M.E.J.; Lewis, H. Mapping sub-pixel proportional land cover with AVHRR imagery. Int. J. Remote Sens. 1997, 18, 917–935. [Google Scholar] [CrossRef]
- Wang, Q.; Zhang, C.; Atkinson, P.M. Sub-pixel mapping with point constraints. Remote Sens. Environ. 2020, 244, 111817. [Google Scholar] [CrossRef]
- Wu, S.; Ren, J.; Chen, Z.; Jin, W.; Liu, X.; Li, H.; Pan, H.; Guo, W. Influence of reconstruction scale, spatial resolution and pixel spatial relationships on the sub-pixel mapping accuracy of a double-calculated spatial attraction model. Remote Sens. Environ. 2018, 210, 345–361. [Google Scholar] [CrossRef]
- Yu, W.; Li, J.; Liu, Q.; Zeng, Y.; Zhao, J.; Xu, B.; Yin, G. Global Land Cover Heterogeneity Characteristics at Moderate Resolution for Mixed Pixel Modeling and Inversion. Remote Sens. 2018, 10, 856. [Google Scholar] [CrossRef] [Green Version]
- He, Y.; Yang, J.; Guo, X. Green Vegetation Cover Dynamics in a Heterogeneous Grassland: Spectral Unmixing of Landsat Time Series from 1999 to 2014. Remote Sens. 2020, 12, 3826. [Google Scholar] [CrossRef]
- Shao, Y.; Lan, J. A Spectral Unmixing Method by Maximum Margin Criterion and Derivative Weights to Address Spectral Variability in Hyperspectral Imagery. Remote Sens. 2019, 11, 1045. [Google Scholar] [CrossRef] [Green Version]
- Craig, M.D. Minimum-Volume Transforms for Remotely Sensed Data. IEEE Trans. Geosci. Remote Sens. 1994, 32, 542–552. [Google Scholar] [CrossRef]
- Nascimento, J.M.P.; Dias, J.M.B. Vertex component analysis: A fast algorithm to unmix hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2005, 43, 898–910. [Google Scholar] [CrossRef] [Green Version]
- Chang, C.I.; Wu, C.C.; Liu, W.; Ouyang, Y.C. A New Growing Method for Simplex-Based Endmember Extraction Algorithm. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2804–2819. [Google Scholar] [CrossRef]
- Miao, L.; Qi, H. Endmember Extraction From Highly Mixed Data Using Minimum Volume Constrained Nonnegative Matrix Factorization. IEEE Trans. Geosci. Remote Sens. 2007, 45, 765–777. [Google Scholar] [CrossRef]
- Zhang, J.; Rivard, B.; Rogge, D.M. The Successive Projection Algorithm (SPA), an Algorithm with a Spatial Constraint for the Automatic Search of Endmembers in Hyperspectral Data. Sensors 2008, 8, 1321–1342. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Winter, M.E. N-FINDR: An algorithm for fast autonomous spectral end-member determination in hyperspectral data. In Proceedings of the SPIE Conference on lmacjincj Spectrometry V, Denver, CO, USA, 18–23 July 1999; pp. 266–275. [Google Scholar]
- Atkinson, P.M. Sub-pixel Target Mapping from Soft-classified, Remotely Sensed Imagery. Photogramm. Eng. Remote Sens. 2005, 71, 839–846. [Google Scholar] [CrossRef] [Green Version]
- Wang, Q.M.; Atkinson, P.M. The effect of the point spread function on sub-pixel mapping. Remote Sens. Environ. 2017, 193, 127–137. [Google Scholar] [CrossRef] [Green Version]
- Kumar, U.; Ganguly, S.; Nemani, R.R.; Raja, K.S.; Milesi, C.; Sinha, R.; Michaelis, A.; Votava, P.; Hashimoto, H.; Li, S.; et al. Exploring Subpixel Learning Algorithms for Estimating Global Land Cover Fractions from Satellite Data Using High Performance Computing. Remote Sens. 2017, 9, 1105. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Chen, Q.; Ding, M.; Li, J. High Precision Dimensional Measurement with Convolutional Neural Network and Bi-Directional Long Short-Term Memory (LSTM). Sensors 2019, 19, 5302. [Google Scholar] [CrossRef] [Green Version]
- Hu, C. A novel ocean color index to detect floating algae in the global oceans. Remote Sens. Environ. 2009, 113, 2118–2129. [Google Scholar] [CrossRef]
- Salomonson, V.V.; Appel, I. Estimating fractional snow cover from MODIS using the normalized difference snow index. Remote Sens. Environ. 2004, 89, 351–360. [Google Scholar] [CrossRef]
- Salomonson, V.V.; Appel, I. Development of the Aqua MODIS NDSI fractional snow cover algorithm and validation results. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1747–1756. [Google Scholar] [CrossRef]
- He, Y.; Chen, G.; Potter, C.; Meentemeyer, R.K. Integrating multi-sensor remote sensing and species distribution modeling to map the spread of emerging forest disease and tree mortality. Remote Sens. Environ. 2019, 231, 111238. [Google Scholar] [CrossRef]
- Li, L.; Chen, Y.; Xu, T.; Shi, K.; Liu, R.; Huang, C.; Lu, B.; Meng, L. Remote Sensing of Wetland Flooding at a Sub-Pixel Scale Based on Random Forests and Spatial Attraction Models. Remote Sens. 2019, 11, 1231. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Chen, R.; Foody, G.M.; Wang, L.; Yang, X.; Du, Y.; Ling, F. Spatio-Temporal Sub-Pixel Land Cover Mapping of Remote Sensing Imagery Using Spatial Distribution Information From Same-Class Pixels. Remote Sens. 2020, 12, 503. [Google Scholar] [CrossRef] [Green Version]
- Ling, F.; Li, X.; Foody, G.M.; Boyd, D.; Ge, Y.; Li, X.; Du, Y. Monitoring surface water area variations of reservoirs using daily MODIS images by exploring sub-pixel information. ISPRS J. Photogramm. Remote Sens. 2020, 168, 141–152. [Google Scholar] [CrossRef]
- Deng, C.; Zhu, Z. Continuous subpixel monitoring of urban impervious surface using Landsat time series. Remote Sens. Environ. 2020, 238, 110929. [Google Scholar] [CrossRef]
- Bessho, K.; Date, K.; Hayashi, M.; Ikeda, A.; Imai, T.; Inoue, H.; Kumagai, Y.; Miyakawa, T.; Murata, H.; Ohno, T.; et al. An Introduction to Himawari-8/9—Japan’s New-Generation Geostationary Meteorological Satellites. J. Meteorol. Soc. Japan. Ser. II 2016, 94, 151–183. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Zhang, Q.; Zhang, G.; Nie, Z.; Gui, Z.; Que, H. A Novel Hybrid Data-Driven Model for Daily Land Surface Temperature Forecasting Using Long Short-Term Memory Neural Network Based on Ensemble Empirical Mode Decomposition. Int. J. Environ. Res. Public Health 2018, 15, 1032. [Google Scholar] [CrossRef] [Green Version]
- Wang, F.; Yang, M.; Ma, L.; Zhang, T.; Qin, W.; Li, W.; Zhang, Y.; Sun, Z.; Wang, Z.; Li, F.; et al. Estimation of Above-Ground Biomass of Winter Wheat Based on Consumer-Grade Multi-Spectral UAV. Remote Sens. 2022, 14, 1251. [Google Scholar] [CrossRef]
- Vafaei, S.; Soosani, J.; Adeli, K.; Fadaei, H.; Naghavi, H.; Pham, T.; Tien Bui, D. Improving Accuracy Estimation of Forest Aboveground Biomass Based on Incorporation of ALOS-2 PALSAR-2 and Sentinel-2A Imagery and Machine Learning: A Case Study of the Hyrcanian Forest Area (Iran). Remote Sens. 2018, 10, 172. [Google Scholar] [CrossRef] [Green Version]
- Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE)?—Arguments against avoiding RMSE in the literature. Geosci. Model Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef] [Green Version]
- Li, H.; Kato, T.; Hayashi, M.; Wu, L. Estimation of Forest Aboveground Biomass of Two Major Conifers in Ibaraki Prefecture, Japan, from PALSAR-2 and Sentinel-2 Data. Remote Sens. 2022, 14, 468. [Google Scholar] [CrossRef]
- An, G.; Xing, M.; He, B.; Liao, C.; Huang, X.; Shang, J.; Kang, H. Using Machine Learning for Estimating Rice Chlorophyll Content from In Situ Hyperspectral Data. Remote Sens. 2020, 12, 3104. [Google Scholar] [CrossRef]
- Kurihara, Y.; Tanada, K.; Murakami, H.; Kachi, M. Australian bushfire captured by AHI/Himawari-8 and SGLI/GCOM-C. In Proceedings of the JpGU-AGU Joint Meeting 2020, Chiba, Japan, 24–28 May 2020. [Google Scholar]
- JAXA Himawari Monitor User’s Guide. Available online: https://www.eorc.jaxa.jp/ptree/userguide.html (accessed on 26 December 2021).
- Wu, X.; Gao, N.; Zheng, X.; Tao, X.; He, Y.; Liu, Z.; Wang, Y. Self-Powered and Green Ionic-Type Thermoelectric Paper Chips for Early Fire Alarming. ACS Appl. Mater. Interfaces 2020, 12, 27691–27699. [Google Scholar] [CrossRef] [PubMed]
- Yao, J.; Raffuse, S.M.; Brauer, M.; Williamson, G.J.; Bowman, D.M.J.S.; Johnston, F.H.; Henderson, S.B. Predicting the minimum height of forest fire smoke within the atmosphere using machine learning and data from the CALIPSO satellite. Remote Sens. Environ. 2018, 206, 98–106. [Google Scholar] [CrossRef]
- Li, X.; Song, W.; Lian, L.; Wei, X. Forest Fire Smoke Detection Using Back-Propagation Neural Network Based on MODIS Data. Remote Sens. 2015, 7, 4473–4498. [Google Scholar] [CrossRef] [Green Version]
- Ciullo, V.; Rossi, L.; Pieri, A. Experimental Fire Measurement with UAV Multimodal Stereovision. Remote Sens. 2020, 12, 3546. [Google Scholar] [CrossRef]
- Rosas-Romero, R. Remote detection of forest fires from video signals with classifiers based on K-SVD learned dictionaries. Eng. Appl. Artif. Intell. 2014, 33, 53. [Google Scholar] [CrossRef]
- Ruescas, A.B.; Sobrino, J.A.; Julien, Y.; Jiménez-Muñoz, J.C.; Sòria, G.; Hidalgo, V.; Atitar, M.; Franch, B.; Cuenca, J.; Mattar, C. Mapping sub-pixel burnt percentage using AVHRR data. Application to the Alcalaten area in Spain. Int. J. Remote Sens. 2010, 31, 5315–5330. [Google Scholar] [CrossRef]


| Satellite | Sensor | Band Number | Band Width (μm) | Spatial Resolution (m) |
|---|---|---|---|---|
| Himawari-8 | AHI | 7 | 3.74~3.96 | 2000 |
| 14 | 11.10~11.30 | 2000 | ||
| Sentinel 2 | MSI | 2 | 0.46~0.52 | 10 |
| 3 | 0.54~0.58 | 10 | ||
| 4 | 0.65~0.68 | 10 | ||
| 8 | 0.79~0.90 | 10 | ||
| Landsat 8 | OLI | 2 | 0.45~0.51 | 30 |
| 3 | 0.53~0.59 | 30 | ||
| 4 | 0.64~0.67 | 30 | ||
| 5 | 0.85~0.88 | 30 | ||
| 8 | 0.50~0.68 | 15 |
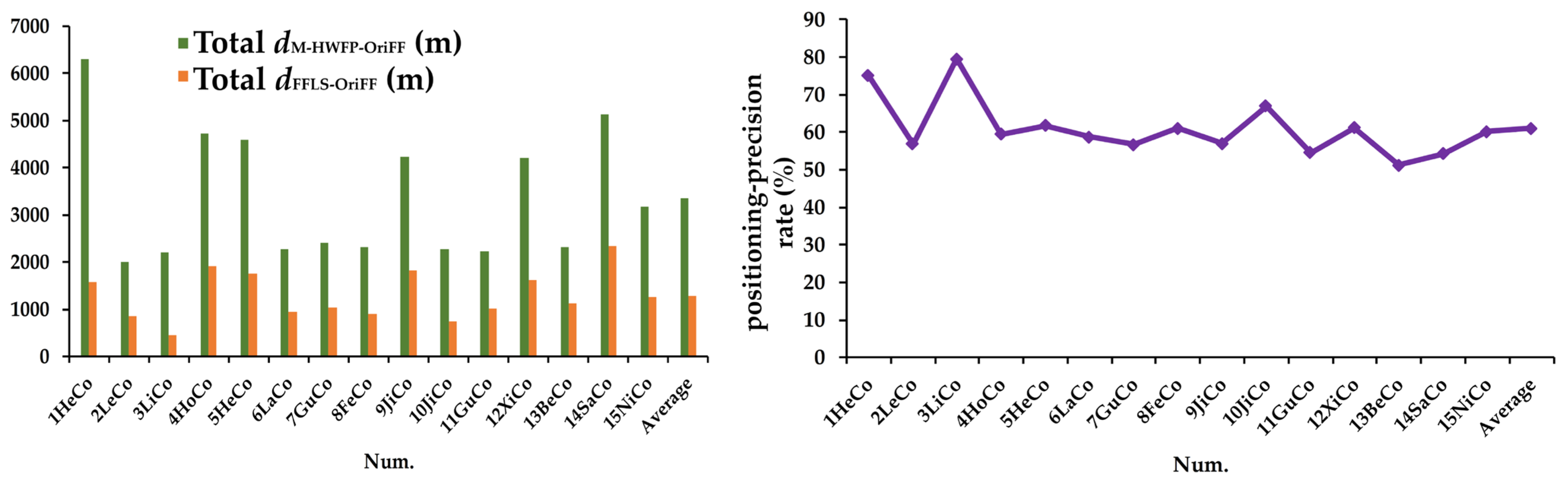
| Num. | Easting and Northing | Total dM-HWFP-OriFF (m) | Total dFFLS-OriFF (m) | PPR (%) | |||||
|---|---|---|---|---|---|---|---|---|---|
| OriFF | M-HWFP | FFLS | |||||||
| Easting (m) | Northing (m) | Easting (m) | Northing (m) | Easting (m) | Northing (m) | ||||
| 1HeCo | 705,596.58 | 3,006,410.92 | 704,082.66 | 3,008,048.47 | 704,954.05 | 3,006,231.03 | 6294.90 | 1573.00 | 75.01 |
| 705,596.58 | 3,006,410.92 | 706,064.56 | 3,008,081.20 | 705,343.10 | 3,006,680.72 | ||||
| 705,596.58 | 3,006,410.92 | 704,119.06 | 3,005,832.40 | 705,739.46 | 3,006,687.27 | ||||
| 705,596.58 | 3,006,410.92 | 706,101.31 | 3,005,865.10 | 705,746.79 | 3,006,244.13 | ||||
| 2LeCo | 702,756.60 | 2,923,687.72 | 701,458.01 | 2,923,778.10 | 702,698.15 | 2,924,196.13 | 2008.86 | 866.57 | 56.86 |
| 702,756.60 | 2,923,687.72 | 703,453.15 | 2,923,809.56 | 703,104.11 | 2,923,759.34 | ||||
| 3LiCo | 731,319.58 | 3,035,796.60 | 731,290.37 | 3,037,348.07 | 731,360.44 | 3,035,955.75 | 2216.78 | 452.59 | 79.58 |
| 731,319.58 | 3,035,796.60 | 731,332.09 | 3,035,131.68 | 731,368.78 | 3,035,512.54 | ||||
| 4HoCo | 389,661.48 | 3,015,656.00 | 387,151.62 | 3,015,747.42 | 390,419.76 | 3,015,657.80 | 4722.92 | 1912.50 | 59.51 |
| 389,661.48 | 3,015,656.00 | 389,111.73 | 3,013,514.02 | 390,815.69 | 3,015,654.38 | ||||
| 5HeCo | 708,216.34 | 2,960,200.00 | 706,831.09 | 2,961,544.35 | 707,705.02 | 2,959,734.72 | 4592.03 | 1754.73 | 61.79 |
| 708,216.34 | 2,960,200.00 | 706,867.31 | 2,959,328.37 | 708,095.58 | 2,960,184.38 | ||||
| 708,216.34 | 2,960,200.00 | 708,856.95 | 2,959,361.04 | 708,508.02 | 2,959,304.68 | ||||
| 6LaCo | 630,975.42 | 2,807,970.71 | 630,761.87 | 2,809,876.75 | 630,434.73 | 2,808,518.79 | 2281.77 | 942.67 | 58.69 |
| 630,975.42 | 2,807,970.71 | 630,783.42 | 2,807,661.70 | 630,841.40 | 2,808,079.76 | ||||
| 7GuCo | 688,789.37 | 2,866,830.81 | 688,294.29 | 2,868,175.04 | 688,365.96 | 2,866,811.21 | 2419.37 | 1046.73 | 56.74 |
| 688,789.37 | 2,866,830.81 | 688,326.07 | 2,865,959.45 | 688,372.32 | 2,866,368.16 | ||||
| 8FeCo | 369,975.51 | 3,102,917.48 | 370,279.78 | 3,104,551.89 | 370,363.30 | 3,102,703.42 | 2307.95 | 897.46 | 61.11 |
| 369,975.51 | 3,102,917.48 | 370,255.77 | 3,102,336.03 | 370,368.09 | 3,103,146.51 | ||||
| 9JiCo | 631,515.70 | 2,846,529.30 | 630,393.03 | 2,847,533.50 | 631,671.98 | 2,846,185.04 | 4242.42 | 1821.94 | 57.05 |
| 631,515.70 | 2,846,529.30 | 630,414.86 | 2,845,318.35 | 631,680.80 | 2,845,299.13 | ||||
| 631,515.70 | 2,846,529.30 | 632,421.46 | 2,845,338.26 | 632,077.63 | 2,845,746.08 | ||||
| 10JiCo | 645,860.26 | 2,839,339.22 | 644,533.72 | 2,838,818.48 | 645,793.16 | 2,839,244.63 | 2269.30 | 747.91 | 67.04 |
| 645,860.26 | 2,839,339.22 | 646,541.41 | 2,838,840.48 | 646,199.49 | 2,838,806.07 | ||||
| 11GuCo | 790,268.92 | 2,875,627.18 | 790,351.29 | 2,876,689.63 | 790,025.81 | 2,874,871.95 | 2230.77 | 1013.74 | 54.56 |
| 790,268.92 | 2,875,627.18 | 790,400.46 | 2,874,473.01 | 790,416.67 | 2,875,324.08 | ||||
| 12XiCo | 631,319.73 | 2,845,985.37 | 630,393.03 | 2,847,533.50 | 631,671.99 | 2,846,185.04 | 4206.16 | 1631.44 | 61.21 |
| 631,319.73 | 2,845,985.37 | 630,414.86 | 2,845,318.35 | 631,676.40 | 2,845,742.08 | ||||
| 631319.73 | 2,845,985.37 | 632,421.46 | 2,845,338.26 | 632,077.64 | 2,845,746.07 | ||||
| 13BeCo | 687,060.14 | 2,844,208.01 | 686,604.09 | 2,845,990.97 | 686,280.65 | 2,844,182.18 | 2320.74 | 1130.68 | 51.28 |
| 687,060.14 | 2,844,208.01 | 686,635.30 | 2,843,775.45 | 686,675.78 | 2,844,630.86 | ||||
| 14SaCo | 404,309.30 | 3,255,150.96 | 403,012.85 | 3,257,151.48 | 405,033.63 | 3,255,261.12 | 5136.11 | 2351.74 | 54.21 |
| 404,309.30 | 3,255,150.96 | 404,952.70 | 3,257,135.00 | 404,653.13 | 3,256,150.69 | ||||
| 404,309.30 | 3,255,150.96 | 404,934.07 | 3,254,918.86 | 404,261.44 | 3,255,710.81 | ||||
| 15NiCo | 599,212.52 | 3,119,992.26 | 598,124.89 | 3,121,978.22 | 598,986.92 | 3,120,578.12 | 3183.05 | 1266.23 | 60.22 |
| 599,212.52 | 3,119,992.26 | 600,106.15 | 3,119,778.82 | 599,779.36 | 3,119,698.53 | ||||
| Average | 3362.21 | 1294.00 | 60.99 | ||||||
| Num. | RMSE | MAE | ||||
|---|---|---|---|---|---|---|
| M-HWFP (m) | FFLS (m) | Decrease of RMSE (%) | M-HWFP (m) | FFLS (m) | Decrease of MAE (%) | |
| 1HeCo | 1486.79 | 381.95 | 74.31 | 1258.98 | 314.60 | 75.01 |
| 2LeCo | 855.29 | 359.53 | 57.96 | 669.62 | 288.86 | 56.86 |
| 3LiCo | 1193.77 | 234.63 | 80.35 | 1108.39 | 226.30 | 79.58 |
| 4HoCo | 1673.17 | 690.51 | 58.73 | 1180.73 | 478.13 | 59.51 |
| 5HeCo | 1218.20 | 525.25 | 56.88 | 918.41 | 350.95 | 61.79 |
| 6LaCo | 1380.39 | 557.94 | 59.58 | 1140.88 | 471.34 | 58.69 |
| 7GuCo | 1230.04 | 532.74 | 56.69 | 1209.69 | 523.37 | 56.74 |
| 8FeCo | 891.70 | 317.33 | 64.41 | 576.99 | 224.36 | 61.11 |
| 9JiCo | 1251.74 | 550.63 | 56.01 | 1060.61 | 455.49 | 57.06 |
| 10JiCo | 740.75 | 287.33 | 61.21 | 453.86 | 149.58 | 67.04 |
| 11GuCo | 596.27 | 295.13 | 50.50 | 318.68 | 144.82 | 54.56 |
| 12XiCo | 1240.13 | 495.49 | 60.05 | 1051.54 | 407.86 | 61.21 |
| 13BeCo | 1345.00 | 568.12 | 57.76 | 1160.37 | 565.34 | 51.28 |
| 14SaCo | 1868.81 | 810.39 | 56.64 | 1712.04 | 783.91 | 54.21 |
| 15NiCo | 1410.81 | 516.95 | 63.36 | 1061.02 | 422.08 | 60.22 |
| Average | 1225.52 | 474.93 | 60.96 | 992.12 | 387.13 | 60.99 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, H.; Zhang, G.; Zhou, Z.; Zhou, X.; Zhou, C. Forest Fire Monitoring and Positioning Improvement at Subpixel Level: Application to Himawari-8 Fire Products. Remote Sens. 2022, 14, 2460. https://doi.org/10.3390/rs14102460
Xu H, Zhang G, Zhou Z, Zhou X, Zhou C. Forest Fire Monitoring and Positioning Improvement at Subpixel Level: Application to Himawari-8 Fire Products. Remote Sensing. 2022; 14(10):2460. https://doi.org/10.3390/rs14102460
Chicago/Turabian StyleXu, Haizhou, Gui Zhang, Zhaoming Zhou, Xiaobing Zhou, and Cui Zhou. 2022. "Forest Fire Monitoring and Positioning Improvement at Subpixel Level: Application to Himawari-8 Fire Products" Remote Sensing 14, no. 10: 2460. https://doi.org/10.3390/rs14102460
APA StyleXu, H., Zhang, G., Zhou, Z., Zhou, X., & Zhou, C. (2022). Forest Fire Monitoring and Positioning Improvement at Subpixel Level: Application to Himawari-8 Fire Products. Remote Sensing, 14(10), 2460. https://doi.org/10.3390/rs14102460









