Precipitation-Use Efficiency and Its Conversion with Climate Types in Mainland China
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data
2.3. Methods
3. Results
3.1. ETa Estimation and Its Change Characteristics
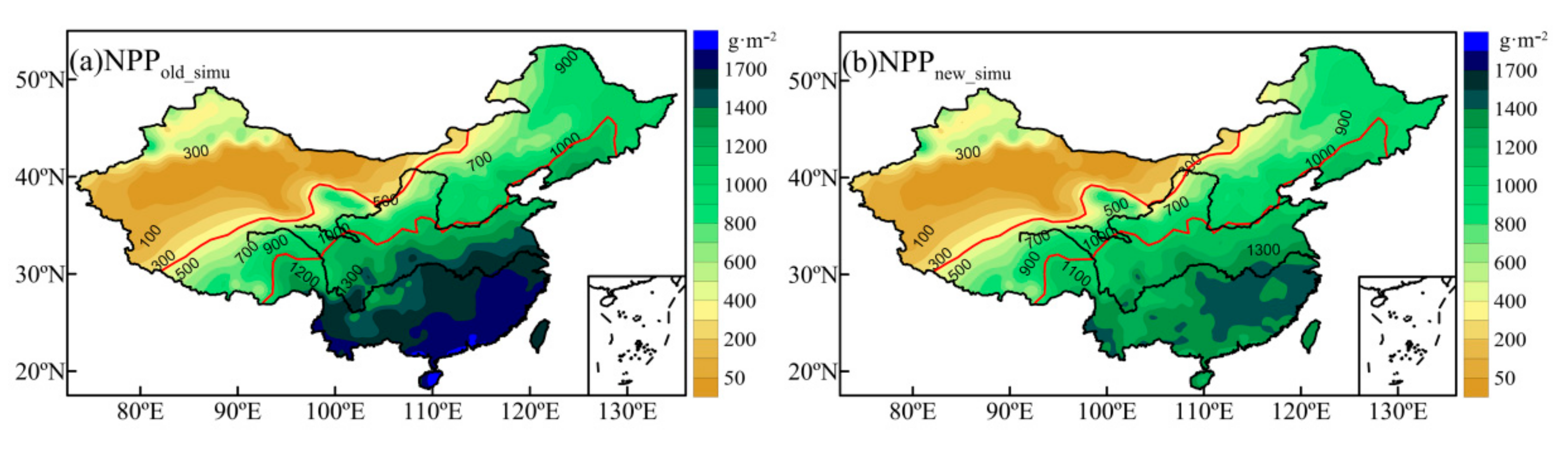
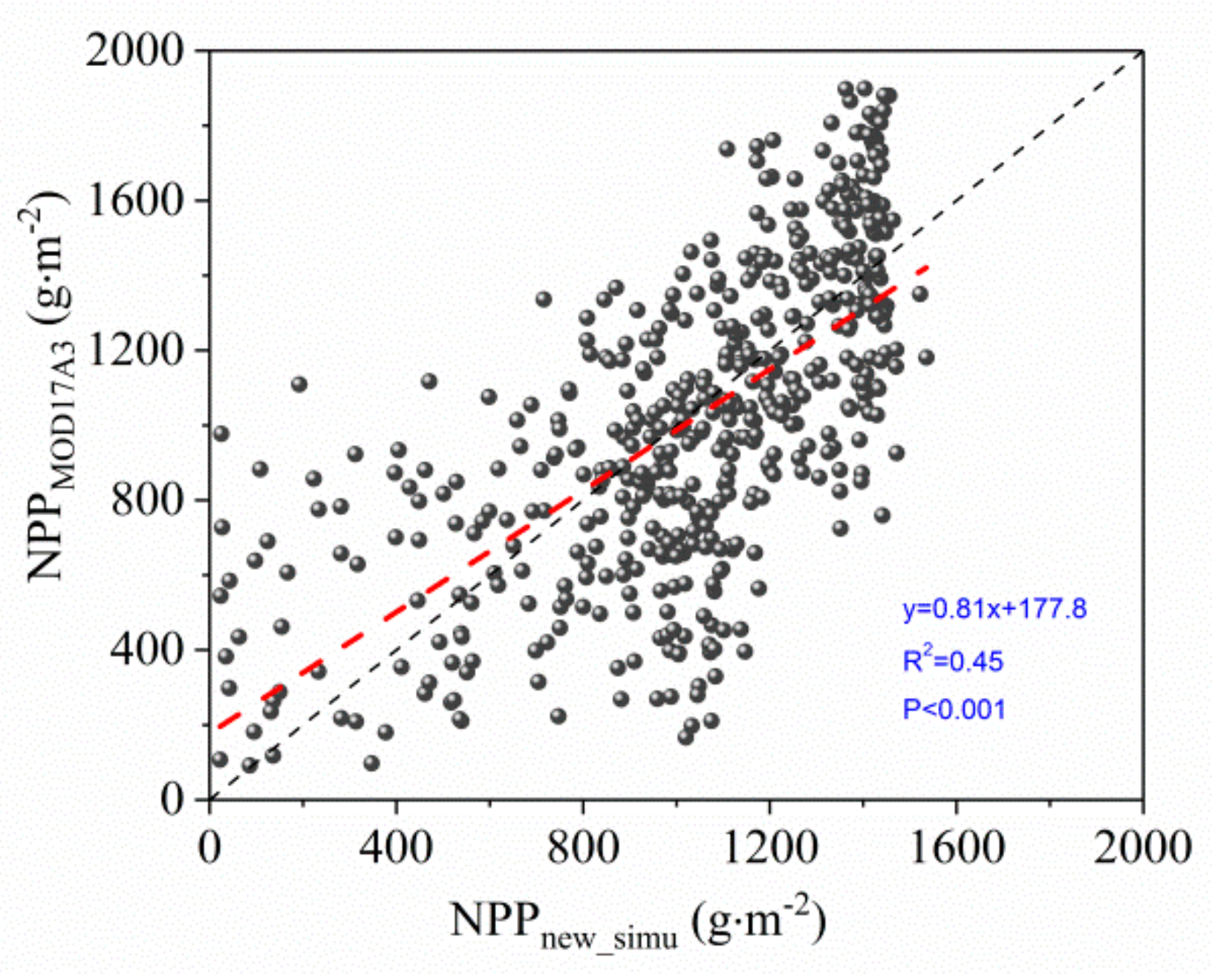
3.2. NPP Estimation and Change Characteristics
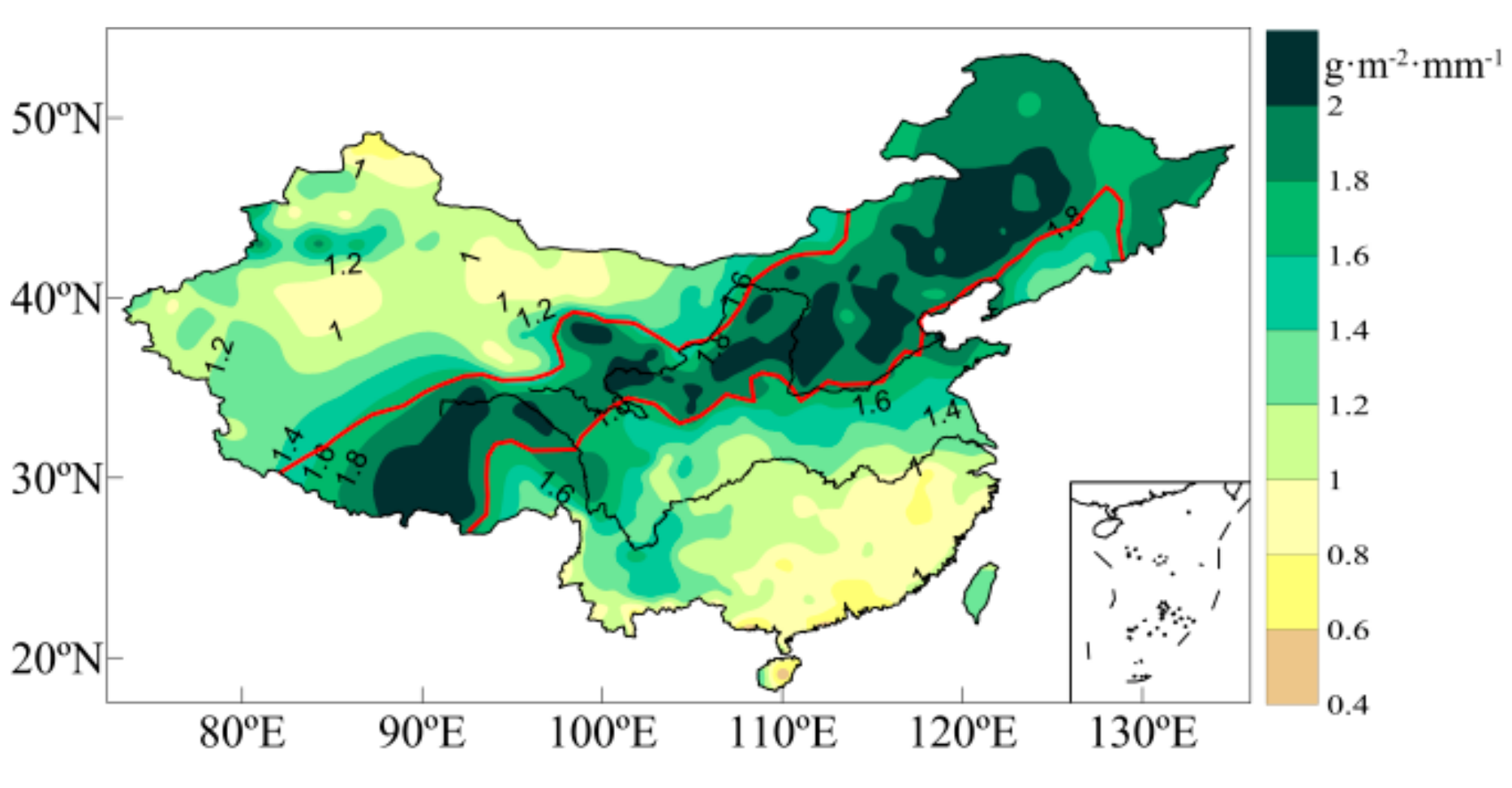
3.3. Spatial Distribution and Temporal Variation in PUE
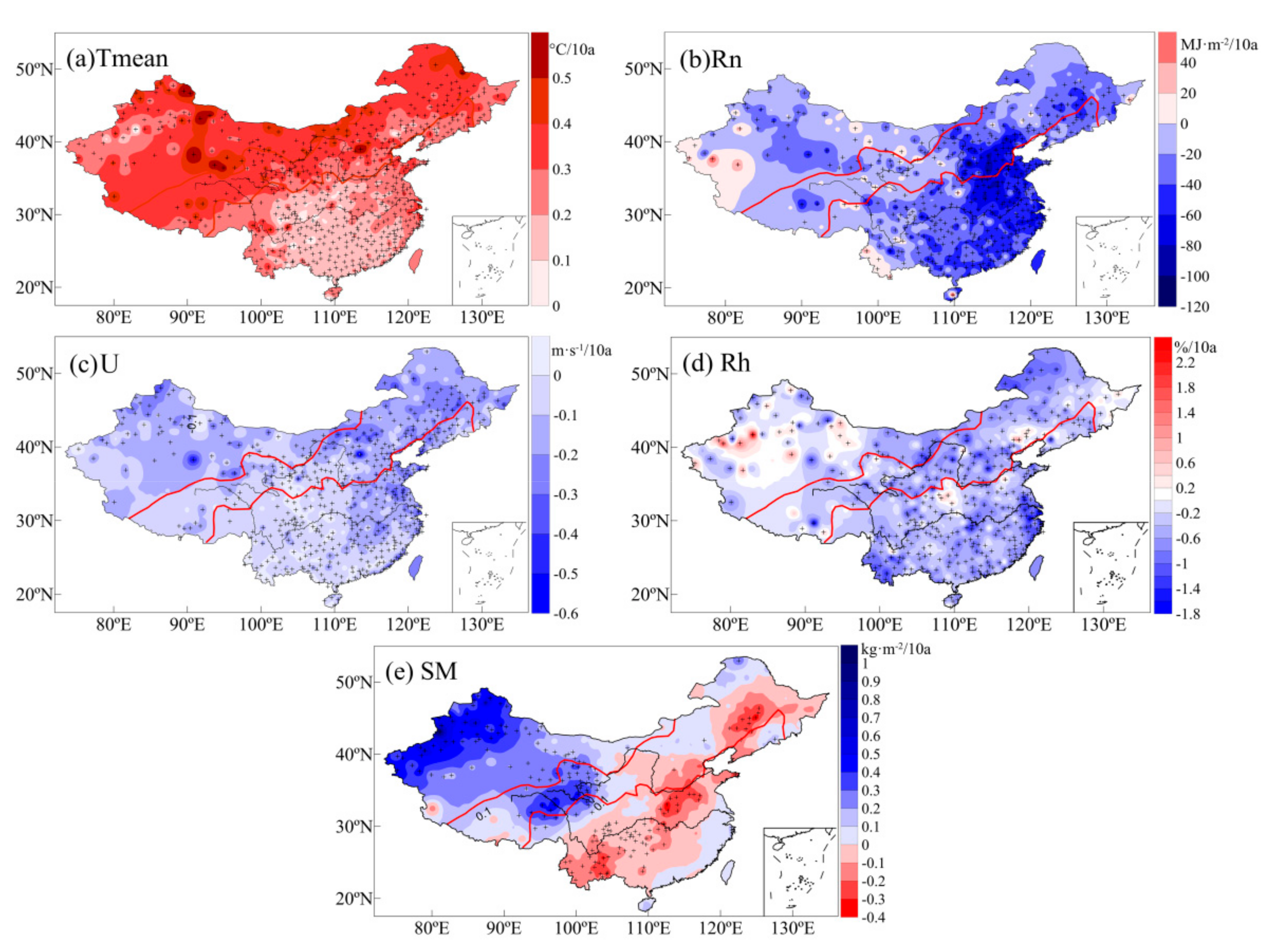
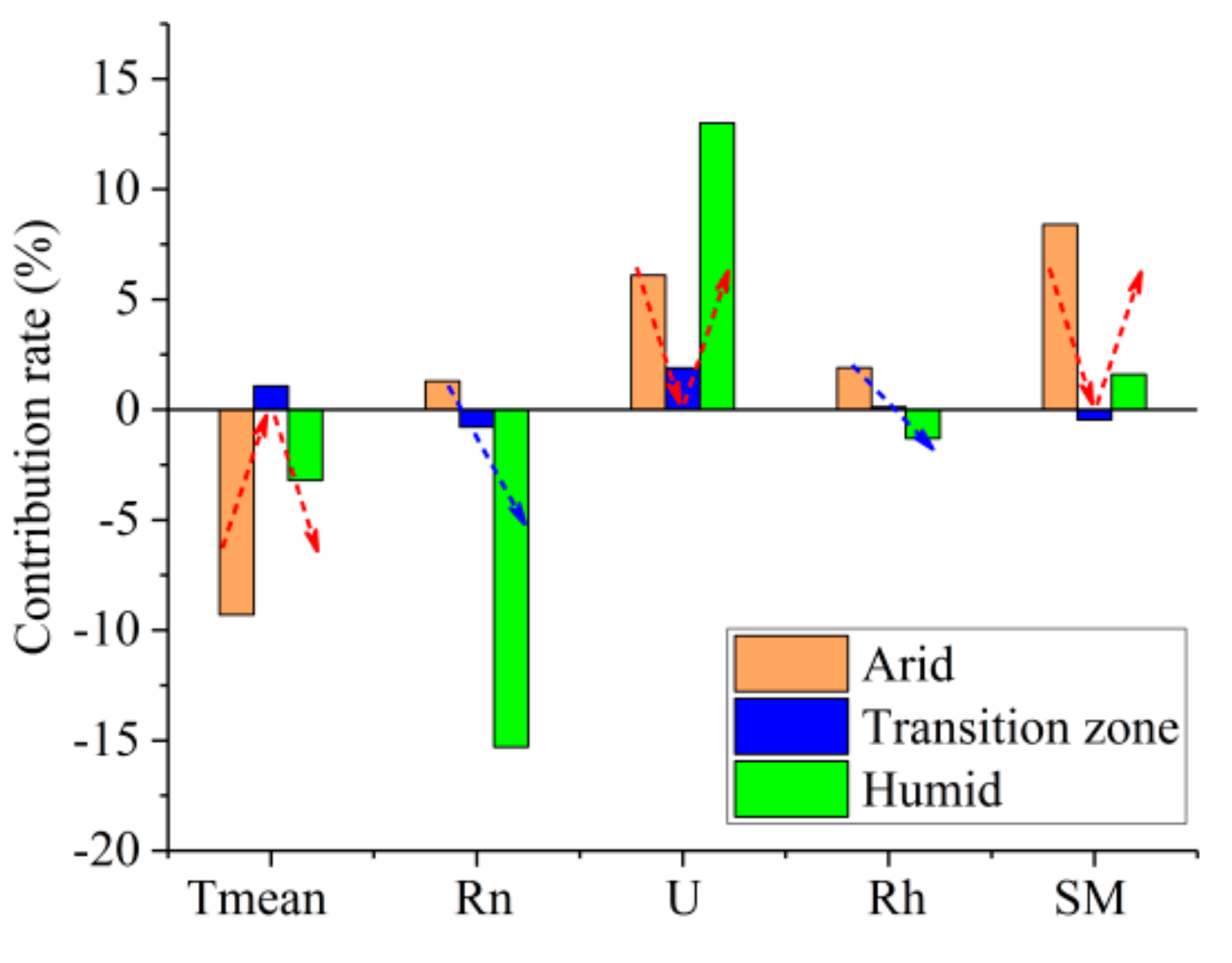
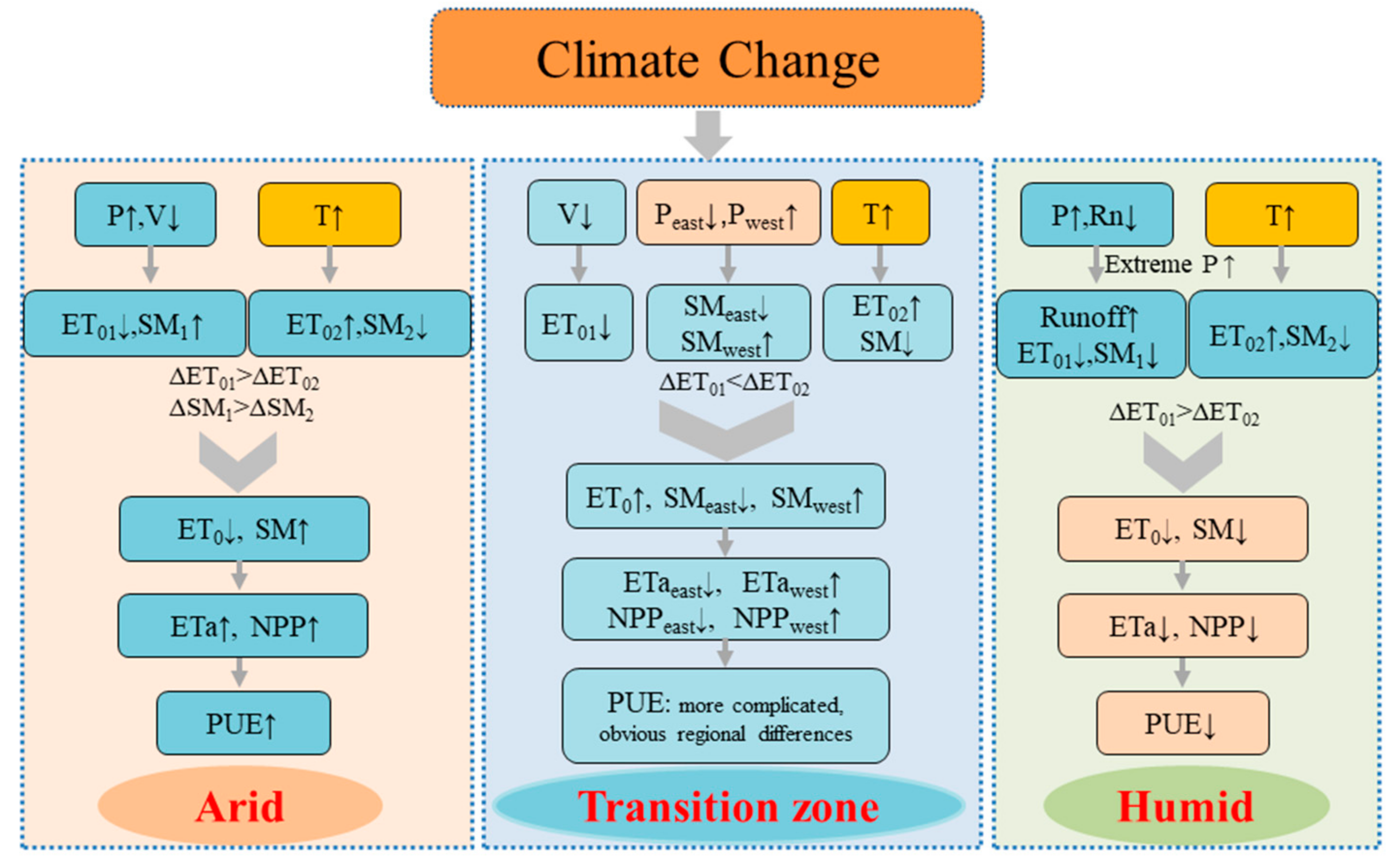
3.4. Driving Force of PUE Changes and Its Corresponding Conversion Characteristics
4. Discussion
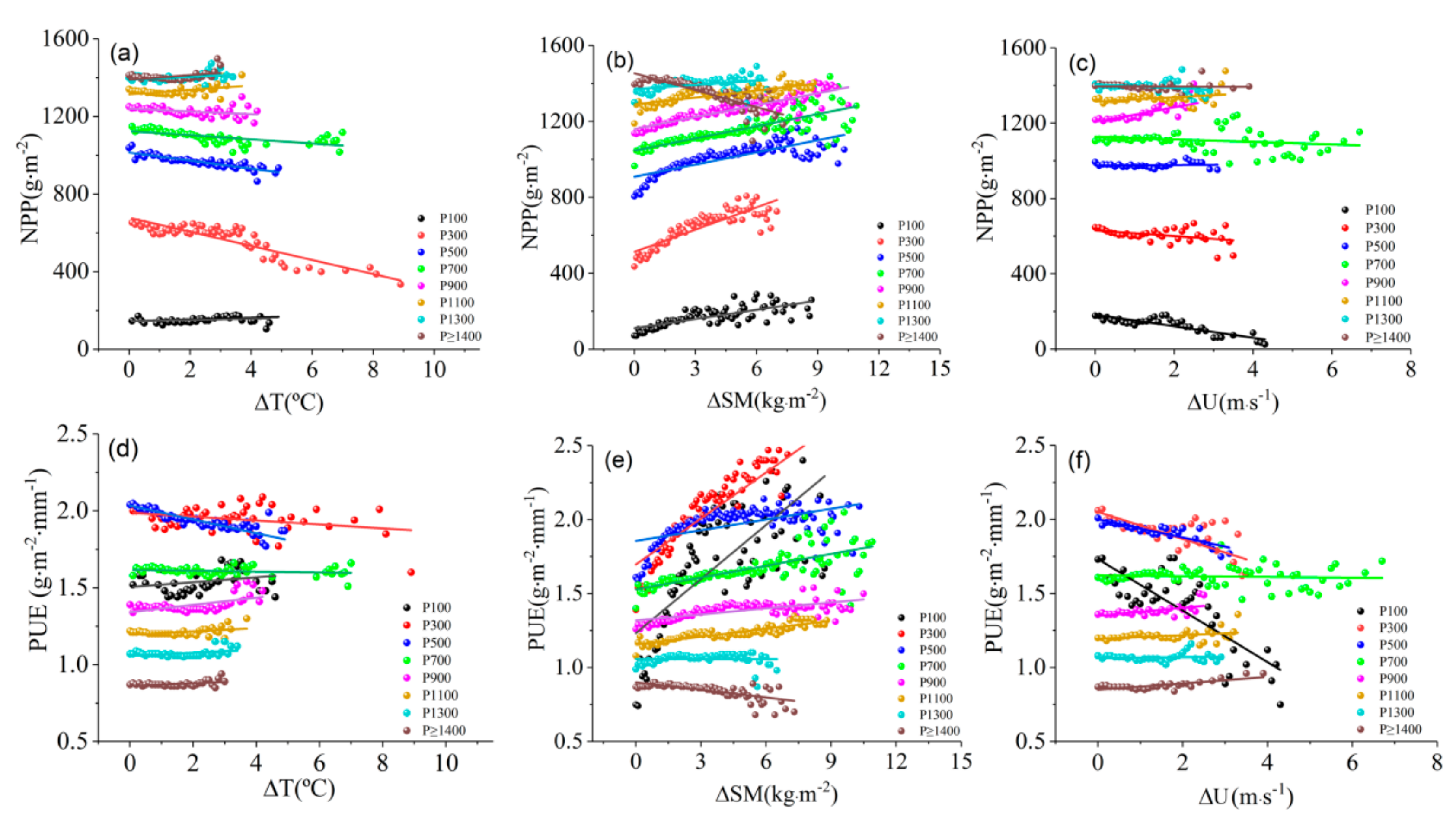
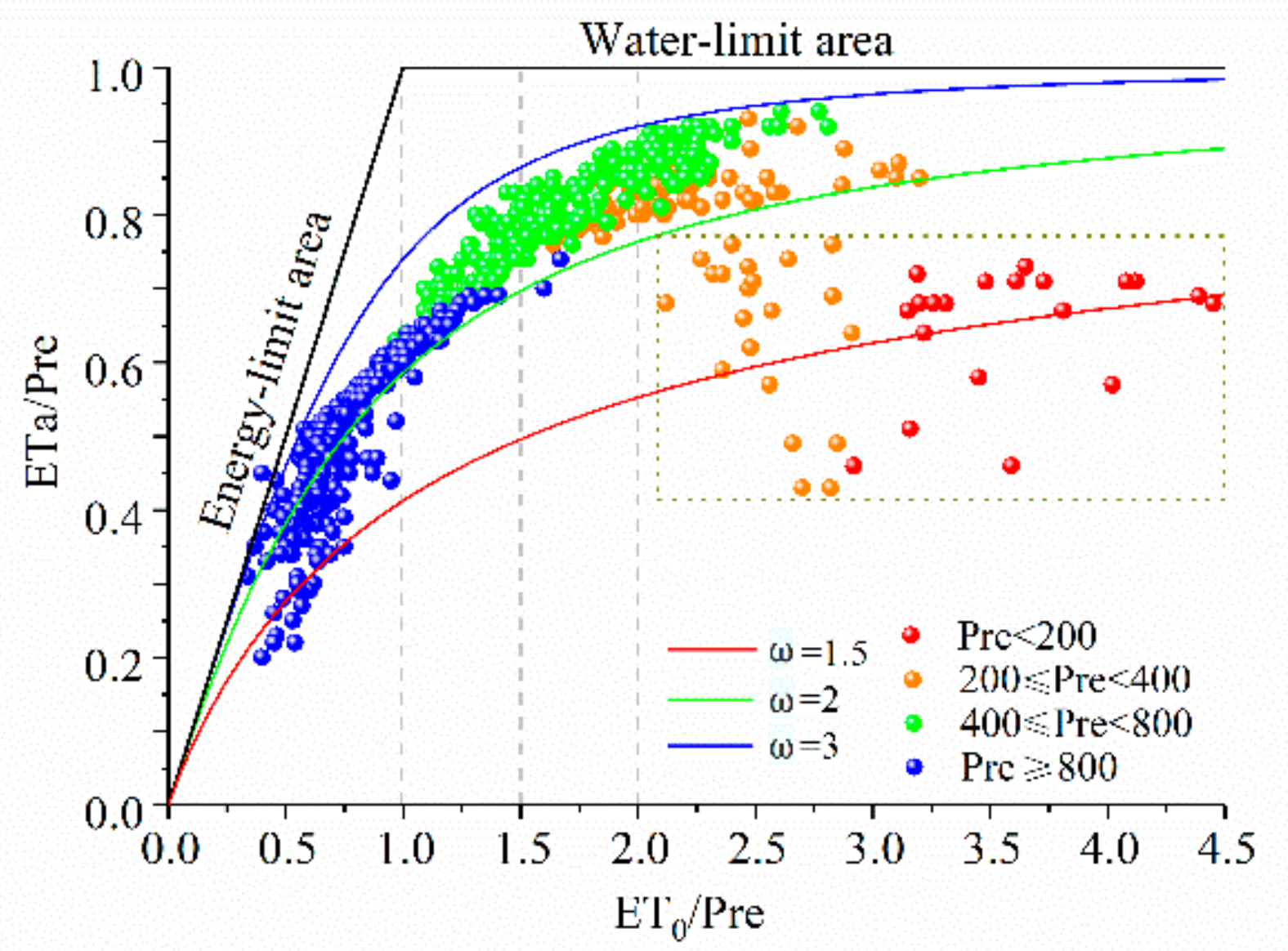
4.1. Effect of Energy and Water on ETa in Different Climatic Regions of China
4.2. Complexity of PUE Change in Transition Zone
4.3. Transformation Characteristics of PUE
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Piao, S.L.; Zhang, X.P.; Chen, A.P.; Liu, Q.; Lian, X.; Wang, H.X.; Peng, S.S.; Wu, X.C. The impacts of climate extremes on the terrestrial carbon cycle: A review. Sci. China Earth Sci. 2019, 62, 1551–1563. [Google Scholar] [CrossRef]
- IPCC. Climate Change 2021: The Physical Science Basis. M/OL]. 2021 [2021-08-09]. Available online: https://www.ipcc.ch/report/ar6/wg1/downloads/report/IPCC_AR6_WGI_Full_Report.pdf (accessed on 9 August 2021).
- Mu, Q.Z.; Zhao, M.S.; Running, S.W.; Liu, M.L.; Tian, H.Q. Contribution of increasing CO2 and climate change to the carbon cycle in China’s ecosystems. J. Geophys. Res. Biogeosci. 2015, 113, G01018. [Google Scholar] [CrossRef] [Green Version]
- Xu, X.T.; Piao, S.L.; Wang, X.H.; Chen, A.P.; Ciais, P.; Myneni, R.B. Spatio-temporal patterns of the area experiencing negative vegetation growth anomalies in China over the last three decades. Environ. Res. Lett. 2012, 7, 035701. [Google Scholar] [CrossRef]
- Hao, Y.B.; Wang, Y.F.; Cui, X.Y. Drought stress reduces the carbon accumulation of the Leymus chinensis steppe in Inner Mongolia, China. Chin. J. Plant Ecol. 2010, 34, 898–906. (In Chinese) [Google Scholar]
- Yuan, W.P.; Cai, W.W.; Chen, Y.; Liu, S.G.; Dong, W.J.; Zhang, H.C.; Yu, G.R.; Chen, Z.Q.; He, H.L.; Guo, W.D.; et al. Severe summer heatwave and drought strongly reduced carbon uptake in Southern China. Sci. Rep. 2016, 6, 18813. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xu, X.J.; Zhou, G.M.; Liu, S.G.; Du, H.Q.; Mo, L.F.; Shi, Y.J.; Jiang, H.; Zhou, Y.F.; Liu, E.B. Implications of ice storm damages on the water and carbon cycle of bamboo forests in southeastern China. Agric. For. Meteorol. 2013, 177, 35–45. [Google Scholar] [CrossRef]
- Turner, N.C. Agronomic options for improving rainfall-use efficiency of crops in dryland farming systems. J. Exp. Bot. 2004, 55, 2413–2425. [Google Scholar] [CrossRef] [Green Version]
- Keenan, T.F.; Hollinger, D.Y.; Bohrer, G.; Dragoni, D.; Munger, J.W.; Schmid, H.P.; Richardson, A.D. Increase in forest water-use efficiency as atmospheric carbon dioxide concentrations rise. Nature 2013, 499, 324–327. [Google Scholar] [CrossRef]
- Wang, L.M.; Li, M.Y.; Wang, J.X.; Li, X.G.; Wang, L.C. An analytical reductionist framework to separate the effects of climate change and human activities on variation in water use efficiency. Sci. Total Environ. 2020, 727, 138306. [Google Scholar] [CrossRef]
- Bai, Y.F.; Wu, J.G.; Qi, X.; Pan, Q.M.; Huang, J.H.; Yang, D.L.; Han, X.G. Primary production and rain use efficiency across a precipitation gradient on the Mongolia Plateau. Ecology 2008, 89, 2140–2153. [Google Scholar] [CrossRef]
- Hu, Z.M.; Yu, G.R.; Fan, J.W.; Zhong, H.P.; Wang, S.Q.; Li, S.G. Precipitation-use efficiency along a 4500-km grassland transect: Rain-use efficiency in Chinese grasslands. Glob. Ecol. Biogeogr. 2010, 19, 842–851. [Google Scholar]
- Huxman, T.E.; Smith, M.D.; Fay, P.A.; Knapp, A.K.; Shaw, M.R.; Loik, M.E.; Smith, S.D.; Tissue, D.T.; Zak, J.C.; Weltzin, J.F. Convergence across biomes to a common rain-use efficiency. Nature 2004, 429, 651–654. [Google Scholar] [CrossRef] [PubMed]
- Lauenroth, W.K.; Paruelo, B. Patterns of production and precipitation-use efficiency of winter wheat and native grasslands in the central great plains of the United States. Ecosystems 2000, 3, 344–351. [Google Scholar] [CrossRef]
- Paruelo, J.M.; Lauenroth, W.K.; Burke, I.C.; Sala, O.E. Grassland precipitation-use efficiency varies across a resource gradient. Ecosystems 1999, 2, 64–68. [Google Scholar] [CrossRef]
- Zhang, X.K.; Du, X.D.; Zhu, Z.M. Effects of precipitation and temperature on precipitation use efficiency of alpine grassland in northern Tibet, China. Sci. Rep. 2020, 10, 20309. [Google Scholar] [CrossRef]
- Khan, R.S.; Bhuiyan, M.A.E. Artificial Intelligence-Based Techniques for Rainfall Estimation Integrating Multisource Precipitation Datasets. Atmosphere 2021, 12, 1239. [Google Scholar] [CrossRef]
- Derin, Y.; Yilmaz, K.K. Evaluation of multiple satellite-based precipitation products over complex topography. J. Hydrometeorol. 2014, 15, 1498–1516. [Google Scholar] [CrossRef] [Green Version]
- Mei, Y.W.; Nikolopoulos, E.I.; Anagnostou, E.N.; Borga, M. Evaluating satellite precipitation error propagation in runoff simulations of mountainous basins. J. Hydrometeorol. 2016, 17, 1407–1423. [Google Scholar] [CrossRef]
- Chen, T.; Bao, A.M.; Jiapaer, G.; Guo, H.; Zheng, G.; Jiang, L.; Chang, C.; Tuerhanjiang, T. Disentangling the relative impacts of climate change and human activities on arid and semiarid grasslands in Central Asia during 1982–2015. Sci. Total Environ. 2019, 653, 1311–1325. [Google Scholar] [CrossRef]
- Yu, G.R.; Song, X.; Wang, Q.F.; Liu, Y.F.; Guan, D.X.; Yan, J.H.; Sun, X.M.; Zhang, L.M.; Wen, X.F. Water use efficiency of forest ecosystems in eastern China and its relations to climatic variables. New Phytol. 2008, 177, 927–937. [Google Scholar] [CrossRef]
- Li, H.X.; Liu, G.H.; Fu, B.J. Spatial variations of rain-use efficiency along a climate gradient on the Tibetan Plateau: A satellite-based analysis. Int. J. Remote Sens. 2013, 34, 7487–7503. [Google Scholar] [CrossRef]
- Cramer, W.; Kicklighter, D.W.; Bondeau, A.; Iii, B.M.; Churkina, G.; Nemry, B.; Ruimy, A.; Schloss, A.L. The Participants of the Potsdam NPP Model Intercomparison, Comparing global models of terrestrial net primary productivity (NPP): Overview and key results. Glob. Chang. Biol. 1999, 5 (Suppl. S1), 1–15. [Google Scholar] [CrossRef]
- McGuire, A.D.; Melillo, J.M.; Kicklighter, D.W.; Joyce, L.A. Equilibrium Responses of Soil Carbon to Climate Change: Empirical and Process-Based Estimates. J. Biogeogr. 1995, 22, 785–796. [Google Scholar] [CrossRef]
- Piao, S.L.; Fang, J.Y.; Guo, Q.H. Application of casa model to the estimation of Chinese terrestrial net primary productivity. Acta Phytoecol. Sin. 2001, 25, 603–608. (In Chinese) [Google Scholar]
- Turner, D.P.; Ritts, W.D.; Cohen, W.B.; Gower, S.T.; Running, S.W.; Zhao, M.S.; Costa, M.H.; Kirschbaum, A.A.; Ham, J.M. Evaluation of MODIS NPP and GPP products across multiple biomes. Remote Sens. Environ. 2006, 102, 282–292. [Google Scholar] [CrossRef]
- Zhang, Q.; Yang, J.H.; Wang, W.; Ma, P.L.; Lu, G.Y.; Liu, X.Y.; Yu, H.P.; Fang, F. Climatic Warming and Humidification in the Arid Region of Northwest China: Multi-Scale Characteristics and Impacts on Ecological Vegetation. J. Meteor. Res. 2021, 35, 113–127. [Google Scholar] [CrossRef]
- Li, Z.; Yan, Z.W. Homogenized China daily mean/maximum/mini-mum temperature series 1960–2008. Atmos. Ocean. Sci. Lett. 2009, 2, 237–243. [Google Scholar]
- Zhang, Y. Energy and Water Budget of a Poplar Plantation in Suburban Beijing; Beijing Forestry University: Beijing, China, 2010. (In Chinese) [Google Scholar]
- Zhu, G.F.; Lu, L.; Su, Y.H.; Wang, X.F.; Cui, X.; Ma, J.Z.; Zhang, K.; Li, C.B. Energy flux partitioning and evapotranspiration in a sub-alpine spruce forest ecosystem. Hydrol. Process. 2014, 28, 5093–5104. [Google Scholar]
- Wang, Z.Y. Energy Balance and Water Vapor Flux of Snail Control and Schistosomiasis Prevention Forests Ecosystem in Yangtze River Beach Land; Chinese Academy of Forestry: Beijing, China, 2008. (In Chinese) [Google Scholar]
- Wilske, B.; Lu, N.; Wei, L.; Chen, S.P.; Zha, T.G.; Liu, C.F.; Xu, W.T.; Noormets, A.; Huang, J.H.; Wei, Y.F.; et al. Poplar plantation has the potential to alter the water balance in semiarid Inner Mongolia. J. Environ. Manag. 2009, 90, 2762–2770. [Google Scholar] [CrossRef]
- Guo, L. The Variations of Water Use Efficiency and Evapotranspiration over a Plantation in Southern Part of Hilly Areas of North-China Master; Chinese Academy of Forestry: Beijing, China, 2010. (In Chinese) [Google Scholar]
- Lin, Y.; Wang, G.X.; Guo, J.Y.; Sun, X.Y. Quantifying evapotranspiration and its components in a coniferous subalpine forest in Southwest China. Hydrol. Process. 2012, 26, 3032–3040. [Google Scholar] [CrossRef]
- Han, S.; Huang, L.L.; Wang, Z.Y.; Wei, Y.; Zhang, X.D. Ecosystem respiration and its controlling factors in the riparian wetland of Yangtze River. Acta Ecol. Sin. 2009, 29, 3621–3628. (In Chinese) [Google Scholar]
- Wang, W.Z.; Zhao, Z.H.; Kang, W.X.; Tian, D.L.; Xiang, W.H.; Yan, W.D. Characteristics of latent heat flux over Cunninghamia lanceolata plantations in Huitong county. J. Cent. South Univ. Fores. Tech. 2011, 31, 192–197. (In Chinese) [Google Scholar]
- Cui, S. Study on the CO2 Flux of a Larch Plantation in NE China by the Micrometeorological Method; Northeast Forestry University: Harbin, China, 2007. (In Chinese) [Google Scholar]
- Liu, S.M.; Xu, Z.W.; Zhu, Z.L.; Jia, Z.Z.; Zhu, M.J. Measurements of evapotranspiration from eddy-covariance systems and large aperture scintillometers in the Hai River Basin, China. J. Hydrol. 2013, 487, 24–38. [Google Scholar] [CrossRef]
- Lin, E.J.; Jiang, H.; Chen, Y.F. Water vapor flux variation and net radiation for a Phyllostachys violascens stand in Taihuyuan. J. Zhejiang Agric. For. Univ. 2013, 30, 313–318. (In Chinese) [Google Scholar]
- Dong, G.; Guo, J.X.; Chen, J.Q.; Sun, G.; Gao, S.; Hu, L.J.; Wang, Y.L. Effects of spring drought on carbon sequestration, evapotranspiration and water use efficiency in the Songnen meadow steppe in Northeast China. Ecohydrology 2011, 4, 211–224. [Google Scholar] [CrossRef]
- Chen, S.P.; Chen, J.Q.; Lin, G.H.; Zhang, W.L.; Miao, H.X.; Wei, L.; Huang, J.H.; Han, X.G. Energy balance and partition in Inner Mongolia steppe ecosystems with different land use types. Agric. For. Meteorol. 2009, 149, 1800–1809. [Google Scholar] [CrossRef]
- Gu, S.; Tang, Y.H.; Cui, X.Y.; Du, M.Y.; Zhao, L.; Li, Y.Q.; Xu, S.X.; Zhou, H.K.; Kato, T.; Qi, P.T.; et al. Characterizing evapotranspiration over a meadow ecosystem on the Qinghai-Tibetan Plateau. J. Geophys. Res. 2008, 113, D08118. [Google Scholar] [CrossRef]
- Shao, C.L.; Chen, J.Q.; Li, L.H. Grazing alters the biophysical regulation of carbon fluxes in a desert steppe. Environ. Res. Lett. 2013, 8, 025012. [Google Scholar] [CrossRef]
- Wang, Y.L.; Zhou, G.S.; Wang, Y.H. Environmental effects on net ecosystem CO2 exchange at half-hour and month scales over Stipa krylovii steppe in northern China. Agric. For. Meteorol. 2008, 148, 714–722. [Google Scholar] [CrossRef]
- Liu, H.Z.; Feng, J.W. Seasonal and interannual variations of evapotranspiration and energy exchange over different land surfaces in a semi-arid area of China. J. Appl. Meteorol. Climatol. 2012, 51, 1875–1888. [Google Scholar]
- Yue, P.; Zhang, Q.; Zhang, L. Biometeorological effects on carbon dioxide and water-use efficiency within a semiarid grassland in the Chinese Loess Plateau. J. Hydrol. 2020, 590, 125520. [Google Scholar] [CrossRef]
- Wang, W.Z.; Xu, Z.W.; Liu, S.M.; Li, X.M.; Ma, M.G.; Wang, J.M. The characteristics of heat and water vapor fluxes over different surfaces in the Heihe River Basin. Adv. Earth Sci. 2009, 24, 714–723. (In Chinese) [Google Scholar]
- Liu, K. Multi-Time Scale Characteristics of Evapotranspiration of Artificial Caragana Korshinskii Forests in Desert Steppe; Ningxia University: Yinchuan, China, 2018. (In Chinese) [Google Scholar]
- Liu, R.; Li, Y.; Wang, Q.X. Variations in water and CO2 fluxes over a saline desert in western China. Hydrol. Process. 2012, 26, 513–522. [Google Scholar] [CrossRef]
- Zhang, F.; Zhou, G.S.; Wang, Y.; Yang, F.L.; Nilsson, C. Evapotranspiration and crop coefficient for a temperate desert steppe ecosystem using eddy covariance in Inner Mongolia, China. Hydrol. Process. 2012, 26, 379–386. [Google Scholar] [CrossRef]
- Li, J.M.; Cai, H.; Cheng, Q.; Qiao, C.L.; Chu, H.; Chen, D.D.; Xu, S.X.; Zhao, X.Q.; Zhao, L. Characterizing the evapotranspiration of a degraded grassland in the Sanjiangyuan Region of Qinghai province. Acta Pratacult. Sin. 2012, 21, 223–233. (In Chinese) [Google Scholar]
- Wu, J.K.; Chen, J.W.; Wu, H.; Zhang, S.Q.; Gao, M.J.; Qin, H. Comparative study of evapotranspiration in an alpine meadow in the upper reach of Shulehe River Basin. Sci. Geogr. Sin. 2013, 33, 97–103. (In Chinese) [Google Scholar]
- Yang, F.L.; Zhang, Q.; Wang, R.Y.; Wang, S.; Yue, P.; Wang, H.L.; Zhao, H. Characteristics of evapotranspiration and crop coefficient of agroecosystems in semi-arid area of Loess Plateau, Northwest China. Chin. J. Appl. Ecol. 2013, 24, 1209–1214. (In Chinese) [Google Scholar]
- Zhou, G.S.; Wang, Y.; Zhou, L. Dynamics of carbon budgets in typical corn and rice ecosystems in Liaohe delta. In Proceedings of the Low Carbon Agriculture Symposium, Beijng, China, 17 June 2010; pp. 265–271. (In Chinese). [Google Scholar]
- Chen, H.; Huang, J.H. Study on in-situ evapotranspiration measurement and its influential factors in farmland in Southern China. Water Resour. Prot. 2017, 33, 79–86. (In Chinese) [Google Scholar]
- Wu, C.; Wang, G.Q.; Hao, Z.C.; Gu, Y.; Liu, P.Y.; Yang, Q.L. Study on the variation regulation and influencing factors of farmland evapotranspiration in gully region of Changwu tableland. J. Water Res. Water Eng. 2017, 28, 37–42. (In Chinese) [Google Scholar]
- Guo, C.M.; Ren, J.Q.; Zhang, T.L.; Yu, H. Dynamic Change of Evapotranspiration and Influenced Factors in the Spring Maize Field in Northeast China. Chin. J. Agrometeorol. 2016, 37, 400–407. (In Chinese) [Google Scholar]
- Guo, Y.D.; Song, C.C.; Zhang, J.S.; Wang, L.L.; Sun, L. Influence of wetland reclamation on land-surface energy exchange and evapotranspiration in the Sanjiang plain, Northeast China. Agric. For. Meteorol. 2021, 296, 108214. [Google Scholar] [CrossRef]
- Zhou, L.; Zhou, G.S.; Liu, S.S.; Sui, X.H. Seasonal contribution and interannual variation of evapotranspiration over a reed marsh (Phragmites australis) in Northeast China from 3−year eddy covariance data. Hydrol. Process. 2010, 24, 1039–1047. [Google Scholar] [CrossRef]
- Guo, H.Q.; Noormets, A.; Zhao, B.; Chen, J.Q.; Sun, G.; Gu, Y.J.; Bo, L.; Chen, J.K. Tidal effects on net ecosystem exchange of carbon in an estuarine wet-land. Agric. For. Meteorol. 2009, 149, 1820–1828. [Google Scholar] [CrossRef]
- Yan, G.Y. Tidal Influence on Energy Balance and Evapotranspiration of Mangrove Ecosystem in Subtropical Area; Xiamen University: Xiamen, China, 2012. (In Chinese) [Google Scholar]
- Chen, H.; Lu, W.Z.; Yan, G.; Yang, S.; Lin, G.H. Typhoons exert significant but differential impacts on net ecosystem carbon exchange of subtropical mangrove forests in China. Biogeosciences 2014, 11, 5323–5333. [Google Scholar] [CrossRef] [Green Version]
- Rodell, M.; Houser, P.R.; Jambor, U.; Gottschalck, J.; Mitchell, K.; Meng, C.J.; Arsenault, K.; Cosgrove, B.; Radkovich, J.; Bosilovich, M.; et al. The Global Land Data Assimilation System. Bull. Amer. Meteor. Soc. 2004, 85, 381–394. [Google Scholar] [CrossRef] [Green Version]
- Lieth, H.; Box, E. Evapotranspiration and primary production. In Thornthwaite W Memorial Model; Publications in Climatology; C.W. Thornthwaite Associates: Centerton-Elmer, NJ, USA, 1972; Volume 25, pp. 37–46. [Google Scholar]
- Zhou, G.S.; Zhang, X.S. A Natural Vegetation NPP Model. Chin. J. Plan. Ecolo. 1995, 19, 193–200. (In Chinese) [Google Scholar]
- Wang, K.C.; Dickinson, R.E. A review of global terrestrial evapotranspiration: Observation, modeling, climatology, and climatic variability. Rev. Geophys. 2012, 50, RG2005. [Google Scholar] [CrossRef]
- Zhang, K.; Kimball, J.S.; Running, S.W. A review of remote sensing based actual evapotranspiration estimation. WIREs Water 2016, 3, 834–853. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Rees, D.; Smith, M. Crop evapotranspiration—Guidelines for computing crop water requirements. In Irrigation and Drainage; FAO: Rome, Italy, 1998; pp. 15–28. [Google Scholar]
- McCuen, R.H. A sensitivity and error analysis of procedures used for estimating evaporation. Water. Res. Bull. 1974, 10, 486–498. [Google Scholar] [CrossRef]
- Zhang, Q.; Yang, Z.S.; Hao, X.C.; Yue, P. Conversion features of evapotranspiration responding to climate warming in transitional climate regions in northern China. Clim. Dyn. 2019, 52, 3891–3903. [Google Scholar] [CrossRef]
- Wang, W.; Cui, W.; Wang, X.J.; Chen, X. Evaluation of GLDAS−1 and GLDAS−2 Forcing Data and Noah Model Simulations over China at the Monthly Scale. J. Hydrometeorol. 2016, 17, 2815–2833. [Google Scholar] [CrossRef]
- Zhang, M.L.; Lai, R.; Zhao, Y.Y.; Jiang, W.L.; Chen, Q.G. Estimating net primary production of natural grassland and its spatio-temporal distribution in China. Sci. Total Environ. 2016, 553, 184–195. [Google Scholar] [CrossRef] [PubMed]
- Churkina, G.; Running, S.W.; Schloss, A.L. The Participants of the Potsdam NPP Model Intercomparison, Comparing global models of terrestrial net primary productivity (NPP): The importance of water availability. Glob. Chang. Biol. 1999, 5 (Suppl. S1), 46–55. [Google Scholar] [CrossRef]
- Fu, C.B.; Dan, L.; Feng, J.M.; Peng, J.; Ying, N. Temporal and spatial variations of total cloud amount and their possible relationships with temperature and water vapor over China during 1960 to 2012. Chin. J. Atmos. Sci. 2019, 43, 87–98. (In Chinese) [Google Scholar]
- Heinsch, F.A.; Zhao, M.S.; Running, S.W.; Kimball, J.S.; Nemani, R.R.; Davis, K.J.; Bolstad, P.V.; Cook, B.D.; Desai, A.R.; Ricciuto, D.M.; et al. Evaluation of remote sensing based terrestrial productivity from MODIS using regional tower eddy flux network observations. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1908–1925. [Google Scholar] [CrossRef] [Green Version]
- Xu, X.C.; Zhang, X.Z.; Dai, E.F.; Song, W. Research of trend variability of precipitation intensity and their contribution to precipitation in China from 1961 to 2010. Geogr. Res. 2014, 33, 1335–1347. (In Chinese) [Google Scholar]
- Du, J.Q.; Shu, J.M.; Zhang, L.B. Analysis of ecosystem degradation and recovery using precipitation use efficiency and NDVI in the headwater catchment of the Yellow River basin. Acta Ecol. Sin. 2012, 32, 3404–3413. (In Chinese) [Google Scholar]
- Liang, F.; Xia, X.A. Long-term trends in solar radiation and the associated climatic factors over China for 1961–2000. Ann. Geophys. 2005, 23, 2425–2432. [Google Scholar] [CrossRef] [Green Version]
- Budyko, M.I. The Heat Balance of the Earth’s Surface; Stepanova, N.A., Translator, Eds.; United States Department of Commerce: Washington, DC, USA, 1958; 259p. (In Russian) [Google Scholar]
- Fu, B.P. On the calculation of the evaporation from land surface. Sci. Atmos. Sin. 1981, 5, 23–31. (In Chinese) [Google Scholar]
- Zhang, L.; Dawes, W.R.; Walker, G.R. Response of mean annual evapotranspiration to vegetation changes at catchment scale. Water Resour. Res. 2001, 37, 701–708. [Google Scholar] [CrossRef]
- Yang, D.F.; Sun, Z.B.; Liu, Z.Y.; Cong, Z.T.; Ni, G.H.; Lei, Z.D. Analyzing spatial and temporal variability of annual water-energy balance in nonhumid regions of China using the Budyko hypothesis. Water Resour. Res. 2007, 43, W04426. [Google Scholar] [CrossRef]
- Gherardi, L.A.; Sala, O.E. Enhanced precipitation variability decreases grass and increases shrub-productivity. Proc. Natl. Acad. Sci. USA 2015, 112, 12735–12740. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Knapp, A.K.; Fay, P.A.; Blair, J.M.; Collins, S.L.; Smith, M.D.; Carlisle, J.D.; Harper, C.W.; Danner, B.T.; Lett, M.S.; McCarron, J.K. Rainfall variability, carbon cycling, and plant species diversity in a mesic grassland. Science 2002, 298, 2202–2205. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Huang, J.J.; Zhang, Q.; Zhang, S.; Chen, X.H. Information entropy-based analysis of spatial and temporal variation in precipitation in Xinjiang. Acta Ecol. Sin. 2017, 37, 4444–4455. (In Chinese) [Google Scholar]
- Yang, J.H.; Zhang, Q.; Lu, G.Y.; Liu, X.Y.; Wang, D.W.; Liu, W.P.; Yue, P.; Zhu, B. Climate Transition from Warm-dry to Warm-wet in Eastern Northwest China. Atmosphere 2021, 12, 548. [Google Scholar] [CrossRef]
- Ahlstrom, A.; Raupach, M.R.; Schurgers, G.; Smith, B.; Arneth, A.; Jung, M.; Reichstein, M.; Canadell, J.G.; Friedlingstein, P.; Jain, A.K.; et al. The dominant role of semi-arid ecosystems in the trend and variability of the land CO2 sink. Science 2015, 348, 895–899. [Google Scholar] [CrossRef] [Green Version]
- Cong, Z.T.; Yang, D.W.; Ni, G.H. Does evaporation paradox exist in China? Hydrol. Earth Syst. Sci. 2008, 13, 357–366. [Google Scholar] [CrossRef] [Green Version]
- Brutsaert, W.; Parlange, M.B. Hydrologic cycle explains the evaporation paradox. Nature 1998, 396, 30. [Google Scholar] [CrossRef]
- Zhang, Q.; Yang, Z.S.; Hao, X.C.; Yue, P. Transition features of surface evapotranspiration responding to climate warming with spatial precipitation–based climate type in Northern China. Chin. Sci. Bull. 2018, 63, 1035–1049. (In Chinese) [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.Y.; Yue, Y.; Wang, Q.; Du, X.L.; Li, J.L.; Gang, C.C.; Zhou, W.; Wang, Z.Q. Evaluating the responses of net primary productivity and carbon use efficiency of global grassland to climate variability along an aridity gradient. Sci. Total Environ. 2019, 652, 671–682. [Google Scholar] [CrossRef]
- Sun, L.; Shen, B.Z.; Sui, B.; Huang, B.H. The influences of East Asian Monsoon on summer precipitation in Northeast China. Clim. Dyn. 2017, 48, 1647–1659. [Google Scholar] [CrossRef]
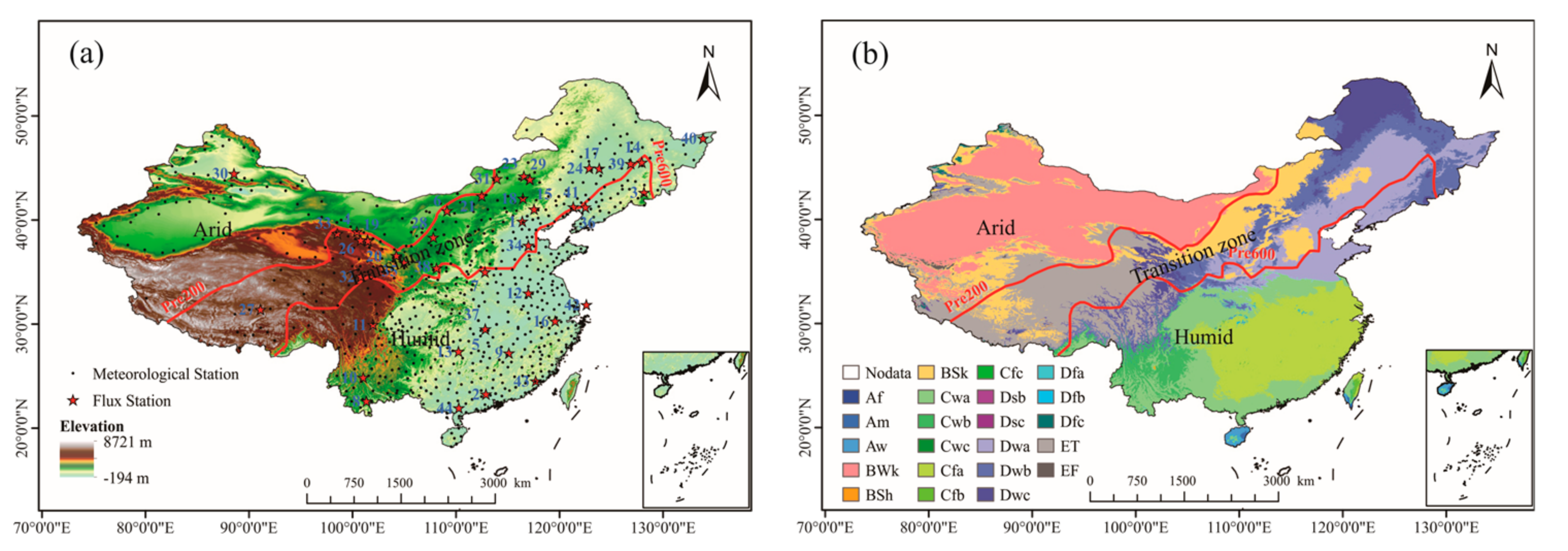
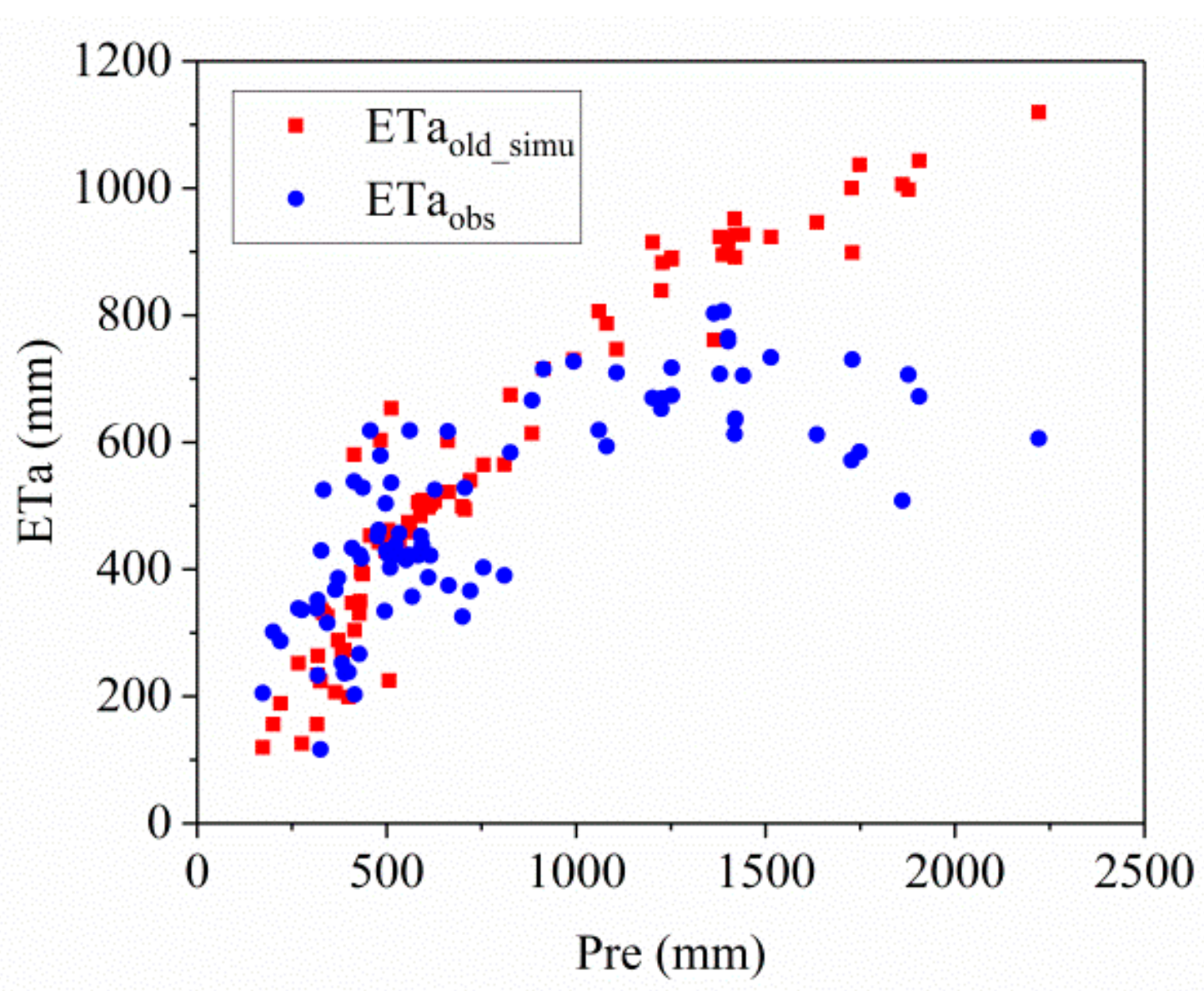
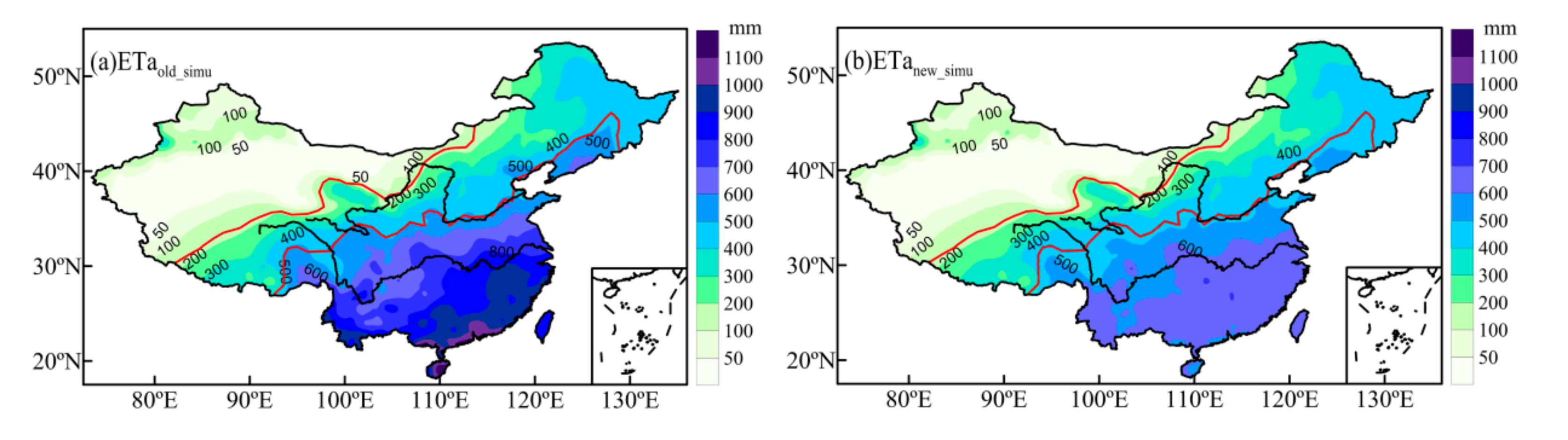

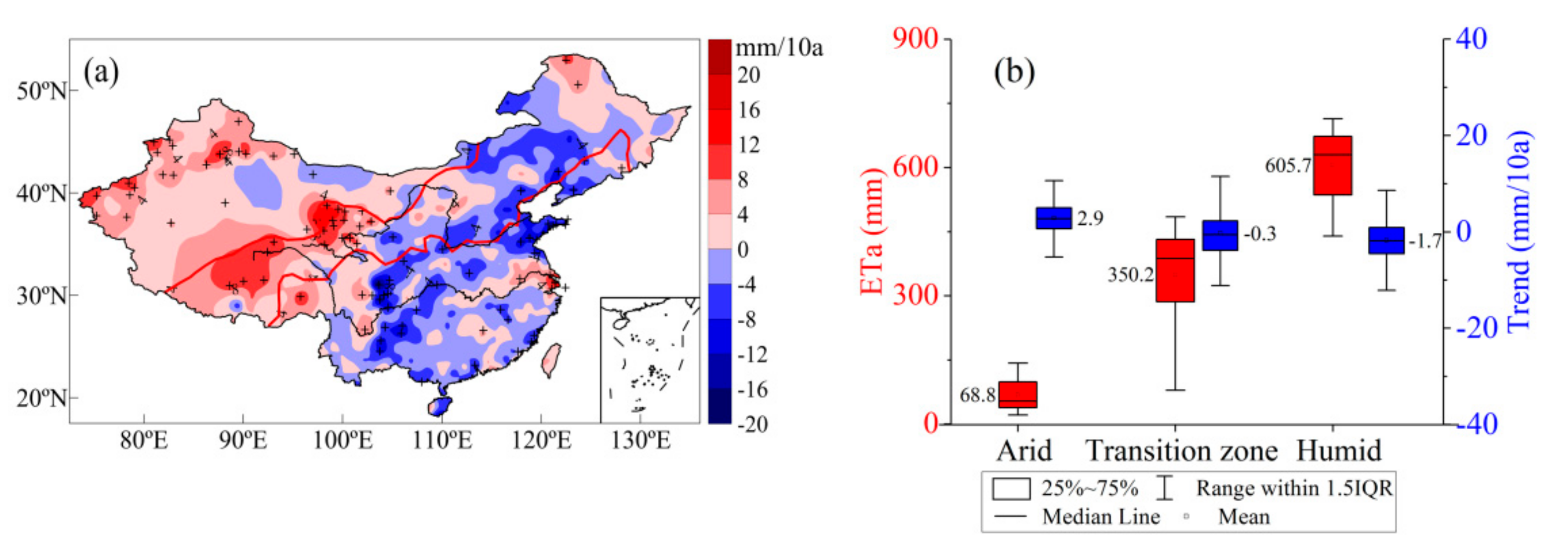


| No. | Stations | Latitude | Longitude | Observational Periods | Reference |
|---|---|---|---|---|---|
| 1 | Daxing | 39.53° N | 116.25° E | 2006 | Zhang [29] |
| 2 | Dinghushan | 23.17° N | 112.53° E | 2003–2010 | China FLUX |
| 3 | Changbaishan | 42.40° N | 128.10° E | 2003–2010 | China FLUX |
| 4 | Guantan | 38.53° N | 100.25° E | 2011 | Zhu et al. [30] |
| 5 | Yueyang | 29.31° N | 112.51° E | 2006 | Wang [31] |
| 6 | Kubiqi | 40.54° N | 108.69° E | 2006 | Wilske et al. [32] |
| 7 | Xiaolangdi | 35.02° N | 112.47° E | 2007–2009 | Guo [33] |
| 8 | Xishuangbannan | 21.96° N | 101.20° E | 2003–2010 | China FLUX |
| 9 | Qianyanzhou | 26.74° N | 115.06° E | 2003–2010 | China FLUX |
| 10 | Ailaoshan | 24.53° N | 101.02° E | 2010 | China FLUX |
| 11 | Gonggashan | 29.58° N | 102.00° E | 2009 | Lin et al. [34] |
| 12 | Huaining | 33.00° N | 117.00° E | 2005–2006 | Han et al. [35] |
| 13 | Huitong | 26.83° N | 109.75° E | 2009 | Wang et al. [36] |
| 14 | Laoshan | 45.33° N | 127.57° E | 2004–2006 | Cui [37] |
| 15 | Miyun | 40.63° N | 117.32° E | 2008–2010 | Liu et al. [38] |
| 16 | Taihuyuan | 30.18° N | 119.34° E | 2011 | Lin et al. [39] |
| 17 | Changling | 44.58° N | 123.50° E | 2007–2008 | Dong et al. [40] |
| 18 | Duolun County | 42.05° N | 116.28° E | 2006 | Chen et al. [41] |
| 19 | Haibei a | 37.66° N | 101.29° E | 2003–2010 | China FLUX |
| 20 | Haibei b | 37.60° N | 101.30° E | 2002–2004 | Gu et al. [42] |
| 21 | Siziwang Banner, grazed | 41.79° N | 111.90° E | 2010 | Shao et al. [43] |
| 22 | Xilinhot, grazed | 43.55° N | 116.67° E | 2006 | Chen et al. [41] |
| 23 | Xilinhot, typical fenced | 44.13° N | 116.33° E | 2004–2006 | Wang et al. [44] |
| 24 | Tongyu | 44.59° N | 122.52° E | 2003–2008 | Liu and Feng [45] |
| 25 | Yuzhong | 35.95° N | 104.14° E | 2007–2012 | Yue et al. [46] |
| 26 | Aro | 38.04° N | 100.46° E | 2008 | Wang et al. [47] |
| 27 | Dangxiong | 30.85° N | 91.08° E | 2003–2010 | China FLUX |
| 28 | Yanchi | 37.81° N | 107.48° E | 2016 | Liu [48] |
| 29 | Xinlin Gol | 43.55° N | 116.68° E | 2003–2010 | China FLUX |
| 30 | Fukang | 44.28° N | 87.93° E | 2004 | Liu et al. [49] |
| 31 | Sunitezuo | 44.00° N | 113.57° E | 2008–2009 | Zhang et al. [50] |
| 32 | Sanjiangyuan | 34.35° N | 100.50° E | 2006–2008 | Li et al. [51] |
| 33 | Tianjun | 38.42° N | 98.32° E | 2011 | Wu et al. [52] |
| 34 | Yucheng | 36.95° N | 116.60° E | 2003–2010 | China FLUX |
| 35 | Dingxi | 35.55° N | 104.58° E | 2010 | Yang et al. [53] |
| 36 | Jinzhou | 41.15° N | 121.20° E | 2006 | Zhou et al. [54] |
| 37 | Yueyang | 29.31° N | 112.51° E | 2015 | Chen and Huang [55] |
| 38 | Changwu | 35.23° N | 107.67° E | 2008 | Wu et al. [56] |
| 39 | Yushu | 44.85° N | 126.52° E | 2009 | Guo et al. [57] |
| 40 | Sanjiang Plains | 47.51° N | 133.51° E | 2017 | Guo et al. [58] |
| 41 | Panjin | 41.14° N | 121.90° E | 2005, 2006–2007 | Zhou et al. [59] |
| 42 | Dongtan | 31.52° N | 121.96° E | 2005 | Guo et al. [60] |
| 43 | Yunxiao | 23.92° N | 117.42° E | 2009–2010 | Yan [61] |
| 44 | Gaoqiao | 21.57° N | 109.76° E | 2010 | Chen et al. [62] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Zhang, Q.; Yue, P.; Wang, J.; Yang, J.; Wang, W.; Zhang, H.; Ren, X. Precipitation-Use Efficiency and Its Conversion with Climate Types in Mainland China. Remote Sens. 2022, 14, 2467. https://doi.org/10.3390/rs14102467
Wang S, Zhang Q, Yue P, Wang J, Yang J, Wang W, Zhang H, Ren X. Precipitation-Use Efficiency and Its Conversion with Climate Types in Mainland China. Remote Sensing. 2022; 14(10):2467. https://doi.org/10.3390/rs14102467
Chicago/Turabian StyleWang, Suping, Qiang Zhang, Ping Yue, Jianshun Wang, Jinhu Yang, Wei Wang, Hongli Zhang, and Xueyuan Ren. 2022. "Precipitation-Use Efficiency and Its Conversion with Climate Types in Mainland China" Remote Sensing 14, no. 10: 2467. https://doi.org/10.3390/rs14102467
APA StyleWang, S., Zhang, Q., Yue, P., Wang, J., Yang, J., Wang, W., Zhang, H., & Ren, X. (2022). Precipitation-Use Efficiency and Its Conversion with Climate Types in Mainland China. Remote Sensing, 14(10), 2467. https://doi.org/10.3390/rs14102467






