Forward-Looking Super-Resolution Imaging for Sea-Surface Target with Multi-Prior Bayesian Method
Abstract
:1. Introduction
2. Method
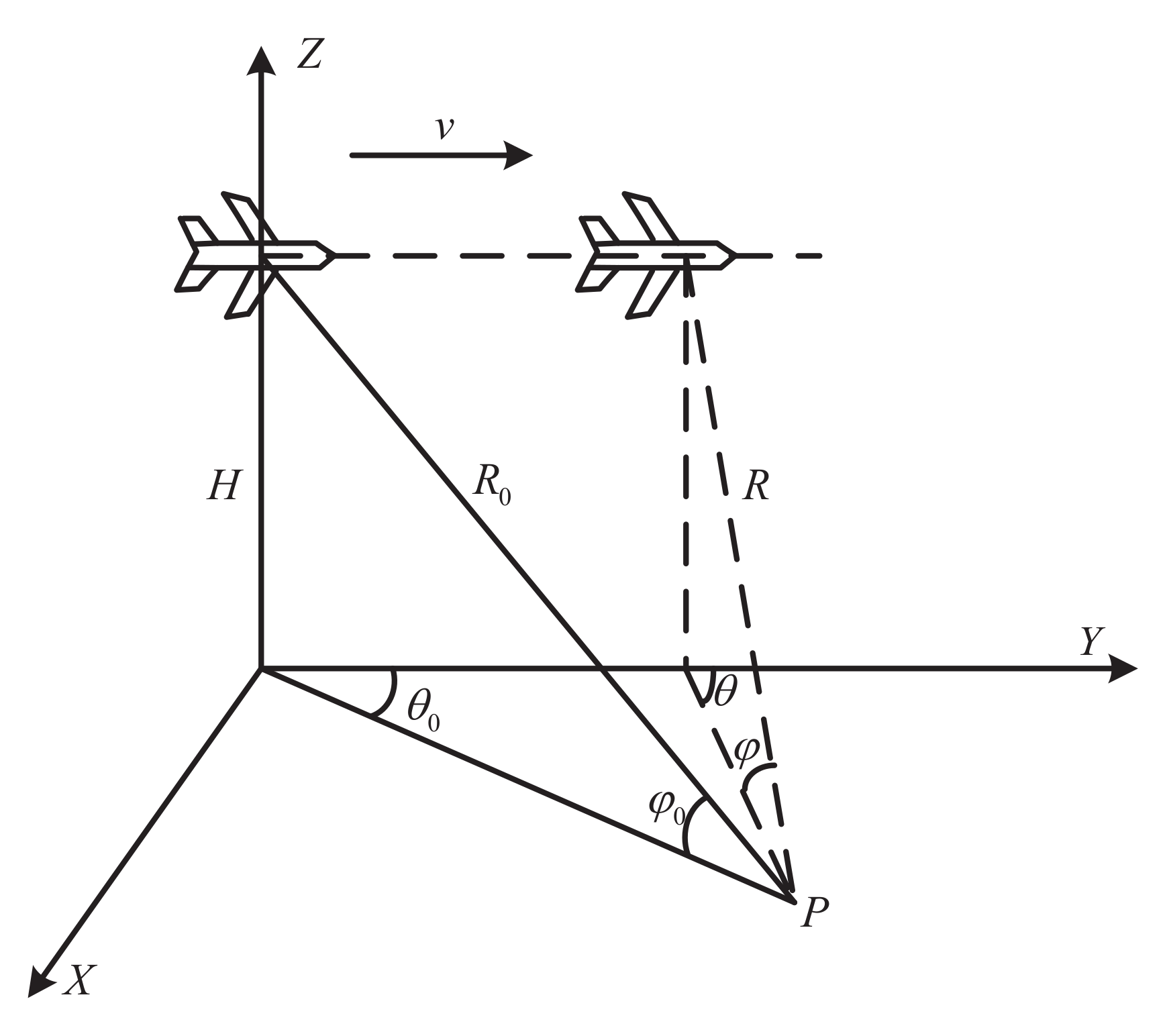
2.1. Azimuth Signal Model for Scanning Radar Forward-Looking Imaging
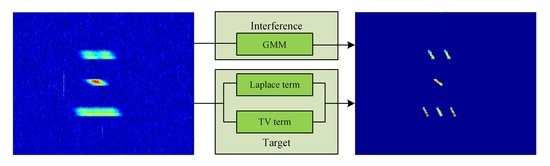
2.2. Bayesian Model for Sea-Surface Target
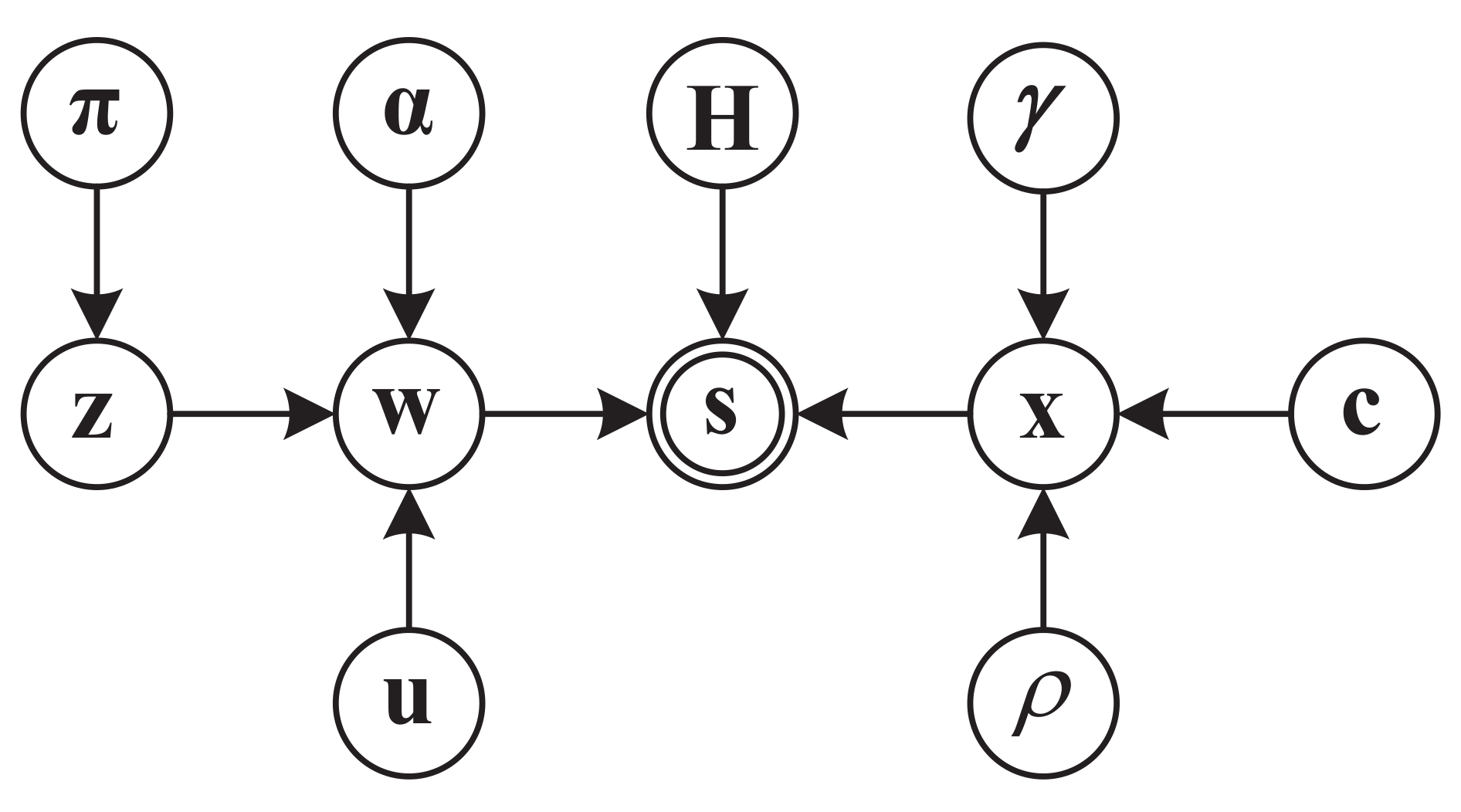
2.2.1. Bayesian Model
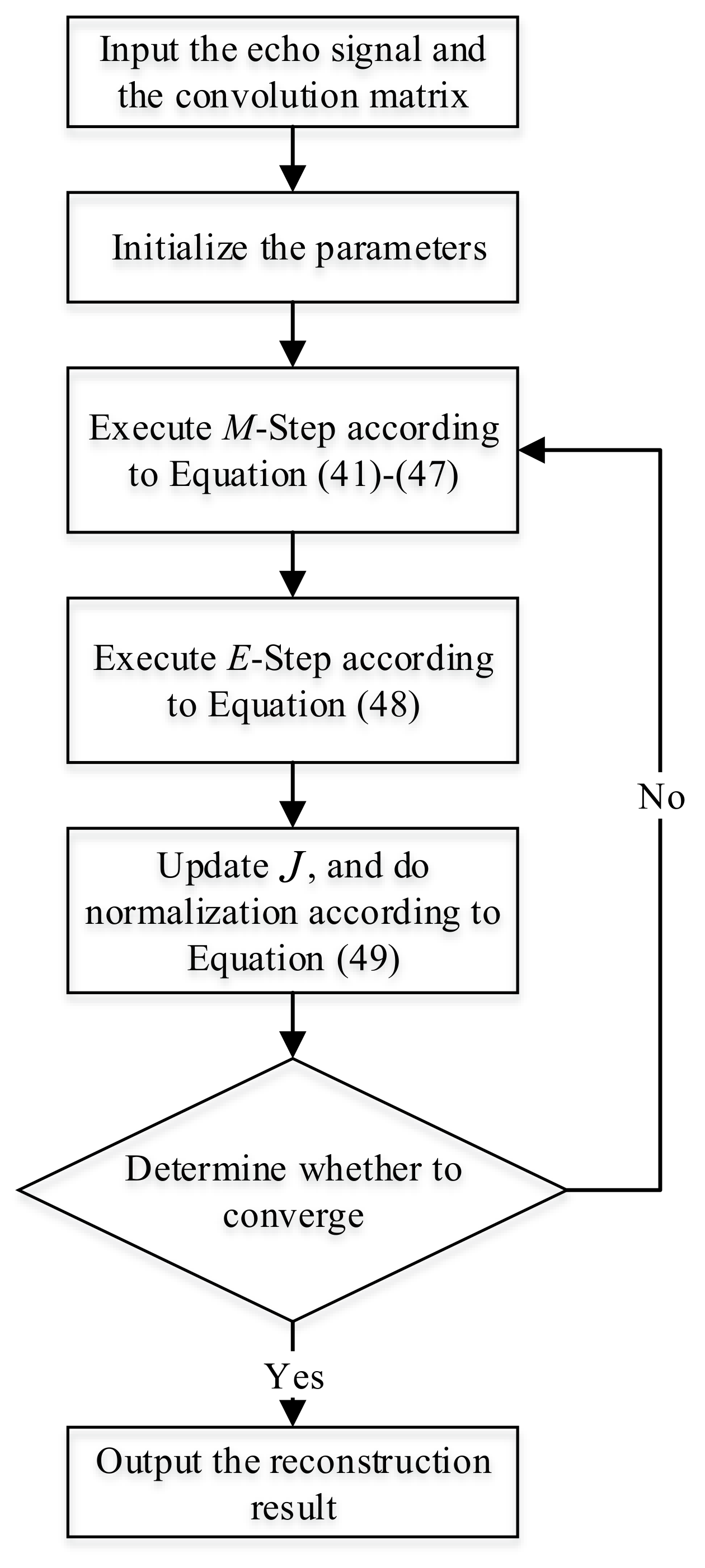
2.2.2. MAP-EM Estimation
3. Experiment Result
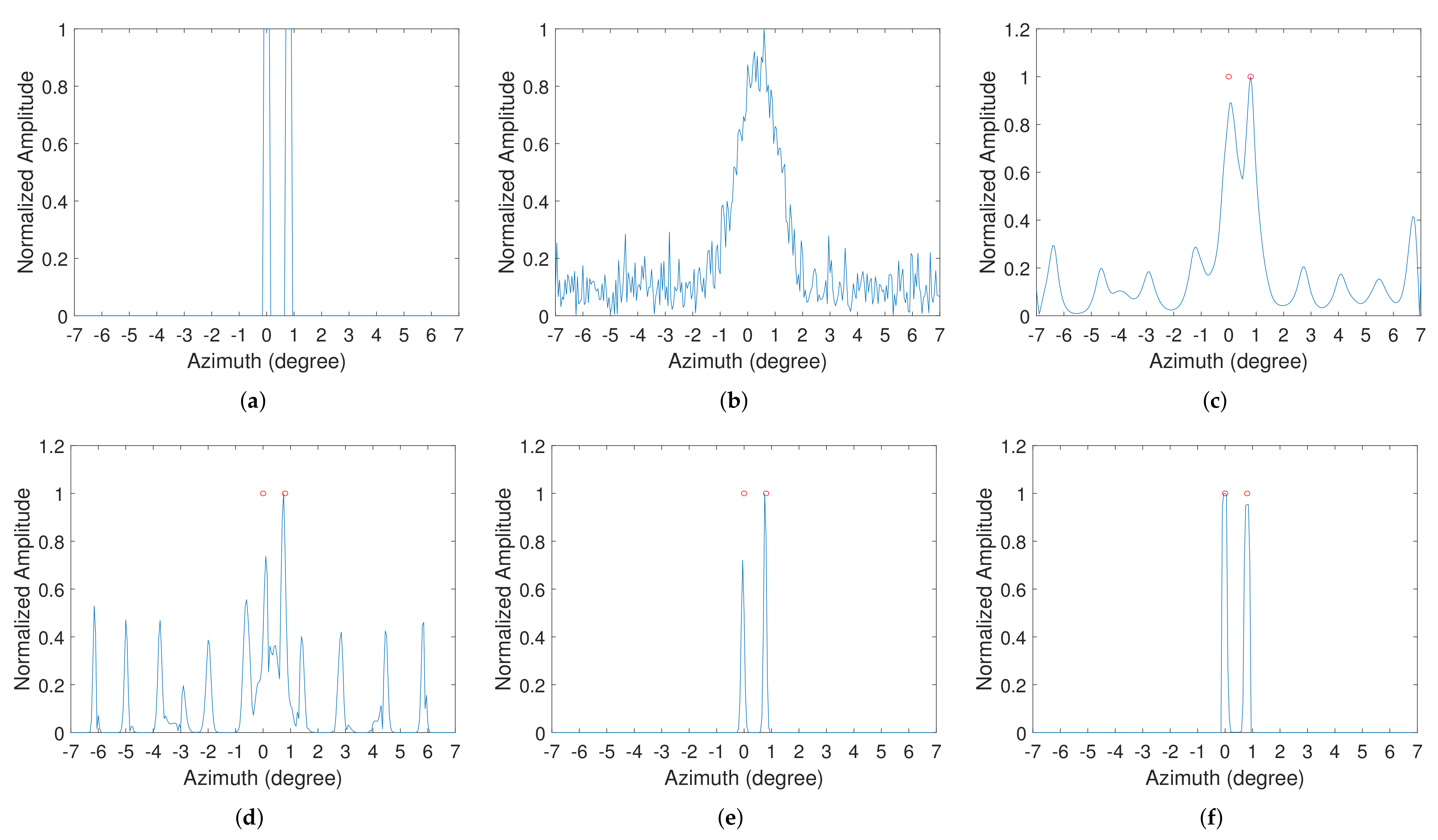
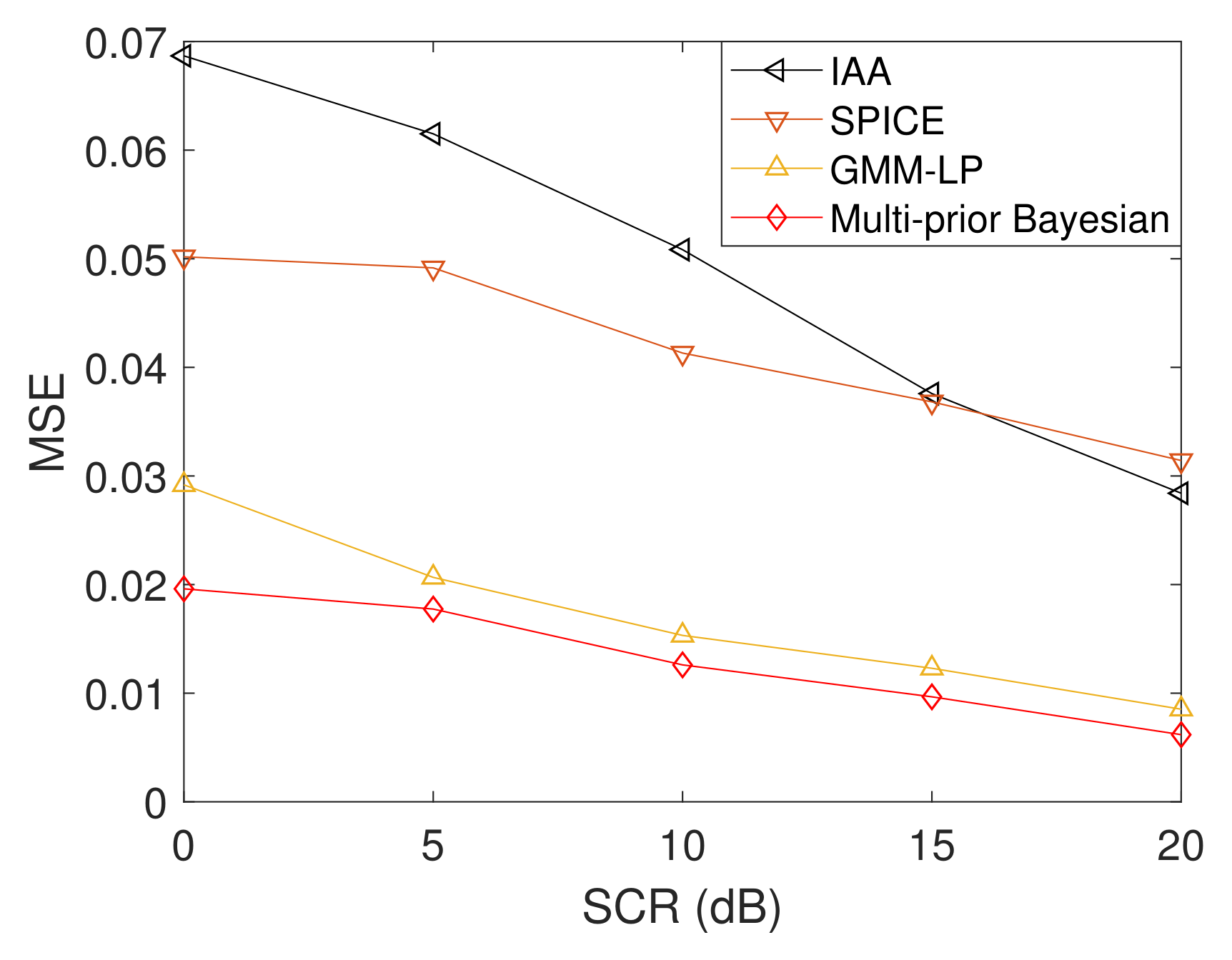
3.1. Point Simulation
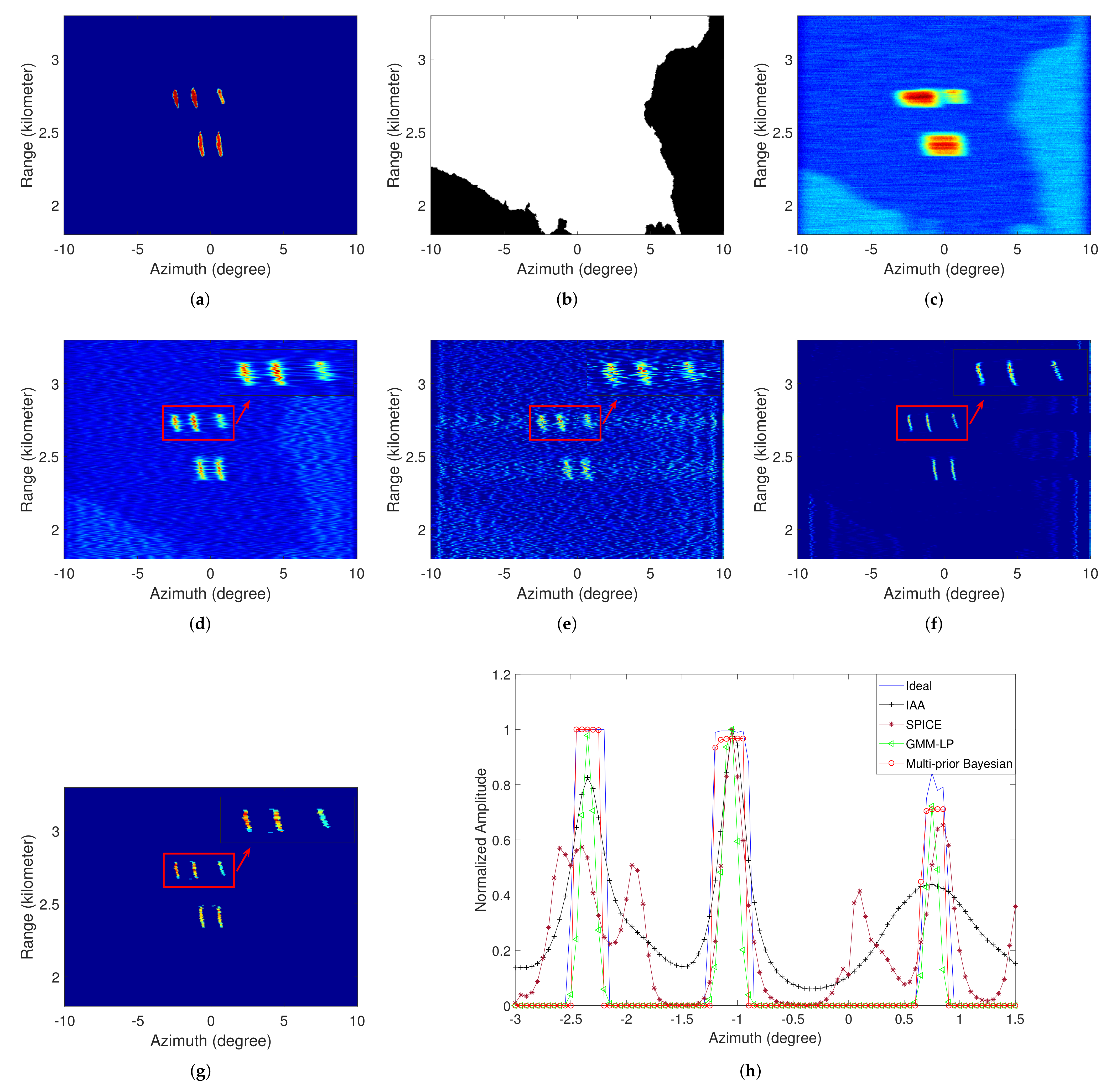
3.2. Area Simulation
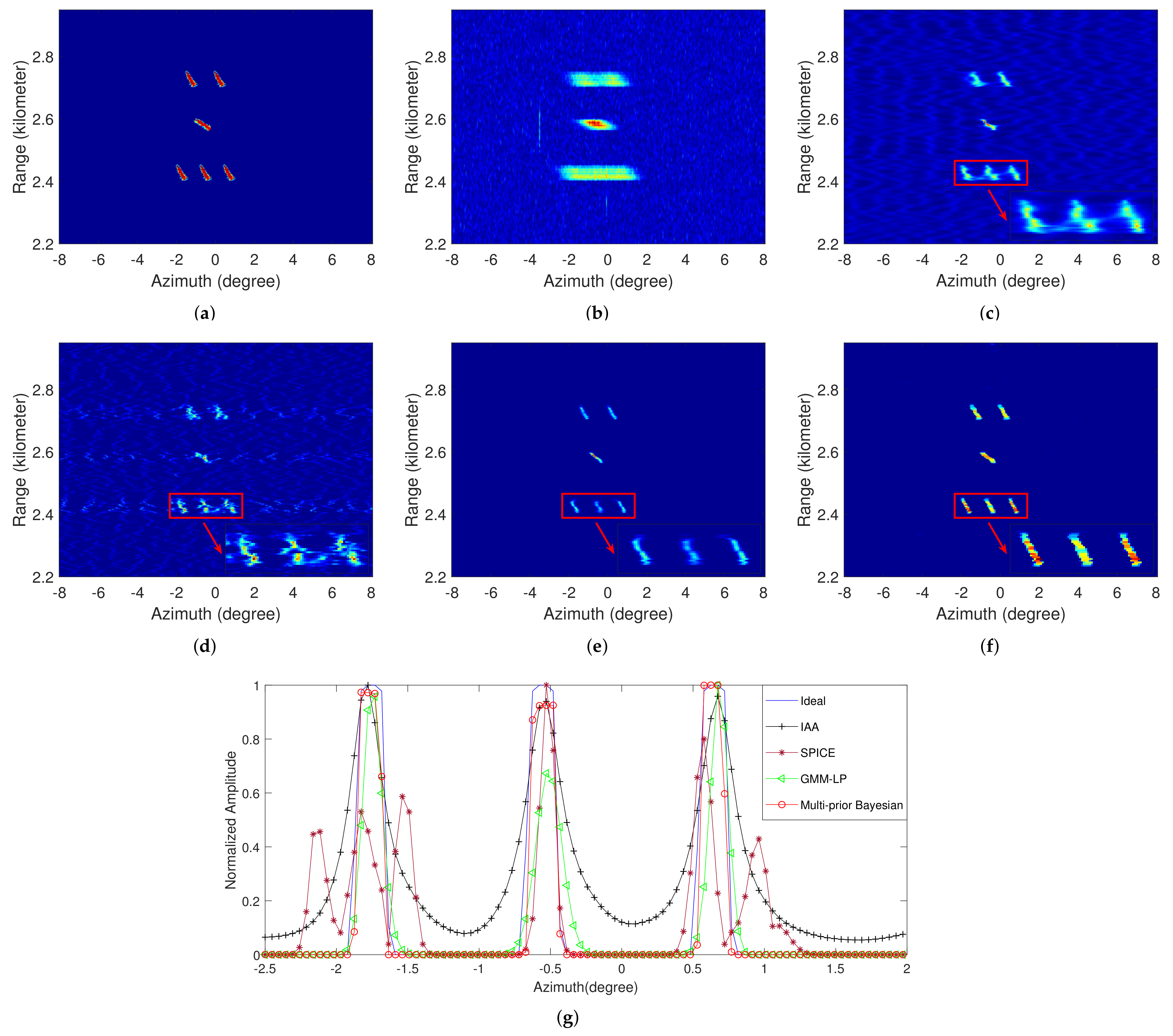
3.3. Semi-Real Data Experiment
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Acronyms
| GMM | Gaussian mixture model |
| TV | total variation |
| MAP-EM | maximum a posterior-expectation maximization |
| LFM | linear frequency modulated |
| TSVD | truncated singular value decomposition |
| IAA | iterative adaptive approach |
| MAP | maximum a posteriori |
| SPICE | sparse iterative covariance-based estimation |
| GMM-LP | Gaussian mixture model-Laplace hierarchical prior |
| SCR | signal to clutter ratio |
| SNR | signal to noise ratio |
| MSE | mean square error |
References
- Chen, H.; Li, M.; Wang, Z.; Lu, Y.; Cao, R.; Zhang, P.; Zuo, L.; Wu, Y. Cross-Range Resolution Enhancement for DBS Imaging in a Scan Mode Using Aperture-Extrapolated Sparse Representation. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1459–1463. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Y.; Huang, Y.; Li, W.; Yang, J. Angular Superresolution for Scanning Radar With Improved Regularized Iterative Adaptive Approach. IEEE Geosci. Remote Sens. Lett. 2016, 13, 846–850. [Google Scholar] [CrossRef]
- Li, W.; Niu, M.; Zhang, Y.; Huang, Y.; Yang, J. Forward-Looking Scanning Radar Superresolution Imaging Based on Second-Order Accelerated Iterative Shrinkage-Thresholding Algorithm. IEEE J. Sel. Topics Appl. Earth Observ. Remote Sens. 2020, 13, 620–631. [Google Scholar] [CrossRef]
- Tan, K.; Li, W.; Pei, J.; Huang, Y.; Yang, J. An I/Q-Channel Modeling Maximum Likelihood Super-Resolution Imaging Method for Forward-Looking Scanning Radar. IEEE Geosci. Remote Sens. Lett. 2018, 15, 863–867. [Google Scholar] [CrossRef]
- Wehner, D.R. High Resolution Radar; Norwood: Boston, MA, USA, 1987. [Google Scholar]
- Li, W.; Zhang, W.; Zhang, Q.; Zhang, Y.; Huang, Y.; Yang, J. Simultaneous Super-Resolution and Target Detection of Forward-Looking Scanning Radar via Low-Rank and Sparsity Constrained Method. IEEE Trans. Geosci. Remote Sens. 2020, 58, 7085–7095. [Google Scholar] [CrossRef]
- Skolnik, M.I. Radar Handbook, 3rd ed.; McGraw-Hill Education: New York, NY, USA, 2008. [Google Scholar]
- Zhang, Q.; Zhang, Y.; Huang, Y.; Zhang, Y. Azimuth Superresolution of Forward-Looking Radar Imaging Which Relies on Linearized Bregman. IEEE J. Sel. Topics Appl. Earth Observ. Remote Sens. 2019, 12, 2032–2043. [Google Scholar] [CrossRef]
- Quan, Y.; Zhang, R.; Li, Y.; Xu, R.; Zhu, S.; Xing, M. Microwave Correlation Forward-Looking Super-Resolution Imaging Based on Compressed Sensing. IEEE Trans. Geosci. Remote Sens. 2021, 59, 8326–8337. [Google Scholar] [CrossRef]
- Dropkin, H.; Ly, C. Superresolution for Scanning Antenna. In Proceedings of the 1997 IEEE National Radar Conference, Syracuse, NY, USA, 13–15 May 1997; pp. 306–308. [Google Scholar]
- Li, Y.; Liu, J.; Jiang, X.; Huang, X. Angular Superresol for Signal Model in Coherent Scanning Radars. IEEE Trans. Aerosp. Electron. Syst. 2019, 55, 3103–3116. [Google Scholar] [CrossRef]
- Ly, C.; Dropkin, H.; Manitius, A.Z. Extension of the Music Algorithm to Millimeter-Wave (Mmw) Real-Beam Radar Scanning Antennas. In Proceedings of the Radar Sensor Technology and Data Visualization, Orlando, FL, USA, 1–5 April 2002; Volume 4744, pp. 96–107. [Google Scholar]
- Zhang, Q.; Zhang, Y.; Zhang, Y.; Huang, Y.; Yang, J. A Sparse Denoising-Based Super-Resolution Method for Scanning Radar Imaging. Remote Sens. 2021, 13, 2768. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhang, Y.; Huang, Y.; Zhang, Y.; Pei, J.; Yi, Q.; Li, W.; Yang, J. TV-Sparse Super-Resolution Method for Radar Forward-Looking Imaging. IEEE Trans. Geosci. Remote Sens. 2020, 58, 6534–6549. [Google Scholar] [CrossRef]
- Chen, H.; Li, Y.; Gao, W.; Zhang, W.; Sun, H.; Guo, L.; Yu, J. Bayesian Forward-Looking Superresolution Imaging Using Doppler Deconvolution in Expanded Beam Space for High-Speed Platform. IEEE Trans. Geosci. Remote Sens. 2021, in press. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Y.; Li, W.; Huang, Y.; Yang, J. Super-Resolution Surface Mapping for Scanning Radar: Inverse Filtering Based on the Fast Iterative Adaptive Approach. IEEE Trans. Geosci. Remote Sens. 2017, 56, 127–144. [Google Scholar] [CrossRef]
- Zhang, Y.; Jakobsson, A.; Zhang, Y.; Huang, Y.; Yang, J. Wideband Sparse Reconstruction for Scanning Radar. IEEE Trans. Geosci. Remote Sens. 2018, 56, 6055–6068. [Google Scholar] [CrossRef]
- Fang, J.; Wang, F.; Shen, Y.; Li, H.; Blum, R.S. Super-Resolution Compressed Sensing for Line Spectral Estimation: An Iterative Reweighted Approach. IEEE Trans. Signal Process. 2016, 64, 4649–4662. [Google Scholar] [CrossRef]
- Goldstein, T.; Osher, S. The split Bregman method for L1-regularized problems. SIAM J. Imag. Sci. 2009, 2, 323–343. [Google Scholar] [CrossRef]
- Shea, J.D.; Van Veen, B.D.; Hagness, S.C. A TSVD Analysis of Microwave Inverse Scattering for Breast Imaging. IEEE Trans. Biomed. Eng. 2011, 59, 936–945. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gambardella, A.; Migliaccio, M. On the Superresolution of Microwave Scanning Radiometer Measurements. IEEE Geosci. Remote Sens. Lett. 2008, 5, 796–800. [Google Scholar] [CrossRef]
- Yardibi, T.; Li, J.; Stoica, P.; Xue, M.; Baggeroer, A.B. Source Localization and Sensing: A Nonparametric Iterative Adaptive Approach Based on Weighted Least Squares. IEEE Trans. Aerosp. Electron. Syst. 2010, 46, 425–443. [Google Scholar] [CrossRef]
- Stoica, P.; Babu, P.; Li, J. SPICE: A Sparse Covariance-Based Estimation Method for Array Processing. IEEE Trans. Signal Process. 2010, 59, 629–638. [Google Scholar] [CrossRef]
- Zhang, Y.; Jakobsson, A.; Yang, J. Range-Recursive IAA for Scanning Radar Angular Super-Resolution. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1675–1679. [Google Scholar] [CrossRef]
- Ghaderpour, E. Multichannel antileakage least-squares spectral analysis for seismic data regularization beyond aliasing. Acta Geophys. 2019, 67, 1349–1363. [Google Scholar] [CrossRef]
- Tipping, M.E. Sparse Bayesian Learning and the Relevance Vector Machine. J. Mach. Learn. Res. 2001, 1, 211–244. [Google Scholar]
- Zhang, Y.; Huang, Y.; Zha, Y.; Yang, J. Superresolution Imaging for Forward-Looking Scanning Radar with Generalized Gaussian Constraint. Prog. Electromagn. Res. 2016, 46, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Bai, X.; Wang, G.; Liu, S.; Zhou, F. High-Resolution Radar Imaging in Low SNR Environments Based on Expectation Propagation. IEEE Trans. Geosci. Remote Sens. 2021, 59, 1275–1284. [Google Scholar] [CrossRef]
- Zhou, F.; Bai, X. High-Resolution Sparse Subband Imaging Based on Bayesian Learning With Hierarchical Priors. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4568–4580. [Google Scholar] [CrossRef]
- Guan, J.; Yang, J.; Huang, Y.; Li, W. Maximum a Posteriori–Based Angular Superresolution for Scanning Radar Imaging. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 2389–2398. [Google Scholar] [CrossRef]
- Chen, H.M.; Li, M.; Wang, Z.; Lu, Y.; Zhang, P.; Wu, Y. Sparse Super-Resolution Imaging for Airborne Single Channel Forward-Looking Radar in Expanded Beam Space via lp Regularisation. Electron. Lett. 2015, 51, 863–865. [Google Scholar] [CrossRef]
- Tuo, X.; Zhang, Y.; Huang, Y.; Yang, J. Fast Sparse-TSVD Super-Resolution Method of Real Aperture Radar Forward-Looking Imaging. IEEE Trans. Geosci. Remote Sens. 2021, 59, 6609–6620. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Q.; Zhang, Y.; Pei, J.; Huang, Y.; Yang, J. Fast Split Bregman Based Deconvolution Algorithm for Airborne Radar Imaging. Remote Sens. 2020, 12, 1747. [Google Scholar] [CrossRef]
- Stoica, P.; Babu, P.; Li, J. New method of sparse parameter estimation in separable models and its use for spectral analysis of irregularly sampled data. IEEE Trans. Signal Process. 2011, 59, 35–47. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Y.; Huang, Y.; Yang, J.; Jakobsson, A. Sparse source location for real aperture radar using generalized sparse covariance fitting. In Proceedings of the IEEE Radar Conference, Seattle, WA, USA, 8–12 May 2017; pp. 1069–1074. [Google Scholar]
- Babacan, S.D.; Molina, R.; Katsaggelos, A.K. Bayesian Compressive Sensing Using Laplace Priors. IEEE Trans. Image Process. 2010, 19, 53–63. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Li, M.; Wang, Z.; Lu, Y.; Wang, S.; Zuo, L.; Zhang, P.; Wu, Y. Super-Resolution Doppler Beam Sharpening Imaging via Sparse Representation. IET Radar Sonar Navigat. 2016, 10, 442–448. [Google Scholar] [CrossRef]
- Xu, G.; Xing, M.; Zhang, L.; Liu, Y.; Li, Y. Bayesian Inverse Synthetic Aperture Radar Imaging. IEEE Geosci. Remote Sens. Lett. 2011, 8, 1150–1154. [Google Scholar] [CrossRef]
- Babacan, S.D.; Molina, R.; Katsaggelos, A.K. Parameter Estimation in TV Image Restoration Using Variational Distribution Approximation. IEEE Trans. Image Process. 2008, 17, 326–339. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Tuo, X.; Huang, Y.; Yang, J. A TV Forward-Looking Super-Resolution Imaging Method Based on TSVD Strategy for Scanning Radar. IEEE Trans. Geosci. Remote Sens. 2020, 58, 4517–4528. [Google Scholar] [CrossRef]
- Huo, W.; Tuo, X.; Zhang, Y.; Zhang, Y.; Huang, Y. Balanced Tikhonov and Total Variation Deconvolution Approach for Radar Forward-Looking Super-Resolution Imaging. IEEE Geosci. Remote Sens. Lett. 2021, in press. [Google Scholar] [CrossRef]
- Xu, S.; Zheng, J.; Pu, J.; Shui, P. Sea-Surface Floating Small Target Detection Based on Polarization Features. IEEE Geosci. Remote Sensing Lett. 2018, 15, 1505–1509. [Google Scholar] [CrossRef]
- Liu, T.; Pang, B.; Ai, S.; Sun, X. Study on Visual Detection Algorithm of Sea Surface Targets Based on Improved YOLOv3. Sensors 2020, 20, 7263. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Q.; Li, C.; Zhang, Y.; Huang, Y.; Yang, J. Sea-Surface Target Angular Superresolution in Forward-Looking Radar Imaging Based on Maximum a Posteriori Algorithm. IEEE J. Sel. Topics Appl. Earth Observ. Remote Sens. 2019, 12, 2822–2834. [Google Scholar] [CrossRef]
- Li, W.; Li, M.; Zuo, L.; Sun, H.; Chen, H.; Lu, X. Azimuth Super-Resolution of Forward-Looking Imaging Based on Bayesian Learning in Complex Scene. Signal Process. 2021, 187, 108141. [Google Scholar] [CrossRef]
- Pedersen, N.L.; Manchón, C.N.; Badiu, M.-A.; Shutin, D.; Fleury, B.H. Sparse Estimation Using Bayesian Hierarchical Prior Modeling for Real and Complex Linear Models. Signal Process. 2015, 115, 94–109. [Google Scholar] [CrossRef] [Green Version]
- Meng, D.; De La Torre, F. Robust Matrix Factorization with Unknown Noise. In Proceedings of the IEEE International Conference on Computer Vision, Sydney, Australia, 2–8 December 2013; pp. 1337–1344. [Google Scholar]
- Bai, X.; Zhang, Y.; Zhou, F. High-Resolution Radar Imaging in Complex Environments Based on Bayesian Learning with Mixture Models. IEEE Trans. Geosci. Remote Sens. 2019, 57, 972–984. [Google Scholar] [CrossRef]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: New York, NY, USA, 2006. [Google Scholar]
- Robert, C.P.; Casella, G. Monte Carlo Statistical Methods; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Ningbo, L.; Yunlong, D.; Guoqing, W.; Hao, D.; Yong, H.; Jian, G.; Xiaolong, C.; You, H. Sea-detecting X-band radar and data acquisition program. J. Radars 2019, 8, 656–667. [Google Scholar]



| Parameter | Value |
|---|---|
| Bandwidth | 60 MHz |
| Scanning speed | |
| Main Lobe Beamwidth | |
| Pulse repetition frequency | 1000 Hz |
| Parameter | Value |
|---|---|
| Bandwidth | 60 MHz |
| Scanning speed | |
| Scanning area | |
| Main Lobe Beamwidth | |
| Pulse repetition frequency | 1000 Hz |
| Methods | MSE () |
|---|---|
| IAA | 2.75 |
| SPICE | 3.91 |
| GMM-LP | 1.41 |
| Multi-prior Bayesia | 0.57 |
| Parameter | Value |
|---|---|
| Bandwidth | 25 MHz |
| Scanning speed | /s |
| Scanning area | |
| Main Lobe Beamwidth | |
| Pulse repetition frequency | 3000 Hz |
| Methods | MSE () |
|---|---|
| IAA | 1.92 |
| SPICE | 2.59 |
| GMM-LP | 0.76 |
| Multi-prior Bayesia | 0.19 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, W.; Li, M.; Zuo, L.; Sun, H.; Chen, H.; Li, Y. Forward-Looking Super-Resolution Imaging for Sea-Surface Target with Multi-Prior Bayesian Method. Remote Sens. 2022, 14, 26. https://doi.org/10.3390/rs14010026
Li W, Li M, Zuo L, Sun H, Chen H, Li Y. Forward-Looking Super-Resolution Imaging for Sea-Surface Target with Multi-Prior Bayesian Method. Remote Sensing. 2022; 14(1):26. https://doi.org/10.3390/rs14010026
Chicago/Turabian StyleLi, Weixin, Ming Li, Lei Zuo, Hao Sun, Hongmeng Chen, and Yachao Li. 2022. "Forward-Looking Super-Resolution Imaging for Sea-Surface Target with Multi-Prior Bayesian Method" Remote Sensing 14, no. 1: 26. https://doi.org/10.3390/rs14010026
APA StyleLi, W., Li, M., Zuo, L., Sun, H., Chen, H., & Li, Y. (2022). Forward-Looking Super-Resolution Imaging for Sea-Surface Target with Multi-Prior Bayesian Method. Remote Sensing, 14(1), 26. https://doi.org/10.3390/rs14010026