Abstract
This study investigated the potential to predict primary production in benthic ecosystems using meteorological variables and spectral indices. In situ production experiments were carried out during the vegetation season of 2020, wherein the primary production and spectral reflectance of different communities of submerged aquatic vegetation (SAV) were measured and chlorophyll (Chl a+b) concentration was quantified in the laboratory. The reflectance of SAV was measured both in air and underwater. First, in situ reflectance spectra of each SAV class were used to calculate different spectral indices, and then the indices were correlated with Chl a+b. Indices using red and blue band combinations such as 650/450 and 650/480 nm explained the largest part of variability in Chl a+b for datasets measured in air and underwater. Subsequently, the best-performing indices were used in boosted regression trees (BRT) models, together with meteorological data to predict the community photosynthesis of different SAV classes. The predictive power (R2) of production models were very high, estimated at the range of 0.82–0.87. The variable contributing the most to the model description was SAV class, followed in most cases by the water temperature. Nevertheless, the inclusion of spectral indices significantly improved BRT models, often by over 20%, and surprisingly their contribution mostly exceeded that of photosynthetically active radiation.
1. Introduction
Primary production is a backbone of life on earth and is a key aspect of the global carbon cycle [1,2]. In aquatic systems, primary production is traditionally mapped in situ using biochemically based techniques, e.g., quantifying changes in oxygen concentration within a sealed environment, incorporation of inorganic carbon into organic matter, or fluorescence kinetics [3]. Although these techniques yield very precise estimates of primary production for the studied locations and times, the methods are not practically feasible for large-scale studies. The patterns of primary production are often highly variable both in time and space. Due to time and budgetary constraints, it becomes unrealistic and inefficient to replicate the measurements to the extent that covers the inherent variability of photosynthetic production at all these scales. Therefore, indirect methods are needed to assess the photosynthetic production at the spatial and temporal scales that remain out of reach of in situ methods. Due to the above-mentioned reasons and the lack of standardized large-scale methods to map the primary production of seascapes, photosynthetic processes are currently among the most important targets of the remote sensing science.
Remote sensing has widely been used for the productivity estimations in terrestrial ecosystems [4]. Several different approaches have been suggested by scientific community for productivity modelling. One of the simplest approaches is a model relying solely on remote sensing data, where the relationship between gross primary productivity (GPP) and various vegetation indices is established [5,6]. However, such relationships allow one to estimate only long-term fluctuations in GPP and may vary significantly between vegetation types and environmental conditions. The inclusion of other meteorological and climate variables, such as land surface temperature or incident photosynthetically active radiation (PAR) [7,8,9,10,11], may allow for accounting for the short-term variability in carbon exchange and result in more accurate and robust models for productivity estimates.
Many current production models use the logic proposed by Monteith [12,13,14,15], where GPP is a function of the PAR, the fraction of PAR absorbed by the vegetation (fAPAR), and the efficiency with which this absorbed light is utilized by vegetation (LUE).
GPP = PAR × fAPAR × LUE,
Different studies use remotely derived spectral indices as proxies for fAPAR and LUE in such models. fAPAR has been shown to be a strong function of the normalized difference vegetation index (NDVI) [14,16,17]. LUE has been proven to be more challenging to estimate from remotely sensed data [5]. Still, photochemical reflectance index (PRI) is considered as a good proxy for LUE [15,18,19,20,21,22]. However, many studies have summarized the difficulties in using those indices at canopy level GPP estimation [7,13,21].
Remotely sensed vegetation indices, used in terrestrial vegetation production models, mostly utilize near infrared (NIR) wavelengths as a reference. As such, those indices are not applicable for benthic productivity assessment because of the effect of water column, which absorbs most of the valuable information in NIR [23,24]. Therefore, benthic vegetation productivity has been assessed through some other remote sensing product (vegetation cover, biomass etc.) in aquatic ecosystems. For example, remote sensing has shown potential to provide information on the biophysical characteristics of benthic vegetation, such as biomass or leaf area index (LAI) [25,26,27,28], as well as benthic types [29,30,31]. For example, the authors of [32] used remotely retrieved products of seagrass leaf area index (LAI) as inputs in benthic ecosystem production models. References [33,34] utilized remotely sensed imagery to map benthic biotopes in a reef environment, which were then coupled with in situ measured community metabolic rates to scale up landscape level benthic productivity. Reference [35] proceeded from the fact that light reaching the water bottom is a fundamental factor driving primary production and studied relationships between light availability and benthic productivity. A version of Monteith model was proposed by the authors of [36] to measure coral reef benthic productivity on the basis of remotely estimated downwelling plane irradiance and optical absorptance of benthic types.
In the current paper, the in situ production estimates of different classes of submerged aquatic vegetation (SAV) were coupled with spectral and meteorological measurements to model SAV GPP. First, we analyzed the measured reflectance spectra of different SAV classes and corresponding laboratory measured pigments to select vegetation indices that have the potential to estimate chlorophylls content in submerged macrophytes. The rationale for using chlorophyll-related indices is that higher chlorophyll content should indicate the higher photosynthesis and thus, higher production rate [7,9]. Secondly, a boosted regression trees (BRT) model was built to assess the sensitivity of meteorological variables (water temperature, PAR) and vegetation indices when predicting the primary production of SAV. Vegetation class was also included in the model to account for variability due to different benthic vegetation classes. Finally, the potential for using remotely sensed vegetation indices in benthic production models was assessed. Current study will help to improve our understanding of the relationships between carbon flux and optical properties of benthic community and develop more efficient algorithms to assess benthic productivity using remote sensing.
2. Materials and Methods
2.1. Experimental Site and Benthic Vegetation Used in the Experiment
The production experiments were carried out in the shallow coastal waters in the Kõiguste Bay, Gulf of Riga, northern Baltic Sea (Figure 1a). The experiments were performed at 0.5–1.0 m water depth on three consecutive days on of the 2–4 June, 3–5 August, and 21–23 September 2020. Experiments were performed in different vegetation periods to account for seasonality in vegetation development stages or vegetation greenness (i.e., canopy chlorophyll content) that can be related to vegetation indices [7]. Three-day continuous measurements were performed to account variability in short term environmental conditions, such as temperature and PAR changes. The short-term variability cannot be estimated from vegetation indices, as greenness remains basically constant over such a short period; however, plant productivity may vary to large extent due to differential availability of light.

Figure 1.
(a) Location of the experimental site in the Baltic Sea. (b) Underwater chamber to quantify the in situ photosynthetic production of plant communities.
Four SAV classes were used in the current experiments: green filamentous macroalgae, brown macroalgae, charophytes, and higher plants, as our previous studies have shown [37] that those are the classes that can be mapped with reasonable accuracy from remote sensing images. Brown macroalgae were represented by the habitat former Fucus vesiculosus and its epiphytes (e.g., Ceramium tenuicorne, Pylaiella littoralis). Green macroalgae class was represented mainly by one dominant species Cladophora glomerata, but this habitat always hosted Ulva intestinalis. In September, however, the green algal community contained only Ulva intestinalis. Fucus vesiculosus and Cladophora glomerata/Ulva intenstinalis habitats are found on hard substrates, such as rocks and stones. Charophytes were represented by the dominant species Chara aspera and subordinate Chara canescens. Higher plant habitat was dominated by Myriophyllum spicatum, and other high plant species were Ruppia maritima and Stuckenia pectinata. Charophyte and high plant species grow on soft sediments.
2.2. Estimating In Situ Production Potential in Plant Communities
The production of plant communities was measured in triplicate from transparent Plexiglas chambers holding 29 L of water with a surface area 850 cm2 (Figure 1b). On soft bottom habitats, the chambers were placed randomly on the seafloor over the homogeneous stands of studied habitat. A rubber seal assured an airtight seal between the chamber and the surrounding environment. On hard bottom habitats, the chamber consisted of a transparent Plexiglas dome and a steel base. Stones with growing macroalgae were collected from a shallow (1 m) adjacent area and were placed on a steel base. Experimental treatments consisted of communities dominated either by F. vesiculosus or C. glomerata. Both habitats had small amounts of epiphytes. An airtight seal between the chamber and the base was achieved using a rubber sealing and steel wing nuts.
Oxygen concentration in the chamber was measured every minute using a calibrated Optode-type oxygen sensor (Aanderaa Instruments) connected to a data logger (data recorder by JFE Advantech Co. Ltd.). This instrument also provides data on water temperature. Changes in dissolved oxygen averaged over minute intervals were used as a proxy of habitat net production. During deployment, irradiance above the plant habitats was measured every minute using a calibrated spherical quantum sensor connected to a data logger (ultra-miniature logger for light intensity by JFE Advantech Co. Ltd.). Each production experiment lasted 24 h on average. The experiment was replicated in three consecutive days under spring, summer, and autumn conditions (June, August, September).
After deployment, plants within incubation chambers were harvested and stored in a deep freezer at −20 °C. The subsequent sorting and determination of species were performed in the laboratory using a stereomicroscope. The dry weight of each species was obtained after drying the individuals at 60 °C for two weeks (i.e., the time needed to achieve the same weight for two consecutive measurements). Combining this information with the oxygen flux measurements described above enabled us to express the habitat net primary production in mg O2 g dry weight of macrophyte−1 min−1.
2.3. Measuring Benthic Vegetation Reflectance
Two types of in situ hyperspectral reflectance measurements of the vegetation canopies were performed shortly after the completion of the production measurements—above water surface (AW dataset) and underwater (UW dataset) reflectance measurements. AW measurements were acquired above the water surface (including 0.5–1.0 m water column) using Ramses upwelling radiance (Lu, W m−2 nm−1 sr−1) and downwelling irradiance (Ed, W m−2 nm−1) sensors. Lu sensor was pointed down to the benthic vegetation canopy, while Ed sensor was pointed to the sky. Reflectance spectra were calculated as Lu/Ed. Throughout the study, 10 replicate scans were taken for each target and the mean values were used in the analyses. AW reflectance spectra contain information from both —water column and water bottom vegetation. However, since we were interested only in the bottom signal, water column signal should be decoupled from benthic vegetation and removed (described in Section 2.4).
UW measurements were obtained below the water surface using Lu sensor and a white SphereOptics panel (99% reflectance) as a reference. Reference measurements were acquired immediately after each target measurement. Reflectance spectra of target vegetation canopies were calculated as Lu(Target)/Lu(Reference). Measurements were performed with negligible distance between the Lu sensor, target, and reference. Therefore, all UW measurements are considered as vegetation reflectance spectra, with minimal water column contribution.
Table 1 shows the number of coincident production and reflectance data for AW and UW datasets. Charophyte data are missing for June, as we were not able to find any charophytes communities from the study area at that time. The AW dataset includes slightly less coincident data, which was mostly driven by the technical problems with Ramses Ed sensor in retrieving reasonable Ed data. Additionally, some reflectance measurements, in both AW and UW dataset, were unusable due to unfavorable weather conditions during the measurements (e.g., strong wind, high waves).

Table 1.
Coincident production and reflectance measurements for AW (above water surface) and UW (underwater) datasets. Coincident measurements available for three days (+++), two days (++), or one day (+) for the vegetation period in June, August, and September. No coincident data (-) available for the period.
2.4. Collection and Processing of Water Column Optical Data
The optical properties of water column were required to apply the water column correction (WCC) to the AW reflectance dataset to retrieve bottom spectra (referred to as AW_bottom). Maritorena [38] WCC algorithm was used to retrieve bottom reflectance (Rb):
where Rw is the measured water surface reflectance, R∞ is the reflectance of optically deep water, Kd is the diffuse downwelling attenuation coefficient, and z is the water depth. z was measured on the location of each production chamber. R∞ and Kd were measured in the deep-water area (>7 m depth), as near as possible to the experimental chambers (within the range of 500 m), to assure similar optical properties between shallow experimental and deep water sites. Still, it needs to be considered that there might have been some differences in water column properties between the location of production chambers and deep water area.
Reflectance spectra of optically deep water (R∞) were acquired above the water surface with Ramses sensors. Reflectance spectra were calculated as Lu/Ed. As the Maritorena model was developed for reflectance just below the water surface, Ramses above water surface reflectance was converted to the below-water-surface reflectance using the approximation of Rw(0−) = Rw(0+)/t, with t = 0.54 [39].
Ramses Ed depth profiles from the surface to the depth of 2.5 m were acquired after every 0.5 m. Ed profiles were used to calculate the diffuse downwelling attenuation coefficient (Kd):
where Δz is the difference in measurement depth, Ed(z1) is the downwelling irradiance at depth z1, and Ed(z2) is the downwelling irradiance at depth z2, while z1 is a reference depth closer to the water surface. Kd value for each 0.5 m depth range along the water column was calculated and, finally, all the values were averaged.
2.5. Pigment Analysis
Vegetation samples collected from the vicinity of each production chamber were taken to the laboratory for pigment analysis. As vegetation greenness (related to pigment content) does not change during a few days, only one sample of each vegetation class per each of the three experiment periods (June, August, September) was collected. In the laboratory, pigments of pre-weighted plant pieces were extracted in methanol (100% pure solvent) for 24 h and analyzed using the PerkinElmer Lambda 35 UV/VIS spectrophotometer (see details in [40]). The concentrations of extracted chlorophylls (Chl a, Chl b) were determined using the equations of [41]. Three replicate measurements were performed per each sample, and average pigment concentrations (mg/g wet weight) were calculated.
2.6. Modelling
2.6.1. Spectral Indices Computation
First, the dataset described in [40] was used to examine relationships between measured SAV spectra and corresponding laboratory measured chlorophylls concentration (Chl a+ b) to select vegetation indices that have the potential to predict Chl a+b in SAV. Green filamentous macroalgae (combining Cladophora glomerata and Ulva intestinalis), brown macroalgae Fucus vesiculosus, and charophyte Chara aspera were used in the analysis. Spectra of vegetation samples were measured in laboratory with hyperspectral imaging device Hyspex (Norsk Elektro Optikk) followed by pigment analysis. As such, this dataset includes SAV spectra measured on leaf level and without the water column influence and is referred to as WW dataset. The details for equipment and measurement methods are provided in [40].
Secondly, the same relationships were studied using the dataset collected in this study, wherein the reflectance spectra were measured under water above the vegetation canopies (UW dataset). An average spectrum of three-day measurements from each of the experiment periods (June, August, September) was used in the analysis to correlate with measured Chl a+b. If less than three measurements per vegetation class and experiment period were available, then an average of two or only single day measurement was used (Table 1, charophytes in August and September, respectively). Due to the limited sample size, all vegetation classes were pooled together for the UW dataset.
Simple ratio (SR) and normalized difference spectral indices (NDSI) were calculated from in situ-measured hyperspectral reflectance spectra using various combinations of wavelengths:
i and j represent wavelengths (i and j nm). Only some pre-selected spectral regions were tested in the current study, as utilizing all the band combinations would have resulted in exhaustive number of indices. The studied macroalgal classes have specific spectral absorption features and reflectance peaks near 450, 480, 550, 570, 600, 650, 680, 704, and 750 nm (Figure 2). Those spectral regions are also affected by the variations in Chl a+b, as seen from Figure 2 and selected for chlorophyll-related indices development.
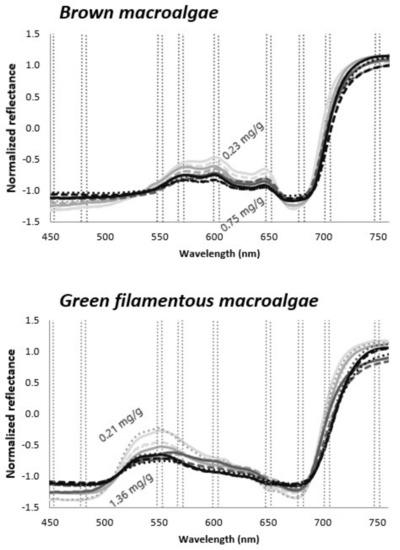
Figure 2.
Examples of normalized reflectance spectra of brown macroalgae and green filamentous macroalgae representing various chlorophyll concentrations; lighter gray—lower concentrations, black—higher concentrations. Spectral regions used for index development are marked with dotted lines. Data taken from the WW dataset.
Both visible (VIS) and NIR spectral regions were used as reference wavelengths in tested indices. However, as the light in the NIR wavelength is almost instantly absorbed by the water, preventing acquiring spectral information from submerged vegetation, even in relatively shallow water depths [23,24], we focused mostly on the VIS wavelength. In addition, indices measuring the height of reflectance peaks (H) near 550, 570, 600, and 650 and the depth of absorption features (D) near 680 nm (Figure 2) were calculated as follows:
where Rλ1 represents the wavelength for which the reflectance height or absorption depth is measured, and Rλ2 and Rλ3 represent reference wavelengths on both sides of the spectral features. It is seen from Figure 2 that H and D should change together with Chl a+b variations. Indices showing the potential to correlate with Chl a+b were used in the production models.
2.6.2. Linking Environmental Condition, Spectral Indices, and Photosynthetic Production of Benthic Communities
When modelling the primary productivity of plant habitats, we used different spectral indices as predictors. However, as the primary production of benthic vegetation is known to be driven by vegetation type, light availability, and water temperature; the productivity model also included plant class, PAR, and water temperature as independent variables. The contribution of different environmental variables on the community photosynthesis of different plant classes was explored using the boosted regression trees technique (BRT).
BRT models are capable of handling different types of predictor variables and their predictive performance is superior to most traditional modelling methods (see, e.g., comparisons with GLM, GAM, and multivariate adaptive regression splines) [42,43]. Importantly, the modelling method enables interactive effects of different independent variables to be accounted for (e.g., the effect of temperature on plant photosynthesis may vary along the PAR gradient). Overfitting is often regarded as a problem in statistical modelling but can be overcome by using independent datasets. The BRT modelling iteratively develops a large ensemble of small regression trees constructed from random subsets of the data. Each successive tree predicts the residuals from the previous tree to gradually boost the predictive performance of the overall model [44]. Important parameters in building BRT models are the learning rate and tree complexity. The learning rate determines the contribution of each tree to the growing model, and tree complexity defines the depth of interactions allowed in a model. A tree complexity of 1 assesses only main effects; a tree complexity >1 includes interactions. Different combinations of these parameters may yield variable predictive performance but generally a lower learning rate and inclusion of interactions gives better results [44].
In the current study, the model learning rate was kept at 0.001, and tree complexity at 5. To avoid potential problems of overfitting, we removed unimportant variables using a simplify tool. To eliminate non-informative variables, the simplify tool progressively simplifies the model, then re-fits the model and sequentially repeats the process until a stopping criterion is reached. Such simplification is most useful for small datasets where redundant predictors may degrade performance by increasing variance. Model performance was evaluated using the cross-validation statistics calculated during model fitting [45]. The BRT modelling was done in R using the gbm package [44]. Standard errors for the predictions and pointwise standard errors for the partial dependence curves, produced by R package “pdp” [46], were estimated using bootstrap (100 replications). Multicollinearity can be an issue with BRT modelling when assessing if and when environmental variables are of ecological interest. Thus, prior to modelling, the Pearson correlation analysis between all environmental variables was calculated in order to avoid including highly correlated variables into the model. The correlation analysis showed that most variables were only weakly intercorrelated (r < 0.5).
3. Results
3.1. Spectral Measurements
Examples of standardized UW reflectance spectra and corresponding endmember spectra are given in Figure 3. Endmember spectra represent the spectra of corresponding vegetation species measured without water column influence. Those endmember spectra, used in the current study, were taken from our spectral library measured over the years from different parts of the Baltic Sea. As shown in Figure 3, UW and endmember spectra display generally similar shape in the VIS spectral range, but distinctive differences occur in the NIR spectral range. Endmember spectra showed high reflectance plateau in NIR, while the effect of water column absorption in UW spectra was most evident at wavelengths longer than 720 nm. Another reflectance peak was apparent near 810–820 nm due to decreased water column absorption [47]. Hence, even though UW measurements were performed with negligible distance between sensor and target, water column still affected the NIR spectral range.
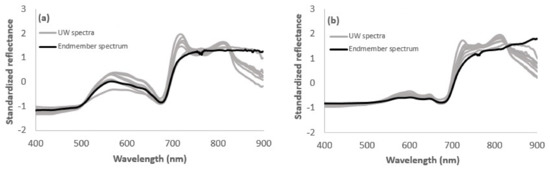
Figure 3.
Comparison of underwater (UW) measured vegetation spectra with corresponding endmember spectrum for (a) green macroalgae (Cladophora glomerata) and (b) brown macroalgae (Fucus vesiculosus).
Examples of AW measured reflectance spectral before and after WCC and corresponding endmember spectra are shown in Figure 4. Again, AW_bottom spectra showed generally similar spectral shape with endmember spectrum in VIS spectral range. WCC model was parameterized with Kd and R∞, which were measured not exactly at the experimental site but at the nearest optically deep-water area. As a result, the water quality may have differed between those sites, resulting in some inaccuracies in retrieved AW_bottom spectra (Figure 4). Considerable discrepancies occur in the NIR spectral range. NIR spectral range is highly sensible to WCC model parameterization. Therefore, even slight inaccuracies in input parameters may have a significant effect on retrieved bottom spectra [48].
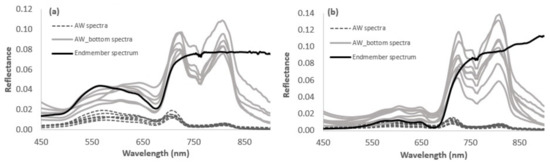
Figure 4.
Comparison of above water surface measured vegetation spectra (AW) with water column corrected (AW_bottom) spectra and corresponding endmember spectrum for (a) green macroalgae (Cladophora glomerata) and (b) brown macroalgae (Fucus vesiculosus).
Figure 4 shows that acceptable bottom spectra can be retrieved for VIS spectral range, as this spectral range is not so sensible to model parameterization. As such, indexes that use VIS bands as reference wavelengths instead of NIR may have a greater potential to predict chlorophyll concentration in benthic vegetation.
3.2. Relationships between Spectral Indices and Chlorophyll a+b Concentrations
Table 2 and Table 3 and Figure 5 show the strengths of correlations between Chl a+b and best performing spectral indices in terms of correlation coefficient (R2) and root mean square error (RMSE). Prior to evaluating the R2 and RMSE, we tested the assumption of normality. The analyses showed that the distribution of means across samples was normal. Table 2 displays the results for the WW dataset for each vegetation class separately and for combined classes. Indices that use NIR wavelength as reference (SR750/705; NDSI750/705) were the most sensitive to variations in Chl a+b if vegetation spectra were measured without water column influence. SR650/680, SR600/680, NDSI650/680, and NDSI600/680 generally correlated well with Chl a+b on the class level, but rather poorly on the combined classes level. SR650/450, SR650/450, NDSI650/480, and NDSI650/480 gave good correlations also on the combined classes level. Height of reflectance peak near 650 nm gave the highest correlation with Chl a+b, while the depth of absorption feature near 680 nm did not provide reasonable correlation, neither on classes nor on the combined classes level. Figure 5 displays scatterplots of regressions between selected spectral indices and Chl a+b.

Table 2.
The coefficient of determination (R2) and root mean square error (RMSE) between chlorophyll concentration (mg/g wet weight Chla a+b) and spectral indices for the WW dataset. R2 and RMSE are given separately for each vegetation class and for combined classes.

Table 3.
The coefficient of determination (R2) and root mean square error (RMSE) between chlorophyll concentration (mg/g wet wt Chl a+b) and spectral indices for the UW dataset. R2 and RMSE are given only for combined classes incorporating green macroalgae, brown macroalgae, charophytes, and higher plants.
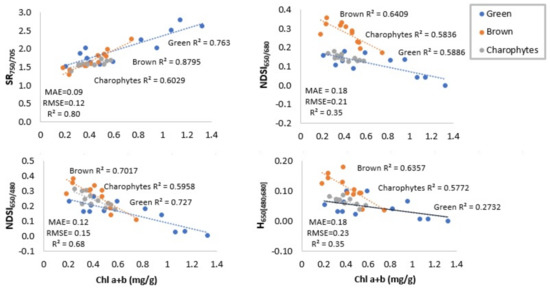
Figure 5.
Relationships between chlorophylls concentration (mg/g wet wt Chl a+b) and selected spectral indices. Indices are calculated from the WW dataset. Root mean square error (RMSE) and mean absolute errors (MAE) are given for combined classes.
The same indices were tested also with the UW dataset to define whether the same relationships exist between indices and Chl a+b if spectra were measured under water at canopy scale (Table 3). Here, only the relationships on combined classes level were assessed, as the limited amount of data did not allow us to perform class level analysis.
Results show that NIR indices gave very poor correlation with Chl a+b concentration in the case of the UW dataset. This indicates that the indices using NIR spectral bands as reference cannot provide prediction for Chl a+b in underwater benthic vegetation, as water absorption interferes spectral information in NIR spectral range. Similar to the WW dataset, indices using information from VIS red and blue spectral range (SR650/450, SR650/450, NDSI650/480, NDSI650/480) were the ones correlating well with Chl a+b if the UW dataset was used. The depth of absorption feature at 680 nm showed the highest sensitivity to variations in Chl a+b concentrations.
3.3. Production Measurements
Photosynthetic production varied largely among different plant classes, with Cladophora glomerata/Ulva intestinalis having the highest rate of photosynthesis, followed by the Chara aspera communities. Fucus vesiculosus and Myriophyllum spicatum had the lowest rates of photosynthesis (Figure 6).
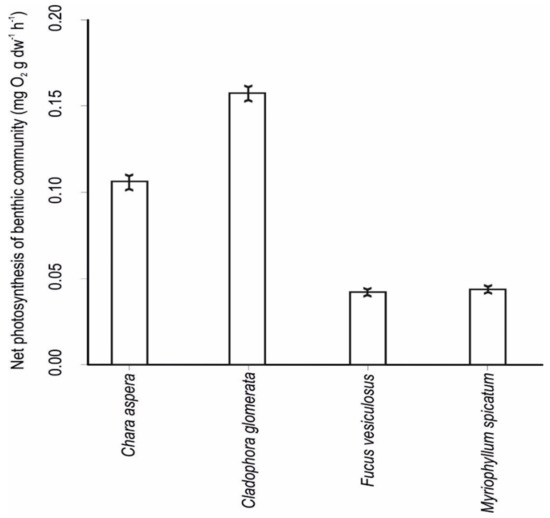
Figure 6.
Community net production rates of different plant classes in the study area (means ± standard error).
Both light and temperature were important predictors of community photosynthesis. For all studied plant classes, improved light availability increased plant productivity up to a threshold of 500 μmol quanta m−2 s−1. Above this tipping point, variability in plant production was largely independent of the ambient PAR. As for Fucus vesiculosus, the community production responded to increased light availability up to 1000 μmol quanta m−2 s−1, but responses were weaker compared to lower light levels (Figure 7).
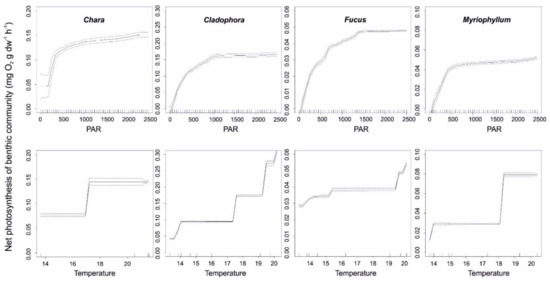
Figure 7.
Standardized functional–form relationships (±standard error) showing the effect of environmental variables on the net photosynthesis of the studied plant classes, whilst all other variables are held at their means. Upward tickmarks on x-axis show the frequency distribution of data along this axis.
The production of plants had clear phases along temperature gradient: low production at <17–19 °C and higher production above this temperature. Cladophora glomerate/Ulva intestinalis responded more gradually to increasing temperature values (Figure 7).
3.4. Model-Based Productivity Assessment
The modelling of the productivity of plant classes was performed separately for UW and AW_bottom datasets. All the spectral indices provided in Table 2 and Table 3 were used as independent variables in the production models. The predictive power of each model (R2) and the relative contribution of different variable to the models’ total variable explained (%) are provided in Table 4.

Table 4.
The predictive power of models (R2) and the relative contribution of different variable to the models’ total variable explained (%) separately for UW and AW_bottom datasets.
The predictive power (R2) of production models were very high and remained in the range of 0.82–0.87 (Table 4). The variable contributing the most to model description was SAV class (38–50%), followed in most cases by water temperature (23–38%). PAR contributed stably at 14–16% to the model. The contribution of spectral indices largely depended on the type of index varying between 4 and 23% of the models’ total variable explained.
The relative contribution of different spectral indices varied more in the UW dataset (5–23%) compared to the AW_bottom dataset (12–20%) (Table 4). The best performing indices in the UW dataset were SR650/450, NDSI650/450, SR650/480, and NDSI650/450, showing the highest contribution to model description. Those indices also performed well in correlation with Chl a+b (Table 3). NIR indices showed low contribution to model description (5%).
The modelling results showed that the best performing indices in AW_bottom dataset were SR650/680, NDSI650/680, and D680[650;705] (Table 4). In AW_bottom dataset, NIR indices showed considerably higher contribution to model’s description compared to UW dataset, although still remaining the lowest if compared to the contribution of VIS indexes.
Examples of the shapes of relationships between best performing spectral indices and the net photosynthesis of the studied plant classes for both datasets (NDSI650/450 for UW and NDSI650/680 for AW_bottom dataset) are given in Figure 8. In UW dataset, NDSI650/450 showed a very good relationship with net photosynthesis, indicating its high ability to improve model’s predictability. In AW_bottom dataset, NDSI650/680 index showed slightly lower response to net photosynthesis. For both indices, elevated values corresponded to high net photosynthesis of the benthic community. However, the responses were largely different between AW and UW datasets. In the AW_bottom dataset, an increasing NDSI650/680 resulted in gradual increase of photosynthesis until a threshold of about 0.1 and then levelled off. On the other hand, in the UW dataset photosynthesis increased with NDSI650/450 in the entire range of index value.
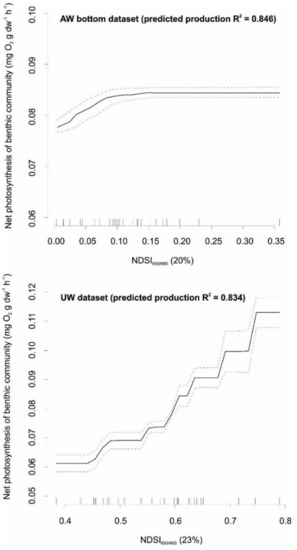
Figure 8.
Standardized functional–form relationships (± standard error) showing the strength (% value in brackets) and shape of relationship between best performing spectral indices and the net photosynthesis of the studied plant classes, whilst all other variables are held at their means. Upward tickmarks on x-axis show the frequency distribution of data along this axis.
4. Discussion
To use remote sensing effectively as an environmental monitoring tool, one must first determine features that are indicative to the studied environmental characteristics and/or processes [47]. In terrestrial ecosystems, spectral vegetation indices have successfully been established and shown to be indicative to primary productivity [5,6,7,8,9,10,11]. The potential for using spectral indices in underwater vegetation production models has hardly been assessed at all.
The existing methodological approaches to assess the spatio-temporal patterns of primary production of terrestrial vegetation assume that remotely sensed indices capture the productivity of vegetation. In order to validate such linkages in benthic ecosystem, it is necessary to first quantify the patterns of remote sensing indices that most likely predict benthic productivity. When the in situ production of the same habitats is assessed, then it enables establishing the functional form relationships between remote sensing indices and primary production of seascapes.
Our first objective was to select vegetation indices that have the ability to estimate chlorophyll content in submerged macrophytes. The rationale for using chlorophyll-related indices is that higher chlorophyll content constitutes a good predictor for higher productivity [7,9]. Vegetation indices that have successfully been applied for productivity assessment in terrestrial vegetation mostly use NIR spectral range as a reference wavelength. However, high water column absorption in NIR spectral range and the need for very precise WCC model parameterization in every image pixel to retrieve acceptable benthic NIR values limits the practical application of such indexes in SAV studies.
Shorter wavelengths are less affected by water column absorption, but they also present a problem with both atmospheric and water column scattering [47]. In addition, colored dissolved organic matter (CDOM) strongly contributes to the absorption at shorter wavelengths in the Baltic Sea. The best performing band combination for benthic vegetation index development lies somewhere in VIS range between the extremes of scattering and absorption properties of atmosphere, water, and water constituents [47,49]. This spectral range also has lower sensitivity to WCC model parameterization, allowing retrieval of bottom spectra with higher accuracy. As such, indexes that use VIS bands (450–700 nm), further from shorter and longer extremes, may have a greater potential to predict chlorophyll concentration and hence productivity in benthic ecosystems.
In this study, reflectance spectra of benthic vegetation with various Chl a+b concentrations were studied to identify a set of spectral bands, with which to formulate vegetation indices that could potentially predict Chl a+b in aquatic vegetation. First, air-measured benthic vegetation dataset (WW dataset) was used to study correlations between Chl a+b and selected band ratios. Developed chlorophyll-related spectral indices were then tested on the UW dataset to define whether the developed indices are applicable if reflectance spectra were measured under the water above the plant canopies.
Our results showed that indices that use NIR wavelength as reference were the most sensitive to variations in Chl a+b in the case when vegetation spectra were measured in air. However, NIR indices did not show high correlations if vegetation spectra were measured underwater, showing the limitation of such indices in underwater applications. Indices using red and blue band combinations such as 650/450 and 650/480 nm gave the best results with Chl a+b for both community scale WW and UW datasets.
The developed indices (Table 2 and Table 3) were then used in BRT models together with meteorological variables to predict benthic vegetation primary productivity. Models were developed separately for two datasets, wherein indices were calculated from UW and AW_bottom reflectance data. Out of the two datasets, the AW dataset is more important from the practical application perspective as this is the information acquired also by remote sensing sensors. WCC processing was required to retrieve AW_bottom spectra from AW spectra, after which the vegetation indices could be calculated. Our previous studies have shown [37] that Maritorena WCC model retrieves reasonable spectral shapes, but not absolute values. As the shape of the reflectance spectra is more important than absolute value while calculating spectral indices, Maritorena WCC model was used in this study.
Modelling results showed that for both datasets, the variable contributing the most to the model description was vegetation class, followed in most cases by the water temperature, the latter probably being a proxy of seasonality in the production of the studied SAV classes. The inclusion of spectral indices significantly improved BRT models, often by over 20%, and surprisingly their contribution mostly exceeded that of PAR. Different indices performed differently and did not quite overlap in the AW_bottom and UW datasets. It is known that benthic primary production is a product of different elements each operating at different temporal scales. The type of SAV defines the generic type of response of the plant to ambient environmental variables (e.g., temperature and PAR) and the maximum production rate [50]. Nevertheless, actual environmental conditions can largely modulate the above responses. For example, plants are often characterized by strong seasonal variation in photosynthesis and growth [51], and this variability is coupled with the quantity of pigments in plant cells [52]. Importantly, the latter defines the daily responses of a plant community to changes in, e.g., PAR.
In the current study, the relationship between vegetation indices and production was established by using an in situ field spectrometer. Subsequent research is needed to investigate the application of this technique to hyperspectral and/or multispectral image data. Several considerations must be taken into account before the developed method can be applied to image data.
First, narrow field spectrometer bands were used to determine vegetation indices suitable for underwater benthic productivity estimation. Spectral resolution of airborne or spaceborne imaging sensors needs to be considered to explore if those sensors have the required bands and/or bandwidths to retrieve indexes that performed well in the current study.
Secondly, acquiring remote sensing images of SAV without the water column influence is not possible. To be able to calculate the spectral indices of SAV, water column signal needs to be removed from the bottom signal. Our experiments were carried out in the depth range of 0.5−1.0 m and applied WCC performed relatively well in retrieving bottom spectra in such a shallow water depth (Figure 4). However, our previous studies [37,48] have shown that WCC in the optically complex waters is a complicated task, and retrieving bottom spectra becomes increasingly harder with increasing water depth. Future work in this area should investigate from what water depth bottom spectra can be retrieved with reasonable accuracy so that spectral indices calculated from those spectra can contribute to productivity models in our waters.
Finally, only pure vegetation spectra were used in the current analysis. In reality, a signal reaching to remote sensing sensor may consist of the combination of vegetation and background (e.g., sand, gravel, mud) signals. This is especially true for sensors with lower spatial resolution. In this case, we need to consider what the vegetation coverage above the substrate should be so that Chl a+b variations are captured by spectral indices.
5. Conclusions
The objective of the current study was to develop spectral indices for the production assessment of benthic vegetation using in situ spectral reflectance data and to test those indices together with other environmental variables (SAV class, temperature, PAR) in productivity models.
Spectral indices were calculated on the basis of in situ-measured benthic vegetation reflectance data and correlated with Chl a+b. Indices using NIR wavelengths (SR750/705; NDSI750/705) gave highest correlations with Chl a+b if vegetation spectra were measured in air, but poor correlations if spectra were measured under water, indicating the limitation of such indices in underwater applications. Indices using red and blue wavelengths (SR650/450, SR650/450, NDSI650/480, and NDSI650/480) gave good correlations for both in air and underwater measured spectra.
Modelling results showed that the primary production of SAV can be effectively and accurately assessed using remote sensing when we have sufficient knowledge on the identity of SAV as well as the levels of environmental variables driving photosynthesis such as temperature and PAR. To date, this poses no difficulties as our recent research demonstrated the ability of remote sensing to distinguish broad SAV classes in the shallow Baltic Sea waters, as well as there being standard products available to map values of temperature and PAR in marine environments (e.g., Copernicus Marine Environment Services products).
This suggests that establishing a relationship between Chl a+b and remote sensing signal is theoretically attainable, providing a quantitative link to relate remotely sensed signal to benthic primary production. However, the practical applicability of methodology in large-scale imaged data requires further investigations. We hope that the current study will help to improve our understanding of the relationships between carbon flux and optical properties of benthic community and develop more efficient algorithms to assess benthic productivity.
Author Contributions
Conceptualization, E.V. and J.K.; methodology, J.K. and E.V.; software, J.K. and M.K.; formal analysis, E.V., J.K., M.K., L.A. and I.K.; investigation, L.A., I.K., M.K. and E.V.; resources, J.K., T.K. and E.V.; writing—E.V.; writing—review and editing, J.K. and T.K.; funding acquisition, E.V. and T.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Estonian Research Council, grant numbers PUT1049 and PUT PRG302.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Thompson, M.V.; Randerson, J.T.; Malmström, C.M.; Field, C.B. Change in net primary production and heterotrophic respiration: How much is necessary to sustain the terrestrial carbon sink? Glob. Biogeochem. Cycles 1996, 10, 711–726. [Google Scholar] [CrossRef]
- Field, C.B.; Behrenfeld, M.J.; Randerson, J.T.; Falkowski, P. Primary Production of the Biosphere: Integrating Terrestrial and Oceanic Components. Science 1998, 281, 237–240. [Google Scholar] [CrossRef]
- Marra, J. Phytoplankton Productivity: Carbon Assimilation in Marine and Freshwater Ecosystems. In Phytoplankton Productivity: Carbon Assimilation in Marine and Freshwater Ecosystems; Williams, P.J.L., Thomas, D.N., Reynolds, C.S., Eds.; Blackwell: Oxford, UK, 2002; pp. 78–108. [Google Scholar]
- Song, C.; Dannenberg, M.P.; Hwang, T. Optical remote sensing of terrestrial ecosystem primary productivity. Prog. Phys. Geogr. Earth Environ. 2013, 37, 834–854. [Google Scholar] [CrossRef]
- Sims, D.A.; Rahman, A.F.; Cordova, V.D.; El Masri, B.; Baldocchi, D.; Flanagan, L.; Goldstein, A.; Hollinger, D.Y.; Misson, L.; Monson, R.K.; et al. On the use of MODIS EVI to assess gross primary productivity of North American ecosystems. J. Geophys. Res. Space Phys. 2006, 111, G04015. [Google Scholar] [CrossRef]
- Hashimoto, H.; Wang, W.; Milesi, C.; White, M.A.; Ganguly, S.; Gamo, M.; Hirata, R.; Myneni, R.B.; Nemani, R.R. Exploring Simple Algorithms for Estimating Gross Primary Production in Forested Areas from Satellite Data. Remote Sens. 2012, 4, 303–326. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Viña, A.; Verma, S.B.; Rundquist, D.C.; Arkebauer, T.J.; Keydan, G.; Leavitt, B.; Ciganda, V.; Burba, G.G.; Suyker, A.E. Relationship between gross primary production and chlorophyll content in crops: Implications for the synoptic monitoring of vegetation productivity. J. Geophys. Res. Atmos. 2006, 111, D08S11. [Google Scholar] [CrossRef]
- Sims, D.A.; Rahman, A.F.; Cordova, V.D.; Elmasri, B.Z.; Baldocchi, D.D.; Bolstad, P.V.; Flanagan, L.B.; Goldstein, A.H.; Hollinger, D.Y.; Misson, L.; et al. A new model of gross primary productivity for North American ecosystems based solely on the enhanced vegetation index and land surface temperature from MODIS. Remote Sens. Environ. 2008, 112, 1633–1646. [Google Scholar] [CrossRef]
- Wu, C.; Niu, Z.; Tang, Q.; Huang, W.; Rivard, B.; Feng, J. Remote estimation of gross primary production in wheat using chlorophyll-related vegetation indices. Agric. For. Meteorol. 2009, 149, 1015–1021. [Google Scholar] [CrossRef]
- Sjöström, M.; Ardö, J.; Arneth, A.; Boulain, N.; Cappelaere, B.; Eklundh, L.; de Grandcourt, A.; Kutsch, W.; Merbold, L.; Nouvellon, Y.; et al. Exploring the potential of MODIS EVI for modeling gross primary production across African ecosystems. Remote Sens. Environ. 2011, 115, 1081–1089. [Google Scholar] [CrossRef]
- Schubert, P.; Lagergren, F.; Aurela, M.; Christensen, T.; Grelle, A.; Heliasz, M.; Klemedtsson, L.; Lindroth, A.; Pilegaard, K.; Vesala, T.; et al. Modeling GPP in the Nordic forest landscape with MODIS time series data—Comparison with the MODIS GPP product. Remote Sens. Environ. 2012, 126, 136–147. [Google Scholar] [CrossRef]
- Monteith, J.L. Solar Radiation and Productivity in Tropical Ecosystems. J. Appl. Ecol. 1972, 9, 747–766. [Google Scholar] [CrossRef]
- Hilker, T.; Coops, N.; Wulder, M.; Black, T.A.; Guy, R.D. The use of remote sensing in light use efficiency based models of gross primary production: A review of current status and future requirements. Sci. Total Environ. 2008, 404, 411–423. [Google Scholar] [CrossRef] [PubMed]
- Wu, C.; Niu, Z.; Gao, S. Gross primary production estimation from MODIS data with vegetation index and photosynthetically active radiation in maize. J. Geophys. Res. Space Phys. 2010, 115, D12127. [Google Scholar] [CrossRef]
- Rossini, M.; Cogliati, S.; Meroni, M.; Migliavacca, M.; Galvagno, M.; Busetto, L.; Cremonese, E.; Julitta, T.; Siniscalco, C.; di Cella, U.M.; et al. Remote sensing-based estimation of gross primary production in a subalpine grassland. Biogeosciences 2012, 9, 2565–2584. [Google Scholar] [CrossRef]
- Viña, A.; Gitelson, A.A. New developments in the remote estimation of the fraction of absorbed photosynthetically active radiation in crops. Geophys. Res. Lett. 2005, 32, L17403. [Google Scholar] [CrossRef]
- Gitelson, A.A. Remote estimation of fraction of radiation absorbed by photosynthetically active vegetation: Generic algorithm for maize and soybean. Remote Sens. Lett. 2018, 10, 283–291. [Google Scholar] [CrossRef]
- Gamon, J.A.; Peñuelas, J.; Field, C.B. A narrow-waveband spectral index that tracks diurnal changes in photosynthetic efficiency. Remote Sens. Environ. 1992, 41, 35–44. [Google Scholar] [CrossRef]
- Gamon, J.A.; Serrano, L.; Surfus, J.S. The photochemical reflectance index: An optical indicator of photosynthetic radiation use efficiency across species, functional types, and nutrient levels. Oecologia 1997, 112, 492–501. [Google Scholar] [CrossRef]
- Penuelas, J.; Filella, I.; Gamon, J.A. Assessment of photosynthetic radiation-use efficiency with spectral reflectance. New Phytol. 1995, 131, 291–296. [Google Scholar] [CrossRef]
- Inoue, Y.; Penuelas, J.; Miyata, A.; Mano, M. Normalized difference spectral indices for estimating photosynthetic efficiency and capacity at a canopy scale derived from hyperspectral and CO2 flux measurements in rice. Remote Sens. Environ. 2008, 112, 156–172. [Google Scholar] [CrossRef]
- Garbulsky, M.F.; Peñuelas, J.; Gamon, J.; Inoue, Y.; Filella, I. The photochemical reflectance index (PRI) and the remote sensing of leaf, canopy and ecosystem radiation use efficiencies: A review and meta-analysis. Remote Sens. Environ. 2011, 115, 281–297. [Google Scholar] [CrossRef]
- Kutser, T.; Dekker, A.G.; Skirving, W. Modeling spectral discrimination of Great Barrier Reef benthic communities by remote sensing instruments. Limnol. Oceanogr. 2003, 48, 497–510. [Google Scholar] [CrossRef]
- Kutser, T.; Vahtmäe, E.; Martin, G. Assessing suitability of multispectral satellites for mapping benthic macroalgal cover in turbid coastal waters by means of model simulations. Estuarine Coast. Shelf Sci. 2006, 67, 521–529. [Google Scholar] [CrossRef]
- Mumby, P.J.; Green, E.P.; Edwards, A.J.; Clark, C. Measurement of seagrass standing crop using satellite and digital airborne remote sensing. Mar. Ecol. Prog. Ser. 1997, 159, 51–60. [Google Scholar] [CrossRef]
- Dierssen, H.M.; Zimmerman, R.C.; Leathers, R.A.; Downes, T.V.; Davis, C.O. Ocean color remote sensing of seagrass and bathymetry in the Bahamas Banks by high-resolution airborne imagery. Limnol. Oceanogr. 2003, 48, 444–455. [Google Scholar] [CrossRef]
- Phinn, S.; Roelfsema, C.; Dekker, A.; Brando, V.; Anstee, J. Mapping seagrass species, cover and biomass in shallow waters: An assessment of satellite multi-spectral and airborne hyper-spectral imaging systems in Moreton Bay (Australia). Remote Sens. Environ. 2008, 112, 3413–3425. [Google Scholar] [CrossRef]
- Wicaksono, P.; Hafizt, M. Mapping Seagrass from Space: Addressing the Complexity of Seagrass LAI Mapping. Eur. J. Remote Sens. 2013, 46, 18–39. [Google Scholar] [CrossRef]
- Benfield, S.L.; Guzman, H.M.; Mair, J.M.; Young, J.A.T. Mapping the distribution of coral reefs and associated sublittoral habitats in Pacific Panama: A comparison of optical satellite sensors and classification methodologies. Int. J. Remote Sens. 2007, 28, 5047–5070. [Google Scholar] [CrossRef]
- Casal, G.; Kutser, T.; Domínguez-Gómez, J.; Sánchez-Carnero, N.; Freire, J. Mapping benthic macroalgal communities in the coastal zone using CHRIS-PROBA mode 2 images. Estuarine Coast. Shelf Sci. 2011, 94, 281–290. [Google Scholar] [CrossRef]
- Vahtmäe, E.; Kutser, T. Classifying the Baltic Sea Shallow Water Habitats Using Image-Based and Spectral Library Methods. Remote Sens. 2013, 5, 2451–2474. [Google Scholar] [CrossRef]
- Hill, V.J.; Zimmerman, R.C.; Bissett, W.P.; Dierssen, H.; Kohler, D.D.R. Evaluating Light Availability, Seagrass Biomass, and Productivity Using Hyperspectral Airborne Remote Sensing in Saint Joseph’s Bay, Florida. Estuaries Coasts 2014, 37, 1467–1489. [Google Scholar] [CrossRef]
- Andréfouët, S.; Payri, C. Scaling-up carbon and carbonate metabolism of coral reefs using in-situ data and remote sensing. Coral Reefs 2001, 19, 259–269. [Google Scholar] [CrossRef]
- Brock, J.; Yates, K.; Halley, R.; Kuffner, I.; Wright, C.; Hatcher, B. Northern Florida reef tract benthic metabolism scaled by remote sensing. Mar. Ecol. Prog. Ser. 2006, 312, 123–139. [Google Scholar] [CrossRef][Green Version]
- Toro-Farmer, G.; Muller-Karger, F.E.; Vega-Rodríguez, M.; Melo, N.; Yates, K.; Cerdeira-Estrada, S.; Herwitz, S.R. Characterization of Available Light for Seagrass and Patch Reef Productivity in Sugarloaf Key, Lower Florida Keys. Remote Sens. 2016, 8, 86. [Google Scholar] [CrossRef]
- Hochberg, E.J.; Atkinson, M.J. Coral reef benthic productivity based on optical absorptance and light-use efficiency. Coral Reefs 2007, 27, 49–59. [Google Scholar] [CrossRef]
- Vahtmäe, E.; Paavel, B.; Kutser, T. How much benthic information can be retrieved with hyperspectral sensor from the optically complex coastal waters? J. Appl. Remote Sens. 2020, 14, 016504. [Google Scholar] [CrossRef]
- Maritorena, S.; Morel, A.; Gentili, B. Diffuse reflectance of oceanic shallow waters: Influence of water depth and bottom albedo. Limnol. Oceanogr. 1994, 39, 1689–1703. [Google Scholar] [CrossRef]
- Mobley, C.D. Estimation of the remote-sensing reflectance from above-surface measurements. Appl. Opt. 1999, 38, 7442–7455. [Google Scholar] [CrossRef] [PubMed]
- Vahtmäe, E.; Kotta, J.; Orav-Kotta, H.; Kotta, I.; Pärnoja, M.; Kutser, T. Predicting macroalgal pigments (chlorophyll a, chlorophyll b, chlorophyll a + b, carotenoids) in various environmental conditions using high-resolution hyperspectral spectroradiometers. Int. J. Remote Sens. 2017, 39, 5716–5738. [Google Scholar] [CrossRef]
- Lichtenthaler, H.K. Chlorophylls and Carotenoids: Pigments of Photosynthetic Biomembranes. Methods Enzymol. 1987, 148, 350–382. [Google Scholar] [CrossRef]
- Elith, J.; Graham, C.H.; Anderson, R.P.; Dudík, M.; Ferrier, S.; Guisan, A.; Hijmans, R.J.; Huettmann, F.; Leathwick, J.R.; Lehmann, A.; et al. Novel methods improve prediction of species’ distributions from occurrence data. Ecography 2006, 29, 129–151. [Google Scholar] [CrossRef]
- Leathwick, J.R.; Elith, J.; Francis, M.P.; Hastie, T.; Taylor, P. Variation in demersal fish species richness in the oceans surrounding New Zealand: An analysis using boosted regression trees. Mar. Ecol. Prog. Ser. 2006, 321, 267–281. [Google Scholar] [CrossRef]
- Elith, J.; Leathwick, J.R.; Hastie, T. A working guide to boosted regression trees. J. Anim. Ecol. 2008, 77, 802–813. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd ed.; Springer: New York, NY, USA, 2009. [Google Scholar]
- Greenwell, B.M. pdp: An R Package for Constructing Partial Dependence Plots. R J. 2017, 9, 421–436. [Google Scholar] [CrossRef]
- Joyce, K.E.; Phinn, S.R. Spectral index development for mapping live coral cover. J. Appl. Remote Sens. 2013, 7, 073590. [Google Scholar] [CrossRef]
- Vahtmäe, E.; Kutser, T.; Paavel, B. Performance and Applicability of Water Column Correction Models in Optically Complex Coastal Waters. Remote Sens. 2020, 12, 1861. [Google Scholar] [CrossRef]
- Kutser, T.; Paavel, B.; Metsamaa, L.; Vahtmäe, E. Mapping coloured dissolved organic matter concentration in coastal waters. Int. J. Remote Sens. 2009, 30, 5843–5849. [Google Scholar] [CrossRef]
- Binzer, T.; Sand-Jensen, K.; Middelboe, A.-L. Community photosynthesis of aquatic macrophytes. Limnol. Oceanogr. 2006, 51, 2722–2733. [Google Scholar] [CrossRef]
- King, R.J.; Schramm, W. Photosynthetic rates of benthic marine algae in relation to light intensity and seasonal variations. Mar. Biol. 1976, 37, 215–222. [Google Scholar] [CrossRef]
- Stengel, D.B.; Dring, M.J. Seasonal variation in the pigment content and photosynthesis of different thallus regions of Ascophyllum nodosum (Fucales, Phaeophyta) in relation to position in the canopy. Phycologia 1998, 37, 259–268. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).