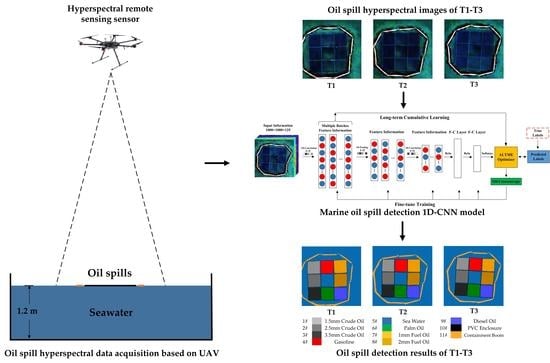
Hyperspectral Remote Sensing Detection of Marine Oil Spills Using an Adaptive Long-Term Moment Estimation Optimizer
Abstract
:1. Introduction
2. Data and Method
2.1. Data
2.2. Adaptive Long-Term Moment Estimation Optimizer
| Algorithm 1 Adaptive Long-term Moment Estimation |
|
1: Input: β = 0.9, λ ∈ [ 1×10−4, 1×10−5 ] 2: Initialize iter = 0, m0 = 0, v0 = 0 3: for λ = 1×10−4 to 1×10−5 do 4: Repeat 5: for t = 1 to T do 6: gt = ▽θ Loss( θt ) 7: mt = βmt-1 + ( 1 - β )gt 8: vt = ( 1 + λ )vt-1 + λgt2 9: mtcorrect = mt / ( 1 - βt ) 10: vtcorrect = vt / (( 1 + λ )t - 1 ) 11: θt = θt-1 - α·mtcorrect / ( + ε ) 12: End for 13: iter ← iter + 1 14: End for |
2.3. Marine Oil-Spill Detection 1D-CNN Model
2.4. Accuracy Evaluation Indexes
3. Results and Discussion
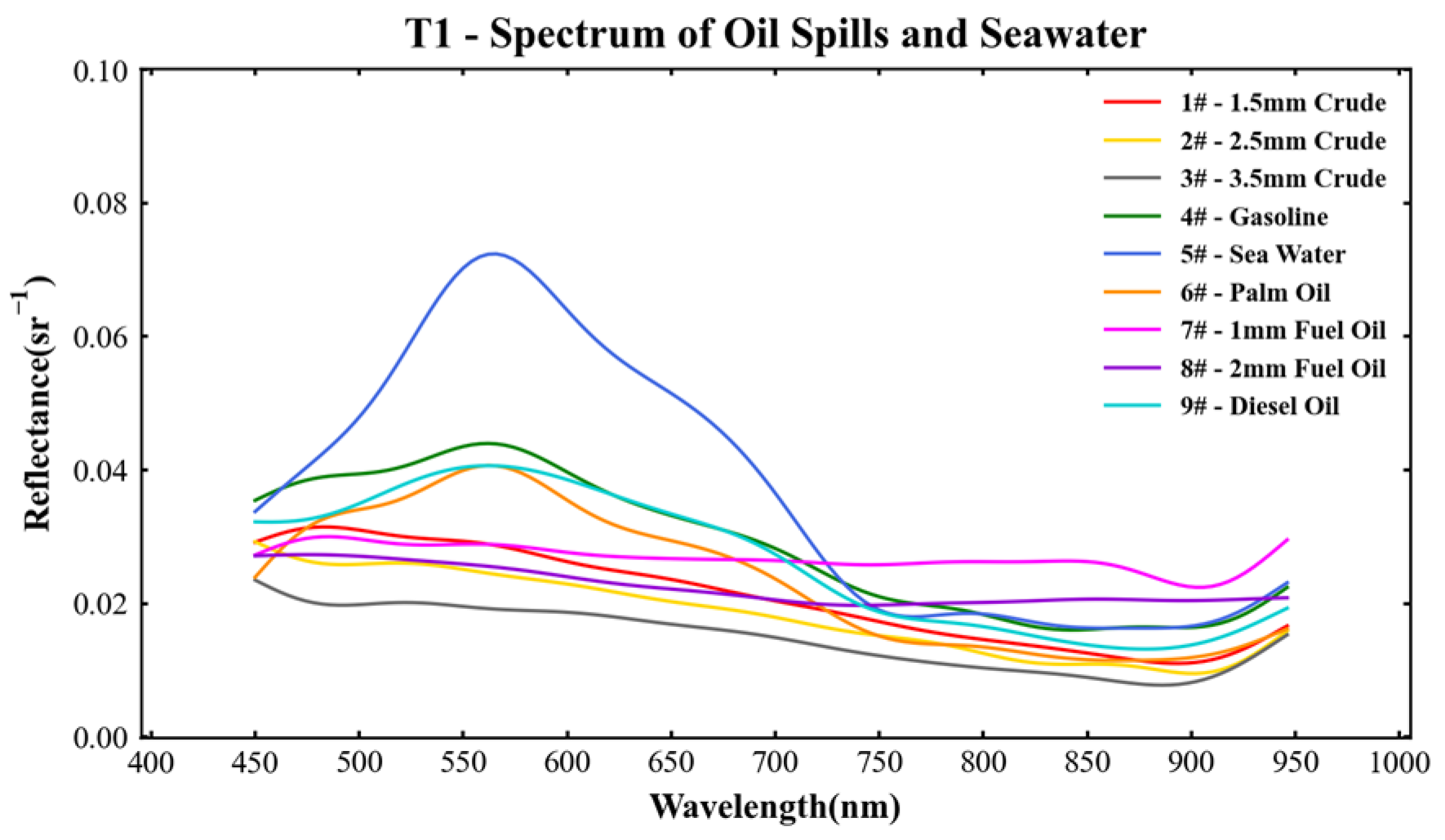
3.1. Analysis of Oil-Spill Spectrum Characteristics
3.1.1. Seawater and Light-Oil Experimental Groups at T1
3.1.2. Crude Oil Experimental Groups at T1
3.1.3. Fuel Oil Experimental Groups at T1
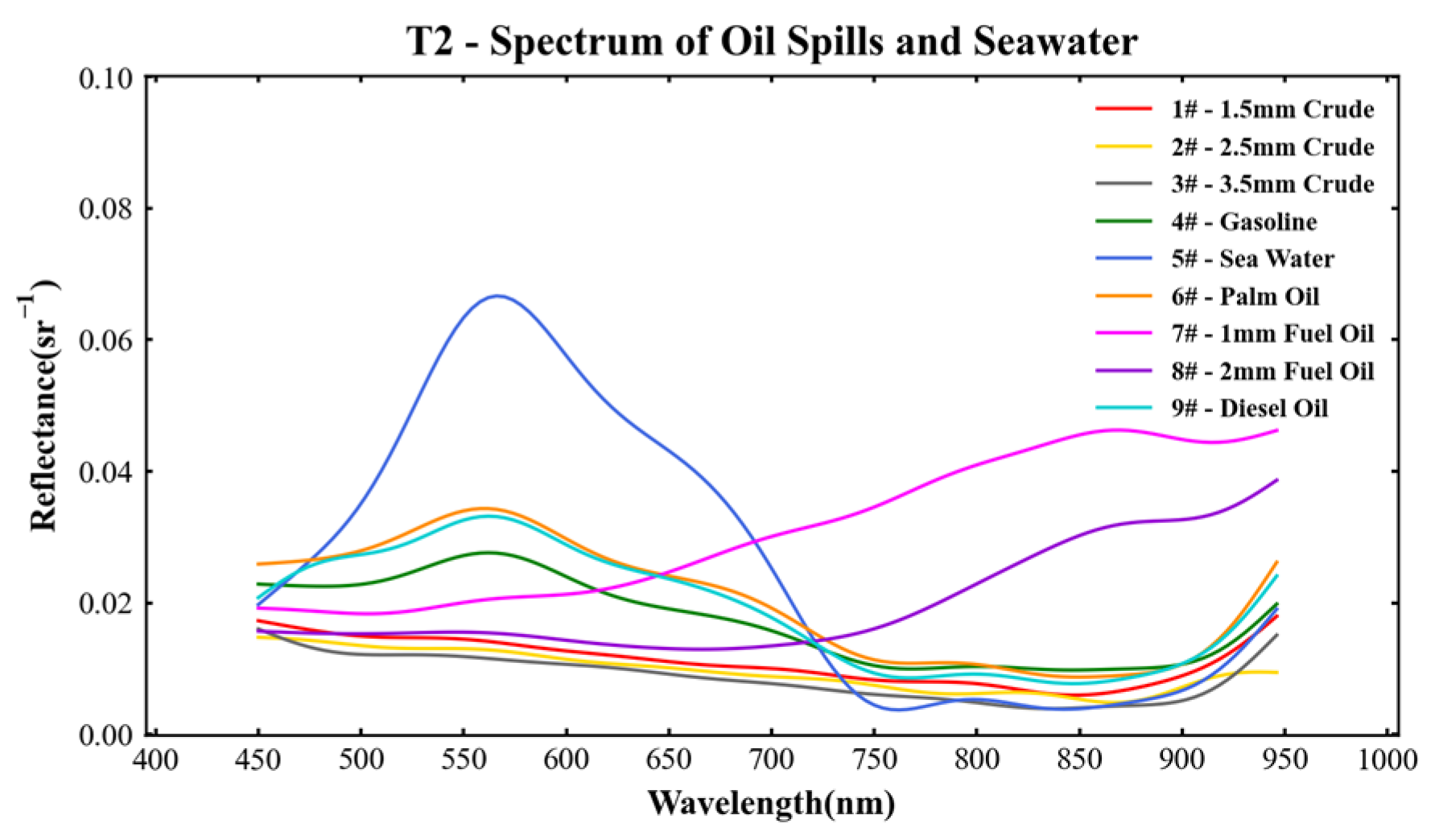
3.1.4. Seawater and Light-Oil Experimental Groups at T2–T3
3.1.5. Crude Oil Experimental Groups at T2–T3
3.1.6. Fuel Oil Experimental Groups at T2–T3
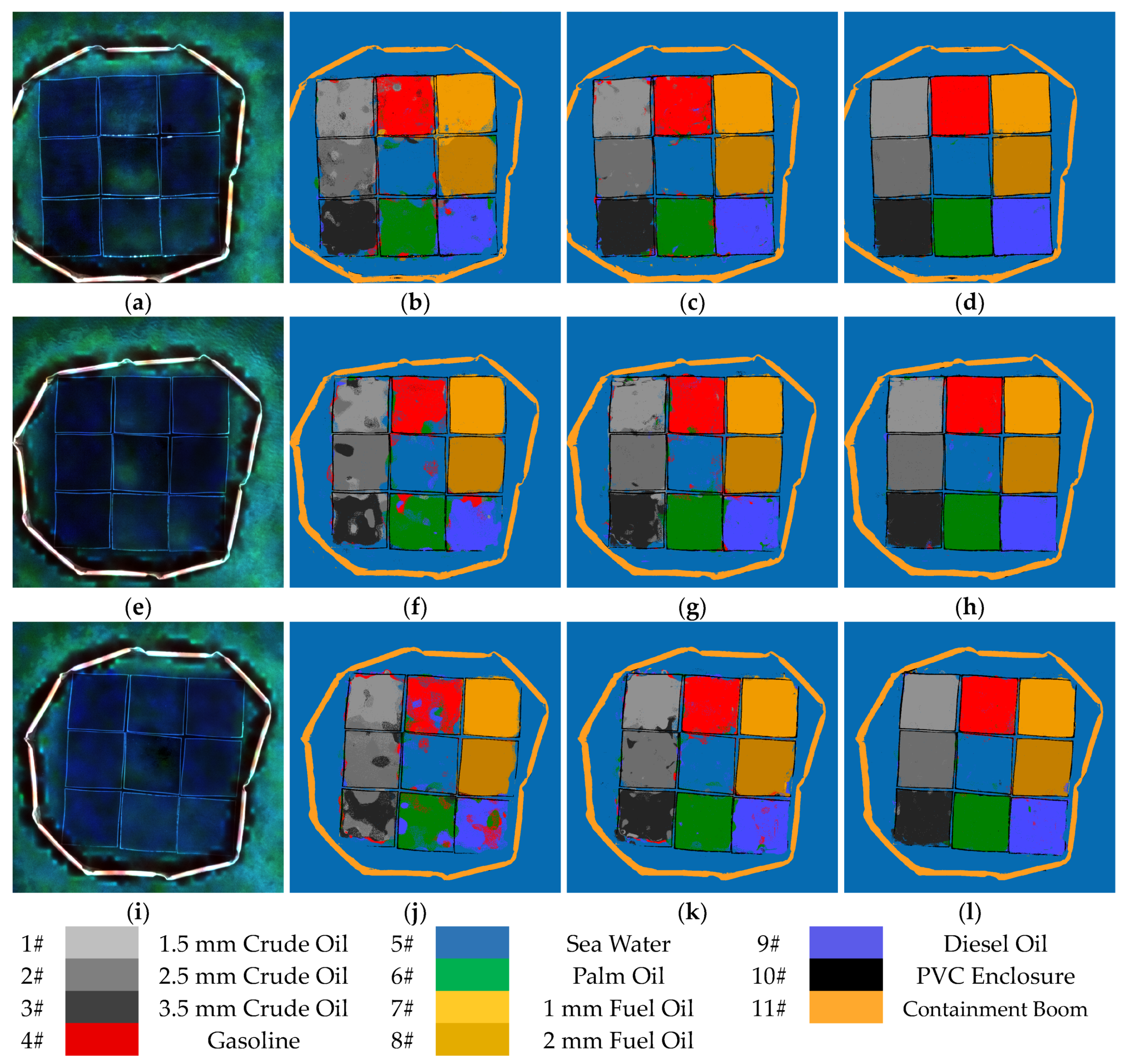
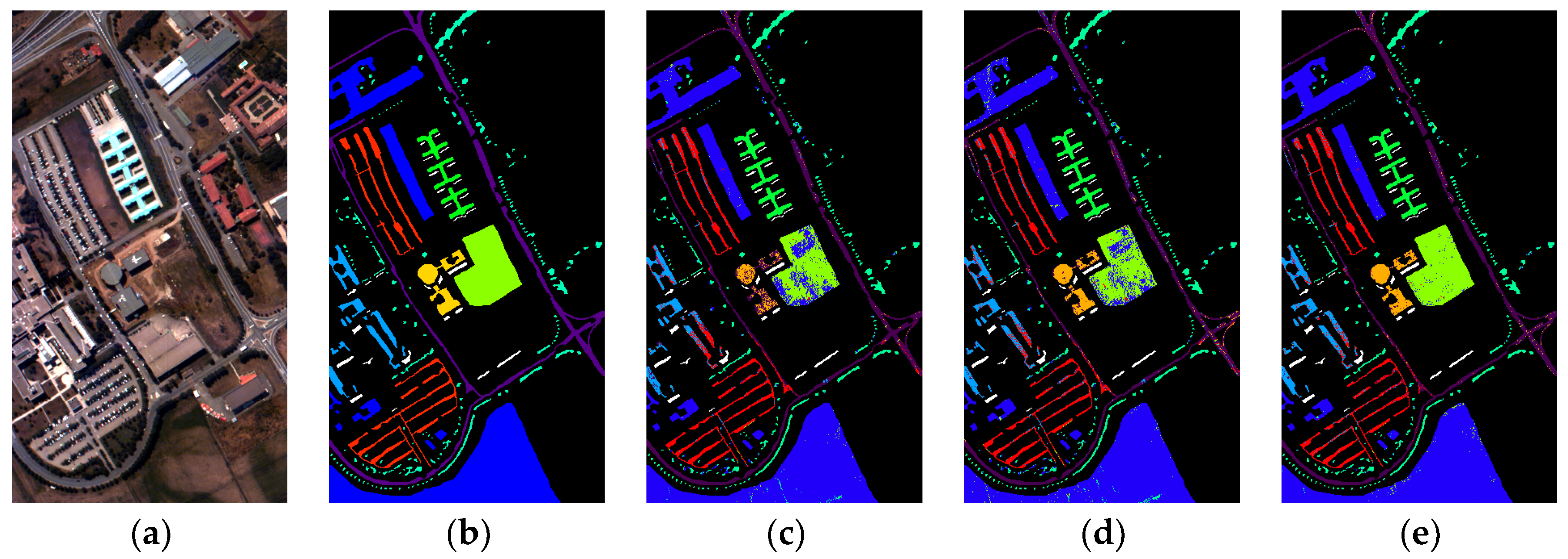
3.2. Selection and Analysis of Basic Oil-Spill Detection Models
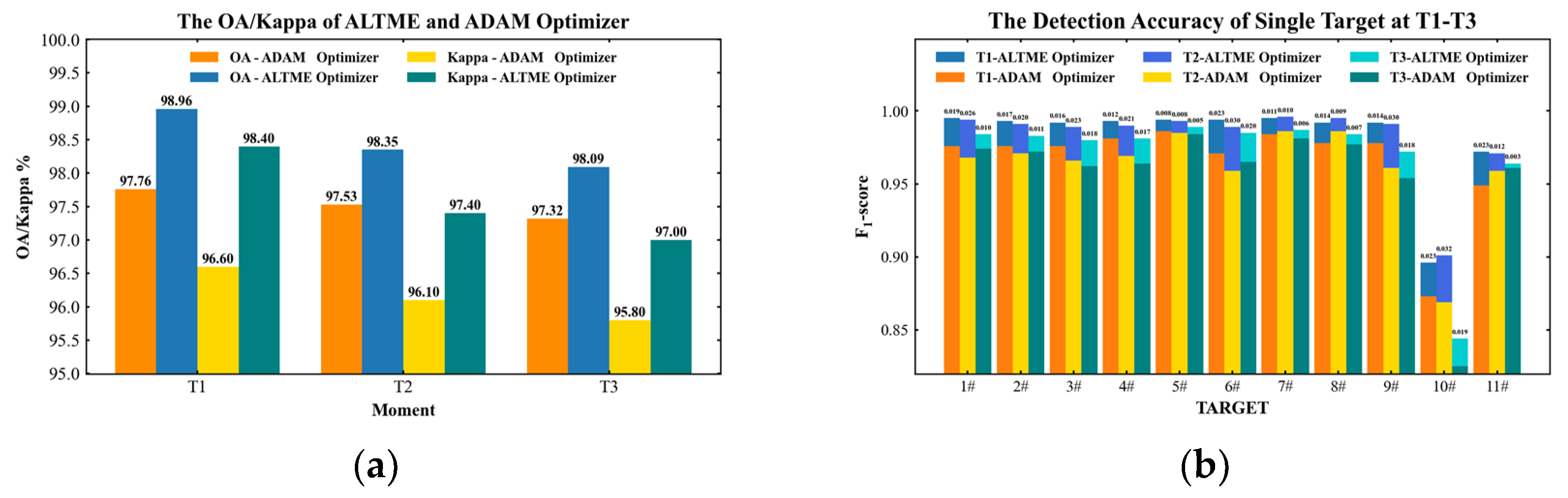
3.3. Adaptive Selection and Analysis of the Cumulative Learning Weight of the ALTME Optimizer
3.4. Analysis of the Stability and Applicability of the ALTME Optimizer
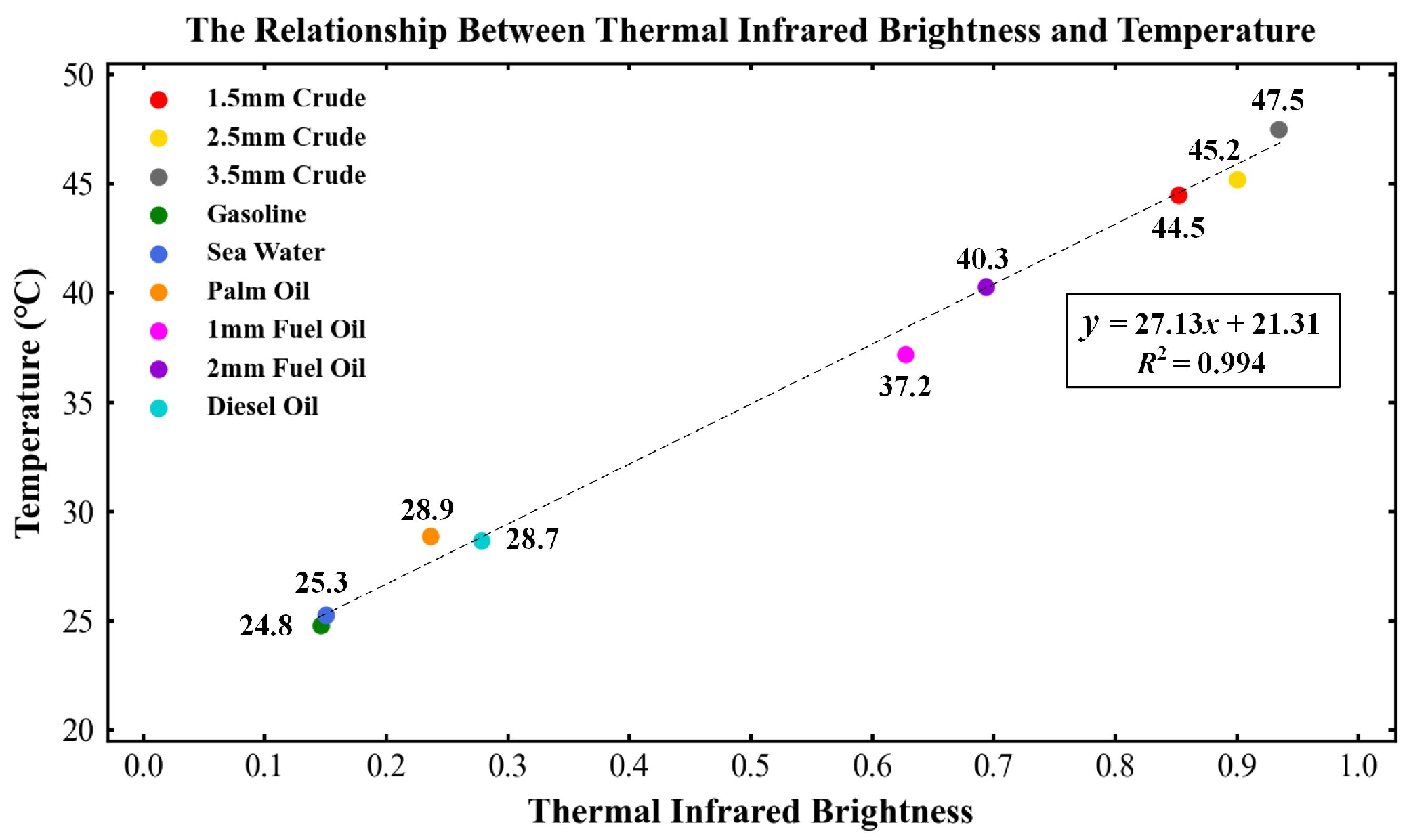
3.5. Feasibility Analysis of Oil-Spill Detection Based on Thermal Infrared Remote Sensing
4. Conclusions
4.1. Conclusions
4.2. Perspectives and Future Works
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Yang, J.F.; Wan, J.-H.; Ma, Y.; Zhang, J.; Hu, Y.-B.; Jiang, Z.-C. Oil Spill Hyperspectral Remote Sensing Detection Based on DCNN with Multi-Scale Features. J. Coast. Res. 2019, 90, 332–339. [Google Scholar] [CrossRef]
- Jiang, Z.C.; Ma, Y. Research on crude oil film absolute thickness inversion based on self-expanding deep confidence network. Ocean. Sci. 2021, 45, 94–107. [Google Scholar]
- Sun, S.J.; Hu, C.M. The Challenges of Interpreting Oil-Water Spatial and Spectral Contrasts for the Estimation of Oil Thick-ness: Examples from Satellite and Airborne Measurements of the Deepwater Horizon Oil Spill. IEEE Trans. Geosci. Remote Sens. 2019, 5, 1–16. [Google Scholar]
- Velotto, D.; Migliaccio, M.; Nunziata, F.; Lehner, S. Dual-Polarized TerraSAR-X Data for Oil-Spill Observation. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4751–4762. [Google Scholar] [CrossRef]
- Marghany, M. Utilization of a genetic algorithm for the automatic detection of oil spill from RADARSAT-2 SAR satellite data. Mar. Pollut. Bull. 2014, 89, 20–29. [Google Scholar] [CrossRef] [PubMed]
- Alpers, W.; Holt, B.; Zeng, K. Oil spill detection by imaging radars: Challenges and pitfalls. Remote Sens. Environ. 2017, 201, 133–147. [Google Scholar] [CrossRef]
- Ren, G.B.; Guo, J.; Ma, Y.; Luo, X.D. Hyperspectral remote sensing detection and thickness estimation method for sea surface oil spilled drones. Acta Oceanol. Sin. 2019, 41, 150–162. [Google Scholar]
- Shi, Q.; Liu, M.; Li, S.; Liu, X.; Wang, F.; Zhang, L. A Deeply Supervised Attention Metric-Based Network and an Open Aerial Image Dataset for Remote Sensing Change Detection. IEEE Trans. Geosci. Remote. Sens. 2021, 61, 1–16. [Google Scholar] [CrossRef]
- Lammoglia, T.; Roberto, C. Spectroscopic characterization of oils yielded from Brazilian offshore basins Potential applications of remote sensing. Remote Sens. Environ. 2011, 115, 2525–2535. [Google Scholar] [CrossRef]
- Yang, Q.Q. Application of Hyperspectral Oil Spill Image Feature Extraction in Oil Species Identification. Master’s Thesis, Dalian Maritime University, Dalian, China, 2010. [Google Scholar]
- Han, Z.; Wan, J.; Deng, L.; Liu, K. Oil Adulteration Identification by Hyperspectral Imaging Using QHM and ICA. PLoS ONE 2016, 11, e0146547. [Google Scholar] [CrossRef] [Green Version]
- Wu, X.; Song, J.M.; Li, X.G.; Yuan, H.M.; Li, N. Technical methods for obtaining oil spill volume at sea. Ocean. Technol. 2011, 30, 50–54. [Google Scholar]
- Song, S.S.; An, W.; Li, J.W.; Zhao, Y.P.; Jin, W.W. A review of research on marine oil spill assessment methods. Coast. Eng. 2017, 36, 83–88. [Google Scholar]
- Lu, Y.C.; Hu, C.M.; Zhan, W.F. Detecting and quantifying oil slick thickness by thermal remote sensing: A ground-based experiment. Remote Sens. Environ. 2016, 181, 207–217. [Google Scholar] [CrossRef]
- Lu, Y.; Shi, J.; Wen, Y.; Hu, C.; Zhou, Y.; Sun, S.; Zhang, M.; Mao, Z.; Liu, Y. Optical interpretation of oil emulsions in the ocean—Part I: Laboratory measurements and proof-of-concept with AVIRIS observations. Remote Sens. Environ. 2019, 230, 111183. [Google Scholar] [CrossRef]
- Lu, Y.C.; Shi, J.; Hu, C.M.; Zhang, M.W.; Sun, S.J.; Liu, Y.X. Optical interpretation of oil emulsions in the ocean-Part II: Ap-plications to multi-band coarse-resolution imagery. Remote Sens. Environ. 2020, 242, 111778. [Google Scholar] [CrossRef]
- Texeira, C.; Santos, S.; Aquino, N. Source identification of sea surface oil with geochemical data in Cantarell, Mexico. Micro-Chem. J. 2014, 117, 202–213. [Google Scholar] [CrossRef]
- Bayona, J.M.; Domínguez, C.; Albaigés, J. Analytical developments for oil spill fingerprinting. Trends Environ. Anal. Chem. 2015, 5, 26–34. [Google Scholar] [CrossRef]
- Yang, J.; Wan, J.; Ma, Y.; Zhang, J.; Hu, Y. Characterization analysis and identification of common marine oil spill types using hyperspectral remote sensing. Int. J. Remote Sens. 2020, 41, 7163–7185. [Google Scholar] [CrossRef]
- Liu, B.X.; Li, Y.; Han, L. Research on the Identification of Surface Oil Species Based on Spectral Reflectance Data. Spectrosc. Spectr. Anal. 2016, 36, 1100–1103. [Google Scholar]
- Shen, Y.F.; Liu, J.Q.; Ding, J.; Jiao, J.N.; Sun, S.J.; Lu, Y.C. HY-1C COCTS and CZI observation of marine oil spills in the South China Sea. J. Remote Sens. 2020, 24, 933–944. [Google Scholar]
- Wan, H.J.; Han, Z.Z.; Song, X.X.; Liu, J. Oil species identification method of marine oil spill hyperspectral imaging based on multi-mode fusion. Acta Lumin. 2016, 97, 473–480. [Google Scholar]
- Shi, J.; Jiao, J.; Lu, Y.; Zhang, M.; Mao, Z.; Liu, Y. Determining spectral groups to distinguish oil emulsions from Sargassum over the Gulf of Mexico using an airborne imaging spectrometer. ISPRS J. Photogramm. Remote Sens. 2018, 146, 251–259. [Google Scholar] [CrossRef]
- Fang, S.A.; Huang, X.X.; Yin, D.; Xu, C.; Feng, X. Research on UV reflectance characteristics of marine oil spill simulation targets. Spectrosc. Spectr. Anal. 2010, 30, 738–742. [Google Scholar]
- Hu, J.C.; Wang, D.F. Monitoring method of ocean oil spilling based on remote sensing. Environ. Prot. Sci. 2014, 40, 68–73. [Google Scholar]
- Shi, J. Study on Hyperspectral Remote Sensing of Marine Oil Emulsion. Master’s Thesis, Nanjing University, Nanjing, China, 2019. [Google Scholar]
- Lu, Y.C.; Tian, Q.J.; Wang, J.J.; Wang, X.C.; Qi, X.P. Experimental study on the spectral response of sea surface oil film. Chin. Sci. Bull. 2008, 9, 111–114. [Google Scholar]
- Lu, Y.C.; Tian, Q.J.; Li, X. Oil film thickness remote sensing inversion theory based on oil slick double-beam interference model. Sci. China Earth Sci. 2011, 41, 541–548. [Google Scholar]
- Lu, S. Research and Application of Hyperspectral Region Growth Algorithm Combined with Unmixing. Ph.D. Dissertation, Dalian Maritime University, Dalian, China, 2015. [Google Scholar]
- Jiang, Z.; Ma, Y.; Yang, J. Inversion of the Thickness of Crude Oil Film Based on an OG-CNN Model. J. Mar. Sci. Eng. 2020, 8, 653. [Google Scholar] [CrossRef]
- Chen, Y.; Jiang, H.; Li, C.; Jia, X.; Ghamisi, P. Deep Feature Extraction and Classification of Hyperspectral Images Based on Convolutional Neural Networks. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6232–6251. [Google Scholar] [CrossRef] [Green Version]
- Hu, F.; Xia, G.-S.; Hu, J.; Zhang, L. Transferring Deep Convolutional Neural Networks for the Scene Classification of High-Resolution Remote Sensing Imagery. Remote Sens. 2015, 7, 14680–14707. [Google Scholar] [CrossRef] [Green Version]
- Yang, X.F.; Ye, Y.M.; Li, X.T.; Raymond, Y.; Zhang, X.F.; Huang, X.H. Hyperspectral Image Classification with Deep Learning Models. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5408–5423. [Google Scholar] [CrossRef]
- Jiang, Z.; Ma, Y. Accurate extraction of offshore raft aquaculture areas based on a 3D-CNN model. Int. J. Remote Sens. 2020, 41, 5457–5481. [Google Scholar] [CrossRef]
- Zhang, H.; Li, Y.; Jiang, Y.; Wang, P.; Shen, Q.; Shen, C. Hyperspectral Classification Based on Lightweight 3-D-CNN With Transfer Learning. IEEE Trans. Geosci. Remote Sens. 2019, 57, 5813–5828. [Google Scholar] [CrossRef] [Green Version]
- Hu, A.N.; Xie, Z.; Xu, Y.Y.; Xie, M.Y.; Wu, L.; Qiu, Q.J. Unsupervised Haze Removal for High-Resolution Optical Remote-Sensing Images Based on Improved Generative Adversarial Networks. Remote Sens. 2020, 12, 4162. [Google Scholar] [CrossRef]
- Zorzi, S.; Maset, E.; Fusiello, A.; Crosilla, F. Full-Waveform Airborne LiDAR Data Classification Using Convolutional Neural Networks. IEEE Trans. Geosci. Remote Sens. 2019, 57, 8255–8261. [Google Scholar] [CrossRef]
- Yang, J.F. Marine Oil Spill Detection and Oil Types Identification Using Multi-Dimensional Optical Remote Sensing. Ph.D. Thesis, China University of Petroleum, Qingdao, China, 2021. [Google Scholar]
- Ling, J.M.; Li, L.; Wang, H.Y. Improved Fusion of Spatial Information into Hyperspectral Classification through the Aggregation of Constrained Segment Trees: Segment Forest. Remote Sens. 2021, 13, 4816. [Google Scholar] [CrossRef]
- Zhang, T.; Shi, C.; Liao, D.; Wang, L. Deep Spectral Spatial Inverted Residual Network for Hyperspectral Image Classification. Remote Sens. 2021, 13, 4472. [Google Scholar] [CrossRef]
- Fingas, M. The Challenges of Remotely Measuring Oil Slick Thickness. Remote Sens. 2018, 10, 319. [Google Scholar] [CrossRef] [Green Version]
- Hu, C.M.; Lu, Y.C.; Sun, S.J.; Liu, Y.X. Optical Remote Sensing of Oil Spills in the Ocean: What Is Really Possible? J. Remote Sens. 2021, 2021, 9141902. [Google Scholar] [CrossRef]
- Li, W.J.; Zhang, Z.Y.; Wang, X.J.; Luo, P. AdaX: Adaptive Gradient Descent with Exponential Long Term Memory. Comput. Sci. 2020, 5, 9740. [Google Scholar]
- Shazeer, N.; Stern, M. Adafactor: Adaptive Learning Rates with Sublinear Memory Cost. Comput. Sci. 2018, 4, 4235. [Google Scholar]
- Shi, Q.; Tang, X.; Yang, T.; Liu, R.; Zhang, L. Hyperspectral Image Denoising Using a 3-D Attention Denoising Network. IEEE Trans. Geosci. Remote Sens. 2021, 59, 10348–10363. [Google Scholar] [CrossRef]
- Liu, B.X. Extraction and Analysis of Oil Film on Water Based on Hyperspectral Characteristics. Ph.D. Thesis, Dalian Maritime University, Dalian, China, 2013. [Google Scholar]
- Sun, P.; Song, M.-P.; An, J.-B. Study of prediction models for oil thickness based on spectral curve. Spectrosc. Spectr. Anal. 2013, 33, 1881–1885. [Google Scholar]














| Parameter | Index | |
|---|---|---|
| Cubert-S185 | Spectral range (nm) | 450~950 |
| Spectral resolution (nm) | 4 | |
| Number of bands | 125 | |
| IFOV (°) | 23 | |
| Imaging method | Frame imaging | |
| Imaging size (pixel) | 1000 × 1000 | |
| M600PRO | Maximum load (kg) | 6 |
| Flight duration (min) | 16 | |
| Maximum wind resistance level (m/s) | 8 | |
| Maximum ascent/descend speed (m/s) | 5/3 | |
| Maximum flight altitude (m) | 4500 | |
| Maximum horizontal speed (km/h) | 65 | |
| Group | M1 (kg) | M2 (kg) | M (kg) | ρOil (kg/L) | V (L) | hOil (mm) |
|---|---|---|---|---|---|---|
| 1#-1.5 mm Crude | 1.90 | 0.66 | 1.24 | 0.81 | 1.53 | 1.53 |
| 2#-2.5 mm Crude | 2.74 | 0.65 | 2.09 | 0.81 | 2.58 | 2.58 |
| 3#-3.5 mm Crude | 4.10 | 1.21 | 2.89 | 0.81 | 3.57 | 3.57 |
| 7#-2 mm Fuel Oil | 1.41 | 0.58 | 0.83 | 0.85 | 0.98 | 0.98 |
| 8#-3 mm Fuel Oil | 2.30 | 0.58 | 1.72 | 0.85 | 2.06 | 2.06 |
| Moment | Wind Speed (m/s) | Cross Wind (m/s) | Upwind (m/s) | Temp (°C) | Solar Elevation Angle (°) | Solar Azimuth Angle (°) | Weather |
|---|---|---|---|---|---|---|---|
| 11:30 | 0.80 | 0.70 | −0.30 | 26.80 | 53.82 | 12.77 | Sunny |
| 13:50 | 1.50 | 0.80 | 1.30 | 26.90 | 45.92 | −41.59 | Sunny |
| 16:21 | 1.80 | 1.00 | 1.50 | 24.50 | 19.84 | −74.89 | Sunny |
| Layer | Number | Kernel | Stride |
|---|---|---|---|
| Convolutional layer-1 | 150 | 1 × 5 | 1 |
| MaxPooling layer-1 | - | 1 × 5 | 3 |
| Convolutional layer-2 | 100 | 1 × 5 | 1 |
| MaxPooling layer-2 | - | 1 × 5 | 3 |
| Convolutional layer-3 | 50 | 1 × 5 | 1 |
| MaxPooling layer-3 | - | 1 × 5 | 1 |
| Fully connected layer-1 | 200 | - | - |
| Fully connected layer-2 | 100 | - | - |
| Index | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Model | SVM | GRU | 1D-CNN | ||||||
| Group | Recall | Precision | F1-Score | Recall | Precision | F1-Score | Recall | Precision | F1-Score |
| 1#-1.5 mm Crude | 85.93 | 83.88 | 0.849 | 90.07 | 95.98 | 0.929 | 98.75 | 96.42 | 0.976 |
| 2#-2.5 mm Crude | 78.95 | 79.33 | 0.791 | 93.98 | 89.84 | 0.919 | 97.40 | 97.73 | 0.976 |
| 3#-3.5 mm Crude | 85.84 | 83.08 | 0.844 | 93.41 | 95.52 | 0.945 | 97.05 | 98.07 | 0.976 |
| 4#-Gasoline | 87.45 | 86.89 | 0.872 | 92.80 | 89.84 | 0.913 | 98.55 | 97.62 | 0.981 |
| 5#-Seawater | 96.82 | 95.57 | 0.962 | 97.75 | 97.82 | 0.978 | 98.48 | 98.63 | 0.986 |
| 6#-Palm Oil | 84.65 | 87.21 | 0.859 | 95.43 | 91.79 | 0.936 | 99.03 | 95.31 | 0.971 |
| 7#-1 mm Fuel Oil | 93.48 | 89.47 | 0.914 | 98.32 | 97.48 | 0.979 | 98.27 | 98.56 | 0.984 |
| 8#-2 mm Fuel Oil | 90.26 | 95.47 | 0.928 | 95.56 | 97.79 | 0.967 | 98.52 | 97.02 | 0.978 |
| 9#-Diesel Oil | 82.14 | 92.21 | 0.869 | 94.61 | 92.34 | 0.935 | 98.16 | 97.45 | 0.978 |
| 10#-PVC | 79.40 | 86.76 | 0.829 | 82.55 | 88.88 | 0.856 | 85.52 | 89.13 | 0.873 |
| 11#-Oil Boom | 92.8 | 94.93 | 0.939 | 95.58 | 94.51 | 0.951 | 93.51 | 96.39 | 0.949 |
| OA (%) | 92.34 | 95.97 | 97.76 | ||||||
| Kappa | 0.882 | 0.939 | 0.966 | ||||||
| Time (min) | 19.12 | 4.79 | 11.68 | ||||||
| Index | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Model | SVM | GRU | 1D-CNN | ||||||
| Group | Recall | Precision | F1-Score | Recall | Precision | F1-Score | Recall | Precision | F1-Score |
| 1#-1.5 mm Crude | 71.92 | 80.13 | 0.758 | 85.12 | 89.73 | 0.874 | 95.66 | 98.05 | 0.968 |
| 2#-2.5 mm Crude | 85.77 | 76.07 | 0.806 | 97.23 | 88.65 | 0.927 | 98.55 | 95.76 | 0.971 |
| 3#-3.5 mm Crude | 66.77 | 82.21 | 0.737 | 83.45 | 89.70 | 0.865 | 96.00 | 97.23 | 0.966 |
| 4#-Gasoline | 80.36 | 78.95 | 0.797 | 92.40 | 88.65 | 0.905 | 97.56 | 96.30 | 0.969 |
| 5#-Seawater | 97.68 | 94.80 | 0.962 | 97.56 | 97.61 | 0.976 | 98.30 | 98.62 | 0.985 |
| 6#-Palm Oil | 83.90 | 81.74 | 0.828 | 95.96 | 87.08 | 0.913 | 98.72 | 93.24 | 0.959 |
| 7#-1 mm Fuel Oil | 97.06 | 97.10 | 0.971 | 98.41 | 97.60 | 0.980 | 98.28 | 98.84 | 0.986 |
| 8#-2 mm Fuel Oil | 96.66 | 96.69 | 0.967 | 97.79 | 97.37 | 0.976 | 98.92 | 98.32 | 0.986 |
| 9#-Diesel Oil | 71.93 | 87.68 | 0.790 | 88.48 | 93.74 | 0.910 | 97.80 | 94.46 | 0.961 |
| 10#-PVC | 76.00 | 92.73 | 0.835 | 80.99 | 90.31 | 0.854 | 83.08 | 91.09 | 0.869 |
| 11#-Oil Boom | 94.84 | 95.93 | 0.954 | 96.14 | 95.92 | 0.960 | 96.27 | 95.56 | 0.959 |
| OA (%) | 91.76 | 95.31 | 97.53 | ||||||
| Kappa | 0.869 | 0.927 | 0.961 | ||||||
| Time (min) | 18.15 | 4.95 | 11.77 | ||||||
| Index | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Model | SVM | GRU | 1D-CNN | ||||||
| Group | Recall | Precision | F1-Score | Recall | Precision | F1-Score | Recall | Precision | F1-Score |
| 1#-1.5 mm Crude | 74.79 | 79.05 | 0.769 | 88.38 | 94.64 | 0.914 | 98.40 | 96.44 | 0.974 |
| 2#-2.5 mm Crude | 79.48 | 65.54 | 0.718 | 92.05 | 87.19 | 0.896 | 98.37 | 96.09 | 0.972 |
| 3#-3.5 mm Crude | 53.16 | 76.10 | 0.626 | 81.36 | 87.59 | 0.844 | 95.10 | 97.36 | 0.962 |
| 4#-Gasoline | 71.69 | 70.41 | 0.710 | 91.74 | 88.54 | 0.901 | 96.76 | 95.94 | 0.964 |
| 5#-Seawater | 97.79 | 93.95 | 0.958 | 97.75 | 97.15 | 0.975 | 98.52 | 98.36 | 0.984 |
| 6#-Palm Oil | 74.03 | 78.47 | 0.762 | 95.57 | 88.74 | 0.920 | 98.26 | 94.86 | 0.965 |
| 7#-1 mm Fuel Oil | 95.60 | 96.17 | 0.959 | 97.59 | 96.24 | 0.969 | 98.34 | 97.75 | 0.981 |
| 8#-2 mm Fuel Oil | 91.79 | 95.20 | 0.935 | 95.36 | 96.67 | 0.960 | 98.52 | 96.96 | 0.977 |
| 9#-Diesel Oil | 58.73 | 66.98 | 0.626 | 89.78 | 86.85 | 0.883 | 96.90 | 94.00 | 0.954 |
| 10#-PVC | 67.24 | 95.08 | 0.788 | 71.85 | 93.22 | 0.812 | 73.94 | 93.22 | 0.825 |
| 11#-Oil Boom | 95.57 | 96.55 | 0.961 | 97.07 | 95.48 | 0.963 | 96.89 | 95.38 | 0.961 |
| OA (%) | 89.23 | 94.84 | 97.32 | ||||||
| Kappa | 0.829 | 0.920 | 0.958 | ||||||
| Time (min) | 17.08 | 4.88 | 11.73 | ||||||
| Index | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Moment | T1 | T2 | T3 | ||||||
| λ | 3 × 10−4 | 3 × 10−4 | 2 × 10−4 | ||||||
| Group | Recall | Precision | F1-Score | Recall | Precision | F1-Score | Recall | Precision | F1-Score |
| 1#-1.5 mm Crude | 99.42 | 99.53 | 0.995 | 99.28 | 99.54 | 0.994 | 99.14 | 97.59 | 0.984 |
| 2#-2.5 mm Crude | 99.56 | 99.08 | 0.993 | 99.63 | 98.67 | 0.991 | 98.91 | 97.78 | 0.983 |
| 3#-3.5 mm Crude | 99.49 | 98.85 | 0.992 | 99.58 | 98.13 | 0.989 | 98.29 | 97.69 | 0.980 |
| 4#-Gasoline | 99.46 | 99.19 | 0.993 | 99.44 | 98.61 | 0.990 | 98.82 | 97.44 | 0.981 |
| 5#-Seawater | 99.42 | 99.31 | 0.994 | 99.32 | 99.27 | 0.993 | 98.89 | 98.90 | 0.989 |
| 6#-Palm Oil | 99.67 | 99.11 | 0.994 | 99.85 | 97.92 | 0.989 | 98.52 | 98.38 | 0.985 |
| 7#-1 mm Fuel Oil | 99.66 | 99.30 | 0.995 | 99.74 | 99.39 | 0.996 | 98.78 | 98.65 | 0.987 |
| 8#-2 mm Fuel Oil | 99.69 | 98.67 | 0.992 | 99.65 | 99.38 | 0.995 | 99.35 | 97.52 | 0.984 |
| 9#-Diesel Oil | 99.40 | 98.99 | 0.992 | 99.50 | 98.66 | 0.991 | 98.88 | 95.56 | 0.972 |
| 10#-PVC | 86.84 | 92.52 | 0.896 | 87.04 | 93.32 | 0.901 | 77.93 | 92.13 | 0.844 |
| 11#-Oil Boom | 96.80 | 97.62 | 0.972 | 96.37 | 97.90 | 0.971 | 97.11 | 95.75 | 0.964 |
| OA (%) | 98.96 | 98.35 | 98.09 | ||||||
| Kappa | 0.984 | 0.974 | 0.970 | ||||||
| Time (min) | 12.15 | 12.22 | 12.07 | ||||||
| Time (min) | ||||||
|---|---|---|---|---|---|---|
| Optimizer | ADAM | ALTME (λ) | ||||
| Moment | 1 × 10−4 | 2 × 10−4 | 3 × 10−4 | 4 × 10−4 | 5 × 10−4 | |
| T1 | 11.68 | 11.97 | 12.09 | 12.19 | 12.29 | 12.41 |
| T2 | 11.77 | 12.01 | 12.12 | 12.22 | 12.35 | 12.43 |
| T3 | 11.63 | 11.93 | 12.07 | 12.18 | 12.27 | 12.39 |
| Group | Class | Samples | Colors |
|---|---|---|---|
| 1# | Asphalt | 6631 | |
| 2# | Meadows | 18,649 | |
| 3# | Gravel | 2099 | |
| 4# | Trees | 3064 | |
| 5# | Painted metal sheets | 1345 | |
| 6# | Bare Soil | 5029 | |
| 7# | Bitumen | 1330 | |
| 8# | Self-Blocking Bricks | 3682 | |
| 9# | Shadows | 947 |
| Index | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Model | SVM | 1D-CNN | 1D-CNN-ALTME (λ = 2 × 10−4) | ||||||
| Group | Recall | Precision | F1-Score | Recall | Precision | F1-Score | Recall | Precision | F1-Score |
| 1#-Asphalt | 93.68 | 87.44 | 0.905 | 92.34 | 93.79 | 0.931 | 94.87 | 96.47 | 0.957 |
| 2#-Meadows | 99.05 | 90.50 | 0.946 | 97.28 | 93.35 | 0.953 | 98.49 | 98.28 | 0.984 |
| 3#-Gravel | 67.72 | 82.96 | 0.746 | 77.14 | 82.28 | 0.796 | 80.38 | 90.85 | 0.853 |
| 4#-Trees | 90.25 | 96.59 | 0.933 | 89.52 | 94.60 | 0.920 | 96.48 | 97.49 | 0.970 |
| 5#-Painted metal sheets | 99.67 | 99.83 | 0.998 | 99.26 | 97.72 | 0.985 | 99.55 | 99.85 | 0.997 |
| 6#-Bare Soil | 68.39 | 96.33 | 0.800 | 79.94 | 90.32 | 0.848 | 95.11 | 95.22 | 0.952 |
| 7#-Bitumen | 48.29 | 89.20 | 0.627 | 87.05 | 86.54 | 0.868 | 91.88 | 89.99 | 0.909 |
| 8#-Self-Blocking Bricks | 89.92 | 80.65 | 0.850 | 88.44 | 84.78 | 0.866 | 93.32 | 85.69 | 0.893 |
| 9#-Shadows | 99.88 | 100.00 | 0.999 | 99.88 | 99.65 | 0.998 | 99.79 | 100.00 | 0.999 |
| OA (%) | 90.12 | 91.97 | 95.91 | ||||||
| Kappa | 0.866 | 0.893 | 0.946 | ||||||
| Time (min) | 4.46 | 2.21 | 2.63 | ||||||
| Temperature (°C) | |||
|---|---|---|---|
| Group | T1 | T2 | T3 |
| 1#-1.5 mm Crude | 44.5 | 41.6 | 30.7 |
| 2#-2.5 mm Crude | 45.2 | 42.5 | 30.9 |
| 3#-3.5 mm Crude | 47.5 | 43.1 | 30.9 |
| 4#-Gasoline | 24.8 | 24.7 | 23.4 |
| 5#-Seawater | 25.3 | 24.9 | 24.5 |
| 6#-Palm Oil | 28.9 | 28.1 | 26.0 |
| 7#-1 mm Fuel Oil | 37.2 | 36.8 | 29.4 |
| 8#-2 mm Fuel Oil | 40.3 | 39.5 | 29.9 |
| 9#-Diesel Oil | 28.7 | 26.5 | 25.9 |
| Temperature Information (°C) | ||||
|---|---|---|---|---|
| Group | Average | Max | Min | STD |
| 1#-1.5 mm Crude | 44.4 | 46.0 | 42.3 | 0.97 |
| 2#-2.5 mm Crude | 45.7 | 47.2 | 44.6 | 0.61 |
| 3#-3.5 mm Crude | 46.6 | 48.1 | 43.1 | 1.06 |
| 4#-Gasoline | 25.3 | 25.5 | 24.8 | 0.13 |
| 5#-Seawater | 25.4 | 25.7 | 25.2 | 0.06 |
| 6#-Palm Oil | 27.7 | 30.1 | 26.7 | 0.83 |
| 7#-1 mm Fuel Oil | 38.3 | 40.9 | 37.4 | 0.79 |
| 8#-2 mm Fuel Oil | 40.1 | 41.2 | 36.1 | 1.19 |
| 9#-Diesel Oil | 28.8 | 29.1 | 27.3 | 0.48 |
| Index | |||
|---|---|---|---|
| Group | Recall (%) | Precision (%) | F1-Score |
| 1#-1.5 mm Crude | 74.24 | 68.37 | 0.712 |
| 2#-2.5 mm Crude | 67.68 | 59.56 | 0.634 |
| 3#-3.5 mm Crude | 68.18 | 87.66 | 0.767 |
| 4#-Gasoline | 38.38 | 97.44 | 0.551 |
| 5#-Seawater | 98.99 | 61.64 | 0.760 |
| 6#-Palm Oil | 84.85 | 80.38 | 0.826 |
| 7#-1 mm Fuel Oil | 85.35 | 76.82 | 0.809 |
| 8#-2 mm Fuel Oil | 74.24 | 83.52 | 0.786 |
| 9#-Diesel Oil | 79.29 | 83.96 | 0.816 |
| OA (%) | 74.58 | ||
| Kappa | 0.714 | ||
| Time (min) | 1.19 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, Z.; Zhang, J.; Ma, Y.; Mao, X. Hyperspectral Remote Sensing Detection of Marine Oil Spills Using an Adaptive Long-Term Moment Estimation Optimizer. Remote Sens. 2022, 14, 157. https://doi.org/10.3390/rs14010157
Jiang Z, Zhang J, Ma Y, Mao X. Hyperspectral Remote Sensing Detection of Marine Oil Spills Using an Adaptive Long-Term Moment Estimation Optimizer. Remote Sensing. 2022; 14(1):157. https://doi.org/10.3390/rs14010157
Chicago/Turabian StyleJiang, Zongchen, Jie Zhang, Yi Ma, and Xingpeng Mao. 2022. "Hyperspectral Remote Sensing Detection of Marine Oil Spills Using an Adaptive Long-Term Moment Estimation Optimizer" Remote Sensing 14, no. 1: 157. https://doi.org/10.3390/rs14010157
APA StyleJiang, Z., Zhang, J., Ma, Y., & Mao, X. (2022). Hyperspectral Remote Sensing Detection of Marine Oil Spills Using an Adaptive Long-Term Moment Estimation Optimizer. Remote Sensing, 14(1), 157. https://doi.org/10.3390/rs14010157