Improving Leaf Area Index Retrieval Using Multi-Sensor Images and Stacking Learning in Subtropical Forests of China
Abstract
:1. Introduction
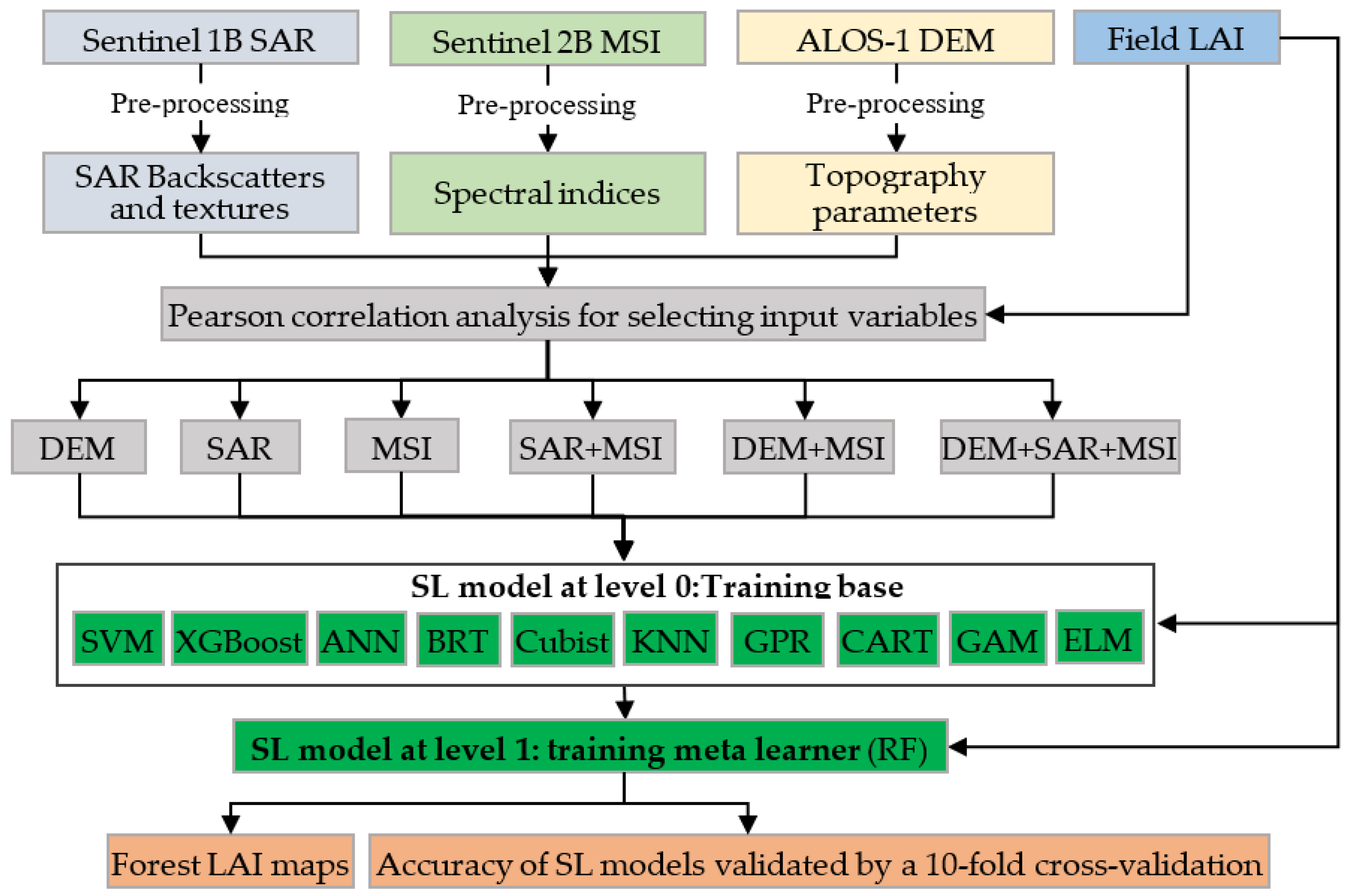
2. Materials and Methods
2.1. Study Areas
2.2. Data
2.2.1. In Situ LAI Measurements
2.2.2. Sentinel-1 Data and Preprocessing
2.2.3. Sentinel-2 Data and Preprocessing
2.2.4. ALOS-1 DEM Data
2.3. Variable Selection and Variables Importance
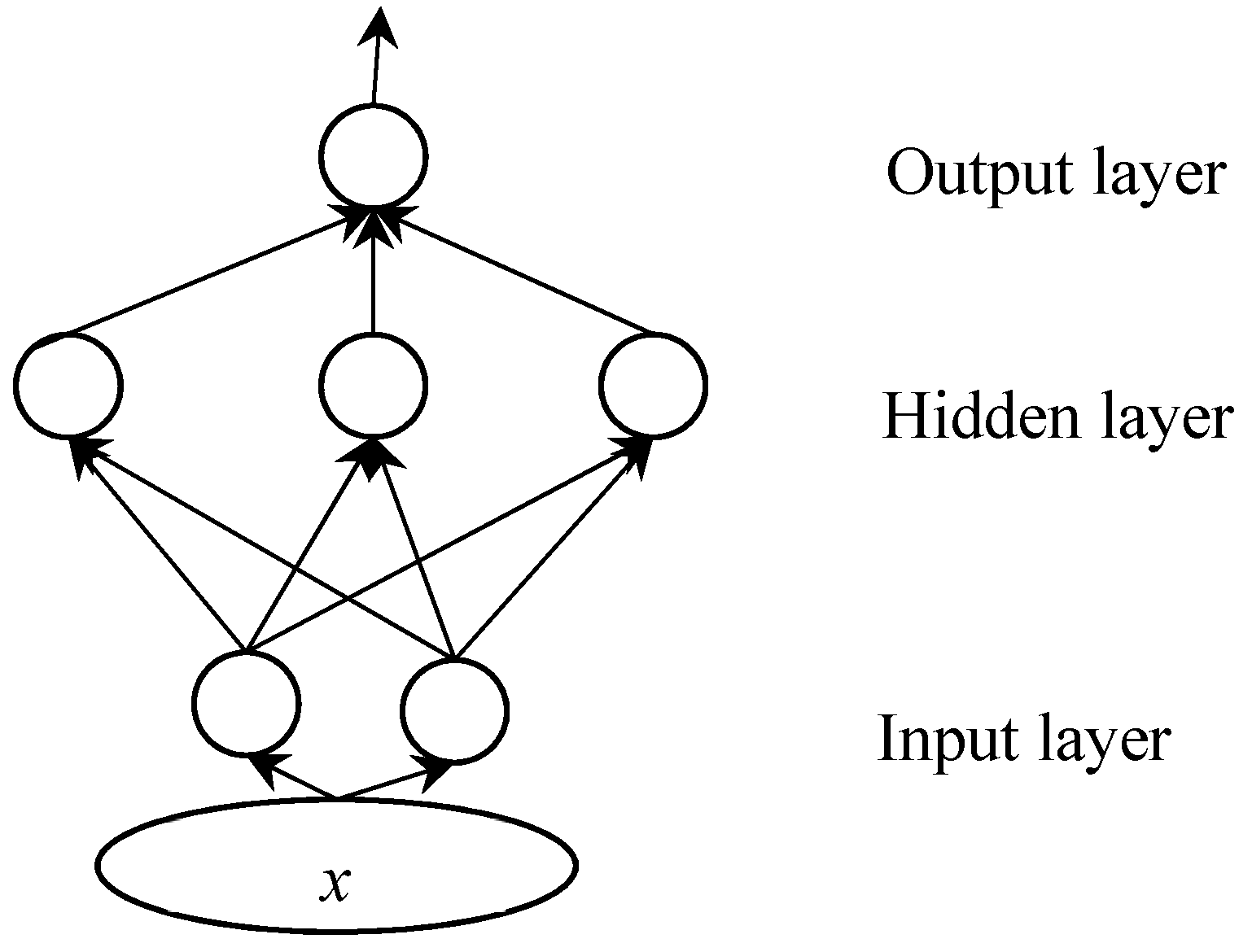
2.4. Stacking Learning
2.5. Forest LAI Mapping
2.5.1. Tuning the Hyperparameters for the Stacking Learning Models
2.5.2. Model Accuracy Assessment
3. Results
3.1. Correlation Analysis and Variable Selection
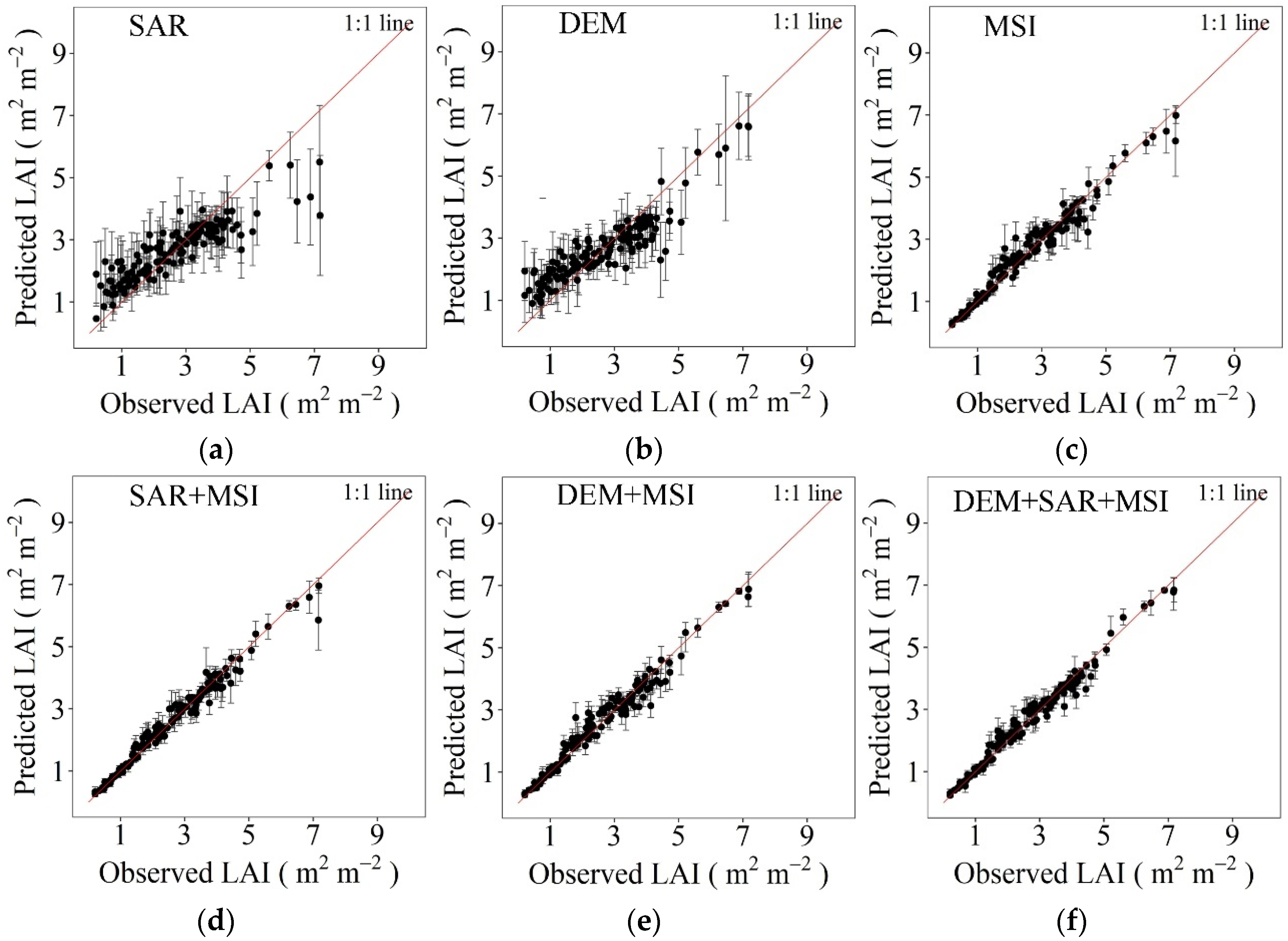
3.2. Evaluation and Comparison of Different Models and Datasets
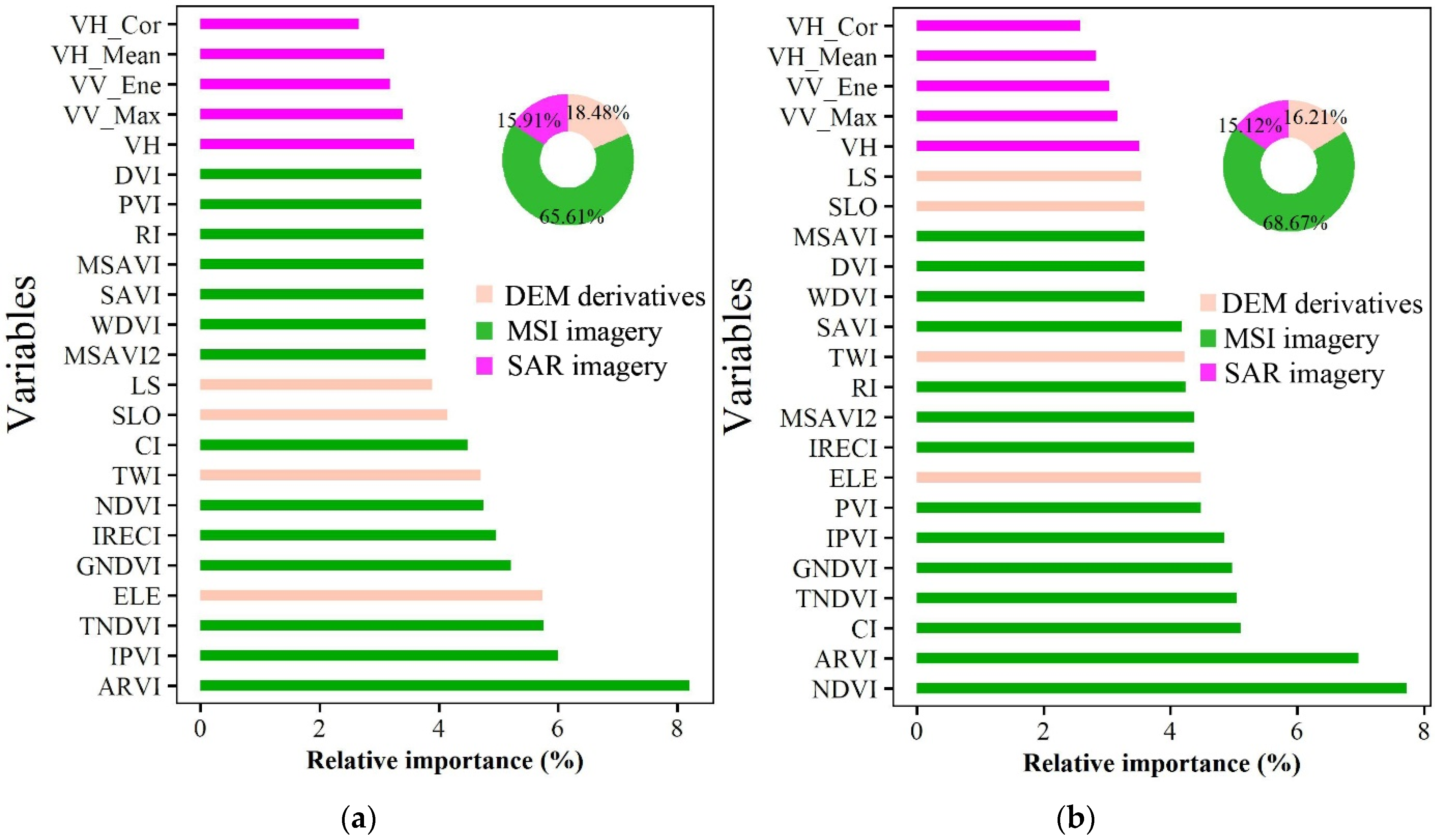
3.3. Variable Importance
3.4. LAI Maps
4. Discussion
4.1. Roles of Sentinel-1 and 2 and ALOS-DEM in Forest LAI Estimation
4.2. Usefulness of Stacking Learning Models for Forest LAI Quantification
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A

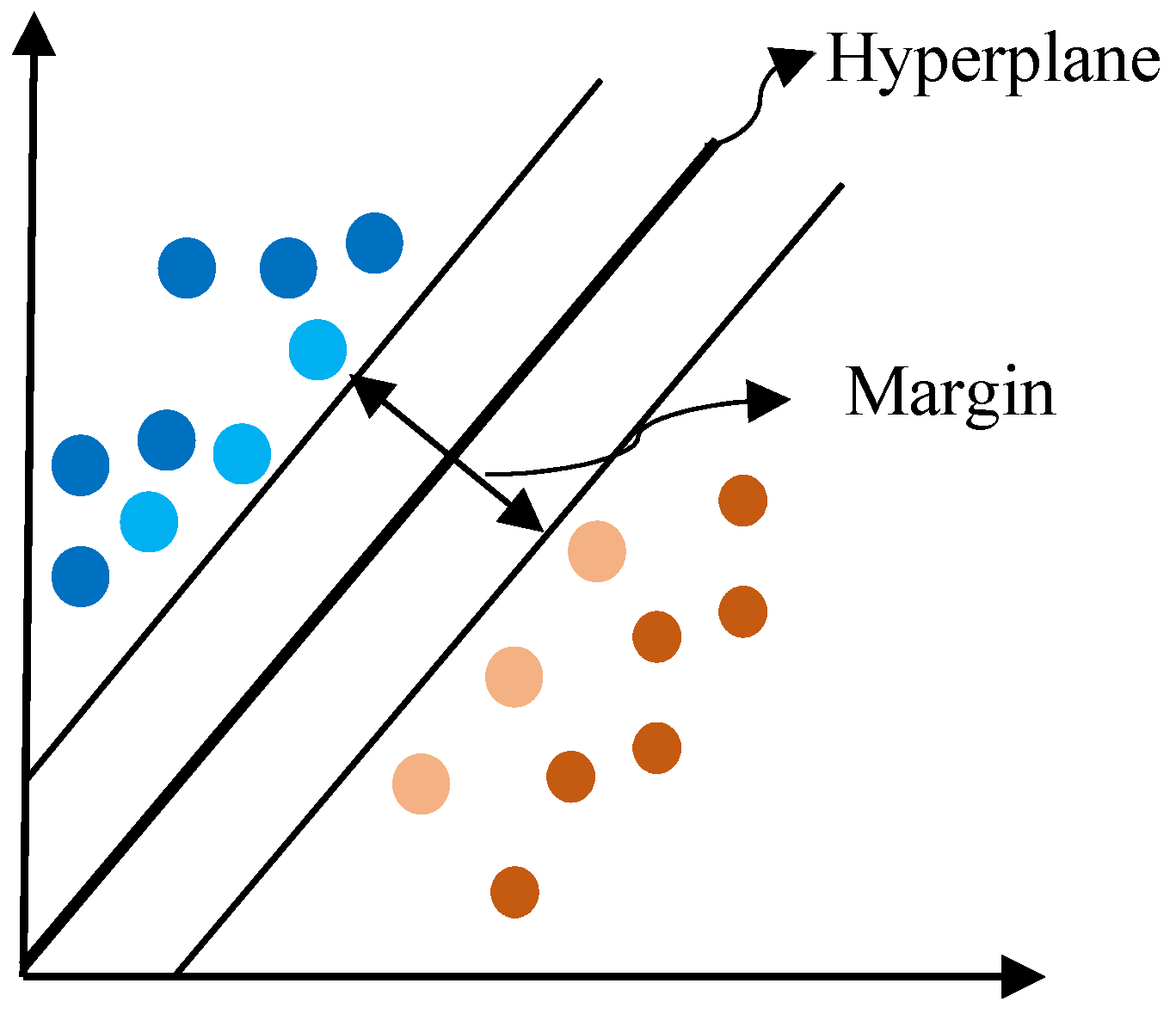


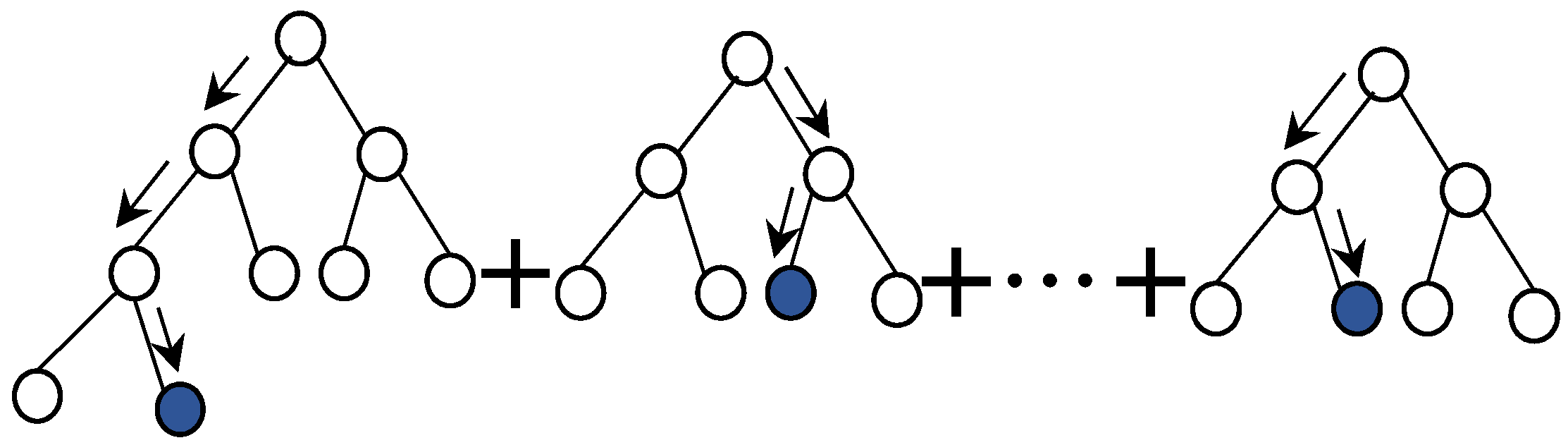
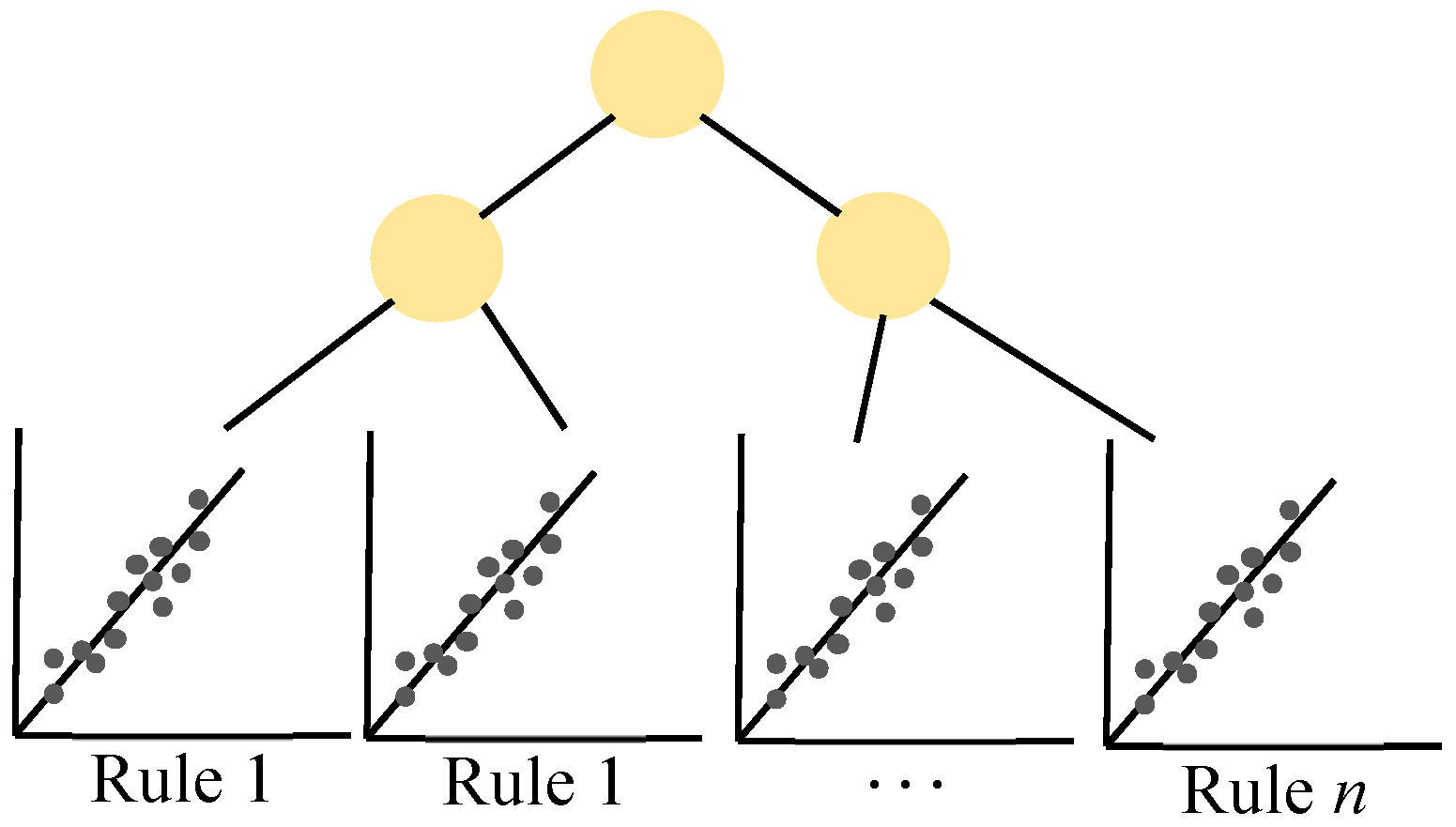
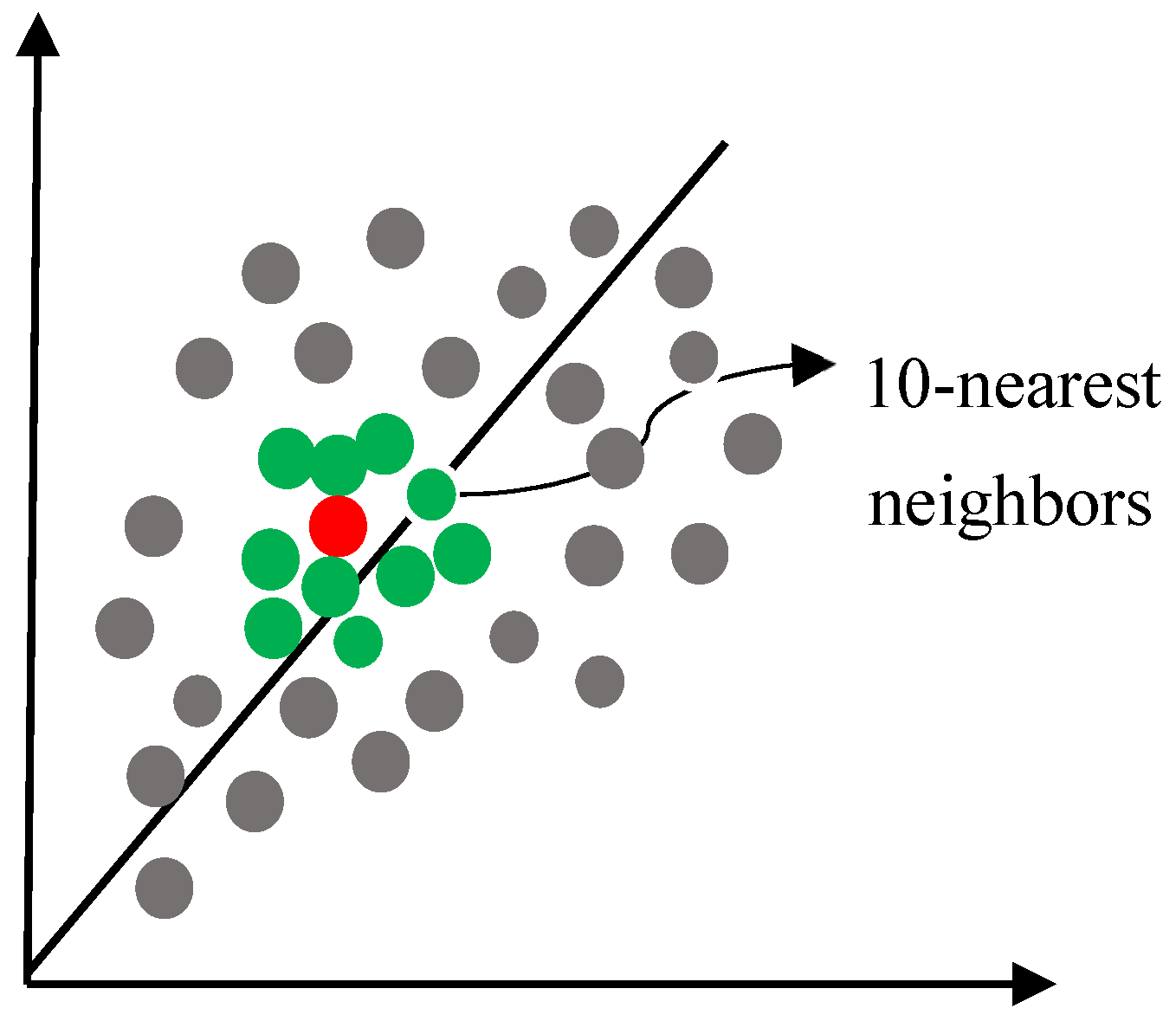


Appendix B
References
- Zhou, G.; Houlton, B.Z.; Wang, W.; Huang, W.; Xiao, Y.; Zhang, Q.; Liu, S.; Cao, M.; Wang, X.; Wang, S. Substantial reorganization of China’s tropical and subtropical forests: Based on the permanent plots. Glob. Change Biol. 2014, 20, 240–250. [Google Scholar] [CrossRef] [PubMed]
- Harris, N.L.; Gibbs, D.A.; Baccini, A.; Birdsey, R.A.; De Bruin, S.; Farina, M.; Fatoyinbo, L.; Hansen, M.C.; Herold, M.; Houghton, R.A. Global maps of twenty-first century forest carbon fluxes. Nat. Clim. Change 2021, 11, 234–240. [Google Scholar] [CrossRef]
- Mori, A.S.; Dee, L.E.; Gonzalez, A.; Ohashi, H.; Cowles, J.; Wright, A.J.; Loreau, M.; Hautier, Y.; Newbold, T.; Reich, P.B. Biodiversity-productivity relationships are key to nature-based climate solutions. Nat. Clim. Change 2021, 11, 543–550. [Google Scholar] [CrossRef]
- Wenhua, L. Degradation and restoration of forest ecosystems in China. For. Ecol. Manag. 2004, 201, 33–41. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, K.; Lin, Y.; Shi, W.; Song, Y.; He, X. Balancing green and grain trade. Nat. Geosci. 2015, 8, 739–741. [Google Scholar] [CrossRef]
- Tong, X.; Brandt, M.; Yue, Y.; Ciais, P.; Jepsen, M.R.; Penuelas, J.; Wigneron, J.-P.; Xiao, X.; Song, X.-P.; Horion, S. Forest management in southern China generates short term extensive carbon sequestration. Nat. Commun. 2020, 11, 129. [Google Scholar] [CrossRef]
- Soudani, K.; François, C.; Le Maire, G.; Le Dantec, V.; Dufrêne, E. Comparative analysis of IKONOS, SPOT, and ETM+ data for leaf area index estimation in temperate coniferous and deciduous forest stands. Remote Sens. Environ. 2006, 102, 161–175. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.M.; Rich, P.M.; Gower, S.T.; Norman, J.M.; Plummer, S. Leaf area index of boreal forests: Theory, techniques, and measurements. J. Geophys. Res. Atmos. 1997, 102, 29429–29443. [Google Scholar] [CrossRef]
- Lama, G.F.C.; Crimaldi, M.; Pasquino, V.; Padulano, R.; Chirico, G.B. Bulk drag predictions of Riparian Arundo donax stands through UAV-acquired multispectral images. Water 2021, 13, 1333. [Google Scholar] [CrossRef]
- Box, W.; Järvelä, J.; Västilä, K. Flow resistance of floodplain vegetation mixtures for modelling river flows. J. Hydrol. 2021, 601, 126593. [Google Scholar] [CrossRef]
- Yan, G.; Hu, R.; Luo, J.; Weiss, M.; Jiang, H.; Mu, X.; Xie, D.; Zhang, W. Review of indirect optical measurements of leaf area index: Recent advances, challenges, and perspectives. Agric. For. Meteorol. 2019, 265, 390–411. [Google Scholar] [CrossRef]
- Haboudane, D.; Miller, J.R.; Pattey, E.; Zarco-Tejada, P.J.; Strachan, I.B. Hyperspectral vegetation indices and novel algorithms for predicting green LAI of crop canopies: Modeling and validation in the context of precision agriculture. Remote Sens. Environ. 2004, 90, 337–352. [Google Scholar] [CrossRef]
- Wang, J.; Xiao, X.; Bajgain, R.; Starks, P.; Steiner, J.; Doughty, R.B.; Chang, Q. Estimating leaf area index and aboveground biomass of grazing pastures using Sentinel-1, Sentinel-2 and Landsat images. ISPRS J. Photogramm. Remote Sens. 2019, 154, 189–201. [Google Scholar] [CrossRef] [Green Version]
- Vreugdenhil, M.; Wagner, W.; Bauer-Marschallinger, B.; Pfeil, I.; Teubner, I.; Rüdiger, C.; Strauss, P. Sensitivity of Sentinel-1 backscatter to vegetation dynamics: An Austrian case study. Remote Sens. 2018, 10, 1396. [Google Scholar] [CrossRef] [Green Version]
- Lu, B.; He, Y. Leaf area index estimation in a heterogeneous grassland using optical, SAR, and DEM data. Can. J. Remote Sens. 2019, 45, 618–633. [Google Scholar] [CrossRef]
- Selkowitz, D.J.; Green, G.; Peterson, B.; Wylie, B. A multi-sensor lidar, multi-spectral and multi-angular approach for mapping canopy height in boreal forest regions. Remote Sens. Environ. 2012, 121, 458–471. [Google Scholar] [CrossRef]
- Chen, L.; Wang, Y.; Ren, C.; Zhang, B.; Wang, Z. Assessment of multi-wavelength SAR and multispectral instrument data for forest aboveground biomass mapping using random forest kriging. For. Ecol. Manag. 2019, 447, 12–25. [Google Scholar] [CrossRef]
- Debastiani, A.B.; Sanquetta, C.R.; Corte, A.P.D.; Pinto, N.S.; Rex, F.E. Evaluating SAR-optical sensor fusion for aboveground biomass estimation in a Brazilian tropical forest. Ann. For. Res. 2019, 62, 109–122. [Google Scholar] [CrossRef]
- Dente, L.; Satalino, G.; Mattia, F.; Rinaldi, M. Assimilation of leaf area index derived from ASAR and MERIS data into CERES-wheat model to map wheat yield. Remote Sens. Environ. 2008, 112, 1395–1407. [Google Scholar] [CrossRef]
- Chen, W.; Yin, H.; Moriya, K.; Sakai, T.; Cao, C. Retrieval and comparison of forest leaf area index based on remote sensing data from AVNIR-2, Landsat-5 TM, MODIS, and PALSAR sensors. ISPRS Int. J. Geo-Inf. 2017, 6, 179. [Google Scholar] [CrossRef] [Green Version]
- Houborg, R.; McCabe, M.F. A hybrid training approach for leaf area index estimation via Cubist and random forests machine-learning. ISPRS J. Photogramm. Remote Sens. 2018, 135, 173–188. [Google Scholar] [CrossRef]
- Li, D.; Gu, X.; Pang, Y.; Chen, B.; Liu, L. Estimation of forest aboveground biomass and leaf area index based on digital aerial photograph data in Northeast China. Forests 2018, 9, 275. [Google Scholar] [CrossRef] [Green Version]
- Xie, R.; Darvishzadeh, R.; Skidmore, A.K.; Heurich, M.; Holzwarth, S.; Gara, T.W.; Reusen, I. Mapping leaf area index in a mixed temperate forest using Fenix airborne hyperspectral data and Gaussian processes regression. Int. J. Appl. Earth Obs. Geoinf. 2021, 95, 102242. [Google Scholar] [CrossRef]
- Breiman, L. Stacked regressions. Mach. Learn. 1996, 24, 49–64. [Google Scholar] [CrossRef] [Green Version]
- Alebele, Y.; Zhang, X.; Wang, W.; Yang, G.; Yao, X.; Zheng, H.; Zhu, Y.; Cao, W.; Cheng, T. Estimation of canopy biomass components in paddy rice from combined optical and SAR data using multi-target gaussian regressor stacking. Remote Sens. 2020, 12, 2564. [Google Scholar] [CrossRef]
- Schwenker, F. Ensemble methods: Foundations and algorithms. IEEE Comput. Intell. Mag. 2013, 8, 77–79. [Google Scholar] [CrossRef]
- Healey, S.P.; Cohen, W.B.; Yang, Z.; Brewer, C.K.; Brooks, E.B.; Gorelick, N.; Hernandez, A.J.; Huang, C.; Hughes, M.J.; Kennedy, R.E. Mapping forest change using stacked generalization: An ensemble approach. Remote Sens. Environ. 2018, 204, 717–728. [Google Scholar] [CrossRef]
- Jiang, F.; Zhao, F.; Ma, K.; Li, D.; Sun, H. Mapping the forest canopy height in Northern China by synergizing ICESat-2 with Sentinel-2 using a stacking algorithm. Remote Sens. 2021, 13, 1535. [Google Scholar] [CrossRef]
- Patil, P.R.; Sivagami, M. Forest cover classification using stacking of ensemble learning and neural networks. In Artificial Intelligence and Evolutionary Computations in Engineering Systems; Springer: Singapore, 2020; pp. 89–102. [Google Scholar] [CrossRef]
- Li, X.; Liu, Z.; Lin, H.; Wang, G.; Sun, H.; Long, J.; Zhang, M. Estimating the growing stem volume of Chinese pine and larch plantations based on fused optical data using an improved variable screening method and stacking algorithm. Remote Sens. 2020, 12, 871. [Google Scholar] [CrossRef] [Green Version]
- Džeroski, S.; Ženko, B. Is combining classifiers with stacking better than selecting the best one? Mach. Learn. 2004, 54, 255–273. [Google Scholar] [CrossRef] [Green Version]
- Dale, V.H.; Joyce, L.A.; McNulty, S.; Neilson, R.P.; Ayres, M.P.; Flannigan, M.D.; Hanson, P.J.; Irland, L.C.; Lugo, A.E.; Peterson, C.J. Climate change and forest disturbances: Climate change can affect forests by altering the frequency, intensity, duration, and timing of fire, drought, introduced species, insect and pathogen outbreaks, hurricanes, windstorms, ice storms, or landslides. BioScience 2001, 51, 723–734. [Google Scholar] [CrossRef] [Green Version]
- Wang, K.; Wang, H.; Shi, X.; Weindorf, D.; Yu, D.; Liang, Y.; Shi, D. Landscape analysis of dynamic soil erosion in Subtropical China: A case study in Xingguo County, Jiangxi Province. Soil Tillage Res. 2009, 105, 313–321. [Google Scholar] [CrossRef]
- Wen, H.; Ni, S.; Wang, J.; Cai, C. Changes of soil quality induced by different vegetation restoration in the collapsing gully erosion areas of southern China. Int. Soil Water Conserv. Res. 2021, 9, 195–206. [Google Scholar] [CrossRef]
- Decagon Devices. AccuPAR PAR/LAI Ceptometer, Model LP-80. Operator’s Manual Version 1.0. 2003. Available online: https://www.manualslib.com/manual/1288172/Decagon-Devices-Accupar-Lp-80.html (accessed on 1 November 2021).
- Lee, J.-S.; Jurkevich, L.; Dewaele, P.; Wambacq, P.; Oosterlinck, A. Speckle filtering of synthetic aperture radar images: A review. Remote Sens. Rev. 1994, 8, 313–340. [Google Scholar] [CrossRef]
- Filipponi, F. Sentinel-1 GRD preprocessing workflow. Proceedings 2019, 18, 11. [Google Scholar] [CrossRef] [Green Version]
- Simard, M.; Saatchi, S.S.; De Grandi, G. The use of decision tree and multiscale texture for classification of JERS-1 SAR data over tropical forest. IEEE Trans. Geosci. Remote Sens. 2000, 38, 2310–2321. [Google Scholar] [CrossRef] [Green Version]
- Haralick, R.M.; Shanmugam, K.; Dinstein, I.H. Textural features for image classification. IEEE Trans. Syst. Man Cybern. 1973, SMC-3, 610–621. [Google Scholar] [CrossRef] [Green Version]
- Akbari, E.; Darvishi, B.; Neysani, S.; Hamzeh, S.; Soufizadeh, S.; Pignatti, S. Crop mapping using random forest and particle swarm optimization based on multi-temporal Sentinel-2. Remote Sens. 2020, 12, 1449. [Google Scholar] [CrossRef]
- Rosenqvist, A.; Shimada, M.; Ito, N.; Watanabe, M. ALOS PALSAR: A pathfinder mission for global-scale monitoring of the environment. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3307–3316. [Google Scholar] [CrossRef]
- Tadono, T.; Ishida, H.; Oda, F.; Naito, S.; Minakawa, K.; Iwamoto, H. Precise global DEM generation by ALOS PRISM. ISPRS Ann. Photogramm. Remote. Sens. Spat. Inf. Sci. 2014, 2, 71. [Google Scholar] [CrossRef] [Green Version]
- Xu, L.; Shi, Y.; Fang, H.; Zhou, G.; Xu, X.; Zhou, Y.; Tao, J.; Ji, B.; Xu, J.; Li, C. Vegetation carbon stocks driven by canopy density and forest age in subtropical forest ecosystems. Sci. Total Environ. 2018, 631, 619–626. [Google Scholar] [CrossRef]
- Fisher, A.; Rudin, C.; Dominici, F. All models are wrong, but many are useful: Learning a variable’s importance by studying an entire class of prediction models simultaneously. J. Mach. Learn. Res. 2019, 20, 1–81. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Wolpert, D.H. Stacked generalization. Neural Netw. 1992, 5, 241–259. [Google Scholar] [CrossRef]
- Hutter, F.; Lücke, J.; Schmidt-Thieme, L. Beyond manual tuning of hyperparameters. Künstliche Intell. 2015, 29, 329–337. [Google Scholar] [CrossRef]
- Stone, M. Cross-validatory choice and assessment of statistical predictions. J. R. Stat. Soc. Ser. B Methodol. 1974, 36, 111–133. [Google Scholar] [CrossRef]
- Tillack, A.; Clasen, A.; Kleinschmit, B.; Förster, M. Estimation of the seasonal leaf area index in an alluvial forest using high-resolution satellite-based vegetation indices. Remote Sens. Environ. 2014, 141, 52–63. [Google Scholar] [CrossRef]
- Chen, J.M. Optically-based methods for measuring seasonal variation of leaf area index in boreal conifer stands. Agric. For. Meteorol. 1996, 80, 135–163. [Google Scholar] [CrossRef]
- Ni-Meister, W.; Jupp, D.L.; Dubayah, R. Modeling lidar waveforms in heterogeneous and discrete canopies. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1943–1958. [Google Scholar] [CrossRef] [Green Version]
- Luo, P.; Liao, J.; Shen, G. Combining spectral and texture features for estimating leaf area index and biomass of maize using Sentinel-1/2, and Landsat-8 data. IEEE Access 2020, 8, 53614–53626. [Google Scholar] [CrossRef]
- Chauhan, S.; Darvishzadeh, R.; Lu, Y.; Boschetti, M.; Nelson, A. Understanding wheat lodging using multi-temporal Sentinel-1 and Sentinel-2 data. Remote Sens. Environ. 2020, 243, 111804. [Google Scholar] [CrossRef]
- Scholten, T.; Goebes, P.; Kühn, P.; Seitz, S.; Assmann, T.; Bauhus, J.; Bruelheide, H.; Buscot, F.; Erfmeier, A.; Fischer, M. On the combined effect of soil fertility and topography on tree growth in subtropical forest ecosystems—A study from SE China. J. Plant Ecol. 2017, 10, 111–127. [Google Scholar] [CrossRef]
- Jordan, M.I.; Mitchell, T.M. Machine learning: Trends, perspectives, and prospects. Science 2015, 349, 255–260. [Google Scholar] [CrossRef] [PubMed]
- Amit, Y.; Geman, D. Shape quantization and recognition with randomized trees. Neural Comput. 1997, 9, 1545–1588. [Google Scholar] [CrossRef] [Green Version]
- Meyer, D.; Leisch, F.; Hornik, K. The support vector machine under test. Neurocomputing 2003, 55, 169–186. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar] [CrossRef] [Green Version]
- Pham, T.D.; Yokoya, N.; Xia, J.; Ha, N.T.; Le, N.N.; Nguyen, T.T.T.; Dao, T.H.; Vu, T.T.P.; Pham, T.D.; Takeuchi, W. Comparison of Machine learning methods for estimating mangrove above-ground biomass using multiple source remote sensing data in the red river delta biosphere reserve, Vietnam. Remote Sens. 2020, 12, 1334. [Google Scholar] [CrossRef] [Green Version]
- Jain, A.K.; Mao, J.; Mohiuddin, K.M. Artificial neural networks: A tutorial. Computer 1996, 29, 31–44. [Google Scholar] [CrossRef] [Green Version]
- Neinavaz, E.; Skidmore, A.K.; Darvishzadeh, R.; Groen, T.A. Retrieval of leaf area index in different plant species using thermal hyperspectral data. ISPRS J. Photogramm. Remote Sens. 2016, 119, 390–401. [Google Scholar] [CrossRef]
- Elith, J.; Leathwick, J.R.; Hastie, T. A working guide to boosted regression trees. J. Anim. Ecol. 2008, 77, 802–813. [Google Scholar] [CrossRef] [PubMed]
- Minasny, B.; McBratney, A.B. Regression rules as a tool for predicting soil properties from infrared reflectance spectroscopy. Chemom. Intell. Lab. Syst. 2008, 94, 72–79. [Google Scholar] [CrossRef]
- Chirici, G.; Mura, M.; McInerney, D.; Py, N.; Tomppo, E.O.; Waser, L.T.; Travaglini, D.; McRoberts, R.E. A meta-analysis and review of the literature on the k-Nearest Neighbors technique for forestry applications that use remotely sensed data. Remote Sens. Environ. 2016, 176, 282–294. [Google Scholar] [CrossRef]
- Rasmussen, C.E. Gaussian Processes in Machine Learning; Springer: Berlin/Heidelberg, Germany, 2003; pp. 63–71. [Google Scholar] [CrossRef] [Green Version]
- Strobl, C.; Malley, J.; Tutz, G. An introduction to recursive partitioning: Rationale, application, and characteristics of classification and regression trees, bagging, and random forests. Psychol. Methods 2009, 14, 323. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rätsch, G.; Onoda, T.; Müller, K.-R. Soft margins for AdaBoost. Mach. Learn. 2001, 42, 287–320. [Google Scholar] [CrossRef]
- Huang, G.-B.; Zhu, Q.-Y.; Siew, C.-K. Extreme learning machine: Theory and applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]



| Study Area | Sensor | Remote Sensing Images | Product Type | Sensing Date | Season |
|---|---|---|---|---|---|
| Xingguo | Sentinel-1B | SAR | GRDH/IW | 16 November 2019 | Winter |
| 23 November 2019 | |||||
| Sentinel-2B | MSI | S2MSI1C | 06 December 2019 | ||
| 13 December 2019 | |||||
| 06 December 2019 | |||||
| Gandong | Sentinel-1B | SAR | GRDH/IW | 15 July 2020 | Summer |
| 21 July 2020 | |||||
| Sentinel-2B | MSI | S2MSI1C | 13 July 2020 | ||
| 19 August 2020 | |||||
| 30 July 2020 | |||||
| 30 July 2020 |
| Sensor | Types | Indices | Definition |
|---|---|---|---|
| Sentinel-1 | Backscatter | VH | Normalized backscatter coefficient of VH channel (dB) |
| VV | Normalized backscatter coefficient of VV channel (dB) | ||
| V/H | VV/VH | ||
| VV_CON | Contrast, measure the statistics derived from the GLCM | ||
| Texture | VV_DIS | Dissimilarity | |
| VV_IDM | Inverse difference moment | ||
| VV_ASM | Angular second moment | ||
| VV_ ENT | Entropy | ||
| VV_AVG | Mean | ||
| VV_COR | Correlation | ||
| VH_CON | Same with above-mentioned texture | ||
| VH_DIS | |||
| VH_IDM | |||
| VH_ASM | |||
| VH_ ENT | |||
| VH_AVG | |||
| VH_COR | |||
| ARVI | Atmospherically resistant vegetation index, (B8 − B5 − y(B5 − B1))/(B8 + B5 − y(B5 − B1)) | ||
| Sentinel-2 | Vegetation indices | CI | Coloration Index, (B4 − B2)/B4 |
| DVI | Difference vegetation index, B8 − B4 | ||
| NDVI | Normalized difference vegetation index, (B8 − B4)/(B8 + B4) | ||
| GNDVI | Green normalized difference vegetation index, (B8a − B3)/(B8a + B3) | ||
| IPVI | Infrared percentage vegetation index, B8/2(B8 + B4) × (NDVI + 1) | ||
| IRECI | Inverted red-edge chlorophyll index, (B7 − B4)/(B5/B6) | ||
| MSAVI | Modified soil-adjusted vegetation index, B8 + 0.5 − [(2B8 + 1)2 − 8(B8 − B5)]0.5 | ||
| MSAVI2 | Modified soil-adjusted vegetation index 2, B8 + 0.5 − [(2B8 + 1)2 − 8(B8 − B4)]0.5 | ||
| PVI | Perpendicular vegetation index, 1/(α0.5 + 1) × (B8a – αr − β) | ||
| SAVI | Soil adjusted vegetation index, (B8 − B4)/(B8 + B5 + L) × (1 + L) | ||
| TNDVI | Transformed NDVI, [(B8a − B4)/(B8a + B4) + 0.5]0.5 | ||
| WDVI | Weighted difference vegetation index, B8a − αB5, α = nir soil/red soil | ||
| RVI | Simple ratio vegetation index, B8/B4 | ||
| RI | Normalized difference red/green redness index, (B4 − B3)/(B4 + B3) | ||
| MTCI | Meris terrestrial chlorophyll index, (B6 − B5)/(B5 − B4) | ||
| REIP | REIP Red-edge infection point index, 700 + 40 × [(B4 + B7)/2− B5]/(B6−B5) | ||
| NDVI2 | Normalized difference vegetation index 2, (B12 − B8)/(B12 + B8) | ||
| RDVI | Renormalized difference vegetation index, (B8 − B4)/[(B8 + B4)0.5] | ||
| MSBI | Misra soil brightness index, 0.406B3 + 0.600B4 + 0.645B6 + 0.643B8a | ||
| ALOS-1 DEM | Topographical parameters | TWI | Topographic wetness index |
| ELE | Elevation | ||
| SLO | Slope | ||
| ASP | Aspect | ||
| PRC | Profile curvature | ||
| PLC | Plan curvature | ||
| RLS | Relief of land surface | ||
| TWI | Topographic wetness index | ||
| SPI | Stream power index | ||
| SL | Slope length, a factor calculated by Universal Soil Loss Equation | ||
| TRI | Terrain ruggedness index |
| Algorithm | R Package | Hyperparameters Tuned | Range |
|---|---|---|---|
| CART | rpart | cp, the complexity parameter. | 0.048 |
| Cubist | cubist | committees, the number of committee models. | 1–100 |
| neighbors, the number of neighbors used to correct the model predictions. | 0–10 | ||
| BRT | GBM | n.trees, the number of trees to fit. | 50–1000 |
| interaction.depth, the number of splits in each tree. | 1–20 | ||
| shrinkage, the rate at which the model descends along the gradient. | 0.01–1 | ||
| n.minobsinnode, the minimum number of observations of the terminal node of the tree. | 1–50 | ||
| RF | randomForest | ntree, the number of trees to grow into a forest. | 50–1000 |
| mtry, the number of variables to be considered at each split. | 1–30 | ||
| XGBoost | xgboost | nrounds, the maximum number of iterations. | 1–1000 |
| max_depth, the depth of the tree. | 1–10 | ||
| eta, the learning rate. | 0.01–0.5 | ||
| gamma, prevents overfitting. | 0–1 | ||
| colsample_bytree, the number of variables supplied to a tree. | 0.1–1 | ||
| min_child_weight, the minimum number of instances required in a child node. | 0–3 | ||
| ANN | nnet | size, the number of units in the hidden layer. | 1–10 |
| decay, parameter for weight decay. | 0.001–0.05 | ||
| KNN | caret | k, number of neighbors considered. | 1–20 |
| SVM | e1071 | sigma, scaling parameters of the hypothetical Laplace distribution. | 0.01–0.5 |
| C, the regularization term in the Lagrange formulation | 1–10 | ||
| GPR | kernlab | degree, parameter for the Polynomial kernel “polydot”. | 1–10 |
| scale, parameter for the Polynomial kernel “polydot”. | 0.001–0.5 | ||
| ELM | elmNN | nhid, number of hidden Units, numeric.Activation Function (actfun, character) | 1–100 |
| actfun, activation function. | linear | ||
| ABCT | adaboost | mstop, number of boosting iterations. | 50–1000 |
| AIC prune. | yes |
| Group | Types | Variable | Xingguo | Gandong |
|---|---|---|---|---|
| ALOS-1 | Topographic parameters | LS | 0.27 * | 0.44 ** |
| SLO | 0.28 * | 0.46 ** | ||
| ELE | 0.36 ** | 0.47 ** | ||
| TWI | −0.30 ** | −0.32 ** | ||
| Sentinel-1 | Backscatter | VH | 0.24 * | 0.20 * |
| Texture | VH_cor | 0.30 * | 0.24 * | |
| VH_Mean | 0.29 ** | 0.19 * | ||
| VV_Ene | 0.33 ** | 0.20 * | ||
| VV_Max | 0.27 ** | 0.19 * | ||
| Sentinel-2 | Soil indices | RI | −0.43 ** | −0.30 * |
| CI | −0.72 ** | −0.58 ** | ||
| Vegetation indices | ARVI | 0.61 ** | 0.73 ** | |
| DVI | 0.36 ** | 0.43 ** | ||
| GNDVI | 0.62 ** | 0.66 ** | ||
| IPVI | 0.54 ** | 0.71 ** | ||
| IRECI | 0.29 * | 0.72 ** | ||
| MSAVI | 0.26 * | 0.53 ** | ||
| MSAVI2 | 0.28 * | 0.55 ** | ||
| NDVI | 0.79 ** | 0.70 ** | ||
| PVI | 0.56 ** | 0.43 ** | ||
| SAVI | 0.27 * | 0.56 ** | ||
| TNDVI | 0.55 ** | 0.68 ** | ||
| WDVI | 0.25 * | 0.52 ** |
| Inputs | Model | Xingguo | Gandong | ||||
|---|---|---|---|---|---|---|---|
| R2 | MAE | RMSE | R2 | MAE | RMSE | ||
| DEM | ANN | 0.27 | 1.15 | 1.40 | 0.13 | 1.87 | 2.34 |
| KNN | 0.20 | 1.15 | 1.39 | 0.11 | 1.89 | 2.29 | |
| SVM | 0.18 | 1.19 | 1.47 | 0.16 | 1.76 | 2.27 | |
| GPR | 0.31 | 1.15 | 1.39 | 0.17 | 1.81 | 2.24 | |
| CART | 0.28 | 1.23 | 1.52 | 0.11 | 1.92 | 2.37 | |
| BRT | 0.30 | 1.12 | 1.36 | 0.14 | 1.97 | 2.44 | |
| Cubist | 0.30 | 1.12 | 1.37 | 0.15 | 1.84 | 2.31 | |
| XGBoost | 0.29 | 1.27 | 1.54 | 0.15 | 2.18 | 2.40 | |
| ABCT | 0.32 | 1.08 | 1.32 | 0.17 | 1.85 | 2.22 | |
| ELM | 0.28 | 1.11 | 1.34 | 0.13 | 1.86 | 2.30 | |
| SL | 0.72 | 0.56 | 0.79 | 0.57 | 1.12 | 1.54 | |
| Sentinel-1 (SAR) | ANN | 0.11 | 1.19 | 1.51 | 0.08 | 2.06 | 2.58 |
| KNN | 0.11 | 1.17 | 1.46 | 0.08 | 1.88 | 2.32 | |
| SVM | 0.12 | 1.18 | 1.48 | 0.11 | 1.94 | 2.41 | |
| GPR | 0.20 | 1.17 | 1.44 | 0.15 | 1.84 | 2.26 | |
| CART | 0.13 | 1.24 | 1.56 | 0.11 | 2.01 | 2.45 | |
| BRT | 0.19 | 1.12 | 1.43 | 0.10 | 1.95 | 2.41 | |
| Cubist | 0.18 | 1.17 | 1.45 | 0.12 | 2.05 | 2.47 | |
| XGBoost | 0.17 | 1.32 | 1.64 | 0.09 | 2.04 | 2.29 | |
| ABCT | 0.21 | 1.11 | 1.40 | 0.14 | 1.89 | 2.29 | |
| ELM | 0.19 | 1.17 | 1.46 | 0.11 | 2.01 | 2.45 | |
| SL | 0.66 | 0.60 | 0.89 | 0.62 | 1.07 | 1.46 | |
| Sentinel-2 (MSI) | ANN | 0.81 | 0.74 | 0.76 | 0.81 | 0.93 | 1.26 |
| KNN | 0.72 | 0.66 | 0.84 | 0.71 | 1.25 | 1.33 | |
| SVM | 0.73 | 0.72 | 1.01 | 0.74 | 1.10 | 1.37 | |
| GPR | 0.77 | 0.89 | 1.25 | 0.76 | 1.15 | 1.27 | |
| CART | 0.64 | 1.01 | 1.28 | 0.75 | 1.15 | 1.41 | |
| BRT | 0.81 | 0.61 | 0.70 | 0.81 | 0.89 | 1.14 | |
| Cubist | 0.80 | 0.59 | 0.81 | 0.82 | 0.87 | 1.11 | |
| XGBoost | 0.79 | 0.64 | 0.77 | 0.81 | 1.01 | 1.27 | |
| ABCT | 0.82 | 0.58 | 0.78 | 0.84 | 0.79 | 1.03 | |
| ELM | 0.80 | 0.61 | 0.79 | 0.82 | 0.97 | 1.29 | |
| SL | 0.95 | 0.23 | 0.34 | 0.95 | 0.34 | 0.51 | |
| DEM + MSI | ANN | 0.82 | 0.49 | 0.67 | 0.82 | 0.89 | 1.20 |
| KNN | 0.73 | 0.64 | 0.84 | 0.73 | 1.01 | 1.30 | |
| SVM | 0.75 | 0.67 | 0.92 | 0.76 | 1.08 | 1.25 | |
| GPR | 0.79 | 0.86 | 1.09 | 0.80 | 1.14 | 1.18 | |
| CART | 0.67 | 0.98 | 1.26 | 0.75 | 1.26 | 1.38 | |
| BRT | 0.81 | 0.53 | 0.68 | 0.82 | 0.86 | 1.12 | |
| Cubist | 0.81 | 0.58 | 0.76 | 0.82 | 0.83 | 1.10 | |
| XGBoost | 0.80 | 0.59 | 0.76 | 0.82 | 0.99 | 1.19 | |
| ABCT | 0.83 | 0.48 | 0.65 | 0.84 | 0.78 | 1.02 | |
| ELM | 0.82 | 0.51 | 0.67 | 0.84 | 0.90 | 1.20 | |
| SL | 0.96 | 0.20 | 0.30 | 0.95 | 0.33 | 0.50 | |
| SAR + MSI | ANN | 0.81 | 0.58 | 0.67 | 0.81 | 0.92 | 1.23 |
| KNN | 0.73 | 0.65 | 0.84 | 0.72 | 1.09 | 1.31 | |
| SVM | 0.74 | 0.68 | 0.92 | 0.74 | 1.08 | 1.34 | |
| GPR | 0.78 | 0.87 | 1.14 | 0.80 | 1.14 | 1.18 | |
| CART | 0.66 | 1.00 | 1.26 | 0.75 | 1.53 | 1.39 | |
| BRT | 0.81 | 0.54 | 0.69 | 0.82 | 0.87 | 1.13 | |
| Cubist | 0.80 | 0.59 | 0.80 | 0.82 | 0.86 | 1.11 | |
| XGBoost | 0.80 | 0.59 | 0.77 | 0.81 | 1.01 | 1.24 | |
| ABCT | 0.82 | 0.48 | 0.65 | 0.84 | 0.79 | 1.03 | |
| ELM | 0.81 | 0.52 | 0.67 | 0.82 | 0.92 | 1.23 | |
| SL | 0.95 | 0.21 | 0.33 | 0.94 | 0.33 | 0.52 | |
| DEM + SAR + MSI | ANN | 0.83 | 0.48 | 0.67 | 0.82 | 0.88 | 1.18 |
| KNN | 0.75 | 0.62 | 0.81 | 0.79 | 0.97 | 1.27 | |
| SVM | 0.77 | 0.65 | 0.91 | 0.76 | 1.03 | 1.14 | |
| GPR | 0.81 | 0.84 | 1.08 | 0.82 | 1.05 | 1.18 | |
| CART | 0.69 | 0.98 | 1.24 | 0.75 | 1.26 | 1.29 | |
| BRT | 0.82 | 0.52 | 0.67 | 0.82 | 0.85 | 1.11 | |
| Cubist | 0.81 | 0.54 | 0.73 | 0.83 | 0.83 | 1.09 | |
| XGBoost | 0.81 | 0.59 | 0.75 | 0.82 | 0.95 | 1.13 | |
| ABCT | 0.83 | 0.47 | 0.64 | 0.84 | 0.78 | 1.01 | |
| ELM | 0.84 | 0.51 | 0.65 | 0.83 | 0.86 | 1.15 | |
| SL | 0.96 | 0.17 | 0.28 | 0.96 | 0.30 | 0.47 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Ma, L.; Yu, D.; Feng, K.; Wang, X.; Song, J. Improving Leaf Area Index Retrieval Using Multi-Sensor Images and Stacking Learning in Subtropical Forests of China. Remote Sens. 2022, 14, 148. https://doi.org/10.3390/rs14010148
Chen Y, Ma L, Yu D, Feng K, Wang X, Song J. Improving Leaf Area Index Retrieval Using Multi-Sensor Images and Stacking Learning in Subtropical Forests of China. Remote Sensing. 2022; 14(1):148. https://doi.org/10.3390/rs14010148
Chicago/Turabian StyleChen, Yang, Lixia Ma, Dongsheng Yu, Kaiyue Feng, Xin Wang, and Jie Song. 2022. "Improving Leaf Area Index Retrieval Using Multi-Sensor Images and Stacking Learning in Subtropical Forests of China" Remote Sensing 14, no. 1: 148. https://doi.org/10.3390/rs14010148
APA StyleChen, Y., Ma, L., Yu, D., Feng, K., Wang, X., & Song, J. (2022). Improving Leaf Area Index Retrieval Using Multi-Sensor Images and Stacking Learning in Subtropical Forests of China. Remote Sensing, 14(1), 148. https://doi.org/10.3390/rs14010148






