Abstract
Global Navigation Satellite System (GNSS) Precise Point Positioning (PPP) is an attractive positioning technology due to its high precision and flexibility. However, the vulnerability of PPP brings a safety risk to its application in the field of life safety, which must be evaluated quantitatively to provide integrity for PPP users. Generally, PPP solutions are processed recursively based on the extended Kalman filter (EKF) estimator, utilizing both the previous and current measurements. Therefore, the integrity risk should be qualified considering the effects of all the potential observation faults in history. However, this will cause the calculation load to explode over time, which is impractical for long-time missions. This study used the innovations in a time window to detect the faults in the measurements, quantifying the integrity risk by traversing the fault modes in the window to maintain a stable computation cost. A non-zero bias was conservatively introduced to encapsulate the effect of the faults before the window. Coping with the multiple simultaneous faults, the worst-case integrity risk was calculated to overbound the real risk in the multiple fault modes. In order to verify the proposed method, simulation and experimental tests were carried out in this study. The results showed that the fixed and hold mode adopted for ambiguity resolution is critical to an integrity risk evaluation, which can improve the observation redundancy and remove the influence of the biased predicted ambiguities on the integrity risk. Increasing the length of the window can weaken the impact of the conservative assumption on the integrity risk due to the smoothing effect of the EKF estimator. In addition, improving the accuracy of observations can also reduce the integrity risk, which indicates that establishing a refined PPP random model can improve the integrity performance.
1. Introduction
Precise single positioning (PPP) technology can provide high-precision positioning for Global Navigation Satellite System (GNSS) users with the help of precise correction information, and by utilizing the code and carrier phase observations [1,2,3]. Generally, the positioning accuracy of the kinematic PPP solution with float-ambiguity after convergence can reach the decimeter to centimeter level. An even better solution and shorter convergence time can be obtained with the integer carrier-phase ambiguities resolved correctly [4,5,6,7,8]. Unlike traditional differential positioning, such as real time kinematic (RTK) and network RTK, PPP is an absolute positioning technology that requires no reference stations and can be applied anywhere in the world. Moreover, PPP can also be augmented by a regional reference station network or integrated with satellite based augmentation system services [9,10,11,12,13,14]. Benefiting from the high precision and flexibility, the application range of PPP is gradually expanding, even moving toward the life-critical field, such as in automotive, maritime and air navigation applications [15,16,17,18]. For users in the field relating to life safety, the accuracy is no longer the most concerning requirement but the safety, which means the positioning solution must be reliable and trustworthy [19,20]. Compared with single point positioning (SPP), PPP is more vulnerable because there are more potential sources of failure, which are categorized into the following five groups in [21]: satellite and signal faults, atmosphere anomalies, product and correction faults, work environment anomalies, and user-end faults. These faults may contaminate observations and result in unsafe PPP location results. Typically, observation faults can be detected, to some extent, based on the data quality control algorithms in PPP [22,23]. Unfortunately, the ones that successfully escape detection may cause a hazardous position error (PE) to the unaware users due to poor observation geometries. In GNSS integrity monitoring, this situation is called hazardous misleading information (HMI), defined as the user’s PE exceeding the alert limit (AL, defined by the requirements), while no timely alarm is triggered. For life-critical applications, the HMI events can cause great potential dangers to the user’s positioning safety. Therefore, it is of vital importance to evaluate the probability of HMI (also called integrity risk) quantitatively to provide confidence on the current positioning results.
Receiver autonomous integrity monitoring (RAIM) is a user-level algorithm to ensure the reliability of positioning that originates in the field of civil aviation [24]. RAIM contains two basic functions; one is fault detection and exclusion, and the other is the evaluation of integrity risk. The former is realized by the designed fault detector and threshold. The latter quantifies the risk of the undetected faults by providing an upper bound of the real integrity risk, or equivalently, providing the protection level (PL) to overbound the PE according to the integrity risk requirement [25]. After decades of development, RAIM has evolved from traditional RAIM to Advanced RAIM (ARAIM) [26]. The former was originally designed to provide services for GPS (Global Positioning System) aviation users during the on route phase calculating the PL under no more than one undetected fault hypothesis [27,28]. The latter was developed with the emergence of multi-frequency and multi-constellation to provide integrity for flight phases with more stringent requirements (for instance, Localizer Performance with Vertical Guidance 200 foot minima, LPV-200) considering multiple simultaneous undetected faults [29,30]. The aviation RAIM algorithms are implemented for SPP with the least-squares estimator (snapshot estimator), which only uses the observations at the current moment. Differently, the extended Kalman filter (EKF) estimator is widely adopted for PPP positioning, which is a recursive estimator utilizing both the previous and current measurements [31]. Indeed, the EKF solution coincides with the batch least square solution that uses the current and all the previous measurements as well as the propagation equations [32]. However, it is unsuitable to directly apply the existing snapshot RAIM algorithms to PPP in the batch least square form because of the increasing amount of matrix storage and calculation over time, especially for the long-time mission. To provide integrity for EKF applications, Tanil et al. [33,34] proposed a sequential integrity monitoring method using chi-square detection considering all the measurement faults in history. However, it still cannot avoid the problem of the increasing computation load. In this regard, Arana et al. [35] introduced a time window monitoring method to maintain the constant computation requirements. Meanwhile, it is robust against faults prior to the window, which is important for the practical implement of integrity monitoring for the EKF estimator.
Limited studies for PPP integrity have been conducted in recent years and have not been well-accepted in models and methods. The authors of [36,37] adopted the traditional RAIM algorithms directly in PPP, which potentially assumed that the predicted states were fault-free and only a single fault in the current observations. However, the assumptions are not appropriate for PPP because the predicted states may contain biases caused by the previous undetected faults. Moreover, the use of observations from multi-frequency and multi-constellation will increase the possibility of instantaneous multiple faults, especially when utilizing the phase observations. Based on the ARAIM algorithms developed earlier, Gunning et al. [38] initially designed the integrity monitoring for PPP using the multiple hypothesis solution separation algorithm, but brought a computational burden due to the use of a bank of parallel filters. Accordingly, Blanch et al. [39] chose the suboptimal filters to reduce the calculation cost and, therefore, degraded the integrity performance due to the increased PL. However, the results suggested that the degradation may be acceptable given the potential computational load savings. To provide PL for PPP in multipath prone environments, Blanch et al. [40] further modified the threat model to better account for local threats to guarantee the integrity in challenging environments such as urban and suburban roads. Facing the challenge of providing the integrity for land users, the Spanish company GMV proposed their own integrity concept, which was a little different from that commonly used in the aviation field [41]. The PL they constructed claimed to have good performance under different test conditions; however, adequate mathematical explanations of the related methods rarely appear in the literature.
In order to extend PPP to the life-critical field, the integrity risk of the PPP solution should be evaluated quantitatively to ensure the users’ safety. The evaluation method should not only adapt to the characteristics of the PPP processing, but also have an appropriate calculation cost for practical applications. This study evaluated the integrity risk considering multiple simultaneous undetected faults under the conservative assumption that the predicted states in the EKF are biased, which are caused by the previous measurement faults. Based on a previous study [35], a time monitoring window was adopted to reduce the impact of the conservative assumption and maintain the computation load. Moreover, the influence of ambiguity was also considered. The remainder of this contribution is organized as follows. First, Section 2 introduces the EKF processing and the method of integrity risk evaluation. Secondly, the PPP simulation experiment is designed, and the related results are analyzed in Section 3. Finally, some conclusions and future work are given in Section 4.
2. Methods
2.1. EKF Processing
EKF estimator is widely adopted in PPP algorithms, which is implemented based on the following prediction model:
and the following observation model:
where the subscript stands for the current epoch; is the true states including the user’s coordinates, receiver clock or other estimates; is the state evolution matrix and is the noise coupling matrix; represents the linearized observation vector and is the linearized design matrix; and denote the nominal process noise and observation error, which are both assumed to be white Gaussian noise with the covariance matrix and , respectively; and is the observation fault vector caused by the various anomalies mentioned in the introduction part. Generally, is modeled as an unknown bias vector whose elements are nonzero only when measurements are contaminated. This means that under a fault-free condition, is a zero vector. In this study, the state evolution model was assumed to not have any faults, and the faults only appeared in the observations. The EKF processing can be implemented using the following equations:
where the superscript (−) and (+) denote the predicted and updated values, respectively; is the variance covariance matrix that contains the uncertainties of the states; is the weight matrix of the innovation vector ; and is the Kalman gain matrix. The EKF can be operated recursively once and are initialized.
2.2. Integrity Risk Evaluation
For integrity monitoring, an integrity risk evaluation is required to quantitatively describe the impact of undetected faults on the safety of current positioning, which is expressed as the probability of HMI as follows:
where is the PE in the direction of interest and is the EKF estimated state error. is the corresponding extraction vector; for instance, is set for the PE in the first direction. is the designed fault detector and is the corresponding threshold. To calculate (10), the probability distributions of and are required, which will be demonstrated next.
2.2.1. The Distribution of PE and Detector
Under the normality of the observation error and process noise, PE is normally distributed as follows:
where is the expectation of . As shown in Appendix A, is influenced by the current and all previous observation faults. Given a time window of epochs prior to , can be expressed as follows:
where is a known matrix containing EKF information in the window as shown in Appendix A. is the combined fault vector that contains the faults in the window and encapsulates the faults prior to the window into the bias at epoch.
The fault detector should react when a fault occurs. In the EKF, the innovations measure the consistency between the actual measurements and the predicted ones. As a result, in this study, the fault detector was defined as the sum of squares of the normalized innovations in the time window as follows:
where denotes the innovations in the window. is the correspond weight matrix expressed as , where means forming a diagonal block matrix. Since the innovations at different epochs are independent [33], the detector follows a non-central chi-squared distribution as follows:
where is the degree of freedom, which is equal to the number of observations in the window. is the non-centrality parameter as follows:
where is a known term derived in Appendix B. Under the fault-free condition (), the detector follows a central chi-squared distribution and the threshold can be determined for a given false alarm requirement, , as follows:
where is the inverse central chi-squared cumulative distribution function with the degree of freedom of .
One advantage of selecting an innovation-based detector is that the PE and fault detector are independent [33]. Therefore, the Equation (10) becomes the following:
Under the fault-free condition, Equation (17) can be calculated directly based on the known distributions of the PE and detector. However, the distributions are not clear for the faulted conditions due to the unknown , which is the difficulty for integrity risk evaluation.
2.2.2. Fault Mode
To simplify the problem, the integrity risk can be evaluated under all potential fault modes, which are all combinations of observation faults in history. However, as the number of observations used by EKF estimator increases, the number of fault modes rises exponentially, which will cause the calculation load to explode over time [31]. In this regard, this study only considered the fault modes within the time window to maintain the computation cost, since the number of fault modes within the time window was relatively stable [35]. In addition, a non-zero bias was conservatively introduced to contain the effect of the observation faults prior to the window. This conservative assumption is reasonable, because, on the one hand, the integrity risk can be appropriately given a conservative value; on the other hand, its impact can be weakened by the window due to the smoothing effect of the EKF estimator.
Using the total probability rule, the integrity risk can be expressed as follows:
where represents the i-th fault mode and, in particular, means the observations in the window are fault free. Given the independence of different observation faults, indicates the probability of instantaneous faults as follows [29]:
where and is the probability of the fault on the s-th observation. In ARAIM, is obtained from the integrity support message [30]. However, in this study, was given by a prior value for the purpose of algorithm research.
Although a time window was adopted, evaluating the integrity risk under all fault modes was still computationally intensive. Fortunately, it was unnecessary because the probability of a large number of instantaneous faults was very low. Therefore, this study only evaluated the risk for the modes with no more than simultaneous faults, and conservatively overbounded the risk for the modes with more than faults as using the following equation [29]:
where is the user defined integrity risk allocation that accounts for the risk of unevaluated fault modes and can be determined as the largest integer that from Equation (20). Therefore, can be overbounded as follows:
where denotes the number of fault modes with no more than faults.
2.2.3. The Worst-Case Integrity Risk
In the i-th fault mode, the unknown fault vector is still left to be determined to calculate the term in Equation (21). In this regard, the concept of “worst-case” commonly used in integrity monitoring is introduced to determine the worst-case integrity risk. Angus et al. [42] showed that the direction of that maximizes is the one that results in the highest slope, which is defined as follows:
where the numerator is the squared expectation of the PE, and the denominator is the non-centrality parameter of the fault detector. For , the denominator of Equation (22) is positive. Therefore, is a positive definite matrix that can be orthogonally decomposed as , where is a diagonal matrix composed of the eigenvalues of , and is an orthogonal matrix composed of the corresponding eigenvectors. Equation (22) can be expressed further as follows:
where and . For the expression of Equation (23), the maximum slope is the maximum eigenvalue of and the worst direction of is that of the corresponding eigenvector . Therefore, the worst direction of can be expressed as follows:
and the worst can be obtained by searching the magnitude of () along :
where and . Ultimately, the integrity risk output to the user is as follows:
Once exceeds the requirement, the current positioning solution will be considered unreliable, and the system will be declared unavailable.
3. Experiments
3.1. Design of the Simulated PPP
In this section, a simulated PPP was designed to verify the method of integrity risk evaluation. The reason for adopting a simulation test is that on the one hand, it can strictly guarantee the normality of the errors, which is the precondition for integrity monitoring; on the other hand, it is more effective to control the changing of inputs in order to validate the performance of the algorithm. In this study, a simulated dynamic ionosphere-free (IF) PPP was designed and the states included the receiver coordinates, velocities, accelerations, receiver clock, zenith tropospheric delay (ZTD), and IF ambiguities.
Figure 1 shows the entire simulation process, including the prediction of states, observation simulation, linearization, fault detection, update, and risk evaluation. The process started with the prediction of the states. The coordinates, velocities, and accelerations were predicted using a constant acceleration model. The receiver clock error was modeled by the white noise. ZTD was modeled as random-walk noise using a Saastamoinen model and Niell Mapping Function [43,44]. The ambiguities were considered to be time invariant. In the observation simulation part, the IF code and phase observations were generated based on the truth of states and the satellite precise orbit and clock products provided by the GeoForschungsZentrum Potsdam (GFZ) center. The observation errors were randomly generated by the given covariance. The generation of process noise in the prediction part was similar but is not shown in the figure for brevity. In the update part, the fixed and hold mode was adopted for an ambiguity resolution. That is, if the ambiguity change of a certain satellite is continuously smaller than the given threshold for epochs, the ambiguity will be fixed and no longer be estimated in the EKF until the satellite descends. Table 1 shows the configuration of the related parameters for the simulated PPP positioning and integrity risk evaluation.
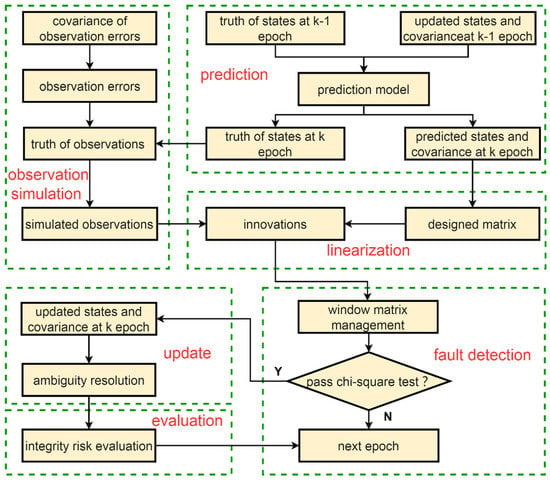
Figure 1.
The simulation process for the simulated dynamic PPP.

Table 1.
Configuration of the parameters for the simulated PPP and integrity risk evaluation.
3.2. Experimental PPP Test
To verify the effect of the proposed method in the real environment, the static IF PPP experiments were carried out using the data collected by four International GNSS Service (IGS) tracking stations (as shown in Figure 2). The observation data and precise products could be accessed from the Crustal Dynamics Data Information System (CDDIS) center. The state parameters contained receiver coordinates, a receiver clock, ZTD, and IF ambiguities. The receiver coordinates were considered to be time invariant, and the other parameters were modeled in line with the description in the simulated PPP. The fixed and hold mode was still adopted for the ambiguity resolution. Moreover, the ambiguity parameters would be reinitialized when a new satellite rose, and a cycle slip occurred. The detailed processing strategies for the experimental PPP are listed in Table 2. The configuration of parameters for integrity risk evaluation is the same as that set for the simulated PPP in Table 1.
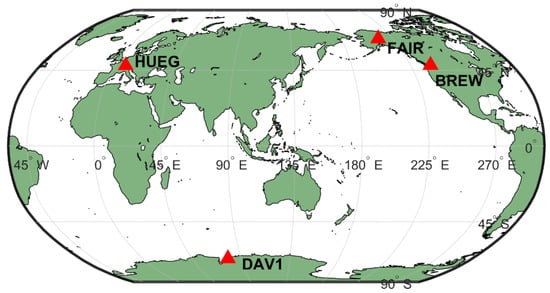
Figure 2.
The distribution of the four IGS stations used for experimental PPP test.

Table 2.
Detailed processing strategies for the experimental static PPP.
4. Results and Discussion
4.1. Simulated Results
This section shows the results of the simulated PPP. Figure 3 shows the PEs, three times of updated standard deviations (STDs) and ALs for the east (E), north (N) and up (U) directions. After a period of convergence (about 15 min), the accuracy of the PEs can reach the centimeter level and the RMSs are 1.0, 0.8 and 2.5 cm for the E, N and U directions, respectively. Figure 4 demonstrates the integrity risk evaluated for the E, N, and U directions. The green solid lines and blue dotted lines show the output integrity risk with and without ambiguity fixed, respectively. It can be seen that if the strategy of ambiguity fixed is not adopted, the integrity risk is almost equal to one all the time, which means that the algorithm will not be available. This is because when the ambiguities are estimated as floating points in the EKF, there are fewer redundant observations. In addition, the algorithm assumes, conservatively, that the updated states before the window are biased, which amplifies the impact of ambiguities on the integrity risk. Therefore, the ambiguities are partially fixed in this study and, subsequently, are no longer estimated in order to reduce the number of states in the EKF and improve the observation redundancy. From Figure 5, it can be seen that as the filtering progresses, the ambiguities begin to be partially fixed, and the number of estimates in the EKF decreases accordingly. After about 17 min, all the ambiguities are fixed, and the integrity risk is drastically reduced correspondingly, as shown by the green solid lines in Figure 4.
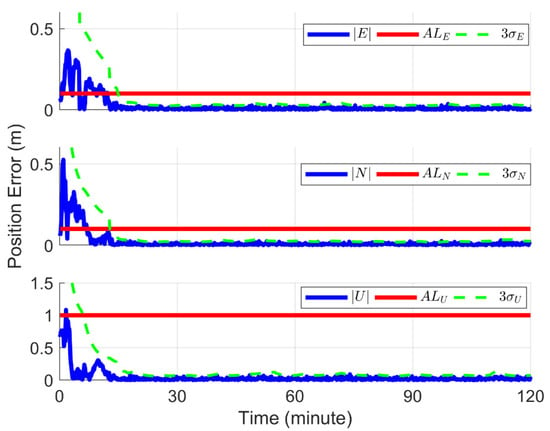
Figure 3.
The PEs, three times of updated STDs and ALs for the east (E, top), north (N, middle) and up (U, bottom) directions of the simulated PPP.
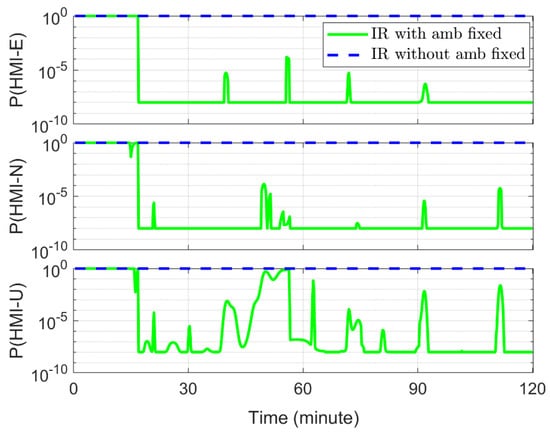
Figure 4.
The output integrity risk (IR) for the east (top), north (middle) and up (bottom) direction. The green solid lines and blue dotted lines show the output integrity risk with and without ambiguity fixed, respectively.
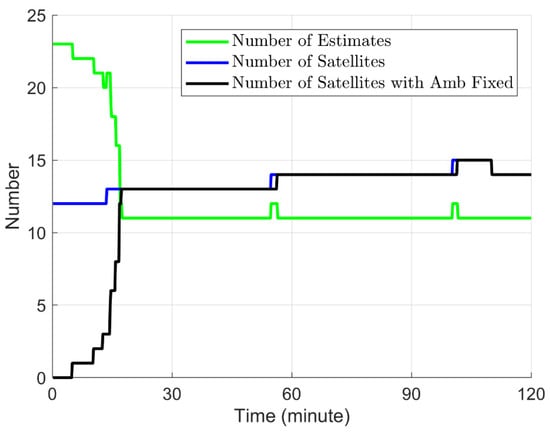
Figure 5.
The change of the number of states estimated in the EKF (green), satellites (blue), and satellites with ambiguity fixed (black).
Figure 6 demonstrates the change of the fault detector and threshold. Since no faults were added into the simulated observations, the chi-square test statistic is always less than the threshold. For the strategy of ambiguity fixed adopted in this study, the fault detector can protect the PE from the contamination of the ambiguity fixed error. Furthermore, even if the ambiguity fixed error escapes detection, the integrity risk caused by the wrong ambiguities can be quantified to ensure the reliability of the positioning.
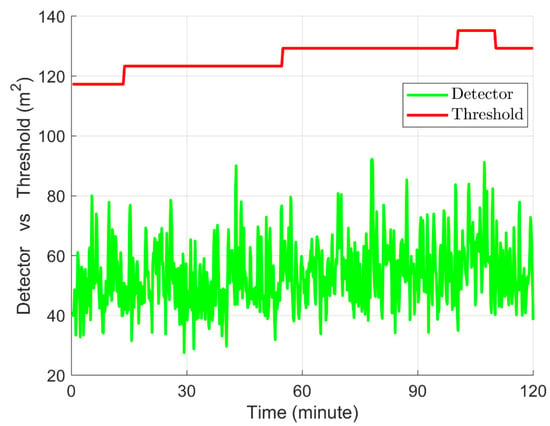
Figure 6.
Time series of the fault detector and threshold.
Figure 7 shows the integrity risk evaluated using the configuration in Table 1 but with windows of different lengths. It can be seen that increasing the length of the window will reduce the integrity risk, since the longer window reduces the impact of the conservative assumption that the undetected faults prior to the window always exist and result in the worst estimate bias at the epoch. However, increasing the length of the window without a limit will result in a computational burden due to the increased number of fault modes. Therefore, the length of the window should be selected appropriately, trading off the computing performance of the hardware and the actual integrity requirements.
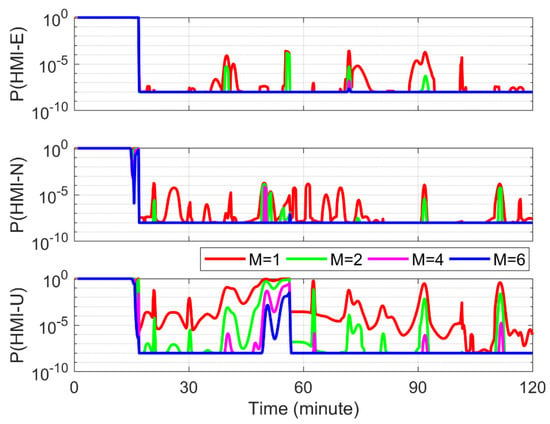
Figure 7.
The integrity risk for the east (top), north (middle) and up (bottom) direction using windows of different lengths.
To quantify the effect of the random model, the configuration in Table 1 is used but with different STDs of the raw observations to evaluate the integrity risk and accuracy of the PE. Figure 8 and Table 3 show the corresponding integrity risk and RMSs of the PE, respectively. It can be seen that reducing the STD of the raw observations can not only improve the accuracy of the positioning result, but also reduce the risk of integrity. Therefore, the establishment of a reliable and refined PPP random model is very important to improve the performance of accuracy and integrity.
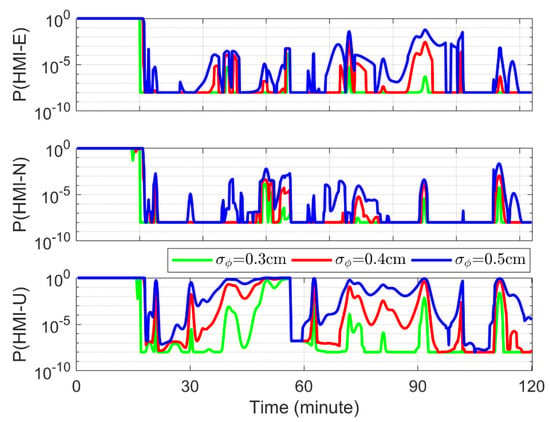
Figure 8.
The integrity risk for the east (E, top), north (N, middle) and up (U, bottom) directions using different STDs of raw observations.

Table 3.
The RMS of the PEs using different STDs of raw observations after convergence (unit: cm).
4.2. Experimental Results
This section shows the results of the experimental PPP. Figure 9 displays the static PPP positioning results of the four IGS stations. It can be seen that after about 15 min of convergence, the positioning accuracy can reach the centimeter level. The RMSs of the E, N and U directions are 3.1, 2.2 and 2.8 cm for the BREW station, 1.6, 2.6 and 2.6 cm for the FAIR station, 2.5, 1.0 and 6.1 cm for the HUEG station, and 0.8, 0.5 and 4.8 cm for the DAV1 station, respectively. Figure 10 shows the time series of the fault detectors and thresholds using the window length of 2, 4 and 6 epochs for the four stations. No obvious observation faults were detected in this experimental stage. Some obvious protrusions on the change curves of the detector are caused by the initialization of the ambiguities of the newly rising satellites.
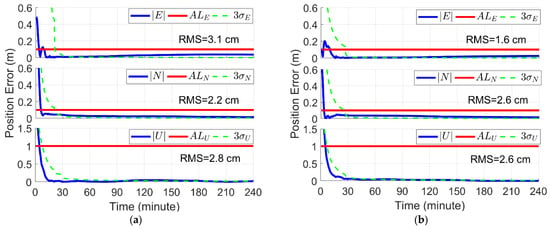
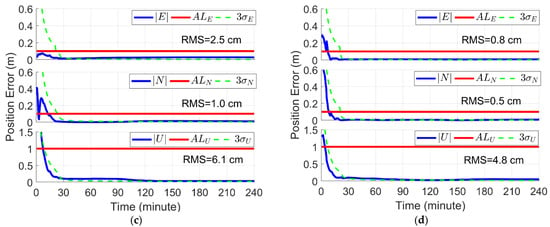
Figure 9.
The three PEs, including the updated STDs and ALs of the: (a) BREW station; (b) FAIR station; (c) HUEG station; and (d) DAV1 station. The top, middle and bottom panels of each figure represent the east (E), north (N) and up (U) directions. The RMSs of the PEs after convergence are noted on the panel, respectively.
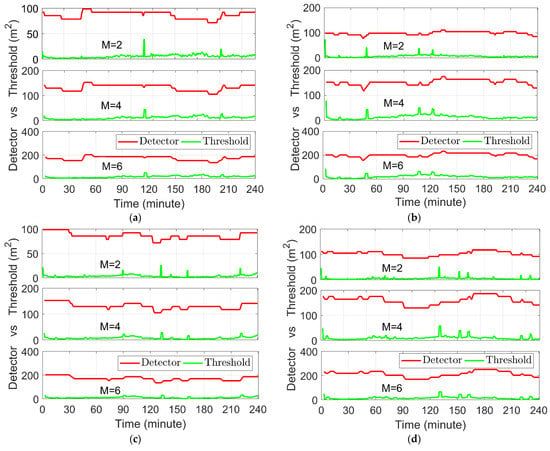
Figure 10.
Time series of the fault detector and threshold of the: (a) BREW station; (b) FAIR station; (c) HUEG station; and (d) DAV1 station. The top, middle and bottom panels of each figure represent the length of time windows of 2, 4 and 6 epochs, respectively.
Figure 11 shows the integrity risk evaluated using the corresponding lengths of the window for the four stations. All the stations complete the initialization (ambiguity resolution) before 30 min and then start the integrity risk evaluation. It can be seen that the integrity risk results of the different stations are inconsistent during the same positioning period. This is mainly because, on the one hand, the different observation geometries are caused by the different positions of the stations; on the other hand, the difference in the ambiguity resolution results in a different observation redundancy, especially the reinitialization of the ambiguities caused by the rise of new stars and cycle slips. Noted by different colors, the integrity risk evaluated using different lengths of window for each station are also shown in Figure 11. It can be seen that increasing the length of the window can reduce the integrity risk, which is consistent with the results of the simulated PPP. However, there are periods when the degree of risk reduction is not obvious, such as from 50 to 70 min in the N direction of the HUEG station and from 90 to 120 min in the U direction of the DAV1 station. This is related to the poor observation geometries during these periods, requiring a longer window to further reduce the risk.
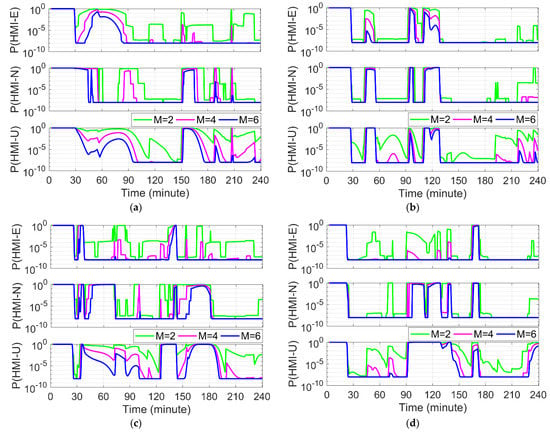
Figure 11.
The integrity risk of the: (a) BREW station; (b) FAIR station; (c) HUEG station; and (d) DAV1 station. The top, middle and bottom panels of each figure represent the east (E), north (N) and up (U) directions. Different colors represent time windows of different lengths, respectively.
5. Conclusions
In this study, the integrity risk of PPP was evaluated quantitatively considering the recursive characteristics of the EKF solution. A time window was employed to maintain the computation load by traversing the fault modes limited within the window. To account for the impact of the faults prior to the window, a non-zero bias was conservatively introduced. Dealing with the multiple instantaneous potential faults, the worst-case integrity risk was quantified to overbound the real risk in multiple fault modes. Moreover, the fixed and hold mode was adopted for an ambiguity resolution to remove the influence of the ambiguities in the integrity risk.
The methodology of the integrity risk evaluation for PPP was derived rigorously. The effect was validated in both the simulated and experimental tests, which show a good consistency. The results suggest that the fixed and hold strategy adopted for the ambiguity resolution is the key to applying this method to PPP, as it can increase the observation redundancy and thereby reduce the integrity risk. Moreover, it can also remove the influence of the biased predicted ambiguities on the integrity risk under the conservative assumption. Increasing the length of the window can further weaken the impact of the bias on the integrity risk because of the smoothing effect of the EKF estimator. However, selecting the length of the window should weigh the computing load and the given integrity requirements. The STD of the raw observations was changed to investigate the influence of the random model on the integrity risk. The result shows that reducing the STD cannot only improve the positioning accuracy, but also decrease the integrity risk. This indicates that establishing a refined PPP random model can improve the PPP positioning and integrity performance, which will be studied in future work.
Author Contributions
Conceptualization, B.X. and H.W. (Haitao Wang); methodology, H.W. (Haitao Wang); software, B.X.; validation, Y.Y. and H.W. (Haitao Wang); formal analysis, B.X.; investigation, B.X. and Y.Y.; resources, H.W. (Han Wang); data curation, H.W. (Han Wang); writing—original draft preparation, B.X.; writing—review and editing, Y.Y. and H.W. (Haitao Wang); visualization, B.X.; supervision, Y.Y.; project administration, Y.Y.; funding acquisition, Y.Y. and H.W. (Haitao Wang). All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (No. 41974008, 41474029 and 42074045), the foundation of the State Key Laboratory of Geodesy and Earth’s Dynamics (No. E025011002) and the National Key Research Program of China “Collaborative Precision Positioning Project” (No. 2016YFB0501900).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
The datasets analyzed in this study can be made available by the corresponding author on request.
Acknowledgments
The authors would like to thank the IGS for providing the observation data and precise products.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
This appendix shows that the bias of the current EKF estimates can be expressed as a function of the current and all the previous observation faults. Given a time window of epochs, the current estimated bias can be expressed by the faults in the window and the bias at the epoch.
First, by substituting Equations (2) and (7) into (8), the EKF estimate at epoch can be expressed as follows:
Then, by subtracting the truth of state from both sides of Equation (A1), the EKF estimate error can be obtained as follows:
Taking the expectation of both sides of Equation (A2), the estimate bias can be expressed as follows:
Therefore, the current estimate bias is not only affected by the current observation faults, but also by the bias of the predicted state. Using Equations (1) and (3), the prediction bias can be expressed further by the estimate bias at the last epoch as follows:
Finally, by substituting Equation (A4) into (A3), can be expressed as follows:
where , and . Noting the recursive feature of Equation (A5), can be further expressed by the current and all the previous faults. Given the time window of epochs, can be expressed as follows:
where and is the combined fault vector, which contains the faults in the window and encapsulates the faults prior to the window into the bias at the epoch.
Appendix B
This appendix shows that the non-centrality parameter of the fault detector’s distribution can also be expressed as a function of the combined fault vector shown in Appendix A.
Based on Equations (2), (3) and (5), the innovation vector at the epoch, , can be shown as follows:
The expectation of can be expressed as follows:
Thus, is also affected by the current observation faults and the bias of the predicted state. Given Equation (A4), can be further expressed as follows:
Similarly, can be also expressed by the combined fault vector as follows:
where . For 1 ≤ i ≤ , can be expressed as . Thus, the expectation of the innovation sequences in the window, , can be shown as follows:
where and means forming an upper triangular matrix. By substituting Equation (A11) into (15), the non-centrality parameter can be expressed by the combined fault vector as follows:
where .
References
- Kouba, J.; Héroux, P. Precise Point Positioning Using IGS Orbit and Clock Products. GPS Solut. 2001, 5, 12–28. [Google Scholar] [CrossRef]
- An, X.; Meng, X.; Jiang, W. Multi-constellation GNSS precise point positioning with multi-frequency raw observations and dual-frequency observations of ionospheric-free linear combination. Satell. Navig. 2020, 1, 7. [Google Scholar] [CrossRef]
- Jin, S.; Su, K. PPP models and performances from single- to quad-frequency BDS observations. Satell. Navig. 2020, 1, 16. [Google Scholar] [CrossRef]
- Choy, S.; Bisnath, S.; Rizos, C. Uncovering common misconceptions in GNSS Precise Point Positioning and its future prospect. GPS Solut. 2017, 21, 13–22. [Google Scholar] [CrossRef]
- Ge, M.; Gendt, G.; Rothacher, M.; Shi, C.; Liu, J. Resolution of GPS carrier-phase ambiguities in Precise Point Positioning (PPP) with daily observations. J. Geod. 2008, 82, 389–399. [Google Scholar] [CrossRef]
- Liu, S.; Yuan, Y. A Method to Accelerate the Convergence of Satellite Clock Offset Estimation Considering the Time-Varying Code Biases. Remote Sens. 2021, 13, 2714. [Google Scholar] [CrossRef]
- Liu, T.; Yuan, Y.; Zhang, B.; Wang, N.; Tan, B.; Chen, Y. Multi-GNSS precise point positioning (MGPPP) using raw observations. J. Geod. 2017, 91, 253–268. [Google Scholar] [CrossRef]
- Geng, J.; Guo, J.; Meng, X.; Gao, K. Speeding up PPP ambiguity resolution using triple-frequency GPS/BeiDou/Galileo/QZSS data. J. Geod. 2020, 94, 6. [Google Scholar] [CrossRef]
- Chen, Y.; Gao, W.; Chen, X.; Liu, T.; Liu, C.; Su, C.; Lu, J.; Wang, W.; Mu, S. Advances of SBAS authentication technologies. Satell. Navig. 2021, 2, 12. [Google Scholar] [CrossRef]
- Heßelbarth, A.; Wanninger, L. SBAS orbit and satellite clock corrections for precise point positioning. GPS Solut. 2013, 17, 465–473. [Google Scholar] [CrossRef]
- Zhang, B.; Chen, Y.; Yuan, Y. PPP-RTK based on undifferenced and uncombined observations: Theoretical and practical aspects. J. Geod. 2019, 93, 1011–1024. [Google Scholar] [CrossRef]
- Geng, J.; Teferle, F.N.; Meng, X.; Dodson, A.H. Towards PPP-RTK: Ambiguity resolution in real-time precise point positioning. Adv. Space Res. 2011, 47, 1664–1673. [Google Scholar] [CrossRef]
- Li, X.; Li, X.; Huang, J.; Shen, Z.; Wang, B.; Yuan, Y.; Zhang, K. Improving PPP–RTK in urban environment by tightly coupled integration of GNSS and INS. J. Geod. 2021, 95, 132. [Google Scholar] [CrossRef]
- Khodabandeh, A. Single-station PPP-RTK: Correction latency and ambiguity resolution performance. J. Geod. 2021, 95, 42. [Google Scholar] [CrossRef]
- De Groot, L.; Infante, E.; Jokinen, A.; Kruger, B.; Norman, L. Precise Positioning for Automotive with Mass Market GNSS Chipsets. In Proceedings of the 31st International Technical Meeting of the Satellite Division of the Institute of Navigation, Miami, FL, USA, 24–28 September 2018; pp. 596–610. [Google Scholar]
- Murrian, M.; Gonzalez, C.W.; Humphreys, T.E.; Pesyna, K.M.; Shepard, D.P.; Kerns, A.J. Low-cost precise positioning for automated vehicles. GPS World 2016, 27, 32–39. [Google Scholar]
- Alkan, R.M.; Saka, M.H.; Ozulu, İ.M.; İlçi, V. Kinematic precise point positioning using GPS and GLONASS measurements in marine environments. Measurement 2017, 109, 36–43. [Google Scholar] [CrossRef]
- Yang, Y.; Mao, Y.; Sun, B. Basic performance and future developments of BeiDou global navigation satellite system. Satell. Navig. 2020, 1, 1–8. [Google Scholar] [CrossRef]
- Zhu, N.; Marais, J.; Betaille, D.; Berbineau, M. GNSS Position Integrity in Urban Environments: A Review of Literature. IEEE Trans. Intell. Transp. Syst. 2018, 19, 2762–2778. [Google Scholar] [CrossRef]
- Norman, L.; Infante, E.; De Groot, L. Integrity performance for precise positioning in automotive. In Proceedings of the 32nd International Technical Meeting of the Satellite Division of the Institute of Navigation, Miami, FL, USA, 16–20 September 2019; pp. 1653–1663. [Google Scholar]
- Du, Y.; Wang, J.; Rizos, C.; El-Mowafy, A. Vulnerabilities and integrity of precise point positioning for intelligent transport systems: Overview and analysis. Satell. Navig. 2021, 2, 3. [Google Scholar] [CrossRef]
- El-Mowafy, A. On detection of observation faults in the observation and position domains for positioning of intelligent transport systems. J. Geod. 2019, 93, 2109–2122. [Google Scholar] [CrossRef]
- Li, B.; Qin, Y.; Liu, T. Geometry-based cycle slip and data gap repair for multi-GNSS and multi-frequency observations. J. Geod. 2019, 93, 399–417. [Google Scholar] [CrossRef]
- Ochieng, W.Y.; Sauer, K.; Walsh, D.; Brodin, G.; Griffin, S.; Denney, M. GPS Integrity and Potential Impact on Aviation Safety. J. Navig. 2003, 56, 51–65. [Google Scholar] [CrossRef]
- Pullen, S.; Joerger, M. GNSS Integrity and Receiver Autonomous Integrity Monitoring (RAIM). In Position, Navigation, and Timing Technologies in the 21st Century; Wiley: Piscataway, NJ, USA, 2020; pp. 591–617. [Google Scholar]
- Zabalegui, P.; De Miguel, G.; Perez, A.; Mendizabal, J.; Goya, J.; Adin, I. A Review of the Evolution of the Integrity Methods Applied in GNSS. IEEE Access 2020, 8, 45813–45824. [Google Scholar] [CrossRef]
- Parkinson, B.; Axelrad, P. Autonomous GPS Integrity Monitoring Using the Pseudorange Residual. Navigation 1988, 35, 255–274. [Google Scholar] [CrossRef]
- Walter, T.; Enge, P. Weighted RAIM for Precision Approach. In Proceedings of the 8th International Technical Meeting of the Satellite Division of the Institute of Navigation, Palm Springs, CA, USA, 12–15 September 1996; pp. 1995–2004. [Google Scholar]
- Blanch, J.; Walker, T.; Enge, P.; Lee, Y.; Pervan, B.; Rippl, M.; Spletter, A.; Kropp, V. Baseline advanced RAIM user algorithm and possible improvements. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 713–732. [Google Scholar] [CrossRef]
- Blanch, J.; Walter, T.; Enge, P.; Lee, Y.; Pervan, B.; Rippl, M.; Spletter, A. Advaced RAIM User Algorithm Description: Integrity Support Message Processing, Fault Detection, Exclusion, and Protection Level Calculation. In Proceedings of the 25th International Technical Meeting of the Satellite Division of the Institute of Navigation, Nashville, TN, USA, 17–21 September 2012; pp. 2828–2849. [Google Scholar]
- Joerger, M.; Pervan, B. Kalman Filter Residual-Based Integrity Monitoring against Measurement Faults. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Minneapolis, MN, USA, 13–16 August 2012. [Google Scholar]
- Joerger, M.; Pervan, B. Integrity risk of Kalman filter-based RAIM. In Proceedings of the 24th International Technical Meeting of the Satellite Division of the Institute of Navigation, Portland, OR, USA, 19–23 September 2011; pp. 3856–3867. [Google Scholar]
- Tanil, C. Detecting GNSS Spoofing Attacks Using INS Coupling. Ph.D. Thesis, Illinois Institute of Technology, Chicago, IL, USA, December 2016. [Google Scholar]
- Tanil, C.; Khanafseh, S.; Joerger, M.; Pervan, B. Sequential Integrity Monitoring for Kalman Filter Innovations-based Detectors. In Proceedings of the 31st International Technical Meeting of the Satellite Division of the Institute of Navigation, Miami, FL, USA, 24–28 September 2018; pp. 2440–2455. [Google Scholar]
- Arana, G.D.; Hafez, O.A.; Joerger, M.; Spenko, M. Recursive Integrity Monitoring for Mobile Robot Localization Safety. In Proceedings of the 2019 International Conference on Robotics and Automation, Montreal, QC, Canada, 20–24 May 2019; pp. 305–311. [Google Scholar]
- Feng, S.; Jokinen, A.; Ochieng, W. Integrity Monitoring for Precise Point Positioning. In Proceedings of the the 27th International Technical Meeting of The Satellite Division of the Institute of Navigation, Tampa, FL, USA, 8–12 September 2014; pp. 986–1007. [Google Scholar]
- Jokinen, A.; Feng, S.; Schuster, W.; Ochieng, W.; Hide, C.; Moore, T.; Hill, C. Integrity monitoring of fixed ambiguity Precise Point Positioning (PPP) solutions. Geo-Spat. Inf. Sci. 2013, 16, 141–148. [Google Scholar] [CrossRef][Green Version]
- Gunning, K.; Blanch, J.; Walter, T.; Groot, L.; Norman, L. Design and evaluation of integrity algorithms for PPP in kinematic applications. In Proceedings of the 31st International Technical Meeting of the Satellite Division of the Institute of Navigation, Miami, FL, USA, 24–28 September 2018; pp. 1910–1939. [Google Scholar]
- Blanch, J.; Gunning, K.; Walter, T.; Groot, L.; Norman, L. Reducing computational load in solution separation for Kalman flters and an application to PPP integrity. In Proceedings of the 32nd International Technical Meeting of the Satellite Division of the Institute of Navigation, Miami, FL, USA, 16–20 September 2019; pp. 720–729. [Google Scholar]
- Blanch, J.; Walter, T.; Norman, L.; Gunning, K.; de Groot, L. Solution Separation-Based FD to Mitigate the Effects of Local Threats on PPP Integrity. In Proceedings of the 2020 IEEE/ION Position, Location and Navigation Symposium, Portland, OR, USA, 20–23 April 2020; pp. 1085–1092. [Google Scholar]
- Madrid, P.F.N.; Fernandez, L.M.; Lopez, M.A.; Samper, M.D.L.; Merino, M.M.R.; Madrid, P.F.N.; Fernndez, L.M.; Lpez, M.A.; Samper, L.; Merino, M.M.R. PPP Integrity for Advanced Applications, Including Field Trials with Galileo, Geodetic and Low-Cost Receivers, and a Preliminary Safety Analysis. In Proceedings of the 29th International Technical Meeting of the Satellite Division of the Institute of Navigation, Portland, OR, USA, 12–16 September 2016; pp. 3332–3354. [Google Scholar]
- Angus, J.E. RAIM with Multiple Faults. Navigation 2006, 53, 249–257. [Google Scholar] [CrossRef]
- Saastamoinen, J. Contributions to the theory of atmospheric refraction. Bulletin Géodésique 1972, 105, 279–298. [Google Scholar] [CrossRef]
- Niell, A.E. Global mapping functions for the atmosphere delay at radio wavelengths. J. Geophys. Res. Solid Earth 1996, 101, 3227–3246. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).