Attitude Determination for GRACE-FO: Reprocessing the Level-1A SC and IMU Data
Abstract
:1. Introduction
2. Data
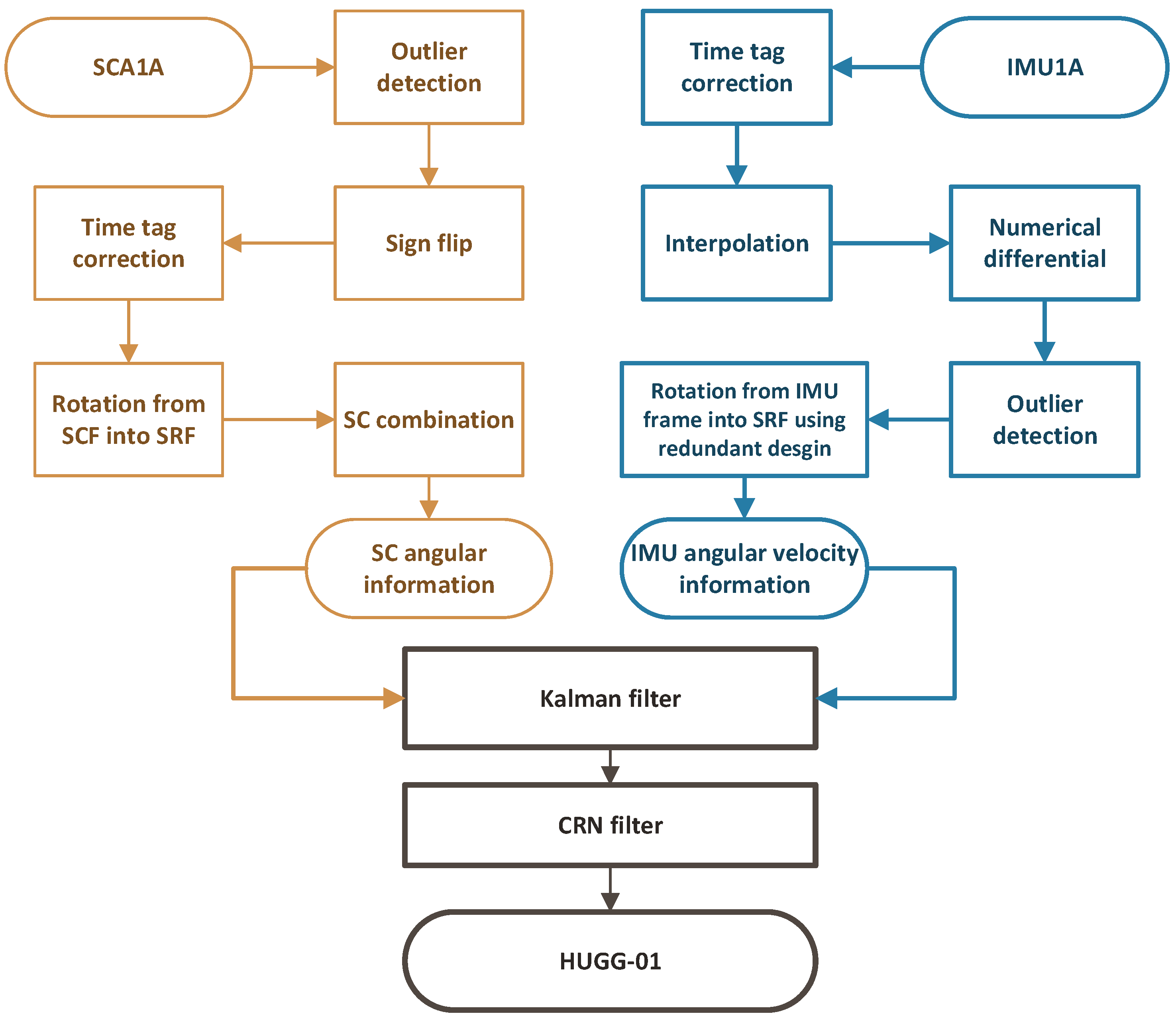
3. Method
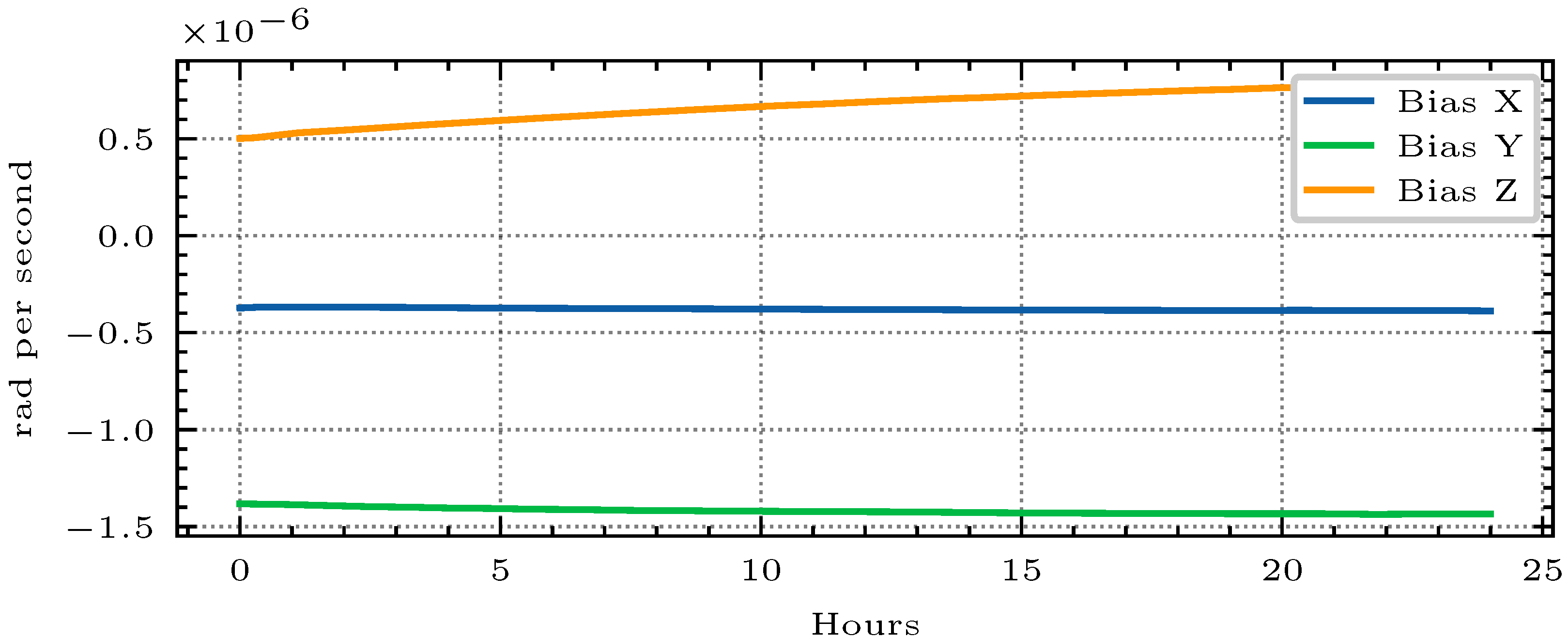
3.1. IMU Processing
3.2. SC Processing
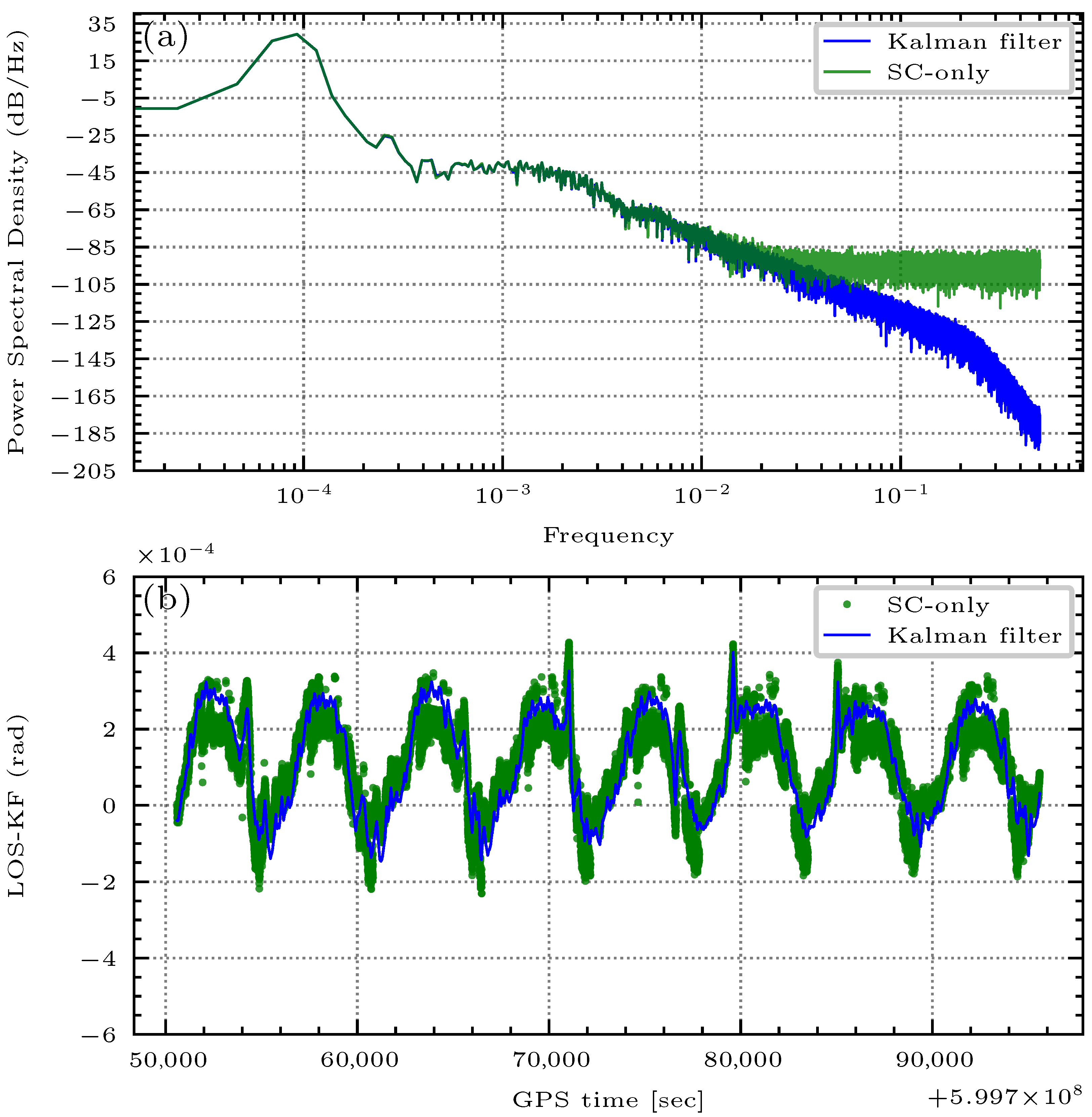
3.3. Kalman Filter
3.4. Metrics
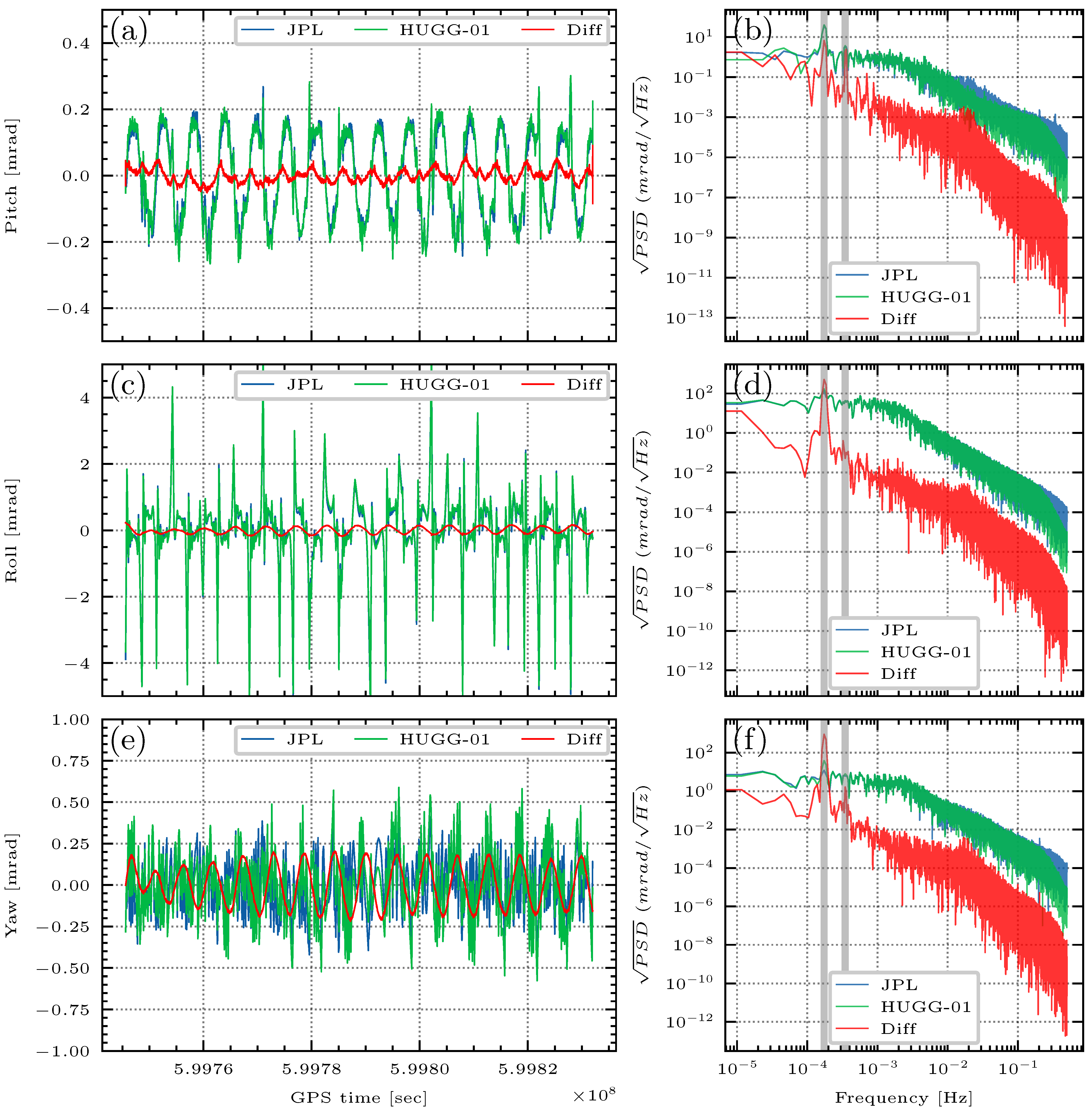
3.4.1. Inter-Satellite Pointing Variation
3.4.2. Inter-Satellite Range Rate Residual
4. Analysis
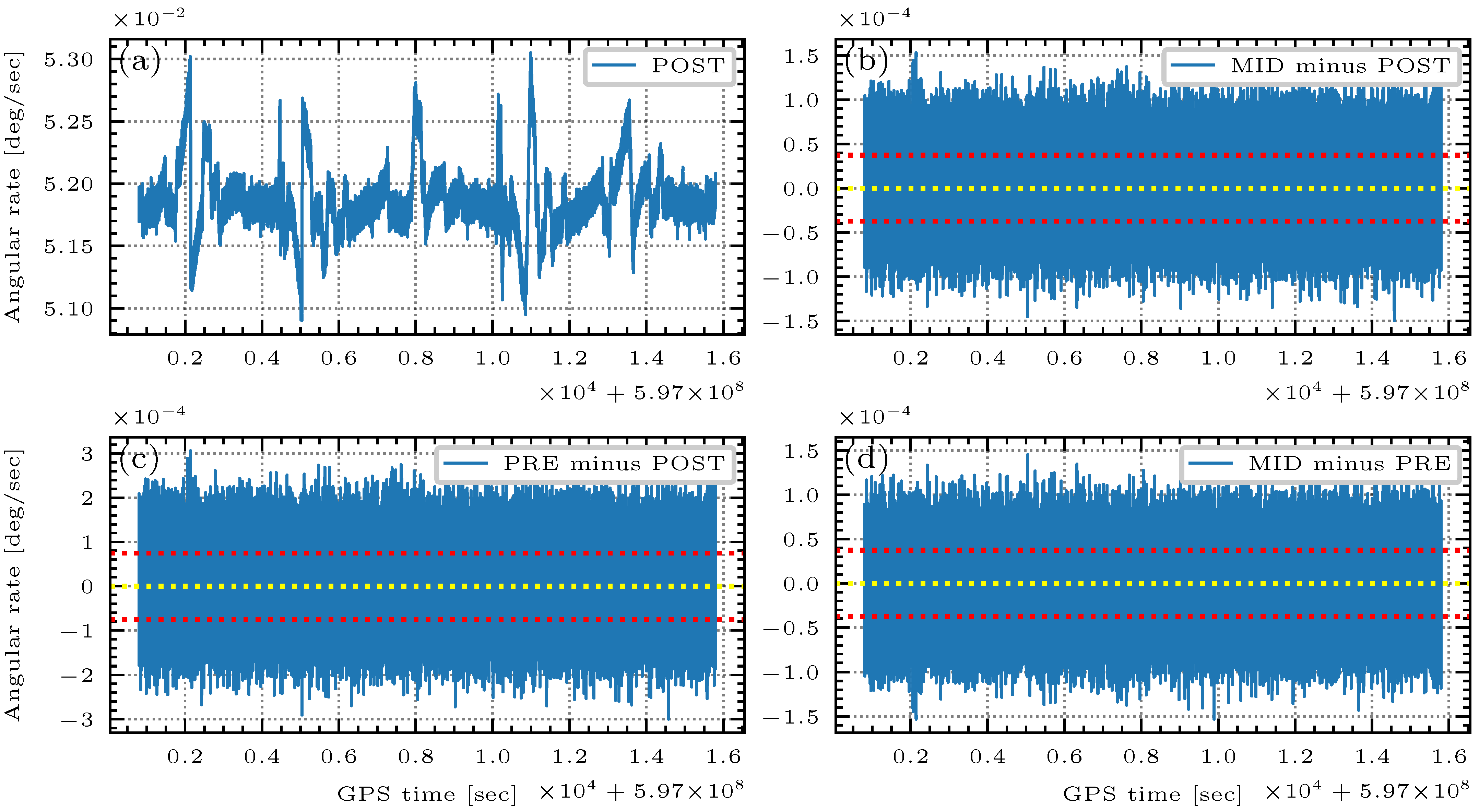
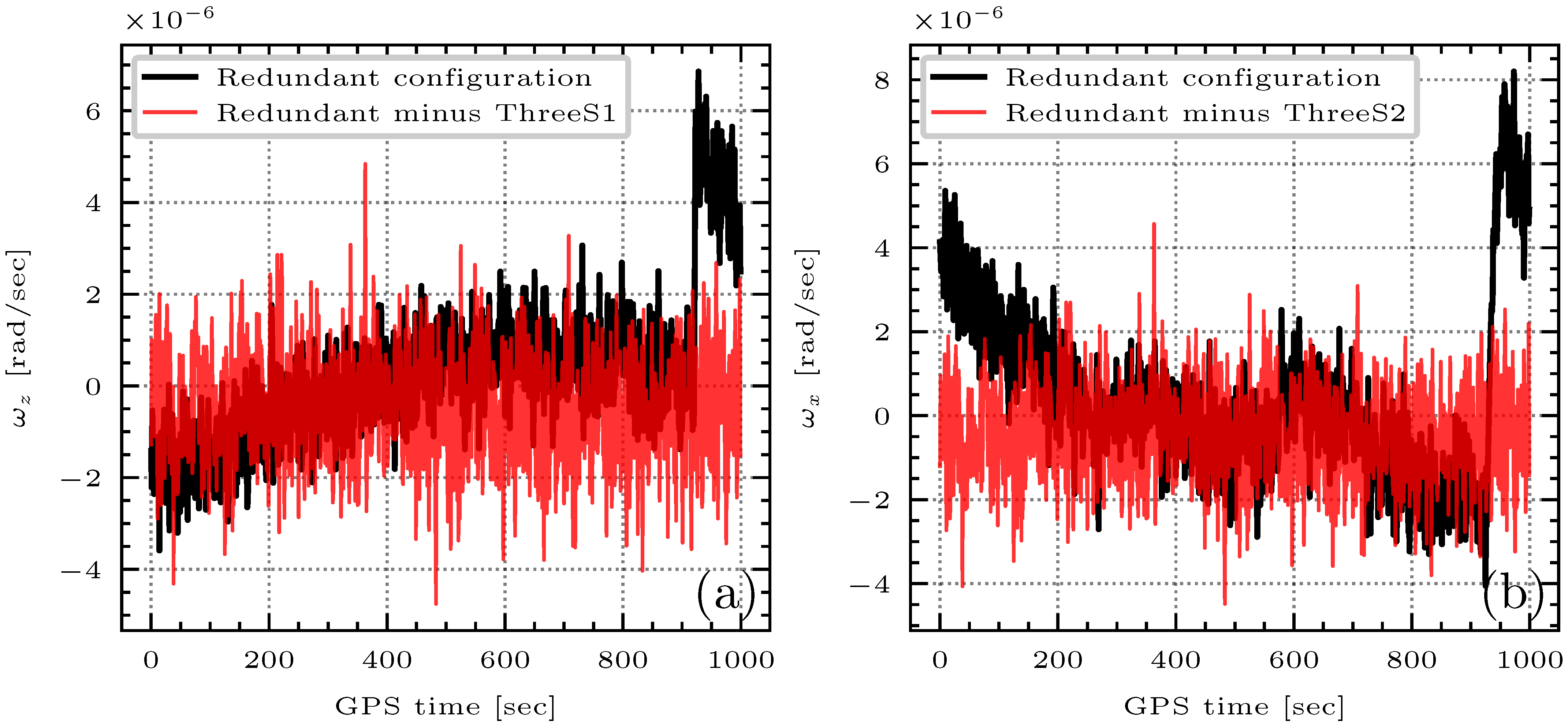
4.1. IMU Processing
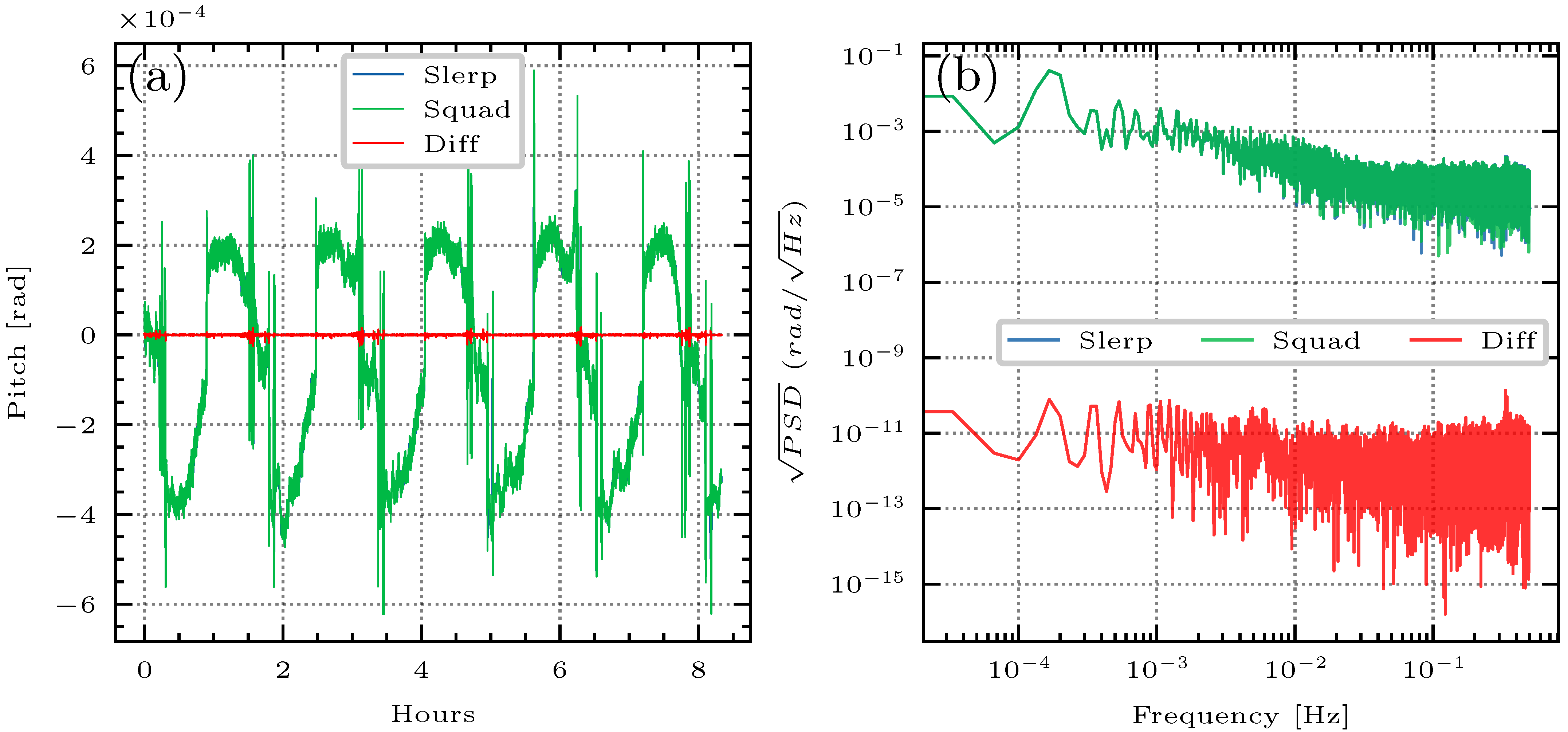
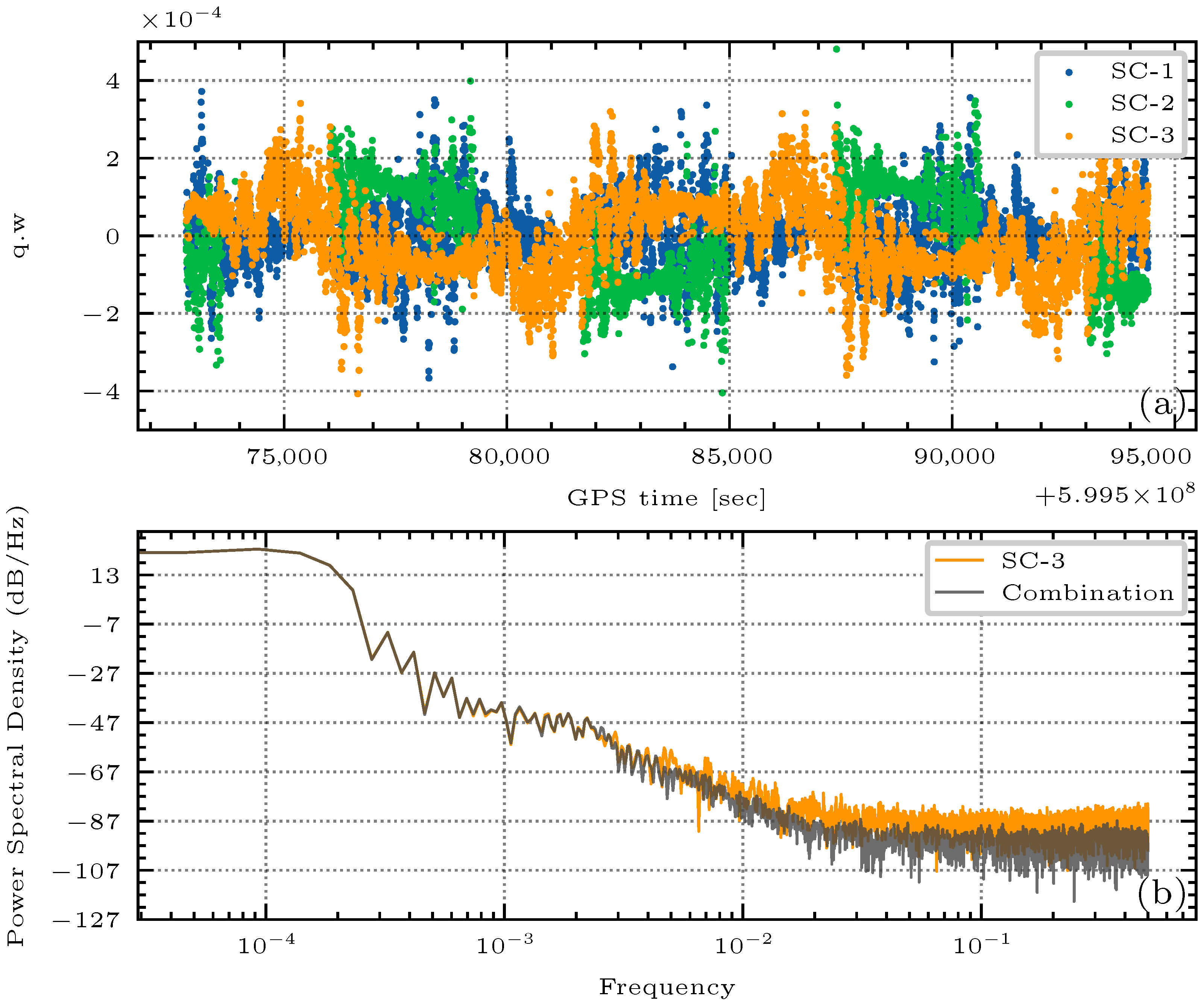
4.2. SC Processing
4.3. Kalman Filter
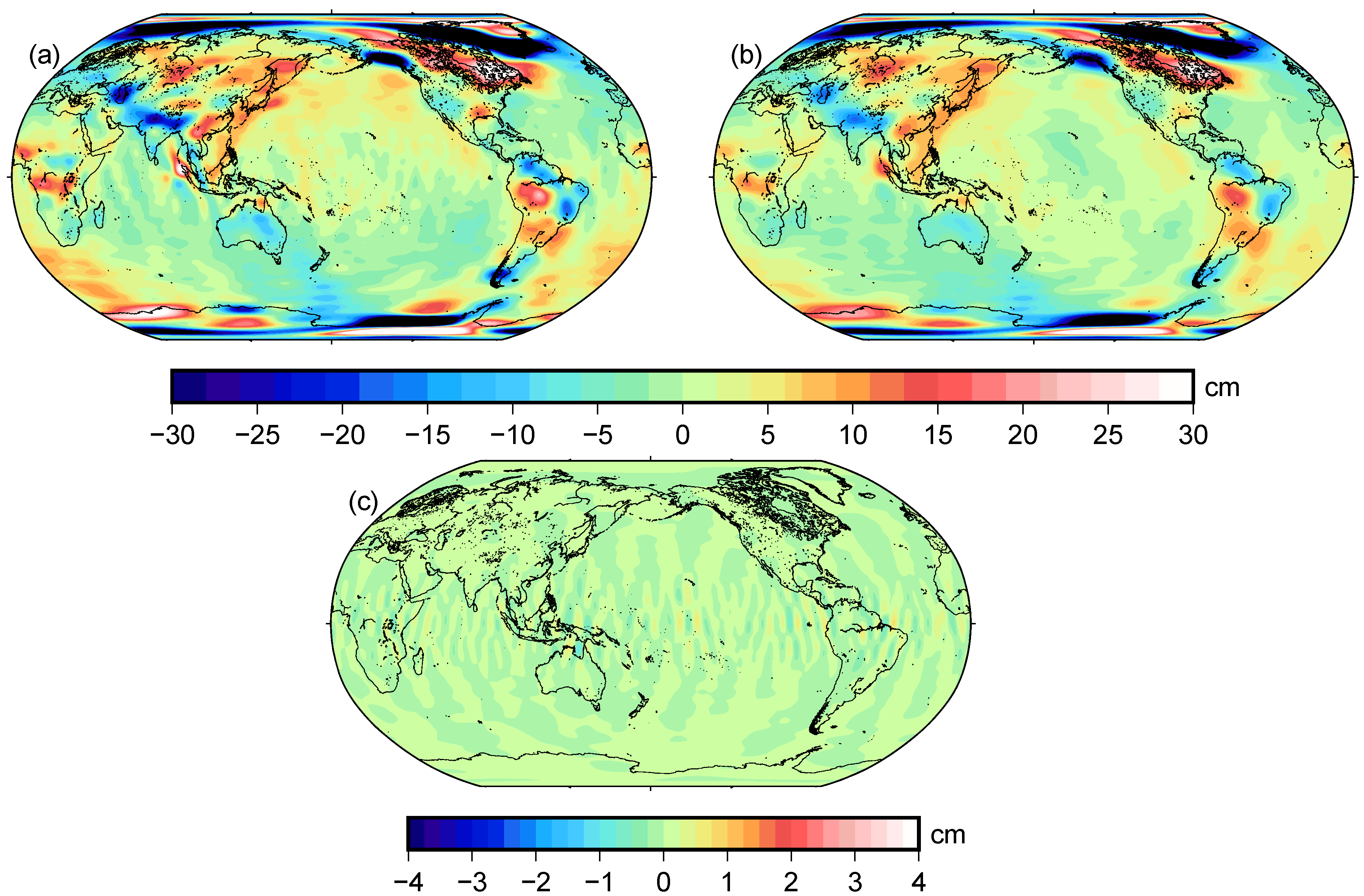
5. Assessments
5.1. Inter-Satellite Pointing Analysis
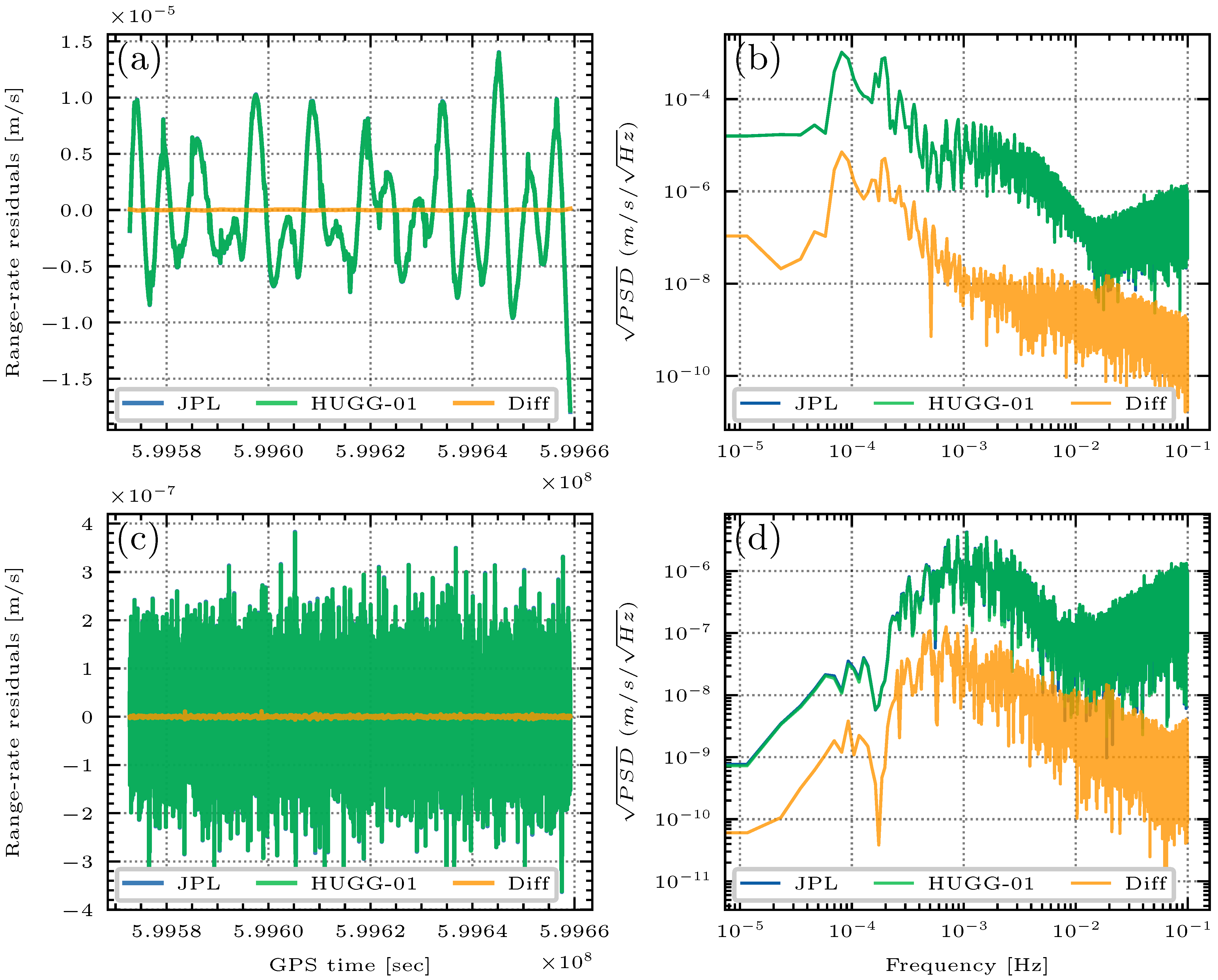
5.2. K-Band Range-Rate Residual Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tapley, B.D.; Bettadpur, S.; Watkins, M.; Reigber, C. The gravity recovery and climate experiment: Mission overview and early results. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef] [Green Version]
- Kornfeld, R.P.; Arnold, B.W.; Gross, M.A.; Dahya, N.T.; Klipstein, W.M.; Gath, P.F.; Bettadpur, S. GRACE-FO: The Gravity Recovery and Climate Experiment Follow-On Mission. J. Spacecr. Rocket. 2019, 56, 931–951. [Google Scholar] [CrossRef]
- Kusche, J.; Klemann, V.; Bosch, W. Mass distribution and mass transport in the Earth system. J. Geodyn. 2012, 59, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Tapley, B.; Watkins, M.; Flechtner, F.; Reigber, C.; Bettadpur, S.; Rodell, M.; Sasgen, I.; Famiglietti, J.S.; Landerer, F.W.; Chambers, D.P.; et al. Contributions of GRACE to understanding climate change. Nat. Clim. Chang. 2019, 9, 358–369. [Google Scholar] [CrossRef]
- Dahle, C.; Murböck, M.; Flechtner, F.; Dobslaw, H.; Michalak, G.; Neumayer, K.; Abrykosov, O.; Reinhold, A.; König, R.; Sulzbach, R.; et al. The GFZ GRACE RL06 Monthly Gravity Field Time Series: Processing Details and Quality Assessment. Remote Sens. 2019, 11, 2116. [Google Scholar] [CrossRef] [Green Version]
- Ramillien, G.; Biancale, R.; Gratton, S.; Vasseur, X.; Bourgogne, S. GRACE-derived surface water mass anomalies by energy integral approach: Application to continental hydrology. J. Geod. 2011, 85, 313–328. [Google Scholar] [CrossRef]
- Famiglietti, J.S.; Rodell, M. Water in the balance. Science 2013, 340, 1300–1301. [Google Scholar] [CrossRef] [PubMed]
- Rodell, M.; Famiglietti, J.S.; Wiese, D.N.; Reager, J.T.; Beaudoing, H.K.; Landerer, F.W.; Lo, M.H. Emerging trends in global freshwater availability. Nature 2018, 557, 651–659. [Google Scholar] [CrossRef]
- Sasgen, I.; Konrad, H.; Ivins, E.; Van den Broeke, M.; Bamber, J.; Martinec, Z.; Klemann, V. Antarctic ice-mass balance 2003 to 2012: Regional reanalysis of GRACE satellite gravimetry measurements with improved estimate of glacial-isostatic adjustment based on GPS uplift rates. Cryosphere 2013, 7, 1499–1512. [Google Scholar] [CrossRef] [Green Version]
- Velicogna, I.; Mohajerani, Y.; Landerer, F.; Mouginot, J.; Noel, B.; Rignot, E.; Sutterley, T.; van den Broeke, M.; van Wessem, M.; Wiese, D. Continuity of Ice Sheet Mass Loss in Greenland and Antarctica From the GRACE and GRACE Follow-On Missions. Geophys. Res. Lett. 2020, 47, e2020GL087291. [Google Scholar] [CrossRef] [Green Version]
- Panet, I.; Sylvain, B.; Narteau, C.; Rémy, D.; Lemoine, J.M. Migrating pattern of deformation prior to the Tohoku-Oki earthquake revealed by GRACE data. Nat. Geosci. 2018, 11, 367–373. [Google Scholar] [CrossRef]
- Cambiotti, G.; Douch, K.; Cesare, S.; Haagmans, R.; Sneeuw, N.; Anselmi, A.; Anna Maria, M.; Sabadini, R. On Earthquake Detectability by the Next-Generation Gravity Mission. Surv. Geophys. 2020, 41, 1049–1074. [Google Scholar] [CrossRef]
- Kim, J. Simulation Study of a Low-Low Satellite-to-Satellite Tracking Mission. Ph.D. Thesis, The University of Texas at Austin, Austin, TX, USA, 2000. [Google Scholar]
- Goswami, S.; Francis, S.P.; Bandikova, T.; Spero, R.E. Analysis of GRACE Follow-On Laser Ranging Interferometer derived inter-satellite pointing angles. IEEE Sens. J. 2021, 21, 19209–19221. [Google Scholar] [CrossRef]
- Flechtner, F.; Neumayer, K.H.; Dahle, C.; Dobslaw, H.; Fagiolini, E.; Raimondo, J.C.; Güntner, A. What Can be Expected from the GRACE-FO Laser Ranging Interferometer for Earth Science Applications? Surv. Geophys. 2016, 37, 453–470. [Google Scholar] [CrossRef] [Green Version]
- Dobslaw, H.; Bergmann-Wolf, I.; Dill, R.; Poropat, L.; Thomas, M.; Dahle, C.; Esselborn, S.; König, R.; Flechtner, F. A new high-resolution model of non-tidal atmosphere and ocean mass variability for de-aliasing of satellite gravity observations: AOD1B RL06. Geophys. J. Int. 2017, 211, 263–269. [Google Scholar] [CrossRef] [Green Version]
- Behzadpour, S.; Mayer-Gürr, T.; Flury, J.; Klinger, B.; Goswami, S. Multiresolution wavelet analysis applied to GRACE range-rate residuals. Geosci. Instrum. Methods Data Syst. 2019, 8, 197–207. [Google Scholar] [CrossRef] [Green Version]
- Yang, F.; Forootan, E.; Wang, C.; Kusche, J.; Luo, Z. A New 1-Hourly ERA5-Based Atmosphere De-Aliasing Product for GRACE, GRACE-FO, and Future Gravity Missions. J. Geophys. Res. Solid Earth 2021, 126, e2021JB021926. [Google Scholar] [CrossRef]
- Frommknecht, B. Integrated Sensor Analysis of the GRACE Mission. Ph.D. Thesis, Leibniz University Hannover, Hanover, Germany, 2007. [Google Scholar]
- Bandikova, T.; Flury, J. Improvement of the GRACE star camera data based on the revision of the combination method. Adv. Space Res. 2014, 54, 1818–1827. [Google Scholar] [CrossRef]
- Gruber, T.; Team, N.D. e2. Motion: Earth System Mass Transport Mission (Square)—Concept for a Next Generation Gravity Field Mission—Final Report of Project Satellite Gravimetry of the Next Generation (NGGM-D). Deutsche Geodätische Kommission der Bayerischen Akademie der Wissenschaften, Reihe B Angewandte Geodäsie Heft Nr. 318, München; Technical Report; Deutsche Geodätische Kommission der Bayerischen Akademie der Wissenschaften: Munich, Germany, 2014; ISBN 978-3-7696-8597-8. [Google Scholar]
- Pail, R.; Chen, Q.; Engels, J.; Hauk, M.; Liu, W.; Purkhauser, A.; Saemian, P.; Sneeuw, N.; Tourian, M.; Visser, P.; et al. Additional Constellation and Scientific Analysis of the Next Generation Gravity Mission Concept (ADDCON); Technical Report; Issue 3.1, ESA Contract No. 4000118480/16/NL/FF/gp; Technical University of Munich: Munich, Germany, 2018. [Google Scholar]
- Zhou, H.; Luo, Z.; Zhou, Z.; Yang, F.; Yang, S. What Can We Expect from the Inclined Satellite Formation for Temporal Gravity Field Determination? Surv. Geophys. 2021, 42, 699–726. [Google Scholar] [CrossRef]
- Wiese, D.N.; Visser, P.; Nerem, R.S. Estimating low resolution gravity fields at short time intervals to reduce temporal aliasing errors. Adv. Space Res. 2011, 48, 1094–1107. [Google Scholar] [CrossRef]
- Purkhauser, A.; Pail, R. Next generation gravity missions: Near-real time gravity field retrieval strategy. Geophys. J. Int. 2019, 217, 1314–1333. [Google Scholar] [CrossRef]
- Abich, K.; Abramovici, A.; Amparan, B.; Baatzsch, A.; Okihiro, B.; Barr, D.; Bize, M.; Bogan, C.; Braxmaier, C.; Burke, M.; et al. In-Orbit Performance of the GRACE Follow-on Laser Ranging Interferometer. Phys. Rev. Lett. 2019, 123, 031101. [Google Scholar] [CrossRef] [Green Version]
- Save, H. Status of CSR RL06 GRACE reprocessing and preliminary results. In Proceedings of the Agu Fall Meeting, New Orleans, LA, USA, 1–15 December 2017. [Google Scholar]
- Kruizinga, G.L.; Bertiger, W.I.; Case, K.E.; Finch, C.J.; Wu, S.C. GRACE Level-1 Processing Status. In Proceedings of the AGU Fall Meeting Abstracts, San Francisco, CA, USA, 8–12 December 2003. [Google Scholar]
- Wu, S.C.; Kruizinga, G.; Bertiger, W. Algorithm Theoretical Basis Document for GRACE Level-1B Data Processing V1.2. GRACE Technical Report; Jet Propulsion Laboratory, California Institute of Technology: Pasadena, CA, USA, 2006. [Google Scholar]
- Horwath, M.; Lemoine, J.M.; Biancale, R.; Bourgogne, S. Improved GRACE Science Results After Adjustment Of Geometric Biases In The Level-1b K-Band Ranging Data. J. Geod. 2011, 85, 23–38. [Google Scholar] [CrossRef]
- Bandikova, T.; Flury, J.; Ko, U.D. Characteristics and accuracies of the GRACE inter-satellite pointing. Adv. Space Res. 2012, 50, 123–135. [Google Scholar] [CrossRef]
- Inácio, P.; Ditmar, P.; Klees, R.; Farahani, H.H. Analysis of star camera errors in GRACE data and their impact on monthly gravity field models. J. Geod. 2015, 89, 551–571. [Google Scholar] [CrossRef] [Green Version]
- Harvey, N. GRACE star camera noise. Adv. Space Res. 2016, 58, 408–414. [Google Scholar] [CrossRef]
- Chen, Q.; Shen, Y.; Chen, W.; Zhang, X.; Hsu, H. An improved GRACE monthly gravity field solution by modeling the non-conservative acceleration and attitude observation errors. J. Geod. 2016, 90, 503–523. [Google Scholar] [CrossRef]
- Romans, L. Optimal Combination of Quaternions from Multiple Star Cameras; JPL Internal Memorandum; NASA Jet Propulsion Laboratory: Pasadena, CA, USA, 2003.
- Harvey, N.; Sakumura, C. Results from a GRACE/GRACE-FO attitude reconstruction Kalman filter. J. Geod. 2019, 93, 1881–1896. [Google Scholar] [CrossRef]
- Klinger, B.; Mayer-Gürr, T. Combination of GRACE star camera and angular acceleration data. In Proceedings of the EGU General Assembly, Vienna, Austria, 27 April–2 May 2014. [Google Scholar]
- Goswami, S.; Klinger, B.; Weigelt, M.; Mayer-Gürr, T. Analysis of attitude errors in GRACE range-rate residuals—A comparison between SCA1B and the reprocessed attitude fused product (SCA1B +ACC1B). IEEE Sens. Lett. 2018, 2, 1–4. [Google Scholar] [CrossRef]
- Wen, H.Y.; Kruizinga, G.; Paik, M.; Landerer, F.; Bertiger, W.; Sakumura, C.; Bandikova, T.; Mccullough, C. Gravity Recovery and Climate Experiment Follow-On (GRACE-FO) Level-1 Data Product User Handbook; Technical Report, GRACE Technical Report, JPL D-56935 (URS270772); USA, 2019. Available online: https://podaac-tools.jpl.nasa.gov/drive/files/allData/gracefo/docs/GRACE-FO_L1_Handbook.pdf (accessed on 9 November 2021).
- Patel, C.R. Analyzing and Monitoring GRACE-FO Star Camera Performance in a Changing Environment. Master’s Thesis, The University of Texas at Austin, Austin, TX, USA, 2020. [Google Scholar]
- Yang, F.; Kusche, J.; Forootan, E.; Rietbroek, R. Passive-ocean radial basis function approach to improve temporal gravity recovery from GRACE observations. J. Geophys. Res. Solid Earth 2017, 122, 6875–6892. [Google Scholar] [CrossRef] [Green Version]
- Yang, F.; Forootan, E.; Schumacher, M.; Shum, C.; Zhong, M. Evaluating non-tidal atmospheric products by measuring GRACE K-band range rate residuals. Geophys. J. Int. 2018, 215, 1132–1147. [Google Scholar] [CrossRef]
- Jafari, M. Optimal redundant sensor configuration for accuracy increasing in space inertial navigation system. Aerosp. Sci. Technol. 2015, 47, 467–472. [Google Scholar] [CrossRef] [Green Version]
- Trawny, N.; Roumeliotis, S. Indirect Kalman Filter for 3D Attitude Estimation. A Tutorial for Quaternion Algebra; Technical Report Number 2005-002, Rev. 57; University of Minnesota: Minneapolis, MN, USA, 2005. [Google Scholar]
- Mandea, M.; Holschneider, M.; Lesur, V.; Luhr, H. The Earth’s magnetic field at the CHAMP satellite epoch. In System Earth via Geodetic-Geophysical Space Techniques; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Siemes, C. GOCE Gradiometer Calibration and Level 1b Data Processing; Technical Report EWP-2384; European Space Agency: Paris, France, 2011. [Google Scholar]
- Stummer, C.; Fecher, T.; Pail, R. Alternative method for angular rate determination within the GOCE gradiometer processing. J. Geod. 2011, 85, 585–596. [Google Scholar] [CrossRef]
- Lefferts, E.J.; Markley, F.L.; Shuster, M. Kalman Filtering for Spacecraft Attitude Estimation. J. Guid. Control Dyn. 1982, 5, 536–542. [Google Scholar] [CrossRef]
- Wang, F. Study on Center of Mass Calibration and K-band Ranging System Calibration of the GRACE Mission. Ph.D. Thesis, The University of Texas at Austin, Austin, TX, USA, 2003. [Google Scholar]
- Liang, L.; Yang, F. An alternative SCA1B product for GRACE-FO from 2018-06 to 2020-12. Figshare 2021. [Google Scholar] [CrossRef]
- Liang, L.; Yu, J.; Wang, C.; Zhong, M.; Feng, W.; Wan, X.; Chen, W.; Yan, Y. Influence of the Low-Frequency Error of the Residual Orbit on Recovering Time-Variable Gravity Field from the Satellite-To-Satellite Tracking Mission. Remote Sens. 2021, 13, 1118. [Google Scholar] [CrossRef]
- Zhao, Q.; Guo, J.; Hu, Z.; Shi, C.; Liu, J.; Cai, H.; Liu, X. GRACE gravity field modeling with an investigation on correlation between nuisance parameters and gravity field coefficients. Adv. Space Res. 2011, 47, 1833–1850. [Google Scholar] [CrossRef]
- Wahr, J.; Molenaar, M.; Bryan, F. Time variability of the Earth’s gravity field: Hydrological and oceanic effects and their possible detection using GRACE. J. Geophys. Res. Solid Earth 1998, 103, 30205–30229. [Google Scholar] [CrossRef]

| Difference Value | One Day | One Month |
|---|---|---|
| =0 | 44.38% | 44.12% |
| = | 55.62% | 55.50% |
| = | 0% | 0.38% |
| ≥3 | 0% | 0% |
| Axis | Sat | Bias Drift Rate | Bias |
|---|---|---|---|
| X | C | ||
| Y | C | ||
| Z | C | ||
| X | D | ||
| Y | D | ||
| Z | D |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, F.; Liang, L.; Wang, C.; Luo, Z. Attitude Determination for GRACE-FO: Reprocessing the Level-1A SC and IMU Data. Remote Sens. 2022, 14, 126. https://doi.org/10.3390/rs14010126
Yang F, Liang L, Wang C, Luo Z. Attitude Determination for GRACE-FO: Reprocessing the Level-1A SC and IMU Data. Remote Sensing. 2022; 14(1):126. https://doi.org/10.3390/rs14010126
Chicago/Turabian StyleYang, Fan, Lei Liang, Changqing Wang, and Zhicai Luo. 2022. "Attitude Determination for GRACE-FO: Reprocessing the Level-1A SC and IMU Data" Remote Sensing 14, no. 1: 126. https://doi.org/10.3390/rs14010126
APA StyleYang, F., Liang, L., Wang, C., & Luo, Z. (2022). Attitude Determination for GRACE-FO: Reprocessing the Level-1A SC and IMU Data. Remote Sensing, 14(1), 126. https://doi.org/10.3390/rs14010126






