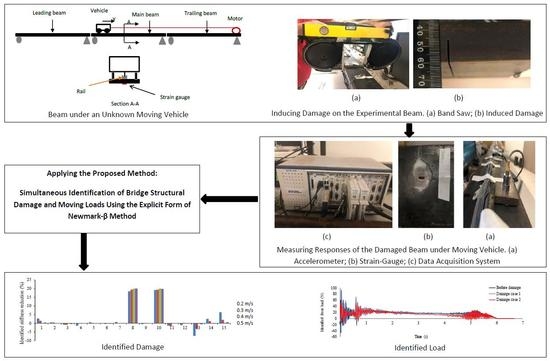
Simultaneous Identification of Bridge Structural Damage and Moving Loads Using the Explicit Form of Newmark-β Method: Numerical and Experimental Studies
Abstract
:1. Introduction
- (1)
- There are no traffic interruptions;
- (2)
- Analysis is performed under operational environment conditions;
- (3)
- Analysis is performed continuously;
- (4)
- There is no need for exceptional experimental arrangements or techniques;
- (5)
- The number of sensors and amount of expense is reduced;
- (6)
- There is the ability for excitation of structural vibrations with a large amplitude and high signal-to-noise ratio.
- (1)
- Sensors should be available at the location of dynamic forces,
- (2)
- One input force-time history should be known,
- (3)
- The known load should be in the range of 0.6 times to 1.5 times of the unknown forces. In practice however, these assumptions are not so simple to apply. Wang et al. [30] developed a method for simultaneous identification of the load and unknown parameters where the excitation source is non-moving.
2. Dynamics of the Vehicle-Bridge Interaction System
2.1. Bridge Model
2.2. Vehicle Model and Vehicle-Bridge Coupled Model
3. Moving Load Identification Formula Based on the Explicit Form of Newmark-β Method
4. Simultaneous Identification of Structural Damage and Moving Loads
4.1. Element Damage Index
4.2. Structural Response Sensitivities
4.3. Damage Detection Applying Dynamic Response Sensitivity Analysis
- Step 1: Conduct a dynamic measurement of the structure and guess the initial value of EI.
- Step 2: Obtain the matrix of system Markov parameters, H, from Equation (7).
- Step 3: Identifying moving loads from Equation (6).
- Step 4: Compute the responses of the structure from Equation (1).
- Step 5: Compute structural response sensitivities from Equation (12).
- Step 6: Calculate structural parameters perturbation from Equation (14).
- Step 7: Update the Finite element model.
- Step 8: Repeat Steps 2–6 until the convergence condition is met.
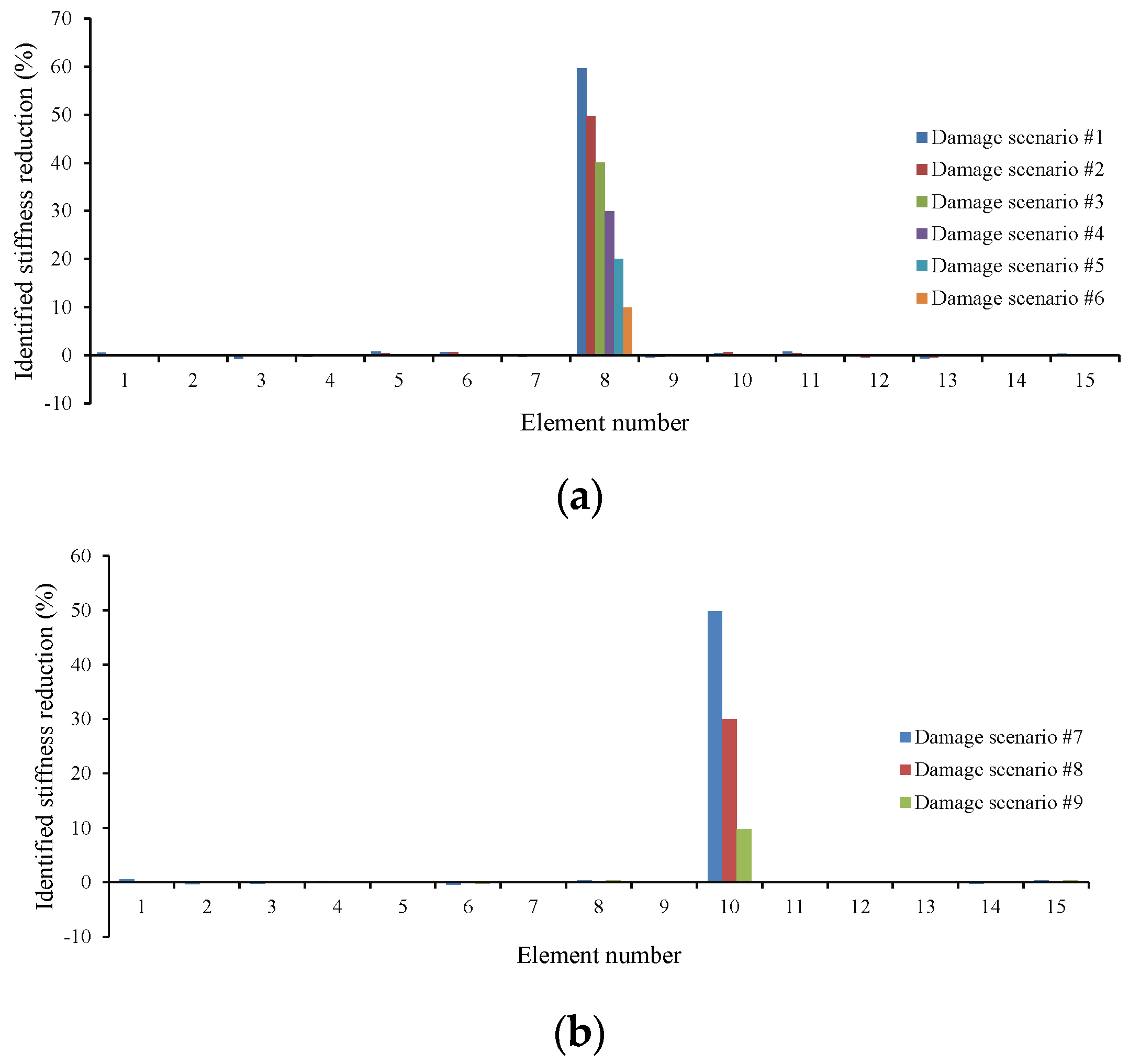
5. Numerical Example I: Simply Supported Single Span Bridge
5.1. Identification Results
5.1.1. Effect of Damage Type
5.1.2. Effect of Sensor Placements
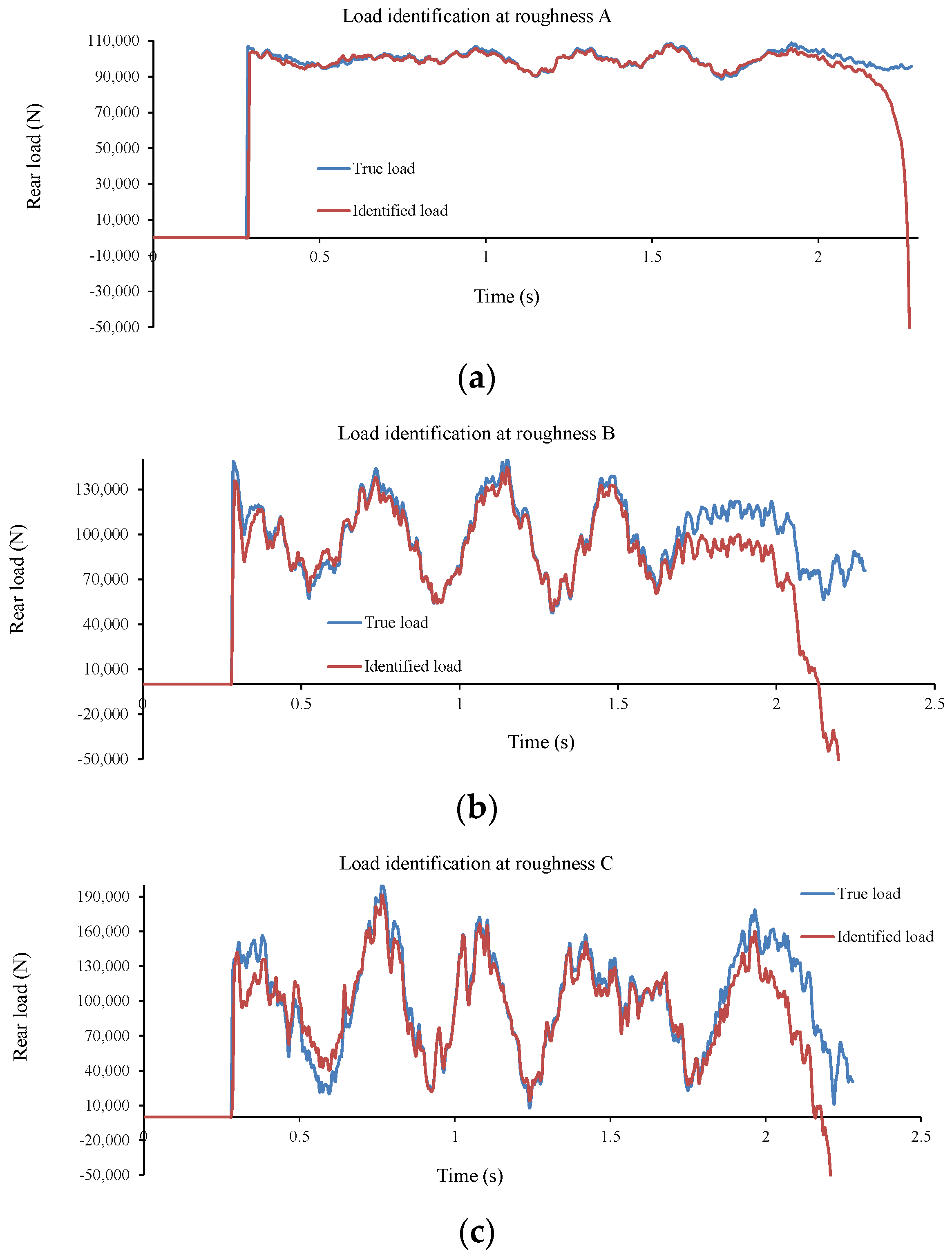
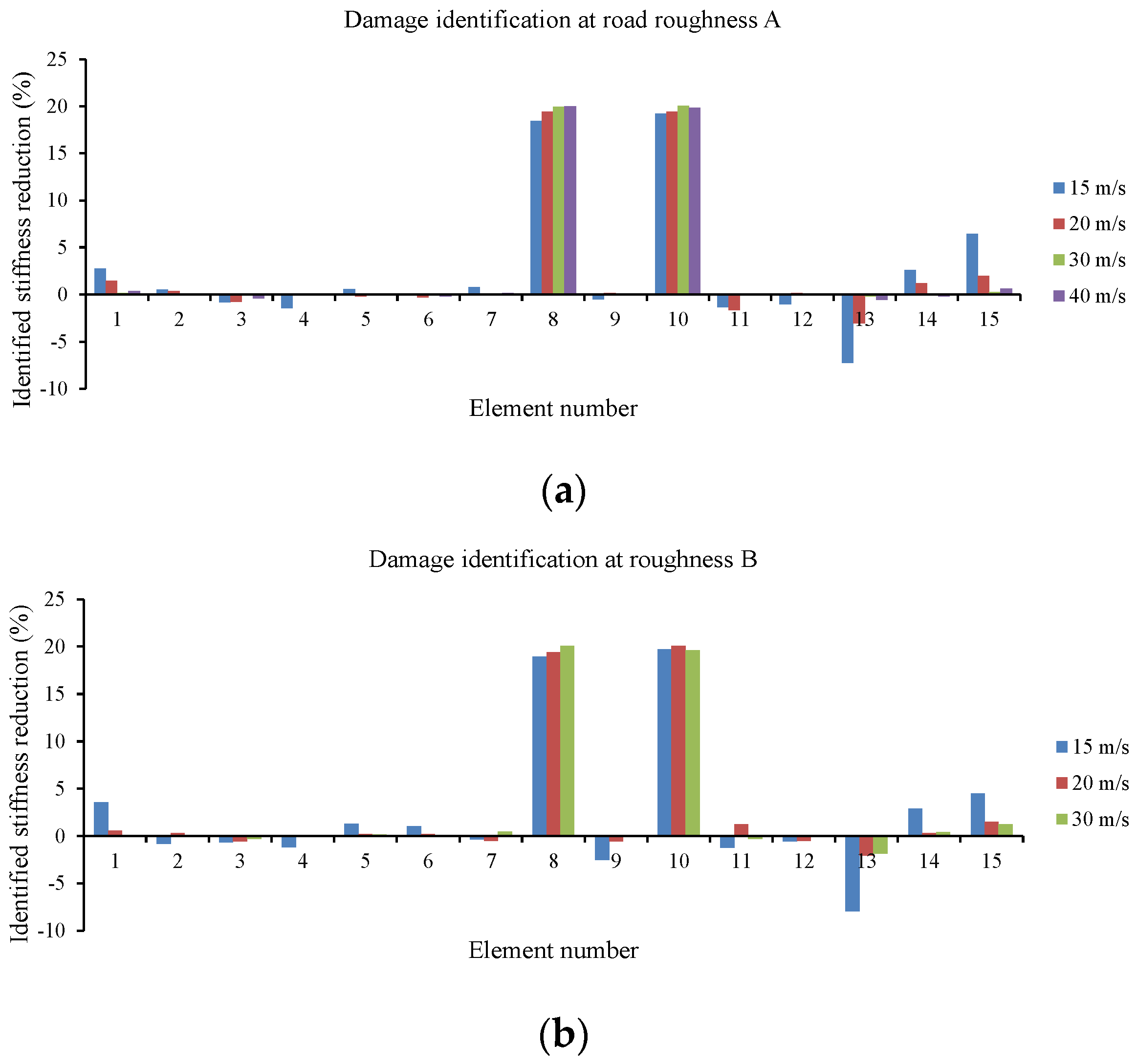
5.1.3. Effect of Vehicle Speed and Road Surface Roughness
5.1.4. Effect of Measurement Noise
5.2. Results Discussion
5.2.1. Effect of Damage Type
5.2.2. Effect of Sensor Placement
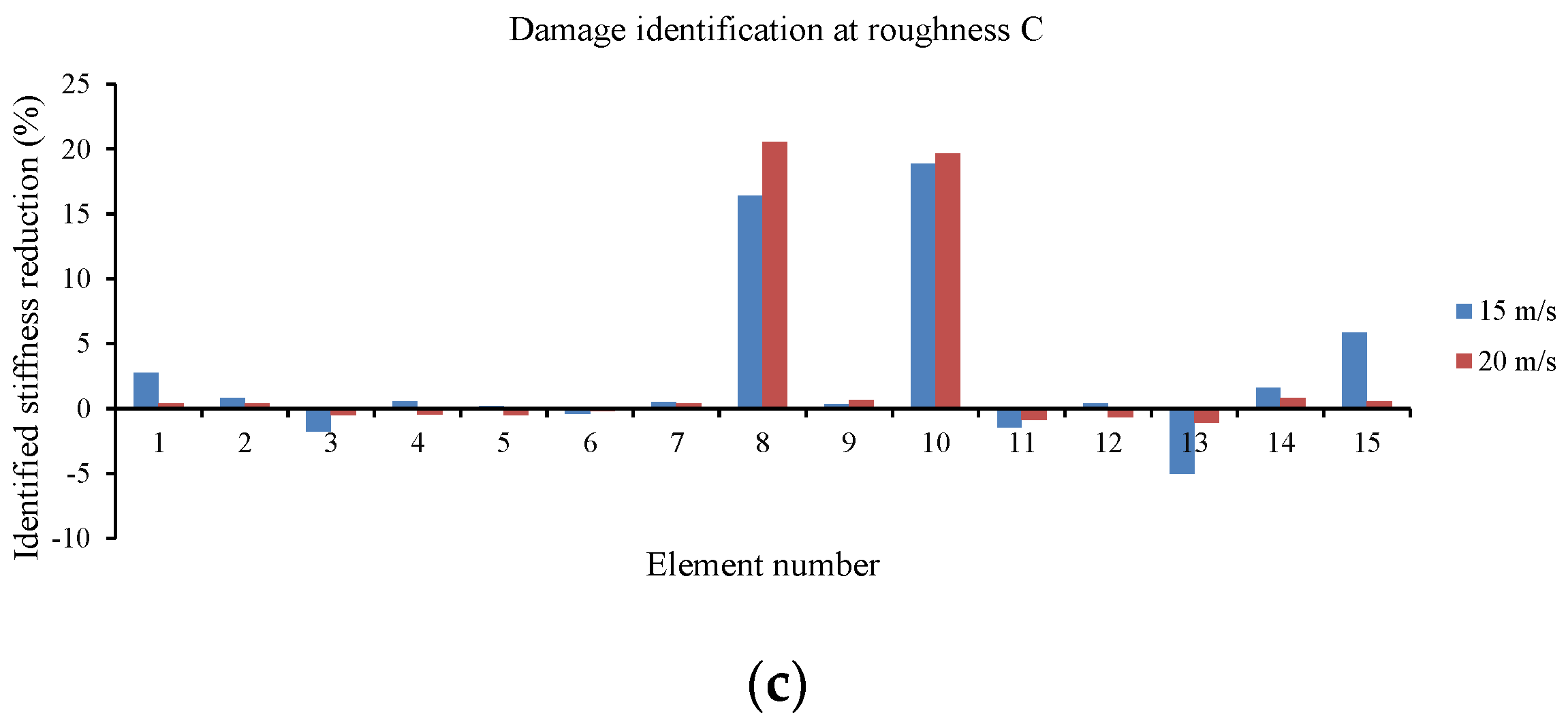
5.2.3. Effect of Vehicle Speed and Road Surface Roughness
5.2.4. Effect of Measurement Noise
6. Numerical Example II: Two-Span Continuous Bridge
Results Discussion
- (a)
- (b)
- (c)
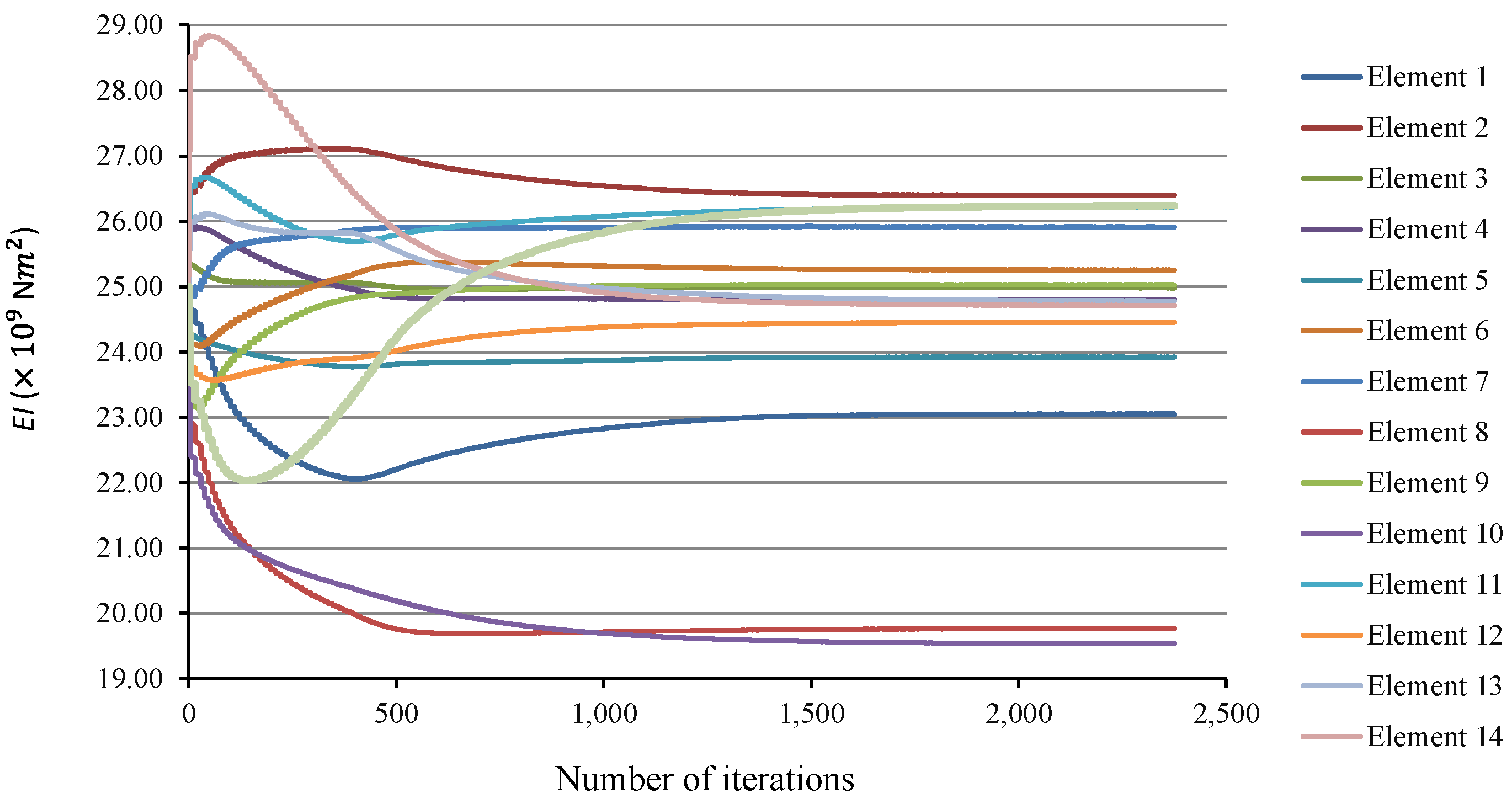
- Figure 11 shows how well the stiffness of all elements is converged at 5% noise.
- (d)
- Referring to Table 9 and comparing with the single span simply supported bridge results, it can be seen that identification errors fall in the same range and very close to each other, showing that the method performs well for continuous bridges, as well;
7. Experimental Studies
7.1. Experimental Test Set-Up and Measurements
7.2. Modal Test of the Beam
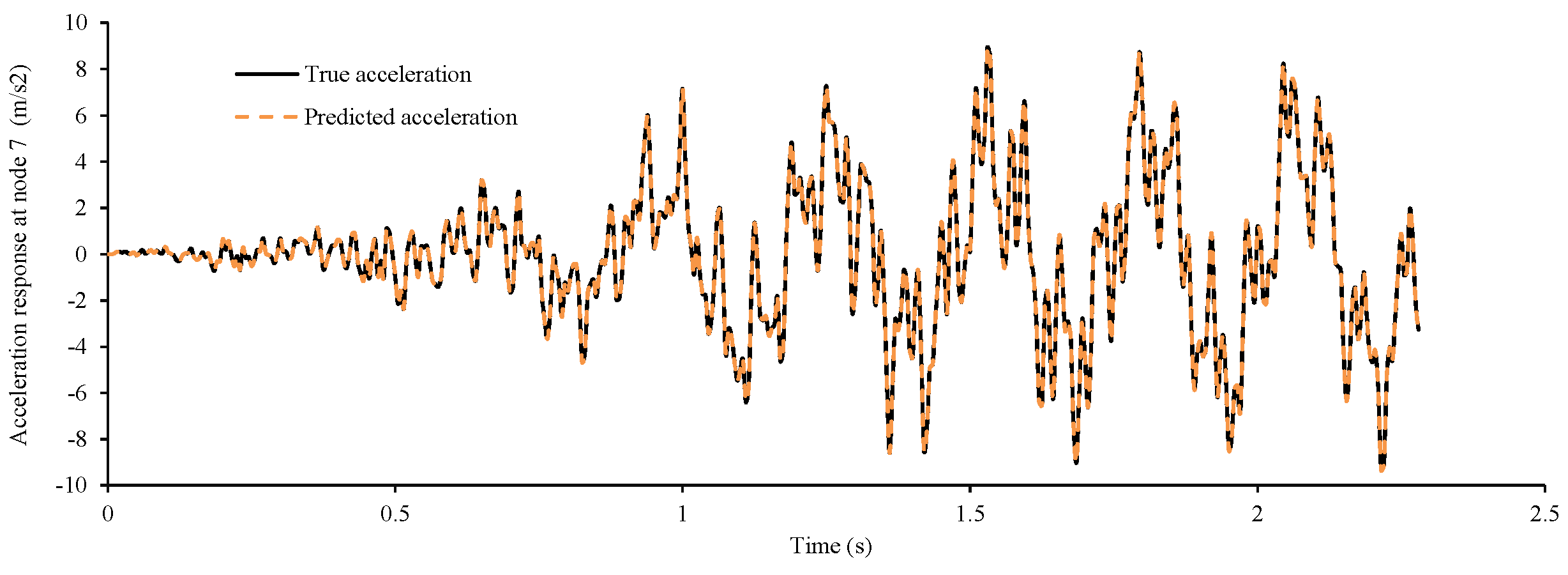
7.3. Identification Verification
7.4. Identification Results
7.5. Results Discussion
- (a)
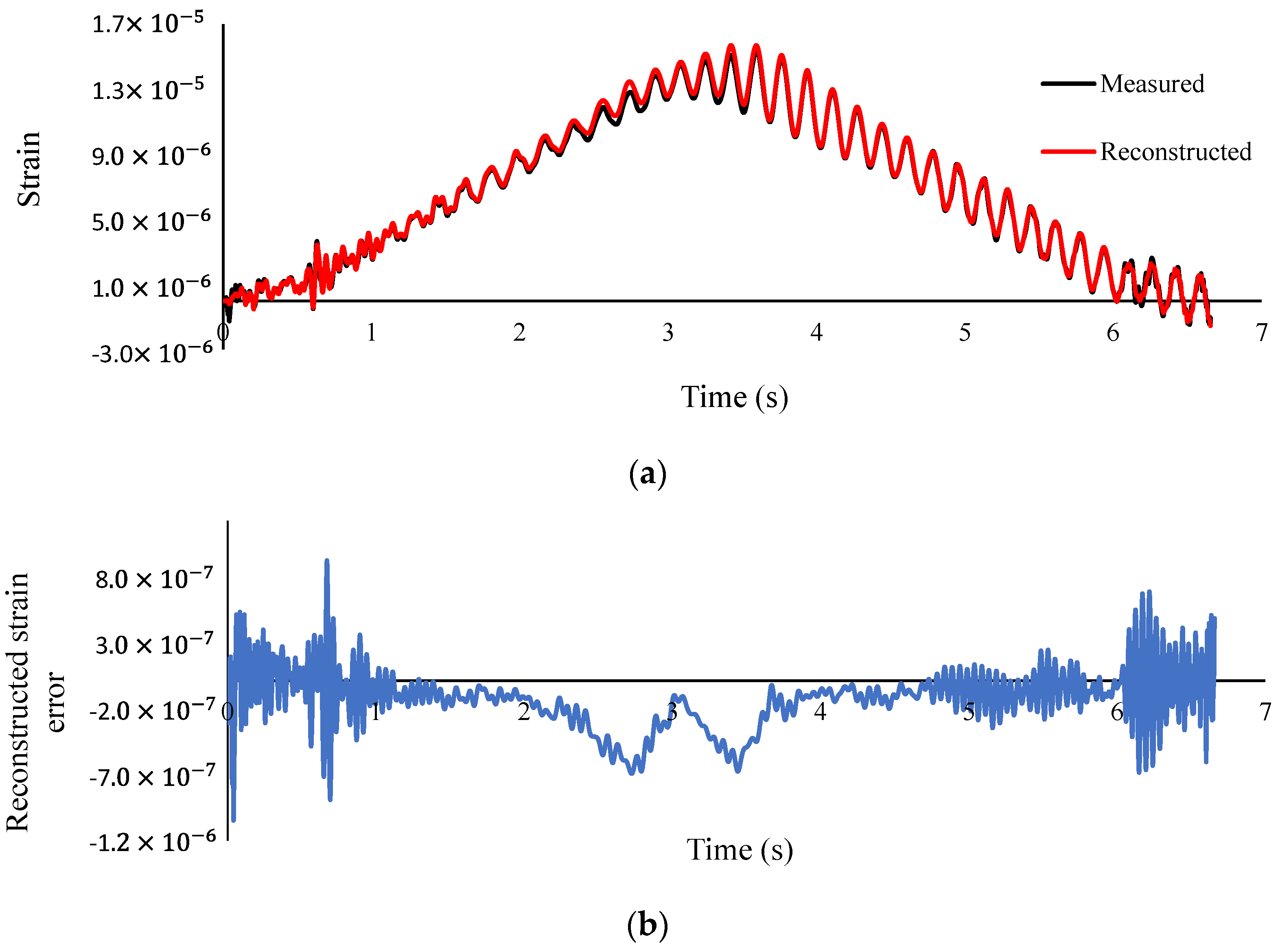
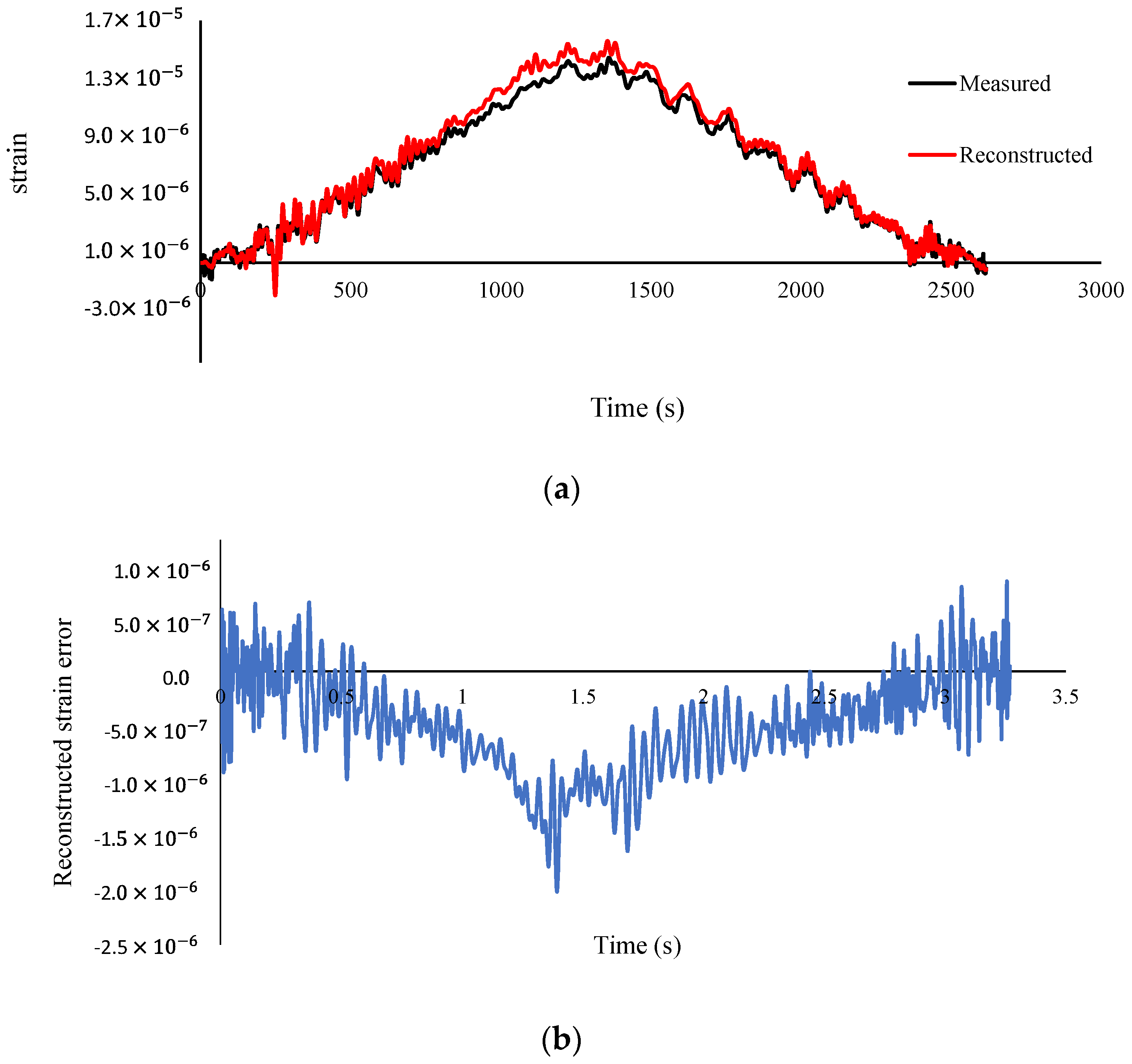
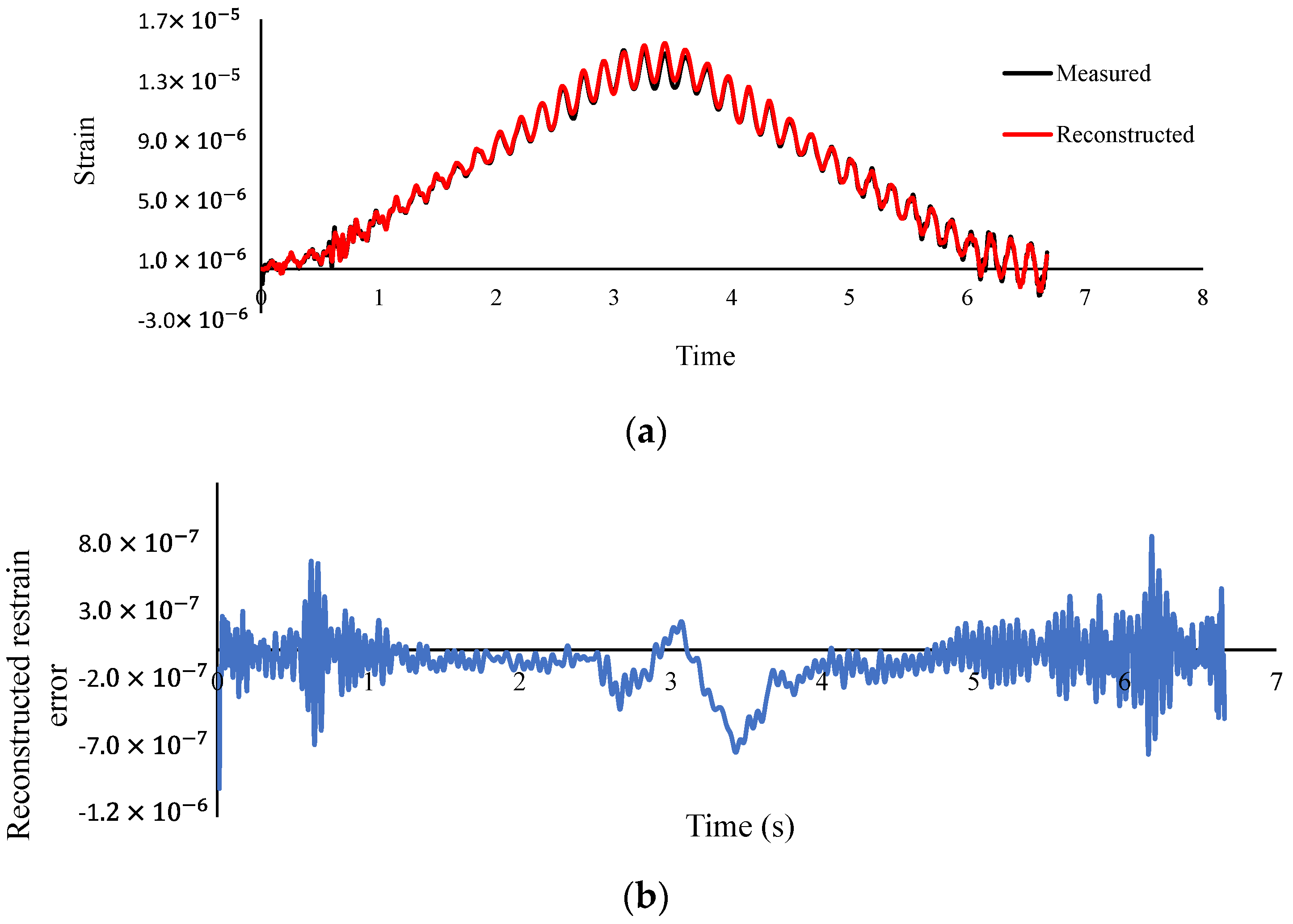
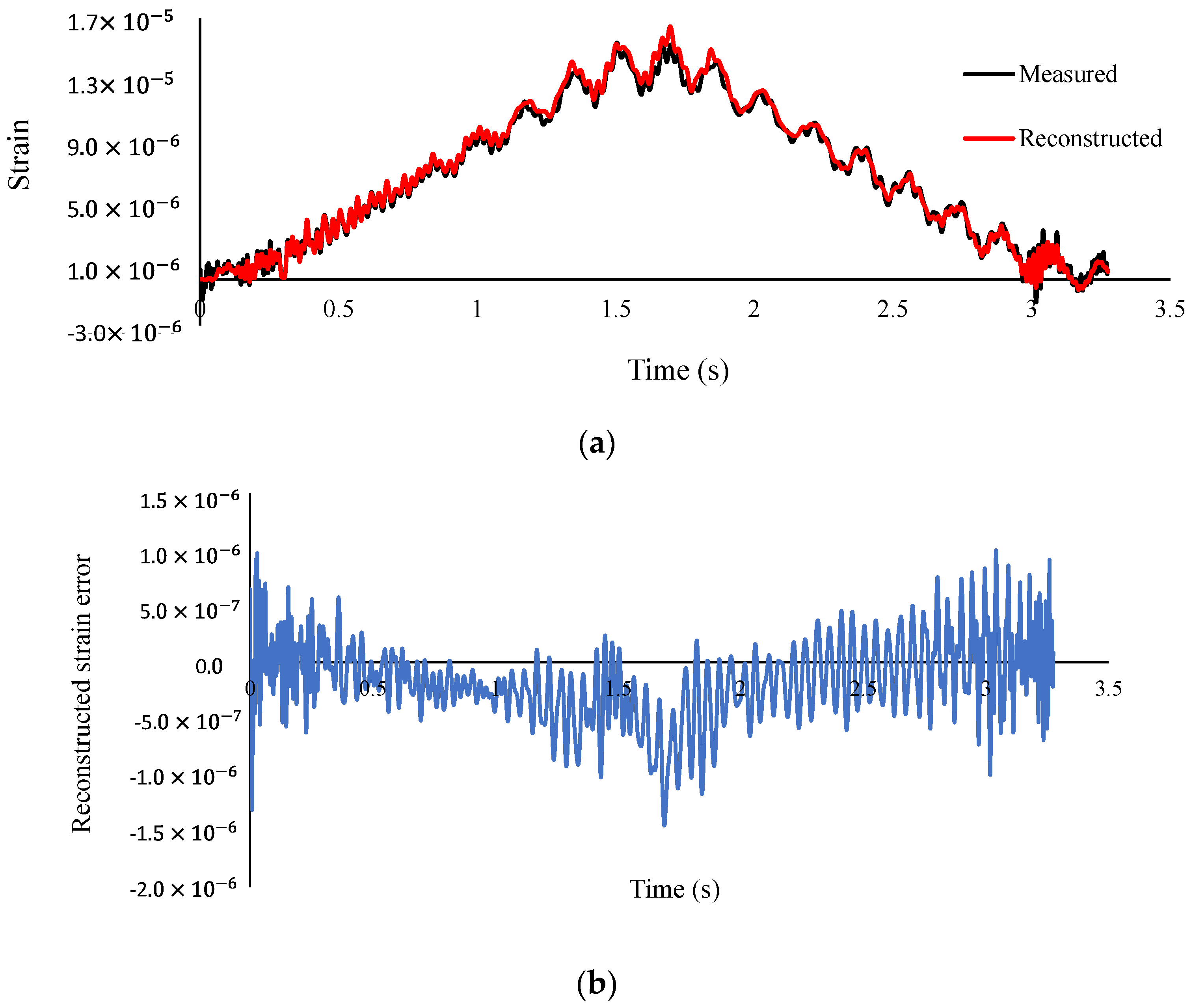
- According to Table 12, the total time of calculation rises with the decrease in speed and increase in the sampling frequency. The error of the reconstructed strain at mid-span is increased with an increase in speed;
- (b)
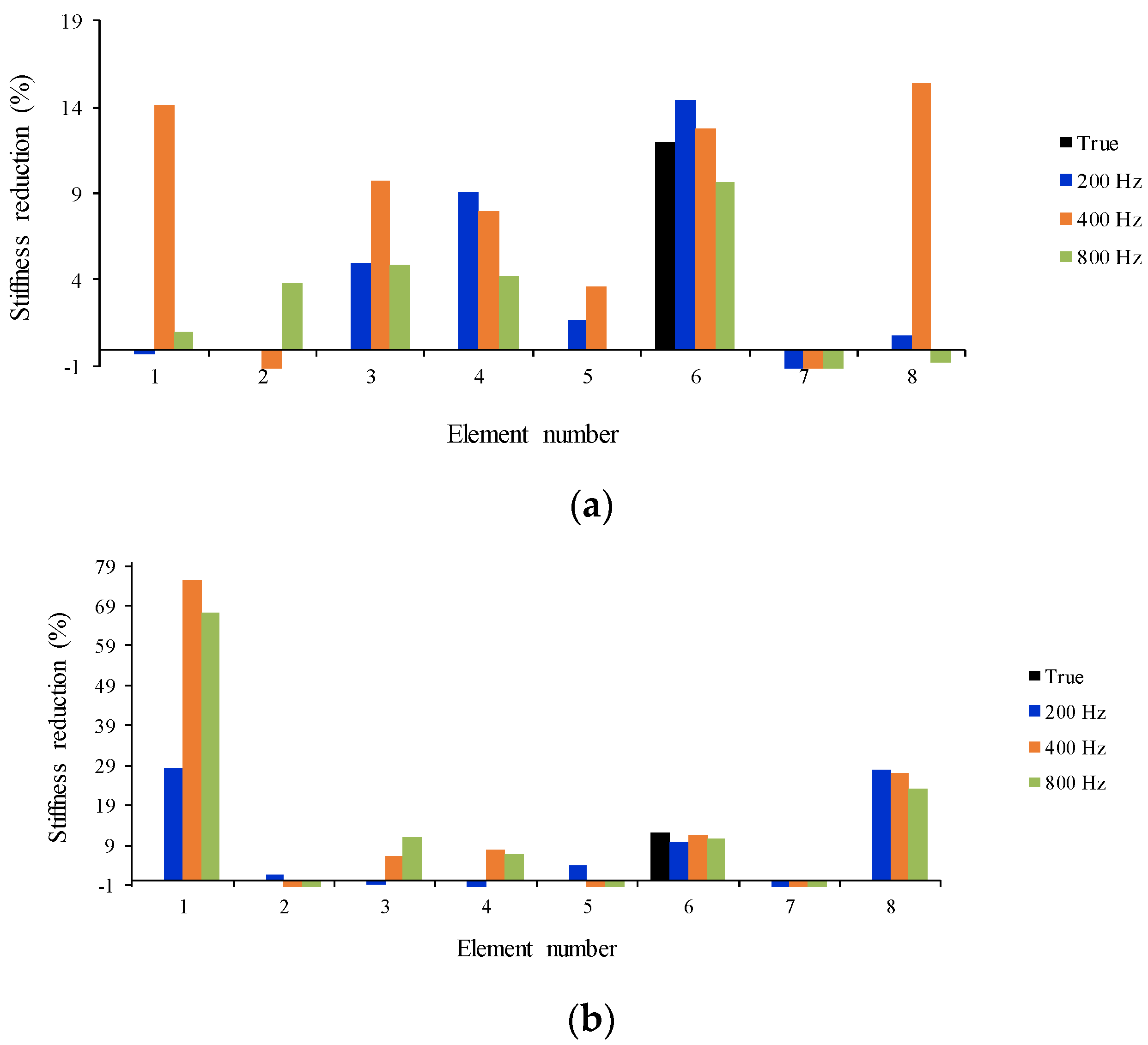
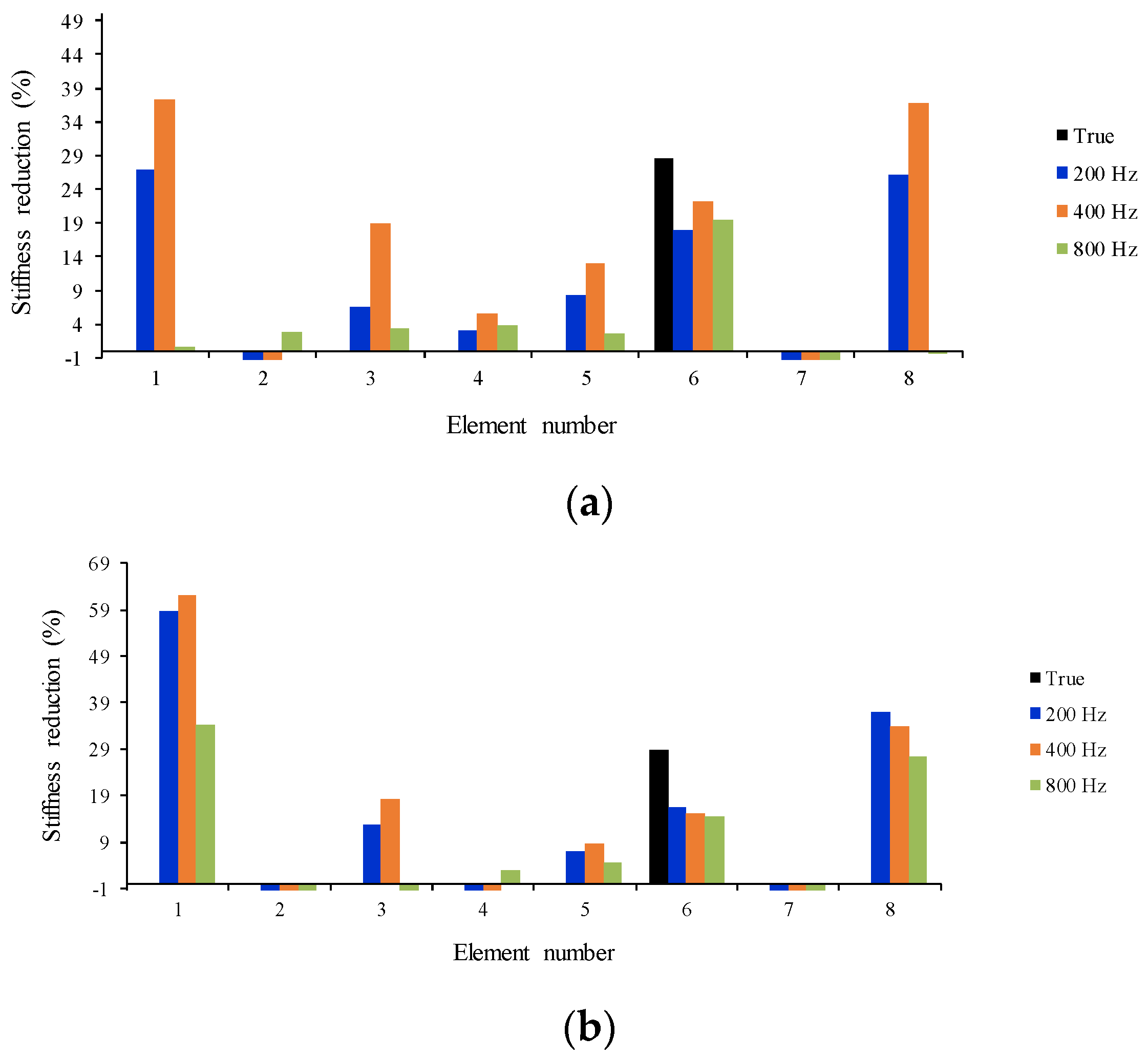
- According to Figure 20 and Figure 21, element six is detected as a damaged element and its extension is quantified reasonably at all sampling frequencies and vehicle speeds, however, there are large false positives at other elements due to measurement noise and modeling errors of the boundary conditions;
- (c)
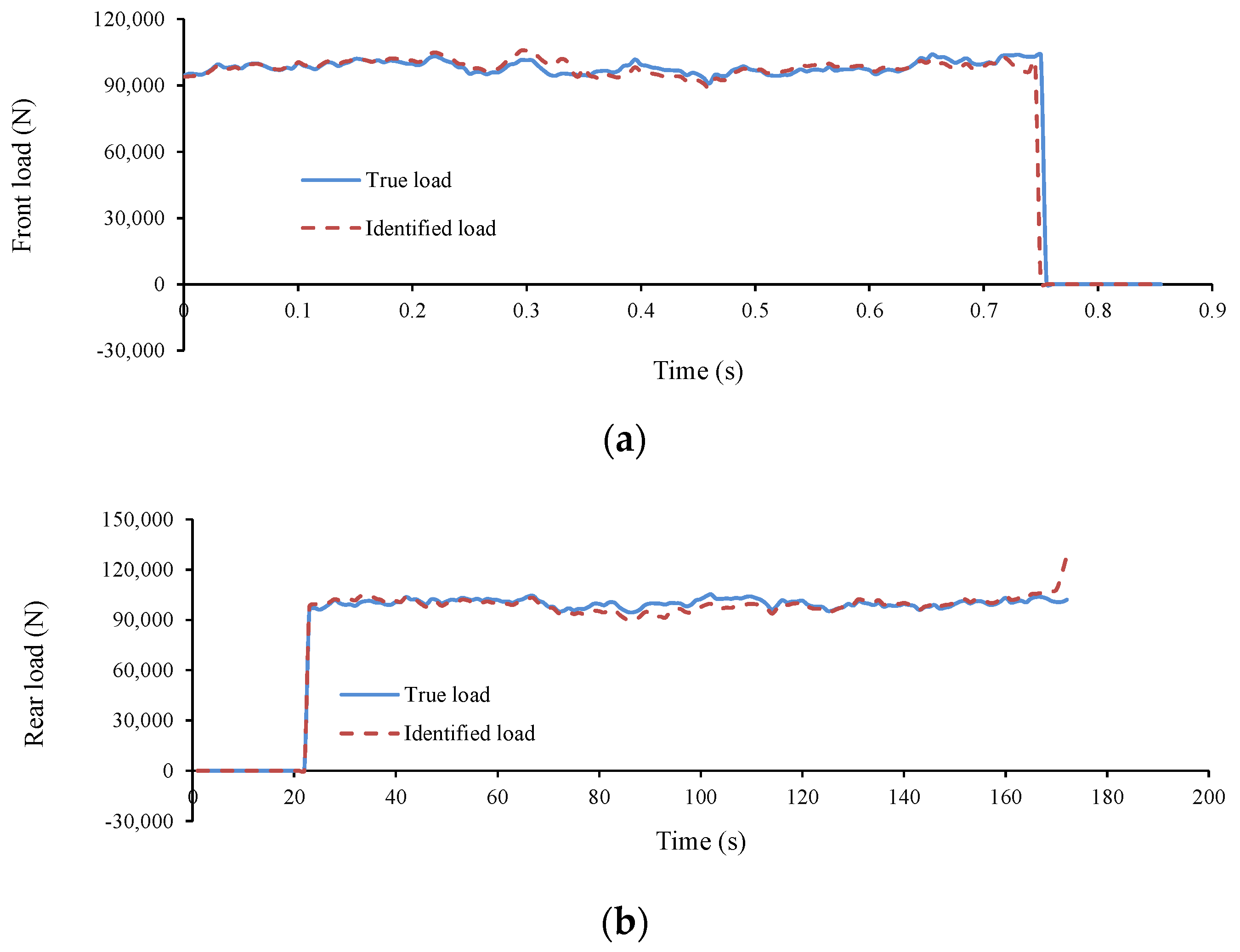
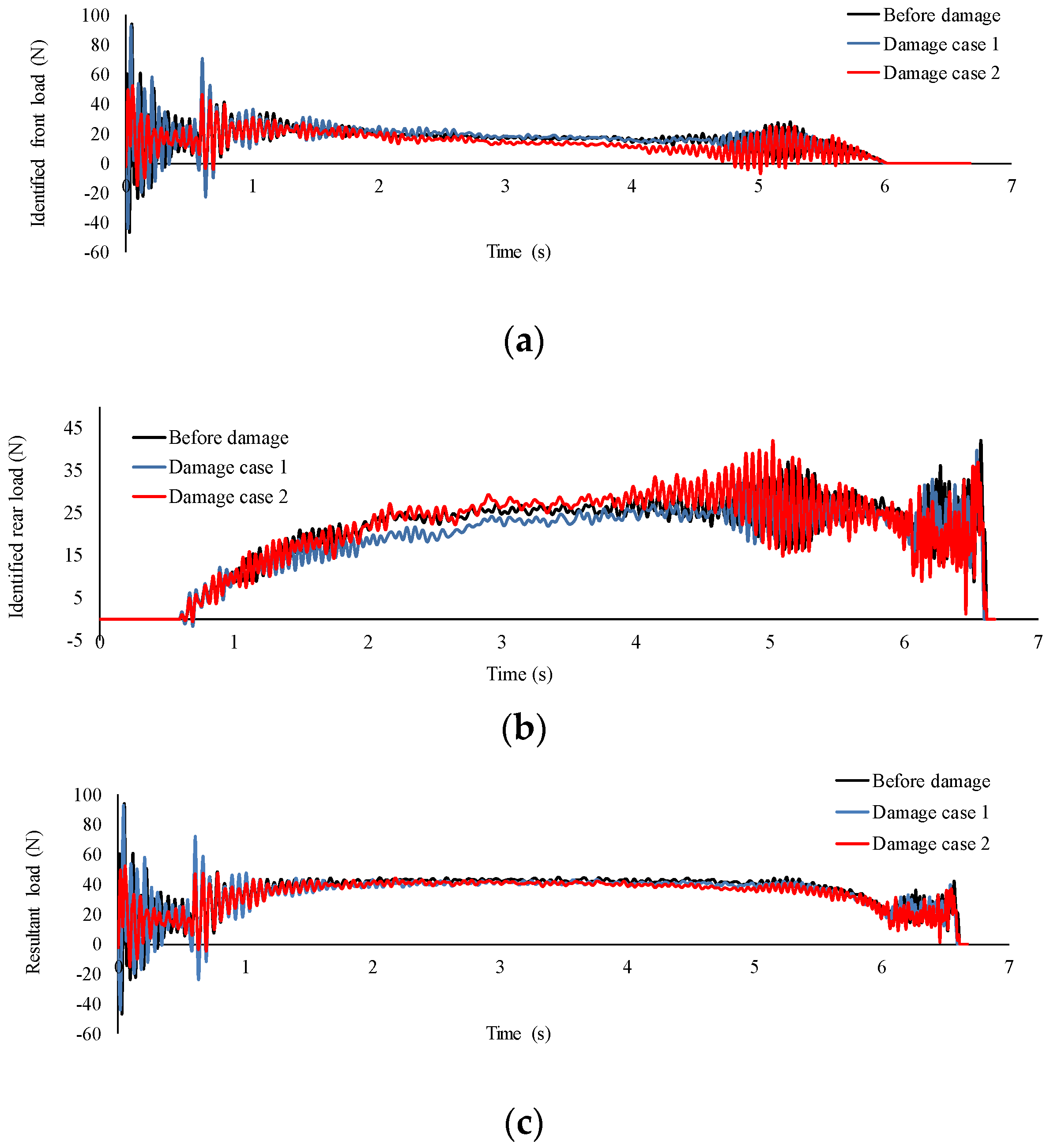
- According to Figure 22 and Figure 23, both the front and rear identified loads are fluctuating around the static axle values (22 N), and the identified resultant load is fluctuating around the total static weight of the vehicle (44 N), showing the accuracy of the method. It can be seen that damage has caused a slight increase in the interaction forces of the vehicle and bridge, which is more visible at the speed of 0.94 m/s in comparison with the speed of 0.47 m/s.
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, J.; Zhao, X. A super-element approach for structural identification in time domain. Front. Mech. Eng. China 2006, 1, 215–221. [Google Scholar] [CrossRef]
- Link, M.; Weiland, M. Damage identification by multi-model updating in the modal and in the time domain. Mech. Syst. Signal Process. 2009, 23, 1734–1746. [Google Scholar] [CrossRef]
- Ouyang, H. Moving-load dynamic problems: A tutorial (with a brief overview). Mech. Syst. Signal Process. 2011, 25, 2039–2060. [Google Scholar] [CrossRef]
- Zhu, X.Q.; Law, S.S. Structural Health Monitoring Based on Vehicle-Bridge Interaction: Accomplishments and Challenges. Adv. Struct. Eng. 2015, 18, 1999–2015. [Google Scholar] [CrossRef]
- He, W.-Y.; Ren, W.-X.; Zhu, S. Baseline-free damage localization method for statically determinate beam structures using dual-type response induced by quasi-static moving load. J. Sound Vib. 2017, 400, 58–70. [Google Scholar] [CrossRef]
- Zhu, X.; Cao, M.; Ostachowicz, W.; Xu, W. Damage Identification in Bridges by Processing Dynamic Responses to Moving Loads: Features and Evaluation. Sensors 2019, 19, 463. [Google Scholar] [CrossRef] [Green Version]
- Mohammadi, M.; Rashidi, M.; Mousavi, V.; Karami, A.; Yu, Y.; Samali, B. Quality Evaluation of Digital Twins Generated Based on UAV Photogrammetry and TLS: Bridge Case Study. Remote Sens. 2021, 13, 3499. [Google Scholar] [CrossRef]
- Rashidi, M.; Mohammadi, M.; Sadeghlou Kivi, S.; Abdolvand, M.M.; Truong-Hong, L.; Samali, B. A Decade of Modern Bridge Monitoring Using Terrestrial Laser Scanning: Review and Future Directions. Remote Sens. 2020, 12, 3796. [Google Scholar] [CrossRef]
- Kalhori, H.; Makki Alamdari, M.; Zhu, X.; Samali, B.; Mustapha, S. Non-intrusive schemes for speed and axle identification in bridge-weigh-in-motion systems. Meas. Sci. Technol. 2017, 28, 025102. [Google Scholar] [CrossRef]
- Pnevmatikos, N.; Konstandakopoulou, F.; Blachowski, B.; Papavasileiou, G.; Broukos, P. Multifractal analysis and wavelet leaders for structural damage detection of structures subjected to earthquake excitation. Soil Dyn. Earthq. Eng. 2020, 139, 106328. [Google Scholar] [CrossRef]
- Chan, T.H.T.; Yu, L.; Law, S.S. Comparative studies on moving force identification from bridge strains in laboratory. J. Sound Vib. 2000, 235, 87–104. [Google Scholar] [CrossRef]
- Chan, T.H.T.; Yu, L.; Law, S.S.; Yung, T.H. Moving force identification studies, ii: Comparative studies. J. Sound Vib. 2001, 247, 77–95. [Google Scholar] [CrossRef]
- Yu, L.; Chan, T.H.T. Recent research on identification of moving loads on bridges. J. Sound Vib. 2007, 305, 3–21. [Google Scholar] [CrossRef]
- Law, S.S.; Zhu, X.Q. Moving Loads- Dynamic Analysis and Identification Techniques, 1st ed.; Structures and Infrastructures Book Series; CRC Press: London, UK, 2011; Volume 8. [Google Scholar] [CrossRef]
- Zhu, X.Q.; Law, S.S. Recent developments in inverse problems of vehicle–bridge interaction dynamics. J. Civ. Struct. Health Monit. 2016, 6, 107–128. [Google Scholar] [CrossRef]
- Daniel, Ľ.; Kortiš, J. The Comparison of Different Approaches to Model Vehicle-Bridge Interaction. Procedia Eng. 2017, 190, 504–509. [Google Scholar] [CrossRef]
- Lu, Z.R.; Law, S.S. Identification of system parameters and input force from output only. Mech. Syst. Signal Process. 2007, 21, 2099–2111. [Google Scholar] [CrossRef]
- Zhang, Q.; Jankowski, Ł.; Duan, Z. Simultaneous identification of moving masses and structural damage. Struct. Multidiscip. Optim. 2010, 42, 907–922. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Q.; Jankowski, Ł.; Duan, Z. Identification of coexistent load and damage. Struct. Multidiscip. Optim. 2010, 41, 243–253. [Google Scholar] [CrossRef]
- Zhang, Q.; Jankowski, Ł.; Duan, Z. Simultaneous identification of excitation time histories and parametrized structural damages. Mech. Syst. Signal Process. 2012, 33, 56–68. [Google Scholar] [CrossRef]
- Sun, H.; Betti, R. Simultaneous identification of structural parameters and dynamic input with incomplete output-only measurements. Struct. Control. Health Monit. 2014, 21, 868–889. [Google Scholar] [CrossRef]
- Jayalakshmi, V.; Rao, A.R. Simultaneous identification of damage and input dynamic force on the structure for structural health monitoring. Struct. Multidiscip. Optim. 2017, 55, 2211–2238. [Google Scholar] [CrossRef]
- Hoshiya, M.; Maruyama, O. Identification of Running Load and Beam System. J. Eng. Mech. 1987, 113, 813–824. [Google Scholar] [CrossRef]
- Zhu, X.; Law, S. Damage Detection in Simply Supported Concrete Bridge Structure under Moving Vehicular Loads. J. Vib. Acoust. 2007, 129, 58–65. [Google Scholar] [CrossRef]
- Law, S.S.; Li, J. Updating the reliability of a concrete bridge structure based on condition assessment with uncertainties. Eng. Struct. 2010, 32, 286–296. [Google Scholar] [CrossRef]
- Zhang, Q.; Jankowski, Ł.; Duan, Z. Simultaneous Identification of Moving Vehicles and Bridge Damages Considering Road Rough Surface. Math. Probl. Eng. 2013, 2013, 963424. [Google Scholar] [CrossRef] [Green Version]
- Feng, D.; Sun, H.; Feng, M.Q. Simultaneous identification of bridge structural parameters and vehicle loads. Comput. Struct. 2015, 157, 76–88. [Google Scholar] [CrossRef]
- Abbasnia, R.; Mirzaee, A.; Shayanfar, M. Simultaneous identification of moving loads and structural damage by adjoint variable. Struct. Eng. Mech. 2015, 56, 871–897. [Google Scholar] [CrossRef]
- OBrien, E.; Carey, C.; Keenahan, J. Bridge damage detection using ambient traffic and moving force identification. Struct. Control. Health Monit. 2015, 22, 1396–1407. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.; Du, C.; Jiang, S. Simultaneous identification of the load and unknown parameters of the structure based on the perturbation method. Adv. Mech. Eng. 2018, 10, 1687814018805664. [Google Scholar] [CrossRef]
- Liu, K.; Law, S.S.; Zhu, X.Q.; Xia, Y. Explicit form of an implicit method for inverse force identification. J. Sound Vib. 2014, 333, 730–744. [Google Scholar] [CrossRef]
- Pourzeynali, S.; Zhu, X.; Ghari Zadeh, A.; Rashidi, M.; Samali, B. Comprehensive Study of Moving Load Identification on Bridge Structures Using the Explicit Form of Newmark-β Method: Numerical and Experimental Studies. Remote Sens. 2021, 13, 2291. [Google Scholar] [CrossRef]
- Zhu, X.; Hao, H. Damage Detection of Bridge Beam Structures under Moving Loads; Conference Proceedings of the Society for Experimental Mechanics Series; Springer: Bethel, CT, USA, 2007. [Google Scholar]
- Mulcahy, N.L. Bridge response with tractor-trailer vehicle loading. Earthq. Eng. Struct. Dyn. 1983, 11, 649–665. [Google Scholar] [CrossRef]






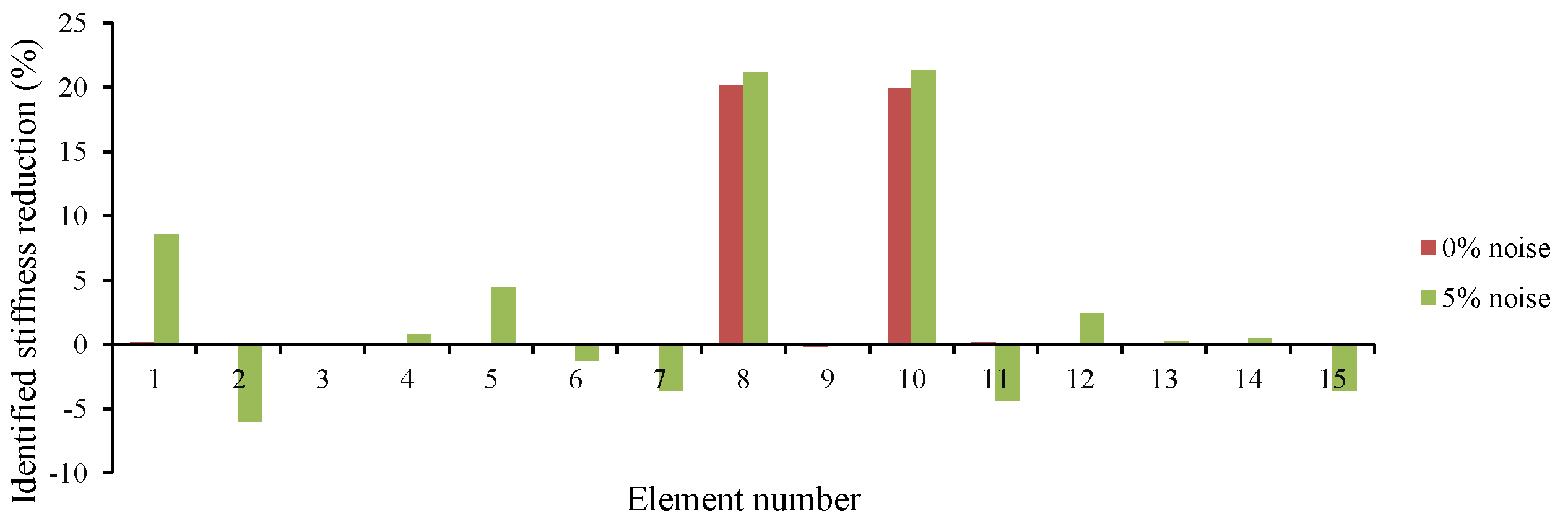




| mv = 17,735 kg | mt1 = 1500 kg | Mt2 = 1000 kg |
| Iv = 1.47 × 105 Nm2 | Ks1 = 2.47 × 106 N/m | Ks2 = 4.23 × 106 N/m |
| a1 = 0.519 m | Kt1 = 1.75 × 106 N/m | Kt2 = 3.5 × 106 N/m |
| a2 = 0.481 m | Cs1 = 3 × 104 N/m/s | Cs2 = 4 × 104 N/m/s |
| S = 4.27 m | Ct1 = 3.9 × 103 N/m/s | Ct2 = 4.3 × 103 N/m/s |
| L = 30 m | EI 1010 N m2 | ρA 103 kg/m | Damping ratio for all modes = 0.02 |
| Damage Scenario | Damage Type | Damage Location | Reduction in Elastic Modulus (%) | Noise |
|---|---|---|---|---|
| #1 | Single | Element 8 | 60 | Nil |
| #2 | 50 | |||
| #3 | 40 | |||
| #4 | 30 | |||
| #5 | 20 | |||
| #6 | 10 | |||
| #7 | Single | Element 10 | 50 | Nil |
| #8 | 30 | |||
| #9 | 10 | |||
| #10 | Single | Element 12 | 50 | Nil |
| #11 | 30 | |||
| #12 | 10 | |||
| #13 | Single | Element 15 | 50 | Nil |
| #14 | 30 | |||
| #15 | 10 | |||
| #16 | Multiple | Elements 8 and 10 | 20 | Nil |
| #17 | 10 |
| Damage Scenario | Total Time h:min:s | N.I. | I.L. Error (%) | D.I. Error (%) | Rec. Acc. Error (%) | |
|---|---|---|---|---|---|---|
| Front | Rear | |||||
| #1 | 1:00:42 | 4518 | 0.33 | 1.01 | 0.44 | 0.15 |
| #2 | 1:06:39 | 4136 | 0.21 | 0.91 | 0.36 | 0.12 |
| #3 | 0:23:06 | 1688 | 0.06 | 0.78 | 0.07 | 0.02 |
| #4 | 0:25:54 | 1971 | 0.13 | 0.78 | 0.03 | 0.00 |
| #5 | 0:24:05 | 1705 | 0.05 | 0.76 | 0.03 | 0.01 |
| #6 | 0:31:54 | 2402 | 0.03 | 0.79 | 0.08 | 0.03 |
| #7 | 00:34:50 | 2677 | 0.1 | 0.83 | 0.24 | 0.06 |
| #8 | 00:40:08 | 3013 | 0.01 | 0.78 | 0.06 | 0.02 |
| #9 | 00:21:06 | 1574 | 0.15 | 0.86 | 0.15 | 0.05 |
| #10 | 00:50:06 | 3440 | 0.05 | 0.77 | 0.07 | 0.02 |
| #11 | 00:26:27 | 1962 | 0.02 | 0.76 | 0.04 | 0.01 |
| #12 | 00:26:26 | 1928 | 0.08 | 0.82 | 0.04 | 0.02 |
| #13 | 00:25:58 | 2017 | 0.07 | 0.83 | 0.11 | 0.05 |
| #14 | 00:26:32 | 1798 | 0.07 | 0.77 | 0.05 | 0.01 |
| #15 | 00:13:51 | 1094 | 0.07 | 0.77 | 0.04 | 0.02 |
| #16 | 00:28:22 | 2273 | 0.1 | 0.85 | 0.20 | 0.06 |
| #17 | 00:27:23 | 1868 | 0.09 | 0.86 | 0.15 | 0.04 |
| Case Number | Number of Sensors | Nodes with Accelerometers |
|---|---|---|
| S14 | 14 | All nodes except supports |
| S3 | 3 | 5, 9,13 |
| S4 | 4 | 4, 7, 10, 13 |
| S5 | 5 | 3, 6, 8, 11, 14 |
| S6 | 6 | 3, 5, 7, 10, 12, 14 |
| Sensor Placement | Total Time h:min:s | N.I. | I.L. Error (%) | D.I. Error (%) | Rec. Acc. Error (%) | Noise | |
|---|---|---|---|---|---|---|---|
| Front | Rear | ||||||
| S3 | 1:23:57 | 6373 | 0.06 | 0.78 | 0.07 | 0.00 | 0% |
| S4 | 00:39:39 | 3224 | 0.82 | 0.13 | 0.54 | 0.07 | |
| S5 | 00:53:14 | 4046 | 0.88 | 0.04 | 0.12 | 0.03 | |
| S6 | 00:25:37 | 2307 | 0.08 | 0.86 | 0.20 | 0.05 | |
| S14 | 00:28:22 | 2273 | 0.1 | 0.8 | 0.20 | 0.06 | |
| Roughness | Speed (m/s) | Total Time h:min:s | N.I. | I.L. Error (%) | D.I. Error (%) | Rec. Acc. Error (%) | |
|---|---|---|---|---|---|---|---|
| Front | Rear | ||||||
| A | 15 | 07:42:07 | 5014 | 1.99 | 1.44 | 1.94 | 0.27 |
| 20 | 4:31:36 | 5370 | 1.08 | 0.89 | 0.84 | 0.17 | |
| 30 | 1:22:51 | 3622 | 0.02 | 0.63 | 0.11 | 0.02 | |
| 40 | 00:25:37 | 2307 | 0.08 | 0.86 | 0.21 | 0.05 | |
| B | 15 | 09:09:30 | 6474 | 4.65 | 5.89 | 2.88 | 0.39 |
| 20 | 06:37:27 | 7673 | 2.93 | 1.11 | 0.84 | 0.22 | |
| 30 | 1:19:41 | 3571 | 1.36 | 1.11 | 0.38 | 0.11 | |
| C | 15 | 10:37:47 | 7595 | 5.95 | 4.73 | 2.53 | 0.41 |
| 20 | 06:37:37 | 7812 | 2.57 | 1.71 | 0.62 | 0.11 | |
| Roughness-Speed (m/s) | Total Time h:min:s | N.I. | I.L. Error (%) | D.I. Error (%) | Rec. Acc. Error (%) | Noise | |
|---|---|---|---|---|---|---|---|
| Front | Rear | ||||||
| A-40 | 00:32:50 | 3404 | 1.91 | 1.10 | 0.45 | 0.82 | 1% |
| 00:18:50 | 1660 | 1.27 | 2.25 | 1.6747 | 4.08 | 5% | |
| 00:26:41 | 2725 | 2.01 | 2.31 | 5.38 | 8.46 | 10% | |
| Roughness | Speed (m/s) | Total Time h:min:s | N.I. | I.L. Error (%) | D.I. Error (%) | Rec. Acc. Error (%) | Noise | |
|---|---|---|---|---|---|---|---|---|
| Front | Rear | |||||||
| A | 40 | 00:28:03 | 2375 | 2.81 | 2.3 | 3.61 | 4.2 | 5% |
| Modal Frequency | 1st | 2nd | 3rd |
|---|---|---|---|
| Measured frequencies (Hz) | 6.27 | 27 | 61.17 |
| Calculated frequencies (Hz) | 6.48 | 25.78 | 57.38 |
| Error | 3.34% | 4.52% | 6.19% |
| Modal Frequency | 1st | 2nd | 3rd | 4th |
|---|---|---|---|---|
| Intact beam frequencies (Hz) | 6.3 | 27 | 61.2 | 104.7 |
| Damaged beam case 1 frequencies (Hz) | 6.2 | 26.4 | 66.6 | 99.9 |
| Damaged beam case 2 frequencies (Hz) | 6.03 | 26.5 | 61.8 | 102.9 |
| Damage Case | Speed (m/s) | Sampling Frequency (Hz) | Total Time h:min:s | Convergence Rate | Reconstructed Strain Error (%) |
|---|---|---|---|---|---|
| 1 | 0.47 | 200 | 00:10:19 | 0.001 | 2.65 |
| 400 | 00:51:52 | 0.001 | 3.48 | ||
| 800 | 02:45:05 | 0.002 | 2.99 | ||
| 0.94 | 200 | 00:00:32 | 0.003 | 5.55 | |
| 400 | 00:15:16 | 0.00004 | 10.3 | ||
| 800 | 01:05:49 | 0.00004 | 8.22 | ||
| 2 | 0.47 | 200 | 00:07:15 | 0.006 | 3.09 |
| 400 | 00:52:48 | 0.001 | 3.29 | ||
| 800 | 04:20:26 | 0.003 | 2.33 | ||
| 0.94 | 200 | 00:03:59 | 0.00008 | 5.35 | |
| 400 | 00:19:55 | 0.00006 | 6.55 | ||
| 800 | 02:19:58 | 0.006 | 4.53 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pourzeynali, S.; Zhu, X.; Ghari Zadeh, A.; Rashidi, M.; Samali, B. Simultaneous Identification of Bridge Structural Damage and Moving Loads Using the Explicit Form of Newmark-β Method: Numerical and Experimental Studies. Remote Sens. 2022, 14, 119. https://doi.org/10.3390/rs14010119
Pourzeynali S, Zhu X, Ghari Zadeh A, Rashidi M, Samali B. Simultaneous Identification of Bridge Structural Damage and Moving Loads Using the Explicit Form of Newmark-β Method: Numerical and Experimental Studies. Remote Sensing. 2022; 14(1):119. https://doi.org/10.3390/rs14010119
Chicago/Turabian StylePourzeynali, Solmaz, Xinqun Zhu, Ali Ghari Zadeh, Maria Rashidi, and Bijan Samali. 2022. "Simultaneous Identification of Bridge Structural Damage and Moving Loads Using the Explicit Form of Newmark-β Method: Numerical and Experimental Studies" Remote Sensing 14, no. 1: 119. https://doi.org/10.3390/rs14010119
APA StylePourzeynali, S., Zhu, X., Ghari Zadeh, A., Rashidi, M., & Samali, B. (2022). Simultaneous Identification of Bridge Structural Damage and Moving Loads Using the Explicit Form of Newmark-β Method: Numerical and Experimental Studies. Remote Sensing, 14(1), 119. https://doi.org/10.3390/rs14010119