SNR-Based Water Height Retrieval in Rivers: Application to High Amplitude Asymmetric Tides in the Garonne River
Abstract
1. Introduction
2. Study Area and Datasets
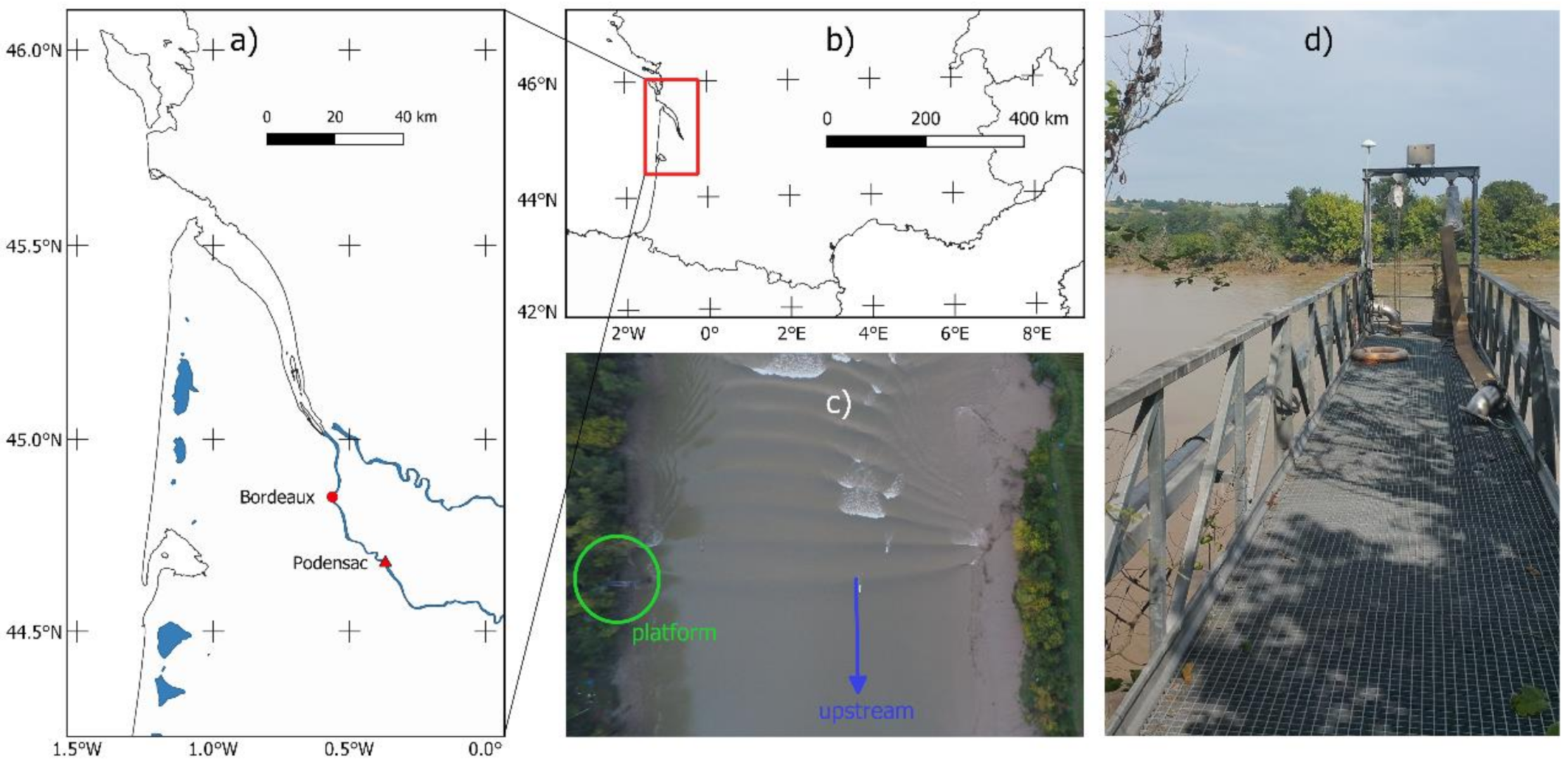
2.1. Study Area
2.2. GNSS-IR Data
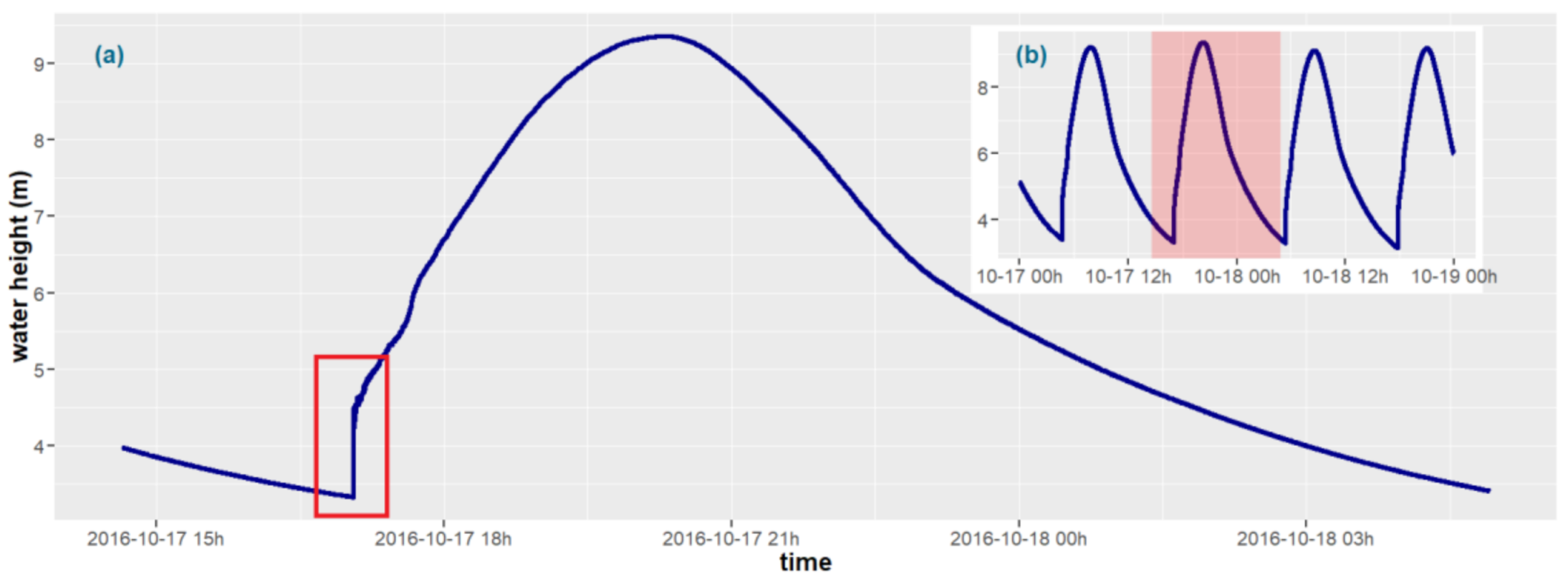
2.3. Validation: Pressure Data
3. Methods
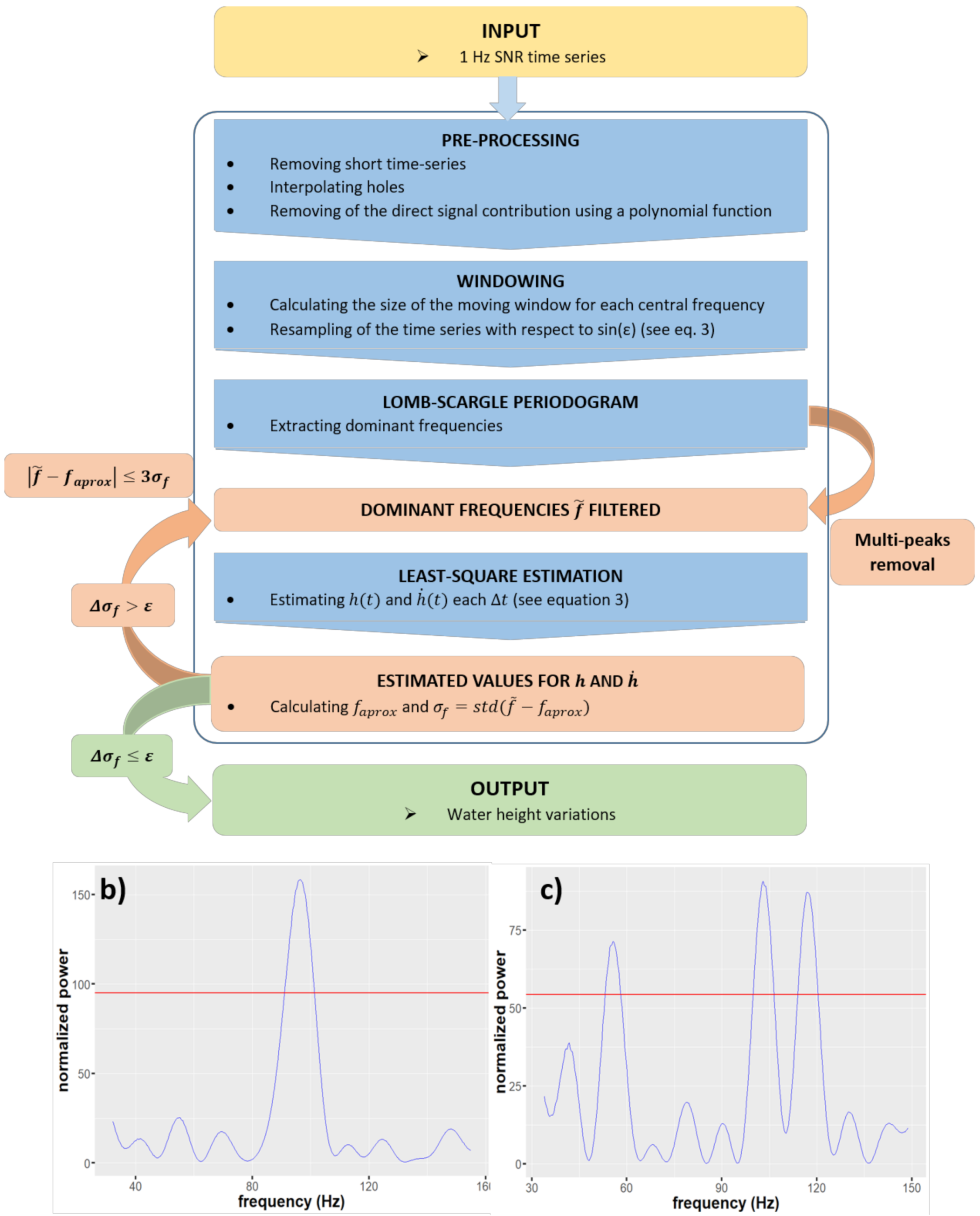
3.1. Preprocessing
3.2. Dynamic SNR Inversion
3.3. Improvements on the Dynamic SNR Approach
3.4. Validation
4. Results
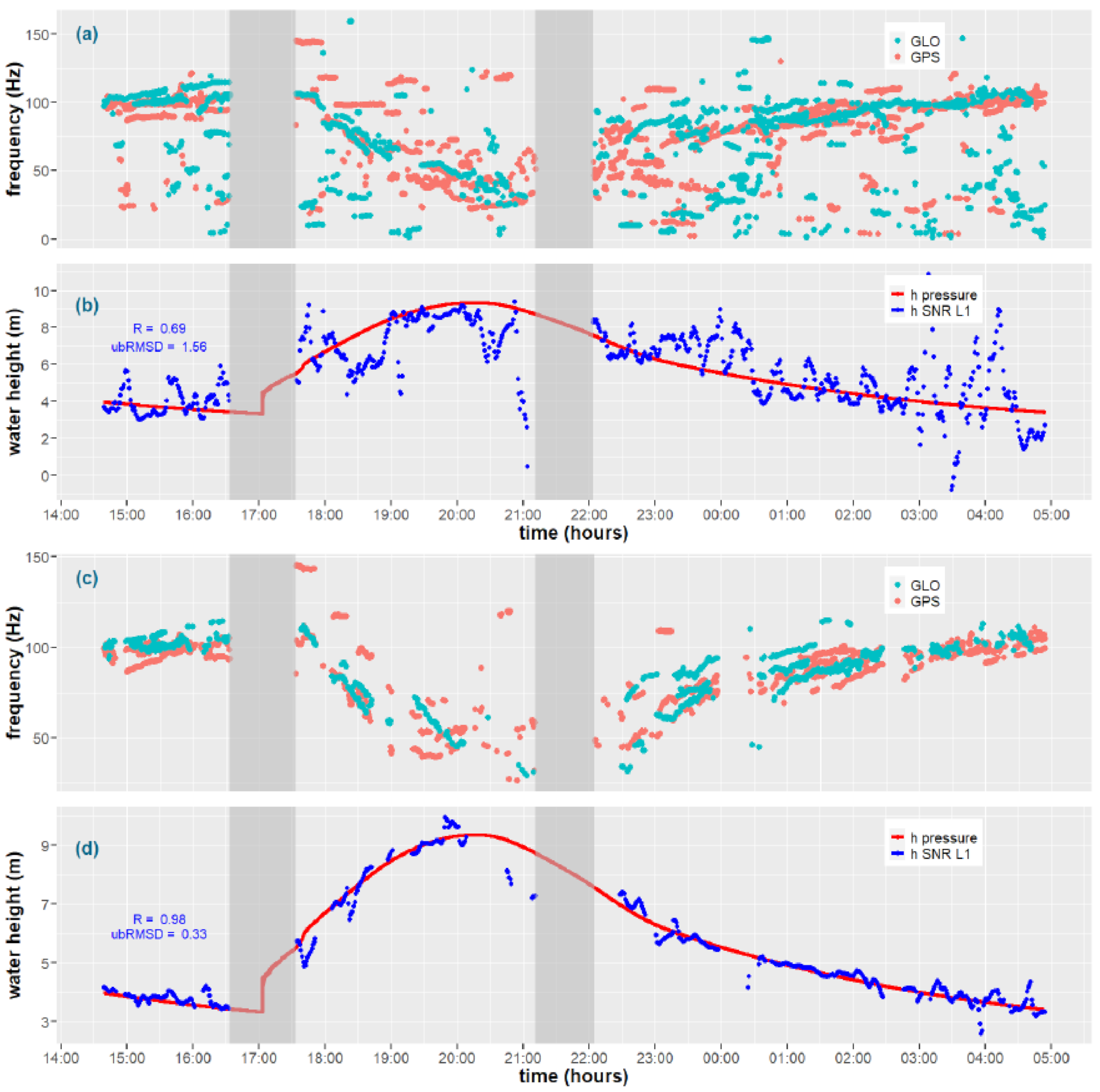
4.1. Preliminary Filtering of the Dominant Frequencies
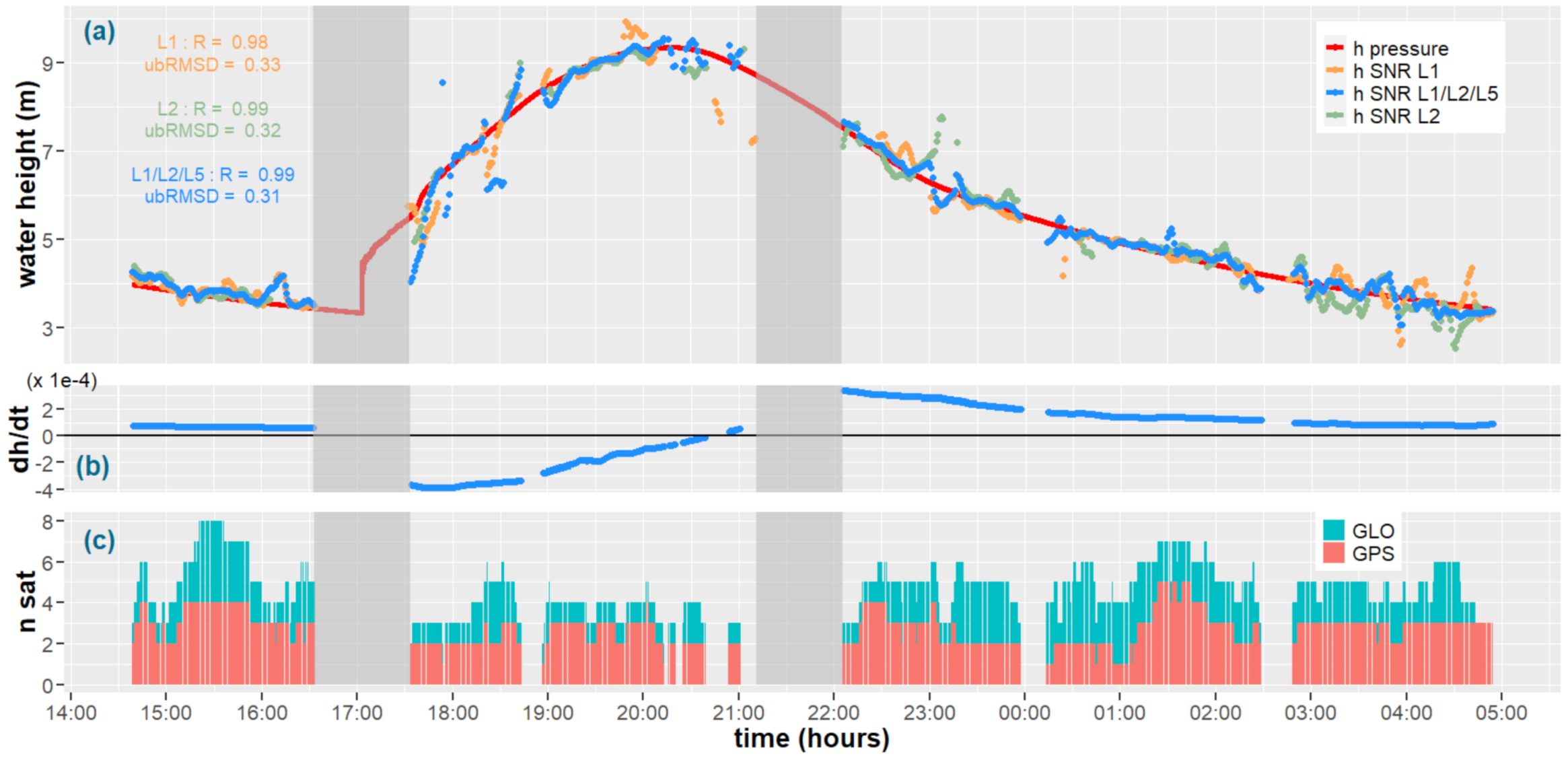
4.2. Comparison Between L1, L2 and L5 GNSS Frequencies
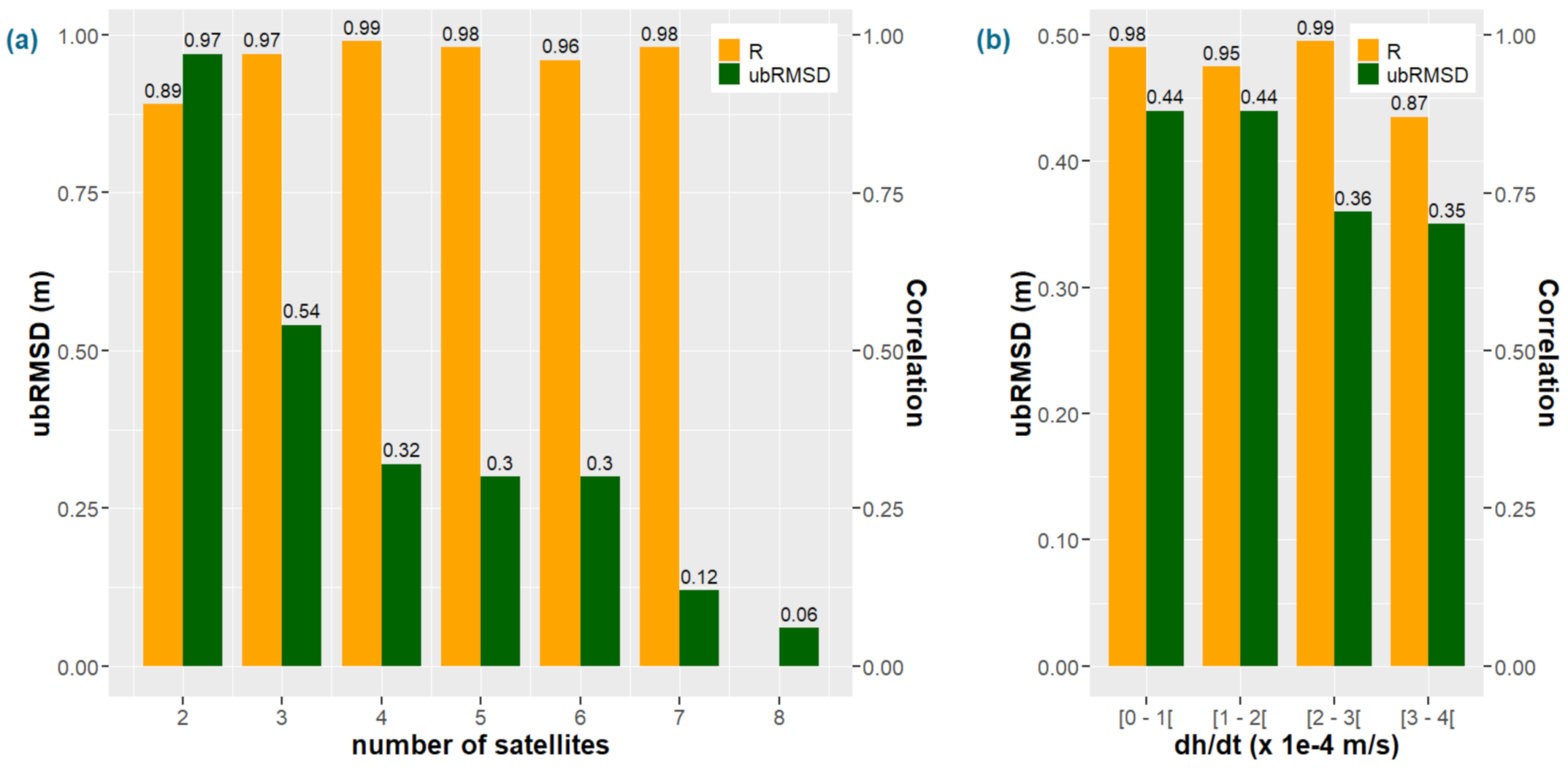
4.3. Influence of the Number of Satellites and Elevation Rate in the LSE Inversion
5. Discussion
5.1. Retrieving Water Heights in Rivers with GNSS-R
5.2. Influence of the GNSS Band, the Number of Satellites Visible and the Vertical Velocity
5.3. The Dynamic SNR Method
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bevis, M.; Businger, S.; Herring, T.A.; Rocken, C.; Anthes, R.A.; Ware, R.H. GPS Meteorology: Remote Sensing of Atmospheric Water Vapor Using the Global Positioning System. J. Geophys. Res. Atmos. 1992, 97, 15787–15801. [Google Scholar] [CrossRef]
- Wickert, J.; Cardellach, E.; Martin-Neira, M.; Bandeiras, J.; Bertino, L.; Andersen, O.B.; Camps, A.; Catarino, N.; Chapron, B.; Fabra, F.; et al. GEROS-ISS: GNSS REflectometry, Radio Occultation, and Scatterometry Onboard the International Space Station. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4552–4581. [Google Scholar] [CrossRef]
- Lestarquit, L.; Peyrezabes, M.; Darrozes, J.; Motte, E.; Roussel, N.; Wautelet, G.; Frappart, F.; Ramillien, G.; Biancale, R.; Zribi, M. Reflectometry With an Open-Source Software GNSS Receiver: Use Case With Carrier Phase Altimetry. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4843–4853. [Google Scholar] [CrossRef]
- Hall, C.D.; Cordey, R.A. Multistatic Scatterometry. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Edinburgh, UK, 12–16 September 1988; pp. 561–562. [Google Scholar]
- Martin-Neira, M. A Passive Reflectometry and Interferometry System (PARIS): Application to Ocean Altimetry. ESA J. 1993, 17, 331–335. [Google Scholar]
- Kavak, A.; Vogel, W.J.; Xu, G. Using GPS to Measure Ground Complex Permittivity. Electron. Lett. 1998, 34, 254–255. [Google Scholar] [CrossRef]
- Larson, K.M.; Small, E.E.; Gutmann, E.D.; Bilich, A.L.; Braun, J.J.; Zavorotny, V.U. Use of GPS Receivers as a Soil Moisture Network for Water Cycle Studies. Geophys. Res. Lett. 2008, 35, L24405. [Google Scholar] [CrossRef]
- Rodriguez-Alvarez, N.; Camps, A.; Vall-Llossera, M.; Bosch-Lluis, X.; Monerris, A.; Ramos-Perez, I.; Valencia, E.; Martinez-Fernandez, J.; Baroncini-Turricchia, G.; Perez-Gutierrez, C.; et al. Land Geophysical Parameters Retrieval Using the Interference Pattern GNSS-R Technique. IEEE Trans. Geosci. Remote Sens. 2011, 49, 71–84. [Google Scholar] [CrossRef]
- Chew, C.C.; Small, E.E.; Larson, K.M.; Zavorotny, V.U. Effects of Near-Surface Soil Moisture on GPS SNR Data: Development of a Retrieval Algorithm for Soil Moisture. IEEE Trans. Geosci. Remote Sens. 2014, 52, 537–543. [Google Scholar] [CrossRef]
- Roussel, N.; Frappart, F.; Ramillien, G.; Darrozes, J.; Baup, F.; Lestarquit, L.; Ha, M.C. Detection of Soil Moisture Variations Using GPS and GLONASS SNR Data for Elevation Angles Ranging from 2° to 70°. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4781–4794. [Google Scholar] [CrossRef]
- Zhang, S.; Calvet, J.C.; Darrozes, J.; Roussel, N.; Frappart, F.; Bouhours, G. Deriving Surface Soil Moisture from Reflected GNSS Signal Observations from a Grassland Site in Southwestern France. Hydrol. Earth Syst. Sci. 2018, 22, 1931–1946. [Google Scholar] [CrossRef]
- Larson, K.M.; Gutmann, E.D.; Zavorotny, V.U.; Braun, J.J.; Williams, M.W.; Nievinski, F.G. Can We Measure Snow Depth with GPS Receivers? Geophys. Res. Lett. 2009, 36, L17502. [Google Scholar] [CrossRef]
- Rodriguez-Alvarez, N.; Aguasca, A.; Valencia, E.; Bosch-Lluis, X.; Camps, A.; Ramos-Perez, I.; Park, H.; Vall-llossera, M. Snow Thickness Monitoring Using GNSS Measurements. IEEE Geosci. Remote Sens. Lett. 2012, 9, 1109–1113. [Google Scholar] [CrossRef]
- Small, E.E.; Larson, K.M.; Braun, J.J. Sensing Vegetation Growth with Reflected GPS Signals. Geophys. Res. Lett. 2010, 37, L12401. [Google Scholar] [CrossRef]
- Zhang, S.; Roussel, N.; Boniface, K.; Cuong Ha, M.; Frappart, F.; Darrozes, J.; Baup, F.; Calvet, J.C. Use of Reflected GNSS SNR Data to Retrieve Either Soil Moisture or Vegetation Height from a Wheat Crop. Hydrol. Earth Syst. Sci. 2017, 21, 4767–4784. [Google Scholar] [CrossRef]
- Anderson, K.D. Determination of Water Level and Tides Using Interferometric Observations of GPS Signals. J. Atmos. Ocean. Technol. 2000, 17, 1118–1127. [Google Scholar] [CrossRef]
- Larson, K.M.; Ray, R.D.; Nievinski, F.G.; Freymueller, J.T. The Accidental Tide Gauge: A GPS Reflection Case Study From Kachemak Bay, Alaska. IEEE Geosci. Remote Sens. Lett. 2013, 10, 1200–1204. [Google Scholar] [CrossRef]
- Löfgren, J.S.; Haas, R. Sea Level Measurements Using Multi-Frequency GPS and GLONASS Observations. EURASIP J. Adv. Signal Process. 2014, 2014, 50. [Google Scholar] [CrossRef]
- Vu, P.L.; Ha, M.C.; Frappart, F.; Darrozes, J.; Ramillien, G.; Dufrechou, G.; Gegout, P.; Morichon, D.; Bonneton, P. Identifying 2010 Xynthia Storm Signature in GNSS-R-Based Tide Records. Remote Sens. 2019, 11, 782. [Google Scholar] [CrossRef]
- Purnell, D.; Gomez, N.; Chan, N.H.; Strandberg, J.; Holland, D.M.; Hobiger, T. Quantifying the Uncertainty in Ground-Based GNSS-Reflectometry Sea Level Measurements. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 4419–4428. [Google Scholar] [CrossRef]
- Tabibi, S.; Geremia-Nievinski, F.; Francis, O.; van Dam, T. Tidal Analysis of GNSS Reflectometry Applied for Coastal Sea Level Sensing in Antarctica and Greenland. Remote Sens. Environ. 2020, 248, 111959. [Google Scholar] [CrossRef]
- Geremia-Nievinski, F.; Hobiger, T.; Haas, R.; Liu, W.; Strandberg, J.; Tabibi, S.; Vey, S.; Wickert, J.; Williams, S. SNR-Based GNSS Reflectometry for Coastal Sea-Level Altimetry: Results from the First IAG Inter-Comparison Campaign. J. Geod. 2020, 94, 70. [Google Scholar] [CrossRef]
- Larson, K.M.; Löfgren, J.S.; Haas, R. Coastal Sea Level Measurements Using a Single Geodetic GPS Receiver. Adv. Space Res. 2013, 51, 1301–1310. [Google Scholar] [CrossRef]
- Beckheinrich, J.; Hirrle, A.; Schon, S.; Beyerle, G.; Semmling, M.; Wickert, J. Water Level Monitoring of the Mekong Delta Using GNSS Reflectometry Technique. In Proceedings of the 2014 IEEE Geoscience and Remote Sensing Symposium, Quebec City, QC, Canada, 13–18 July 2014; pp. 3798–3801. [Google Scholar]
- Tabibi, S.; Francis, O. Can GNSS-R Detect Abrupt Water Level Changes? Remote Sens. 2020, 12, 3614. [Google Scholar] [CrossRef]
- Bonneton, P.; Bonneton, N.; Parisot, J.-P.; Castelle, B. Tidal Bore Dynamics in Funnel-Shaped Estuaries. J. Geophys. Res. Ocean. 2015, 120, 923–941. [Google Scholar] [CrossRef]
- Martins, K.; Bonneton, P.; Frappart, F.; Detandt, G.; Bonneton, N.; Blenkinsopp, C.E. High Frequency Field Measurements of an Undular Bore Using a 2D LiDAR Scanner. Remote Sens. 2017, 9, 462. [Google Scholar] [CrossRef]
- Frappart, F.; Roussel, N.; Darrozes, J.; Bonneton, P.; Bonneton, N.; Detandt, G.; Perosanz, F.; Loyer, S. High Rate GNSS Measurements for Detecting Non-Hydrostatic Surface Wave. Application to Tidal Borein the Garonne River. Eur. J. Remote Sens. 2016, 49, 917–932. [Google Scholar] [CrossRef]
- Roussel, N.; Ramillien, G.; Frappart, F.; Darrozes, J.; Gay, A.; Biancale, R.; Striebig, N.; Hanquiez, V.; Bertin, X.; Allain, D. Sea Level Monitoring and Sea State Estimate Using a Single Geodetic Receiver. Remote Sens. Environ. 2015, 171, 261–277. [Google Scholar] [CrossRef]
- Vu, P.-L.; Frappart, F.; Darrozes, J.; Ha, M.-C.; Dinh, T.-B.-H.; Ramillien, G. Comparison of Water Level Changes in the Mekong River Using Gnss Reflectometry, Satellite Altimetry and in-Situ Tide/River Gauges. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 8408–8411. [Google Scholar]
- Bonneton, P.; Filippini, A.G.; Arpaia, L.; Bonneton, N.; Ricchiuto, M. Conditions for Tidal Bore Formation in Convergent Alluvial Estuaries. Estuar. Coast. Shelf Sci. 2016, 172, 121–127. [Google Scholar] [CrossRef]
- Bishop, G.J.; Klobuchar, J.A.; Doherty, P.H. Multipath Effects on the Determination of Absolute Ionospheric Time Delay from GPS Signals. Radio Sci. 1985, 20, 388–396. [Google Scholar] [CrossRef]
- Strandberg, J.; Hobiger, T.; Haas, R. Improving GNSS-R Sea Level Determination through Inverse Modeling of SNR Data: GNSS-R INVERSE MODELING. Radio Sci. 2016, 51, 1286–1296. [Google Scholar] [CrossRef]
- Santamaría-Gómez, A.; Watson, C.; Gravelle, M.; King, M.; Wöppelmann, G. Levelling Co-Located GNSS and Tide Gauge Stations Using GNSS Reflectometry. J. Geod. 2015, 89, 241–258. [Google Scholar] [CrossRef]
| GNSS Bands Used | k | Iterative LSE | Min Number of Satellites | Nh—Number of deTerminations of h | Maximum Error (m) | R (Pearson) | ubRMSD (m) |
|---|---|---|---|---|---|---|---|
| L1 | 1 | No | / | 738 | 8.37 | 0.69 | 1.57 |
| Yes | 2 | 735 | 10.45 | 0.73 | 1.64 | ||
| 4 | 620 | 10.60 | 0.91 | 0.91 | |||
| L1 | 0.90 | No | / | 733 | 3.82 | 0.90 | 0.85 |
| Yes | 2 | 730 | 3.34 | 0.96 | 0.54 | ||
| 4 | 643 | 3.32 | 0.97 | 0.47 | |||
| L1 | 0.75 | No | / | 723 | 8.64 | 0.85 | 1.09 |
| Yes | 2 | 720 | 8.46 | 0.88 | 0.96 | ||
| 4 | 606 | 2.93 | 0.97 | 0.44 | |||
| L1 | 0.60 | No | / | 715 | 20.64 | 0.83 | 1.19 |
| Yes | 2 | 688 | 8.57 | 0.93 | 0.76 | ||
| 4 | 529 | 1.59 | 0.98 | 0.33 | |||
| L1 | 0.50 | No | / | 688 | 4.56 | 0.91 | 0.83 |
| Yes | 2 | 660 | 5.28 | 0.93 | 0.72 | ||
| 4 | 465 | 2.81 | 0.98 | 0.35 | |||
| L2 | 0.60 | No | / | 702 | 21.60 | 0.77 | 1.48 |
| Yes | 2 | 686 | 12.05 | 0.84 | 1.21 | ||
| 4 | 476 | 1.59 | 0.99 | 0.32 | |||
| L1, L2, L5 | 0.60 | No | / | 742 | 2.38 | 0.95 | 0.62 |
| Yes | 2 | 741 | 2.16 | 0.98 | 0.44 | ||
| 4 | 662 | 2.08 | 0.99 | 0.31 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeiger, P.; Frappart, F.; Darrozes, J.; Roussel, N.; Bonneton, P.; Bonneton, N.; Detandt, G. SNR-Based Water Height Retrieval in Rivers: Application to High Amplitude Asymmetric Tides in the Garonne River. Remote Sens. 2021, 13, 1856. https://doi.org/10.3390/rs13091856
Zeiger P, Frappart F, Darrozes J, Roussel N, Bonneton P, Bonneton N, Detandt G. SNR-Based Water Height Retrieval in Rivers: Application to High Amplitude Asymmetric Tides in the Garonne River. Remote Sensing. 2021; 13(9):1856. https://doi.org/10.3390/rs13091856
Chicago/Turabian StyleZeiger, Pierre, Frédéric Frappart, José Darrozes, Nicolas Roussel, Philippe Bonneton, Natalie Bonneton, and Guillaume Detandt. 2021. "SNR-Based Water Height Retrieval in Rivers: Application to High Amplitude Asymmetric Tides in the Garonne River" Remote Sensing 13, no. 9: 1856. https://doi.org/10.3390/rs13091856
APA StyleZeiger, P., Frappart, F., Darrozes, J., Roussel, N., Bonneton, P., Bonneton, N., & Detandt, G. (2021). SNR-Based Water Height Retrieval in Rivers: Application to High Amplitude Asymmetric Tides in the Garonne River. Remote Sensing, 13(9), 1856. https://doi.org/10.3390/rs13091856







