Study on Radar Echo-Filling in an Occlusion Area by a Deep Learning Algorithm
Abstract
1. Introduction
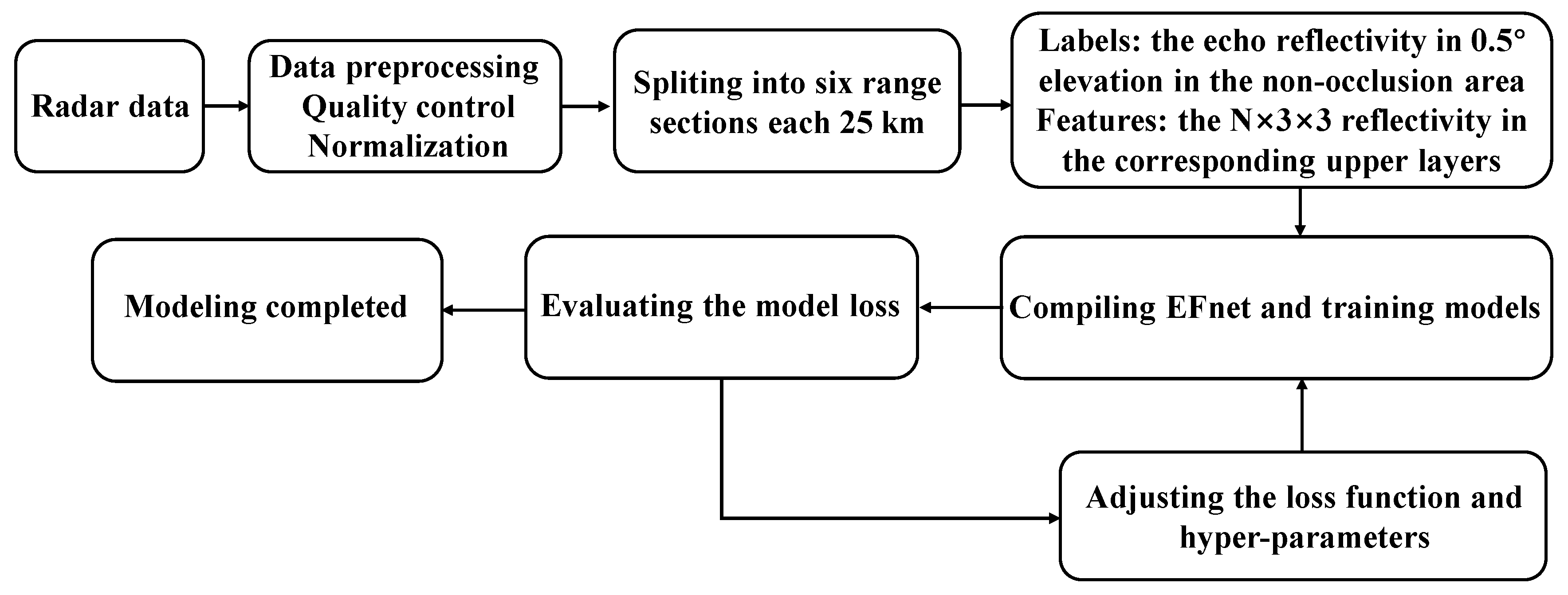
2. Construction of the Training Dataset
2.1. Data Sources
2.2. Data Preprocessing
2.3. Building the Training Dataset
3. Building the Echo-Filling Model
3.1. Model Network Architecture Design
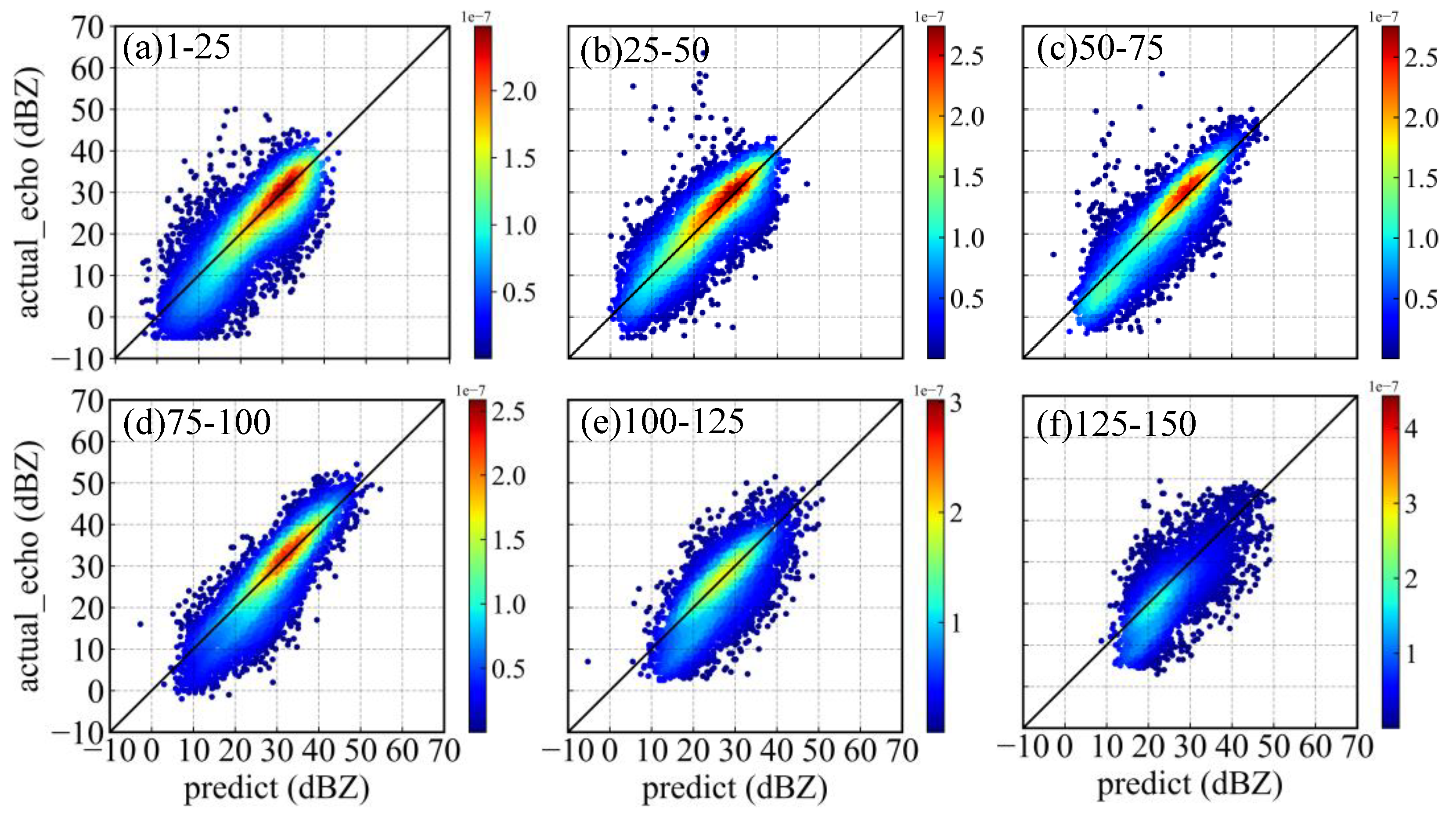
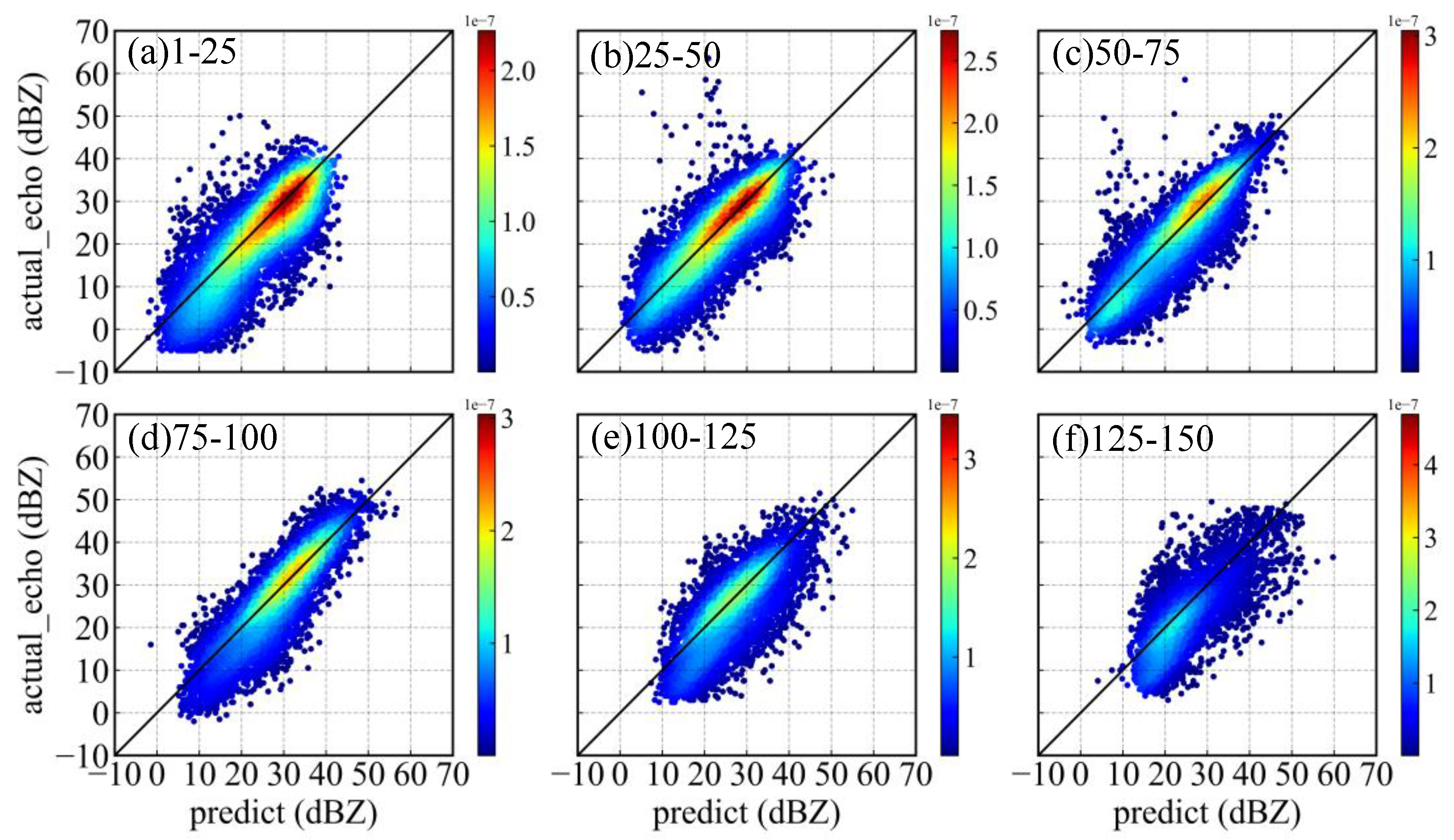
3.2. Self-Defined Loss Function
3.3. Model Hyperparameters Setting and Training
3.4. Comparing with Multivariable Linear Regression Models
4. Case Study
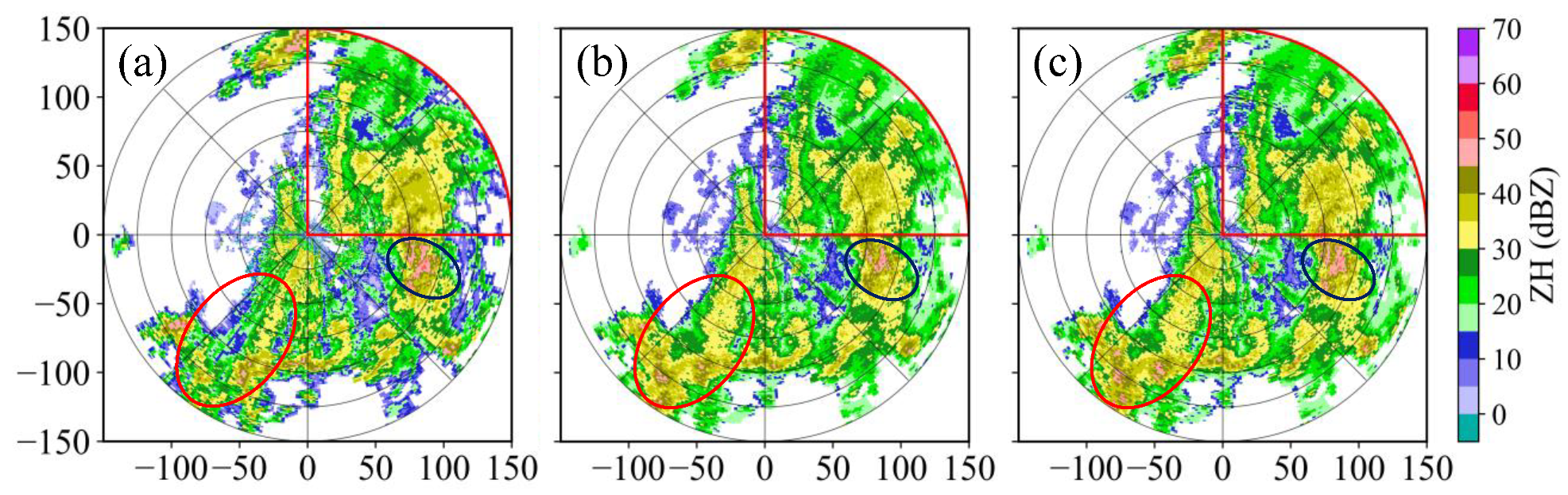
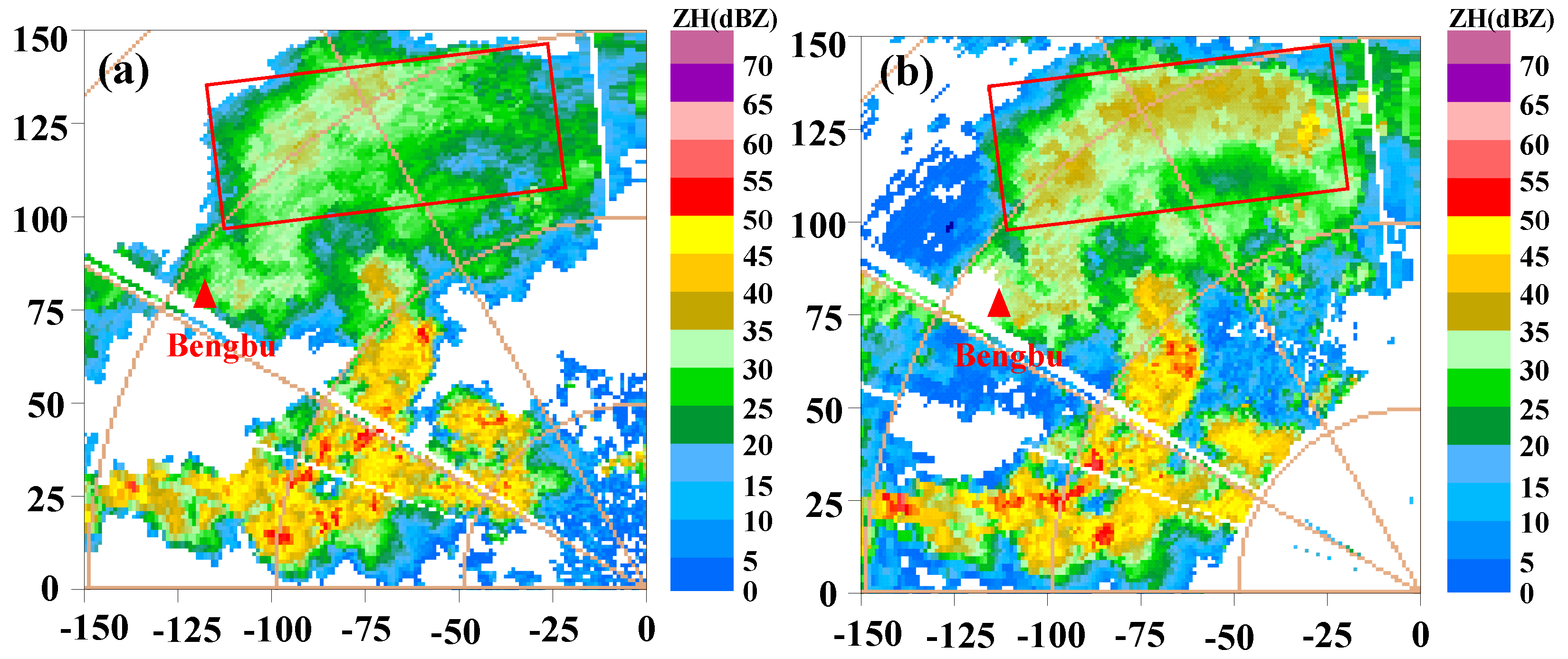
4.1. Weak Echoes-Dominated Case
4.2. Strong Echoes-Dominated Case
5. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yu, X.D.; Yao, X.P.; Xiong, T.N.; Zhou, X.G.; Wu, H.; Deng, B.S.; Song, Y. Principle and Application of Doppler Weather Radar; China Meteorological Press: Beijing, China, 2006; pp. 63–72. [Google Scholar]
- Westrick, K.J.; Mass, C.F.; Colle, B.A. The Limitations of the WSR-88D Radar Network for Quantitative Precipitation Measurement over the Coastal Western United States. Bull. Amer. Meteor. Soc. 1999, 80, 2289–2298. [Google Scholar] [CrossRef]
- Germann, U.; Joss, J. Operational Measurement of Precipitation in Mountainous Terrain; Springer: Berlin/Heidelberg, Germany, 2004; pp. 52–77. [Google Scholar]
- Battan, L.J. Radar Observation of the Atmosphere; The University of Chicago Press: Chicago, IL, USA, 1973. [Google Scholar]
- Lang, T.J.; Nesbitt, S.W.; Carey, L.D. On the Correction of Partial Beam Blockage in Polarimetric Radar Data. J. Atmos. Ocean. Technol. 2009, 26, 943–957. [Google Scholar] [CrossRef]
- Luo, L.; Jing, G.F.; Guo, J.; You, Y. Frequency of the “Cross Points” of Rayleigh Wave Dispersion Curves in Multi-layered Medium with Low Velocity Layer. Sci. Technol. Eng. 2016, 16, 12–19. (In Chinese) [Google Scholar]
- Lee, J.; Jung, S.H.; Kim, H.L.; Lee, S.K. Improved Rainfall Estimation Based on Corrected Radar Reflectivity in Partial Beam Blockage Area of S-band Dual-Polarization Radar. Korean Meteorol. Soc. 2017, 27, 467–481. [Google Scholar]
- Zhang, Y.P.; Liu, J.; Xia, W.M.; Gu, S.S. The Calculation of Beam Blockage Coefficients in Estimating Regional Precipitation with Radar. J. Nanjing Inst. Meteorol. 2002, 25, 67–74. (In Chinese) [Google Scholar]
- Yang, H.P.; Zhang, P.Y.; Cheng, M.H.; Li, B.; Xiong, Y.; Gao, Y.C.; Chen, D.R. The Valid Mosaic Data Region of the CINRAD Network. J. Appl. Meteorol. Sci. 2009, 20, 47–55. (In Chinese) [Google Scholar]
- Shakti, P.C.; Maki, M.; Shimizu, S.; Maesaka, T.; Kim, D.-S.; Lee, D.-I.; Iida, H. Correction of Reflectivity in the Presence of Partial Beam Blockage over a Mountainous Region Using X-Band Dual Polarization Radar. J. Hydrometeorol. 2013, 14, 744–764. [Google Scholar]
- Gou, Y.B.; Liu, L.P.; Li, R.Y.; Du, M.Y.; Duan, Y.P. Radar Partial Shielding Region Identification Algorithm Based on the Probability Characteristics of Radar Echoes. Plateau Meteorol. 2015, 34, 556–567. (In Chinese) [Google Scholar]
- Huang, X.Y.; Ma, L.; Yang, M.; Yin, J.N.; Liu, Y.F. Recognition and correction of beam blockage of weather radar based on spatial correlation. Sci. Meteorol. Sinica 2019, 39, 532–539. (In Chinese) [Google Scholar]
- Germann, U.; Galli, G.; Boscacci, M.; Bolliger, M. Radar precipitation measurement in a mountainous region. Quart. J. Roy. Meteorol. Soc. 2006, 132, 1669–1692. [Google Scholar] [CrossRef]
- Tabary, P. The New French Operational Radar Rainfall Product. Part I: Methodology. Weather Forecast. 2007, 22, 393–408. [Google Scholar] [CrossRef]
- Germann, U.; Joss, J. Mesobeta Profiles to Extrapolate Radar Precipitation Measurements above the Alps to the Ground Level. J. Appl. Meteorol. 2002, 41, 542–557. [Google Scholar] [CrossRef]
- Yang, F.; Gu, S.S.; Huang, X.Y.; Sun, Q.; Wu, L.L.; Xia, W.M. Determination of Vertical Profiles of Reflectivity for Estimation of Stratiform Cloud Precipitation in Ground Clutter Areas. J. Nanjing Inst. Meteorol. 2009, 32, 145–150. (In Chinese) [Google Scholar]
- Andrieu, H.; Creutin, J.D.; Delrieu, G.; Faure, D. Use of a weather radar for the hydrology of a mountainous area. Part I: Radar measurement interpretation. J. Hydrol. 1997, 193, 1–25. [Google Scholar] [CrossRef]
- Creutin, J.D.; Andrieu, H.; Faure, D. Use of a weather radar for the hydrology of a mountainous area. Part II: Radar measurement validation. J. Hydrol. 1997, 193, 26–44. [Google Scholar] [CrossRef]
- Yang, L.; Liu, L.P.; Wang, H.Y. Filling-up of Occultation Regions Using Vertical Profile of Reflectivity Factor. Meteor. Sci. Technol. 2015, 43, 788–793. (In Chinese) [Google Scholar]
- Tan, C.; Feng, X.; Long, J.; Geng, L. FORECAST-CLSTM: A New Convolutional LSTM Network for Cloudage Nowcasting. In Proceedings of the 2018 IEEE Visual Communications and Image Processing (VCIP), Taichung, Taiwan, 9–12 December 2018; pp. 1–4. [Google Scholar]
- Gorooh, V.A.; Kalia, S.; Nguyen, P.; Hsu, K.; Sorooshian, S.; Ganguly, S.; Nemani, R. Deep Neural Network Cloud-Type Classification (DeepCTC) Model and Its Application in Evaluating PERSIANN-CCS. Remote Sens. 2020, 12, 316. [Google Scholar] [CrossRef]
- Lee, J.; In, J.; Cha, D.H.; Park, H.; Sim, S. Tropical Cyclone Intensity Estimation Using Multi-Dimensional Convolutional Neural Networks from Geostationary Satellite Data. Remote Sens. 2020, 12, 108. [Google Scholar] [CrossRef]
- Fabry, F. Radar Meteorology—Principles and Practice; Cambridge University Press: Cambridge, UK, 2015; p. 272. [Google Scholar]
- Shi, X.; Chen, Z.; Wang, H.; Yeung, D.Y.; Wong, W.K.; Woo, W.C. Convolutional LSTM network: A machine learning approach for precipitation nowcasting. In Proceedings of the 28th International Conference on Neural Information Processing Systems (NeurIPS), Montreal, QC, Canada, 7–12 December 2015; pp. 802–810. [Google Scholar]
- Zhou, K.H.; Zheng, Y.G.; Li, B.; Dong, W.; Zhang, X.L. Forecasting different types of convective weather: A deep learning approach. J. Meteorol. Res. 2019, 33, 797–809. [Google Scholar] [CrossRef]
- Tran, Q.K.; Song, S.K. Multi-Channel Weather Radar Echo Extrapolation with Convolutional Recurrent Neural Networks. Remote Sens. 2019, 11, 2303. [Google Scholar] [CrossRef]
- Wei, C.C.; Hsieh, P.Y. Estimation of Hourly Rainfall during Typhoons Using Radar Mosaic-Based Convolutional Neural Networks. Remote Sens. 2020, 12, 896. [Google Scholar] [CrossRef]
- Bouget, V.; Béréziat, D.; Brajard, J.; Charantonis, A.; Filoche, A. Fusion of Rain Radar Images and Wind Forecasts in a Deep Learning Model Applied to Rain Nowcasting. Remote Sens. 2021, 13, 246. [Google Scholar] [CrossRef]
- Liu, L.P.; Wu, L.L.; Yang, Y.M. Development of Fuzzy-logical Two-step Ground Clutter Detection Algorithm. Acta Meteorol. Sinica. 2007, 65, 252–260. (In Chinese) [Google Scholar]
- Li, F.; Liu, L.P.; Wang, H.Y.; Jiang, Y. Identification of Non-precipitation Meteorological Echoes with Doppler Weather Radar. J. Appl. Meteor. Sci. 2012, 23, 147–158. (In Chinese) [Google Scholar]
- Wen, H.; Liu, L.P.; Zhang, Y. Improvements of ground clutter identification algorithm for Doppler Weather Radar. Plateau Meteor. 2017, 36, 736–746. (In Chinese) [Google Scholar]
- Zhang, P.C.; Dai, T.P.; Du, B.Y. Radar Meteorology; China Meteorological Press: Beijing, China, 2001; pp. 100–103. [Google Scholar]
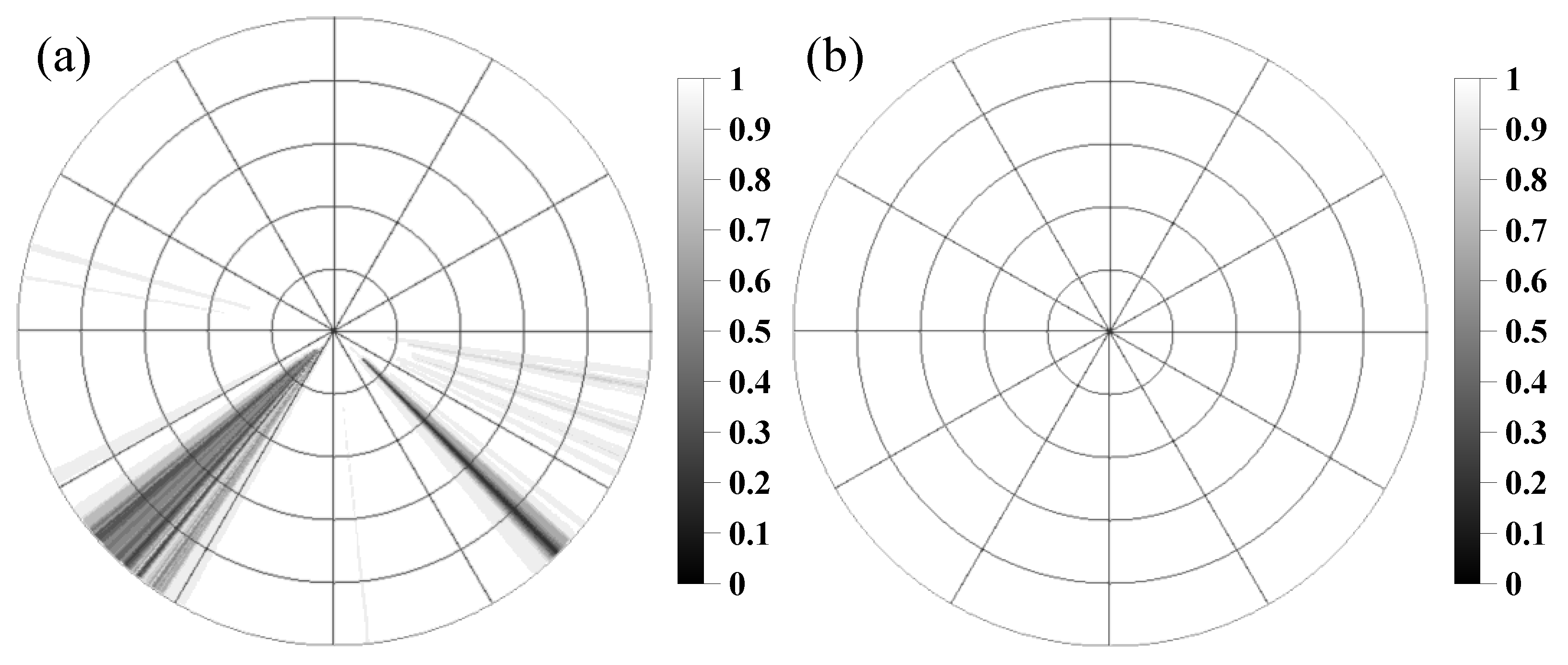




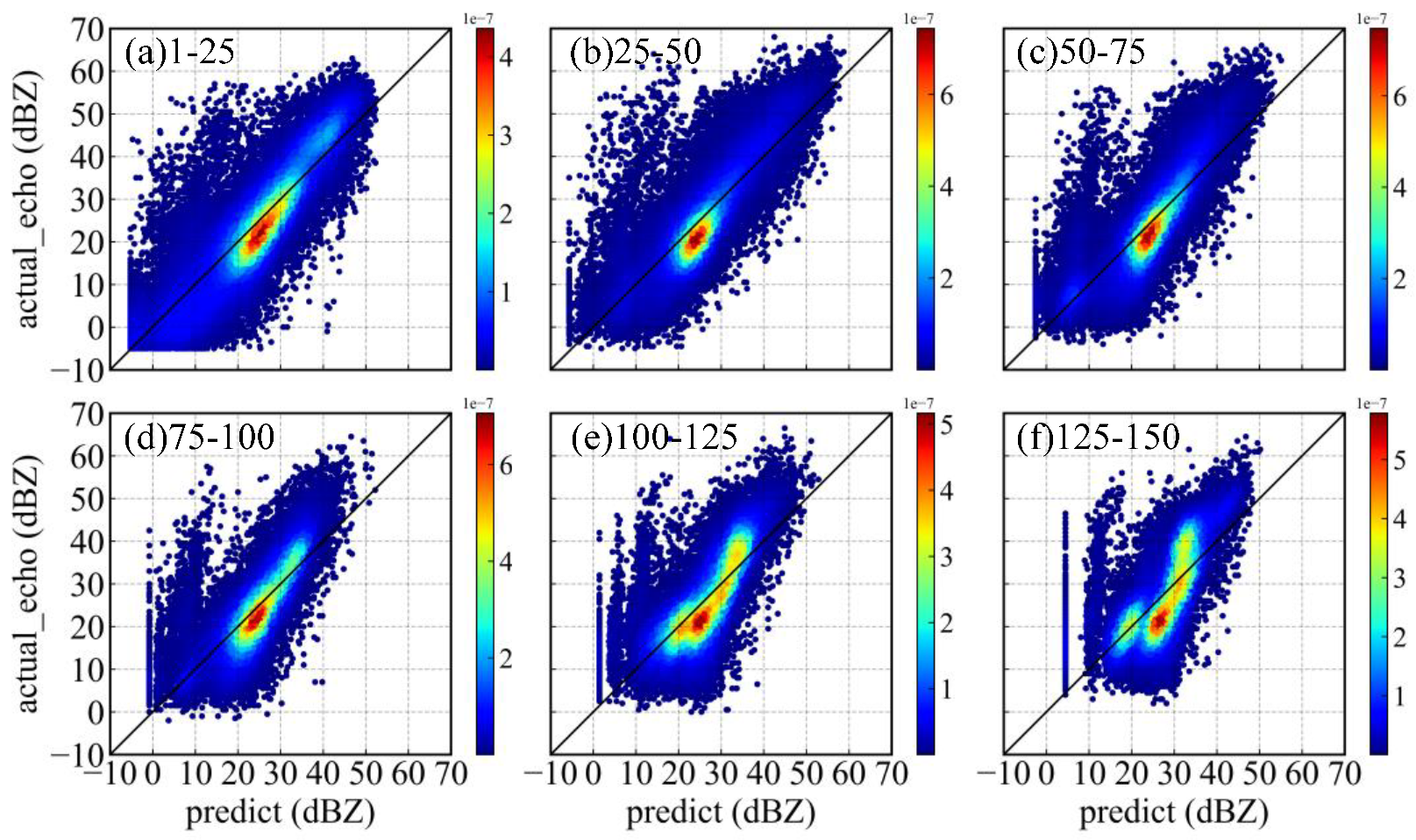



| Range (km) | 1–25 | 25–50 | 50–75 | 75–100 | 100–125 | 125–150 |
|---|---|---|---|---|---|---|
| Using elevation layer number | 7 | 6 | 5 | 4 | 3 | 2 |
| Data size (group) | 171,887 | 190,182 | 199,830 | 185,808 | 201,990 | 182,676 |
| Training set size (80%) | 137,510 | 152,146 | 159,864 | 148,646 | 161,592 | 146,141 |
| Test set size (20%) | 34,377 | 38,036 | 39,966 | 37,162 | 40,398 | 36,535 |
| Range (km) | 1–25 | 25–50 | 50–75 | 75–100 | 100–125 | 125–150 |
|---|---|---|---|---|---|---|
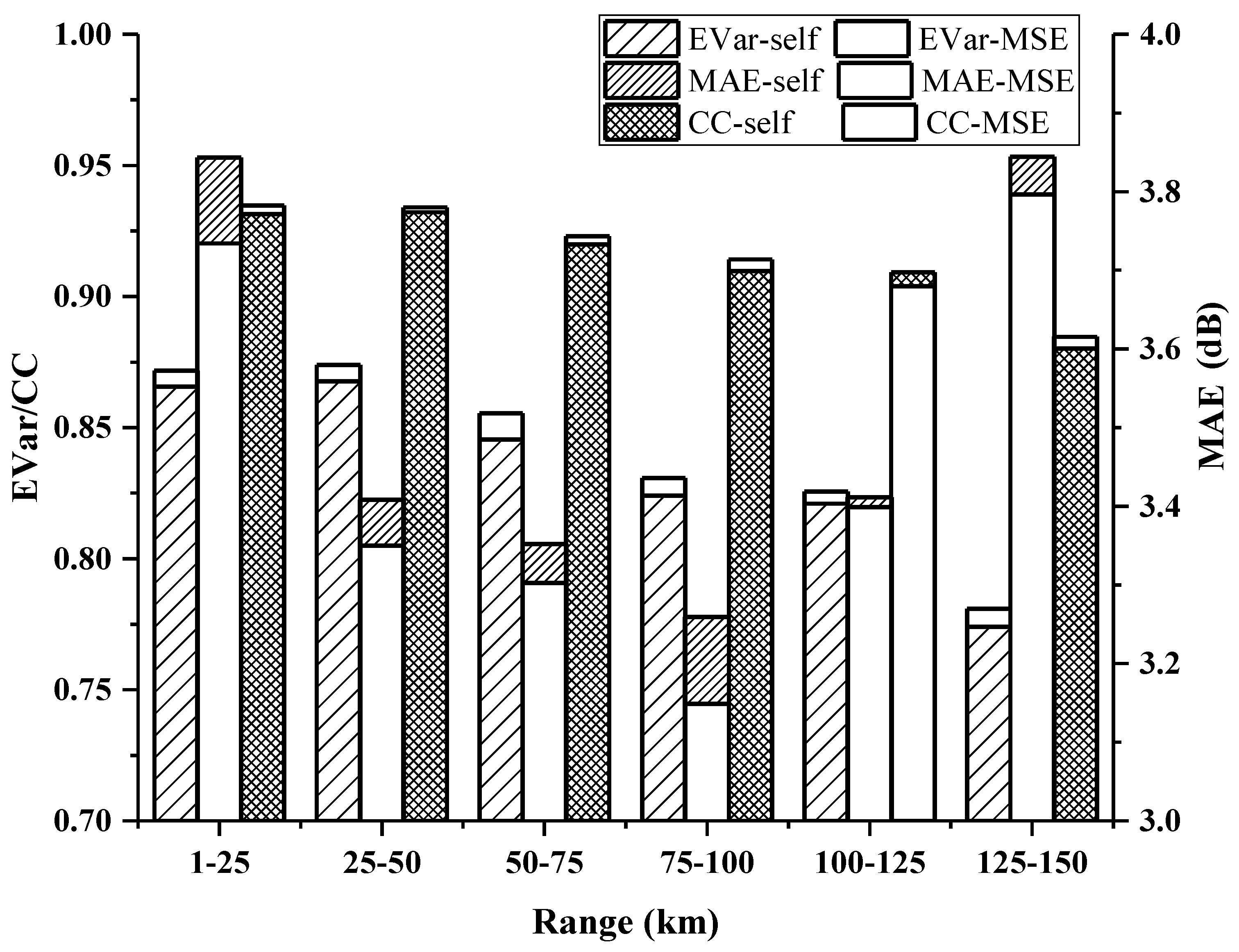
| EVar | 0.8717 | 0.8739 | 0.8555 | 0.8309 | 0.8256 | 0.7809 |
| MAE | 3.7340 | 3.3501 | 3.3028 | 3.1489 | 3.3989 | 3.7964 |
| CC | 0.9346 | 0.9340 | 0.9230 | 0.9142 | 0.9039 | 0.8846 |
| Range (km) | 1–25 | 25–50 | 50–75 | 75–100 | 100–125 | 125–150 |
|---|---|---|---|---|---|---|
| EVar | 0.8656 | 0.8677 | 0.8455 | 0.8241 | 0.8210 | 0.7740 |
| MAE | 3.8435 | 3.4084 | 3.3520 | 3.2592 | 3.4112 | 3.8445 |
| CC | 0.9314 | 0.9321 | 0.9199 | 0.9097 | 0.9092 | 0.8802 |
| Range (km) | 1–25 | 25–50 | 50–75 | 75–100 | 100–125 | 125–150 | |
|---|---|---|---|---|---|---|---|
| MSE loss function | EVar | 0.9156 | 0.9481 | 0.8652 | 0.8373 | 0.8809 | 0.9029 |
| MAE | 4.2895 | 3.1031 | 3.2099 | 3.9277 | 3.9277 | 4.3006 | |
| CC | 0.9610 | 0.9735 | 0.9378 | 0.9415 | 0.9415 | 0.9505 | |
| Self-defined loss function | EVar | 0.9243 | 0.9486 | 0.8685 | 0.8562 | 0.8696 | 0.9496 |
| MAE | 4.0580 | 2.9573 | 3.2546 | 2.9447 | 3.9176 | 4.2122 | |
| CC | 0.9635 | 0.9749 | 0.9341 | 0.9375 | 0.9423 | 0.9012 | |
| Range (km) | 1–25 | 25–50 | 50–75 | 75–100 | 100–125 | 125–150 | |
|---|---|---|---|---|---|---|---|
| MSE loss function | EVar | 0.8709 | 0.9284 | 0.9497 | 0.9488 | 0.9488 | 0.9354 |
| MAE | 4.4745 | 4.4930 | 3.8682 | 4.3950 | 3.9859 | 4.4552 | |
| CC | 0.9333 | 0.9636 | 0.9745 | 0.9746 | 0.9743 | 0.9671 | |
| Self-defined loss function | EVar | 0.8763 | 0.9301 | 0.9535 | 0.9535 | 0.9483 | 0.9342 |
| MAE | 4.3681 | 4.5081 | 3.6362 | 4.1202 | 3.8835 | 4.5047 | |
| CC | 0.9374 | 0.9647 | 0.9767 | 0.9765 | 0.9756 | 0.9666 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, X.; Hu, Z.; Zheng, J.; Li, B.; Zuo, Y. Study on Radar Echo-Filling in an Occlusion Area by a Deep Learning Algorithm. Remote Sens. 2021, 13, 1779. https://doi.org/10.3390/rs13091779
Yin X, Hu Z, Zheng J, Li B, Zuo Y. Study on Radar Echo-Filling in an Occlusion Area by a Deep Learning Algorithm. Remote Sensing. 2021; 13(9):1779. https://doi.org/10.3390/rs13091779
Chicago/Turabian StyleYin, Xiaoyan, Zhiqun Hu, Jiafeng Zheng, Boyong Li, and Yuanyuan Zuo. 2021. "Study on Radar Echo-Filling in an Occlusion Area by a Deep Learning Algorithm" Remote Sensing 13, no. 9: 1779. https://doi.org/10.3390/rs13091779
APA StyleYin, X., Hu, Z., Zheng, J., Li, B., & Zuo, Y. (2021). Study on Radar Echo-Filling in an Occlusion Area by a Deep Learning Algorithm. Remote Sensing, 13(9), 1779. https://doi.org/10.3390/rs13091779