Sensitivity of Near-Infrared Permanent Laser Scanning Intensity for Retrieving Soil Moisture on a Coastal Beach: Calibration Procedure Using In Situ Data
Abstract
1. Introduction
2. Test Site
2.1. Permanent Laser Scanner
2.2. In Situ TDR Measurements
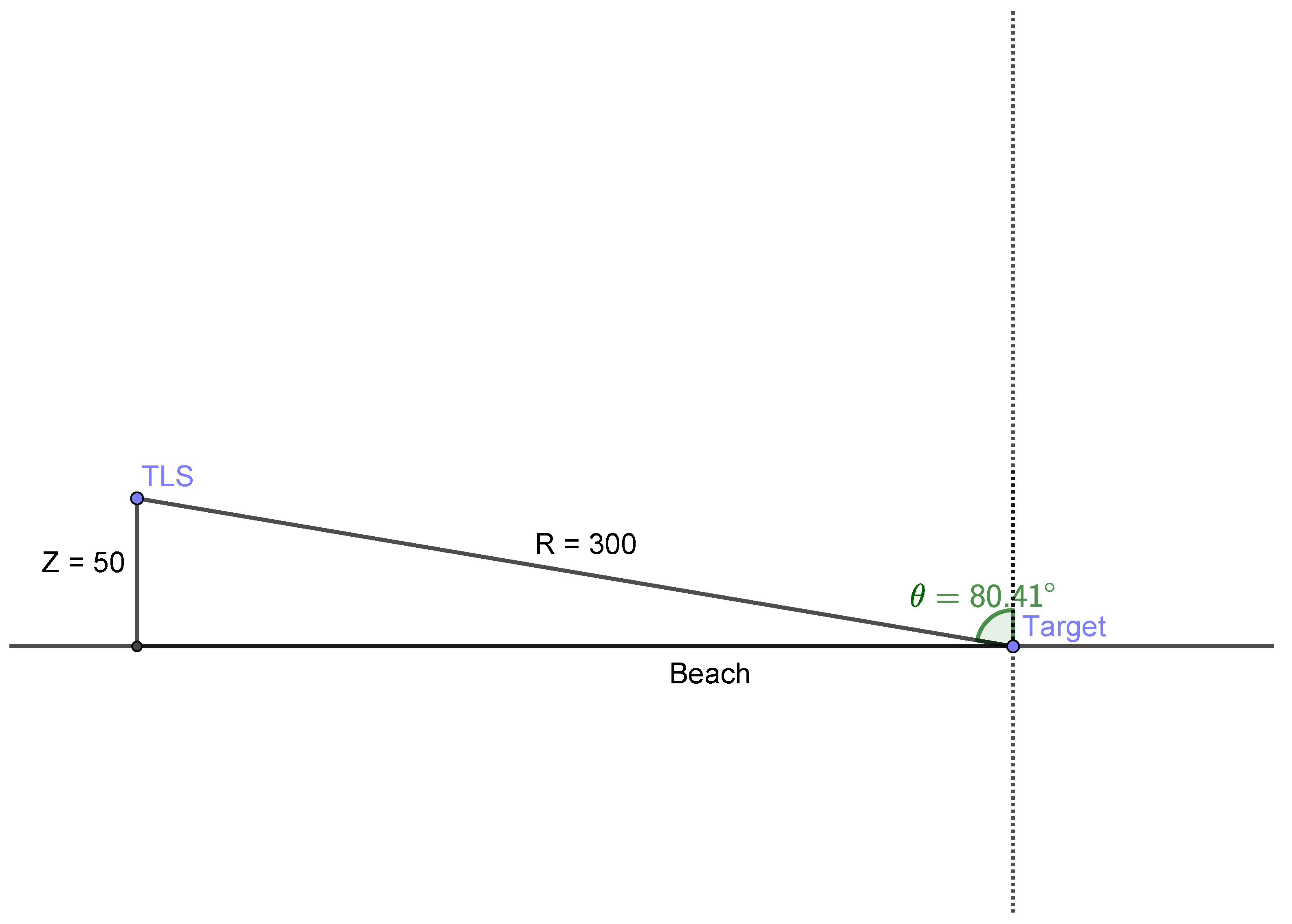
2.3. Incidence Angle and Distance from the TLS
3. Methods
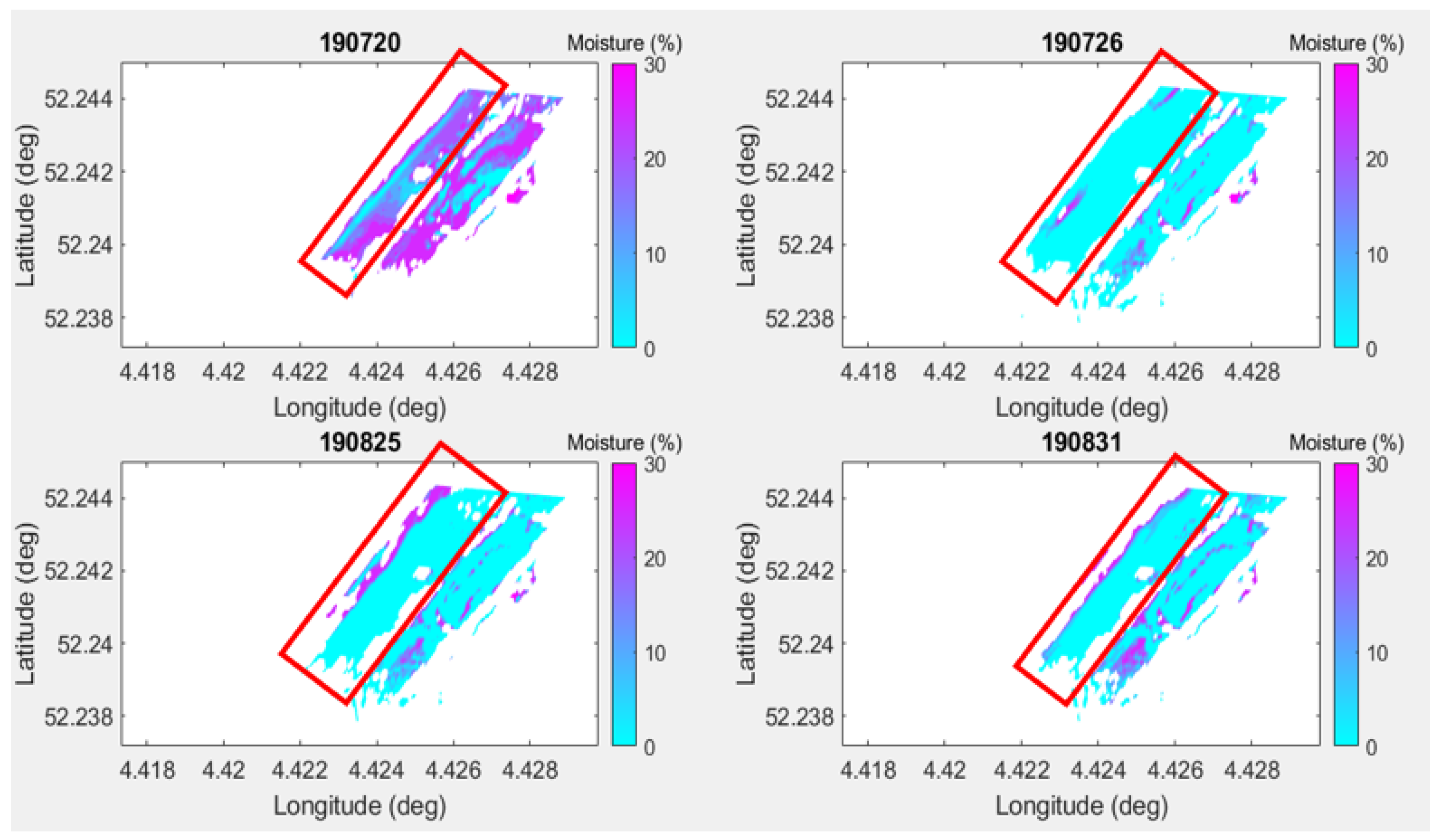
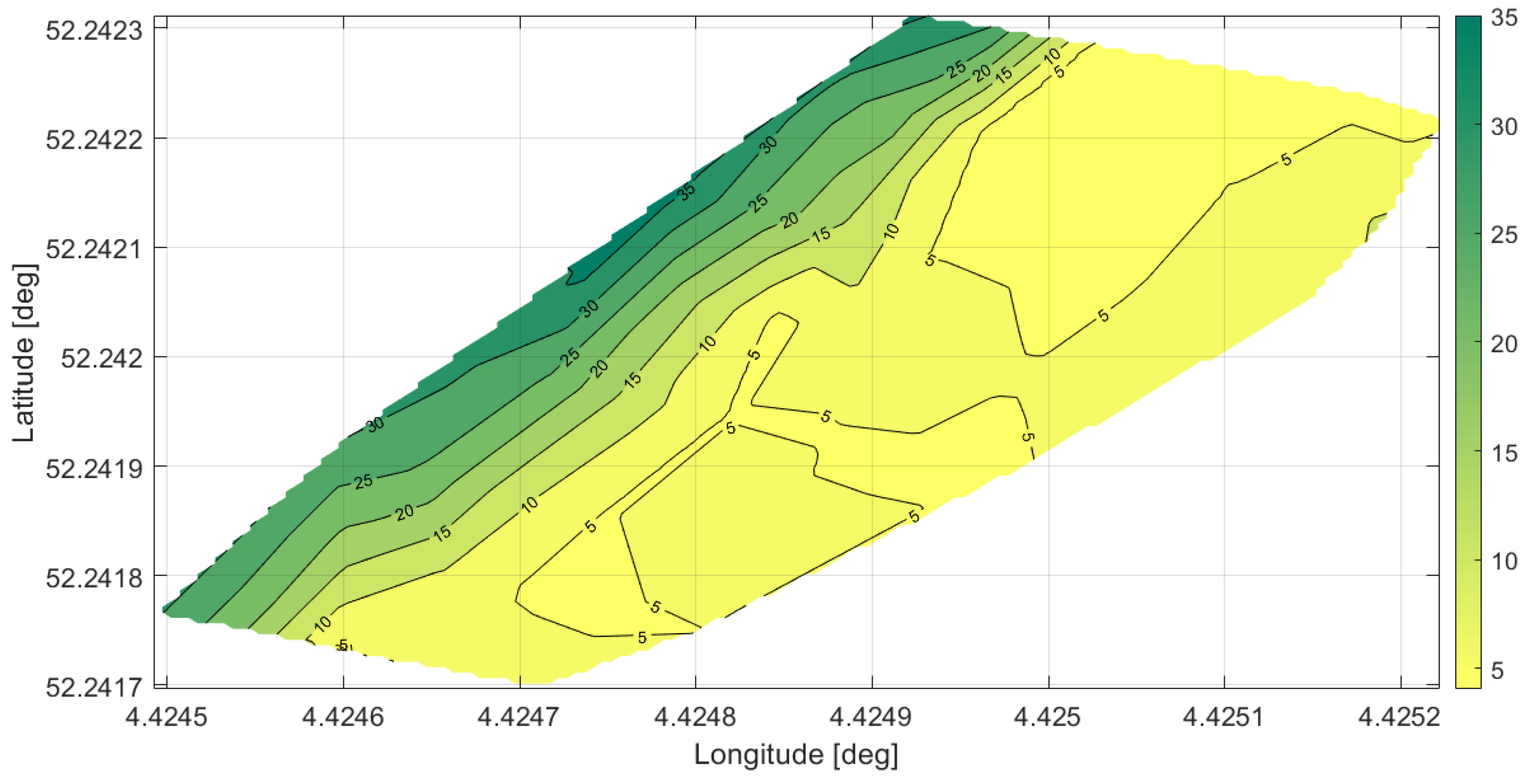
4. Results and Validation
4.1. Validation
4.2. Environmental and Meteorological Conditions
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Keijsers, J.; De Groot, A.; Riksen, M. Modeling the biogeomorphic evolution of coastal dunes in response to climate change. J. Geophys. Res. Earth Surf. 2016, 121, 1161–1181. [Google Scholar] [CrossRef]
- Nickling, W.G.; Davidson-Arnott, R. Beaches and coastal sand dunes. In Proceedings of the Canadian Symposium on Coastal Sand Dunes, Guelph, ON, Canada, 12–14 September 1990; p. 1. [Google Scholar]
- Sherman, D.J.; Bauer, B.O. Dynamics of beach-dune systems. Prog. Phys. Geogr. 1993, 17, 413–447. [Google Scholar] [CrossRef]
- Bauer, B.O.; Davidson-Arnott, R.G. A general framework for modeling sediment supply to coastal dunes including wind angle, beach geometry, and fetch effects. Geomorphology 2003, 49, 89–108. [Google Scholar] [CrossRef]
- Anthony, E.J.; Ruz, M.H.; Vanhée, S. Aeolian sand transport over complex intertidal bar-trough beach topography. Geomorphology 2009, 105, 95–105. [Google Scholar] [CrossRef]
- Namikas, S.; Edwards, B.; Bitton, M.; Booth, J.; Zhu, Y. Temporal and spatial variabilities in the surface moisture content of a fine-grained beach. Geomorphology 2010, 114, 303–310. [Google Scholar] [CrossRef]
- Van der Wal, D. Effects of fetch and surface texture on aeolian sand transport on two nourished beaches. J. Arid Environ. 1998, 39, 533–547. [Google Scholar] [CrossRef]
- Neuman, C.M.; Scott, M.M. A wind tunnel study of the influence of pore water on aeolian sediment transport. J. Arid Environ. 1998, 39, 403–419. [Google Scholar] [CrossRef]
- Jackson, N.L.; Nordstrom, K.F. Effects of time-dependent moisture content of surface sediments on aeolian transport rates across a beach, Wildwood, New Jersey, USA. Earth Surf. Process. Landf. J. Br. Geomorphol. Group 1997, 22, 611–621. [Google Scholar] [CrossRef]
- Wiggs, G.; Baird, A.; Atherton, R. The dynamic effects of moisture on the entrainment and transport of sand by wind. Geomorphology 2004, 59, 13–30. [Google Scholar] [CrossRef]
- Delgado-Fernandez, I. Meso-scale modelling of aeolian sediment input to coastal dunes. Geomorphology 2011, 130, 230–243. [Google Scholar] [CrossRef]
- Sarre, R. Evaluation of aeolian sand transport equations using intertidal zone measurements, Saunton Sands, England. Sedimentology 1988, 35, 671–679. [Google Scholar] [CrossRef]
- Namikas, S.L.; Sherman, D.J. A review of the effects of surface moisture content on aeolian sand transport. In Desert Aeolian Processes; Springer: Berlin, Germany, 1995; pp. 269–293. [Google Scholar]
- Cornelis, W.; Gabriels, D. The effect of surface moisture on the entrainment of dune sand by wind: An evaluation of selected models. Sedimentology 2003, 50, 771–790. [Google Scholar] [CrossRef]
- McKenna-Neuman, C.; Nickling, W. A theoretical and wind tunnel investigation of the effect of capillary water on the entrainment of sediment by wind. Can. J. Soil Sci. 1989, 69, 79–96. [Google Scholar] [CrossRef]
- Kaleita, A.L.; Heitman, J.L.; Logsdon, S.D. Field calibration of the theta probe for Des Moines lobe soils. Appl. Eng. Agric. 2005, 21, 865–870. [Google Scholar] [CrossRef]
- Brakenhoff, L.B.; Smit, Y.; Donker, J.J.; Ruessink, G. Tide-induced variability in beach surface moisture: Observations and modelling. Earth Surf. Process. Landf. 2019, 44, 317–330. [Google Scholar] [CrossRef]
- Atherton, R.J.; Baird, A.J.; Wiggs, G.F. Inter-tidal dynamics of surface moisture content on a meso-tidal beach. J. Coast. Res. 2001, 17, 482–489. [Google Scholar]
- Schmutz, P.P.; Namikas, S.L. Measurement and modeling of moisture content above an oscillating water table: Implications for beach surface moisture dynamics. Earth Surf. Process. Landf. 2013, 38, 1317–1325. [Google Scholar] [CrossRef]
- Famiglietti, J.S.; Ryu, D.; Berg, A.A.; Rodell, M.; Jackson, T.J. Field observations of soil moisture variability across scales. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Hájek, M.; Hájková, P.; Kočí, M.; Jiroušek, M.; Mikulášková, E.; Kintrová, K. Do we need soil moisture measurements in the vegetation–environment studies in wetlands? J. Veg. Sci. 2013, 24, 127–137. [Google Scholar] [CrossRef]
- Yang, X.; Yu, Y.; Li, M. Estimating soil moisture content using laboratory spectral data. J. For. Res. 2019, 30, 1073–1080. [Google Scholar] [CrossRef]
- Zhao, Y.; Peth, S.; Hallett, P.; Wang, X.; Giese, M.; Gao, Y.; Horn, R. Factors controlling the spatial patterns of soil moisture in a grazed semi-arid steppe investigated by multivariate geostatistics. Ecohydrology 2011, 4, 36–48. [Google Scholar] [CrossRef]
- Bretreger, D.; Yeo, I.Y.; Melchers, R. Terrain wetness indices derived from LiDAR to inform soil moisture and corrosion potential for underground infrastructure. Sci. Total Environ. 2021, 756, 144138. [Google Scholar] [CrossRef] [PubMed]
- Walker, I.; Davidson-Arnott, R.; Hesp, P.; Bauer, B.; Ollerhead, J. Mean flow and turbulence responses in airflow over foredunes: New insights from recent research. J. Coast. Res. 2009, I, 366–370. [Google Scholar]
- Hoonhout, B.M.; Vries, S.D. A process-based model for aeolian sediment transport and spatiotemporal varying sediment availability. J. Geophys. Res. Earth Surf. 2016, 121, 1555–1575. [Google Scholar] [CrossRef]
- Hoonhout, B.; de Vries, S. Field measurements on spatial variations in aeolian sediment availability at the Sand Motor mega nourishment. Aeol. Res. 2017, 24, 93–104. [Google Scholar] [CrossRef]
- Cohn, N.; Ruggiero, P.; de Vries, S.; Kaminsky, G.M. New insights on coastal foredune growth: The relative contributions of marine and aeolian processes. Geophys. Res. Lett. 2018, 45, 4965–4973. [Google Scholar] [CrossRef]
- Nield, J.M.; Wiggs, G.F.; Squirrell, R.S. Aeolian sand strip mobility and protodune development on a drying beach: Examining surface moisture and surface roughness patterns measured by terrestrial laser scanning. Earth Surf. Process. Landf. 2011, 36, 513–522. [Google Scholar] [CrossRef]
- Yang, Y.; Davidson-Arnott, R.G. Rapid measurement of surface moisture content on a beach. J. Coast. Res. 2005, 21, 447–452. [Google Scholar] [CrossRef]
- Davidson-Arnott, R.G.; Yang, Y.; Ollerhead, J.; Hesp, P.A.; Walker, I.J. The effects of surface moisture on aeolian sediment transport threshold and mass flux on a beach. Earth Surf. Process. Landf. J. Br. Geomorphol. Res. Group 2008, 33, 55–74. [Google Scholar] [CrossRef]
- Dwevedi, A.; Kumar, P.; Kumar, P.; Kumar, Y.; Sharma, Y.K.; Kayastha, A.M. Soil sensors: Detailed insight into research updates, significance, and future prospects. In New Pesticides and Soil Sensors; Elsevier: Hoboken, NJ, USA, 2017; pp. 561–594. [Google Scholar]
- Edwards, B.L.; Namikas, S.L. Small-scale variability in surface moisture on a fine-grained beach: Implications for modeling aeolian transport. Earth Surf. Process. Land. 2009, 34, 1333–1338. [Google Scholar] [CrossRef]
- Sheng, W.; Zhou, R.; Sadeghi, M.; Babaeian, E.; Robinson, D.A.; Tuller, M.; Jones, S.B. A TDR array probe for monitoring near-surface soil moisture distribution. Vadose Zone J. 2017, 16, 1–8. [Google Scholar] [CrossRef]
- Edwards, B.L.; Schmutz, P.P.; Namikas, S.L. Comparison of surface moisture measurements with depth-integrated moisture measurements on a fine-grained beach. J. Coast. Res. 2013, 29, 1284–1291. [Google Scholar]
- Ångström, A. The albedo of various surfaces of ground. Geogr. Ann. 1925, 7, 323–342. [Google Scholar]
- Twomey, S.A.; Bohren, C.F.; Mergenthaler, J.L. Reflectance and albedo differences between wet and dry surfaces. Appl. Opt. 1986, 25, 431–437. [Google Scholar] [CrossRef] [PubMed]
- Lobell, D.B.; Asner, G.P. Moisture effects on soil reflectance. Soil Sci. Soc. Am. J. 2002, 66, 722–727. [Google Scholar] [CrossRef]
- Philpot, W. Spectral reflectance of wetted soils. Proc. ASD IEEE GRS 2010, 2, 1–12. [Google Scholar]
- Nolet, C.; Poortinga, A.; Roosjen, P.; Bartholomeus, H.; Ruessink, G. Measuring and modeling the effect of surface moisture on the spectral reflectance of coastal beach sand. PLoS ONE 2014, 9, e112151. [Google Scholar] [CrossRef]
- Williams, R.; Brasington, J.; Vericat, D.; Hicks, D. Hyperscale terrain modelling of braided rivers: Fusing mobile terrestrial laser scanning and optical bathymetric mapping. Earth Surf. Process. Landf. 2014, 39, 167–183. [Google Scholar] [CrossRef]
- Darke, I.; Davidson-Arnott, R.; Ollerhead, J. Measurement of beach surface moisture using surface brightness. J. Coast. Res. 2009, 25, 248–256. [Google Scholar] [CrossRef]
- Delgado-Fernandez, I.; Davidson-Arnott, R. Sediment input to foredunes: Description and frequency of transport events at Greenwich Dunes, PEI, Canada. J. Coast. Res. 2009, 1, 302–306. [Google Scholar]
- McKenna Neuman, C.; Langston, G. Measurement of water content as a control of particle entrainment by wind. Earth Surf. Process. Landf. J. Br. Geomorphol. Res. Group 2006, 31, 303–317. [Google Scholar] [CrossRef]
- Lookingbill, T.; Urban, D. An empirical approach towards improved spatial estimates of soil moisture for vegetation analysis. Landsc. Ecol. 2004, 19, 417–433. [Google Scholar] [CrossRef]
- Jaboyedoff, M.; Oppikofer, T.; Abellán, A.; Derron, M.H.; Loye, A.; Metzger, R.; Pedrazzini, A. Use of LIDAR in landslide investigations: A review. Nat. Hazards 2012, 61, 5–28. [Google Scholar] [CrossRef]
- Bretreger, D.; Yeo, I.Y.; Melchers, R. LiDAR derived terrain wetness indices to infer soil moisture above underground pipelines. Int. J. Smart Sens. Intell. Syst. 2020, 13. [Google Scholar] [CrossRef]
- Kemppinen, J.; Niittynen, P.; Riihimäki, H.; Luoto, M. Modelling soil moisture in a high-latitude landscape using LiDAR and soil data. Earth Surf. Process. Landf. 2018, 43, 1019–1031. [Google Scholar] [CrossRef]
- Hardy, A.J.; Barr, S.L.; Mills, J.P.; Miller, P.E. Characterising soil moisture in transport corridor environments using airborne LIDAR and CASI data. Hydrol. Process. 2012, 26, 1925–1936. [Google Scholar] [CrossRef]
- Wehr, A.; Lohr, U. Airborne laser scanning—An introduction and overview. ISPRS J. Photogramm. Remote Sens. 1999, 54, 68–82. [Google Scholar] [CrossRef]
- Leempoel, K.; Parisod, C.; Geiser, C.; Daprà, L.; Vittoz, P.; Joost, S. Very high-resolution digital elevation models: Are multi-scale derived variables ecologically relevant? Methods Ecol. Evolut. 2015, 6, 1373–1383. [Google Scholar] [CrossRef]
- Jiang, Y.; Weng, Q. Estimation of hourly and daily evapotranspiration and soil moisture using downscaled LST over various urban surfaces. GISci. Remote Sens. 2017, 54, 95–117. [Google Scholar] [CrossRef]
- Baldwin, D.; Naithani, K.J.; Lin, H. Combined soil-terrain stratification for characterizing catchment-scale soil moisture variation. Geoderma 2017, 285, 260–269. [Google Scholar] [CrossRef]
- Li, X.; Liu, S.; Xiao, Q.; Ma, M.; Jin, R.; Che, T.; Wang, W.; Hu, X.; Xu, Z.; Wen, J.; et al. A multiscale dataset for understanding complex eco-hydrological processes in a heterogeneous oasis system. Sci. Data 2017, 4, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Vosselman, G.; Maas, H.G. Airborne and Terrestrial Laser Scanning; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- French, J.; Burningham, H. Coastal geomorphology: Trends and challenges. Prog. Phys. Geogr. 2009, 33, 117–129. [Google Scholar] [CrossRef]
- Zelaya Wziątek, D.; Terefenko, P.; Kurylczyk, A. Multi-temporal cliff erosion analysis using airborne laser scanning surveys. Remote Sens. 2019, 11, 2666. [Google Scholar] [CrossRef]
- de Sanjosé Blasco, J.J.; Serrano-Cañadas, E.; Sánchez-Fernández, M.; Gómez-Lende, M.; Redweik, P. Application of Multiple Geomatic Techniques for Coastline Retreat Analysis: The Case of Gerra Beach (Cantabrian Coast, Spain). Remote Sens. 2020, 12, 3669. [Google Scholar] [CrossRef]
- Kaasalainen, S.; Niittymaki, H.; Krooks, A.; Koch, K.; Kaartinen, H.; Vain, A.; Hyyppa, H. Effect of target moisture on laser scanner intensity. IEEE Trans. Geosci. Remote Sens. 2009, 48, 2128–2136. [Google Scholar] [CrossRef]
- Tan, K.; Chen, J.; Zhang, W.; Liu, K.; Tao, P.; Cheng, X. Estimation of soil surface water contents for intertidal mudflats using a near-infrared long-range terrestrial laser scanner. ISPRS J. Photogramm. Remote Sens. 2020, 159, 129–139. [Google Scholar] [CrossRef]
- Nield, J.M.; King, J.; Jacobs, B. Detecting surface moisture in aeolian environments using terrestrial laser scanning. Aeol. Res. 2014, 12, 9–17. [Google Scholar] [CrossRef]
- Smit, Y.; Ruessink, G.; Brakenhoff, L.B.; Donker, J.J. Measuring spatial and temporal variation in surface moisture on a coastal beach with a near-infrared terrestrial laser scanner. Aeol. Res. 2018, 31, 19–27. [Google Scholar] [CrossRef]
- Ruessink, G.; Brakenhoff, L.; van Maarseveen, M. Measurement of surface moisture using infra-red terrestrial laser scanning. In EGU General Assembly Conference Abstracts; NASA: Washington, DC, USA, 2014; p. 2797. [Google Scholar]
- Kukko, A.; Kaasalainen, S.; Litkey, P. Effect of incidence angle on laser scanner intensity and surface data. Appl. Opt. 2008, 47, 986–992. [Google Scholar] [CrossRef]
- Franceschi, M.; Teza, G.; Preto, N.; Pesci, A.; Galgaro, A.; Girardi, S. Discrimination between marls and limestones using intensity data from terrestrial laser scanner. ISPRS J. Photogramm. Remote Sens. 2009, 64, 522–528. [Google Scholar] [CrossRef]
- Kaasalainen, S.; Kukko, A.; Lindroos, T.; Litkey, P.; Kaartinen, H.; Hyyppa, J.; Ahokas, E. Brightness measurements and calibration with airborne and terrestrial laser scanners. IEEE Trans. Geosci. Remote Sens. 2008, 46, 528–534. [Google Scholar] [CrossRef]
- González-Jorge, H.; Gonzalez-Aguilera, D.; Rodriguez-Gonzalvez, P.; Arias, P. Monitoring biological crusts in civil engineering structures using intensity data from terrestrial laser scanners. Constr. Build. Mater. 2012, 31, 119–128. [Google Scholar] [CrossRef]
- Kaasalainen, S.; Jaakkola, A.; Kaasalainen, M.; Krooks, A.; Kukko, A. Analysis of incidence angle and distance effects on terrestrial laser scanner intensity: Search for correction methods. Remote Sens. 2011, 3, 2207–2221. [Google Scholar] [CrossRef]
- Jin, J.; De Sloover, L.; Verbeurgt, J.; Stal, C.; Deruyter, G.; Montreuil, A.L.; De Maeyer, P.; De Wulf, A. Measuring Surface Moisture on a Sandy Beach based on Corrected Intensity Data of a Mobile Terrestrial LiDAR. Remote Sens. 2020, 12, 209. [Google Scholar] [CrossRef]
- Vos, S.; Lindenbergh, R.; de Vries, S.; Aagaard, T.; Deigaard, R.; Fuhrman, D. Coastscan: Continuous monitoring of coastal change using terrestrial laser scanning. In Proceedings of the Coastal Dynamics, Helsingor, Danmark, 12–16 June 2017; pp. 12–16. [Google Scholar]
- Eisma, D. Composition, origin and distribution of Dutch coastal sands between Hoek van Holland and the island of Vlieland. Neth. J. Sea Res. 1968, 4, 123–267. [Google Scholar] [CrossRef]
- Wagner, W.; Ullrich, A.; Ducic, V.; Melzer, T.; Studnicka, N. Gaussian decomposition and calibration of a novel small-footprint full-waveform digitising airborne laser scanner. ISPRS J. Photogramm. Remote Sens. 2006, 60, 100–112. [Google Scholar] [CrossRef]
- RIEGL. Data Sheet, RIEGL VZ-2000; RIEGL: Horn, Austria, 2000. [Google Scholar]
- Singh, J.; Levick, S.R.; Guderle, M.; Schmullius, C. Moving from plot-based to hillslope-scale assessments of savanna vegetation structure with long-range terrestrial laser scanning (LR-TLS). Int. J. Appl. Earth Obs. Geoinf. 2020, 90, 102070. [Google Scholar] [CrossRef]
- IMKO. Manual TRIME-PICO 64/32; IMKO Micromodultechnik GmbH: Ettlingen, Germany, 2017. [Google Scholar]
- Schmutz, P.P.; Namikas, S.L. Utility of the Delta-T Theta Probe for obtaining surface moisture measurements from beaches. J. Coast. Res. 2011, 27, 478–484. [Google Scholar]
- Hillel, D. Soil and Water: Physical Principles and Processes; Elsevier: Hoboken, NJ, USA, 2012. [Google Scholar]
- Davidson-Arnott, R.; Bauer, B.; Houser, C. Introduction to Coastal Processes and Geomorphology; Cambridge University Press: Cambridge, UK, 2019. [Google Scholar]
- Pesci, A.; Teza, G. Effects of surface irregularities on intensity data from laser scanning: An experimental approach. Ann. Geophys. 2008, 51, 839–848. [Google Scholar]

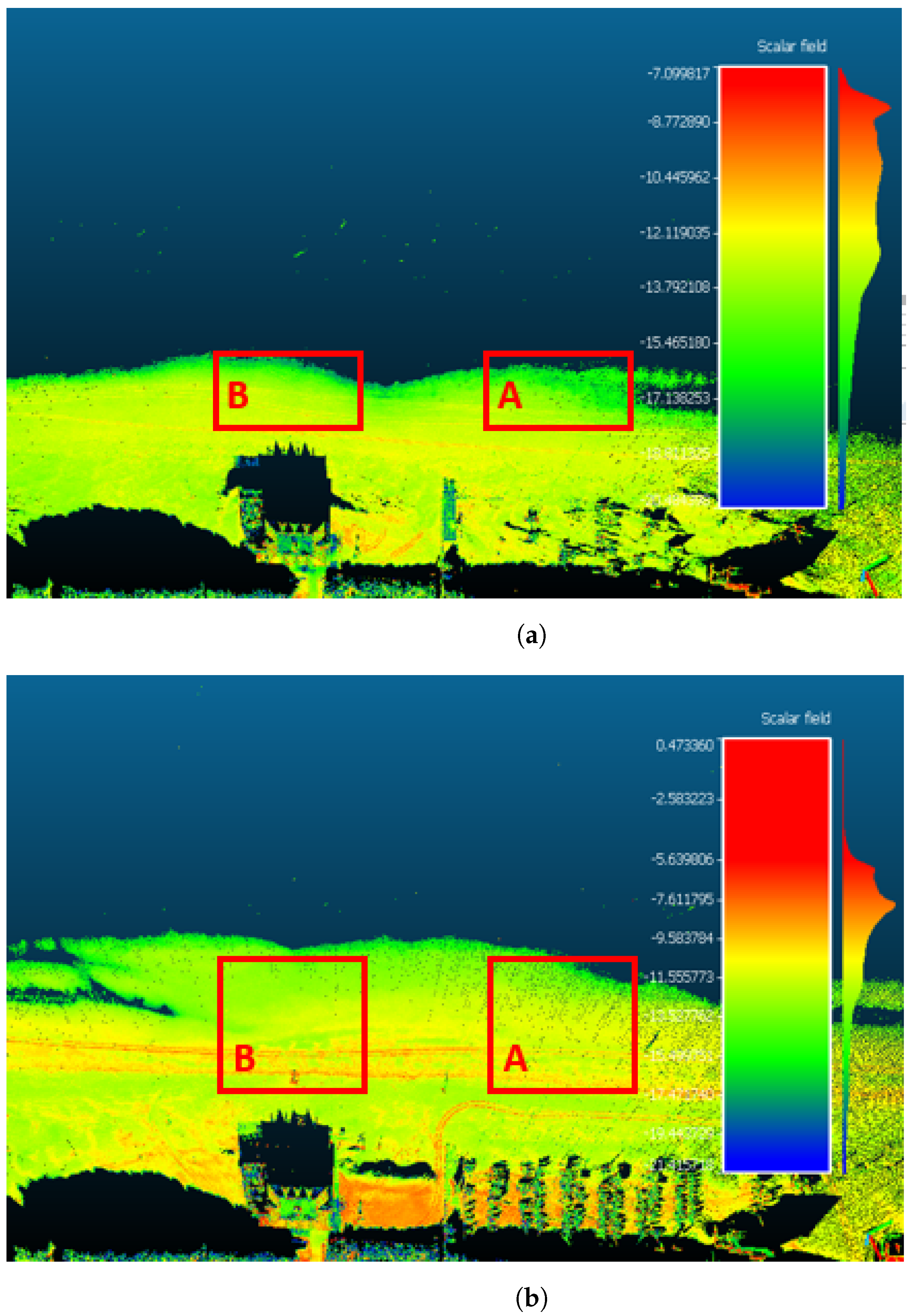

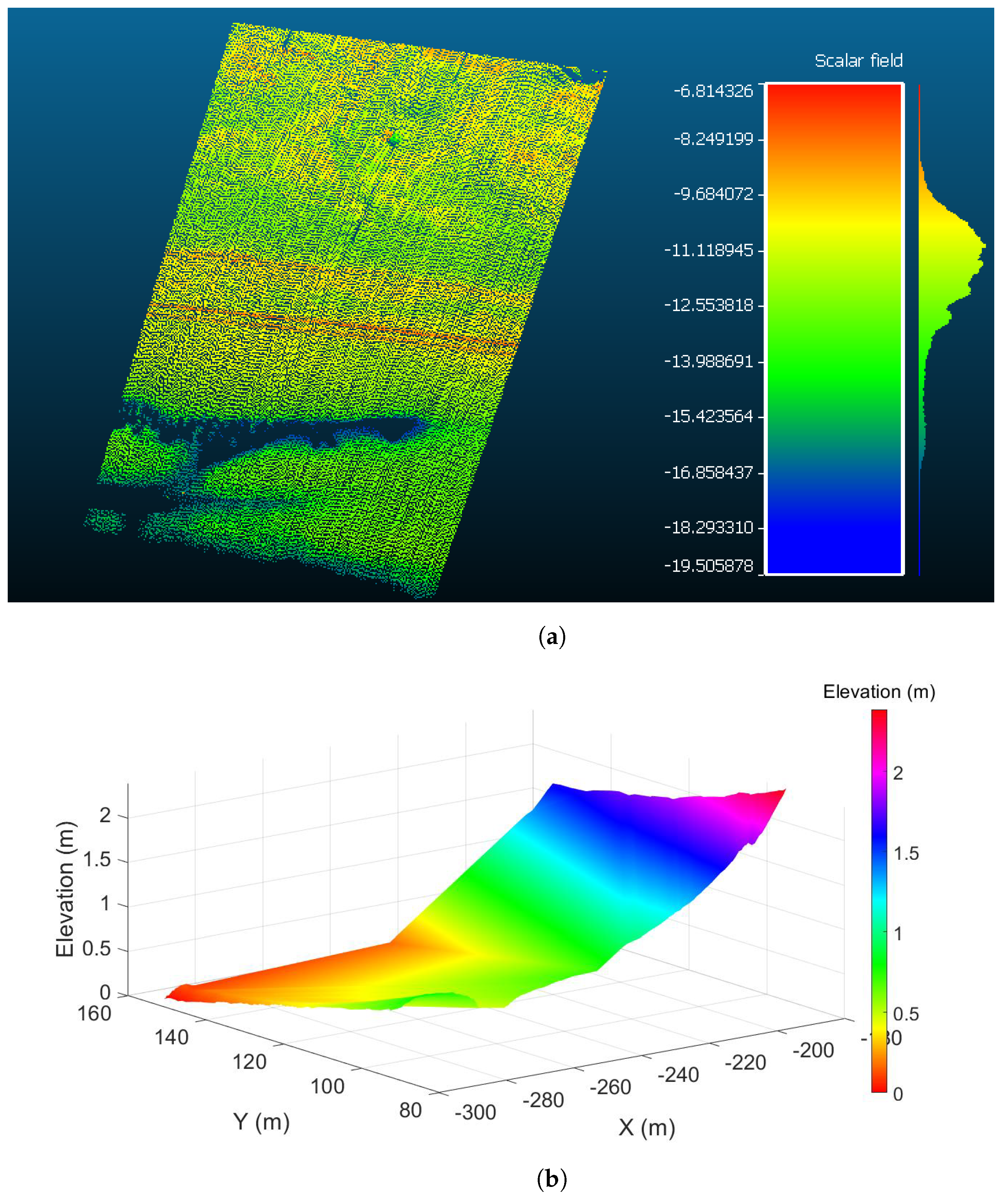
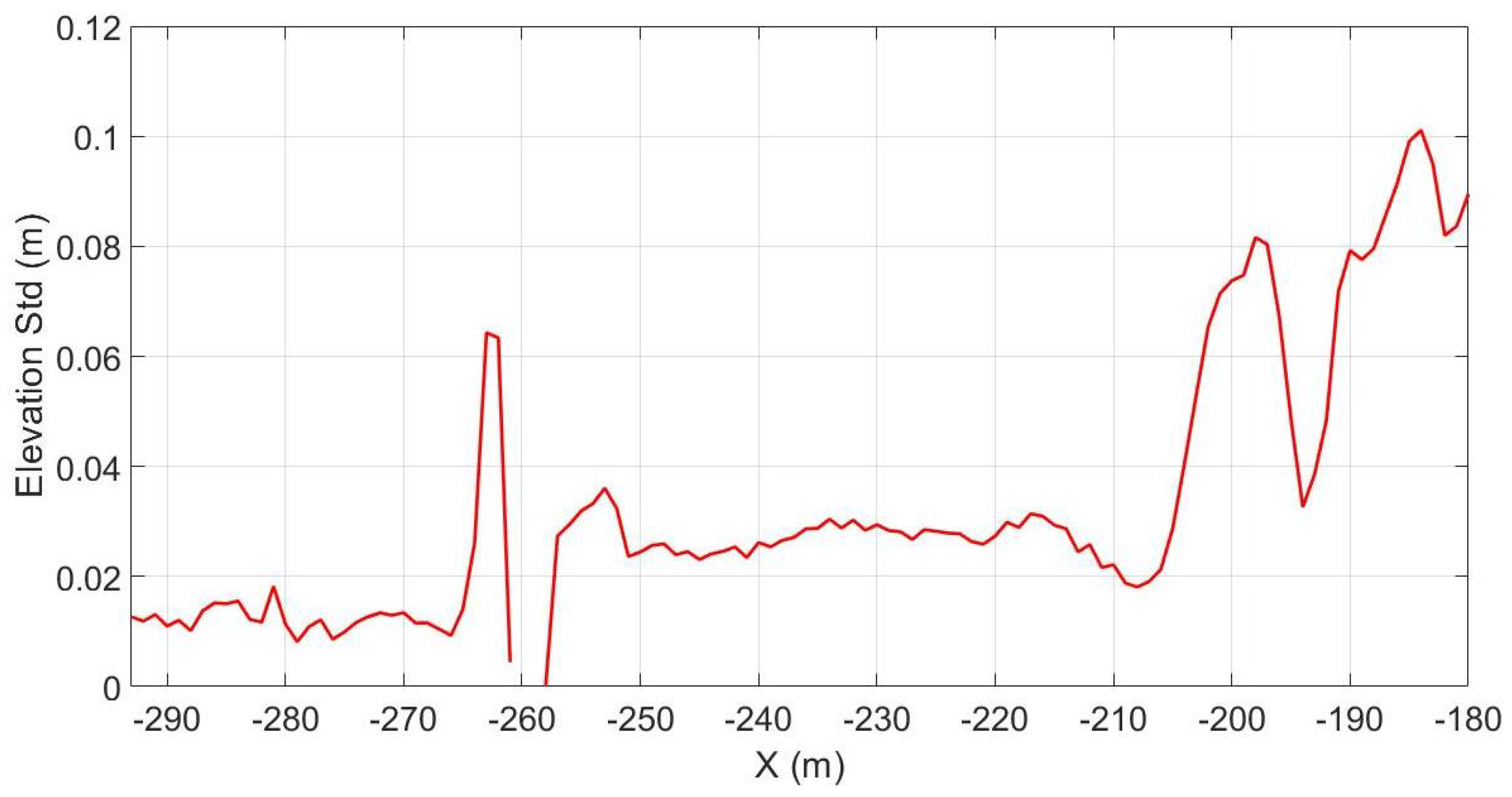



| Parameter Value | |||||||
|---|---|---|---|---|---|---|---|
| w | RMSE | R-Square | |||||
| 0.86 | 0 | ||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Di Biase, V.; Hanssen, R.F.; Vos, S.E. Sensitivity of Near-Infrared Permanent Laser Scanning Intensity for Retrieving Soil Moisture on a Coastal Beach: Calibration Procedure Using In Situ Data. Remote Sens. 2021, 13, 1645. https://doi.org/10.3390/rs13091645
Di Biase V, Hanssen RF, Vos SE. Sensitivity of Near-Infrared Permanent Laser Scanning Intensity for Retrieving Soil Moisture on a Coastal Beach: Calibration Procedure Using In Situ Data. Remote Sensing. 2021; 13(9):1645. https://doi.org/10.3390/rs13091645
Chicago/Turabian StyleDi Biase, Valeria, Ramon F. Hanssen, and Sander E. Vos. 2021. "Sensitivity of Near-Infrared Permanent Laser Scanning Intensity for Retrieving Soil Moisture on a Coastal Beach: Calibration Procedure Using In Situ Data" Remote Sensing 13, no. 9: 1645. https://doi.org/10.3390/rs13091645
APA StyleDi Biase, V., Hanssen, R. F., & Vos, S. E. (2021). Sensitivity of Near-Infrared Permanent Laser Scanning Intensity for Retrieving Soil Moisture on a Coastal Beach: Calibration Procedure Using In Situ Data. Remote Sensing, 13(9), 1645. https://doi.org/10.3390/rs13091645







