Monocular Visual-Inertial Navigation for Dynamic Environment

Abstract

Simultaneous localization and mapping (SLAM) systems have been generally limited to static environments. Moving objects considerably reduce the location accuracy of SLAM systems, rendering them unsuitable for several applications. Using a combined vision camera and inertial measurement unit (IMU) to separate moving and static objects in dynamic scenes, we improve the location accuracy and adaptability of SLAM systems in these scenes. We develop a moving object-matched feature points elimination algorithm that uses IMU data to eliminate matches on moving objects but retains them on stationary objects. Moreover, we develop a second algorithm to validate the IMU data to avoid erroneous data from influencing image feature points matching. We test the new algorithms with public datasets and in a real-world experiment. In terms of the root mean square error of the location absolute pose error, the proposed method exhibited higher positioning accuracy for the public datasets than the traditional algorithms. Compared with the closed-loop errors obtained by OKVIS-mono and VINS-mono, those obtained in the practical experiment were lower by 50.17% and 56.91%, respectively. Thus, the proposed method eliminates the matching points on moving objects effectively and achieves feature point matching results that are realistic.

1. Introduction

Simultaneous location and mapping (SLAM) is the “holy grail” of autonomous driving research [1]. In an unknown environment, SLAM enables a robot to perceive its own position and posture and map the environment at the same time. It is one of the key technologies of augmented reality (AR), positioning, and navigation. Visual SLAM mainly uses visual data fused with other sensor data for positioning and mapping [2]. Depending on the type and number of cameras used, visual SLAM can be divided into RGB-D SLAM, stereo SLAM, and monocular SLAM. RGB-D SLAM directly obtains a precise feature point depth using a depth camera. However, the depth camera is short-ranged and difficult to use outdoors. Stereo SLAM obtains the depth of the feature point via two offset cameras, and the distance between them is the baseline for depth calculation. However, the computation requirements and algorithmic complexity of such systems are high. In contrast to stereo SLAM, monocular SLAM uses only one camera; therefore, it is a low-cost, lightweight, and low-power solution. It is also easier to integrate into AR helmets and other devices, making it widely applicable. However, by relying only on monocular camera information, the system cannot obtain the true scale of the motion trajectory [3]. To solve this problem, various multisensor fusion methods have been applied. Among the many different sensor combinations, the combination of a camera and inertial measurement unit (IMU) is the most robust and least expensive. The visual data obtained by the camera can reduce the drift of the IMU data, whereas the IMU data can recover the scale of the visual data. The VINS-Fusion [4,5,6,7] proposed by the Hong Kong University of Science and Technology is a SLAM system based on optimized multisensor fusion. The system is an extension of VINS-Mono [5] and supports multiple modes: monocular camera + IMU, stereo camera, and stereo camera + IMU. The system uses IMU preintegration and feature point observations to achieve precise device self-location. It supports the calibration of the extrinsic parameters between the camera and IMU and the time offset between different sensors online. MSCKF [8], proposed by Mourikis et al., is a real-time visual-inertial navigation algorithm based on an extended Kalman filter (EKF). MSCKF integrates IMU and visual information under the EKF framework. It can adapt to some violent movements of the equipment, lack of texture in experimental scenes, and changes in lighting.

Most existing SLAM methods assume that all objects in a scene are static [9]. Therefore, they are unable to determine whether objects in the environment are moving. However, in the real world, there are many moving objects, and the assumption of a static environment is impractical. With many moving objects in the environment, image feature point matching is affected; the system’s location accuracy suffers, and the SLAM system is degraded. This limits the application of SLAM technology in many fields, such as robotic navigation [10], autonomous driving [11], AR [12], human following [13], and navigation assistance for the visually impaired [14]. Therefore, the construction of a SLAM system that has high precision in a dynamic environment has been the focus of many studies in recent years. Researchers have proposed many solutions that can be broadly divided into two categories: geometric constraints-based and deep learning-based.

Many researchers have attempted to develop SLAM systems for dynamic environments from the perspective of geometric constraints. Kim et al. proposed a background-model-based dense-visual odometry (BaMVO) [15], which uses an RGB-D camera in dynamic environments. First, a background model is estimated using a nonparametric model. Then, the background model is used to estimate the location and posture of the sensor to reduce the impact of moving objects. Sun et al. [16] proposed an RGB image and depth data-based method for removing moving objects. They incorporated this method into the RGB-D SLAM process in the preprocessing stage to remove data related to moving objects. Li et al. [17] proposed a real-time RGB-D SLAM system suitable for dynamic environments by using a static weighting method for edge points in the keyframe. This static weight is added to the intensity-assisted iterative closest point method used for the registration task. Tan et al. [18] presented a real-time monocular SLAM system with an online keyframe representation and updating method that reliably detects changed features from the key frames by projecting them to the current frame. In addition, they proposed a novel prior-based adaptive random sampling consensus (RANSAC) algorithm to efficiently remove match outliers. Shimamura et al. [19] introduced weighted tentative initial values of a camera pose and three-dimensional point cloud map to reduce user operation loading. Their study also distinguished outliers of feature points to stably estimate camera poses in dynamic scenes. Kim et al. [20] fused depth information into the RGB image based on the sped up robust features [21] descriptor. An IMU was used to rotate the feature points. To remove dynamic feature points and retain static feature points that are used to calculate the motion of the device (via the RANSAC algorithm) [22], they used a filtering method. Wang et al. [9] proposed a moving object detection algorithm for RGB-D SLAM based on mathematical models and geometric constraints.

Researchers have also proposed many deep learning-based methods. Yu et al. [23] proposed a robust semantic visual SLAM for dynamic environments called DS-SLAM, which combines the semantic segmentation network and moving consistency check method to reduce the impact of moving objects and improve the localization accuracy in a dynamic environment. Wang et al. [24] proposed a moving-target segmentation method that can be combined with dense SLAM. To address the problem of unsatisfactory segmentation results, Bescos et al. [25] proposed a visual SLAM system, DynaSLAM, which builds on ORB-SLAM2 [26] and adds dynamic object detection and background inpainting functions. It can run on dynamic scenes in monocular, stereo, and RGB-D modes. Further, it detects moving objects either by multiview geometry, deep learning, or both. Zhao et al. [27] proposed a dynamic environment-oriented semantic visual inertial system that uses pixel-level results of semantic segmentation for real-time locations. The system integrates feature points extraction and matching algorithms into the SLAM process and combines pixel-level features in the dynamic feature detection module. It excludes dynamic feature points by using semantic segmentation results and multiview geometric constraints. Cheng et al. [2] proposed a feature-based method called DM-SLAM, which supports monocular, stereo, and RGB-D sensor modes. The semantic segmentation module obtains the pixel segmentation results of potential dynamic objects. In the case of the RGB-D or stereo modes, the method uses a reprojection error to distinguish dynamic points. In the case of the monocular mode, the method uses epipolar constraints. Then, static feature points are inputted into the SLAM framework to obtain the position and posture of the system. Khan et al. [28] proposed a coarse-to-fine pupil localization method using a composite of machine learning and image processing algorithms. The machine learning method they developed can be applied to dynamic SLAM.

Although many current solutions for dynamic environments have achieved good results, they still have some shortcomings. For methods based on geometric constraints, most current methods use only RGB or RGB-D cameras. This makes the system behave poorly in some complex environments, limiting the system’s usage scenarios. Most methods also assume that there are far more static objects than moving objects in the scene; thus, the motion model of the camera is determined by the most matched feature points. The matched feature points that do not satisfy the model are eliminated. However, this assumption is often incorrect. Though deep learning methods are superior to the traditional ones in many aspects, works utilizing them in SLAM systems are few. Besides the system tuning requirements, deep learning methods require a GPU or other hardware accelerators for real-time inference [29], which may limit their application in AR, obstacle avoidance navigation, and other fields. Additionally, because most deep learning-based methods are based on object detection, the deep learning models used must be pretrained to classify predetermined moving objects. Not only does it make the system powerless against moving objects the models were not trained for, but also not all the objects the models are trained to recognize are always in motion. Therefore, it is difficult to guarantee the accuracy of the point features matching. In summary, it is still necessary to study high-precision match elimination algorithms for moving object feature points in complex environments.

To improve the system’s location accuracy in complex scenes, we need to eliminate the feature matches on moving objects and use the static scene information for system location. This paper proposes a method for eliminating feature points on moving objects using IMU data. The translation and rotation of the system in the corresponding time period of the two frames can be obtained using the IMU data and the motion state at the last moment of the device. Then, we can use the translation and rotation of the system to obtain the transformation matrix of motion during this period. The distance between the feature matches and transformation matrix is calculated one by one, and the number of matching point features supporting the transformation matrix is determined. When the number is sufficiently high, the IMU data is considered valid. In this case, the feature point matches having large distances to the transformation matrix are considered abnormal matches (located on a moving object or erroneous match) that need to be eliminated.

To summarize, the main contributions of this study are as follows:

• An algorithm for validating IMU data is proposed. By calculating the number of image feature matches that support the transformation matrix, we can validate the IMU data.
• A feature point matches elimination algorithm for dynamic scenes is proposed. By calculating the distance between the feature point matches on the RGB image and the transformation matrix, we can determine whether the feature match is on the moving object.
• The proposed algorithm is integrated into a visual inertial navigation system. Consequently, the number of feature points matches on moving objects in a complex environment is reduced and location accuracy is significantly improved.

The remainder of this paper is structured as follows. The Section 2 describes how to use IMU data to reduce the influence of moving objects. The Section 3 introduces the experimental plan for the public dataset and real-world experiment. The Section 4 presents the experimental process and results. Finally, the Section 5 summarizes the study.

2. Methods

2.1. Overview

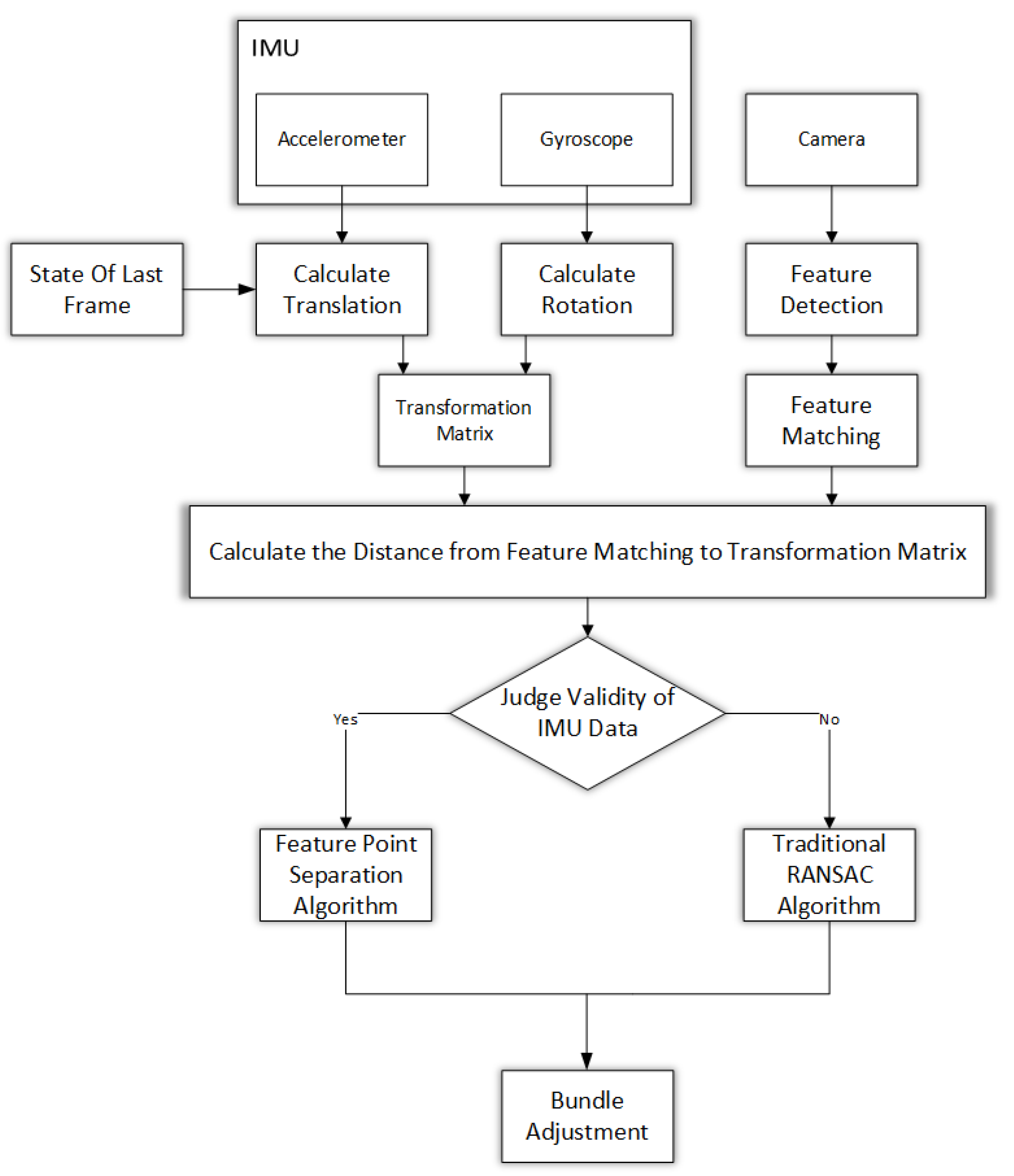
Due to moving objects, corresponding feature points will move in the image, significantly reducing the accuracy of point features matching. To effectively reduce the impact of moving objects and improve the location accuracy of a SLAM system, we propose a method for eliminating feature point matches on moving objects in dynamic scenes. The method uses IMU data to obtain the motion transformation matrix of the camera. Then, high-precision feature point matches are obtained by using the transformation matrix under polar geometry constraints. Figure 1 depicts the SLAM system using the proposed dynamic feature matches culling algorithm. First, feature points were extracted and matched according to the RGB image. The angular velocity and acceleration can be obtained from the IMU data, which are used to calculate the translation and rotation between the two frames and the corresponding transformation matrix with the system’s motion state at the last moment. Then, the distances between the feature matches and the transformation matrix were calculated one at a time to determine whether the two are consistent. If enough feature matches support the matrix, the IMU data are considered valid and abnormal matches are eliminated according to the distance between the feature matches and the transformation matrix. By contrast, if the IMU data are invalid, the RANSAC algorithm is used to eliminate the erroneous matches. Finally, the rest of the feature matches are input to the optimization equations to calculate the device’s pose, motion state, and coordinates of three-dimensional feature points through bundle adjustment.

2.2. Obtaining the Transformation Matrix from IMU Data

The gyroscope measures the angular velocity of the device. By integrating the angular velocity, the rotation of the device between the two frames can be obtained. The following equation [30] was used to calculate the posture according to the last frame of the image.

$$q_{b_{k+1}}^w=q_{b_k}^w\otimes {{\displaystyle \int }}_{t\in \left[t_k,t_{k+1}\right]}\frac{1}{2}\Omega \left({\omega }_t\right)q_t^{b_k}dt$$

(1)

where:

$$\Omega \left(\omega \right)=\left|\begin{array}{cc}-\lfloor \omega {\rfloor }_{\times }& \omega \\ -{\omega }^T& 0\end{array}\right|$$

(2)

$$\lfloor \omega {\rfloor }_{\times }=\left|\begin{array}{ccc}0& -{\omega }_z& {\omega }_y\\ {\omega }_z& 0& -{\omega }_x\\ -{\omega }_y& {\omega }_x& 0\end{array}\right|$$

(3)

In Equation (1), $q_{b_k}^w$ represents the posture of the IMU at frame k in the world coordinate system. $\omega$ is the angular velocity of the device measured by the gyroscope. ${\omega }_x$, ${\omega }_y$, and ${\omega }_z$ represent the angular velocities in the x, y, and z directions, respectively. The rotation of the system in the time period can be calculated according to the current posture of the system and the previous posture of the system.

Similarly, according to Equation (4), the speed of the system at the current frame can be obtained by integrating the acceleration measured by the accelerometer. By integrating the speed, the translation amount of the system between two frames can be obtained using Equation (5).

$$v_{b_{k+1}}^w=v_{b_k}^w+{{\displaystyle \int }}_{t_k}^{t_{k+1}}\left(R_t^w{a}_t-g^w\right)dt$$

(4)

$$\begin{array}{cc}{p}_{b_{k+1}}^w=p_{b_k}^w& +v_{b_k}^w\Delta t_k+{{\displaystyle \iint }}_{t\in \left[t_k,t_{k+1}\right]}\left(R_t^w{a}_t-g^w\right)d{t}^2\end{array}$$

(5)

Here, $v_{b_k}^w$ is the velocity at frame k in the world coordinate system. $R_t^w$ is the posture of the device represented by the rotation matrix in the world coordinate system at time t, and a is the acceleration. g is the gravity vector in the world frame. $p_{b_k}^w$ is the position at frame k in the world coordinate system, and $\Delta t_k$ is the time interval from $t_k$ to $t_{k+1}$.

The rotations and translations of the device are in the global coordinate system. Because the camera and the IMU are rigidly connected and the relative position is fixed, the rotation matrix and translation in the camera’s coordinate system can be obtained by transforming the location and posture of the IMU using the extrinsic parameters of the camera-IMU. According to the translation and rotation of the camera and the camera’s internal parameter matrix, the fundamental matrix of the camera motion between two adjacent frames can be obtained by the following equations:

$$E_{b_{k+1}}^c=t_{b_{k+1}}^c{}^{\wedge }{R}_{b_{k+1}}^c$$

(6)

$$F_{b_{k+1}}^c=K^{-T}{E}_{b_{k+1}}^c{K}^{-1}$$

(7)

Here, E is the essential matrix of camera movement. $t^{\wedge }$ is the antisymmetric matrix of translation t. F is the fundamental matrix of camera movement. K is the internal parameter matrix of the camera.

2.3. Distances between Feature Matches and the Fundamental Matrix

Geometrically, the fundamental matrix is a projective map that maps points to straight lines. In this case, point x in the first frame determines the epipolar line on the second frame as:

$$l^{\prime }=Fx.$$

(8)

Therefore, if the feature point $P_i$ is in a static state, the feature point will satisfy the epipolar geometric constraint in an ideal situation [31]:

$$p_{k+1,i}^{T}F{p}_{k,i}=0,i=1,2,3,\dots ,m.$$

(9)

For the fundamental matrix F, the distance from the corresponding feature matches to the epipolar line can be obtained as follows:

$$d=\frac{\left|p_{k+1,i}^{T}F{p}_{k,i}\right|}{\sqrt{{||x||}^2+{||y||}^2}},i=1,2,3,\dots ,m,$$

(10)

where

$$F{p}_{k,i}={[x,y,z]}^T.$$

(11)

The steps for calculating the distance between the feature point matches and the fundamental matrix are as follows. First, the fundamental matrix is calculated using IMU data. According to Equation (10), the distance between the corresponding feature points in the latter image and the polar line is calculated and denoted as $d_1$. Similarly, the fundamental matrix of motion from the current frame to the previous image is calculated. We calculate the distance between the feature point matches in the previous image and the corresponding polar line according to Equation (11), denoted as $d_2$. The larger of the variables $d_1$ and $d_2$ is defined as the distance $d$ from the feature matches to the fundamental matrix. Algorithm 1 describes the steps of the calculation in detail.

Algorithm 1: Calculating distances between feature matches and the fundamental matrix

Input: Matched feature points of adjacent frames: $PointSe{t}_k=\left\{P_{k,1},P_{k,2},\cdots ,P_{k,n}\right\}$, $PointSe{t}_{k+1}=\left\{P_{k+1,1},P_{k+1,2},\cdots ,P_{k+1,n}\right\}$

Fundamental matrix F

Output: The distance of every feature matches to F

Step 1:

for each $P_{k,i}\in PointSe{t}_k$ do

${\left[x,y,z\right]}^T=F{P}_{k,i}$

$d_{k,i}^1=\frac{\left|P_{k+1,i}^{T}F{P}_{k,i}\right|}{\sqrt{{||x||}^2+{||y||}^2}}$

end

Step 2:

$F^{\prime }=F^T$

Step 3:

for each $P_{k,i}\in PointSe{t}_k$ do

${\left[x,y,z\right]}^T=F^{\prime }{P}_{k+1,i}$

$d_{k,i}^2=\frac{\left|P_{k,i}^T{F}^{\prime }{P}_{k+1,i}\right|}{\sqrt{{||x||}^2+{||y||}^2}}$

end

Step 4:

if $d_{k,i}^1<d_{k,i}^2$ do

$d_{k,i}=d_{k,i}^2$

else

$d_{k,i}=d_{k,i}^1$

2.4. Eliminating Abnormal Matches Using IMU Data

Because the IMU can only measure the angular velocity and linear acceleration of the system movement, the drift of IMU data will increase over time. Additionally, as many things can interfere with IMUs, the data from IMUs can be very noisy and unreliable. Therefore, IMU data should be validated before use to constrain the feature point matching.

To determine whether the feature match is consistent with the fundamental matrix, we calculate the distance $d$ from the feature match to the fundamental matrix. If the distance is smaller than $a$, a given threshold, the feature match is consistent with the fundamental matrix; otherwise, it is not consistent. The value ${\phi }_{k,i}$ is set to 0 when the i-th feature point $u_{k,i}$ of the k-th frame is consistent with the fundamental matrix; otherwise, it is set to 1.

$${\phi }_{k,i}=\{\begin{array}{c}1, d_{k,i}\ge a\\ 0, d_{k,i}<a\end{array}$$

(12)

The consistency of the feature matches in the image with the fundamental matrix derived from the IMU data is calculated one by one. Given a threshold b, when the valid feature matches count is not less than b, the IMU data are considered valid; otherwise, they are considered invalid. The value of ${\theta }_k$ is set to 0 if the feature point matches of the k-th and the k + 1-th frames are consistent with the fundamental matrix in the corresponding time period; otherwise, it is set to 1.

$${\theta }_k=\{\begin{array}{c}0, {\displaystyle {\displaystyle \sum }_{i=1}^m}{\phi }_{k,i}<b\\ 1,{\displaystyle {\displaystyle \sum }_{i=1}^m}{\phi }_{k,i}\ge b\end{array}$$

(13)

If the IMU data are valid (i.e., ${\theta }_k=0$), the fundamental matrix calculated from the IMU data is accurate, and the IMU data is trustworthy. In this case, the distance between the feature points matches and the fundamental matrix is used to determine whether the feature points matches are correct. For each set of feature matches, if the distance to the fundamental matrix calculated by the IMU is less than c, the feature match will be consistent with the movement of the system between the two frames calculated by the IMU data and is considered correct. Otherwise, the feature match is incorrect, or the matched point is located on a dynamic object and needs to be eliminated.

When the IMU data is invalid (i.e., ${\theta }_k=1$), the fundamental matrix calculated from the IMU data is inaccurate and the IMU data is untrustworthy. Therefore, the visual data is used instead. Here, the RANSAC algorithm, which uses the feature point matches of the visual data, is used to calculate the motion matrix that is supported by most feature point matches and eliminate abnormal matches.

3. Materials and Experimental Setup

An Intel(R) Core(TM) i7-7700HQ CPU @ 2.80 GHz computer with 16 GB RAM and Ubuntu 16.04 LTS was used for the experiment. The experiment was composed of two parts. The first part used the ADVIO public dataset [32]. A detailed introduction of the dataset is provided in Section 3.1. Select feature matches data collected when the ADVIO dataset was ran through the SLAM system were extracted to verify the performance of our algorithm. At the same time, the dataset’s ground truth was used to quantitatively evaluate the location accuracy. The second part involved using self-collected data. We selected feature matches data during the experiment to verify the performance of our algorithm. By setting the origin and destination of the experiment to the same point, we can use the closed-loop error to verify the location accuracy of the system, as discussed in in Section 3.2.

We selected VINS-mono [5] proposed by Qin et al., ROVIO [33] proposed by Bloesch et al., and OKVIS [34] proposed by Leutenegger et al., which are all state-of-the-art projects, to compare with the proposed algorithm. In VINS-Mono, a tightly coupled, nonlinear optimization–based method is employed to obtain high accuracy visual-inertial odometry by fusing preintegrated IMU measurements and feature observations. ROVIO is a monocular visual-inertial odometry algorithm, which, by directly using pixel intensity errors of image patches, achieves accurate tracking performance while exhibiting extremely high robustness. OKVIS is a novel approach to tightly integrate visual measurements with readings from an IMU in SLAM.

3.1. ADVIO Dataset Experiment

The sensor data for the ADVIO dataset were collected using an iPhone 6s. The sequences collected totaled 4.5 km. The ground truth was obtained by combining a pure inertial navigation system with frequent manual positioning based on precise planes [35]. The dataset contained 23 separate recordings captured in six different locations, and all had complete six degree-of-freedom location and posture true values. The dataset was not limited to small spaces and covered a variety of indoor and outdoor scenarios, including stairs, escalators, elevators, offices, shopping malls, and subway stations. The dataset provides a variety of sensor data from cameras, accelerometers, gyroscopes, magnetic sensors, and barometers.

We selected eight data sequences (sequence 1, 2, 6, 9, 11, 13, 18, and 21) to test the location accuracy of the algorithm in different application scenarios. Sequences 1, 2, 6, and 9 were shopping mall scenes. Sequence 11 was a subway station. Sequences 13 and 18 were office areas. Sequence 21 was an outdoor scene. Sequences 1 and 9 contained escalators. Sequences 13 and 18 contained stairs. Sequence 18 contained elevators. Sequences 6 and 11 contained many pedestrians. Sequences 1 and 2 contained a medium number of pedestrians. Sequences 9, 13, and 21 contained a small number of pedestrians. Sequence 18 was devoid of pedestrians. Sequences 11 and 21 contained many moving vehicles. As the selected sequences contained different kinds of objects, we can detect the adaptability and robustness of the algorithm.

3.2. Real-World Experiment

To verify our algorithm’s accuracy in the real world, an on-site experiment with equipment was conducted. The experimental data were collected at the Chinese Academy of Sciences, Datun Road, Chaoyang District, Beijing, China. The experiment was conducted at lunchtime; therefore, there were many pedestrians on the road. Hence, it was a challenging dynamic scene for the SLAM system. The experimenter held the equipment in the park along a closed-loop path to collect the data. An Intel RealSense D435i camera [36] was used for data collection, as shown in Figure 2. It is a monocular camera with an accelerometer, gyroscope, and depth camera. Only visual, accelerometer, and gyroscope data were used. The resolution of the visual data was 640 × 480 pixels with a frequency of 15 Hz. The accelerometer’s frequency was 60 Hz. The frequency of the gyroscope was 200 Hz.

It was necessary to calibrate the equipment in advance. This included calibrating the internal parameters of the camera, IMU, and the camera-IMU extrinsic parameters. We used the imu_utils [37] library and the MATLAB-based calibration toolbox [38] to calibrate the IMU and camera internal parameters, respectively. The results are presented in

Table 1. Internal parameters and distortion coefficients of the RGB cameras.

Name	${\mathit{f}}_{\mathit{x}}$	${\mathit{f}}_{\mathit{y}}$	${\mathit{c}}_{\mathit{x}}$	${\mathit{c}}_{\mathit{y}}$	${\mathit{k}}_1$	${\mathit{k}}_2$	${\mathit{p}}_1$	${\mathit{p}}_2$
Value	601.75	603.59	336.28	242.99	0.1630	−0.328	−0.006	0.007

The unit of $f_x,f_y,c_x$ and $c_y$ is pixel.

and

Table 2. Noise density and random walk from IMU calibration.

Name	Accelerometer Noise Density	Accelerometer Random Walk	Gyroscope Noise Density	Gyroscope Random Walk
Value	1.083−2	9.131−4	1.682−3	1.468−5

.

Then, the Kalibr library [39] was used to calibrate the camera-IMU’s extrinsic parameters. The calibration results are as follows:

$$\left[\begin{array}{cccc}0.99911& -0.03830& 0.01725& -0.00003\\ 0.03849& 0.99920& -0.01052& 0.00011\\ -0.01683& 0.01118& 0.99980& 0.00001\\ 0& 0& 0& 1\end{array}\right]$$

(14)

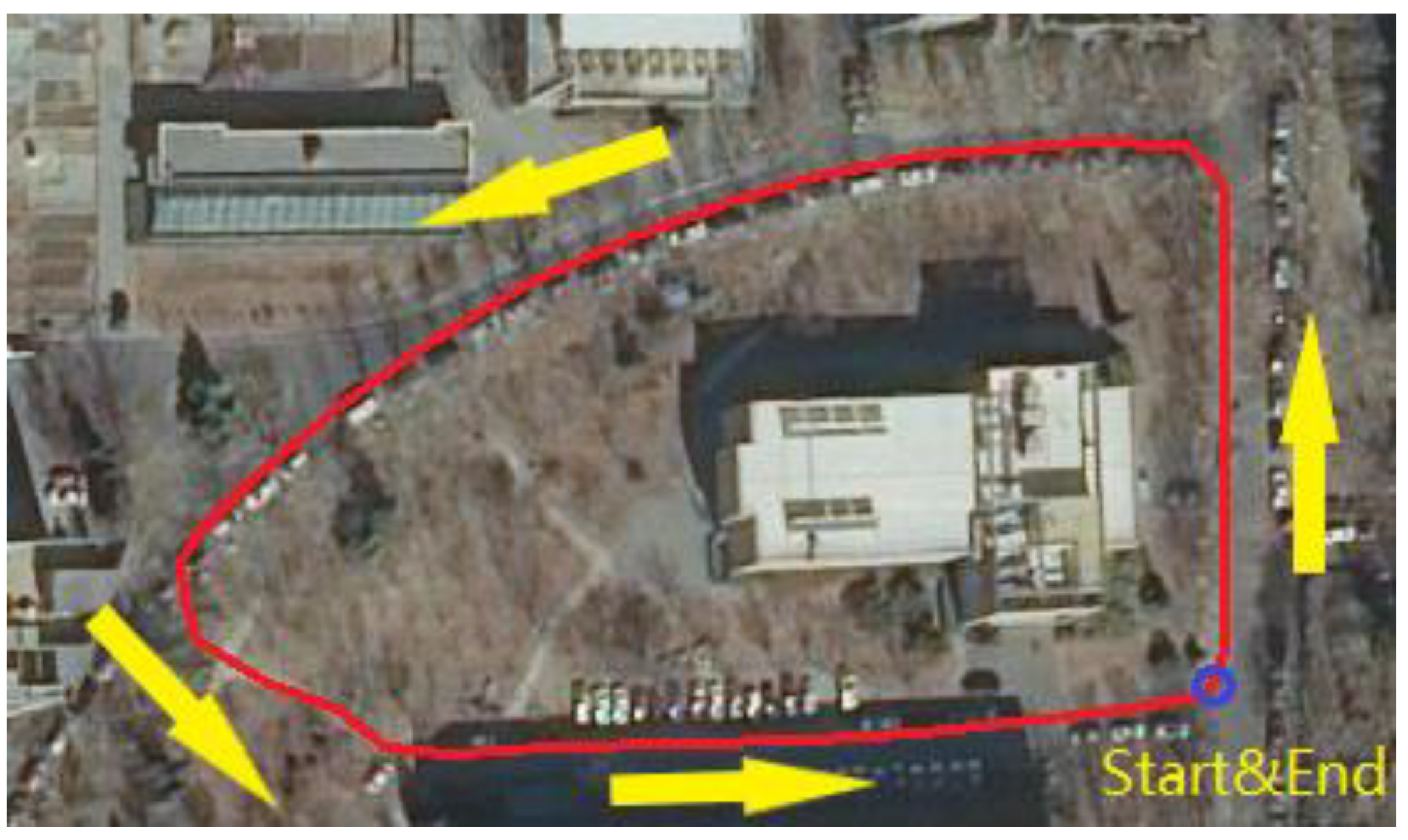
Figure 3 shows the track used in the experiment. The blue circle at the lower right corner of the track indicates the start and end points of the loop. The arrow indicates the direction of travel, and the red line is the approximate path traveled. The beginning of the dataset (about 1 s in length) is usually poor in quality with insufficient exposure or excessive exposure of visual photos, because the device has just been turned on. Therefore, the initial stage of the data was processed. Then we used the methods described in [5] to unify the frequencies of the accelerometer and gyroscope and align the time stamps. Subsequently, the data were used by the location system to locate the trajectory.

4. Results

4.1. ADVIO Public Data Set

We selected two adjacent frames in sequence 2. Figure 4 shows the raw frame images, where Figure 4a is the previous frame, and Figure 4b is the current frame. During the experiment, the system performed feature points extraction, matching, and abnormal feature point match elimination.

Figure 5 shows the results of feature matches for the two image frames. The rightmost images show the feature matches; the leftmost images show the matched feature points on the previous frames; the middle images show the matched feature points on the current frames. Figure 5a shows the results without the elimination of feature matches. Figure 5b shows the results of with the elimination of feature points matches, which was realized using the RANSAC algorithm. Figure 5c shows the results of with the elimination of feature points matches, which was realized using the proposed method.

The pedestrian in motion interfered with the feature point matching accuracy. The other objects in the scene were static. Therefore, if the feature point is located on the pedestrian, the feature point matching accuracy and the system’s location accuracy will be reduced. Comparing Figure 5a,b, we see that while the number of matched feature points on the pedestrian was reduced after using the RANSAC algorithm to eliminate abnormal feature matches, there are still many points on the pedestrian, especially on the pedestrian’s left arm and bag. In Figure 5c, the matched feature points on the pedestrian are almost completely nil, and the feature points on the stationary objects in the scene are retained. Therefore, our algorithm is more accurate than the RANSAC algorithm. Hence, when the vision camera is disturbed by a moving object, our proposed algorithm eliminates the matched feature points on the moving object better and obtains higher-precision feature point matches.

For a comprehensive evaluation of our method’s performance, we used the root mean square error (RMSE) and mean of the absolute pose error. We used the open-source library evo [40] to evaluate the location trajectory.

The dataset we selected is challenging for the SLAM system. First, because the dataset is collected via a hand-held method, the data has some shaking. Second, dynamic information is present, such as the pedestrian and vehicle in the scene. Third, the shaking of the equipment also poses a big challenge to the SLAM system. Therefore, not all SLAM systems can run perfectly in all datasets. OKVIS-mono cannot run in sequences 11 and 21, while ROVIO-mono can only run in sequences 1, 9, 13, and 21.

Table 3. Performance of the traditional algorithms and the proposed algorithm on the ADVIO dataset (unit in meters).

Sequence	Venue	Object	Pedestrian	OKVIS-Mono		VINS-Mono		ROVIO-Mono		Proposed
				RMSE	Mean	RMSE	Mean	RMSE	Mean	RMSE	Mean
1	Mall	Escalator	Moderate	1.661	1.502	1.872	1.641	2.599	2.452	1.814	1.588
2	Mall	None	Moderate	7.273	6.827	2.655	2.278	-	-	2.516	2.136
6	Mall	None	High	4.545	4.313	3.807	3.623	-	-	3.669	3.486
9	Mall	Escalator	Low	18.779	18.258	2.544	1.949	2.159	2.024	1.952	1.552
11	Metro	Vehicles	High	-	-	5.960	5.423	-	-	5.830	5.301
13	Office	Stairs	Low	1.917	1.691	1.781	1.661	4.729	4.247	1.703	1.576
18	Office	Stairs Elevator	None	23.456	20.245	14.629	13.211	-	-	12.174	10.730
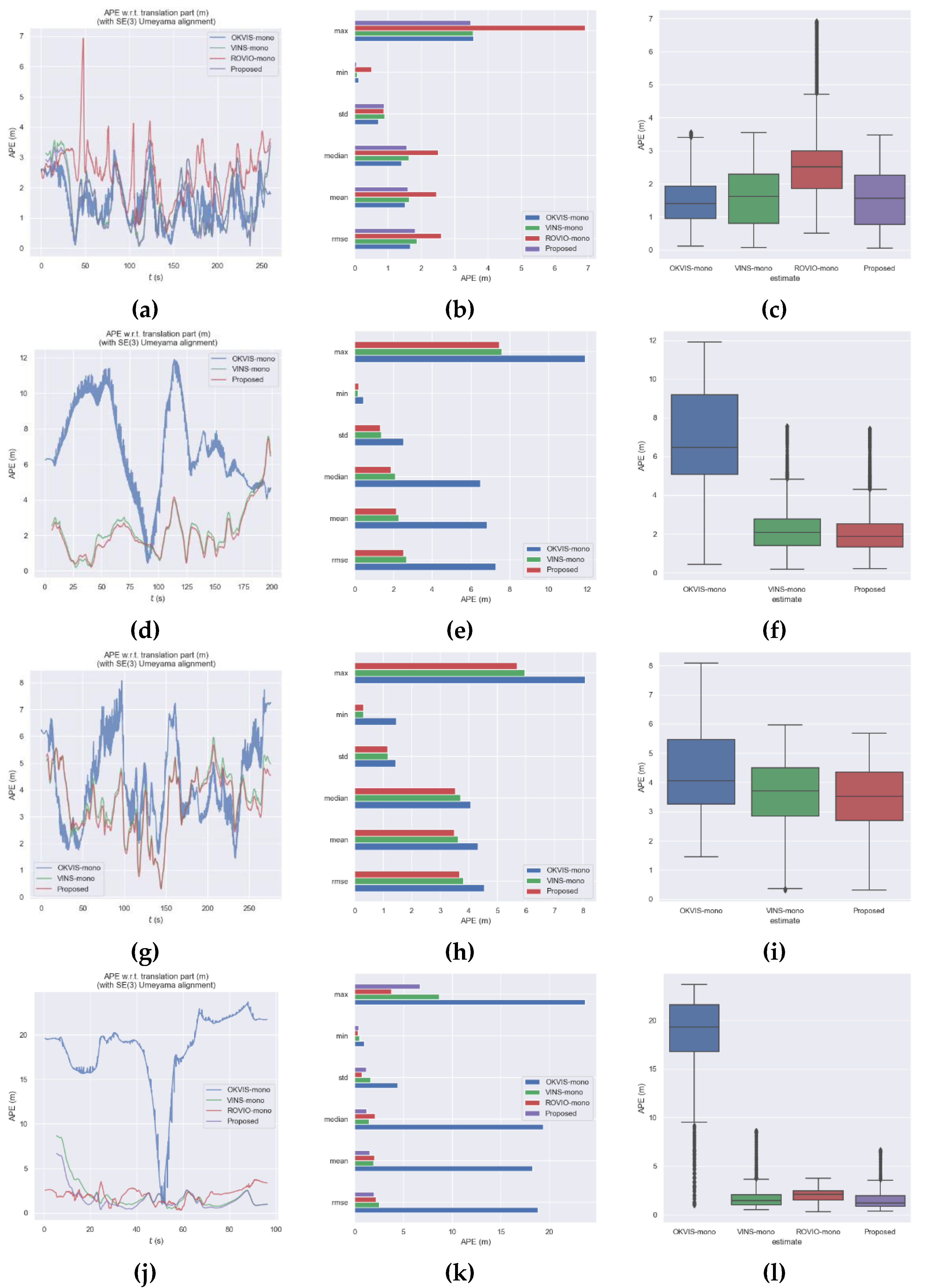
21	Outdoor (urban)	Vehicles	Low	-	-	15.973	15.643	20.524	17.842	15.889	15.568

summarizes the error comparison data of the proposed method and the three monocular state-of-the-art SLAM systems for the eight sequences of the ADVIO dataset we preselected for performance testing. The numbers in bold indicate that the proposed method performed better than the other methods, in terms of these values.

Table 3 summarizes that the proposed method performs considerably better than the other traditional methods for the eight preselected data sequences. In terms of system robustness, both OKVIS-mono and ROVIO-mono have dataset sequences that cannot be implemented, but the proposed method can run perfectly in all eight sequences, which implies that the SLAM system using the proposed method is considerably robust. In terms of system location accuracy, that of the SLAM system using the proposed method is the best for all seven dataset sequences, apart from being the second-best accuracy in the first sequence. The SLAM system integrated with the proposed algorithm had higher location accuracies than VINS-mono, which can also run perfectly in all datasets.

Figure 6 shows the location trajectory and error data. The leftmost images show the absolute position errors of the four methods. The abscissa is the system’s running time in seconds, while the ordinate is the system’s absolute position error in meters. The middle images denote the statistics for the absolute error of the trajectory. The statistics are, from top to bottom, the maximum error value, minimum error value, standard deviation, median, average error, and RMSE. The horizontal axis is the magnitude of the errors in meters. The last column is the boxplot of the four methods. The abscissa is the four systems, while the ordinate is the system’s absolute position error in meters. The figure does not show the systems that cannot run in the dataset sequence.

For sequence 1 and sequence 13, ROVIO-mono has the lowest positioning accuracy, and the other three exhibit slight differences. FOR sequence 2 and sequence 6, ROVIO-mono cannot be implemented. Although OKVIS-mono can barely run, the positioning accuracy is considerably lower than that of VINS-mono and the proposed method, and the positioning accuracy of the proposed method is the best. In sequence 9, the positioning error of OKVIS-mono is considerably larger than the other three. For sequence 11, because it is in the subway station, there is a lot of motion information in the scene, such as trains and pedestrians; thus, only VINS-mono and the proposed method can run. In sequence 18 and 21, the robustness and positioning accuracy of VINS-mono and the proposed method are better than those of OKVIS-mono and ROVIO-mono.

In summary, the performance of the proposed method is the best in terms of robustness and positioning accuracy.

4.2. Self-Collected Data

We selected two adjacent frames from the real-world experiment data. The raw images are shown in Figure 7, where Figure 7a is the previous frame, and Figure 7b is the current frame. During the experiment, the system performed feature point extraction, matching, and abnormal feature point matching elimination.

Figure 8 shows the feature matches for the two frames. The rightmost images show the feature points matches; the leftmost images show the matched feature points in the previous frame; the middle images show the matched feature points in the current frames. Figure 8a shows the results without feature points matches elimination. Figure 8b shows the results with feature points matches elimination using the RANSAC algorithm. Figure 8c shows the results with the feature points match elimination using the proposed method.

In the two adjacent frames, the elements that interfere with the accuracy of feature points matching are the two pedestrians close to the lens in the middle and on the right-hand side of the frame. Although there are other pedestrians moving farther in the distance, the pixel changes from those pedestrians can be ignored as they are too far away and can be considered static objects. Thus, only the feature points match on the two pedestrians close to the camera will affect the accuracy of feature point matching and the systems’ location accuracy. Figure 8a,b show that there are hardly any benefits to using the RANSAC algorithm to remove abnormal feature point matches. Figure 8c shows that our algorithm almost completely removes abnormal feature points matches on the two pedestrians while retaining the feature points on the static objects in the scene. Thus, our algorithm has an obvious removal effect on feature points matches on moving objects.

To facilitate the evaluation of the location accuracy of the system, the start and end points were the same in the experiment. Therefore, the accuracy of the algorithm was evaluated by comparing the distance between the start and end points. To make datasets more challenging, we use the hand-held method to collect data; thus, vibration inevitably exists, which will cause the drastic change of accelerometer value and hinder the tracking of feature points. In such cases, ROVIO-mono cannot be implemented; thus, we only compared the proposed method with OKVIS-mono and VINS-mono.

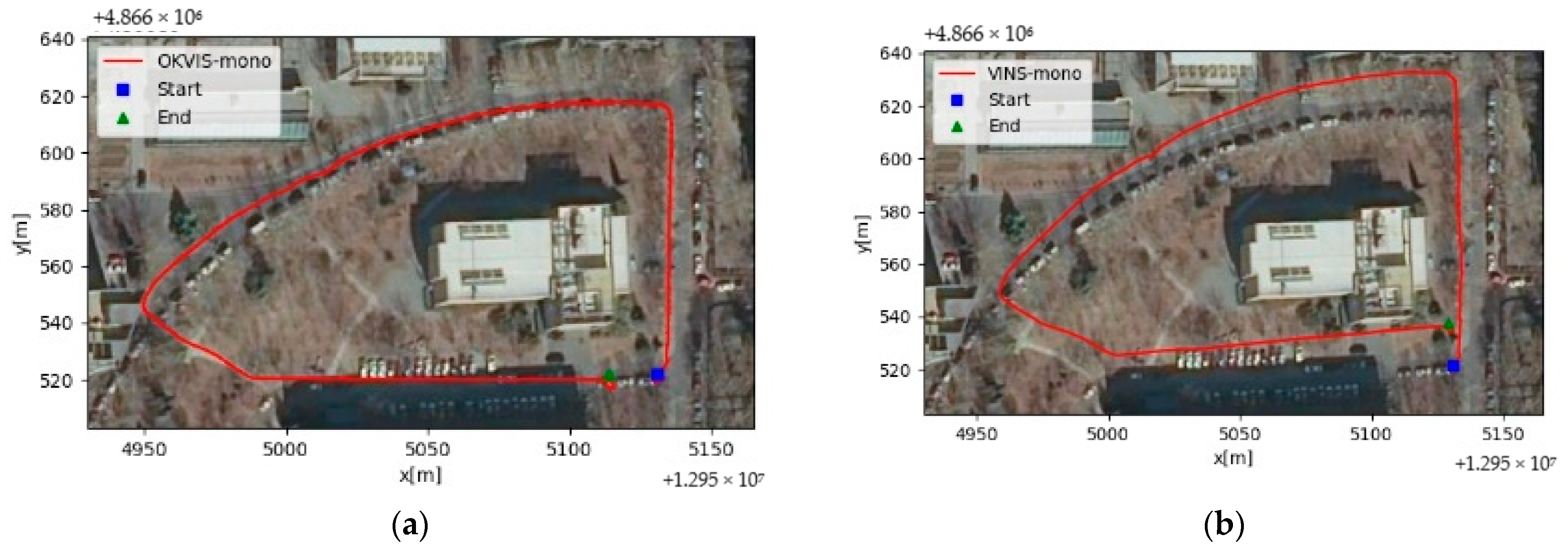
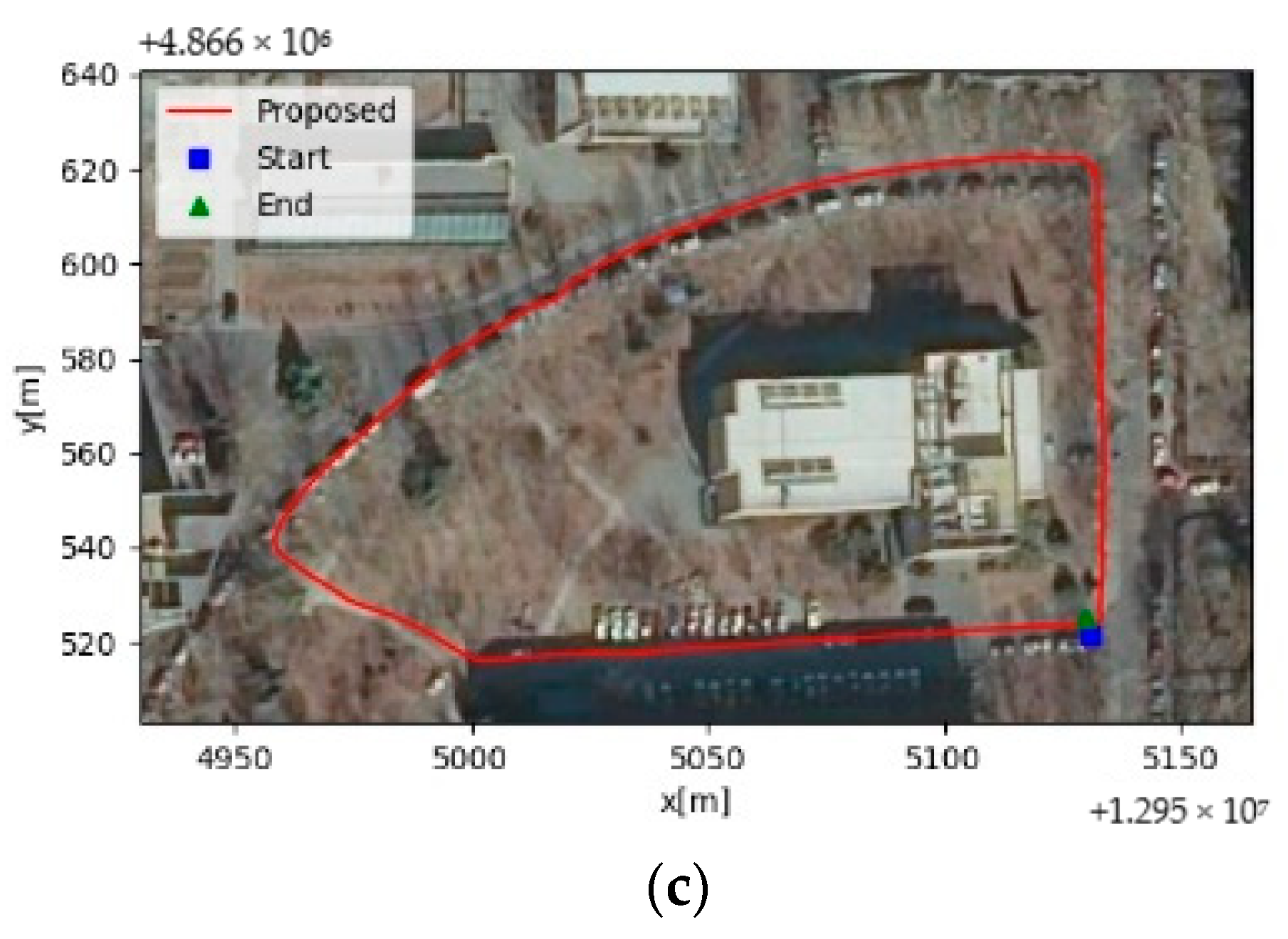
The experimental results are shown in Figure 9. Figure 9a shows the location trajectory of OKVIS-mono, Figure 9b shows the location trajectory of VINS-mono, and Figure 9c shows the location trajectory of the SLAM system using our algorithm. The blue square is the calculated start point, and the green triangle is the calculated end point. The red line shows the trajectory of the positioning results.

Figure 9 shows that our algorithm has higher location accuracy than the traditional algorithm as the start and end points are closer to each other, and the closed-loop error is smaller.

To quantitatively evaluate the accuracies of the three methods, the difference between the location of the end point and the start point was calculated and used as an indicator of the location accuracy of the three methods.

When we evaluate the positioning accuracy, we need to consider the total positioning error of the three XYZ axes. If the total positioning error of the three directions decreases, the positioning accuracy of the system improves. The closed-loop errors of OKVIS-mono and VINS-mono are 11.52 m and 13.32 m, which are 50.17% and 56.91% higher, respectively, than that of the proposed algorithm, which is 5.74 m.

The experiment proves that the proposed abnormal feature matching elimination algorithm is valid and can significantly improve the location accuracy of SLAM systems in complex environments.

5. Conclusions

This paper proposed an algorithm for eliminating feature matches on moving objects with the help of IMU data. The proposed algorithm has two main advantages. First, the algorithm uses the distance from the feature that matches the fundamental matrix calculated by the IMU data as an indicator. Then, it uses feature point matching data to validate the IMU data. Second, with the help of the valid IMU data, the transformation matrix separates the dynamic matched feature points from the static matched feature points, reducing the influence of the moving objects on feature point matching. Therefore, the proposed algorithm can obtain feature points that are realistic.

Our experiment tested a SLAM system with our algorithm integrated on the ADVIO dataset and in the real world. The experiments show that even with moving objects in the scene, our algorithm can accurately separate dynamic elements from static elements and eliminate abnormal matches. Therefore, it can improve the accuracy of feature points matches and increase the location accuracy of SLAM systems in complex environments. This investigation would have wider implications for indoor and outdoor navigation, AR, and location services.

In the future, we plan to introduce deep learning to combine the geometric constraint and object detection methods. By detecting dynamic objects in the scene to improve moving objects recognition, further accuracy gains in feature matching and location accuracy are achievable.