1. Introduction
Plastics are synthetic and made of high molecular weight organic polymers [
1,
2]. More than 300 million tonnes of plastic are produced worldwide, from which around 60 million tonnes are produced in Europe [
3]. Plastic compounds are durable and inexpensive compared to other counterparts, aiding in their wide viability and usage [
4]. Around 240 million tonnes of plastic are discarded annually [
5,
6,
7], of which around 32 million tonnes of plastic enter the ocean every year as waste [
3,
8]. The economic cost to marine natural capital is estimated to range from
$3300 to
$33,000 per ton of plastic per year [
9]. Larger plastics entering ocean waters have two fates—floating on the surface or sinking due to bio-fouling and/or ballasting [
10,
11]. Plastic litter has been found in the deepest parts of the oceans, the seabed, and continental shelves [
3,
12]. Larger marine debris, as compared to microplastics, is more frequently reported by deep diving expeditions in deep-sea environments [
13]. The decay process of plastics has been estimated to be a hundred thousand years [
14]. Plastics can easily sediment in terrestrial and marine environments [
2].
Plastics can be categorized into macroplastics, mesoplastics, microplastics, and nanoplastics [
4,
15]. Macroplastics are of a size more than 25 mm and can be classified as litter such as plastic bags and bottles, discarded fishing nets, plastic toys, and sections of plastic piping [
4,
16]. Mesoplastics range from 5 to 25 mm in diameter, while microplastics or microliters are around 0.5–1 mm in diameter and many a time have been misidentified as food by marine biota [
17]. Nanoplastics are plastic particles of size up to or less than 100 nm in at least one of the dimensions [
18]. If not removed by clean-up operations, macroplastics (>5 mm) may harm many types of marine life through entanglement or ingestion. They also fragment and degrade into microplastics [
19,
20,
21,
22] that can be ingested and incorporated into the bodies and tissues of many organisms. Some of the plastic debris has less density than water, and as a result, it transports more easily and floats on the water surface [
16]. Plastic entanglement of the marine ecosystem [
19] and ingestion of plastic debris and death of marine animals is a growing threat to the environment [
23]. Once ingested, small microplastic fragments may cause physical harm to the digestive systems of animals [
24]. Plastic ingestion can also lead to chemical poisoning of living animals [
25]. Microplastics have also become a threat to human health when marine species ingested with microplastics are consumed [
26]. Studies have shown that plastics have affected the growth and reproduction of at least some aquatic invertebrates [
27]. Furthermore, macroplastics in the environment have been responsible for emission of climate-relevant trace gases, which is because of the breaking of macromolecular chains of plastic through degraded habitat and harmed micro-organisms [
28].
The marine plastic signature was not well documented in the 1940s–1950s [
2], as its usage was limited and the environmental impact was still unrealized. However, in the past few decades, beaches have been found to be the most approachable area for studying plastic debris, as a large fraction of plastic from the marine environment accumulates in that area [
29]. Plastic debris has been found in patches near the sea with varying density depending on wind and current conditions [
30]. In addition, the coastline and distance from trade routes and urban areas can impact the distribution of plastic debris [
31]. Past studies have shown the presence of various plastic accumulation zones near the Atlantic Ocean and Mediterranean Sea [
32]. The presence of high densities of plastic in these regions has been attributed to large-scale residual ocean circulation patterns [
33]. Human activities such as tourism, urban growth, and fishing activities have also contributed to patterns of marine and seabed plastic debris [
2]. Plastics enter the sea via rivers and via ships. To alleviate plastic pollution, illegal dumping has been banned by international law and shipping regulations [
23]. Despite regulatory measures, studies have found more than 6 million tonnes of plastic enter the sea annually, and projections claim that amounts are set to rise significantly by 2025 [
34].
Being able to detect larger floating plastics in coastal waters before they become entangled, ingested, exported, and/or fragmented may help to answer key questions about sources, pathways, and trends. Furthermore, actions that highlight and reduce marine plastic pollution in the context of an increasingly stressed marine environment can be counted as investments toward the health and future resilience of global marine ecosystem services. The challenge is to detect the presence of floating plastics in waterbodies and consider appropriate measures to reduce plastics in oceans via a removal process.
This study considers the use of Sentinel-2 remote sensing data to detect the presence of floating plastics near coastal waterbodies. The Sentinel-2 satellite has a 12-band multi-spectral instrument (MSI) sensor and collects data at a spatial resolution of 10 m, which allows for detecting small features and objects in the marine environment, including river plumes, boats, and patches of macroalgae. Topouzelis et al. [
35] confirmed that floating rafts composed of plastic bottles, bags, and fishing nets reflected light in the near infrared (NIR) band that could be seen from space. The intensity of reflectance appeared to be dependent on the proportion of floating plastic within grids/pixels. Consequently, once water composed more than 50 to 70% of a given grid, poor reflectance in the NIR band was noted. In pixels filled with at least 30% bottles or bags or 50% fishing net, the characteristic reflectance and absorption features of floating plastics are observable. In the ocean, natural and anthropogenic materials tend to be aggregated together, generating patches of mixed objects including natural sources of debris and litter dominated by macroplastics. Once aggregated into sufficiently large patches of varying shapes and sizes, detection from Sentinel-2 is possible.
The objective of this study is to detect floating plastics based on freely available, optical remote sensing satellite data. Detection of floating plastics in coastal waters can be performed using a variety of classification algorithms. However, it is not known a priori which of those algorithms are better suited for the analysis. This study considers four classification algorithms to detect floating plastics using Sentinel-2 remote sensing and in situ data and compares the performance of each of these algorithms. Furthermore, the classification algorithms can be developed based on all or a subset of the multi-spectral band data obtained from the optical satellite sensors as well as a set of indices that can be derived from the satellite data. Since the best combination of the bands and indices were not known a priori, this study considered several combinations of multi-spectral bands and indices to identify the optimal combinations to detect floating plastics in coastal waterbodies. To compare the results obtained by using different classification algorithms and bands and indices combinations, real-world, in situ data that was not considered in the development of the classification algorithm needed to be used for the performance evaluation of each developed model. For this purpose, two locations (Limassol, Cyprus and Mytilene, Greece) were identified where in situ experimental data on floating plastics in the coastal water were available. Details on the Sentinel-2 data and in situ data on the chosen two locations are described in
Section 2.
Section 3 provides details on the four classification algorithms used in the study and the performance evaluation. Results and the discussion are provided in
Section 4 and
Section 5, respectively, while conclusions are drawn in
Section 6.
3. Methodology
The goal of this study was to identify the presence of floating plastics in a sea/ocean waterbody using Sentinel-2 remote sensing imagery. This study considered the use of two unsupervised classification/clustering algorithms and two supervised classification algorithm to detect floating plastics in coastal waters by using the Sentinel-2 remote sensing data. The supervised classification algorithms required a predefined training dataset wherein information on the presence/absence of floating plastics in a set of grids in the waterbody was available based on in situ data. The training dataset was used to calibrate the model parameters of the supervised classification. Once the model was calibrated and validated, it could be used to detect the presence of floating plastics in other grids in the study area that did not belong to the training dataset. On the other hand, the development of an unsupervised classification algorithm (also termed as unsupervised clustering) used only the remote sensing data and did not require any in situ prior information to develop the model. In situations where limited/no training data are available, unsupervised clustering is the only option to develop a model to detect floating plastics in a waterbody. Since real-world information is being used to develop the supervised classification algorithm, it is expected that the performance would be better for detecting floating plastics when compared to unsupervised classification models.
The two clustering algorithms used for unsupervised classification were K-means hard clustering and fuzzy c-means (FCM) clustering. In the literature, these two approaches are found to be robust in forming clusters [
45,
46]. The supervised classifications considered in this study were the support vector regression (SVR)-based algorithm and the semi-supervised fuzzy c-means (SFCM) algorithm. The major advantage of the SVR model is that it can quantify nonlinear relationships between the set of predictors and predictand using a kernel function [
47]. The SFCM is a modification of the unsupervised FCM in which information on the classification is used to form clusters [
48,
49]. In the case of supervised classification, the predictors in the modelling were the Sentinel-2 data obtained at different bands/wavelengths, while the predictand was the presence/absence of floating plastic in a chosen grid/location in the waterbody. Since the optimal combination of Sentinel-2 bands data to produce the highest efficiency in detecting floating plastics in a waterbody was not known a priori, different combinations of available remote sensing band data and a set of indices that were found to be useful in detecting floating plastics were considered in this study. Subsequently, the best-suited algorithm and best combinations of bands and indices were identified to detect floating plastics at an arbitrary location using the Sentinel-2 dataset.
The literature revealed [
50] that a newly proposed index called the Floating Debris Index (FDI) was useful in the identification of floating plastics in waterbodies using remote sensing imagery. The FDI can be estimated as:
where
,
and
denote the reflectance values measured using the satellite per grid corresponding to near infrared (NIR), red edge 2 (RE2,) and short wave infrared 1 (SWIR1) bands, respectively.
,
and
are, respectively, the central wavelengths (in nanometres) corresponding to the NIR, red and SWIR1 bands measured by the satellite. The central wavelengths corresponding to different bands for the Sentinel-2 satellite are provided in
Table 1.
Another index that was found to be useful in detecting plastics was the Normalized Difference Vegetation Index (NDVI), given as:
Biermann et al. [
50] considered the two indices FDI and NDVI along with the reflectance values obtained for the bands red, red edge 2, NIR, and SWIR1 and developed a naïve Bayesian model to predict the presence of floating plastics in waterbodies using Sentinel-2 data. Since the algorithm was a supervised classification algorithm, it required a set of training databases wherein the presence/absence of plastics in a set of grids needed to be used to estimate the model parameters.
The development of the classification model to predict the presence/absence of floating plastics required a set of attributes that were useful in detecting floating plastics. From a literature review [
50], it has been found that the FDI takes a high value and the NDVI takes a low value in grids with the presence of floating plastics. Furthermore, reflectance values corresponding to bands red, NIR, RE2 and SWIR1 have also been used, as they have been found to be useful for detecting floating plastics. However, the optimal band combinations to produce the highest efficiency in detecting floating plastics in waterbodies were not known a priori. This study considers three combinations of bands/indices to develop the attribute sets and perform supervised and unsupervised classification. The three attribute sets considered in this study are shown in
Table 3.
Details of the four classification algorithms and their performance evaluations are provided in the following subsections.
3.1. K-means Clustering Algorithm
This section presents a K-means clustering method [
51] that yield hard clusters through a deterministic search procedure. The method assumes that points in the attribute space can be segregated by using straight lines or linear planes and that the points can be segregated into clusters such that points in a cluster fully resemble each other and those in different clusters do not have any resemblance.
Let denote a vector containing attributes for a grid , with representing the value of the th attribute for the grid. The attribute can be the reflectance value corresponding to a given remote sensing band (e.g., blue, green, red, NIR, SWIR1, etc.) or value of an index (e.g., FDI, NDVI) at the grid . Once the attribute values for each site are obtained, a feature matrix containing vectors from all the sites can be prepared.
The K-means algorithm partitions the feature matrix
into
number of clusters by minimizing the following objective function:
where
denote the
i-th hard cluster,
is an indicator function where
if
is true and
otherwise;
is a matrix containing centroids of
K clusters such that
and
is the square of the Euclidean distance between two vectors.
The optimal number of clusters
can be identified using the Davies–Bouldin (
) cluster validity index [
52]. The index is a function of the ratio of the sum of within-cluster scatter to between-cluster separation and is computed as:
where
and
are within cluster scatter for the
i-th and
l-th clusters, respectively. In general,
is computed as
;
is the number of points in cluster
i and
is the Euclidean distance between the centroids of the
i-th and
l-th clusters. A feature vector can be assigned to the cluster whose centroid is closest to the vector. Optimal clusters should have the lowest
value.
3.2. Fuzzy c-means Clustering Algorithm
This section presents a fuzzy c-means (FCM) clustering method [
53] that is designed to be useful in real world scenarios where a chosen grid may be partially filled with floating plastics. Let
N denote the number of feature vectors prepared as described in
Section 3.1. To form clusters, the FCM method involves partitioning of the feature matrix
into
c clusters by executing the following steps. The method attempts to minimize the following objective function:
subject to the following constraints,
where
is the fuzzy partition matrix in which
denotes the membership of
in the
i-th fuzzy cluster,
is a matrix containing centroids of
c clusters in the
m-dimensional feature space such that
,
refers to the fuzzifier that depicts fuzziness of the clusters, and
is the Euclidean distance between two vectors. The memberships tend to either 1 or 0 as the value of
tends to 1.
The optimal number of clusters and optimal fuzzifier value can be identified for situations where the value of Xie-Beni cluster validity index
[
54] is minimal.
3.3. Support Vector Regression (SVR) Algorithm
The support vector regression (SVR) develops a nonlinear relationship [
55] between an input vector
and output
.
The relationship can be expressed as:
where
is a nonlinear transformation function [
55] and
is white noise whose expected value
is 0. The relationship is developed based on
n number of training data where the presence of floating plastic for grid
s is known. In this study,
Details of the SVR algorithm can be found in Vapnik [
55].
3.4. Semi-Supervised Fuzzy c-means (SFCM) Algorithm
The semi-supervised fuzzy c-means (SFCM) algorithm is an extension of the FCM clustering wherein a portion of the data, termed as a training set that is used for clustering, are known to belong to a given cluster a priori [
48]. The SFCM algorithm is a hybrid clustering algorithm which can extract the hidden pattern present in the data by using FCM clustering on the non-trained data and use the training data to improve the cluster formation. The SFCM algorithm minimizes the following objective function:
where
is a scaling factor that maintains balance between the training and non-training data,
are the membership values of the training dataset, and
is a Boolean indicator that takes a value equal to 1 if the data belongs to a training set and zero if the data is non-trained.
3.5. Performance Evaluation
In order to evaluate the performance of a chosen algorithm for detecting the floating plastics in coastal waterbodies, the total available training data needed to be subdivided into two sets. The first set, termed the calibration set, was used to develop the model using a chosen algorithm (either supervised or unsupervised) and estimate the model parameters. Subsequently, the developed model was implemented for the remotely sensed bands and indices to predict presence/absence of floating plastics in grids belonging to the second set, called the validation set. Subdividing the total training data into the calibration and validation sets was necessary to ensure that the validation set data that were used for performance evaluation of the model had not been used to develop the model.
The effectiveness of the classification approach in detecting presence/absence of floating plastics was evaluated in terms of the error/confusion matrix, overall accuracy, and F-score statistic based on the validation set data. The error matrix consisted of 2 rows and 2 columns (
Table 4). Along the row-wise direction, the observed/in situ information on the presence/absence of floating plastics was indicated, while in the column-wise direction, the model predicted values were noted. In situations where the model predicted the presence/absence of floating plastic at the grid where in situ observations agreed with the predictions, the algorithm could be considered to be efficient. In the error matrix, true positive (TP) indicates that the model correctly predicts the presence of floating plastics, while true negative (TN) means the model correctly predicts the absence of floating plastic in a grid. On the other hand, false positive (FP) means the model wrongly predicts the presence of floating plastic in a grid where plastic is absent based on the in situ ground truth data, whereas false negative (FN) indicates the algorithm fails to detect floating plastic in a grid.
The overall accuracy could be estimated by summing the number of grids where the model predicted correctly and dividing that value by the total number of grids. Based on the table, the overall accuracy = 100 × (TP + TN)/(TP + TN + FP + FN). The overall accuracy ranges from 0 to 100%.
Subsequently, the F-score can be estimated based on the results as:
The F-score value ranges from 0 to 1. In situations where the model performance was better, the overall accuracy tended toward 100% while the F-score approached unity.
4. Results
This study considered data from two locations, Limassol, Cyprus and Mytilene, Greece, to investigate the effectiveness of the four classification algorithms. The reason for selecting those two locations was that a real-world experiment was performed in the coastal waters of those two locations and the presence of floating plastics was verified by using in situ observations. In Limassol, plastics were detected in 4 grids on 15 December 2018 based on in situ observations, while clear water was detected in 95 grids based on aerial and Sentinel images (
Figure 2a). Similarly, in Mytilene, in situ floating plastic was detected in 12, 6, 25, and 12 grids respectively on 7 June 2018, 18 April 2019, 3 May 2019, and 7 June 2019, respectively (
Figure 2b–e). The number of grids with clean water at Mytilene on the aforementioned four dates were 92, 86, 94, and 91 respectively. Based on the in situ database, 59 grids were identified to have floating plastics, while based on aerial and Sentinel images, 458 grids were found to have clean water without the presence of floating plastics. In total, the training dataset consisted of 517 grids. In this study, 75% of the entire training data were considered as the calibration set, and the remaining 25% data was selected as the validation set. The calibration set consisted of 388 grid data points, and the validation set had 129 grids. Based on in situ information, it was noted that out of 388 grids, 44 grids had floating plastics, whereas the remaining 344 grids did not contain any plastic. It can be noted that the supervised SVR algorithm has been developed based on the 388-grid calibration set data, whereas the remaining 129-grid data, in which 15 grids had floating plastics and the remaining 114 grids did not have plastics, were solely used for performance evaluation.
The total number of 28,797 unsupervised/untrained grids have been considered in the study along with the 517 trained grids. The untrained grids were located within a distance of 500 m from the grids where floating plastic was detected. Those grids were considered to be untrained, as in situ information on floating plastic at those grids was unknown; however, the reflectance values and the FDI and NVDI values at each of the grids were available from the Sentinel-2 remote sensing data. This untrained database of 28,797 grids was combined with the 388 grid data from the calibration set to perform the two unsupervised classifications and the semi-supervised fuzzy c-means classification. The reason for using the untrained data was that both K-means and FCM algorithms, as well as the SFCM algorithm, require a considerable number of datasets to form clusters. Since the SVR-based supervised classification algorithm cannot use an untrained database for parameter estimation, the SVR model was developed by using data from the calibration set only.
A comparison of the performance of each of the four classification algorithms with the three different attribute sets A, B, and C was investigated using the 129-grid validation set data. The classification algorithm could be considered to perform correctly when it predicted the presence of floating plastics in grids where plastic was found to be present by using in situ data. In addition, the algorithm worked properly when it did not detect floating plastics in clean water. Error occurred when the algorithm failed to detect floating plastics in grids where they were present or predicted the presence of floating plastics in clean water.
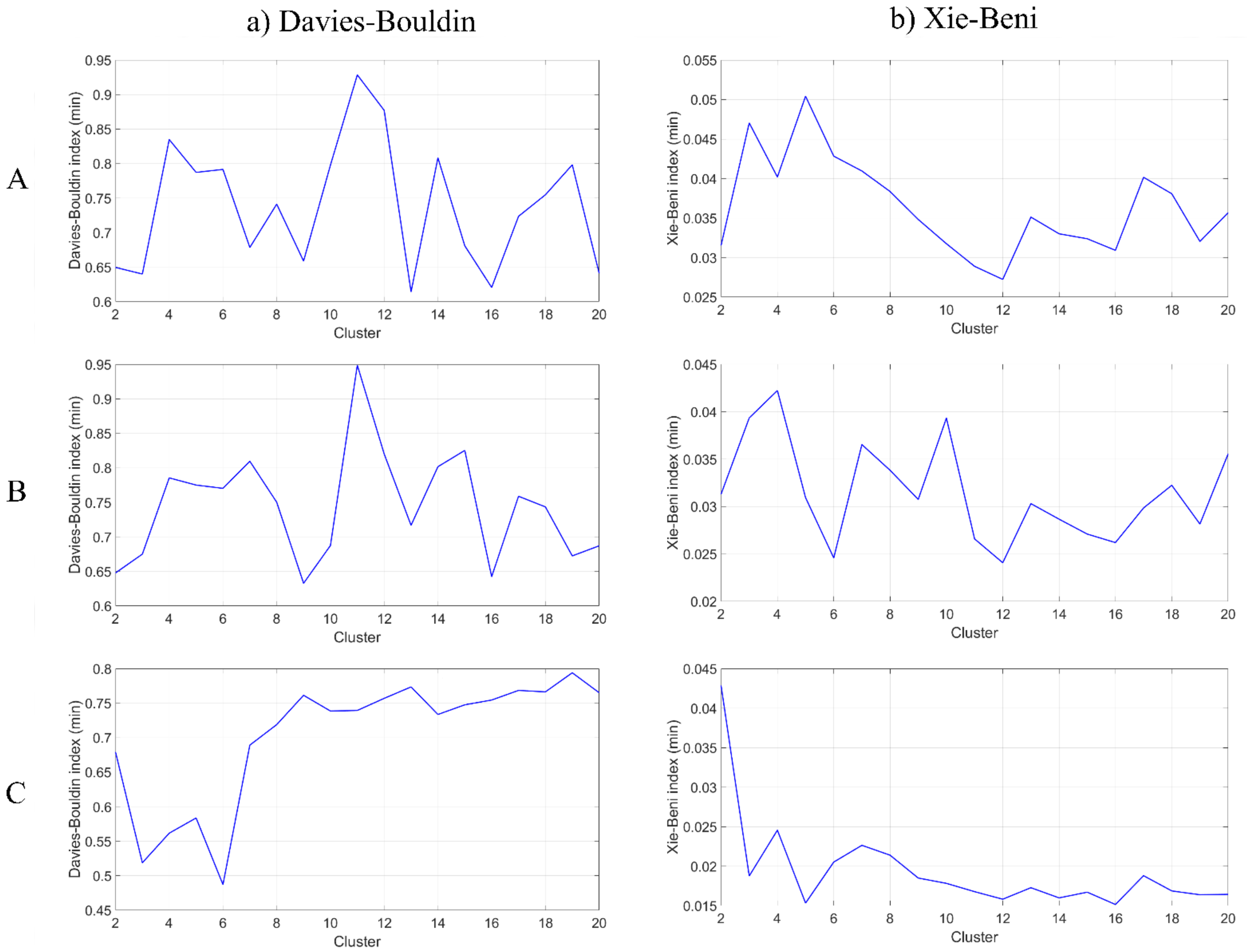
Based on the untrained dataset and the calibrating data, the K-means clustering algorithm was developed by separately using the three attribute sets A, B, and C. Since the optimal number of clusters were not known a priori, the cluster values K ranging from 2 to 20 were considered, and the clusters were formed. The optimal cluster numbers K_opt were identified based on the Davies–Bouldin cluster validity index (
Figure 3a). The optimal K-means cluster numbers were found to be 13, 9, and 6 for attribute sets A, B, and C, respectively. Based on the analysis, the clusters that represented the floating plastics were identified, and the cluster centroids were noted. Based on the cluster centroids, the data from the validation set were reclassified to predict the presence/absence of floating plastics. A performance matrix (error/confusion matrix) was developed to estimate the performance of the algorithm in predicting the presence/absence of floating plastics. The performance matrix based on K-means clustering using each of the three attribute sets is shown in
Table 5. The overall accuracies obtained using K-means clustering were found to be 81.4%, 78.3%, and 69.8%, respectively, while using attribute sets A, B, and C, and for those sets, the algorithm wrongly predicted 21, 25, and 36 times the presence of plastics at locations where plastic was absent in the real-world scenario. The F-scores for the three attribute sets were found to be 0.5, 0.46, and 0.38, respectively.
Similar to the K-means clustering, the fuzzy c-means (FCM) clustering algorithm was applied to each of the three attribute sets to form clusters. Since the optimal number of clusters and the optimal fuzzifier values were not known a priori, the clustering was performed by considering a different combination of those values. In this study, the cluster number varied from 2 to 20. However, since the objective was to identify whether plastic was present/absent in a chosen grid, a fuzzifier value closer to 1 needed to be considered because a higher fuzzifier value tended to assign nearby membership to all clusters. Hence, the fuzzifier value was not varied, and a single value equal to 1.05 was selected for the analysis. The optimal cluster number was identified based on the Xie–Beni cluster validity index (
Figure 3b) and was found to be 12, 12, and 5 for attribute sets A, B, and C, respectively. Following this, the performance matrix was estimated using the validation set data (
Table 5). While using attribute sets A, B, and C, the overall accuracy was estimated as 82.2%, 81.4% and 69.8%, respectively. It can be noted that the accuracy was slightly better than that obtained from K-means clustering while using attribute sets A and B, whereas both the clustering algorithms produced similar results when only the indices (attribute C) were used for model development. The number of times the FCM predicted the presence of plastics in grids where plastic was not present in reality were 21, 21, and 36 for sets A, B, and C respectively. The F-score for the three cases using FCM was found to be 0.53, 0.5, and 0.38 respectively.
The support vector regression(SVR)-based supervised classification algorithm was developed based on the calibration data only. The SVR model had two parameters, γ and C. Since the optimal values of those parameters were not known a priori, the model was run by selecting different combinations of the two parameter values, and the best-fit model was identified. The values of γ were considered to be 1, 10, 100, and 1000, while the value of C ranged from 0.1 to 10 with an increment of 0.1. The optimal model parameter values were found to be γ_opt = 100, C_opt = 1.1 for attribute set A, γ_opt = 100, C_opt = 1.0 for attribute set B, and γ_opt = 10, C_opt = 1.5 for attribute set C. Once the model was developed, it was used to predict the presence/absence of floating plastic by using the validation set data, and the performance matrix was estimated (
Table 5).
Table 5 indicates that out of the 15 grids where floating plastic was found to be present based on in situ observations, the SVR supervised classification algorithm detected the presence of plastics in 13 (86.7% accuracy) grids when reflectance values from 6 bands and the two indices were used. The accuracy in detecting plastics reduced to 80% (12 out of 15 grids) when blue and green band reflectance data was discarded (set B) and to 73.3% (set C) when only the indices were used to develop the SVR model. One point to be noted is that each of the three SVR models that were developed using different attribute sets managed to correctly identify grids where no floating plastic was present. The overall accuracy of the SVR models was 98.4%, 97.7% and 96.9% while using attribute sets A, B and C, respectively. High values of overall accuracy were obtained, as all three models developed based on the SVR algorithm successfully identified all the grids where plastic was absent in real-world scenarios. The F-score values for attribute sets A, B and C using the SVR algorithm were 0.93, 0.89 and 0.95 respectively.
In the case of SFCM classification, only two clusters were formed, as the calibration set training data had only two classes, presence and absence of floating plastics. The error matrix obtained for the validation set data is shown in
Table 5. The overall accuracy and the F-score were found to be low for the SFCM classification.
The FCM algorithm also managed to locate 13 grids where plastic was present while using set A data. However, both FCM and K-means algorithms wrongly predicted the presence of floating plastics in several grids where no plastic was present. The performance of both the supervised and unsupervised algorithms was the best when set A was used and the worst when only the indices were considered to develop the algorithm. The performance of K-means and FCM were similar, with FCM being slightly better. In general, the results indicated the use of blue and green band data along with the red, red edge 2, NIR, and SWIR 1 as well as the two indices FDI and NDVI could provide better plastic detection. The supervised classification algorithm was considerably better when compared to unsupervised clustering. However, it needs to be noted that the supervised classification algorithm can only be developed in situations where substantial training data are available.
In order to visualize the results, a portion of the validation set data obtained based on in situ observations was plotted in
Figure 4. Grids where plastic was found to be present using in situ data are shown in red, while grids with no plastics are shown in blue.
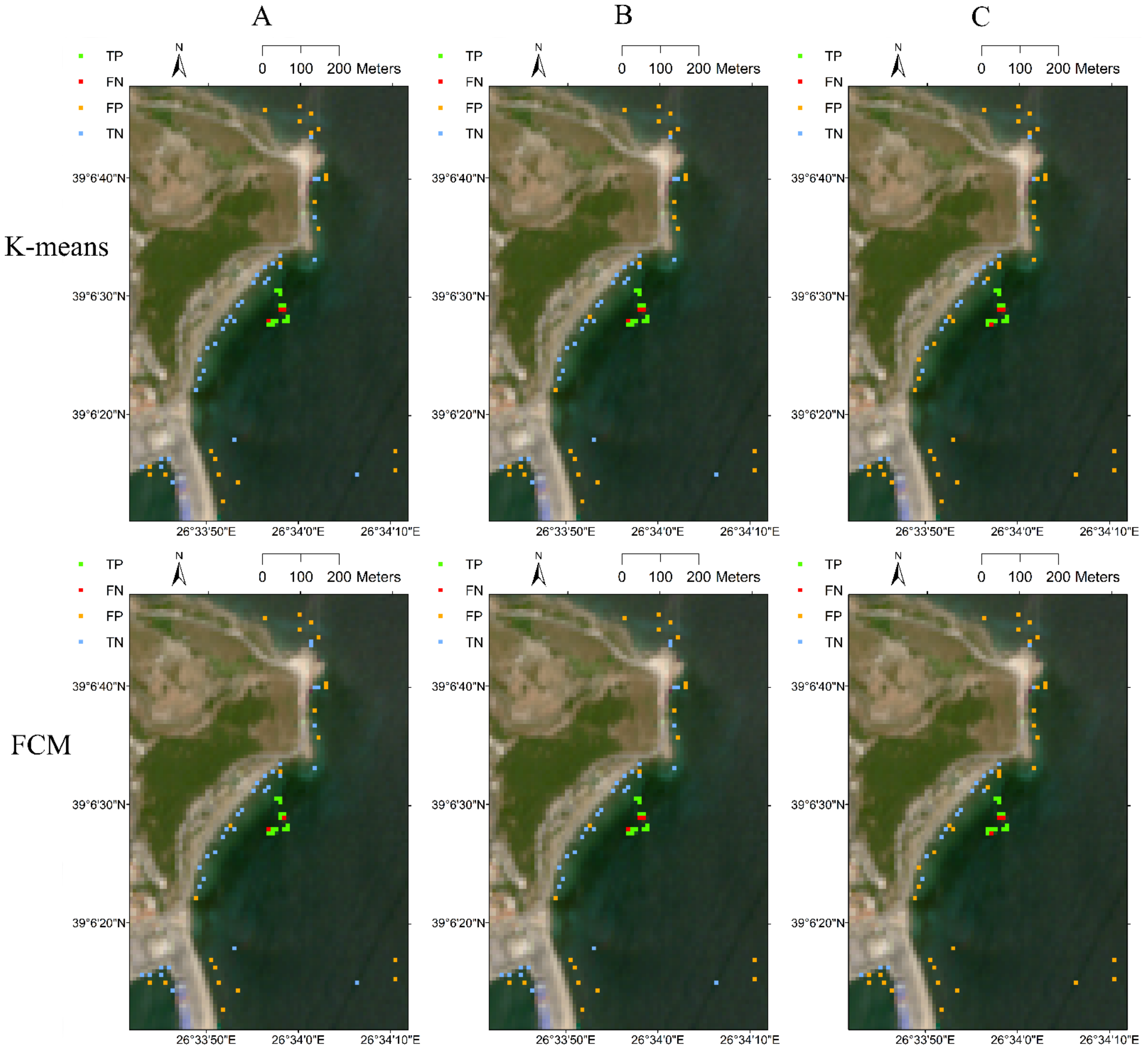
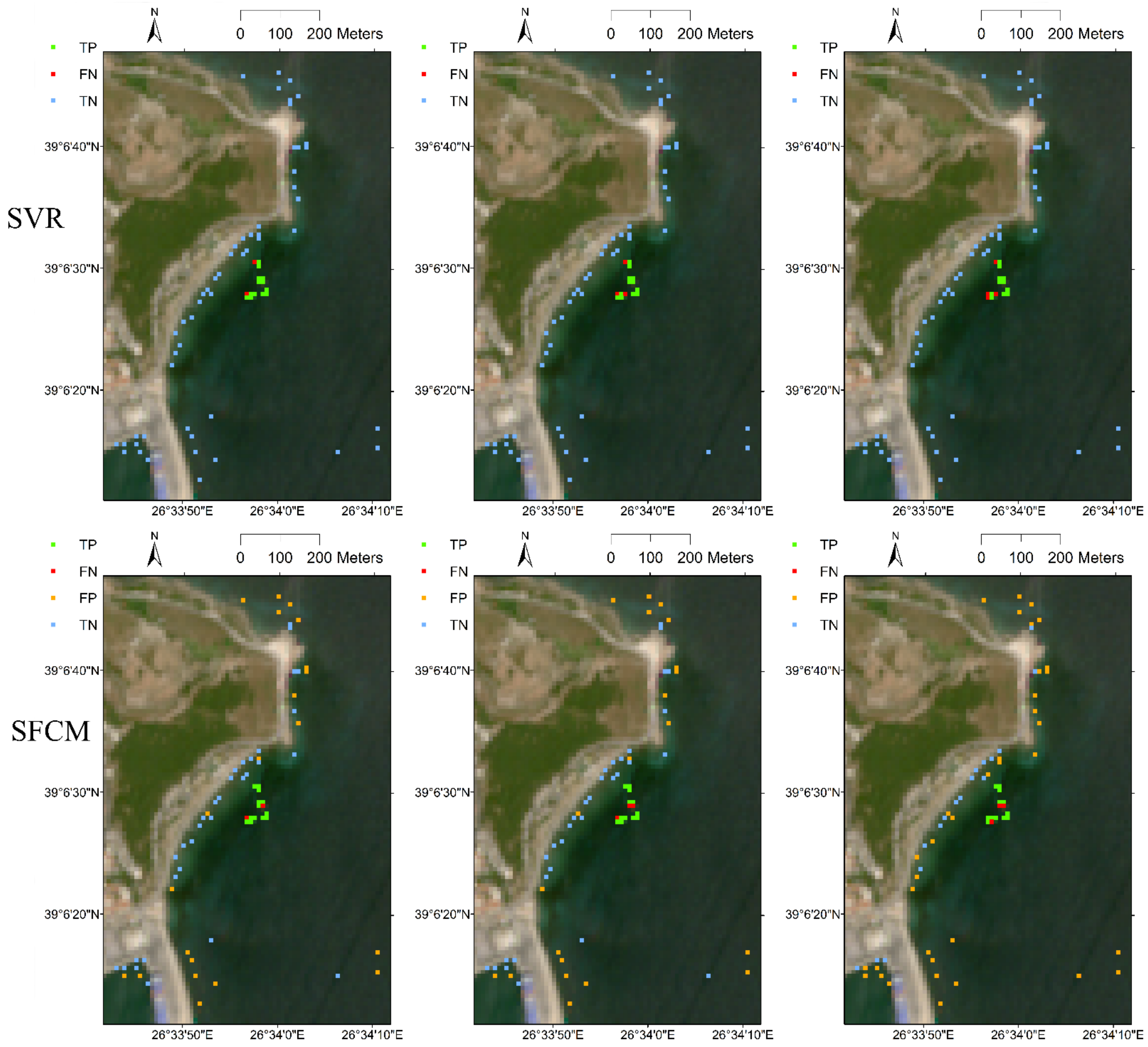
Similar plots were prepared based on classifications obtained using K-means, FCM, SVR and SFCM based classification algorithms and by using each of the three attribute sets A, B, and C (
Figure 5). In this figure, grids were plotted as true positive (TP) where the model correctly detected the floating plastics, true negative (TN) where the model correctly predicted the absence of floating plastics, false positive (FP) where the model wrongly predicted the presence of floating plastics, and false negative (FN) where the model failed to detect floating plastics. The figure is useful for locating the correctly classified and misclassified grids from the validation set.
It can be noted from
Figure 5 and
Table 5 that the supervised SVR algorithm managed to predict the absence of floating plastics in all the grids accurately. One point to be noted here is that in the training dataset that consisted of 517 grids, only 59 of those grids had floating plastics, while the remaining 458 grids had an absence of plastics. The number of grids with floating plastics in the training dataset was considerably low, which may have affected the performance of the developed model. Furthermore, the number of grids without plastic was considerably high (458 grids) when compared to the number of grids with the presence of floating plastics (59 grids). In order to perform a sensitivity analysis, another model was developed wherein an equal number of grids with plastics and without plastics were considered. In the new training data, the existing 59 grids where floating plastics were present were considered, whereas only 59 grids out of the 458 available grids with no plastics were randomly selected to construct the new training set database. Since SVR is the only supervised classification algorithm, it was selected to develop the new mode. Furthermore, as attribute set A was found to provide superior results when compared to attribute sets B and C, only attribute set A was chosen to develop the SVR model. The newly created training set consisting of 118 grid datapoints was subdivided into two sets, the calibration set and the validation set, in a ratio of 3:1. The calibration set consisted of 88 grid points, wherein 44 grids had floating plastics and the remaining 44 grids had no plastics, while the validation set had 30 grid points (15 grids with plastics and 15 without plastics). The performance of the developed model was estimated based on the validation set data and is shown in
Table 6 and
Figure 6.
5. Discussion
Comparative analysis between the two unsupervised clustering algorithms (K-means and fuzzy c-means) and the two supervised classifications (support vector regression and semi-supervised fuzzy c-means) for detecting floating plastics in coastal waterbodies revealed that overall, the supervised classification outperformed the unsupervised clustering algorithm. This can be concluded based on the significant differences in the overall accuracy and the F-score statistic obtained by using the different models. The overall accuracy and the F-score were found to be the highest for the SVR model, followed by FCM, K-means, and the SFCM algorithm. The performance of a chosen classification algorithm for detecting floating plastics by considering the three different attribute sets A, B, and C revealed that all the algorithms performed better when attribute set A was selected to develop the classification model. It can be noted from
Table 3 that set A contained reflectance information corresponding to six bands (blue, green, red, NIR, RE2, and SWIR1) as well as two indices (FDI and NDVI). The other two sets, B and C, were subsets of set A and contained less information. The performance of a chosen classification algorithm did not always improve with availability of a higher amount of attribute data. A proper selection of attributes was essential to obtain better performance. A lower number of attributes might not have sufficient information to form effective classifiers, whereas more information might become redundant and mislead the classifiers [
56,
57]. Superior performance of classification models using set A data indicated that all six bands and the two indices were important and provided independent information to detect the presence/absence of floating plastics in the coastal waterbodies. The reflectance value of waterbodies with and without the presence of floating plastics corresponding to those six bands were different, and they were necessary for the segregation of the grids with plastics from grids without plastics [
50].
The validation set consisted of a total of 129 grids, out of which 15 grids had floating plastics, and 114 grids had no plastics present. In situations where attribute set A was considered, the SVR model successfully detected 13 of the 15 grids where plastic was present and failed to detect two grids. However, the algorithm completely detected all the grids with no plastics and did not predict the presence of floating plastics in clear waterbodies. The SFCM algorithm managed to detect 14 grids with plastics; however, it falsely predicted the presence of plastics in clear waterbodies for 45 grids, which led to its poor overall accuracy and F-score. The other two unsupervised algorithms also exhibited several misclassifications wherein the model predicted the presence of plastics in clear waterbodies as well as failed to detect plastics. The SVR model had the advantage of developing nonlinear relationships between the predictor and predictand sets and always reached the global optimal solution while solving the classification algorithm [
55], which led to its better performance in detecting floating plastics. The unsupervised classification algorithm was developed solely based on the remote sensing data and did not include information from the training set, which led to its inferior performance. In general, better performance from the SFCM algorithm is expected when compared to that from unsupervised FCM. However, while developing the SFCM clusters, only two clusters were formed in this study, as the calibration set data had only two classes, presence and absence of floating plastics. It can be noted that the SFCM algorithm managed to detect 14 grids with plastics and failed to detect only 1 grid with plastic, while the other algorithms detected 13 or 12 grids and failed to detect 2–3 grids. The error in SFCM arose as it falsely predicted the presence of plastics in clear waterbodies. This is because of the fact that even though those grids did not have plastics present, they may not have been classified as clear water due to the presence of other forms such as seaweed, foam, timber, etc. The performance of SFCM could be considerably improved with better training datasets. Furthermore, it is not definite that the same set of band and index combinations would produce similar accuracy in detecting floating plastics in coastal areas across the world. Detailed research needs to be conducted by performing similar experiments to those conducted in Cyprus and Greece at a global scale to explore the effectiveness of the models used in this study.
Another point to be noted is that the performance of the algorithms was sensitive to the atmospheric corrections applied when processing the Sentinel-2 remote sensing data. In situations where remote sensing images are the solely available data for the identification of floating plastics, the presence of cloud cover and water vapor can be a major issue in obtaining accurate data. The selection of an effective atmospheric correction algorithm for coastal waterbodies is essential to improve the accuracy in detecting floating plastics from remote sensing images.
Another challenge is that most of the open access remote sensing satellite data are available at a spatial resolution of 10 m or coarser range, indicating that one single spectral reflectance value is available over an area of 100 square meters or more. In a real-world scenario, it is extremely likely that floating plastics might be present only in some portion of the area of each remote sensing grid. This makes the detection process extremely challenging. Furthermore, different types of plastics such as bottles, bags, fishnets, etc. would have different reflectance values at multiple wavelengths. Further research needs to be performed to create plastic targets for training datasets wherein a mixture of plastic materials is present and the target covers only a fraction of the remote sensing grids.
6. Conclusions
Based on an advanced machine learning algorithm (support vector regression) and clustering techniques (K-means, fuzzy c-means), the potential application of open source Sentinel data in detecting marine floating plastic at the remote sensing grid scale was thoroughly examined. Despite uncertainties and data limitations, the present research successfully demonstrates the application and functional usability of these machine learning and clustering techniques in detecting floating marine debris. Replicability and easy transferability of the models and approaches have been the key focus of this study. The analysis also demonstrates that the developed models can be used to detect floating plastics across the world as a real-time solution if real-time satellite data can be fed into the algorithms. Additionally, since the algorithms developed in this study are primarily based on remote sensing spectral bands, the same can be applied to any similar remote sensing data (Landsat or other high-resolution satellite data with spectral bands identical to Sentinel-2).
The study investigated the effectiveness of two unsupervised (K-means and FCM) and two supervised classification algorithms (SVR and SFCM) in detecting floating plastics in coastal waterbodies. Based on data from the coastline of Cyprus and Greece, 59 grids were located with the presence of floating plastics. Out of those 59 grids, 44 grids were used to develop the models, while 15 grids were considered as a validation set for performance evaluation of the models. Three different attribute sets were chosen to develop each of the classification models. The biggest attribute set considered 6-band reflectance data from Sentinel-2 images and two indices estimated from the Sentinel-2 data, while the other two attribute sets were subsets of the biggest attribute set. The performance of each of these models was found to be superior when the biggest attribute set was chosen. The model performance was categorized based on its accuracy in identifying grids with plastics and grids without plastics, while the errors in misclassification were also noted. Out of the 15 grids with plastics, SFCM detected 14 grids correctly, SVR and FCM detected 13 grids correctly, and K-means detected 12 grids. The SVR model didn’t predict floating plastic in any grids with clear water; however, the other three algorithms wrongly predicted the presence of plastics in grids where plastic was absent in real world scenarios. It can be noted that some of those grids might exhibit other types of materials such as foam, timber, and seaweed. Further analysis needs to be performed with bigger training samples collected across the world to develop better classification algorithms. Current research is focusing on creating a new training dataset in Ireland and exploring the opportunity of using higher resolution, multispectral, commercially available remote sensing data to develop a better classification algorithm.