A Higher-Order Graph Convolutional Network for Location Recommendation of an Air-Quality-Monitoring Station
Abstract
1. Introduction
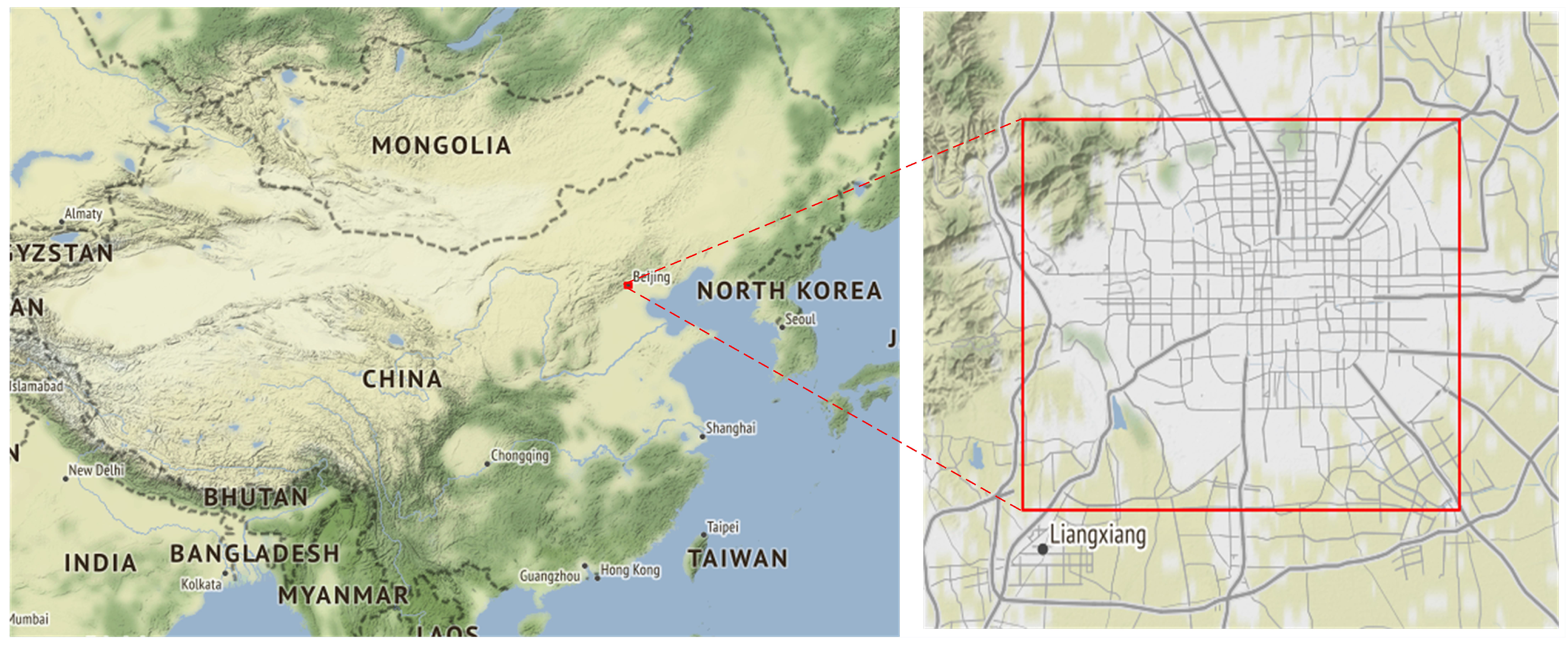
2. Study Area and Data Requirement
2.1. Study Area
2.2. Data Requirement
3. Preliminary and Methodology
3.1. Preliminary
3.1.1. Air-Quality Index
3.1.2. Graph Convolutional Networks
3.1.3. Urban Spatiotemporal Graph
3.1.4. Inference Problem of Air Quality
3.1.5. Location Recommendation for the Monitoring Station
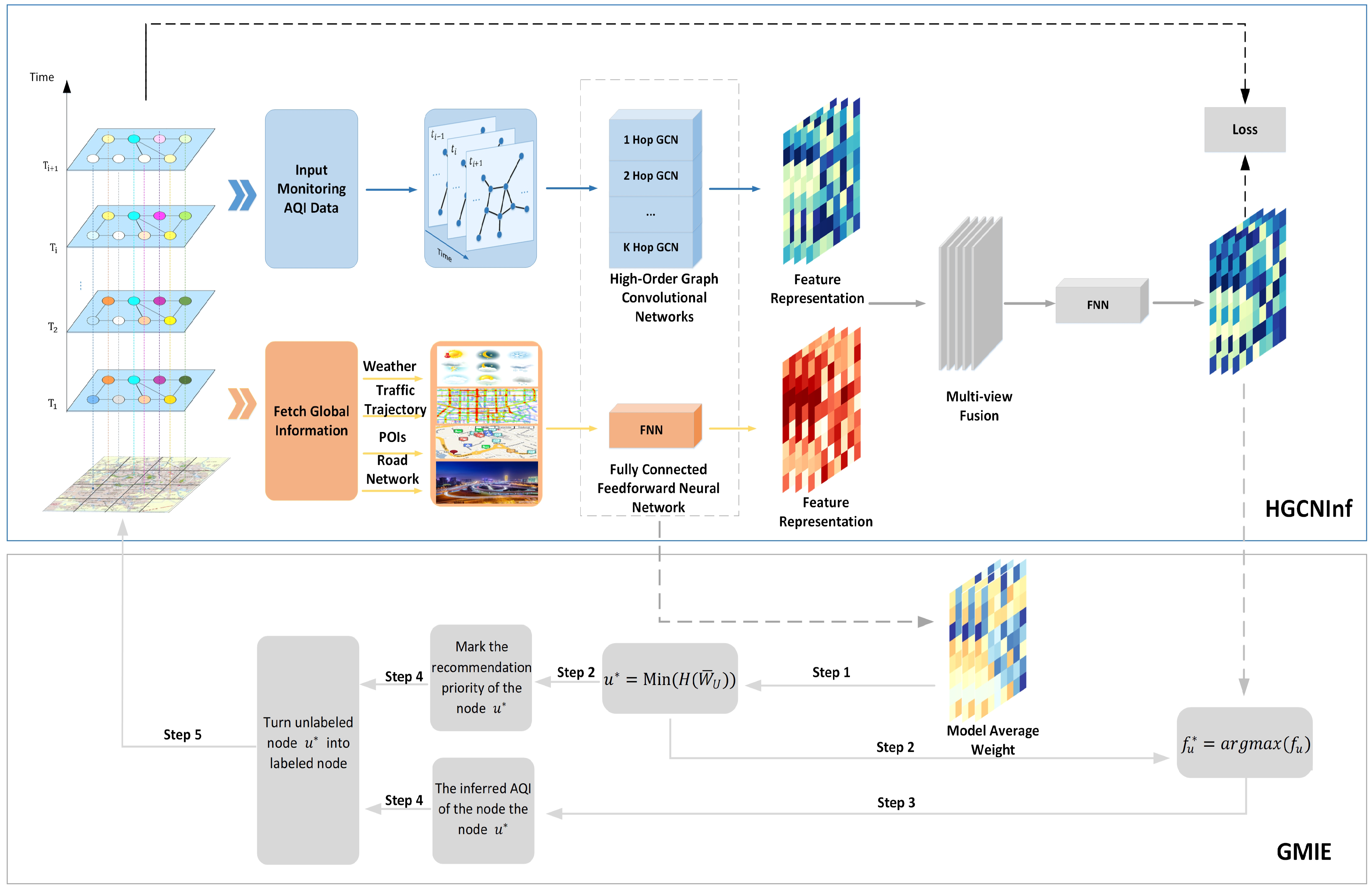
3.2. Methodology
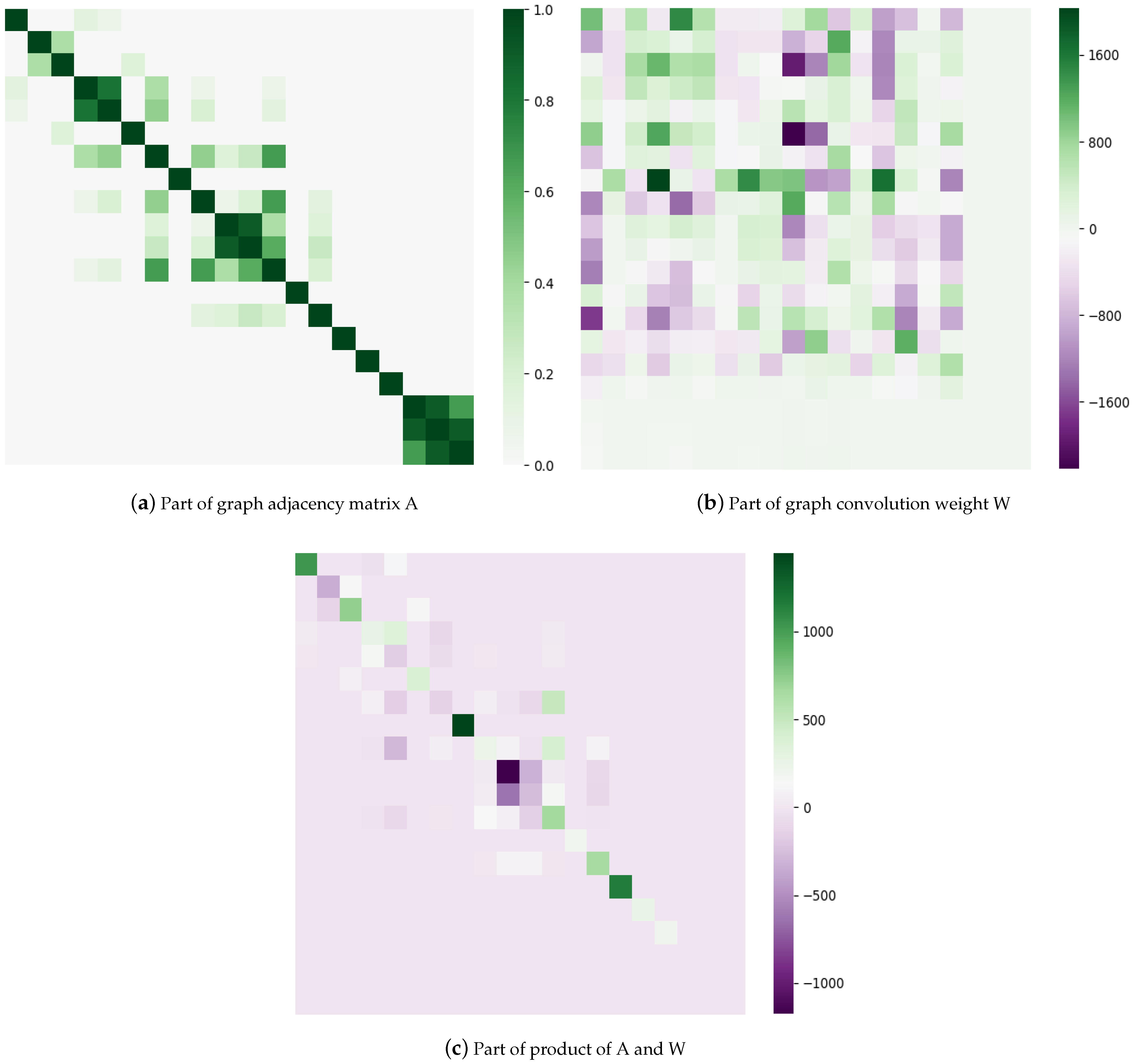
3.2.1. Higher-Order Graph Convolutional Network
3.2.2. The Air-Quality Graph Convolution
3.2.3. Air-Quality-Monitoring Station Location Recommendation
4. Experiments and Results
4.1. Data Processing
4.2. Experimental Settings
4.2.1. Evaluation
4.2.2. Baselines
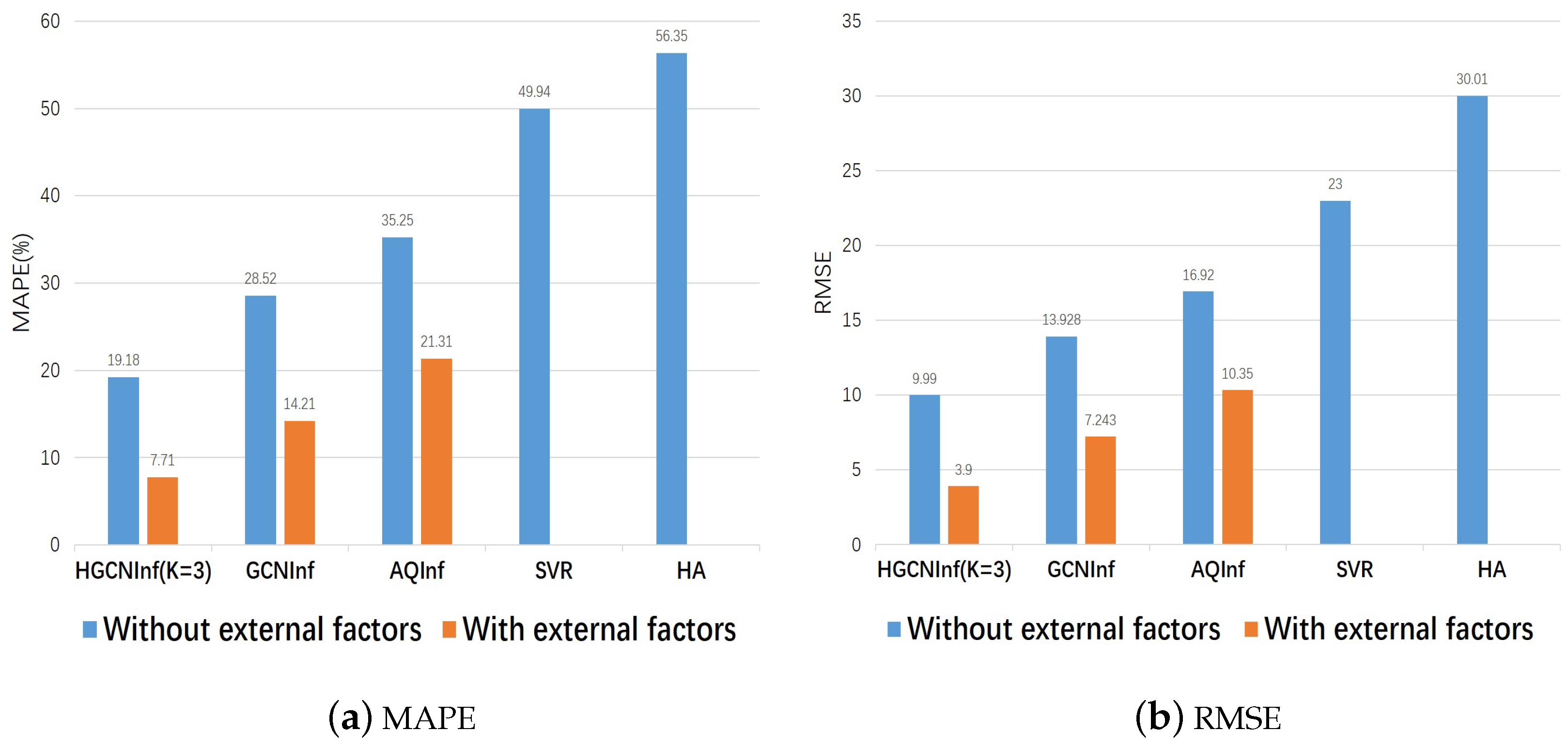
4.3. Experimental Results
4.3.1. The Effectiveness of HCNInf
4.3.2. The Effectiveness of GMIE
5. Discussion
5.1. Air-Quality Inference
5.2. Air-Quality-Monitoring Station Location Recommendation
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Li, W.; Shao, L.; Wang, W.; Li, H.; Wang, X.; Li, Y.; Li, W.; Jones, T.; Zhang, D. Air quality improvement in response to intensified control strategies in Beijing during 2013–2019. Sci. Total. Environ. 2020, 744, 140776. [Google Scholar] [CrossRef]
- Shi, K.; Wu, L. Forecasting air quality considering the socio-economic development in Xingtai. Sustain. Cities Soc. 2020, 61, 102337. [Google Scholar] [CrossRef]
- Suman. Air quality indices: A review of methods to interpret air quality status. Mater. Today Proc. 2021, 34, 863–868. [Google Scholar] [CrossRef]
- Xu, Z.; Kang, Y.; Cao, Y.; Li, Z. Deep amended COPERT model for regional vehicle emission prediction. Sci. China Inf. Sci. 2021, 64, 1–3. [Google Scholar] [CrossRef]
- Reames, T.G.; Bravo, M.A. People, place and pollution: Investigating relationships between air quality perceptions, health concerns, exposure, and individual-and area-level characteristics. Environ. Int. 2019, 122, 244–255. [Google Scholar] [CrossRef]
- Yang, X. The relationship between air pollution and human health. Green Build. Mater. 2019, 154, 53–56. [Google Scholar]
- Bai, L.; Shin, S.; Burnett, R.T.; Burnett, R.T.; Kwong, J.C.; Hystad, P.; Donkelaar, A.V.; Goldberg, M.S.; Lacigne, E.; Copes, R.; et al. Exposure to ambient air pollution and the incidence of congestive heart failure and acute myocardial infarction: A population-based study of 5.1 million Canadian adults living in Ontario. Environ. Int. 2019, 132, 105004. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Y.; Liu, F.; Hsieh, H.P. U-air: When urban air quality inference meets big data. In Proceedings of the 19th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Chicago, IL, USA, 11–14 August 2013; pp. 1436–1444. [Google Scholar]
- Qin, Y.; Qian, Y.; Rong, T. Research on the optimization of monitoring site selection based on atmospheric pollutants. China Environ. Sci. 2015, 35, 1056–1064. [Google Scholar]
- Liu, P.; Zheng, J.; Li, Z.; Zhong, L.; Wang, X. Research on Optimal Distribution Method of Regional Air Quality Monitoring Network. China Environ. Sci. 2010, 30, 907–913. [Google Scholar]
- Luo, H.; Feng, H.; Yan, X. Application of air quality prediction model for monitoring site selection. In Proceedings of the 2012 Annual Conference of Chinese Society for Environmental Sciences, Sapporo, Japan, 1–4 August 2012. [Google Scholar]
- USEPA. Fresno Supersite Final Report; Desert Research Institute for the OAQPS, U.S. Environmental Protection Agency: Research Triangle Park, NC, USA, 2005.
- Europe Environment Agency. The European Environment. State and Outlook 2005 [EB/OL]. Available online: http://www.eea.europa.eu/highlights/20051122115248 (accessed on 29 November 2005).
- Fukushima, H. Air pollution monitoring in East Asia. Sci. Technol. Trend 2006, 18, 55–63. [Google Scholar]
- Raffuse, S.M.; Sullivan, D.C.; McCarthy, M.C. Ambient Air Monitoring Network Assessment Guidance; U.S. Environmental Protection Agency: Washington, DC, USA, 2006.
- Arbeloa, S.F.J.; Caseiras, P.C.; Andres, L.P.M. Air quality monitoring: Optimization of a network around a hypothetical potash plant in open countryside. Atmos. Environ. 1993, 27A, 729–738. [Google Scholar] [CrossRef]
- Kao, J.J.; Hsieh, M.R. Utilizing multiobjective analysis to determine an air quality monitoring network in an industrial district. Atmos. Environ. 2006, 40, 1092–1103. [Google Scholar] [CrossRef]
- Sarigiannis, D.A.; Saisana, M. Multi-objective optimization of air quality monitoring. Environ. Monit. Assess. 2008, 136, 87–99. [Google Scholar] [CrossRef] [PubMed]
- Xu, Z.; Kang, Y.; Cao, Y. Emission stations location selection based on conditional measurement GAN data. Neurocomputing 2020, 388, 170–180. [Google Scholar] [CrossRef]
- Liu, D.; Weng, D.; Li, Y.; Bao, J.; Zheng, Y.; Qu, H.; Wu, Y. Smartadp: Visual analytics of large-scale taxi trajectories for selecting billboard locations. IEEE Trans. Vis. Comput. Graph. 2016, 23, 1–10. [Google Scholar] [CrossRef]
- Li, Y.; Zheng, Y.; Ji, S.; Wang, W.; U, L.H.; Gong, Z. Location selection for ambulance stations: A data-driven approach. In Proceedings of the 23rd SIGSPATIAL International Conference on Advances in Geographic Information Systems, Seattle, WA, USA, 3–6 November 2015; pp. 1–4. [Google Scholar]
- Kang, Y.; Li, Z.; Zhao, Y.; Qin, J.; Song, W. A novel location strategy for minimizing monitors in vehicle emission remote sensing system. IEEE Trans. Syst. Man Cybern. Syst. 2017, 48, 500–510. [Google Scholar] [CrossRef]
- Hsieh, H.P.; Lin, S.D.; Zheng, Y. Inferring air quality for station location recommendation based on urban big data. In Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Sydney, NSW, Australia, 10–13 August 2015; pp. 437–446. [Google Scholar]
- Zhu, X.; Ghahramani, Z.; Lafferty, J.D. Semi-supervised learning using gaussian fields and harmonic functions. In Proceedings of the 20th International Conference on Machine Learning (ICML-03), Washington, DC, USA, 21–24 August 2003; pp. 912–919. [Google Scholar]
- Vardoulakis, S.; Fisher, B.E.A.; Pericleous, K.; Gonzalez-Flesca, N. Modelling air quality in street canyons: A review. Atmos. Environ. 2003, 37, 155–182. [Google Scholar] [CrossRef]
- Bruna, J.; Zaremba, W.; Szlam, A.; LeCun, Y. Spectral networks and locally connected networks on graphs. arXiv 2013, arXiv:1312.6203. [Google Scholar]
- Defferrard, M.; Bresson, X.; Vandergheynst, P. Convolutional neural networks on graphs with fast localized spectral filtering. In Proceedings of the Advances in Neural Information Processing Systems, Bracelona, Spain, 9–10 December 2016; pp. 3844–3852. [Google Scholar]
- Hammond, D.K.; Vandergheynst, P.; Gribonval, R. Wavelets on graphs via spectral graph theory. Appl. Comput. Harmon. Anal. 2011, 30, 129–150. [Google Scholar] [CrossRef]
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- Yu, B.; Yin, H.; Zhu, Z. Spatio-temporal graph convolutional networks: A deep learning framework for traffic forecasting. arXiv 2017, arXiv:1709.04875. [Google Scholar]
- Xu, Z.; Kang, Y.; Cao, Y.; Li, Z. Spatiotemporal Graph Convolution Multifusion Network for Urban Vehicle Emission Prediction. IEEE Trans. Neural Networks Learn. Syst. 2021. [Google Scholar] [CrossRef]
- Sun, J.; Zhang, J.; Li, Q.; Yi, X.; Liang, Y.; Zheng, Y. Predicting citywide crowd flows in irregular regions using multi-view graph convolutional networks. arXiv 2019, arXiv:1903.07789. [Google Scholar] [CrossRef]
- Cui, Z.; Henrickson, K.; Ke, R.; Wang, Y. Traffic graph convolutional recurrent neural network: A deep learning framework for network-scale traffic learning and forecasting. IEEE Trans. Intell. Transp. Syst. 2019, 21, 4883–4894. [Google Scholar] [CrossRef]
- Abu-El-Haija, S.; Perozzi, B.; Al-Rfou, R.; Alemi, A. Watch your step: Learning graph embeddings through attention. arXiv 2017, arXiv:1710.09599. [Google Scholar]
- Grover, A.; Leskovec, J. node2vec: Scalable feature learning for networks. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 855–864. [Google Scholar]
- Perozzi, B.; Al-Rfou, R.; Skiena, S. DeepWalk: Online Learning of Social Representations; ACM: New York, NY, USA, 2014; pp. 701–710. [Google Scholar]
- Shuman, D.I.; Narang, S.K.; Frossard, P.; Ortega, A.; Vandergheynst, P. The Emerging Field of Signal Processing on Graphs: Extending High-Dimensional Data Analysis to Networks and Other Irregular Domains. IEEE Signal Process. Mag. 2013, 30, 83–98. [Google Scholar] [CrossRef]
- Smola, A.J.; Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef]
- Gibson, M.D.; Kundu, S.; Satish, M. Dispersion model evaluation of PM2.5, NOx and SO2 from point and major line sources in Nova Scotia, Canada using AERMOD Gaussian plume air dispersion model. Atmos. Pollut. Res. 2013, 4, 157–167. [Google Scholar] [CrossRef]
- Rakowska, A.; Wong, K.C.; Townsend, T.; Chan, K.L.; Westerdahl, D.; Ng, S.; Močnik, G.; Drinovec, L.; Ning, Z. Impact of traffic volume and composition on the air quality and pedestrian exposure in urban street canyon. Atmos. Environ. 2014, 98, 260–270. [Google Scholar] [CrossRef]
- Blum, A.; Mitchell, T. Combining labeled and unlabeled data with co-training. In Proceedings of the 11th Annual Conference on Computational Learning Theory, Madison, WI, USA, 24–26 July 1998; pp. 92–100. [Google Scholar]
- Chen, L.; Cai, Y.; Ding, Y.; Lv, M.; Yuan, C.; Chen, G. Spatially fine-grained urban air quality estimation using ensemble semi-supervised learning and pruning. In Proceedings of the Acm International Joint Conference on Pervasive & Ubiquitous Computing, Heidelberg, Germany, 12–16 September 2016; pp. 1076–1087. [Google Scholar]
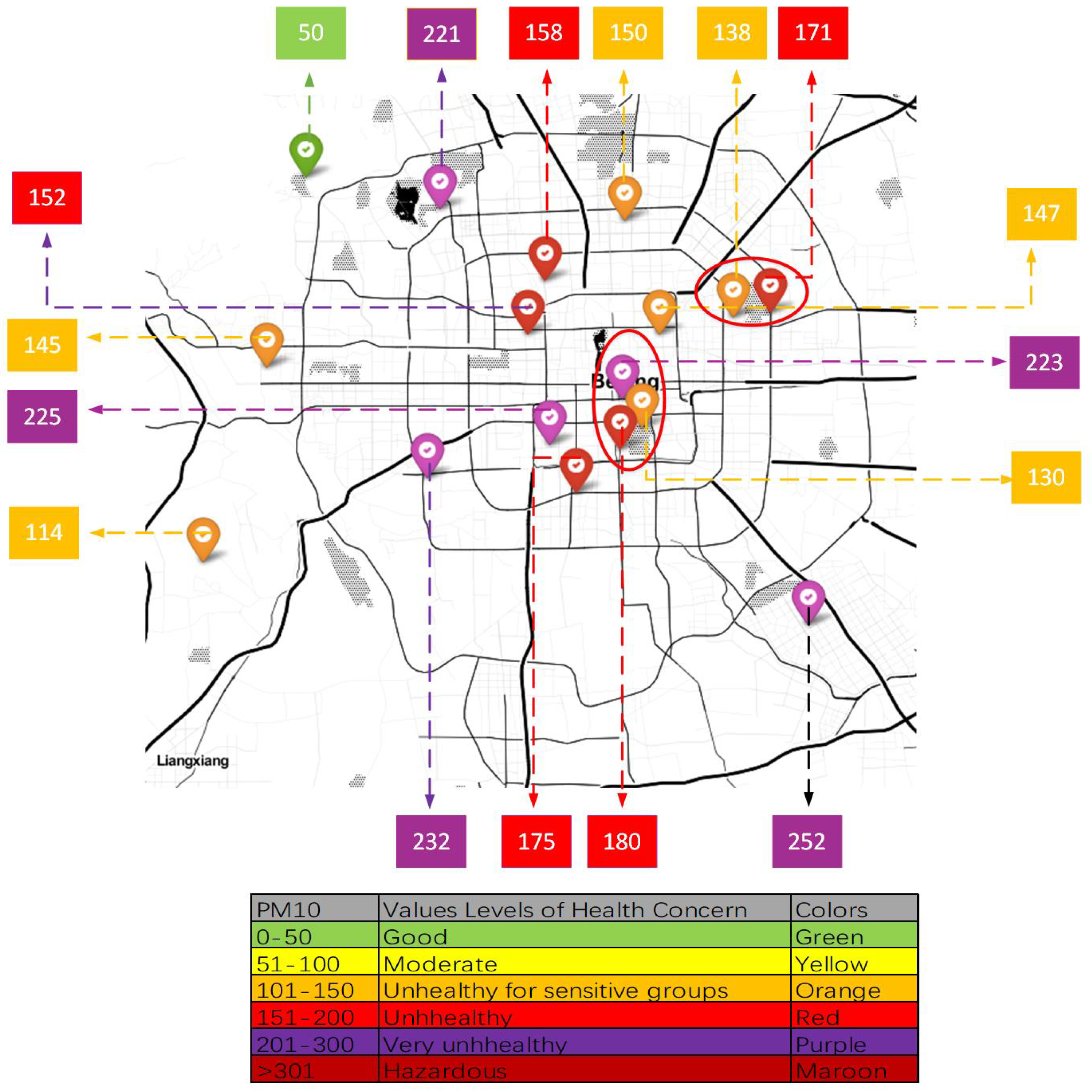








| 1. | Parks | 6. | Companies |
| 2. | Schools | 7. | Hotels |
| 3. | Stadium | 8. | Supermarkets |
| 4. | Restaurants | 9. | Vehicle repair stations |
| 5. | Business center | 10. | Gas stations |
| Model | Beijing Air-Quality Data Evaluation | |||
|---|---|---|---|---|
| MAPE (%) | RMSE | |||
| Without External Factors | With External Factors | Without External Factors | With External Factors | |
| HA | 56.35 | / | 30.01 | / |
| SVR | 49.94 | / | 23.00 | / |
| AQInf | 35.25 | 21.31 | 16.92 | 10.35 |
| GCNInf | 28.52 | 14.10 | 13.93 | 7.24 |
| HGCNInf | 19.18 | 7.71 | 9.99 | 3.90 |
| The Robustness of Each Air Quality Inference Model | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Model | HA | SVR | AQInf | GCNInf | HGCNInf | ||||||
| Metric | MAPE (%) | RMSE | MAPE (%) | RMSE | MAPE (%) | RMSE | MAPE (%) | RMSE | MAPE (%) | RMSE | |
| Number | |||||||||||
| 0 | 56.35 | 30.01 | 49.94 | 23.00 | 21.31 | 10.35 | 14.10 | 7.24 | 7.71 | 3.90 | |
| 1 | 59.45 | 31.50 | 51.75 | 24.40 | 23.75 | 11.41 | 15.82 | 7.74 | 9.01 | 3.98 | |
| 2 | 63.38 | 34.02 | 52.15 | 26.4 | 24.15 | 12.01 | 16.13 | 7.82 | 11.63 | 6.62 | |
| 3 | 69.67 | 37.99 | 55.18 | 29.00 | 27.18 | 13.39 | 18.31 | 8.61 | 12.07 | 6.66 | |
| 4 | 95.05 | 42.96 | 62.00 | 33.00 | 40.68 | 19.52 | 20.27 | 10.69 | 15.18 | 7.52 | |
| 5 | 131.92 | 50.18 | 73.01 | 40.18 | 61.06 | 27.18 | 26.42 | 12.34 | 22.94 | 11.67 | |
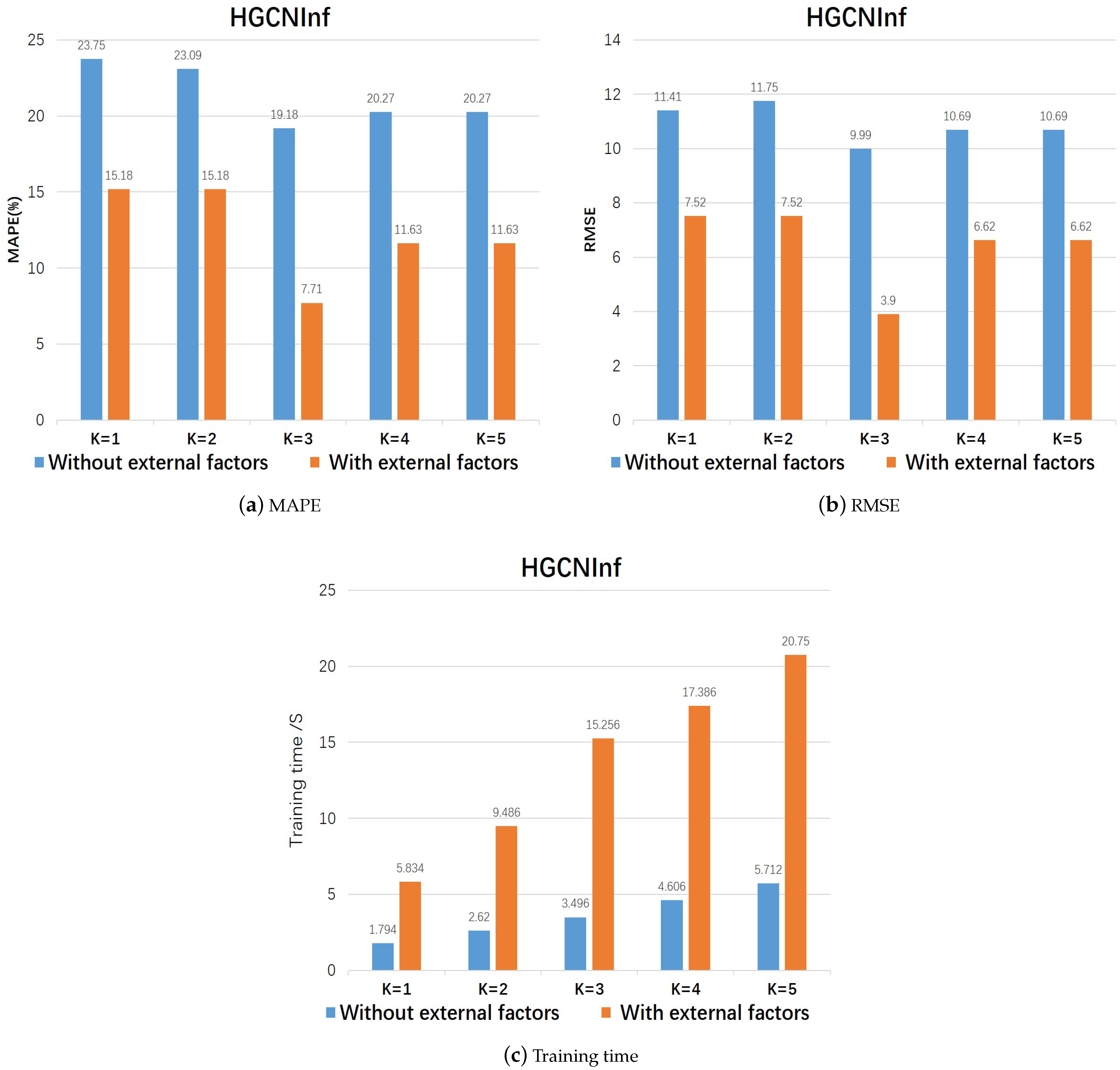
| Order | K = 1 | K = 2 | K = 3 | K = 4 | K = 5 | |
|---|---|---|---|---|---|---|
| Metric | ||||||
| MAPE (%) | Without external factors | 23.75 | 23.09 | 19.18 | 20.27 | 20.27 |
| With external factors | 15.18 | 15.18 | 7.71 | 11.63 | 11.63 | |
| RMSE | Without external factors | 11.41 | 11.75 | 9.99 | 10.69 | 10.69 |
| With external factors | 7.52 | 7.52 | 3.90 | 6.62 | 6.62 |
| Training Time/(s) | K = 1 | K = 2 | K = 3 | K = 4 | K = 5 |
|---|---|---|---|---|---|
| Without external factors | 1.79 | 2.62 | 3.50 | 4.61 | 5.71 |
| With external factors | 5.83 | 9.49 | 15.26 | 17.39 | 20.75 |
| The Improved MAPE and RMSE Results with the Increase in the Number of Recommended Nodes | |||||||
|---|---|---|---|---|---|---|---|
| Model | HGCNInf+GMIE | GCNInf+GMIE | AQInf+GEM | ||||
| Metric | MAPE (%) | RMSE | MAPE (%) | RMSE | MAPE (%) | RMSE | |
| Number | |||||||
| 0 | 21.57 | 10.83 | 23.31 | 11.26 | 24.15 | 12.01 | |
| 1 | 12.94 | 6.84 | 20.48 | 10.13 | 23.75 | 11.41 | |
| 2 | 9.01 | 4.27 | 18.30 | 8.61 | 22.80 | 11.22 | |
| 3 | 8.00 | 3.98 | 16.37 | 7.82 | 22.10 | 10.69 | |
| 4 | 7.71 | 3.90 | 14.70 | 7.40 | 21.60 | 10.47 | |
| 5 | 7.71 | 3.90 | 14.10 | 7.42 | 21.31 | 10.35 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, Y.; Chen, J.; Cao, Y.; Xu, Z. A Higher-Order Graph Convolutional Network for Location Recommendation of an Air-Quality-Monitoring Station. Remote Sens. 2021, 13, 1600. https://doi.org/10.3390/rs13081600
Kang Y, Chen J, Cao Y, Xu Z. A Higher-Order Graph Convolutional Network for Location Recommendation of an Air-Quality-Monitoring Station. Remote Sensing. 2021; 13(8):1600. https://doi.org/10.3390/rs13081600
Chicago/Turabian StyleKang, Yu, Jie Chen, Yang Cao, and Zhenyi Xu. 2021. "A Higher-Order Graph Convolutional Network for Location Recommendation of an Air-Quality-Monitoring Station" Remote Sensing 13, no. 8: 1600. https://doi.org/10.3390/rs13081600
APA StyleKang, Y., Chen, J., Cao, Y., & Xu, Z. (2021). A Higher-Order Graph Convolutional Network for Location Recommendation of an Air-Quality-Monitoring Station. Remote Sensing, 13(8), 1600. https://doi.org/10.3390/rs13081600







