A Hybrid Model Consisting of Supervised and Unsupervised Learning for Landslide Susceptibility Mapping
Abstract
1. Introduction
2. Materials
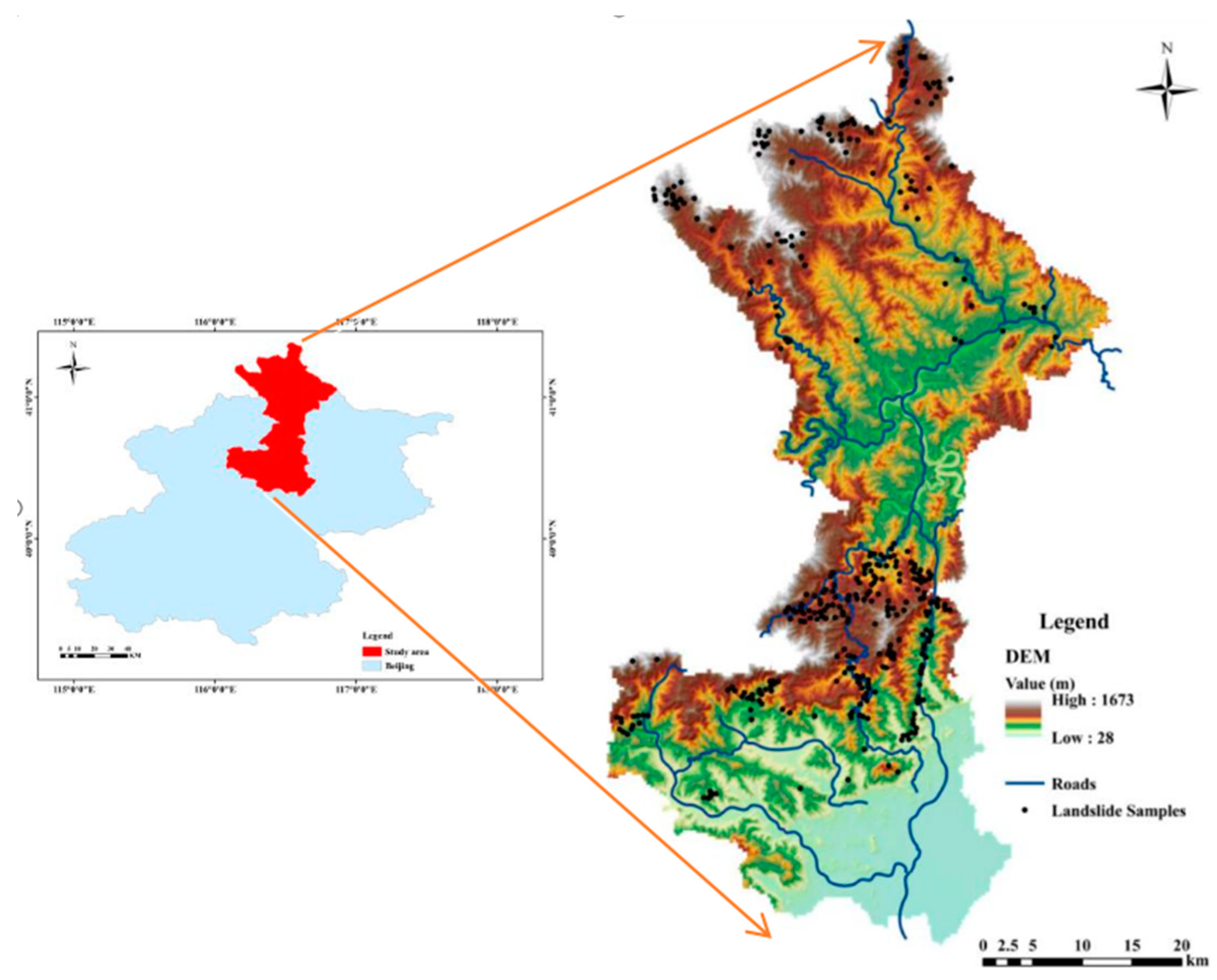
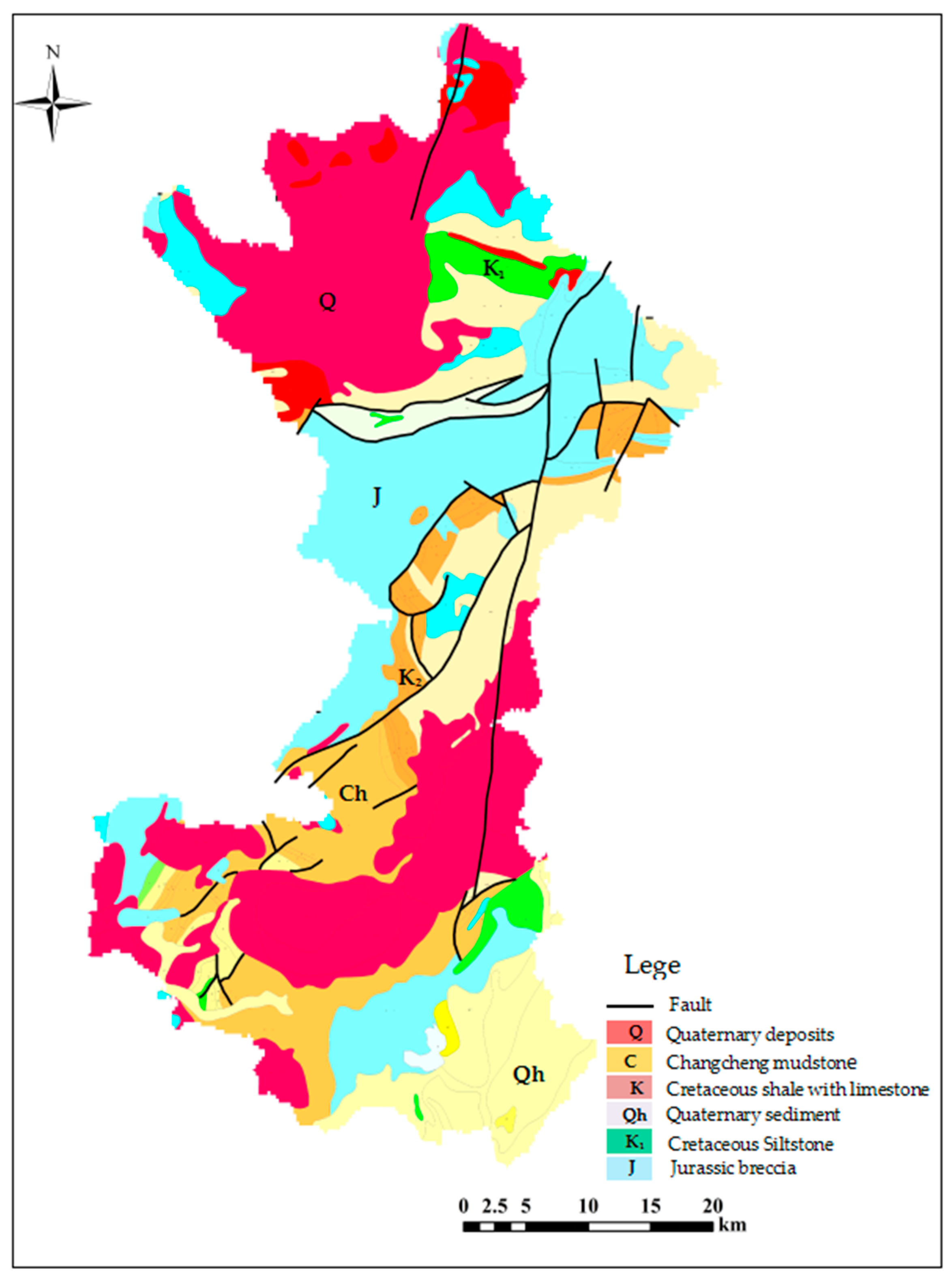
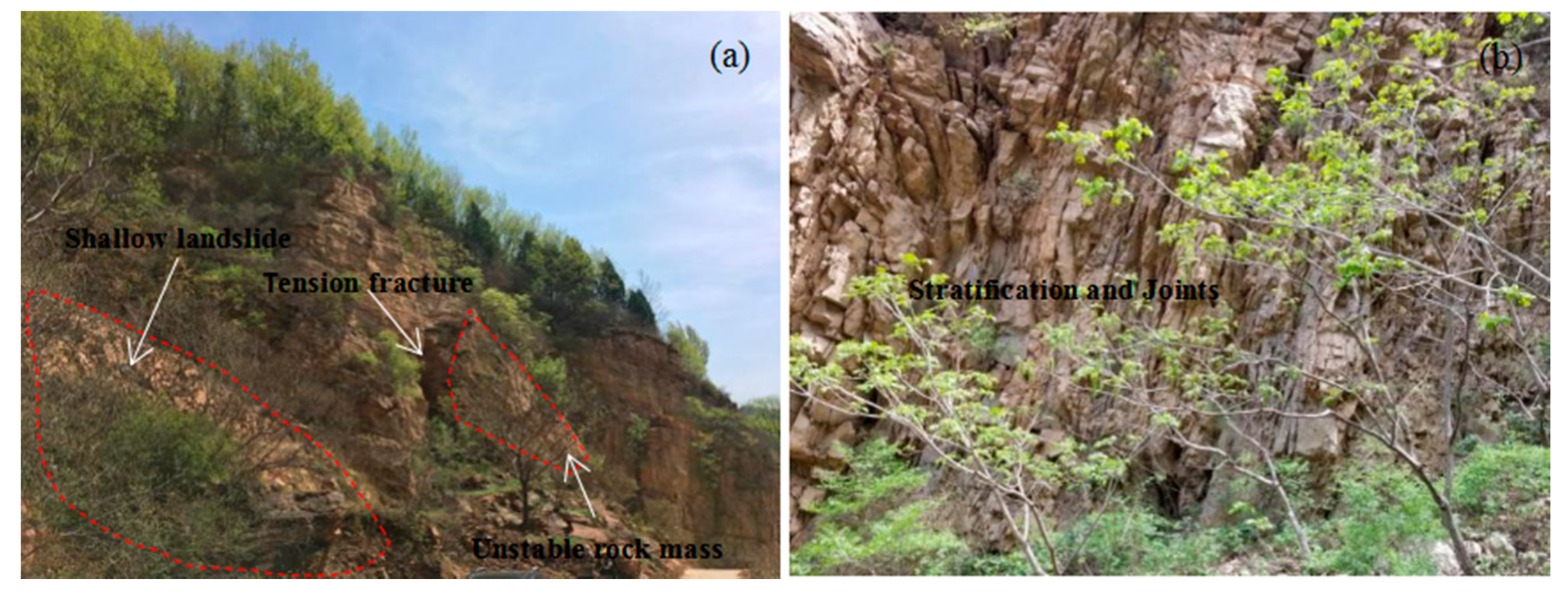
2.1. Study Area and Landslide Inventories
2.2. Data Preparation
2.2.1. Mapping Units
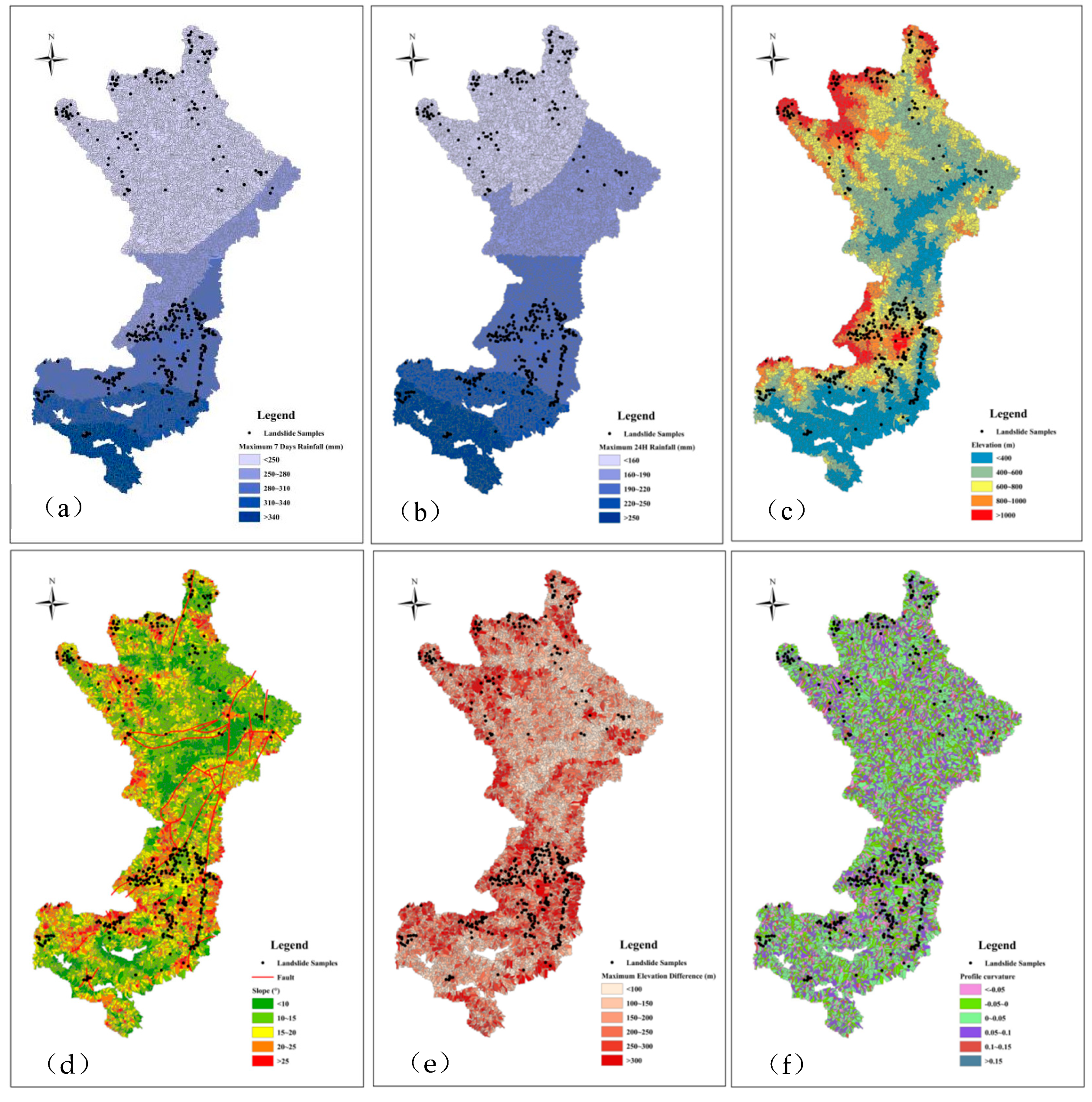
2.2.2. Conditioning Factors
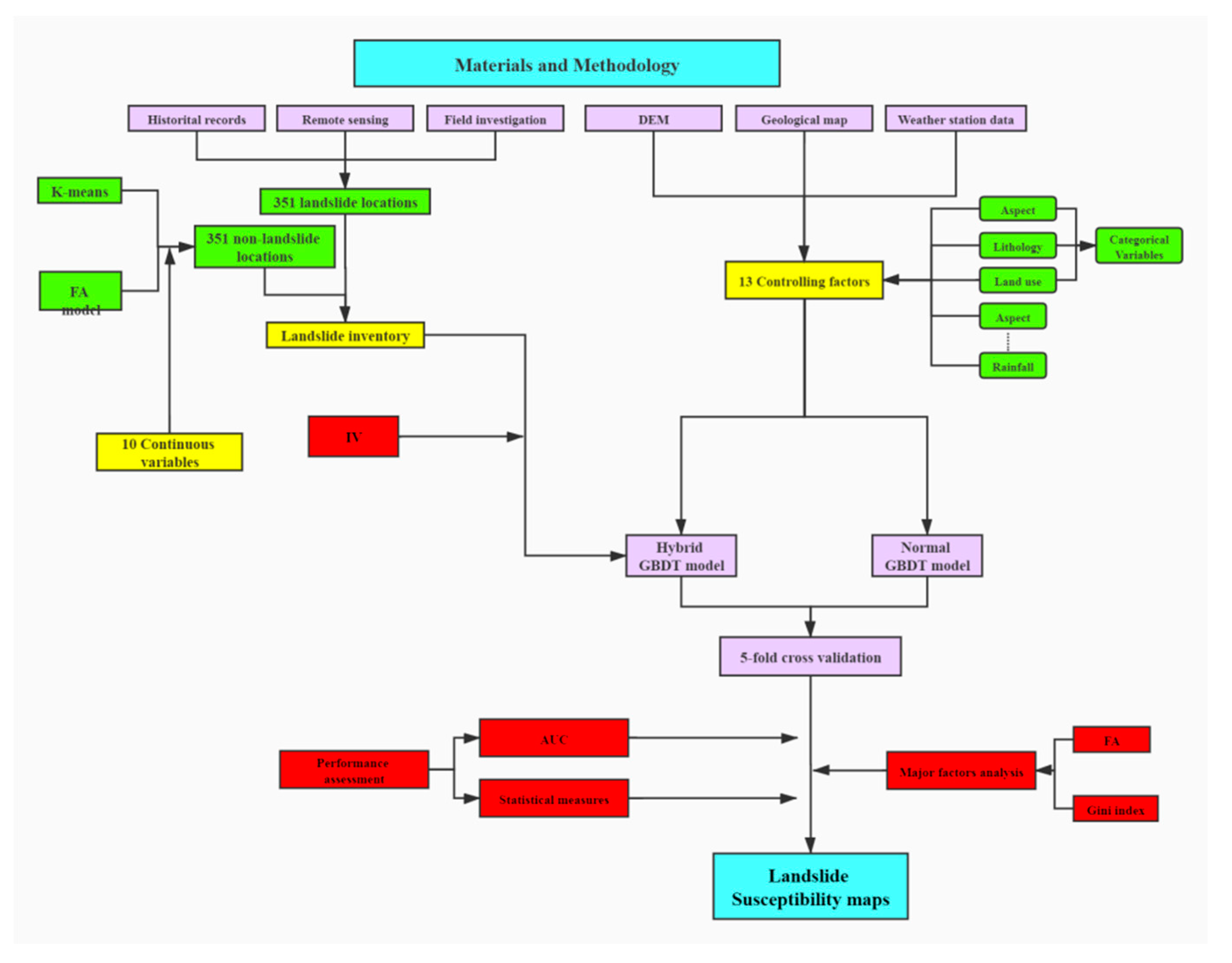
3. Methodology
3.1. FA
- (1)
- Test the fitness of applying FA.
- (2)
- Extraction factor.
- (3)
- Orthogonal rotation.
- (4)
- Calculating factor scores.
3.2. K-Means Clustering
- (1)
- Determining the initial clustering centers;
- (2)
- Calculating the Euclidean distances between samples and the clustering center;
- (3)
- Retrieves the centers for each new cluster and iterates until it meets the following equation:where un+1 is the sum of squares of distances after the nth iteration; is the precision.
3.3. Sampling and Validation Strategy
3.4. GBDT
3.5. Information Value Model
3.6. Model Performance
4. Results
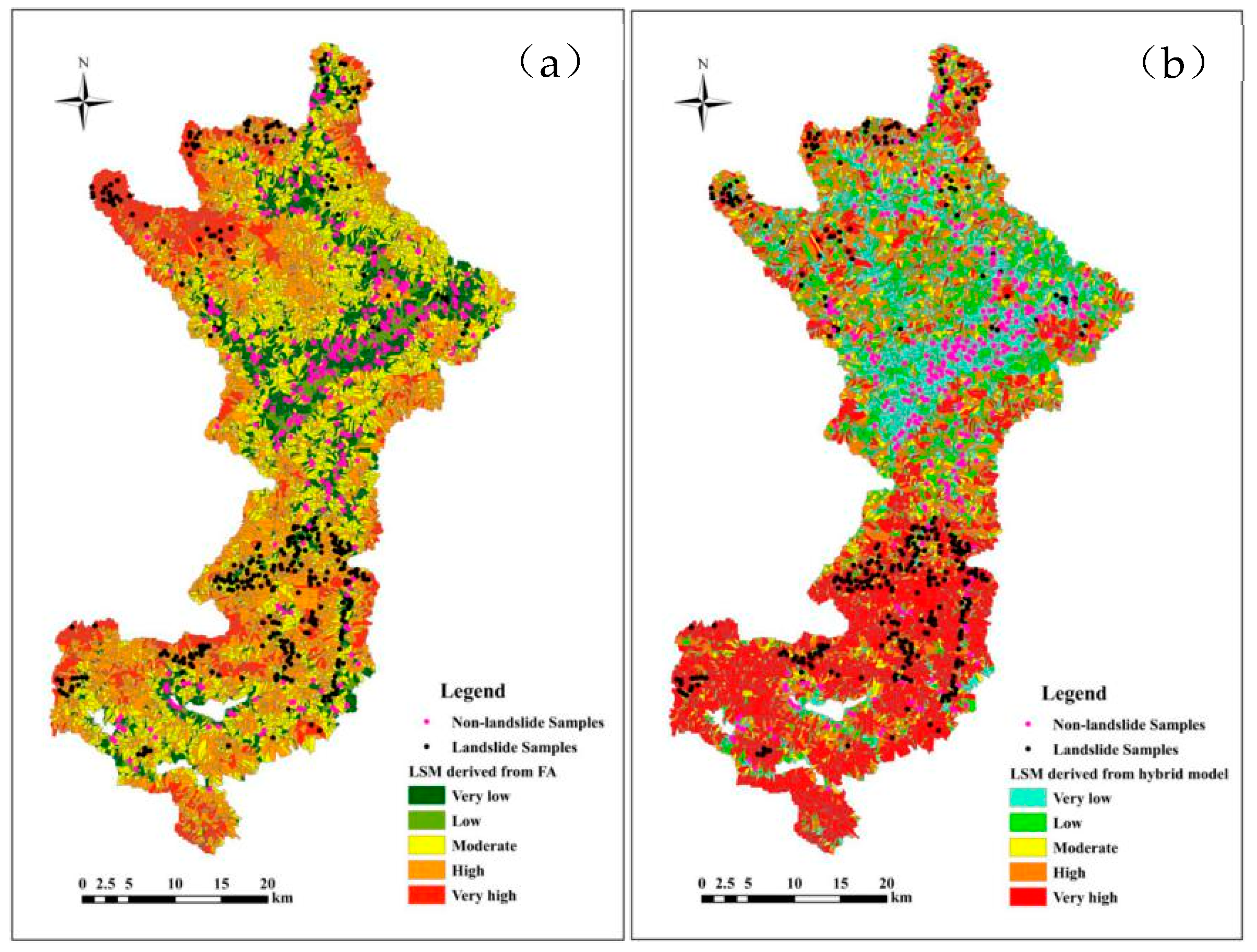
4.1. LSM Obtained by the ULM
4.2. LSM Obtained by GBDT
4.3. Comparison of Different Models for LSM
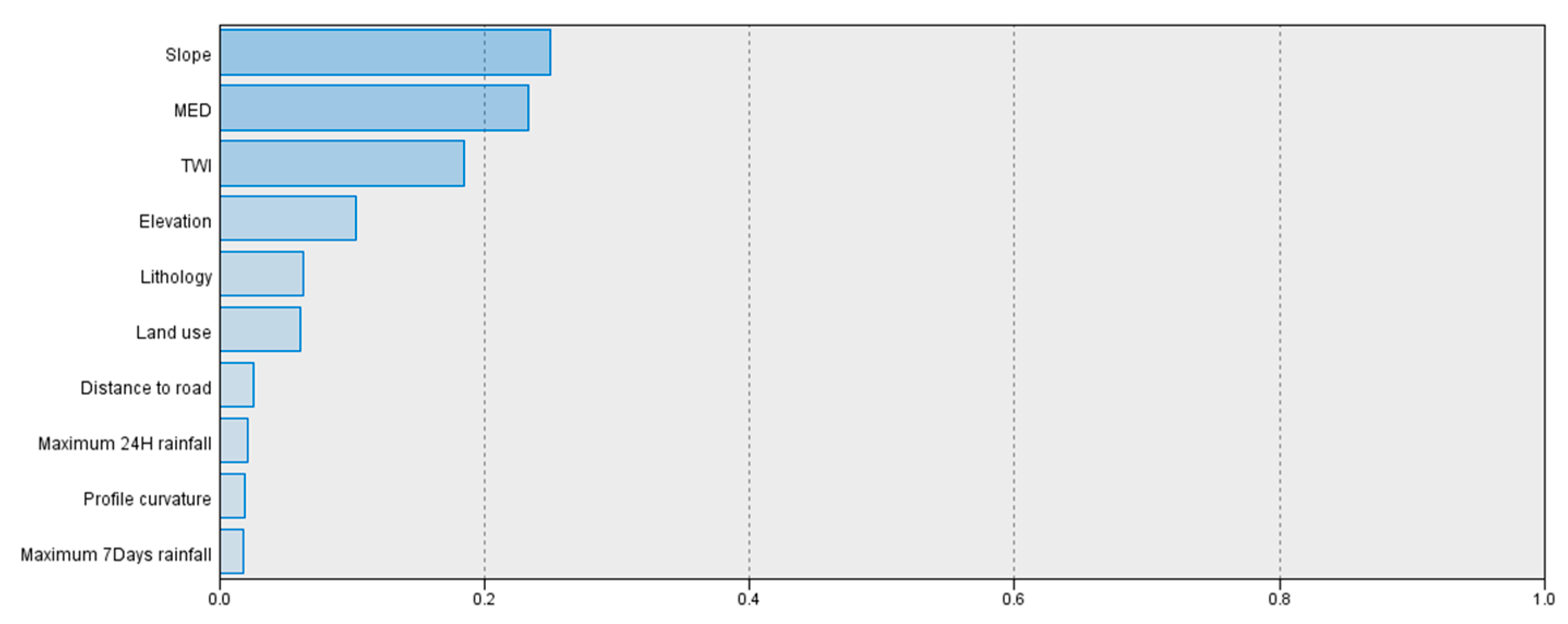
4.3.1. Selection of the Major Conditioning Factors
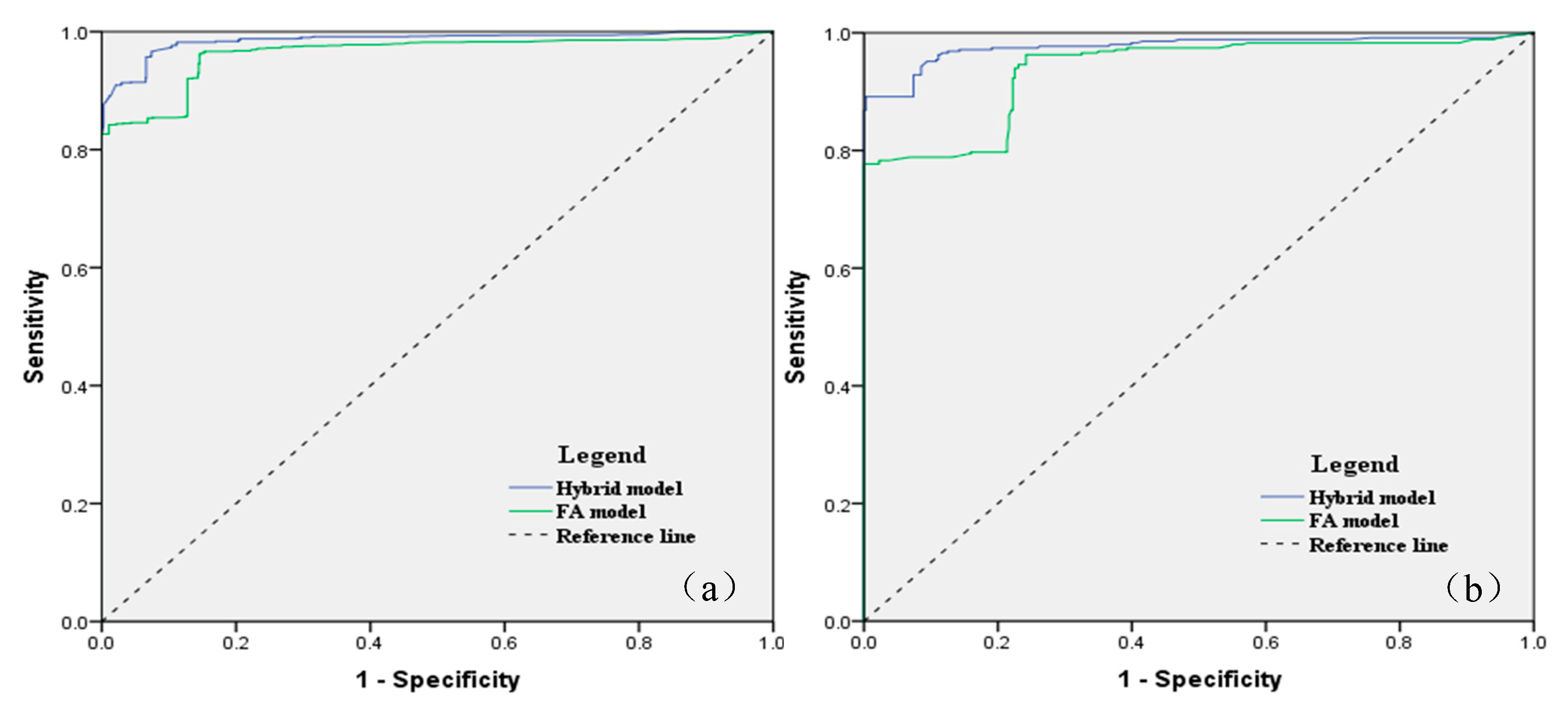
4.3.2. Accuracy and Rationality of LSM
5. Discussion
5.1. Comparison of Unsupervised and Supervised Learning for LSM
5.2. Further Use of Prior Conditions
6. Conclusions
- FA performs well in dimensionality reduction and major conditioning factors analysis. Rainfall, slope, MED and DTR were considered as the major conditioning factors;
- The performance of the GBDT mode can be improved in terms of accuracy and generalization ability for the conditions that the quality of samples are guaranteed. The non-landslide samples selected from the very low susceptibility area predicted by the verified FA model were effective;
- The full utilization of prior conditions enhances the logicality of the models. Labeled samples were valuable in the validation of ULM and modeling of SLM;
- A hybrid model is recommended due to its high accuracy and reasonable explanation of major conditioning factors.
- More advanced methods need to be discussed and compared;
- The effect of other factors like mapping unit and interpretation accuracy of DEM was not considered;
- The hybrid model is not applied to other study area.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| LSM | Landslide susceptibility mapping |
| GBDT | Gradient boosting decision tree |
| SLM | Supervised learning model |
| ULM | Unsupervised learning model |
| ROC | Receiver operating characteristic curve |
| AUC | Area under the curve |
| FA | Factor analysis |
| DT | Decision tree |
| BHH | Beijing Hydrology Handbook |
| DEM | Digital elevation model |
| DNRB | Department of Natural Resources of Beijing |
| IV | Information value |
| TWI | Topographic wetness index |
| MED | Maximum elevation difference |
| DTR | Distance to road |
| DTF | Distance to fault |
| TP | True positive |
| TN | True negative |
| FN | False negative |
| FP | False positive |
References
- Haque, U.; Silva, P.F.; Devoli, G.; Pilz, J.; Zhao, B.; Khaloua, A.; Wilopo, W.; Andersen, P.; Lu, P.; Lee, J.; et al. The human cost of global warning: Deadly landslides and their triggers (1995–2014). Sci. Total Environ. 2019, 682, e673–e684. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Peng, J.; Hong, H.; Shahabi, H.; Pradhan, B.; Liu, J.; Zhu, A.-X.; Pei, X.; Duan, Z. Landslide susceptibility modelling using GIS-based machine learning techniques for Chongren County, Jiangxi Province, China. Sci. Total Environ. 2018, 626, 1121–1135. [Google Scholar] [CrossRef]
- Reichenbach, P.; Rossi, M.; Malamud, B.D.; Mihir, M.; Guzzetti, F. A review of statistically-based landslide susceptibility models. Earth Sci. Rev. 2018, 180, 60–91. [Google Scholar] [CrossRef]
- Merghadi, A.; Abderrahmane, B.; Bui, D.T. Landslide Susceptibility Assessment at Mila Basin (Algeria): A Comparative Assessment of Prediction Capability of Advanced Machine Learning Methods. ISPRS Int. J. Geo-Inf. 2018, 7, 268. [Google Scholar] [CrossRef]
- Yi, Y.; Zhang, Z.; Zhang, W.; Xu, Q.; Deng, C.; Li, Q. GIS-based earthquake-triggered-landslide susceptibility mapping with an integrated weighted index model in Jiuzhaigou region of Sichuan Province, China. Nat. Hazards Earth Syst. Sci. 2019, 19, 1973–1988. [Google Scholar] [CrossRef]
- Shi, M.; Chen, J.; Song, Y.; Zhang, W.; Song, S.; Zhang, X. Assessing debris flow susceptibility in Heshigten Banner, Inner Mongolia, China, using principal component analysis and an improved fuzzy C -means algorithm. Bull. Eng. Geol. Environ. 2016, 75, 909–922. [Google Scholar] [CrossRef]
- Liang, Z.; Wang, C.; Han, S.; Khan, K.U.J.; Liu, Y. Classification and susceptibility assessment of debris flow based on a semi-quantitative method combination of the fuzzy C-means algorithm, factor analysis and efficacy coefficient. Nat. Hazards Earth Syst. Sci. 2020, 20, 1287–1304. [Google Scholar] [CrossRef]
- Karimi, V.; Khatibi, R.; Ghorbani, M.A.; Bui, D.T.; Darbandi, S. Strategies for Learning Groundwater Potential Modelling Indices under Sparse Data with Supervised and Unsupervised Techniques. Water Resour. Manag. 2020, 34, 2389–2417. [Google Scholar] [CrossRef]
- Wang, Q.; Kong, Y.; Zhang, W.; Chen, J.; Xu, P.; Li, H.; Xue, Y.; Yuan, X.; Zhan, J.; Zhu, Y. Regional debris flow susceptibility analysis based on principal component analysis and self-organizing map: A case study in Southwest China. Arab. J. Geosci. 2016, 9, 718. [Google Scholar] [CrossRef]
- Levada, A.L. Parametric PCA for unsupervised metric learning. Pattern Recognit. Lett. 2020, 135, 425–430. [Google Scholar] [CrossRef]
- Bui, D.T.; Tuan, T.A.; Klempe, H.; Pradhan, B.; Revhaug, I. Spatial prediction models for shallow landslide hazards: A comparative assessment of the efficacy of support vector machines, artificial neural networks, kernel logistic regression, and logistic model tree. Landslides 2016, 13, 361–378. [Google Scholar] [CrossRef]
- Jiang, S.-H.; Huang, J.; Qi, X.-H.; Zhou, C.-B. Efficient probabilistic back analysis of spatially varying soil parameters for slope reliability assessment. Eng. Geol. 2020, 271, 105597. [Google Scholar] [CrossRef]
- Trigila, A.; Iadanza, C.; Esposito, C.; Scarascia-Mugnozza, G. Comparison of Logistic Regression and Random Forests techniques for shallow landslide susceptibility assessment in Giampilieri (NE Sicily, Italy). Geomorphology 2015, 249, 119–136. [Google Scholar] [CrossRef]
- Choubin, B.; Moradi, E.; Golshan, M.; Adamowski, J.; Sajedi-Hosseini, F.; Mosavi, A. An ensemble prediction of flood susceptibility using multivariate discriminant analysis, classification and regression trees, and support vector machines. Sci. Total Environ. 2019, 651, 2087–2096. [Google Scholar] [CrossRef] [PubMed]
- Liang, Z.; Wang, C.-M.; Zhang, Z.-M.; Khan, K.-U.-J. A comparison of statistical and machine learning methods for debris flow susceptibility mapping. Stoch. Environ. Res. Risk Assess. 2020, 34, 1887–1907. [Google Scholar] [CrossRef]
- Hong, H.; Pourghasemi, H.R.; Pourtaghi, Z.S. Landslide susceptibility assessment in Lianhua County (China): A comparison between a random forest data mining technique and bivariate and multivariate statistical models. Geomorphology 2016, 259, 105–118. [Google Scholar] [CrossRef]
- Ali, S.; Biermanns, P.; Haider, R.; Reicherter, K. Landslide susceptibility mapping by using a geographic information system (GIS) along the China–Pakistan Economic Corridor (Karakoram Highway), Pakistan. Nat. Hazards Earth Syst. Sci. 2019, 19, 999–1022. [Google Scholar] [CrossRef]
- Huang, F.; Cao, Z.; Guo, J.; Jiang, S.-H.; Li, S.; Guo, Z. Comparisons of heuristic, general statistical and machine learning models for landslide susceptibility prediction and mapping. Catena 2020, 191, 104580. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Guzzetti, F.; Reichenbach, P.; Ardizzone, F.; Cardinali, M.; Galli, M. Estimating the quality of landslide susceptibility models. Geomorphology 2006, 81, 166–184. [Google Scholar] [CrossRef]
- Guzzetti, F.; Galli, M.; Reichenbach, P.; Ardizzone, F.; Cardinali, M. Landslide hazard assessment in the Collazzone area, Umbria, Central Italy. Nat. Hazards Earth Syst. Sci. 2006, 6, 115–131. [Google Scholar] [CrossRef]
- Rossi, M.; Guzzetti, F.; Salvati, P.; Donnini, M.; Napolitano, E.; Bianchi, C. A predictive model of societal landslide risk in Italy. Earth Sci. Rev. 2019, 196, 102849. [Google Scholar] [CrossRef]
- Mondini, A.; Guzzetti, F.; Reichenbach, P.; Rossi, M.; Cardinali, M.; Ardizzone, F. Semi-automatic recognition and mapping of rainfall induced shallow landslides using optical satellite images. Remote. Sens. Environ. 2011, 115, 1743–1757. [Google Scholar] [CrossRef]
- Dou, J.; Yunus, A.P.; Xu, Y.; Zhu, Z.; Chen, C.-W.; Sahana, M.; Khosravi, K.; Yang, Y.; Pham, B.T. Torrential rainfall-triggered shallow landslide characteristics and susceptibility assessment using ensemble data-driven models in the Dongjiang Reservoir Watershed, China. Nat. Hazards 2019, 97, 579–609. [Google Scholar] [CrossRef]
- Hong, H.; Pradhan, B.; Xu, C.; Bui, D.T. Spatial prediction of landslide hazard at the Yihuang area (China) using two-class kernel logistic regression, alternating decision tree and support vector machines. Catena 2015, 133, 266–281. [Google Scholar] [CrossRef]
- Soeters, R.; van Westen, C.J. Slope Instability Recognition, Analysis, and Zonation in Landslides: Investigation and Mitigation; Transport Research Board: Washington, DC, USA, 1996; Volume 8. [Google Scholar]
- Dou, J.; Yunus, A.P.; Bui, D.T.; Merghadi, A.; Sahana, M.; Zhu, Z.; Chen, C.-W.; Khosravi, K.; Yang, Y.; Pham, B.T. Assessment of advanced random forest and decision tree algorithms for modeling rainfall-induced landslide susceptibility in the Izu-Oshima Volcanic Island, Japan. Sci. Total Environ. 2019, 662, 332–346. [Google Scholar] [CrossRef]
- Wilson, J.P.; Gallant, J.C. Digital terrain analysis. In Terrain Analysis; Wilson, J.P., Gallant, J.C., Eds.; John Wiley & Sons: New York, NY, USA, 2000; pp. 1–27. [Google Scholar]
- Vahidnia, M.H.; Alesheikh, A.A.; Alimohammadi, A.; Hosseinali, F. A GIS-based neuro-fuzzy procedure for integrating knowledge and data in landslide susceptibility mapping. Comput. Geosci. 2010, 36, 1101–1114. [Google Scholar] [CrossRef]
- Pham, B.T.; Prakash, I. A novel hybrid model of Bagging-based Naïve Bayes Trees for landslide susceptibility assessment. Bull. Int. Assoc. Eng. Geol. 2019, 78, 1911–1925. [Google Scholar] [CrossRef]
- Yesilnacar, E.; Topal, T. Landslide susceptibility mapping: A comparison of logistic regression and neural networks methods in a medium scale study, Hendek region (Turkey). Eng. Geol. 2005, 79, 251–266. [Google Scholar] [CrossRef]
- Catani, F.; Lagomarsino, D.; Segoni, S.; Tofani, V. Landslide susceptibility estimation by random forests technique: Sensitivity and scaling issues. Nat. Hazards Earth Syst. Sci. 2013, 13, 2815–2831. [Google Scholar] [CrossRef]
- Can, A.; Dagdelenler, G.; Ercanoglu, M.; Sonmez, H. Landslide susceptibility mapping at Ovacık-Karabük (Turkey) using different artificial neural network models: Comparison of training algorithms. Bull. Eng. Geol. Environ. 2019, 78, 89–102. [Google Scholar] [CrossRef]
- Nedbal, V.; Brom, J. Impact of highway construction on land surface energy balance and local climate derived from LANDSAT satellite data. Sci. Total Environ. 2018, 633, 658–667. [Google Scholar] [CrossRef]
- Nasiri, V.; Darvishsefat, A.A.; Rafiee, R.; Shirvany, A.; Hemat, M.A. Land use change modeling through an integrated Multi-Layer Perceptron Neural Network and Markov Chain analysis (case study: Arasbaran region, Iran). J. For. Res. 2019, 30, 943–957. [Google Scholar] [CrossRef]
- Ding, C.; He, X. K-means clustering via principal component analysis. In Proceedings of the Twenty-first international conference on Machine learning—ICML ’04, Banff, AB, Canada, 4–7 July 2004. [Google Scholar]
- Kornejady, A.; Ownegh, M.; Bahremand, A. Landslide susceptibility assessment using maximum entropy model with two different data sampling methods. Catena 2017, 152, 144–162. [Google Scholar] [CrossRef]
- Chung, C.-J.F.; Fabbri, A.G. Validation of Spatial Prediction Models for Landslide Hazard Mapping. Nat. Hazards 2003, 30, 451–472. [Google Scholar] [CrossRef]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning; Springer: New York, NY, USA, 2013; Volume 112, p. 18. [Google Scholar]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Wang, Y.; Feng, L.; Li, S.; Ren, F.; Du, Q. A hybrid model considering spatial heterogeneity for landslide susceptibility mapping in Zhejiang Province, China. Catena 2020, 188, 104425. [Google Scholar] [CrossRef]
- Sharma, S.; Mahajan, A.K. A comparative assessment of information value, frequency ratio and analytical hierarchy process models for landslide susceptibility mapping of a Himalayan watershed, India. Bull. Eng. Geol. Environ. 2019, 78, 2431–2448. [Google Scholar] [CrossRef]
- Merghadi, A.; Yunus, A.P.; Dou, J.; Whiteley, J.; ThaiPham, B.; Bui, D.T.; Avtar, R.; Abderrahmane, B. Machine learning methods for landslide susceptibility studies: A comparative overview of algorithm performance. Earth Sci. Rev. 2020, 207, 103225. [Google Scholar] [CrossRef]
- Liu, C.; Li, W.; Wu, H.; Lu, P.; Sang, K.; Sun, W.; Chen, W.; Hong, Y.; Li, R. Susceptibility evaluation and mapping of China’s landslides based on multi-source data. Nat. Hazards 2013, 69, 1477–1495. [Google Scholar] [CrossRef]
- Jaafari, A.; Najafi, A.; Rezaeian, J.; Sattarian, A.; Ghajar, I. Planning road networks in landslide-prone areas: A case study from the northern forests of Iran. Land Use Policy 2015, 47, 198–208. [Google Scholar] [CrossRef]
- Bui, D.T.; Pradhan, B.; Lofman, O.; Revhaug, I.; Dick, O.B. Landslide susceptibility assessment in the Hoa Binh province of Vietnam: A comparison of the Levenberg–Marquardt and Bayesian regularized neural networks. Geomorphology 2012, 171–172, 12–29. [Google Scholar]
- Liang, Z.; Wang, C.; Khan, K.U.J. Application and comparison of different ensemble learning machines combining with a novel sampling strategy for shallow landslide susceptibility mapping. Stoch. Environ. Res. Risk Assess. 2020, 1–14. [Google Scholar] [CrossRef]
- Peng, L.; Niu, R.; Huang, B.; Wu, X.; Zhao, Y.; Ye, R. Landslide susceptibility mapping based on rough set theory and support vector machines: A case of the Three Gorges area, China. Geomorphology 2014, 204, 287–301. [Google Scholar] [CrossRef]
- Omta, W.A.; Van Heesbeen, R.G.; Shen, I.; De Nobel, J.; Robers, D.; Van Der Velden, L.M.; Medema, R.H.; Siebes, A.P.J.M.; Feelders, A.J.; Brinkkemper, S.; et al. Combining Supervised and Unsupervised Machine Learning Methods for Phenotypic Functional Genomics Screening. SLAS Discov. Adv. Sci. Drug Discov. 2020, 25, 655–664. [Google Scholar] [CrossRef]
- Chang, Z.; Du, Z.; Zhang, F.; Huang, F.; Chen, J.; Li, W.; Guo, Z. Landslide Susceptibility Prediction Based on Remote Sensing Images and GIS: Comparisons of Supervised and Unsupervised Machine Learning Models. Remote Sens. 2020, 12, 502. [Google Scholar] [CrossRef]
- Sabokbar, H.F.; Roodposhti, M.S.; Tazik, E. Landslide susceptibility mapping using geographically-weighted principal component analysis. Geomorphology 2014, 226, 15–24. [Google Scholar] [CrossRef]
- Tang, Y.; Feng, F.; Guo, Z.; Feng, W.; Li, Z.; Wang, J.; Sun, Q.; Ma, H.; Li, Y. Integrating principal component analysis with statistically-based models for analysis of causal factors and landslide susceptibility mapping: A comparative study from the loess plateau area in Shanxi (China). J. Clean. Prod. 2020, 277, 124159. [Google Scholar] [CrossRef]
- Vasu, N.N.; Lee, S.-R. A hybrid feature selection algorithm integrating an extreme learning machine for landslide susceptibility modeling of Mt. Woomyeon, South Korea. Geomorphology 2016, 263, 50–70. [Google Scholar] [CrossRef]
- Pham, B.T.; Bui, D.T.; Prakash, I.; Dholakia, M. Hybrid integration of Multilayer Perceptron Neural Networks and machine learning ensembles for landslide susceptibility assessment at Himalayan area (India) using GIS. Catena 2017, 149, 52–63. [Google Scholar] [CrossRef]
- Erener, A.; Sivas, A.A.; Selcuk-Kestel, A.S.; Düzgün, H.S. Analysis of training sample selection strategies for regression-based quantitative landslide susceptibility mapping methods. Comput. Geosci. 2017, 104, 62–74. [Google Scholar] [CrossRef]
- Zhu, A.-X.; Miao, Y.; Yan, L.; Bai, S.; Liu, J.; Hong, H. Comparison of the presence-only method and presence-absence method in landslide susceptibility mapping. Neural Comput. 2018, 171, 222–233. [Google Scholar] [CrossRef]

| Category | Conditioning Factors | Type | Data Source | Values |
|---|---|---|---|---|
| Topographical | Altitude (m) | Continuous | DEM | 23–4413 |
| Slope angle (°) | Continuous | DEM | 0–87 | |
| MED (m) | Continuous | DEM | 12–652 | |
| Plan curvature | Continuous | DEM | −0.51–0.64 | |
| Profile curvature | Continuous | DEM | −0.86–0.56 | |
| Aspect | Categorical | DEM | East; Northeast; North; West; Northwest; South; Southwest; Southeast | |
| TWI | Continuous | DEM | 5.13–17.94 | |
| Geological | Distance to faults (km) | Continuous | Geological map | <1; 1–2; 2–3; 3–4; 4–5; >5 |
| Lithology | Categorical | GESI | 0–2.5; 2.5–5; 5–7.5; 7.5–10; 10–12.5; 12.5–15; 15–17.5; >17.5 | |
| Triggering factors | Maximum 24 h rainfall (mm) | Continuous | BHH | 148.02–304.36 |
| Maximum 7 days rainfall (mm) | Continuous | BHH | 211.36–376.44 | |
| Distance to roads (km) | Continuous | DNRB | <1; 1–2; 2–3; 3–4; 4–5; >5 | |
| Land use | Categorical | DNRB | Artificial Surfaces; Cropland; Forests; Grasslands |
| Factor | C1 | C2 | C3 | C4 | C5 |
|---|---|---|---|---|---|
| Distance to fault (F1) | −0.032 | 0.027 | 0.895 | 0.021 | 0.005 |
| Plan curvature (F2) | −0.004 | −0.004 | −0.028 | −0.135 | 0.983 |
| Profile curvature (F3) | 0.002 | 0.007 | −0.032 | 0.940 | −0.091 |
| Distance to road (F4) | −0.177 | 0.067 | 0.831 | −0.070 | −0.030 |
| Slope (F5) | 0.024 | 0.909 | 0.046 | −0.168 | −0.049 |
| Elevation (F6) | −0.544 | 0.438 | 0.409 | −0.264 | −0.170 |
| MED (F7) | 0.050 | 0.875 | 0.048 | 0.069 | 0.017 |
| Maximum 7 days rainfall (F8) | 0.977 | 0.057 | −0.133 | −0.017 | −0.015 |
| Maximum 24H rainfall (F9) | 0.979 | 0.070 | −0.053 | −0.023 | −0.022 |
| TWI (F10) | 0.008 | −0.593 | −0.051 | 0.658 | −0.131 |
| Contribution rate (%) | 28.993 | 22.842 | 14.598 | 11.974 | 8.121 |
| Accumulative contribution (%) | 28.993 | 51.834 | 66.433 | 78.380 | 86.501 |
| Model | Class | Total Area (m2) | Percentage of Area (%) | Landslide Area (m2) | Percentage of Landslide Area (%) | IV |
|---|---|---|---|---|---|---|
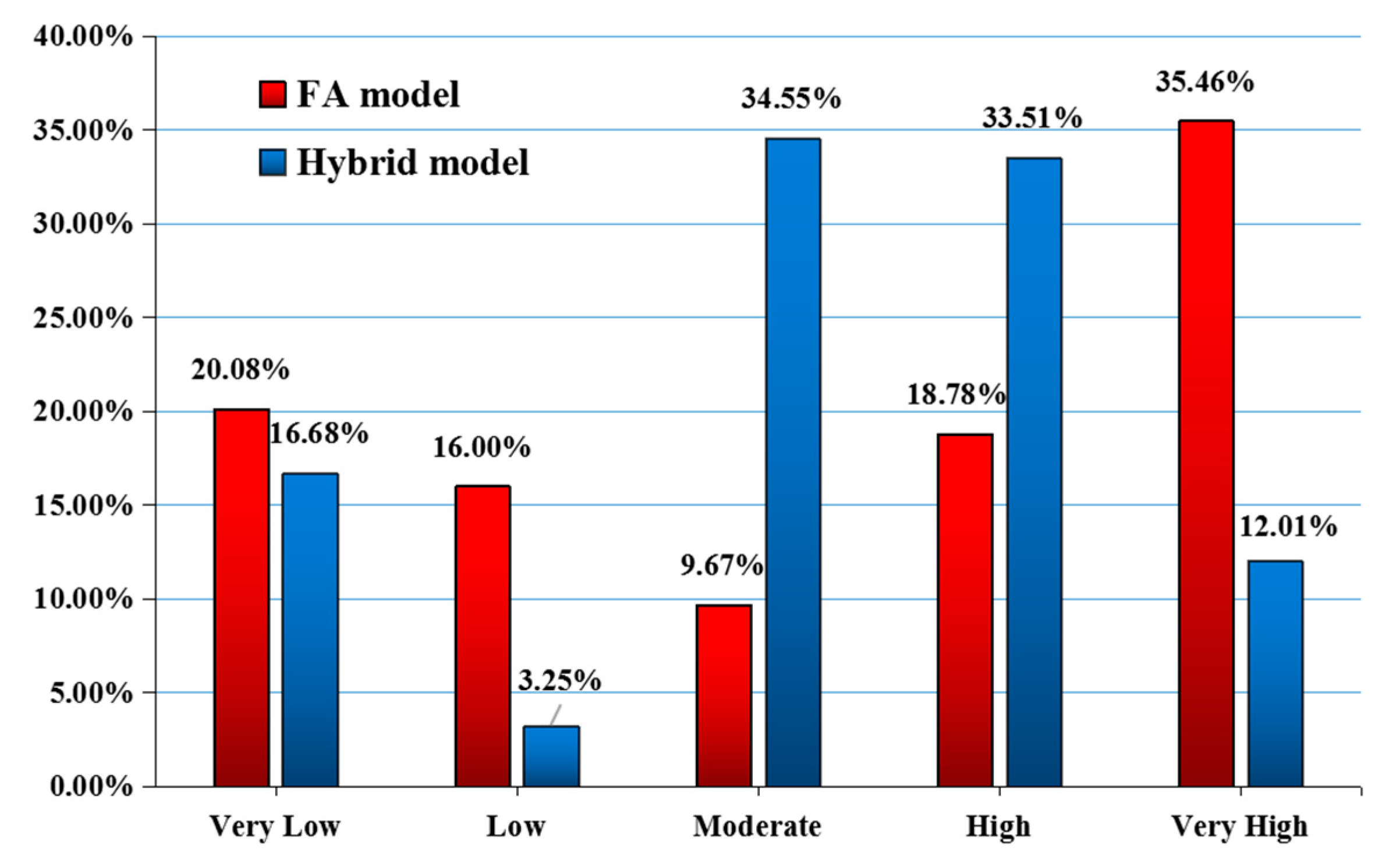
| FA | Very low | 299,175,346 | 16.80 | 6,615,258 | 7.25 | −0.84 |
| Low | 58,195,125 | 3.25 | 1,023,304 | 1.12 | −1.07 | |
| Moderate | 619,590,418 | 34.55 | 24,292,631 | 26.64 | −0.26 | |
| High | 601,033,643 | 33.51 | 39,841,031 | 43.69 | 0.27 | |
| Very high | 215,547,446 | 12.01 | 19,415,340 | 21.29 | 0.57 | |
| FA+ GBDT | Very low | 360,203,145 | 20.08 | 2,802,398 | 3.08 | −1.87 |
| Low | 286,967,956 | 16.00 | 2,640,178 | 2.9 | −1.71 | |
| Moderate | 173,449,271 | 9.67 | 4,451,170 | 4.9 | −0.68 | |
| High | 325,321,468 | 18.78 | 10,752,965 | 19.38 | 0.03 | |
| Very high | 647,600,138 | 35.46 | 73,787,162 | 69.72 | 0.68 |
| Dataset | Metrics | Normal GBDT | Hybrid Model |
|---|---|---|---|
| Training | Sensitivity | 88.51% | 92.29% |
| Specificity | 90.24% | 90.52% | |
| Accuracy | 89.38% | 91.69% | |
| AUC | 0.963 | 0.986 | |
| Test | Sensitivity | 83.73% | 88.60% |
| Specificity | 85.47% | 92.59% | |
| Accuracy | 84.62% | 90.60% | |
| AUC | 0.937 | 0.976 |
| Method | Slope | MED | TWI | Elevation | Lithology | land Use | DTR | Maximum 24 h Rainfall | Profile Curvature | Maximum 7 Days Rainfall |
|---|---|---|---|---|---|---|---|---|---|---|
| Gini index | 0.26 | 0.24 | 0.19 | 0.1 | 0.06 | 0.06 | 0.03 | 0.02 | 0.02 | 0.02 |
| Factor | Rainfall | Slope | MED | DTR | DTF | Curvature | TWI | Elevation | Lithology | Land Use | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Method | |||||||||||
| FA | 1 | 2 | 3 | 4 | 5 | 6 | |||||
| Gini index | 7 | 1 | 2 | 7 | 7 | 3 | 4 | 5 | 6 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, Z.; Wang, C.; Duan, Z.; Liu, H.; Liu, X.; Ullah Jan Khan, K. A Hybrid Model Consisting of Supervised and Unsupervised Learning for Landslide Susceptibility Mapping. Remote Sens. 2021, 13, 1464. https://doi.org/10.3390/rs13081464
Liang Z, Wang C, Duan Z, Liu H, Liu X, Ullah Jan Khan K. A Hybrid Model Consisting of Supervised and Unsupervised Learning for Landslide Susceptibility Mapping. Remote Sensing. 2021; 13(8):1464. https://doi.org/10.3390/rs13081464
Chicago/Turabian StyleLiang, Zhu, Changming Wang, Zhijie Duan, Hailiang Liu, Xiaoyang Liu, and Kaleem Ullah Jan Khan. 2021. "A Hybrid Model Consisting of Supervised and Unsupervised Learning for Landslide Susceptibility Mapping" Remote Sensing 13, no. 8: 1464. https://doi.org/10.3390/rs13081464
APA StyleLiang, Z., Wang, C., Duan, Z., Liu, H., Liu, X., & Ullah Jan Khan, K. (2021). A Hybrid Model Consisting of Supervised and Unsupervised Learning for Landslide Susceptibility Mapping. Remote Sensing, 13(8), 1464. https://doi.org/10.3390/rs13081464







