Abstract
This paper discusses the potential of L-band Advanced Land Observing Satellite-2 (ALOS-2) and C-band Sentinel-1 radar data for retrieving soil parameters over cereal fields. For this purpose, multi-incidence, multi-polarization and dual-frequency satellite data were acquired simultaneously with in situ measurements collected over a semiarid area, the Merguellil Plain (central Tunisia). The L- and C-band signal sensitivity to soil roughness, moisture and vegetation was investigated. High correlation coefficients were observed between the radar signals and soil roughness values for all processed multi-configurations of ALOS-2 and Sentinel-1 data. The sensitivity of SAR (Synthetic Aperture Radar) data to soil moisture was investigated for three classes of the normalized difference vegetation index (NDVI) (low vegetation cover, medium cover and dense cover), illustrating a decreasing sensitivity with increasing NDVI values. The highest sensitivity to soil moisture under the dense cover class is observed in L-band data. For various vegetation properties (leaf area index (LAI), height of vegetation cover (H) and vegetation water content (VWC)), a strong correlation is observed with the ALOS-2 radar signals (in HH(Horizontal-Horizontal) and HV(Horizontal-Vertical) polarizations). Different empirical models that link radar signals (in the L- and C-bands) to soil moisture and roughness parameters, as well as the semi-empirical Dubois modified model (Dubois-B) and the modified integral equation model (IEM-B), over bare soils are proposed for all polarizations. The results reveal that IEM-B performed a better accuracy comparing to Dubois-B. This analysis is also proposed for covered surfaces using different options provided by the water cloud model (WCM) (with and without the soil–vegetation interaction scattering term) coupled with the best accuracy bare soil backscattering models: IEM-B for co-polarization and empirical models for the entire dataset. Based on the validated backscattering models, different options of coupled models are tested for soil moisture inversion. The integration of a soil–vegetation interaction component in the WCM illustrates a considerable contribution to soil moisture precision in the HV polarization mode in the L-band frequency and a neglected effect on C-band data inversion.
Keywords:
radar; ALOS-2; L-band; Sentinel-1; C-band; soil moisture; soil roughness; vegetation; water cloud model 1. Introduction
Soil moisture is a key parameter for various processes in the continental water cycle. It plays an essential role in the separation of precipitation between runoff, infiltration and evaporation from surfaces. It is also a key parameter in water resource management, especially in the estimation of irrigation needs and monitoring of flood events [,,,,,]. Considerable effort has been devoted to estimate soil moisture in a context of limited contribution of punctual ground measurements.
Over the last thirty years, remote sensing has shown a high potential to retrieve soil moisture. Operational algorithms have also been principally proposed using low-spatial resolution microwave radiometer or scatterometer instruments. In the L-band, satellites such as Soil Moisture and Ocean Salinity (SMOS) and Soil Moisture Active Passive (SMAP) have demonstrated a strong potential for soil moisture retrieval, with a spatial resolution ranging between 25 and 36 km by a revisit time of up to one day [,]. Scatterometers, such as ASCAT [], have provided different products principally based on change detection algorithms. These low-resolution products are particularly adapted to global and regional applications [].
SAR (Synthetic Aperture Radar) high-resolution data have been particularly adapted to estimate soil moisture at the agricultural field scale. In the last three decades, many experimental and theoretical research studies have proposed methodologies to retrieve soil moisture [,,,,,,,,,,,,,,]. These studies are based on a succession of radar missions, mainly in the C- and X-bands (ERS, ASAR/ENVISAT, RADARSAT-1, RADARSAT-2, TERRASAR-X, SKYMED, Sentinel-1, etc.).
For bare soils, different models have been proposed to understand and characterize the relationship between radar signals and soil properties, i.e., soil moisture and surface roughness are generally estimated by statistical parameters such as root mean square height (Hrms) and correlation length (Lc). Among these models, there are empirical [,] and semi-empirical approaches, such as Dubois and Oh models [,], and physical approaches that consider different types of physical approximations, such as the small perturbation model, Kirchhoff [] or the integral equation model [], which are the most frequently used by the scientific community. These models have been tested and validated by numerous scientific studies [,,,]. These studies have demonstrated the limitations of these different models, especially for characterizing scattering over surfaces with a high roughness. Different approaches have been proposed to improve these simulations. Baghdadi et al. [,] replaced in the IEM-B version the correlation length by a fitting parameter function of Hrms, incidence angle, polarization and radar wavelength.
For surfaces with vegetation cover, backscattering analysis should consider the effect of vegetation cover in addition to that of soil. In this framework, different models have been developed to simulate the radar signal scattered by the surface. These are physical models such as the Karam model [], Michigan microwave canopy scattering (MIMCS) [] or semi-empirical or empirical models. The most known among the latter is the water cloud model (WCM) proposed by Attema and Ulaby in 1978 [].
The WCM considers the total backscattering signal as the sum of a first component, soil scattering attenuated with the vegetation effect, a second component, vegetation volume scattering, and, finally, a third term describing the interactions between soil and vegetation. This last component is generally neglected in scientific studies that use the WCM []. For this model, vegetation effect quantification requires the use of vegetation biophysical properties such as leaf area index (LAI), vegetation water content (VWC) or vegetation height (H) [,,,]. In this context, for an operational objective, spectral indices calculated from optical images such as the normalized difference vegetation index (NDVI) are often considered for this description [,]. Several studies have highlighted the strong contribution of the synergy of radar and optical data to properly characterize the scattering of surfaces with vegetation cover [,]. However, this approach has some limitations due to the saturation of optical indices and is unable to reproduce all the dynamics of vegetation cover with high density levels [].
The inversion of the radar signal to estimate the soil water content at the agricultural plot scale is essentially based on three types of approaches: (1) a direct inversion approach of the backscattering models described above [,], (2) an approach based on machine learning approaches, notably through the use of neural networks [,,] and (3) approaches that use change detection techniques [,,].
With the arrival of the Sentinel 1 and 2 Copernicus constellations, these approaches have been tested by several scientific studies. The authors of [] proposed approaches for the direct inversion of S1 data using backscatter models. They illustrated accuracies on the order of 5 vol.%. However, this methodology remains relatively fragile in applications outside the calibration sites of the model’s parameters. The authors of [] proposed an algorithm based on neural networks and learning using the coupling of the IEM-B and WCM models. This approach provides soil moisture estimates with an accuracy on the order of 5 vol.% for surfaces with NDVI < 0.7. The authors of [] proposed an adapted high-resolution approach to change detection, illustrating a precision on the order of 6 vol.%. At a scale of 1 km, [] also proposed an operational approach based on this change detection technique, and operational products have already been available across Europe.
Most of those approaches considered for backscatter model validation or radar data inversion to retrieve land surface parameters are mainly based on data acquired in the C- and X-bands. Concerning the L-band, data availability remains relatively limited to a few space missions, notably the ALOS and ALOS-2 Japanese missions. In the near future, different L-band missions, such as NISAR and ROSE-L, should be launched. One of the objectives of these missions is to contribute to improving the estimation of land surface parameters, notably soil moisture. Many studies have been proposed to analyze the L-band data potential over agricultural surfaces [,,,,,,]. The authors of [] used fully polarized L-band airborne observations to evaluate the IEM, Dubois and Oh backscatter models. The authors of [] investigated and confirmed the potential of ALOS-2 L-band data in retrieving soil moisture even for dense vegetation (NDVI > 0.7). The authors of [], in a tropical context, tested the WCM on covered fields using the LAI parameter for vegetation effect simulation. An accuracy of 6.7 vol.% for HH(Horizontal-Horizontal) polarization and 7.9 vol.% for HV(Horizontal-Vertical) polarization was reported over marigold crop fields. For turmeric crop fields, RMSE values ranged between 8.7 and 11 vol.% for HH and HV polarization, respectively. They particularly illustrated its high sensitivity to soil moisture even for vegetation with LAI > 2.5. The authors of [] developed an approach based on polarimetric decomposition over many cultures, leading to RMSE values between 6 and 8 vol.%.
The use of L-band signals still needs to be explored, especially in terms of the potential of the L-band to retrieve surface parameters, compared to that of the C-band. This work aims to contribute to a better understanding of the potential of L-band compared to C-band radar data in terms of sensitivities to soil and vegetation properties, as well as their inversion for retrieving soil moisture. It discusses the scattering behavior, particularly the term of interaction between soil and vegetation often neglected in experimental studies. It focuses on cereal fields. Section 2 of this paper describes the study site and collected satellite and in situ database. Section 3 details the methodology proposed in this study. Section 4 presents the results and discussions in three parts: sensitivity analysis of radar data to surface parameters, simulation of radar signals using backscattering models and inversion applications to retrieve soil moisture over cereal fields. The conclusions are gathered in Section 5.
2. Study Zone Description and Database
2.1. Study Zone Description
The study was performed on the Merguellil Plain (9°23′–10°17′E, 35°1′–35°55′N), which is a flat landscape covering 3000 km2 (Figure 1). It is classified as a semiarid zone with a rainy season ranging from September to April and a summer season with almost no rainfall. The mean annual precipitation is 300 mm per year. The average temperature in the coldest months (December, January and February) is 11 °C and can reach 30 °C in summer. The reference evapotranspiration is estimated to be 1600 mm according to the Penman method. The main land use is cereal, olive tree and market garden crops. The plain is a basin that was fed by surface water infiltration before the construction of the El Haouareb and Sidi Saad dams at the level of the Merguellil and Zeroud rivers, respectively. Moreover, it is the confluence zone of several underground water tables (Bouhaffna, Haffouz–Cherichira and Ain El Bidha) that drain into the Sabkhet El Kalbia outlet [].
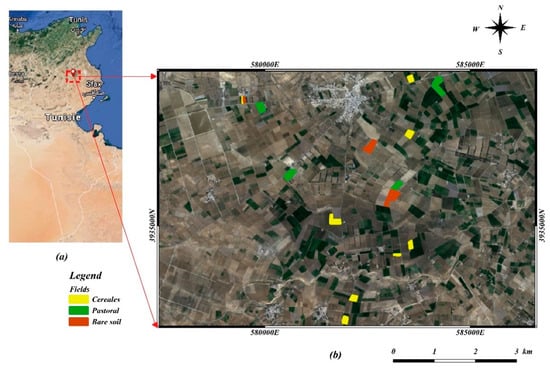
Figure 1.
(a) Location of study site in the Merguellil area (dashed rectangle colored in red) in central Tunisia. (b) Reference fields on the study site (in the front RGB colored map derived from a Sentinel-2 image).
2.2. Dataset Description
2.2.1. Radar Images
- (a)
- ALOS-2 Radar Data
Multi-incidence images were acquired by the Advanced Land Observing Satellite-2 (ALOS-2) using the L-band SAR antenna Phased Array Synthetic Aperture Radar (PALSAR), which was launched by the Japan Aerospace Exploration Agency (JAXA), with a revisit cycle frequency of 1/14 days−1. The ALOS-2 images used, in the strip map operation mode, offer a spatial resolution of 6 x 6 m in dual polarizations HH (horizontal–horizontal) and HV (horizontal–vertical) and various incidence angles (28°, 32.5° and 36°). Table 1 summarizes the main characteristics of the L-band SAR images recorded at the Kairouan site.

Table 1.
Radar parameters of satellite images acquired in 2014–2016, 2019 and 2020 (incidence angle, polarization, path, spatial resolution, acquisition mode and ascending or descending).
Images were radiometrically corrected to convert the digital values into backscatter coefficients on a linear scale. This correction was followed by georeferencing according to the UTM projection system, using the control point method, referenced on an NDVI image calculated from the Sentinel 2 optical images. The root mean square (RMSE) control point error is close to 0.5 pixels.
- (b)
- Sentinel-1 Constellation Radar Data
Owing to the launch of the Sentinel-1 A (S-1 A) on 3 April 2014 and Sentinel-1 B (S-1 B) on 25 April 2016, C-band SAR images are available with a revisit cycle frequency of 6 days in dual-polarization VV (vertical–vertical) and VH (vertical–horizontal) modes, with an incidence angle of approximately 39°. In the present study, we used seven images in the interferometric wide swath mode (IW) with a spatial resolution of 10 × 10 m, as described in Table 1.
Acquired level 1 ground range detected (GRD) images were processed to derive backscattering coefficients in each pixel through the following steps: thermal noise removal, radiometric calibration followed by terrain correction and speckle filtering (Lee filter).
2.2.2. Sentinel-2 Optic Data
Optical images were acquired by Sentinel-2A, launched on 23/06/2015, and Sentinel-2B, launched on 07/03/2017. They offer images with a 10 m resolution and a passage frequency of 1/5 days−1. S2 surface reflectance images, cloud free selected, were downloaded from the THEIA-LAND site and orthorectified and corrected for atmospheric effects using the MAJA processor for cloud detection and atmospheric correction (https://www.theia-land.fr, accessed on 31 March 2021).
The NDVI vegetation index, expressed as NDVI = (RNIR − RRED)/(RNIR + RRED), where RNIR is the near-infrared (NIR) reflectance and RRED is the red reflectance, was calculated from the optical images. The NDVI pixel values were then averaged for each reference field and each acquisition date [,,].
2.2.3. In Situ Measurements
In situ campaigns were carried out at the same time as the ALOS-2 acquisitions (two dates in 2014/2015, two dates in 2016 and eight dates in 2019/2020) and Sentinel-1 satellite acquisitions (7 dates in 2019/2020). Seventeen reference fields were considered with 8 bare soil fields with different types of roughness, ranging from smooth to ploughed surfaces, and 9 irrigated cereal fields. The surface areas of these study fields ranged between 0.5 and 7 ha.
The in situ measurements made in the test fields involved the characterization of the following parameters: moisture and roughness measurements were carried out for the soil characterization, and LAI, VWC and H vegetation property measurements were recorded for the fields with vegetation cover. Table 2 provides details of the dates of the field campaigns and the corresponding types of measurement.

Table 2.
In situ measurements (min-max) during campaigns from 2014 to 2020 with the roughness parameters (root mean square height (Hrms), correlation length (Lc)), soil moisture (Mv) and cereal parameters (vegetation height (H), leaf area index (LAI) and vegetation water content (VWC)).
- (a)
- Roughness
Roughness is a measure of microtopographic height variations at the soil surface. This was characterized by means of a 1-m-long pin profiler with a resolution equal to 2 cm. Six roughness profiles, 3 parallel and 3 perpendicular to the tillage row direction, were established in all reference fields during three different ground campaigns. The test fields are totally flat and homogenous with soil tillage with very limited directional structures. The proposed number of profiles is a priori sufficient to allow an accurate estimation of the roughness, as shown by [] over the same site.
Two main surface roughness parameters, Hrms and Lc, were determined from the mean height correlation function, which was computed from the digitized soil profiles []. Significant variations in the values of Hrms were observed between successive ground campaigns, ranging from 0.46 (very smooth soils) to 6.46 cm (ploughed soils), resulting mainly from the influence of rain and cultural practices (tillage, sowing, etc.).
- (b)
- Soil Moisture (Mv)
Soil moisture measurements were collected from each reference field at 20 randomly distributed points using a hand-held Theta probe for each considered date. These moisture measurements were calibrated by gravimetric measurements recorded during previous campaigns simultaneously over the same reference fields []. During the missions, moisture measurements were taken at the same image acquisition time with a time lag of approximately 2 h in order to limit any temporal variation in soil water content. In the case of the presence of precipitations or irrigations exactly during the satellite acquisitions, the data are generally not considered because the temporal variations could be very strong on a very limited duration. The recorded volumetric values varied between 3.0 vol.% issued in dry conditions and 42.9 vol.% in wet conditions due to precipitation or irrigation (Table 2).
- (c)
- Vegetation Parameters
• Vegetation Heights (H):
In each cereal plot, 20 height measurements were taken, which were well distributed spatially. The height values reached 1 m towards the end of February during the stem extension growth stage.
• Leaf Area Index (LAI):
LAI is defined as the total one-sided area of leaf tissue per unit ground surface area. According to this definition, LAI is dimensionless. For each reference field, we considered approximately twenty hemispherical digital images, which were processed to retrieve this vegetation parameter based on the vegetation gap fraction []. LAI measurements were performed during the 2019–2020 agricultural season. During all measurement campaigns, the computed value of LAI ranged between 0 and 4.5 (Table 2). The highest values of LAI were observed mainly in the irrigated reference fields.
• Vegetation Water Content (VWC):
Measurement of the water content of the vegetation was based on fresh surface vegetation sampling. The spatial limits of this sampling were defined by a wooden frame. We took 3 samples per plot and weighed the fresh material collected. The samples were dried in an oven at 80 °C for 72 h and reweighed again as dry matter. The water content was calculated according to the following equation in terms of kilograms of water per m2 of surface area:
where is the weight of the fresh material, is the weight of the dry vegetation and is the surface area of the wooden frame. The obtained values ranged between 0.07 kg of water/m2 at the start of the cycle to 1.09 kg of water/m2 in February.
3. Methodology
In this section, we present different backscattering models that are validated by our ground truth collected data in the Results section. In the case of bare soils, different empirical, semi-empirical and physical backscattering models are considered. In the case of surfaces with vegetation coverage, the water cloud model (WCM) with various options is discussed.
3.1. Bare Soil Backscattering Models
3.1.1. Empirical Relationships
Empirical models used to characterize the relationship between the backscattering coefficients σ and soil surface parameters are presented as follows:
where Mv is the soil moisture (vol.%), Hrms is the root mean square of heights (cm), pq is the radar polarization and αpq, βpq and γpq and α’pq, β’pq and γ’pq are constants requiring calibration and validation.
The roughness effect is introduced by a logarithmic regression between the Hrms or Zs parameter, defined as Hrms2/Lc [], and the radar signal. This empirical relation is generally considered to be logarithmic because of the strong saturation of the radar signal for high roughness levels [].
3.1.2. Dubois Calibrated Model (Dubois-B)
The Dubois model is a semi-empirical model applied for copolarized radar signals over bare soils. Its input variables include radar parameters (polarization, incidence angle and wavelength), soil moisture and roughness Hrms measurements []. The Dubois model validity range includes soil moisture values <35 vol.%, k.Hrms value <2.5 and incidence angles Ѳ > 30°.
A modified version of the Dubois model (Dubois-B) was proposed by [] in the three polarizations of HH, VV and HV to minimize the discrepancy between simulated and real backscattering coefficients. For HH, VV and HV polarizations, expressions are written as follows:
where k is the wavenumber, which is equal to , is the wavelength, θ is the incidence angle in radian, Mv is in vol.% and Hrms is in cm.
3.1.3. IEM-B Model
The IEM, proposed by [], is a physical model. It calculates the backscattering coefficient over bare soils. Its inputs include the dielectric constant retrieved from soil moisture and the height correlation function (exponential or Gaussian), as well as the radar parameters (polarization, wavelength and incidence angle). The IEM validity range is limited by k.Hrms > 3.
The IEM is expressed as []
where is the backscattering coefficient at pp polarization, is the radar incidence angle, is the wavenumber, , , and is the root mean surface height. is a function of the radar incidence angle, the relative dielectric constant of the soil εr, and the Fresnel reflection coefficient. is the Fourier transform of the th power of the surface correlation function.
Despite the important contribution of this model to simulations with high-precision backscattering over bare soils, different studies have shown some limitations in adequately describing soil geometry [,,], particularly for high roughness levels. Over the years, many studies have updated versions of the IEM to minimize discrepancies with SAR backscattered coefficients over natural areas. The authors of [] proposed a modified advanced integrated equation model (AIEM) by considering a transitional model to calculate the Fresnel reflection coefficient. Other improvements were focused on the IEM inputs. Correlation length (Lc) measurements are, in general, uncertain. The authors of [] replaced Lc with an optimized parameter, Lopt, that was directly linked to the Hrms roughness parameter in the IEM-B version in the C-band (Equations (8) and (9)):
In the L-band, the authors of [] used a fitting parameter, Lopt, for HH polarization and a Gaussian correlation function, as shown in equation (10):
3.2. Water Cloud Model (WCM) Backscattering Model over Vegetation Cover
The WCM was used to model the radar signal backscattered for vegetation-covered surfaces. Vegetation is described as a set of identical, spherical water droplets characterized by their density and canopy height []. The total backscattering coefficient is expressed as follows:
where is the vegetation contribution component and is the two-way vegetation attenuation of the bare soil backscattering coefficient . Multi-backscattering effects are considered in the term .
where A and B are parameters that depend on the characteristics of the vegetation canopy and V1 and V2 are vegetation descriptors. The impact of the choice of descriptors was discussed in []. In the present case, we consider the NDVI, which is strongly related to the vegetation parameters, as shown in Section 2.
The multi-scattering term is generally neglected in experimental studies, and total backscattering is then written as follows:
However, a number of studies have illustrated the importance of the multi-scattering term, notably in HV polarization. The authors of [] considered the following term, describing the coherent interaction between the canopy and ground:
where is the volume scattering coefficient, d is the canopy depth and is the Fresnel reflectivity in the pq polarization mode.
In this study, we propose an approximation of this term by considering a third term to calibrate:
in which the Cpq parameter is dependent on the characteristics of the vegetation cover, and the α parameter is estimated directly from the linear relationship between the radar signal and soil moisture in dB/vol.%.
In this approximation, the formulation of the volume scattering coefficient is deduced from Expression (12), V2 is the vegetation descriptor, directly related to the canopy depth, and, finally, the expression of the Fresnel coefficient is expressed from the relationship between the soil moisture and radar signal.
3.3. Statistical Parameters for Accuracy Assessment
Datasets were subdivided into two parts: 70% of the database for model calibration, and 30% for validation. The training data were used to calculate the different parameters to be estimated in the empirical and semi-empirical models.
The root mean square error (RMSE) and bias were considered to estimate the precision of the models.
where N is the number of data samples, is the estimated value of sample i and is the measured value of sample i.
4. Results and Discussion
4.1. Relationship between NDVI and Vegetation Parameters
Analysis of the optical data potential was conducted by plotting the NDVI index as a function of the vegetation parameters measured in the test field (Figure 2). The NDVI values covered an interval starting from 0.2 for cereals after sowing to values of approximately 0.8 at the stem extension phase.
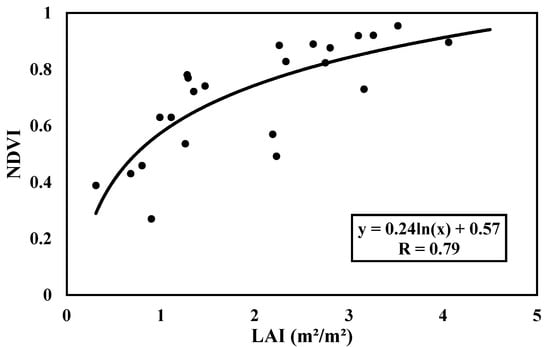
Figure 2.
Relationship between LAI in situ measurements and normalized difference vegetation index (NDVI) derived from Sentinel 2 images.
The NDVI values show moderate correlations with R values of 0.74 and 0.59 for H and VWC, respectively. Figure 2 illustrates this strong relationship between NDVI and LAI, generally considered for modeling of the vegetation backscattering contribution, with a high correlation equal to 0.79. We consider NDVI as a key parameter for describing vegetation cover, basing on the results observed in many other studies [,], in the remainder of this study, concerning backscattering and inversion models.
4.2. Sensitivity of Radar Signal to Surface Properties
4.2.1. Sensitivity to Soil Roughness
Signal behavior is strongly influenced by soil roughness and moisture. Figure 3 shows the sensitivity of L-band SAR data as a function of roughness parameters (Hrms and Zs). To avoid the impact of soil moisture on this backscattering behavior, we analyzed the relationship between the roughness and radar signal only with moisture values less than 10 vol.%. Table 3 details the statistical correlation coefficients for all relationships between roughness parameters (Hrms and Zs) and the dual-frequency radar signals with ALOS-2 in dual polarizations HH and HV according to three incidence angles (28°, 32.5° and 36°) and Sentinel-1 data in VV and VH polarizations at a 39° incidence angle.
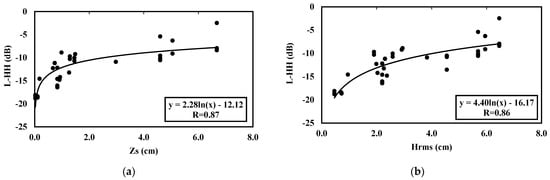
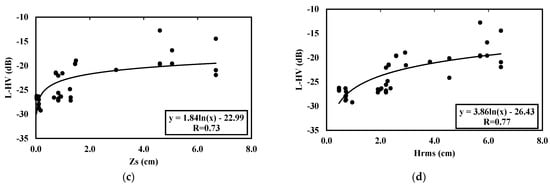
Figure 3.
ALOS-2 radar data (28° incidence angle) as a function of roughness parameters Zs and Hrms. (a) Zs and HH polarization, (b) Hrms and HH polarization, (c) Zs and HV polarization, (d) Hrms and HV polarization.

Table 3.
Statistics of relationships between radar signal and roughness parameters (Hrms and Zs), for L-HH and L-HV (ALOS-2), at three incidence angles, 28°, 32.5° and 36°, and for C-VV and C-VH (Sentinel-1), at a 39° incidence angle where soil moisture values are under 10 vol.%.
Using the Hrms parameter, high correlation coefficients ranging between 0.83 and 0.93 in L-HH multi-incidence data and between 0.77 and 0.83 in L-HV multi-incidence data can be observed. Using the Zs parameter, correlation coefficients between 0.7 and 0.92 are observed for the multi-incidence L-HH data and between 0.73 and 0.82 for the L-HV data. We observe approximately the same level of correlation for the two roughness parameters. We also observe a range of radar signals related to the variation in roughness approximately equal to 10 dB and 8 dB for L-HH and L-HV, respectively.
For Sentinel-1 C-VV data, we observe high correlation coefficients equal to 0.88 and 0.85 for the Zs and Hrms parameters, respectively. A lower level of correlation is observed for the C-VH data, where the R values reach a maximum of 0.56 for the same roughness range.
Different reasons can degrade the correlation observed between the radar signals and the roughness parameters: the absence of information on the shape of the height correlation function, the complexity of the scattering for strong roughness levels and, finally, the possible uncertainties in the roughness ground measurements.
Under low-soil moisture conditions, according to Table 3, we observe a signal dynamic due to soil roughness approximately equal to 8 dB and 6 dB for C-VV and C-VH, respectively, which is close to the observed range in []. This could give more weight to the use of L-band data in mapping soil practices and, at the same time, be considered a probable, more important noise factor in estimating soil moisture from L-band radar data.
4.2.2. Sensitivity to Soil Moisture
In this section, we analyze the sensitivity of L- and C-band radar data to soil moisture. In this context, to avoid the vegetation cover effect, we consider three classes of vegetation: a first class of bare soil or very dispersed vegetation (NDVI < 0.3), a second class with medium density (0.3 < NDVI < 0.6) and, finally, a third class with dense vegetation (NDVI > 0.6). Only surfaces after tillage for cereal sowing, with approximately the same roughness, are considered in this analysis to avoid other effects due to roughness for bare soils.
Figure 4 illustrates the relationships found for the L-HH and L-HV data for the three considered classes. We first observe a decrease in the sensitivity of the radar signal to soil moisture with an increase in vegetation cover for both polarizations. This sensitivity decreases by 0.31 and 0.18 dB/vol.% (NDVI < 0.3) to 0.27 and 0.15 dB/vol.% for NDVI values between 0.3 and 0.6 and finally to 0.19 and 0.16 dB/vol.% (NDVI > 0.6) in HH and HV, respectively. All statistics are also illustrated in Table 4.
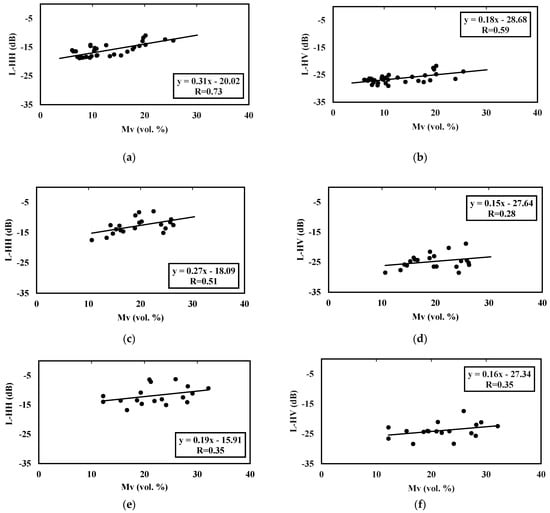
Figure 4.
ALOS-2 radar data as a function of soil moisture: NDVI < 0.3 (HH (a); HV (b)), 0.3 < NDVI < 0.6 (HH (c); HV (d)) and NDVI > 0.6 (HH (e); HV (f)).

Table 4.
Radar data linear relationship as a function of soil moisture for ALOS-2 data in dual polarizations HH and HV at a 28° incidence angle and for Sentinel-1 data in VV and VH polarizations at an approximately 39° incidence angle.
The moisture sensitivity is generally lower for HV polarization, which could be explained by the volume scattering effect in the cross-polarization case, especially in the presence of the canopy. This last result is generally observed by experimental scientific studies [,]. For the densest canopies (NDVI > 0.6), the sensitivity of L-HH data to soil moisture remains significant. However, the correlation is weak (R = 0.35), which makes the conclusion about the sensitivity of the radar signal to moisture rather fragile.
In the C-band, Table 4 shows that the sensitivity of the radar signal to soil moisture decreased by 0.26 and 0.24 dB/vol.% to 0.17 and 0.08 dB/vol.% for the vegetation medium density class and finally to 0.07 and 0.09 dB/vol.% for the denser canopy classes in VV and VH, respectively.
The inter-comparison of the results obtained for the L- and C-bands shows a higher sensitivity of the L-band in HH polarization to soil moisture for the high density covered soils (0.19 dB/vol.% for L-HH configuration and 0.07 dB/vol.% for C-VV configuration). In the case of HV polarization, a lower sensitivity to soil moisture is generally observed for all tested configurations. This is particularly due to the effect of stronger volume scattering in cross-polarization.
In all studied cases, the correlations observed for all configurations remain relatively moderate even in the case of bare soil. This could be explained, in particular, by the effect of the surface roughness, illustrated earlier in this section. These results are in agreement with other studies [,,,].
In the case of tropical crops (marigold and turmeric), [] confirmed the strong sensitivity of the L-band radar signal to soil moisture for LAI values greater than 2.5. The authors of [] also observed a high potential of L-band data in HH polarization to penetrate wheat and grassland covers, even where NDVI > 0.7.
These results confirm the contribution of L-band data compared to C-band data in estimating soil moisture, especially in the densest canopies.
4.2.3. Sensitivity of Radar Signal to Vegetation Parameters
In this section, we evaluate the sensitivity of ALOS-2 and S-1 radar data as a function of vegetation parameters (VWC, LAI and H). To limit the effect due to soil moisture, we considered data at only high moisture levels (greater than 20 vol.%). In this context, the radar signal is close to saturation with respect to the effect of soil moisture. Figure 5 represents radar signals and L-HH, L-HV, C-VV and C-VH data as a function of vegetation parameters under the considered wet soil moisture conditions.
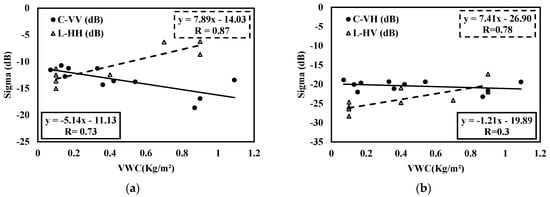
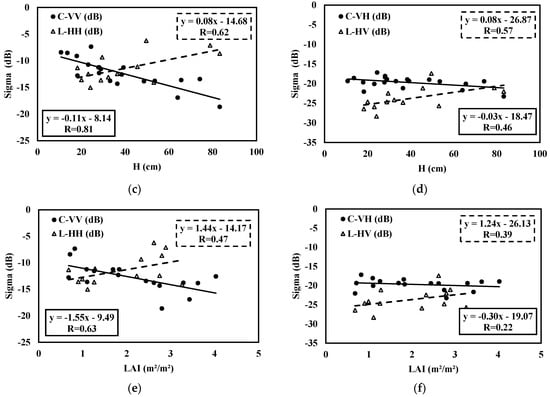
Figure 5.
Radar data as a function of vegetation parameters using linear regression with continuous line for C-band data and dashed line for L-band data: (a) L-HH (ALOS-2) and C-VV (Sentinel-1) as a function of VWC, (b) L-HV and C-VH as a function of VWC, (c) L-HH and C-VV as a function of vegetation height (H), (d) L-HV and C-VH as a function of H, (e) L-HH and C-VV as a function of LAI, (f) L-HV and C-VH.
Despite a relatively limited number of samples (between 9 and 13 samples), a sensitivity of the radar signal to canopy properties is observed with ALOS-2 SAR data for both L-HH and L-HV configurations. This sensitivity is relatively the same for both polarizations. The correlation is weaker for the L-HV configuration than for the L-HH configuration. This could be explained particularly by the complex volume scattering behavior observed in the HV polarization mode.
The L-band trends show the strongest correlation with VWC, with R values equal to 0.87 and 0.78 in the HH and HV polarizations, respectively, followed by height and then LAI (Figure 5).
The L-band data have a higher penetration of radar waves into the canopy compared to C data. Therefore, the correlation with LAI, which displays information more related to leaf superior cover without information about the cover structure, is weakest.
An increase in the L-HH radar signal is observed with increasing cereal canopy parameters. This trend has already been observed, in particular, in [] over wheat fields, where the L-HH signal increases as a function of LAI and vegetation height. In contrast to the VV polarization data, which illustrate a decrease in the radar signal for the first period of growth due to a strong attenuation of the signal over cereals with vertical geometry, the HH polarization data show weak attenuation and then a more dominant contribution due to volumetric scattering. This behavior with a decrease in the radar signal with the growth of the vegetation cover is clearly observed in the S1 data (Figure 5) and in other studies using X-band data []. However, we also observe in different studies a reversal of the trend with the development of cereals, probably related to a stronger dominance of volume scattering [].
In contrast to the L-band data, a moderate correlation is observed between the radar signals in the C-VV configuration and LAI parameter (R equal to 0.63). This result is consistent with other past studies performed with S1 data. This correlation remains relatively strong for the other vegetation parameters (H and VWC). However, the C-VH data illustrate a weak correlation with the different vegetation parameters analyzed, with an R value less than 0.46.
Comparing the cross-polarization results for the L- and C-bands, we note that different behaviors are mainly attributed to penetration depths with different contributions of volume scattering and sensor configurations, such as incident angles, since we worked on the same cereal fields.
4.3. Simulations of Radar Backscattering Coefficients
In this section, after a relatively simple analysis of radar signals’ sensitivities to the different surface parameters, separately, the objective is to use different backscattering models for a global analysis of relationships between surface parameters and multi-configuration radar signals. Simulations concern two different types of land use: bare soil and soil covered by cereals.
4.3.1. Case of Bare Soils
In this section, we first validate the Dubois-B and IEM-B models using our multi-incidence, multi-polarization and dual-frequency database acquired on bare soil.
Figure 6 illustrates the results retrieved for L-band data for the two tested models. For the L-HH configuration, we observe a better consistency between the data and the IEM-B model compared to the results obtained using the semi-empirical Dubois-B model. For the three incidence angles (28°, 32.5° and 36°), the simulations in the L-HH configuration show an RMSE lower than 2.1 dB with IEM-B, while with Dubois-B, the RMSE is between 2.4 and 2.7 dB. Table 5 gives statistical parameters regarding the comparison between the measured ALOS-2 data and simulated L-band signal with the IEM-B and Dubois-B models in dual polarization. In the L-HV configuration, the IEM-B model presents very low performances compared to the L-HH results for the three incidence angles with RMSE values between 3.2 and 4.5 dB.
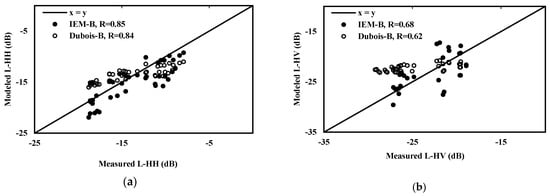
Figure 6.
Comparison between modeled (with Dubois-B and IEM-B) and measured radar backscattering coefficients in L-band: (a) L-HH, (b) L-HV. Only incidence angle of 28° is illustrated.

Table 5.
Statistical precision coefficients with IEM-B and Dubois-B models for ALOS-2 data (L-HH and L-HV) and Sentinel-1 data (C-VV and C-VH).
As illustrated in Figure 7 and Table 5, IEM-B and Dubois-B exhibit the best performances with the C-VV data configuration, with RMSE values between 1.3 and 1.5 dB, respectively. For the C-VH configuration, we note a high discrepancy between simulations and real data, with RMSE values equal to 1.7 and 2.3 dB for the IEM-B and Dubois-B models, respectively, and bias exceeding −3.5 dB.
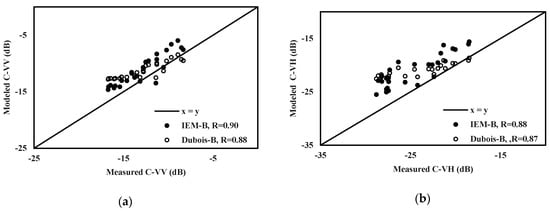
Figure 7.
Comparison between modeled (with Dubois-B and IEM-B) and measured radar backscattering coefficients: (a) C-VV, (b) C-VH.
Based on these results, only the IEM-B model in the polarizations (HH and VV) is considered further in the simulation of the scattered signal from the bare soil coupled with the WCM model. The other simulations of IEM-B and Dubois-B are considered too degraded to contribute to the overall simulation of the total radar signal over a surface with vegetation cover.
The empirical expressions proposed in Section 3.1.1. are tested on the 39° incidence angle Sentinel-1 data and 28° incidence angle L-band data acquired during 2019–2020. The use of empirical equations first requires parameter calibration. In this context, the actual dataset is divided randomly into two parts: the first part for model calibration (70% of the data) and 30% for empirical model validation.
Table 6 illustrates the calibration parameters and statistical precision (RMSE and R) between the calibrated empirical expressions (Equations (2) and (3)) and L-band data considered for calibration. The calibrated relationship h(Mv, Zs) between the radar signal and the Mv and Zs parameters shows RMSE values equal to 1.2 dB in L-HH and 1.0 dB in L-HV. On the other hand, for the g(Mv, Hrms) calibrated relationship, RMSEs of 1.4 dB in L-HH and 1.0 dB in HV are retrieved.

Table 6.
Calibration parameters and statistical precision coefficients with the proposed empirical expressions h and g for ALOS-2 (L-HH and L-HV) and for Sentinel-1 (C-VV and C-VH) data.
Empirical models are also tested for Sentinel-1 data, showing high accuracy in simulating signals over bare soils. In the C-VV configuration, RMSE values are equal to 1.2 dB and 1.3 dB using g(Mv, Hrms) and h(Mv, Zs) relationships, respectively. In the C-VH polarization, RMSE values are equal to 1.3 dB for the h(Mv, Zs) case and 1.4 dB for the g(Mv, Hrms) case, where R is approximately 0.89 and 0.9, respectively. The results show very similar accuracies with the two empirical expressions h and g.
Figure 8 illustrates comparisons between the calibrated empirical models and radar datasets considered just for validation (30% of database, 9 samples for each polarization). We observe a good agreement between the calibrated models and radar data, with RMSE ranging from 1.4 dB to 2.0 dB for the L-HH and L-HV configurations using h(Mv, Zs) and 1.3 dB and 1.8 dB with g(Mv, Hrms), respectively. For the S-1 data, h(Mv, Zs) relationship validation using real data gives RMSE values equal to 1.0 and 1.9 dB for the C-VV and C-VH configurations, respectively. Similar statistical precision ranges characterize g(Mv, Hrms) validation, where RMSE values are equal to 1.1 and 1.9 dB for the C-VV and C-VH configurations, respectively. Having two empirical models g and h with very similar accuracies, only the model g is kept afterwards for coupling with the WCM model.
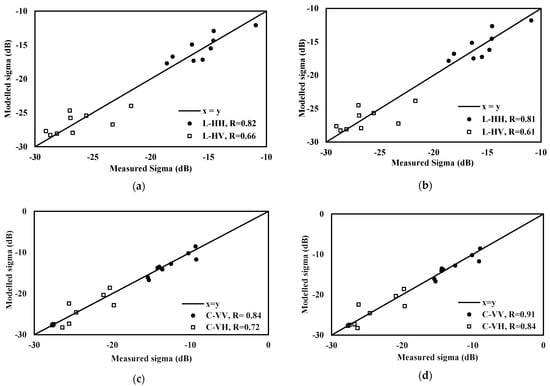
Figure 8.
Validation of the empirical backscattering models with multi-configuration real data: (a) L-HH and L-HV data with g(Mv, Hrms), (b) L-HH and L-HV data with h(Mv, Zs), (c) C-VV and C-VH data with g(Mv, Hrms), (d) C-VV and C-VH data with h(Mv, Zs).
4.3.2. Case of Vegetation-Covered Soil
In this section, we analyze simulations of L- and C-band radar signals over fields with vegetation cover. To represent the soil contribution to the total backscattering coefficients, we use the aforementioned results retrieved in Section 4.3.1. Referring to bare soil model outcomes, in Section 4.3.1., IEM-B (for L-HH and C-VV configurations) and the empirical model g(Mv, Hrms) (for all configurations, L-HH, L-HV, C-VV, C-VH), for which the results illustrate good consistency over bare soils, are considered for bare soil component modeling.
By considering these various models for soil backscattering, using WCM option 1 (without an interaction component) illustrated in equation 14 and NDVI as a vegetation descriptor, the calibration of the A and B coefficients is proposed by using 70% of the dataset and the least square method. Table 7 summarizes the retrieved A and B parameters for different options and the corresponding statistical parameters (RMSE and R) of the comparison between the calibrated models and the dataset used for calibration.

Table 7.
WCM option 1 parameters A and B calibration, with statistical precision coefficients for the case of two soil backscattering models, for ALOS-2 and Sentinel-1 data multi-polarizations.
The term B, related to the attenuation of the soil backscattered signal by the vegetation cover, is approximately at the same level for L-band configurations in the tested models. For L-HH and L-HV cases, with all proposed soil models, the B values ranged between 0.34 and 0.76 and 0.53 and 1.54 for the Sentinel-1 data in the C-VV and C-VH configurations, respectively.
Concerning the backscattering associated with the vegetation cover, the A parameter is certainly lower in the L-HV polarization than in L-HH, in agreement with the levels of the total L-HV signal compared to the L-HH signal. The same conclusions are observed for the C-VV and C-VH configurations. The A and B parameters retrieved with the S-1 data are close to those retrieved by Bousbih et al. (2017) over the same site with measurements realized in 2015–2016.
The use of the empirical model g(Mv, Hrms) for soil backscattering allows good agreement between the calibrated WCM model and the real data, with an RMSE lower than 1.7 dB for both the L-HH and L-HV configurations and reaching an RMSE maximum value of 1.4 dB for the C-VV and C-VH configurations. The IEM-B model applied to the co-polarizations also shows a reasonable performance with RMSE and R values equal to 2.0 dB and 0.72, respectively, for L-HH and 1.3 dB and 0.86 for the C-VV data.
In the second part of this section, we propose WCM calibration when the second option with soil–vegetation interaction is added, as described by equation (16). In this case, the total backscattering over cereal test fields is the sum of backscattering over bare soils attenuated by vegetation cover, the contribution of vegetation covers and, finally, the multiscattering component. With the added soil–vegetation interaction term in the WCM expression, three parameters (A, B and a newly added parameter, C, which also depends on vegetation properties) require calibration.
Table 8 illustrates the three calibrated parameters of A, B and C and the statistical coefficients (R and RMSE) when considering the two soil backscattering models (g(Mv, Hrms) and IEM-B). According to Table 8, RMSE values range from 1.6 to 2.4 dB in the L-HH configuration and equal 1.6 dB in L-HV for g(Mv, Hrms).

Table 8.
Calibration parameters and statistical precision coefficients with the second WCM option 2 in L-HH, L-HV, C-VV and C-VH.
For the L-HH case, the attenuated B parameter values range between 1.4 and 2.8. For the L-HV configuration, the B value is equal to 2.28 for the g soil model. The A parameter values (ranging between 0.023 and 0.052) in the L-HH configuration are higher than those retrieved with the L-HV case (equal to 0.004). The C parameter records values between 0.054 and 0.128 in the L-HH case and equal to 0.009 in the L-HV case.
In the C-band case, the A parameter values vary between 0.09 and 0.13 in the VV polarization and equal 0.025 for the VH polarization. The B parameter values are close to those found in the L-band, indicating large signal attenuation by vegetation [].
For the C-VV and C-VH configurations, the C values are weak, resigning the negligence of the soil–vegetation interaction contribution to the total backscattering coefficients. In the following section, we evaluate the soil moisture inversion capabilities using the two WCM options with calibrated parameters in multiple configurations.
4.4. Soil Moisture Estimation
In this section, we aim to use different validated backscattering models for soil moisture estimation. For this section, two methods of inversion were carried out on over 30% of the dataset. Knowing the backscattered radar signal (in the L-HH, C-VV, L-HV or C-VH configurations), the NDVI characterizing the vegetation cover and the soil roughness, we estimate the soil moisture through a direct inversion of the calibrated expressions in the case of semi-empirical models or through look-up tables for IEM-B. Both options of the WCM are tested (with and without the addition of the soil–vegetation interaction term). Table 9 focuses on statistical parameters by representing bias and RMSE values for different inversion configurations and dual-frequency data.

Table 9.
Inversion statistical precision coefficients in L-HH, L-HV, C-VV and C-VH configurations in the case of two options of the WCM.
Considering option 1 of the WCM model, we observe satisfactory results with estimated moisture accuracies between moderate and high for the L-HH configuration, with RMSEs between 4.9 and 6.4 vol.%, by considering IEM-B and g(Mv, Hrms) models, respectively.
The best estimates are made by the IEM-B model, with RMSE values ranging between 3.4 and 4.9 vol.% for C-VV and L-HH polarizations, respectively. With the semi-empirical approach for soil scattering, there is a degradation that could be explained by less precision in the simulation of roughness behavior, particularly for low-frequency data. In fact, the precision of the C-VV configuration is equal to 4.7 vol.% with the g soil model. On the other hand, a lower accuracy is retrieved for the L-HH configuration, with RMSEs equal to 6.4 vol.% for the g model.
The application of this WCM option in cross-polarization concerns only the g soil semi-empirical model. In this case, the results are strongly degraded compared to the results in C-VV and L-HH, with accuracies (RMSE) on the order of 13 vol.% for the ALOS-2 data and 7.1 vol.% for the Sentinel-1 data. These results are consistent with previous studies showing the poorer accuracy of moisture inversion using cross-polarization. They are also consistent with many studies showing the importance of taking into account the soil–vegetation interaction component in the simulation of canopy scattering for the case of a cross-polarization configuration.
The application of WCM option 2 illustrates performances relatively close to those retrieved for the WCM option 1 in the case of the L-HH configuration, with RMSEs relatively stable between 4.8 and 6.1 vol.% and also the same precision quality as the C-VV configuration. However, for the case of the L-HV configuration, the effect of taking into account the ground–vegetation interaction is very important. Indeed, this integration makes it possible to go from very degraded to moderate accuracies between 6 and 7 vol.%.
In contrast, the integration of the soil–vegetation component into the WCM model induces a limited improvement when retrieving soil moisture in the C-VH polarization and insists on the adequacy of simplified WCM use in the C-band frequency. This could be explained by the limited contribution of soil–vegetation interactions in the context of a limited wave penetration ability.
Figure 9 shows the inter-comparison between the in situ soil moisture and estimated values for the application of WCM option 2 with different types of soil scattering models at the L- and C-band frequencies. Each point corresponds to one tested field.
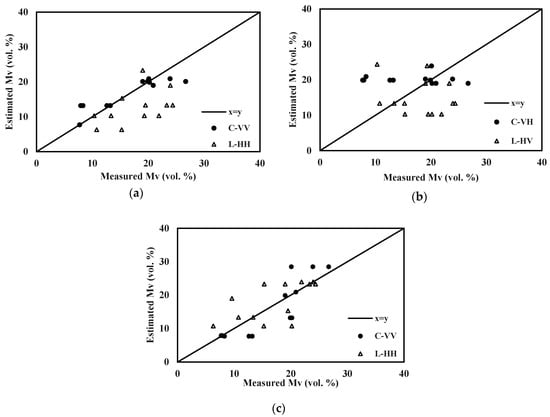
Figure 9.
Inter-comparison between ground measurements and estimated soil moisture values using different inversion approaches based on WCM option 2 (with interaction component contribution) (a) with g model, L-HH and C-VV, (b) with g model, L-HV and C-VH and (c) with IEM-B model, L-HH and C-VV.
This result highlights the importance of considering the soil–vegetation interaction component in the modeling of the radar signal, especially in the L-HV configuration. The best performance is illustrated with IEM-B coupled to WCM option 1 in the C-VV configuration, with an RMSE value of approximately 3.3 vol.%, and coupled to WCM option 2 in the L-HH configuration, with an RMSE of less than 5 vol.%.
The contribution of the L-band seems evident for dense covers; however, noise coming from vegetation volume scattering and a more important effect due to roughness could degrade the precision of soil moisture estimation. To analyze the benefits and limitations of the L-band compared to other frequency bands and particularly the C-band, it will be very useful in the future to analyze polarimetric measurements acquired in different frequency bands.
5. Conclusions
In the present study, we analyzed the potential of L- and C-band radar data for soil moisture estimation over cereal agricultural fields in the semiarid plain of Kairouan (central Tunisia).
Based on multi-incidence, multi-polarization and dual-frequency data, an analysis of the sensitivities of radar signals to soil parameters (roughness and moisture) and vegetation properties was proposed. For the L-band, multi-incidence (28°, 32.5° and 36°) dual-polarization (HH and HV) data are strongly influenced by soil roughness. According to the analyzed results under low-soil moisture conditions, statistical values show high correlations between radar signals and roughness parameters (Hrms and Zs). A range of approximately 10 dB in radar signals is observed for the roughness effect. For the same range of roughness parameters, S-1 radar data, acquired in the C-band, show a lower dynamic range, between 8 and 6 dB, for VV and VH polarizations, respectively. The sensitivity of the ALOS-2 signal to soil moisture decreases with vegetation development by 0.31 and 0.18 dB/vol.% (NDVI < 0.3) to 0.27 and 0.15 dB/vol.% for NDVI values between 0.3 and 0.6 and finally to 0.19 and 0.16 dB/vol.% (NDVI > 0.6) in HH and HV, respectively. The sensitivity of the Sentinel-1 signal to soil moisture decreases by 0.26 and 0.24 dB/vol.% in the bare soil class and low vegetation density to 0.17 and 0.08 dB/vol.% for the medium density vegetation class and finally to 0.07 and 0.09 dB/vol.% for the denser canopy class in VV and VH polarizations, respectively.
The observed results underline the L-band signal sensitivity to vegetation parameters (VWC, LAI and vegetation height). The highest correlations, equal to 0.87 and 0.78, for HH and HV polarizations, respectively, are observed with the VWC parameter. This could be particularly explained by the high penetration of L-band radar signals in vegetation covers.
The simulation of L- and C-band radar signals was discussed for bare and covered soils. For bare soils, two empirical models dependent on roughness (Hrms or Zs parameters) and soil moisture, the semi-empirical Dubois-B model and, finally, the IEM-B model were tested. The best simulations are found with the two empirical approaches calibrated in the available polarizations and the IEM-B model in only like-polarization. Validations with a set of real data different from those used for calibration illustrate, for example, an RMSE equal to 1.3 dB, 1.8dB, 1.1dB and 1.9dB for L-HH, L-HV, C-VV and C-VH for empirical model g(Mv, Hrms), respectively.
Concerning the surfaces with vegetation cover, two options were considered for the WCM: option 1 with two components in which the soil component is attenuated by the vegetation cover, and option 2, which includes the addition of the soil–vegetation interaction to the first two components.
After calibration of the two WCM options, the proposed models were tested to invert the radar signal and estimate the soil moisture.
Concerning the L-HH configuration, the use of option 1 enables an estimation with a high to moderate precision between 4.9 and 6.4 vol.% for the different types of considered soil scattering models. The L-HV configuration, on the other hand, shows very degraded results with this WCM first option. Regarding the C-VV configuration, the same WCM option grants soil moisture retrieval with RMSE values varying between 3.3 and 4.7 vol.% for different soil backscattering models facing approximately 7 vol.% C-VH polarization. The use of WCM option 2 maintains a relatively stable accuracy for the case of the L-HH configuration. It enables a clear improvement in the estimates in the L-HV data case with an RMSE between 6 and 7 vol.% for different types of soil backscattering models. According to the present results, consideration of the soil–vegetation interaction component seems essential for the exploitation of L-HH data in soil moisture estimation.
In the future, a simultaneous inversion approach for the two parameters roughness and moisture will be proposed, with the use of the artificial neural network (NN) technique to firstly derive the soil roughness (Hrms) from the L-HH data in order to then consider the derived Hrms and C-band data for soil moisture estimation. Moreover, this proposed estimate of soil moisture will be considered for irrigation mapping and detection over the studied site.
Author Contributions
E.A., M.Z., Z.K. and Z.L.-C. conceived and designed the experiments; E.A. and S.B. performed the experiments; E.A. and M.Z. analyzed the data; E.A., M.Z., Z.K., Z.L.-C. and N.B. contributed to the materials/analysis tools; E.A. and M.Z. wrote the paper. All authors have read and agreed to the published version of the manuscript.
Funding
This study was funded by the Viana (ERA-Net ARIMNet) Project; the PHC Utique IPASS Project; the Chaams (ERANET3-602 CHAAMS) Project; the Irrigation+ ((ESA n°4000129870/20/I-NB) Project; and the TAPAS TOSCA/CNES project.
Data Availability Statement
Data are available in Theia Land site https://www.theia-land.fr/ (accessed on 31 March 2021) and Environment Information System of CESBIO site http://osr-cesbio.ups-tlse.fr/portailsie/ (accessed on 31 March 2021).
Acknowledgments
We extend our warm thanks to the technical teams at the IRD and INAT (Institut National Agronomique de Tunisie) who participated in the ground truth measurement campaigns and data processing.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Koster, R.D.; Dirmeyer, P.A.; Guo, Z.; Bonan, G.; Chan, E.; Cox, P.; Gordon, C.T.; Kanae, S.; Kowalczyk, E.; Lawrence, D.; et al. Regions of Strong Coupling Between Soil Moisture and Precipitation. Science 2004, 305, 1138–1140. [Google Scholar] [CrossRef] [PubMed]
- Anguela, T.P.; Zribi, M.; Hasenauer, S.; Habets, F.; Loumagne, C. Analysis of surface and root-zone soil moisture dynamics with ERS scatterometer and the hydrometeorological model SAFRAN-ISBA-MODCOU at Grand Morin watershed (France). Hydrol. Earth Syst. Sci. 2008, 12, 1415–1424. [Google Scholar] [CrossRef]
- Saux-Picart, S.; Ottlé, C.; Decharme, B.; André, C.; Zribi, M.; Perrier, A.; Coudert, B.; Boulain, N.; Cappelaere, B.; Descroix, L.; et al. Water and energy budgets simulation over the AMMA-Niger super-site spatially constrained with remote sensing data. J. Hydrol. 2009, 375, 287–295. [Google Scholar] [CrossRef]
- Manfreda, S.; Scanlon, T.M.; Caylor, K.K. On the importance of accurate depiction of infiltration processes on modelled soil moisture and vegetation water stress. Ecohydrology 2009, 3, 155–165. [Google Scholar] [CrossRef]
- Massari, C.; Brocca, L.; Moramarco, T.; Tramblay, Y.; Lescot, J.F.D. Potential of soil moisture observations in flood modelling estimating initial conditions and correcting rainfall. Adv. Water Resour. 2014, 74, 44–53. [Google Scholar] [CrossRef]
- Habets, F.; Gascoin, S.; Korkmaz, S.; Thiéry, D.; Zribi, M.; Amraoui, N.; Carli, M.; Ducharne, A.; Leblois, E.; LeDoux, E.; et al. Multi-model comparison of a major flood in the groundwater-fed basin of the Somme River (France). Hydrol. Earth Syst. Sci. 2010, 14, 99–117. [Google Scholar] [CrossRef]
- Kerr, Y.H.; Waldteufel, P.; Wigneron, J.-P.; Delwart, S.; Cabot, F.; Boutin, J.; Escorihuela, M.-J.; Font, J.; Reul, N.; Gruhier, C.; et al. The SMOS Mission: New Tool for Monitoring Key Elements of the Global Water Cycle. Proc. IEEE 2010, 98, 666–687. [Google Scholar] [CrossRef]
- Entekhabi, D.; Njoku, E.G.; O’Neill, P.E.; Kellogg, K.H.; Crow, W.T.; Edelstein, W.N.; Entin, J.K.; Goodman, S.D.; Jackson, T.J.; Johnson, J.; et al. The Soil Moisture Active Passive (SMAP) Mission. Proc. IEEE 2010, 98, 704–716. [Google Scholar] [CrossRef]
- Wagner, W.; Lemoine, G.; Rott, H. A Method for Estimating Soil Moisture from ERS Scatterometer and Soil Data. Remote Sens. Environ. 1999, 70, 191–207. [Google Scholar] [CrossRef]
- Brocca, L.; Hasenauer, S.; Lacava, T.; Melone, F.; Moramarco, T.; Wagner, W.; Dorigo, W.; Matgen, P.; Martínez-Fernández, J.; Llorens, P.; et al. Soil moisture estimation through ASCAT and AMSR-E sensors: An intercomparison and validation study across Europe. Remote Sens. Environ. 2011, 115, 3390–3408. [Google Scholar] [CrossRef]
- Chen, K.; Yen, S.; Huang, W. A simple model for retrieving bare soil moisture from radar-scattering coefficients. Remote Sens. Environ. 1995, 54, 121–126. [Google Scholar] [CrossRef]
- McNairn, H.; Brisco, B. The application of C-band polarimetric SAR for agriculture: A review. Can. J. Remote Sens. 2004, 30, 525–542. [Google Scholar] [CrossRef]
- Srivastava, H.S.; Patel, P.; Sharma, Y.; Navalgund, R.R. Large-Area Soil Moisture Estimation Using Multi-Incidence-Angle RADARSAT-1 SAR Data. IEEE Trans. Geosci. Remote Sens. 2009, 47, 2528–2535. [Google Scholar] [CrossRef]
- Pierdicca, N.; Pulvirenti, L.; Bignami, C. Soil moisture estimation over vegetated terrains using multitemporal remote sensing data. Remote Sens. Environ. 2010, 114, 440–448. [Google Scholar] [CrossRef]
- Du, J.; Shi, J.; Sun, R. The development of HJ SAR soil moisture retrieval algorithm. Int. J. Remote Sens. 2010, 31, 3691–3705. [Google Scholar] [CrossRef]
- Balenzano, A.; Mattia, F.; Satalino, G.; Davidson, M.W.J. Dense Temporal Series of C- and L-band SAR Data for Soil Moisture Retrieval Over Agricultural Crops. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2011, 4, 439–450. [Google Scholar] [CrossRef]
- Santi, E.; Dabboor, M.; Pettinato, S.; Paloscia, S. Combining Machine Learning and Compact Polarimetry for Estimating Soil Moisture from C-Band SAR Data. Remote Sens. 2019, 11, 2451. [Google Scholar] [CrossRef]
- Gorrab, A.; Zribi, M.; Baghdadi, N.; Mougenot, B.; Lili-Chaabane, Z. Retrieval of both soil moisture and texture using TerraSAR-X images. Remote Sens. 2015, 7, 10098–10116. [Google Scholar] [CrossRef]
- Wang, H.; Magagi, R.; Goita, K.; Jagdhuber, T.; Hajnsek, I. Evaluation of Simplified Polarimetric Decomposition for Soil Moisture Retrieval over Vegetated Agricultural Fields. Remote Sens. 2016, 8, 142. [Google Scholar] [CrossRef]
- Wang, H.; Magagi, R.; Goita, K.; Jagdhuber, T. Refining a Polarimetric Decomposition of Multi-Angular UAVSAR Time Series for Soil Moisture Retrieval Over Low and High Vegetated Agricultural Fields. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 1431–1450. [Google Scholar] [CrossRef]
- Verhoest, N.E.C.; Lievens, H.; Wagner, W.; Alvarez-Mozos, J.; Moran, M.S.; Mattia, F. On the soil roughness parameterization problem in soil moisture retrieval of bare surfaces from Synthetic Aperture Radar. Sensors 2008, 8, 4213–4248. [Google Scholar] [CrossRef]
- Ma, C.; Li, X.; McCabe, M.F. Retrieval of High-Resolution Soil Moisture through Combination of Sentinel-1 and Sentinel-2 Data. Remote Sens. 2020, 12, 2303. [Google Scholar] [CrossRef]
- Shi, J.; Wang, J.; Hsu, A.Y.; O’Neill, P.E.; Engman, E.T. Estimation of bare surface soil moisture and surface roughness parameter using L-band SAR image data. IEEE Trans. Geosci. Remote Sens. 1997, 35, 1254–1266. [Google Scholar]
- El Hajj, M.; Baghdadi, N.; Zribi, M.; Rodríguez-Fernández, N.; Wigneron, J.P.; Al-Yaari, A.; Al Bitar, A.; Albergel, C.; Calvet, J.-C. Evaluation of SMOS, SMAP, ASCAT and Sentinel-1 Soil Moisture Products at Sites in Southwestern France. Remote Sens. 2018, 10, 569. [Google Scholar] [CrossRef]
- Mohanty, B.P.; Cosh, M.H.; Lakshmi, V.; Montzka, C. Soil Moisture Remote Sensing: State-of-the-Science. Vadose Zone J. 2017, 16, 1–9. [Google Scholar] [CrossRef]
- Zribi, M.; Dechambre, M. A new empirical model to retrieve soil moisture and roughness from C-band radar data. Remote Sens. Environ. 2003, 84, 42–52. [Google Scholar] [CrossRef]
- Bousbih, S.; Zribi, M.; Lili-Chabaane, Z.; Baghdadi, N.; El Hajj, M.; Gao, Q.; Mougenot, B. Potential of Sentinel-1 Radar Data for the Assessment of Soil and Cereal Cover Parameters. Sensors 2017, 17, 2617. [Google Scholar] [CrossRef] [PubMed]
- Dubois, P.; Van Zyl, J.; Engman, T. Measuring soil moisture with imaging radars. IEEE Trans. Geosci. Remote Sens. 1995, 33, 915–926. [Google Scholar] [CrossRef]
- Oh, Y.; Sarabandi, K.; Ulabz, F.T. An emprical model and an inversion technique for radar scattering from bare soil surfaces. IEEE Trans. Geosci. Remote Sens. 1992, 30, 370–381. [Google Scholar] [CrossRef]
- Ulaby, F.T.; Moore, R.K.; Fung, A.K. Microwave Remote Sensing: Active and Passive. 3-From Theory to Applications; Artech House: Norwood, MA, USA, 1986. [Google Scholar]
- Fung, A.; Li, Z.; Chen, K. Backscattering from a randomly rough dielectric surface. IEEE Trans. Geosci. Remote Sens. 1992, 30, 356–369. [Google Scholar] [CrossRef]
- Zribi, M.; Taconet, O.; Le Hégarat-Mascle, S.; Vidal-Madjar, D.; Emblanch, C.; Loumagne, C.; Normand, M. Backscattering behavior and simulation comparison over bare soils using SIR-C/X-SAR and ERASME 1994 data over Orgeval. Remote Sens. Environ. 1997, 59, 256–266. [Google Scholar] [CrossRef]
- Baghdadi, N.; Zribi, M. Evaluation of radar backscatter models IEM, OH and Dubois using experimental observations. Int. J. Remote Sens. 2006, 27, 3831–3852. [Google Scholar] [CrossRef]
- Baghdadi, N.; Saba, E.; Aubert, M.; Zribi, M.; Baup, F. Evaluation of Radar Backscattering Models IEM, Oh, and Dubois for SAR Data in X-Band Over Bare Soils. IEEE Geosci. Remote Sens. Lett. 2011, 8, 1160–1164. [Google Scholar] [CrossRef]
- Choker, M.; Baghdadi, N.; Zribi, M.; El Hajj, M.; Paloscia, S.; Verhoest, N.E.C.; Lievens, H.; Mattia, F. Evaluation of the Oh, Dubois and IEM Backscatter Models Using a Large Dataset of SAR Data and Experimental Soil Measurements. Water 2017, 9, 38. [Google Scholar] [CrossRef]
- Baghdadi, N.; Gherboudj, I.; Zribi, M.; Sahebi, M.; King, C.; Bonn, F. Semi-empirical calibration of the IEM backscattering model using radar images and moisture and roughness field measurements. Int. J. Remote Sens. 2004, 25, 3593–3623. [Google Scholar] [CrossRef]
- Baghdadi, N.; Zribi, M.; Paloscia, S.; Verhoest, N.E.C.; Lievens, H.; Baup, F.; Mattia, F. Semi-Empirical Calibration of the Integral Equation Model for Co-Polarized L-Band Backscattering. Remote Sens. 2015, 7, 13626–13640. [Google Scholar] [CrossRef]
- Karam, M.; Fung, A.; Antar, Y. Electromagnetic wave scattering from some vegetation samples. IEEE Trans. Geosci. Remote Sens. 1988, 26, 799–808. [Google Scholar] [CrossRef]
- Ulaby, F.; McDonald, K.; Sarabandi, K.; Dobson, M. Michigan Microwave Canopy Scattering Models (MIMICS). Int. J. Remote Sens. 1990, 11, 1223–1253. [Google Scholar] [CrossRef]
- Attema, E.P.W.; Ulaby, F.T. Vegetation modeled as a water cloud. Radio Sci. 1978, 13, 357–364. [Google Scholar] [CrossRef]
- Graham, A.J.; Harris, R. Extracting biophysical parameters from remotely sensed radar data: A review of the water cloud model. Prog. Phys. Geogr. Earth Environ. 2003, 27, 217–229. [Google Scholar] [CrossRef]
- Baghdadi, N.; El Hajj, M.; Zribi, M.; Bousbih, S. Calibration of the Water Cloud Model at C-Band for Winter Crop Fields and Grasslands. Remote Sens. 2017, 9, 969. [Google Scholar] [CrossRef]
- Weiß, T.; Ramsauer, T.; Löw, A.; Marzahn, P. Evaluation of Different Radiative Transfer Models for Microwave Backscatter Estimation of Wheat Fields. Remote Sens. 2020, 12, 3037. [Google Scholar] [CrossRef]
- Ouaadi, N.; Jarlan, L.; Ezzahar, J.; Zribi, M.; Khabba, S.; Bouras, E.; Bousbih, S.; Frison, P.-L. Monitoring of wheat crops using the backscattering coefficient and the interferometric coherence derived from Sentinel-1 in semi-arid areas. Remote Sens. Environ. 2020, 251, 112050. [Google Scholar] [CrossRef]
- Zribi, M.; Chahbi, A.; Shabou, M.; Lilichabaane, Z.; Duchemin, B.; Baghdadi, N.; Amri, R.; Chehbouni, A. Soil surface moisture estimation over a semi-arid region using ENVISAT ASAR radar data for soil evaporation evaluation. Hydrol. Earth Syst. Sci. 2011, 15, 345–358. [Google Scholar] [CrossRef]
- Fieuzal, R.; Baup, F.; Marais-Sicre, C. Monitoring wheat and rapeseed by using synchronous optical and radar satellite data—From temporal signatures to crop parameters estimation. Adv. Remote Sens. 2013, 2, 162–180. [Google Scholar] [CrossRef]
- Kim, S.B.; Moghaddam, M.; Tsang, L.; Burgin, M.; Xu, X.; Njoku, E.G. Models of L-band radar backscattering coefficients over global terrain for soil moisture retrieval. IEEE Trans. Geosci. Remote Sens. 2014, 52, 1381–1396. [Google Scholar] [CrossRef]
- Kim, S.B.; van Zyl, J.J.; Johnson, J.T.; Moghaddam, M.; Tsang, L.; Colliander, A.; Dunbar, R.S.; Jackson, T.J.; Jaruwatanadilok, S.; West, R.; et al. Surface Soil Moisture Retrieval Using the L-Band Synthetic Aperture Radar Onboard the Soil Moisture Active–Passive Satellite and Evaluation at Core Validation Sites. IEEE Trans. Geosci. Remote Sens. 2017, 55, 1897–1914. [Google Scholar] [CrossRef] [PubMed]
- Notarnicola, C.; Angiulli, M.; Posa, F. Soil moisture retrieval from remotely sensed data: Neural network approach versus Bayesian method. IEEE Trans. Geosci. Remote Sens. 2008, 46, 547–557. [Google Scholar] [CrossRef]
- Santi, E.; Paloscia, S.; Pettinato, S.; Fontanelli, G. Application of artificial neural networks for the soil moisture retrieval from active and passive microwave spaceborne sensors. Int. J. Appl. Earth Obs.Geoinf. 2016, 48, 61–73. [Google Scholar] [CrossRef]
- El Hajj, M.; Baghdadi, N.; Zribi, M.; Bazzi, H. Synergic use of Sentinel-1 and Sentinel-2 images for operational soil moisture mapping at high spatial resolution over agricultural areas. Remote Sens. 2017, 9, 1292. [Google Scholar] [CrossRef]
- Gao, Q.; Zribi, M.; Escorihuela, M.J.; Baghdadi, N. Synergetic Use of Sentinel-1 and Sentinel-2 Data for Soil Moisture Mapping at 100 m Resolution. Sensors 2017, 17, 1966. [Google Scholar] [CrossRef] [PubMed]
- Bauer-Marschallinger, B.; Freeman, V.; Cao, S.; Paulik, C.; Schaufler, S.; Stachl, T.; Modanesi, S.; Massari, C.; Ciabatta, L.; Brocca, L.; et al. Toward Global Soil Moisture Monitoring With Sentinel-1: Harnessing Assets and Overcoming Obstacles. IEEE Trans. Geosci. Remote Sens. 2018, 57, 520–539. [Google Scholar] [CrossRef]
- Foucras, M.; Zribi, M.; Albergel, C.; Baghdadi, N.; Calvet, J.-C.; Pellarin, T. Estimating 500-m Resolution Soil Moisture Using Sentinel-1 and Optical Data Synergy. Water 2020, 12, 866. [Google Scholar] [CrossRef]
- Bousbih, S.; Zribi, M.; El Hajj, M.; Baghdadi, N.; Lili-Chabaane, Z.; Gao, Q.; Fanise, P. Soil Moisture and Irrigation Mapping in A Semi-Arid Region, Based on the Synergetic Use of Sentinel-1 and Sentinel-2 Data. Remote Sens. 2018, 10, 1953. [Google Scholar] [CrossRef]
- Panciera, R.; Tanase, M.A.; Lowell, K.; Walker, J.P. Evaluation of IEM, Dubois, and Oh Radar Backscatter Models Using Airborne L-Band SAR. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4966–4979. [Google Scholar] [CrossRef]
- Dabrowska-Zielinska, K.; Inoue, Y.; Kowalik, W.; Gruszczynska, M. Inferring the effect of plant and soil variables on C- and L-band SAR backscatter over agricultural fields, based on model analysis. Adv. Space Res. 2007, 39, 139–148. [Google Scholar] [CrossRef]
- Jagdhuber, T.; Hajnsek, I.; Bronstert, A.; Papathanassiou, K.P. Soil Moisture Estimation under Low Vegetation Cover Using a Multi-Angular Polarimetric Decomposition. IEEE Trans. Geosci. Remote Sens. 2012, 51, 2201–2215. [Google Scholar] [CrossRef]
- El Hajj, M.; Baghdadi, N.; Bazzi, H.; Zribi, M. Penetration Analysis of SAR Signals in the C and L Bands for Wheat, Maize, and Grasslands. Remote Sens. 2018, 11, 31. [Google Scholar] [CrossRef]
- El Hajj, M.; Baghdadi, N.; Zribi, M. Comparative analysis of the accuracy of surface soil moisture estimation from the C- and L-bands. Int. J. Appl. Earth Obs.Geoinf. 2019, 82, 101888. [Google Scholar] [CrossRef]
- Zribi, M.; Muddu, S.; Bousbih, S.; Al Bitar, A.; Tomer, S.K.; Baghdadi, N.; Bandyopadhyay, S. Analysis of L-Band SAR Data for Soil Moisture Estimations over Agricultural Areas in the Tropics. Remote Sens. 2019, 11, 1122. [Google Scholar] [CrossRef]
- Sekertekin, A.; Marangoz, A.M.; Abdikan, S. ALOS-2 and Sentinel-1 SAR data sensitivity analysis to surface soil moisture over bare and vegetated agricultural fields. Comput. Electron. Agric. 2020, 171, 105303. [Google Scholar] [CrossRef]
- Amri, R.; Zribi, M.; Duchemin, B.; Lili-Chabaane, Z.; Gruhier, C.; Chebouni, A. Analysis of vegetation behaviour in a semi-arid region, using SPOT-VEGETATION NDVI data. Remote Sens. 2011, 3, 2568–2590. [Google Scholar] [CrossRef]
- Zribi, M.; Gorrab, A.; Baghdadi, N. A new soil roughness parameter for the modelling of radar backscattering over bare soil. Remote Sens. Environ. 2014, 152, 62–73. [Google Scholar] [CrossRef]
- Baghdadi, N.; Choker, M.; Zribi, M.; El Hajj, M.; Paloscia, S.; Verhoest, N.E.C.; Lievens, H.; Baup, F.; Mattia, F. A New Empirical Model for Radar Scattering from Bare Soil Surfaces. Remote Sens. 2016, 8, 920. [Google Scholar] [CrossRef]
- Wu, T.-D.; Chen, K.; Shi, J.; Fung, A. A transition model for the reflection coefficient in surface scattering. IEEE Trans. Geosci. Remote Sens. 2001, 39, 2040–2050. [Google Scholar] [CrossRef]
- El Hajj, M.; Baghdadi, N.; Zribi, M.; Belaud, G.; Cheviron, B.; Courault, D.; Charron, F. Soil moisture retrieval over irrigated grassland using X-band SAR data. Remote Sens. Environ. 2016, 176, 202–218. [Google Scholar] [CrossRef]
- Fontanelli, G.; Paloscia, S.; Zribi, M.; Chahbi, A. Sensitivity analysis of X-band SAR to wheat and barley leaf area index in the Merguellil Basin. Remote Sens. Lett. 2013, 4, 1107–1116. [Google Scholar] [CrossRef]
- El Hajj, M.; Baghdadi, N.; Belaud, G.; Zribi, M.; Cheviron, B.; Courault, D.; Hagolle, O.; Charron, F. Irrigated Grassland Monitoring Using a Time Series of TerraSAR-X and COSMO-SkyMed X-Band SAR Data. Remote Sens. 2014, 6, 10002–10032. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).