Strategies for the Development of Spectral Models for Soil Organic Matter Estimation
Abstract
1. Introduction
2. Materials and Methods
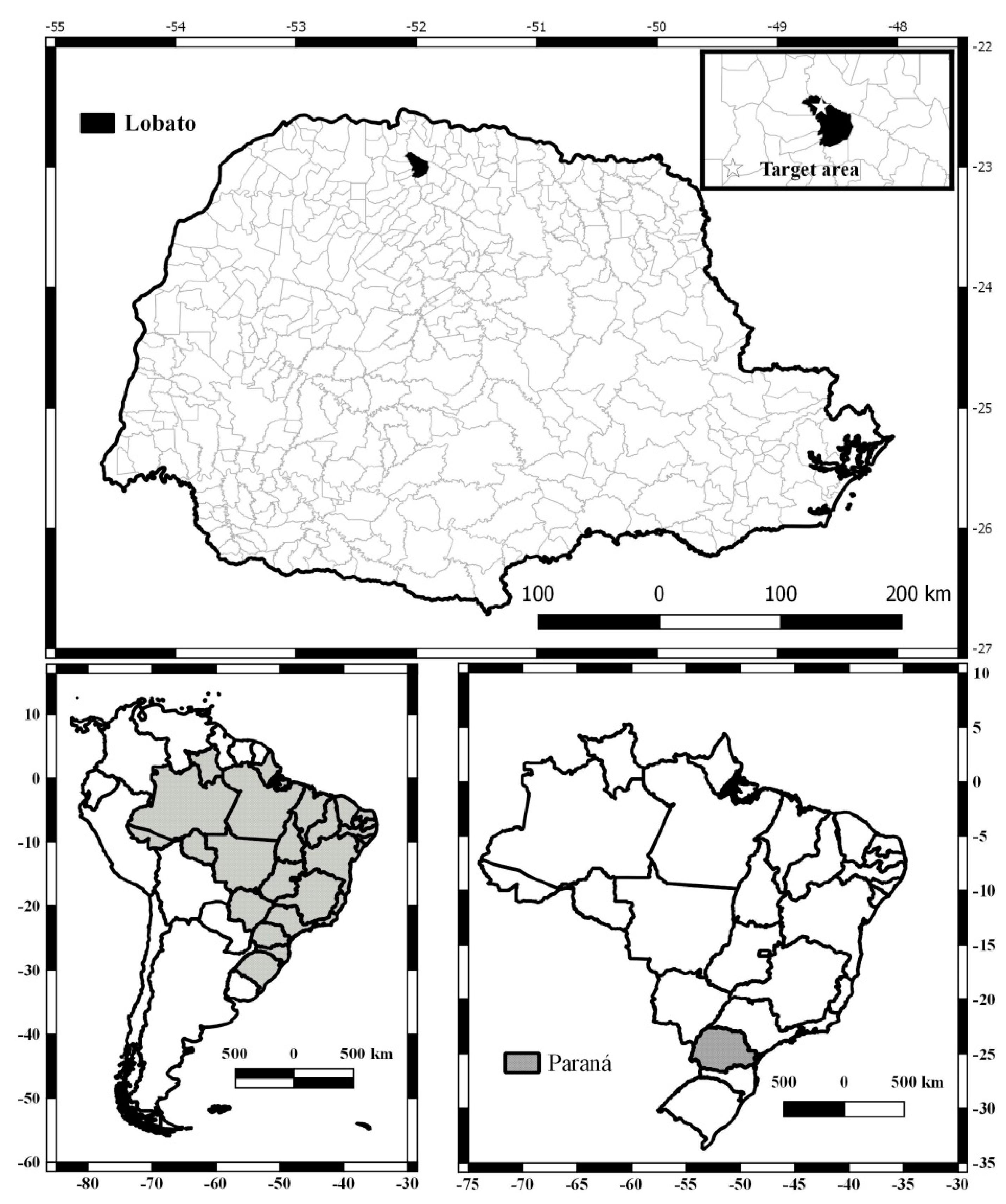
2.1. Soil Sampling
2.2. Organic Matter and Spectral Analyses
2.3. Data Processing and Statistical Analyses
2.4. State Model
Recalibrated State Model
3. Results and Discussions
3.1. Statistical Soil Sample Characterization
3.2. Spectral Soil Sample Characterization
3.3. Unspiked State Model
Calibration and Prediction
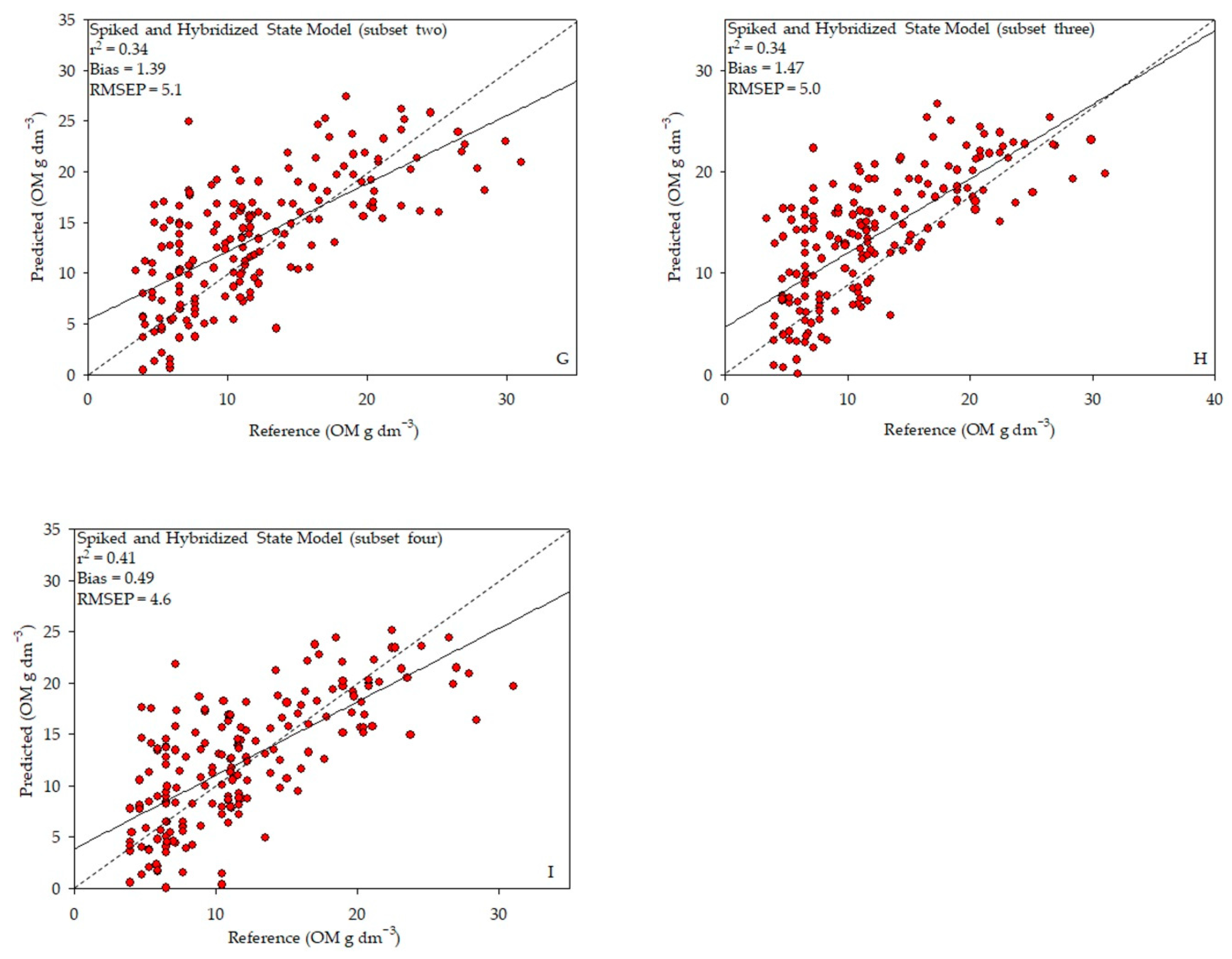
3.4. Spiked State Model/Spiked and Hybridized State Model
3.4.1. Recalibration
3.4.2. Prediction
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Viscarra Rossel, R.A.; Walvoort, D.J.J.; McBratney, A.B.; Janik, L.J.; Skjemstad, J.O. Visible, near infrared, mid infrared or combined diffuse reflectance spectroscopy for simultaneous assessment of various soil properties. Geoderma 2006, 131, 59–75. [Google Scholar] [CrossRef]
- Sousa Junior, J.G.; Demattê, J.A.M.; Araújo, S.R. Modelos espectrais terrestres e orbitais na determinação de teores de atributos dos solos: Potencial e custos. Bragantia 2011, 70, 610–621. [Google Scholar] [CrossRef]
- Sun, W.; Li, X.; Niu, B. Prediction of soil organic carbon in a coal mining area by VIS-NIR spectroscopy. PLoS ONE 2018, 13, e0196198. [Google Scholar] [CrossRef]
- Lazaar, A.; Mahyou, H.; Gholizadeh, A.; Elhammouti, K.; Bilal, M.; Andich, K.; Roger, J.M.; Monir, A.; Kouotou, D. Potential of VIS-NIR spectroscopy to characterize and discriminate topsoils of different soil types in the Triffa Plain (Morocco). Soil Sci. Annu. 2019, 70, 54–73. [Google Scholar] [CrossRef]
- Janik, L.J.; Merry, R.H.; Skjemstad, J.O. Can mid infra-red diffuse reflectance analysis replace soil extractions? Aust. J. Exp. Agric. 1998, 38, 681–696. [Google Scholar] [CrossRef]
- O’Rourke, S.M.; Holden, N.M. Optical sensing and chemometric analysis of soil organic carbon e a cost effective alternative to conventional laboratory methods? Soil Use Manag. 2011, 27, 143–155. [Google Scholar] [CrossRef]
- Islam, K.; Singh, B.; Mcbratney, A. Simultaneous estimation of several soil properties by ultraviolet, visible, and near-infrared reflectance spectroscopy. Aust. J. Soil Res. 2003, 41, 1101–1114. [Google Scholar] [CrossRef]
- Mcbratney, A.B.; Minasny, B.; Viscarra Rossel, R. Spectral soil analysis and inference systems: A powerful combination for solving the soil data crisis. Geoderma 2006, 136, 272–278. [Google Scholar] [CrossRef]
- Brown, D.J.; Bricklemyer, R.S.; Millar, P.R. Validation requirements for diffuse reflectance soil characterization models with a case study of VNIR soil C prediction in Montana. Geoderma 2005, 129, 251–267. [Google Scholar] [CrossRef]
- Viscarra Rossel, R.A.; Jeon, Y.S.; Odeh, I.O.A.; McBratney, A.B. Using a legacy soil sample to develop a mid-IR spectral library. Aust. J. Soil. Res. 2008, 46, 1–16. [Google Scholar] [CrossRef]
- Wetterlind, J.; Stenberg, B.; Söderström, M. Increased sample point density in farm soil mapping by local calibration of visible and near infrared prediction models. Geoderma 2010, 156, 152–160. [Google Scholar] [CrossRef]
- Sankey, J.B.; Brown, D.J.; Bernard, M.L.; Lawrence, R.L. Comparing local vs. global visible and near-infared (VisNIR) diffuse reflectance spectroscopy (DRS) calibrations for the prediction of soil clay, organic C and inorganic C. Geoderma 2008, 148, 149–158. [Google Scholar] [CrossRef]
- D’Acqui, L.P.; Pucci, A.; Janik, L.J. Soil properties of western Mediterranean islands with similar climatic environments by means of mid-infrared diffuse reflectance spectroscopy. Eur. J. Soil Sci. 2010, 61, 865–876. [Google Scholar] [CrossRef]
- Wetterlind, J.; Stenberg, B. Near-infrared spectroscopy for within-field soil characterization: Small local calibrations compared with national libraries spiked with local samples. Eur. J. Soil Sci. 2010, 61, 823–843. [Google Scholar] [CrossRef]
- Guerrero, C.; Stenberg, B.; Wetterlind, J.; Viscarra Rossel, R.A.; Maestre, F.T.; Mouazen, A.M.; Zornoza, R.; Ruiz Sinoga, J.D.; Kuang, B. Assessment of soil organic carbon at local scale with spiked NIR calibrations: Effects of selection and extra-weighting on the spiking subset. Eur. J. Soil Sci. 2014, 65, 248–263. [Google Scholar] [CrossRef]
- Guerrero, C.; Wetterlind, J.; Stenberg, B.; Mouazen, A.M.; Gabarrón-Galeote, M.A.; RuizSinoga, J.D.; Zornoza, R.; Viscarra Rossell, R.A. Do we really need large spectral libraries for local scale SOC assessment with NIR spectroscopy? Soil Tillage Res. 2016, 155, 501–509. [Google Scholar] [CrossRef]
- Hong, Y.; Chen, Y.; Zhang, Y.; Liu, Y.; Liu, Y.; Yu, L.; Liu, Y.; Cheng, H. Transferability of Vis-NIR models for Soil Organic Carbon Estimation between Two Study Areas by using Spiking. Soil Sci. Soc. Am. J. 2018, 82, 1231–1242. [Google Scholar] [CrossRef]
- Guy, A.L.; Siciliano, S.D.; Lamb, E.G. Spiking regional VIS-NIR calibration models with local samples to predict soil organic carbon in two High Arctic polar deserts using a vis-NIR probe. Can. J. Soil Sci. 2015, 95, 237–249. [Google Scholar] [CrossRef]
- Guerrero, C.; Zornoza, R. Extending the geographical validity of NIR models by spiking: Can hybrids spectra act as bridges between sets? A case study for soil organic carbon. Geophysical Research Abstracts; EGU General Assembly: Vienna, Austria, 2011. [Google Scholar]
- Hong, Y.; Chen, S.; Zhang, Y.; Chen, Y.; Yu, L.; Liu Yanfang Liu, Y.; Cheng, H.; Liy, Y. Rapid identification of soil organic matter level via visible and near-infrared spec-troscopy: Effects of two-dimensional correlation coefficient and extremelearning machine. Sci. Total Environ. 2018, 644, 1232–1243. [Google Scholar] [CrossRef]
- Memon, M.S.; Guo, J.; Tagar, A.A.; Perveen, N.; Ji, C.; Memon, S.A.; Memon, N. The effects of tillage and straw incorporation on soil organic carbon status, rice crop productivity, and sustainability in the rice-wheat cropping system of eastern China. Sustainability 2018, 10, 961. [Google Scholar] [CrossRef]
- Walkley, A.; Black, I.A. An examination of the Degtjareff method for determining soil organic matter, and proposed modification of the chromic acid titration method. Soil Sci. 1934, 37, 29–38. [Google Scholar] [CrossRef]
- Rosin, N.A.; Dalmolin, R.S.N.; Horst-Heinen, T.Z.; Moura-Bueno, J.M.; da Silva-Sangoi, D.V.; da Silva, L.S. Diffuse reflectance spectroscopy for estimating soil organic carbon and make nitrogen recommendations. Sci. Agric. 2020, 78, 1–13. [Google Scholar] [CrossRef]
- St Luce, M.; Ziadi, N.; Zebarth, B.J.; Grant, C.A.; Tremblay, G.F.; Gregorich, E.G. Rapid determination of soil organic matter quality indicators using visible near infrared reflectance spectroscopy. Geoderma 2014, 232–234, 449–458. [Google Scholar] [CrossRef]
- Empresa Brazileira de Pesquisa Agropecuária. Mapa de Solos Do Estado Do Paraná; Embrapa Solos: Rio de Janeiro, Brazil, 2007. [Google Scholar]
- Mineropar. Atlas Geológico Do Estado Do Paraná; Mineropar: Curitiba, Brazil, 2001; pp. 1–116. [Google Scholar]
- World Reference Base for Soil Resources. International Soil Classification System for Naming Soils and Creating Legends for Soil Maps, 3rd ed.; FAO: Rome, Italy, 2014; ISBN 978-92-5-108369-7. [Google Scholar]
- Empresa Brazileira de Pesquisa Agropecuária. Manual de Métodos E Análise de Solo, 2nd ed.; Revista e atualizada; Embrapa: Rio de Janeiro, Brazil, 1997; pp. 1–211. [Google Scholar]
- Epiphânio, J.C.N.; Formaggio, A.R.; Valeriano, M.D.M.; Oliveira, J.D. Comportamento Espectral de Solos Do Estado de São Paulo, 1st ed.; INPE: São José dos Campos, Brazil, 1992. [Google Scholar]
- Labsphere Reflectance Calibration Laboratory. Spectral Reflectance Target Calibrated from 0.25–2.5 nm Reported in 0.050 nm Intervals, 1st ed.; Labsphere Inc.: North Sutton, London, UK, 2009. [Google Scholar]
- Nanni, M.R.; Cezar, E.; Silva Junior, C.A.D.; Silva, G.F.C.; Gualberto, A.A.S. Partial least squares regression (PLSR) associated with spectral response to predict soil attributes in transitional lithologies. Arch. Agron. Soil Sci. 2017, 64, 682–695. [Google Scholar] [CrossRef]
- Nanni, M.R.; Demattê, J.A.M. Comportamento da linha do solo obtida por espectrorradiometria laboratorial para diferentes classes de solo. Rev. Bras. Ciênc. Do Solo 2006, 30, 1031–1038. [Google Scholar] [CrossRef]
- Lee, K.S.; Sudduth, K.A.; Drummond, T.S.; Lee, D.H.; Kitchen, N.R.; Chung, S.O. Calibration methods for soil property estimation using reflectance spectroscopy. ASABE 2010, 53, 675–684. [Google Scholar] [CrossRef]
- Buddenbaum, H.; Steffens, M. The effects of spectral pretreatments on chemometric analyses of soil profiles using laboratory imaging spectroscopy. Appl. Environ. Soil Sci. 2012, 2012, 1–12. [Google Scholar] [CrossRef]
- Savitzky, A.; Golay, M.J.E. Smoothing and differentiation of data by simplified least squares procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Cezar, E.; Nanni, M.R.; Guerrero, C.; da Silva Junior, C.A.; Cruciol, L.G.T.; Chicati, M.L.; Silva, G.F.C. Organic matter and sand estimates by spectroradiometry: Strategies for the development of models with applicability at a local scale. Geoderma 2019, 340, 224–233. [Google Scholar] [CrossRef]
- Wrege, M.S.; Steinmetz, S.; Reiser Júnior, C.; de Almeida, I.R. Atlas Climático da Região Sul do Brazil: Estados do Paraná, Santa Catarina e Rio Grande do Sul, 2nd ed.; Brasília: Embrapa, Brazil, 2012; pp. 1–331. [Google Scholar]
- Martínez, I.; Chervet, A.; Weisskopf, P.; Sturny, W.G.; Etana, A.; Stettler, M.; Forkman, J.; Keller, T. Two decades of no-till in the Oberacker long-term field experiment: Part I. Crop yield, soil organic carbon and nutrient distribution in the soil profile. Soil Till. Res. 2016, 163, 141–151. [Google Scholar] [CrossRef]
- Latz, K.; Weismiller, R.A.; Van Scoyoc, G.E.; Baumgardner, M.F. Characteristic variations in spectral reflectance of selected eroded Alfisols. Soil Sci. Soc. Am. J. 1984, 48, 1130–1134. [Google Scholar] [CrossRef]
- Bowers, S.A.; Hanks, R.J. Reflection of radiant energy from soils. Soil Sci. 1965, 100, 130–138. [Google Scholar] [CrossRef]
- Vitorrelo, I.; Galvão, L.S. Spectral properties of geologic materials in the 400 to 2500 nm range: Review for applications to mineral exploration and lithologic mapping. Phot. Int. 1996, 2, 77–96. [Google Scholar]
- Demattê, J.A.M.; Garcia, G.J. Alteration of soil properties through a weathering sequence as evaluated by spectral reflectance. Soil Sci. Soc. Amer. J. 1999, 63, 327. [Google Scholar] [CrossRef]
- Baumgardner, M.F.; Kristof, S.J.; Johannsen, C.J.; Zachary, A.L. Effects of organic matter on the multispectral properties of soils. Ind. Acad. Sci. 1969, 79, 413–422. [Google Scholar]
- Bilgili, A.V.; Van Es, H.M.; Akbas, F.; Durak, A.; Hively, W.D. Visible-near infrared reflectance spectroscopy for assessment of soil properties in a semi-arid area of Turkey. J. Arid Environ. 2010, 74, 229–238. [Google Scholar] [CrossRef]
- Viscarra Rossel, R.A.; Cattle, S.R.; Ortega, A.; Fouad, Y. In situ measurements of soil colour, mineral composition and clay content by vis–NIR spectroscopy. Geoderma 2009, 150, 253–266. [Google Scholar] [CrossRef]
- Guerrero, C.; Zornoza, R.; Gómez, I.; Mataix-Beneyto, J. Spiking of NIR regional models using simples from target sites: Effect of model size on prediction accuracy. Geoderma 2010, 158, 66–77. [Google Scholar] [CrossRef]
- Lazzareti, B.P.; Da Silva, L.S.; Drescher, G.L.; Dotto, A.C.; Nörnberg, D.B.J.L. Prediction of soil organic matter and clay contents by near-infrared spectroscopy—NIRS. Cienc. Rural 2020, 50, 1–8. [Google Scholar] [CrossRef]
- Lazaar, A.; Mouazen, A.M.; Hammouti, K.E.; Fullen, M.; Pradhan, B.; Memon, M.S.; Andich, K.; Monir, A. The application of proximal visible and near-infrared spectroscopy to estimate soil organic matter on the triffa plain of Morocco. Int. Soil Water Conse. Res. 2020, 8, 195–204. [Google Scholar] [CrossRef]
- Qiao, X.X.; Wang, C.; Feng, M.C.; Yang, W.D.; Ding, G.W.; Sun, H.; Liang, Z.Y.; Shi, C.C. Hyperspectral estimation of soil organic matter based on different spectral preprocessing techniques. Spectrosc. Lett. 2017, 50, 156–163. [Google Scholar] [CrossRef]
- Nawar, S.; Mouazen, A.M. Optimal sample selection for measurement of soil organic carbon using online Vis-NIR spectroscopy. Comput. Electron. Agric. 2018, 151, 469–477. [Google Scholar] [CrossRef]
- Kuang, B.; Mouazen, A.M. Influence of the number of samples on prediction error of visible and near infrared spectroscopy of selected soil properties at the farm scale. Eur. J. Soil Sci. 2012, 63, 421–429. [Google Scholar] [CrossRef]
- Nawar, S.; Mouazen, A.M. Predictive performance of mobile vis-near infrared spectroscopy for key soil properties at different geographical scales by using spiking and data mining techniques. Catena 2017, 151, 118–129. [Google Scholar] [CrossRef]
- Daniel, K.W.; Tripathi, N.K.; Honda, K. Artificial neural network analysis of laboratory and in situ spectra for the estimation of macronutrients in soils of Lop Buri (Thailand). Aust. J. Soil Res. 2003, 41, 47–59. [Google Scholar] [CrossRef]
- Wang, Y.; Lu, C.; Wang, L.; Song, L.; Wang, R.; Ge, Y. Prediction of Soil Organic Matter Content Using VIS/NIR Soil Sensor. Sens. Trans. J. 2014, 168, 113–119. [Google Scholar]
- Kuang, B.; Mouazen, A.M. Effect of spiking strategy and ratio on calibration of online visible and near infrared soil sensor for measurement in European farms. Soil Tillage Res. 2013, 128, 125–136. [Google Scholar] [CrossRef]
- Gogé, F.; Gomez, C.; Jolivet, C.; Jofre, R. Which strategy is best to predict soil properties of a local site from a national Vis–NIR database? Geoderma 2014, 213, 1–9. [Google Scholar] [CrossRef]





| Calibration | |||||||
| n | r2 (1) | RMSEC (2) | SEC (3) | BIAS (4) | R (5) | RPD (6) | Nº factors |
| 425 | 0.86 | 10.2 | 10.2 | 6.05 × 10−4 | 0.77 | 1.63 | 10 |
| Prediction | |||||||
| n | r2 | RMSEP (7) | SEP (8) | BIAS | R | RPD | Nº factors |
| 200 | 0.30 | 5.2 5.2 | 5.2 | −0.43 | 0.67 | 1.42 | 7 |
| Spiked State Model | |||||||
| Subset | r2 (1) | RMSEC (2) | SEC (3) | BIAS (4) | R (5) | RPD (6) | Nº factors |
| 1 | 0.87 | 9.8 | 9.8 | 6.91 × 10−4 | 0.80 | 1.68 | 14 |
| 2 | 0.87 | 9.7 | 9.7 | 2.18 × 10−4 | 0.79 | 1.66 | 14 |
| 3 | 0.86 | 9.9 | 9.9 | −3.25 × 10−4 | 0.78 | 1.65 | 14 |
| 4 | 0.88 | 9.6 | 9.6 | −3.58 × 10−5 | 0.80 | 1.72 | 14 |
| Spiked and Hybridizated State Model | |||||||
| Subset | r2 (1) | RMSEC (2) | SEC (3) | BIAS (4) | R (5) | RPD (6) | Nº factors |
| 1 | 0.87 | 9.9 | 9.9 | 2.40 × 10−3 | 0.79 | 1.66 | 14 |
| 2 | 0.88 | 9.6 | 9.7 | 9.46 × 10−5 | 0.80 | 1.68 | 14 |
| 3 | 0.87 | 9.8 | 9.8 | 4.75 × 10−4 | 0.78 | 1.66 | 11 |
| 4 | 0.87 | 9.7 | 9.7 | 2.41 × 10−4 | 0.79 | 1.65 | 11 |
| Spiked State Model | |||||||
| Subset | r2 (1) | RMSEP (2) | SEP (3) | BIAS (4) | R (5) | RPD (6) | Nº factors |
| 1 | 0.41 | 4.8 | 4.8 | 0.33 | 0.68 | 1.52 | 7 |
| 2 | 0.38 | 4.9 | 4.9 | −0.41 | 0.70 | 1.28 | 7 |
| 3 | 0.37 | 4.9 | 5.3 | 1.20 | 0.68 | 1.37 | 7 |
| 4 | 0.43 | 4.4 | 4.7 | 0.94 | 0.76 | 1.36 | 6 |
| Spiked and Hybridized State Model | |||||||
| Subset | r2 (1) | RMSEP (2) | SEP (3) | BIAS (4) | R (5) | RPD (6) | Nº factors |
| 1 | 0.32 | 6.2 | 6.7 | 1.37 | 0.62 | 1.22 | 10 |
| 2 | 0.34 | 5.1 | 5.6 | 1.39 | 0.69 | 1.21 | 7 |
| 3 | 0.34 | 5.0 | 5.6 | 1.47 | 0.71 | 1.23 | 6 |
| 4 | 0.41 | 4.6 | 4.7 | 0.49 | 0.71 | 1.55 | 7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cezar, E.; Nanni, M.R.; Crusiol, L.G.T.; Sun, L.; Chicati, M.S.; Furlanetto, R.H.; Rodrigues, M.; Sibaldelli, R.N.R.; Silva, G.F.C.; Oliveira, K.M.d.; et al. Strategies for the Development of Spectral Models for Soil Organic Matter Estimation. Remote Sens. 2021, 13, 1376. https://doi.org/10.3390/rs13071376
Cezar E, Nanni MR, Crusiol LGT, Sun L, Chicati MS, Furlanetto RH, Rodrigues M, Sibaldelli RNR, Silva GFC, Oliveira KMd, et al. Strategies for the Development of Spectral Models for Soil Organic Matter Estimation. Remote Sensing. 2021; 13(7):1376. https://doi.org/10.3390/rs13071376
Chicago/Turabian StyleCezar, Everson, Marcos Rafael Nanni, Luís Guilherme Teixeira Crusiol, Liang Sun, Mônica Sacioto Chicati, Renato Herrig Furlanetto, Marlon Rodrigues, Rubson Natal Ribeiro Sibaldelli, Guilherme Fernando Capristo Silva, Karym Mayara de Oliveira, and et al. 2021. "Strategies for the Development of Spectral Models for Soil Organic Matter Estimation" Remote Sensing 13, no. 7: 1376. https://doi.org/10.3390/rs13071376
APA StyleCezar, E., Nanni, M. R., Crusiol, L. G. T., Sun, L., Chicati, M. S., Furlanetto, R. H., Rodrigues, M., Sibaldelli, R. N. R., Silva, G. F. C., Oliveira, K. M. d., & Demattê, J. A. M. (2021). Strategies for the Development of Spectral Models for Soil Organic Matter Estimation. Remote Sensing, 13(7), 1376. https://doi.org/10.3390/rs13071376









