High Spatial and Temporal Resolution Energy Flux Mapping of Different Land Covers Using an Off-the-Shelf Unmanned Aerial System
Abstract
1. Introduction
2. Materials and Methods
2.1. Methodological Overview
2.2. Eddy Covariance Reference Datasets
2.2.1. Eddy Covariance Station Sites
2.2.2. EC Station data and Footprint Delineation
2.3. EC Station Energy Balance Closure
- No correction
- Increased H and LE to close the energy balance, but maintain the Bowen Ratio (H/LE)
- Added the residual imbalance flux to H, and used uncorrected LE
- Added the residual imbalance flux to LE, and used uncorrected H
2.4. Unmanned Aerial System
2.4.1. Unmanned Aerial Vehicle
2.4.2. Sensors
2.4.3. Surveys and Flight Parameters
2.4.4. Orthomosaic and Point Cloud Production
2.5. Spatially Distributed Energy Fluxes
2.5.1. Two Source Energy Balance Model
2.5.2. Overview of Inputs
2.5.3. Radiometric Surface Temperature
2.5.4. Canopy Height Model (CHM)
2.5.5. Land Cover Map (LCM) and Vegetation Masks
2.5.6. Leaf Area Index (LAI)
2.5.7. Green Fraction
2.6. EC Station-UAS Flux Comparisons
3. Results and Discussion
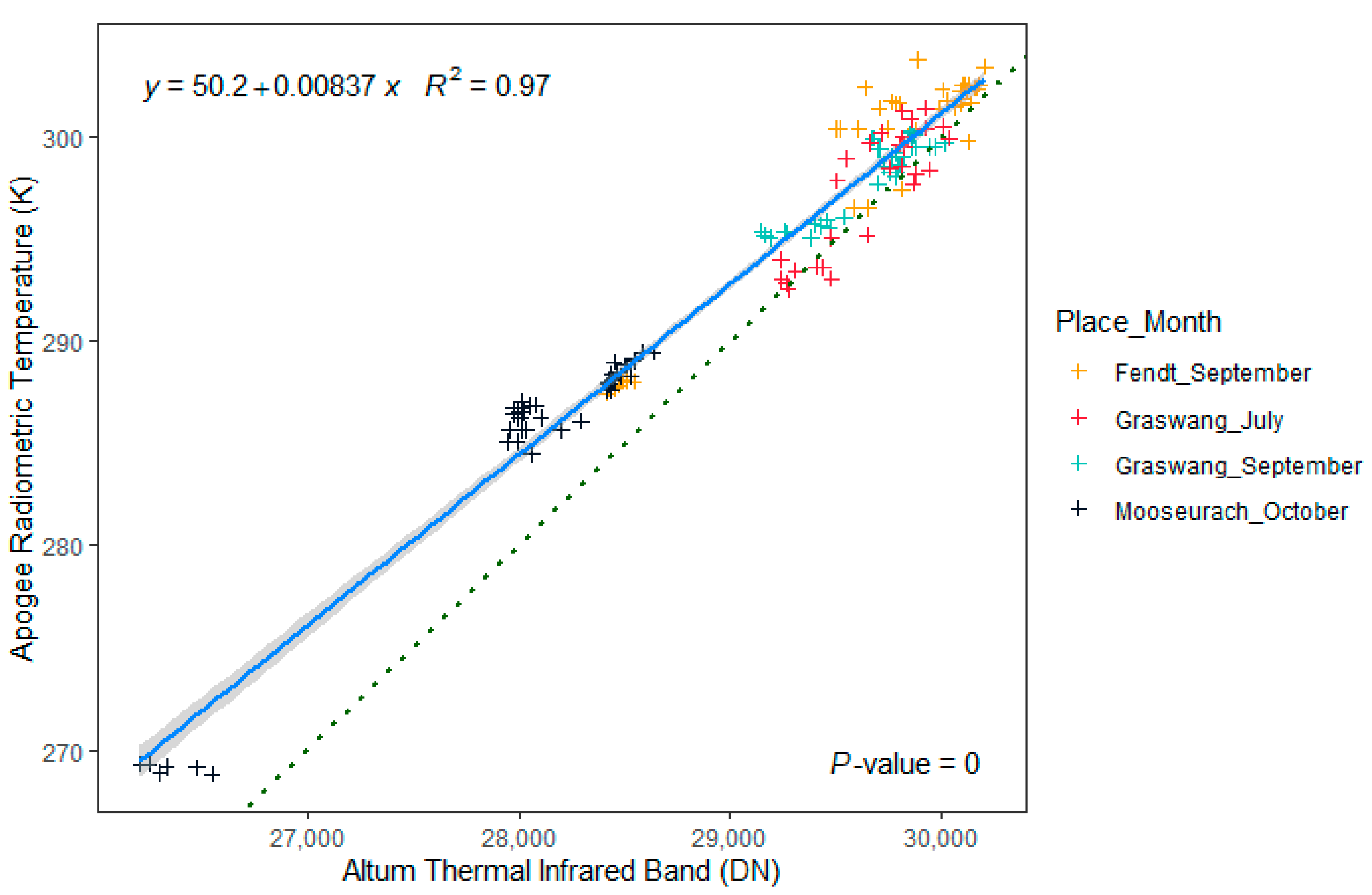
3.1. Conversion Factor for Altum Thermal Infrared Band
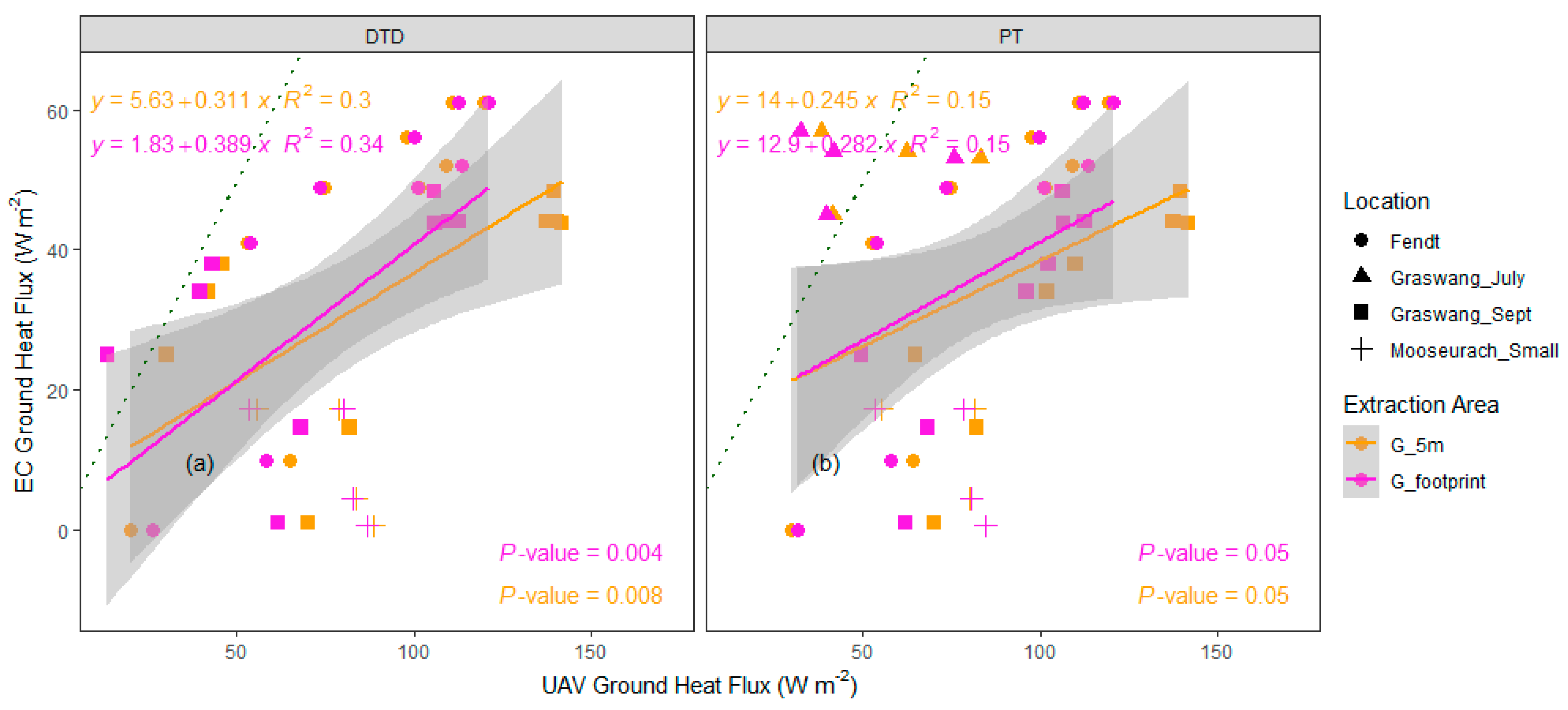
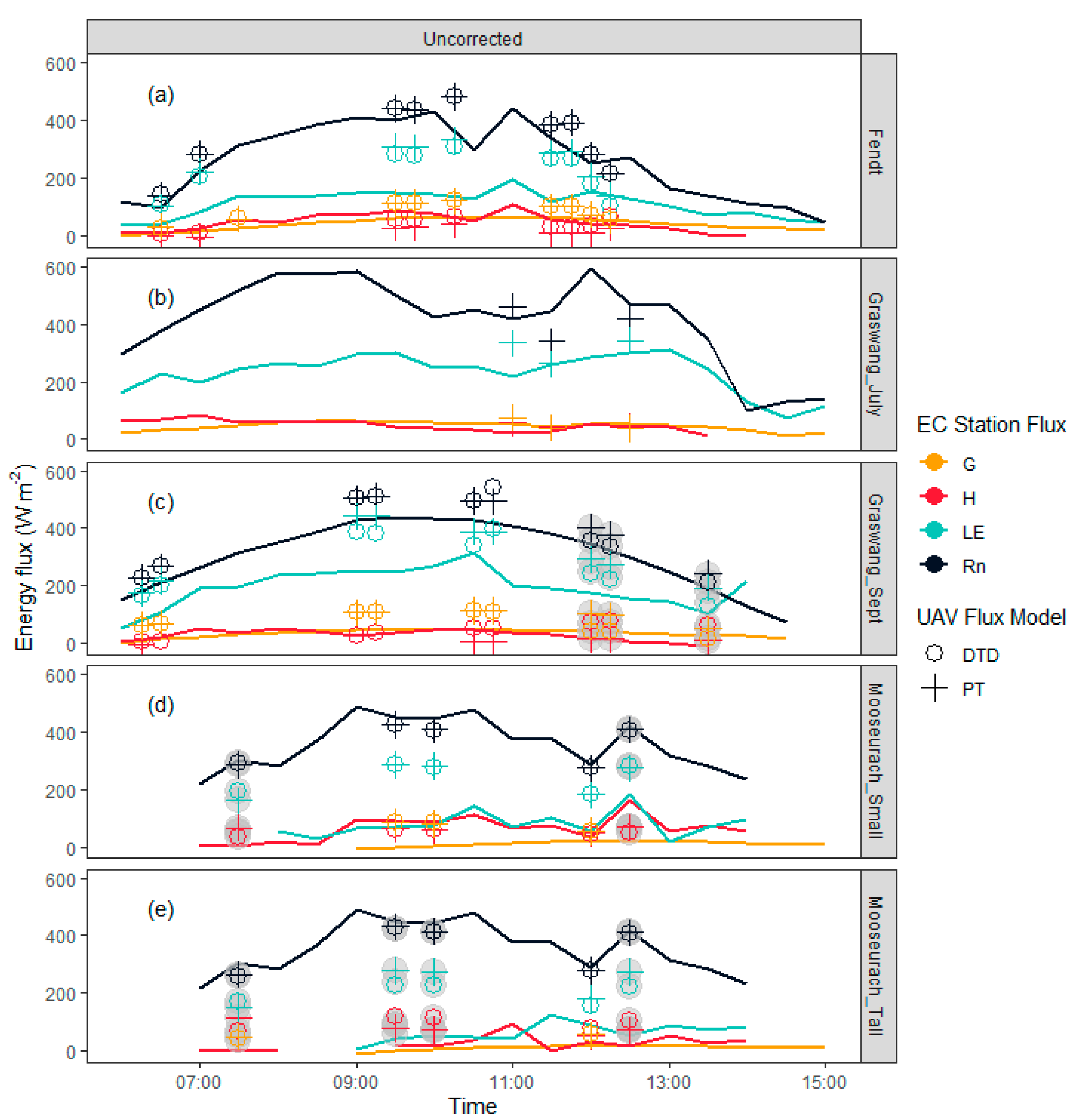
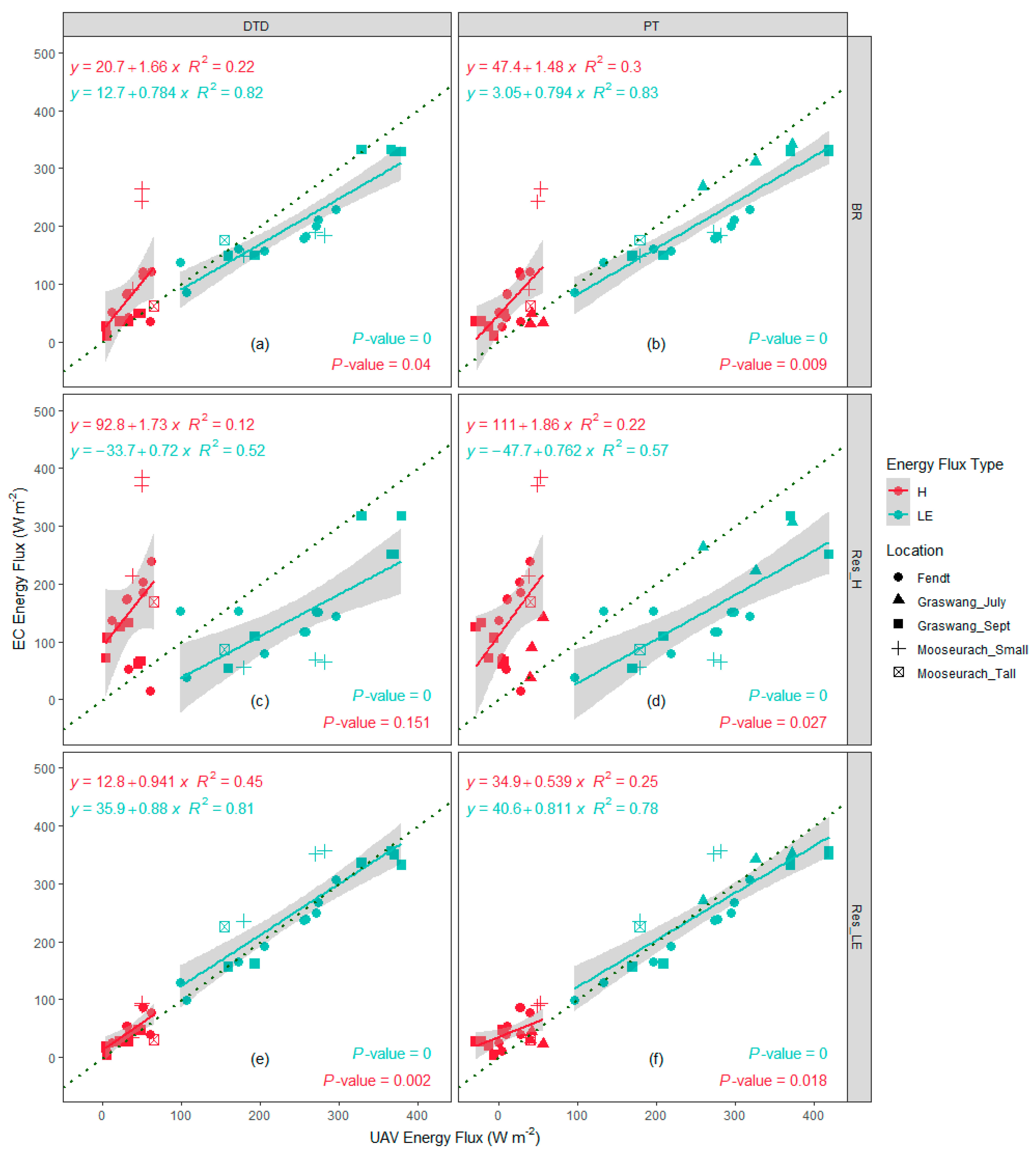
3.2. UAS vs. EC Station Flux Estimates
- adding imbalance residuals (Imb) to H (Res_H) and using uncorrected LE;
- adding imbalance residuals (Imb) to LE (Res_LE) and using uncorrected H;
- by maintaining the Bowen Ratio (BR);
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A



| Flux | Model | RMSE | Mean Bias | Standard Deviation |
|---|---|---|---|---|
| (W m−2) | ||||
| Rn | DTD | 64.6 | 51.2 | 40.6 |
| H | 28.9 | 4.4 | 29.3 | |
| LE | 119.4 | 97.3 | 71.2 | |
| G | 64.6 | 61.9 | 19.2 | |
| Rn | PT | 56.1 | 44.5 | 35.1 |
| H | 50.2 | −41.5 | 28.9 | |
| LE | 150.0 | 134.3 | 35.1 | |
| G | 60.5 | 54.0 | 27.9 | |
| Flux | EC Correction Type | Model | RMSE | Combined RMSE | Mean Bias | Standard Deviation |
|---|---|---|---|---|---|---|
| (W m−2) | ||||||
| H | BR | DTD | 73.2 | 73.6 | −31.2 | 68.1 |
| LE | 74.1 | −63.8 | 39.1 | |||
| H | BR | PT | 94.6 | 90.0 | −71.9 | 62.9 |
| LE | 85.1 | 74.3 | 42.6 | |||
| H | Res_H | DTD | 145.3 | 133.0 | −108.0 | 100 |
| LE | 119.4 | 97.3 | 71.2 | |||
| H | Res_H | PT | 170.7 | 160.7 | −144.0 | 92.8 |
| LE | 150.0 | 134.3 | 68.5 | |||
| H | Res_LE | DTD | 28.9 | 39.4 | 4.4 | 29.3 |
| LE | 47.7 | −15.2 | 46.5 | |||
| H | Res_LE | PT | 50.2 | 50.9 | −41.5 | 28.9 |
| LE | 51.5 | 31.7 | 41.5 | |||

References
- Duveiller, G.; Hooker, J.; Cescatti, A. The mark of vegetation change on Earth’s surface energy balance. Nat. Commun. 2018, 9, 1–12. [Google Scholar] [CrossRef]
- Lawrence, P.J.; Chase, T.N. Investigating the climate impacts of global land cover change in the community climate system model. Int. J. Climatol. 2010, 30, 2066–2087. [Google Scholar] [CrossRef]
- Shukla, J.; Mintz, Y.; Guo, Z.; Bonan, G.; Chan, E.; Cox, P.; Gordon, C.T.; Kanae, S.; Kowalczyk, E.; Lawrence, D.; et al. Influence of Land-Surface Evapotranspiration on the Earth’s Climate. Science 1982, 215, 1498–1501. [Google Scholar] [CrossRef] [PubMed]
- Bonan, G.B. Forests and Climate Change: Forcings, Feedbacks, and the Climate Benefits of Forests. Science 2008, 320, 1444–1449. [Google Scholar] [CrossRef] [PubMed]
- Perugini, L.; Caporaso, L.; Marconi, S.; Cescatti, A.; Quesada, B.; de Noblet-Ducoudré, N.; House, J.I.; Arneth, A. Biophysical effects on temperature and precipitation due to land cover change. Environ. Res. Lett. 2017, 12, 053002. [Google Scholar] [CrossRef]
- Spracklen, D.V.; Baker, J.C.A.; Garcia-Carreras, L.; Marsham, J.H. The Effects of Tropical Vegetation on Rainfall. Annu. Rev. Environ. Resour. 2018, 43, 193–218. [Google Scholar] [CrossRef]
- Norman, J.M.; Kustas, W.P.; Humes, K.S. Source approach for estimating soil and vegetation energy fluxes in observations of directional radiometric surface temperature. Agric. For. Meteorol. 1995, 77, 263–293. [Google Scholar] [CrossRef]
- Quattrochi, D.A.; Luvall, J.C. Thermal infrared remote sensing for analysis of landscape ecological processes: Methods and applications. Landsc. Ecol. 1999, 14, 577–598. [Google Scholar] [CrossRef]
- Lin, B.B. Agroforestry management as an adaptive strategy against potential microclimate extremes in coffee agriculture. Agric. For. Meteorol. 2007, 144, 85–94. [Google Scholar] [CrossRef]
- Lawrence, D.; Vandecar, K. Effects of tropical deforestation on climate and agriculture. Nat. Clim. Chang. 2015, 5, 27–36. [Google Scholar] [CrossRef]
- Liang, S.; Wang, J. Advanced Remote Sensing: Terrestrial Information Extraction and Applications; Elsevier: Amsterdam, The Netherlands, 2019; ISBN 9780128158265. [Google Scholar]
- Kiese, R.; Fersch, B.; Baessler, C.; Brosy, C.; Butterbach-Bahl, K.; Chwala, C.; Dannenmann, M.; Fu, J.; Gasche, R.; Grote, R.; et al. The TERENO pre-alpine observatory: Integrating meteorological, hydrological, and biogeochemical measurements and modeling. Vadose Zone J. 2018, 17, 1–17. [Google Scholar] [CrossRef]
- Rebmann, C.; Aubinet, M.; Schmid, H.; Arriga, N.; Aurela, M.; Burba, G.; Clement, R.; De Ligne, A.; Fratini, G.; Gielen, B.; et al. ICOS eddy covariance flux-station site setup: A review. Int. Agrophysics 2018, 32, 471–494. [Google Scholar] [CrossRef]
- Allen, R.G.; Tasumi, M.; Morse, A.; Trezza, R.; Wright, J.L.; Bastiaanssen, W.; Kramber, W.; Lorite, I.; Robison, C.W. Satellite-Based Energy Balance for Mapping Evapotranspiration with Internalized Calibration (METRIC)—Applications. J. Irrig. Drain. Eng. 2007, 133, 395–406. [Google Scholar] [CrossRef]
- Reis, T.G.; Monteiro, R.O.C.; Albuquerque, M.G.; Espinoza, J.M.A.; Ferreira, J.A.C.; Moreria, E.G. Actual Evapotranspiration Estimated By Orbital Sensors, Uav and Meteorological Station for Vineyards in the Southern Brazil. In Proceedings of the IV Inovagri International Meeting, Fortaleza, Brazil, 2–6 October 2017. [Google Scholar]
- Hoffmann, H.; Nieto, H.; Jensen, R.; Guzinski, R.; Zarco-Tejada, P.; Friborg, T. Estimating evaporation with thermal UAV data and two-source energy balance models. Hydrol. Earth Syst. Sci. 2016, 20, 697–713. [Google Scholar] [CrossRef]
- Guzinski, R.; Nieto, H.; Jensen, R.; Mendiguren, G. Remotely sensed land-surface energy fluxes at sub-field scale in heterogeneous agricultural landscape and coniferous plantation. Biogeosciences 2014, 11, 5021–5046. [Google Scholar] [CrossRef]
- Nieto, H.; Kustas, W.P.; Torres-rúa, A.; Alfieri, J.G.; Gao, F.; Anderson, M.C.; Alex, W.; Song, L. Evaluation of TSEB turbulent fluxes using different methods for the retrieval of soil and canopy component temperatures from UAV thermal and multispectral imagery. Irrig. Sci. 2019, 37, 389–406. [Google Scholar] [CrossRef]
- Brenner, C.; Zeeman, M.; Bernhardt, M.; Schulz, K. Estimation of evapotranspiration of temperate grassland based on high-resolution thermal and visible range imagery from unmanned aerial systems. Int. J. Remote Sens. 2018, 39, 5141–5174. [Google Scholar] [CrossRef]
- Brenner, C.; Thiem, C.E.; Wizemann, H.-D.; Bernhardt, M.; Schulz, K. Estimating spatially distributed turbulent heat fluxes from high-resolution thermal imagery acquired with a UAV system. Int. J. Remote Sens. 2017, 38, 3003–3026. [Google Scholar] [CrossRef]
- Niu, H.; Zhao, T.; Wang, D.; Chen, Y. Evapotranspiration Estimation with UAVs in Agriculture: A Review. Preprints 2019. [Google Scholar] [CrossRef]
- Andreu, A.; Dube, T.; Nieto, H.; Mudau, A.E.; González-Dugo, M.P.; Guzinski, R.; Hülsmann, S. Remote sensing of water use and water stress in the African savanna ecosystem at local scale – Development and validation of a monitoring tool. Phys. Chem. Earth 2019. [Google Scholar] [CrossRef]
- Burchard-Levine, V.; Nieto, H.; Riaño, D.; Migliavacca, M.; El-Madany, T.S.; Perez-Priego, O.; Carrara, A.; Martín, M.P. Seasonal adaptation of the thermal-based two-source energy balance model for estimating evapotranspiration in a semiarid tree-grass ecosystem. Remote Sens. 2020, 12, 904. [Google Scholar] [CrossRef]
- Xia, T.; Kustas, W.P.; Anderson, M.C.; Alfieri, J.G.; Gao, F.; McKee, L.; Prueger, J.H.; Geli, H.M.E.; Neale, C.M.U.; Sanchez, L.; et al. Mapping evapotranspiration with high-resolution aircraft imagery over vineyards using one-and two-source modeling schemes. Hydrol. Earth Syst. Sci. 2016, 20. [Google Scholar] [CrossRef]
- Alhassan, A.; Jin, M. Evapotranspiration in the Tono Reservoir Catchment in Upper East Region of Ghana Estimated by a Novel TSEB Approach from ASTER Imagery. Remote Sens. 2020, 12, 569. [Google Scholar] [CrossRef]
- Chávez, J.L.; Gowda, P.H.; Howell, T.A.; Neale, C.M.U.; Copeland, K.S. Estimating hourly crop ET using a two-source energy balance model and multispectral airborne imagery. Irrig. Sci. 2009, 28, 79–91. [Google Scholar] [CrossRef]
- Kafle, H.K.; Yamaguchi, Y. Effects of topography on the spatial distribution of evapotranspiration over a complex terrain using two-source energy balance model with ASTER data. Hydrol. Process. 2009, 23, 2295–2306. [Google Scholar] [CrossRef]
- Torres-Rua, A. Vicarious Calibration of sUAS Microbolometer Temperature Imagery for Estimation of Radiometric Land Surface Temperature. Sensors 2017, 17, 1499. [Google Scholar] [CrossRef] [PubMed]
- Weslien, P.; Klemedtsson, L.; Eklundh, L.; Kelly, J.; Kljun, N.; Olsson, P.O.; Mihai, L.; Liljeblad, B.; Weslien, P.; Klemedtsson, L.; et al. Challenges and best practices for deriving temperature data from an uncalibrated UAV thermal infrared camera. Remote Sens. 2019, 11, 567. [Google Scholar] [CrossRef]
- Sagan, V.; Maimaitijiang, M.; Sidike, P.; Eblimit, K.; Peterson, K.; Hartling, S.; Esposito, F.; Khanal, K.; Newcomb, M.; Pauli, D.; et al. UAV-Based High Resolution Thermal Imaging for Vegetation Monitoring, and Plant Phenotyping Using ICI 8640 P, FLIR Vue Pro R 640, and thermoMap Cameras. Remote Sens. 2019, 11, 330. [Google Scholar] [CrossRef]
- Guzinski, R.; Nieto, H.; Sandholt, I.; Karamitilios, G. Modelling high-resolution actual evapotranspiration through Sentinel-2 and Sentinel-3 data fusion. Remote Sens. 2020, 12, 1433. [Google Scholar] [CrossRef]
- He, R.; Jin, Y.; Kandelous, M.M.; Zaccaria, D.; Sanden, B.L.; Snyder, R.L.; Jiang, J.; Hopmans, J.W. Evapotranspiration estimate over an almond orchard using Landsat satellite observations. Remote Sens. 2017, 9, 436. [Google Scholar] [CrossRef]
- Alfieri, J.G.; Kustas, W.P.; Nieto, H.; Prueger, J.H.; Hipps, L.E.; McKee, L.G.; Gao, F.; Los, S. Influence of wind direction on the surface roughness of vineyards. Irrig. Sci. 2019, 37, 359–373. [Google Scholar] [CrossRef]
- Kormann, R.; Meixner, F.X. An analytical footprint model for non-neutral stratification. Boundary-Layer Meteorol. 2001, 99, 207–224. [Google Scholar] [CrossRef]
- Mauder, M.; Foken, T.; Cuxart, J. Surface-Energy-Balance Closure over Land: A Review. Boundary-Layer Meteorol. 2020, 177, 395–426. [Google Scholar] [CrossRef]
- Morillas, L.; García, M.; Nieto, H.; Villagarcia, L.; Sandholt, I.; Gonzalez-Dugo, M.P.; Zarco-Tejada, P.J.; Domingo, F. Using radiometric surface temperature for surface energy flux estimation in Mediterranean drylands from a two-source perspective. Remote Sens. Environ. 2013, 136, 234–246. [Google Scholar] [CrossRef]
- Tilahun, T. High-Resolution Mapping of Subsurface Tile Drainage in Agricultural Fields Using an Unmanned Aerial System (UAS). Univ. Res. Symp. 2019. [Google Scholar] [CrossRef]
- Hutton, J.J.; Lipa, G.; Baustian, D.; Sulik, J.; Bruce, R.W. High Accuracy Direct Georeferencing of the Altum Multispectral UAV Camera and its Application to High Throughput Plant Phenotyping. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2020. [Google Scholar] [CrossRef]
- Honkavaara, E.; Näsi, R.; Oliveira, R.; Viljanen, N.; Suomalainen, J.; Khoramshahi, E.; Hakala, T.; Nevalainen, O.; Markelin, L.; Vuorinen, M.; et al. Using multitemporal hyper-and multispectral UAV imaging for detecting bark beetle infestation on norway spruce. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, 43, 429–434. [Google Scholar] [CrossRef]
- Miller, I.J.; Schieber, B.; De Bey, Z.; Benner, E.; Ortiz, J.D.; Girdner, J.; Patel, P.; Coradazzi, D.G.; Henriques, J.; Forsyth, J. Analyzing crop health in vineyards through a multispectral imaging and drone system. In Proceedings of the 2020 Systems and Information Engineering Design Symposium, SIEDS, Charlottesville, VA, USA, 24–24 April 2020. [Google Scholar]
- ICOS-Deutschland ICOS: Graswang (C3). Available online: https://www.icos-infrastruktur.de/en/icos-d/komponenten/oekosysteme/beobachtungsstandorte/graswang-c3/ (accessed on 18 January 2021).
- ICOS-Deutschland ICOS: Fendt (C1). Available online: https://www.icos-infrastruktur.de/en/icos-d/komponenten/oekosysteme/beobachtungsstandorte/fendt-c1/ (accessed on 18 January 2021).
- ICOS-Deutschland ICOS: Mooseurach (C3). Available online: https://www.icos-infrastruktur.de/en/icos-d/komponenten/oekosysteme/beobachtungsstandorte/mooseurach-c3/ (accessed on 18 January 2021).
- Hommeltenberg, J.; Schmid, H.P.; Drösler, M.; Werle, P. Can a bog drained for forestry be a stronger carbon sink than a natural bog forest? Biogeosciences 2014, 11, 3477–3493. [Google Scholar] [CrossRef]
- Fratini, G.; Mauder, M. Towards a consistent eddy-covariance processing: An intercomparison of EddyPro and TK3. Atmos. Meas. Tech. 2014, 7, 2273–2281. [Google Scholar] [CrossRef]
- Foken, T.; Aubinet, M.; Leuning, R. The Eddy Covariance Method. In Eddy Covariance; Springer: Berlin/Heidelberg, Germany, 2012; pp. 1–19. [Google Scholar]
- Mauder, M.; Cuntz, M.; Drüe, C.; Graf, A.; Rebmann, C.; Schmid, H.P.; Schmidt, M.; Steinbrecher, R. A strategy for quality and uncertainty assessment of long-term eddy-covariance measurements. Agric. For. Meteorol. 2013, 169, 122–135. [Google Scholar] [CrossRef]
- Heidbach, K.; Schmid, H.P.; Mauder, M. Experimental evaluation of flux footprint models. Agric. For. Meteorol. 2017, 246, 142–153. [Google Scholar] [CrossRef]
- Kljun, N.; Calanca, P.; Rotach, M.W.; Schmid, H.P. A simple two-dimensional parameterisation for Flux Footprint Prediction (FFP). Geosci. Model Dev. 2015, 8, 3695–3713. [Google Scholar] [CrossRef]
- Templeton, R.C.; Vivoni, E.R.; Méndez-Barroso, L.A.; Pierini, N.A.; Anderson, C.A.; Rango, A.; Laliberte, A.S.; Scott, R.L. High-resolution characterization of a semiarid watershed: Implications on evapotranspiration estimates. J. Hydrol. 2014, 509, 306–319. [Google Scholar] [CrossRef]
- Foken, T. The energy balance closure problem: An overview. Ecol. Appl. 2008, 18, 1351–1367. [Google Scholar] [CrossRef] [PubMed]
- Mauder, M.; Genzel, S.; Fu, J.; Kiese, R.; Soltani, M.; Steinbrecher, R.; Zeeman, M.; Banerjee, T.; De Roo, F.; Kunstmann, H. Evaluation of energy balance closure adjustment methods by independent evapotranspiration estimates from lysimeters and hydrological simulations. Hydrol. Process. 2018, 32, 39–50. [Google Scholar] [CrossRef]
- Shuttleworth, W.J.; Wallace, J.S. Evaporation from sparse crops-an energy combination theory. Q. J. R. Meteorol. Soc. 1985, 111, 839–855. [Google Scholar] [CrossRef]
- Priestley, C.H.B.; Taylor, R.J. On the Assessment of Surface Heat Flux and Evaporation Using Large-Scale Parameters. Mon. Weather Rev. 1972, 100, 81–92. [Google Scholar] [CrossRef]
- Bellvert, J.; Jofre-Ĉekalović, C.; Pelechá, A.; Mata, M.; Nieto, H. Feasibility of Using the Two-Source Energy Balance Model (TSEB) with Sentinel-2 and Sentinel-3 Images to Analyze the Spatio-Temporal Variability of Vine Water Status in a Vineyard. Remote Sens. 2020, 12, 2299. [Google Scholar] [CrossRef]
- Colaizzi, P.; Kustas, W.P.; Anderson, M.C. Two-source energy balance model estimates of evapotranspiration using component and composite surface temperatures. Adv. Water Resour. 2012, 50, 134–151. [Google Scholar] [CrossRef]
- Kustas, W.; Anderson, M. Advances in thermal infrared remote sensing for land surface modeling. Agric. For. Meteorol. 2009, 149, 2071–2081. [Google Scholar] [CrossRef]
- Wind Energy Data for Switzerland. Available online: https://wind-data.ch/tools/profile.php?h=3.25&v=2.17&z0=0.2&abfrage=Aktualisieren (accessed on 5 January 2021).
- FLIR Tech Note: Radiometric Temperature Measurements. Available online: https://www.flir.com/globalassets/guidebooks/suas-radiometric-tech-note-en.pdf (accessed on 7 May 2020).
- Schmugge, T.; French, A.; Ritchie, J.C.; Rango, A.; Pelgrum, H. Temperature and emissivity separation from multispectral thermal infrared observations. Remote Sens. Environ. 2002, 79, 189–198. [Google Scholar] [CrossRef]
- Nolan, R.; Padilla-Parra, S. ijtiff: An R package providing TIFF I/O for ImageJ users. J. Open Source Softw. 2018, 3, 633. [Google Scholar] [CrossRef]
- RStudio Team RStudio: Integrated Development for R.; RStudio, Inc.: Boston, MA, USA, 2016; Volume 42, p. 14.
- CloudCompare 3D Point Cloud and Mesh Processing Software; 2021. Available online: https://www.danielgm.net/cc/ (accessed on 13 November 2020).
- Isenburg, M. LAStools—Efficient LiDAR Processing Software; 2011. Available online: https://rapidlasso.com/lastools/ (accessed on 20 November 2020).
- Roussel, J.-R.; Auty, D.; Coops, N.C.; Tompalski, P.; Goodbody, T.R.H.; Meador, A.S.; Bourdon, J.-F.; de Boissieu, F.; Achim, A. lidR: An R package for analysis of Airborne Laser Scanning (ALS) data. Remote Sens. Environ. 2020, 251, 112061. [Google Scholar] [CrossRef]
- Pareeth, S.; Karimi, P.; Shafiei, M.; De Fraiture, C.; Pareeth, S.; Karimi, P.; Shafiei, M.; De Fraiture, C. Mapping Agricultural Landuse Patterns from Time Series of Landsat 8 Using Random Forest Based Hierarchial Approach. Remote Sens. 2019, 11, 601. [Google Scholar] [CrossRef]
- Stefan, V. R—Using Random Forests, Support Vector Machines and Neural Networks for a Pixel Based Supervised Classification of Sentinel-2 Multispectral Images. Available online: https://valentinitnelav.github.io/satellite-image-classification-r/#visualize-classifications (accessed on 2 March 2021).
- Byrne, K.A.; Kiely, G.; Leahy, P. CO2 fluxes in adjacent new and permanent temperate grasslands. Agric. For. Meteorol. 2005, 135, 82–92. [Google Scholar] [CrossRef]
- Mauder, M.; Foken, T.; Clement, R.; Elbers, J.A.; Eugster, W.; Grünwald, T.; Heusinkveld, B.; Kolle, O. Quality control of CarboEurope flux data - Part 2: Inter-comparison of eddy-covariance software. Biogeosciences 2008, 5, 451–462. [Google Scholar] [CrossRef]
- Kalma, J.D.; McVicar, T.R.; McCabe, M.F. Estimating Land Surface Evaporation: A Review of Methods Using Remotely Sensed Surface Temperature Data. Surv. Geophys. 2008, 29, 421–469. [Google Scholar] [CrossRef]
- Piñeiro, G.; Perelman, S.; Guerschman, J.P.; Paruelo, J.M. How to evaluate models: Observed vs. predicted or predicted vs. observed? Ecol. Modell. 2008, 216, 316–322. [Google Scholar] [CrossRef]
- Wohlfahrt, G.; Irschick, C.; Thalinger, B.; Hörtnagl, L.; Obojes, N.; Hammerle, A. Insights from Independent Evapotranspiration Estimates for Closing the Energy Balance: A Grassland Case Study. Vadose Zo. J. 2010, 9, 1025–1033. [Google Scholar] [CrossRef]
- Calders, K.; Origo, N.; Disney, M.; Nightingale, J.; Woodgate, W.; Armston, J.; Lewis, P. Variability and bias in active and passive ground-based measurements of effective plant, wood and leaf area index. Agric. For. Meteorol. 2018, 252, 231–240. [Google Scholar] [CrossRef]
- Kustas, W.P.; Alfieri, J.G.; Nieto, H.; Wilson, T.G.; Gao, F.; Anderson, M.C. Utility of the two-source energy balance (TSEB) model in vine and interrow flux partitioning over the growing season. Irrig. Sci. 2019, 37, 375–388. [Google Scholar] [CrossRef]
- Hirschi, M.; Michel, D.; Lehner, I.; Seneviratne, S.I. A site-level comparison of lysimeter and eddy covariance flux measurements of evapotranspiration. Hydrol. Earth Syst. Sci 2017, 21, 1809–1825. [Google Scholar] [CrossRef]
- Burchard-Levine, V.; Nieto, H.; Riaño, D.; Migliavacca, M.; El-Madany, T.S.; Perez-Priego, O.; Carrara, A.; Martín, M.P. Adapting the thermal-based two-source energy balance model to estimate energy fluxes in a complex tree-grass ecosystem. Hydrol. Earth Syst. Sci. Discuss. 2019, 1–37. [Google Scholar] [CrossRef]
- Guzinski, R.; Nieto, H. Evaluating the feasibility of using Sentinel-2 and Sentinel-3 satellites for high-resolution evapotranspiration estimations. Remote Sens. Environ. 2019, 221, 157–172. [Google Scholar] [CrossRef]
- Nieto, H.; Kustas, W.P.; Alfieri, J.G.; Gao, F.; Hipps, L.E.; Los, S.; Prueger, J.H.; McKee, L.G.; Anderson, M.C. Impact of different within-canopy wind attenuation formulations on modelling sensible heat flux using TSEB. Irrig. Sci. 2019, 37. [Google Scholar] [CrossRef]

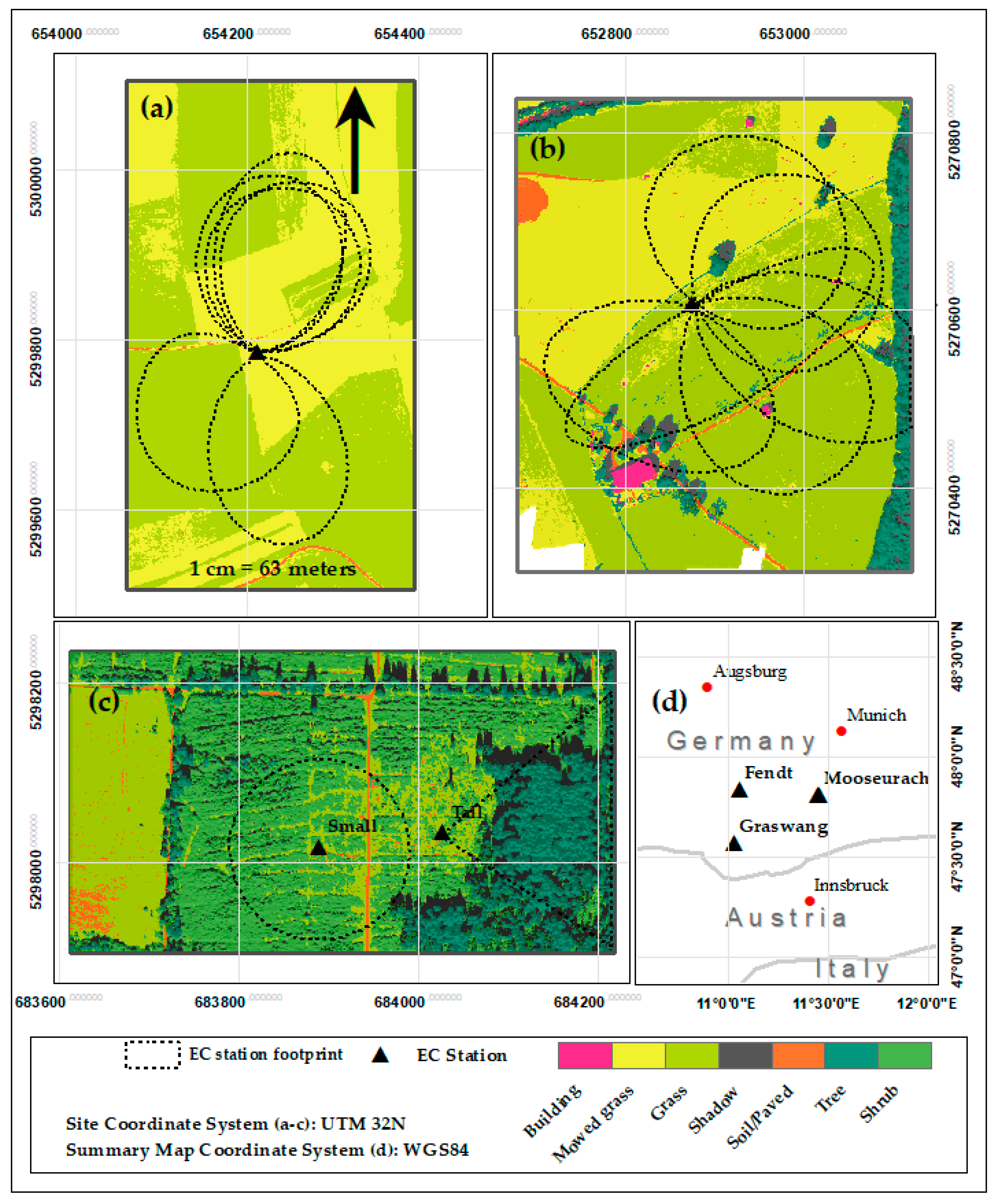



| EC Station Name | Elevation (m AMSL) | Location | Vegetation Type | Tower Height (m) | Equipment Used for Flux Measurements |
|---|---|---|---|---|---|
| Graswang | 869 | 47.571312° 11.031706° | Grass, Trees | 3 | LI-7500 1, CSAT3 2, CNR4 3 |
| Fendt | 595 | 47.832905° 11.060738° | Grass | 3 | LI-7500 1, CSAT3 2, CNR4 3 |
| Mooseurach Small | 599 | 47.809127° 11.457864° | Grass, Shrub, Trees | 6 | LI-7200 1 CNR4 3, HS-50 4 |
| Mooseurach Tall | 599 | 47.809272° 11.456149° | Grass, Shrub, trees | 30 | LI-7500 1, CSAT3 2 |
| Sensor | Bands | Image Resolution (Pixels) | Sensor Size (mm) | Focal Length (mm) | Field of View (°) | Centre Wavelength (nm) | Band Width (nm) | GSD at 100 m Altitude (m) |
|---|---|---|---|---|---|---|---|---|
| Micasense Altum | Blue | 2064 × 1544 | 7.12 × 5.33 | 8 | 48 × 37 | 475 | 32 | 0.04 |
| Green | 560 | 27 | ||||||
| Red | 668 | 16 | ||||||
| Red-edge | 717 | 12 | ||||||
| Near Infrared | 840 | 57 | ||||||
| Thermal Infrared | 160 × 120 | 1.92 × 1.44 | 1.77 | 57 × 44 | 11,000 | 60 | 0.67 | |
| Sony RX1RII | RGB | 7952 × 5304 | 35.9 × 24 | 35 | 63 | NA | NA | 0.01 |
| Location | Date | Time | Duration (Minutes) | Weather | Air Temperature (°C) | Survey Area Overpasses | Images Taken | Average Flying Height (m AGL) |
|---|---|---|---|---|---|---|---|---|
| Graswang | 20 July 2020 | 12:00 | 20 | Sunny | 25.8 | 1 | 382 | 100 |
| 12:30 | 20 | Sunny | 26.0 | 1 | 566 | |||
| 13:30 | 40 | Sun/cloud | 26.4 | 2 | 863 | |||
| Graswang | 15 September 2020 | 07:15 | 40 | Sunny | 18.0 | 2 | 818 | 120 |
| 10:00 | 40 | Sunny | 25.9 | 2 | 756 | |||
| 11:30 | 40 | Sunny | 27.9 | 2 | 775 | |||
| 13:30 | 40 | Sun/cloud | 28.0 | 2 | 754 | |||
| Fendt | 17 September 2020 | 07:30 | 30 | Overcast | 19.9 | 1 | 837 | 110 |
| 08:30 | 30 | Overcast | 21.0 | 1 | 842 | |||
| 10:30 | 40 | Sunny | 21.0 | 2 | 738 | |||
| 11:15 | 20 | Sunny | 24.5 | 1 | 482 | |||
| 12:30 | 40 | Sunny | 26.1 | 2 | 757 | |||
| 13:30 | 40 | Sunny | 26.3 | 2 | 893 | |||
| Mooseurach | 20 October 2020 | 08:00 | 30 | Sunny | 0.9 | 1 | 672 | 100 |
| 10:30 | 60 | Overcast | 10.8 | 2 | 667 | |||
| 11:30 | 60 | Overcast | 11.0 | 2 | 970 | |||
| 13:00 | 30 | Sunny | 14.3 | 2 | 962 |
| Main Input | Input Type | Unit | Source | Sensor |
|---|---|---|---|---|
| View Zenith Angle | SV | ° | Default = 0 | |
| Surface temperature | Raster | K | UAV Radiometrically calibrated TIR | Altum |
| Processing mask | Raster | Land Cover Map | Altum & RX1 | |
| Effective Leaf Area Index | Raster | m2/m2 | eLAI and Land Cover Map | LI-COR LAI2200 |
| Vegetation Fractional Cover | Raster | 0–1 | Default = 1 | Altum |
| Canopy Height | Raster | m | DSM-DTM | RX1RII |
| Canopy Height/Width ratio | SV | m m−1 | Default = 1 | |
| Green Fraction | SV | 0–1 | NDVI map | Altum |
| Latitude/longitude | SV | ° | Centroid of survey area | GNSS |
| Altitude | SV | m (AMSL) | Centroid of survey area | GNSS |
| Solar zenith angle | SV | ° | Estimated by pyTSEB | |
| Solar azimuth angle | SV | ° | Estimated by pyTSEB | |
| Day of year | SV | Day | Julian day | |
| Standardised Longitude/Time | SV | h | Decimal solar time | |
| Air temperature | SV | K | EC station | Thermometer |
| Wind speed | SV | m s−1 | EC station | Sonic anemometer |
| Atmospheric pressure | SV | Pa | EC instrument | Barometer |
| Vapor pressure | SV | Pa | Calculated from RH and air temperature | |
| Incoming SW irradiance | SV | W m−2 | EC station or hand held instrument | Pyranometer |
| Incoming LW irradiance | SV | W m−2 | EC station |
| Flux | Model | Location with Highest Errors | RMSE | Mean Bias | Standard Deviation |
|---|---|---|---|---|---|
| (W m−2) | |||||
| Rn | DTD | Graswang | 53.0 | 35.2 | 40.8 |
| H | Mooseurach | 23.1 | −10.8 | 21.0 | |
| LE | Mooseurach | 121.6 | 103.7 | 65.2 | |
| G | Mooseurach | 56.3 | 53.5 | 17.9 | |
| Rn | PT | Graswang | 44.9 | 29.4 | 34.7 |
| H | Mooseurach | 36.1 | −26.2 | 25.4 | |
| LE | Mooseurach | 128.1 | 112.0 | 63.6 | |
| G | Mooseurach | 51.6 | 45.1 | 25.7 | |
| Flux | EC Correction Type | Model | Location with Highest Errors | RMSE | Combined RMSE | Mean Bias | Standard Deviation |
|---|---|---|---|---|---|---|---|
| (W m−2) | |||||||
| H | BR | DTD | Mooseurach | 77.4 | 75.5 | −46.1 | 64.0 |
| LE | Mooseurach | 73.1 | −62.8 | 38.4 | |||
| H | BR | PT | Mooseurach | 79.0 | 71.9 | −56.4 | 56.6 |
| LE | Fendt | 64.0 | 52.7 | 37.1 | |||
| H | Res_H | DTD | Mooseurach | 153.9 | 138.7 | −122.0 | 96.6 |
| LE | Mooseurach | 121.6 | 103.7 | 65.2 | |||
| H | Res_H | PT | Mooseurach | 153.7 | 141.5 | −127.7 | 25.4 |
| LE | Fendt | 128.1 | 112.0 | 63.6 | |||
| H | Res_LE | DTD | Graswang | 23.1 | 31.9 | −10.8 | 21.0 |
| LE | Mooseurach | 38.7 | −7.5 | 39.0 | |||
| H | Res_LE | PT | Fendt | 36.1 | 39.5 | −26.2 | 25.4 |
| LE | Mooseurach | 42.6 | 10.5 | 42.3 | |||
| Location | Model | BR | Res_LE | ||
|---|---|---|---|---|---|
| RMSE | Mean Bias | RMSE | Mean Bias | ||
| (W m−2) | |||||
| Graswang | DTD | 59.1 | 19.3 | 51.6 | 38.4 |
| Fendt | 48.6 | −2.8 | 33.2 | 16.6 | |
| Mooseurach | 97.4 | −46.1 | 53.0 | −11.7 | |
| All sites | 75.3 | −5.0 | 44.7 | 17.6 | |
| Graswang | PT | 50.9 | 26.8 | 47.4 | 24.9 |
| Fendt | 56.6 | −19.9 | 37.8 | 16 | |
| Mooseurach | 87.2 | −7.9 | 49.5 | −11.4 | |
| All sites | 71.9 | 17.7 | 44.2 | 14.7 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Simpson, J.E.; Holman, F.; Nieto, H.; Voelksch, I.; Mauder, M.; Klatt, J.; Fiener, P.; Kaplan, J.O. High Spatial and Temporal Resolution Energy Flux Mapping of Different Land Covers Using an Off-the-Shelf Unmanned Aerial System. Remote Sens. 2021, 13, 1286. https://doi.org/10.3390/rs13071286
Simpson JE, Holman F, Nieto H, Voelksch I, Mauder M, Klatt J, Fiener P, Kaplan JO. High Spatial and Temporal Resolution Energy Flux Mapping of Different Land Covers Using an Off-the-Shelf Unmanned Aerial System. Remote Sensing. 2021; 13(7):1286. https://doi.org/10.3390/rs13071286
Chicago/Turabian StyleSimpson, Jake E., Fenner Holman, Hector Nieto, Ingo Voelksch, Matthias Mauder, Janina Klatt, Peter Fiener, and Jed O. Kaplan. 2021. "High Spatial and Temporal Resolution Energy Flux Mapping of Different Land Covers Using an Off-the-Shelf Unmanned Aerial System" Remote Sensing 13, no. 7: 1286. https://doi.org/10.3390/rs13071286
APA StyleSimpson, J. E., Holman, F., Nieto, H., Voelksch, I., Mauder, M., Klatt, J., Fiener, P., & Kaplan, J. O. (2021). High Spatial and Temporal Resolution Energy Flux Mapping of Different Land Covers Using an Off-the-Shelf Unmanned Aerial System. Remote Sensing, 13(7), 1286. https://doi.org/10.3390/rs13071286







