A New CBAM-P-Net Model for Few-Shot Forest Species Classification Using Airborne Hyperspectral Images

Abstract

High-precision automatic identification and mapping of forest tree species composition is an important content of forest resource survey and monitoring. The airborne hyperspectral image contains rich spectral and spatial information, which provides the possibility of high-precision classification and mapping of forest tree species. Few-shot learning, as an application of deep learning, has become an effective method of image classification. Prototypical networks (P-Net) is a simple and practical deep learning network, which has significant advantages in solving few-shot classification problems. Considering the high band correlation and large data volume associated with airborne hyperspectral images, how to fully extract effective features, filter or reduce redundant features is the key to improving the classification accuracy of P-Net, in order to extract effective features in hyperspectral images and obtain a high-precision forest tree species classification model with limited samples. In this research, we embedded the convolutional block attention module (CBAM) between the convolution blocks of P-Net, the CBAM-P-Net was constructed, and a method to improve the feature extraction efficiency of the P-Net was proposed, although this method makes the network more complex and increases the computational cost to a certain extent. The results show that the combination strategy using Channel First for CBAM greatly improves the feature extraction efficiency of the model. In different sample windows, CBAM-P-Net has an average increase of 1.17% and 0.0129 in testing overall accuracy (OA) and kappa coefficient (Kappa). The optimal classification window is 17 × 17, the OA reaches 97.28%, and Kappa reaches 0.97, which is an increase of 1.95% and 0.0214 along with just 49 s of training time expended, respectively, compared with P-Net. Therefore, using a suitable sample window and applying the proposed CBAM-P-Net to classify airborne hyperspectral images can achieve high-precision classification and mapping of forest tree species.

1. Introduction

Fine-grained tree species classification is the basis of forest management planning and interference monitoring, which is conducive to the scientific management and effective use of forest resources. Numerous continuous narrow spectral bands and high spatial resolution of hyperspectral images (HSI) can provide a wealth of available spectral information for each pixel on the land cover mapping [1]. Forest-type recognition is an important aspect of hyperspectral image application [1,2,3], and it plays an important role in the fine-grained classification of tree species [4].

Deep learning can extract high-level and semantic features [5,6]. Its objective function focuses directly on classification, and completes the process of data feature extraction and classifier training automatically. The complex feature extraction and selection process is replaced by a simple end-to-end deep workflow [7,8].

Recently, convolution neural networks (CNNs) for hyperspectral classification have made significant developments [9,10,11,12,13,14,15]. For instance, Chen et al. [10] addressed the classification problem of three hyperspectral public data sets (Indian Pines, University of Pavia, and Kennedy Space Center) by making use of 1D, 2D, and 3D CNNs and found that the 3D CNN can obtain the best classification effect, whereas the 2D CNN is superior to the 1D CNN. In [16], Zhang et al. explored an improved 3D CNN, named 3D-1D CNN, for tree species classification, which converts the joint spatial-spectral feature extracted by the last Conv3D layer into a 1D feature. This model can shorten the training time of the 3D CNN model by 60%, although it loses some classification accuracy.

Deep learning has achieved inspiring results in classification applications, but when there are few training examples, its classification performance will still decrease [17]. In the forest, sample collection will be hindered due to the complex terrain and stand structure. At the same time, the heterogeneity of structure and tree species composition and the similarity of image features make it difficult to label the samples when classifying forest tree species. Therefore, the problem of tree species classification based on a few-shot set of deep learning methods needs to be solved urgently [18,19].

Few-shot learning refers to performing related learning tasks when there are fewer training samples in categories. According to the different application scenarios, the number of categories and the sample size within a category show differences in the few-shot public data sets given at present. They mainly include Omniglot [20], CIFAR-100 [21], MiniImageNet [19], Tiered-ImageNet [22], and CUB-200 [23]. The overall classification results show that the more categories and more samples in the categories, the more conducive to few-shot image classification [24]. Hyperspectral images processing presents many challenges, including high data dimensionality and usually low numbers of training samples [25]. Currently, public hyperspectral remote sensing image data sets include Indian Pines [9,10,26,27,28,29], Salinas [9,27], Pavia University [9,10,26,27,28,29,30,31], and the Kennedy Space Center (KSC) [10,30], etc.

Table 1. Public hyperspectral data set and its parameters.

Data	Indian Pines	Salinas	Pavia University	KSC
Image size/pixels	145 × 145	512 × 217	610 × 340	512 × 614
Wavelength range/nm	400–2500	400–2500	430–860	400–2500
Bands	220	224	115	224
Spatial resolution	20	3.7	1.3	18
Sensor	AVIRIS	AVIRIS	ROSIS	AVIRIS
Region	Indian	California	Pavia	Florida
Number of classes	16	16	9	13

shows the detailed information of the four hyperspectral data sets. In general, these data sets have low spatial resolution, significant differences between categories, and regular boundaries, and are mainly used in the classification of urban ground objects and crops. When applied to the classification of forestry tree species, the accuracy often decreases because the spectral response of different plants of the same family and genus are very similar, especially under the fragmented species distribution, complex topography, and the occluded canopy [16]. Therefore, establishing a hyperspectral data set suitable for forest tree classification is the primary problem of our research. In the complex forest stand structure, the uneven distribution of samples and the noise generated by the background pixels are difficult to identify directly through hyperspectral images. It is necessary to rely on data collected by ground plot surveys and forest sub-compartment surveys, etc., but the sample points obtained in this way are difficult and relatively scarce. Therefore, in the process of making samples, it is necessary to comprehensively consider the complexity of the hundreds of dimensional bands of hyperspectral remote sensing images and the limitations of obtaining prior knowledge in forest stands, and to establish a data set with the number of categories in line with the actual situation and the size of the samples within the category as sufficient as possible. The data set can be applied to the classification of tropical and subtropical forest species similar to those of this study area.

Attention plays an important role in human perception. A significant characteristic of the human visual system is that it does not try to process the entire scene immediately, but selectively focuses on the salient parts in order to better capture the visual structure. Attention can be directed to the focal point, and the expression ability can be improved by using the attention mechanism, that is, focusing on important features and suppressing unnecessary features. Convolutional block attention module (CBAM) is a simple and effective attention module for feedforward convolutional neural networks [32]. Given an intermediate feature map, CBAM will sequentially infer the attention map along two separate dimensions (channel and spatial) [32] and then multiply the attention map by the input feature map for adaptive feature refinement [33]. Since CBAM is a lightweight general-purpose module, it can be seamlessly integrated into any convolutional neural network (CNN) architecture [25,34], while the overhead is negligible, and it can engage in end-to-end training together with the basic CNN [35,36,37]. Applying CBAM to the tree species classification of hyperspectral images aims to overcome the dimensional dilemma, adaptively reduce the impact of redundant bands on classification, and achieve a precise and efficient feature extraction so as to improve classification performance.

Matching networks uses the latest advances in attention to achieve fast learning. It is a weighted nearest-neighbor classifier applied within an embedding space. During the training process, the model imitates the test scenario of the few-shot task by sub-sampling the class labels and samples [19]. The training process of the network is to establish the relationship or mapping between labels and samples in the training set, and directly apply it to the test set in the same way. Prototypical networks is part of special matching networks and has a simple network structure, which does not require complex hyper-parameters, guiding the learning of new tasks using past prior knowledge and experience [38]. Moreover, it has great potential for solving few-shot classification problems. Compared with matching networks, it has fewer parameters and is more convenient to train. However, for the classification of hyperspectral images, the general prototypical networks structure is simple, and the problem of weak model generalization is prone to occur [39].

Considering the large and fine-grained spatial and spectral characteristics of airborne hyperspectral images, we are faced with two major challenges:

• Extracting effective features for classification based on a large amount of spatial and spectral information of hyperspectral images.
• Obtaining a high-precision forest tree species classification model with limited samples.

In this study, we proposed a CBAM-P-Net model by embedding a CBAM module into the prototypical networks, analyzed the influence of the convolutional attention module on the network operation efficiency and results, optimized the prototypical networks structure and tuning parameters, proposed a training sample size and method suitable for tree species classification based on airborne hyperspectral data, and discussed the classification performance of CBAM-P-Net on hyperspectral images under the condition of few-shot. The results show that our method improved the efficiency of feature extraction, although it makes the network more complex and increases the computational cost to a certain extent.

2. Materials and Methods

2.1. Study Area

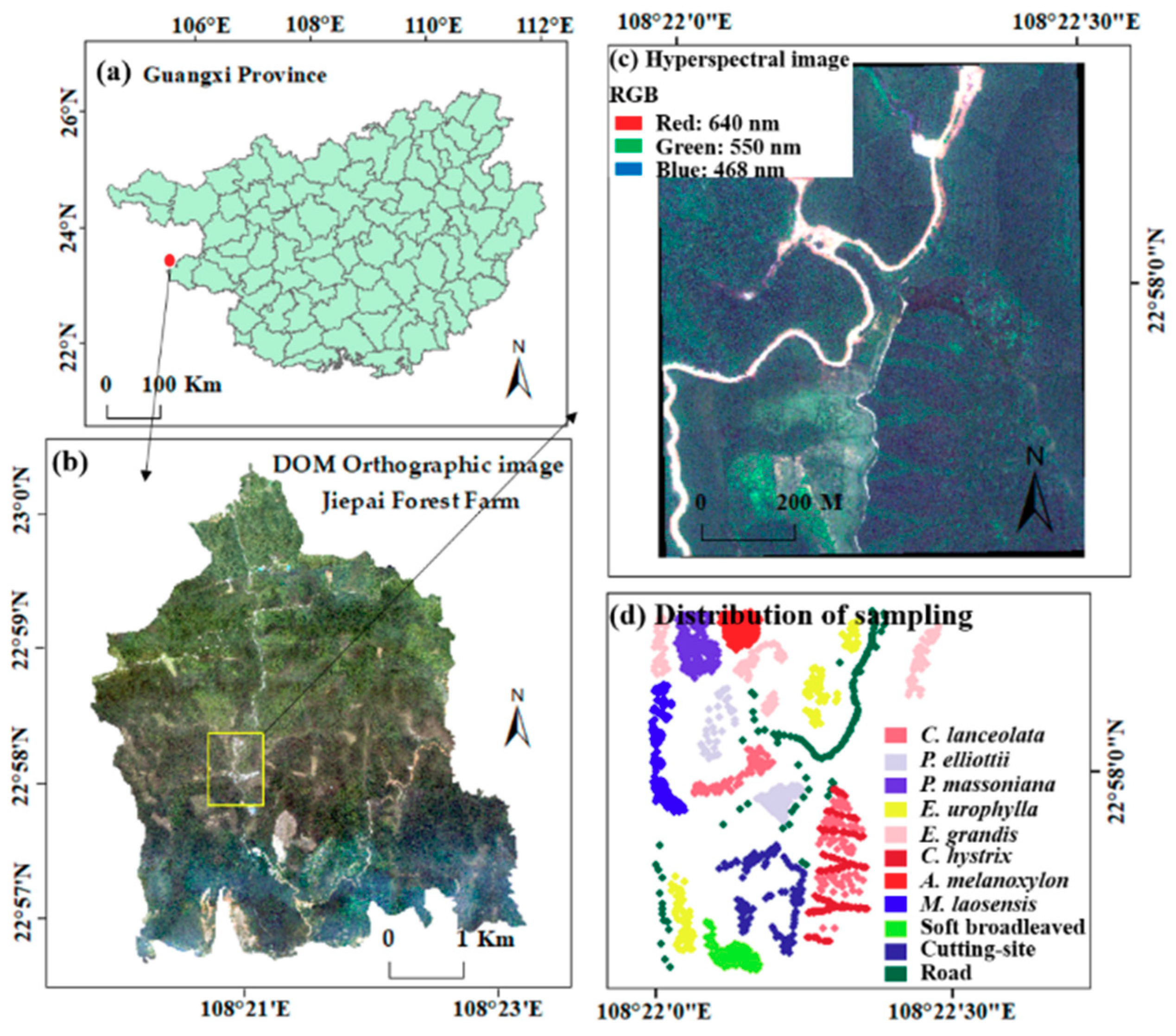
The study area is a sub-area of the Jiepai branch of Gaofeng Forest Farm in Nanning City, Guangxi Province, China (108°22′1″~108°22′30″ E, 22°57′42″~22°58′13″ N), belonging to the subtropical monsoon climate, with an area of 74.1 hm2. The average temperature is 21.6 °C, the average annual precipitation is 1200–1500 mm, and the average relative humidity is 79%. It is a hilly landform with an altitude of 149–263 m and a slope of 6~35°. The forest composition and structure in the study area have the typical characteristics of subtropical forests, with diverse tree species, fragmented and irregular distribution, complex tree structure, and a varied and luxuriant understory vegetation, which brings challenges to the classification of tree species. This paper classifies 11 categories in the study area, including 9 tree species, cutover land, and road. Of these, coniferous species include Cunninghamia lanceolate (C. lanceolate, CL), Pinus elliottii (P. elliottii, PE), and Pinus massoniana (P. massoniana, PM), and broadleaf species include Eucalyptus urophylla (E. urophylla, EU), Eucalyptus grandis (E. grandis, EG), Castanopsis hystrix (C. hystrix, CH), Acacia melanoxylon (A. melanoxylon, AM), Mytilaria laosensis (M. laosensis, ML), and other soft broadleaf species (SB). C. lanceolate, P. elliottii, P. massoniana, A. melanoxylon, and M. laosensis are mixed forests, and the remains are pure forests. Exploring the high-precision classification method of tree species in the study area has important guiding significance for the classification and mapping of forest stands with complex structures and composition.

2.2. Data Collection and Processing

2.2.1. Airborne Hyperspectral Data

The hyperspectral data acquisition was conducted on 13 January and 30 January 2019, under cloudless conditions, at noon. The hyperspectral equipment was equipped with the CAF’s (Chinese Academy of Forestry) LiCHy (LiDAR, CCD and Hyperspectral) system integrated by the German IGI company, including LiDAR sensors (LMS-Q680i, produced by RIEGL company), CCD cameras (DigiCAM-60), AISA Eagle II hyperspectral sensors (produced by Finland SPECIM company), and inertial navigation units (IMU). The aircraft had a flying speed of 180 km/h, a relative altitude of 750 m, an absolute altitude of 1000 m, and a course spacing of 400 m. The hyperspectral data is the radiance data after radiometric calibration and geometric correction. It contained 125 bands with a wavelength range of 400–987 nm, a spectral resolution of 3.3 nm, and a spatial resolution of 1 m.

Table 2. Parameters of the hyperspectral sensors in the LiCHy system.

Hyperspectral: AISA Eagle II
Spectral Resolution	3.3 nm	Spatial Resolution	1 m
Angle of view	37.7°	Spatial pixels	1024
Instantaneous angle of view	0.646 mrad	Spectral sampling interval	4.6 nm
Focal length	18.5 mm	Bit depth	12 bits

summarizes the detailed parameters of the hyperspectral sensors.

The Quick Atmospheric Correction (QUAC) method was used to perform atmospheric correction on hyperspectral images to eliminate the interference of light and the atmosphere on the reflectivity of ground objects. Due to the complex terrain of the study area, the brightness value of the images was uneven, so the hyperspectral image was corrected by the DEM based on the synchronously acquired LiDAR data, which eliminated the changes in the image radiance value caused by the undulation of the terrain. Savitzky-GOlay (SG) filtering [40] was used to smooth the spectral data and effectively remove the noise caused by various factors.

2.2.2. Field Survey Data

The field data survey was conducted at the Jiepai branch of Gaofeng Forest Farm from 16 January 16 to 5 February 2019. First, through the visual interpretation of GF-2 satellite images with a resolution of 1 m, the sample plots were set up with uniform distribution. Ten plots with the size of 25 m × 25 m and nine plots with 25 m × 50 m were laid out, of which seven were C. lanceolate pure forest, three were E. urophylla pure forests, three were E. grandis pure forests, and the remaining six were other forest stands and mixed forests. The tree species mainly included C. lanceolate and P. massoniana, E. urophylla, E. grandis, C. hystrix, etc., with a total of 1657 trees. In the plot, each tree was positioned using the China Sanding STS-752 Series Total Station and measured including tree species, tree height, crown width, branch height, diameter at breast height, and other factors. At the same time, for areas where it was not possible to set up plots due to the complex terrain, a field positioning survey was conducted by handheld GPS, with 10–20 points for each tree species.

In order to keep the number of sample points of each feature category consistent and evenly distributed, for categories with too many sample points, the points located at plot edges and that were too densely distributed were deleted. For categories where the number of sample points was too few, based on field survey GPS location points and sample site survey data, combined with a 0.2 m resolution digital orthophoto map (DOM) and forest sub-compartments survey data, the sample points were manually marked on the image of the study area. In this way, 112 sample points were obtained for each category, a total of 1232 sample points (Figure 1).

2.3. Sample Data and Prototypical Networks Construction

In the previous research, we have produced a complete set of sample data and constructed the classification framework of the prototypical networks [39]. The sample data set is based on hyperspectral images, as the data source, centered on the screen coordinate representation of the actual measured point’s latitude and longitude, and clipped with different window sizes through the open source framework GDAL. The window size starts from 5 × 5, with a step length of 2 m, and then clips the sample data until 31 × 31, when the clipping area exceeds the study area. Finally, a sample data set (11 classes, 112 samples in each class, a total of 1232 samples) consistent with the number of sample points was obtained in different window sizes. The sample data were divided into training samples and test samples according to the ratio of 80% and 20%.

The classification principle of the prototypical networks is that the points of each class are clustered around a prototype. Specifically, the neural network learns the nonlinear mapping of the input to the embedding space and uses the average value of the support set as the prototype of its class in the embedding space. Next, the nearest class prototype is found to classify the embedded query points [39]. 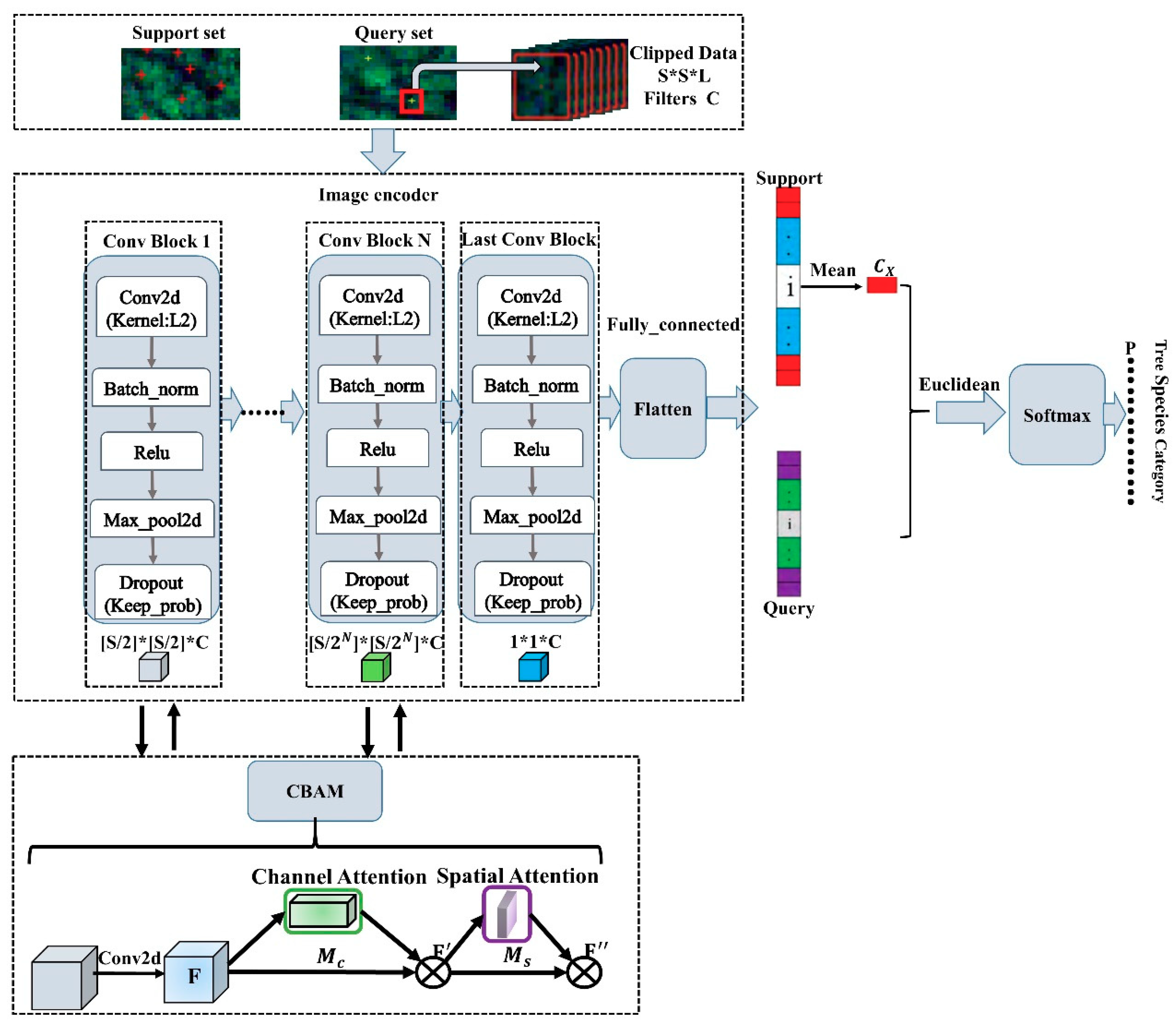The classification framework of the prototypical networks is shown in Figure 2, which mainly includes three parts: sample data input, image feature extraction, distance measurement and classification. In the prototypical networks, the sample data are divided into a support set and a query set. The support set is used to calculate the prototype, and the query set is used to optimize the prototype. If there are A classes and B samples in each class as the support set, it is A-way-B-shot. The image feature extraction part is to construct the embedding function ($f_{\varnothing }:R^D\to R^M$, $\varnothing$ is the learning parameter) to calculate the M-dimensional representation of each sample, that is, the image feature, and each class prototype ($c_kϵR^M$) is the mean value of the feature vector obtained by the embedding function of the support set samples of its class. The square of the Euclidean distance is used to construct a linear classifier. From the projection of the sample to the embedding space, prototypical networks uses the distance function to calculate the distance from the query set x to the prototype, and then uses the softmax to calculate the probability of belonging to the category.

This research uses slice data of H × W × C (Height × Width × Channels) as the input of prototypical networks. The image feature extraction architecture is composed of different numbers of convolution blocks (Conv Block 1...Conv Block N, Last Conv Block) according to the size of the clipped data window. Each convolution block includes a convolution layer (Conv2d, output dimension F is 64, convolution kernel is 3 × 3), a batch normalization layer (Batch_norm), a non-linear activation function (ReLU), and a maximum Pooling layer (Max_pool2d, pooling kernel is 2 × 2). At the same time, in order to avoid model overfitting, the L2 regularization (${\alpha }_2$ = 0.001) of the convolution kernel is added to the convolution layer, and Dropout is added after the maximum pooling layer (Keep_prob is 0.7). Feature values are processed through the fully connected layer (Flatten) and softmax as the basis for classification. The same embedding function is taken to operate the support set and the query set, then using them it as input parameters for the loss and precision calculations. All models are trained through Adam-SGD. The initial learning rate is 10⁻⁴, halving the learning rate every 2000 training sessions. Euclidean distance is used as the measurement function, and the loss function is a negative log likelihood function to train the prototypical networks.

2.4. Convolutional Block Attention Module

Convolutional Block Attention Module (CBAM) is an attention module that combines the spatial and channel dimensions (Figure 3). CBAM can achieve better results compared with SENet [41] because the attention mechanism adopted by the latter only focuses on channels. In addition, MaxPool is added to the network structure of CBAM, which makes up for the information lost by AvgPool to a certain extent. It can be seen from Figure 3 that taking the feature map ($\mathrm{F}\in R^{H\times W\times C}$) extracted by CNN as input, CBAM sequentially obtains a one-dimensional Channel Attention feature map ($M_c\in R^{1\times 1\times C}$) and a two-dimensional Spatial Attention feature map ($M_s\in R^{H\times W\times 1}$). The entire attention process can be summarized as:

$$F^{\prime }=M_c\left(F\right)\otimes F,$$

(1)

$$F^{″}=M_s\left(F^{\prime }\right)\otimes F^{\prime }$$

(2)

The symbol $\otimes$ means multiply by element, and $F^{\prime }$ represents a new feature obtained through channel attention, which is used as the input of spatial attention. Finally, the feature $F^{″}$ of the entire CBAM output is obtained.

The soft mask mechanism proposed by Wang et al. [42] can guarantee a better performance of the attention module. The equation is modified as:

$$F^{\prime }=M_c\left(F\right)\otimes F+ F,$$

(3)

$$F^{″}=M_s\left(F^{\prime }\right)\otimes F^{\prime }+ F^{\prime }$$

(4)

2.4.1. Channel Attention

Producing a channel attention map by exploiting the inter-channel relationship of the features (Figure 4). In order to effectively calculate channel attention, the spatial size of the input feature map needs to be compressed, and average pooling and maximum pooling are commonly used. It can be seen from Figure 4 that the module takes the feature map as input, and obtains the features ($F_{max}^c\in R^{1\times 1\times C}, F_{avg}^c\in R^{1\times 1\times C}$, C represents the number of channels) through spatial-based global maximum pooling and global average pooling. Then, through a multi-layer perceptron (MLP) composed of two dense layers, the features output by the MLP are element-wise summation multiplication, and then, through the sigmoid activation function, the channel attention feature map ($M_c\in R^{1\times 1\times C}$) is generated. The feature map will multiply the input feature by the element to obtain a new feature ($F^{\prime }$). The calculation equation is indicated by Formula (5).

$$\begin{array}{ll}{M}_c(F)& =\sigma (MLP(AvgPool(F))+MLP(MaxPool(F)))\\ & =\sigma (W_1(W_0(F_{avg}^c))+W_1(W_0(F_{max}^c)))\end{array}$$

(5)

where $\sigma$ represents the sigmoid activation function, $W_0ϵR^{C/r\times C}$ is the weight of the first hidden layer in the MLP, r is the feature compression rate, and $W_1ϵR^{C\times C/r}$ is the weight of the second hidden layer in the MLP.

2.4.2. Spatial Attention

Generating a spatial attention map by utilizing the inter-spatial relationship of the features (Figure 5). First, average pooling and maximum pooling operations along the channel axis are applied to generate the corresponding feature vectors, which are connected according to the channel axis to form an effective feature descriptor. On this basis, the convolutional layer is applied to generate the spatial attention feature map ($M_s\in R^{H\times W\times 1}$), which will be multiplied by the input feature to obtain a new feature ($F^{″}$). The calculation equation is indicated in Formula (6).

$$\begin{array}{ll}{M}_{\mathrm{s}}(F)& =\sigma (f^{7\ast 7}([AvgPool(F);MaxPool(F)]))\\ & =\sigma (f^{7\ast 7}([F_{avg}^c;F_{max}^c]))\end{array}$$

(6)

where $\mathsf{\sigma }$ represents the sigmoid activation function, and $f^{7\ast 7}$ is a convolution operation with a kernel size of 7 × 7.

As shown in Figure 6, this study inserts CBAM between the convolution blocks of the prototypical networks to construct CBAM-P-Net. CBAM focuses on channel and spatial features. In addition, the soft mask mechanism is used in each convolution block attention sub-module to ensure the performance of the model.

2.5. Accuracy Verification

The classification accuracy of CBAM-P-Net includes training accuracy and testing accuracy. The training accuracy is expressed by last epoch accuracy (LEA). The testing accuracy is expressed by average accuracy (AA, Equation (7)), overall accuracy (OA, Equation (8)), and Kappa coefficient (Kappa, Equation (9)).

$$AA=\frac{X_{ii}}{X_{i+}},$$

(7)

$$OA=\frac{{{\displaystyle \sum }}_{i=1}^n{X}_{ii}}{M}$$

(8)

$$Kappa=\frac{M{{\displaystyle \sum }}_{i=1}^n{X}_{ii}-{{\displaystyle \sum }}_{i=1}^n(X_{i+}\times X_{+i})}{M^2-{{\displaystyle \sum }}_{i=1}^n(X_{i+}\times X_{+i})}$$

(9)

where n is the number of categories, X_ii is the number of correct classifications of a category in the error matrix, X_+i is the total number of true reference samples of that category, X_i+ is the total number of categories classified into this category, and M is the total number of samples.

2.6. Experiments Design

In this study, we designed four experimental schemes, as shown in

Table 3. Experimental schemes.

Experiments	Name	Description
A	Classification using the prototypical networks in different windows	Rotating (the image of each band is rotated 90, 180, and 270 degrees with the center as the axis) and flipping (the image of each band are flipped up-down and left-right respectively) training samples in different windows (from 5 × 5 to 29 × 29). Then, using 11-way-5-shot, and the optimal number of iterations is sought to train the prototypical networks.
B	CBAM combination strategy selection	B1: Channel attention prior to spatial attention.
		B2: Spatial attention prior to channel attention.
		B3: Channel attention parallel with spatial attention.
C	The effect of training set ratio on CBAM-P-Net classification accuracy	Divide the sample into proportions, set the training set to 20%, 40%, 60%, and 80%, and divide the rest into the test set for experimentation.
D	Comparative experiment	Using the same sample and computer configuration, train the 2D CNN, 3D CNN, and 3D-1D CNN matching networks and combine the matching networks with CBAM to compare the classification accuracy with CBAM-P-Net.

.

3. Results

3.1. Classification Using Prototypical Networks in Different Windows

Taking the sample data from the 5 × 5 to the 29 × 29 window as the input, rotating (the image of each band is rotated 90, 180, and 270 degrees with the center point as the axis) and flipping (the image of each band is flipped up-down and left-right, respectively) the sample, and applying prototypical networks for classification, the results are shown in

Table 4. Classification accuracy using the prototypical networks in different windows.

Sample Windows	Epochs/Iterations	LEA (%)	Training Times (s)	OA (%)	Kappa
5 × 5	70/100	95.89	279	79.39	0.7733
7 × 7	70/100	96.58	546	86.00	0.8460
9 × 9	35/100	97.31	479	88.97	0.8786
11 × 11	25/100	97.16	486	89.92	0.8891
13 × 13	25/100	97.18	696	92.15	0.9136
15 × 15	25/100	97.84	938	91.87	0.9106
17 × 17	15/100	99.46	731	95.33	0.9486
19 × 19	15/100	99.84	944	95.50	0.9505
21 × 21	10/100	99.22	765	94.80	0.9428
23 × 23	10/100	99.96	872	94.40	0.9384
25 × 25	10/100	99.53	1059	95.40	0.9494
27 × 27	10/100	99.75	1229	96.37	0.9600
29 × 29	10/100	99.69	1435	96.92	0.9661

. As the sample window increases, the model training time gradually increases. The model training accuracy (LEA), testing accuracy OA, and Kappa are above 95.89%, 79.39%, and 0.7733, respectively. Figure 7 illustrates the changes of the classification accuracy in different windows, showing an overall upward trend. The testing accuracy of samples from the 5 × 5 to the 17 × 17 window is obviously improved, slightly increases in the 19 × 19 window compared to the 17 × 17 window, and decreases from the 21 × 21 to the 23 × 23 window, increases again from the 25 × 25 to the 29 × 29 window, and the testing accuracy reaches the maximum in the 29 × 29 window.

3.2. CBAM Combination Strategy Selection

3.2.1. Channel Attention Prior to Spatial Attention

Taking channel attention prior to spatial attention (Channel First), the CBAM is inserted between the convolutional blocks of the prototypical networks to classify samples in different windows, and the results are shown in

Table 5. Classification accuracy of Channel First.

Sample Windows	Epochs/Iterations	LEA (%)	Training Times (s)	OA (%)	Kappa
5 × 5	70/100	96.66	298	81.23 +1.84	0.7935 +0.0202
7 × 7	70/100	97.04	541	86.15 +0.15	0.8476 +0.0016
9 × 9	35/100	98.53	504	90.47 +1.50	0.8951 +0.0165
11 × 11	25/100	97.36	534	90.95 +1.04	0.9005 +0.0114
13 × 13	25/100	97.31	706	93.53 +1.38	0.9288 +0.0152
15 × 15	25/100	97.84	988	94.64 +2.77	0.9410 +0.0305
17 × 17	15/100	100.00	780	97.28 +1.95	0.9700 +0.0214
19 × 19	15/100	100.00	858	96.63 +1.12	0.9629 +0.0123
21 × 21	10/100	100.00	779	96.40 +1.59	0.9603 +0.0175
23 × 23	10/100	99.36	942	95.38 +0.98	0.9492 +0.0107
25 × 25	10/100	99.98	1121	95.76 +0.37	0.9534 +0.0040
27 × 27	10/100	99.69	1313	96.81 +0.44	0.9649 +0.0048
29 × 29	10/100	99.82	1536	97.04 +0.12	0.9674 +0.0013
OA Average Growth: +1.17% Kappa Average Growth: +0.0129

. The testing accuracy (OA, Kappa) of the model has been improved to a certain extent, with an average increase of 1.17% for OA and 0.0129 for Kappa. Figure 8 illustrates the change trend of the classification accuracy in different windows. It can be seen that the testing accuracy of samples from the 5 × 5 to the 17 × 17 window increases tremendously, decreases slightly from the 19 × 19 to the 23 × 23 window, and successively improves from the 25 × 25 to the 29 × 29 window. The testing accuracy reaches the highest value, and the model training time is short when the sample window size is 17 × 17.

3.2.2. Spatial Attention Prior to Channel Attention

The CBAM of spatial attention prior to channel attention (Spatial First) is inserted between the convolutional blocks of the prototypical networks to classify samples in different windows, and the results are shown in

Table 6. Classification accuracy of Spatial First.

Sample Windows	Epochs/Iterations	LEA (%)	Training Times (s)	OA (%)	Kappa
5 × 5	70/100	96.93	301	81.17 +1.78	0.7976 +0.0243
7 × 7	70/100	97.75	576	86.21 +0.22	0.8504 +0.0044
9 × 9	35/100	98.31	505	89.84 +0.87	0.8872 +0.0086
11 × 11	25/100	98.58	522	91.05 +1.13	0.9023 +0.0133
13 × 13	25/100	98.09	742	92.50 +0.35	0.9174 +0.0038
15 × 15	25/100	98.00	1015	92.39 +0.52	0.9141 +0.0035
17 × 17	15/100	100.00	853	96.84 +1.52	0.9637 +0.0151
19 × 19	15/100	100.00	996	96.37 +0.87	0.9601 +0.0095
21 × 21	10/100	99.40	786	95.60 +0.80	0.9516 +0.0088
23 × 23	10/100	99.51	941	96.44 +2.03	0.9608 +0.0224
25 × 25	10/100	99.86	1128	96.04 +0.64	0.9564 +0.0071
27 × 27	10/100	99.85	1335	96.78 +0.41	0.9633 +0.0033
29 × 29	10/100	99.73	1533	96.93 +0.02	0.9662 +0.0001
OA Average Growth: +0.86% Kappa Average Growth: +0.0096

. The testing accuracy (OA, Kappa) of the model has been improved, and OA and Kappa increased by 0.86% and 0.0096, on average, which is lower than in Channel First. Figure 9 shows the change trend of the classification accuracy in different windows. We found that the variation trend of the classification accuracy of samples in different windows is consistent with the results of Channel First. The testing accuracy reaches the highest value in 29 × 29, followed by 17 × 17. The OA and Kappa of 17 × 17 are about 0.09% and 0.0025, lower than those of the 29 × 29 window, but the training time is nearly halved. Therefore, we can consider 17 × 17 to be the best window size for classification with high testing accuracy and short model training time.

3.2.3. Channel Attention Parallel with Spatial Attention

CBAM paralleled by channel attention and spatial attention is inserted between the convolutional blocks of the prototypical networks to classify samples in different windows. The results are shown in

Table 7. Classification accuracy of Parallel.

Sample Windows	Epochs/Iterations	LEA (%)	Training Times (s)	OA (%)	Kappa
5 × 5	70/100	96.29	297	80.05 +0.66	0.7806 +0.0073
7 × 7	70/100	97.42	573	86.40 +0.40	0.8484 +0.0024
9 × 9	35/100	98.55	672	89.53 +0.57	0.8848 +0.0062
11 × 11	25/100	98.55	534	90.92 +1.00	0.9001 +0.0110
13 × 13	25/100	97.67	755	92.63 +0.49	0.9190 +0.0053
15 × 15	25/100	98.22	991	92.99 +1.12	0.9229 +0.0123
17 × 17	15/100	100.00	818	96.97 +1.65	0.9667 +0.0181
19 × 19	15/100	100.00	986	95.63 +0.13	0.9520 +0.0014
21 × 21	10/100	100.00	789	96.32 +1.52	0.9587 +0.0159
23 × 23	10/100	100.00	942	96.87 +2.47	0.9656 +0.0271
25 × 25	10/100	100.00	1138	96.16 +0.76	0.9588 +0.0094
27 × 27	10/100	99.78	1324	96.37 +0.01	0.9601 +0.0001
29 × 29	10/100	99.91	1535	97.04 +0.13	0.9681 +0.0020
OA Average Growth: +0.84% Kappa Average Growth: +0.0091

. To a certain degree, the testing accuracy (OA, Kappa) of the model has been improved, OA and Kappa increased by 0.84% and 0.0091, on average, which is even worse than in Spatial First. The change trend of the classification accuracy in different windows using Parallel can be seen in Figure 10. Consistent with Spatial First, the OA and Kappa of the 17 × 17 window are about 0.07% and 0.0014, lower than those of the 29 × 29 window, but the training time is nearly halved. It is obvious that 17 × 17 is the best window size for classification with high testing accuracy and short model training time.

Therefore, adding CBAM to the prototypical networks can play a positive role in the classification results. From a spatial perspective, channel attention is applied globally and represents feature information, whereas spatial attention is applied locally and represents location information. It is obvious that the weight of local information is determined on the global feature distribution. For this reason, Channel First has the most significant role in improving the classification accuracy, followed by Spatial First. Adding channel attention and spatial attention to prototypical networks in parallel results only in a slight of improvement in the classification accuracy.

3.3. The Effect of Training Set Ratio on CBAM-P-Net Classification Accuracy

Inserting CBAM between the various convolution blocks of the prototypical networks to construct CBAM-P-Net with Channel First. The best window of sample is 17 × 17. This study classified 11 categories, and each category selected 5, 10, and 15 samples as the support set, so three scenarios of 11-way-5-shot, 11-way-10-shot, and 11-way-15-shot were taken into trials. At the same time, in order to verify the impact of the number of training samples on the classification accuracy of the prototypical networks, we conducted classification tests on all ground-measured samples according to the proportions of 80%, 60%, 40%, and 20%. The results are shown in

Table 8. Classification accuracy of different training set ratio.

Training Sample	80%			60%			40%			20%
Shot	5	10	15	5	10	15	5	10	15	5	10	15
Epochs/iterations	15/100	15/100	15/100	15/100	15/100	15/100	15/100	15/100	15/100	15/100	15/100	15/100
Training Times(s)	780	1209	1641	781	1209	1621	771	1210	1627	776	1191	1609
OA (%)	97.28	97.28	96.00	96.02	96.21	94.12	94.64	94.83	93.57	92.05	92.08	90.47
Kappa	0.9700	0.9701	0.9560	0.9562	0.9583	0.9354	0.9410	0.9432	0.9293	0.9125	0.9129	0.8951
C. lanceolate (%)	98.42	93.34	83.24	96.54	97.98	92.96	98.46	86.56	86.82	89.04	83.74	83.02
P. elliottii (%)	83.82	91.30	85.28	88.32	88.72	88.94	88.90	90.00	91.16	81.36	89.46	82.92
P. massoniana (%)	98.86	97.08	96.48	96.56	99.92	100.00	96.94	97.00	95.26	96.86	92.44	92.66
E. urophylla (%)	96.82	96.90	99.90	94.26	95.12	89.60	86.08	89.42	93.08	84.50	92.78	84.38
E. grandis (%)	100.00	99.74	99.86	97.56	92.42	91.02	89.30	95.32	91.62	93.34	89.08	91.34
C. hystrix (%)	92.14	92.00	96.08	98.82	98.80	97.54	97.78	93.72	94.16	88.76	88.80	94.40
A. melanoxylon (%)	100.00	99.96	100.00	96.90	95.04	94.46	97.36	99.88	96.36	95.84	94.72	91.40
M. laosensis (%)	100.00	99.92	99.98	89.16	96.16	90.58	95.42	96.00	84.40	90.06	89.20	83.02
Soft broadleaved (%)	99.96	99.86	95.18	98.16	94.40	90.26	93.68	96.76	96.42	95.74	93.24	95.24
cutting-site (%)	100.00	100.00	100.00	99.86	100.00	100.00	99.30	100.00	100.00	99.96	99.40	100.00
Road (%)	100.00	100.00	100.00	100.00	99.76	100.00	97.80	98.50	100.00	97.04	100.00	96.76

.

It can be seen from Table 8 that when the number of training samples drops from 80% of the actual measured samples to 20%, the testing accuracy of CBAM-P-Net also decreases sequentially. Yet even when 20% of the samples are used for training, the testing accuracy of CBAM-P-Net still reaches more than 90%. From the testing accuracy of different tree species, it can be found that among the coniferous species, the testing accuracy of C. lanceolata is the highest, and the testing accuracy of P. elliottii is the lowest; among the broad-leaved species, 80% and 60% of the samples are used for training, and the testing accuracy is above 90%. However, when the training samples are 40% and 20%, the testing accuracy of A. melanoxylon and soft broadleaved species is still above 90%, but is decreases in other tree species.

3.4. Comparative Experiments

The optimal window of the sample is 17 × 17. Under the same experimental conditions, we compared different models for hyperspectral image classification tasks.

Below are the methods included in our comparison.

• 2D CNN: The architecture of the 2D CNN used three convolutional blocks and 3 × 3 filters for all the blocks. A max-pooling layer follows each block. It has two convolutional layers, and 32, 64, and 128 filters are used for the convolutional layers of those three blocks, respectively [13].
• 3D CNN: Five convolution blocks are considered, each of which includes a 3D convolutional layer with a kernel of 3 × 3 × 3, a nonlinear activation function (ReLU), and a batch normalization layer. The first and last convolution blocks set a maximum pooling layer, which was used to rapidly reduce the data dimension. Subsequently, we flattened the feature output by the last 3D convolutional layer and transformed the 3D feature cube into features with dimensions of 1 × 128 through the first dense layer. These feature vectors passed the linear activation function and entered the second dense layer, obtaining the features with the dimension of 1 × 11. We used the activation function (Softmax) to calculate the probability of belonging to each category as the basis for classification [16,39].
• 3D-1D CNN: This network converts the joint spatial-spectral feature extracted by the last 3D convolutional layer into a 1D feature. In this way, 3D-1D CNN reduces the training parameters [16].
• Matching networks: It is a weighted nearest-neighbor classifier applied within an embedding space. The training process of the network is to establish the relationship or mapping between labels and samples in the training set, and directly apply it to the test set in the same way. We trained the matching networks and the matching networks combined with CBAM for classification schemed with [19].

The results are shown in

Table 9. Comparison of classification accuracy between matching networks and prototypical networks.

Model	Shot	Epochs/Iterations	Training Times	OA (%)	Kappa
2D CNN	32 (per batch)	50 (Epochs)	1020 s	86.74	0.8542
3D CNN	32 (per batch)	20 (Epochs)	3.8 h	90.91	0.9000
3D-1D CNN	32 (per batch)	20 (Epochs)	2.9 h	89.77	0.8875
Matching Networks	5	100/100	37.4 h	91.96	0.9120
	10	100/100	37.7 h	91.83	0.9113
	15	100/100	38.4 h	90.79	0.9011
CBAM-M-Net	5	100/100	38.5 h	92.25	0.9172
	10	100/100	38.9 h	92.27	0.9179
	15	100/100	40.4 h	91.42	0.9085
Prototypical Networks	5	15/100	731 s	95.33	0.9486
	10	15/100	1142 s	95.34	0.9487
	15	15/100	1526 s	94.59	0.9405
CBAM-P-Net	5	15/100	780 s	97.28	0.9700
	10	15/100	1209 s	97.28	0.9701
	15	15/100	1641 s	96.00	0.9560

and

Table 10. Comparison of classification accuracy between CBAM-M-Net and CBAM-P-Net.

	2D CNN	3D CNN	3D-1D CNN	CBAM-M-Net	CBAM-P-Net
Trainable params	467307	280275	206491	33989754	306726
C. lanceolate (%)	89.80	89.80	80.95	82.68	93.34
P. elliottii (%)	81.82	76.92	80.00	74.14	91.30
P. massoniana (%)	82.93	95.65	95.65	96.06	97.08
E. urophylla (%)	89.36	90.20	84.44	90.75	96.90
E. grandis (%)	88.00	93.62	94.12	91.93	99.74
C. hystrix (%)	80.70	79.17	82.14	91.41	92.00
A. melanoxylon (%)	81.36	94.12	94.12	98.25	99.96
M. laosensis (%)	81.82	88.46	91.67	97.55	99.92
Soft broadleaved (%)	78.05	89.80	83.72	98.50	99.86
cutting-site (%)	100.00	100.00	100.00	99.89	100.00
Road (%)	100.00	100.00	100.00	100.00	100.00

. In CNNs, 3D CNN outperform 2D CNN, whereas 3D-1D CNN reduces training time and brings about a 1% accuracy loss compared with 3D CNN. However, the few-shot learning method, i.e., matching networks and prototypical networks, obtained a higher testing accuracy than CNNs in the case of few samples. A comparison of few-shot learning methods shows that the model training time of the matching networks is much longer than that of the prototypical networks, and the testing accuracy is less than that of the prototypical networks. In different training scenarios, the matching networks and the prototypical networks have a high testing accuracy when the shot is 5 and 10, and the classification testing is low when the shot is 15. Inserting CBAM into matching networks and prototypical networks, the testing accuracy of the model is obviously improved, and it still shows that CBAM-P-Net is obviously better than CBAM-M-Net in training time cost and classification performance. In terms of network structure, the trainable parameters of CBAM-P-Net are at the hundred thousand level, which is far lower than the tens of millions in CBAM-M-Net. The testing accuracy of different tree species also proved that CBAM-P-Net is higher than CBAM-M-Net.

3.5. Classification Results

Taking each pixel as the sample center point and the window size (17 × 17) as the best sample window, the classification maps of CBAM-P-Net constructed with 20%, 40%, 60%, and 80% of the training samples and P-Net constructed with 80% of the samples were generated, respectively (Figure 11).

From the classification maps, it can be seen that, when CBAM-P-Net is trained with 20% (Figure 11a), 40% (Figure 11b), and 60% (Figure 11c) samples, and P-Net is trained with 80% samples (Figure 11d), the boundaries of the coniferous species C. lanceolate and P. elliottii are not clear, there is confusion between C. hystrix and A. melanoxylon, and E. urophylla and E. grandis are also mixed together. When CBAM-P-Net is trained with 80% (Figure 11e) samples, C. lanceolate, P. elliottii, E. urophylla, and E. grandis can be well distinguished. When there are fewer training samples, the elliptical box area in Figure 11a,b is classified as C. hystrix. However, as the number of training samples increases (Figure 11c–e) elliptical boxes), the area is classified as soft broadleaved, and the classification accuracy is high, which is more in line with the distribution of tree species in real life.

4. Discussion

4.1. The Size of the Sample Windows on the Classification of Prototypical Networks

When using prototypical networks to classify airborne hyperspectral images, the different window sizes show significant diversities in classification accuracy (Figure 7). Appropriately increasing the window size helps to improve the classification performance of prototypical networks, but samples with an excessively large window may cause extra noise. In addition, the increase of the window will also increase the time for network training and the prediction calculations. In this study, with the increase of the window size, the classification accuracy of the samples obviously improved till the window was 17 × 17, indicating that the spatial feature and channel feature extraction of the prototypical networks for this window size basically meets the requirements of high-precision classification. When the window size increased to 25 × 25, the classification accuracy fluctuated. This is because the data noise caused by the enlarged window affects the classification performance. Classification accuracy increases with the window from 25 × 25 to 29 × 29, especially in the 29 × 29 window, where the classification accuracy reaches the maximum. On the one hand, this shows that the spatial characteristics of the samples using this window size are enough to cover the data noise, which reflects the classification potential of prototypical networks; on the other hand, it also shows that the current prototypical networks model still has potential for improvement in feature extraction. Improving its feature extraction method can fully mine the feature information of samples on a small window in further study.

4.2. The Influence of Convolutional Attention Module on Prototypical Networks

In the field of image classification based on deep learning, the output of each layer in the network can be represented as a three-dimensional feature map. In order to improve the effectiveness of the image features, the attention mechanism [43] is applied to few-shot image classification algorithms as a form of image feature enhancement. The previous research achieved a single attention mechanism [44] and a multiple attention mechanism [45], and compared these two methods. The experimental results show that the model based on the hybrid attention mechanism can extract image information more sufficiently and achieve a better classification performance [35,36,45]. Therefore, our research focuses on the hybrid attention mechanism. In this experiment, we compared three different arrangements of the channel attention and spatial attention submodules in CBAM-P-Net: Channel First, Spatial First, and Parallel. The three combination methods have shown an improvement in classification performance, and the best classification performance has been obtained in the 17 × 17 window, which is consistent with our expectations. Since each module has different functions, we speculate that the performance improvement comes from accurate attention and noise reduction of irrelevant clutter. From a spatial perspective, channel attention is applied globally, while spatial attention is applied locally. Combining two attention outputs to construct a three-dimensional attention map, it can be predicted that the sequential mode should be better than the parallel mode, and the application mode of Channel First is more in line with our optimal arrangement strategy. The average growth of Channel First and Spatial First in OA and Kappa is higher than that of Parallel, and the best classification performance obtained by Channel First shows the better interpretability of CBAM.

4.3. The Effect of the Number of Training Samples on Classification Accuracy

In the deep learning algorithm, a large number of training samples are the guarantee for obtaining the optimal model, and the training samples need to contain a variety of different scenarios, so that the testing model has sufficient robustness [46]. Therefore, more effective sample information is of great significance to the training of a high-precision classification model. In this study, we re-divided the sample ratio, and the overall classification performance showed a gradient decline with the reduction of training samples, which demonstrated the importance of training samples for the CBAM-P-Net model. When we use 80% (96 samples per class, 1056 samples in total) of samples as training samples, we get 97.28% as the highest OA and 0.9701 as the highest Kappa, whereas using 40% (48 samples per class, 528 samples in total) of samples, the highest OA is 94.83%, and the highest Kappa is 0.9432. In the same research area, Zhang et al. [16] constructed a 3D-CNN model for 12 categories of classification using 5342 training samples, and the OA and Kappa were 95.74% and 0.9705, respectively. Another study [39] used the training samples consistent with this paper (96 samples per class, 1056 samples in total), but over-fitting occurred when the original hyperspectral image was classified. The OA and Kappa were 71.08% and 0.6819, respectively. This confirms the advantages of CBAM-P-Net proposed in this paper for classifying few-shot data sets. Due to the different application scenarios, this research aims to consider the equilibrium of various categories of samples. Therefore, there are differences in the number of categories and the number of samples within the category from the data set constructed by the previous researches. When the training sample is reduced to 20% (24 training samples for each class), the classification accuracy increases up to 92%, which shows that the CBAM-P-Net is practical and that the model still has a large improvement.

4.4. Comparison of Prototypical Networks and Matching Networks

The comparison of the proposed method with those in the literature is presented in Table 9 and Table 10. Generally speaking, our method performs better than other methods with significant margins in terms of training time cost and test accuracy. The performance improvements of the proposed method are mainly due to the effectiveness of the proposed model. Furthermore, two few-shot learning methods are compared. Prototypical networks and matching networks have the same structure in the feature extraction part, and so the way to insert CBAM is also consistent. In this study, under the same experimental conditions, we constructed prototypical networks and matching networks, as well as CBAM-P-Net and CBAM-M-Net after joining CBAM. Although the model after joining CBAM has caused a certain consumption of training time, the advantages of CBAM-P-Net and CBAM-M-Net in classification accuracy are inspiring enough to show the positive effect of CBAM on feature extraction. In terms of network structure, prototypical networks unifies the coding layer and the classification layer, which has fewer parameters than matching networks. This is particularly evident for 125-bands hyperspectral images, which directly reflected the huge difference in training time between our model and the matching networks model. CBAM-P-Net is superior to CBAM-M-Net in the classification accuracy of different tree species, which not only illustrates the advantages of the prototypical networks in the classification performance compared with the matching networks, but also shows that the Euclidean distance that satisfies the Bregman divergences is better than cosine measurement distance in clustering.

5. Conclusions

The CBAM-P-Net proposed in this paper has a great performance in the forest tree species classification. When using the optimized prototypical networks to classify nine complex forest tree species, cutover land, and roads in the 74.1 hm2 study area with airborne hyperspectral images, training only takes 1209 s. The highest testing accuracy OA reaches 97.28%, and Kappa reaches 0.9701, which can be used for the regional fine-grained classification and mapping of tree species.

• When samples of different window sizes are input into prototypical networks, there is an optimal window for classification. The window size should be determined according to the area size and forest stand distribution pattern.
• For the classification of hyperspectral remote sensing images with hundreds of bands, the feature extraction method of conventional prototypical networks is slightly insufficient. Adding CBAM between the convolutional blocks of prototypical networks and configuring channel attention prior to spatial attention (Channel First) can improve the feature extraction efficiency. Thus, the proposed CBAM-P-Net can effectively solve the few-shot classification problem.
• Compared with matching networks, prototypical networks has shorter training time and higher testing accuracy for tree species classification using hyperspectral images. From tens of millions of training parameters to one hundred thousand, the training time of the prototypical networks is shortened by thousands of times, and the classification accuracy of the prototypical networks is higher. Compared with CBAM-M-Net, CBAM-P-Net shows a higher classification accuracy on different tree species. Therefore, using CBAM-P-Net to classify and map tree species distribution based on airborne hyperspectral images can achieve better results.