Modelling the Diameter Distribution of Savanna Trees with Drone-Based LiDAR
Abstract
1. Introduction
2. Materials and Methods
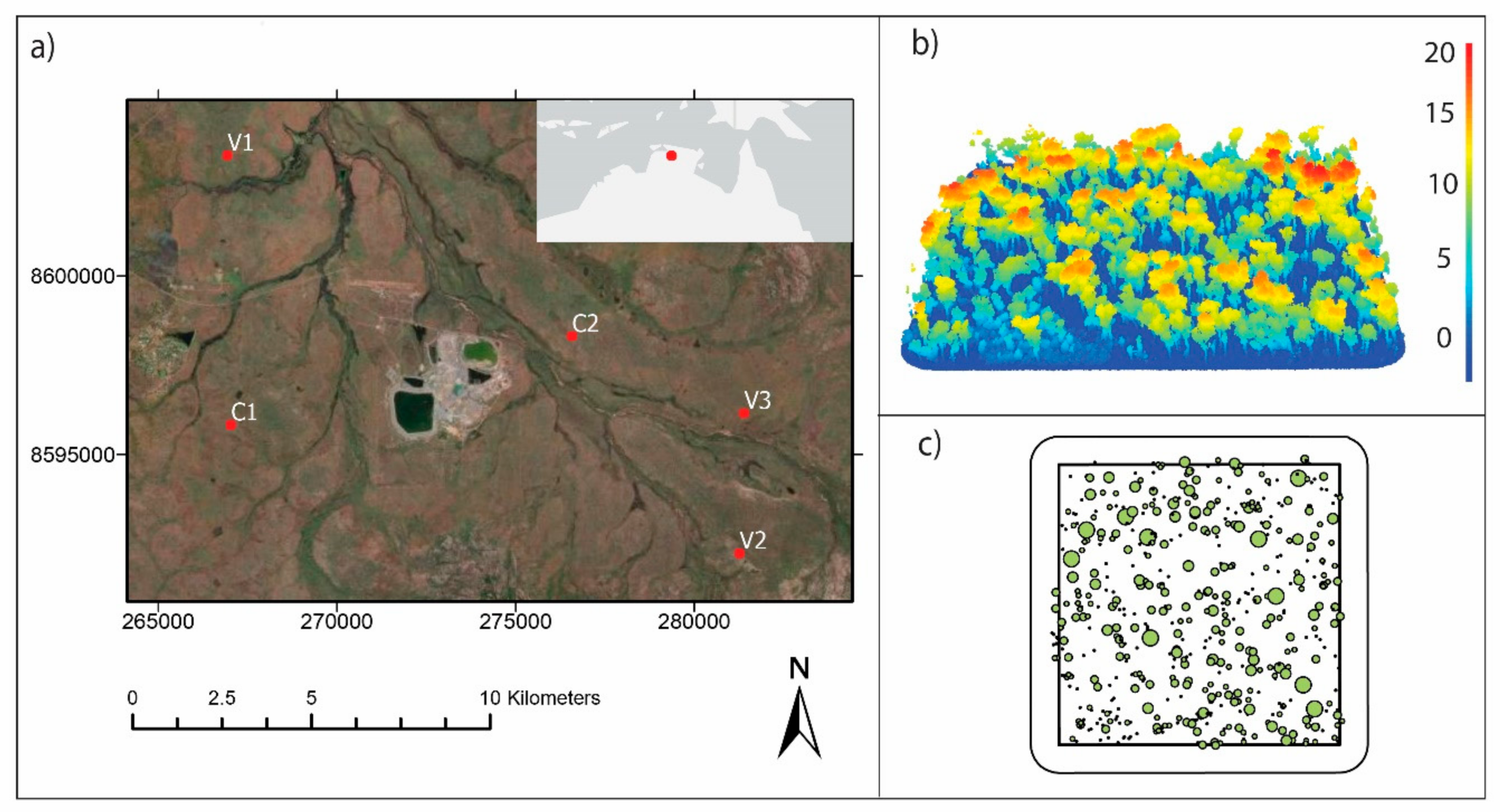
2.1. Study Site
2.2. Remote Sensing Data Collection
2.3. Field Data Collection
2.4. Data Analysis Overview
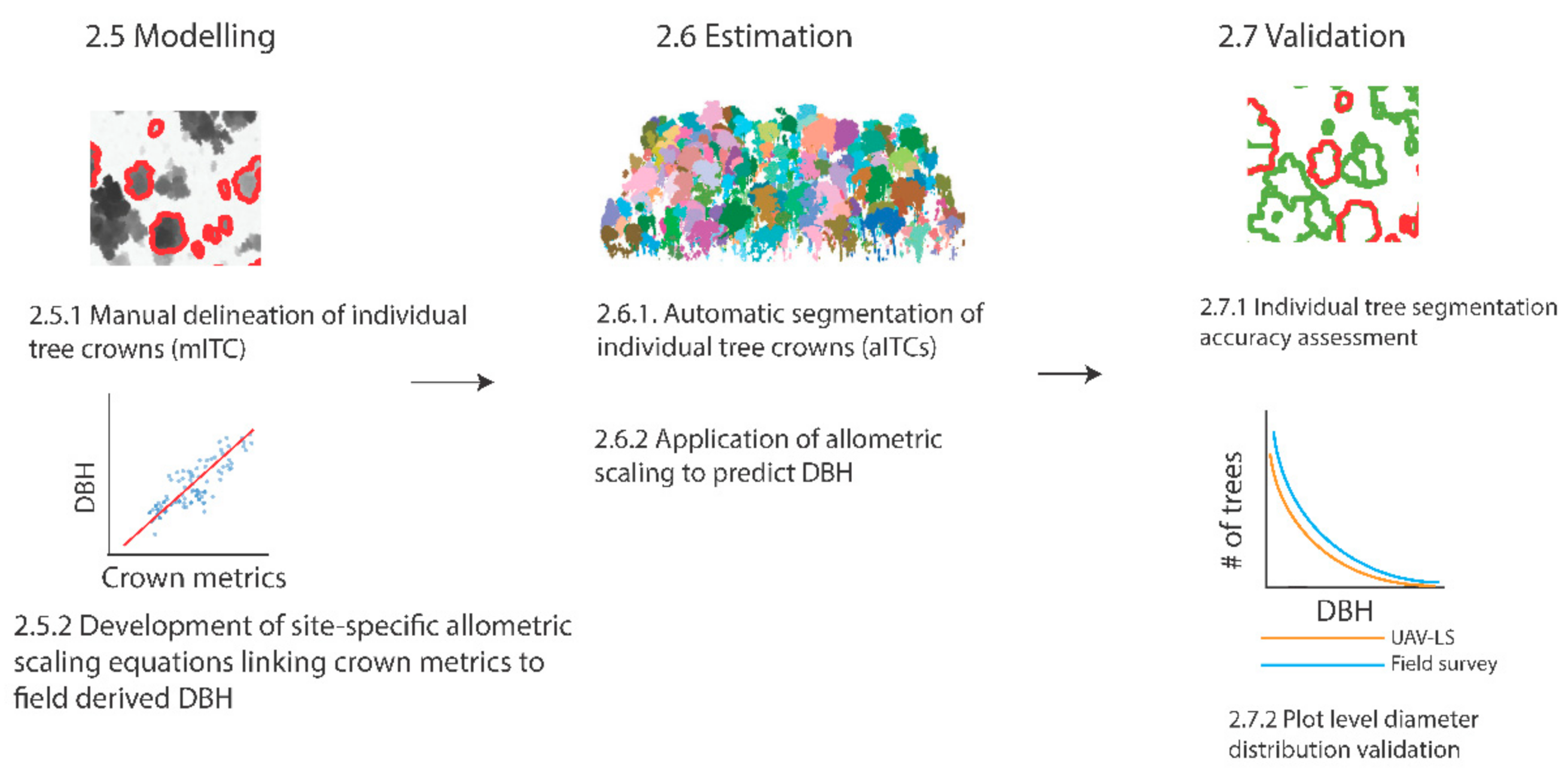
2.5. Modelling
2.5.1. Manual Delineation of Individual Tree Crowns (mITC)
2.5.2. Development of Site-Specific Allometric Scaling Equations Linking Crown Metrics to Field Derived DBH
2.6. Estimation
2.6.1. Automatic Segmentation of Individual Tree Crowns (aITCs)
2.6.2. Application of Allometric Scaling to Predict DBH
2.7. Validation
2.7.1. Individual Tree Segmentation Accuracy Assessment
2.7.2. Plot Level Diameter Distribution Validation
3. Results
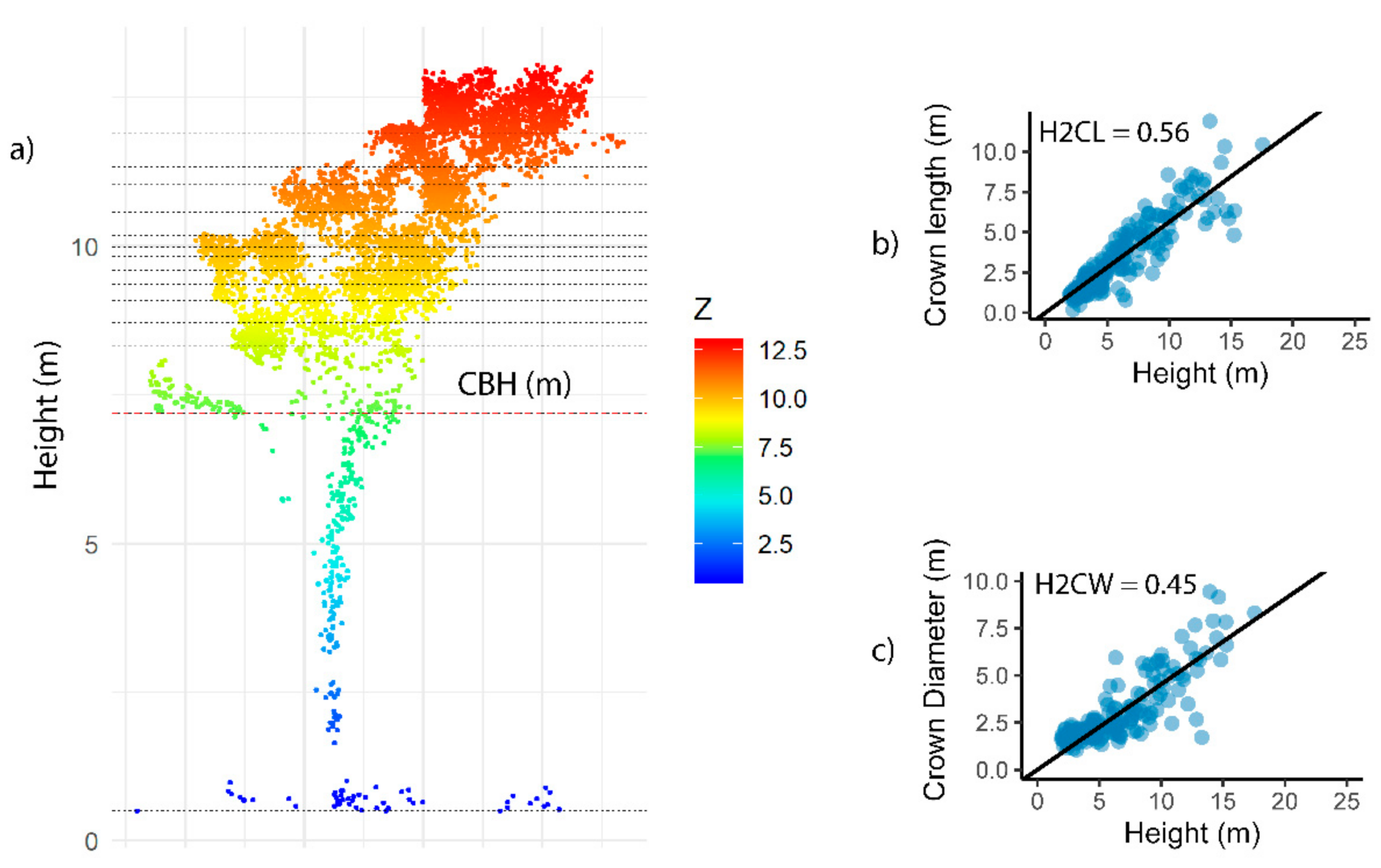
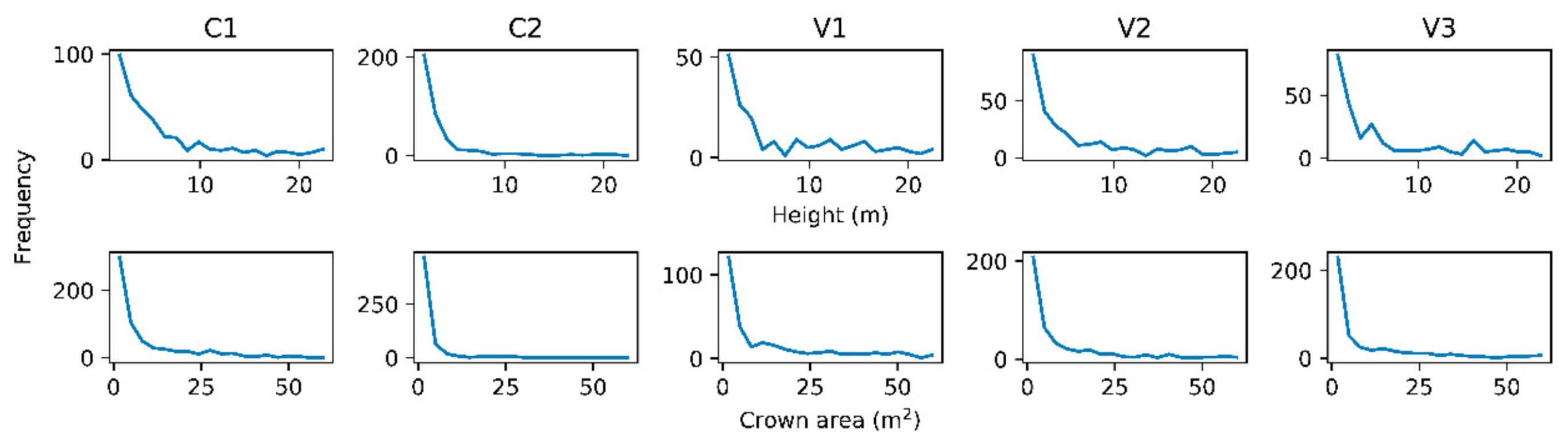
3.1. Development of Allometry to Predict DBH from Crown Metrics
3.2. Individual Tree Level Segmentation Accuracy Assessment
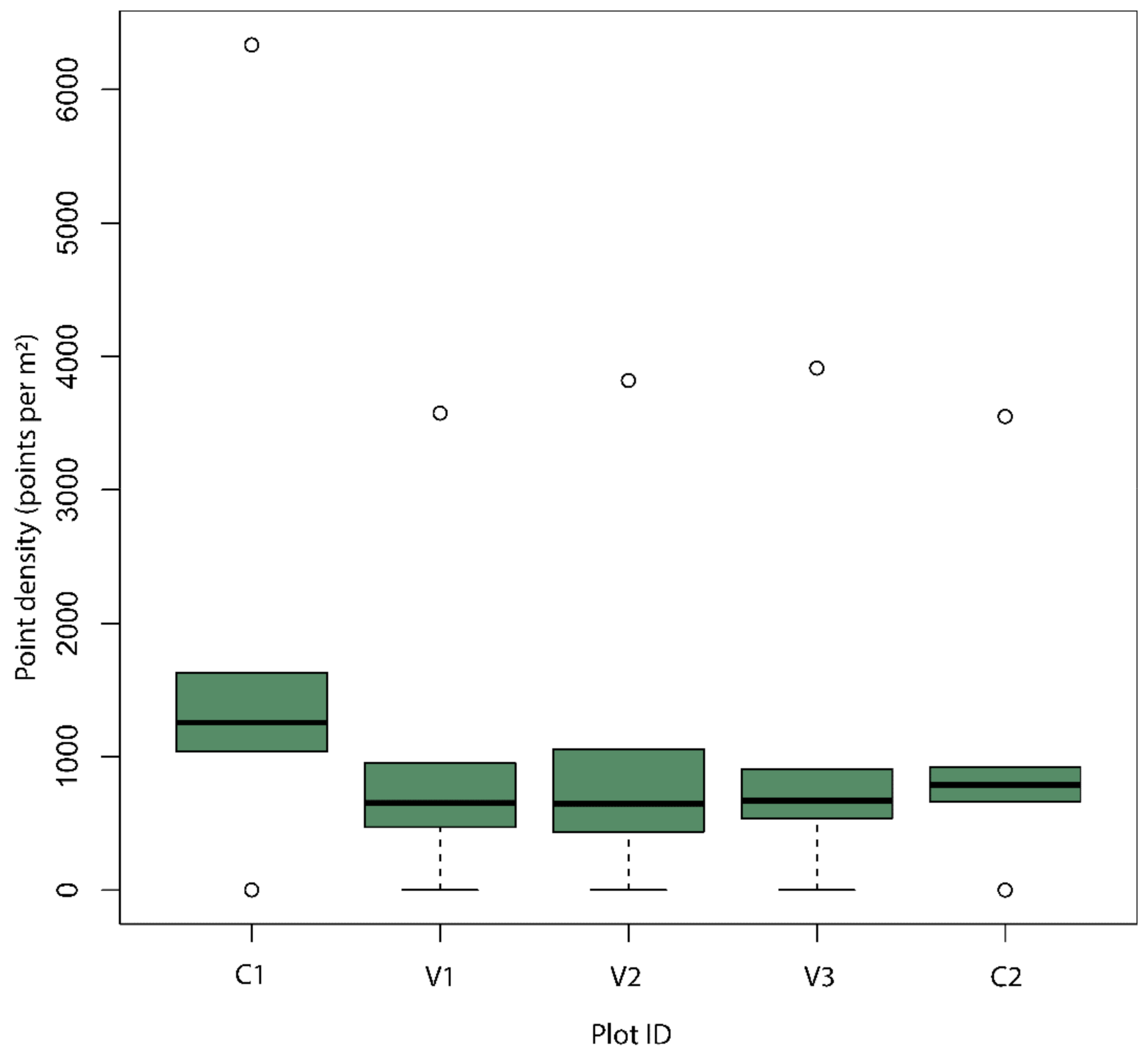
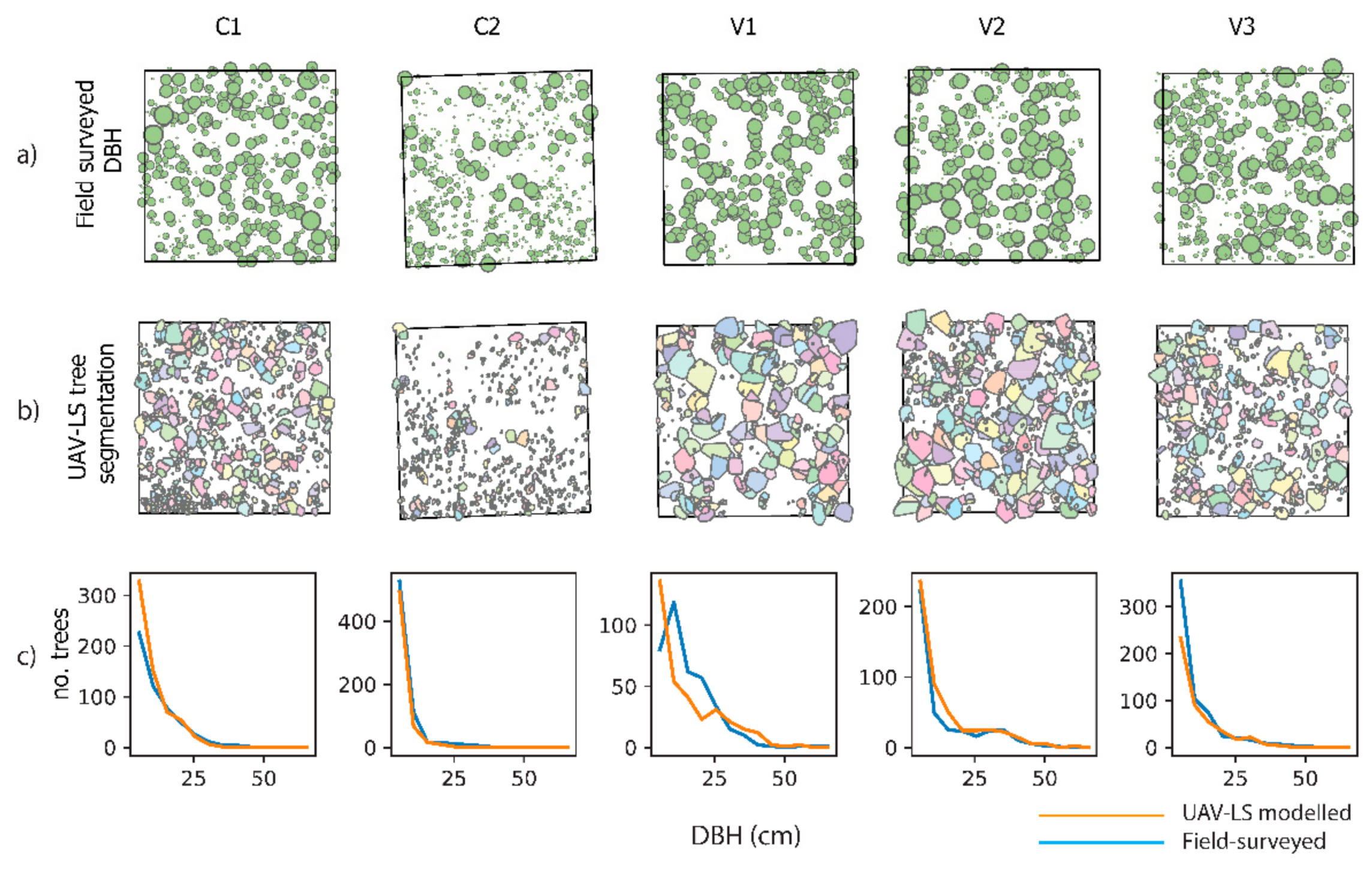
3.3. Plot Level Tree Detection and Diameter Distribution Accuracy Assessment
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

Appendix B
References
- Scholes, R.J.; Archer, S.R. Tree-Grass Interactions in Savannas. Annu. Rev. Ecol. Syst. 1997, 28, 517–544. [Google Scholar] [CrossRef]
- Grace, J.; José, J.S.; Meir, P.; Miranda, H.S.; Montes, R.A. Productivity and Carbon Fluxes of Tropical Savannas. J. Biogeogr. 2006, 33, 387–400. [Google Scholar] [CrossRef]
- Sankaran, M.; Ratnam, J.; Hanan, N.P. Tree-Grass Coexistence in Savannas Revisited—Insights from an Examination of Assumptions and Mechanisms Invoked in Existing Models. Ecol. Lett. 2004, 7, 480–490. [Google Scholar] [CrossRef]
- Scheiter, S.; Higgins, S.I. Impacts of Climate Change on the Vegetation of Africa: An Adaptive Dynamic Vegetation Modelling Approach. Glob. Chang. Biol. 2009, 15, 2224–2246. [Google Scholar] [CrossRef]
- Lehmann, C.E.R.; Archibald, S.A.; Hoffmann, W.A.; Bond, W.J. Deciphering the Distribution of the Savanna Biome. New Phytol. 2011, 191, 197–209. [Google Scholar] [CrossRef]
- Murphy, B.P.; Bowman, D.M.J.S. What Controls the Distribution of Tropical Forest and Savanna? Ecol. Lett. 2012, 15, 748–758. [Google Scholar] [CrossRef]
- Woinarski, J.C.Z.; Risler, J.; Kean, L. Response of Vegetation and Vertebrate Fauna to 23 Years of Fire Exclusion in a Tropical Eucalyptus Open Forest, Northern Territory, Australia. Austral. Ecol. 2004, 29, 156–176. [Google Scholar] [CrossRef]
- Murphy, B.P.; Russell-Smith, J.; Prior, L.D. Frequent Fires Reduce Tree Growth in Northern Australian Savannas: Implications for Tree Demography and Carbon Sequestration. Glob. Chang. Biol. 2010, 16, 331–343. [Google Scholar] [CrossRef]
- Lykke, A.M. Assessment of Species Composition Change in Savanna Vegetation by Means of Woody Plants’ Size Class Distributions and Local Information. Biodivers. Conserv. 1998, 7, 1261–1275. [Google Scholar] [CrossRef]
- Holdo, R.M.; Anderson, T.M.; Morrison, T. Precipitation, Fire and Demographic Bottleneck Dynamics in Serengeti Tree Populations. Landsc. Ecol. 2014, 29, 1613–1623. [Google Scholar] [CrossRef]
- Roitman, I.; Felfili, J.M.; Rezende, A.V. Tree Dynamics of a Fire-Protected Cerrado Sensu Stricto Surrounded by Forest Plantations, over a 13-Year Period (1991–2004) in Bahia, Brazil. Plant Ecol. 2008, 197, 255–267. [Google Scholar] [CrossRef]
- Levick, S.R.; Baldeck, C.A.; Asner, G.P. Demographic Legacies of Fire History in an African Savanna. Funct. Ecol. 2015, 29, 131–139. [Google Scholar] [CrossRef]
- Staver, C. Prediction and Scale in Savanna Ecosystems. New Phytol. 2018, 219, 52–57. [Google Scholar] [CrossRef] [PubMed]
- Maltamo, M.; Gobakken, T. Predicting Tree Diameter Distributions. In Forestry Applications of Airborne Laser Scanning: Concepts and Case Studies; Maltamo, M., Næsset, E., Vauhkonen, J., Eds.; Springer: Heidelberg, Germany, 2014; pp. 177–191. [Google Scholar] [CrossRef]
- Dalponte, M.; Coomes, D.A. Tree-Centric Mapping of Forest Carbon Density from Airborne Laser Scanning and Hyperspectral Data. Methods Ecol. Evol. 2016, 7, 1236–1245. [Google Scholar] [CrossRef]
- Silva, C.A.; Hudak, A.T.; Vierling, L.A.; Loudermilk, E.L.; O’Brien, J.J.; Hiers, J.K.; Jack, S.B.; Gonzalez-Benecke, C.; Lee, H.; Falkowski, M.J.; et al. Imputation of Individual Longleaf Pine (Pinus Palustris Mill.) Tree Attributes from Field and LiDAR Data. Can. J. Remote Sens. 2016, 42, 554–573. [Google Scholar] [CrossRef]
- Li, W.; Guo, Q.; Jakubowski, M.K.; Kelly, M. A New Method for Segmenting Individual Trees from the Lidar Point Cloud. Photogramm. Eng. Remote Sens. 2012, 78, 75–84. [Google Scholar] [CrossRef]
- Roussel, J.R.; Auty, D.; Coops, N.C.; Tompalski, P.; Goodbody, T.R.H.; Meador, A.S.; Bourdon, J.F.; de Boissieu, F.; Achim, A. LidR: An R Package for Analysis of Airborne Laser Scanning (ALS) Data. Remote Sens. Environ. 2020, 251, 112061. [Google Scholar] [CrossRef]
- Ferraz, A.; Saatchi, S.; Mallet, C.; Meyer, V. Lidar Detection of Individual Tree Size in Tropical Forests. Remote Sens. Environ. 2016, 183, 318–333. [Google Scholar] [CrossRef]
- Knapp, N. MeanShiftR. Available online: https://github.com/niknap/MeanShiftR (accessed on 15 November 2020).
- Jucker, T.; Caspersen, J.; Chave, J.; Antin, C.; Barbier, N.; Bongers, F.; Dalponte, M.; van Ewijk, K.Y.; Forrester, D.I.; Haeni, M.; et al. Allometric Equations for Integrating Remote Sensing Imagery into Forest Monitoring Programmes. Glob. Chang. Biol. 2017, 23, 177–190. [Google Scholar] [CrossRef] [PubMed]
- Dalponte, M.; Frizzera, L.; Ørka, H.O.; Gobakken, T.; Næsset, E.; Gianelle, D. Predicting Stem Diameters and Aboveground Biomass of Individual Trees Using Remote Sensing Data. Ecol. Indic. 2018, 85, 367–376. [Google Scholar] [CrossRef]
- Goldbergs, G.; Maier, S.; Levick, S.; Edwards, A.; Goldbergs, G.; Maier, S.W.; Levick, S.R.; Edwards, A. Efficiency of Individual Tree Detection Approaches Based on Light-Weight and Low-Cost UAS Imagery in Australian Savannas. Remote Sens. 2018, 10, 161. [Google Scholar] [CrossRef]
- Torresan, C.; Carotenuto, F.; Chiavetta, U.; Miglietta, F.; Zaldei, A.; Gioli, B. Individual Tree Crown Segmentation in Two-Layered Dense Mixed Forests from UAV LiDAR Data. Drones 2020, 4, 10. [Google Scholar] [CrossRef]
- Camarretta, N.; Harrison, P.A.; Lucieer, A.; Potts, B.M.; Davidson, N.; Hunt, M. From Drones to Phenotype: Using UAV-LiDAR to Detect Species and Provenance Variation in Tree Productivity and Structure. Remote Sens. 2020, 12, 3184. [Google Scholar] [CrossRef]
- Puliti, S.; Breidenbach, J.; Astrup, R. Estimation of Forest Growing Stock Volume with UAV Laser Scanning Data: Can It Be Done without Field Data? Remote Sens. 2020, 12, 1245. [Google Scholar] [CrossRef]
- Moncrieff, G.R.; Lehmann, C.E.R.; Schnitzler, J.; Gambiza, J.; Hiernaux, P.; Ryan, C.M.; Shackleton, C.M.; Williams, R.J.; Higgins, S.I. Contrasting Architecture of Key African and Australian Savanna Tree Taxa Drives Intercontinental Structural Divergence. Glob. Ecol. Biogeogr. 2014, 23, 1235–1244. [Google Scholar] [CrossRef]
- Arzai, A.; Aliyu, B. The Relationship between Canopy Width, Height and Trunk Size in Some Tree Species Growing in the Savana Zone of Nigeria. Bayero J. Pure Appl. Sci. 2010, 3. [Google Scholar] [CrossRef]
- Wells, M. Soil Studies in the Magela Creek Catchment 1978: Part 1; Land Conservation Unit, Territory Parks and Wildlife Commission: Darwin, NT, USA, 1979.
- White, A.; Sparrow, B.; Leitch, E.; Foulkes, J.; Flitton, R.; Lowe, A.J.; Caddy-Retalic, S. AUSPLOTS Rangelands Survey Protocols Manual; University of Adelaide Press: Adelaide, Australia, 2012. [Google Scholar]
- Hernandez-Santin, L.; Rudge, M.L.; Bartolo, R.E.; Whiteside, T.G.; Erskine, P.D. Reference Site Selection Protocols for Mine Site Ecosystem Restoration. Restor. Ecol. 2020. [Google Scholar] [CrossRef]
- Khosravipour, A.; Skidmore, A.K.; Isenburg, M.; Wang, T.; Hussin, Y.A. Generating Pit-Free Canopy Height Models from Airborne Lidar. Photogramm. Eng. Remote Sens. 2014, 80, 863–872. [Google Scholar] [CrossRef]
- Awang, K.; Venkateswarlu, P.; Nor Aini, A.S.; Adjers, G.; Bhumibhamon, S.; Kietvuttinon, B.; Pan, F.J.; Pitpreecha, K.; Simsiri, A. Three Year Performance of International Provenance Trials of Acacia Auriculiformis. For. Ecol. Manag. 1994, 70, 147–158. [Google Scholar] [CrossRef]
- Seabold, S.; Perktold, J. Statsmodels: Econometric and Statistical Modeling with Python. In Proceedings of the 9th Python in Science Conference, Austin, TX, USA, 28 June–3 July 2010; Volume 57, p. 61. [Google Scholar]
- Cleveland, W.S. Robust Locally Weighted Regression and Smoothing Scatterplots. J. Am. Stat. Assoc. 1979, 74, 829–836. [Google Scholar] [CrossRef]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef] [PubMed]
- Aubry-Kientz, M.; Dutrieux, R.; Ferraz, A.; Saatchi, S.; Hamraz, H.; Williams, J.; Coomes, D.; Piboule, A.; Vincent, G. A Comparative Assessment of the Performance of Individual Tree Crowns Delineation Algorithms from ALS Data in Tropical Forests. Remote Sens. 2019, 11, 1086. [Google Scholar] [CrossRef]
- Solberg, S.; Naesset, E.; Bollandsas, O.M. Single Tree Segmentation Using Airborne Laser Scanner Data in a Structurally Heterogeneous Spruce Forest. Photogramm. Eng. Remote Sens. 2006, 72, 1369–1378. [Google Scholar] [CrossRef]
- Chamberlain, C.P.; Sánchez Meador, A.J.; Thode, A.E. Airborne Lidar Provides Reliable Estimates of Canopy Base Height and Canopy Bulk Density in Southwestern Ponderosa Pine Forests. For. Ecol. Manag. 2021, 481. [Google Scholar] [CrossRef]
- Hastings, J.H.; Ollinger, S.V.; Ouimette, A.P.; Sanders-DeMott, R.; Palace, M.W.; Ducey, M.J.; Sullivan, F.B.; Basler, D.; Orwig, D.A. Tree Species Traits Determine the Success of LiDAR-Based Crown Mapping in a Mixed Temperate Forest. Remote Sens. 2020, 12, 309. [Google Scholar] [CrossRef]
- Yin, D.; Wang, L. How to Assess the Accuracy of the Individual Tree-Based Forest Inventory Derived from Remotely Sensed Data: A Review. Int. J. Remote Sens. 2016, 37, 4521–4553. [Google Scholar] [CrossRef]
- Hodges, J.L. The Significance Probability of the Smirnov Two-Sample Test. Ark. För Mat. 1958, 3, 469–486. [Google Scholar] [CrossRef]
- Luck, L.; Hutley, L.B.; Calders, K.; Levick, S.R. Exploring the Variability of Tropical Savanna Tree Structural Allometry with Terrestrial Laser Scanning. Remote Sens. 2020, 12, 3893. [Google Scholar] [CrossRef]
- Hutley, L.; Beringer, J. Disturbance and Climatic Drivers of Carbon Dynamics of a North Australian Tropical Savanna. Ecosyst. Funct. Savannas 2010, 2014, 57–75. [Google Scholar] [CrossRef]
- Brede, B.; Calders, K.; Lau, A.; Raumonen, P.; Bartholomeus, H.M.; Herold, M.; Kooistra, L. Non-Destructive Tree Volume Estimation through Quantitative Structure Modelling: Comparing UAV Laser Scanning with Terrestrial LIDAR. Remote Sens. Environ. 2019, 233, 111355. [Google Scholar] [CrossRef]
- The United Nations Department of Economic and Social Affairs. Sustainable Development Goals. Available online: https://sdgs.un.org/goals (accessed on 20 October 2020).
- Windrim, L.; Bryson, M. Detection, Segmentation, and Model Fitting of Individual Tree Stems from Airborne Laser Scanning of Forests Using Deep Learning. Remote Sens. 2020, 12, 1469. [Google Scholar] [CrossRef]
- Levick, S.R.; Whiteside, T.; Loewensteiner, D.A.; Rudge, M.; Bartolo, R. Leveraging TlS as a Calibration and Validation Tool for MlS and UlS Mapping of Savanna Structure and Biomass at Landscape-Scales. Remote Sens. 2021, 13, 257. [Google Scholar] [CrossRef]
- Williams, R.J.; Zerihun, A.; Montagu, K.D.; Hoffman, M.; Hutley, L.B.; Chen, X. Allometry for Estimating Aboveground Tree Biomass in Tropical and Subtropical Eucalypt Woodlands: Towards General Predictive Equations. Aust. J. Bot. 2005, 53, 607–619. [Google Scholar] [CrossRef]
- Ocer, N.E.; Kaplan, G.; Erdem, F.; Kucuk Matci, D.; Avdan, U. Tree Extraction from Multi-Scale UAV Images Using Mask R-CNN with FPN. Remote Sens. Lett. 2020, 11, 847–856. [Google Scholar] [CrossRef]


| Calibration Plots | Validation Plots | |||
|---|---|---|---|---|
| DBH size class (cm) | Number crowns accurately segmented | Accuracy % | Number of accurately segmented crowns | Accuracy % |
| <10 | 41 (137) | 30 | 38 (56) | 68 |
| 10–20 | 37 (47) | 79 | 15 (25) | 60 |
| >20 | 18 (21) | 86 | 14 (17) | 82 |
| All sizes | 96 (205) | 47 | 67 (98) | 68 |
| Plot ID | DBH Size Class | <10 cm | 10–20 cm | >20 cm | Total |
|---|---|---|---|---|---|
| C1 | No. field survey | 268 | 187 | 64 | 519 |
| No. UAV-LS segmentation | 397 | 178 | 56 | 631 | |
| % segmented | 148 | 95 | 88 | 122 | |
| C2 | No. field survey | 607 | 51 | 36 | 694 |
| No. UAV-LS segmentation | 531 | 51 | 6 | 588 | |
| % segmented | 87 | 100 | 17 | 85 | |
| V1 | No. field survey | 128 | 162 | 93 | 383 |
| No. UAV-LS segmentation | 154 | 83 | 101 | 338 | |
| % segmented | 120 | 51 | 109 | 88 | |
| V2 | No. field survey | 248 | 60 | 93 | 401 |
| No. UAV-LS segmentation | 269 | 117 | 111 | 497 | |
| % segmented | 108 | 195 | 119 | 124 | |
| V3 | No. field survey | 407 | 135 | 71 | 613 |
| No. UAV-LS segmentation | 280 | 114 | 69 | 463 | |
| % segmented | 69 | 84 | 97 | 76 |
| All Size Classes | >10 cm DBH | >20 cm DBH | ||||
|---|---|---|---|---|---|---|
| Plot | D | p value | D | p value | D | p value |
| C1 | 0.170 | <0.001 | 0.065 | 0.651 | 0.234 | 0.063 |
| C2 | 0.251 | <0.001 | 0.344 | 0.001 | 0.583 | 0.041 |
| V1 | 0.198 | <0.001 | 0.221 | <0.001 | 0.249 | 0.004 |
| V2 | 0.180 | <0.001 | 0.160 | 0.016 | 0.106 | 0.569 |
| V3 | 0.246 | <0.001 | 0.101 | 0.252 | 0.163 | 0.272 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rudge, M.L.M.; Levick, S.R.; Bartolo, R.E.; Erskine, P.D. Modelling the Diameter Distribution of Savanna Trees with Drone-Based LiDAR. Remote Sens. 2021, 13, 1266. https://doi.org/10.3390/rs13071266
Rudge MLM, Levick SR, Bartolo RE, Erskine PD. Modelling the Diameter Distribution of Savanna Trees with Drone-Based LiDAR. Remote Sensing. 2021; 13(7):1266. https://doi.org/10.3390/rs13071266
Chicago/Turabian StyleRudge, Mitchel L. M., Shaun R. Levick, Renee E. Bartolo, and Peter D. Erskine. 2021. "Modelling the Diameter Distribution of Savanna Trees with Drone-Based LiDAR" Remote Sensing 13, no. 7: 1266. https://doi.org/10.3390/rs13071266
APA StyleRudge, M. L. M., Levick, S. R., Bartolo, R. E., & Erskine, P. D. (2021). Modelling the Diameter Distribution of Savanna Trees with Drone-Based LiDAR. Remote Sensing, 13(7), 1266. https://doi.org/10.3390/rs13071266








