SNR Enhancement of Back Scattering Signals for Bistatic Radar Based on BeiDou GEO Satellites

Abstract

Using scattering signals of the global navigation satellite system (GNSS) for target detection has become one of the research hotspots. This technology faces the difficulty of low signal-to-noise ratio (SNR) target echoes. Since BeiDou geostationary orbit (GEO) satellites provide the opportunity to form a bistatic radar with some advantages, such as fixed coverage area and quasi monostatic configuration to avoid the interference from the direct signals, the target echoes may have regular phases that are beneficial to SNR enhancement. This study uses BeiDou GEO satellites and ground fixed receivers to form a bistatic radar and analyzes the phase changes in the reflected signal caused by the target, then gives two methods for SNR enhancement corresponding to two applications: deformation monitoring and ship detection. This paper first introduces the basic signal processing including the intermediate frequency (IF) signal collector and the range compression in the software receiver, then describes the basic SNR enhancement method, i.e., increasing coherence integration time (CIT), and shows its limitation by two target cases: static metal reflector on the land and ships in the water. After that, this study provides an improved SNR enhancement method based on Doppler and range compensation in the moving ship detection case. The experiment shows that by the SNR enhancement, the SNRs of target echo signals in range/Doppler domain increase more than 4 dB on average. This study also demonstrates the bistatic radar’s potential for monitoring surface deformation.

1. Introduction

Using global navigation satellite system (GNSS) reflected signals to construct a bistatic radar for remote sensing on an object is a popular issue. When the radio signal transmitted from the navigation satellite impinges on the target, it is reflected and contains the target information, then a satellite-based, aircraft-based, or ground-based receiver is employed to capture this signal and retrieve the physical parameters such as vegetation optical depth, soil moisture, sea ice surface, and ocean surface wind speed [1,2]. Especially, when the receiver is installed at a fixed position on the ground, the receiver can be used for target imaging [3,4,5,6], maritime target detection [7,8], and surface deformation monitoring [9,10]. GNSS signals are particularly attractive given their advantages of multiple frequencies, low cost, and global coverage.

At present, the research of ground-based bistatic radar has commonly faced the challenge of low signal-to-noise ratio (SNR) target echo due to the following reasons: (1) Unfixed coverage areas lead the coherent and incoherent components of the reflected signal to change with the ground. For example, Global Position System (GPS), GLONASS, and Galileo mainly use moving satellites. Their coverage area varies with the geometric configuration of satellite and receiver. The unfixed configuration leads to the reflected signal not coming from the same area, which results in phase coherence not being guaranteed. The proportion of the coherent and incoherent components in the reflected signal changes with ground targets. As a result, the phase stability of the signal not only needs to be evaluated but also needs to be separated from the phase caused by the motion of the satellite, which brings limitation to coherent integration time (CIT). (2) The radio waves emitted by the satellite are continuous, and no time-division exists between the received and transmitted signals, which result in the interference between the reflected signal and the direct signal; (3) The GNSS signals are not designed for radar, so the power reaching the ground is not strong.

Several methods have been used to solve these challenges. For example, to study the deformation applications based on BeiDou system (BDS) inclined geosynchronous orbit (IGSO) satellites, a dedicated transponder with amplifier is constructed to simulate the displacement device which can generate strong reflected signals [11], but the drawback of this method is the need of supply power to the transponder. Moreover, some signal processing methods are presented, for example, the long accumulation time method based on the short-time Fourier transform (STFT) and the Keystone transform are used to correct the range cell migration [12], but this method is only effective for signals with high radial velocity and relatively high bandwidth; also, fractional Fourier transform (FrFT) is employed for long time integration [13]. Although simulation results prove its validity, multiple targets in close range will lead to errors in the results in actual measurement. To overcome the interference between direct and reflected signals, several studies use the backscattering model instead of the front scattering model [14], but the geometric limitations caused by the motion of the satellite still exist. Furthermore, the idea of using specially designed geostationary orbit (GEO) satellites to construct a bistatic radar for target detection in a fixed area has also been proposed and simulated [15], but more experiments with existing GNSS satellites are needed to verify it.

The BDS has five GEO satellites (C01, C02, C03, C04, and C05) with nearly unchanged azimuths and elevations compared with medium Earth orbit (MEO) or IGSO satellites when observed in central China. Thus, a GEO satellite and a fixed ground-based receiver can construct a bistatic radar, which has two characteristics. The first one is that this radar has a fixed covering area for long-term monitoring. So, it can provide an opportunity to study the phase stability of static target echoes over a period of time, similar to the study of permanent scatterers in synthetic aperture radar (SAR) images. The second one is that it can easily distinguish the movement of the target by the Doppler frequency (the phase change rate). To avoid the interference from the direct signal, the radar can be configured to backscatter radar (quasi monostatic radar) [16]. The above characteristics provide a possibility of signal processing to improve SNR.

The purposes of this study are to analyze the phase characteristics of scattered signals from GEO satellites and provide two methods to increase SNR for static and moving targets, this paper will also show the potential of GEO bistatic radar in deformation measurement and ship detection. The remaining content of this paper is organized as follows. Section 2 describes the basic signal processing including the intermediate frequency (IF) signal collector and the range compression in the software receiver. Section 3 describes the first basic SNR enhance method, i.e., increasing CIT, and shows its limitation by two target cases: metal reflector on the land and the ships on the water. Section 4 provides the improved SNR enhancement method based on Doppler and range offsets compensation in the moving ship detection case. Section 5 gives some discussions on the radar cross section (RCS) and application scenario. Lastly, Section 6 concludes the paper.

2. GNSS IF Signal Collector and Range Compression Based on the Software Receiver

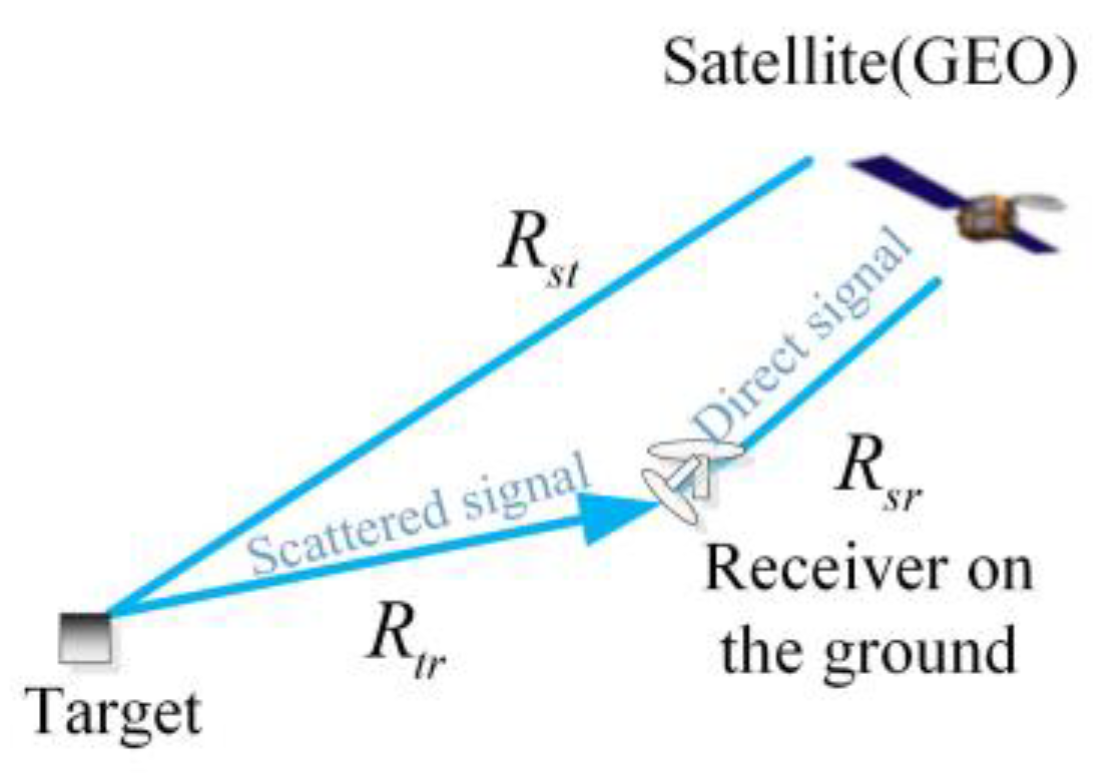
In this study, a generally bistatic radar geometric configuration is shown in Figure 1 where $R_{sr}$, $R_{st}$, and $R_{tr}$ are the distances among the satellite, the receiving antennas, and the target. The bistatic range ($R_{\Delta }$) of the target at time t can be written as:

$$R_{\Delta }\left(t\right)=R_{st}\left(t\right)+R_{tr}\left(t\right)-R_{sr}\left(t\right).$$

(1)

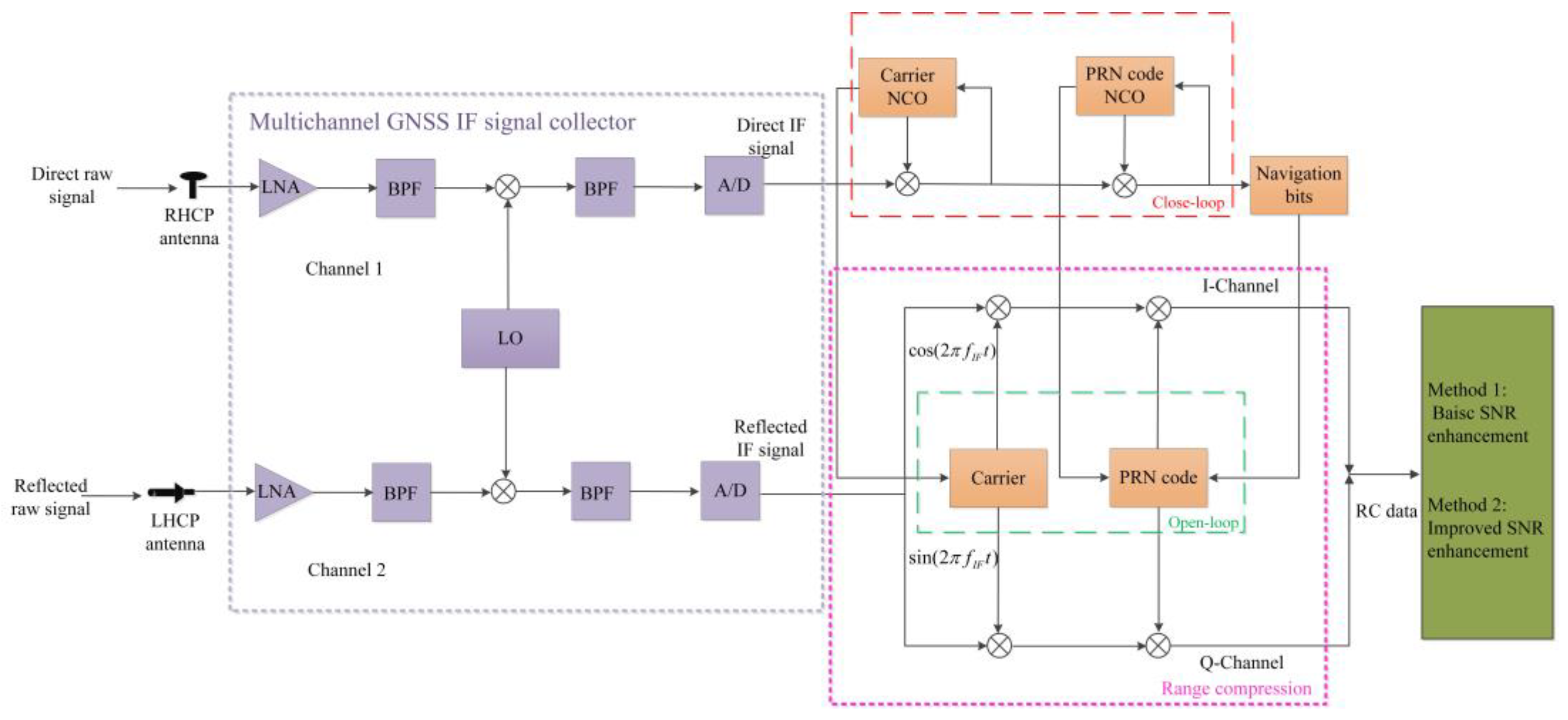
Figure 2 shows two key components of the software receiver: the multichannel GNSS IF signal collector and range compression. In each channel, the GNSS IF signal collector utilizes a combination of low-noise amplifier (LNA), band-pass filter (BPF), mixer, and its local oscillator (LO) to down-convert the input raw signal on the antenna into IF frequency and employs an analog-to-digital (A/D) converter to convert the analog signal to digital samples. These samples are then transferred to the computer. Here, the direct and reflected signals go through the same process in the different channel and share the same clock and LO.

Range compression is conducted in the computer where different signal processes are used; e.g., direct signal acquisition and closed-loop tracking are conducted to find suitable GEO satellites and reconstruct the local carrier signal and pseudo random noise (PRN) code as the reference signal; the detail can be referred to [17]. For the reflected signals, open-loop tracking, named range compression, is conducted.

The direct IF signal with a zero initial phase can be written as:

$$S_{IF,d}\left(t\right)=AC\left(t\right)D\left(t\right)\mathit{cos}\left(2\pi f_{IF}t\right)$$

(2)

which is used as the reference signal, where $A$ is the amplitude of the signal, $C\left(t\right)$ is the PRN code, and $D\left(t\right)$ is the navigation bit. The reflected signals from the target located on the bistatic range $R_{\Delta }$ can be written as:

$$S_{IF,r}\left(t\right)=AC\left[t-\frac{R_{\Delta }}{c}\right]D\left[t-\frac{R_{\Delta }}{c}\right]\mathit{cos}\left\{2\pi (f_{IF}+f_d)\left[t-\frac{R_{\Delta }}{c}\right]\right\}$$

(3)

where $c$ is the speed of light, and $f_d$ is Doppler frequency. The direct IF signals are processed with closed-loop processing to obtain the local carrier phase and PRN codes. The data are multiplied by navigation bits to solve the problem of phase inversion caused by navigation bits. Then, the reflected IF signal is processed by stripping off the carrier with the local carriers [$\mathit{cos}\left(2\pi f_{IF}t\right)$ and $\mathit{sin}\left(2\pi f_{IF}t\right)$] and being correlated with the PRN codes of the reflected signal to obtain complex echo signals with in-phase and quadrature components. PRN code has a strong nature of self-correlation; hence, the PRN code delay with the highest correlation peak intensity means the bistatic range of the reflector. In this way, the range compression of each sampling dataset in 1 ms is realized. The range compressed (RC) data can be denoted as a 2D matrix, as shown as follows:

$$\begin{array}{cc}\hfill S\left(n,t\right)& =A\Lambda \left[t-\frac{R_{\Delta }\left(n\right)}{c}\right]\mathit{exp}\left\{j\left[2\pi f_d\left(n\right)t+2\pi \frac{R_{\Delta }\left(n\right)}{\lambda }\right]\right\}\hfill \\ & =A\Lambda \left[t-\frac{R_{\Delta }\left(n\right)}{c}\right]\mathit{exp}\left[j2\pi f_d\left(n\right)t+j2\pi N\left(n\right)+j\varphi \right]\hfill \end{array}$$

(4)

where n is the index of the period of PRN codes (ms), t is the index of the sampling time in the PRN code period, and $\Lambda (·)$ is the amplitude of the cross-correlation function of PRN codes. $f_d$ is the Doppler frequency caused by the target movement. $N$ is the integer which means ambiguity, and $\varphi$ is the phase in a cycle.

3. Method 1: Basic SNR Enhancement Method-Increasing CIT

To overcome the problem of weak navigation scattering signal, SNR enhancement is necessary. A basic SNR enhancement method for static target is coherent accumulation process (CAP), i.e., increasing the coherence integration time. In the conventional navigation receiver, the CIT is generally limited by the navigation bit length (20 ms for GPS L1) because a change of navigation bit sign during the CIT would destroy the correlation. However, in our software receiver, thanks to correcting the phase inversion, we can conduct a long CAP beyond 20 ms to increase the process gain.

The RC data $S\left(n,t\right)$ can be stored in a matrix form $S\left(n,m\right)$ by transforming the time delay to the bistatic range cell, where m is the index of the range cell. When defining the consecutive target echoes in time T as a frame and assuming that there is no Doppler on the echo during the p-th frame time, the CAP of echo signal is expressed as:

$$S\left(p,m\right) ={{\displaystyle \sum }}_{n=\left(\mathrm{p}-1\right)\times \mathrm{T}+1}^{p\times T}S\left(n,m\right),$$

(5)

where T is the CIT of a frame and $p\in 1,2,\cdots ,n_{max}$ is the index of the frame.

3.1. Increasing CIT for Ground Target

We first illustrate CAP application and limitation with an example of a metal reflector as a static target. Figure 3 shows the isosceles triangle metal reflector with a side length of 1.5 m and three antennas mounted on a T-shaped support—one white right-handed circularly polarized (RHCP) patch antenna for direct signal and two high-gain left-handed circularly polarized (LHCP) helical antennas for reflected signal. The included angle ($\gamma$) between the metal reflector and the ground is about 60°, the azimuth of the metal reflector is approximately 180°. The sampling frequency of the receiver is 32.738 MHz.

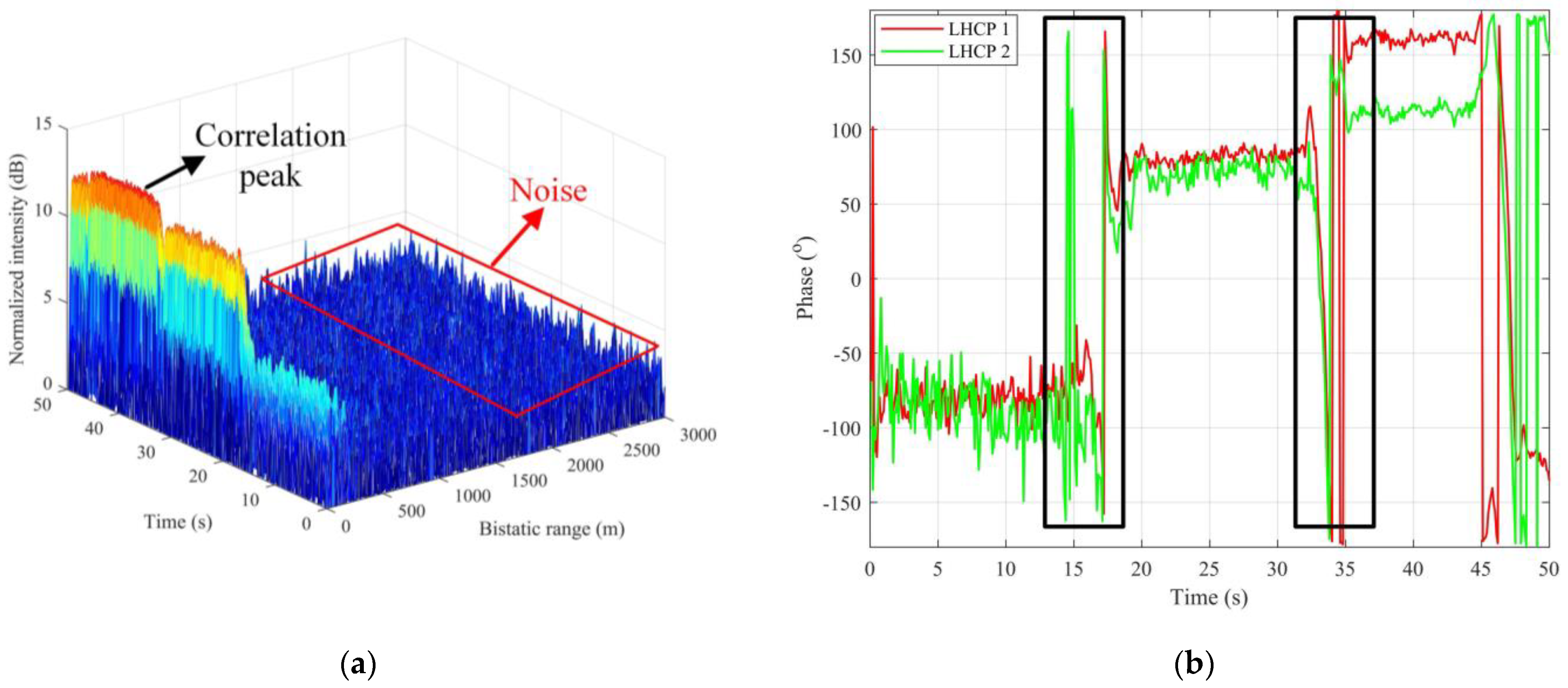
The data are recorded continuously for 50 s. During this period, the metal reflector is moved toward the LHCP antennas twice to simulate a real deformation scenario and it remains static in three positions 1, 2, 3 for 18, 18, and 14 s, respectively. Therefore, the coherence of the signal is guaranteed in each period. We adopt the CIT of 200 ms (ten times of the CIT of ordinary navigation receivers). We regard the data of C01 as an example. The 3D correlation peaks of LHCP 1 are shown in Figure 4a. At the sixth range cell (with a bistatic distance of 54.96 m), three step-shaped continuous correlation peaks occur during the entire time, which represent the three positions of the reflector. Signals received by LHCP 2 also show a similar result. Since our software receiver outputs complex signals, we can extract the phase of the signals. Figure 4b shows the phase variations of the signals received by the two LHCP antennas. The phase changes occur at 18 and 36 s. For the signals of LHCP 1, from 0 to 18 s, the mean value of the phase is −82.68°, and the RMSE is 8.20°, ignoring the data around the abrupt change. From 18 to 36 s, the mean value of the phase is 81.18°, and the RMSE is 3.43°. From 36 to 50 s, the mean phase is 160.90°, and the RMSE is 2.72°. For LHCP 2, the mean value of the phase is −87.48° and the RMSE is 9.50° from 0 to 18 s. The mean phase is 71.25° and the RMSE is 5.90° from 18 to 36 s. The mean phase is 112.21° and the RMSE is 2.82° from 36 to 50 s. The phase changes marked by the black rectangle in the figure are due to the instability during the movement of the metal reflector.

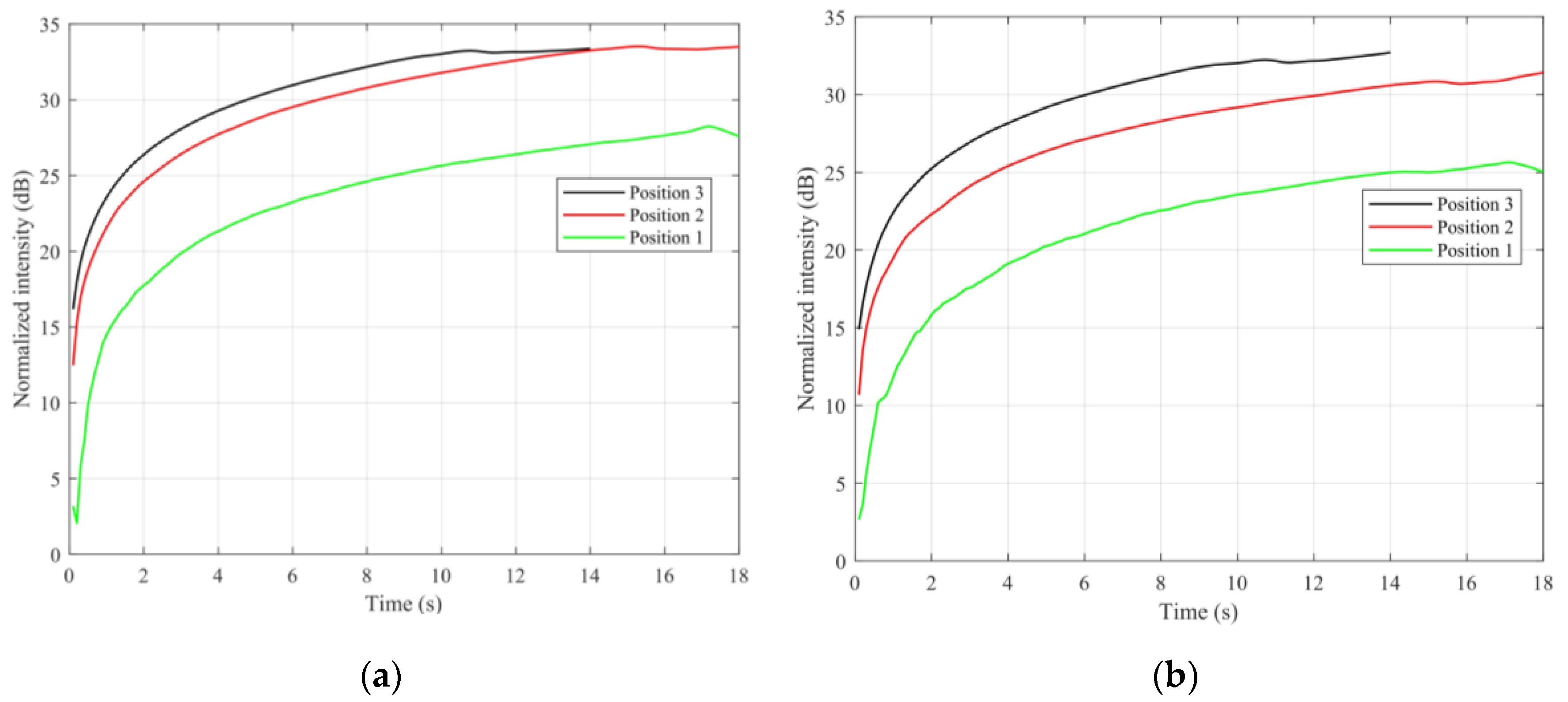
Given the stability of the phase of the static target, the SNR of the correlation peak can be enhanced by CAP. We regard three different periods as examples (0–18 s, 18–36 s, and 36–50 s). Figure 5 shows the SNR results of the reflected signals received versus CIT by LHCP 1 and 2. The x-axis is the CIT. When the CIT of each period is increased, the SNR is improved. When the CIT reaches the moment of the movement, the SNR enhancement reaches the maximum limitation.

As illustrated in Figure 4 and Figure 5 above, when the metal reflector is moving, the phase of the reflected signal will change. Since the phase change interrupts the continuity of the signal, it limits the CIT, i.e., simply increasing the CIT can no longer increase the SNR. New approaches need to be considered.

3.2. Application and Limitation of Increasing CIT for Targets in the Water

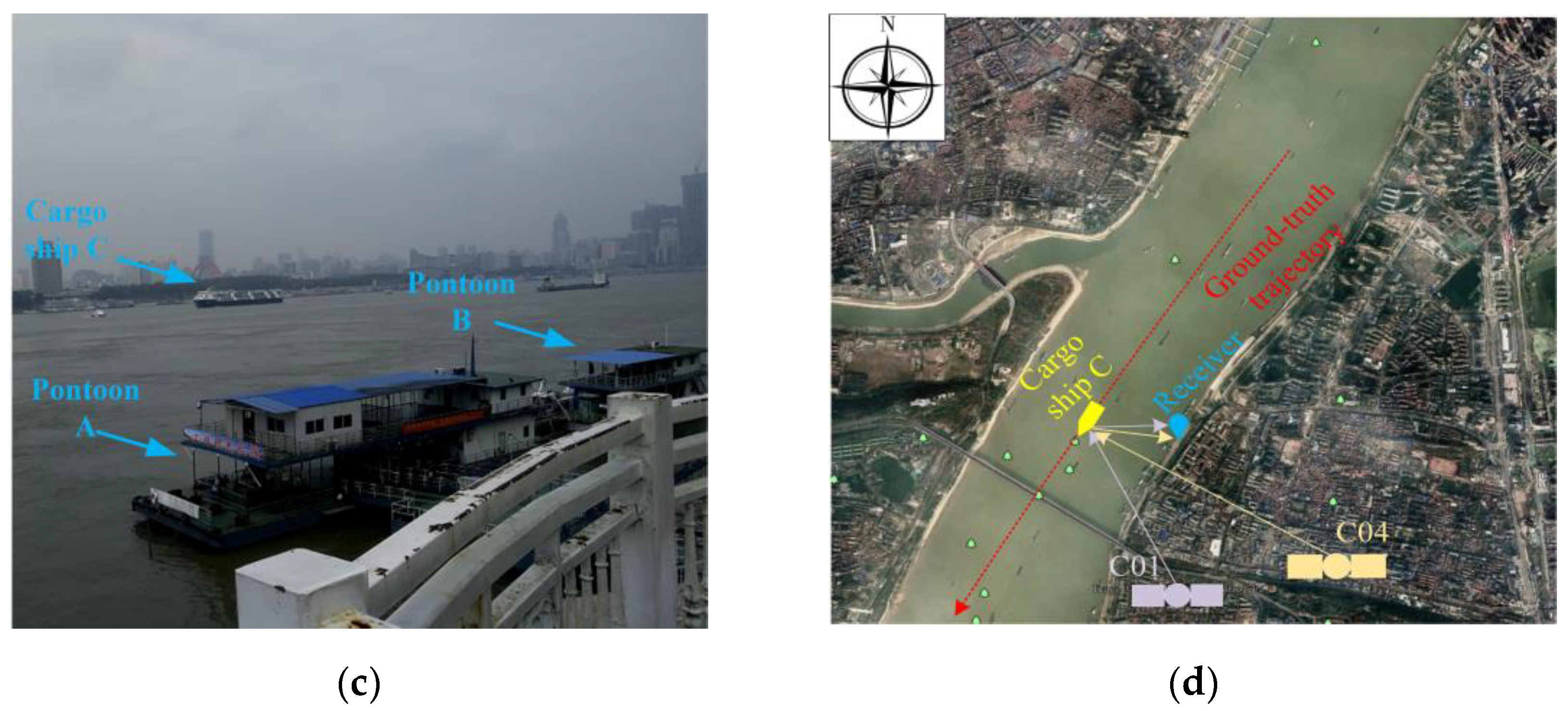
We conduct an experiment and apply the CAP to ships on the Changjiang River. Figure 6a shows the RHCP and LHCP antenna for the experiment. Figure 6b shows the two-channel GNSS IF signal collector and the process computer, the collector is with a sampling rate of 62 MHz, and the distance resolution between adjacent range cells is 4.8 m. We choose the signals of the C01 and C04 satellites as data sources. Figure 6c shows three targets (two pontoons and one cargo ship) on the river for the experiment. Pontoons A and B are stationary, and cargo ship C moves from northeast to southwest. Pontoon A is approximately 55 m from the receiver, pontoon B is approximately 80 m, and cargo ship C is more than 700 m. Figure 6d depicts the positions of the receiver and the cargo ship C, and the orientations of C01 and C04 satellites.

We collect 100 s data for analysis. After processed with range compression, as mentioned in Section 2, the RC data are stored in $S\left(n,m\right)$, where n is the index of the PRN period (n = 1, 2, …, 100,000), and m is the index of the range cells. Only 600 range cells are considered for processing in each millisecond to reduce the total amount of data, namely, m = 1, 2, …, 600.

CIT in Equation (5) depends on the radial velocity of the target. For pontoons A and B, their velocity is zero. For moving cargo ship C, we cannot acquire the prior information of radial velocity; accordingly, the traversal method is adopted to set the basic CIT, such as CIT = 10 ms, CIT = 50 ms, and CIT = 100 ms. The results show that when CIT = 50 ms, CAP is efficient for pontoons A and B, and the correlation peaks of reflected signals are visible. Consequently, we consider CIT = 50 ms and split up the data into 2000 frames. 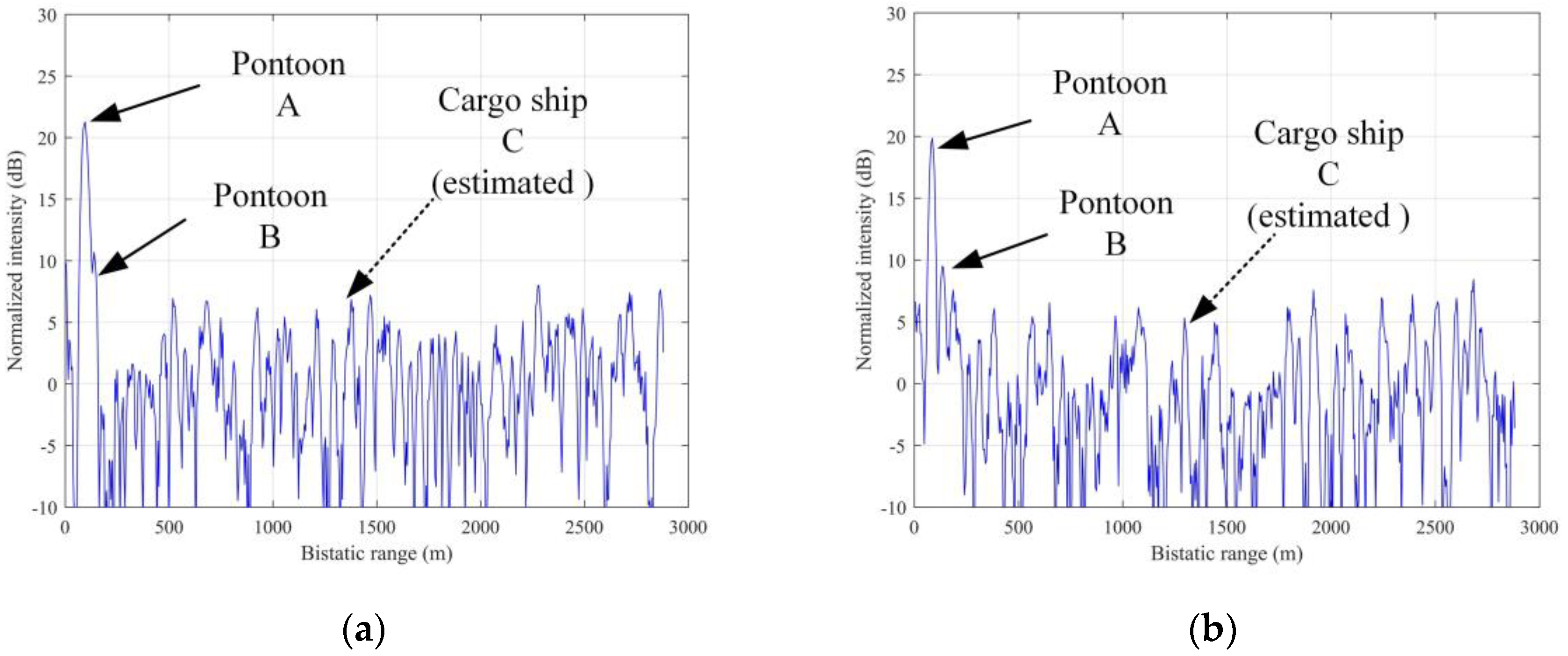Two examples of the cross sections of the correlation peak (0–50 ms) are shown in Figure 7. In Figure 7a, the correlation peak formed by the reflected signal of pontoon A can be observed at the 19th range cell (the bistatic range is 91.2 m, and the SNR is 19.85 dB). At the 30th range cell (the bistatic range is 144 m, and the SNR is 9.37 dB), the correlation peak of pontoon B can be observed. In Figure 7b, at the 18th range cell (the bistatic range is 86.4 m, and the SNR is 21.26 dB), the highest correlation peak is formed by the reflected signal of pontoon A. At the 26th range cell (the bistatic range is 124.8 m, and the SNR is 10.69 dB), the correlation peak of pontoon B occurs. But in these figures, the bistatic range of cargo ship C is difficult to distinguish because the reflected signal of cargo ship C is submerged under the noise (we mark the estimated range cell of C with dash arrow line).

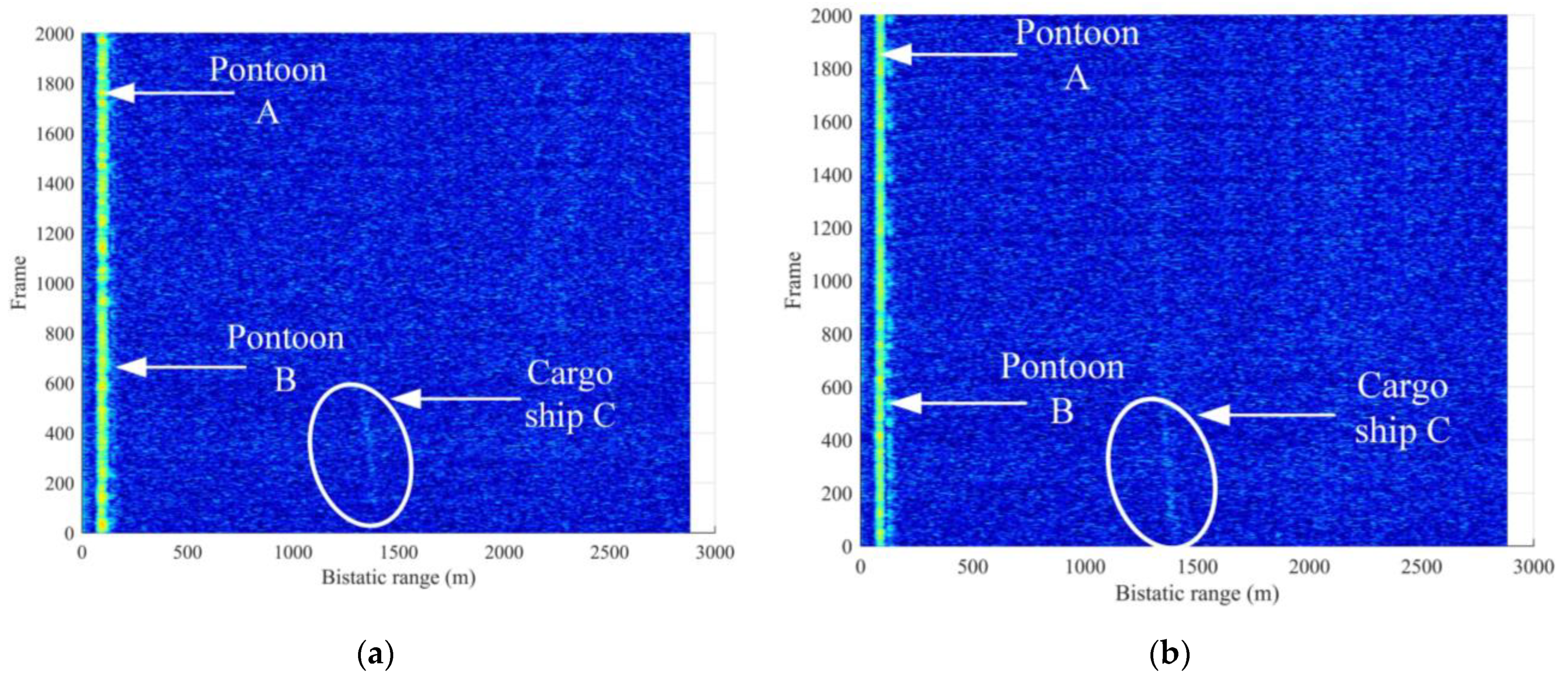
However, when the RC data in continuous frames are plotted in 2D range/time maps, we can find correlation peaks of cargo ship C, although, sometimes, it has low SNRs. Figure 8 shows the range compression maps of cargo ship C marked with an ellipse. Although the correlation peaks are less obvious than those of pontoons A and B, its bistatic range can be confirmed from 1200 to 1500 m.

The reason for the failure of the CAP for cargo ship C is that its velocity is not zero and the echo phase changes with the bistatic range, so the CAP cannot reach the effect of SNR enhancement.

4. Method 2: Improved SNR Enhancement Method for Moving Target

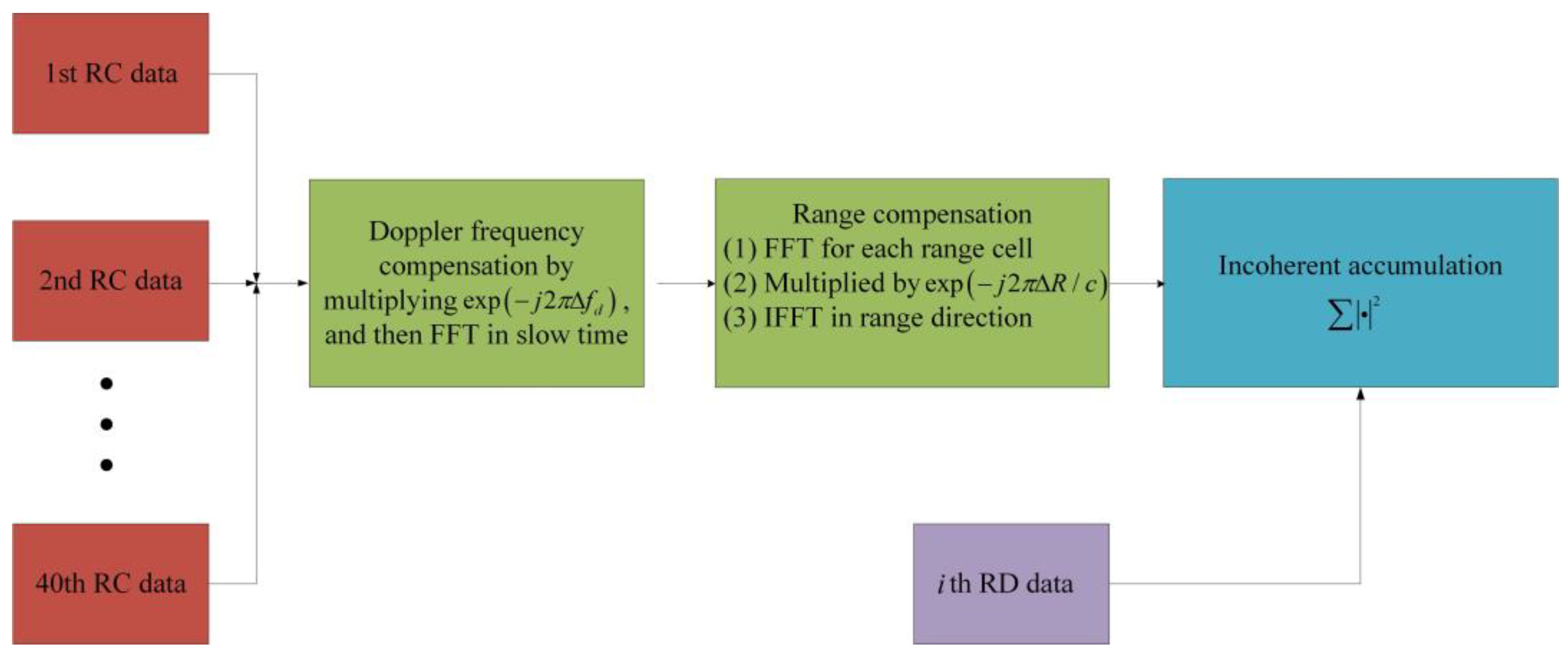
As mentioned above, for moving target, a new approach must be adopted. In this paper, the SNR enhancement considering the velocity of the target includes two steps: In the first step, the recorded data are divided into multiple frames and fast Fourier transform (FFT) is employed to calculate the Doppler frequencies; In the second step, both the Doppler frequency offset and range offset of each frame are compensated. The entire compensation process is shown in Figure 9. In the following subsections, we will detail the process for each step.

4.1. Doppler Processing in Frames

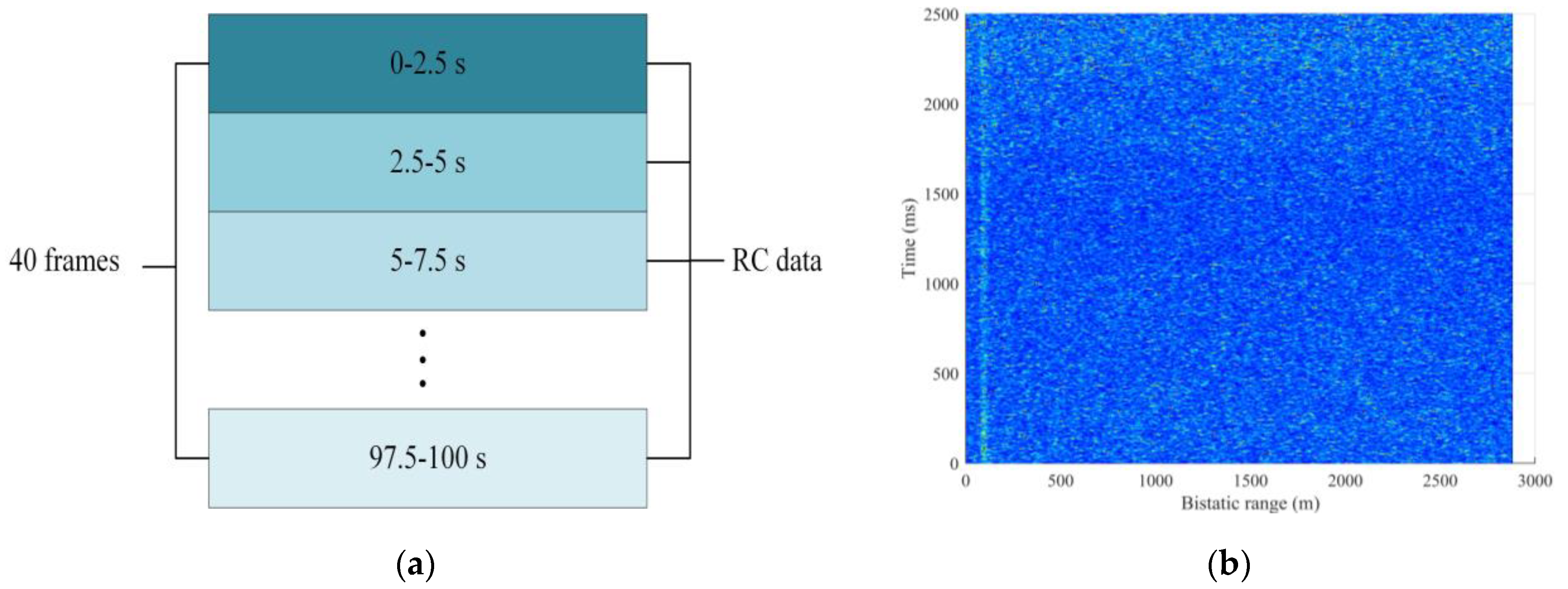
Since the bistatic range of cargo ship C is continually changing, as shown in Figure 8. It is reasonable to assume that the target will not extend a range cell of 4.8 m in a short time, e.g., 2.5 s. Then, the 100 s data of RC data are divided into 40 frames, with each frame corresponding to 2500 ms, as shown in Figure 10a. The RC matrix of the i-th frame is denoted as:

$$\mathit{R}\mathit{C}= \left[\begin{array}{cccc}S\left(T\left(i-1\right)+1,1\right)& S\left(T\left(i-1\right)+1,2\right)& \cdots & S\left(T\left(i-1\right)+1,1\right)\\ S\left(T\left(i-1\right)+2,1\right)& S\left(T\left(i-1\right)+2,2\right)& \cdots & S\left(T\left(i-1\right)+2,\mathrm{m}\right)\\ ⋮& ⋮& \ddots & ⋮\\ S\left(T\left(i-1\right)+\mathrm{T},1\right)& S\left(T\left(i-1\right)+\mathrm{T},2\right)& \cdots & S\left(T\left(i-1\right)+\mathrm{T},\mathrm{m}\right)\end{array}\right]$$

(6)

where $i=1,2,\cdots ,n_{max}$; $T$ is 2500 ms; and m is the index of range cells. Figure 10b is an example of raw RC data of the 5th frame of C01 (10~12.5 s) before FFT, where the target of cargo ship C can not be distinguished. Afterward, FFT is performed in the slow time for each column, which results in a range-Doppler (RD) map in the range/Doppler domain written as $\mathit{R}{\mathit{D}}_i^j=\mathrm{FFT}\left(\mathit{R}{\mathit{C}}_i^j\right)$, where $j$ is the index of GEO satellite.

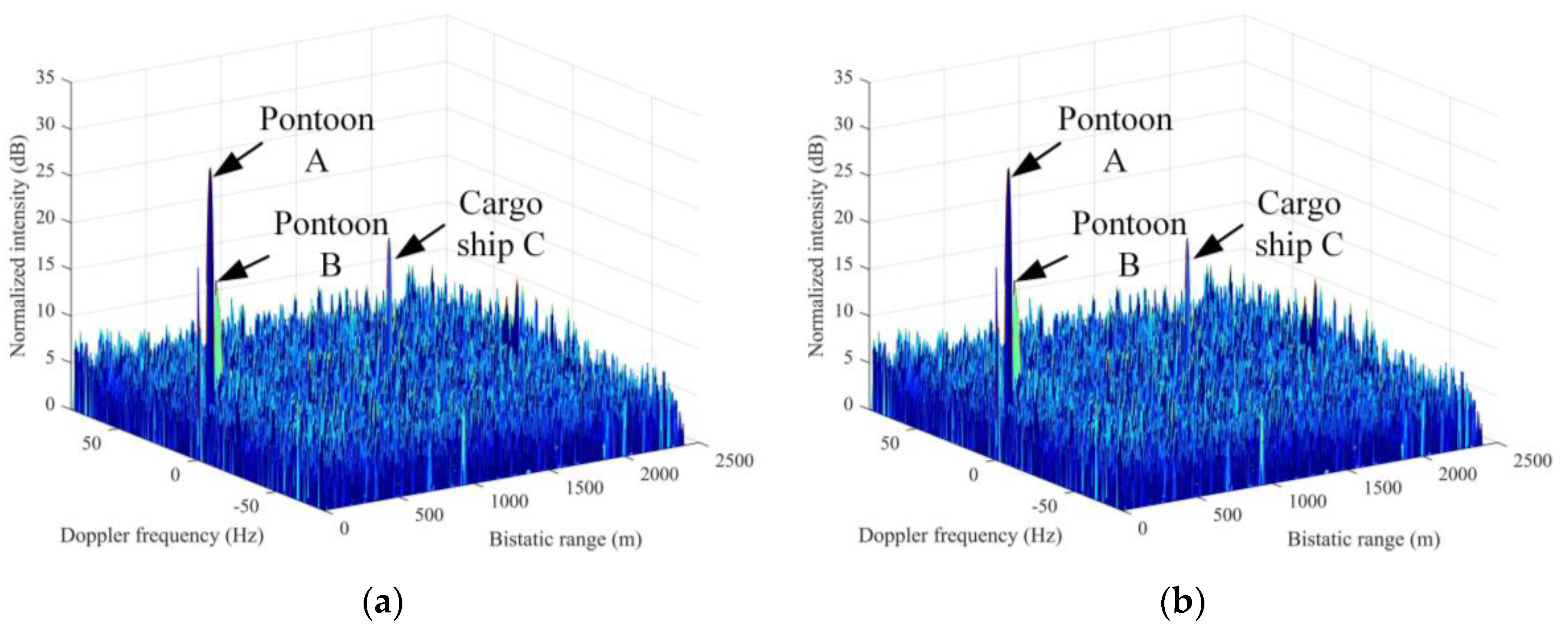
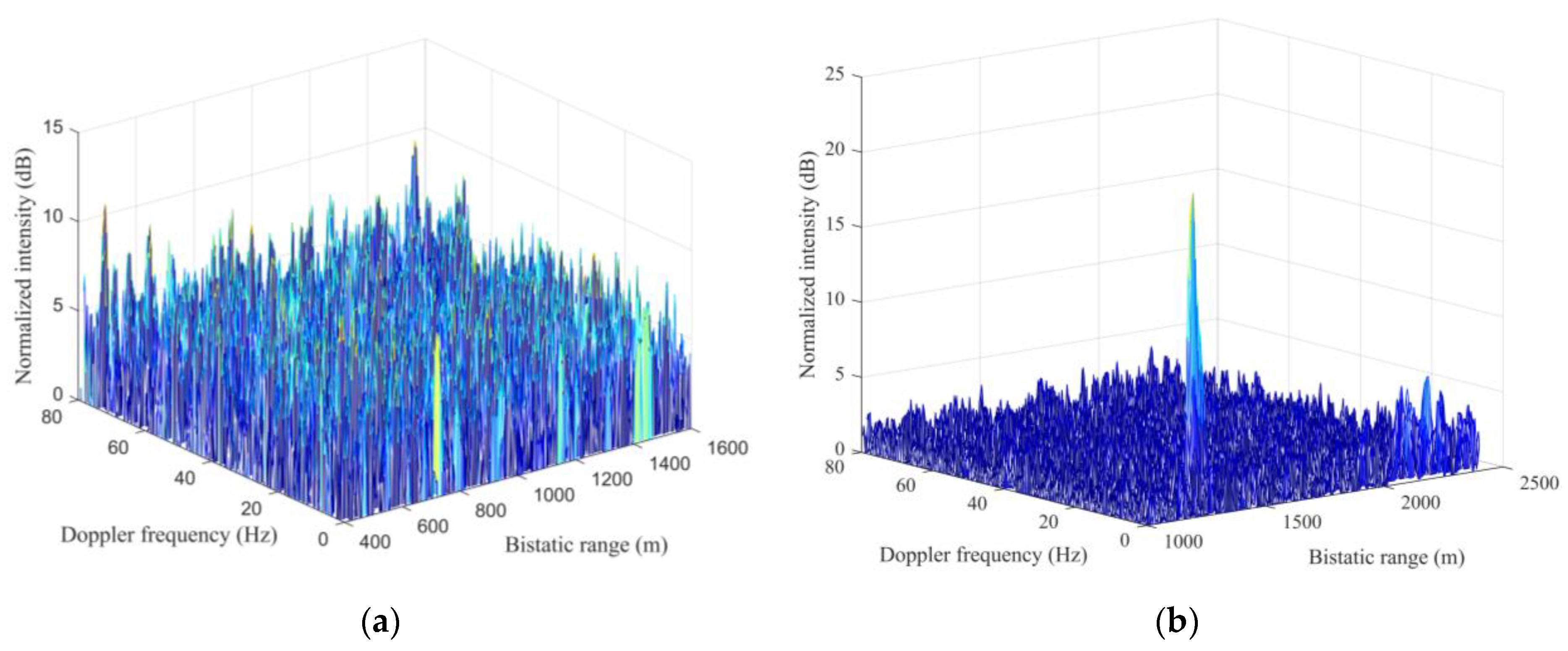
As examples, Figure 11 shows the obtained fifth RD map of $\mathit{R}{\mathit{D}}_5^1$ and $\mathit{R}{\mathit{D}}_5^4$ from C01 and C04, respectively. We only draw part of the Doppler frequency range (−80 Hz, 80 Hz) where the target is located. In Figure 11a, the highest peak locates at the bistatic range of 91.2 m, with the Doppler frequency of 0 Hz representing pontoon A. The peak at the bistatic range of 144 m and the Doppler frequency of 0 Hz corresponds to pontoon B. A low peak with a bistatic range of 1368 m and a Doppler frequency of 14.8 Hz is also determined, which corresponds to cargo ship C. Compared with the raw RC data as shown in Figure 10b, the cargo ship C in Figure 11a is observable after FFT. In Figure 11b, the highest peak locates at the bistatic range of 86.4 m and the Doppler frequency of 0 Hz, which is caused by pontoon A. The peak at the bistatic range of 124.8 m and the Doppler frequency of 0 Hz corresponds to pontoon B. The low peak with a bistatic range of 1373 m and a Doppler frequency of 9.2 Hz corresponds to cargo ship C.

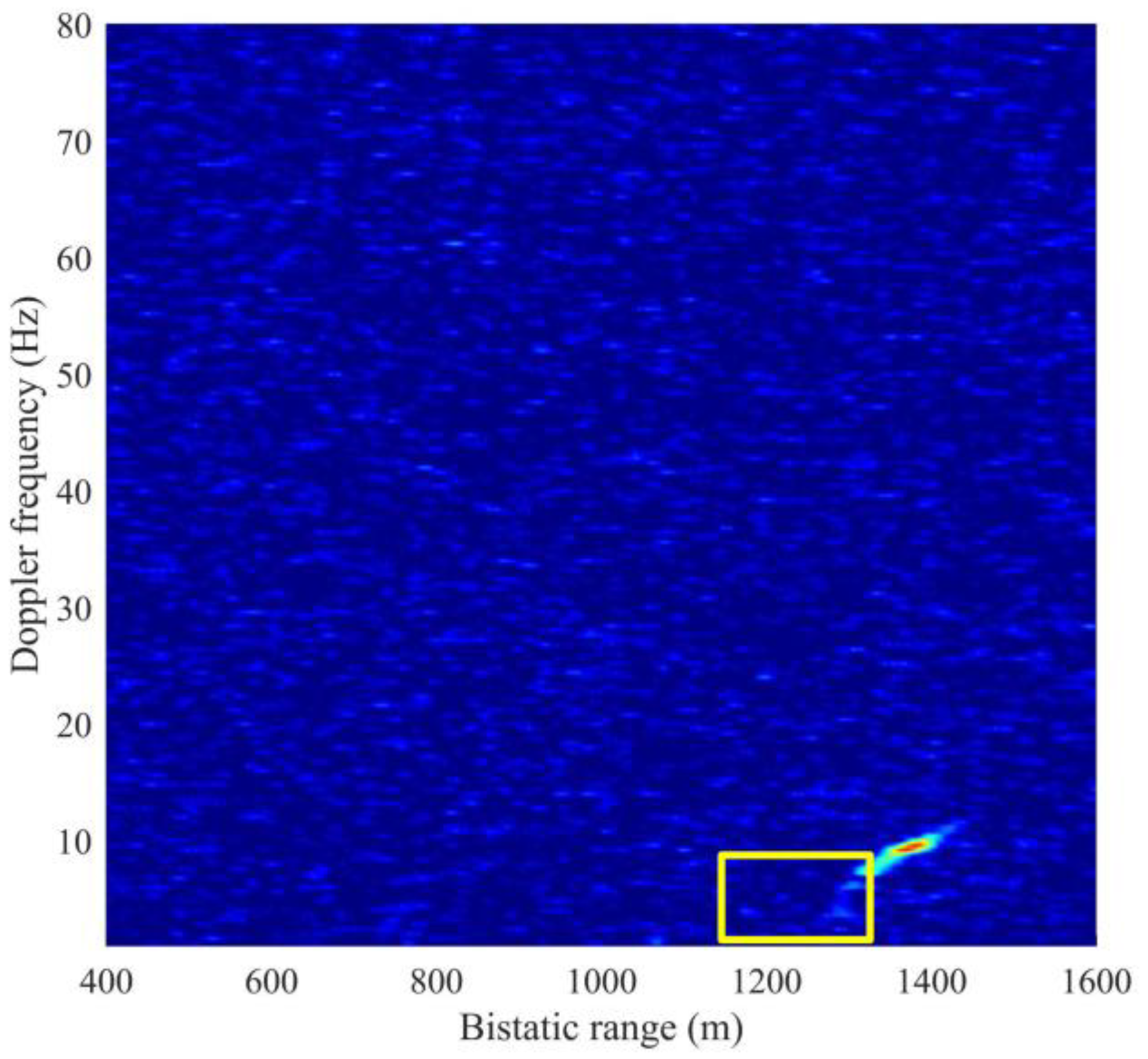
The RD maps of $\mathit{R}{\mathit{D}}_5^1$ and $\mathit{R}{\mathit{D}}_5^4$ are two examples with high SNR data. In the entire 40 frames, not all frames have high SNRs; consequently, the correlation peaks of several time intervals cannot be observed. We superpose all frames of the RD data of C01 as examples, as shown in Figure 12. The area marked with yellow rectangle has correlation peaks of low intensity, and the target cannot be detected. SNR enhancement thus needs to be performed.

4.2. SNR Enhancement

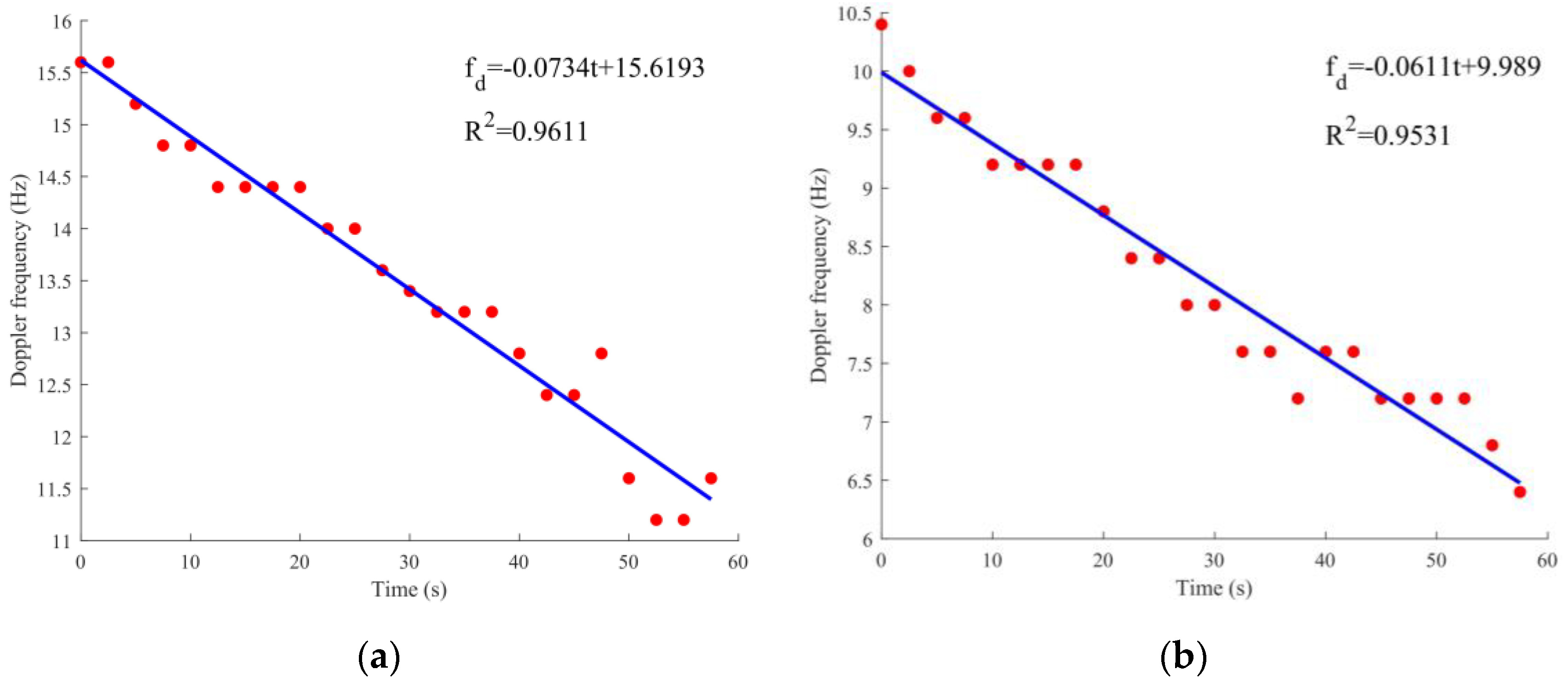
To find the relationship between the Doppler frequency and the time of cargo ship C marked in Figure 12, the Doppler frequency of the first 24 frames of C01 and C04 is first calculated, and the Doppler frequency is then depicted in Figure 13. The x-axis is the time length of 24 frames (time length of 60 s), and the y-axis is the Doppler frequency. The relationship between the Doppler frequency and the time is linear, resulting in the linear fit results. The Doppler rate is −0.0734 Hz/s corresponding to C01 data, and −0.0611 Hz/s to C04 data. $R^2$ of the figures are 0.96112 and 0.9531, illustrating high linearity.

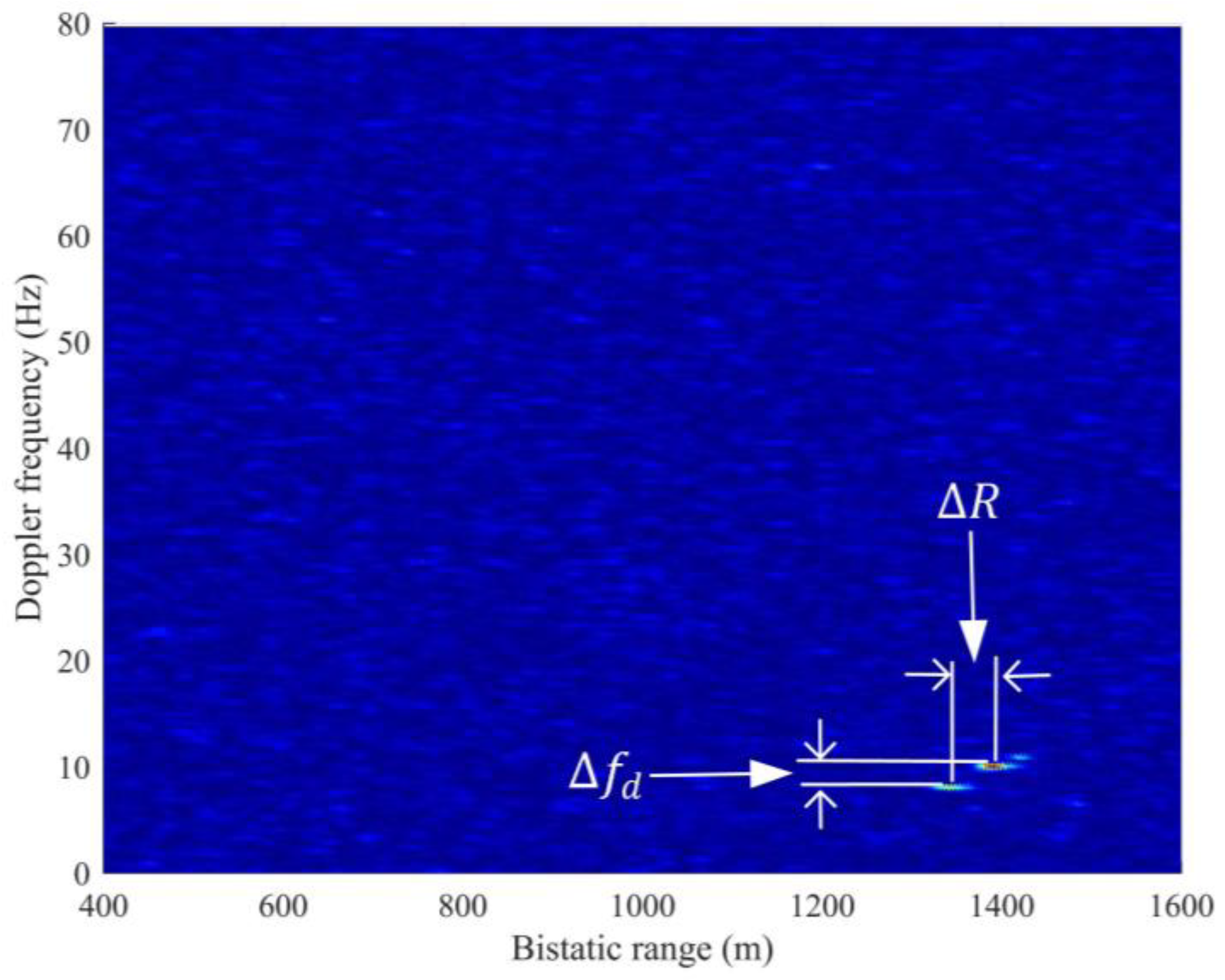
Given that the correlation peaks of cargo ship C appear in the adjacent frames, the main idea of SNR enhancement is to compensate for the Doppler frequency offset and range offset of other frames. Then, the SNR is enhanced by accumulating the frames. Three different RD maps are superposed as an example in Figure 14. Three correlation peaks caused by cargo ship C appear at the different range and Doppler frequency cells at diverse times. The differences among these peaks are the Doppler offset ($\Delta f_d$) and range offset ($\Delta R$). The SNR enhancement algorithm is based on range and Doppler offsets compensation.

We aim to compensate for those weak target correlation peaks in the 40 frames with strong correlation peaks. The basic idea is that for each of the 40 RD maps, the remaining 39 RD maps are compensated in the offset of range and Doppler frequency, then incoherent accumulation is performed.

For example, $\mathit{R}{\mathit{D}}_{40}$ is the 40th frame RD matrix before the compensation, and $facte{r}_{40}^l$ is the compensation operator using the $l$ th frame data. The compensated 40th frame data can be written as:

$$\mathit{R}{\mathit{D}}_{40}^{Comped}=\frac{1}{40}\left\{\left|\mathit{R}{\mathit{D}}_{40}\right|+{\displaystyle \sum }_{l=1}^{39}\left|\mathit{R}{\mathit{D}}_l\ast facte{r}_{40}^l\right|\right\}$$

(7)

where $*$ is the compensation operation. Then, in the same way, the compensated $i$ th frame data can be written as:

$$\mathit{R}{\mathit{D}}_i^{Comped}=\frac{1}{40}\left\{\left|\mathit{R}{\mathit{D}}_i\right|+{{\displaystyle \sum }}_{l\ne i}^{40}\left|\mathit{R}{\mathit{D}}_l\ast facte{r}_i^l\right|\right\}.$$

(8)

$facte{r}_{40}^l$ includes two steps, the offsets compensation of the Doppler frequency and range. We assume that the data will be compensated is $\mathit{R}{\mathit{D}}_i$. The $l$ th RD map ($\mathit{R}{\mathit{D}}_l$) is reference used for compensation. Given that Doppler frequency changes linearly with time, the following expression can be obtained: $f_d\left(t\right)=k_d\times t+f_d{}_0$, where $k_d$ is the Doppler rate, and $f_{d0}$ is the initial Doppler frequency. Hence, the Doppler frequency compensation factor is $\mathit{exp}\left(-j2\pi \Delta f_d\right)$, where:

$$\Delta f_d=f_d\left(l\right)-f_d\left(i\right)=k_d\times \left(l-i\right).$$

(9)

The phase of the reflected signal corresponding to the bistatic range in the $l$ th frame is denoted as ${\Phi }_d\left(l\right)$, the phase of the echo signal in the $i$ th frame is denoted as ${\Phi }_d\left(i\right)$, and the difference of phase from $l$ to $i$ is denoted as:

$$\begin{array}{cc}\hfill \Delta {\Phi }_d& ={\Phi }_d\left(l\right)-{\Phi }_d\left(i\right)\hfill \\ & =2\pi \left[{\displaystyle {\int }_0^l{f}_d\left(t\right)dt}-{\displaystyle {\int }_0^i{f}_d\left(t\right)dt}\right]\hfill \\ & =2\pi \left\{\frac{1}{2}\times k_d\times \Delta p^2+\left[f_d\left(l\right)-k_d\times \Delta p\right]\times \Delta p\right\}\hfill \end{array}$$

(10)

where $\Delta p=l-i$. Consequently, in accordance with Equation (3), the range compensation factor is $\mathit{exp}\left(-j2\pi \Delta R/c\right)$, and $\Delta R$ can be derived as:

$$\Delta R=\frac{\lambda \Delta {\Phi }_d}{2\pi }=-\lambda \left[-\frac{1}{2}\times k_d\times \Delta p^2+f_d\left(l\right)\times \Delta p\right].$$

(11)

Afterward, the range compensation and Doppler frequency compensation are conducted. The $i$ th frame RC data will be compensated as follows: (1) Doppler frequency compensation. On the basis of the RC data, each column is multiplied by the Doppler frequency compensation factor $\mathit{exp}\left(-j2\pi \Delta f_d\right)$, then each column is processed with FFT to convert the RC data into RD data. (2) Range compensation. This compensation uses the property of Fourier transform, namely, multiplying $F\left(j\omega \right)e^{\pm i\omega t_0}$, written as $F\left[f\left(t-t_0\right)\right]=F\left(j\omega \right)e^{-j\omega t_0}$. First, for each row in the RD matrix, we perform FFT to convert it into the range–frequency domain. Then, it is multiplied by the range compensation factor in each arrow. Lastly, inverse FFT (IFFT) is conducted in the range–frequency domain to convert into RD data, and the range compensation is finished.

With the compensation of range and Doppler frequency, the amplitude of the signal is focused on the same range and Doppler frequency cells. Then, the SNR is enhanced by accumulating the frames, and we can observe the bistatic range information in the 40 RD maps.

4.3. SNR Enhancement Results

To describe the experimental results specifically, we first consider the enhancement results of the 22nd frame $\mathit{R}{\mathit{D}}_{22}^4$ as an example and then show the SNR enhancement statistics results. Lastly, we compare the RD maps before and after the enhancement.

Figure 15 illustrates the SNR of $\mathit{R}{\mathit{D}}_{22}^4$ before and after the enhancement. In Figure 15a, the SNR of the reflected signal from cargo ship C is 6.1 dB, which is easily confused with the surrounding interference signal. Thus, the bistatic range and Doppler frequency of the correlation peak cannot be directly observed from the RD map. However, after the enhancement step, as shown in Figure 15b, a clear peak exists at the bistatic range of 1291 m (Doppler frequency of 6.4 Hz), with an SNR of 10.5 dB, which is increased by 4.4 dB.

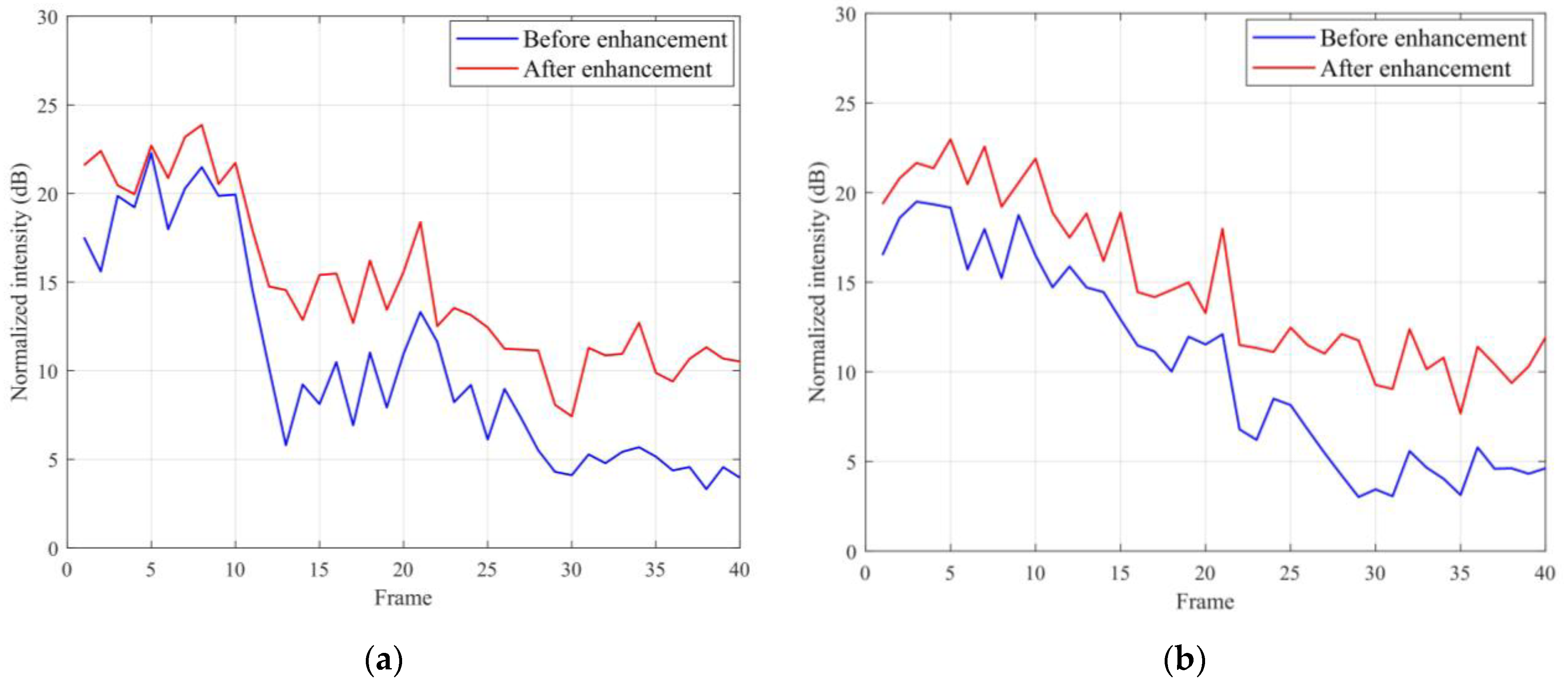
The statistical distribution after SNR enhancement is shown in Figure 16 to show the overall effect of the enhancement. The blue line represents the SNR before the enhancement, and the red one is the result after the enhancement. Because the SNRs of the first ten frames are high before the enhancement, Figure 16a,b show smaller increase in the first ten frames compared to the remaining frames. The SNRs of C01 reflected signal are increased by 4.46 dB on average, and that of C04 reflected signal are increased by approximately 4.52 dB on average.

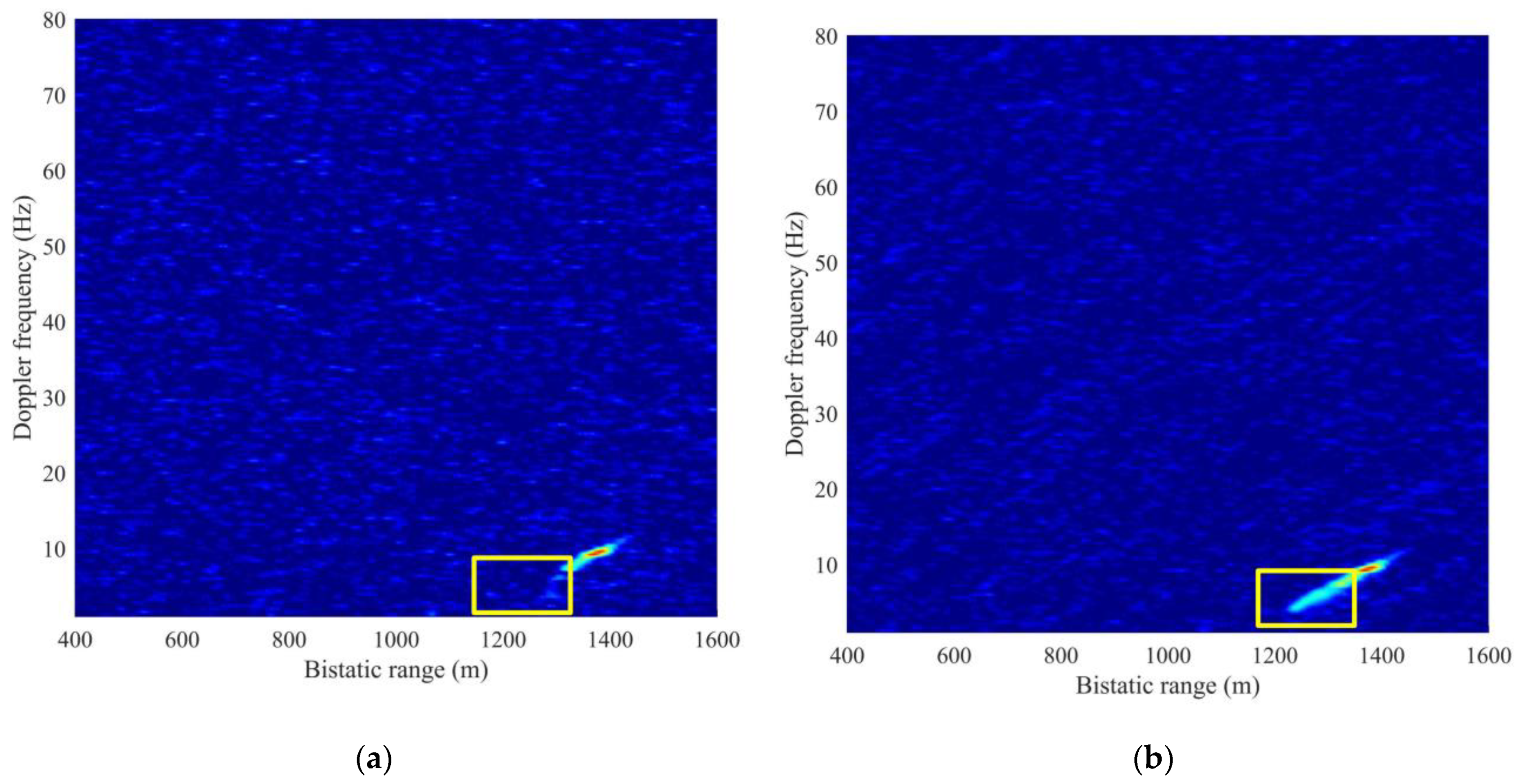
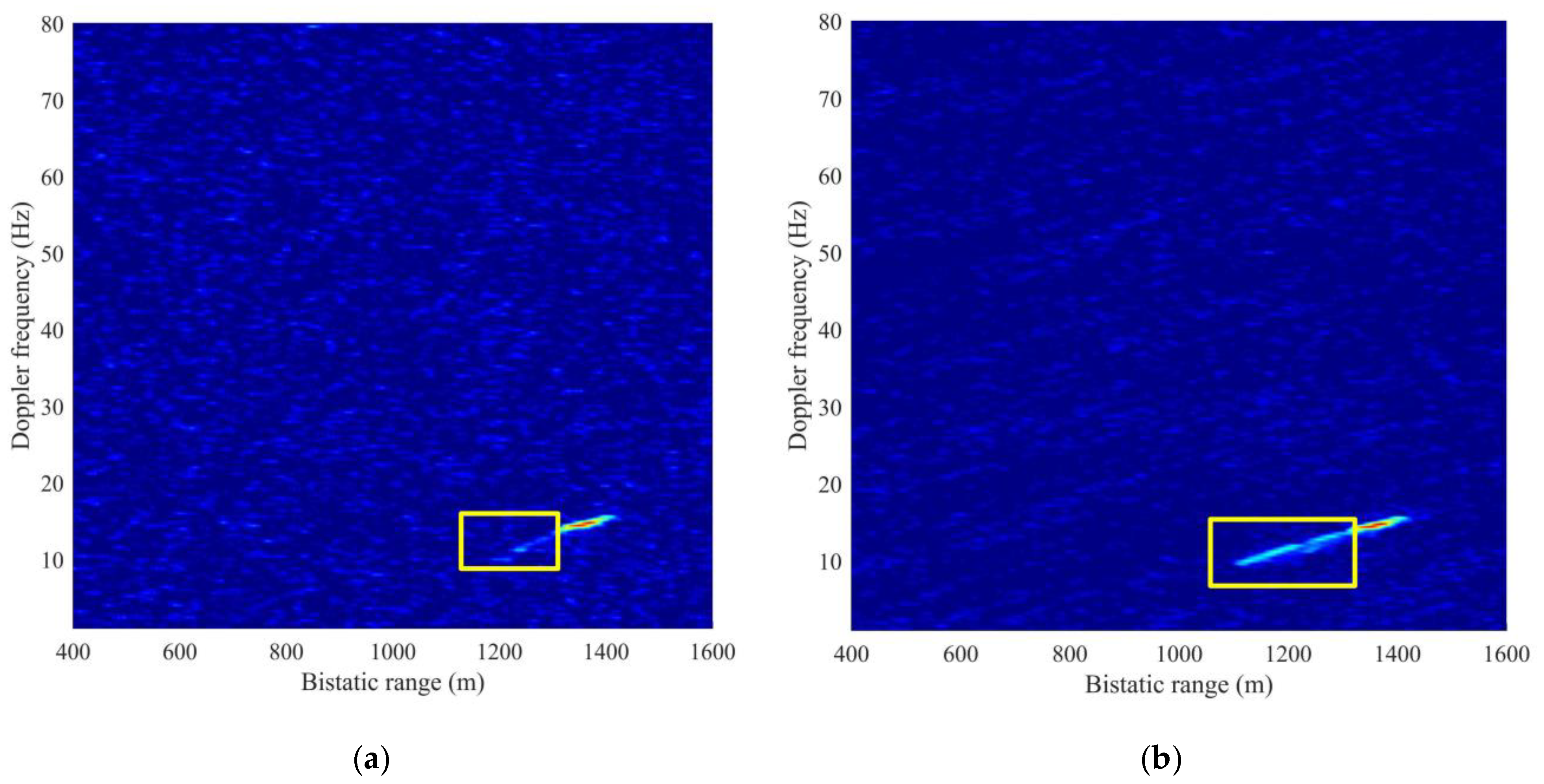
To show the effectiveness of the algorithm in this paper intuitively, the 40 frames of the same target before and after SNR enhancement are rearranged together in one RD map. Figure 17 shows the RD maps of C01 data. In Figure 17a, the correlation peak of reflected signal from cargo ship C cannot be observed (SNR < 10 dB) in the area (bistatic 1118 to 1320 m) marked by a yellow rectangle. Nevertheless, in Figure 17b, after the SNR enhancement, a continuous peak can be observed (SNR ≥ 10 dB) in the region circled by the yellow rectangle, and the track formed by the continuous peak can also be determined in the marked region. Moreover, in Figure 17b, the Doppler frequency shows a linear change with bistatic range. Figure 18 illustrates the RD maps of C04 data. A continuous correlation peak can be observed (SNR ≥ 10 dB) in the yellow rectangle marked area (bistatic range 1230 to 1320 m) in Figure 18b. The trajectory formed by the peak is clearly visible, and the relation between Doppler frequency and the bistatic range is linear.

5. Discussion

5.1. RCS of Metal Reflector and Deformation Detection Accuracy

In this paper, the metal reflector is a finite surface as shown in Figure 3, which can be taken as a perfectly conducting isosceles triangle. Another point worth noting is that although the bistatic radar system is adopted in this paper, we try to maintain a small bistatic angle in geometry, for example, the bistatic angle is about 24° in deformation detection, resulting in the incident angle being almost perpendicular to the surface. Therefore, for simplification, the metal reflector can be modelled as a triangular flat plate and the RCS is [18]:

$$\sigma =\frac{\pi a^4}{{\lambda }^2}{\left(\mathit{cos}{\theta }^{\prime }\right)}^2\left[\frac{{\left(\mathit{sin}\rho \right)}^4}{{\rho }^4}\right],$$

(12)

where a is the side length of the metal reflector; $\rho =2\pi \mathit{sin}{\theta }^{\prime }\mathit{sin}\eta /\lambda$, $\eta$ is determined by azimuth angle of satellite signals and ${\theta }^{\prime }$ is the aspect angle. In our experiment, $\eta =\pi /2$, and the aspect angle is 12°, RCS = 0.1332 m² When the aspect angle increases, i.e., the incident direction deviates from the normal direction, the RCS deceases rapidly.

It is worth mentioning that the phase change of metal reflector as in Figure 4b can be used to simulate a deformation detection. We conduct a quantitative test, as in Section 3.1, the metal reflector is moved twice (less than a wavelength), and the data are collected 3 times. Each time, 10 s data are collected. The phase difference between two successive movements is extracted as ${\phi }_{dif}$, using the equation $\Delta R_{\Delta }={\phi }_{dif}\lambda /2\pi$, we get the calculated deformation results as shown in

Table 1. Calculated deformation of the metal reflector in the normal line direction.

Antenna	The First Calculated Deformation Value (cm)	The Second Calculated Deformation Value (cm)	The Ground-Truth Deformation Value (cm)
LHCP 1	−3.85	−3.20	−3.46
LHCP 2	−3.37	−5.28	−3.46

. The deviation between the estimated deformation (normal line direction) and the ground-truth measurement is less than 0.8 cm.

The accuracy of this result is similar to that of the reference [11]. When this result is compared with the deformation results of SAR data such as Sentinel-1, we find that the accuracy of this result is worse than that of SAR data (The deformation measurement accuracy of SAR is in the millimeter level) [19]. The reason is that the bandwidth of BeiDou 3 signal (20.46MHz) is far lower than that of SAR signal. But given that it is a passive radar that does not require a high-powered transmitter, it can be used for stable measurements with an accuracy of several centimeters over a long period of time.

5.2. RCS of Ship and Target Detectability

Now considering the ships in the water. When researchers study the ice edge in the Ocean, they use a trihedral model with an approximately infinite plane to calculate the RCS [20]. Whereas in our experiments the ships are in freshwater, and the geometry relationship among the GEO satellite, ships, and receiver are configured as quasi monostatic radar, so for simplification, the surface of cargo ship can be modeled as a trihedral corner reflector as shown in Figure 19. The RCS of this ship is:

$$\sigma =\frac{12\pi a^4}{{\lambda }^2},$$

(13)

where a is the edge length of the trihedral corner reflector, which depends on the height of ship about 15 m; $\lambda$ is the wavelength of the incident radiation about 24 cm for BeiDou B3 signals. The basic RCS is calculated to be approximately 3.4 × 10⁷ m² under the condition of BeiDou B3 signals.

The reference [21] gives the target detectability when constructing bistatic SAR radar, and the gain of azimuth compression is taken into account. Additionally, the reference [22] has given a relatively detailed discussion about detectability in a GNSS Bistatic radar. Here, we discuss the target detectability based on the SNR prediction of the BeiDou GEO satellite.

After the range compression, the final SNR can be written as:

$$\frac{S}{N}=\frac{P_t{G}_t}{4\pi R_{st}^2}\cdot \frac{4\pi }{{\lambda }^2}\frac{G_r\sigma }{4\pi R_{tr}{}^2}\cdot \frac{1}{K{T}_{0}B}\cdot G_{sp}$$

(14)

where $R_{st}$, $R_{tr}$ are the ranges among the satellite and the target; and the receiver; the first item ($P_t{G}_t/4\pi R_{st}^2$) is energy density when GNSS signal reaches the surface of the Earth; then $P_{\mathrm{Earth}}=\frac{P_t{G}_t}{4\pi R_{st}^2}\cdot \frac{4\pi }{{\lambda }^2}$ is the signal power near the Earth surface (−163 dBw as shown in the BeiDou interface control document (http://www.beidou.gov.cn/xt/gfxz/index_2.html, accessed on 1 February 2021) [23]); $G_r$ is the gain of the receiving LHCP antenna (14 dB), the thermal noise $K{T}_{0}B=-131$ dB, where $K$ is the Boltzmann coefficient; $T_0$ is equivalent noise temperature; $B$ is the receiver bandwidth. For our receiver, the frequency bandwidth of BeiDou B3 signals is 20.46 MHz; $G_{sp}$ is the signal processing gain based on CIT or FFT, which depends on the coherent processing interval (CPI). In our experiment, when CPI = 50 ms, $G_{sp}$ is about 17dB. According to the above parameters, the final SNR after range compressing of cargo ship C is about 5.55 dB.

It is worth mentioning that different azimuths and elevations of GEO satellites will influence the RCS and final SNR. For example, in our experiment, the boresight axis of the LHCP antenna points to 317°, along the opposite of the azimuth of C01 satellite (137°), so the C01 satellite, the target ship, and the fixed receiver constitute a quasi-single station radar system. Therefore, the LHCP antenna can receive the reflected signals in azimuths of 301° to 333° (the main lobe beamwidth of receiving LHCP antenna is 32°). If the target is 700 m away, the detected trajectory range is equal to arc length (about 390 m). However, for the satellite C04, there is a deviation. The azimuth is different from C01 resulting in an attenuation of SNR with a factor of ${\left(\mathit{cos}{\eta }^{\prime }\right)}^2$, where ${\eta }^{\prime }$ is the equivalent aspect angle depending on the azimuth of satellite, the elevation of satellite, and the positions of target and the receiver.

For convenience, the power estimations of ships with different RCSs are given for reference as shown in

Table 2. The power estimations of different ships.

The Height of Ship (m)	Range (m)	CPI (ms)	SNR (dB)	RCS (m2)
8	400	50	−0.51	2324633
	800	50	−6.53
16	400	50	11.5293	37194138
	800	50	5.5087
24	400	50	18.57	188295324
	800	50	12.55

. The table shows that when the height of the ship is more than 16 m, it is possible for us to detect the ship in the range of more than 400 m.

6. Conclusions

In this work, we study SNR enhancement algorithm and applications of reflected signals under the condition of a bistatic radar system consisting of BeiDou GEO satellites and a fixed receiver. For a static target, the basic SNR enhancement method—increasing CIT—is used. An experimental scene using a metal reflector is conducted showing the effectiveness until the metal reflector movement which results in a phase discontinues. For moving targets, we take a cargo ship as an example and model it as a trihedral corner reflector, then calculate Doppler frequency in every frame and compensate the Doppler frequency and range offset based on the echo phase to achieve the purpose of SNR enhancement. Results show that the average SNR increases by more than 4 dB.

The study shows the potential application of the phase discontinues for deformation detection. When the metal reflector is moved to a distance, the phase changes with the deformation. When calculating the deformation on the basis of the phase difference by using the geometry of reflected signals, the deviation between the estimated deformation and the ground-truth measurement is less than 0.8 cm. Compared with other deformation-monitoring methods, such as using SAR data (e.g., Sentinel-1) with a long revisiting period of several days, this method of using GNSS signals has a shorter revisiting time, leading to a long-time continuous monitoring. One limitation of this method is that the change in the bistatic range of the surface cannot exceed one integer wavelength (24 cm).

This study also discusses the RCS of ship and the power estimations in different ships, which reveal the potential application for monitoring the ships in inland river.

When multiple satellites are used, multiple frequency signals from different directions will provide more opportunities. So our future research will focus on detailed industry application of GNSS-based bistatic radar and try to solve some technical problems such as the integer ambiguity of phase, etc.