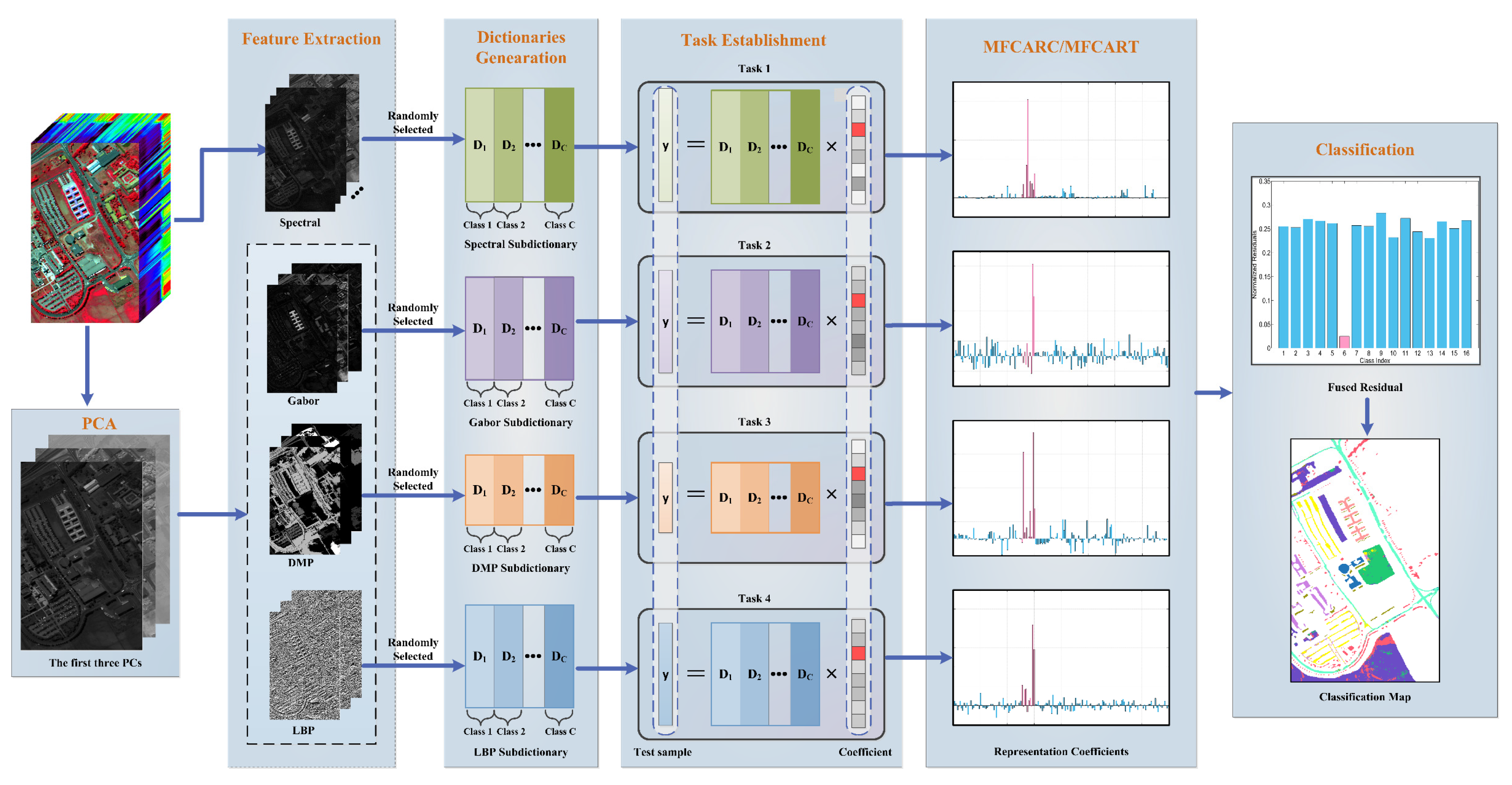
1. Introduction
Hyperspectral images (HSIs) provide valuable spectral information by using the hyperspectral imaging sensors to capture data at hundreds of narrow contiguous bands from the same spatial location. In the past few years, HSIs have been extensively applied in various fields [
1,
2,
3,
4,
5]. Among them, HSI classification is a crucial task for a wide variety of real-world applications, such as ecological science, mineralogy, and precision agriculture [
6]. However, there exist open challenges in the HSI classification task. For example, although the hundreds of spectral bands provide sufficient information, it results in the Hughes phenomenon. Additionally, given that the practical sample labeling is difficult and expensive, lacking sufficient labeled samples is another major challenge in HSI classification techniques.
In recent years, deep-learning-based techniques have aroused broad interests in the geoscience and remote sensing community. It shows the effectiveness in HSI classification due to a powerful ability of learning high-level and abstract features from the HSI data automatically [
7]. Compared with traditional classification methods, deep learning-based approaches normally require higher computation power and a larger number of training samples to learn the massive tuning parameters, resulting from the manner in deep hierarchical networks [
8]. According to the fact that available training samples are limited in hyperspectral data, it is still challenging to use deep learning approaches to fulfill the HSI classification task with high accuracy.
Currently, representation-based classification methods have been successfully applied to HSI classification and numerous representation-based classifiers have been investigated extensively. Started by Wright et al. [
9], sparse representation-based classifier (SRC) was proposed for face recognition. Later on, Chen et al. [
10] explored a joint sparse representation model into the HSI classification. In recent years, many variants of SRC have been designed for the HSI classification, such as joint SRC (JSRC) [
11,
12], robust SRC (RSRC) [
13] and group SRC (GSRC) [
14,
15]. Zhang et al. [
16] investigated the core principle of SRC and asserted that it was the collaborative representation (CR) mechanism deduced by
rather than the
based sparsity constraint to improve the final classification performance. Similar to the query-adapted technique adopted in weighted SRC (WSRC) [
17], the nearest regularized subspace (NRS) [
18] was presented by introducing the distance-weighted Tikhonov regularization into CRC. Then the CR with Tikhonov regularization (CRT) [
19] and different kernel versions of CRC and CRT [
20,
21,
22] were introduced in the HSI classification.
According to the above-mentioned discussion, for the representation-based classifiers, one of the crucial issues is to seek for a suitable representation for any test sample and derive the discriminative representation coefficients to achieve the subsequent classification task. Note, when applying SRC to hyperspectral data, whether a useful sparse solution can be obtained or not mostly depends on the degree of coherence of the dictionary [
23]. Specifically, when the samples from the same subspace within the dictionary are highly correlated, SR tends to select one atom at random for representation and overlooks other correlated atoms. It leads to SR suffering from the instability problem. Besides, SR lacks the ability to reveal the correlation structure of the dictionary due to the sparsity [
24]. On the other hand, when applying CRC to the HSI classification, CR tends to group correlated samples together but lacks the ability of sample selection, which potentially introduces the between-class interference, resulting in poor classification performance.
Given that both SR and CR have their intrinsic limitations, there are some attempts to achieve the balance between SR and CR for better performance. Li et al. [
25] presented a fused representation-based classifier (FRC) by combining SR and CR in the spectral residual domain and Gan et al. [
26] developed a kernel version of FRC (KFRC) to attain the balance in the kernel residual domain. Liu et al. [
27] extended the KFRC from the spectral kernel residual domain to the composite kernel with ideal regularization (CKIR)-based residual domain to further enhance the class separability. Although these fusion-based classifiers have been demonstrated to perform better than the individual representation-based classifiers, they still cannot perform sample selection and group correlated samples simultaneously. As a remedy, the elastic net representation (ENR) model [
24] was proposed to encourage the sparsity and the grouping effect via a combination of the LASSO and the Ridge regression. Inspired from the elastic net, several variants of the ENR-based classification methods have been developed for HSIs to take full advantages of SRC and CRC [
28,
29,
30]. However, the ENR model benefits from both the
and the
at the cost of having two regularization parameters to tune. In addition, the ENR model is blind to the exact correlation structure of the data and thus fails to balance between SR and CR adaptively according to the precise correlation structure of the dictionary.
To tackle the above-mentioned issues, in this paper, a correlation adaptive representation (CAR) solution and CAR-based classifier (CARC) are proposed by exploring the precise correlation structure of the dictionary effectively. Specifically, we introduce a data correlation adaptive penalty by utilizing the advantage of the correlation adaptive behavior and thus make the model adaptive to the correlation structure of the dictionary. Different from ENR-based classifiers, the proposed CARC is capable of performing sample selection and grouping correlated samples jointly with a single regularization parameter to be tuned. By capturing the correlation structure of data samples, the CARC is able to balance SR and CR adaptively, producing more discriminative representation coefficients for the classification task.
Moreover, as an effective solution to the small training samples issue in HSI classification techniques, the multi-task representation mechanism is employed by integrating the discriminative capabilities of complementary features to augment the training samples [
31,
32]. As a result, it leads to a new trend to exploit the complementarity contained in multi-feature for the HSI classification [
33]. Zhang et al. [
34] and Jia et al. [
35] respectively proposed a multi-feature joint SRC (MF-JSRC) and a 3-D Gabor cube selection based multitask joint SRC model for hyperspectral data. Fang et al. [
36] presented a multi-feature based adaptive sparse representation (MFASR) method to exploit the correlations among features. He et al. [
37,
38] introduced a class-oriented multitask learning based classifier and a kernel low-rank multitask learning (KL-MTL) method to handle multiple features. To deal with the nonlinear distribution of multiple features, Gan et al. [
39] developed a multiple feature kernel SRC for HSI classification. Although these multi-feature based classification algorithms employ the multi-task representation mechanism to improve the classification accuracy, the traditional representation models lead to unsatisfactory performance.
In this paper, a multi-feature correlation adaptive representation-based classifier (MFCARC) is proposed to enhance the classification accuracy under the small size samples situations by employing the multi-task representation mechanism. More importantly, the distance-weighted Tikhonov regularization is introduced to MFCARC, namely, multi-feature correlation adaptive representation with Tikhonov regularization (MFCART) classifier, leading to better performance. The main contributions are summarized as follows.
A new representation-based classifier CARC is proposed to possess the ability of performing sample selection and grouping correlated samples together simultaneously. It overcomes the intrinsic limitations of the traditional SRC & CRC methods and makes the model balance between SR & CR adaptively according to the precise correlation structure of the dictionary.
A dissimilarity-weighted Tikhonov regularization is integrated into the MFCARC framework to integrate the locality structure information and encode the correlation between the test sample and the training samples effectively, revealing the true geometry of feature space and thus further improving the class separability.
A multi-task representation strategy is incorporated into CARC and a correlation adaptive representation with Tikhonov regularization (CART) classifier, respectively, enhancing the classification accuracy under the small size samples situations.
The rest of this paper is organized as follows.
Section 2 briefly introduces the extraction of multiple features and the conventional representation-based classifiers. In
Section 3, the proposed MFCARC and MFCART algorithms are described. The experimental results on real hyperspectral datasets are present in
Section 4.
Section 5 provides a discussion of the results and conclusions are drawn in
Section 6.
4. Results
In this section, we examine the effectiveness of the proposed methods on three real hyperspectral data sets, including the Indian Pines data set, the University of Paiva data set, and the Salinas data set. State-of-the-art classification algorithms are used as the benchmark, including kernel sparse representation classification (KSRC) [
54], multiscale adaptive sparse representation classification (MASR) [
55], collaborative representation classification with Tikhonov regularization (CRT) [
19], kernel fused representation classification via the composite kernel with ideal regularization (KFRC-CKIR) [
27], multiple feature sparse representation classification (MF-SRC) [
34], multiple feature joint sparse representation classification (MF-JSRC) [
34], and multi-feature based adaptive sparse representation classification (MFASR) [
36]. To further demonstrate the effectiveness of the proposed methods, the classification performance of several recent deep-learning-based classifiers is also compared, including two convolutional neural networks (2-D CNN and 3-D CNN) [
56], a spatial prior generalized fuzziness extreme learning machine autoencoder (GFELM-AE) based active learning method [
57], a spatial–spectral convolutional long short-term memory (ConvLSTM) 2-D neural network (SSCL2DNN) [
58] and a spatial–spectral ConvLSTM 3-D neural network (SSCL3DNN) [
58]. In addition, four widely used metrics, the overall accuracy (OA), the average accuracy (AA), the kappa coefficient, and the class-specific accuracy (CA) are utilized for evaluation.
4.1. Hyperspectral Data Sets
4.1.1. Indian Pines Data Set
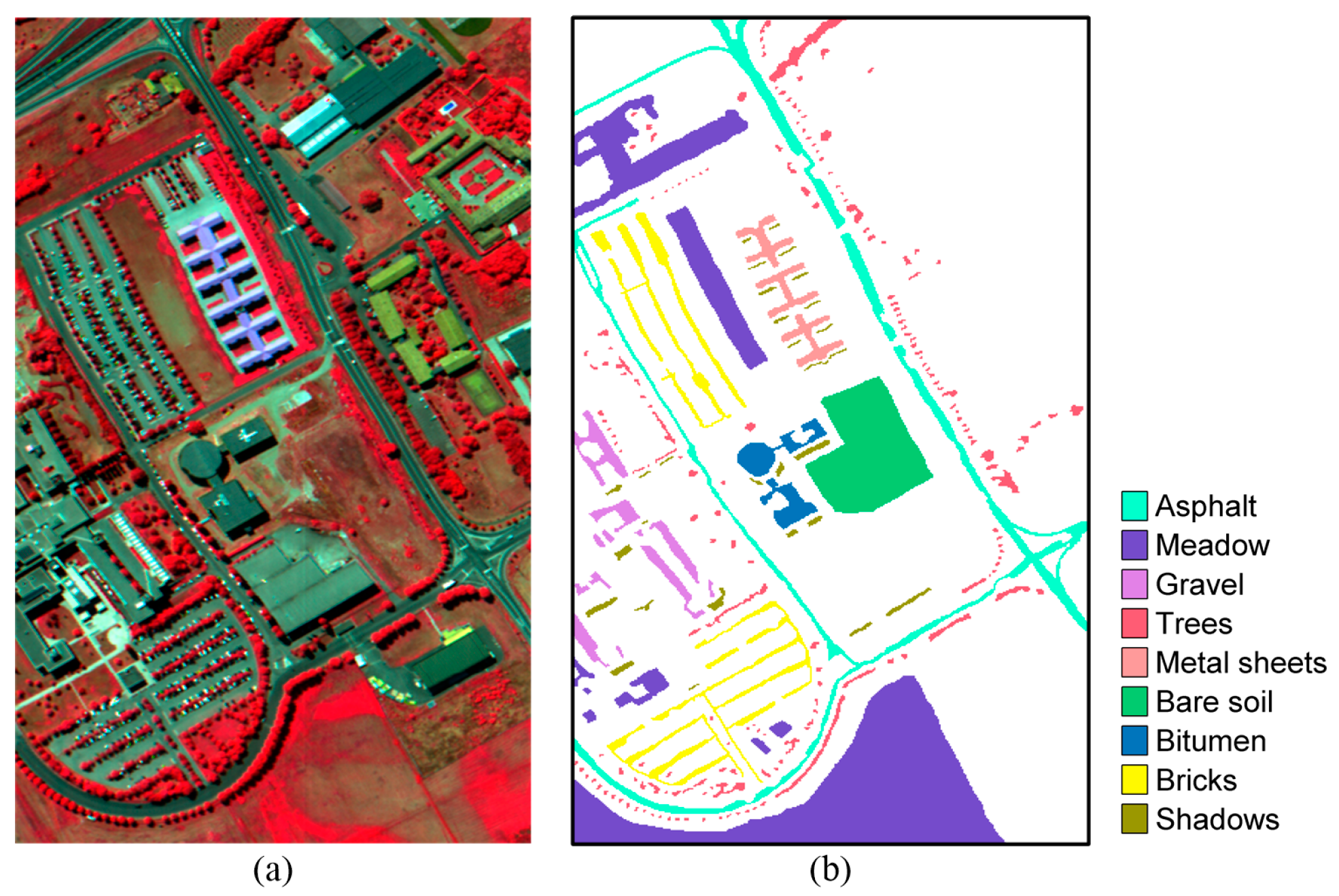
This data set was gathered by the Airborne Visible Infrared Imaging Spectrometer (AVIRIS) sensor over the agricultural regions in northwest Indiana’s Indian Pines test site. The spatial size of the data set is
pixels. Considering the effect of water absorption, 20 water absorption bands are removed, leaving 200 spectral bands for the HSI classification. The scene contains 16 land-cover classes. The detailed information of the ground-truth classes and the number of labeled samples are shown in
Table 1. The false-color composite image and the corresponding ground-truth map are shown in
Figure 2. As the small size samples situation is mainly concerned in our work, ten samples from each class are randomly picked up to constitute the dictionary, and the remaining samples are used for testing.
4.1.2. University of Pavia Data Set
This data set was acquired by the Reflective Optics System Imaging Spectrometer (ROSIS) sensor over the urban area of the University of Pavia, Northern Italy. The original data set contains
pixels and 115 spectral bands, with 103 spectral bands reserved for analysis after removing 12 noisy bands. The nine ground-truth classes and the number of labeled samples from each class are listed in
Table 2.
Figure 3 displays the false color image and the ground truth map. As for the number of training and testing samples, we randomly pick up ten labeled samples from each class for training and the rest for testing.
4.1.3. Salinas Data Set
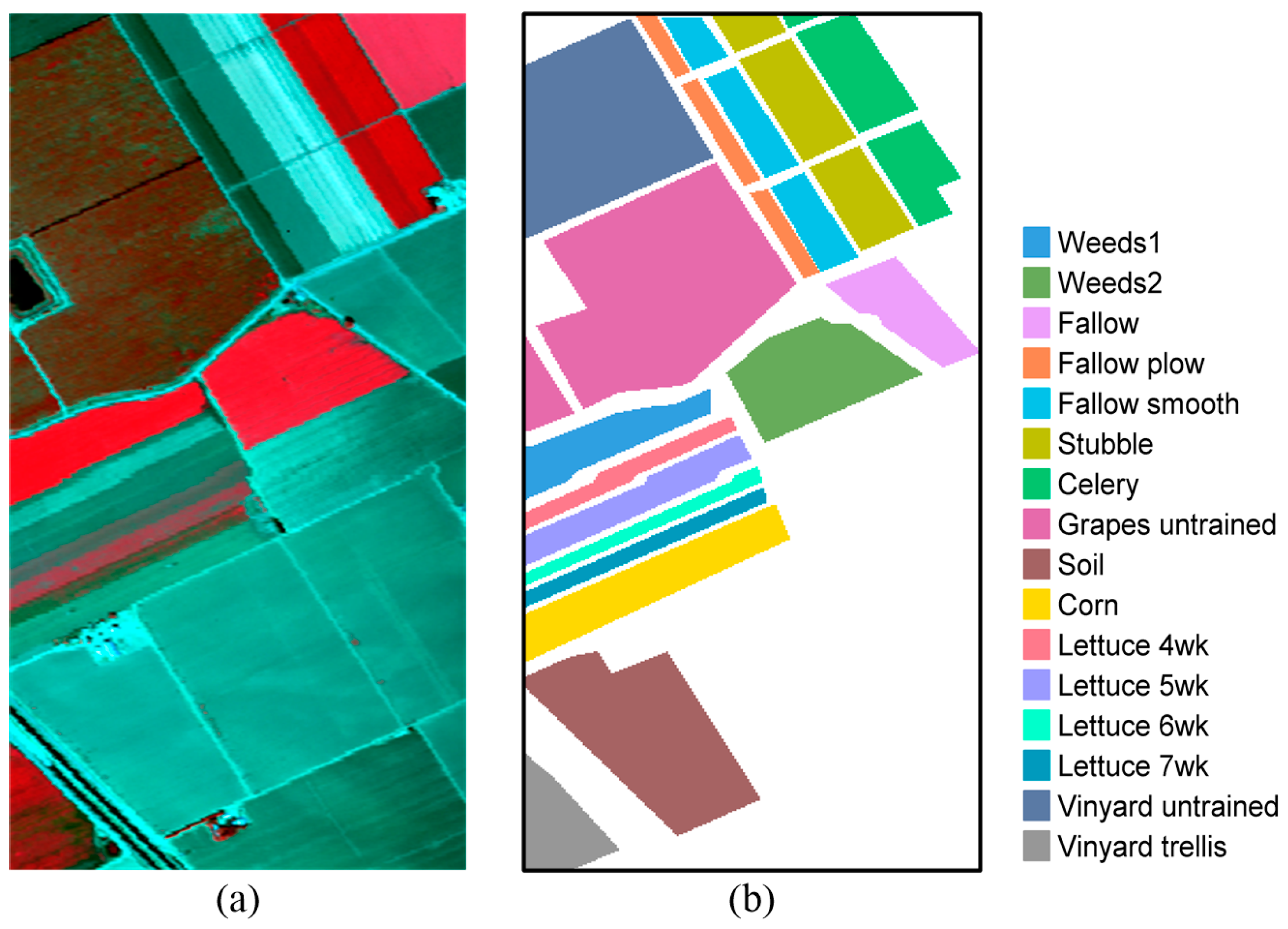
This data set was also collected by the AVIRIS sensor over the area of Salinas Valley, CA, USA. The data contains
pixels and 224 spectral bands. Like the Indian Pines data set, we also remove 20 water absorption spectral bands and keep 204 spectral bands preserved for the HSI classification. The thorough description of labeled samples from the 16 ground-truth classes is provided in
Table 3. The false-color image and the corresponding ground-truth map are shown in
Figure 4. Likewise, ten labeled samples from each class are chosen at random as the training dictionary and the remaining samples as the testing set.
4.2. Experimental Setting
4.2.1. Feature Extraction
For the proposed multi-feature-based representation methods, four features need to be extracted from the hyperspectral data, respectively. As described in
Section 2.1, the Gabor texture feature, LBP feature and DMP shape feature are extracted from the first three principal components of the HSIs by using the principal component analysis. The detailed parameter values used in our work for the four feature descriptors are listed in
Table 4.
4.2.2. Parameter Tuning
The impact of the two regularization parameters
λ and
β on the classification performance of the proposed algorithms with the three hyperspectral data sets need to be investigated. The range of the parameter
λ in the proposed MFCARC and MFCART algorithms is set as “
”. For the parameter
β in the MFCART, the candidate set is set as “
1, 5, 10”. Considering that the value of the parameter
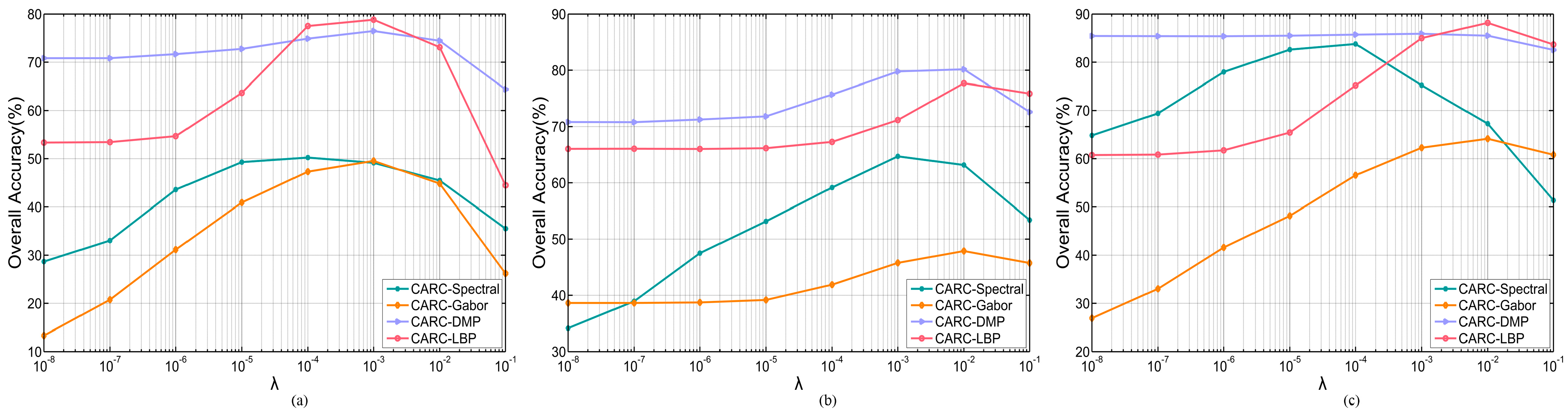
λ involved in the single-feature-based CARC methods (i.e., CARC-Spectral, CARC-Gabor, CARC-DMP, and CARC-LBP) has great influence on the performance of the proposed multi-feature based representation methods, we examine the effect of
λ on the performance of the CARC with four features, respectively. The overall accuracy tendencies of the single-feature-based CARC methods versus varying
λ with three data sets are illustrated in
Figure 5. As observed, the overall accuracies of the single-feature-based CARC methods generally increase significantly with the growing
λ and then begin to decrease after the maximum value.
The influence of the regularization parameter
β on the classification performance of the MFCART algorithm is also evaluated with all three data sets. As illustrated in
Figure 6, the single-feature-based CART methods generally achieve better performance when the parameter
β ranges from
to
except for the CART-spectral, as the CART-spectral achieves the best performance when
β = 5 on the Indian Pines data set. The optimal parameter values of
λ and
β for the proposed MFCARC and MFCART algorithms on the three data sets are summarized in
Table 5.
4.3. Classification Results
First, classification performance of the proposed CARC with the four features, i.e., CARC-Spectral, CARC-Gabor, CARC-DMP, and CARC-LBP is compared with the performance of the proposed MFCARC and MFCART, as shown in
Table 6. The experiments of the proposed methods are conducted under the optimal parameters listed in
Table 5. For the Salinas data set, ten labeled samples from each class are chosen at random for training and the rest for testing. It is observed that the proposed MFCARC and MFCART outperform the single-feature-based CARC methods, which demonstrates the effectiveness of combining multiple complementary features in the multi-task representation model. Besides, among those features, DMP and LBP features have superior performance and stronger class separability.
Subsequently, we compare the classification performance of the proposed MFCARC and MFCART methods with KSRC, MASR, CRT, KFRC-CKIR, MF-SRC, MF-JSRC, and MFASR. To avoid any bias, we repeat all the experiments ten times and record the averaged classification results, including the mean and standard deviation of OA, AA, CA, and the kappa coefficient. Classification performance of the proposed methods and its competitors for the Indian Pines data set is listed in
Table 7. From
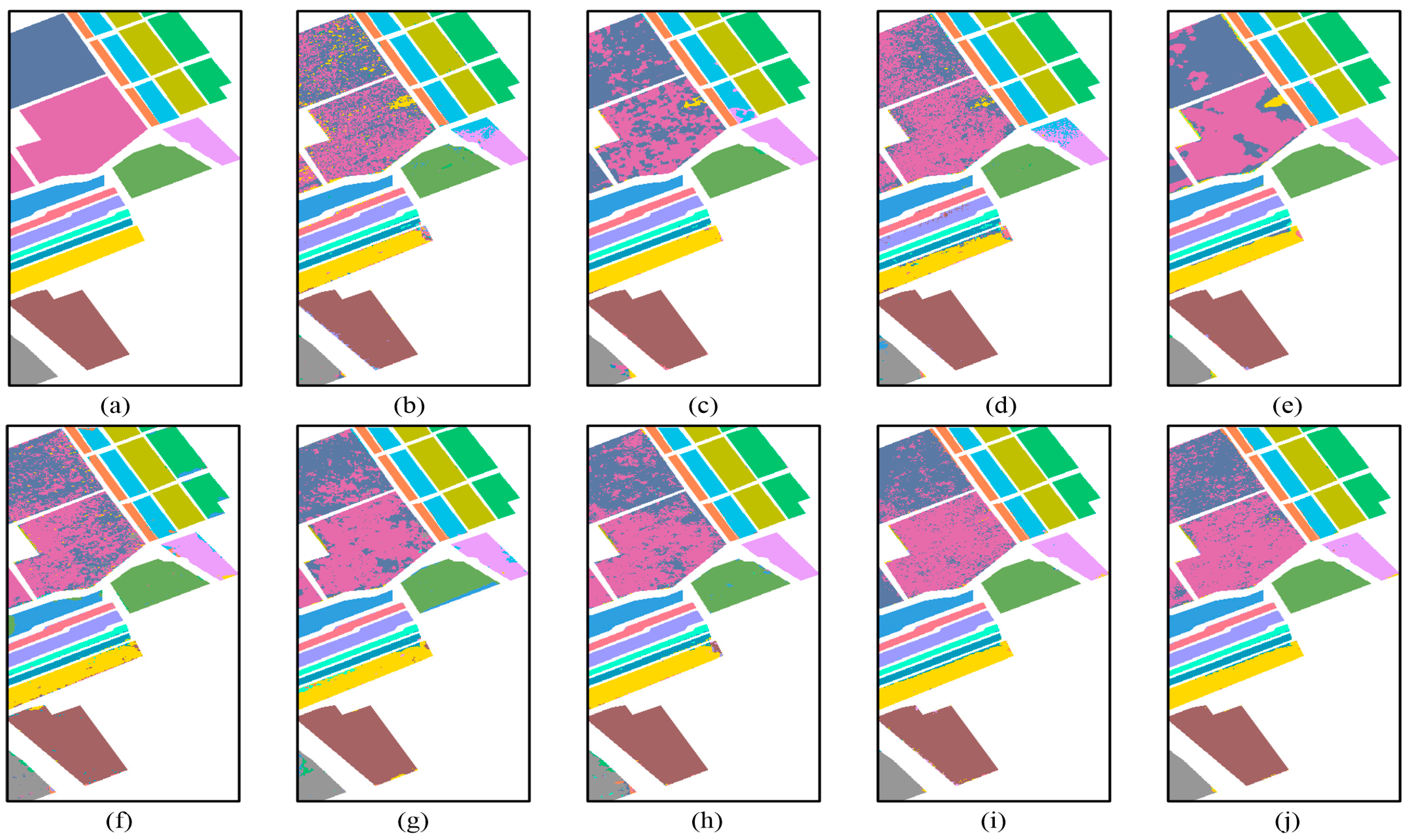
Table 7, it is observed that the proposed methods provide remarkable performance with approximately 20% higher improvement in terms of OA compared with the state-of-the-art KSRC, CRT, and MF-SRC. In addition, when compared with the multi-feature-based classification algorithms such as MF-SRC, MF-JSRC, and MFASR, our proposed methods show better performance. Besides, the classification maps generated by the proposed methods and other comparative methods are shown in
Figure 7b–j. It shows that the proposed methods achieve promising performance in both large homogeneous regions and regions of small objects.
The detailed classification performance for the University of Pavia data set is given in
Table 8, and the classification maps are shown in
Figure 8b‒j. The proposed methods achieve the best performance with the OA value reaching about 90%. There exists significant improvement when compared with multi-feature-based classification methods. Specifically, our methods produce nearly 11%, 8%, and 6% improvement in terms of OA compared with MF-SRC, MF-JSRC, and MFASR. As illustrated in
Figure 8, our methods result in more accurate classification maps than other classifiers.
The classification performance for Salinas data set is listed in
Table 9, and the classification maps generated by different classifiers are shown in
Figure 9b–j. From
Table 9, it is seen that the proposed MFCARC and MFCART methods outperform other comparative algorithms. For the Salinas data, there are two classes that are very difficult to be distinguished, i.e., class 8 (Grapes untrained) and class 15 (Vinyard untrained). This is because these two classes are not only spatially adjacent, but also have very similar spectral reflectance curves. From the classification maps, we can see that our proposed methods produce satisfactory results. The accuracy for class 15 of MFCART improves nearly 6% compared with MFCARC, which validates the effectiveness of the MFCART.
To further validate the effectiveness of the proposed methods, we compare our methods with several recent deep-learning-based classifiers. The experimental results over the Indian Pines data set and the University of Paiva data set are reported in
Table 10 and
Table 11. From
Table 10 and
Table 11, it is observed that the proposed methods outperform deep-learning-based models on both data sets. Specifically, compared with the state-of-the-art GFELM-AE, SSCL2DNN and SSCL3DNN algorithms, MFCART obtains 25.93%, 26.76%, and 16.07% gains in OA on the Indian Pines data set. For the University of Pavia data set, the proposed MFCARC yields an accuracy of 90.59%, achieving 46.29%, 32.09%, and 9.48% improvement over the 2-D CNN, 3-D CNN, and SSCL3DNN methods, respectively. Based on the experimental results, it demonstrates the effectiveness and the superiority of the proposed MFCARC and MFCART methods.
6. Conclusions
In this paper, a new representation-based classifier CARC is proposed to perform sample selection and group correlated samples simultaneously. Owing to the adaptive property of the regularization, CARC is capable of balancing between SRC and CRC adaptively according to the precise correlation structure of the dictionary, which overcomes the intrinsic limitations of the traditional SR- and CR-based classification methods in HSI classification. In addition, by taking the correlation between the test sample and the training samples into consideration, CART is developed to make the representation model reveal the true geometry of feature space. Moreover, aiming at solving the small training samples issue, multi-feature representation frameworks are constructed according to the proposed CARC and CART, leading to MFCARC and MFCART frameworks, which can build more accurate representation models for hyperspectral data under the small size samples situations. Experimental results show that the MFCARC and MFCART achieve superior performance than state-of-the-art algorithms.
However, there also exist certain limitations for the proposed methods. In our proposed methods, training samples are directly used as training atoms of the dictionary and the random sampling strategy is adopted for constructing the dictionary. Considering that constructing a compact and representative dictionary is beneficial for the sample representation, our future research will focus on the design of the discriminative dictionary and the integration of the dictionary learning process to further improve the classification performance under the small size samples situations.