Interannual Climate Variability in the West Antarctic Peninsula under Austral Summer Conditions
Abstract
1. Introduction
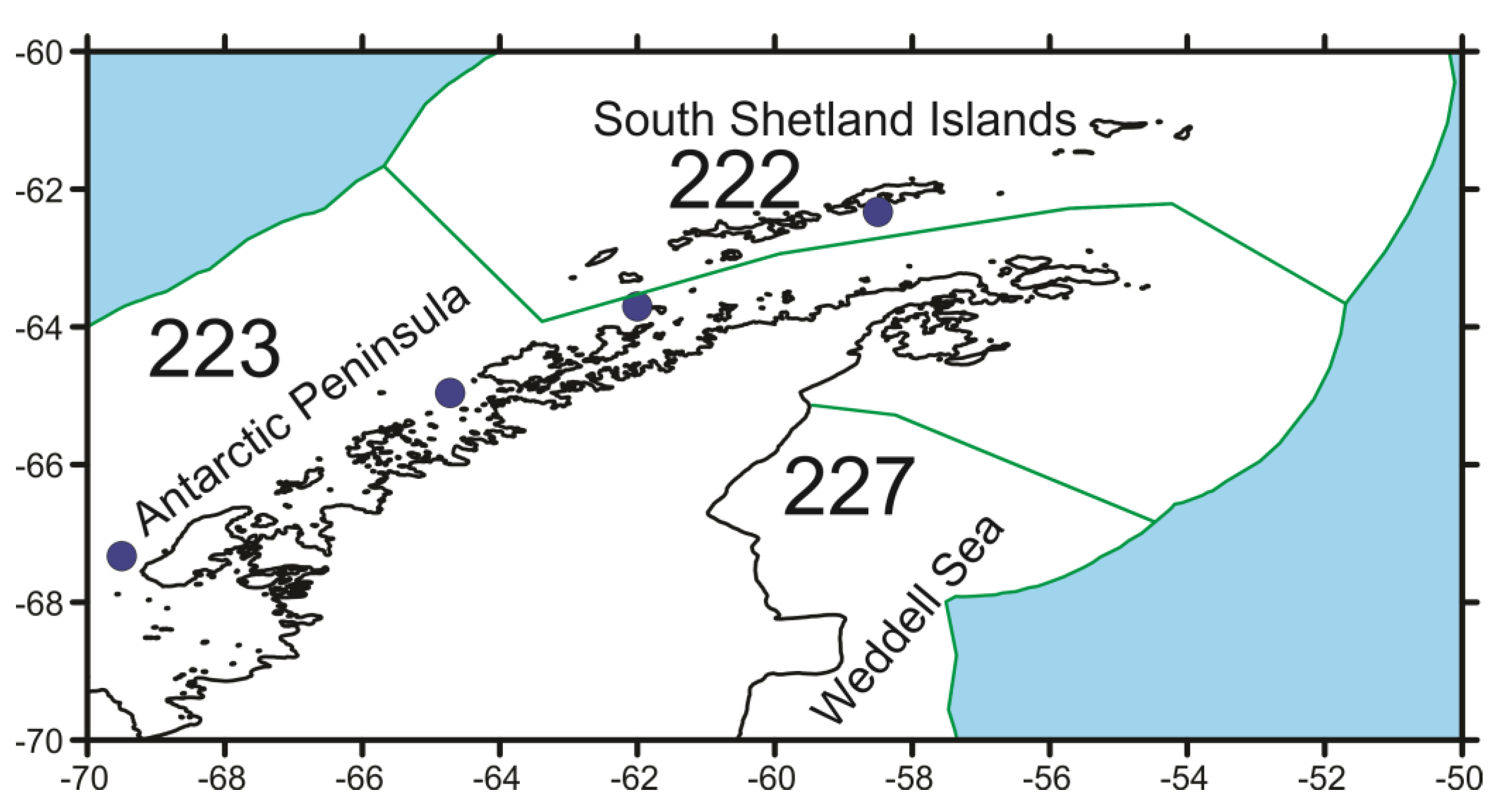
2. Materials and Methods
3. Results
4. Discussion
- The SOI [40] is an index based on atmospheric pressure at sea level in Tahiti and Darwin, with a time series since January 1876.
- The Oceanic Niño Index (ONI; El Niño 3–4) is listed as an index based on sea-surface temperature in the region 3-4 in the equator [92] and has been calculated since 1950. One of the main weaknesses of this index is that it is calculated based on the Extended Reconstructed Sea-Surface Temperature (ERSST).
- The Multivariate ENSO Index (MEI) [93] combines oceanic and atmospheric variables using an orthogonal empirical function (OEF), encompassing the time period from 1979 to date.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Farman, J.C.; Gardiner, B.G.; Shanklin, J.D. Large losses of total ozone in Antarctica reveal seasonal ClOx/NOx interaction. Nat. Cell Biol. 1985, 315, 207–210. [Google Scholar] [CrossRef]
- Brook, E.J.; Buizert, C. Antarctic and global climate history viewed from ice cores. Nat. Cell Biol. 2018, 558, 200–208. [Google Scholar] [CrossRef] [PubMed]
- Moore, J.K.; Fu, W.; Primeau, F.; Britten, G.L.; Lindsay, K.; Long, M.; Doney, S.C.; Mahowald, N.; Hoffman, F.; Randerson, J.T. Sustained climate warming drives declining marine biological productivity. Science 2018, 359, 1139–1143. [Google Scholar] [CrossRef] [PubMed]
- Bornman, J.F.; Barnes, P.W.; Robson, T.M.; Robinson, S.A.; Jansen, M.A.K.; Ballaré, C.L.; Flint, S.D. Linkages between stratospheric ozone, UV radiation and climate change and their implications for terrestrial ecosystems. Photochem. Photobiol. Sci. 2019, 18, 681–716. [Google Scholar] [CrossRef] [PubMed]
- COMNAP. COMNAP Antarctic Station Catalogue. 2017. Available online: https://www.comnap.aq/Members/Shared%20Documents/COMNAP_Antarctic_Station_Catalogue.pdf (accessed on 20 November 2020).
- King, J.C. Recent climate variability in the vicinity of the Antarctic Peninsula. Int. J. Clim. 1994, 14, 357–369. [Google Scholar] [CrossRef]
- Saba, G.K.; Fraser, W.R.; Saba, V.S.; Iannuzzi, R.A.; Coleman, K.E.; Doney, S.C.; Ducklow, H.W.; Martinson, D.G.; Miles, T.N.; Patterson-Fraser, D.L.; et al. Winter and spring controls on the summer food web of the coastal West Antarctic Peninsula. Nat. Commun. 2014, 5, 4318. [Google Scholar] [CrossRef]
- Kim, H.; Ducklow, H.W.; Abele, D.; Ruiz Barlett, E.M.; Buma, A.G.; Meredith, M.P.; Rozema, P.D.; Schofield, O.M.; Venables, H.J.; Schloss, I.R. Inter-decadal variability of phytoplankton biomass along the coastal West Antarctic Peninsula. Philos. Trans. R. Soc. A 2018, 376, 20170174. [Google Scholar] [CrossRef]
- Montes-Hugo, M.; Doney, S.C.; Ducklow, H.W.; Fraser, W.R.; Martinson, D.G.; Stammerjohn, S.E.; Schofield, O. Recent Changes in Phytoplankton Communities Associated with Rapid Regional Climate Change Along the Western Antarctic Peninsula. Science 2009, 323, 1470–1473. [Google Scholar] [CrossRef]
- Whitehouse, M.; Meredith, M.; Rothery, P.; Atkinson, A.; Ward, P.; Korb, R. Rapid warming of the ocean around South Georgia, Southern Ocean, during the 20th century: Forcings, characteristics and implications for lower trophic levels. Deep. Sea Res. Part I Oceanogr. Res. Pap. 2008, 55, 1218–1228. [Google Scholar] [CrossRef]
- Cañon-Páez, M.L.; Santamaría-del-Ángel, E.; Lopez Calderón, J.M.; González-Silveira, A.G.; Camacho-Ibar, V.F.; Fran-co-Herrera, A. Changes in Community Structure Based on the Reconstruction of Type Spectra of the Specific Absorption Coefficient of Phytoplankton in the Gerlache Strait. (in preparation). March 2021. [Google Scholar]
- Vaughan, D.G.; Marshall, G.J.; Connolley, W.M.; King, J.C.; Mulvaney, R. Climate change: Devil in the Detail. Science 2001, 293, 1777–1779. [Google Scholar] [CrossRef] [PubMed]
- Marshall, G.J.; Lagun, V.; Lachlan-Cope, T.A. Changes in Antarctic Peninsula tropospheric temperatures from 1956 to 1999: A synthesis of observations and reanalysis data. Int. J. Clim. 2002, 22, 291–310. [Google Scholar] [CrossRef]
- Vaughan, D.G.; Marshall, G.J.; Connolley, W.M.; Parkinson, C.; Mulvaney, R.; Hodgson, D.A.; King, J.C.; Pudsey, C.J.; Turner, J. Recent Rapid Regional Climate Warming on the Antarctic Peninsula. Clim. Chang. 2003, 60, 243–274. [Google Scholar] [CrossRef]
- Meredith, M.P.; King, J.C. Rapid climate change in the ocean west of the Antarctic Peninsula during the second half of the 20th century. Geophys. Res. Lett. 2005, 32, 19. [Google Scholar] [CrossRef]
- Smith, R.C.; Stammerjohn, S.E.; Baker, K.S. Surface air temperature variations in the Western Antarctic Peninsula region, in Foundations for Ecological Research West of the Antarctic Peninsula. Antarct. Res. Ser. 1996, 70, 105–121. [Google Scholar]
- Turner, J.; Colwell, S.R.; Marshall, G.J.; Lachlan-Cope, T.A.; Carleton, A.M.; Jones, P.D.; Lagun, V.; Reid, P.A.; Iagovkina, S. Antarctic climate change during the last 50 years. Int. J. Clim. 2005, 25, 279–294. [Google Scholar] [CrossRef]
- Clarke, A.; Griffiths, H.J.; Barnes, D.K.A.; Meredith, M.P.; Grant, S.M. Spatial variation in seabed temperatures in the Southern Ocean: Implications for benthic ecology and biogeography. J. Geophys. Res. Space Phys. 2009, 114, 03003. [Google Scholar] [CrossRef]
- Moffat, C.; Meredith, M. Shelf–ocean exchange and hydrography west of the Antarctic Peninsula: A review. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2018, 376, 20170164. [Google Scholar] [CrossRef] [PubMed]
- Vazquez, J.; Li, X. (Eds.) Sea Surface Temperature Retrievals from Remote Sensing. Remote Sens. 2018, 340. [Google Scholar] [CrossRef]
- Santamaría-del-Angel, E.; Soto, I.; Millán-Nuñez, R.; González-Silvera, A.; Wolny, J.; Cerdeira-Estrada, S.; Cajal-Medrano, R.; Muller-Karger, F.; Cannizzaro, J.; Padilla-Rosas, Y.X.S.; et al. Anthropocentric bias in management policies. Are we efficiently monitoring our ecosystem? In Coastal Ecosystems: Experiences and Recommendations for Environmental Monitoring Programs; Sebastiá-Frasquet, M.T., Ed.; Nova Science Publishers: New York, NY, USA, 2015; Chapter 1; pp. 1–12. ISBN 978-1-63482-189-6i. [Google Scholar]
- Palmer Long-Term Ecological Research. Available online: https://pal.lternet.edu/ (accessed on 4 August 2020).
- Ocean Color Data. Available online: https://oceancolor.gsfc.nasa.gov/ (accessed on 4 August 2020).
- Walton, C.C.; Pichel, W.G.; Sapper, J.F.; May, D.A. The development and operational application of nonlinear algorithms for the measurement of sea surface temperatures with the NOAA polar-orbiting environmental satellites. J. Geophys. Res. Space Phys. 1998, 103, 27999–28012. [Google Scholar] [CrossRef]
- Kilpatrick, K.; Podestá, G.; Walsh, S.; Williams, E.; Halliwell, V.; Szczodrak, M.; Brown, O.; Minnett, P.; Evans, R. A decade of sea surface temperature from MODIS. Remote Sens. Environ. 2015, 165, 27–41. [Google Scholar] [CrossRef]
- Kahru, M.; Di Lorenzo, E.; Manzano-Sarabia, M.; Mitchell, B.G. Spatial and temporal statistics of sea surface temperature and chlorophyll fronts in the California Current. J. Plankton Res. 2012, 34, 749–760. [Google Scholar] [CrossRef]
- Kahru, M.; Kudela, R.M.; Anderson, C.R.; Mitchell, B.G. Optimized Merger of Ocean Chlorophyll Algorithms of MODIS-Aqua and VIIRS. IEEE Geosci. Remote Sens. Lett. 2015, 12, 2282–2285. [Google Scholar] [CrossRef]
- Wim Software. Available online: https://www.wimsoft.com (accessed on 20 November 2020).
- Santamaría-del-Ángel, E.; Sebastia-Frasquet, M.-T.; González-Silvera, A.; Aguilar-Maldonado, J.; Mercado-Santana, A.; Herrera-Carmona, J.C. Uso potencial de las anomalías estandarizadas en la interpretación de fenómenos oceanográficos globales a escalas locales. Chapter Procesos y ciclos en la costa; In Tópicos de Agenda para la Sostenibilidad de Costas y Mares Mexicanos; Rivera-Arriaga, E., Sánchez-Gil, P., Gutiérrez, J., Eds.; Universidad Autónoma de Campeche: Campeche, Mexico, 2019; pp. 193–212, 334. ISBN 978-607-8444-57-1. [Google Scholar]
- Chen, S.; Wu, R. Impacts of winter NPO on subsequent winter ENSO: Sensitivity to the definition of NPO index. Clim. Dyn. 2017, 50, 375–389. [Google Scholar] [CrossRef]
- Morales-Acuña, E.; Torres, C.R.; Delgadillo-Hinojosa, F.; Linero-Cueto, J.R.; Santamaría-Del-Ángel, E.; Castro, R. The Baja California Peninsula, a Significant Source of Dust in Northwest Mexico. Atmosphere 2019, 10, 582. [Google Scholar] [CrossRef]
- Di Matteo, S.; Viall, N.M.; Kepko, L. Power Spectral Density Background Estimate and Signal Detection via the Multitaper Method. J. Geophys. Res. Space Phys. 2021, 126, e2020JA028748. [Google Scholar] [CrossRef]
- Schonlau, M. The Clustergram: A Graph for Visualizing Hierarchical and Nonhierarchical Cluster Analyses. Stata J. 2002, 2, 391–402. [Google Scholar] [CrossRef]
- Jamshidian, M.; Jalal, S. Tests of Homoscedasticity, Normality, and Missing Completely at Random for Incomplete Multivariate Data. Psychometrika 2010, 75, 649–674. [Google Scholar] [CrossRef]
- Liang, J.; Pan, W.S.; Yang, Z.H. Characterization-based Q–Q plots for testing multinormality. Stat. Probabil. Lett. 2004, 70, 183–190. [Google Scholar] [CrossRef]
- Bureau of Meteorology. Available online: http://www.bom.gov.au/climate/current/soihtm1.shtml (accessed on 4 August 2020).
- Marshall, G.J. Trends in the Southern Annular Mode from observations and reanalyses. J. Clim. 2003, 16, 4134–4143. [Google Scholar] [CrossRef]
- Climate Date Guide. Available online: https://climatedataguide.ucar.edu/climate-data/marshall-southern-annular-mode-sam-index-station-based (accessed on 4 August 2020).
- SAM Index. Available online: https://legacy.bas.ac.uk/met/gjma/sam.html (accessed on 8 August 2020).
- Bureau Meteorology. Available online: http://www.bom.gov.au/climate/enso/history/ln-2010-12/SAM-what.shtml (accessed on 12 August 2020).
- Santamaría-del-Angel, E.; Millán-Núñez, R.; González-Silvera, A.; Cajal-Medrano, R. A comparison of Chl a concentrations estimated in situ and Chl a concentrations determined via remote sensing: A statistical examination of the match-up approach. In Handbook of Satellite Remote Sensing Image Interpretation: Applications for Marine Living Resources Conservation and Management; Morales, J., Stuart, V., Platt, T., Sathyendranath, S.J., Eds.; EU PRESPO and IOCCG: Dartmouth, NS, Canada, 2011; Chapter 17; pp. 241–259. Available online: https://www.ioccg.org/handbook/casestudy17_angel_etal.pdf (accessed on 2 December 2020).
- Perdices, M. Null Hypothesis Significance Testing, p-values, Effects Sizes and Confidence Intervals. Brain Impair. 2018, 19, 70–80. [Google Scholar] [CrossRef]
- Mu, Y.; Liu, X.; Wang, L. A Pearson’s correlation coefficient based decision tree and its parallel implementation. Inf. Sci. 2018, 435, 40–58. [Google Scholar] [CrossRef]
- Farnsworth, D.L.; Triola, M.F. Elementary Statistics. Technometrics 1990, 32, 456. [Google Scholar] [CrossRef]
- Kokoska, S.; Nevison, C. Critical values for Spearman’s rank correlation coefficient. In Statistical Tables and Formulae; Springer: New York, NY, USA, 1989. [Google Scholar] [CrossRef]
- Santamaría-del-Ángel, E.; González-Silvera, A.; Millán-Núñez, R.; Callejas-Jiménez, M.E.; Cajal-Medrano, R. Determining dynamic biogeographic regions using remote sensing data. In Handbook of Satellite Remote Sensing Image Interpretation: Applications for Marine Living Resources Conservation and Management; Morales, J., Stuart, V., Platt, T., Sathyendranath, S.J., Eds.; EU PRESPO and IOCCG: Dartmouth, NS, Canada, 2011; Chapter 19; pp. 273–293. Available online: https://www.ioccg.org/handbook/casestudy19_angel_etal.pdf (accessed on 2 December 2020).
- Kaiser, H.F. The varimax criterion for analytic rotation in factor analysis. Psychometrika 1958, 23, 187–200. [Google Scholar] [CrossRef]
- Yeomans, K.A.; Golder, P.A. The Guttman-Kaiser Criterion as a Predictor of the Number of Common Factors. Amer. Statist. 1982, 31, 221. [Google Scholar] [CrossRef]
- Ferré, L. Selection of components in principal component analysis: A comparison of methods. Comput. Stat. Data Anal. 1995, 19, 669–682. [Google Scholar] [CrossRef]
- Kanyongo, G.Y. Determining the correct number of components to extract from a principal components analysis: A Monte Carlo study of the accuracy of the scree plot. J Mod. Appl. Stat. Methods 2005, 4, 120–133. [Google Scholar] [CrossRef]
- Schreiber, J.B. Issues and recommendations for exploratory factor analysis and principal component analysis. Res. Soc. Adm. Pharm. 2020. [Google Scholar] [CrossRef] [PubMed]
- Navarro Fierro, R. Introducción a la bioestadística: Análisis de variables binarias; McGRAW-Hill: Ciudad de Mexico, Mexico, 1988; 170p, ISBN 968-422-387-0. [Google Scholar]
- Santamaría-Del-Angel, E.; Alvarez-Borrego, S.; Muller-Karger, F.E. The 1982–1984 El Niño in the Gulf of California as seen in coastal zone color scanner imagery. J. Geophys. Res. Space Phys. 1994, 99, 7423–7431. [Google Scholar] [CrossRef]
- Turner, J.; Marshall, G.J.; Clem, K.; Colwell, S.; Phillips, T.; Lu, H. Antarctic temperature variability and change from station data. Int. J. Clim. 2020, 40, 2986–3007. [Google Scholar] [CrossRef]
- Ducklow, H.W.; Baker, K.; Martinson, D.G.; Quetin, L.B.; Ross, R.M.; Smith, R.C.; Stammerjohn, S.E.; Vernet, M.; Fraser, W. Marine pelagic ecosystems: The West Antarctic Peninsula. Philos. Trans. R. Soc. B Biol. Sci. 2006, 362, 67–94. [Google Scholar] [CrossRef] [PubMed]
- Atkinson, A.; Siegel, V.; Pakhomov, E.; Rothery, P. Long-term decline in krill stock and increase in salps within the Southern Ocean. Nat. Cell Biol. 2004, 432, 100–103. [Google Scholar] [CrossRef] [PubMed]
- Suprenand, P.M.; Ainsworth, C.H. Trophodynamic effects of climate change-induced alterations to primary production along the western Antarctic Peninsula. Mar. Ecol. Prog. Ser. 2017, 569, 37–54. [Google Scholar] [CrossRef]
- Clarke, A.; Murphy, E.J.; Meredith, M.P.; King, J.C.; Peck, L.S.; Barnes, D.K.A.; Smith, R.C. Climate change and the marine ecosystem of the western Antarctic Peninsula. Philos. Trans. R. Soc. B Biol. Sci. 2006, 362, 149–166. [Google Scholar] [CrossRef]
- White, W.B.; Peterson, R.G. An Antarctic circumpolar wave in surface pressure, wind, temperature and sea-ice extent. Nature 1996, 380, 699–702. [Google Scholar] [CrossRef]
- Donohue, K.A.; Tracey, K.L.; Watts, D.R.; Chidichimo, M.P.; Chereskin, T.K. Mean Antarctic Circumpolar Current transport measured in Drake Passage. Geophys. Res. Lett. 2016, 43, 11–760. [Google Scholar] [CrossRef]
- Constantin, A.; Johnson, R.S. An Exact, Steady, Purely Azimuthal Flow as a Model for the Antarctic Circumpolar Current. J. Phys. Oceanogr. 2016, 46, 3585–3594. [Google Scholar] [CrossRef]
- Tarakanov, R.Y.; Gritsenko, A.M. Jets of the Antarctic Circumpolar Current in the Drake Passage Based on Hydrographic Section Data. Oceanology 2018, 58, 503–516. [Google Scholar] [CrossRef]
- Giglio, D.; Johnson, G.C. Subantarctic and Polar Fronts of the Antarctic Circumpolar Current and Southern Ocean Heat and Freshwater Content Variability: A View from Argo. J. Phys. Oceanogr. 2016, 46, 749–768. [Google Scholar] [CrossRef]
- Haziot, S.V.; Marynets, K. Applying the stereographic projection to modeling of the flow of the Antarctic Circumpolar Current. Oceanography 2018, 31, 68–75. [Google Scholar] [CrossRef]
- Quirchmayr, R. A steady, purely azimuthal flow model for the Antarctic Circumpolar Current. Mon. Math. 2017, 187, 565–572. [Google Scholar] [CrossRef]
- Marynets, K. The Antarctic Circumpolar Current as a shallow-water asymptotic solution of Euler’s equation in spherical coordinates. Deep. Sea Res. Part II Top. Stud. Oceanogr. 2019, 160, 58–62. [Google Scholar] [CrossRef]
- Haziot, S.V. Study of an elliptic partial differential equation modelling the Antarctic Circumpolar Current. Discret. Contin. Dyn. Syst. A 2019, 39, 4415–4427. [Google Scholar] [CrossRef]
- Koshlyakov, M.N.; Savchenko, D.S.; Tarakanov, R.Y. Energy Exchange between Jets of the Antarctic Circumpolar Current and Synoptic Eddies in the Drake Passage and Scotia Sea. Oceanology 2018, 58, 329–339. [Google Scholar] [CrossRef]
- Song, H.; Long, M.C.; Gaube, P.; Frenger, I.; Marshall, J.; McGillicuddy, D.J., Jr. Seasonal Variation in the Correlation Between Anomalies of Sea Level and Chlorophyll in the Antarctic Circumpolar Current. Geophys. Res. Lett. 2018, 45, 5011–5019. [Google Scholar] [CrossRef]
- Balwada, D.; Speer, K.G.; LaCasce, J.H.; Owens, W.B.; Marshall, J.C.; Ferrari, R. Circulation and Stirring in the Southeast Pacific Ocean and the Scotia Sea Sectors of the Antarctic Circumpolar Current. J. Phys. Oceanogr. 2016, 46, 2005–2027. [Google Scholar] [CrossRef]
- King, J.C.; Turner, J.; Marshall, G.J.; Connolley, W.M.; Lachlan-Cope, T.A.; King, J.C.; Turner, J.; Marshall, G.J.; Connolley, W.M.; Lachlan-Cope, T.A. Antarctic Peninsula climate variability and its causes as revealed by analysis of instrumental records. In Antarctic Peninsula Climate Variability: Historical and Paleoenvironmental Perspectives; American Geophysical Union: Washington, DC, USA, 2003; Volume 79, pp. 17–30. [Google Scholar] [CrossRef]
- Barnes, D.K.; Fuentes, V.; Clarke, A.; Schloss, I.R.; Wallace, M.I. Spatial and temporal variation in shallow seawater temperatures around Antarctica. Deep. Sea Res. Part II Top. Stud. Oceanogr. 2006, 53, 853–865. [Google Scholar] [CrossRef]
- Thompson, A.F.; Stewart, A.L.; Spence, P.; Heywood, K.J. The Antarctic Slope Current in a Changing Climate. Rev. Geophys. 2018, 56, 741–770. [Google Scholar] [CrossRef]
- Kim, Y.S.; Orsi, A.H. On the Variability of Antarctic Circumpolar Current Fronts Inferred from 1992–2011 Altimetry. J. Phys. Oceanogr. 2014, 44, 3054–3071. [Google Scholar] [CrossRef]
- Kim, H.; Doney, S.C.; Iannuzzi, R.A.; Meredith, M.P.; Martinson, D.G.; Ducklow, H.W. Climate forcing for dynamics of dissolved inorganic nutrients at Palmer Station, Antarctica: An interdecadal (1993–2013) analysis. J. Geophys. Res. Biogeosciences 2016, 121, 2369–2389. [Google Scholar] [CrossRef]
- Jones, M.E.; Bromwich, D.H.; Nicolas, J.P.; Carrasco, J.; Plavcová, E.; Zou, X.; Wang, S.-H. Sixty Years of Widespread Warming in the Southern Middle and High Latitudes (1957–2016). J. Clim. 2019, 32, 6875–6898. [Google Scholar] [CrossRef]
- Stammerjohn, S.E.; Martinson, D.G.; Smith, R.C.; Yuan, X.; Rind, D. Trends in Antarctic annual sea ice retreat and advance and their relation to El Niño–Southern Oscillation and Southern Annular Mode variability. J. Geophys. Res. Space Phys. 2008, 113, 4603. [Google Scholar] [CrossRef]
- Clem, K.R.; Renwick, J.A.; McGregor, J.; Fogt, R.L. The relative influence of ENSO and SAM on Antarctic Peninsula climate. J. Geophys. Res. Atmos. 2016, 121, 9324–9341. [Google Scholar] [CrossRef]
- Fogt, R.L.; Bromwich, D.H.; Hines, K.M. Understanding the SAM influence on the South Pacific ENSO teleconnection. Clim. Dyn. 2011, 36, 1555–1576. [Google Scholar] [CrossRef]
- Kwok, R.; Comiso, J.C. Spatial patterns of variability in Antarctic surface temperature: Connections to the Southern Hemisphere Annular Mode and the Southern Oscillation. Geophys. Res. Lett. 2002, 29, 50–51. [Google Scholar] [CrossRef]
- Pezza, A.B.; Rashid, H.A.; Simmonds, I. Climate links and recent extremes in antarctic sea ice, high-latitude cyclones, Southern Annular Mode and ENSO. Clim. Dyn. 2012, 38, 57–73. [Google Scholar] [CrossRef]
- Yeo, S.-R.; Kim, K.-Y. Decadal changes in the Southern Hemisphere sea surface temperature in association with El Niño–Southern Oscillation and Southern Annular Mode. Clim. Dyn. 2015, 45, 3227–3242. [Google Scholar] [CrossRef]
- Fogt, R.L.; Bromwich, D.H. Decadal Variability of the ENSO Teleconnection to the High-Latitude South Pacific Governed by Coupling with the Southern Annular Mode. J. Clim. 2006, 19, 979–997. [Google Scholar] [CrossRef]
- Lachlan-Cope, T.; Connolley, W. Teleconnections between the tropical Pacific and the Amundsen-Bellinghausens Sea: Role of the El Niño/Southern Oscillation. J. Geophys. Res. Space Phys. 2006, 111, 111. [Google Scholar] [CrossRef]
- Yiu, Y.Y.S.; Maycock, A.C. The linearity of the El Niño teleconnection to the Amundsen Sea region. Q. J. R. Meteorol. Soc. 2020, 146, 1169–1183. [Google Scholar] [CrossRef]
- Sexton, D.M.H. The effect of stratospheric ozone depletion on the phase of the Antarctic Oscillation. Geophys. Res. Lett. 2001, 28, 3697–3700. [Google Scholar] [CrossRef]
- Gillett, N.P.; Allen, M.R.; Williams, K.D. Modelling the atmospheric response to doubled CO2 and depleted stratospheric ozone using a stratosphere-resolving coupled GCM. Q. J. R. Meteorol. Soc. 2003, 129, 947–966. [Google Scholar] [CrossRef]
- Chipperfield, M.P.; Dhomse, S.S.; Feng, W.; McKenzie, R.L.; Velders, G.; Pyle, J.A. Quantifying the ozone and ultraviolet benefits already achieved by the Montreal Protocol. Nat. Commun. 2015, 6, 7233. [Google Scholar] [CrossRef] [PubMed]
- Spalding, M.D.; Fox, H.E.; Allen, G.R.; Davidson, N.; Ferdaña, Z.A.; Finlayson, M.; Halpern, B.S.; Jorge, M.A.; Lombana, A.; Lourie, S.A.; et al. Marine Ecoregions of the World: A Bioregionalization of Coastal and Shelf Areas. Bioscience 2007, 57, 573–583. [Google Scholar] [CrossRef]
- Nature Conservancy. Available online: https://geospatial.tnc.org/datasets/ed2be4cf8b7a451f84fd093c2e7660e3_0 (accessed on 4 August 2020).
- Koenig, Z.; Provost, C.; Ferrari, R.; Sennéchael, N.; Park, Y.-H. Anatomy of the Antarctic Circumpolar Current volume transports through Drake Passage. J. Geophys. Res. Oceans 2016, 121, 2572–2595. [Google Scholar] [CrossRef]
- National Weather Service Climate Prediction Center. Available online: https://origin.cpc.ncep.noaa.gov/products/analysis_monitoring/ensostuff/ONI_v5.php (accessed on 14 January 2021).
- Physical Sciences Laboratory. Available online: https://psl.noaa.gov/enso/mei (accessed on 14 January 2021).
- Welhouse, L.J.; Lazzara, M.A.; Keller, L.M.; Tripoli, G.J.; Hitchman, M.H. Composite analysis of the effects of ENSO events on Antarctica. J. Clim. 2016, 29, 1797–1808. [Google Scholar] [CrossRef]
- Yu, J.Y.; Paek, H.; Saltzman, E.S.; Lee, T. The early 1990s change in ENSO–PSA–SAM relationships and its impact on Southern Hemisphere climate. J. Clim. 2015, 28, 9393–9408. [Google Scholar] [CrossRef]
- Scott, R.C.; Nicolas, J.P.; Bromwich, D.H.; Norris, J.R.; Lubin, D. Meteorological Drivers and Large-Scale Climate Forcing of West Antarctic Surface Melt. J. Clim. 2019, 32, 665–684. [Google Scholar] [CrossRef]
- National Oceanic and Atmospheric Administration. Available online: https://www.ncdc.noaa.gov/data-access/marineocean-data/extended-reconstructed-sea-surface-temperature-ersst-v5 (accessed on 7 August 2020).
- Ding, Q.; Steig, E.J. Temperature Change on the Antarctic Peninsula Linked to the Tropical Pacific. J. Clim. 2013, 26, 7570–7585. [Google Scholar] [CrossRef]
- National Snow & Ice Data Center. Available online: Nsidc.org/data/avhrr (accessed on 9 August 2020).
- National Oceanic and Atmospheric Administration. Available online: https://www.nodc.noaa.gov/sog/pathfinder4km/userguide.html (accessed on 10 August 2020).
- Kilpatrick, K.A.; Podestá, G.P.; Evans, R. Overview of the NOAA/NASA advanced very high resolution radiometer Pathfinder algorithm for sea surface temperature and associated matchup database. J. Geophys. Res. Space Phys. 2001, 106, 9179–9197. [Google Scholar] [CrossRef]
- Vincent, R.F.; Marsden, R.F.; Minnett, P.J.; Creber, K.A.M.; Buckley, J.R. Arctic waters and marginal ice zones: A composite Arctic sea surface temperature algorithm using satellite thermal data. J. Geophys. Res. Space Phys. 2008, 113, 04021. [Google Scholar] [CrossRef]
- Vincent, R.F.; Marsden, R.F.; Minnett, P.J.; Buckley, J.R. Arctic waters and marginal ice zones: 2. An investigation of arctic atmospheric infrared absorption for advanced very high resolution radiometer sea surface temperature estimates. J. Geophys. Res. Space Phys. 2008, 113, 08044. [Google Scholar] [CrossRef]
- Vincent, R. The Case for a Single Channel Composite Arctic Sea Surface Temperature Algorithm. Remote Sens. 2019, 11, 2393. [Google Scholar] [CrossRef]
- Kilpatrick, K.A.; Minnett, P.J.; Luo, B. Validation of NASA MODIS R2019.0 reprocessed SST products. In Proceedings of the 18th International GHRSST Science Team Meeting (GHRSST XVIII), Frascati, Italy, 6–10 June 2019. [Google Scholar]
- Jia, C.; Minnett, P.J. High latitude sea surface temperatures derived from MODIS infrared measurements. Remote Sens. Environ. 2020, 251, 112094. [Google Scholar] [CrossRef]
- Palmer Station Antarctica. Available online: https://oceaninformatics.ucsd.edu/datazoo/catalogs/pallter/datasets/28/datatables/28/download (accessed on 12 August 2020).
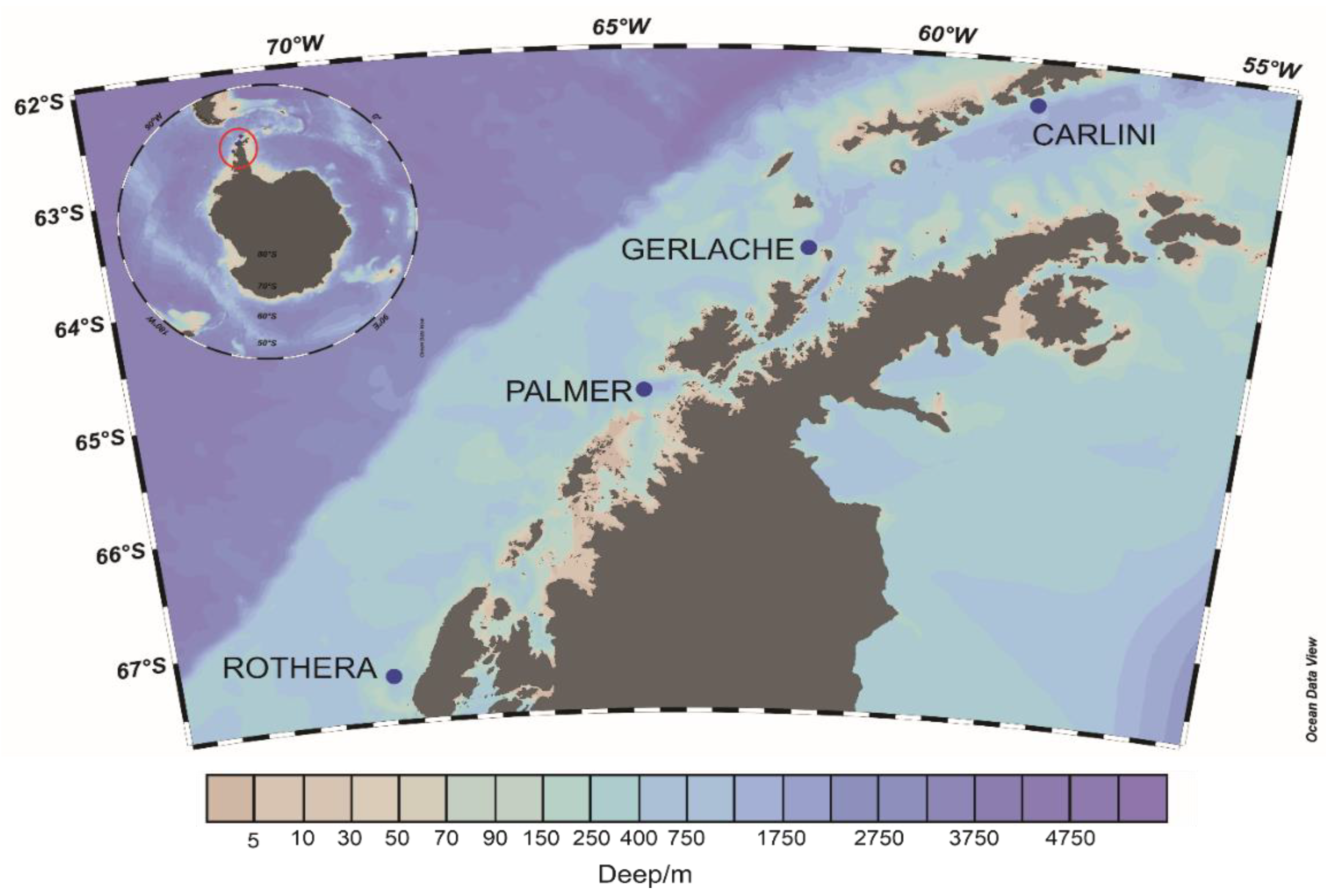

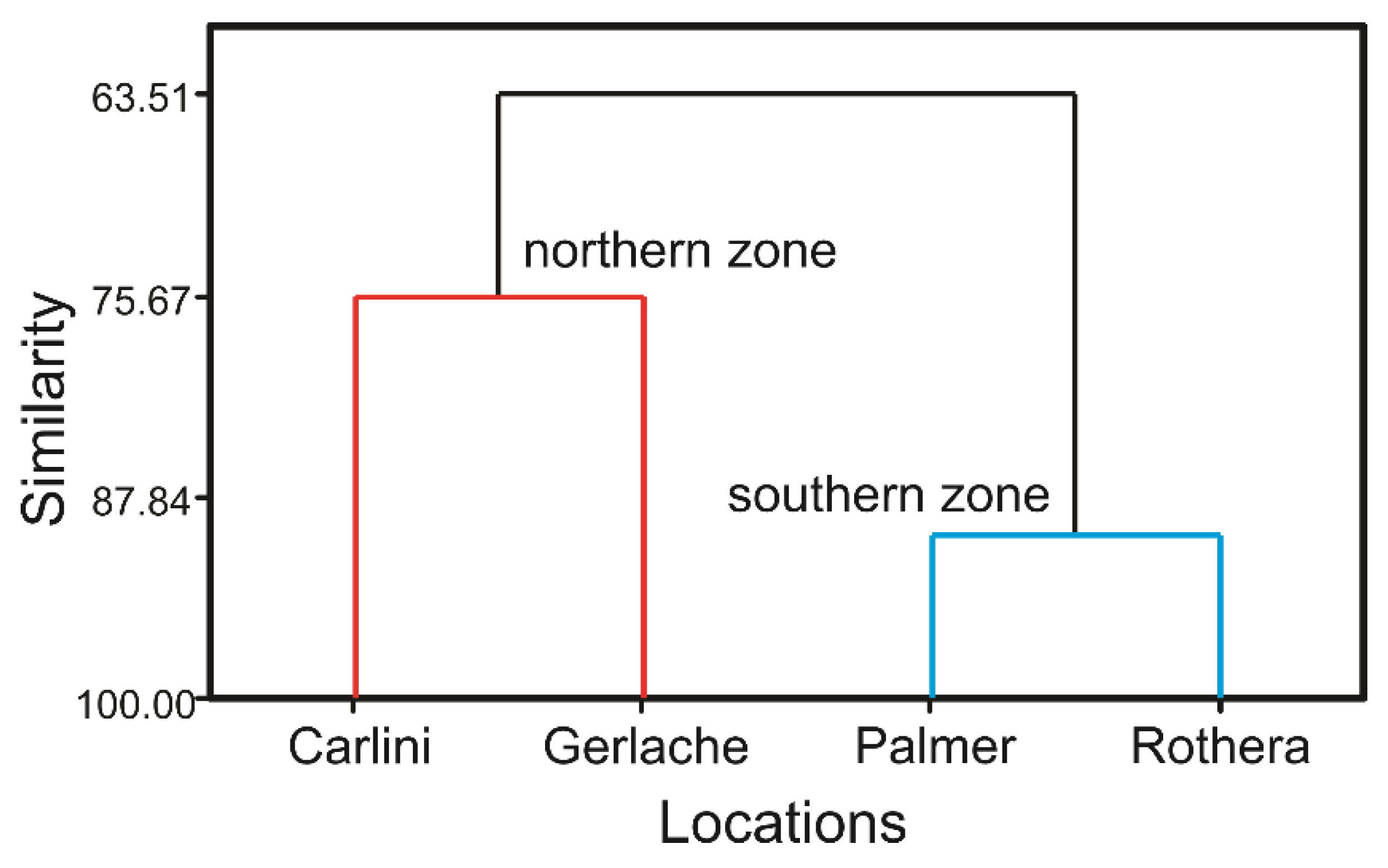


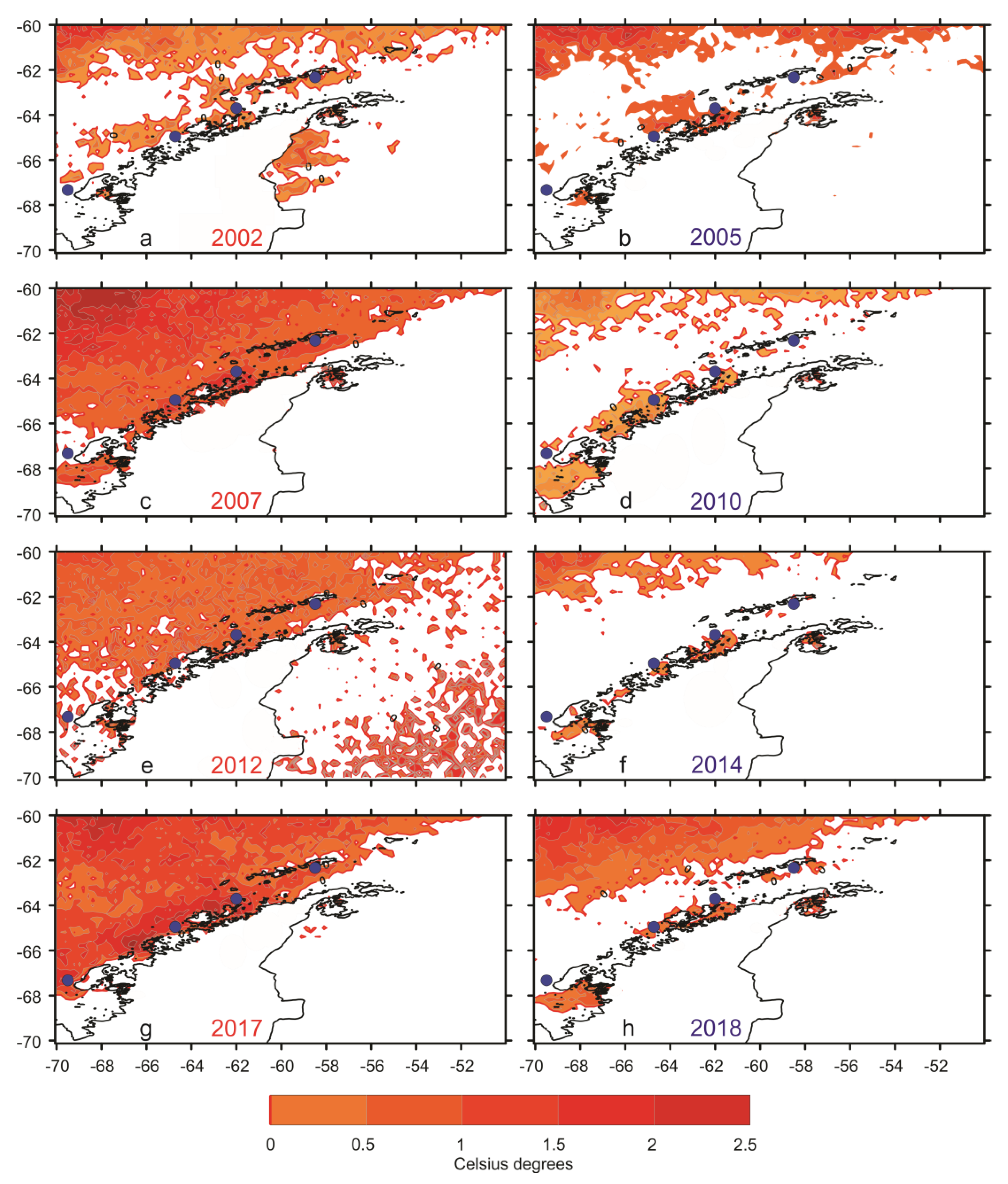
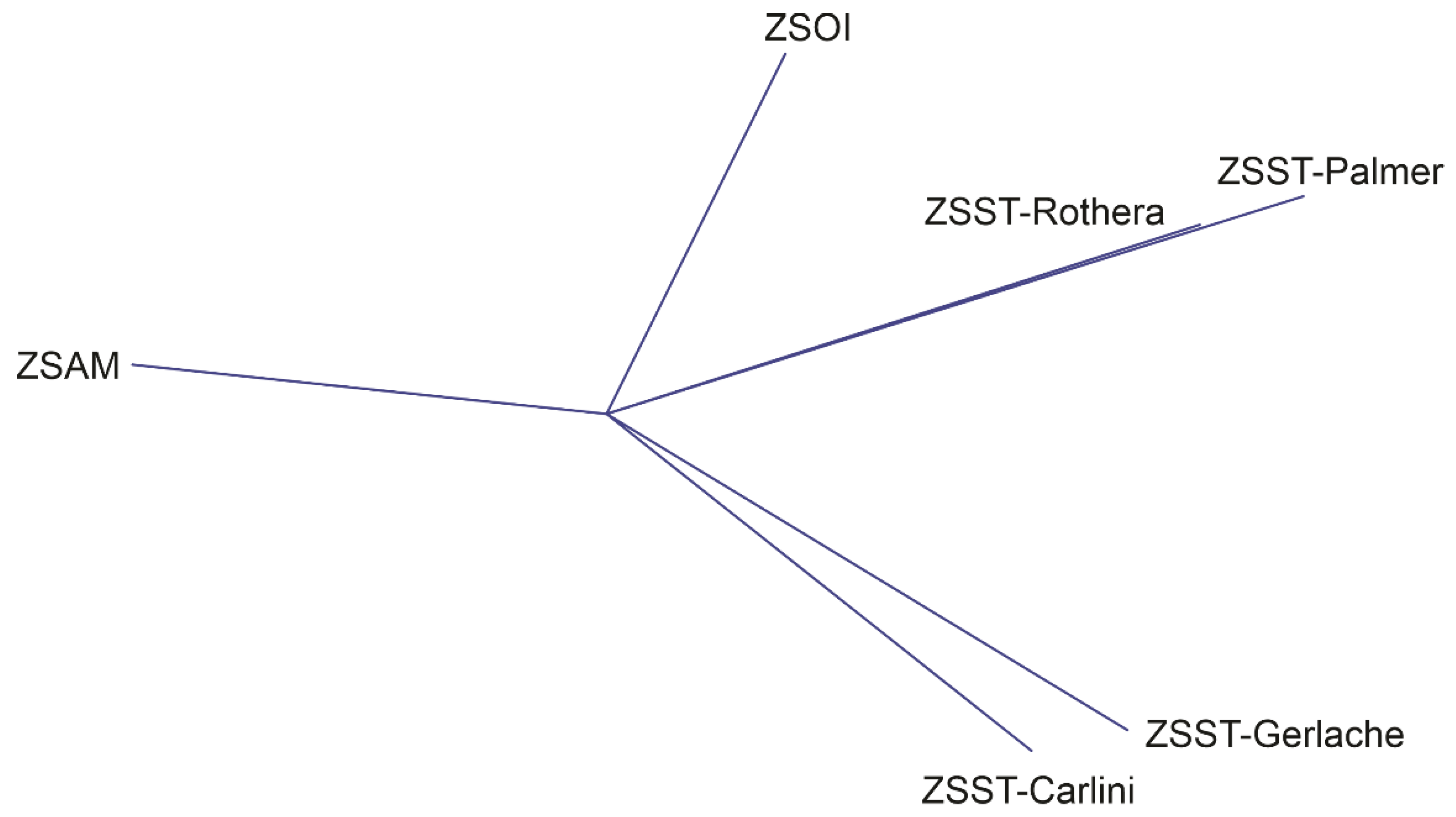
| Station | n | Mean (°C) | SD (°C) | Minimum (°C) | Maximum (°C) |
|---|---|---|---|---|---|
| Carlini | 20 | −0.022 | 0.330 | −0.533 | 0.517 |
| Gerlache | 20 | 0.226 | 0.400 | −0.283 | 1.233 |
| Palmer | 20 | 0.181 | 0.727 | −1.417 | 1.550 |
| Rothera | 20 | −0.467 | 0.876 | −1.650 | 1.250 |
| Q-Qcal | Q-Qcrit | Comparison | Decision | |
|---|---|---|---|---|
| Carlini | 0.97.98 | 0.9498 | Q-Qcal > Q-Qcrit | The data have a G.D. |
| Gerlache | 0.954112 | 0.9498 | Q-Qcal > Q-Qcrit | The data have a G.D. |
| Palmer | 0.992129 | 0.9498 | Q-Qcal > Q-Qcrit | The data have a G.D. |
| Rothera | 0.975972 | 0.9498 | Q-Qcal > Q-Qcrit | The data have a G.D. |
| Contrast | Fcal | Fcrit | Comparison | Decision |
|---|---|---|---|---|
| Carlini vs. Gerlache | 1.470 | 2.168 | Fcal < Fcrit | Equal variances |
| Carlini vs. Palmer | 4.851 | 2.168 | Fcal > Fcrit | Different variances |
| Carlini vs. Rothera | 7.047 | 2.168 | Fcal > Fcrit | Different variances |
| Gerlache vs. Palmer | 3.301 | 2.168 | Fcal > Fcrit | Different variances |
| Gerlache vs. Rothera | 4.795 | 2.168 | Fcal > Fcrit | Different variances |
| Palmer vs. Rothera | 1.453 | 2.168 | Fcal < Fcrit | Equal variances |
| Station | SAM | SOI | ||
|---|---|---|---|---|
| rPearson | rSpearman | rPearson | rSpearman | |
| Carlini | −0.258 | −0.209 | 0.087 | 0.071 |
| Gerlache | −0.264 | −0.103 | −0.070 | 0.038 |
| Palmer | −0.476 | −0.424 | 0.331 | 0.120 |
| Rothera | −0.233 | −0.207 | 0.049 | −0.064 |
| Carlini | Gerlache | Palmer | Rothera | SOI | SAM | |
|---|---|---|---|---|---|---|
| Carlini | 1.000 | 0.516 | 0.301 | 0.055 | 0.087 | −0.258 |
| Gerlache | 0.516 | 1.000 | 0.331 | 0.394 | −0.070 | −0.264 |
| Palmer | 0.301 | 0.331 | 1.000 | 0.803 | 0.331 | −0.476 |
| Rothera | 0.055 | 0.394 | 0.803 | 1.000 | 0.049 | −0.233 |
| SOI | 0.087 | −0.070 | 0.331 | 0.049 | 1.000 | −0.030 |
| SAM | −0.258 | −0.264 | −0.476 | −0.233 | −0.030 | 1.000 |
| Eigenanalysis of the Correlation Matrix | |||
|---|---|---|---|
| PC1 | PC2 | PC3 | |
| Eigenvalue | 2.526 | 1.202 | 1.002 |
| Proportion of total variance accounted for | 0.421 | 0.200 | 0.167 |
| Cumulative proportion of total variance accounted for | 0.421 | 0.621 | 0.788 |
| Loadings of the Variables on Each Component | |||
| PC1 | PC2 | PC3 | |
| SOI | −0.229 | −0.605 | 0.723 |
| SAM | 0.605 | −0.083 | −0.007 |
| Carlini | −0.561 | 0.544 | 0.499 |
| Gerlache | −0.667 | 0.528 | −0.035 |
| Palmer | −0.889 | −0.366 | −0.064 |
| Rothera | −0.759 | −0.320 | −0.475 |
| Negative | Positive | Positive |
|---|---|---|
| −0.909 | 0.000 | |
| −0.309 | 0.143 | |
| 0.318 | 0.428 | |
| 0.318 | 0.428 |
| Positive | Negative | Negative |
|---|---|---|
| −0.833 | 0.000 | |
| −0.629 | 0.250 | |
| 0.388 | 0.500 | |
| 0.388 | 0.500 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Santamaría-del-Ángel, E.; Cañon-Páez, M.-L.; Sebastiá-Frasquet, M.-T.; González-Silvera, A.; Gutierrez, A.-L.; Aguilar-Maldonado, J.-A.; López-Calderón, J.; Camacho-Ibar, V.; Franco-Herrera, A.; Castillo-Ramírez, A. Interannual Climate Variability in the West Antarctic Peninsula under Austral Summer Conditions. Remote Sens. 2021, 13, 1122. https://doi.org/10.3390/rs13061122
Santamaría-del-Ángel E, Cañon-Páez M-L, Sebastiá-Frasquet M-T, González-Silvera A, Gutierrez A-L, Aguilar-Maldonado J-A, López-Calderón J, Camacho-Ibar V, Franco-Herrera A, Castillo-Ramírez A. Interannual Climate Variability in the West Antarctic Peninsula under Austral Summer Conditions. Remote Sensing. 2021; 13(6):1122. https://doi.org/10.3390/rs13061122
Chicago/Turabian StyleSantamaría-del-Ángel, Eduardo, Mary-Luz Cañon-Páez, Maria-Teresa Sebastiá-Frasquet, Adriana González-Silvera, Angelica-L. Gutierrez, Jesús-A. Aguilar-Maldonado, Jorge López-Calderón, Víctor Camacho-Ibar, Andrés Franco-Herrera, and Alejandra Castillo-Ramírez. 2021. "Interannual Climate Variability in the West Antarctic Peninsula under Austral Summer Conditions" Remote Sensing 13, no. 6: 1122. https://doi.org/10.3390/rs13061122
APA StyleSantamaría-del-Ángel, E., Cañon-Páez, M.-L., Sebastiá-Frasquet, M.-T., González-Silvera, A., Gutierrez, A.-L., Aguilar-Maldonado, J.-A., López-Calderón, J., Camacho-Ibar, V., Franco-Herrera, A., & Castillo-Ramírez, A. (2021). Interannual Climate Variability in the West Antarctic Peninsula under Austral Summer Conditions. Remote Sensing, 13(6), 1122. https://doi.org/10.3390/rs13061122









