An Efficient Method for Ground Maneuvering Target Refocusing and Motion Parameter Estimation Based on DPT–KT–MFP
Abstract
1. Introduction
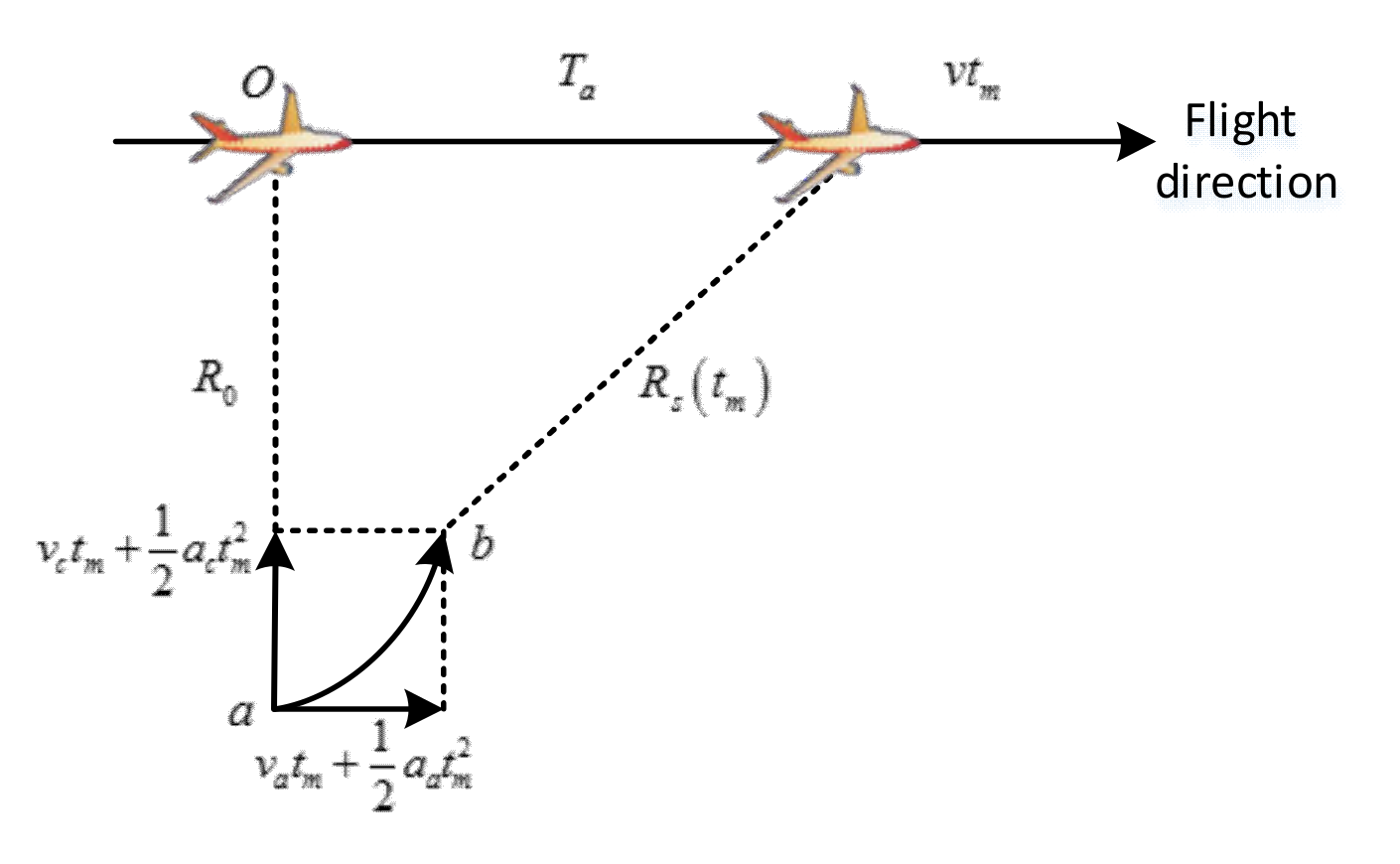
2. Signal Model
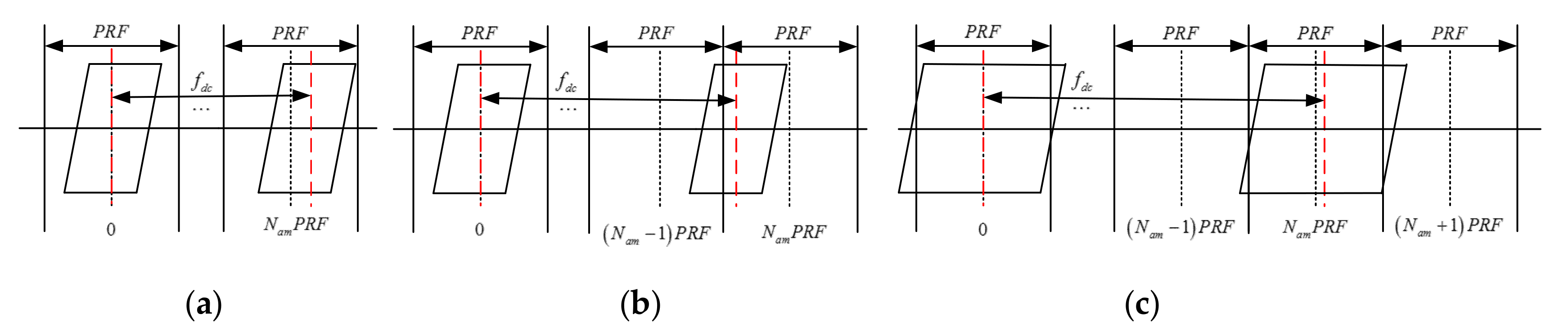
3. Algorithm Description
3.1. DPT–KT–MFP Algorithm with Single Target
3.2. DPT–KT–MFP Algorithm with Multiple Targets
3.3. Computational Complexity Analysis
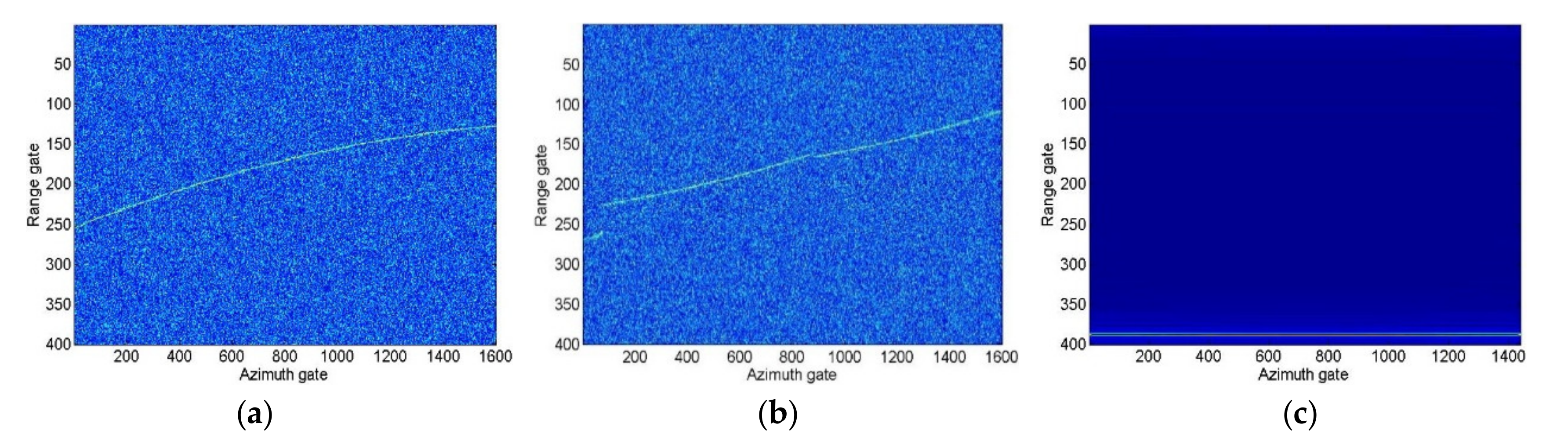
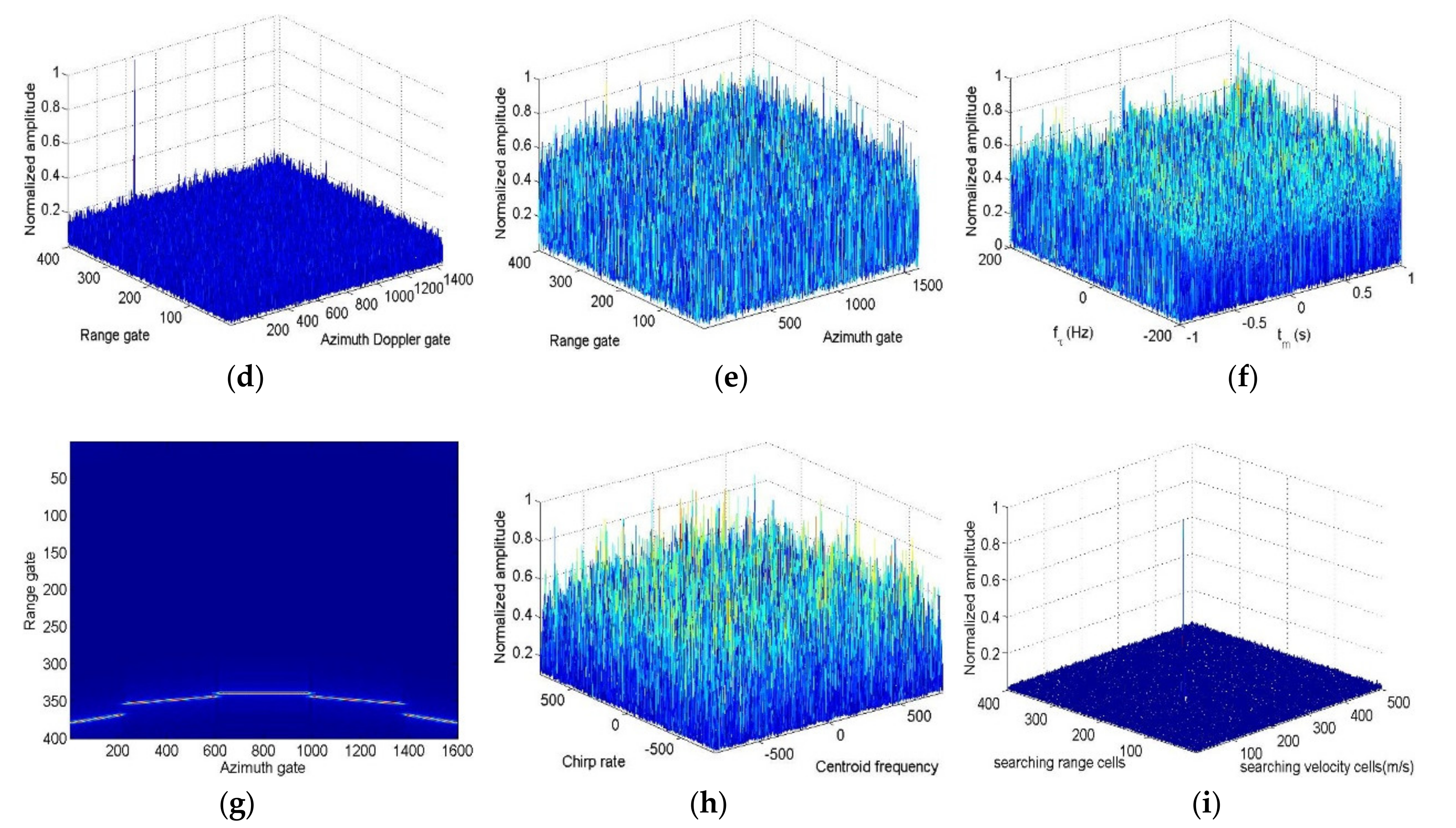
4. Simulation and Real Data Processing Results
4.1. Analysis and Discussion of Simulation Results
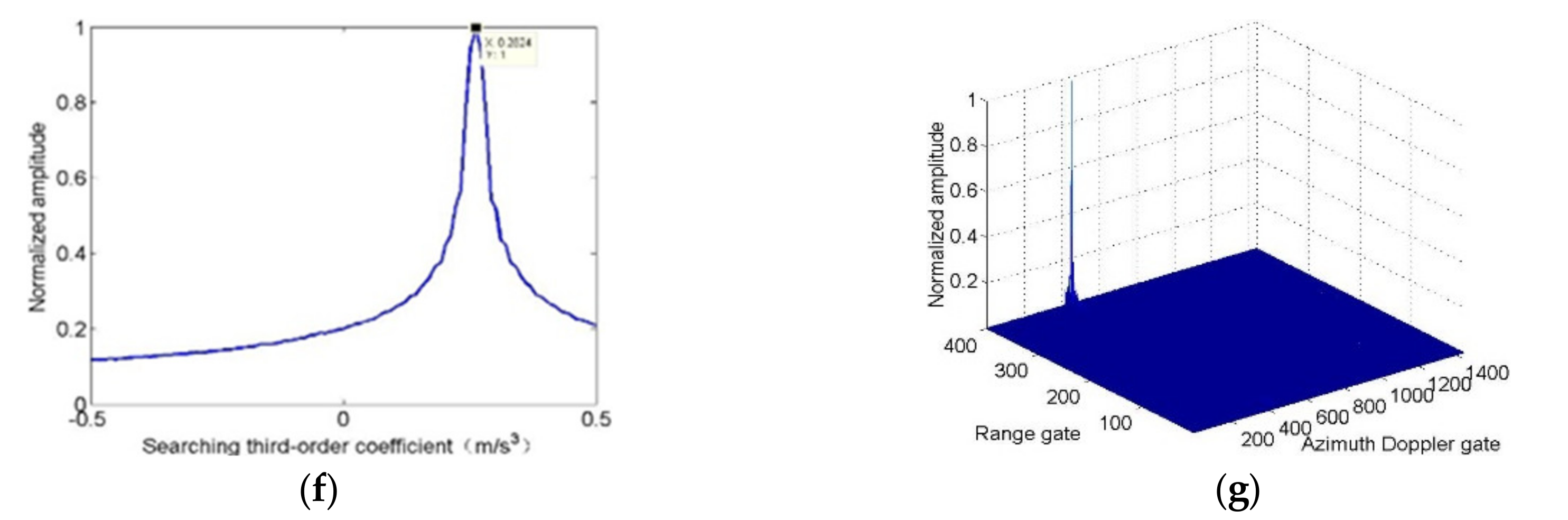
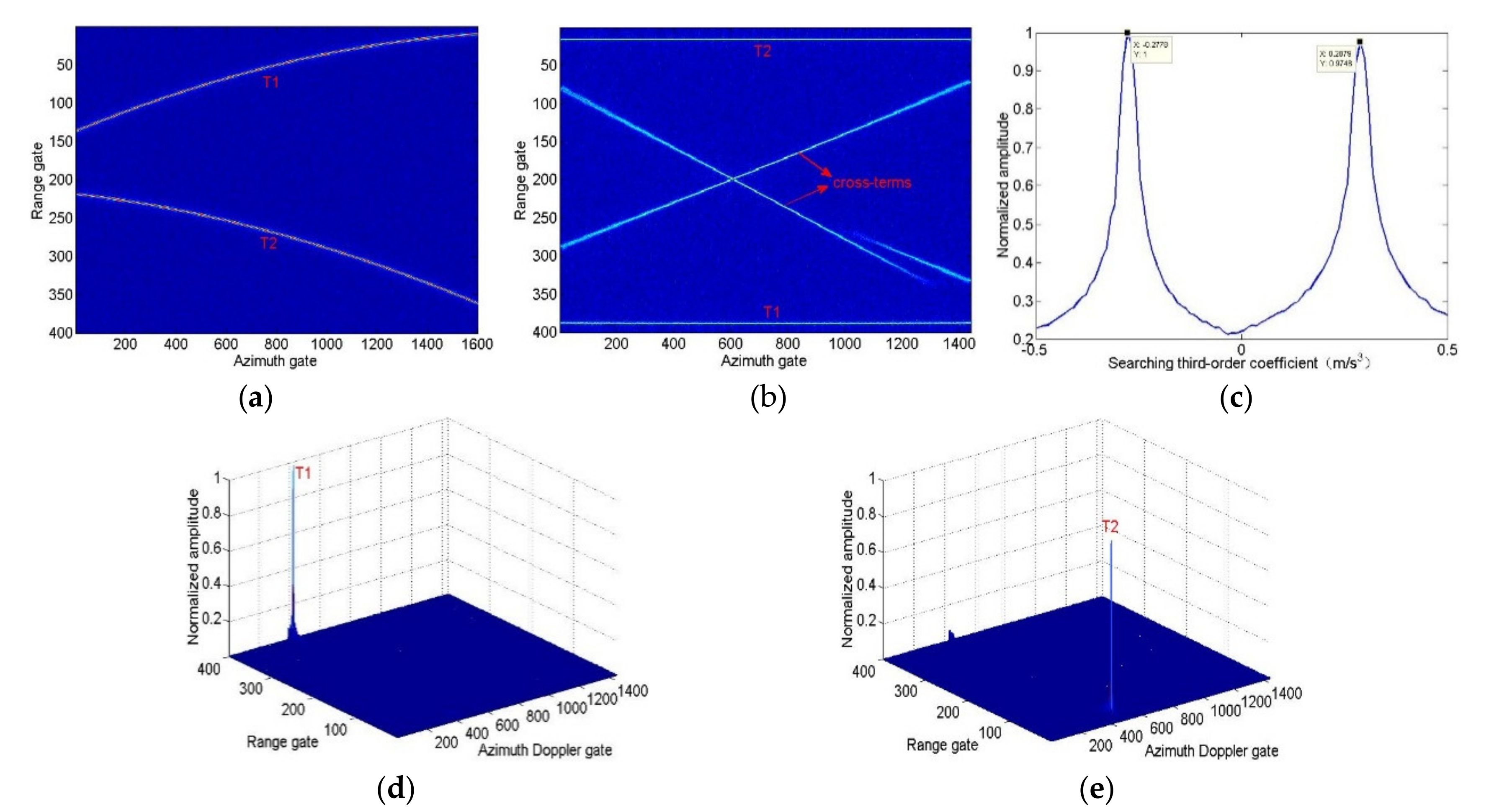
4.1.1. Maneuvering Target Integration Performance
4.1.2. Maneuvering Target Detection Ability
4.1.3. Motion Parameter Estimation Performance
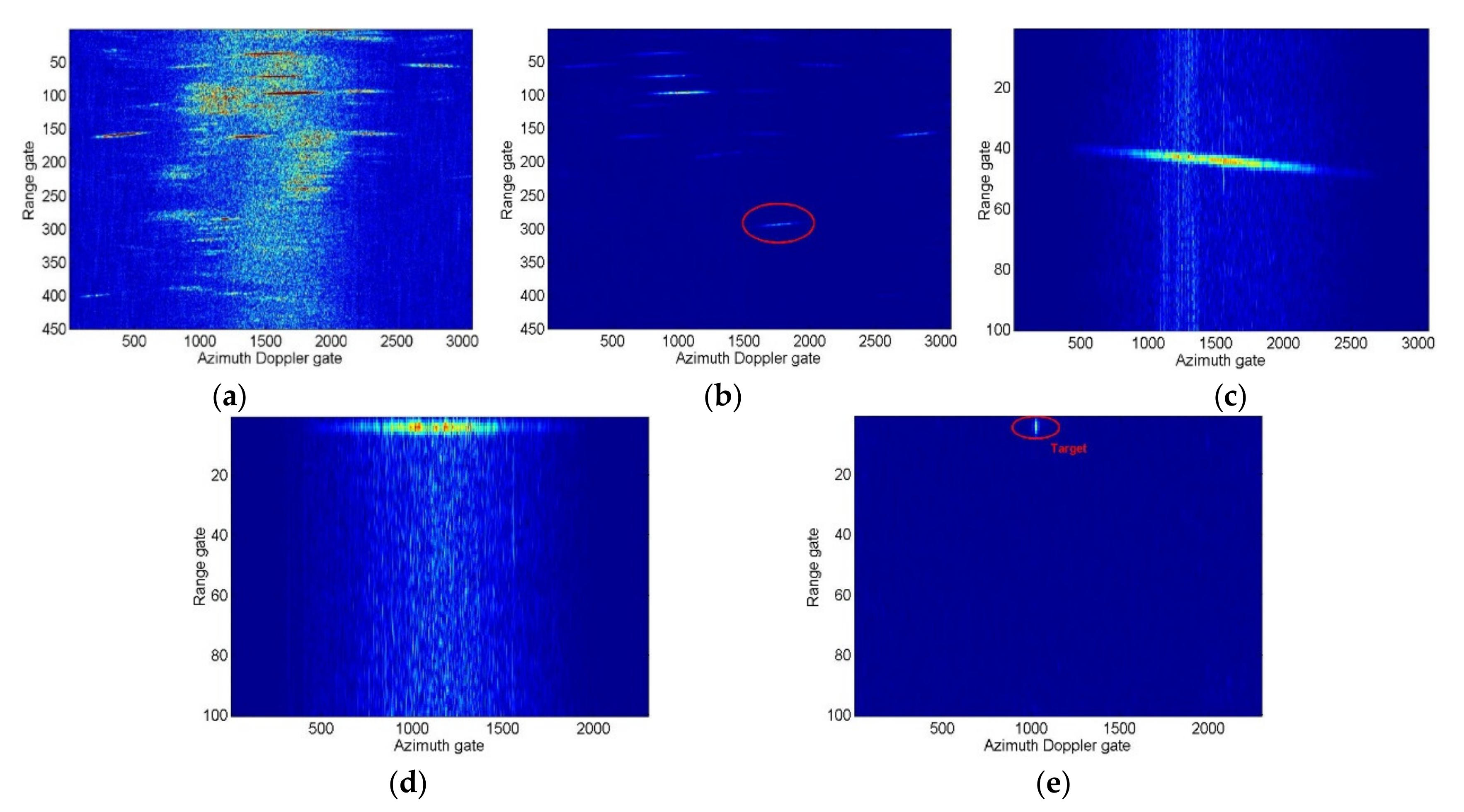
4.2. Analysis and Discussion of Real Data Processing Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhu, S.; Liao, G.; Qu, Y.; Zhou, Z.; Liu, X. Ground moving targets imaging algorithm for synthetic aperture radar. IEEE Trans. Geosci. Remote Sens. 2011, 49, 462–477. [Google Scholar] [CrossRef]
- Bovenga, F.; Derauw, D.; Rana, F.M.; Barbier, C.; Refice, A.; Veneziani, N.; Vitulli, R. Multi-chromatic analysis of SAR images for coherent target detection. Remote Sens. 2014, 6, 8822–8843. [Google Scholar] [CrossRef]
- Filippo, B. COSMO-SkyMed staring spotlight SAR data for micro-motion and inclination angle estimation of ships by pixel tracking and convex optimization. Remote Sens. 2019, 11, 766. [Google Scholar] [CrossRef]
- Wan, J.; Zhou, Y.; Zhang, L.; Chen, Z. A doppler ambiguity tolerated method for radar sensor maneuvering target focusing and detection. IEEE Sens. J. 2019, 19, 6691–6704. [Google Scholar] [CrossRef]
- Huang, Y.; Liao, G.; Xu, J.; Li, J.; Yang, D. GMTI and parameter estimation for MIMO SAR system via fast interferometry RPCA method. IEEE Trans. Geosci. Remote Sens. 2018, 56, 1774–1787. [Google Scholar] [CrossRef]
- Zhang, X.; Liao, G.; Zhu, S.; Zeng, C.; Shu, Y. Geometry-information-aided efficient radial velocity estimation for moving target imaging and location based on Radon transform. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1105–1117. [Google Scholar] [CrossRef]
- Li, D.; Zhan, M.; Liu, H.; Liao, Y.; Liao, G. A Robust Translational Motion Compensation Method for ISAR Imaging Based on Keystone Transform and Fractional Fourier Transform Under Low SNR Environment. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 2140–2156. [Google Scholar] [CrossRef]
- Tian, M.; Liao, G.; Zhu, S.; He, X.; Li, Y. A novel method for high-speed maneuvering target detection and motion parameters estimation. Multidimens. Syst. Signal Process. 2020, 4, 1625–1647. [Google Scholar] [CrossRef]
- Li, D.; Ma, H.; Liu, H.; Chen, Z.; Yang, Z. An efficient ground manoeuvring target refocusing method based on principal component analysis and motion parameter estimation. Remote Sens. 2020, 12, 378. [Google Scholar] [CrossRef]
- Perry, R.P.; DiPietro, R.C.; Fante, R.L. SAR imaging of moving targets. IEEE Trans. Aerosp. Electron. Syst. 1999, 35, 188–200. [Google Scholar] [CrossRef]
- Zhu, D.; Li, Y.; Zhu, Z. A keystone transform without interpolation for SAR ground moving-target imaging. IEEE Geosci. Remote Sens. Lett. 2007, 4, 18–22. [Google Scholar] [CrossRef]
- Li, G.; Xia, X.; Peng, Y. Doppler keystone transform: An approach suitable for parallel implementation of SAR moving target imaging. IEEE Geosci. Remote Sens. Lett. 2008, 5, 573–577. [Google Scholar] [CrossRef]
- Sun, Z.; Li, X.; Yi, W.; Gui, G. Detection of weak maneuvering target based on keystone transform and matched filtering process. Signal Process. 2017, 140, 127–138. [Google Scholar] [CrossRef]
- Huang, P.; Liao, G.; Yang, Z.; Xia, X.; Ma, J.; Zhang, X. An approach for refocusing of ground moving target without target motion parameter estimation. IEEE Trans. Geosci. Remote Sens. 2017, 55, 336–350. [Google Scholar] [CrossRef]
- Rao, X.; Tao, H.; Su, J.; Guo, X.; Zhang, J. Axis rotation MTD algorithm for weak target detection. Digit. Signal Process. 2014, 26, 81–86. [Google Scholar] [CrossRef]
- Xu, J.; Yu, J.; Peng, Y.; Xia, X. Radon–Fourier transform for radar target detection, I: Generalized Doppler filter bank. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 1186–1202. [Google Scholar] [CrossRef]
- Xu, J.; Yu, J.; Peng, Y.; Xia, X. Radon–Fourier transform for radar target detection (II): Blind speed sidelobe suppression. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 2473–2489. [Google Scholar] [CrossRef]
- Yu, J.; Xu, J.; Peng, Y.; Xia, X. Radon-Fourier transform for radar target detection (III): Optimality and fast implementations. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 991–1004. [Google Scholar] [CrossRef]
- Zheng, J.; Su, T.; Liu, H.; Liao, G. Radar high-speed target detection based on the frequency-domain deramp-keystone transform. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 285–294. [Google Scholar] [CrossRef]
- Zhou, F.; Wu, R.; Xing, M.; Bao, Z. Approach for single channel SAR ground moving target imaging and motion parameter estimation. IET Radar Sonar Navig. 2007, 1, 59–66. [Google Scholar] [CrossRef]
- Kirkland, D. Imaging moving targets using the second-order keystone transform. IET Radar Sonar Navig. 2011, 5, 902–910. [Google Scholar] [CrossRef]
- Tian, J.; Cui, W.; Xia, X.; Wu, S. A novel method for parameter estimation of space moving targets. IEEE Geosci. Remote Sens. Lett. 2013, 11, 389–393. [Google Scholar] [CrossRef]
- Chen, X.; Guan, J.; Liu, N.; He, Y. Maneuvering target detection via Radon-fractional Fourier transform-based long-time coherent integration. IEEE Trans. Signal Process. 2014, 62, 939–953. [Google Scholar] [CrossRef]
- Huang, P.; Liao, G.; Yang, Z.; Xia, X.; Ma, J.; Zhang, X. A fast SAR imaging method for ground moving target using a second-order WVD transform. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1940–1956. [Google Scholar] [CrossRef]
- Tian, M.; Liao, G.; Zhu, S.; Liu, Y.; He, X.; Li, Y. Long-time coherent integration and motion parameters estimation of radar moving target with unknown entry/departure time based on SAF-WLVT. Digit. Signal Process. 2020, 107, 102854. [Google Scholar] [CrossRef]
- Li, X.; Sun, Z.; Yi, W.; Cui, G.; Kong, L.; Yang, X. Computationally efficient coherent detection and parameter estimation algorithm for maneuvering target. Signal Process. 2019, 155, 130–142. [Google Scholar] [CrossRef]
- He, X.; Liao, G.; Zhu, S.; Xu, J.; Guo, Y.; Wei, J. Fast non-searching method for ground moving target refocusing and motion parameters estimation. Digit. Signal Process. 2018, 79, 152–163. [Google Scholar] [CrossRef]
- Xu, J.; Xia, X.; Peng, S.; Yu, J.; Peng, Y.; Qian, L. Radar maneuvering target motion estimation based on generalized Radon–Fourier transform. IEEE Trans. Signal Process. 2012, 60, 6190–6201. [Google Scholar]
- Huang, P.; Liao, G.; Yang, Z.; Xia, X.; Ma, J. Long-time coherent integration for weak maneuvering target detection and high-order motion parameter estimation based on keystone transform. IEEE Trans. Signal Process. 2015, 64, 4013–4026. [Google Scholar] [CrossRef]
- Kong, L.; Li, X.; Cui, G.; Yi, W.; Yang, Y. Coherent integration algorithm for a maneuvering target with high-order range migration. IEEE Trans. Signal Process. 2015, 63, 4474–4486. [Google Scholar] [CrossRef]
- Huang, P.; Liao, G.; Yang, Z.; Xia, X.; Ma, J.; Zheng, J. Ground maneuvering target imaging and high-order motion parameter estimation based on second-order keystone and generalized Hough-HAF transform. IEEE Trans. Geosci. Remote Sens. 2017, 55, 320–335. [Google Scholar] [CrossRef]
- Huang, P.; Xia, X.; Liao, G.; Yang, Z.; Zhang, Y. Long-Time Coherent Integration Algorithm for Radar Maneuvering Weak Target with Acceleration Rate. IEEE Trans. Geosci. Remote Sens. 2019, 57, 3528–3542. [Google Scholar] [CrossRef]
- Li, X.; Cui, G.; Yi, W.; Kong, L. Fast coherent integration for maneuvering target with high-order range migration via TRT-SKT-LVD. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 2803–2814. [Google Scholar] [CrossRef]
- Li, X.; Cui, G.; Kong, L.; Yi, W. Fast non-searching method for maneuvering target detection and motion parameters estimation. IEEE Trans. Signal Process. 2016, 64, 2232–2244. [Google Scholar] [CrossRef]
- Fang, X.; Min, R.; Cao, Z.; Pi, Y. High-order RM and DFM correction method for long-time coherent integration of highly maneuvering target. Signal Process. 2019, 162, 221–233. [Google Scholar] [CrossRef]
- Sun, G.; Xing, M.; Xia, X.; Wu, Y.; Bao, Z. Robust ground moving-target imaging using deramp–keystone processing. IEEE Trans. Geosci. Remote Sens. 2013, 51, 966–982. [Google Scholar] [CrossRef]
- Chen, Z.; Zhou, Y.; Zhang, L.; Lin, C.; Huang, Y.; Tang, S. Ground moving target imaging and analysis for near-space hypersonic vehicle-borne synthetic aperture radar system with squint angle. Remote Sens. 2018, 10, 1996. [Google Scholar] [CrossRef]
- Xin, Z.; Liao, G.; Yang, Z.; Huang, P.; Ma, J. A fast ground moving target focusing method based on first-order discrete polynomial-phase transform. Digit. Signal Process. 2017, 60, 287–295. [Google Scholar] [CrossRef]
- Yu, W.; Su, W.; Gu, H. Ground maneuvering target detection based on discrete polynomial-phase transform and Lv’s distribution. Signal Process. 2018, 144, 364–372. [Google Scholar] [CrossRef]
- Su, J.; Xing, M.; Wang, G.; Bao, Z. High-speed multi-target detection with narrowband radar. IET Radar Sonar Navig. 2010, 4, 595–603. [Google Scholar] [CrossRef]
- DiPietro, R.C. Extended factored space–time processing for airborne radar systems. In Proceedings of the 26th Asilomar Conference on Signals, Systems & Computers, Pacific Grove, CA, USA, 26–28 October 1992; pp. 425–430. [Google Scholar]




| Parameter | Value |
|---|---|
| Carrier frequency | 6 GHZ |
| Range bandwidth | 200 MHZ |
| Range sampling frequency | 300 MHZ |
| Pulse repetition frequency | 800 HZ |
| Pulse width | 1 µs |
| Synthetic aperture time | 2 s |
| Platform velocity | 250 m/s |
| Methods | Computational Complexity |
|---|---|
| GRFT | |
| SOKT–GHHAF | |
| TRT–SOKT–LVD | |
| Proposed |
| Methods | Computational Time (s) |
|---|---|
| GRFT | 3382 |
| SOKT–GHHAF | 279.2 |
| TRT–SOKT–LVD | 36.5 |
| Proposed | 3.49 |
| Parameter | Value |
|---|---|
| Carrier frequency | |
| Range bandwidth | |
| Range sampling frequency | |
| Pulse repetition frequency | |
| Pulse width | 10 µs |
| Platform velocity | |
| Swath central range |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, M.; Liao, G.; Zhu, S.; He, X.; Liu, Y.; Li, Y. An Efficient Method for Ground Maneuvering Target Refocusing and Motion Parameter Estimation Based on DPT–KT–MFP. Remote Sens. 2021, 13, 1092. https://doi.org/10.3390/rs13061092
Tian M, Liao G, Zhu S, He X, Liu Y, Li Y. An Efficient Method for Ground Maneuvering Target Refocusing and Motion Parameter Estimation Based on DPT–KT–MFP. Remote Sensing. 2021; 13(6):1092. https://doi.org/10.3390/rs13061092
Chicago/Turabian StyleTian, Mingming, Guisheng Liao, Shengqi Zhu, Xiongpeng He, Yongjun Liu, and Yunpeng Li. 2021. "An Efficient Method for Ground Maneuvering Target Refocusing and Motion Parameter Estimation Based on DPT–KT–MFP" Remote Sensing 13, no. 6: 1092. https://doi.org/10.3390/rs13061092
APA StyleTian, M., Liao, G., Zhu, S., He, X., Liu, Y., & Li, Y. (2021). An Efficient Method for Ground Maneuvering Target Refocusing and Motion Parameter Estimation Based on DPT–KT–MFP. Remote Sensing, 13(6), 1092. https://doi.org/10.3390/rs13061092







